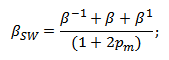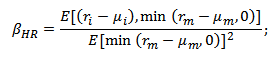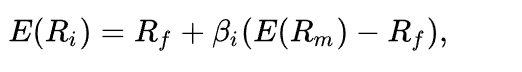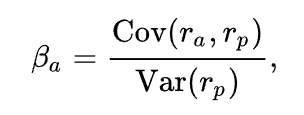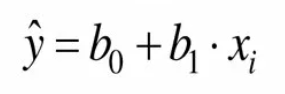На чтение 9 мин Просмотров 97.6к.
Разберем такой инвестиционный показатель как – коэффициент бета, рассчитаем его на реальном пример с помощью Excel и рассмотрим различные современные модификации.
Содержание
- Инфографика: Коэффициент бета
- Коэффициент бета. Определение
- Формула расчета коэффициента бета
- Анализ уровня риска по значению коэффициента бета (β)
- Данные для построения коэффициента бета информационными компаниями
- Коэффициент бета в модели оценки капитальных активов –CAPM
- Пример расчета коэффициента бета вExcel
- Недостатки использования коэффициента бета в модели CAPM
- Модификация коэффициента бета
- Коэффициент бета для акций США
- Где посмотреть коэффициент бета для российских акций
Инфографика: Коэффициент бета
Коэффициент бета. Определение
Коэффициент бета (англ. Beta, β, beta coefficient) – определяет меру риска акции (актива) по отношению к рынку и показывает чувствительность изменения доходности акции по отношению к изменению доходности рынка. Коэффициент бета может быть рассчитан не только для отдельной акции, но также и для инвестиционного портфеля. Коэффициент используется как мера систематического риска, и применяется в модели У.Шарпа – оценки капитальных активов CAPM (Capital Assets Price Model). В первые, коэффициент бета рассмотрел Г. Марковиц для оценки систематического риска акций, который получил называние индекс недиверсифицируемого риска. Коэффициент бета позволяет сравнивать между собой акции различных компаний по степени их риска.
Формула расчета коэффициента бета
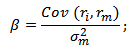
β – коэффициент бета, мера систематического риска (рыночного риска);
ri – доходность i-й акации (инвестиционного портфеля);
rm – рыночная доходность;
σ2m – дисперсия рыночной доходности.
Анализ уровня риска по значению коэффициента бета (β)
Коэффициент бета показывает рыночный риск акции и отражает чувствительность изменения акции по отношению к изменению доходности рынка. В таблице ниже показана оценка уровня риска по коэффициенту бета. Коэффициент бета может иметь как положительный, так и отрицательный знак, который показывает положительную или отрицательную корреляцию между акцией и рынком. Положительный знак отражает, что доходность акций и рынка изменяются в одном направлении, отрицательный – разнонаправленное движение.
|
Значение показателя |
Уровень риска акции |
Направление изменения доходности акции |
|
β > 1 |
Высокий |
Однонаправленное |
|
β = 1 |
Умеренный |
Однонаправленное |
|
0 < β < 1 |
Низкий |
Однонаправленное |
| -1 < β < 0 |
Низкий |
Разнонаправленное |
| β = -1 |
Умеренный |
Разнонаправленное |
|
β < -1 |
Высокий |
Разнонаправленное |
Данные для построения коэффициента бета информационными компаниями
Коэффициент бета используется многими информационно-инвестиционными компаниями для оценки систематического риска: Bloomberg, Barra, Value Line и др . Для построения коэффициента бета используются месячные/недельные данные за несколько лет. В таблице показаны основные параметры оценки показателя различными информационными компаниями.
★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут
|
Информационные компании |
Исторический период наблюдения | Частота |
|
Bloomberg |
2 года |
Неделя |
| Barra | 5 лет |
Месяц |
| Value Line | 5 лет |
Месяц |
Можно заметить, что Bloomberg проводит краткосрочную оценку показателя, тогда как Barra и Value Line используют месячные данные доходностей акций и рынка за последние пять лет. Долгосрочная оценка может сильно быть искажена вследствие влияния на акции компании различных кризисов и негативных факторов.
Коэффициент бета в модели оценки капитальных активов – CAPM
Формула расчета доходности акций по модели капитальных активов CAPM (Capital Assets Price Model, модель У.Шарпа) имеет следующий вид:
где:
r – будущая ожидаемая доходность акций компании;
rf – доходность по безрисковому активу;
rm – доходность рынка;
β – коэффициент бета (мера рыночного риска), отражает чувствительность изменения стоимости акций компании в зависимости от изменения доходности рынка (индекса);
Модель CAPM была создана У.Шарпом (1964) и Дж. Линтером (1965) и позволяет спрогнозировать будущее значение доходности акции (актива) на основании линейной регрессии. Модель отражает линейную взаимосвязь планируемой доходности с уровнем рыночного риска, выраженного коэффициентом бета.
Доходность по безрисковому активу, на практике, берется как доходность по государственным ценным бумагам ГКО, ОФЗ. Доходность по ним в России составляет около 12%. Доходность можно посмотреть на сайте ЦБ в разделе «Ставки рынка ГКО-ОФЗ».
Для расчета рыночной доходности используют доходность индекса или фьючерса на индекс (индекс ММВБ, РТС – для России, S&P500 – США).
Пример расчета коэффициента бета в Excel
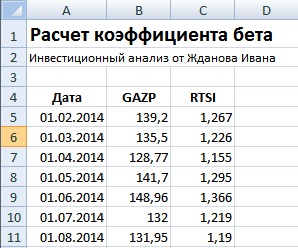
Рассчитаем коэффициент бета в Excel для отечественной компании ОАО «Газпром». Данная компания имеет обыкновенные акции, котировки которых можно посмотреть на сайте finam.ru в разделе «Экспорт данных». Для расчета были взяты месячные котировки акции ОАО «Газпром» (GAZP) и индекса РТС (RTSI) за период с 31.01.2014 по 31.01.2015 г.
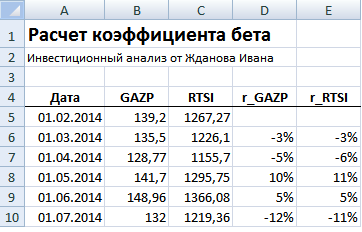
Далее необходимо рассчитать доходности по акции и индексу, для этого воспользуемся формулами:
D6=LN(B6/B5)
E6=LN(C6/C5)
Для расчета коэффициента бета необходимо рассчитать коэффициент линейной регрессии между доходностью акций ОАО «Газпром» и индекса РТС. Рассмотрим два варианта расчета коэффициента бета средствами Excel.
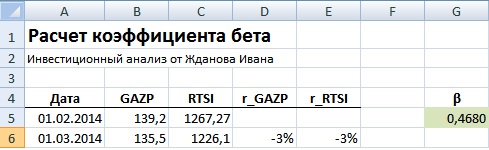
Вариант №1. Расчет через формулу Excel
Расчет через формулы Excel выглядит следующим образом:
=ИНДЕКС(ЛИНЕЙН(D6:D17;E6:E17);1)
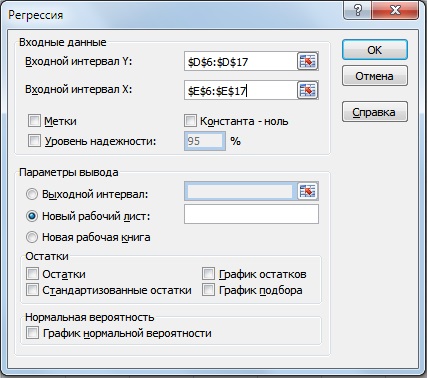
Вариант №2. Расчет через надстройку «Анализ данных»
Второй вариант расчета коэффициента бета использует надстройку Excel «Анализ данных». Для этого необходимо перейти в главном меню программы в раздел «Данные», выбрать опцию «Анализ данных» (если данная надстройка включена) и в инструментах анализа выделить «Регрессия». В поле «Входной интервал Y» выбрать доходности акции ОАО «Газпром», а в поле «Выходные интервал X» выбрать доходности индекса РТС.
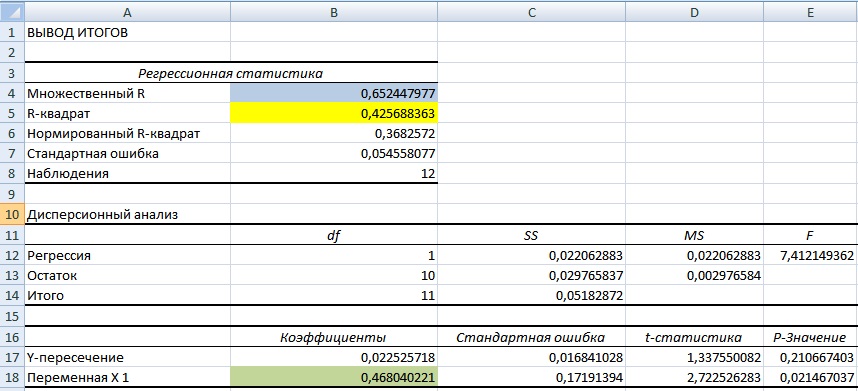
Далее мы получим отчет по регрессии на отдельном листе. В ячейке В18 показано значение коэффициента линейной регрессии, который равен коэффициенту бета = 0,46. Также проанализируем другие параметры модели, так показатель R-квадрат (коэффициент детерминированности) показывает силу взаимосвязи между доходностью акции ОАО «Газпром» и индекса РТС. Коэффициент детерминированности равен 0,4, что является довольно мало для точного прогнозирования будущей доходности по модели CAPM. Множественный R – коэффициент корреляции (0,6), который показывает наличие зависимости между акцией и рынком.
Значение 0,46 коэффициента бета для акции свидетельствует о умеренном риске и в тоже время сонаправленность изменения доходностей.
Недостатки использования коэффициента бета в модели CAPM
Рассмотрим ряд недостатков присущих данному коэффициенту:
- Сложность использования коэффициента бета для оценки низколиквидных акций. Данная ситуация характерна для развивающихся рынков капитала, в частности: России, Индии, Бразилии и т.д.
- Не возможность оценки малых компаний, не имеющих эмиссий обыкновенных акций. Большинство отечественных компаний не проходили процедуры IPO.
- Неустойчивость прогноза коэффициента бета. Использование линейной регрессии для оценки рыночного риска по ретроспективным данным не позволяет получать точные прогнозы риска. Как правило, трудно прогнозировать коэффициент бета более 1 года.
- Не возможность учета несистематических рисков компании: рыночной капитализации, исторической доходности, отраслевой принадлежности, критериев P/E и т.д., которые оказывает влияние на величину ожидаемой доходности.
Модификация коэффициента бета
Так как коэффициент, предложенный У. Шарпов не имел должной устойчивости и не мог использоваться для прогнозирования будущей доходности в модели CAPM, различными учеными были предложены модификации и корректировки данного показателя (англ. adjusted beta, modified beta).Рассмотрим скорректированные коэффициенты бета:
Модификация коэффициента бета от М.Блюма (1971)
Маршал Блюм показал, что со временем коэффициенты бета компаний стремятся к 1. Формула расчета скорректированного показателя следующая:
Использование данных весовых значений позволяет более точно спрогнозировать будущий систематический риск. Так данную модификацию используют многие информационные агентства, такие как: Bloomberg, Value Line и Merrill Lynch.
Модификация коэффициента бета от Бава-Линдсберга (1977)
В своей корректировке Линдсберг предложил рассчитывать односторонний коэффициент бета. Главный постулат заключался в том, что изменение доходности выше определенного уровня большинство инвесторов не рассматривают как риск, а риском считается только то, что ниже уровня. За минимальный уровень риска в данной модели был доходность безрискового актива.
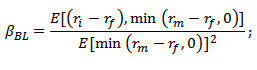
ri – доходность акции; rm – доходность рынка; rf – доходность безрискового актива.
Модификация коэффициента бета от Шоулза-Виллимса
β-1, β, β1 – коэффициенты беты для предыдущего (-1) текущего и следующего (1) периода;
ρm – коэффициент автокорреляции рыночной доходности.
Модификация коэффициента бета от Харлоу-Рао (1989)
Формула отражает одностороннюю бету, с предположением, что инвесторы рассматривают риск только как отклонение от среднерыночной доходности вниз. В отличие от модели Бава-Линдсберга за минимальный уровень риска брался уровень среднерыночной доходности.
где: μi – средняя доходность акции; μm – средняя доходность рынка;
Помимо коэффициента бета на практике используют другие показатели риска-доходности инвестиционного портфеля, ПИФа, более подробно узнать про современные показатели оценки инвестиций вы можете в моей статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«. О практике оценке риска инвестиции читайте в статье: «Методы оценки риска VaR (Value at Risk). Рыночный риск. Пример расчета в Excel «.
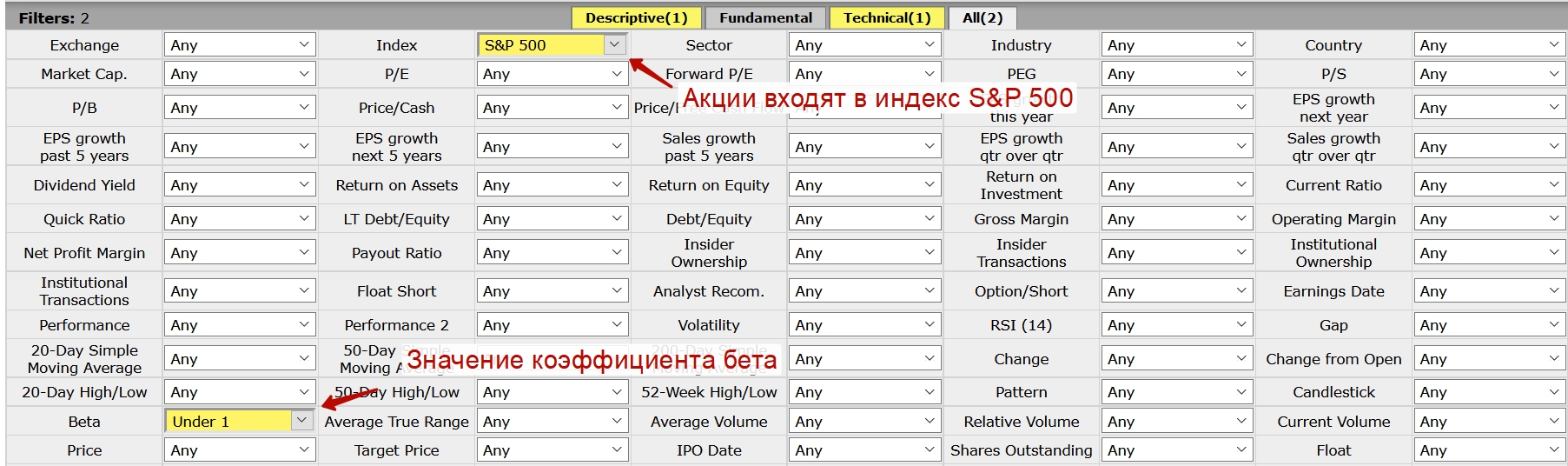
Коэффициент бета для акций США
Существуют сервисы позволяющие оценить коэффициент бета для множества компаний и выделить наиболее интересные. Будем применять сервис Finviz. Чтобы найти акции менее чувствительные чем колебания фондового рынка необходимо установить коэффициент бета меньше 1.
Где посмотреть коэффициент бета для российских акций
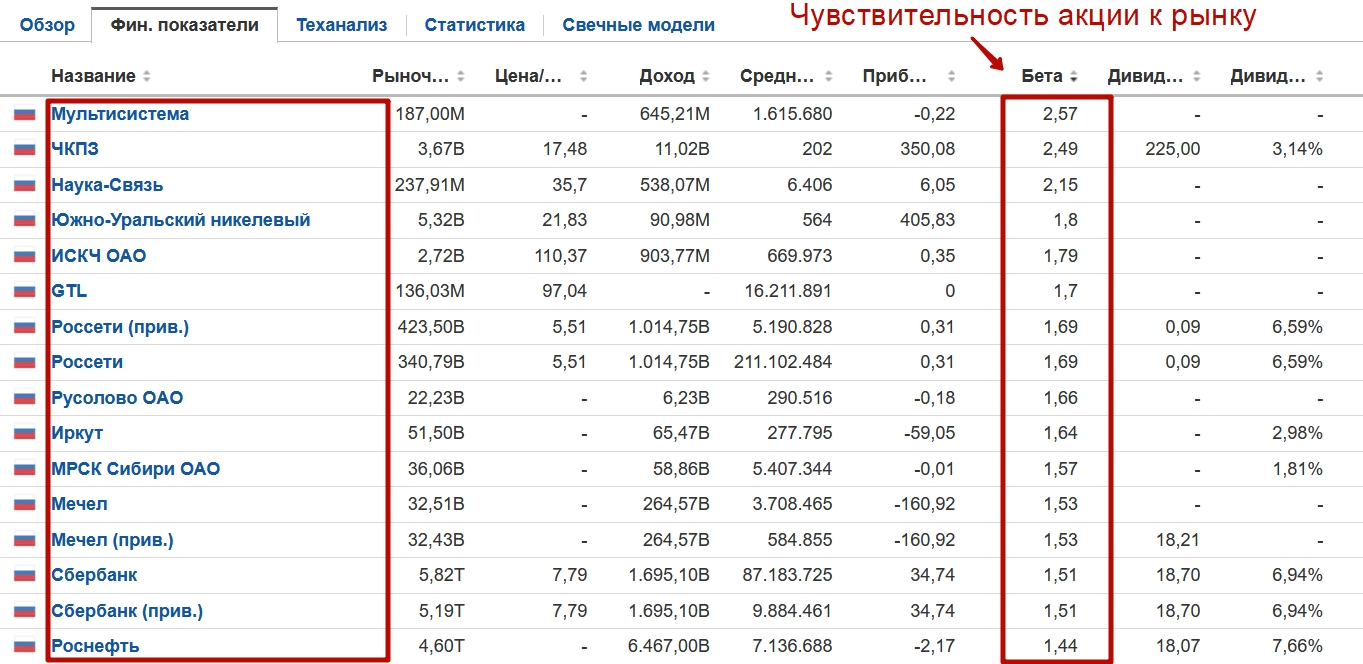
Если цель узнать коэффициент бета для российских акций, то для этого можно воспользоваться сервисом investing.com. Помимо отечественных компаний коэффициент бета можно определить для иностранных. Как мы видим для акции Мультисистемы коэффициент равен 2,57 – это значит, что она в 2,5 раза более изменчивая по отношению к рыночному изменению (индексу ММВБ).
Проанализировать акции на бета можно по ссылке.
Высокие значения коэффициента бета при растущем рынке будут обеспечивать дополнительную прибыль, при коррекциях такие акции как правило имеют больше убытков.
Резюме
Коэффициент бета является одним из классических мер рыночного риска для оценки доходности акций, инвестиционных портфелей и ПИФов. Несмотря на сложность использования данного инструмента для оценки отечественных низколиквидных акций и неустойчивость его изменения во времени, коэффициент бета является ключевым показателем оценки инвестиционных рисков. Рассмотренные модификации коэффициента позволяют скорректировать и дать более оценку систематическому риску. С вами был Иван Жданов, спасибо за внимание.
Автор: к.э.н. Жданов Иван Юрьевич
What Is Beta?
Peering through Yahoo (YHOO) Finance, Google (GOOG) Finance, or other financial data feeders, one may see a variable called beta amid other financial data, such as stock price or market value.
In finance, the beta of a firm refers to the sensitivity of its share price with respect to an index or benchmark. Generally, the index of 1.0 is selected for the market index (usually the S&P 500 index), and if the stock behaved with more volatility than the market, its beta value will be greater than one. If the opposite is the case, its beta will be a value less than one. A company with a beta of greater than one will tend to amplify market movements (for instance the case for the banking sector), and a business with a beta of less than one will tend to ease market movements.
Beta can be seen as a measure of risk: the higher the beta of a company, the higher the expected return should be to compensate for the excess risk caused by volatility.
Therefore, from a portfolio management or investment perspective, one wants to analyze any measures of risk associated with a company to gain a better estimation of its expected return.
Key Takeaways
- Beta is a measure of how sensitive a firm’s stock price is to an index or benchmark.
- A beta greater than 1 indicates that the firm’s stock price is more volatile than the market, and a beta less than 1 indicates that the firm’s stock price is less volatile than the market.
- A beta may produce different results because of the variations in estimating it, such as different time spans used to calculate data.
- Microsoft Excel serves as a tool to quickly organize data and calculate beta.
- Low beta stocks are less volatile than high beta stocks and offer more protection during turbulent times.
How Do You Calculate Beta In Excel?
Different Results for the Same Beta
Incidentally, it is important to differentiate the reasons why the beta value that is provided on Google Finance may be different from the beta on Yahoo Finance or Reuters.
This is because there are several ways to estimate beta. Multiple factors, such as the duration of the period taken into account, are included in the computation of the beta, which creates various results that could portray a different picture. For example, some calculations base their data on a three-year span, while others may use a five-year time horizon. Those two extra years may be the cause of two vastly different results. Therefore, the idea is to select the same beta methodology when comparing different stocks.
Calculation of Beta Using Excel
It’s simple to calculate the beta coefficient over a certain time period. The beta coefficient needs a historical series of share prices for the company that you are analyzing. In our historical example, we will use Apple (AAPL) stock prices from 2012 through 2015 as our object of analysis and the S&P 500 as our historical index. To get this data, go to:
- Yahoo! Finance –> Historical prices, and download the time series «Adj Close» for the S&P 500 and the firm Apple.
We only provide a small snippet of the data over 750 rows as it is extensive:
Once we have the Excel table, we can reduce the table data to three columns: the first is the date, the second is the Apple stock, and the third is the price of the S&P 500.
There are then two ways to determine beta. The first is to use the formula for beta, which is calculated as the covariance between the return (ra) of the stock and the return (rb) of the index divided by the variance of the index (over a period of three years).
β
a
=
Cov
(
r
a
,
r
b
)
Var
(
r
b
)
begin{aligned} &beta_a = frac { text{Cov} ( r_a, r_b ) }{ text{Var} ( r_b ) } \ end{aligned}
βa=Var(rb)Cov(ra,rb)
To do so, we first add two columns to our spreadsheet; one with the index return r (daily in our case), (column D in Excel), and with the performance of Apple stock (column E in Excel).
At first, we only consider the values of the last three years (about 750 days of trading) and a formula in Excel, to calculate beta.
BETA FORMULA = COVAR (D1: D749; E1: E749) / VAR (E1: E749)
The second method is to perform a linear regression, with the dependent variable performance of Apple stock over the last three years as an explanatory variable and the performance of the index over the same period.
Now that we have the results of our regression, the coefficient of the explanatory variable is our beta (the covariance divided by variance).
With Excel, we can pick a cell and enter the formula: «SLOPE» which represents the linear regression applied between the two variables; the first for the series of daily returns of Apple (here: 750 periods), and the second for the daily performance series of the index, which follows the formula:
BETA FORMULA = SLOPE (E1: E749; D1:D749)
Here, we have just computed a beta value for Apple’s stock (0.77 in our example, taking daily data and an estimated period of three years, from April 9, 2012, to April 9, 2015).
Low Beta–High Beta
Many investors found themselves with heavy losing positions as part of the global financial crisis that began in 2007. As part of those collapses, low beta stocks dove down much less than higher beta stocks during periods of market turbulence. This is because their market correlation was much lower, and thus the swings orchestrated through the index were not felt as acutely for those low beta stocks.
However, there are always exceptions given the industry or sectors of low beta stocks, and so, they might have a low beta with the index but a high beta within their sector or industry.
Therefore, incorporating low beta stocks versus higher beta stocks could serve as a form of downside protection in times of adverse market conditions. Low beta stocks are much less volatile; however, another analysis must be done with intra-industry factors in mind.
On the other hand, higher beta stocks are selected by investors who are keen and focused on short-term market swings. They wish to turn this volatility into profit, albeit with higher risks. Such investors would select stocks with a higher beta, which offer more ups and downs and entry points for trades than stocks with lower beta and lower volatility.
What Does a Stock’s Beta Tell You?
The Beta of a stock indicates its relative volatility compared to the broader equity market, as measured by the S&PO 500 (which has a beta of 1.0). A beta greater than one would indicate that the stock will go up more (in percentage terms) than the index when the index goes up, but also fall more than the index when it declines. A beta of less than one would suggest more muted movements relative to the index.
How Is Beta Computed?
Beta is essentially the regression coefficient of a stock’s historical returns compared to those of the S&P 500 index. This coefficient represents the slope of a line of best fit correlating the stock’s returns against the index’s. Because regression coefficients are called «betas» (β) in statistics, the terminology was carried over to investing.
How Is Beta Used in Practice?
Beta is used to gauge the relative riskiness of a stock. As an example, consider the hypothetical firm US CORP (USCS). Financial websites provide a current beta for this company at 5.48, which means that with respect to the historical variations of the stock compared to the Standard & Poor’s 500, US CORP increased on average by 5.48% if the S&P 500 rose by 1%. Conversely, when the S&P 500 is down 1%, US CORP Stock would tend to average a decline of 5.48%. If the index rose by 0,2%, USGC rose, on average, by 1.1%. As a result, one may conclude that USGC is a fairly risky investment.
The Bottom Line
It is important to follow strict trading strategies and rules and apply a long-term money management discipline in all beta cases. Employing beta strategies can be useful as part of a broader investment plan to limit downside risk or realize short-term gains, but it’s important to remember that it is also subject to the same levels of market volatility as any other trading strategy.
Бета-коэффициент (по англ. beta) – это показатель чувствительности цены акции относительно всего фондового рынка (или широкого индекса акций). Бета измеряет систематический риск, то есть риск, присущий всей финансовой системе. Бета-коэффициент является важным компонентом модели оценки капитальных активов CAPM при расчете требуемой нормы прибыли. Математически, бета представляет собой коэффициент наклона Линии рынка ценных бумаг (по англ. Security Market Line).
Формула
Бета-коэффициент рассчитывается как ковариация между доходностью акции и доходностью рынка, разделенная на дисперсию рыночной доходности.
Небольшая модификация данной формулы позволит выявить еще одно ключевое соотношение: коэффициент бета равен коэффициенту корреляции, умноженному на стандартное отклонение доходности акций, разделенное на стандартное отклонение рыночных доходностей.
Анализ
Бета-коэффициент равный 1 предполагает, что акция имеет такой же риск, что и общий рынок, и доходность акции будет сопоставима с доходностью рынка. Коэффициент ниже единицы указывает на пониженный риск и более низкую потенциальную доходность относительно рынка. С другой стороны, β выше 1, более высокий риск инвестирования в данную акцию.
В 2017 году акция Chevron (тикер CVX) имела бета коэффициент 1.17. Это свидетельствует о том, что акция компании немного более рискованна, чем индекс акций S&P 50. Marathon Oil (тикер на бирже NYSE: MRO), с другой стороны, имеет β в размере 3.02. Можно заключить, что эта акция более рискованная, чем рынок в целом.
Расчет бета-коэффициента
Пример. Предположим, что коэффициент корреляции между рынком и ценой акций компании ABC составляет 0.83, стандартное отклонение рынка составляет 12%, а отклонение цены акций – 9%. Бета может составлять:
0.83 * 9%/12% = 0.63
Если у нас нет информации по стандартному отклонению и корреляции для расчета бета коэффициента, необходимо выполнить следующие простые шаги в Excel:
1) Найдите данные о исторической динамике цены акции
2) Получите исторические значения соответствующего индекса (например, S&P500).
3) Определяем дневную доходность цены акции, используя следующую формулу:
Доходность = (Цена закрытия – Цена открытия)/Цена открытия
4) Аналогичным образом преобразуйте значения цены индекса в доходности.
5) Сопоставляем полученные доходности по датам.
6) При помощи функции НАКЛОН (в англоязычной версии – SLOPE) определяем коэффициент наклона между массивами данных. Итоговое значение и является бета коэффициентом.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает функцию бета-распределения.
Функция бета-распределения обычно используется для изучения вариации в процентах какой-либо величины между выборками — например, части дня, которую люди проводят у телевизора.
Синтаксис
БЕТА.РАСП(x;альфа;бета;интегральная;[A];[B])
Аргументы функции БЕТА.РАСП описаны ниже.
-
X — обязательный аргумент. Значение в интервале между A и B, для которого вычисляется функция.
-
Альфа — обязательный аргумент. Параметр распределения.
-
Бета — обязательный аргумент. Параметр распределения.
-
Накопительное — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция БЕТА.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается функция плотности распределения.
-
A — необязательный аргумент. Нижняя граница интервала изменения x.
-
B — необязательный аргумент. Верхняя граница интервала изменения x.
Замечания
-
Если какой-либо из аргументов не является числом, аргумент БЕТА. DIST возвращает #VALUE! значение ошибки.
-
Если альфа ≤ 0 или бета ≤ 0, то бета. DIST возвращает #NUM! значение ошибки.
-
Если x < A, x > B или A = B, БЕТА. DIST возвращает #NUM! значение ошибки.
-
Если значения A и B не указаны, функция БЕТА.РАСП использует стандартное интегральное бета-распределение (A = 0, B = 1).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
2 |
Значение, для которого рассчитывается функция |
|
|
8 |
Параметр распределения |
|
|
10 |
Параметр распределения |
|
|
1 |
Нижний предел |
|
|
3 |
Верхний предел |
|
|
Формула |
Описание |
Результат |
|
=БЕТА.РАСП(A2;A3;A4;ИСТИНА;A5;A6) |
Интегральная функция плотности бета-вероятности для указанных выше параметров (0,68547058) |
0,6854706 |
|
=БЕТА.РАСП(A2;A3;A4;ЛОЖЬ;A5;A6) |
Функция плотности бета-вероятности для указанных выше параметров |
1,4837646 |
Нужна дополнительная помощь?
При оценке компании доходным методом, то есть путем дисконтирования будущих денежных потоков, очевидно значимым моментом является определение ставки дисконтирования, с помощью которой эти самые будущие денежные потоки будут приводиться к текущей стоимости.
Не вдаваясь в подробности расчета дисконтированных денежных потоков, скажу, что базово потоки делятся на два вида: денежные потоки на собственный капитал и денежные потоки на инвестированный капитал (собственный капитал + заемное финансирование). Отличаются и ставки дисконтирования для двух разновидностей потоков. Поскольку речь далее пойдет про смысл и методику расчета коэффициента бета, то обратимся к ставке дисконтирования для собственного капитала. Она, к слову, нужна и для расчета ставки дисконтирования для капитала инвестированного.
В современной практике для расчета ставки дисконтирования денежный потоков на собственный капитал в большинстве случаев применяется модель CAPM (Capital Asset Pricing Model), что в дословном переводе означает «модель ценообразования капитальных активов».
Концепция CAPM была разработана на основе портфельной теории Г. Марковица, наиболее применимая на сегодняшний день интерпретация данной концепции принадлежит У. Шарпу, поэтому она зачастую называется его именем. Ставка доходности, рассчитанная по модели CAPM, определяет, какой должна быть доходность актива, добавляемого к портфелю, с учетом его рыночного риска. Поскольку именно требуемой доходностью определяется ставка дисконтирования будущих денежных потоков, рассчитанная по описываемой модели доходность может использоваться в качестве такой ставки. Рассчитанная по модели CAPM требуемая норма доходности в отношении актива является, таким образом, общей для рынка, то есть лишена субъективной составляющей.
Ниже приведена формула расчета доходности по CAPM:
Где:
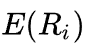
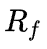
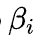
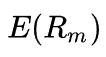
Выражение в скобках представляет собой премию за риск для определенного рынка (рынка, для которого мы берем рыночную доходность и безрисковую ставку). Бета-коэффициент, таким образом, выступает мерой рыночного риска: он определяет, в какой степени конкретный актив подвержен рыночному риску, то есть как соотносится изменение доходности актива с изменением доходности рыночного портфеля.
Поскольку доходность актива в случае с акциями определяется движением котировок, коэффициент бета также часто интерпретируют как волатильность: чем выше коэффициент – тем волатильнее акция, для которой он рассчитан. Волатильность же измеряется в данном случае относительно рыночного портфеля.
Расчет бета-коэффициента:
Где:
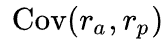
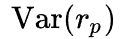
Коэффициент бета, таким образом, может принимать любое значение, однако чаще всего находится в диапазоне от -1 до 1, или, еще чаще, в диапазоне от 0 до 1. Ниже приведена интерпретация основных интервалов значений.
-
Бета 0. Такое значение коэффициента означает, что доходность актива не изменяется вовсе, то есть он является безрисковым. Если подставить такое значение в первую формулу, мы получим доходность, равную безрисковой ставке.
-
Бета в диапазоне от 0 до 1. Такое значение коэффициента означает, что доходность актива и рыночного портфеля изменяются сонаправленно, однако изменение доходности актива (волатильность) ниже, чем у рыночного портфеля.
-
Бета равна 1. Означает, что доходности актива и рыночного портфеля меняются одинаково, то есть корреляция 100%.
-
Бета коэффициент больше 1. Означает, что доходность актива и рыночного портфеля меняются сонаправленно, однако изменчивость доходности актива выше, нежели рыночного портфеля. То есть, выше его риск.
-
Бета в диапазоне от -1 до 0. Выводы аналогичны диапазону от 0 до 1, однако движение доходностей является противоположным.
-
Бета равна -1. Означает, что доходности актива и рыночного портфеля изменяются в одинаковой мере, но разнонаправленно.
-
Бета меньше -1. Выводы аналогичны значению больше 1, однако движение доходностей разнонаправленное.
Поскольку, как сказано выше, доходность определяется движением котировок, под изменением доходности следует понимать изменение котировок.
Как рассчитать бета-коэффициент?
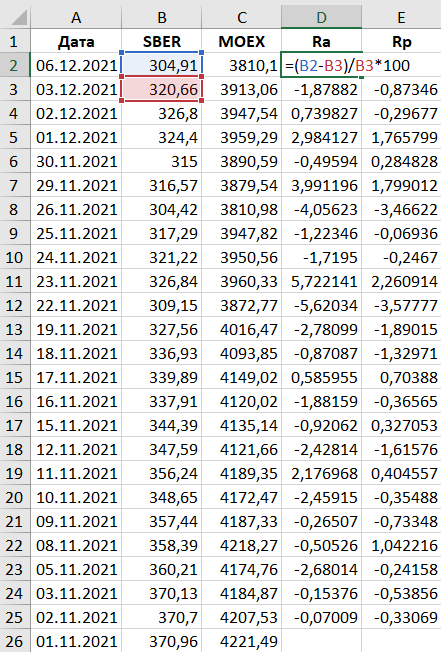
Поскольку расчет бета-коэффициента – достаточно трудоемкое занятие, сегодня это проще всего сделать с помощью Excel. В таблице ниже для примера взяты данные по торгам с 1 ноября 2021 года, однако на практике лучше использовать более длительный период, хотя бы от 100 торговых дней.
Для каждого периода рассчитываем доходности Ra (доходность акции) и Rp (доходность портфеля).
Далее есть два способа рассчитать бета-коэффициент.
Способ №1
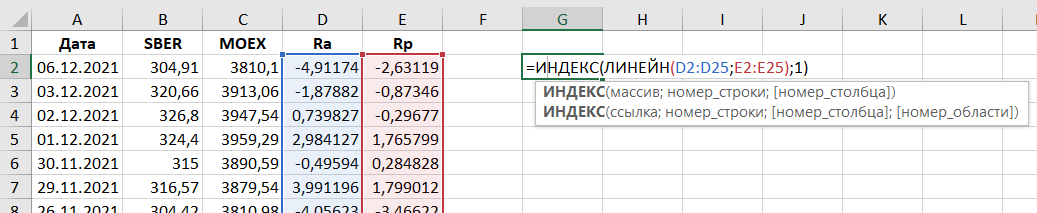
Для расчета коэффициента будем использовать формулы Excel «ИНДЕКС» и «ЛИНЕЙН», в значениях из таблицы выше формула примет вид:
Получаем значение бета-коэффициента, равное 1,56, что в соответствии с описанной выше интерпретацией говорит нам о том, что на данном временном промежутке акции Сбера были более волатильными, чем рыночный портфель, в качестве которого использовался индекс Московской биржи.
Способ №2
На зависимость между доходностями акции и рыночного портфеля можно смотреть как на линейную регрессию.
Уравнение простой (парной) линейной регрессии имеет следующий общий вид:
Коэффициент b1 и определяет тесноту связи переменных. Он и будет бета-коэффициентом в случае построения парной линейной регрессии для наших значений доходностей. Чтобы построить регрессию в Excel потребуется подключить в настройках пакет анализа данных.
На вкладке «Файл» необходимо найти раздел «Параметры».
Он находится в левом нижнем углу.
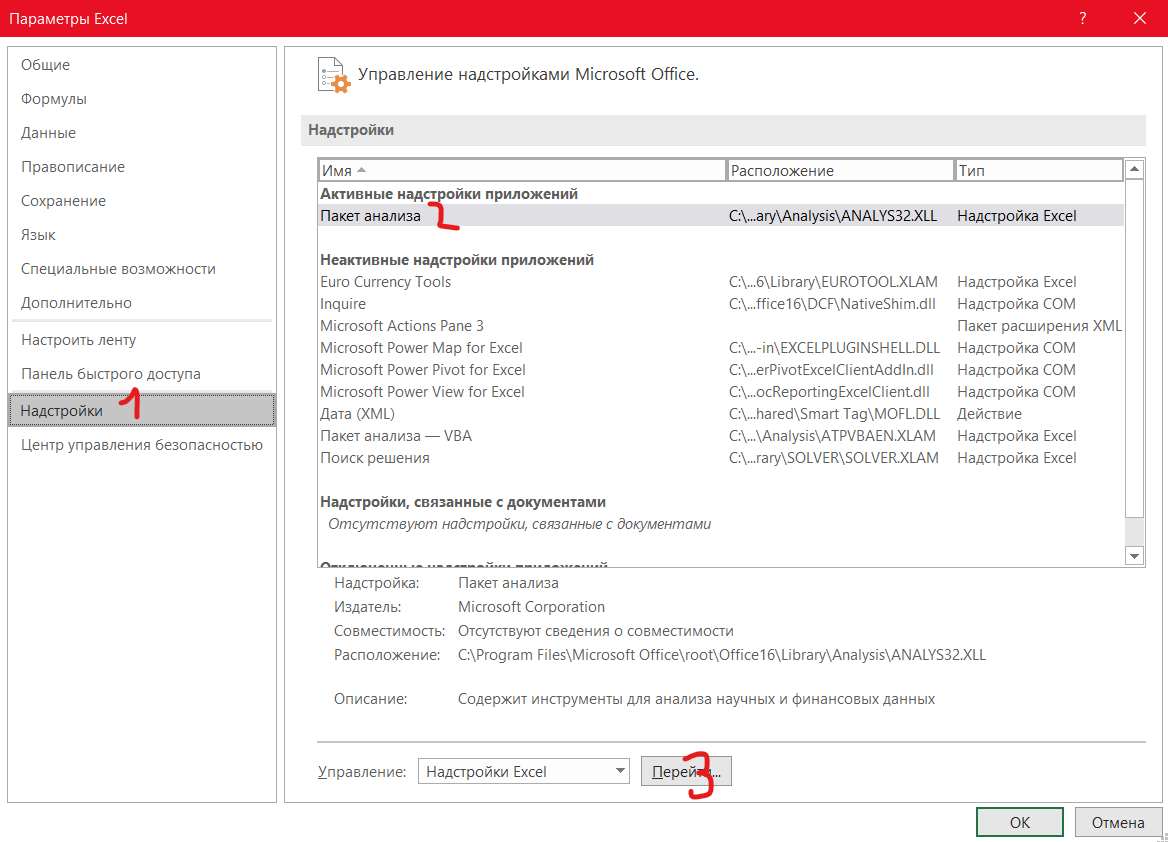
В появившемся окне переходим в раздел «Настройки» и нажимаем последовательно как на картинке:
В появившемся окне ставим галочку в поле «Пакет анализа».
Теперь пакет анализа включен и найти его можно на вкладке «Данные» в правом верхнем углу.
Далее дело за малым. Нажимаем на «Анализ данных». Выбираем в списке «Регрессия».
Заполняем входные диапазоны: Y – это значения доходностей акции, X – значения доходностей индекса (рыночного портфеля). Ставим галочку в разделе «Параметры вывода» в графе «Новый рабочий лист», нажимаем «Ок».
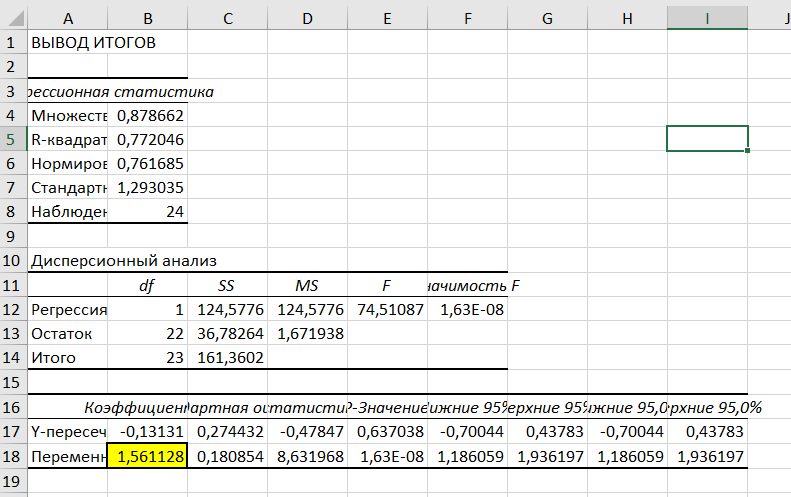
Открывается новый рабочий лист, на котором мы видим множество различных параметров нашей регрессии. Нас же интересует бета-коэффициент, который выделен желтым цветом.
В целом способы по своей сути одинаковые, просто во втором случае мы получаем дополнительные данные, которые будут интересны разве что тем, что хорошо разбирается в статистике. Приведенные данные позволяют оценить достоверность выявленной зависимости, статистическую значимость результата.
Бета-коэффициент можно считать для различных периодов, в зависимости от того, насколько сильно в представлении считающего менялся характер связи между акцией и индексом. Так, чем стабильнее и рынок и чем он более развит – тем больше может быть период для расчета коэффициента.
Если деятельность компании претерпела серьезные изменения, которые позволяют предположить, что степень влияния на ее деятельность рыночных рисков изменилась, не стоит принимать к расчету большой период до соответствующих изменений, так как такие значения могут исказить результат и «перевесить» более поздние и актуальные значения при расчете.