From Wikipedia, the free encyclopedia
The bag-of-words model is a simplifying representation used in natural language processing and information retrieval (IR). In this model, a text (such as a sentence or a document) is represented as the bag (multiset) of its words, disregarding grammar and even word order but keeping multiplicity. The bag-of-words model has also been used for computer vision.[1]
The bag-of-words model is commonly used in methods of document classification where the (frequency of) occurrence of each word is used as a feature for training a classifier.[2]
An early reference to «bag of words» in a linguistic context can be found in Zellig Harris’s 1954 article on Distributional Structure.[3]
The Bag-of-words model is one example of a Vector space model.
Example implementation[edit]
The following models a text document using bag-of-words. Here are two simple text documents:
(1) John likes to watch movies. Mary likes movies too.
(2) Mary also likes to watch football games.
Based on these two text documents, a list is constructed as follows for each document:
"John","likes","to","watch","movies","Mary","likes","movies","too" "Mary","also","likes","to","watch","football","games"
Representing each bag-of-words as a JSON object, and attributing to the respective JavaScript variable:
BoW1 = {"John":1,"likes":2,"to":1,"watch":1,"movies":2,"Mary":1,"too":1}; BoW2 = {"Mary":1,"also":1,"likes":1,"to":1,"watch":1,"football":1,"games":1};
Each key is the word, and each value is the number of occurrences of that word in the given text document.
The order of elements is free, so, for example {"too":1,"Mary":1,"movies":2,"John":1,"watch":1,"likes":2,"to":1} is also equivalent to BoW1. It is also what we expect from a strict JSON object representation.
Note: if another document is like a union of these two,
(3) John likes to watch movies. Mary likes movies too. Mary also likes to watch football games.
its JavaScript representation will be:
BoW3 = {"John":1,"likes":3,"to":2,"watch":2,"movies":2,"Mary":2,"too":1,"also":1,"football":1,"games":1};
So, as we see in the bag algebra, the «union» of two documents in the bags-of-words representation is, formally, the disjoint union, summing the multiplicities of each element.

Application[edit]
In practice, the Bag-of-words model is mainly used as a tool of feature generation. After transforming the text into a «bag of words», we can calculate various measures to characterize the text. The most common type of characteristics, or features calculated from the Bag-of-words model is term frequency, namely, the number of times a term appears in the text. For the example above, we can construct the following two lists to record the term frequencies of all the distinct words (BoW1 and BoW2 ordered as in BoW3):
(1) [1, 2, 1, 1, 2, 1, 1, 0, 0, 0] (2) [0, 1, 1, 1, 0, 1, 0, 1, 1, 1]
Each entry of the lists refers to the count of the corresponding entry in the list (this is also the histogram representation). For example, in the first list (which represents document 1), the first two entries are «1,2»:
- The first entry corresponds to the word «John» which is the first word in the list, and its value is «1» because «John» appears in the first document once.
- The second entry corresponds to the word «likes», which is the second word in the list, and its value is «2» because «likes» appears in the first document twice.
This list (or vector) representation does not preserve the order of the words in the original sentences. This is just the main feature of the Bag-of-words model. This kind of representation has several successful applications, such as email filtering.[1]
However, term frequencies are not necessarily the best representation for the text. Common words like «the», «a», «to» are almost always the terms with highest frequency in the text. Thus, having a high raw count does not necessarily mean that the corresponding word is more important. To address this problem, one of the most popular ways to «normalize» the term frequencies is to weight a term by the inverse of document frequency, or tf–idf. Additionally, for the specific purpose of classification, supervised alternatives have been developed to account for the class label of a document.[4] Lastly, binary (presence/absence or 1/0) weighting is used in place of frequencies for some problems (e.g., this option is implemented in the WEKA machine learning software system).
n-gram model[edit]
The Bag-of-words model is an orderless document representation — only the counts of words matter. For instance, in the above example «John likes to watch movies. Mary likes movies too», the bag-of-words representation will not reveal that the verb «likes» always follows a person’s name in this text. As an alternative, the n-gram model can store this spatial information. Applying to the same example above, a bigram model will parse the text into the following units and store the term frequency of each unit as before.
[ "John likes", "likes to", "to watch", "watch movies", "Mary likes", "likes movies", "movies too", ]
Conceptually, we can view bag-of-word model as a special case of the n-gram model, with n=1. For n>1 the model is named w-shingling (where w is equivalent to n denoting the number of grouped words). See language model for a more detailed discussion.
Python implementation[edit]
# Make sure to install the necessary packages first # pip install --upgrade pip # pip install tensorflow from tensorflow import keras from typing import List from keras.preprocessing.text import Tokenizer sentence = ["John likes to watch movies. Mary likes movies too."] def print_bow(sentence: List[str]) -> None: tokenizer = Tokenizer() tokenizer.fit_on_texts(sentence) sequences = tokenizer.texts_to_sequences(sentence) word_index = tokenizer.word_index bow = {} for key in word_index: bow[key] = sequences[0].count(word_index[key]) print(f"Bag of word sentence 1:n{bow}") print(f"We found {len(word_index)} unique tokens.") print_bow(sentence)
Hashing trick[edit]
A common alternative to using dictionaries is the hashing trick, where words are mapped directly to indices with a hashing function.[5] Thus, no memory is required to store a dictionary. Hash collisions are typically dealt via freed-up memory to increase the number of hash buckets. In practice, hashing simplifies the implementation of bag-of-words models and improves scalability.
Example usage: spam filtering[edit]
In Bayesian spam filtering, an e-mail message is modeled as an unordered collection of words selected from one of two probability distributions: one representing spam and one representing legitimate e-mail («ham»).
Imagine there are two literal bags full of words. One bag is filled with words found in spam messages, and the other with words found in legitimate e-mail. While any given word is likely to be somewhere in both bags, the «spam» bag will contain spam-related words such as «stock», «Viagra», and «buy» significantly more frequently, while the «ham» bag will contain more words related to the user’s friends or workplace.
To classify an e-mail message, the Bayesian spam filter assumes that the message is a pile of words that has been poured out randomly from one of the two bags, and uses Bayesian probability to determine which bag it is more likely to be in.
See also[edit]
- Additive smoothing
- Bag-of-words model in computer vision
- Document classification
- Document-term matrix
- Feature extraction
- Hashing trick
- Machine learning
- MinHash
- n-gram
- Natural language processing
- Vector space model
- w-shingling
- tf-idf
Notes[edit]
- ^ a b Sivic, Josef (April 2009). «Efficient visual search of videos cast as text retrieval» (PDF). IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 31, NO. 4. opposition. pp. 591–605.
- ^ McTear et al 2016, p. 167.
- ^ Harris, Zellig (1954). «Distributional Structure». Word. 10 (2/3): 146–62. doi:10.1080/00437956.1954.11659520.
And this stock of combinations of elements becomes a factor in the way later choices are made … for language is not merely a bag of words but a tool with particular properties which have been fashioned in the course of its use
- ^ Youngjoong Ko (2012). «A study of term weighting schemes using class information for text classification». SIGIR’12. ACM.
- ^ Weinberger, K. Q.; Dasgupta A.; Langford J.; Smola A.; Attenberg, J. (2009). «Feature hashing for large scale multitask learning». Proceedings of the 26th Annual International Conference on Machine Learning: 1113–1120. arXiv:0902.2206. Bibcode:2009arXiv0902.2206W.
References[edit]
- McTear, Michael (et al) (2016). The Conversational Interface. Springer International Publishing.
Мешок слов (BoW) – это способ представления текстовых данных при моделировании в Машинном обучении (ML).
Модель набора слов проста для понимания и реализации и зарекомендовала себя с большим успехом в таких задачах, как Языковое моделирование (Language Modeling) и Классификация документов (Document Classification).
Проблема с текстом
Проблема с моделированием текста заключается в том, что он беспорядочный, а большинство Алгоритмов (Algorithm) машинного обучения предпочитают входные и выходные данные фиксированной длины.
Алгоритмы машинного обучения не могут работать напрямую с необработанным текстом: его необходимо преобразовать в числа а точнее, в векторы чисел. При языковой обработке векторы выводятся из текстовых данных, чтобы отразить различные лингвистические свойства текста. Это называется извлечением или Кодированием (Encoding) признаков. BoW – как раз и есть один из таких методов.
Подход очень простой и гибкий, и его можно использовать множеством способов для извлечения функций из документов.
Пакет слов – это представление текста, которое описывает «характер» присутствия слов в документе. Это подразумевает две вещи:
- Словарь – список уникальных присутствующих в тексте слов
- Мера присутствия таких слов в тексте
Это называется «мешком» слов, потому что всякая информация о порядке или структуре слов в документе отбрасывается. Модель заботится только о том, встречаются ли известные слова в документе, а не об их положении. В этом подходе мы изучаем на гистограмму частоты употребления слов в тексте, то есть рассматриваем ее как признак-столбец.
Интуиция подсказывает человеку, что тексты похожи, если имеют похожее содержание. Кроме того, только по содержанию мы можем кое-что узнать о значении документа.
Пакет слов может быть настолько простым или сложным, насколько нам хочется. Сложность возникает как при принятии решения о том, как составить словарь известных слов – Токенов (Token), так и при оценке меры их «присутствия». Мы рассмотрим обе эти проблемы более подробно.
Пример модели мешка слов
Шаг 1. Соберите данные
Ниже приведен фрагмент книги Чарльза Диккенса «Повесть о двух городах»:
It was the best of times,
It was the worst of times,
It was the age of wisdom,
It was the age of foolishness,
В этом небольшом примере давайте рассматривать каждую строку как отдельный «документ», а все четверостишие – как Корпус (Corpus) документов.
Шаг 2: Составьте словарь
Теперь мы можем составить список всех слов:
- “it”
- “was”
- “the”
- “best”
- “of”
- “times”
- “worst”
- “age”
- “wisdom”
- “foolishness”
Это словарь из 10 лексем корпуса, содержащего 24 слова.
Шаг 3. Создайте векторы документа
Следующим шагом будет оценка слов в каждом документе. Цель состоит в том, чтобы превратить каждый документ с произвольным текстом в вектор, который мы можем использовать в качестве Входных данных (Input Data) для Модели (Model) машинного обучения.
Самый простой метод оценки – отметить наличие слов как логическое значение, 0 – отсутствие, 1 – присутствие. Поскольку в словаре есть 10 слов, мы создадим таблицу, описывающую присутствие того или иного слова в документе № 1, то есть первой строке:
Двоичный вектор документа будет выглядеть следующим образом:
[1, 1, 1, 1, 1, 1, 0, 0, 0, 0]Остальные три документа выглядели бы следующим образом:
"it was the worst of times" = [1, 1, 1, 0, 1, 1, 1, 0, 0, 0]
"it was the age of wisdom" = [1, 1, 1, 0, 1, 0, 0, 1, 1, 0]
"it was the age of foolishness" = [1, 1, 1, 0, 1, 0, 0, 1, 0, 1]Теперь у нас есть последовательный способ извлечения функций из любого документа в нашем корпусе, и эти вектора подходят для моделирования.
Новые документы, слова из которых лишь отчасти «покрыты» ранее составленным словарем, по-прежнему могут кодироваться, при этом оцениваются только вхождение известных слов, а неизвестные игнорируются.
Управление словарным запасом
По мере увеличения размера словаря увеличивается и векторное представление документов.
В предыдущем примере длина вектора документа равна количеству известных слов.
Для очень большого корпуса, например, тысячи книг, длина вектора – тысячи или миллионы позиций. Кроме того, каждый документ может содержать очень мало известных слов. В результате получается вектор с множеством нулевых оценок, называемый Разреженным вектором (Sparse Vector).
Для разреженных векторов требуется больше памяти и вычислительных ресурсов при моделировании, а огромное количество позиций или измерений может сделать процесс моделирования очень сложным для традиционных алгоритмов. Таким образом, при использовании мешка слов возникает необходимость уменьшить размер словарного запаса.
Существуют простые методы очистки текста, которые можно использовать в качестве первого шага, например:
- Игнорирование регистра
- Игнорирование знаков препинания
- Игнорирование часто используемых неинформативных так называемых стоп-слов, например «а», «из» и т.д.
- Исправление слов с ошибками
- Сокращение слов до их граммтической основы – Cnемминг (Stemming)
Более сложный подход – создать словарь сгруппированных слов. Это одновременно изменяет объем словарного запаса и позволяет мешку слов выделить больше смысла из документа.
При таком подходе каждое слово или лексема называются «грамм». Создание словаря пар из двух слов, в свою очередь, называется моделью Биграмм (Bigram). Опять же, моделируются только биграммы, которые появляются в корпусе, а не все возможные биграммы.
N-грамм – это последовательность слов из N-знаков: биграмма – это последовательность из двух слов, таких как «пожалуйста, переверни», «переверни это» или «домашнее задание»; и триграмма – это последовательность из трех слов, например «пожалуйста, переверни свою» или «своя домашняя работа».
Например, биграммы в первой строке текста в предыдущем разделе: «Это были лучшие времена» выглядят следующим образом:
- “it was”
- “was the”
- “the best”
- “best of”
- “of times”
Словарь, который затем отслеживает тройки слов, называется моделью триграммы, а общий подход называется моделью N-граммы (N-gram), где N – количество сгруппированных слов.
Часто биграммы показывают лучшие результаты, чем модели Ngram, где N равен 1.
Оценка слов
После того, как словарный запас выбран, необходимо подсчитать наличие слов в примерах документов. В проработанном выше примере мы уже видели один очень простой подход к оценке: бинарная оценка наличия или отсутствия слов.
Некоторые дополнительные простые методы оценки включают в себя:
- Подсчет: сколько раз каждое слово встречается в документе.
- Частота появления каждого слова в документе
Хэширование слов
Хэш-функция сопоставляет данные с набором чисел фиксированного размера. Например, мы используем их , преобразуя имена в числа для скорейшего поиска.
Мы можем использовать Хеширование слов (Word Hashing) в нашем словаре. Это решает проблему наличия очень большого словарного запаса для большого текстового корпуса, потому что мы можем выбрать размер хэш-пространства, который, в свою очередь, равен размеру векторного представления документа.
TF-IDF
Проблема с оценкой частоты слов заключается в том, что в документе преобладают очень часто встречающиеся слова, но они могут не содержать столько информации для модели, сколько более редкие, специфические для предметной области слова.
Один из подходов состоит в том, чтобы изменить частоту слов в зависимости от того, как часто они появляются во всех документах, тем самым «штрафуя» часто встречающиеся предлоги («at»), артикли («the») и т.д. Такой подход к оценке называется Мера оценки важности слова в контексте документа (TF-IDF), где:
- Term Frequency (TF) –оценка частоты встречаемости слова в текущем документе.
Inverse Document Frequency (IDF) – оценка того, насколько редко слово встречается в документах.
Ограничения мешка слов
Модель набора слов очень проста для понимания и реализации и предлагает большую гибкость для настройки ваших конкретных текстовых данных. Тем не менее, она страдает некоторыми недостатками, такими как:
- Словарь требует тщательного проектирования, особенно управления размером, что влияет на разреженность представлений документа.
- Редкость: разреженные представления труднее моделировать как по вычислительным (пространственная и временная сложность), так и по информационным причинам. Модели должны использовать так мало информации в таком большом пространстве представлений.
- Значение: при отказе от порядка слов игнорируется контекст и, в свою очередь, значение слов в документе. Контекст и значение могут многое дать нашей модели. Человеку очевидна разница между фразами «this is interesting» и «is this interesting».
Автор оригинальной статьи: Jason Brownlee
Предобработка данных
Начнем с подключения необходимых библиотек и модулей:
import pandas as pd import seaborn as sns from tqdm import tqdm from sklearn.datasets import fetch_20newsgroups from sklearn.model_selection import train_test_split from sklearn.linear_model import Ridge from sklearn.metrics import mean_squared_error
Работа с текстовыми данными
Как правило, модели машинного обучения действуют в предположении, что
матрица «объект-признак» является вещественнозначной, поэтому при
работе с текстами сперва для каждого из них необходимо составить его
признаковое описание. Для этого широко используются техники
векторизации, tf-idf и пр.
Сперва загрузим данные:
data = fetch_20newsgroups(subset='all', categories=['comp.graphics', 'sci.med'])
Данные содержат тексты новостей, которые надо классифицировать на разделы.
texts = data['data'] target = data['target']
Например:
data['target_names'][target[0]]
Bag-of-words
Самый очевидный способ формирования признакового описания текстов —
векторизация. Простой способ заключается в подсчёте, сколько раз встретилось каждое слово
в тексте. Получаем вектор длиной в количество уникальных слов, встречающихся во
всех объектах выборки. В таком векторе много нулей, поэтому его удобнее хранить
в разреженном виде.
Пусть у нас имеется коллекция текстов ( D = {d_i}_{i=1}^l )
и словарь всех слов, встречающихся в выборке ( V = {v_j}_{j=1}^d. ) В
этом случае некоторый текст ( d_i ) описывается вектором
( (x_{ij})_{j=1}^d, ) где
$$
x_{ij} = sum_{v in d_i} [v = v_j].
$$
Таким образом, текст ( d_i ) описывается вектором количества вхождений
каждого слова из словаря в данный текст.
from sklearn.feature_extraction.text import CountVectorizer vectorizer = CountVectorizer(encoding='utf8', min_df=1) _ = vectorizer.fit(texts)
Результатом является разреженная матрица.
vectorizer.transform(texts[:1])
print(vectorizer.transform(texts[:1]).indptr) print(vectorizer.transform(texts[:1]).indices) print(vectorizer.transform(texts[:1]).data)
Такой способ представления текстов называют мешком слов (bag-of-words).
TF-IDF
Очевидно, что не все слова полезны в задаче прогнозирования. Например, мало
информации несут слова, встречающиеся во всех текстах. Это могут быть
как стоп-слова, так и слова, свойственные всем текстам выборки (в
текстах про автомобили употребляется слово «автомобиль»). Эту проблему
решает TF-IDF (*T*erm *F*requency–*I*nverse *D*ocument *F*requency)
преобразование текста.
Рассмотрим коллекцию текстов ( D ). Для каждого уникального слова ( t )
из документа ( d in D ) вычислим следующие величины:
- TD (Term Frequency) – количество вхождений слова в отношении к общему числу слов в тексте:
$$
textrm{tf}(t, d) = frac{n_{td}}{sum_{t in d} n_{td}},
$$
где ( n_{td} ) — количество вхождений слова ( t ) в текст ( d ).
- IDF (Inverse Document Frequency):
$$
textrm{idf}(t, D) = log frac{left| D right|}{left| {din D: t in d} right|},
$$
где ( left| {din D: t in d} right| ) – количество текстов в коллекции, содержащих слово ( t ).
Тогда для каждой пары (слово, текст) ( (t, d) ) вычислим величину:
$$
textrm{tf-idf}(t,d, D) = text{tf}(t, d)cdot text{idf}(t, D).
$$
Отметим, что значение ( text{tf}(t, d) ) корректируется для часто
встречающихся общеупотребимых слов при помощи значения
( textrm{idf}(t, D) ).
from sklearn.feature_extraction.text import TfidfVectorizer vectorizer = TfidfVectorizer(encoding='utf8', min_df=1) _ = vectorizer.fit(texts)
На выходе получаем разреженную матрицу.
vectorizer.transform(texts[:1])
print(vectorizer.transform(texts[:1]).indptr) print(vectorizer.transform(texts[:1]).indices) print(vectorizer.transform(texts[:1]).data)
Заметим, что оба метода возвращают вектор длины 32548 (размер нашего словаря).
Заметим, что одно и то же слово может встречаться в различных формах
(например, «сотрудник» и «сотрудника»), но описанные выше методы
интерпретируют их как различные слова, что делает признаковое описание
избыточным. Устранить эту проблему можно при помощи лемматизации и
стемминга.
Стемминг
Стемминг — это процесс нахождения основы слова. В результате применения
данной процедуры однокоренные слова, как правило, преобразуются к одинаковому
виду.
Таблица 1. Примеры стемминга
| Слово | Основа |
| вагон | вагон |
| вагона | вагон |
| вагоне | вагон |
| вагонов | вагон |
| вагоном | вагон |
| вагоны | вагон |
| важная | важн |
| важнее | важн |
| важнейшие | важн |
| важнейшими | важн |
| важничал | важнича |
| важно | важн |
Snowball — фрэймворк для написания
алгоритмов стемминга (библиотека nltk). Алгоритмы стемминга отличаются для разных языков
и используют знания о конкретном языке — списки окончаний для разных
чистей речи, разных склонений и т.д. Пример алгоритма для русского
языка – Russian stemming.
import nltk stemmer = nltk.stem.snowball.RussianStemmer()
print(stemmer.stem(u'машинное'), stemmer.stem(u'обучение'))
stemmer = nltk.stem.snowball.EnglishStemmer() def stem_text(text, stemmer): tokens = text.split() return ' '.join(map(lambda w: stemmer.stem(w), tokens)) stemmed_texts = [] for t in tqdm(texts[:1000]): stemmed_texts.append(stem_text(t, stemmer))
Как видим, стеммер работает не очень быстро и запускать его для всей
выборки достаточно накладно.
Лематизация
Лемматизация — процесс приведения слова к его нормальной форме (лемме):
- для существительных — именительный падеж, единственное число;
- для прилагательных — именительный падеж, единственное число, мужской род;
- для глаголов, причастий, деепричастий — глагол в инфинитиве.
Лемматизация — процесс более сложный по сравнению со стеммингом. Стеммер
просто «режет» слово до основы.
Например, для русского языка есть библиотека pymorphy2.
import pymorphy2 morph = pymorphy2.MorphAnalyzer()
morph.parse('играющих')[0]
Сравним работу стеммера и лемматизатора на примере:
stemmer = nltk.stem.snowball.RussianStemmer() print(stemmer.stem('играющих'))
print(morph.parse('играющих')[0].normal_form)
Трансформация признаков и целевой переменной
Разберёмся, как может влиять трансформация признаков или целевой
переменной на качество модели.
Логарифмирование
Воспользуется датасетом с ценами на дома, с которым мы уже
сталкивались ранее
(House Prices: Advanced Regression Techniques).
data = pd.read_csv('train.csv') data = data.drop(columns=["Id"]) y = data["SalePrice"] X = data.drop(columns=["SalePrice"])
Посмотрим на распределение целевой переменной
plt.figure(figsize=(12, 5)) plt.subplot(1, 2, 1) sns.distplot(y, label='target') plt.title('target') plt.subplot(1, 2, 2) sns.distplot(data.GrLivArea, label='area') plt.title('area') plt.show()
Видим, что распределения несимметричные с тяжёлыми правыми хвостами.
Оставим только числовые признаки, пропуски заменим средним значением.
X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.3, random_state=10) numeric_data = X_train.select_dtypes([np.number]) numeric_data_mean = numeric_data.mean() numeric_features = numeric_data.columns X_train = X_train.fillna(numeric_data_mean)[numeric_features] X_test = X_test.fillna(numeric_data_mean)[numeric_features]
Если разбирать линейную регрессия с
вероятностной точки зрения, то можно получить, что шум должен быть
распределён нормально. Поэтому лучше, когда целевая переменная
распределена также нормально.
Если прологарифмировать целевую переменную, то её распределение станет
больше похоже на нормальное:
sns.distplot(np.log(y+1), label='target') plt.show()
Сравним качество линейной регрессии в двух случаях:
- Целевая переменная без изменений.
- Целевая переменная прологарифмирована.
Предупреждение
Не забудем во втором случае взять экспоненту от предсказаний!
model = Ridge() model.fit(X_train, y_train) y_pred = model.predict(X_test) print("Test RMSE = %.4f" % mean_squared_error(y_test, y_pred) ** 0.5)
model = Ridge() model.fit(X_train, np.log(y_train+1)) y_pred = np.exp(model.predict(X_test))-1 print("Test RMSE = %.4f" % mean_squared_error(y_test, y_pred) ** 0.5)
Попробуем аналогично логарифмировать один из признаков, имеющих также
смещённое распределение (этот признак был вторым по важности!)
X_train.GrLivArea = np.log(X_train.GrLivArea + 1) X_test.GrLivArea = np.log(X_test.GrLivArea + 1)
model = Ridge() model.fit(X_train[numeric_features], y_train) y_pred = model.predict(X_test[numeric_features]) print("Test RMSE = %.4f" % mean_squared_error(y_test, y_pred) ** 0.5)
model = Ridge() model.fit(X_train[numeric_features], np.log(y_train+1)) y_pred = np.exp(model.predict(X_test[numeric_features]))-1 print("Test RMSE = %.4f" % mean_squared_error(y_test, y_pred) ** 0.5)
Как видим, преобразование признаков влияет слабее. Признаков много, а
вклад размывается по всем. К тому же, проверять распределение
множества признаков технически сложнее, чем одной целевой переменной.
Бинаризация
Мы уже смотрели, как полиномиальные признаки могут помочь при
восстановлении нелинейной зависимости линейной моделью. Альтернативный
подход заключается в бинаризации признаков. Мы разбиваем ось значений
одного из признаков на куски (бины) и добавляем для каждого куска-бина
новый признак-индикатор попадения в этот бин.
from sklearn.linear_model import LinearRegression np.random.seed(36) X = np.random.uniform(0, 1, size=100) y = np.cos(1.5 * np.pi * X) + np.random.normal(scale=0.1, size=X.shape)
X = X.reshape((-1, 1)) thresholds = np.arange(0.2, 1.1, 0.2).reshape((1, -1)) X_expand = np.hstack(( X, ((X > thresholds[:, :-1]) & (X <= thresholds[:, 1:])).astype(int)))
from sklearn.model_selection import KFold from sklearn.model_selection import cross_val_score
-np.mean(cross_val_score( LinearRegression(), X, y, cv=KFold(n_splits=3, random_state=123), scoring='neg_mean_squared_error'))
-np.mean(cross_val_score( LinearRegression(), X_expand, y, cv=KFold(n_splits=3, random_state=123), scoring='neg_mean_squared_error'))
Так линейная модель может лучше восстанавливать нелинейные зависимости.
Транзакционные данные
Напоследок посмотрим, как можно извлекать признаки из транзакционных данных.
Транзакционные данные характеризуются тем, что есть много строк,
характеризующихся моментов времени и некоторым числом (суммой денег,
например). При этом если это банк, то каждому человеку принадлежит не
одна транзакция, а чаще всего надо предсказывать некоторые сущности
для клиентов. Таким образом, надо получить признаки для пользователей
из множества их транзакций. Этим мы и займёмся.
Для примера возьмём данные отсюда. Задача
детектирования фродовых клиентов.
customers = pd.read_csv('Retail_Data_Response.csv') transactions = pd.read_csv('Retail_Data_Transactions.csv')
transactions.trans_date = transactions.trans_date.apply( lambda x: datetime.datetime.strptime(x, '%d-%b-%y'))
Посмотрим на распределение целевой переменной:
customers.response.mean()
Получаем примерно 1 к 9 положительных примеров. Если такие данные
разбивать на части для кросс валидации, то может получиться так, что в
одну из частей попадёт слишком мало положительных примеров, а в другую
— наоборот. На случай такого неравномерного баланса классов есть
StratifiedKFold, который бьёт данные так, чтобы баланс классов во всех
частях был одинаковым.
from sklearn.model_selection import StratifiedKFold
Когда строк на каждый объект много, можно считать различные
статистики. Например, средние, минимальные и максимальные суммы,
потраченные клиентом, количество транзакий, …
agg_transactions = transactions.groupby('customer_id').tran_amount.agg( ['mean', 'std', 'count', 'min', 'max']).reset_index() data = pd.merge(customers, agg_transactions, how='left', on='customer_id') data.head()
from sklearn.linear_model import LogisticRegression np.mean(cross_val_score( LogisticRegression(), X=data.drop(['customer_id', 'response'], axis=1), y=data.response, cv=StratifiedKFold(n_splits=3, random_state=123), scoring='roc_auc'))
Но каждая транзакция снабжена датой! Можно посчитать статистики только
по свежим транзакциям. Добавим их.
transactions.trans_date.min(), transactions.trans_date.max()
agg_transactions = transactions.loc[transactions.trans_date.apply( lambda x: x.year == 2014)].groupby('customer_id').tran_amount.agg( ['mean', 'std', 'count', 'min', 'max']).reset_index()
data = pd.merge(data, agg_transactions, how='left', on='customer_id', suffixes=('', '_2014')) data = data.fillna(0)
np.mean(cross_val_score( LogisticRegression(), X=data.drop(['customer_id', 'response'], axis=1), y=data.response, cv=StratifiedKFold(n_splits=3, random_state=123), scoring='roc_auc'))
Можно также считать дату первой и последней транзакциями
пользователей, среднее время между транзакциями и прочее.
From Wikipedia, the free encyclopedia
The bag-of-words model is a simplifying representation used in natural language processing and information retrieval (IR). In this model, a text (such as a sentence or a document) is represented as the bag (multiset) of its words, disregarding grammar and even word order but keeping multiplicity. The bag-of-words model has also been used for computer vision.[1]
The bag-of-words model is commonly used in methods of document classification where the (frequency of) occurrence of each word is used as a feature for training a classifier.[2]
An early reference to «bag of words» in a linguistic context can be found in Zellig Harris’s 1954 article on Distributional Structure.[3]
The Bag-of-words model is one example of a Vector space model.
Example implementation[edit]
The following models a text document using bag-of-words. Here are two simple text documents:
(1) John likes to watch movies. Mary likes movies too.
(2) Mary also likes to watch football games.
Based on these two text documents, a list is constructed as follows for each document:
"John","likes","to","watch","movies","Mary","likes","movies","too" "Mary","also","likes","to","watch","football","games"
Representing each bag-of-words as a JSON object, and attributing to the respective JavaScript variable:
BoW1 = {"John":1,"likes":2,"to":1,"watch":1,"movies":2,"Mary":1,"too":1}; BoW2 = {"Mary":1,"also":1,"likes":1,"to":1,"watch":1,"football":1,"games":1};
Each key is the word, and each value is the number of occurrences of that word in the given text document.
The order of elements is free, so, for example {"too":1,"Mary":1,"movies":2,"John":1,"watch":1,"likes":2,"to":1} is also equivalent to BoW1. It is also what we expect from a strict JSON object representation.
Note: if another document is like a union of these two,
(3) John likes to watch movies. Mary likes movies too. Mary also likes to watch football games.
its JavaScript representation will be:
BoW3 = {"John":1,"likes":3,"to":2,"watch":2,"movies":2,"Mary":2,"too":1,"also":1,"football":1,"games":1};
So, as we see in the bag algebra, the «union» of two documents in the bags-of-words representation is, formally, the disjoint union, summing the multiplicities of each element.

Application[edit]
In practice, the Bag-of-words model is mainly used as a tool of feature generation. After transforming the text into a «bag of words», we can calculate various measures to characterize the text. The most common type of characteristics, or features calculated from the Bag-of-words model is term frequency, namely, the number of times a term appears in the text. For the example above, we can construct the following two lists to record the term frequencies of all the distinct words (BoW1 and BoW2 ordered as in BoW3):
(1) [1, 2, 1, 1, 2, 1, 1, 0, 0, 0] (2) [0, 1, 1, 1, 0, 1, 0, 1, 1, 1]
Each entry of the lists refers to the count of the corresponding entry in the list (this is also the histogram representation). For example, in the first list (which represents document 1), the first two entries are «1,2»:
- The first entry corresponds to the word «John» which is the first word in the list, and its value is «1» because «John» appears in the first document once.
- The second entry corresponds to the word «likes», which is the second word in the list, and its value is «2» because «likes» appears in the first document twice.
This list (or vector) representation does not preserve the order of the words in the original sentences. This is just the main feature of the Bag-of-words model. This kind of representation has several successful applications, such as email filtering.[1]
However, term frequencies are not necessarily the best representation for the text. Common words like «the», «a», «to» are almost always the terms with highest frequency in the text. Thus, having a high raw count does not necessarily mean that the corresponding word is more important. To address this problem, one of the most popular ways to «normalize» the term frequencies is to weight a term by the inverse of document frequency, or tf–idf. Additionally, for the specific purpose of classification, supervised alternatives have been developed to account for the class label of a document.[4] Lastly, binary (presence/absence or 1/0) weighting is used in place of frequencies for some problems (e.g., this option is implemented in the WEKA machine learning software system).
n-gram model[edit]
The Bag-of-words model is an orderless document representation — only the counts of words matter. For instance, in the above example «John likes to watch movies. Mary likes movies too», the bag-of-words representation will not reveal that the verb «likes» always follows a person’s name in this text. As an alternative, the n-gram model can store this spatial information. Applying to the same example above, a bigram model will parse the text into the following units and store the term frequency of each unit as before.
[ "John likes", "likes to", "to watch", "watch movies", "Mary likes", "likes movies", "movies too", ]
Conceptually, we can view bag-of-word model as a special case of the n-gram model, with n=1. For n>1 the model is named w-shingling (where w is equivalent to n denoting the number of grouped words). See language model for a more detailed discussion.
Python implementation[edit]
# Make sure to install the necessary packages first # pip install --upgrade pip # pip install tensorflow from tensorflow import keras from typing import List from keras.preprocessing.text import Tokenizer sentence = ["John likes to watch movies. Mary likes movies too."] def print_bow(sentence: List[str]) -> None: tokenizer = Tokenizer() tokenizer.fit_on_texts(sentence) sequences = tokenizer.texts_to_sequences(sentence) word_index = tokenizer.word_index bow = {} for key in word_index: bow[key] = sequences[0].count(word_index[key]) print(f"Bag of word sentence 1:n{bow}") print(f"We found {len(word_index)} unique tokens.") print_bow(sentence)
Hashing trick[edit]
A common alternative to using dictionaries is the hashing trick, where words are mapped directly to indices with a hashing function.[5] Thus, no memory is required to store a dictionary. Hash collisions are typically dealt via freed-up memory to increase the number of hash buckets. In practice, hashing simplifies the implementation of bag-of-words models and improves scalability.
Example usage: spam filtering[edit]
In Bayesian spam filtering, an e-mail message is modeled as an unordered collection of words selected from one of two probability distributions: one representing spam and one representing legitimate e-mail («ham»).
Imagine there are two literal bags full of words. One bag is filled with words found in spam messages, and the other with words found in legitimate e-mail. While any given word is likely to be somewhere in both bags, the «spam» bag will contain spam-related words such as «stock», «Viagra», and «buy» significantly more frequently, while the «ham» bag will contain more words related to the user’s friends or workplace.
To classify an e-mail message, the Bayesian spam filter assumes that the message is a pile of words that has been poured out randomly from one of the two bags, and uses Bayesian probability to determine which bag it is more likely to be in.
See also[edit]
- Additive smoothing
- Bag-of-words model in computer vision
- Document classification
- Document-term matrix
- Feature extraction
- Hashing trick
- Machine learning
- MinHash
- n-gram
- Natural language processing
- Vector space model
- w-shingling
- tf-idf
Notes[edit]
- ^ a b Sivic, Josef (April 2009). «Efficient visual search of videos cast as text retrieval» (PDF). IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 31, NO. 4. opposition. pp. 591–605.
- ^ McTear et al 2016, p. 167.
- ^ Harris, Zellig (1954). «Distributional Structure». Word. 10 (2/3): 146–62. doi:10.1080/00437956.1954.11659520.
And this stock of combinations of elements becomes a factor in the way later choices are made … for language is not merely a bag of words but a tool with particular properties which have been fashioned in the course of its use
- ^ Youngjoong Ko (2012). «A study of term weighting schemes using class information for text classification». SIGIR’12. ACM.
- ^ Weinberger, K. Q.; Dasgupta A.; Langford J.; Smola A.; Attenberg, J. (2009). «Feature hashing for large scale multitask learning». Proceedings of the 26th Annual International Conference on Machine Learning: 1113–1120. arXiv:0902.2206. Bibcode:2009arXiv0902.2206W.
References[edit]
- McTear, Michael (et al) (2016). The Conversational Interface. Springer International Publishing.
Обработка естественного языка или NLP (Natural Language Processing) занимается применением алгоритмов Machine Learning для текстовых данных. Как правило, модели машинного обучения работают с числами. В этой статье поговорим о 4-х наиболее применяемых методах для перевода текстов в числовые тензоры.
Сначала текст разбивается на текстовые единицы (токены), например, символы, слова, словосочетания, предложения, абзацы и т.д. Чаще всего разбивают на слова. Токены образуют словарь, который может быть отсортирован по алфавиту.
Также в NLP применяются термины «документ» и «корпус». Документ – это совокупность токенов, которые принадлежат одной смысловой единице. В качестве документа может выступать предложение, комментарий или пост пользователя. Корпус – это генеральная совокупность всех документов.
Рассмотрим пример. Допустим имеется два предложения: “Пес сел на пень”, “Кот сел на ель”. Выберем в качестве токенов слова, тогда получится следующий словарь:
{Пес, Кот, ель, на, сел, пень} # Словарь
и два документа, которые составляют корпус:
[Пес, сел, на, пень] # Первый документ [Кот, сел, на, ель] # Второй документ [[Пес, сел, на, пень], [Кот, сел, на, ель]] # Корпус
В последующих методах кодирования слов мы также будем использовать два этих предложения в качестве примера.
1. Прямое кодирование
Прямое кодирование (one-hot encoding) считается самым простым способом преобразования токенов в тензоры и выполняется следующим образом:
- каждый токен представляет бинарный вектор (значения 0 или 1);
- единица ставится тому элементу, который соответствует номеру токена в словаре.
С нашими предложениями это выглядит так:
{Пес, Кот, ель, на, сел, пень} # Словарь
# Первый документ
[[1, 0, 0, 0, 0, 0] # Пес
[0, 0, 0, 0, 0, 0] # Кот (нет в предложении)
[0, 0, 0, 0, 0, 0] # ель (нет в предложении)
[0, 0, 0, 1, 0, 0] # на
[0, 0, 0, 0, 1, 0] # сел
[0, 0, 0, 0, 0, 1]] # пень
# Второй документ
[[0, 0, 0, 0, 0, 0] # Пес (нет в предложении)
[0, 1, 0, 0, 0, 0] # Кот
[0, 0, 1, 0, 0, 0] # ель
[0, 0, 0, 1, 0, 0] # на
[0, 0, 0, 0, 1, 0] # сел
[0, 0, 0, 0, 0, 0]] # пень (нет в предложении)
Проблемой прямого кодирования является размерность. Каждое предложение состоит всего из 4 слов, но в итоге получилась большая матрица для каждого документа. Количество строк регулируется словарем, поэтому чем больше слов в словаре, тем больше будет матрица.
2. Bag of words
В отличие от прямого кодирования, мешок слов (Bag of words) выделяет вектору весь документ, и каждый элемент кодируется 1 по порядку следования слов в словаре:
{Пес, Кот, ель, на, сел, пень} # Словарь
# Корпус:
[[1, 0, 0, 1, 1, 1] # Первый документ
[0, 1, 1, 1, 1, 0]] # Второй документ
Bag of words решает проблему размерности по одной оси. Количество строк определяется количеством документов. Однако, этот метод не учитывает важность того или иного токена, ведь одно слово может повторятся по несколько раз. В этом случае пригодится альтернативный способ, рассмотренный далее.
3. TF-IDF
TF-IDF состоит из двух компонентов: Term Frequency (частотность слова в документе) и Inverse Document Frequency (инверсия частоты документа). Они считаются следующим образом:
где — сколько раз встречается токен в
-ом документе,
— общее количество токенов в
-ом документе,
— количество документов, в которых встречается токен,
— общее количеств документов.
В конечном счете, TF-IDF – это произведение TF на IDF:
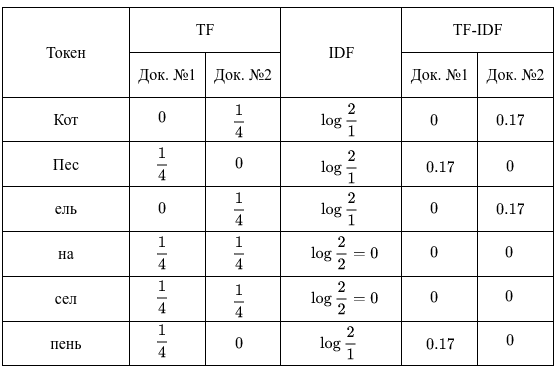
Стоит отметить, что TF считается для токенов документа, тогда как IDF – токенов всего корпуса. Итак, у нас имеется 2 документа, в каждом из которых оказалось по 4 слова. В этом случае вычисления будут следующими:
В результате получили для 1-го документа такие важные слова, как “Пес” и “пень”, для 2-го — “Кот” и “ель”. В TF-IDF редкие слова и слова, которые встречаются во всех документах, несут мало информации. Кроме того, IDF можно считать и другими способами, например, в Python-библиотеке Scikit-learn этот параметр гибко регулируется.
4. Word Embeddings
Все вышерассмотренные NLP-методы отличаются следующими недостатками:
- не зависят от контекста – например, оба анализируемых предложения отражают примерно одно и то же: “что-то куда-то село”;
- не учитывают порядок слов в предложении;
- обладают высокой размерностью в случае большого словаря, что может снизить производительность модели глубокого обучения (Deep Learning).
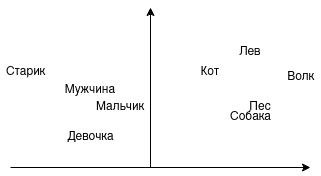
На практике все чаще используется word embeddings – векторное представление слов. Векторы можно складывать, вычитать, сравнивать. Например, можно ли сложить слова “Король” и “Женщина”? Можно предположить, что будет “Королева”. А можно ли сравнить близость слов “мужчина”, “мальчик”, “девочка”? Напрашивается, что “мужчина” и “мальчик” стоят ближе друг к другу. На изображении показано, как это выглядит графически:
В этом примере на одной стороне животные, на другой люди. Со стороны животных возможен переход от домашних к диким или от псовых к кошачьим. Со стороны людей возможен переход по полу и возрасту. Именно так и работают word embeddings, представляя слова (токены) в векторы.
Самой распространенной реализацией векторного представления слов является Word2vec. Архитектура Word2vec подразделяется на два вида — Skip-gram и Continuous Bag of Words (CBOW).
Skip-gram получает на вход одно слово и предсказывает подходящий контекст. Например, предсказываем контекст к слову “Пес”, он может выглядеть так:
[сел] [сел на] [пень] [сел на пень] ...
В свою очередь, CBOW пытается угадать слово, исходя из контекста. Например, следующее слово в предложении “Кот сел на […]” может быть следующим:
[ель] [стул] [пень] ...
Контекст для word embeddings является очень важным. Юридические документы отличаются от комментариев в социальных сетях, поэтому и результат может быть разным.
В следующей статье поговорим об первичной обработке текстов. А получить практические навыки работы с текстами в NLP на реальных задачах Data Science вы сможете на наших курсах по Python в лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов в Москве.
Анализ текстовой информации — весьма полезный инструмент. Я ранее публиковал уже статьи на тему анализа текстов. Например, анализ авторства текста, генеративные сети с условием (в этих GAN-ах использовался слой embedding), чатботы и пр. Пора систематизировать способы представления текстов в числовой форме и попробовать понять что «под капотом», т.е. как это все работает.
One-hot encoding (OHE)
Самый простой подход :
- Выделить в исходном тексте split-ом все слова.
- Создать из них словарь.
- Закодировать слова с помощью 0 и 1 («one-hot»). Это не двоичное представление индекса слова в словаре, поскольку единица в векторе только одна, остальные — 0!
Например, есть текст «The cat sat on the mat». Чтобы представить каждое слово для обучения нейронной сети, создадим вектор из нулей с длиной равной размеру словаря. Единица будет на позиции соответствующей слову.

Чтобы создать вектор, который кодировал бы всю фразу достаточно объединить (concatenate) one-hot вектор каждого из слов. Очевидно, что при этом полностью теряется информация о последовательности слов в тексте. Остается только информация о наборе слов («bag of words»).
Подход крайне неэффективен. Слово закодированное с помощью one-hot кодирования — это гигантский (длина равна количеству слов в тексте) разреженный (sparse — большая часть 0 и в одной позиции 1-ца) вектор. Под него уходит очень много памяти.
Кодирование словаря уникальными индексами
Другой распространенный подход — кодировать каждое слово некоторым уникальным числом. В примере выше можно было-бы слову «cat» сопоставить с 1, 2-ку присвоить для «mat» и т.д.
В этом случае можно было-бы закодировать фразу «The cat sat on the mat» плотным (dense) вектором, скажем, [5, 1, 4, 3, 5, 2]. Этот подход эффективен с т.з. использования памяти.
Однако, этот подход имеет несколько минусов:
- Кодирование целыми числами не учитывает взаимосвязи между словами. Впрочем, one-hot encoding его тоже не учитывает.
- Нейронная сеть плохо воспринимает целочисленное кодирование. Для нейронки число сложно интерпретировать, они для неё все как-бы одинаковые. Собственно, поэтому при классификации, например, картинок в тестовой базе MNIST при обучении номер на картинке кодируется в OHE. Например, методами tokenizer-а Keras: to_categorical.
Чтобы нейронная сеть корректно воспринимала выходные значения представленные в числовом виде без предварительного кодирования в OHE используется специальная функция loss: sparse_categorical_crossentropy. Она работает только для выходных значений и вычисляет cross-entropy между реальными и предсказанными сетью значениями.
Bag Of Words
Кодирование входных данных в OHE приводит к серьезной проблемой с нехваткой памяти при обработке данных. Например, рассмотрим для примера задачу эмоционального анализа текстов (sentiment snalysis). Например, есть отзывы клиентов на продукт. Они могут быть положительные, отрицательные и нейтральные.
Типовой механизм преобразования текстов для обработки нейронной сетью будет следующим:
- Текст разбивается (split) на слова с параллельной очисткой от лишних символов. Например, используется токенизатор Keras:
tokenizer = Tokenizer(num_words=num_words, filters='!"#$%&()*+,-—./:;<=>?@[\]^_`{|}~tnxa0????????????☝️?✌️?????♂️♂️?????♂️‼️♥❤️?????????????????????', lower=True, split=' ', char_level=False) #, oov_token='unknown'
- Словам в соответствие ставятся индексы (числовые значения):
tokenizer.texts_to_matrix(texts, mode='count')
- По умолчанию в токенизаторе параметр reserve_zero=True, поэтому первым элементом в матрице индексов будет стоять 0, зарезервированный в качестве значения для максирования (masking). Следующий слой нейронной сети должен понимать, что 0 — это не реальные данные, а искусственно дополненные. Полученная матрица индексов будет длиннее по горизонтали на 1.
- Предложения выравниваются по длине с помощью Keras pad_sequences, добавлением 0-ей в начале или конце массива (padding=’post’). Кроме того фраза может быть урезана по длине с начала или с конца (truncating=’post’).
x_train = pad_sequences(x_train_tokenized, maxlen=max_len) #, padding='post', truncating='post')
- Полученная матрица индексов, выровненная по длине преобразуется в OHE. На выходе получится гигантская разреженная матрица (sparse) заполненная 0-ми и лишь одной 1-ей, стоящей в позиции равной индексу слова. Это удобно, поскольку если взять argmax от такого вектора, то он вернет позицию в которой стоит 1, т.е. индекс слова.
- Каждому слову будет поставлен в соответствие вектор равный длине используемого словаря. Например, в обработанном тексте содержалось 20000 слов (словарь), соответственно, каждое слово будет представлено вектором длиной 20000.
Размерность полученной OHE матрицы:
- Максимальная длина фразы в отзывах — 500 слов. После pad_sequences все фразы в матрице будут длиной 500.
- Размер словаря — 20000 слов, те. каждое слово будет представлено вектором длиной 20000.
- Отзывов — 10000 шт.
OHE_shape = 500 * 20000 x 10000 = 10 000 000 x 10000.
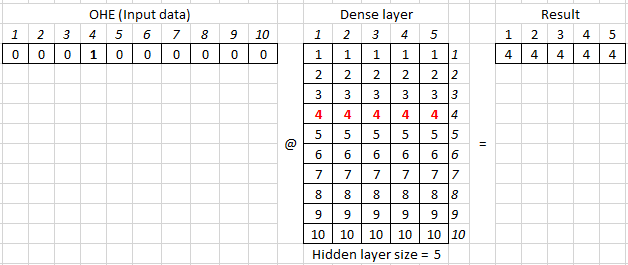
Визуализация такого способа подачи текстового представления на нейронную сеть:
Исходная матрица подается на Dense слой и веса этого слоя в процессе обучения принимают значения, которые некоторым образом описывают фразу в слове.
Сравнительно небольшой текст преобразовался в гигантскую матрицу, где каждая фраза представлена вектором из 0 и одной 1. Длина вектора 10 млн. и количество таких векторов 10 000. Под такую матрицу расходовалось бы гигантское количество памяти. На практике для подачи текста на нейронную сеть используют подход Bag of Words [BOW].
При Bag Of Words последовательность слов в фразе убирается, поэтому фраза (на картинке Document1, Document2) представляется в виде вектора. Его длина равной размеру общего словаря всех анализируюмых текстов. В полученном векторе на позициях, соответствующих словам присутствующим в тексте стоят 1, а если слово в тексте не встретилось — 0.
В результате размерность матрицы, которая подается на нейронную сеть равна размер словаря х количество фраз (документов) или для нашего примера с отзывами 20000 х 10000.
Embedding
Ранее при обработке текстов, например, при рассмотрении рекуррентных сетей использовалась следующая преобраотка входной последовательности:
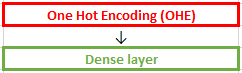
Рассмотрим как это выглядит в коде. Поскольку Dense слой — это матрица весов, сгенерируем такую рандомную матрицу:
hidden_size = 5 num_words = 10 dense_weights = np.random.normal(0, 1, (10, hidden_size))
array([[-1.32707206, 0.10119344, 1.79757198, 0.34618246, -1.54246334],
[-1.71555483, -0.41435209, 1.55291255, 0.45605782, -0.38036262],
[ 0.1468921 , -1.70855181, -0.11037113, -0.0230945 , 0.08609408],
[-2.00268987, 0.83066333, -0.11383054, -0.52439005, 1.92159762],
[ 0.83877495, -1.13184209, 0.60702018, -0.13582864, -0.4720022 ],
[-1.68540624, 0.4514039 , 0.141728 , -0.56166716, -0.08567821],
[-1.12092014, -0.89378575, -1.01579628, 0.28156886, 0.4657587 ],
[-0.97334435, -0.00635427, -0.06353585, -0.44005828, -1.48547527],
[-2.10256962, 0.80774305, -1.50179081, 0.63876112, 0.53071349],
[ 0.7122738 , 0.1074994 , 0.57170802, -0.47366115, -2.34293163]])
На входе dense слоя (матрицы весов) подаются входные данные представленные в виде OHE. Например, для кодирования 10 слов используется следующая матрица OHE — по-сути, единичная квадратная матрица. У неё по диагонали стоят единицы:
I = np.eye(num_words)
array([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 1., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 1., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 1., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]])
Для обратного преобразования из матрицы OHE в порядковый номер слова в словаре (индекс) используется код:
np.argmax(I, axis = 1) array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
Соответственно, чтобы получить OHE соответствующий произвольному индексу, нужно взять из матрицы строку или столбец по нему:
def custom_OHE(index, num_classes): return np.eye(num_classes)[index]
token = 5 #Индекс нужного слова OHE_vector = custom_OHE(token, num_words) OHE_vector @ dense_weights array([-1.68540624, 0.4514039 , 0.141728 , -0.56166716, -0.08567821])
где @ — матричное умножение, аналог numpy.dot.
В параметрах dense слоя задается только размерность hidden size (в примере = 5). Вторую размерность (в данном случае = 10) dense слой берет из предыдущего слоя, выступающего для него в качестве входа.
Поскольку перемножение OHE на матрицу весов описывающих dense слой эквивалентно взятию из матрицы весов строки соответствующей индексу, то операция получения вектора (embedding) описыващего слово с выбранным индексом упрощается:
embedding = dense_weights token = 5 #Индекс нужного слова embedding [token] array([-1.68540624, 0.4514039 , 0.141728 , -0.56166716, -0.08567821])
По-сути, получаем словарь где слову с определенным индексом поставлен в соотвествие вектор с размерностью заданной для embedding-а.
model = Sequential() model.add(Embedding(num_words, embedding_size, input_length=max_len))
где
- num_words — количество слов в словаре,
- embedding_size — размерность embedding-а равна размеру скрытого слоя (hidden_size) dense слоя внутри embedding.
- max_len — размер входных данных. Например, тот-же max_len используется при выравнивании длины фраз x_train = pad_sequences(x_train_tokenized, maxlen=max_len).
Представление слов в виде embedding-ов — способ эффективно с точки зрения использования памяти представить слово в виде понятном для нейронной сети. При этом одинаковые слова имеют одинаковый вектор их представляющий.
Размер вектора задается исследователем и чаще всего варьируется от 8-ми мерного для небольших датасетов (текстов) до 1024 в случае больших текстовых баз. Embedding-и с высокой размерностью позволяют вычленять тонкие нюансы во взаимосвязях между словами, но требуют очень больших баз для обучения.
Физический смысл embedding
Помимо значительно большей эффективности использования оперативной памяти embedding-и обладают ещё одним полезным свойством.
Поскольку каждое слово из словаря раскладывается в виде многомерного вектора размерностью embedding_size, то можно предположить, что величина по каждой из осей что-то означает.
Важный момент, в embedding слову может соотвествовать только один вектор. Т.е. не смысловое значение для слова может быть только одно.
Например, был взят embedding_size = 2 и после тренировки embedding получен словарь двумерных векторов соответствующих слову. Их разместили на графике, отложив по оси X — одну координату вектора, а по Y — другую. После анализа слов получили, например, что ось X определяет определяет степень новизны слова, а по Y — насколько слово эмоционально положительное.
Для вектора работают математические операции сложения и вычитания. Кроме того можно вычислить угол между векторами для определения насколько они сонаправлены или ортогональны.
Но, что важно, вектора в многомерном пространстве можно сравнивать, используя косинусную меру.
Если угол между двумя векторами равен 0, то они сонаправлены и значение cos(0) будет равно 1, если ортогональны, то cos(pi/2) = 0, а если противоположно направлены, то cos(pi) = -1.
Косинусную меру можно использовать и как метрику и как loss. Как метрика она используется в исходном виде, как задан по формуле, поскольку метрика должна максимизироваться, т.е. стремится к 1.
В случае с loss его минимизируют, поэтому косинусную меру нужно вычесть из 1. В этом случае при максимальном сходстве векторов значение будет стремится к 0, когда вектора ортогональны, то к 1, а когда противоположно направлены = 2.
Если косинусная мера показывает меру смыслового сходства, то длина вектора дает степень окраски. Например, красивый, прекрасный, прекраснейший и пр. эпитеты ранжируются по степени.
Поскольку embedding может быть предобучен на больших корпусах (объемах) текстов с использованием специальных моделей, а затем выгружен в виде словаря, где слову ставится в соответствие вектор, то появляется возможность получать качественные предобученные embedding-и без необходимости их повторного обучения (веса слоя можно заморозить trainable = False).
from keras.layers import Embedding
embedding_layer = Embedding(len(word_index) + 1,
EMBEDDING_DIM,
weights=[embedding_matrix],
input_length=MAX_SEQUENCE_LENGTH,
trainable=False)
Тренировка embedding в зависимости от его размера занимает немало времени, поэтому такая оптимизация крайне полезна.
Word2Vec
Теперь проверим насколько теория о том, что полученные нейронкой вектора embedding-а действительно отражают что-то. Для этого воспользуемся моделью word2vec. При тренировке модели использовалось два подхода. Первый использовал метод continuous bag of words (CBOW), который по контексту пытается предсказать слово. Второй — использовать слово для предсказания контекста — skip-gram.
Word2Vec — это не предобученные эмбеддинги (файл с векторами), а подход к их формированию. Этот подход реализован, например, в библиотеке Gensim. Используя этот подход и большие корпуса текстов разного типа (например, новости) были созданы готовые файлы embedding-ов. Если посмотреть такой файл, то вначале идет слово, а затем набор чисел описывающих его векторное представление. Размерность embedding чаще всего от 100 до 1024.
Выше была дана формула косинусного расстояния. В Python она выглядит следующим образом:
def cos_distance(a , b): #метрика косинусного расстояния return a@b/((a@a)*(b@b))**0.5
Подгрузим embedding-и. Файл порядка 1,6 Гб, там только английские слова. При желании легко найти предобученные embedding-и для русского языка. В наименовании embedding указано 300 — это размерность векторов в embedding.
import gensim.downloader as api
wv = api.load('word2vec-google-news-300') #загружаем w2v
Широко известный культовый пример для модели Word2Vec.
Посмотрим косинусное расстояние между
cos_distance(wv['king']-wv['man'], wv['queen']-wv['woman']) 0.7580350416366332
Действительно получаем высокое значение косинусного расстояния. Найдем меру сходства между walking и walked:
cos_distance(wv['walking'], wv['walked']) 0.6706871263449815
или то-же самое вычислим с помощью встроенной функции Word2Vec:
wv.similarity('walking', 'walked')
0.6706871
В процессе обучения добавились того, чтобы если прибавление некоторого вектора к embedding слова «walking» приводил к появлению embedding слова «walked», то прибавление того-же вектора к слову swimming -> swam. Это называется «параллельный перенос«.
Найдем слово, которое выбивается из ряда слов:
print(wv.doesnt_match(['fire', 'water', 'land', 'man', 'sea', 'air'])) man
Или найдем слова, наиболее близкие по смыслу с точки зрения нейронной сети:
wv.similar_by_vector(wv['king'])
[('king', 0.9999999403953552),
('kings', 0.7138046026229858),
('queen', 0.6510956883430481),
('monarch', 0.6413194537162781),
('crown_prince', 0.6204219460487366),
('prince', 0.6159993410110474),
('sultan', 0.5864822864532471),
('ruler', 0.5797566771507263),
('princes', 0.5646551847457886),
('Prince_Paras', 0.543294370174408)]
С русскими словами результат сходный:
Встраивание embedding в нейронную сеть
При работе с готовыми embedding-ами нужно их как-то подать в нейронную сеть. Используется два основных подхода. В первом исходные фразы конвертируются в массив векторов и уже этот массив подается на вход нейронной сети вместо комбинации OHE + Dense. В этом случае полученные вектора не будут тренироваться при тренировки нейронной сети. Они уже подготовлены и считается, что обучение произведено качественно, поскольку для этого использовались гигантские корпуса текстов и тренировка проводилась долго.
Сконвертируем слова в векторное представление:
sentence = 'I would like to have the flat'
x_sent = sentence.split(' ')
x_sent
['I', 'would', 'like', 'to', 'have', 'the', 'flat']
И затем:
x_emb = []
for word in x_sent:
if word in wv.vocab:
x_emb.append(wv[word])
x_emb = np.array(x_emb)
x_emb.shape
(6, 300)
Обращаю внимание на проверку if word in wv.vocab. Например, в примере частица to является стоп словом (stop-word) с минимальной для модели смысловой нагрузкой. Поэтому эта частица отсуствует в скаченном эмбеддинге.
Если запустить код без этой проверки, то он выпадет с ошибкой, что слово не найдено. Поэтому при трансформации я это слово пропускаю и поэтому в shape-е только 6, а не 7 векторов размерностью 300.
Второй подход — это встроить embedding в качестве слоя в архитектуру нейронной сети Keras. Для этого используется метод:
x = wv.get_keras_embedding(train_embeddings=True) #можно сразу получить embedding keras
Чтобы преобразовать слово в индекс в скаченном embedding используется следующий метод:
word_index = wv.vocab['king'].index #Преобразование слова -> индекс
print("Индекс:", word_index)
word = wv.index2word[word_index] #Обратное преобразование индекс -> слово
print("Слово:", word)
Индекс: 6147
Слово: king
Встраивание предоубченного embedding в нейронную сетью (Keras)
Есть два способа подать анализируемый текст на нейронку, используя предобученный embedding. В первом подходе входные данные адаптируются под слой embedding-а, а во втором — слой embedding-а подстраивается под входные индексы.
Первый способ состоит в конвертации входного текста с помощью словаря embedding-а и подаче подготовленного текста на слой с весами embedding в модели:
- Предложения в тексте разбить на последовательность слов c помощью Keras text_to_word_sequence. Словарь частотности не формируется. Если нужно ограничить словарь, то придется использовать Tokenizer.
- Преобразовать слова в индексы с помощью словаря предобученного embedding-а.
- Получить слой embedding-а с помощью get_keras_embedding().
- Встроить его первым слоем в модель. С весами слоя ничего не делаем!
- Подать на вход модели массив индексов полученных в п. 2.
Второй способ состоит в том, чтобы для индексов полученных токенизатором, например, Keras-а, поменять веса в матрице embedding-а, чтобы индекс определенного слова в embedding-е соответствовал индексу слова после токенизатора:
- Получить массив индексов с помощью Tokenizer. В этом случае словарь упорядочен по частоте появления слов в тексте, поэтому можно обрезать словарь с конца если нужно получить укороченный вариант.
- Получить предобученный embedding (обучить самому или скачать готовый).
- Адаптировать матрицу весов слоя embedding таким образом, чтобы индексу определенного слова после Tokenizer-а в слое embedding соответствовало то-же слово из словаря embedding-а.
Первый способ подготовки данных я рассмотрю в этой статье, а второй — в следующей.
Слой полученный get_keras_embedding() принимает на вход индексы из скаченного embedding-а. Для преобразования текст в последовательность индексов на которых тренировался скаченный embedding:
padding_index = 0 #Just for example
x_sent_arr = []
x_sent_arr.append('I would like to have the flat'.split(' '))
x_sent_arr.append('I would like to eat the apple'.split(' '))
x_train = []
for index, line in enumerate(x_sent_arr):
print(index, ':', line)
sentence = []
for word in line:
if word in wv.vocab:
sentence.append(wv.vocab[word].index)
else:
sentence.append(padding_index) # Do something. For example, leave it blank or replace with padding character's index.
x_train.append(sentence)
print(x_train)
0 : ['I', 'would', 'like', 'to', 'have', 'the', 'flat'] 1 : ['I', 'would', 'like', 'to', 'eat', 'the', 'apple'] [[20, 47, 87, 0, 21, 11, 2532], [20, 47, 87, 0, 2785, 11, 13467]]
В некоторых случаях нужно подгрузить текст убрав лишние символы и пр. Если делать это Keras токенизатором, то для передачи индексов на embedding слой word2vec нужно слегка извратится, поскольку я не нашел нормального метода у Tokenizator для получения списка слов.
tokenizer = Tokenizer(filters='!–"—#$%&()*+,-./:;<=>?@[\]^_`{|}~tnr«»', lower=True, split=' ', char_level=False)
tokenizer.fit_on_texts(x_sent_arr)
seq = tokenizer.texts_to_sequences(x_sent_arr)
text = tokenizer.sequences_to_texts(seq)
text = [line.split() for line in text]
print(text)
x_train = []
padding_index = 0
for line in text:
sentence = []
for word in line:
if word in wv.vocab:
sentence.append(wv.vocab[word].index)
else:
sentence.append(padding_index) # Do something. For example, leave it blank or replace with padding character's index.
x_train.append(sentence)
print(x_train)
[['i', 'would', 'like', 'to', 'have', 'the', 'flat'], ['i', 'would', 'like', 'to', 'eat', 'the', 'apple']] [[4501, 47, 87, 0, 21, 11, 2532], [4501, 47, 87, 0, 2785, 11, 13467]]
Или без использования Tokenizer, взяв функцию text_to_word_sequence:
from keras.preprocessing.text import text_to_word_sequence
x_sent_arr = []
x_sent_arr.append('I would like to have the flat')
x_sent_arr.append('I would like to eat the apple')
text = [text_to_word_sequence(line, filters='!"#$%&()*+,-./:;<=>?@[\]^_`{|}~tn', lower=True, split=' ') for line in x_sent_arr]
print(text)
x_train = []
padding_index = 0
for line in text:
sentence = []
for word in line:
if word in wv.vocab:
sentence.append(wv.vocab[word].index)
else:
sentence.append(padding_index) # Do something. For example, leave it blank or replace with padding character's index.
x_train.append(sentence)
print(x_train)
[['i', 'would', 'like', 'to', 'have', 'the', 'flat'], ['i', 'would', 'like', 'to', 'eat', 'the', 'apple']]
[[4501, 47, 87, 0, 21, 11, 2532], [4501, 47, 87, 0, 2785, 11, 13467]]
Если объем текста большой, а памяти GPU мало, то нужно использовать вариант с генератором. В этом случае данные будут подгружаться в нейронку batch-ами:
from keras.preprocessing.text import text_to_word_sequence
x_sent_arr = []
x_sent_arr.append('I would like to have the flat')
x_sent_arr.append('I would like to eat the apple')
def texts_to_sequences(texts, word2vec):
for text in texts:
tokens = text_to_word_sequence(text)
yield [word2vec.vocab[w].index for w in tokens if w in word2vec.vocab]
sequence = texts_to_sequences(x_sent_arr, wv)
for b in sequence:
print(b)
[4501, 47, 87, 21, 11, 2532]
[4501, 47, 87, 2785, 11, 13467]
Продолжение следует.
Полезные ссылки
- TensorFlow — Word Embedding.
- Word2vec в картинках.
- Vector Semantics and Embeddings.
- RusVectōrēs: семантические модели для русского языка.
- Comparison of Top 6 Python NLP Libraries
- Using pre-trained word embeddings in a Keras model.
- GloVe: Global Vectors for Word Representation
- A Detailed Guide to understand the Word Embeddings and Embedding Layer in Keras.
- Using a Keras Embedding Layer to Handle Text Data.
- Чудесный мир Word Embeddings: какие они бывают и зачем нужны? — толковая статья.
- https://pathmind.com/wiki/word2vec
Нежное введение в модель «мешок слов»
Перевод
Ссылка на автора
Модель мешка слов — это способ представления текстовых данных при моделировании текста с помощью алгоритмов машинного обучения.
Модель «мешок слов» проста для понимания и реализации и имеет большой успех в таких проблемах, как моделирование языка и классификация документов.
В этом руководстве вы познакомитесь с моделью мешков слов для извлечения функций в обработке естественного языка.
После завершения этого урока вы узнаете:
- Что такое модель мешка слов и почему она нужна для представления текста.
- Как разработать модель пакета слов для коллекции документов.
- Как использовать разные техники для подготовки словарного запаса и оценки слов.
Давайте начнем.
Обзор учебника
Этот урок разделен на 6 частей; они есть:
- Проблема с текстом
- Что такое мешок слов?
- Пример модели мешка слов
- Управляющий словарь
- Подсчет слов
- Ограничения Мешка Слова
Проблема с текстом
Проблема с моделированием текста заключается в том, что он грязный, а методы, такие как алгоритмы машинного обучения, предпочитают четко определенные входы и выходы фиксированной длины.
Алгоритмы машинного обучения не могут работать с необработанным текстом напрямую; текст должен быть преобразован в числа. Конкретно векторы чисел.
При обработке языка векторы x извлекаются из текстовых данных, чтобы отражать различные лингвистические свойства текста.
— Страница 65, Методы нейронной сети в обработке естественного языка, 2017
Это называется извлечением или кодированием объектов.
Популярный и простой метод извлечения признаков из текстовых данных называется текстовой моделью мешка слов.
Что такое мешок слов?
Модель мешка слов, или сокращенно BoW, — это способ извлечения особенностей из текста для использования в моделировании, например, в алгоритмах машинного обучения.
Подход очень прост и гибок, и его можно использовать множеством способов для извлечения функций из документов.
Мешок слов — это представление текста, который описывает вхождение слов в документ. Это включает в себя две вещи:
- Словарь известных слов.
- Мера наличия известных слов.
Это называется «мешокСлов, потому что любая информация о порядке или структуре слов в документе отбрасывается. Модель касается только того, встречаются ли в документе известные слова, а не где в документе.
Очень распространенная процедура извлечения предложений и документов — это метод «мешка слов» (BOW). При таком подходе мы смотрим на гистограмму слов в тексте, то есть рассматриваем каждое слово как особенность.
— Страница 69, Методы нейронной сети в обработке естественного языка, 2017
Интуиция заключается в том, что документы похожи, если они имеют похожее содержание. Далее, что из одного только содержания мы можем узнать кое-что о значении документа.
Мешок слов может быть простым или сложным, как вам нравится. Сложность заключается как в определении словарного запаса известных слов (или токенов), так и в том, как оценивать наличие известных слов.
Мы подробнее рассмотрим обе эти проблемы.
Пример модели мешка слов
Давайте сделаем модель мешка слов конкретной с проработанным примером.
Шаг 1: Сбор данных
Ниже приведен фрагмент первых нескольких строк текста из книги « Повесть о двух городах Чарльза Диккенса, взято из проекта Гутенберга.
Это были лучшие времена,
это было худшее время,
это был век мудрости,
это был век глупости,
Для этого небольшого примера давайте рассмотрим каждую строку как отдельный «документ», а 4 строки — как весь наш набор документов.
Шаг 2. Составьте словарь
Теперь мы можем составить список всех слов в нашем модельном словаре.
Уникальные слова здесь (игнорируя регистр и знаки препинания):
- «Это»
- «было»
- «»
- «Лучший»
- «Из»
- «времена»
- «наихудший»
- «возраст»
- «Мудрость»
- «Глупость»
Это словарь из 10 слов из корпуса, содержащего 24 слова.
Шаг 3. Создание векторов документов
Следующим шагом является оценка слов в каждом документе.
Цель состоит в том, чтобы превратить каждый документ свободного текста в вектор, который мы можем использовать в качестве входных или выходных данных для модели машинного обучения.
Поскольку мы знаем, что в словаре 10 слов, мы можем использовать представление документа фиксированной длины, равное 10, с одной позицией в векторе для оценки каждого слова.
Самый простой метод оценки — пометить присутствие слов как логическое значение, 0 для отсутствия, 1 для настоящего.
Используя произвольный порядок слов, перечисленных выше в нашем словаре, мы можем пройти первый документ («Это были лучшие времена«) И преобразовать его в двоичный вектор
Оценка документа будет выглядеть следующим образом:
- «Это» = 1
- «Был» = 1
- «The» = 1
- «Лучший» = 1
- «Из» = 1
- «Времена» = 1
- «Худший» = 0
- «Возраст» = 0
- «Мудрость» = 0
- «Глупость» = 0
В качестве двоичного вектора это будет выглядеть следующим образом:
[1, 1, 1, 1, 1, 1, 0, 0, 0, 0]Остальные три документа будут выглядеть следующим образом:
"it was the worst of times" = [1, 1, 1, 0, 1, 1, 1, 0, 0, 0]
"it was the age of wisdom" = [1, 1, 1, 0, 1, 0, 0, 1, 1, 0]
"it was the age of foolishness" = [1, 1, 1, 0, 1, 0, 0, 1, 0, 1]Все упорядочения слов номинально отбрасываются, и у нас есть последовательный способ извлечения функций из любого документа в нашем корпусе, готового для использования в моделировании.
Новые документы, которые пересекаются со словарем известных слов, но могут содержать слова вне словаря, все еще могут быть закодированы, где только вхождение известных слов оценивается, а неизвестные слова игнорируются.
Вы можете видеть, как это может естественным образом масштабироваться до больших словарей и больших документов.
Управляющий словарь
По мере увеличения словарного запаса увеличивается и векторное представление документов.
В предыдущем примере длина вектора документа равна количеству известных слов.
Вы можете себе представить, что для очень большого корпуса, такого как тысячи книг, длина вектора может составлять тысячи или миллионы позиций. Кроме того, каждый документ может содержать очень мало известных слов в словаре.
В результате получается вектор с множеством нулевых оценок, называемый разреженным вектором или разреженным представлением.
При моделировании разреженные векторы требуют больше памяти и вычислительных ресурсов, а огромное количество позиций или измерений может сделать процесс моделирования очень сложным для традиционных алгоритмов.
Таким образом, существует необходимость уменьшить размер словарного запаса при использовании модели с набором слов.
В качестве первого шага можно использовать простые методы очистки текста, такие как:
- Игнорирование дела
- Игнорирование знаков препинания
- Игнорирование частых слов, которые не содержат много информации, называемых стоп-словами, такими как «а», «из» и т. Д.
- Исправление слов с ошибками.
- Сокращение слов до их основы (например, «игра» от «игра») с использованием алгоритмов
Более сложный подход заключается в создании словаря сгруппированных слов. Это одновременно изменяет объем словарного запаса и позволяет сумме слов захватить немного больше смысла из документа.
При таком подходе каждое слово или токен называется «грамм». Создание словаря пар из двух слов, в свою очередь, называется биграмной моделью. Опять же, моделируются только биграммы, которые появляются в корпусе, а не все возможные биграммы.
N-грамм — это последовательность из N-токенов слов: 2-грамм (чаще называемый биграммой) — это последовательность из двух слов, таких как «пожалуйста, включите», «переверните» или «домашнее задание» и 3 грамма (чаще называемый триграммой) — это последовательность из трех слов, например «пожалуйста, включите свою работу» или «включите свою домашнюю работу».
— страница 85, Обработка речи и языка, 2009.
Например, биграммы в первой строке текста предыдущего раздела: «Это были лучшие времена»:
- «это было»
- «был»
- «лучшее»
- «лучшее из»
- «Времен»
Затем словарь отслеживает триплеты слов, называется моделью триграмм, а общий подход называется моделью n-граммы, где n относится к числу сгруппированных слов.
Часто простой биграмный подход лучше, чем 1-граммовая модель мешка слов для таких задач, как классификация документации.
представление о мешке с биграммами намного мощнее, чем орудие слова, и во многих случаях оказывается очень трудно победить.
— страница 75, Методы нейронной сети в обработке естественного языка, 2017
Подсчет слов
После того, как словарь был выбран, необходимо оценивать вхождение слов в пример документов.
В проработанном примере мы уже видели один очень простой подход к оценке: двоичная оценка наличия или отсутствия слов.
Некоторые дополнительные простые методы оценки включают в себя:
- Графы, Подсчитайте, сколько раз каждое слово появляется в документе.
- частоты, Вычислите частоту появления каждого слова в документе среди всех слов в документе.
Хеширование слов
Вы можете помнить из информатики, что хэш-функция немного математики, которая отображает данные в набор чисел фиксированного размера.
Например, мы используем их в хеш-таблицах при программировании, где, возможно, имена преобразуются в числа для быстрого поиска.
Мы можем использовать хэш-представление известных слов в нашем словаре. Это решает проблему наличия очень большого словарного запаса для большого текстового корпуса, потому что мы можем выбрать размер хеш-пространства, который, в свою очередь, равен размеру векторного представления документа.
Слова хешируются детерминистически в один и тот же целочисленный индекс в целевом хэш-пространстве Затем для оценки слова можно использовать двоичную оценку или счет.
Это называется «хэш трюк» или же «функция хеширования«.
Задача состоит в том, чтобы выбрать хеш-пространство для размещения выбранного размера словаря, чтобы минимизировать вероятность коллизий и компромисса.
TF-IDF
Проблема с оценкой частоты слов заключается в том, что в документе начинают доминировать очень часто встречающиеся слова (например, большее количество баллов), но они могут содержать не столько «информационное содержание» модели, сколько более редкие, но, возможно, специфичные для предметной области слова.
Один из подходов заключается в том, чтобы изменить частоту слов по частоте их появления во всех документах, чтобы штрафы за такие частые слова, как «the», которые также встречаются во всех документах.
Этот подход к скорингу называется Term Frequency — Inverse Document Frequency, или сокращенно TF-IDF, где:
- Срок Частота: оценка частоты появления слова в текущем документе.
- Частота обратных документов: оценка того, насколько редко это слово встречается в документах.
Баллы — это вес, в котором не все слова одинаково важны или интересны.
Баллы имеют эффект выделения слов, которые отличаются (содержат полезную информацию) в данном документе.
Таким образом, idf редкого термина является высоким, тогда как idf частого термина, вероятно, будет низким.
— страница 118, Введение в поиск информации, 2008.
Ограничения Мешка Слова
Модель пакета слов очень проста для понимания и реализации и предлагает большую гибкость для настройки ваших конкретных текстовых данных.
Он с большим успехом использовался для задач прогнозирования, таких как моделирование языка и классификация документации.
Тем не менее, он страдает некоторыми недостатками, такими как:
- Запас слов: Словарь требует тщательного проектирования, особенно для того, чтобы управлять размером, что влияет на разреженность представлений документа.
- разреженность: Разреженные представления сложнее моделировать как по вычислительным причинам (пространственная и временная сложность), так и по информационным причинам, где задача состоит в том, чтобы модели использовали так мало информации в таком большом репрезентативном пространстве.
- Имея в виду: При отбрасывании порядка слов игнорируется контекст и, в свою очередь, значение слов в документе (семантика). Контекст и значение могут многое предложить модели: если смоделированный может сказать разницу между одними и теми же словами, расположенными по-разному («это интересно» против «это интересно»), синонимами («старый велосипед» против «подержанный велосипед») , и многое другое.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по этой теме, если вы хотите углубиться.
статьи
- Мешок с словами в Википедии
- N-грамм в Википедии
- Функция хеширования в Википедии
- tf – idf в Википедии
книги
- Глава 6, Методы нейронной сети в обработке естественного языка, 2017
- Глава 4, Обработка речи и языка, 2009.
- Глава 6, Введение в поиск информации, 2008.
- Глава 6, Основы статистической обработки естественного языка, 1999.
Резюме
В этом уроке вы обнаружили модель мешка слов для извлечения объектов с текстовыми данными.
В частности, вы узнали:
- Что такое модель мешка слов и зачем она нам нужна.
- Как работать с применением модели пакета слов в коллекции документов.
- Какие приемы можно использовать для составления словарного запаса и набора слов.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.