Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
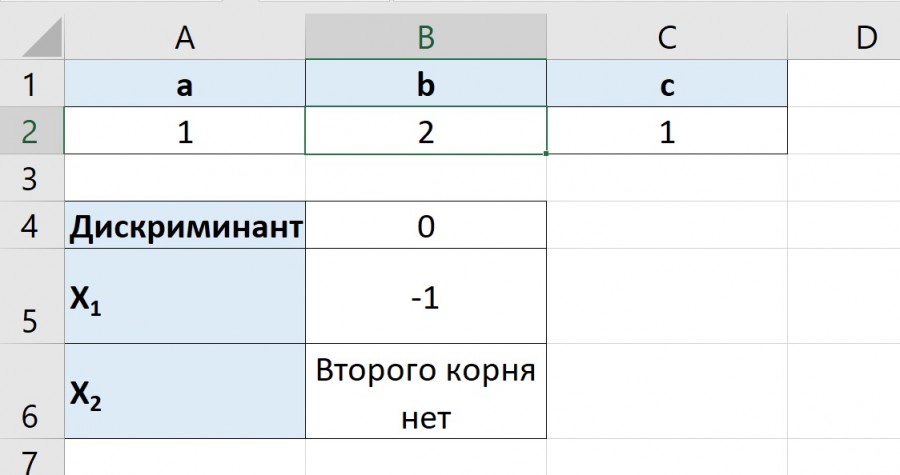
Получим формулу вида ax 2 +bx+c=0
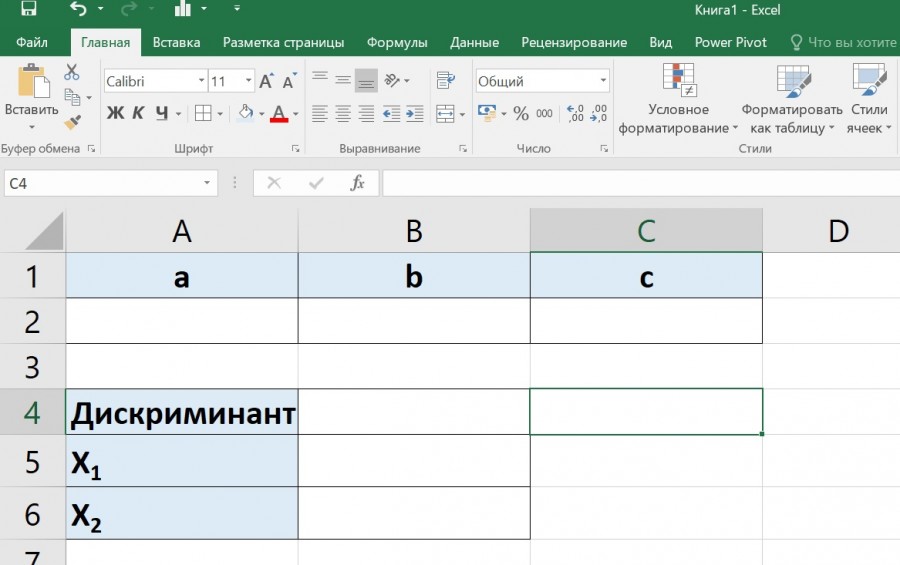
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
Как решить квадратное уравнение в экселе?
Чтобы решать любое квадратное уравнение в программе эксель, необходимо сначала подготовить универсальную форму, а потом подставлять нужные значения и получать решения. И давайте рассмотрим инструкцию, как это сделать.
Первый шаг. Квадратное уравнение представляется собой следующие уравнение: a*x 2 +b*х+с=0. Поэтому создадим форму, чтобы можно было вводить коэффициенты: a, b, c. А также формы в которых будет выводится дискриминант.
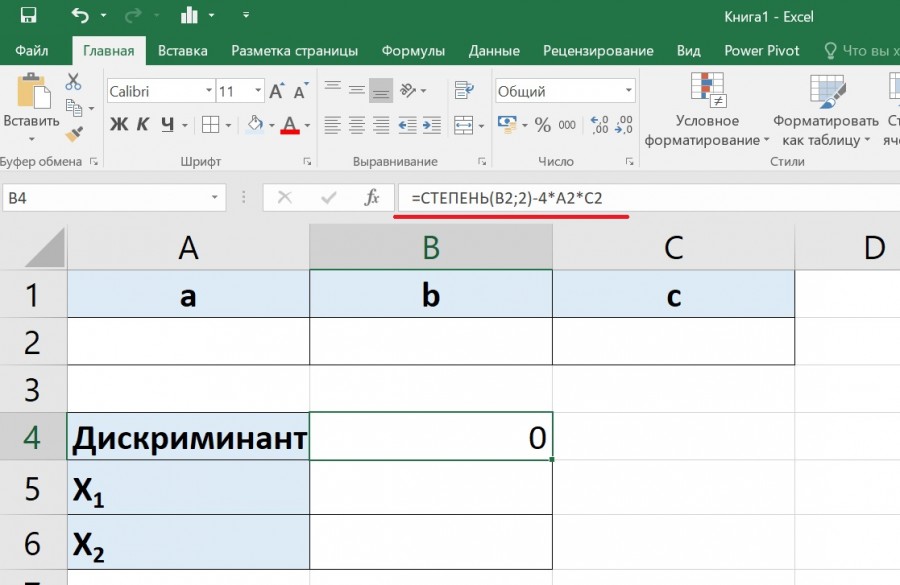
Второй шаг. Теперь нужно прописать формулы, которые будут решать квадратное уравнение. Начнем с дискриминант, он по правилам математики равен b 2 -4*a*c. Поэтому в ячейке «B4» пишем формулу: =СТЕПЕНЬ(B2;2)-4*A2*C2, где b 2 – это СТЕПЕНЬ(B2;2), a – это A2, с – это C2.
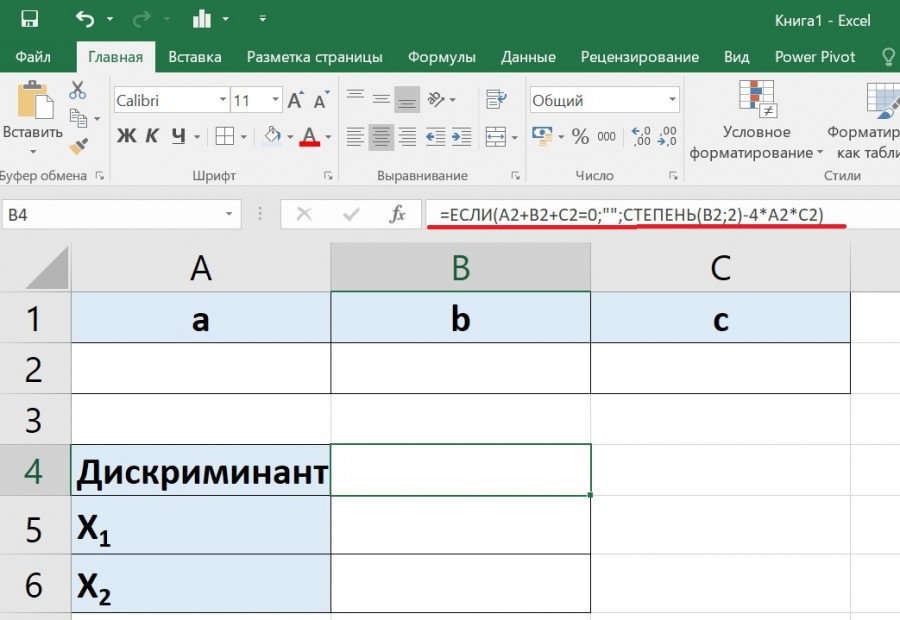
Третий шаг. Чтобы, когда поля были пустые у коэффициентов a, b, c, дискриминант не считался, добавил проверку на условия и перепишем формулу в ячейке «В4» на =ЕСЛИ(A2+B2+C2=0;»»;СТЕПЕНЬ(B2;2)-4*A2*C2). Т.е. проверяем, что если поля пустые, то выходи пустота.
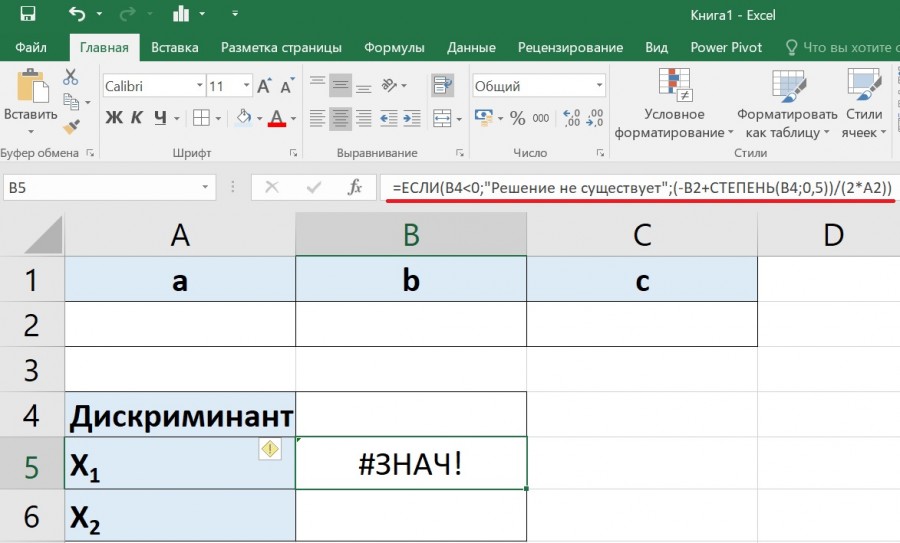
Четвертый шаг. Теперь найдем первый корень, при этом нужно учесть тот факт, что если дискриминант меньше нуля, то решения у уравнения не существует. Поэтому в ячейке «B5» пишем формулу =ЕСЛИ(B4 2 +D 0,5 )/2a.
Пятый шаг. Чтобы убрать ошибку #ЗНАЧ!, заключим формулу из четвертого шага в функцию ЕСЛИОШИБКА и напишем формулу: =ЕСЛИОШИБКА(ЕСЛИ(B4 2 +2*x+1=0.
Видео как решить квадратное уравнение в экселе.
Квадратное уравнение. Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D 2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень

Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
источники:
http://portalonline.ru/kompyutery-i-programmy/5337-kak-reshit-kvadratnoe-uravnenie-v-eksele.html
http://wpcalc.com/kvadratnoe-uravnenie-excel/
Содержание
- 0.1 Шаг 1. Организация таблицы
- 0.2 Шаг 2. Проверка равенства Дискриминанта.
- 0.3 Формула дискриминанта
- 0.4 Шаг 3. Вычисляем корни уравнения.
- 1 Перейдем к вводу формул для решения
- 1.1 Защита листа в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
В этой статье вы узнаете как решить квадратное уравнение на конкретном примере.
Постановка задачи: решить квадратное уравнение в Excel
Ход решения: Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b2-4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
=B3^2-4*B2*B4
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
=ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Для расчета x2 введем похожую формулу, но со знаком плюс
=ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)
Соответственно при введенных значениях a,b,cсначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c,то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK,подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
На примере квадратного уравнения х2 — 3х + 2 = 0 рассмотрим как решить квадратное уравнение в Excel.
1. В ячейки А1:А4 введите соответственно тексты
«а=», «b=», «c=», «D=».
2. В ячейки В1:ВЗ введите соответствующие значения
коэффициентов: 1; -3; 2.
3. В ячейку В4 введите формулу =В2^2-4*В1*В3
(Если все сделали правильно, то в ячейке B4 будет число 1).
4. В ячейку А5 введите текст «Есть ли корни?».
5. В ячейку В5 введите формулу =ЕСЛИ(В4=0;«х1=»;»»).
7. В ячейку В7 введите формулу = ЕСЛИ(В4>=0;«х2=»;»»),
8. В ячейку С6 введите формулу
= ЕСЛИ(В4>=0;(-В2+КОРЕНЬ(В4))/(2*В1);»»).
9. В ячейку С7 введите формулу
= ЕСЛИ(В4>=0;(-В2-КОРЕНЬ(В4))/(2*В1);»»).
This is the second part of the how to solve quadratic equations in Excel guide. Here, we are going to be focusing on how to do this manual and VBA method, whereas the first part shows how to do this using the Goal Seek feature. In this guide, we are going to show you a different approach to solving quadratic equations in Excel using formulas and VBA.
If you missed the first part:
A quadratic function is a type of equation that contains a squared variable. It is called quadratic because quad means square in Latin. The quadratic functions usually have a structure like ax² + bx + c = 0, where x represents an unknown variable, and a, b, and c represent known constants. Excel can help you easily solve these types of equations for x.
Download Workbook
The Quadratic Formula
A quadratic function’s variable can take 2 values, meaning that there can be 2 solutions. To find these values, you can use the quadratic formula:
The plus/minus operator (±) means the formula should be executed twice. Once with plus (+):
And once with minus (-):
The a, b and c values are known numbers where a ≠ 0. Since we know the formula representation and the values, we can now create a formula for solving quadratic equations.
The Standard Formula
For this first approach, you essentially need to replicate the quadratic formula in Excel. You can enter the known values (a, b and c) right away into the formula. However, this means that the formula will be static and you will need to change the values one-by-one again when you need to solve for another equation.
Alternatively, you can pull the input values from cells to place the constants a, b and c and use those references inside the formula. Changing the cell value is usually a lot easier than changing all values one-by-one, especially with complex formulas.
Let’s assume that our constant values are in cells C7, D7 and E7. In this example, we also named these cells as a_1, b_1 and c_1 to make the formula easier to read. The formulas will be,
=(-b_1 + SQRT(POWER(b_1,2) — 4*a_1*c_1)) / (2*a_1)
=(-b_1 — SQRT(POWER(b_1,2) — 4*a_1*c_1)) / (2*a_1)
As you can see, one of the formulas uses plus and the other uses minus. This is how you can create a structure to solve the quadratic equations using traditional formulas. You can learn more about the POWER and SQRT functions in the respective pages.
Solving Quadratic Equations using VBA
The standard formula method is effective and dynamic. However, it may be hard to remember or use. While Excel doesn’t have a function that allows solving quadratic equations with one click, you can create yourself one!
To start working with VBA, you need to enable the Visual Basic for Applications (VBA) window. When your workbook is open, press the Alt + F11 key combination. Once the VBA window is active, add a module. Modules are pages where you can write your VBA code.
Copy and paste the code below into the module you’ve just added:
Function SolveQuadraticEquation(a As Integer, b As Integer, c As Integer, result As Integer)
If result = 1 Then
SolveQuadraticEquation = (-b + Sqr(b * b — 4 * a * c)) / (2 * a)
ElseIf result = 2 Then
SolveQuadraticEquation = (-b — Sqr(b * b — 4 * a * c)) / (2 * a)
Else
SolveQuadraticEquation = «Invalid result value. It should be 1 or 2.»
End If
End Function
This code creates a new function named SolveQuadraticEquation. This function has 4 arguments — 3 for known values, and 1 for selecting the plus/minus sign.
After pasting the code, return to the Excel window and test your new function. First, enter the 3 known values, a, b and c. Set 1 or 2 to select between plus and minus respectively.
Лабораторная
работа № 1
«Решение
квадратного уравнения в Ms.excel»
Задание (по Excel).
Решение квадратного уравнения.
Необходимо изобразить общую схему для
решения уравнений вида ax2
+ bx + c =
0.
1. В ячейке А1 записать – Решение
уравнения вида:
Объедините ячейки А1, В1, С1, Д1 измените
шрифт и цвет надписи.
В ячейке В2 записать ax2+bx+c=0.
Выделите цифру 2, щелкните правой кнопкой
мыши, выберете команду Формат ячеек
и во вкладке Шрифт команду Верхний
индекс. Измените цвет и размер шрифта
по вашему усмотрению.
2. Введите следующие значения в
ячейки:
В А3 а= В А5 с= В А7 х1=
В А4 b= В А6 D=
В А8 х2=
Выровняйте
текст в этих ячейках по правому краю, а
в ячейках А7 и А8 сделайте цифры 1 и 2
нижними индексами (аналогично как
написано в пункте 1).
3. В ячейку В6 введем формулу для
вычисления дискриминанта (b2
-4*a*c)
Формулу вводим с использованием мастера
функций:
В ячейках В7 и В8 напишите формулы для
вычисления х1 и х2 ()
4. Отобразите корни уравнения с
точностью до четвертого знака после
запятой. Выделите ячейки в которых
содержится вычисление корней уравнения.
Щелкаем правой кнопкой мыши. В появившемся
меню выбираем Формат ячеек. Выбираем
вкладку число и числовой формат.
Устанавливаем число десятичных знаков
– 4.
5. С использованием логической
функции ЕСЛИ в ячейках для расчета
корней уравнения отобразить “решения
нет” для случая, когда дискриминант
отрицательный.
6.
Попробуйте несколько вариантов решения
уравнения.
Пример исполнения работы представлен
на рисунках (см ниже)
Соседние файлы в папке Lab_R_Excel
- #
- #
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 2 мин
Квадратное уравнение принимает следующий вид:
ах 2 + Ьх + с = у
Часто вам будет дано значение y и вас попросят найти значение x .
Например, предположим, что у нас есть следующее квадратное уравнение:
4x 2 – 20x + 16 = -8
Оказывается, установка x = 3 или x = 2 решит это уравнение.
Для решения квадратных уравнений в Excel можно использовать функцию поиска цели .
В следующем пошаговом примере показано, как использовать функцию поиска цели на практике.
Шаг 1: введите уравнение
Во-первых, давайте введем случайное значение для x и формулу квадратного уравнения для y:
Шаг 2: Найдите первое значение X, используя поиск цели
Затем щелкните вкладку « Данные » на верхней ленте, затем нажмите кнопку « Анализ «что, если»» и выберите «Поиск цели »:
В появившемся новом окне укажите, что вы хотите установить ячейку B2 равной -8 , изменив значение в ячейке A2 :
Как только мы нажмем OK , функция поиска цели автоматически найдет значение x, которое решает уравнение:
Goal Seek находит, что значение x=2 (при условии, что 1,9999 округляется до 2) решает квадратное уравнение.
Шаг 3: Найдите второе значение X, используя поиск цели
Чтобы найти второе значение x, которое решает квадратное уравнение, установите начальное значение x на другое число.
Например, мы могли бы установить начальное значение x равным 4:
Затем мы можем снова запустить функцию поиска цели и увидеть, что она находит новое решение x=3 :
Таким образом, два значения x, которые могут решить это квадратное уравнение, равны x=2 и x=3 .
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как решить систему уравнений в Excel
Как построить уравнение в Excel
Для решения квадратного уравнения необходимо знать формулу и алгоритм нахождения квадратов уравнения
Шаг 1. Организация таблицы
На первом этапе мы организуем таблицу для ввода данных коэффициентов a,b и c.
- a называют первым или старшим коэффициентом,
- b называют вторым или коэффициентом при x,
- c называют свободным членом.
Шаг 2. Проверка равенства Дискриминанта.
Для того, чтобы вычислить корни уравнения второй степени, необходимо определить значение Дискриминанта.
Формула дискриминанта
D = b2 — 4ac
Вычисление корней уравнения второй степени происходит по формулам при условии величины Дискриминанта
| Условие | D > 0 | D = 0 | D < 0 |
| Число действительных корней | корней два | корень один | Нет решения |
| Формула | X1,2=(- b ±√ (b2 — 4 * a * c)) / (2 * a) | X1=X2=-b/(2*a) |
Шаг 3. Вычисляем корни уравнения.
После определения значения Дискриминанта используем выше приведенные формулы для нахождения корней.
Находим первый корень
Находим второй корень. Формула будет отличаться только в одном знаке.
Итог: с помощью Excel можем создать единожды таблицу и формулы для решения квадратного уравнения (уравнения второй степени) и быстро их решать.
людей нашли эту статью полезной. А Вы?
Администрация городского округа Химки Московской
области
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
СРЕДНЯЯ
ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 20 г. ХИМКИ
ИНН 5047045510 КПП 504701001 141431, МО, г. Химки,
мкрн. Подрезково, ул. Школьная, д. 2,
тел/факс: 8(495)574-13-63, 574-08-80,Е-mail: himkimou20@mail.ru
Открытый интегрированный урок:
«Решение квадратных уравнений в MS Excel».
Авторы:
Учитель информатики
Гуськов Владимир Вячеславович,
Учитель математики
Уварова Марина Константиновна
ТЕМА УРОКА: «Решение
квадратных уравнений в MS Excel »
(интегрированный
урок: математика, информатика)
Цель урока математики
·
Обобщение и систематизация материала по данной
теме;
Учебные задачи
·
Развитие навыков само и взаимоконтроля
Воспитательные задачи
·
Развитие навыков групповой и индивидуальной
деятельности
Цель урока информатики
·
Показать практическое применение электронных таблиц
в вычислительных задачах на примере решения квадратных уравнений.
Учебные задачи
·
Повторить правило ввода формул в ячейку
·
Повторить
типы адресации ячеек; научиться пользоваться мастером функций
Воспитательные задачи
Развитие навыков аккуратного исполнения алгоритма при
работе с компьютером.
Ход урока.
Вступительное
слово психолога. Определение эмоционального состояния
учащихся вначале урока (ученик выбирает полоску любого цвета, из которых
учитель составляет цветовую матрицу класса)
Организационный
момент: с целью проверки домашней работы учащиеся
сдают сообщения по теме «Квадратные уравнения»
Учитель математики:
Являясь
современными, учениками, обладая запасом знаний, накопленных нашими предками, вам
предстоит на этом уроке решать квадратные уравнения различными способами:
1)
Используя формулу корней квадратного уравнения;
2)
Учитывая четность второго коэффициента;
3)
Выделением квадрата двучлена;
4)
Графическим, построением графиков функций;
5)
С помощью компьютера.
Повторение
Квадратным
уравнением называется уравнение вида ах2 + bх
+с=а, где а, b и с – коэффициенты
квадратного уравнения, причём а не равно нулю, х – переменная.
Формула корней
квадратного уравнения ах2 + bх + с=0, при а не равно нулю

D=b2 -4ac
Наличие корней
зависит от знака D
D<0 D=0
D>0
корней нет один корень или два равных два
различных корня
I. Устная
работа с учащимися
Согласны ли вы с утверждением, что если в квадратном уравнении ах2
+ bх +с=0 числа а и с имеют разные знаки, то уравнение
имеет корни?
- Корни какого из уравнений обладают свойством:
а) сумма корней равна 6, а произведение равно –16.
б) один из корней
6; х2 –
6х=0
в) корни
равны х2
– 10х + 25=0
г) корней
нет. х2
– 6х – 16=0
х2 – 2х + 24=0
- Даны квадратные уравнения (D>0)
х2 + 4х – 5=0; 2х2 – 5х +3
=0; х2 – 4х+3=0; — 7х2+ 13х – 6=0
Все они обладают одним и тем же свойством. Каким? Используя это
свойство, решите уравнение: 2006х2 + 19х –
2025=0
- Найдите значение выражения а) (х+4)2
б) х2 – 16
зная, что х2 + 8х + 16=0
Проверка работ по карточкам
*** Физкультминутка (для снятия физического и эмоционального
напряжения).
II. Работа по карточкам.
Карточка 1 и 2
|
№ |
Квадратное |
Найти |
D= >< 0 сравнить значения |
Найти корни квадратного |
|
1 |
х2 – 10х + 25=0 |
|||
|
2 |
5х2 – 8х +3=0 |
|||
|
3 |
х2 – 2х +24=0 |
|
№ |
Уравнение х + рх + |
х1 |
х2 |
|
1 |
х2 – 6х – 16 = 0 |
— 2 |
|
|
2 |
х2 – 2х – 24 = 0 |
6 |
|
|
3 |
х2 – 6х = 0 |
0 |
х1 + х2 = ________
х1 * х2 = ________
III. До сих пор решали квадратные уравнения
только аналитически. Теперь для проверки полученных результатов составим в
электронных таблицах алгоритм решения квадратного уравнения.
Ещё раз обратим
внимание на общий вид уравнения:
ax2 + bx + c = 0
Для составления
электронной таблицы необходимо определить имена переменных величин
·
значения которых являются входными данными
·
значения которых являются выходными данными
Вход: a,
b, c
Выход: d,
x1, x2
Для получения
выходных данных воспользуемся формулами нахождения дискриминанта и корней
квадратного уравнения:
вход преобразование
выход
 |
|
 |
|
 |
Известно, что существование корней квадратного
уравнения зависит от знака дискриминанта. Следовательно, необходимо
исследовать дискриминант, для этого воспользуемся встроенной логической
функцией если.
Графическое
представление функции:
Составим таблицу
для решения уравнения (1): x2 — 10x + 25 = 0
Почему числитель и знаменатель заключены в
скобки?
Верно, чтобы не был нарушен приоритет операций
при вычислении.
Решим уравнение (1) при помощи уже
составленной электронной таблицы.
Сложно составить электронную таблицу для решения
квадратного уравнения?
Верно, необходимо дополнительное время для
изучения новой информации.
Зачем же его тратить? Может быть достаточно
научиться решать уравнения вручную?
Для ответа на этот вопрос решите квадратное
уравнение (2)
357,89 x2 + 823,17x
– 121,23=0
при помощи уже составленной таблицы.
Что для этого необходимо сделать?
Верно, ввести новые входные данные.
Вам понадобилось для этого много времени,
совершенно верно, несколько секунд.
Решение
уравнения (2):
Сколько
времени вам понадобится для решения этого уравнения вручную?
— Гораздо больше.
А
если не пользоваться калькулятором?
— Много.
Таким образом, этот
пример демонстрирует очень важное свойство алгоритма – массовость.
IV. Практическое
задание.
Используя
электронные таблицы, проверить решения квадратных уравнений, выполненных
вручную.
При помощи компьютера учащиеся проверяют
правильность заполнения таблиц, приходят к выводу, что используя информационные
технологии можно очень быстро и качественно решить квадратные уравнения.
V. Итог урока
Учитель: Что нового для себя узнали
на уроке? Что понравилось?
VI. Домашнее задание
Составьте формулы для решения линейного уравнения ах
= b в электронных таблицах.