At risk for excel

In portfolio management, Value-at-Risk (VaR) is a popular metric to quantitatively assess the risk of our holdings.

Originally invented by banks to give some sense to how much lost could be reasonably anticipated across different business, it gained traction in the risk management world and soon become a well-known method to measuring risk and helping traders/portfolio managers to view their portfolio in a different fashion.

Today let’s learn about what is VaR, and how we can compute it in Excel.

You may also be interested in 2021 New Year Resolution List for Excel.

Workbook

What is Value-at-Risk (VaR)?

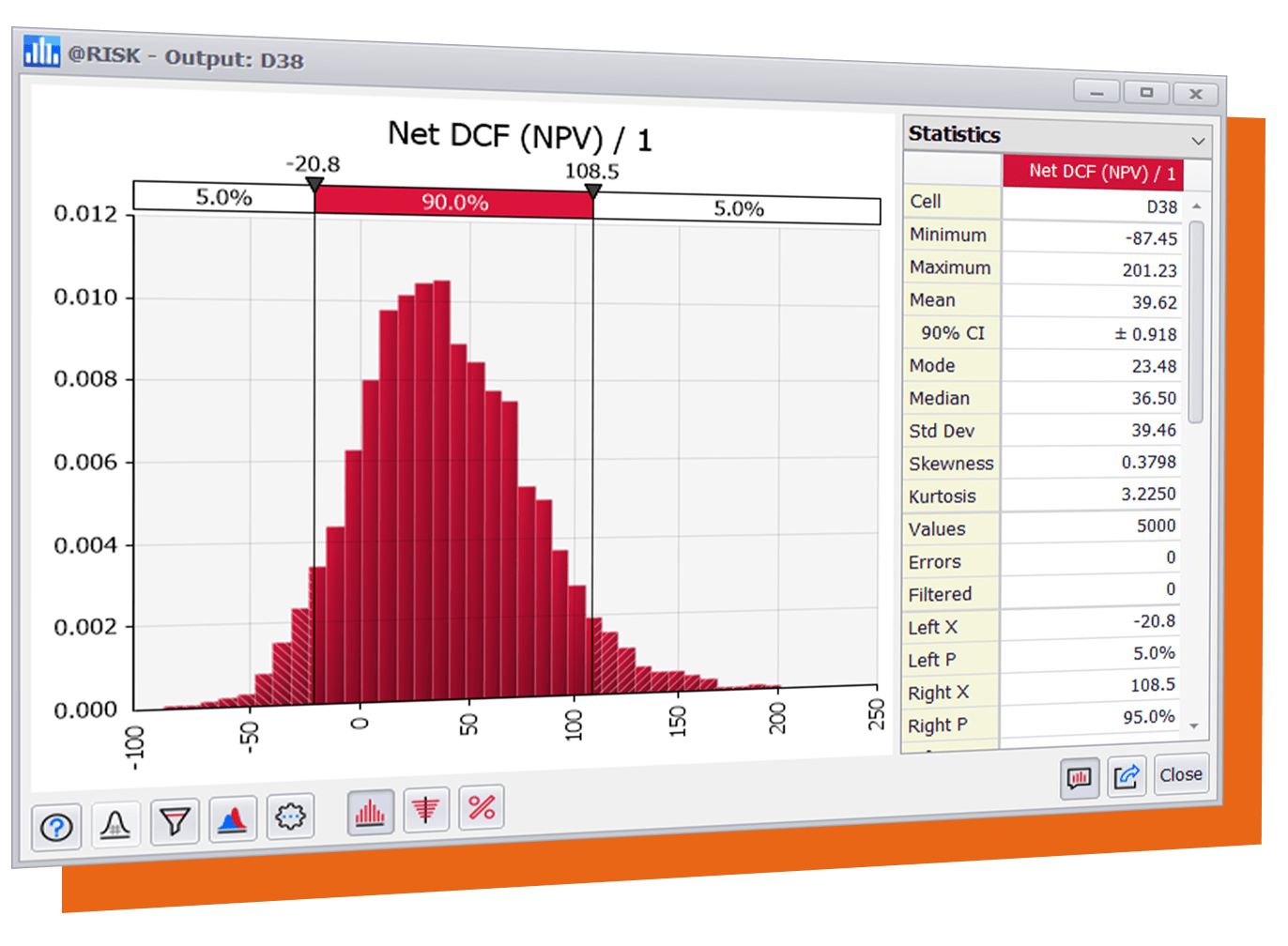
Value-at-Risk (VaR) is, in essence, the X-percentile of the projected Profit-and-loss (PnL) for our portfolio, over a given time horizon. In plain words, if VaR is $100, it tells you that if we are unlucky tomorrow, we expect to lose at a maximum of $100 with X% chance/confidence.

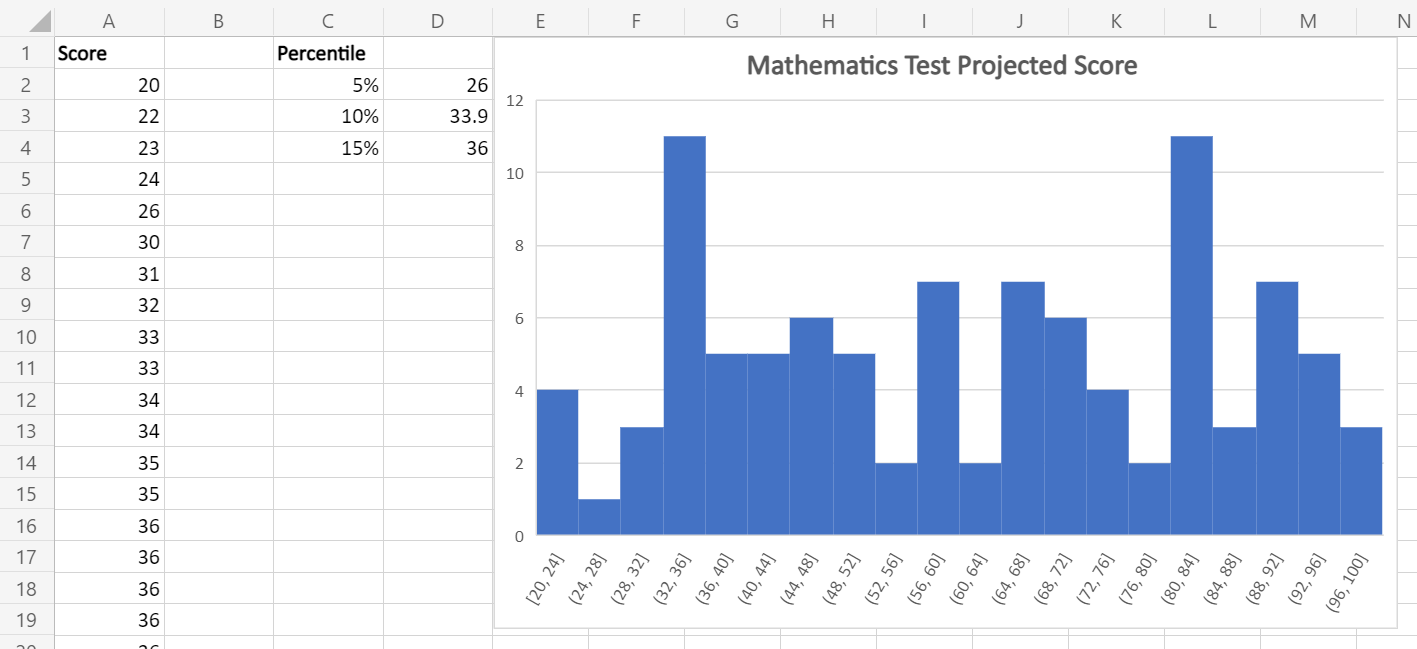
Let’s think about it in a non-financial example. Suppose you have 99 students in a Mathematics class, taking the same test tomorrow. Based on the result of the last test they’ve taken, you obtained a projection of how the class will perform in the coming test.

With the data in our example workbook, we found that the 5th percentile of the score is at 26, which is basically the 5th-lowest score achieved by the class (cell A6). Therefore, we can loosely say that the 5% Value-at-Risk for the class is 26 in the upcoming test, i.e. we have 5% confidence that the lowest score achieved by all students is 26.

You may also be interested in Binomial Option Pricing (Excel formula).

Why do we use Value-at-Risk (VaR)?

Now let’s turn our attention to portfolios of financial instruments. Instead of the score of students, now we look to project the Profit-and-Loss (PnL) of our portfolio, and compute a Value-at-Risk (VaR) based on that.

There are actually good reason to look at Value-at-Risk (VaR), on top of usual metrics like expected return/portfolio standard deviation. VaR is actually a metric to look at heavy-tail events (or black-swan events).

Heavy-tail (or black-swan) events are rare events that have severe consequence. For example, people generally think the stock market would not drop by more than 5% a day, so “Market dropping by more than 5%” is a black-swan event.

While metrics like expected return/portfolio standard deviation give investor a sense of the characteristics of their portfolio, they do not tell you what could happen if you have a really bad day. And VaR is a good metric to tell you that, if you have a really bad day, what is the loss to be expected.

For large investor, heavy-tail events are risks to be managed, and hence heavy-tail metrics like VaR has grown in prominence for risk management.

With this in mind, our problem becomes:

1. How do we present VaR figures?
2. How do we come up with the statistical distribution of the PnL (i.e. the chances of achieving different PnL levels)?

Let’s go through one-by-one in the following section.

You may also be interested in How to Compute IRR in Excel (Basic to Advanced).

How do we present Value-at-Risk (VaR)?

In practice, Value-at-Risk (VaR) often comes in different flavors, and it is important for us to understand how to read into the VaR figures provided.

Confidence Level

VaR is always presented in the manner “X%-VaR“, and we specify the confidence level (i.e. X%) related to a specific VaR. For example, a 95%-VaR would correspond to the 5th-percentile of the PnL distribution, 99%-VaR to the 1st-percentile of the PnL distribution.

There is no one-shoe-fit-all rule that dictates what is the confidence level to use, but practitioners generally quotes multiple confidence level at once (e.g. 95%, 97.5%, 99%) to give a better sense for how heavy-tail events would impact the portfolio.

Time Horizon

VaR is also commonly presented as a “X-day VaR“, although sometimes it is implicitly a 1-day VaR measure. When speaking of the PnL distribution, depending on the frequency of the data (e.g. daily/weekly/monthly), VaR of different time horizon could be calculated.

Majority of the VaR measures in practice is a 1-day metric, as a typical assumption is that risks are reviewed on a daily basis, but longer horizon metrics are often useful as well.

Absolute vs Relative

Absolute and Relative VaR differs in whether you want to benchmark against the expected return.

For example, suppose the 5th percentile of your PnL distribution is -$10, and your expected return (i.e. mean of PnL distribution) is +$2. Your Absolute 95%-VaR would be -$10 (the total loss expected), and your Relative 95%-VaR would be -$8 (a relative figure to the expected return).

You may also be interested in How to Generate Random Variables in Excel.

How do we come up with the statistical distribution?

After we discussed on what are the flavors for Value-at-Risk (VaR), we look at a more fundamental question – how do we come up with the distribution of potential Profit-and-Loss (PnL) in the first place?

Ultimately, the computed VaR depends on your selected PnL distribution: if you select a distribution that there is a high chance of losing (positively skewed), chances are, your VaR computed will be larger than if you have picked a distribution that is more symmetrical.

There are mainly 2 ways which we’ll illustrate with the help of Excel:

1. Historical approach
2. Parametric approach

Historical Approach

As the name suggest, in historical approach, you compute the VaR based on what is available in the past.

In essence, based on the specific portfolio composition, we obtain the daily PnL data, sort them in ascending order, and find the relevant (1-X)-th percentile that translates to our X%-VaR.

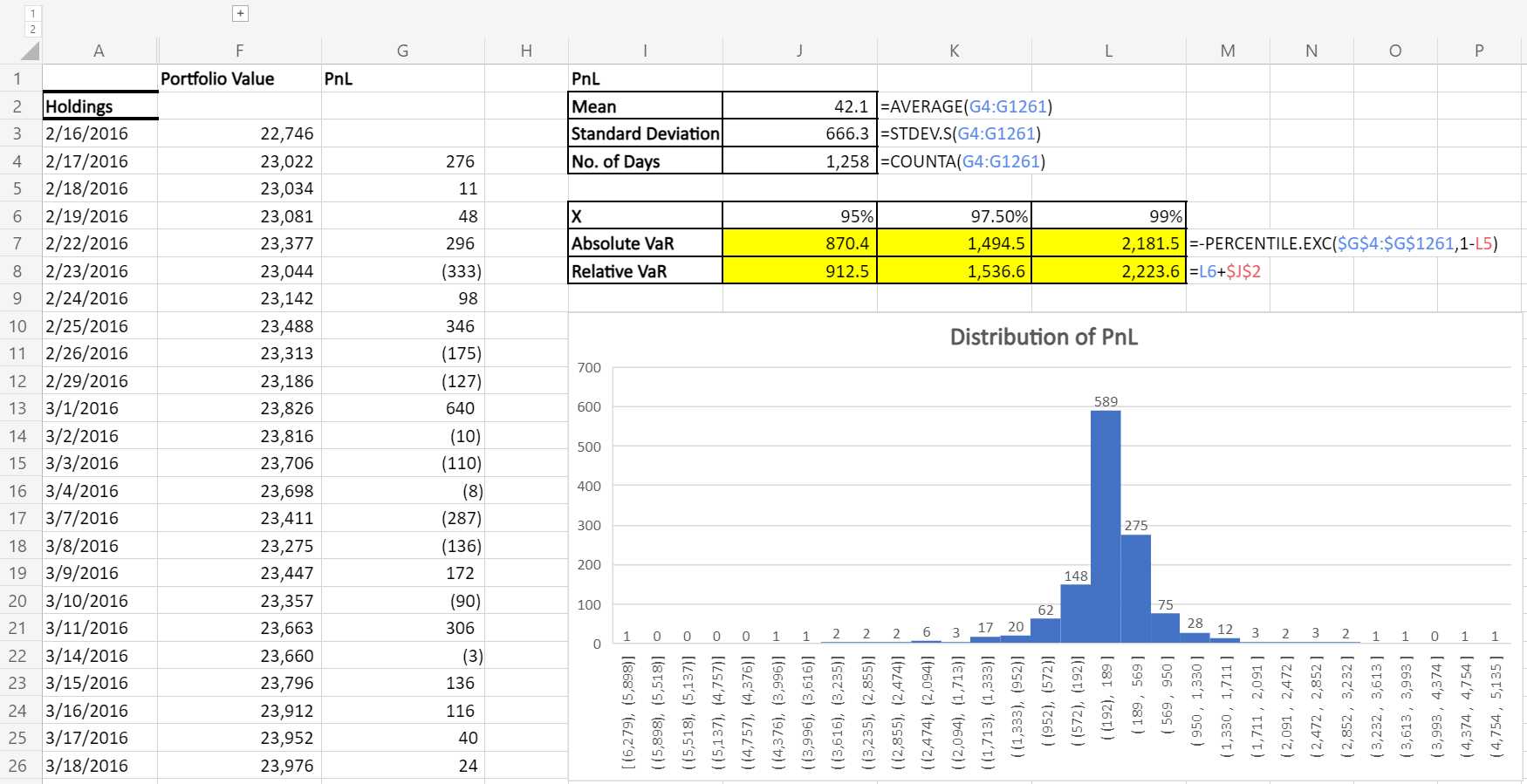
From the Sample Workbook, you’ll find an example where we have a portfolio with 4 stocks. With Yahoo Finance stock price data, we compute the day-on-day change as our PnL distribution.

Based on the calculation, we found that the 1-day 95%-VaR is $870.4, which means on a given day, we expect that the maximum loss is $870.4 with 5% confidence. Similarly we have the 97.5%-VaR and 99%-VaR for side-by-side comparison.

As you’ve guessed, there are several limitation of using a historical approach:

1. The computed VaR is heavily influenced by the timeframe you’ve selected.
2. Past performance of the portfolio does not necessarily link closely to future performance
3. Most importantly, sampling of the negative outliers (i.e. days with large loss) may be biased as we usually have too few observations.

With that in mind, we introduce the alternative approach: the parametric approach.

You may also be interested in Black-Scholes Option Pricing (Excel formula).

Parametric Approach

The parametric approach is a fancy way to say that we make some statistical assumption with the PnL distribution.

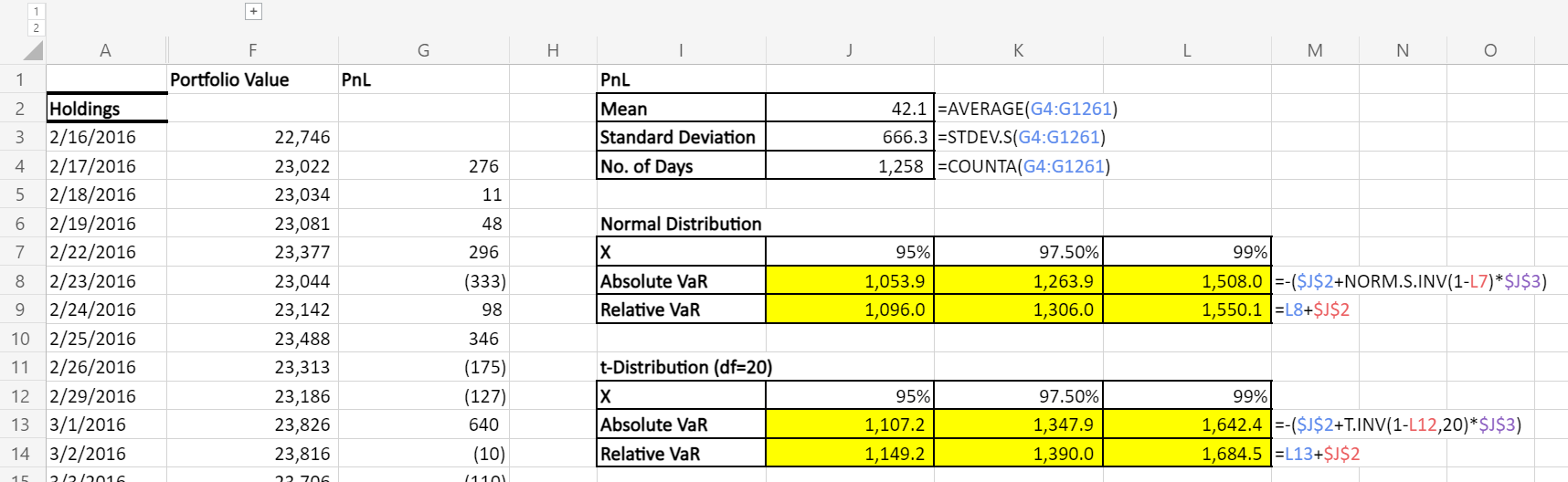
For example, in our sample workbook, we’ve presented VaR computed from 2 commonly-used parametric distribution: the Normal distribution and the t-distribution.

In the Parametric Approach, we only need to estimate for a couple of parameters (e.g. mean and standard deviation) of the PnL distribution, and apply these parameter to find the expected percentile.

Notice how the VaR computed for t-distribution is larger than the normal distribution, which is due to the fact that t-distribution has heavier tails than the normal distribution. Heavier tail means that there are more chances for outliers (negative outcome in our case).

Comparing what we computed in parametric vs historical approach, while parametric approach seems more prudent than the historical approach for 95%-VaR (1,053.9 vs 870.4, larger means more prudent), for 99%-VaR (1,508.0 vs 2,181.5) the opposite is true.

In this case, we’ll need to re-evaluate whether our choice of parametric PnL distribution (e.g. Normal/t) is representative of the actual PnL distribution, and see if we need to find a more heavy-tailed distribution.

You may also be interested in How to Name Multiple Single Cells in Excel.

Bottomline

Value-at-Risk (VaR) is an important metric in risk management, giving investors/traders the sense of how heavy-tail/black-swan events would impact the portfolio of financial instruments we hold.

There are numerous ways to how VaR can be computed and presented, but we should always compare and contrast VaR computed with different approach and understand what it means for our modelling and how it could be representative of our risks.

You may be interested in How to use REPT functions to the Most.

Hungry for more useful Excel tips like this? Subscribe to our newsletter to make sure you won’t miss out on any of our posts and get exclusive Excel tips!

5 mins read

In this post, we will calculate Value at Risk in EXCEL using the VaR Historical Simulation approach.

1. What is Value at Risk?

Perhaps the simplest and common concept you are likely to see when it comes to financial risk management is Value at Risk or VaR for short.  It represents an educated estimate for:

a)      How bad can prices get when they really get bad? or

b)      What is the most that you can lose on a really bad day on account of price changes? or

c)       What is the worst that can happen when the market hits free fall?

While VaR has received a great deal of negative coverage post 2008, before we discuss issues, it would be useful to first determine how to calculate Value at Risk.

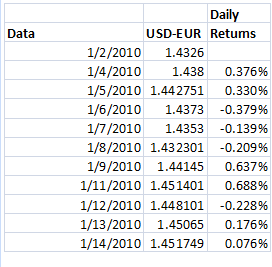
There are three methods for calculating Value at Risk. Variance covariance (VCV), Historical Simulation and Monte Carlo Simulation. In this post,  we will start off with a data series for the USD-EUR Foreign currency exchange rate. Then see what the Value at Risk measure can tell us about the likely (most common) and the worst case (extreme) movement for this exchange rate.

We will calculate Value at Risk using the Historical Simulation approach in EXCEL.

2. Guide to the Value at Risk Historical Simulation Approach

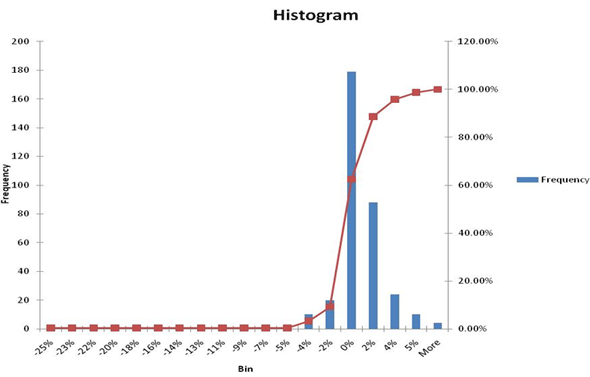
For example, take a look at the following EXCEL histogram.

This histogram is calculated using a series of daily price changes for a given financial security. Within risk terms, we call daily price changes, daily returns, and these returns could be positive or negative.

The histogram above takes a daily return series, sorts the series and then slots each return in a given return bucket.

a. Step 1 – Calculate daily returns

We will first calculate a table of daily returns from the daily USD-EUR exchange rates daily exchange rate series.  Each return is calculated by the application of LN(P1/P0) where LN is the natural log function in EXCEL, P1 is the new exchange rate, P0 is the old exchange rate.  This is approximately equal to the daily % price change in the underlying exchange rate.

We will take this return series and use it to calculate a histogram similar to the one above.

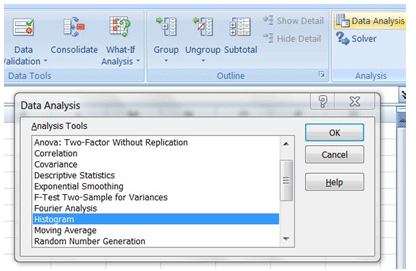
b. Step 2 – Set up & run EXCEL’s Data Analysis Histogram tool

You can find the Histogram tool under the Data Analysis tab in Excel.  If for some reason you don’t see a data analysis tab in your version of EXCEL, to enable the tab do the following:

• Go to EXCEL Options
• Choose Addins, and
• Add the Data Analysis Addin.

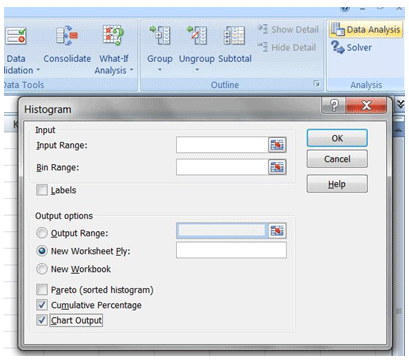
To generate the Histogram select the daily return series by calculating the percentage change in prices from one day to the next. Use that return series as your input range.

Opt for New worksheet ply, cumulative percentage and chart output (see below) to see a graphical representation of the Histogram as well as a supporting table.

When you press ok, EXCEL will create a new tab for you and show the histogram that you see below.

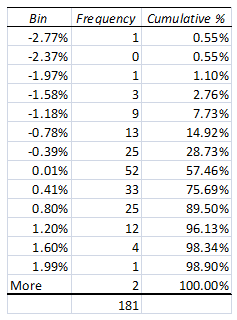
c. Step 3 – Interpreting the results of the histogram

As a risk professional our focus is on the downside which in the histogram below is marked at -2.77%. The upside is about 1.99+%.

i. Worst case loss?

So if I asked you what is the worst that can happen, you can easily tell me that my worst scenario based on historical returns as shown by the above histogram is a loss of over -2.77% (the extreme left corner on the bottom) if I am long (bought) Euro or a loss of 1.99% if I am short (sold) Euro versus the US dollar.

ii. Time period? Odds?

Your next two questions should be, over what time and with what odds?

The returns are calculated on a daily basis hence the answer to the first question is over anyone given trading day.

The second answer requires a bit of work.  There are approximately 300 days (frequency count) in the graph above. Your worst case loss is a once in 300 day event. The probability of you seeing a loss greater than this number is 1/300 or 0.33%.

Fortunately, the EXCEL histogram output worksheet already has a table with these probabilities and numbers in it.

iii. Putting it together

If you put it together there is only a .55% chance that you or I will see a worst case loss of over -2.77% on any given trading day if you bought Euros and a 1.1% chance that you will see a loss of over 1.99% if you have sold Euros.

Congratulations. By adding a holding period (a given trading day) and a probability (0.55% / 1.1%) you have converted your simple what is the worst that can happen statement into a value at risk estimate.

Typically Value at Risk (VaR) is expressed in dollar terms. However, since here we only had percentile returns to work with we have expressed it in percentage terms.

Conceptually Value at Risk represents the projected level of losses a trading desk needs to protect itself against under extreme conditions. It is used as a proxy for the amount of capital required to support such losses.

3. Alternative Value at Risk methods

The approach that we have just used to calculate Value at Risk is also known as the VaR Historical Simulation approach.

You can also calculate Value at Risk using the Variance covariance (VCV) approach or using the Monte Carlo simulation approach.

The VaR Historical simulation approach works with the actual distribution of results (the price and return series), the VCV approach assumes that returns are normally distributed (it imposes the normal distribution) while the Monte Carlo Simulation technique uses a generator function to first simulate a series of prices and then applies the same process we have used above for Historical simulation.

a. Using the right models

As is the case with practitioners, as we solve new problems (sometimes creating other more difficult to solve problems), we build up an inventory of biases and prejudices.

I greatly like Monte Carlo simulation as a tool for dissecting structures and testing pricing and hedging strategies. However, I hate it (Monte Carlo simulation) when it comes to modeling risk. I realize that the Historical Simulation approach has many significant limitations. But over the years, it’s the only approach that has shown some sense of stability. As Nassim Taleb puts it, history is not going to repeat itself, you are not going to be hit by your last worst loss and the next big wave that will wipe you out will not come from where you expect it.

My respect for historical simulation grew when we started modeling Value at Risk for cross currency swaps. Two separate currencies, two separate interest rates, two separate term structures and about a thousand assumptions in between. I would look at the end number our Monte Carlo simulator would throw out in amazement and wonder how could any rationale being put any reliance on something that is literally stitched together by chewing gum and baling wire.

While Historical simulations had its own issues, at least it reduced the assumption set and the usage of historical price data set across currency pairs, rates, term structures and markets made it a lot easier to explain to traders. Traders understand and respect price and price histories. They question assumptions. A model that uses raw prices unfettered by drivers and assumptions for a trader is infinitely superior to a model with more assumptions than equations.

For additional examples and instruction please see the following lessons:

• Calculating value at risk case study and example
• Portfolio Var – Shortcut approach without VCV