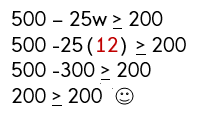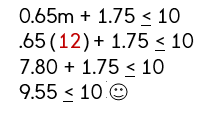Solving Word Problems in Algebra
Inequality Word Problems
How are you with solving word problems in Algebra? Are you ready to
dive into the «real world» of inequalities? I know that solving word
problems in Algebra is probably not your favorite, but there’s no point
in learning the skill if you don’t apply it.
I promise to make this as easy as possible. Pay close attention to
the key words given below, as this will help you to write the
inequality. Once the inequality is written, you can solve the
inequality using the skills you learned in our past lessons.
I’ve tried to provide you with examples that could pertain to your
life and come in handy one day. Think about others ways you might use
inequalities in real world problems. I’d love to hear about them if you do!
Before we look at the examples let’s go over some of the rules and
key words for solving word problems in Algebra (or any math class).
Word Problem Solving Strategies
- Read through the entire problem.
- Highlight the important information and key words that you need to solve the problem.
- Identify your variables.
- Write the equation or inequality.
- Solve.
- Write your answer in a complete sentence.
- Check or justify your answer.
I know it always helps too, if you have key words that help you to write
the equation or inequality. Here are a few key words that we associate
with inequalities! Keep these handy as a reference.
Inequality Key Words
- at least — means greater than or equal to
- no more than — means less than or equal to
- more than — means greater than
- less than — means less than
Ok… let’s put it into action and look at our examples.
Example 1: Inequality Word Problems
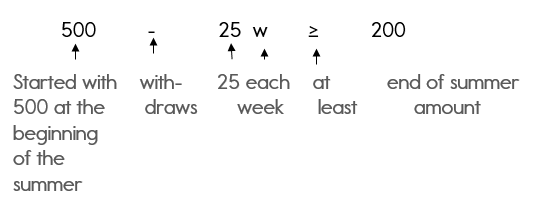
Keith has $500 in a savings account at the beginning of the summer. He wants to have at least $200 in the account by the end of the summer. He withdraws $25 each week for food, clothes, and movie tickets.
- Write an inequality that represents Keith’s situation.
- How many weeks can Keith withdraw money from his account? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: At least is a key word that notes that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know how many weeks.
Let w = the number of weeks
Step 3: Write your inequality.
500 — 25w > 200
I know you are saying, «How did you get that inequality?»
I know the «at least» part is tricky. You would probably think that at least means less than.
But… he wants the amount in his account to be at least $200 which means $200 or greater. So, we must use the greater than or equal to symbol.
Step 4: Solve the inequality.
The number of weeks that Keith can withdraw money from his account is 12 weeks or less.
Step 5: Justify (prove your answer mathematically).
I’m going to prove that the largest number of weeks is 12 by substituting 12 into the inequality for w. You could also substitute any number less than 12.
Since 200 is equal to 200, my answer is correct. Any more than 12 weeks and his account balance would be less than $200. Any number of weeks less than 12 and his account would stay above $200.
That wasn’t too bad, was it? Let’s take a look at another example.
Example 2: More Inequality Word Problems
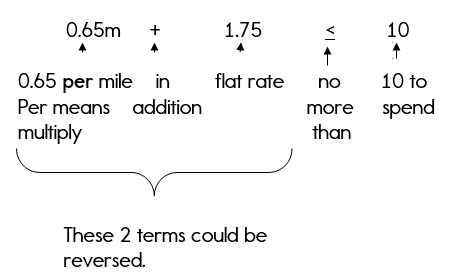
Yellow Cab Taxi charges a $1.75 flat rate in addition to $0.65 per mile. Katie has no more than $10 to spend on a ride.
- Write an inequality that represents Katie’s situation.
- How many miles can Katie travel without exceeding her budget? Justify your answer.
Solution
Step 1: Highlight the important information in this problem.
Note: No more than are key words that note that this problem must be written as an inequality.
Step 2: Identify your variable. What don’t you know? The question verifies that you don’t know the number of miles Katie can travel.
Let m = the number of miles
Step 3: Write the inequality.
0.65m + 1.75 < 10
Are you thinking, «How did you write that inequality?»
The «no more than» can also be tricky. «No more than» means that you can’t have more than something, so that means you must have less than!
Step 4: Solve the inequality.
Since this is a real world problem and taxi’s usually charge by the mile, we can say that Katie can travel 12 miles or less before reaching her limit of $10.
Step 5: Justify (prove your answer mathematically).
Are you ready to try some on your own now? Yes… of course you are! Click here to move onto the word problem practice problems.
Take a look at the questions that other students have submitted:
- Home
- Inequalities
-
Inequality Word Problems
>
>
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
When most people hear “word problems,” they often think of the popular example of trains traveling at different speeds, or unrealistic applications of math. However, word problems represent how most people use math in everyday life, and the SAT includes these problems to test students’ ability to reason logically and solve problems.
For many students, the hardest part of a word problem is figuring out exactly what the word problem is asking of you. Not all word problems are created the same though, so we’re going to break down what you need to know so that you feel confident solving them on the SAT.
Types of Math Word Problems on the SAT
You could divide math word problem in a few different ways. You could do it by topic, for example, such as using the SAT subscores as your guide. Or you could do it by the type of solution the problem requires of you. We’re going to focus on the second way, simply because trying to divide word problems by topic would mean we’d have to cover virtually every math topic the SAT covers, which is way more than we could fit in a single post.
Creating an equation or a formula. In these problems, you’ll be given some information about a scenario and asked to come up with an equation or formula that represents that scenario. In fact, looking for the word “represents” in the question might tip you off that you’re dealing with a problem of this type. These are almost exclusively found in the multiple-choice questions, with different equations or formulas listed as the answer choices.
Solving for a value. This is the most common form of word problem. Based on the information in the word problem, you’ll need to come up with at least one specific value that satisfies the requirements of the problem. Examples include finding “how much” or “how many” of something in the problem, or finding minimums and maximum values.
Defining or interpreting. For these problems, you are often asked to interpret what a variable or a constant means in the situation described, or you might be asked what kinds of conclusions can be drawn from a survey. These types of problems often have no “math” involved, and instead ask you to think logically about a situation.
Tip: Being able to identify problems by type on the SAT is a useful prep exercise and can help you on the day you take the test. You may want to use the Math section from a free practice SAT test and circle all of the word problems. Then, read each word problem and assign it to one of the types. Doing this will help you see the commonalities between different types of questions and will allow you to spend less time on the actual test wondering what type of question you’re dealing with!
How to Approach SAT Math Word Problems
For every SAT Math word problem, there are two things to consider. The first is what we discussed above, which is to figure out what type of problem you’re dealing with to best identify what you need to do. Once you know whether you need to provide a definition, write an equation, or solve for a value, you’ve taken the first step.
The next step will be to do the math that you’ve identified you need to do based on the type of word problem. Let’s take a look at each one:
Write an equation/formula. For problems of this type and for problems that ask you to solve for a specific value, you will often need to understand how to “translate” a word problem into an equation, diagram, or graph that you can work with. Luckily, the SAT is very particular about how it uses words in its word problems, so you can always be sure that certain words are meant to relate to specific mathematical concepts. Here are some of the common phrases used by test makers to clue you in to what kind of math you’re looking for:
| Word/phrase | Mathematical meaning/symbol |
| Is, will be, is equal to, is the same as | Equals, = |
| Plus, sum, increased by, added to, received | Addition, + |
| Minus, fewer, difference, decreased by | Subtraction, – |
| Times, product, multiplied by, of | Multiplication, x |
| Divided by, quotient, per, for | Division, ÷ |
| More than, greater than | Inequality, > |
| At least, minimum | Inequality, ≥ |
| Fewer than, less than | Inequality, < |
| At most, maximum | Inequality, ≤ |
| What, how many | Variable, x (or any other letter) |
Solve for a value. With these problems, you might be given an equation as part of your information, but most likely you have to write an equation or formula and solve for the answer. You may benefit from drawing a diagram on some of these questions, especially if the word problem refers to geometric shapes but doesn’t already include one. This can help you visualize the information you’re looking for (the measure of an angle, for example) and help you focus on the right concepts to find the solution.
When translating a word problem into a diagram, make sure you follow the set-up as described in the word problem to the best of your ability, and don’t be fooled by your own diagram. For example, a problem may mention a right triangle, so you draw one. You may end up drawing a diagram that looks like a 45-45-90 triangle, but the problem is actually dealing with a 30-60-90 triangle. By labeling all of the information on your diagram and making a mental note that your drawings aren’t to scale, you can quickly make sense of most problems.
Defining and interpreting. With these types of problems, you often have the equation or formula given to you, and you just need to explain how a part of it works. If you’re not sure, consider whether you’re being asked about a constant or a variable, and eliminate any choices that don’t correspond to the type of value you’re looking at. You can also test the equation with different numbers to see how the value in question influences the equation.
Some problems involve your knowledge of statistical topics, such as understanding how to draw conclusions from surveys, or what factors affect standard deviation. For many of these problems, you’ll need to review these concepts in order to form the correct conclusion.
Examples of SAT Math Word Problems
The following example problems come from the College Board’s free SAT practice tests.
Example of Creating an Equation/Formula
How to solve: We can tell we need to come up with our own formula based on the answer choices and the word “represents” in the problem’s question. We need to find the formula that represents what the original price of a laptop was in terms of p, what Alma paid for it.
Let’s make x the original price of the laptop. In this case, x would be multiplied by .8 to get to the sales price (representing the 20% discount). The sales prices would then be multiplied by 1.08 to account for sales tax. This means that p=(1.08)(0.8)(x). We need to isolate x, so we need to divide both sides by 1.08 and 0.8. That gives us D as the correct answer.
Alternate method: Many problems requiring you to create your own equation are not too difficult, but they can get tricky when there are several steps involved or several variables. You can substitute a number for the variable you’re solving for to find the solution that way. For example, you can set $100 to be the original price of the laptop. Multiply it by .8 to find the sales price, and then by 1.08 to find the price that Alma paid. Then plug the price Alma paid into the answer choices to find the correct answer.
Example of Solving for a Value
How to solve: The word “maximum” tips us off that we are looking for a specific value and that we’ll be dealing with an inequality (see above). Given the information in the problem, we can write this inequality to start: (weight of driver) + (weight of truck) + (14x, or the weight of the boxes) ≤ 6000.
Because we’re told that the weight of the driver and the truck equals 4,500, we can replace that part of the equation: 4500 + 14x ≤ 6000. Now, all we need to do is solve for x. Subtract 4500 from both sides to get 14x ≤ 1500. Then divide both sides by 14 to get x ≤ 107.14… The answer is thus 107.
Note: Pay close attention to how you need to round when working with inequalities. Although this particular decimal probably wouldn’t have made you think to round up, if the result of the division had been 107.9999 you should still round down in this case because the number you’re looking for needs to be less than that value.
Example of Defining/Interpreting
How to solve: Again, the use of the word “interpretation” lets us know what type of problem we’re dealing with. In this case, 12 is a coefficient for the variables n and h, which are the number of landscapers and the number of hours respectively. We can thus rule out choices B and D, since those answers define 12 as a constant in place of these variables.
Since this equation is used to calculate the price of a job, we can be sure 12 represents a dollar amount as reflected in choices A and C. To figure out how things are affected, we can substitute simple numbers for n and h. When both are equal to 1 (there is one landscaper who works for one hour), then 12nh=12(1)(1)=12. When we increase both of these numbers to two, then 12nh=12(2)(2)=48. We can thus rule out C, because the price increased by more than 12 when we added another hour. Choice A is the best interpretation.
How to solve: This is an interpretation problem dealing with statistical concepts rather than interpreting an equation. To be able to “solve” you’d need to know what factors contribute to a reliable conclusion and see what was missing from this survey set-up. In this case, the correct answer is D.
In order for reliable conclusions to be drawn, a sample must be selected at random from the population to ensure that the sample is representative of the population, which in this case is the entire town. By choosing people at the same restaurant on one day, the researcher is possibly biasing their results by narrowing their sample to “people who like this one restaurant.” Because the sample is not representative, choice D identifies the factor that makes the conclusion unreliable. The other choices are factors that, given what we know from the problem, don’t negatively impact the conclusion.
SAT Math Word Problems Tips
As you may have noticed in the last example, you’ll still need to be familiar with math concepts and understand how they might show up in different situations to really feel confident taking any problem on. Here are a couple of other tips worth mentioning:
For most problems, there is more than one way to solve it. We showed this with the first example, where we provided an alternate method for solving a problem. If you find yourself stumped on a problem (we’ve all been there!), then move on to other problems and return to the one that tripped you up later. You may find that you see what you need to do more clearly.
Read carefully. The SAT test makers put a lot of care into how they write math word problems. Be sure to carefully read the question so that you don’t misread something and solve for the wrong thing. (The test makers may even include the answers that result from these common misreadings in the choices!). It’s difficult to read a question correctly once you’ve misread it. If you’re a fast reader who tends to skip over things, try mouthing the words silently as you read. It will force you to slow down just enough that you won’t miss anything, but not so much that you won’t have time to finish the test.
In general, preparing for the SAT Math section requires a multi-faceted approach. You need to be able to identify the types of questions you’re dealing with, know mathematical concepts and how to use them, and deal with other testing issues like rushing through the end or dealing with test anxiety. To help you get started, check out our free SAT Guide that includes 8 of our best test prep tips!
For more information about preparing for the SAT, check out these posts below:
30 SAT Math Formulas You Need to Know
25 Tips and Tricks for the SAT
5 Common SAT Math Mistakes to Avoid
Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!
Word problems used to be the bane of my existence as a new teacher. Thankfully, I learned new strategies and resources to help me implement and teach word problem strategies all year. To be honest, teaching word problems all year was the ONE thing that I did that had the greatest impact (if you are interested in more information about word problems and how I teach them, see the links at the bottom of this article). On this post, I will share one of those word problem strategies that involves helping students think through and analyze word problems using graphic organizers or word problem mats.
Teaching Word Problem Strategies with Word Problem Organizers
These word problem graphic organizers/mats help walk students through the thinking and analyzing process that is automatic for us. Through this analysis, the students have a better chance of comprehending the word problem, choosing the correct operation to solve it, and determining if their answers make sense.
In the same manner that we teach students to comprehend texts, we should also teach them how to breakdown and analyze a word problem. Using graphic organizers/mats helps break the process down into manageable steps for the students.
The free download (available a few sections down) has several different versions to allow you to choose which works best for your students and their needs. Having the different versions will also allow you to differentiate the organizers.
My go to version to begin with has the students following these steps:
- What operation are you planning to use? Write or underline the evidence from the problem that supports that operation.
- Solve the problem and show your math work.
- Write the answer in a complete sentence.
And here is an example from one of the more advanced organizers with more steps:
- Retell the problem in your own words.
- What operation are you thinking will solve this problem? Why?
- Solve the problem and show your math work.
- Write the answer to the problem in a complete sentence.
- Prove your answer is correct.
Using the Word Problem Organizers
You have a ton of variety in how you choose to use these organizers, however I definitely recommend following this sequence:
- Introduce the organizer/mat by going over the steps and how they help the student comprehend the word problem and/or organize their work. Understanding the purpose behind the organizer is huge with students because you don’t want them to view it as busy work.
- Model how to complete the organizer/mat whole group with at least one word problem (and more if the students need it and depending on the complexity of the organizer you choose).
- Allow the students to work in pairs or triads to complete the organizer as a form of guided practice before they are required to do so independently.
The graphic organizers/mats can also be used as a guide for students when discussing the word problem with partners. They don’t always have to fill in each part of it, but instead they can discuss some of the parts. This will give the same benefits in less time.
Also, placing the word problem organizers/mats in page protectors and letting the students use expo markers instantly makes it more engaging.
Here are some ways you can use these word problem mats to help your students practice analyzing word problems:
- Math centers
- Small group teaching
- Independent work
- Homework – send home a page protector and expo marker and let the students use the mats at home or they can use the mats as a guide as they work through word problems. These organizers will also help parents support students if they struggle with a word problem.
About the Digital Word Problem Organizers
There are digital versions of each of the word problem organizers included in the download below. The digital access link can be found on page 6. Each slide has text boxes for students to type into and interactive ways to complete some of the tasks.
The digital organizers are available in two versions, one with a designated spot to write a word problem and one without the space.
Should the students use the mat with every word problem they solve?
They certainly can (especially if you use dry erase markers and/or have them discuss some of the parts instead of recording it all) but they don’t have to. Using the organizers will help them work through complex problems but will take more time. When I use these in math centers, I only require one word problem to be worked on fully on the more advanced organizers. However this depends on the mat you choose. Some of them are more simple and don’t require any extra work- the mat simply organizes the work they would already do.
Download the Word Problem Strategies Mats
Click here or on the image to download the Word Problem Mats. Remember there are several versions so you can choose the ones that work best for your grade level and your students’ needs.
Need More Word Problem Strategies and Resources?
Check out these helpful resources, blog posts, and freebies for even more help teaching word problems.
Teaching Word Problems without Key Words (And What to Teach Instead)
Word Problem of the Day: FREE Starter Packs
8 Ways to Help Students Be Successful with Word Problems
Show the LOVE with Word Problems: Helping Students Answer Word Problems Effectively
Teaching Students How To Justify Answers in Math
Close Reading in Math Strategies and Freebies
10 Ways to Get Students Writing in Math
Solving Multi-Part Word Problems
4th Grade Word Problem of the Day TpT Resource
5th Grade Word Problem of the Day TpT Resource
The task card word problems shown in the images are part of my task card collections for 3rd-5th grade math. Click on the links below if you wish to see these resources in your grade level.
3rd Grade Common Core Math Task Card Collection
4th Grade Common Core Math Task Card Collection
5th Grade Common Core Math Task Card Collection
In the first post in this series, I spoke about the AND and the OR probability rules. Now, we will focus on probability questions involving the “at least” probability.
The complement rule
There is a very simple and very important rule relating P(A) and P(not A), linking the probability of any event happening with the probability of that same event not happening. For any well-defined event, it’s 100% true that either the event happens or it doesn’t happen.
The GMAT will not ask you probability question about bizarre events in which, for example, you can’t tell whether or not the event happened, or complex events which could, in some sense, both happen and not happen. For any event A in a probability question on the GMAT, the two scenarios “A happens” and “A doesn’t happen” exhaust the possibilities that could take place.
With certainty, we can say: one of those two will occur. In other words:
P(A OR not A) = 1
Having a probability of 1 means guaranteed certainty. Obviously, for a variety of deep logical reasons, the events “A” and “not A” are disjoint and have no overlap. The OR rule, discussed in the last post, implies:
P(A) + P(not A) = 1
Subtract the first term to isolate P(not A).
P(not A) = 1 – P(A)
- That is known in probability as the complement rule, because the probabilistic region in which an event doesn’t occur complements the region in which it does occur.
This is a crucial idea in general, for all GMAT probability questions, and one that will be very important in solving “at least” questions in particular.
The complement of “at least” statements
Suppose event A is a statement involving words “at least”—how would we state what constituted “not A“? In other words, how do we negate an “at least” statement?
Let’s be concrete. Suppose there is some event that involves just two outcomes: success and failure. The event could be, for example, making a basketball free throw, or flipping a coin and getting heads. Now, suppose we have a “contest” involving ten of these events in a row, and we are counting the number of successes in these ten trials.
Let A be the event defined as: A = “there are at least 4 successes in these ten trials.” What outcomes would constitute “not A“? Well, let’s think about it. In ten trials, one could get zero successes, exactly one success, exactly two successes, all the way up to ten successes. There are eleven possible outcomes, the numbers from 0 – 10, for the number of successes one could get in 10 trials.
Consider the following: number of possible successes in ten trials:
0 1 2 3 4 5 6 7 8 9 10
The purple numbers are the members of A, the members of “at least 4 successes” in ten trials. Therefore, the green numbers are the complement space, the region of “not A.” In words, how would we describe the conditions that land you in the green region? We would say: “not A” = “three or fewer success” in ten trials. The negation, the opposite, of “at least four” is “three or fewer.”
Abstracting from this, the negation or opposite of “at least n” is the condition “(n – 1) or fewer.”
- One particularly interesting case of this is n = 1: the negation or opposite of “at least one” is “none.”
That last statement is a hugely important idea, arguably the key to solving most of the “at least” questions you will see on the GMAT.
Solving an “at least” question
The big idea for any “at least” question on the GMAT is:
- It is always easier to figure out the complement probability.
For example, in the above scenario of ten trials of some sort, calculating “at least 4” directly would involve seven different calculations (for the cases from 4 to 10), whereas the calculation of “three or fewer” would involve only four separate calculations (for the cases from 0 to 3).
In the extreme—and extremely common—case of “the probability of at least one”, the direct approach would involve a calculation for almost case, but the complement calculation simply involves calculating the probability for the “none” case, and then subtracting from one.
P(not A) = 1 – P(A)
P(at least one success) = 1 – P(no successes)
This is one of the most powerful time-saving shortcuts on the entire GMAT.
An example calculation
Consider the following simple question.
Two dice are rolled. What is the probability of at least one of the dice rolling a 6?
It turns out, calculating that directly would involve a relatively long calculation — the probability of exactly one 6, on either die, and the rare probability of both coming up 6’s. That calculation easily could take several minutes.
Instead, we will use the shortcut defined above:
P(not A) = 1 – P(A)
P(at least one 6) = 1 – P(no 6’s)
What’s the probability of both dice coming up no 6’s? Well, first, let’s consider one die. The probability of rolling a 6 is 1/6, so the probability of rolling something other than 6 (“not 6”) is 5/6.
P(two rolls, no 6’s) = P(“not 6” on dice #1 AND “not 6” on dice #2)
As we found in the previous post, the word AND means multiply. (Clearly, the outcome of each die is independent of the other). Thus:
P(two rolls, no 6’s) =(5/6)*(5/6) = 25/36
P(at least one 6) = 1 – P(no 6’s) = 1 – 25/36 = 11/36
What could have been a long calculation becomes remarkably straightforward by means of this shortcut. This can be an enormous time-saver on the GMAT!
Practice
Now that you’ve read this post, take shot at these three practice questions before reading the answers and explanations below.
Set #1 = {A, B, C, D, E}
Set #2 = {K, L, M, N, O, P}
- There are these two sets of letters, and you are going to pick exactly one letter from each set. What is the probability of at least one vowel being picked?
- 1/6
- 1/3
- 1/2
- 2/3
- 5/6
Show answer and explanation
P(at least one vowel) = 1 – P(no vowels)
The probability of picking no vowel from the first set is 3/5. The probability of picking no vowel from the second set is 5/6. In order to get no vowels at all, we need no vowels from the first set AND no vowels from the second set. According to the AND rule, we multiply those probabilities.
P(no vowels) = (3/5)*(5/6) = 1/2
P(at least one vowel) = 1 – P(no vowels) = 1 – 1/2 = 1/2
Answer = C
- Suppose you flip a fair coin six times. What is the probability of at least one head in six flips?
- 5/8
- 13/16
- 15/16
- 31/32
- 63/64
Show answer and explanation
P(at least one H) = 1 – P(no H’s)
In one flip, P(“not H”) = P(T) = 1/2. We would need to have this happen six times—that is to say, six independent events joined by AND, which means they are multiplied together.
Answer = E
- In a certain game, you pick a card from a standard deck of 52 cards. If the card is a heart, you win. If the card is not a heart, the person replaces the card to the deck, reshuffles, and draws again. The person keeps repeating that process until he picks a heart, and the point is to measure: how many draws did it take before the person picked a heart and won? What is the probability that one will have at least two “heartless” draws on the first two draws, not picking the first heart until at least the third draw?
- 1/2
- 9/16
- 11/16
- 13/16
- 15/16
Show answer and explanation
A full deck of 52 cards contains 13 cards from each of the four suits. The probability of drawing a heart from a full deck is 1/4. Therefore, the probability of “not heart” is 3/4.
P(at least three draws to win) = 1 – P(win in two or fewer draws)
Furthermore,
P(win in two or fewer draws) = P(win in one draw OR win in two draws)
= P(win in one draw) + P(win in two draws)
Winning in one draw means: I select one card from a full deck, and it turns out to be a heart. Above, we already said: the probability of this is 1/4.
P(win in one draw) = 1/4
Winning in two draws means: my first draw is “not heart”, P = 3/4, AND the second draw is a heart, P = 1/4. Because we replace and re-shuffle, the draws are independent, so the AND means multiply.
P(win in two draws) =(3/4)*(1/4) = 3/16
P(win in two or fewer draws) = P(win in one draw) + P(win in two draws)
= 1/4 + 3/16 = 7/16
P(at least three draws to win) = 1 – P(win in two or fewer draws)
= 1 – 7/16 = 9/16
Answer = B
Bonus Question
The probability is 0.6 that an “unfair” coin will turn up tails on any given toss. If the coin is tossed 3 times, what is the probability that at least one of the tosses will turn up tails?
0.064
0.36
0.64
0.784
0.936
Click here for the answer and video explanation!
The next article in this series will explore probability questions that involve counting techniques.
-
Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as «member of the month» for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.
View all posts
We recommend reading any word problem at least three times. By the conclusion of the third reading, you should be magically whisked away to your home in Kansas.
Read it once…
…to get a general idea of what’s going on. Is the problem about money? Height and width? Distances? Money? Yeah, we already said money, but it’s important. Can you draw a picture in the margin that helps you visualize the problem?
Twice…
…to translate from English into math. Read the problem carefully this time, figuring out which pieces of information are important and which ones aren’t. Then ignore the unnecessary bits. This may sound a bit harsh, but they’re big boys. They’ll get over it.
Three times…
…a lady. Wait, that’s not it.
…to make sure you answered the right question. To be sure, read the question one last time before drawing a box around your final answer. Even if this method of double-checking saves you only once out of every 100 times, it’ll help you in the long run. One out of 100 is better than zero out of 100, but now we’re moving into some advanced mathematics.
Sample Problem
The local department store was having a sale. Holla! Gabe bought a pair of shoes for $21, although they would’ve been cheaper if he’d bought penny loafers. He also bought some shirts that were on sale for 25% off their normal retail price of $18 each. Gabe, always the bargain hunter, spent $75 total. How many shirts did he buy? Also, does he really think any of them will go with those shoes?
Read the problem:
Once…
…for a general idea of what’s going on: Gabe went shopping and spent money. Sounds like an old familiar story. Time for an intervention, friends of Gabe. Preferably before he maxes out his Diner’s Club card.
Now we need to figure out how many shirts he bought, so we read the problem:
Twice…
…to translate from English into math. Remember, we can translate a bit at a time, sort of like how Gabe pays for some of his major purchases when he has them on layaway. Sheesh, Gabe. Get a hold of yourself.
(total amount Gabe spent) = (amount he spent on shoes) + (amount he spent on shirts)
We know he spent $75 total, of which $21 was spent on shoes. This gives us the equation:
$75 = 21 + (amount he spent on shirts)
The problem has gotten smaller. It’s depressing when that happens with cake, but great when it happens to a word problem. Now all we need to do is come up with a symbolic expression for how much Gabe spent on shirts, or the cost per shirt times the number of shirts:
(amount he spent on shirts) = (cost per shirt)(number of shirts)
Since the shirts are 25% off their normal price of $18, they cost $18 – 0.25(18) = $13.50 each. What a deal, and real polyester, too!
We need to introduce a variable for the number of shirts; s will do the trick nicely.
(amount he spent on shirts) = 13.5s
When we plug this into the earlier equation, we find that:
75 = 21 + 13.5s
Finally, we’ve reduced this thing to a super-simple-looking equation! Good riddance, vestiges of language! Begone, nouns and verbs!
Things look much nicer now, right? No worrying about shirts or shoes or prices or Gabe’s uncontrollable shopping addiction. For the moment, we can forget about the word problem and solve the equation. The answer is s = 4, by the way. In case you were interested.
Three times…
…to make sure we’re answering the right question. We want to know how many shirts Gabe bought. Is that the answer we arrived at? We found that s = 4, and s was the number of shirts Gabe bought, so we’re all done. Four new shirts for Gabe, and three of them feature a Hawaiian pattern. Gabe, if you insist on buying far more clothes than you need, can’t you at least have a decent fashion sense?
When translating from English into math, some information can be ignored. We don’t care that «the local department store was having a sale.» Gabe might, but we certainly don’t. We care about statements that tell us numbers, and statements that tell us what the question is. Any extraneous information has been placed there simply as a decoy. We’re not going to fall for that. Wait a second…two for one? We’ll grab our jacket and meet you there.
Some people find it helpful to underline the important pieces of information in a word problem. You’re like an actor highlighting in a script the lines that are important for him to remember. Unlike an actor, however, you can always look back at the original problem if you draw a blank. Also, you don’t need to wear any stage makeup.
In the problem we just did, the important bits might look something like this:
The local department store was having a sale. Gabe bought a pair of shoes for $21 and some shirts that were on sale for 25% off their normal retail price of $18 each. If Gabe spent $75 total, how many shirts did he buy?
As you practice, you’ll become better at figuring out which parts of the word problem you can ignore and which parts are important.