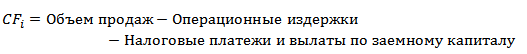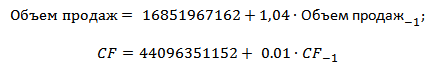Arima в excel пример - Word и Excel - помощь в работе с программами

Модель arima пример в excel

Перед тем, как применять модель необходимо позаботиться о стационарности динамического ряда.

Ряд приводят к стационарности взятием последовательных разностей (вместо исходных 3,5,5,4,8 получится 2,0,-1,4) или преобразованием Бокса-Кокса. Стабилизировать дисперсию помогает логарифмирование.

Критерий Льюнга-Бокса — критерий для выявления автокоррелированности временных рядов.
Критерий KPSS (KPSS test) — критерий для проверки на стационарность (Hо = ряд стационарен).
Критерий Дики-Фулера — критерий для проверки на стационарность (Но = ряд нестационарен).

Лучшая модель подбирается с помощью AIC. Модель с самым низким значением информационного критерия Акаике (не несет абсолютную оценку, используется только для сравнения моделей между собой) нужно проверить на адекватность путем анализа остатков (разницы между фактическими и прогнозными значениями).

Нужно убедиться, что остатки:

имеют низкое абсолютное значение, в них отсутствует тренд и циклы;
распределены нормально со средним

отсутствует автокорреляция (смотрим коррелограмму и тесты «Box-Pierce» «Ljung-Box»).

Если хотя бы что-то не так — значит модель описала не всю структуру и качество можно улучшать. Возвращаемся назад для подбора лучших параметров или преобразования исходных данных.

1. Построить график. Удалить выбросы, заменить пропущенные значения, декомпозировать ряд.

2. Обратить внимание на дисперсию, сезонность и тренд. В случае необходимости применить логарифмирование для стабилизации дисперсии или преобразование Бокса-Кокса / последовательные разности для приведения к стационарности.

3. Убедиться в стационарности ряда при помощи критерия Дики-Фуллера или теста KPSS.

4. Отобразить ACF и PACF функции, сделать предположение о модели и порядке параметров.

5. Использовать информационный критерий AIC выбора лучшей модели.
Или просто воспользоваться автотюнингом: язык программирования R > library(forecast) > auto.arima()

6. Построить ACF график остатков лучшей модели, убедиться в отсутствии корреляции остатков (тест Бокса-Кокса).

7. Если остатки выглядят как белый шум и это подтверждено тестом, то можно приступать к прогнозированию.

8. Оценить точность кросс-валидацией или прогнозом по укороченному ряду.

Некоторые динамические ряды не имеют устойчивой структуры и сильно зависят от влияния внешних факторов (например: погода, рекламный бюджет). В таких случаях целесообразно применить математическое моделирование. Подойдет простая регрессия, нейронные сеточки, случайные леса, ближайшие соседи, SVM или ансамбль из всех перечисленных (зависит от типа, распределения и объема исходных данных).

Алгоритмы будут сопоставлять весь массив входных данных (предикторов) и соответствующих значений целевой переменной (т.е. уровня продаж). Такой процесс называется «обучением». Методы машинного обучения как бы обобщают полученный опыт для ответов на новые вопросы. Гиперпараметры подгоняются так, чтобы ошибка прогнозов была минимальной.

Выбор алгоритмов их их параметров оказывают большое влияние на точность прогнозов, но определяющую роль играет набор признаков, т.е. состав переменных на которых будет будет обучаться алгоритм. При выборе признаков руководствуются физическими ограничениями, так как не все получается оцифровать и измерить (или сделать это за приемлемую цену).

Специалист из предметной области определяет набор данных, которые необходимо получить и использовать для моделирования. Если таких данных много в уже оцифрованном виде, то применяются математические методы селекции: корреляция (correlation), хи-квадрат (chi-square), мера энтропии (Informaition gain), индекс Джини (GINI index), расчет уменьшения предсказательной способности при исключении переменной, рекурсивное разбиение (Recursive partitioning), сети векторного квантования (Learning Vector Quantization) и др.

Перечислим полезные лайфхаки:

Цикличность можно закодировать категориальным фактором (день недели или месяца) или числовой переменной, которая отражает средний уровень целевой переменной за этот период.
Погоду, курсы валют и ставки ЦБ можно получать напрямую через API или скрапингом. Благодаря этому ваша модель будет работать без ручного обогащения новыми данными.
Результаты прогноза по ARIMA-моделям могут быть поданы на вход другим алгоритмам для дальнейшего сокращения остатков.

Планирование денежных потоков по модели AR. Пример расчета в Excel

Рассмотрим планирование продаж и денежных потоков помощью авторегрессионной модели. Оценка будущих денежных поступлений важна как для собственника компании, так и инвесторам для определения ее эффективности в перспективе.

Планирование продаж и денежных потоков предприятия

Прогнозирование продаж и денежных потоков является важной задачей компании. Оценка будущих поступлений от реализации продукции позволяет планировать денежные потоки, которые могут быть направлены на повышение эффективности, производительности и стоимости предприятия для инвесторов.

Цель оценки объема продаж – оценка результативности и эффективности предприятия, точки безубыточности и финансового запаса прочности в перспективе.

Цель оценки денежных потоков – оценка потенциала компании для развития инноваций и реализации инвестиционных проектов.

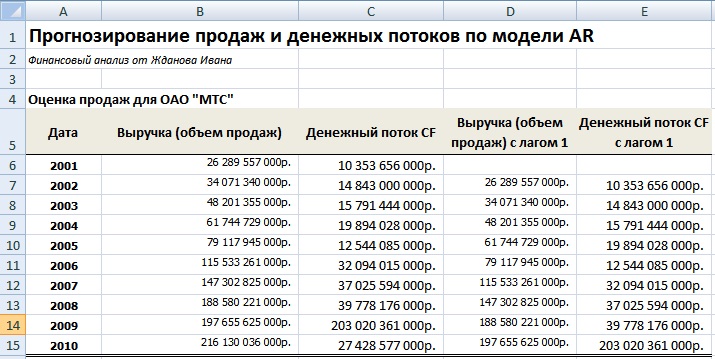
Продажи компании и денежные потоки тесно взаимосвязаны между собой следующей формулой:

Методы планирования продаж и денежных потоков

Существует множество различных методов прогнозирования объема продаж (денежных потоков): модель скользящего среднего (MA, Moving Average), модель авторегрессии (AR, AutoRegressive), модель авторегрессии скользящего среднего (Autoregressive Moving Average model, ARMA), модель Бокса-Дженкинса и др. В данной статье мы более подробно разберем прогнозирование с помощью модели авторегрессии.

Авторегрессионные модели (англ. AR, AutoRegressive model) используются для описания устойчивых (стационарных) процессов в экономике, когда на будущие значения прогнозируемой величины влияют предыдущие значения. Авторегрессионные модели (AR) используются в прогнозировании как макроэкономических показателей (ВВП, инфляция и др.), так и для оценки микроэкономических показателей: объем будущих продаж, чистой прибыли, размера денежных потоков т.д.

Модель прогнозирования продаж и денежных потоков

Авторегрессионная модель планирования объема продаж и денежных потоков имеет следующий аналитический вид:

где:

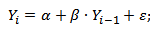
Y_i – прогноз денежного потока или объема продаж;

Y_i_-1 – значение денежного потока и продаж в предыдущем периоде;

α, β – коэффициенты в модели авторегрессии;

ξ – случайная величина (белый шум).

Пример планирования продаж и денежных потоков предприятия ОАО «МТС» в Excel

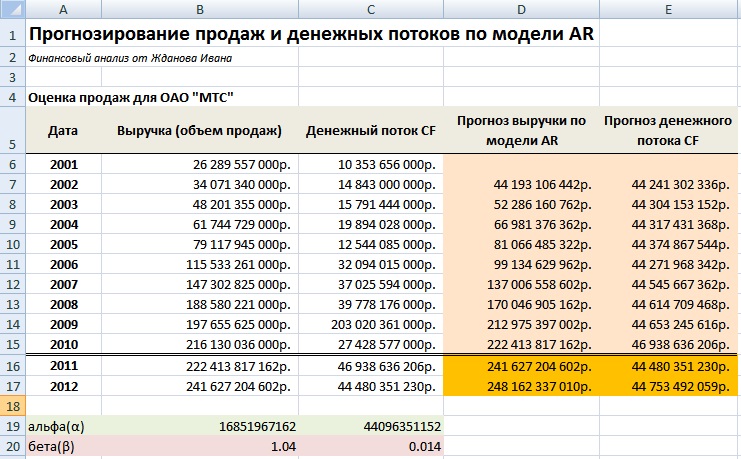
Разберем практический пример планирования продаж (выручки) и объема денежных потоков предприятия ОАО «МТС». Данное предприятие было выбрано для анализа, потому что имеет устойчивую сеть дистрибьюторов и постоянный спрос на продукцию, что позволяет адекватно сделать оценку. На рисунке ниже представлена выручка и денежный поток компании за 10 лет. Данные были взяты из официальной отчетности предприятия. Денежные потоки представляли собой сумму чистой прибыли предприятия и амортизации (Форма №5 стр. 640 + Форма №2 стр. 190).

Объем продаж и денежный поток для ОАО “МТС”

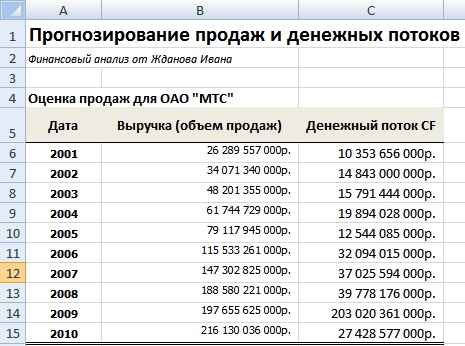
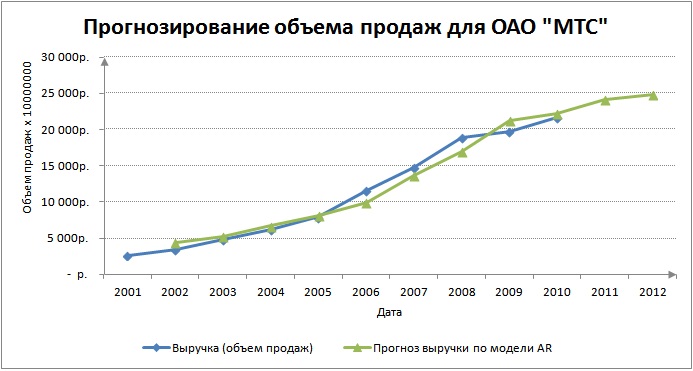
Графически изменение объема продажи и денежного потока имеет следующий вид:

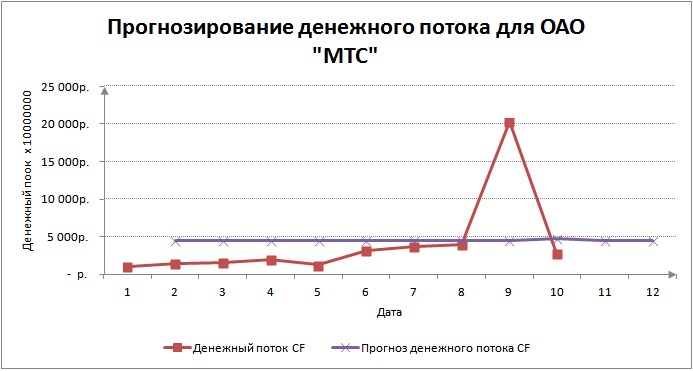
Как мы видим из рисунка, денежный поток компании резко изменился в 2009 году из-за большого размера начисленной амортизации, что сильно искажает динамику изменения денежного потока. Сделаем прогноз на два года вперед объема продаж и денежного потока предприятия по модели AR.

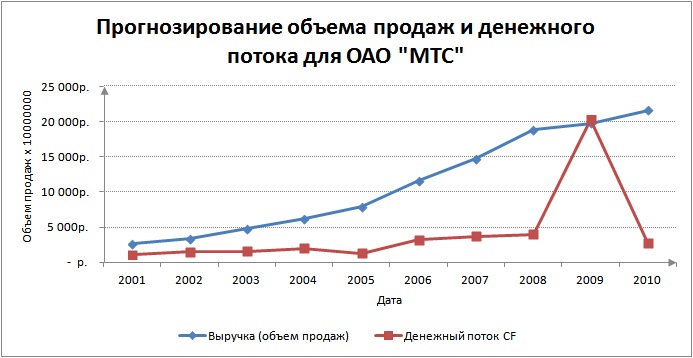
Первоначально для построения модели необходимо определить тесноту связи между ближайшими значениями продаж (денежного потока). Для этого необходимо произвести оценку регрессии со сдвигом ряда объема продаж. Был взят лаг в один год, потому что максимальное влияние на будущие значения оказывают именно предыдущие продажи.

Расчет авторегрессии для объема продаж и денежного потока в Excel

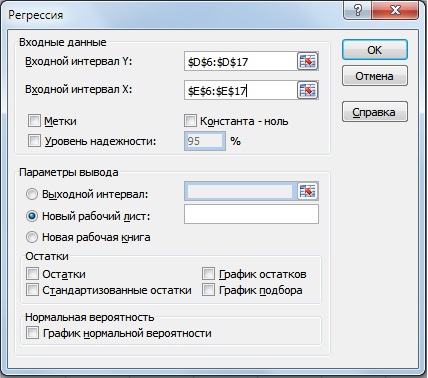
На следующем этапе необходимо рассчитать значения коэффициентов регрессии между рядами и рядами с лагами в один год. Воспользуемся надстройкой: Главное меню Excel → «Данные» → «Анализ данных» → «Регрессия». Рассчитаем параметры отдельно для прогнозирования выручки и денежного потока. Пример оценки объема продаж представлен на рисунке ниже.

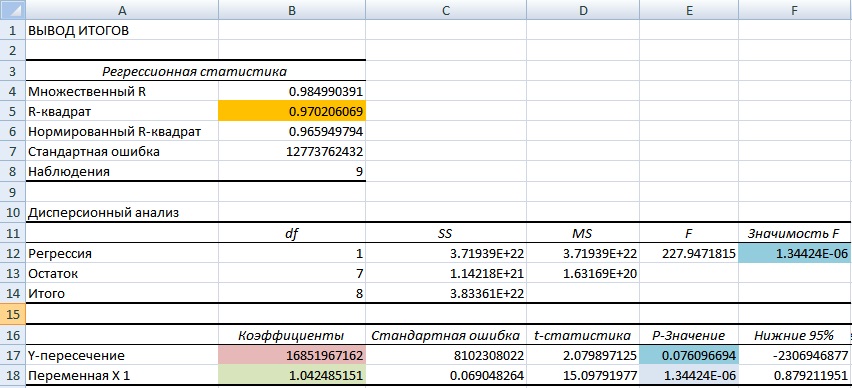
Мы получили базовые значения в модели регрессии для выручки (объема продаж). Так коэффициент альфа (α) в модели регрессии равен 16851967162, а коэффициент бета (β) 1,04. Полученная статистика по регрессионной модели имеет следующие важные показатели оценки ее адекватности и точности прогнозирования. Первое на что следует обратить внимание это показатель R-квадрат (коэффициент детерминации), который показывает качество модели в шкале от 0 до 1. В нашем примере качество модели высокое и составляет 0,97. Показатель модели критерий-F близок к 0, что показывает устойчивость модели. Статистический показатель P-значение отражает адекватность значений данных коэффициент (альфа, бета) для полученной модели он меньше 15% для обоих коэффициентов, что удовлетворяет нормативам.

Показатели оценки качества регрессионной модели в Excel

Аналогично строится модель планирования денежных потоков предприятия. В результате полученные модели прогнозирования объема продаж и денежных потоков описываются с помощью следующих уравнений:

Сделаем прогноз на основе полученных моделей значений объема продажи и денежного потока на два года вперед. С помощью формул в Excel сделаем прогноз по модели.

Прогноз продаж по модели AR =$B$19+B6*$B$20

Планирование продаж и денежных потоков предприятия по модели авторегрессии в Excel

Визуально планирование продаж будет иметь следующий вид. Наблюдается повышающийся тренд на два года вперед.

График прогноза объема продаж (выручки) предприятия

Графически прогноз денежного потока на два года вперед сильно не изменится.

Прогнозирование денежного потока предприятия по модели авторегрессии (AR)

Использование методов прогнозирования денежных потоков позволяет оценить показатели эффективности инвестиционных проектов, более подробно про методы оценки проектов читайте в моей статье: “6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI“. Существуют также другие методы планирования объемов продаж компании: XYZ-анализ, ABC-анализ, которые тоже зарекомендовали себя на практике. Так метод ABC анализа на практическом примере разобран в статье: “ABC анализ продаж. Пример расчета в Excel“.

Мастер-класс: “Как рассчитать план продаж”

Резюме

Использование методов авторегресси (AR) для планирования будущих объемов продаж (денежного потока) обосновано, если предприятие имеет устойчивую сеть дистрибьюторов и покупателей на свою продукцию. Достоинством использования данного метода оценки является возможность учета влияния предыдущего объема продаж (денежного потока) на будущие значения. В ситуациях экономического кризиса и нестабильности оценка может сильно изменяться под воздействием макроэкономических факторов и глобальных трендов.

Автор: к.э.н. Жданов Иван Юрьевич

Модель ARIMA

Модель ARIMA в определенной степени является расширенной версией модели ARMA. Символ I (Integrated) отвечает за порядок оператора последовательной разности. Дело в том, что далеко не все ряды являются стационарными, но некоторые из них могут быть приведены к стационарным путем взятия последовательной разности. Если, например, временной ряд у, стал стационарным после взятия последовательной разности порядка s и для описания уже стационарного ряда может быть использована модель ARMA (р, q), то процессу, называется интегрированным процессом авторегрессии и скользящей средней (ARIMA (р, s, q)).

При этом для оценки модели можно пользоваться несколько модифицированным подходом Бокса – Дженкинса. Непосредственно перед первым этапом необходимо будет привести исследуемый ряд к стационарному путем взятия последовательных разностей. Остальные этапы подхода не изменятся, после этого стационарный ряд нужно будет идентифицировать, оценить, диагностировать и использовать.

Примеры взятия последовательной разности

Рассмотрим примеры простейших нестационарных временных рядов, которые могут быть приведены к стационарным путем взятия последовательной разности.

1. Уравнение с трендом

Временной ряд с трендом имеет вид

где a + βt – временной тренд; ut – белый шум.

Таким образом, временной тренд состоит из детерминированной составляющей линейного тренда и случайной составляющей белого шума (рис. 8.7). Найдем математическое ожидание временного тренда:

Рис. 8.7. Тренд (модельный пример)

Как очевидно, математическое ожидание зависит от времени, следовательно, ряд не является стационарным.

Для того чтобы привести ряд с линейный трендом к стационарному, нужно взять первую разность:

Возможен временной ряд с квадратичным временным трендом и временными трендами высших порядков. Для приведения их к стационарному ряду необходимо взятие последовательной разности тех же порядков. Так, например, чтобы привести к стационарному временной квадратичный тренд, нужно дважды взять последовательную разность:

где вторая последовательная разность – стационарный ряд.

2. Случайное блуждание

Модель случайного блуждания уже описывалась ранее. Уравнение модели имеет вид

где иt – белый шум.

Случайное блуждание – классический пример нестационарного ряда. Однако, чтобы привести его к стационарному, нужно просто взять первую разность:

Первая разность случайного блуждания равняется белому шуму, следовательно, стационарна по определению.

3. Временной ряд с сезонностью•

Сезонность часто встречается в статистических данных.

В различных процессах сезонная составляющая может встречаться практически с любой частотой: месячная сезонная компонента, квартальная сезонная компонента, полугодовая сезонная компонента:

где

Рис. 8.8. Сезонность (модельный пример)

Для того чтобы привести с сезонность к стационарному ряду, необходимо взять сезонную последовательную разность. Так, например, для квартальной сезонной компоненты

При этом сезонная последовательная разность Δ4у, будет стационарным временным рядом (рис. 8.8).

Пример построения модели ARIMA

В качестве иллюстрирующего примера используем модель ARIMA для ряда значений индекса DAX со 2 апреля 1998 г. по 23 октября 2007 г. (рис. 8.9).

Первым шагом необходимо определить, является ли рассматриваемый ряд стационарным. Визуально анализ графика ряда не говорит о стационарности ряда. Необходимо провести дополнительный анализ.

Вторым шагом должно быть построение диаграммы выборочных автокорреляционной и частной автокорреляционной функций.

Рис. 8.9. Индекс DAX со 2 апреля 1998 г. по 23 октября 2007 г.

Таблица 8.13. Диаграмма автокорреляционных функций по лагам для DAX

Документация

Спецификации модели ARIMA

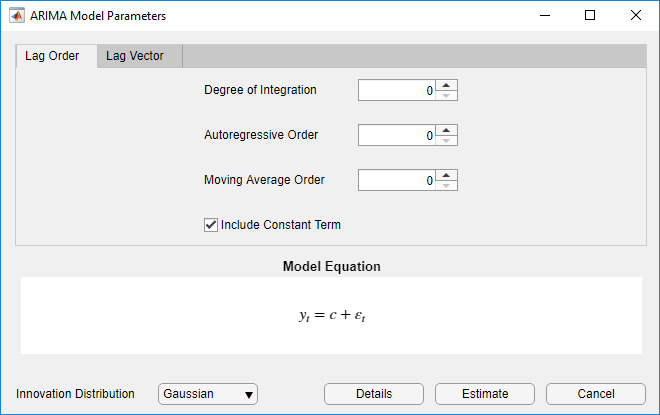
Модель ARIMA по умолчанию

В этом примере показано, как использовать краткий arima(p,D,q) синтаксис, чтобы задать ARIMA по умолчанию ( p , D , q ) модель,

Δ D y t = c + ϕ 1 Δ D y t — 1 + … + ϕ p Δ D y t — p + ε t + θ 1 ε t — 1 + … + θ q ε t — q ,

где Δ D y t isa D t h временные ряды differenced. Можно написать эту модель в сжатой форме с помощью обозначения оператора задержки:

ϕ ( L ) ( 1 — L ) D y t = c + θ ( L ) ε t .

По умолчанию все параметры в созданном объекте модели имеют неизвестные значения, и инновационное распределение является Гауссовым с постоянным отклонением.

Задайте модель ARIMA (1,1,1) по умолчанию:

Выход показывает что созданный объект модели, model , имеет NaN значения для всех параметров модели: постоянный термин, AR и коэффициенты MA и отклонение. Можно изменить созданную модель с помощью записи через точку или ввести его (наряду с данными) к estimate .

Свойство P имеет значение 2 ( p + D ). Это — количество преддемонстрационных наблюдений, должен был инициализировать модель AR.

Модель ARIMA с известными значениями параметров

В этом примере показано, как задать ARIMA ( p , D , q ) модель с известными значениями параметров. Можно использовать такую полностью заданную модель в качестве входа к simulate или forecast .

Задайте модель ARIMA (2,1,1)

Δ y t = 0 . 4 + 0 . 8 Δ y t — 1 — 0 . 3 Δ y t — 2 + ε t + 0 . 5 ε t — 1 ,

где инновационное распределение является t Студента с 10 степенями свободы и постоянным отклонением 0.15.

Аргумент пары «имя-значение» D задает степень несезонного интегрирования (D) .

Поскольку все значения параметров заданы, созданный объект модели не имеет никакого NaN значения. Функции simulate и forecast не принимайте входные модели с NaN значения.

Задайте модель ARIMA Используя приложение Econometric Modeler

В приложении Econometric Modeler можно задать структуру задержки, присутствие константы, и инновационное распределение ARIMA (p, D, q) модель путем выполнения этих шагов. Все заданные коэффициенты являются неизвестными но допускающими оценку параметрами.

В командной строке откройте приложение Econometric Modeler.

В качестве альтернативы откройте приложение из галереи приложений (см. Econometric Modeler).

В Data Browser выберите ряд времени отклика, к которому модель будет подходящей.

На вкладке Econometric Modeler, в разделе Models, нажимают ARIMA. Чтобы создать модели ARIMAX, см. Спецификации Модели ARIMAX.

Диалоговое окно ARIMA Model Parameters появляется.

Задайте структуру задержки. Чтобы задать ARIMA (p, D, q), модель, которая включает все задержки AR от 1 до p и всех задержек MA от 1 до q, использует вкладку Lag Order. Для гибкости, чтобы задать включение особых задержек, используйте вкладку Lag Vector. Для получения дополнительной информации смотрите Полиномы Оператора Задержки Определения В интерактивном режиме. Независимо от вкладки вы используете, можно проверить форму модели путем осмотра уравнения в разделе Model Equation .

Задавать модель ARIMA (3,1,2), которая включает константу, включает весь последовательный AR и задержки MA от 1 до их соответствующих порядков, и имеет Гауссово инновационное распределение:

Установите Degree of Integration на 1 .

Установите Autoregressive Order на 3 .

Установите Moving Average Order на 2 .

Задавать модель ARIMA (3,1,2), которая включает весь AR и задержки MA от 1 до их соответствующих порядков, имеет Распределение Гаусса, но не включает константу:

Установите Degree of Integration на 1 .

Установите Autoregressive Order на 3 .

Установите Moving Average Order на 2 .

Снимите флажок Include Constant Term.

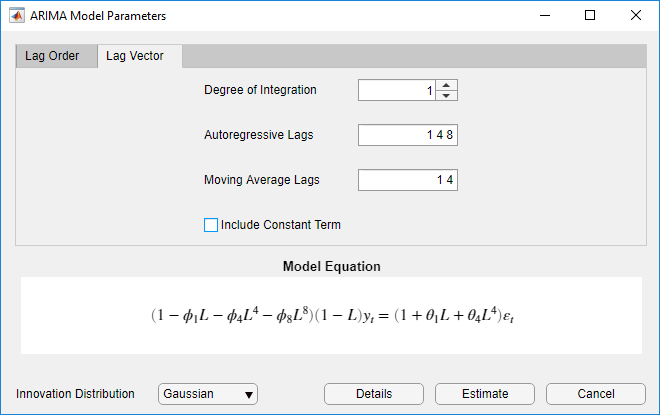
Задавать модель ARIMA (8,1,4), содержащую непоследовательные задержки

( 1 − ϕ 1 L − ϕ 4 L 4 − ϕ 8 L 8 ) ( 1 − L ) y t = ( 1 + θ 1 L 1 + θ 4 L 4 ) ε t ,

где _εt является серией Гауссовых инноваций IID:

Кликните по вкладке Lag Vector.

Установите Degree of Integration на 1 .

Установите Autoregressive Lags на 1 4 8 .

Установите Moving Average Lags на 1 4 .

Снимите флажок Include Constant Term.

Чтобы задать модель ARIMA (3,1,2), которая включает весь последовательный AR и задержки MA через их соответствующие порядки и постоянный термин, и имеет t — инновации распределения:

Установите Degree of Integration на 1 .

Установите Autoregressive Order на 3 .

Установите Moving Average Order на 2 .

Нажмите кнопку Innovation Distribution, затем выберите t .

Параметр степеней свободы распределения t является неизвестным, но допускающим оценку параметром.

После того, как вы зададите модель, нажмите Estimate, чтобы оценить все неизвестные параметры в модели.

Смотрите также

Приложения

Объекты

Функции

Связанные примеры

Больше о

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация Econometrics Toolbox

Поддержка

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

ARIMA

ARIMA models describe phenomena that evolve through time and predict future values. Run them in Excel using the XLSTAT add-on statistical software.

XLSTAT offers a wide selection of ARIMA models such as ARMA (Autoregressive Moving Average), ARIMA (Autoregressive Integrated Moving Average) or SARIMA (Seasonal Autoregressive Integrated Moving Average).

What are ARIMA models

The models of the ARIMA family allow to represent in a synthetic way phenomena that vary with time, and to predict future values with a confidence interval around the predictions.

The mathematical writing of the ARIMA models differs from one author to the other. The differences concern most of the time the sign of the coefficients. XLSTAT is using the most commonly found writing, used by most software. If we define by Xt a series with mean µ, then if the series is supposed to follow an ARIMA(p,d,q)(P,D,Q)s model, we can write:

[ Yt = (1 – B)d (1 – Bs)D Xt — µ ; Φ(B)Ø(Bs))Yt = θ(B) Θ(Bs) Zt, Zt∞N(0,σ2) ]

[ Φ(z) = 1 – Σpi=1 Φi zi, Ø(z)= 1 – Σpi=1 Øi zi ; θ(z) = 1 + Σqi=1 θi zi, Θ(z) = 1 + Σqi=1 Θi zi ]

p is the order of the autoregressive part of the model. q is the order of the moving average part of the model. d is the differencing order of the model. D is the differencing order of the seasonal part of the model. s is the period of the model (for example 12 if the data are monthly data, and if one noticed a yearly periodicity in the data). P is the order of the autoregressive seasonal part of the model. Q is the order of the moving average seasonal part of the model.

Remark 1: the Yt process is causal if and only if for any z such that |z|≤1, f(z)≠0 and q(z)≠0.
Remark 2: if D=0, the model is an ARIMA(p,d,q) model. In that case, P, Q and s are considered as null.
Remark 3: if d=0 and D=0, the model simplifies to an ARMA(p,q) model.
Remark 4: if d=0, D=0 and q=0, the model simplifies to an AR(p) model.
Remark 5: if d=0, D=0 and p=0, the model simplifies to an MA(q) model.

Explanatory variables

XLSTAT allows you to take into account explanatory variables through a linear model. Three different approaches are possible:

OLS: A linear regression model is fitted using the classical linear regression approach, then the residuals are modeled using an (S)ARIMA model.
CO-LS: If d or D and s are not zero, the data (including the explanatory variables) are differenced, then the corresponding ARMA model is fitted at the same time as the linear model coefficients using the Cochrane and Orcutt (1949) approach.
GLS: A linear regression model is fitted, then the residuals are modeled using an (S)ARIMA model, then we loop back to the regression step, in order to improve the likelihood of the model by changing the regression coefficients using a Newton-Raphson approach.

Note: if no differencing is requested (d=0 and D=0), and if there are no explanatory variables in the model, the constant of the model is estimated using CO-LS.

Источник

The forecasting approach is exactly as described in Real Statistics ARMA Data Analysis Tool. The only difference now is that we need to account for the differencing.

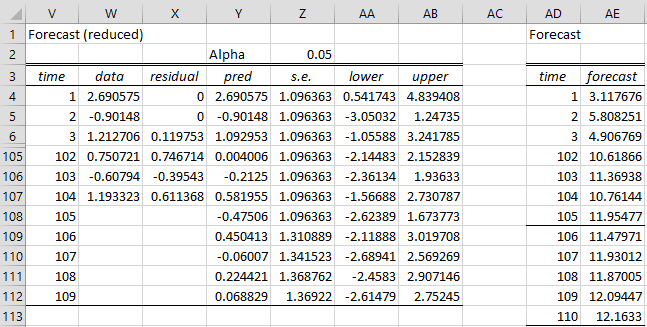
Example 1: Find the forecast for the next five terms in the time series from Example 1 of Real Statistics ARMA Data Analysis Tool based on the ARIMA(2,1,1) model without constant term.

Figure 1 – Forecast for ARIMA(2,1,1) model

The table on the left side is calculated exactly as in Figure 3 of Real Statistics ARMA Data Analysis Tool. The right side undoes the differencing. E.g. Cell AD4 contains the formula =B4 (with reference to the data in Figure 1 of Calculating ARIMA Model Coefficients). Cell AD109 contains the formula =X108+AD108.

Note that if you had not assumed that there was no constant term, cell AD109 would contain the formula =X108+AD108+J$6. If Differences is 2, then AD109 would contain the formula =X107+2*AD108-AD107+J$6.

Источник

Три подхода к прогнозированию продаж чего угодно

Заглядываем в будущее при помощи статистики

Качественные прогнозы приносят деньги

Из знания уровня будущих продаж предприниматели могут извлечь значительную выгоду: направить оборотные средства на более востребованные SKU, избежать упущенной выгоды, сократить долю просроченных и невостребованных товаров.

Методология прогнозирования экспортных продаж нефти и булочек в районном кафе будет отличаться, но в обоих случаях можно построить точные прогнозы при помощи Excel или специального статистического П.О.

Хотите систематизировать свои знания по аналитике?

Встречайте «Анализ данных для хулиганов» ✨
Нескучное онлайн пособие о том, как создавать великолепные продукты и эффективно управлять маркетингом на основе данных

Три подхода

Все модели можно разделить на три типа:

а) Простые и наивные методы. К ним относится простая экстраполяция на основе среднего значения или темпа прироста, подбор коэффициентов сезонности или продолжение тренда. Эти методы подходят для быстрого прогноза «на коленке».

б) Модели класса ARIMA. Особенности временных рядов заключается в том, что прошлые значения связаны с текущими и будущими. Для краткосрочного прогнозирования рядов с устойчивой структурой достаточно данных о продажах в прошлых периодах.

в) Математическое моделирование. Используются в случаях когда прогнозируемая переменная сильно зависит от внешних факторов: погода, ключевая ставка ЦБ, рекламный бюджет, уровень цен…

Подходы можно комбинировать для улучшения точности прогноза.

ОПРЕДЕЛЕНИЕ
Временной ряд (динамический ряд) — это значение признака, измеренного в хронологическом порядке через постоянные временные промежутки.

Главная особенность динамических рядов в том, что они являются зависимыми. Предыдущие показатели связаны с текущими и будущими, а сам ряд можно разложить на компоненты:

тренд;
сезонность;
цикличность;
случайные отклонения.

Визуализация

Порой хороший график приносит больше пользы, чем самые сложные модели. В любом случае перед тем как прогнозировать любые динамические ряды их необходимо изучить визуально.

Посмотрим на ряд при помощи обычного линейного графика. Скользящее среднее или экспоненциальное сглаживание помогают выявить тенденции среди шума.

Сглаживание динамического ряда при помощи скользящей средней

2. Графическая декомпозиция недоступна в Excel, зато гарантированно присутствует в любом статистическом пакете. С ее помощью ряд раскладывается на компоненты.
В данном случае график подсказывает исследователю, что продажи товара Х имеют не только ярко выраженную сезонность, но и стабильную цикличность в рамках недели.

Декомпозиция динамического ряда

3. Коррелограмма — это график автокорреляций. Он помогает понять как значения ряда связаны со своими же значениями в прошлом. Лаг отражает степень запаздывания. Значимый коэффициент корреляции для лагов 7 и 14 также намекает на недельную цикличность.

Модели класса ARIMA

Согласно теореме Вальда любой

стационарный

ряд может быть описан моделью ARMA.
AR – это модель авторегрессии порядка p. Обычное регрессионное уравнение в котором будущие значения ряда линейно зависят от предыдущих.
MA – модель скользящего среднего порядка q. Функция при которой значение в каждой точке ряда равно среднему значению n соседних точек.

СПРАВКА.

ARIMA – расширение моделей ARMA для нестационарных временных рядов.
SARMA / SARIMA – расширение для рядов с сезонной составляющей.
SARIMAX – расширение, позволяющее включить внешнюю регрессионную составляющую.

Стационарный ряд
– это ряд, в котором отсутствует автокорреляция, а среднее и дисперсия не меняются со временем.

Перед тем, как применять модель необходимо позаботиться о стационарности динамического ряда.

Чтобы убедиться, что мы все сделали правильно применяем формальные тесты:

СПРАВКА. Критерий Льюнга-Бокса — критерий для выявления автокоррелированности временных рядов.
Критерий KPSS (KPSS test) — критерий для проверки на стационарность (Hо = ряд стационарен).
Критерий Дики-Фулера — критерий для проверки на стационарность (Но = ряд нестационарен).

Отлично! Теперь нужно подобрать параметры p и q. Это можно сделать вручную, на основе крупнейших лагов автокорреляционной функции ACF и PACF или воспользоваться чудо-функцией

auto.arima

из библиотеки Forecast для R.

Прогнозирование временных рядов в R

Нужно убедиться, что остатки:

имеют низкое абсолютное значение, в них отсутствует тренд и циклы;
распределены нормально со средним ~0;
отсутствует автокорреляция (смотрим коррелограмму и тесты «Box-Pierce» «Ljung-Box»).

Анализ временных рядов в R


Install.packages("forecast"); Install.packages("tseries") #устанавливаем полезные расширения
library(forecast); library(tseries) #задействуем их
my_time_series <- ts(data$sales, frequency = 7)  #кодируем числовой вектор, как временной ряд
my_time_series <- tsclean(my_time_series) #автоматическая замена выбросов и пропущенных значений
plot(my_time_series) #визуализация
plot(decompose(my_time_series)) #график декомпозиции ряда
acf(my_time_series) #построение коррелограммы
fit <- auto.arima(my_time_series) #автоматический подбор модели и оптимальных параметров
fit #модель
tsdisplay(residuals(fit)) #графический анализ остатков
Box.test(residuals(fit)) #формальный тест скоррелированности остатков
my_forecast <- forecast(fit, h=3) #прогноз на 3 периода вперед
plot(forecast(fit, h=3)) #визуализация прогноза с доверительным интервалом
- - - - -
#другие полезные функции:
ets() #экспоненциальное сглаживание 
BoxCox() #преобразование Бокса-Кокса
adf.test()  #проверка стационарности (тест Дики-Фуллера)

Математическое моделирование

Пример регресионной модели прогнозирования продаж

Пример исходных данных для прогнозирования продаж

Перечислим полезные лайфхаки:

Цикличность можно закодировать категориальным фактором (день недели или месяца) или числовой переменной, которая отражает средний уровень целевой переменной за этот период.
Погоду, курсы валют и ставки ЦБ можно получать напрямую через API или скрапингом. Благодаря этому ваша модель будет работать без ручного обогащения новыми данными.
Результаты прогноза по ARIMA-моделям могут быть поданы на вход другим алгоритмам для дальнейшего сокращения остатков.

Заключение

Чтобы быстро прикинуть продажи в следующей неделе / месяце / году воспользуйтесь одним из наивных методов.

Для краткосрочного прогнозирования временных рядов с устойчивой структурой подходят модели класса ARIMA.

Для долгосрочного моделирования сложных и зависимых от внешних факторов процессов используйте модели машинного обучения.

Хотите систематизировать свои знания по аналитике?

Встречайте «Анализ данных для хулиганов»

Онлайн пособие о том, как создавать великолепные продукты и эффективно управлять маркетингом на основе данных⚡

Методики / Фреймворки / Шаблоны для скачивания

Источник

This tutorial will help you set up and interpret an ARIMA — Autoregressive Integrated Moving Average — model in Excel using the XLSTAT software.

Dataset to fit an ARIMA model to a time series

The data have been obtained in [Box, G.E.P. and Jenkins, G.M. (1976). Time Series Analysis: Forecasting and Control. Holden-Day, San Francisco], and correspond to monthly international airline passengers (in thousands) from January 1949 to December 1960.

We notice on the chart, that there is a global upward trend, that every year a similar cycle starts, and that the variability within a year seems to increase over time. Before we fit the ARIMA model, we need to stabilize the variability. To do that, we transform the series using a log transformation. We can see on the chart below that the variability is reduced.

We can now fit an ARIMA(0,1, 1)(0,1,1)12 model which seems to be appropriate to remove the trend effect and the yearly seasonality of the data.

Setting up the fitting of an ARIMA model to a time series

Open XLSTAT
Select the XLSTAT / Time Series Analysis / ARIMA command. Once you’ve clicked on the button, the ARIMA dialog box will appear.
Select the data on the Excel sheet. In the Times series field you can now select the Log(Passengers) data.
Activate the Center option because we want XLSTAT to automatically center the series before optimizing the ARIMA model.
Define the type of ARIMA model by entering the value of the (p,d,q)(P,D,Q)s orders. The period of the series is set to 12, because it seems the cycles are repeated every year (12 months).
Activate the Series labels the first row of the selected data contains the header of the variable.

In the validation tab, enter 12 so that the last 12 values are not used to fit the model, but only to validate the model.
Click OK to launch the computations.

Interpreting the results of an ARIMA model fitting to a time series

After the summary statistics of the series, a table displays the various criteria that allow to evaluate the quality of the fit, and to compare the fit of this model with other models (if available).

The next table displays the parameters of the model. We notice that both the MA(1) and SMA(1) parameters are significantly different from 0 as the 95% confidence interval does not include 0. The confidence intervals are computed using the Hessian after optimization which is what other software usually display, and using an asymptotical method. The constant of the model is fixed as it comes from the removal of the mean.

The ARIMA model writes:

Y(t) = 0.000+Z(t-1)-0.348.Z(t-1)-0.562.Z(t-12)+0.195*Z(t-13) where Z(t) is a white noise N(0, 0.001) Y(t)=(1-B)(1-B12)X(t), and X(t) is the input series.

The forecasting equation for the X(t) series is given by: X(t+1) = Y(t+1)+X(t)+X(t-11)-X(t-12)

A table gives the values of the original series, and the smoothed series (the predictions). Because of the constraints of the model, predictions are not available for the 13 first observations (the predictions are replaced by the values of the input series). Notice that a time variable «T» has been created to facilitate the graphical representation. For the last 12 observations predictions have been computed in validation mode and a confidence range is available. We notice that almost all residuals (in red) are negative. This means that in forecasting mode the model overestimates the traffic.

On the chart below, we can visually see that the predictions (Validation) are very close to the data.

Was this article useful?

Источник

ARIMA — модель авторегрессии скользящего среднего, которая применяется для построения краткосрочных прогнозов величины на основании её предыдущих значений. Разбираем построение модели в Loginom для прогноза объема продаж сезонных товаров зимнего спорта по месяцам.

Исходные данные
Построение модели
Результаты прогнозирования
Построение графика
Анализ полученных результатов
Увеличение точности прогноза
Автоматизация прогнозирования в Loginom

Для большинства бизнесов процесс принятия решений напрямую связан с результатами прогнозирования, которые используются при планировании производства, оптимизации запасов и прочее.

Для этого часто применяются методы анализа временных рядов — математических моделей, в которых определяется зависимость будущего значения от прошлых внутри самого процесса. На основе выявленных зависимостей построится прогноз.

Анализ временных рядов лучше использовать для краткосрочного прогнозирования, т.к. при увеличении горизонта прогноза модель начинает рассчитывать новые значения на основании своих же предсказаний. Это допустимо на определенном временном интервале, но по мере увеличения горизонта прогнозы становятся гораздо менее точными из-за накапливающейся погрешности.

Важно учитывать и ограничения — такой метод подходит только для планирования стохастических (стационарных) процессов, в которых не изменяется распределение вероятности при смещении времени. Например, для расчета объема продаж.

Существует класс моделей, в которых реализуется этот метод:

ARIMA. Авторегрессионная модель скользящего среднего с интеграцией.
ARIMAX. Отличается от ARIMA тем, что дополнительно учитывается воздействие внешних (eXtended) факторов, влияющих на изменение исходного показателя.

Данные аббревиатуры можно расшифровать следующим образом:

AR – модель авторегрессии. Вычисление значения прогнозируемой величины в заданный момент времени на основе её предыдущих значений.
I – интеграция. Изучение не самих значений процесса, а изменений его показателей друг относительно друга.
MA – модель скользящего среднего. Фильтр, сглаживающий выбросы временного ряда посредством замены исходного значения средним арифметическим значением нескольких ближайших к нему членов.
X – расширения. Добавление в модель внешних факторов, влияние которых будет учитываться в прогнозе.

Учет внешнего фактора важен для построения прогнозов высокой точности, но сбор и обработка таких данных как правило занимают время, а в некоторых случаях вообще сложно предсказать их поведение.

Например, при анализе объема продаж товаров для зимнего спорта важным параметром становится температура воздуха, но каждый знает, что метеорологи регулярно ошибаются с прогнозами на день вперед. Поэтому при планировании на несколько месяцев, точность данных о погоде будет настолько низкой, то нет смысла её учитывать.

В данной статье рассмотрим пример прогнозирования значений величины на основе модели ARIMA. В этом случае никаких дополнительных данных, кроме самого прогнозируемого показателя для построения прогноза не требуется.

Оставим за скобками процессы предобработки и дальнейшего использования данных и разберемся, как работает обработчик ARIMAX.

Исходные данные

Для получения корректного прогноза необходимо достаточное количество данных о предыдущих значениях продаж. Важно учитывать, что совсем старые данные не могут быть использованы, иначе прогноз будет недостоверным.

Кроме того, чем больший интервал прогноза будет рассматриваться, тем больше данных потребуется. В нашем случае для прогнозирования потребления на 5 месяцев вперед потребуется информация как минимум о нескольких годовых периодах в прошлом.

Ниже представлена таблица 1, которая состоит из следующих столбцов:

Дата. Первое число каждого месяца, т.к. временной интервал взят помесячно.
Продажи (руб.). Суммарные объемы продаж товаров для зимнего спорта за месяц.

Таблица 1. Исходные данные:

Дата	Продажи (руб.)
01.05.2015	250 127.68
01.06.2015	225 127.56
01.07.2015	184 265.77
01.08.2015	200 792.53
01.09.2015	265 275.44
01.10.2015	339 285.82
01.11.2015	390 677.54
01.12.2015	417 945.20
…	…

Построение модели

В Loginom есть специальный обработчик ARIMAX, который включает в себя математическую модель ARIMA с расширениями, влияние которых будет учитываться при построении прогноза. Если внешних данных не поступает на вход, то он превращается в ARIMA.

Перенесем этот элемент на область построения сценария, подав на вход узла исходные данные.

Настроим обработчик ARIMAX для получения прогнозных данных. Первое окно — «Настройка входных столбцов», здесь каждому столбцу исходных данных нужно задать одно из трех возможных значений:

Не задано. Автоматически устанавливается для всех полей.
Входное. Нужно задать для полей, которые соответствуют внешнему фактору, в нашем примере их нет.
Прогнозируемое. Может быть установлено только для одного поля, в нашем случае «Продажи (руб.)».

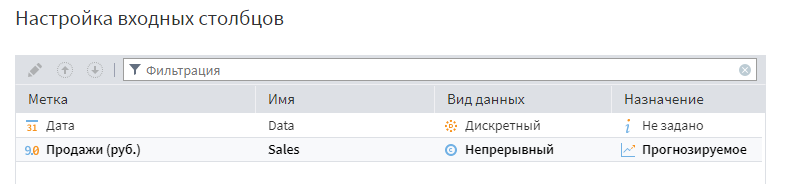
Настройка входных столбцов обработчика ARIMAX

После настройки входных столбцов доступна нормализация входных и выходных полей. В подавляющем большинстве случаев её не нужно применять ни к данным временного поля, ни к внешним параметрам.

Основные настройки задаются в окне «Настройки ARIMAX», причем при отсутствии конкретных критериев прогноза можно установить отметку в поле «Определить структуру автоматически», и обработчик рассчитает необходимые параметры для ваших данных.

По умолчанию значение горизонта прогноза устанавливается равным 1, это значит, что мы получим прогноз на один период вперед. Чтобы нагляднее увидеть работу узла, изменим это значение на 5.

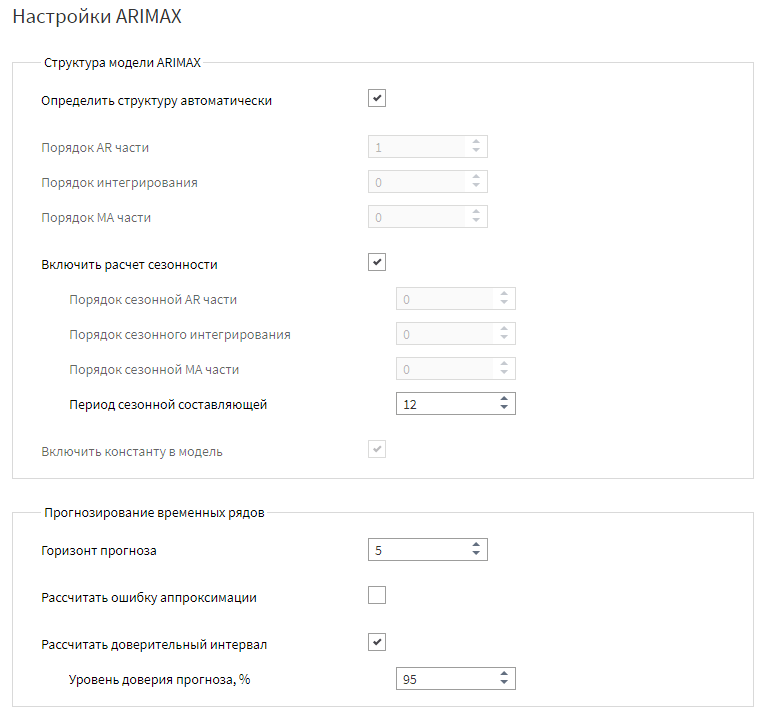
Автоматическая настройка обработчика ARIMAX

Сразу после сохранения настроек элемента запускать на исполнение его нельзя. Сначала нужно обучить данный узел.

Для этого в контекстном меню выберем «Переобучить узел».

Переобучение узла

Результаты прогнозирования

В узле ARIMAX три выходных порта:

Выход модели
Коэффициенты модели
Сводка

После запуска обработчика ARIMAX можно открыть «Быстрый просмотр» на первом выходном порту и увидеть, что исходные данные дополнились следующими выходными столбцами:

Продажи (руб.)ǀПрогноз. Прогноз объема продаж на основе предыдущих периодов.
Продажи (руб.)ǀНижняя граница. Нижняя граница прогноза объема продаж на основе предыдущих периодов.
Продажи (руб.)ǀВерхняя граница. Верхняя граница прогноза объема продаж на основе предыдущих периодов.
Продажи (руб.)ǀОшибка аппроксимации. Среднее отклонение расчетных значений от фактических, будет отображаться, если установлена отметка в «Рассчитать ошибку аппроксимации».

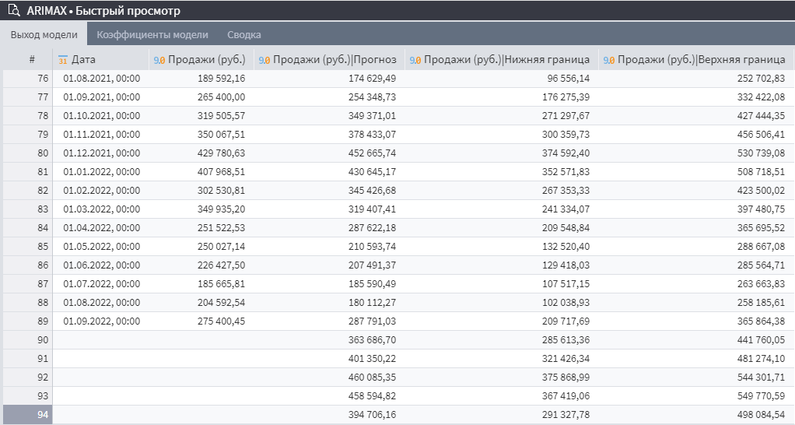
Выход модели ARIMAX

Причем прогнозные данные будут рассчитаны и для тех месяцев, по которым уже известен объем продаж, и для новых периодов. Стоит отметить, что в самом начале таблицы новые столбцы с прогнозами будут пустыми, их количество зависит от установленного значения в поле «Порядок AR части».

Если мы обратимся ко второму выходному порту, то увидим таблицу с коэффициентами модели, а к третьему — сводку значений переменных, показывающих количество примеров, ошибки на обучающем множестве, информационные критерии, коэффициенты детерминации, числа степеней свободы.

Данные выходных портов дают исчерпывающую информацию о выполненном прогнозе, но табличное представление сложно воспринимать, поэтому в большинстве случаев потребуются визуализаторы.

Прежде, чем переходить к построению графиков, необходимо заполнить значения временного ряда для появившихся строк, иначе график прогноза будет отображаться только на исходном временном периоде, а значения на горизонте прогноза не будут отражены. Для этого добавим узел «Калькулятор».

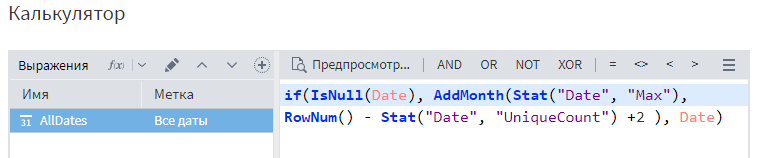
В настройках узла создадим переменную AllDates, которая будет содержать все значения временного ряда. Расчет будет строиться с помощью функции условия If. Если поле даты пустое, то функция AddMonth добавляет необходимое количество месяцев к последнему известному значению, в противном случае вносит ту дату, которая указана в поле.

Для того, чтобы вычислить количество месяцев, необходимо сначала найти разность между номером текущей строки (функция RowNum()) и количеством уникальных значений поля Date (функция Stat(«Date», «UniqueCount»)), а затем добавить к полученному результату 2. Важно учитывать, что нумерация строк начинается с 0, а в количестве уникальных значений присутствуют не только исходные даты, но и пустое значение в появившихся после прогноза строках, именно поэтому вводится цифра 2.

Калькулятор Loginom

После выполнения узла «Калькулятор» в таблице на его выходном порту появится столбец «Все даты».

Построение графика

Для того, чтобы визуально оценить прогнозные значения и их корреляцию с фактическими показателями, построим графики исходных значений объема продаж и прогноза этой величины, полученного в результате использования модели ARIMA.

В результате получим график, на котором отображаются кривые прогноза и исходных значений объема продаж в рублях.

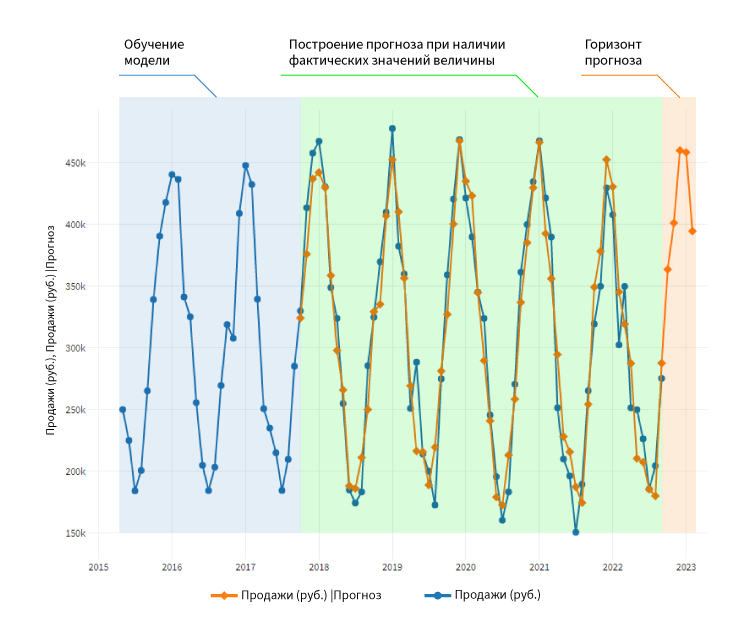
График прогноза продаж

Анализ полученных результатов

На графике отчетливо выделяются 3 временных периода:

Обучение модели. На этом временном отрезке возможно построение только кривой фактических данных.
Построение прогноза при наличии фактических значений величины. На графике присутствуют сразу две кривые, что позволяет визуально оценить, насколько близки полученные в результате работы модуля ARIMA прогнозные значения к фактическим.
Горизонт прогноза — отображается кривая прогноза.

В качестве этапа обучения модели обработчик ARIMAX задал временной промежуток 29 месяцев (около 2 лет). На втором интервале видно, что графики объема продаж и его прогноза имеют одинаковую форму, но при этом значения величин в некоторых точках значительно отличаются. Линия прогноза на 3 временном промежутке визуально повторяет форму кривой исходных значений продаж.

Увеличение точности прогноза

В случае, когда точность прогноза с автоматически заданными параметрами оказалась недостаточной, можно задать эти значения вручную.

Важно понимать, что нет универсальных правил, которые могут быть применимы ко всем задачам прогнозирования, поэтому для каждого набора данных они будут свои. В документации можно подробно ознакомиться с описанием структуры ARIMAX и определениями каждого из настраиваемых параметров.

Изменим показатели в окне настройки ARIMAX, как это показано на рисунке ниже.

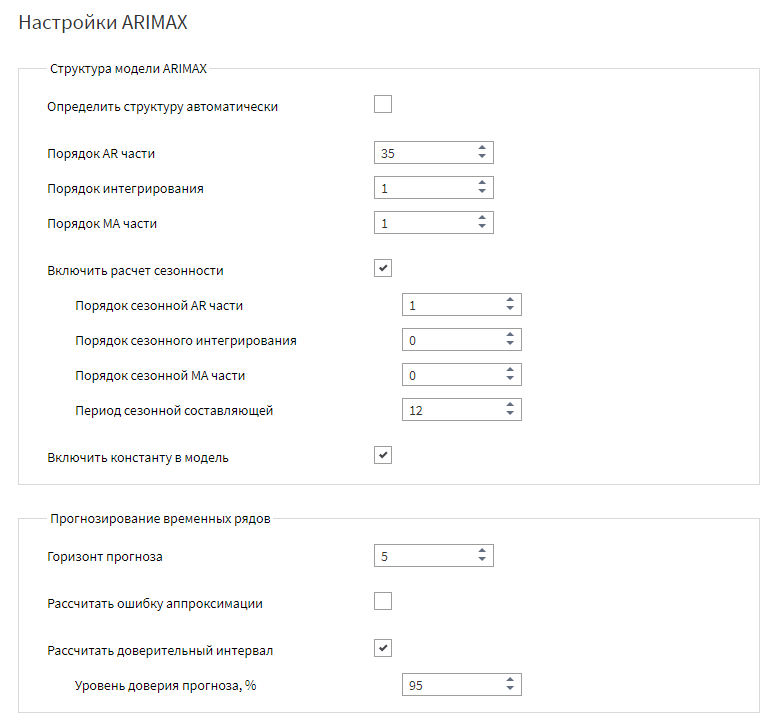
Настройка обработчика ARIMAX

Далее необходимо будет произвести переобучение данного узла.

Значения прогноза будут пересчитаны, и в визуализаторе мы сможем увидеть, что графики кривых на 2 временном периоде приняли почти одинаковый вид. Это говорит о том, что точность прогноза увеличилась.

График прогноза продаж

Чтобы убедиться в том, что прогноз стал точнее, откроем вкладку «Сводка» на третьем выходном порте модели. Значение средней относительной ошибки на обучающем множестве сократились в несколько раз по сравнению с предыдущими.

Ошибки сводки ARIMAX

Автоматизация прогнозирования в Loginom

В данном примере мы построили прогноз объема продаж сезонных товаров для зимнего спорта с помощью модели ARIMA.

При автоматически заданных параметрах обработчика ARIMAX был получен корректный прогноз с минимальным количеством входных данных. Кроме того, удалось добиться увеличения точности прогноза с помощью ручного подбора параметров модели ARIMAX.

Сам обработчик ARIMAX характеризуется простотой использования и быстрой работой, достаточно подать на вход данные и ввести показатели прогнозирования (а можно и не вводить вовсе), и уже через несколько секунд получить корректный прогноз. Кроме того, в Loginom можно построить графики с кривыми фактических и прогнозных значений, что в полной мере позволяет визуально оценить полученный результат.

Другие материалы по теме:

Автоматизация прогнозирования розничных продаж. Кейс Estee Lauder Companies Inc.

Прогнозирование аварий и обнаружение потерь на объектах газоснабжения

Прогнозирование в разрезе SKU. Новые возможности повышения адекватности прогнозов

Источник

Introduction

XLMiner facilitates the analysis of datasets via the use of trend discovery techniques (autocorrelation and partial autocorrelation) and comprehensive modeling methods (ARIMA and exponential smoothing).

ARIMA — AutoRegressive Integrated Moving-Average model — is one of the most popular modeling methods used in time series forecasting, due largely to its focus on using data autocorrelation techniques to achieve high-quality models. XLMiner fully utilizes all aspects of ARIMA implementation, including variable selections, seasonal / non-seasonal parameter definitions, and advanced options such as iteration maximums, output, and forecast options.

ARIMA Modeling in XLMiner

An ARIMA model is a regression-type model that includes autocorrelation. When estimating ARIMA coefficients, the basic assumption is that the data is stationary; meaning, the trend or seasonality cannot affect the variance. This is generally not true. In order to achieve stationary data, XLMiner needs to apply differencing: ordinary, seasonal, or both.

After XLMiner fits the model, various results will be available. The quality of the model can be evaluated by comparing the time plot of the actual values with the forecasted values. If both curves are close, then it can be assumed that the model is a good fit. The model should expose any trends and seasonality, if any exist.

Next an analysis of the residuals should convey whether or not the model is a good fit: random residuals means that the model is accurate, but if the residuals exhibit a trend then the model may be inaccurate. Fitting an ARIMA model with parameters (0,1,1) will give the same results as exponential smoothing, while using the parameters (0,2,2) will give the same results as double exponential smoothing.

How to Access ARIMA Settings in Excel

Launch Excel.
In the toolbar, click XLMINER PLATFORM.
In the ribbon, click ARIMA.
In the drop-down menu, select ARIMA Model.

For usability information, please reference Using Time Series and/or the XLMiner Online Help.

ARIMA Model Summary

ARIMA: AutoRegressive Integrated Moving Average.
Forecasting model used in time-series analysis.
ARIMA Parameter Syntax: ARIMA (p,d,q) where p = the number of auto-regressive terms, d = the number of non-seasonal differences, and q = the number of moving average terms.

Resources

Time Series Example: View an example of how an ARIMA model can be applied.
Using Time Series: How to use time series analysis functionality within XLMiner.
Smoothing Models: How smoothing techniques can be applied to time series forecasting models.
XLMiner Online Help: Help system covering functionality within the XLMiner module.

Источник

На чтение 6 мин Просмотров 10.6к.

Содержание

Планирование продаж и денежных потоков предприятия
Методы планирования продаж и денежных потоков
Модель прогнозирования продаж и денежных потоков
Пример планирования продаж и денежных потоков предприятия ОАО «МТС» в Excel
Мастер-класс: «Как рассчитать план продаж»

Планирование продаж и денежных потоков предприятия

★ ABC и XYZ-анализ товарного ассортимента в Excel за 5 минут

Продажи компании и денежные потоки тесно взаимосвязаны между собой следующей формулой:

где: CF_i (Cash Flow) – денежный поток.

Методы планирования продаж и денежных потоков

Модель прогнозирования продаж и денежных потоков

Авторегрессионная модель планирования объема продаж и денежных потоков имеет следующий аналитический вид:

где:

Y_i – прогноз денежного потока или объема продаж;

Y_i_-1 – значение денежного потока и продаж в предыдущем периоде;

α, β – коэффициенты в модели авторегрессии;

ξ – случайная величина (белый шум).

Пример планирования продаж и денежных потоков предприятия ОАО «МТС» в Excel

Объем продаж и денежный поток для ОАО «МТС»

Графически изменение объема продажи и денежного потока имеет следующий вид:

Расчет авторегрессии для объема продаж и денежного потока в Excel

Показатели оценки качества регрессионной модели в Excel

Прогноз продаж по модели AR =$B$19+B6*$B$20

Прогноз денежного потока по модели AR =$C$19+$C$20*C6

Планирование продаж и денежных потоков предприятия по модели авторегрессии в Excel

Визуально планирование продаж будет иметь следующий вид. Наблюдается повышающийся тренд на два года вперед.

График прогноза объема продаж (выручки) предприятия

Графически прогноз денежного потока на два года вперед сильно не изменится.

Прогнозирование денежного потока предприятия по модели авторегрессии (AR)

Использование методов прогнозирования денежных потоков позволяет оценить показатели эффективности инвестиционных проектов, более подробно про методы оценки проектов читайте в моей статье: «6 методов оценки эффективности инвестиций в Excel. Пример расчета NPV, PP, DPP, IRR, ARR, PI«. Существуют также другие методы планирования объемов продаж компании: XYZ-анализ, ABC-анализ, которые тоже зарекомендовали себя на практике. Так метод ABC анализа на практическом примере разобран в статье: «ABC анализ продаж. Пример расчета в Excel«.

Мастер-класс: «Как рассчитать план продаж»

Резюме

Автор: к.э.н. Жданов Иван Юрьевич

Источник

As Carlos Otero and I mentioned in our talk at MDIS (link), forecasting is an important area of focus for businesses in general across a range of functions: for instance, you can have finance teams forecasting costs, sales teams forecasting revenues, or engineering teams forecasting developer-hours and bug burn downs, etc. In addition, business data often flows through Excel – arguably, Excel is the most widely used tool for business analytics and forecasting. Finally, with the increased importance of Data Science and Machine Learning and the increasing complexity of business data, Business Analysts have taken to more sophisticated methods to do forecasting. Thus, the importance of exploring how to incorporate more sophisticated forecasting models within Excel workflows. The goal of this post is to share a few ideas and tips on how to super-charge your skillsets – in Excel and Machine Learning — to increase your forecasting efficiency.

In this post, we’ll cover:

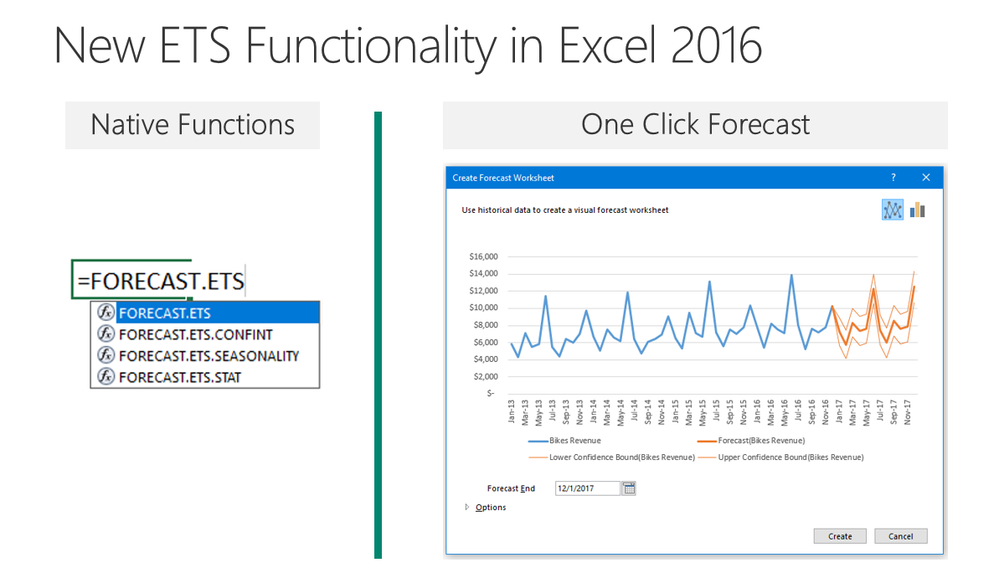
Exponential Triple Smoothing or ETS which is a commonly used forecasting technique that’s natively supported in Excel 2016.
Azure Machine Learning (Azure ML), R, and as an example a popular technique called Auto-Arima. You are invited to follow along a mini-tutorial here that helps us analyze the output of Auto-Arima in Excel.

Note that the sample techniques are commonly used by teams at our company, Microsoft. For purposes of this blog post, we have not focused on stochastic forecasting techniques such as Monte Carlo simulations, although it is possible to extend the work we’re doing here to implement the method in ML if needed and analyze in Excel via an add-in.

Exponential Smoothing (ETS)

Exponential Triple Smoothing (ETS) uses the weighted mean of past values. One reason ETS is popular is that it adjusts for seasonal variation in data. Some trace the origins of exponential smoothing to Poisson, as an extension of a numerical analysis technique from the 17th century, and the technique was later adopted by the telco community in the twentieth century. In Excel, we use a variation of the Holt Winters ETS algorithm.

In Excel 2016, we introduced native ETS functionality. This includes both a set of new functions such as FORECAST.ETS and other supporting functions for additional statistics. Your dataset does not need to be perfect, as the functions will accommodate up to 30% missing data.
Another way of using these capabilities in Excel is via the one click forecasting button in the Data tab, which gives us a forecasting chart at a button press. The visual below shows us the forecast (in orange) vs actual data (in blue) as well as the confidence intervals of the forecast.

Here is a demo on how a Bikes Accessories Analyst uses Excel ETS Forecasting.

Azure Machine Learning + R + Arima

Azure Machine Learning (or Azure ML) is a cloud predictive analytics service that makes it possible to quickly create and deploy predictive models as analytics solutions.

According to a recent survey by KD Nuggets, R and Python feature prominently among tools used by Data Scientists, as does Excel. In addition, based on our research and conversations with Data Scientists and Analysts, there is a need for better integrating workflows between these tools and Excel. While there are several ways of integrating ML workflows into Excel including the work of our partners such Anaconda, XLWings, Pyxll we’ll focus on AzureML in this post.

Azure ML Studio is the tool we use to author machine learning experiments in Azure ML. Studio is a GUI-based cloud IDE for ML, offers one click deployment of Web Services, and supports advanced analytics via R, Python, and packaged modules.

One sample experiment we built for forecasting leverages the R forecast package and the Auto-Arima function – in ML Studio. This experiment is inspired by work done by Lucas A. Meyer of Microsoft. ARIMA stands for AutoRegressive Integrated Moving Averages, and is popularly used for time-based data series predictions.

Now let’s take a quick look at a simple Auto-Arima forecasting experiment. To follow along:

Start at https://studio.azureml.net/ (Azure ML Studio) and create your own subscription & workspace.
Open the sample Experiment here, and click the “Open in Studio” green button.

In the next dialog box, pick your Region and Workspace to successfully copy the Experiment into your account.
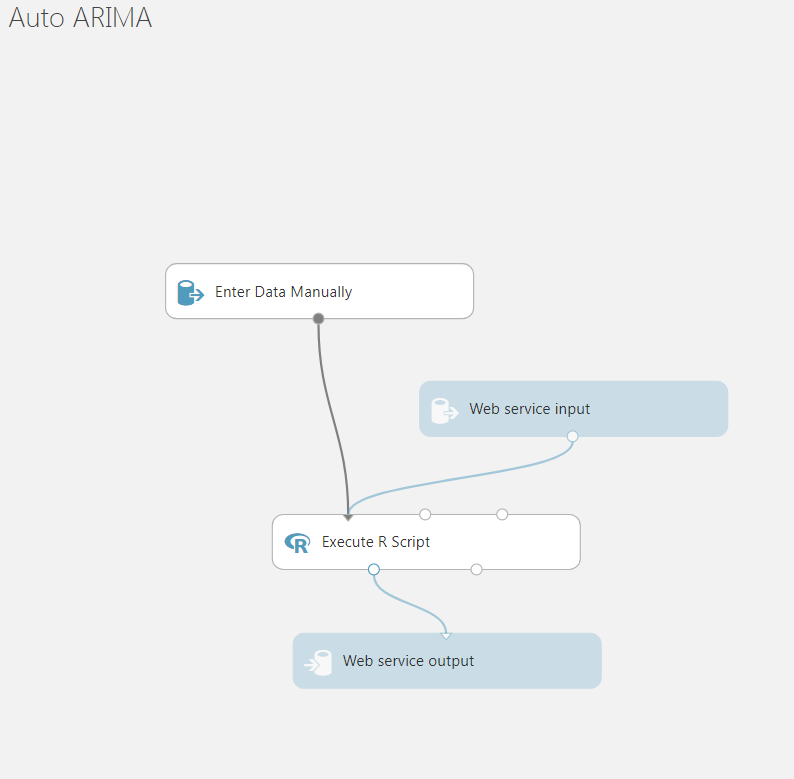
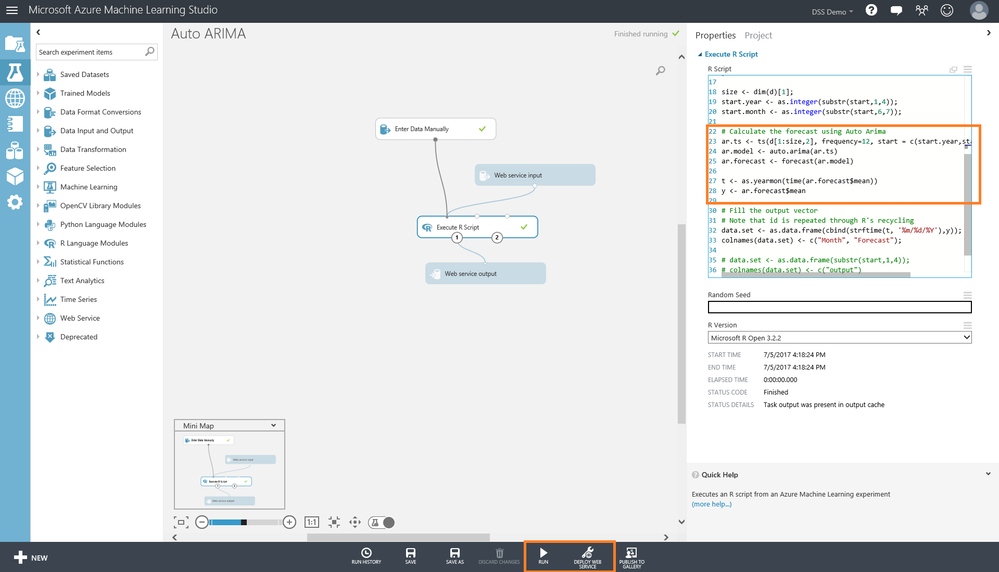
You should now see the different modules in the sample experiment (it should look like the image below).

When you click on the “Execute R Script” module, you’ll see a side pane containing the sample R Script. In the screenshot below, the box on the right shows the place where the Auto Arima forecast functions is invoked.
This experiment has already been set up to provide the output via a web service that can be integrated into Excel using the earlier-mentioned add-in.
Now click “Run”, then “Deploy Webservice” the taskbar below (see box at the bottom). Thus we create a webservice API that apps like Excel can now use to call into the experiment.

Now you’ll see the newly created webservice API details. Click on one of the links under the “Request/Response” and “Apps” area (or right click and select Save target as…). See blue box in the screenshot below.

This will download an Excel file already set up to consume the webservice.
Open the file, and click on “Enable Editing” in the Protected View yellow bar on top.
This will automatically load and open the Azure Machine Learning add-in. Save this file to your local share.
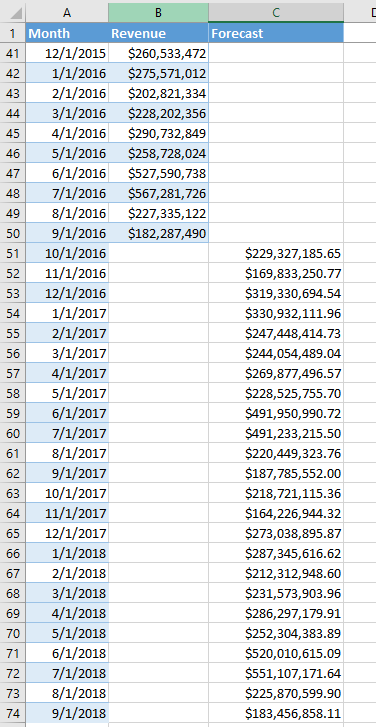
To work on some sample data open this file and copy over the data from A1:B74 to Sheet1 of your file. Adjust the column widths until you see all the data.
On C1 write Forecast. Use Format Painter to copy the format from B1 to C1. Select col C. On the Home tab of Excel, update the number format to Currency.
On the Azure Machine Learning Add-In, select your input range e.g. Sheet1!A2:B50. Uncheck my data has headers.
Under output select the 1^st cell of the range where we want output, e.g. Sheet1!C51. Uncheck Include Headers. The sample data now looks like this –

Hit the “predict” button to get forecast output into the table.

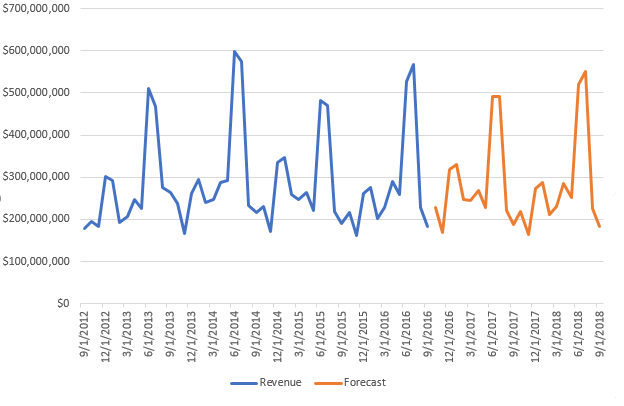
After selecting the data in all 3 columns (Month, Revenue, ForecasT), you can plot a chart of your choice, for e.g. Insert Chart -> Line Chart. The chart shows both blue (actual) and orange (forecast) trends.

Going back to ML Studio, I can share my experiment with others via the Publish to Gallery button which provides access to others via the Cortana Intelligence Gallery.

Besides the example described in this post, several other forecasting methods exist in the Cortana Intelligence Gallery (screenshot below). In addition, other powerful models and techniques for different domains are available if we search in the Gallery. The Azure ML – Excel integration helps bridge the gap between Data Scientists and Analysts. As we’ve seen you can build a model in Azure ML for your dataset, easily deploy it as a web service, and bring the data into Excel via the Excel Azure ML Add in. For more details, you can see the demo recording on AzureML.

In Conclusion…

The full talk at MDIS has more details including some tricks to compare the accuracy of different forecasting techniques (i.e. Mean Absolute Percent Error or MAPE) and how to aggregate multiple forecasts using Excel’s new Get and Transform capabilities. Watch the full talk here. We hope this inspires a few experiments.

Let us know what you think and if you have any questions. Also, given the feedback on the talk this year, we will likely prepare a presentation at other conferences such as next year’s MDIS and would love to start collecting ideas and customer scenarios. We’d love to learn how you use Excel for your forecasting workflows.

Источник