Содержание
- Применение математических функций
- СУММ
- СУММЕСЛИ
- ОКРУГЛ
- ПРОИЗВЕД
- ABS
- СТЕПЕНЬ
- КОРЕНЬ
- СЛУЧМЕЖДУ
- ЧАСТНОЕ
- РИМСКОЕ
- Вопросы и ответы
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
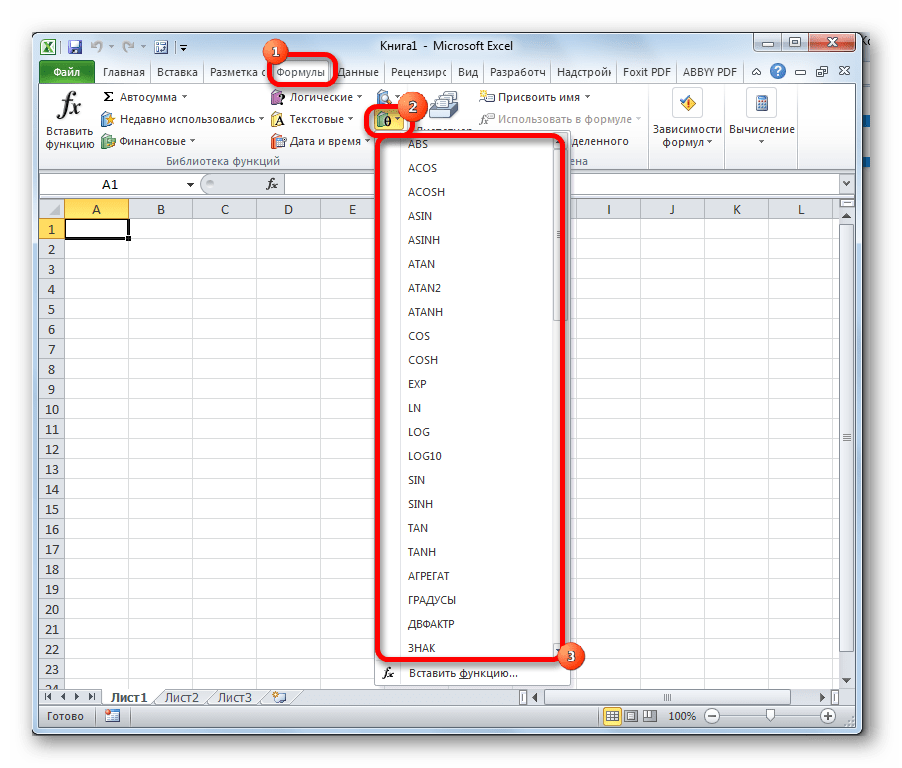
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Урок: Мастер функций в Excel
СУММ
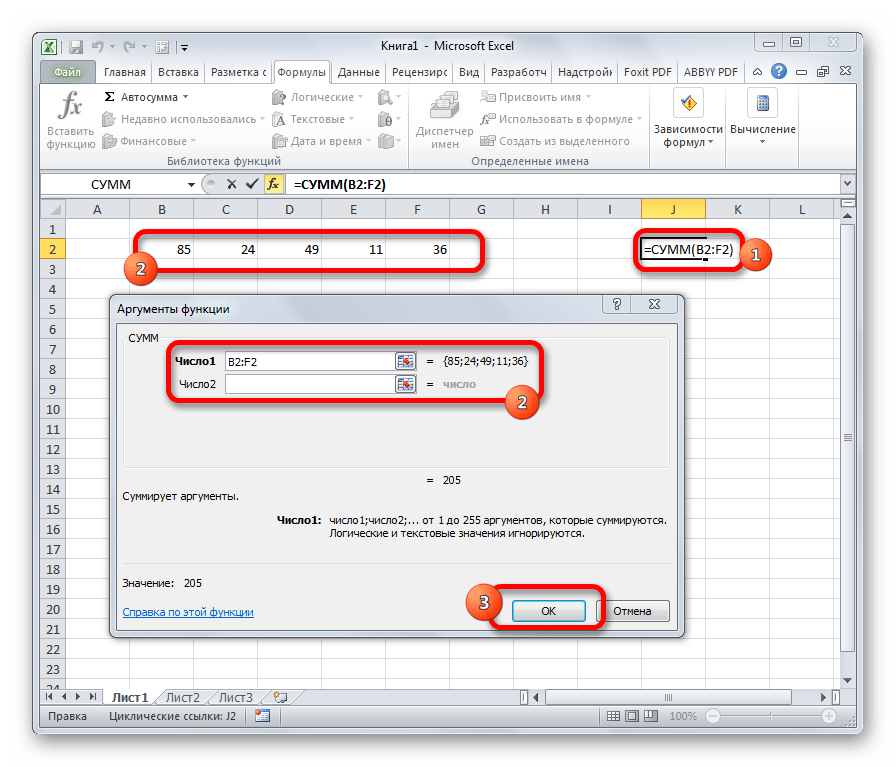
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
=СУММ(число1;число2;…)
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
Урок: Как посчитать сумму в Экселе
СУММЕСЛИ
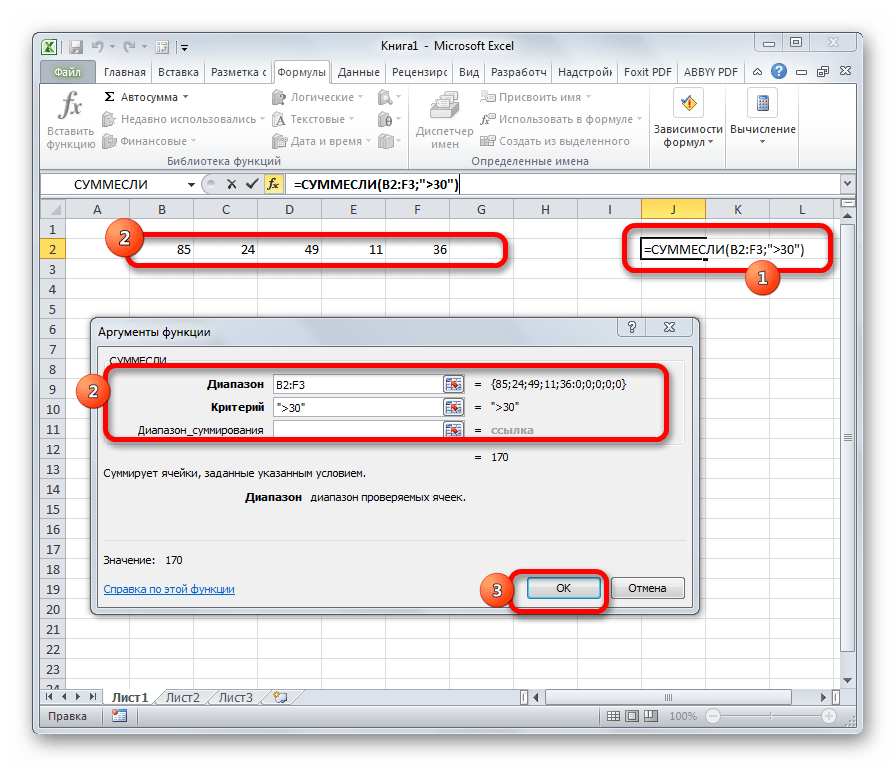
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)
ОКРУГЛ
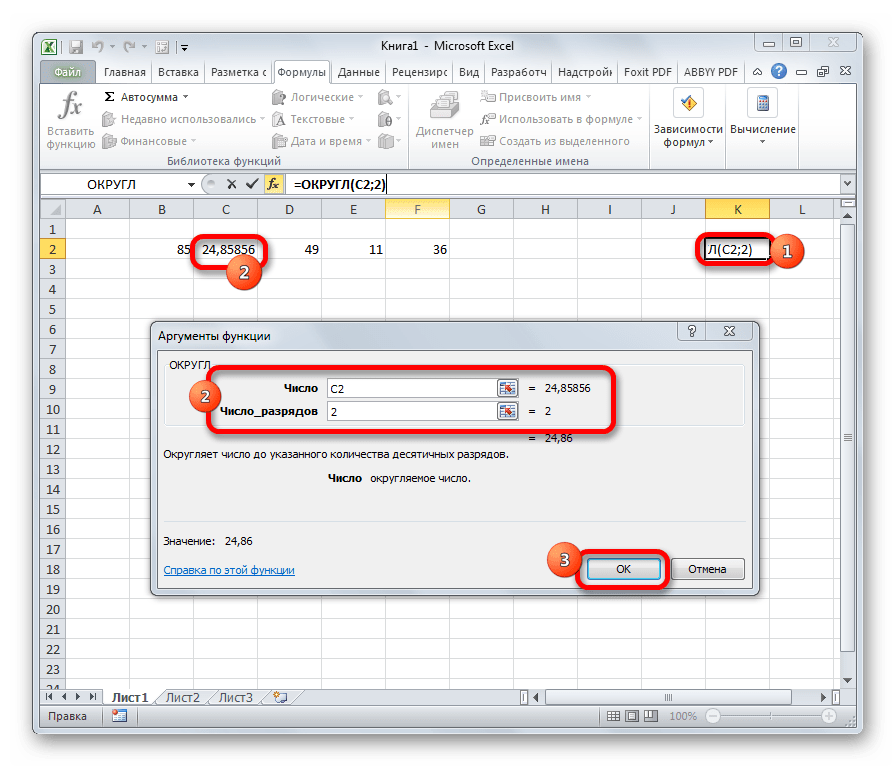
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
=ОКРУГЛ(число;число_разрядов)
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
Урок: Округление чисел в Excel
ПРОИЗВЕД
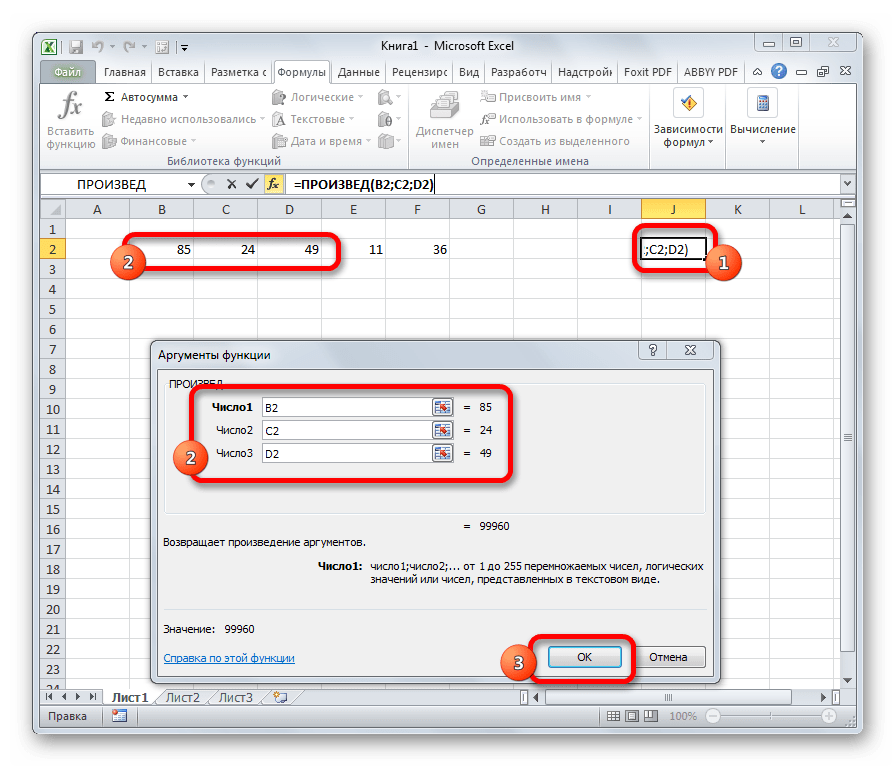
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
=ПРОИЗВЕД(число;число;…)
Урок: Как правильно умножать в Excel
ABS
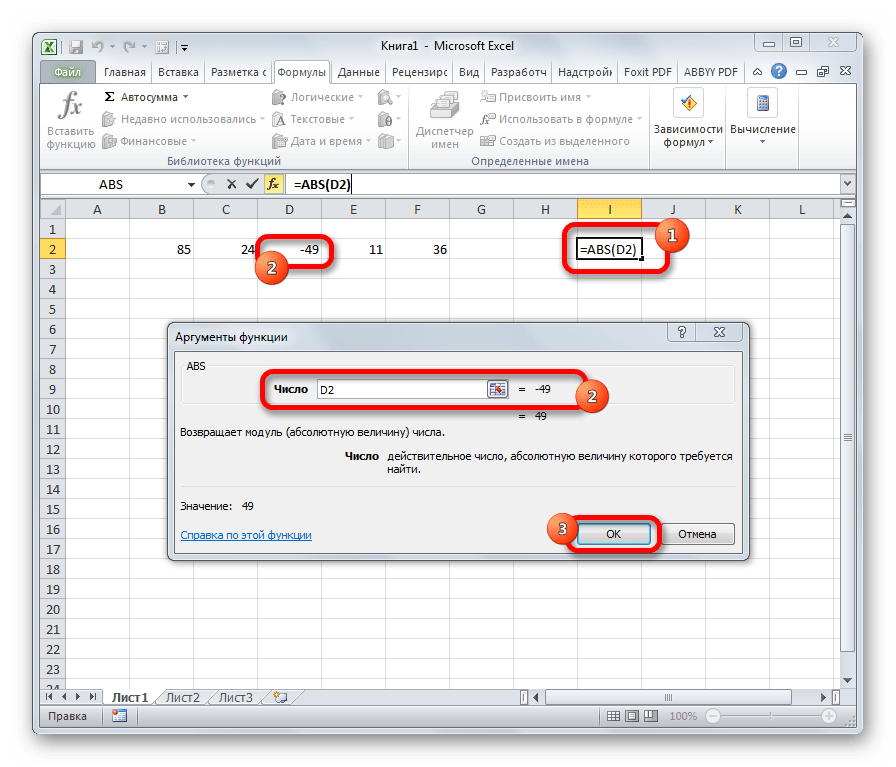
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
=ABS(число)
Урок: Функция модуля в Excel
СТЕПЕНЬ
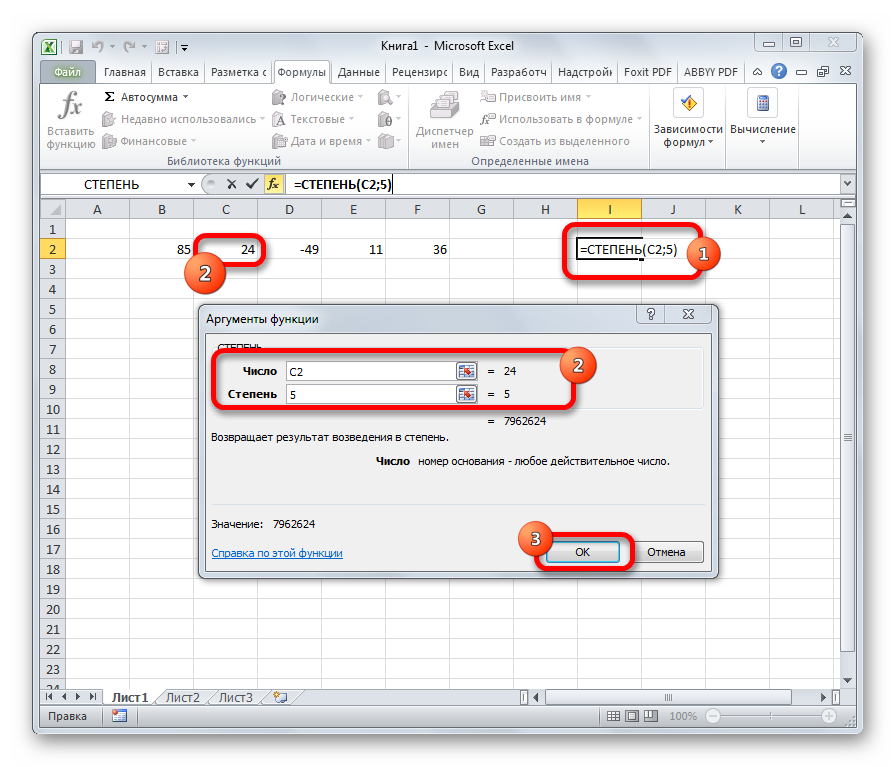
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
=СТЕПЕНЬ(число;степень)
Урок: Как возводить в степень в Экселе
КОРЕНЬ
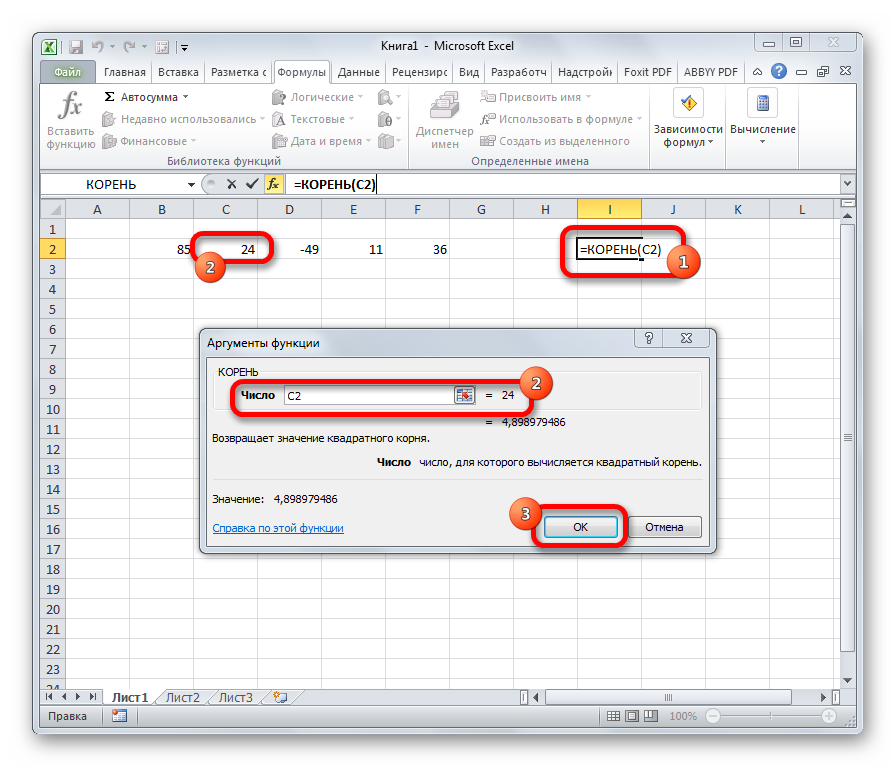
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
=КОРЕНЬ(число)
Урок: Как посчитать корень в Экселе
СЛУЧМЕЖДУ
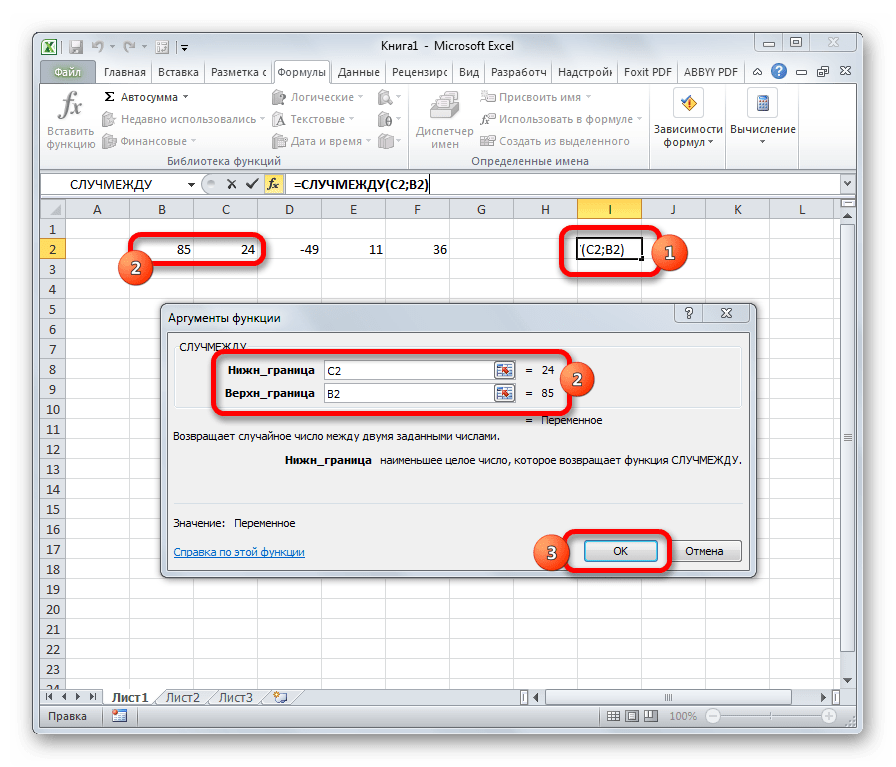
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)
ЧАСТНОЕ
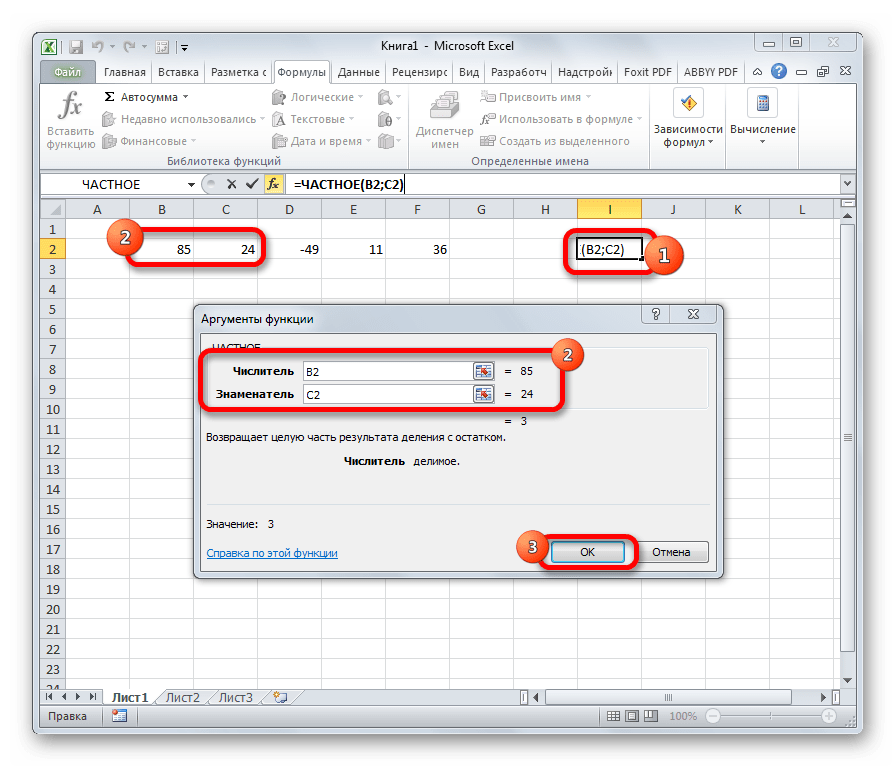
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
=ЧАСТНОЕ(Числитель;Знаменатель)
Урок: Формула деления в Экселе
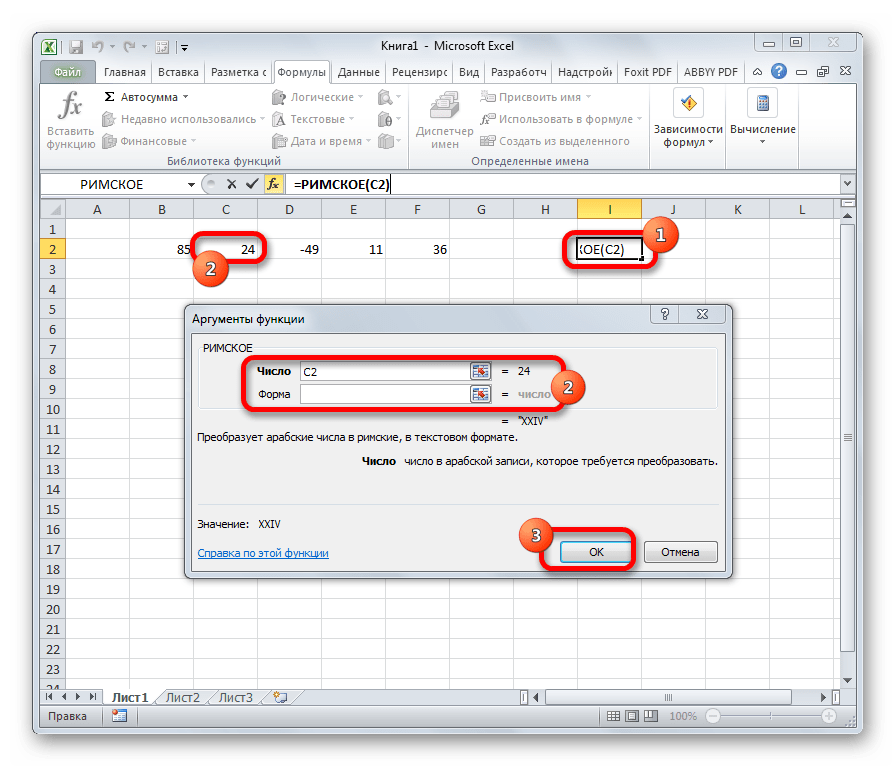
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
=РИМСКОЕ(Число;Форма)
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Редактор таблиц Microsoft Excel имеет очень широкий набор возможностей для решения задач самой разной сложности в различных сферах деятельности. Именно благодаря этому Эксель стал таким популярным среди пользователей по всему миру. Одним из базовых навыков работы с программой является проведение простейших вычислений и математических операций. В этой статье подробно разберём, как выполнять сложение, вычитание, умножение и деление в Excel. Давайте же начнём! Поехали!
Математические операции выполняются без использования калькулятора
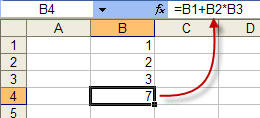
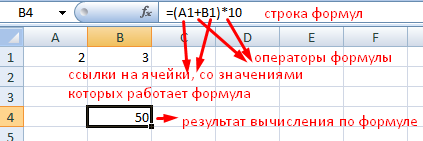
Все расчёты в Экселе основаны на построении простых формул, с помощью которых программа и будет производить вычисления. Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке.
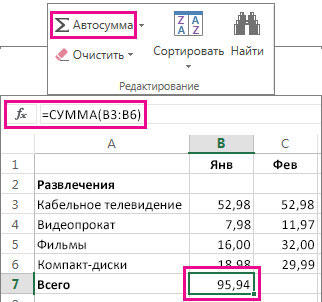
Начнём с самых простых операций — сложения и вычитания. Для сложения чисел можно использовать, так называемую функцию «Автосумма». Ей удобно пользоваться в случаях, когда необходимо посчитать сумму чисел, которые стоят подряд в одной строке, столбце либо в выделенной вами области. Чтобы воспользоваться этим инструментом, перейдите во вкладку «Формулы». Там вы обнаружите кнопку «Автосумма». Выделив участок таблицы со значениями, которые нужно сложить, кликните по кнопке «Автосумма». После этого появится отдельная ячейка, содержащая результат вычисления. Это был первый подход.
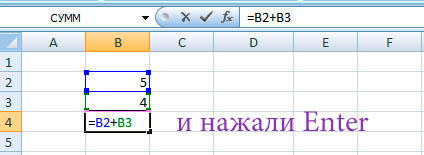
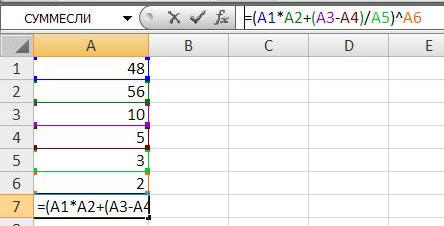
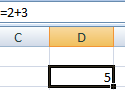
Второй подход заключается в том, что формула для расчёта вводится вручную. Допустим, перед вами стоит задача вычислить сумму чисел, разбросанных по таблице. Для этого сделайте активной (кликните по ней левой кнопкой мыши) ячейку, в которую желаете поместить результат вычисления. Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную. Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей.
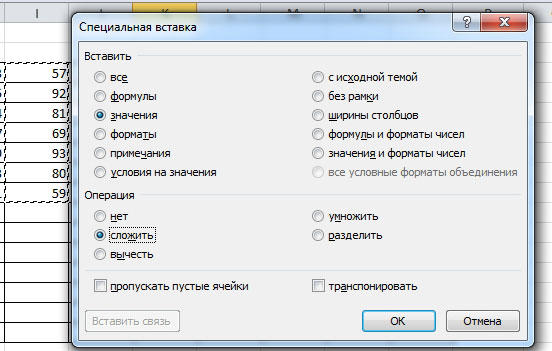
Существует ещё один подход — использование функции «Специальная вставка». Этот способ удобен тем, что позволяет суммировать данные из нескольких отдельных таблиц, при условии, что все их графы одинаковые. Для начала создайте сводную таблицу, в которую вы будете вставлять скопированные данные. Выделите числа одной таблицы и вставьте их в сводную, далее поступите так же со значениями второй таблицы, только в этот раз кликните по ячейке правой кнопкой мыши и выберите пункт «Специальная вставка». В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить. В результате все данные просуммируются.
Вычитание в Excel выполняется таким же способом, как и сложение. Вам понадобится ввести формулу, указав необходимые ячейки, только вместо знака «+» между адресами ставится «–».
Чтобы умножить числа в Экселе, напишите формулу, отмечая нужные данные и ставя между ними знак «*». Формула будет иметь следующий вид: «=A3*A7*B2».
Деление производится аналогичным образом, только используется знак «/». Также вы можете выполнять несколько арифметический операций сразу. Формулы строятся по математическим правилам. Например: «=(B2-B4)*E8/(A1+D1)*D4». Построенная вами формула может быть любой сложности, главное, не забывать основные математические правила, чтобы расчёт был выполнен верно.
Владея навыками простых арифметических вычислений в программе Microsoft Excel, вы уже сможете упростить себе процесс решения некоторых задач и сэкономить время. Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ. Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel. Пишите в комментариях помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12689 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.

Данную систему уравнений можно представить в матричной форме:




Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
Решить систему уравнений:

1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://zf.bsut.by/it/fbo/zb1/lab2.htm
Содержание
- 5.4. Арифметические и логические выражения в Excel
- Глава 6. Вычисления в Excel
- 6.1. Абсолютные, относительные и смешанные адреса
- Работа в Excel с формулами и таблицами для чайников
- Формулы в Excel для чайников
- Как в формуле Excel обозначить постоянную ячейку
- Как составить таблицу в Excel с формулами
- 10 популярных математических функций Microsoft Excel
- Применение математических функций
- СУММЕСЛИ
- ОКРУГЛ
- ПРОИЗВЕД
- СТЕПЕНЬ
- КОРЕНЬ
- СЛУЧМЕЖДУ
- ЧАСТНОЕ
- РИМСКОЕ
5.4. Арифметические и логические выражения в Excel
Арифметическое выражение – это совокупность числовых констант, ссылок на ячейки и функций, связанных арифметическими операциями. Решением арифметического выражения является число.
Арифметические операции: + — * / % ^ (возведение в степень).
Порядок выполнения операций в арифметических выражениях – раскрываются скобки (если они есть), выполняются функции, % , затем возведение в степень, умножение и деление, сложение и вычитание. Приведем пример формулы с арифметическим выражением: =(А1 + В1)/(С1+COS(D1))
Логические выражения (ЛВ). Простое логическое выражение — это выражение отношения или два арифметических выражения, связанные операцией отношения.
Например: А1 > С1 . Если А1 больше С1, то результат решения логического выражения — true, иначе значение false.
Сложное логическое выражение включает логические операции:
И( логическое умножение) , ИЛИ (логическое сложение), НЕ (операция отрицания). Синтаксис логической операции И :
И (логическое выражение 1; логич. выражение 2; . ; логич. выражение 30)
Операция И — возвращает значение ИСТИНА, если все аргументы имеют значение ИСТИНА (возвращает ЛОЖЬ, когда хотя бы один аргумент имеет значение ЛОЖЬ ). Например, значение ячейки А1=95, тогда логическое выражение И(A1 =90) имеет значение – истина.
Синтаксис логической операции ИЛИ:
ИЛИ (логическое выражение 1; логич. выражение 2; . ; логич. выражение 30) Операция ИЛИ — возвращает ИСТИНА, если хотя бы один аргумент имеет значение ИСТИНА (возвращает ЛОЖЬ – когда все аргументы имеют значение ЛОЖЬ). Например,ИЛИ(A1 =90) может иметь значение – истина, когда истинны оба логических выражения, либо одно из выражений.
Операция отрицания НЕ — меняет на противоположное логическое значение своего аргумента. Например, НЕ (ложь) – истина.
Глава 6. Вычисления в Excel
6.1. Абсолютные, относительные и смешанные адреса
Адреса ячеек в формулах. В формуле могут быть записаны относительные и абсолютные адреса ячеек, а также смешанные, содержащие относительные и абсолютные адреса
Абсолютные адреса имеют признак $ перед именем столбца и строки. Например, $A$2. При копировании формулы этот адрес не изменяется.
Относительные адреса – без признака $. Например, А2. Относительные адреса изменяются в зависимости от того, куда копируется формула.
Смешанные адреса – содержат относительную и абсолютную части. Например, $A1 – имя столбца не будет изменяться при копировании, а строка будет. Если адрес будет А$1, то имя столбца будет меняться, а строки нет.
Копирование формулы в смежные ячейки выполняется протягиванием мышкой за маркер ячейки.
Источник
Работа в Excel с формулами и таблицами для чайников
Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе.
Конструкция формулы включает в себя: константы, операторы, ссылки, функции, имена диапазонов, круглые скобки содержащие аргументы и другие формулы. На примере разберем практическое применение формул для начинающих пользователей.
Формулы в Excel для чайников
Чтобы задать формулу для ячейки, необходимо активизировать ее (поставить курсор) и ввести равно (=). Так же можно вводить знак равенства в строку формул. После введения формулы нажать Enter. В ячейке появится результат вычислений.
В Excel применяются стандартные математические операторы:
| Оператор | Операция | Пример |
| + (плюс) | Сложение | =В4+7 |
| — (минус) | Вычитание | =А9-100 |
| * (звездочка) | Умножение | =А3*2 |
| / (наклонная черта) | Деление | =А7/А8 |
| ^ (циркумфлекс) | Степень | =6^2 |
| = (знак равенства) | Равно | |
| Больше | ||
| = | Больше или равно | |
| <> | Не равно |
Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.
Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.
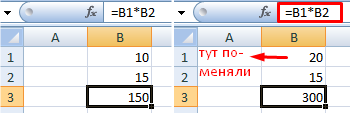
При изменении значений в ячейках формула автоматически пересчитывает результат.
Ссылки можно комбинировать в рамках одной формулы с простыми числами.
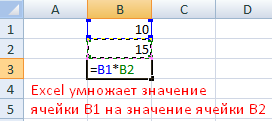
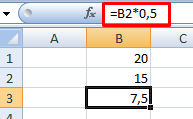
Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке.
В нашем примере:
- Поставили курсор в ячейку В3 и ввели =.
- Щелкнули по ячейке В2 – Excel «обозначил» ее (имя ячейки появилось в формуле, вокруг ячейки образовался «мелькающий» прямоугольник).
- Ввели знак *, значение 0,5 с клавиатуры и нажали ВВОД.
Если в одной формуле применяется несколько операторов, то программа обработает их в следующей последовательности:
Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.
Как в формуле Excel обозначить постоянную ячейку
Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.
Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.
- Вручную заполним первые графы учебной таблицы. У нас – такой вариант:
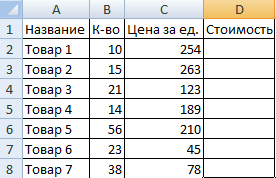
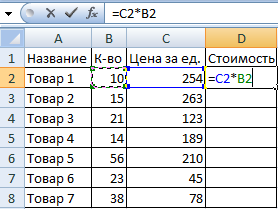
- Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.
- Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.
Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.
Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.
Ссылки в ячейке соотнесены со строкой.
Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).
Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.
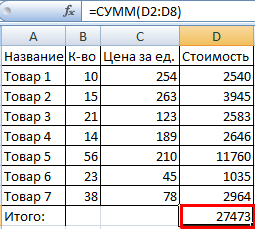
- Создадим строку «Итого». Найдем общую стоимость всех товаров. Выделяем числовые значения столбца «Стоимость» плюс еще одну ячейку. Это диапазон D2:D9
- Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».
- После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.
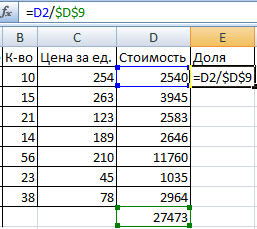
Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:
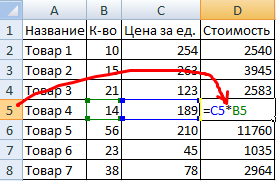
- Разделить стоимость одного товара на стоимость всех товаров и результат умножить на 100. Ссылка на ячейку со значением общей стоимости должна быть абсолютной, чтобы при копировании она оставалась неизменной.
- Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5
- Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.
При создании формул используются следующие форматы абсолютных ссылок:
- $В$2 – при копировании остаются постоянными столбец и строка;
- B$2 – при копировании неизменна строка;
- $B2 – столбец не изменяется.
Как составить таблицу в Excel с формулами
Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.
Простейшие формулы заполнения таблиц в Excel:
- Перед наименованиями товаров вставим еще один столбец. Выделяем любую ячейку в первой графе, щелкаем правой кнопкой мыши. Нажимаем «Вставить». Или жмем сначала комбинацию клавиш: CTRL+ПРОБЕЛ, чтобы выделить весь столбец листа. А потом комбинация: CTRL+SHIFT+»=», чтобы вставить столбец.
- Назовем новую графу «№ п/п». Вводим в первую ячейку «1», во вторую – «2». Выделяем первые две ячейки – «цепляем» левой кнопкой мыши маркер автозаполнения – тянем вниз.
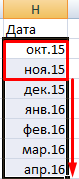
- По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.
- Найдем среднюю цену товаров. Выделяем столбец с ценами + еще одну ячейку. Открываем меню кнопки «Сумма» — выбираем формулу для автоматического расчета среднего значения.
Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.
Источник
10 популярных математических функций Microsoft Excel
Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.
Применение математических функций
С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.
Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.
Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».
Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».
Открывается выпадающий список. Выбираем в нем позицию «Математические».
После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».
Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.
Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:
В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.
СУММЕСЛИ
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), « » («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:
ОКРУГЛ
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:
Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.
ПРОИЗВЕД
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:
СТЕПЕНЬ
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:
КОРЕНЬ
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:
СЛУЧМЕЖДУ
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:
ЧАСТНОЕ
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:
РИМСКОЕ
Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:
Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.
Источник
Содержание
- 1 Автосуммирование
- 2 Тиражирование формул при помощи маркера заполнения
- 3 Относительные и абсолютные ссылки
- 3.1 Создание имени
- 3.2 Создание нескольких имен
- 4 Ошибки в формулах
- 5 Функции в Excel
- 6 Формулы в Excel для чайников
- 7 Как в формуле Excel обозначить постоянную ячейку
- 8 Как составить таблицу в Excel с формулами
- 9 Как вставить формулу
- 10 Из чего состоит формула
- 11 Использование операторов
- 11.1 Арифметические
- 11.2 Операторы сравнения
- 11.3 Математические функции и графики
- 12 Отличие в версиях MS Excel
- 13 Заключение
- 14 Файл примеров
- 15 Видеоинструкция
Формула — это математическое выражение, которое создается для вычисления результата и которое может зависеть от содержимого других ячеек. Формула в ячейке может содержать данные, ссылки на другие ячейки, а также обозначение действий, которые необходимо выполнить.
Использование ссылок на ячейки позволяет пересчитывать результат по формулам, когда происходят изменения содержимого ячеек, включенных в формулы.
В Excel формулы начинаются со знака =. Скобки ( ) могут использоваться для определения порядка математических операции.
Excel поддерживает следующие операторы:
- Арифметические операции:
- сложение (+);
- умножение (*);
- нахождение процента (%);
- вычитание (-);
- деление (/);
- экспонента (^).
- Операторы сравнения:
- = равно;
- < меньше;
- > больше;
- = больше или равно;
- не равно.
- Операторы связи:
- : диапазон;
- ; объединение;
- & оператор соединения текстов.
| Формула | Составляющие элементы |
| =27+36 =А1+А2-АЗ =45%*АЗ , |
Цифры Ссылки на ячейки Цифры и ссылки на ячейки |
| =СУММ(А1:А5), =МАКС(АЗ:А5) |
Предварительно определенные функции |
| =(А1+А2)/АЗ | Ссылки на ячейки при заданном порядке действий |
Таблица 22. Примеры формул
Упражнение
Вставка формулы -25-А1+АЗ
Предварительно введите любые числа в ячейки А1 и A3.
- Выберите необходимую ячейку, например В1.
- Начните ввод формулы со знака=.
- Введите число 25, затем оператор (знак -).
- Введите ссылку на первый операнд, например щелчком мыши на нужную ячейку А1.
- Введите следующий оператор(знак +).
- Щелкните мышью в той ячейке, которая является вторым операндом в формуле.
- Завершите ввод формулы нажатием клавиши Enter. В ячейке В1 получите результат.
Автосуммирование
Кнопка Автосумма (AutoSum) — ∑ может использоваться для автоматического создания формулы, которая суммирует область соседних ячеек, находящихся непосредственно слева в данной строке и непосредственно выше в данном столбце.
- Выберите ячейку, в которую надо поместить результат суммирования.
- Щелкните кнопку Автосумма — ∑ или нажмите комбинацию клавиш Alt+=. Excel примет решение, какую область включить в диапазон суммирования, и выделит ее пунктирной движущейся рамкой, называемой границей.
- Нажмите Enter для принятия области, которую выбрала программа Excel, или выберите с помощью мыши новую область и затем нажмите Enter.
Функция «Автосумма» автоматически трансформируется в случае добавления и удаления ячеек внутри области.
Упражнение
Создание таблицы и расчет по формулам
- Введите числовые данные в ячейки, как показано в табл. 23.
| А | В | С | D | Б | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | |||
| Высшее | 25 | 20 | 9 | |||
| Среднее спец. | 28 | 23 | 21 | |||
| ПТУ | 27 | 58 | 20 | |||
| в | Другое | 8 | 10 | 9 | ||
| Всего | ||||||
| Без высшего |
Таблица 23. Исходная таблица данных
- Выберите ячейку В7, в которой будет вычислена сумма по вертикали.
- Щелкните кнопку Автосумма — ∑ или нажмите Alt+=.
- Повторите действия пунктов 2 и 3 для ячеек С7 и D7.
Вычислите количество сотрудников без высшего образования (по формуле В7-ВЗ).
- Выберите ячейку В8 и наберите знак (=).
- Щелкните мышью в ячейке В7, которая является первым операндом в формуле.
- Введите с клавиатуры знак (-) и щелкните мышью в ячейке ВЗ, которая является вторым операндом в формуле (будет введена формула).
- Нажмите Enter (в ячейке В8 будет вычислен результат).
- Повторите пункты 5-8 для вычислений по соответствующим формулам в ячейках С8 и 08.
- Сохраните файл с именем Образование_сотрудников.х1s.
Таблица 24. Результат расчета
| А | B | С | D | Е | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | |||
| Высшее | 25 | 20 | 9 | |||
| Среднее спец. | 28 | 23 | 21 | |||
| ПТУ | 27 | 58 | 20 | |||
| Другое | 8 | 10 | 9 | |||
| Всего | 88 | 111 | 59 | |||
| Без высшего | 63 | 91 | 50 |
Тиражирование формул при помощи маркера заполнения
Область ячеек (ячейка) может быть размножена при помощи использования маркера заполнения. Как было показано в предыдущем разделе, маркер заполнения представляет собой контрольную точку в правом нижнем углу выделенной ячейки.
Часто бывает необходимо размножать не только данные, но и формулы, содержащие адресные ссылки. Процесс тиражирования формул при помощи маркера заполнения позволяет колировать формулу при одновременном изменении адресных ссылок в формуле.
- Выберите ячейку, содержащую формулу для тиражирования.
- Перетащите маркер заполнения в нужном направлении. Формула будет размножена во всех ячейках.
Обычно этот процесс используется при копировании формул внутри строк или столбцов, содержащих однотипные данные. При тиражировании формул с помощью маркера заполнения меняются так называемые относительные адреса ячеек в формуле (подробно относительные и абсолютные ссылки будут описаны далее).
Упражнение
Тиражирование формул
1.Откройте файл Образование_сотрудников.х1s.
- Введите в ячейку ЕЗ формулу для автосуммирования ячеек =СУММ(ВЗ:03).
- Скопируйте, перетащив маркер заполнения, формулу в ячейки Е4:Е8.
- Просмотрите как меняются относительные адреса ячеек в полученных формулах (табл. 25) и сохраните файл.
| А | В | С | D | Е | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | |||
| Высшее | 25 | 20 | 9 | =СУММ{ВЗ:03) | ||
| Среднее спец. | 28 | 23 | 21 | =СУММ(В4:04) | ||
| ПТУ | 27 | 58 | 20 | =СУММ(В5:05) | ||
| Другое | 8 | 10 | 9 | =СУММ(В6:06) | ||
| Всего | 88 | 111 | 58 | =СУММ(В7:07) | ||
| Без высшего | 63 | 91 | 49 | =СУММ(В8:08) |
Таблица 25. Изменение адресов ячеек при тиражировании формул
Относительные и абсолютные ссылки
Формулы, реализующие вычисления в таблицах, для адресации ячеек используют так называемые ссылки. Ссылка на ячейку может быть относительной или абсолютной.
Использование относительных ссылок аналогично указанию направления движения по улице — «идти три квартала на север, затем два квартала на запад». Следование этим инструкциям из различных начальных мест будет приводить в разные места назначения.
Обычно ссылки на ячейки описываются и используются как относительные (формат записи А1). Когда формула, содержащая эти ссылки, копируется, происходит изменение формулы для поддержания относительности ссылок.
Например, формула, которая суммирует числа в столбце или строке, затем часто копируется для других номеров строк или столбцов. В таких формулах используются относительные ссылки (см. предыдущий пример в табл. 25).
Абсолютная ссылка на ячейку .иди область ячеек будет всегда ссылаться на один и тот же адрес строки и столбца. При сравнении с направлениями улиц это будет примерно следующее: «Идите на пересечение Арбата и Бульварного кольца». Вне зависимости от места старта это будет приводить к одному и тому же месту. Если формула требует, чтобы адрес ячейки оставался неизменным при копировании, то должна использоваться абсолютная ссылка (формат записи $А$1). Например, когда формула вычисляет доли от общей суммы, ссылка на ячейку, содержащую общую сумму, не должна изменяться при копировании.
Абсолютная ссылка может быть создана только при наборе формулы, перед адресом строки и столбца вводится знак доллара — $.
Для создания абсолютной ссылки удобно использовать клавишу абсолютной ссылки F4, которая осуществляет преобразование относительной ссылки в абсолютную и наоборот.
Знак доллара ($) появится как перед ссылкой на столбец, так и перед ссылкой на строку (например, $С$2), Последовательное нажатие F4 будет добавлять или убирать знак перед номером столбца или строки в ссылке (С$2 или $С2 — так называемые смешанные ссылки).
Упражнение
Создание абсолютной ссылки
- Создайте таблицу, аналогичную представленной ниже.
| A | B | C | |
| Часовая ставка | 100р. | ||
| Ф. И. 0 . | Часов | Зарплата | |
| Иванов | 40 | ||
| Петров | 30 | ||
| Сидоров | 25 |
Таблица 26. Расчет зарплаты
- В ячейку СЗ введите формулу для расчета зарплаты Иванова =В1*ВЗ.
При тиражировании формулы данного примера с относительными ссылками в ячейке С4 появляется сообщение об ошибке (#ЗНАЧ!), так как изменится относительный адрес ячейки В1, и в ячейку С4 скопируется формула =В2*В4;
- Задайте абсолютную ссылку на ячейку В1, поставив курсор в строке формул на В1 и нажав клавишу F4, Формула в ячейке СЗ будет иметь вид =$В$1*ВЗ.
- Скопируйте формулу в ячейки С4 и С5.
- Сохраните файл (табл. 27) под именем Зарплата.xls.
| A | B | C | |
| 1 | Часовая ставка | 100р. | |
| ФИО | Часов | Зарплата | |
| 3 | Иванов | 40 | 4000р. |
| 4 | Петров | 30 | 3000р. |
| 5 | Сидоров | 25 | 2500р. |
Таблица 27. Итоги расчета зарплаты
Имена в формулах
Имена в формулах легче запомнить, чем адреса ячеек, поэтому вместо абсолютных ссылок можно использовать именованные области (одна или несколько ячеек). Необходимо соблюдать следующие правила при создании имен:
- имена могут содержать не более 255 символов;
- имена должны начинаться с буквы и могут содержать любой символ, кроме пробела;
- имена не должны быть похожи на ссылки, такие, как ВЗ, С4;
- имена не должны использовать функции Excel, такие, как СУММ, ЕСЛИ и т. п.
В меню Вставка, Имя существуют две различные команды создания именованных областей: Создать и Присвоить.
Команда Создать позволяет задать (ввести) требуемое имя (только одно)команда Присвоить использует метки, размещенные на рабочем листе, в качестве имен областей (разрешается создавать сразу несколько имен).
Создание имени
- Выделите ячейку В1 (табл. 26).
- Выберите в меню Вставка, Имя (Insert, Name) команду Присвоить (Define).
- Введите имя Часовая ставка и нажмите ОК.
- Выделите ячейку В1 и убедитесь, что в поле имени указано Часовая ставка.
Создание нескольких имен
- Выделите ячейки ВЗ:С5 (табл. 27).
- Выберите в меню Вставка, Имя (Insert, Name) команду Создать (Create), появится диалоговое окно Создать имена (рис. 88).
- Убедитесь, что переключатель в столбце слева помечен и нажмите ОК.
- Выделите ячейки ВЗ:СЗ и убедитесь, что в поле имени указано Иванов.
Рис. 88. Диалоговое окно Создать имена
Можно в формулу вставить имя вместо абсолютной ссылки.
- В строке формул установите курсор в то место, где будет добавлено имя.
- Выберите в меню Вставка, Имя (Insert, Name) команду Вставить (Paste), появится диалоговое окно Вставить имена.
- Выберите нужное имя из списка и нажмите ОК.
Ошибки в формулах
Бели при вводе формул или данных допущена ошибка, то в результирующей ячейке появляется сообщение об ошибке. Первым символом всех значений ошибок является символ #. Значения ошибок зависят от вида допущенной ошибки.
Excel может распознать далеко не все ошибки, но те, которые обнаружены, надо уметь исправить.
Ошибка # # # # появляется, когда вводимое число не умещается в ячейке. В этом случае следует увеличить ширину столбца.
Ошибка #ДЕЛ/0! появляется, когда в формуле делается попытка деления на нуль. Чаще всего это случается, когда в качестве делителя используется ссылка на ячейку, содержащую нулевое или пустое значение.
Ошибка #Н/Д! является сокращением термина «неопределенные данные». Эта ошибка указывает на использование в формуле ссылки на пустую ячейку.
Ошибка #ИМЯ? появляется, когда имя, используемое в формуле, было удалено или не было ранее определено. Для исправления определите или исправьте имя области данных, имя функции и др.
Ошибка #ПУСТО! появляется, когда задано пересечение двух областей, которые в действительности не имеют общих ячеек. Чаще всего ошибка указывает, что допущена ошибка при вводе ссылок на диапазоны ячеек.
Ошибка #ЧИСЛО! появляется, когда в функции с числовым аргументом используется неверный формат или значение аргумента.
Ошибка #ССЫЛКА! появляется, когда в формуле используется недопустимая ссылка на ячейку. Например, если ячейки были удалены или в эти ячейки было помещено содержимое других ячеек.
Ошибка #ЗНАЧ! появляется, когда в формуле используется недопустимый тип аргумента или операнда. Например, вместо числового или логического значения для оператора или функции введен текст.
Кроме перечисленных ошибок, при вводе формул может появиться циклическая ссылка.
Циклическая ссылка возникает тогда, когда формула прямо или косвенно включает ссылки на свою собственную ячейку. Циклическая ссылка может вызывать искажения в вычислениях на рабочем листе и поэтому рассматривается как ошибка в большинстве приложений. При вводе циклической ссылки появляется предупредительное сообщение (рис. 89).
Рис. 89. Циклическая ссылка
Индикатор циклической ссылки в строке состояния показывает ««ссылку на последнюю зависимую формулу.
Когда формула, содержащая циклическую ссылку, находится на рабочем листе, появится сообщение, указанное на рис. 89.
Для исправления ошибки удалите ячейку, которая вызвала циклическую ссылку, отредактируйте или введите заново формулу.
Более сложные вычисления в таблицах Excel осуществляются с помощью специальных функций (рис. 90). Список категорий функций доступен при выборе команды Функция в меню Вставка (Insert, Function).
Финансовые функции осуществляют такие расчеты, как вычисление суммы платежа по ссуде, величину выплаты прибыли на вложения и др.
Функции Дата и время позволяют работать со значениями даты и времени в формулах. Например, можно использовать в формуле текущую дату, воспользовавшись функцией СЕГОДНЯ.
Рис. 90. Мастер функций
Математические функции выполняют простые и сложные математические вычисления, например вычисление суммы диапазона ячеек, абсолютной величины числа, округление чисел и др.
Статистические функции позволяют выполнять статистический анализ данных. Например, можно определить среднее значение и дисперсию по выборке и многое другое.
Функции Ссылки и массивы позволяют осуществить поиск данных в списках или таблицах, найти ссылку на ячейку в массиве. Например, для поиска значения в строке таблицы используется функция ГПР.
Функции работы с базами данных можно использовать для выполнения расчетов и для отбора записей по условию.
Текстовые функции предоставляют пользователю возможность обработки текста. Например, можно объединить несколько строк с помощью функции СЦЕПИТЬ.
Логические функции предназначены для проверки одного или нескольких условий. Например, функция ЕСЛИ позволяет определить, выполняется ли указанное условие, и возвращает одно значение, если условие истинно, и другое, если оно ложно.
Функции Проверка свойств и значений предназначены для определения данных, хранимых в ячейке. Эти функции проверяют значения в ячейке по условию и возвращают в зависимости от результата значения ИСТИНА или ЛОЖЬ.
Для вычислений в таблице с помощью встроенных функций рекомендуется использовать мастер функций. Диалоговое окно мастера функций доступно при выборе команды Функция в меню Вставка или нажатии кнопки на стандартной панели инструментов. В процессе диалога с мастером требуется задать аргументы выбранной функции, для этого необходимо заполнить поля в диалоговом окне соответствующими значениями или адресами ячеек таблицы.
Упражнение
Вычисление величины среднего значения для каждой строки в файле Образование.хls.
- Выделите ячейку F3 и нажмите на кнопку мастера функций.
- В первом окне диалога мастера функций из категории Статистические выберите функцию СРЗНАЧ, нажмите на кнопку Далее.
- Во втором диалоговом окне мастера функций должны быть заданы аргументы. Курсор ввода находится в поле ввода первого аргумента. В это поле в качестве аргумента число! введите адрес диапазона B3:D3 (рис. 91).
- Нажмите ОК.
- Скопируйте полученную формулу в ячейки F4:F6 и сохраните файл (табл. 28).
Рис. 91. Ввод аргумента в мастере функций
Таблица 28. Таблица результатов расчета с помощью мастера функций
| А | В | С | D | Е | F | |
| Распределение сотрудников по образованию | ||||||
| Магнолия | Лилия | Фиалка | Всего | Среднее | ||
| Высшее | 25 | 20 | 9 | 54 | 18 | |
| Среднее спец. | 28 | 23 | 21 | 72 | 24 | |
| ПТУ | 27 | 58 | 20 | 105 | 35 | |
| в | Другое | 8 | 10 | 9 | 27 | 9 |
| Всего | 88 | 111 | 59 | 258 | 129 |
Для ввода диапазона ячеек в окно мастера функций можно мышью обвести на рабочем листе таблицы этот диапазон (в примере B3:D3). Если окно мастера функций закрывает нужные ячейки, можно передвинуть окно диалога. После выделения диапазона ячеек (B3:D3) вокруг него появится бегущая пунктирная рамка, а в поле аргумента автоматически появится адрес выделенного диапазона ячеек.
Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе.
Конструкция формулы включает в себя: константы, операторы, ссылки, функции, имена диапазонов, круглые скобки содержащие аргументы и другие формулы. На примере разберем практическое применение формул для начинающих пользователей.
Формулы в Excel для чайников
Чтобы задать формулу для ячейки, необходимо активизировать ее (поставить курсор) и ввести равно (=). Так же можно вводить знак равенства в строку формул. После введения формулы нажать Enter. В ячейке появится результат вычислений.
В Excel применяются стандартные математические операторы:
| Оператор | Операция | Пример |
| + (плюс) | Сложение | =В4+7 |
| — (минус) | Вычитание | =А9-100 |
| * (звездочка) | Умножение | =А3*2 |
| / (наклонная черта) | Деление | =А7/А8 |
| ^ (циркумфлекс) | Степень | =6^2 |
| = (знак равенства) | Равно | |
| Меньше | ||
| > | Больше | |
| Меньше или равно | ||
| >= | Больше или равно | |
| Не равно |
Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.
Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.
При изменении значений в ячейках формула автоматически пересчитывает результат.
Ссылки можно комбинировать в рамках одной формулы с простыми числами.
Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке.
В нашем примере:
- Поставили курсор в ячейку В3 и ввели =.
- Щелкнули по ячейке В2 – Excel «обозначил» ее (имя ячейки появилось в формуле, вокруг ячейки образовался «мелькающий» прямоугольник).
- Ввели знак *, значение 0,5 с клавиатуры и нажали ВВОД.
Если в одной формуле применяется несколько операторов, то программа обработает их в следующей последовательности:
- %, ^;
- *, /;
- +, -.
Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.
Как в формуле Excel обозначить постоянную ячейку
Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.
Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.
- Вручную заполним первые графы учебной таблицы. У нас – такой вариант:
- Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.
- Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.
Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.
Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.
Ссылки в ячейке соотнесены со строкой.
Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).
Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.
- Создадим строку «Итого». Найдем общую стоимость всех товаров. Выделяем числовые значения столбца «Стоимость» плюс еще одну ячейку. Это диапазон D2:D9
- Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».
- После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.
Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:
- Разделить стоимость одного товара на стоимость всех товаров и результат умножить на 100. Ссылка на ячейку со значением общей стоимости должна быть абсолютной, чтобы при копировании она оставалась неизменной.
- Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5
- Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.
При создании формул используются следующие форматы абсолютных ссылок:
- $В$2 – при копировании остаются постоянными столбец и строка;
- B$2 – при копировании неизменна строка;
- $B2 – столбец не изменяется.
Как составить таблицу в Excel с формулами
Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.
Простейшие формулы заполнения таблиц в Excel:
- Перед наименованиями товаров вставим еще один столбец. Выделяем любую ячейку в первой графе, щелкаем правой кнопкой мыши. Нажимаем «Вставить». Или жмем сначала комбинацию клавиш: CTRL+ПРОБЕЛ, чтобы выделить весь столбец листа. А потом комбинация: CTRL+SHIFT+»=», чтобы вставить столбец.
- Назовем новую графу «№ п/п». Вводим в первую ячейку «1», во вторую – «2». Выделяем первые две ячейки – «цепляем» левой кнопкой мыши маркер автозаполнения – тянем вниз.
- По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.
- Найдем среднюю цену товаров. Выделяем столбец с ценами + еще одну ячейку. Открываем меню кнопки «Сумма» — выбираем формулу для автоматического расчета среднего значения.
Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.
Общие сведения о проекте
На сегодняшний день наш сайт является уникальным проектом на просторах российского интернета. На страницах сайта infowall.ru всегда можно найти самую свежую и исчерпывающую информацию о новинках компьютерных программ, а также практические советы по работе в сети Интернет, настройке и использованию компьютера, установке программного обеспечения и другую полезную информацию. Информационное наполнение сайта, а также программы для компьютера рассчитаны как на простых пользователей, так и на людей, имеющих практический опыт в области информационных технологий, программного обеспечения и администрирования сетевых ресурсов (операторов компьютерных систем, программистов, а также системных администраторов). Целью проекта является создание оптимизированного ресурса для размещения актуальной и полезной информации, а также практическая поддержка пользователей сайта.
Практические руководства и инструкции
Многие бесплатные программы, которые размещены на нашем сайте, зачастую требуют от пользователей определенных базовых навыков работы с ними. Для облегчения процесса знакомства с новыми популярными программами в разделе База знаний мы ежедневно размещаем подробные инструкции по использованию тех или иных наиболее востребованных на наш взгляд программ, с которыми приходится сталкиваться в повседневной работе. Все инструкции написаны живым языком и будут интересны как начинающим, так и более опытным пользователям. Кроме того, на сайте пополняется база практических руководств по работе в интернете, обслуживанию компьютера, установке и использованию пакетов популярных и профессиональных программ и многое другое. Отныне сайт infowall.ru станет для вас надежным проводником в мире интернета и персональных компьютеров. И если вы еще новичок в этой области, то с нашим проектом вы незаметно для себя получите практический опыт и обширные знания, посещая наш сайт, хотя бы раз в день!
Программное обеспечение
Наш сайт также содержит регулярно обновляемый каталог программ, которые станут вашими незаменимыми помощниками в процессе практической работы на компьютере, как дома, так и на работе. Наши специалисты тестируют и размещают бесплатные программы для компьютера, различные утилиты, антивирусы и прочий софт. У нас можно скачать офисные программы и приложения, мультимедиа софт, кодеки, утилиты для восстановления данных, файловые менеджеры, архиваторы, программы для интернета, для работы с электронной почтой и многое другое.
Мы стремимся обеспечить максимальный комфорт для наших пользователей, именно поэтому все программы для компьютера, размещенные на нашем сайте, доступны для простого и бесплатного скачивания, а также имеют в своей структуре подробное описание, что позволяет пользователям предварительно ознакомиться с той или иной программой.
Кроме того, если в процессе работы с компьютером у вас возникли какие-либо сложности, то вы всегда можете оставить у нас заявку в специальном разделе Помогите найти или задать вопрос в разделе Вопросы. Мы ежедневно прилагаем все усилия, чтобы в максимально сжатые сроки предоставить вам исчерпывающую и подробную информацию по всем интересующим вопросам.
Развитие проекта
Мы также приветствуем всякую посильную помощь от наших пользователей в развитии проекта. Если у вас есть чем поделиться с другими, вы всегда можете разместить на сайте любую программу, которая, по вашему мнению, будет полезна пользователям и посетителям нашего сайта.
Проект infowall.ru является некоммерческим. При этом его развитие осуществляется благодаря энтузиазму сообщества небезразличных людей. Вы также можете поделиться с нами вашими идеями, статьями, ссылками или любым другим способом принять участие в развитии проекта. Для этого достаточно связаться с администрацией сайта. Мы будем рады любому вашему участию!
Формулы в Excel – одно из самых главных достоинств этого редактора. Благодаря им ваши возможности при работе с таблицами увеличиваются в несколько раз и ограничиваются только имеющимися знаниями. Вы сможете сделать всё что угодно. При этом Эксель будет помогать на каждом шагу – практически в любом окне существуют специальные подсказки.
Как вставить формулу
Для создания простой формулы достаточно следовать следующей инструкции:
- Сделайте активной любую клетку. Кликните на строку ввода формул. Поставьте знак равенства.
- Введите любое выражение. Использовать можно как цифры,
так и ссылки на ячейки.
При этом затронутые ячейки всегда подсвечиваются. Это делается для того, чтобы вы не ошиблись с выбором. Визуально увидеть ошибку проще, чем в текстовом виде.
Из чего состоит формула
В качестве примера приведём следующее выражение.
Оно состоит из:
- символ «=» – с него начинается любая формула;
- функция «СУММ»;
- аргумента функции «A1:C1» (в данном случае это массив ячеек с «A1» по «C1»);
- оператора «+» (сложение);
- ссылки на ячейку «C1»;
- оператора «^» (возведение в степень);
- константы «2».
Использование операторов
Операторы в редакторе Excel указывают какие именно операции нужно выполнить над указанными элементами формулы. При вычислении всегда соблюдается один и тот же порядок:
- скобки;
- экспоненты;
- умножение и деление (в зависимости от последовательности);
- сложение и вычитание (также в зависимости от последовательности).
Арифметические
К ним относятся:
- сложение – «+» (плюс);
=2+2
- отрицание или вычитание – «-» (минус);
=2-2 =-2
Если перед числом поставить «минус», то оно примет отрицательное значение, но по модулю останется точно таким же.
- умножение – «*»;
=2*2
- деление «/»;
=2/2
- процент «%»;
=20%
- возведение в степень – «^».
=2^2
Операторы сравнения
Данные операторы применяются для сравнения значений. В результате операции возвращается ИСТИНА или ЛОЖЬ. К ним относятся:
- знак «равенства» – «=»;
=C1=D1
- знак «больше» – «>»;
=C1>D1
- знак «меньше» — «=D1
- знак «меньше или равно» — «3″;B3:C3)
- Excel может складывать с учетом сразу нескольких условий. Можно посчитать сумму клеток первого столбца, значение которых больше 2 и меньше 6. И ту же самую формулу можно установить для второй колонки.
=СУММЕСЛИМН(B3:B9;B3:B9;»>2″;B3:B9;»3″)
- Результат всех формул получится следующим.
Математические функции и графики
При помощи Экселя можно рассчитывать различные функции и строить по ним графики, а затем проводить графический анализ. Как правило, подобные приёмы используются в презентациях.
В качестве примера попробуем построить графики для экспоненты и какого-нибудь уравнения. Инструкция будет следующей:
- Создадим таблицу. В первой графе у нас будет исходное число «X», во второй – функция «EXP», в третьей – указанное соотношение. Можно было бы сделать квадратичное выражение, но тогда бы результирующее значение на фоне экспоненты на графике практически пропало бы.
- Для того чтобы преобразовать значение «X», нужно указать следующие формулы.
=EXP(B4) =B4+5*B4^3/2
- Дублируем эти выражения до самого конца. В итоге получаем следующий результат.
- Выделяем всю таблицу. Переходим на вкладку «Вставка». Кликаем на инструмент «Рекомендуемые диаграммы».
- Выбираем тип «Линия». Для продолжения кликаем на «OK».
- Результат получился довольно-таки красивый и аккуратный.
Как мы и говорили ранее, прирост экспоненты происходит намного быстрее, чем у обычного кубического уравнения.
Подобным образом можно представить графически любую функцию или математическое выражение.
Отличие в версиях MS Excel
Всё описанное выше подходит для современных программ 2007, 2010, 2013 и 2016 года. Старый редактор Эксель значительно уступает в плане возможностей, количества функций и инструментов. Если откроете официальную справку от Microsoft, то увидите, что они дополнительно указывают, в какой именно версии программы появилась данная функция.
Во всём остальном всё выглядит практически точно так же. В качестве примера, посчитаем сумму нескольких ячеек. Для этого необходимо:
- Указать какие-нибудь данные для вычисления. Кликните на любую клетку. Нажмите на иконку «Fx».
- Выбираем категорию «Математические». Находим функцию «СУММ» и нажимаем на «OK».
- Указываем данные в нужном диапазоне. Для того чтобы отобразить результат, нужно нажать на «OK».
- Можете попробовать пересчитать в любом другом редакторе. Процесс будет происходить точно так же.
Заключение
В данном самоучителе мы рассказали обо всем, что связано с формулами в редакторе Excel, – от самого простого до очень сложного. Каждый раздел сопровождался подробными примерами и пояснениями. Это сделано для того, чтобы информация была доступной даже для полных чайников.
Если у вас что-то не получается, значит, вы допускаете где-то ошибку. Возможно, у вас есть опечатки в выражениях или же указаны неправильные ссылки на ячейки. Главное понять, что всё нужно вбивать очень аккуратно и внимательно. Тем более все функции не на английском, а на русском языке.
Кроме этого, важно помнить, что формулы должны начинаться с символа «=» (равно). Многие начинающие пользователи забывают про это.
Файл примеров
Для того чтобы вам было легче разобраться с описанными ранее формулами, мы подготовили специальный демо-файл, в котором составлялись все указанные примеры. Вы можете скачать его с нашего сайта совершенно бесплатно. Если во время обучения вы будете использовать готовую таблицу с формулами на основании заполненных данных, то добьетесь результата намного быстрее.
Видеоинструкция
Если наше описание вам не помогло, попробуйте посмотреть приложенное ниже видео, в котором рассказываются основные моменты более детально. Возможно, вы делаете всё правильно, но что-то упускаете из виду. С помощью этого ролика вы должны разобраться со всеми проблемами. Надеемся, что подобные уроки вам помогли. Заглядывайте к нам чаще.
- знак «меньше или равно» — «3″;B3:C3)