Last Update: Jan 03, 2023
This is a question our experts keep getting from time to time. Now, we have got the complete detailed explanation and answer for everyone, who is interested!
Asked by: Mrs. Amira McCullough DDS
Score: 4.4/5
(48 votes)
Algebraic word problems are questions that require translating sentences to equations, then solving those equations. and a single variable. Usually, the variable represents an unknown quantity in a real-life scenario.
What is considered algebra?
Algebra is a branch of mathematics dealing with symbols and the rules for manipulating those symbols. In elementary algebra, those symbols (today written as Latin and Greek letters) represent quantities without fixed values, known as variables. … The letters x and y represent the areas of the fields.
What are the 4 types of algebra?
They are elementary algebra, abstract algebra, advanced algebra, communicative algebra, and linear algebra. All these branches have a different formula, different application, and different use in finding out the values of variables.
Is algebra a problem solving?
Using algebra to solve word problems is a very powerful application of mathematics. Unfortunately, many students don’t feel comfortable using algebra to solve real world problems, even though they feel comfortable with their algebra skills.
How do you do algebra word problems?
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
42 related questions found
Why is algebra so hard?
Algebra is thinking logically about numbers rather than computing with numbers. … Paradoxically, or so it may seem, however, those better students may find it harder to learn algebra. Because to do algebra, for all but the most basic examples, you have to stop thinking arithmetically and learn to think algebraically.
Who invented 0?
The first modern equivalent of numeral zero comes from a Hindu astronomer and mathematician Brahmagupta in 628. His symbol to depict the numeral was a dot underneath a number.
Who really invented algebra?
When was algebra invented? Muhammad ibn Musa al-Khwarizmi, a Muslim mathematician wrote a book in 9th century named «Kitab Al-Jabr» from which the word «ALGEBRA» derived. So algebra was invented in the 9th century.
Are algebra numbers countable?
All integers and rational numbers are algebraic, as are all roots of integers. … The set of complex numbers is uncountable, but the set of algebraic numbers is countable and has measure zero in the Lebesgue measure as a subset of the complex numbers. In that sense, almost all complex numbers are transcendental.
Is 0 an algebraic expression?
yes,is zero an algebraic expression.
Is E Pi algebraic?
Possible transcendental numbers
Numbers which have yet to be proven to be either transcendental or algebraic: Most sums, products, powers, etc. of the number π and the number e, e.g. eπ, e + π, π − e, π/e, ππ, ee, πe, π√2, eπ2 are not known to be rational, algebraic, irrational or transcendental.
Is algebra 1a advanced?
Algebra 1 in 9th grade was the old norm when I was in high school. … Good-at-math students were a year advanced, taking algebra 1 in 8th grade leading to calculus in 12th grade as a bonus to get a head start on college level math.
What all comes under algebra?
Advanced algebra will help you to go through the other parts of algebra such as:
- Equations with inequalities.
- Matrices.
- Solving system of linear equations.
- Graphing of functions and linear equations.
- Conic sections.
- Polynomial Equation.
- Quadratic Functions with inequalities.
- Polynomials and expressions with radicals.
Is algebra math in high school?
What is Algebra 1? Algebra 1 is a high school math course exploring how to use letters (called variables) and numbers with mathematical symbols to solve problems. Algebra 1 typically includes evaluating expressions, writing equations, graphing functions, solving quadratics, and understanding inequalities.
Who figured out pi?
The first calculation of π was done by Archimedes of Syracuse (287–212 BC), one of the greatest mathematicians of the ancient world.
Who invented school?
Credit for our modern version of the school system usually goes to Horace Mann. When he became Secretary of Education in Massachusetts in 1837, he set forth his vision for a system of professional teachers who would teach students an organized curriculum of basic content.
Who invented time?
The measurement of time began with the invention of sundials in ancient Egypt some time prior to 1500 B.C. However, the time the Egyptians measured was not the same as the time today’s clocks measure. For the Egyptians, and indeed for a further three millennia, the basic unit of time was the period of daylight.
What is the hardest math ever?
These Are the 10 Toughest Math Problems Ever Solved
- The Collatz Conjecture. Dave Linkletter. …
- Goldbach’s Conjecture Creative Commons. …
- The Twin Prime Conjecture. …
- The Riemann Hypothesis. …
- The Birch and Swinnerton-Dyer Conjecture. …
- The Kissing Number Problem. …
- The Unknotting Problem. …
- The Large Cardinal Project.
What is the hardest math problem?
But those itching for their Good Will Hunting moment, the Guinness Book of Records puts Goldbach’s Conjecture as the current longest-standing maths problem, which has been around for 257 years. It states that every even number is the sum of two prime numbers: for example, 53 + 47 = 100.
Why do students struggle with algebra?
First-time learners find it difficult to grasp the concept of symbols used in algebra. … While this is related to their difficulty in understanding the equal sign, it is also a matter of students finding the use of symbols in Mathematics rather alien.
What is a word problem in maths?
What is a word problem? A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
How do you turn a word problem into an algebraic equation?
How to Translate Word Problems Into Equations
- Step One: Highlight Important Parts of the Text.
- Step Two: Establish your variables. …
- Step Three: Rewrite the Problem as an Equation. …
- Step Four: Substitute. …
- Step Five: Simplify and Combine Terms. …
- Step Six: Divide Each Side of the Equation. …
- Step Seven: Solve.
From Wikipedia, the free encyclopedia
This article is about algorithmic word problems in mathematics and computer science. For other uses, see Word problem.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.[1]
Background and motivation[edit]
In computer algebra one often wishes to encode mathematical expressions using an expression tree. But there are often multiple equivalent expression trees. The question naturally arises of whether there is an algorithm which, given as input two expressions, decides whether they represent the same element. Such an algorithm is called a solution to the word problem. For example, imagine that 

EQUAL, and similarly produce NOT_EQUAL from 
The most direct solution to a word problem takes the form of a normal form theorem and algorithm which maps every element in an equivalence class of expressions to a single encoding known as the normal form — the word problem is then solved by comparing these normal forms via syntactic equality.[1] For example one might decide that 



While the word problem asks whether two terms containing constants are equal, a proper extension of the word problem known as the unification problem asks whether two terms 


while 

History[edit]
One of the most deeply studied cases of the word problem is in the theory of semigroups and groups. A timeline of papers relevant to the Novikov-Boone theorem is as follows:[3][4]
- 1910: Axel Thue poses a general problem of term rewriting on tree-like structures. He states «A solution of this problem in the most general case may perhaps be connected with unsurmountable difficulties».[5][6]
- 1911: Max Dehn poses the word problem for finitely presented groups.[7]
- 1912: Dehn presents Dehn’s algorithm, and proves it solves the word problem for the fundamental groups of closed orientable two-dimensional manifolds of genus greater than or equal to 2.[8] Subsequent authors have greatly extended it to a wide range of group-theoretic decision problems.[9][10][11]
- 1914: Axel Thue poses the word problem for finitely presented semigroups.[12]
- 1930 – 1938: The Church-Turing thesis emerges, defining formal notions of computability and undecidability.[13]
- 1947: Emil Post and Andrey Markov Jr. independently construct finitely presented semigroups with unsolvable word problem.[14][15] Post’s construction is built on Turing machines while Markov’s uses Post’s normal systems.[3]
- 1950: Alan Turing shows the word problem for cancellation semigroups is unsolvable,[16] by furthering Post’s construction. The proof is difficult to follow but marks a turning point in the word problem for groups.[3]: 342
- 1955: Pyotr Novikov gives the first published proof that the word problem for groups is unsolvable, using Turing’s cancellation semigroup result.[17][3]: 354 The proof contains a «Principal Lemma» equivalent to Britton’s Lemma.[3]: 355
- 1954 – 1957: William Boone independently shows the word problem for groups is unsolvable, using Post’s semigroup construction.[18][19]
- 1957 – 1958: John Britton gives another proof that the word problem for groups is unsolvable, based on Turing’s cancellation semigroups result and some of Britton’s earlier work.[20] An early version of Britton’s Lemma appears.[3]: 355
- 1958 – 1959: Boone publishes a simplified version of his construction.[21][22]
- 1961: Graham Higman characterises the subgroups of finitely presented groups with Higman’s embedding theorem,[23] connecting recursion theory with group theory in an unexpected way and giving a very different proof of the unsolvability of the word problem.[3]
- 1961 – 1963: Britton presents a greatly simplified version of Boone’s 1959 proof that the word problem for groups is unsolvable.[24] It uses a group-theoretic approach, in particular Britton’s Lemma. This proof has been used in a graduate course, although more modern and condensed proofs exist.[25]
- 1977: Gennady Makanin proves that the existential theory of equations over free monoids is solvable.[26]
The word problem for semi-Thue systems[edit]
The accessibility problem for string rewriting systems (semi-Thue systems or semigroups) can be stated as follows: Given a semi-Thue system 




The accessibility and word problems are undecidable, i.e. there is no general algorithm for solving this problem.[28] This even holds if we limit the systems to have finite presentations, i.e. a finite set of symbols and a finite set of relations on those symbols.[27] Even the word problem restricted to ground terms is not decidable for certain finitely presented semigroups.[29][30]
The word problem for groups[edit]
Given a presentation 
The word problem in combinatorial calculus and lambda calculus[edit]
One of the earliest proofs that a word problem is undecidable was for combinatory logic: when are two strings of combinators equivalent? Because combinators encode all possible Turing machines, and the equivalence of two Turing machines is undecidable, it follows that the equivalence of two strings of combinators is undecidable. Alonzo Church observed this in 1936.[32]
Likewise, one has essentially the same problem in (untyped) lambda calculus: given two distinct lambda expressions, there is no algorithm which can discern whether they are equivalent or not; equivalence is undecidable. For several typed variants of the lambda calculus, equivalence is decidable by comparison of normal forms.
The word problem for abstract rewriting systems[edit]
Solving the word problem: deciding if 

The word problem for an abstract rewriting system (ARS) is quite succinct: given objects x and y are they equivalent under 

The Knuth-Bendix completion algorithm can be used to transform a set of equations into a convergent term rewriting system.
The word problem in universal algebra[edit]
In universal algebra one studies algebraic structures consisting of a generating set A, a collection of operations on A of finite arity, and a finite set of identities that these operations must satisfy. The word problem for an algebra is then to determine, given two expressions (words) involving the generators and operations, whether they represent the same element of the algebra modulo the identities. The word problems for groups and semigroups can be phrased as word problems for algebras.[1]
The word problem on free Heyting algebras is difficult.[34]
The only known results are that the free Heyting algebra on one generator is infinite, and that the free complete Heyting algebra on one generator exists (and has one more element than the free Heyting algebra).
The word problem for free lattices[edit]
|
|
The word problem on free lattices and more generally free bounded lattices has a decidable solution. Bounded lattices are algebraic structures with the two binary operations ∨ and ∧ and the two constants (nullary operations) 0 and 1. The set of all well-formed expressions that can be formulated using these operations on elements from a given set of generators X will be called W(X). This set of words contains many expressions that turn out to denote equal values in every lattice. For example, if a is some element of X, then a ∨ 1 = 1 and a ∧ 1 = a. The word problem for free bounded lattices is the problem of determining which of these elements of W(X) denote the same element in the free bounded lattice FX, and hence in every bounded lattice.
The word problem may be resolved as follows. A relation ≤~ on W(X) may be defined inductively by setting w ≤~ v if and only if one of the following holds:
- w = v (this can be restricted to the case where w and v are elements of X),
- w = 0,
- v = 1,
- w = w1 ∨ w2 and both w1 ≤~ v and w2 ≤~ v hold,
- w = w1 ∧ w2 and either w1 ≤~ v or w2 ≤~ v holds,
- v = v1 ∨ v2 and either w ≤~ v1 or w ≤~ v2 holds,
- v = v1 ∧ v2 and both w ≤~ v1 and w ≤~ v2 hold.
This defines a preorder ≤~ on W(X), so an equivalence relation can be defined by w ~ v when w ≤~ v and v ≤~ w. One may then show that the partially ordered quotient set W(X)/~ is the free bounded lattice FX.[35][36] The equivalence classes of W(X)/~ are the sets of all words w and v with w ≤~ v and v ≤~ w. Two well-formed words v and w in W(X) denote the same value in every bounded lattice if and only if w ≤~ v and v ≤~ w; the latter conditions can be effectively decided using the above inductive definition. The table shows an example computation to show that the words x∧z and x∧z∧(x∨y) denote the same value in every bounded lattice. The case of lattices that are not bounded is treated similarly, omitting rules 2 and 3 in the above construction of ≤~.
Example: A term rewriting system to decide the word problem in the free group[edit]
Bläsius and Bürckert
[37]
demonstrate the Knuth–Bendix algorithm on an axiom set for groups.
The algorithm yields a confluent and noetherian term rewrite system that transforms every term into a unique normal form.[38]
The rewrite rules are numbered incontiguous since some rules became redundant and were deleted during the algorithm run.
The equality of two terms follows from the axioms if and only if both terms are transformed into literally the same normal form term. For example, the terms
, and
share the same normal form, viz. 
As another example, the term 



| A1 |  |

|
| A2 |  |

|
| A3 |  |

|
| R1 |  |

|
| R2 |  |

|
| R3 |  |

|
| R4 |  |

|
| R8 |  |

|
| R11 |  |

|
| R12 |  |

|
| R13 |  |

|
| R14 |  |

|
| R17 |  |

|
See also[edit]
- Conjugacy problem
- Group isomorphism problem
References[edit]
- ^ a b c d Evans, Trevor (1978). «Word problems». Bulletin of the American Mathematical Society. 84 (5): 790. doi:10.1090/S0002-9904-1978-14516-9.
- ^ Cohen, Joel S. (2002). Computer algebra and symbolic computation: elementary algorithms. Natick, Mass.: A K Peters. pp. 90–92. ISBN 1568811586.
- ^ a b c d e f g Miller, Charles F. (2014). Downey, Rod (ed.). «Turing machines to word problems» (PDF). Turing’s Legacy: 330. doi:10.1017/CBO9781107338579.010. hdl:11343/51723. ISBN 9781107338579. Retrieved 6 December 2021.
- ^ Stillwell, John (1982). «The word problem and the isomorphism problem for groups». Bulletin of the American Mathematical Society. 6 (1): 33–56. doi:10.1090/S0273-0979-1982-14963-1.
- ^ Müller-Stach, Stefan (12 September 2021). «Max Dehn, Axel Thue, and the Undecidable». p. 13. arXiv:1703.09750 [math.HO].
- ^ Steinby, Magnus; Thomas, Wolfgang (2000). «Trees and term rewriting in 1910: on a paper by Axel Thue». Bulletin of the European Association for Theoretical Computer Science. 72: 256–269. CiteSeerX 10.1.1.32.8993. MR 1798015.
- ^ Dehn, Max (1911). «Über unendliche diskontinuierliche Gruppen». Mathematische Annalen. 71 (1): 116–144. doi:10.1007/BF01456932. ISSN 0025-5831. MR 1511645. S2CID 123478582.
- ^ Dehn, Max (1912). «Transformation der Kurven auf zweiseitigen Flächen». Mathematische Annalen. 72 (3): 413–421. doi:10.1007/BF01456725. ISSN 0025-5831. MR 1511705. S2CID 122988176.
- ^ Greendlinger, Martin (June 1959). «Dehn’s algorithm for the word problem». Communications on Pure and Applied Mathematics. 13 (1): 67–83. doi:10.1002/cpa.3160130108.
- ^ Lyndon, Roger C. (September 1966). «On Dehn’s algorithm». Mathematische Annalen. 166 (3): 208–228. doi:10.1007/BF01361168. hdl:2027.42/46211. S2CID 36469569.
- ^ Schupp, Paul E. (June 1968). «On Dehn’s algorithm and the conjugacy problem». Mathematische Annalen. 178 (2): 119–130. doi:10.1007/BF01350654. S2CID 120429853.
- ^ Power, James F. (27 August 2013). «Thue’s 1914 paper: a translation». arXiv:1308.5858 [cs.FL].
- ^ See History of the Church–Turing thesis. The dates are based on On Formally Undecidable Propositions of Principia Mathematica and Related Systems and Systems of Logic Based on Ordinals.
- ^ Post, Emil L. (March 1947). «Recursive Unsolvability of a problem of Thue» (PDF). Journal of Symbolic Logic. 12 (1): 1–11. doi:10.2307/2267170. JSTOR 2267170. S2CID 30320278. Retrieved 6 December 2021.
- ^ Mostowski, Andrzej (September 1951). «A. Markov. Névožmoinost’ nékotoryh algoritmov v téorii associativnyh sistém (Impossibility of certain algorithms in the theory of associative systems). Doklady Akadémii Nauk SSSR, vol. 77 (1951), pp. 19–20». Journal of Symbolic Logic. 16 (3): 215. doi:10.2307/2266407. JSTOR 2266407.
- ^ Turing, A. M. (September 1950). «The Word Problem in Semi-Groups With Cancellation». The Annals of Mathematics. 52 (2): 491–505. doi:10.2307/1969481. JSTOR 1969481.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Proceedings of the Steklov Institute of Mathematics (in Russian). 44: 1–143. Zbl 0068.01301.
- ^ Boone, William W. (1954). «Certain Simple, Unsolvable Problems of Group Theory. I». Indagationes Mathematicae (Proceedings). 57: 231–237. doi:10.1016/S1385-7258(54)50033-8.
- ^ Boone, William W. (1957). «Certain Simple, Unsolvable Problems of Group Theory. VI». Indagationes Mathematicae (Proceedings). 60: 227–232. doi:10.1016/S1385-7258(57)50030-9.
- ^ Britton, J. L. (October 1958). «The Word Problem for Groups». Proceedings of the London Mathematical Society. s3-8 (4): 493–506. doi:10.1112/plms/s3-8.4.493.
- ^ Boone, William W. (1958). «The word problem» (PDF). Proceedings of the National Academy of Sciences. 44 (10): 1061–1065. Bibcode:1958PNAS…44.1061B. doi:10.1073/pnas.44.10.1061. PMC 528693. PMID 16590307. Zbl 0086.24701.
- ^ Boone, William W. (September 1959). «The Word Problem». The Annals of Mathematics. 70 (2): 207–265. doi:10.2307/1970103. JSTOR 1970103.
- ^ Higman, G. (8 August 1961). «Subgroups of finitely presented groups». Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 262 (1311): 455–475. Bibcode:1961RSPSA.262..455H. doi:10.1098/rspa.1961.0132. S2CID 120100270.
- ^ Britton, John L. (January 1963). «The Word Problem». The Annals of Mathematics. 77 (1): 16–32. doi:10.2307/1970200. JSTOR 1970200.
- ^ Simpson, Stephen G. (18 May 2005). «A Slick Proof of the Unsolvability of the Word Problem for Finitely Presented Groups» (PDF). Retrieved 6 December 2021.
- ^ «Subgroups of finitely presented groups». Mathematics of the USSR-Sbornik. 103 (145): 147–236. 13 February 1977. doi:10.1070/SM1977v032n02ABEH002376.
- ^ a b Matiyasevich, Yuri; Sénizergues, Géraud (January 2005). «Decision problems for semi-Thue systems with a few rules». Theoretical Computer Science. 330 (1): 145–169. doi:10.1016/j.tcs.2004.09.016.
- ^ Davis, Martin (1978). «What is a Computation?» (PDF). Mathematics Today Twelve Informal Essays: 257–259. doi:10.1007/978-1-4613-9435-8_10. ISBN 978-1-4613-9437-2. Retrieved 5 December 2021.
- ^ a b Baader, Franz; Nipkow, Tobias (5 August 1999). Term Rewriting and All That. Cambridge University Press. pp. 59–60. ISBN 978-0-521-77920-3.
- ^
- Matiyasevich, Yu. V. (1967). «Простые примеры неразрешимых ассоциативных исчислений» [Simple examples of undecidable associative calculi]. Doklady Akademii Nauk SSSR (in Russian). 173 (6): 1264–1266. ISSN 0869-5652.
- Matiyasevich, Yu. V. (1967). «Simple examples of undecidable associative calculi». Soviet Mathematics. 8 (2): 555–557. ISSN 0197-6788.
- ^ Novikov, P. S. (1955). «On the algorithmic unsolvability of the word problem in group theory». Trudy Mat. Inst. Steklov (in Russian). 44: 1–143.
- ^ Statman, Rick (2000). «On the Word Problem for Combinators». Rewriting Techniques and Applications. Lecture Notes in Computer Science. 1833: 203–213. doi:10.1007/10721975_14. ISBN 978-3-540-67778-9.
- ^ Beke, Tibor (May 2011). «Categorification, term rewriting and the Knuth–Bendix procedure». Journal of Pure and Applied Algebra. 215 (5): 730. doi:10.1016/j.jpaa.2010.06.019.
- ^ Peter T. Johnstone, Stone Spaces, (1982) Cambridge University Press, Cambridge, ISBN 0-521-23893-5. (See chapter 1, paragraph 4.11)
- ^ Whitman, Philip M. (January 1941). «Free Lattices». The Annals of Mathematics. 42 (1): 325–329. doi:10.2307/1969001. JSTOR 1969001.
- ^ Whitman, Philip M. (1942). «Free Lattices II». Annals of Mathematics. 43 (1): 104–115. doi:10.2307/1968883. JSTOR 1968883.
- ^ K. H. Bläsius and H.-J. Bürckert, ed. (1992). Deduktionsssysteme. Oldenbourg. p. 291.; here: p.126, 134
- ^ Apply rules in any order to a term, as long as possible; the result doesn’t depend on the order; it is the term’s normal form.
Asked by: Mrs. Amira McCullough DDS
Score: 4.4/5
(48 votes)
Algebraic word problems are questions that require translating sentences to equations, then solving those equations. and a single variable. Usually, the variable represents an unknown quantity in a real-life scenario.
What is considered algebra?
Algebra is a branch of mathematics dealing with symbols and the rules for manipulating those symbols. In elementary algebra, those symbols (today written as Latin and Greek letters) represent quantities without fixed values, known as variables. … The letters x and y represent the areas of the fields.
What are the 4 types of algebra?
They are elementary algebra, abstract algebra, advanced algebra, communicative algebra, and linear algebra. All these branches have a different formula, different application, and different use in finding out the values of variables.
Is algebra a problem solving?
Using algebra to solve word problems is a very powerful application of mathematics. Unfortunately, many students don’t feel comfortable using algebra to solve real world problems, even though they feel comfortable with their algebra skills.
How do you do algebra word problems?
You can tackle any word problem by following these five steps:
- Read through the problem carefully, and figure out what it’s about.
- Represent unknown numbers with variables.
- Translate the rest of the problem into a mathematical expression.
- Solve the problem.
- Check your work.
42 related questions found
Why is algebra so hard?
Algebra is thinking logically about numbers rather than computing with numbers. … Paradoxically, or so it may seem, however, those better students may find it harder to learn algebra. Because to do algebra, for all but the most basic examples, you have to stop thinking arithmetically and learn to think algebraically.
Who invented 0?
The first modern equivalent of numeral zero comes from a Hindu astronomer and mathematician Brahmagupta in 628. His symbol to depict the numeral was a dot underneath a number.
Who really invented algebra?
When was algebra invented? Muhammad ibn Musa al-Khwarizmi, a Muslim mathematician wrote a book in 9th century named «Kitab Al-Jabr» from which the word «ALGEBRA» derived. So algebra was invented in the 9th century.
Are algebra numbers countable?
All integers and rational numbers are algebraic, as are all roots of integers. … The set of complex numbers is uncountable, but the set of algebraic numbers is countable and has measure zero in the Lebesgue measure as a subset of the complex numbers. In that sense, almost all complex numbers are transcendental.
Is 0 an algebraic expression?
yes,is zero an algebraic expression.
Is E Pi algebraic?
Possible transcendental numbers
Numbers which have yet to be proven to be either transcendental or algebraic: Most sums, products, powers, etc. of the number π and the number e, e.g. eπ, e + π, π − e, π/e, ππ, ee, πe, π√2, eπ2 are not known to be rational, algebraic, irrational or transcendental.
Is algebra 1a advanced?
Algebra 1 in 9th grade was the old norm when I was in high school. … Good-at-math students were a year advanced, taking algebra 1 in 8th grade leading to calculus in 12th grade as a bonus to get a head start on college level math.
What all comes under algebra?
Advanced algebra will help you to go through the other parts of algebra such as:
- Equations with inequalities.
- Matrices.
- Solving system of linear equations.
- Graphing of functions and linear equations.
- Conic sections.
- Polynomial Equation.
- Quadratic Functions with inequalities.
- Polynomials and expressions with radicals.
Is algebra math in high school?
What is Algebra 1? Algebra 1 is a high school math course exploring how to use letters (called variables) and numbers with mathematical symbols to solve problems. Algebra 1 typically includes evaluating expressions, writing equations, graphing functions, solving quadratics, and understanding inequalities.
Who figured out pi?
The first calculation of π was done by Archimedes of Syracuse (287–212 BC), one of the greatest mathematicians of the ancient world.
Who invented school?
Credit for our modern version of the school system usually goes to Horace Mann. When he became Secretary of Education in Massachusetts in 1837, he set forth his vision for a system of professional teachers who would teach students an organized curriculum of basic content.
Who invented time?
The measurement of time began with the invention of sundials in ancient Egypt some time prior to 1500 B.C. However, the time the Egyptians measured was not the same as the time today’s clocks measure. For the Egyptians, and indeed for a further three millennia, the basic unit of time was the period of daylight.
What is the hardest math ever?
These Are the 10 Toughest Math Problems Ever Solved
- The Collatz Conjecture. Dave Linkletter. …
- Goldbach’s Conjecture Creative Commons. …
- The Twin Prime Conjecture. …
- The Riemann Hypothesis. …
- The Birch and Swinnerton-Dyer Conjecture. …
- The Kissing Number Problem. …
- The Unknotting Problem. …
- The Large Cardinal Project.
What is the hardest math problem?
But those itching for their Good Will Hunting moment, the Guinness Book of Records puts Goldbach’s Conjecture as the current longest-standing maths problem, which has been around for 257 years. It states that every even number is the sum of two prime numbers: for example, 53 + 47 = 100.
Why do students struggle with algebra?
First-time learners find it difficult to grasp the concept of symbols used in algebra. … While this is related to their difficulty in understanding the equal sign, it is also a matter of students finding the use of symbols in Mathematics rather alien.
What is a word problem in maths?
What is a word problem? A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
How do you turn a word problem into an algebraic equation?
How to Translate Word Problems Into Equations
- Step One: Highlight Important Parts of the Text.
- Step Two: Establish your variables. …
- Step Three: Rewrite the Problem as an Equation. …
- Step Four: Substitute. …
- Step Five: Simplify and Combine Terms. …
- Step Six: Divide Each Side of the Equation. …
- Step Seven: Solve.
You will encounter these area word problems often in math. Many of
them will require familiarity with basic math, algebra skills, or a
combination of both to solve the problems.
As I solve these area word problems, I will make an attempt to
give you some problems
solving skills
Word problem #1:
The area of a square is 4 inches. What is the length of a side?
Important concept: Square. It
means 4 equal
sides.
Area = s × s= 4 × 4 = 16 inches2
Word problem #2:
A small square is located inside a bigger square. The length of one side of the small square is 3 inches and the length of one side of the big square is 7 inches
What is the area of the region located outside the small square, but inside the big square?
Important concept: Draw a picture and see the problem with your eyes. This is done below:
The area that you are looking for is everything is red. So you need to remove the area of the small square from the area of the big square
Area of big square = s × s = 7 × 7 = 49 inches2
Area of small square = s × s = 3 × 3 = 9 inches2
Area of the region in red = 49 — 9 = 40 inches2
Word problem #3:
A classroom has a length of 20 feet and a width of 30 feet. The headmaster decided that tiles will look good in that class.
If each tile has a length of 24 inches and a width of 36 inches, how many tiles are needed to fill the classroom?
Important concept:
Find area occupied by entire classroom
Find area for one tile
Decide which unit to use. In this case, we could use feet
Area of classroom = length × width = 20 × 30 = 600 ft2
Before we get the area of each tile, convert the dimensions to feet as already stated
Since 1 foot = 12 inches, 36 inches = 3 feet and 24 inches = 2 feet
Area of each tile = length × width = 2 × 3 = 6 ft2
If one tile takes 6 ft2, it takes 100 tiles to cover 600 ft2 (6 × 100 = 600)
Word problem #4:
Sometimes area word problems may require skills in algebra, such as factoring and solving quadratic equations
A room whose area is 24 ft2 has a length that is 2 feet longer than the width. What are the dimensions of the room?
Solution #1 Use of basic math skills and trial and error
Pretend width = 1, then length = 3 ( 1 + 2)
1 × 3 is not equal to 24 and 3 is not close at all to 24. Try bigger numbers
let width = 3, then length = 5 ( 3 + 2)
3 × 5 = 15. It is still not equal to 24
let width = 4, then length = 4 ( 4 + 2)
4 × 6 = 24. We are done!
Solution #2 Use of algebra
Let width = x, so length = x + 2
Area = length × width
24 = x × ( x + 2)
24 = x2 + 2x
x2 + 2x = 24 (swap the left side with the right side)
x2 + 2x — 24 = 0
( x + 6) × ( x — 4 ) = 0
x = -6 and x = 4
So width = 4 and length = 4 + 2 = 6
As you can see area word problems can become very complicated as
shows in the last problem. And the use of basic math skills may not be
the best way to go to solve area word problems. Sometimes algebra
is better because trial and error can take a long time!
Have a question about these area word problems? send me a note.
Recent Articles
-
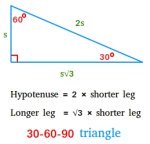
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
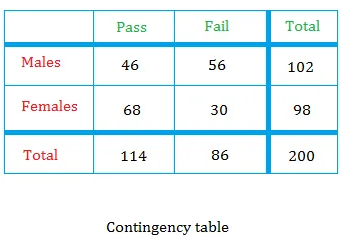
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more