Step 1 – Read through the problem at least three times. The first reading should be a quick scan, and the next two readings should be done slowly to find answers to these questions:
What does the problem ask? (Usually located at the end)
Mark all information and underline all important words or phrases.
Step 2 – Draw a picture. Use arrows, circles, lines, whatever works for you. This makes the problem real.
A favorite word problem is something like, 1 train leaves Station A travelling at 100 km/hr and another train leaves Station B travelling at 60 km/hr. …
Draw a line, the two stations, and the two trains at either end.
Depending on the question, make a table with a blank portion to show information you don’t know.
Step 3 – Assign a single letter to represent each unknown.
You may want to note the unknown that each letter represents so you don’t get confused.
Step 4 – Translate the information into an equation.
Remember that the main problem with word problems is that they are not expressed in regular math equations. Your ability to identify correctly the variables and translate the information into an equation determines your ability to solve the problem.
Step 5 – Check the equation to see if it looks like regular equations that you are used to seeing and whether it looks sensible.
Does the equation appear to represent the information in the question? Take note that you may need to rewrite some formulas needed to solve the word problem equation.
Step 6 – Use algebra rules to solve the equation.
Simplify each side of the equation by removing parentheses and combining like terms.
Use addition or subtraction to isolate the variable term on one side of the equation. If a number crosses to the other side of the equation, the sign changes to the opposite — for example positive to negative.
Use multiplication or division to solve for the variable. What you to once side of the equation you must do for the other.
Where there are multiple unknowns you will need to use elimination or substitution methods to resolve all the equations.
Step 7 – Check your final answers to see if they make sense with the information given in the problem.
For example, if the word problem involves a discount, the final price should be less or if a product was taxed then the final answer has to cost more.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?

3-Step System
1. Read: Read the problem and decide what the question is asking.
- Read the problem 2 times or more.
- Underline or circle key words, phrases, and numbers. Draw a line through irrelevant information.
2. Plan: Think about what the story is asking you to do. What information are you given, and what do you need to find out?
- Draw a picture.
- Circle or underline key words. (Use highlighters or crayons to color-code key numbers and phrases.)
- Write out the question in your own words.
3. Solve: What strategy could you use to find the missing information: addition, subtraction, multiplication, or division?
- Write a number sentence and solve.
- Use counters.
- Create charts.
Check your work by explaining your reasoning. Does your answer make sense?
Download this free strategy checklist from Math Fundamentals to help your child solve word problems.
Different Strategies to Solve Word Problems
Everyone learns in a different way. What makes sense to one individual often isn’t the easiest option for another. Incorporating different strategies to solve word problems can help your child discover what strategy works best for him or her. A few tips to use are:
1. Circle numbers in a story and underline key phrases.
Color coding is a fun method to incorporate to help children decide what operation the question is asking for. Assign a color to each operation and highlight the phrase that identifies it. For example, red links to addition and blue links to subtraction.
2. Incorporate a key word list.
Key word lists are best used for teaching younger children how to solve word problems. As math curriculum advances, children should not be dependent on a key word list to solve a problem. The questions get trickier.
Addition
In all
Together
Total
Altogether
Combine
Sum
Join
Subtraction
Difference
Fewer
How many more
How much more
Left
Remain
Less
3. Visuals
If your child is a visual learner, drawing a picture or using counters can help him or her understand what the problem is asking. Use number lines, charts, or counters or draw a picture.
4. Write your own word problem.
Knowing what is needed to write a word problem is the first step in identifying key words to solve a story. Take turns writing your own word problems with your child and exchange them to solve.
5. Stay organized.
It is important to write clearly and keep work space neat so children can read and follow their own computations. Many children need a separate piece of paper to allow them enough space to solve and understand their answer. Graphing paper is a great option to help students record neat work.
Download this free sample word problem from Math Fundamentals, grade 1.
How to solve a two-step word problem
In a two-step word problem children are being asking to solve two related equations. These can get tricky for children to understand when they transition from one-step to two-step problems. Help your child understand his or her relationships within two-step word problems with these strategies:
1. Circle important information.
Circle numbers and important phrases that ask questions. The number sentences needed to solve these equations are hidden in those asking questions. Identify the first and second questions needed to solve.
2. Distinguish the two parts of the problem.
First identify the first step of the first part of the word problem. Write a number sentence and solve.
3. Use the answer from the first-step solution to the whole problem.
Use the answer from the first question to help you solve the next equation. What operation does the second question require?
Check your work by explaining your reasoning. What was the question answered? Is the answer reasonable for the question being asked?
Download this free sample two-strategy word problem from Math Fundamentals, grade 2
Download this free sample multi-strategy word problem from Math Fundamentals, grade 4
Evan-Moor’s Math Fundamentals is a great resource for training students how to solve word problems in 3 simple steps. It provides step-by-step directions for solving questions and guides children with helpful visuals and key phrases.
Check out Daily Word Problems for consistent practice solving word problems.
For more fun math tips and strategies check out our Math- Ideas, Activities and Lessons Pinterest Board.
Save these tips and Pin It now!

This article is for parents who think about how to help with math and support their children. The math word problems below provide a gentle introduction to common math operations for schoolers of different grades.
What are math word problems?
During long-time education, kids face various hurdles that turn into real challenges. Parents shouldn’t leave their youngsters with their problems. They need an adult’s possible help, but what if the parents themselves aren’t good at mathematics? All’s not lost. You can provide your kid with different types of support. Not let a kid burn the midnight oil! Help him/ her to get over the challenges thanks to these captivating math word examples.
Math word problems are short math questions formulated into one or several sentences. They help schoolers to apply their knowledge to real-life scenarios. Besides, this kind of task helps kids to understand this subject better.
Addition for the first and second grades
These math examples are perfect for kids that just stepped into primary school. Here you find six easy math problems with answers:
1. Peter has eight apples. Dennis gives Peter three more. How many apples does Peter have in all?
Show answer
Answer: 8 apples + 3 apples = 11 apples.
2. Ann has seven candies. Lack gives her seven candies more. How many candies does Ann have in all?
Show answer
Answer: 7 candies + 7 candies = 14 candies.
3. Walter has two books. Matt has nine books. If Matt gives all his books to Walter, how many books will Walter have?
Show answer
Answer: 2 books + 9 books = 11 books.
4. There are three crayons on the table. Albert puts five more crayons on the table. How many crayons are on the table?
Show answer
Answer: 3 crayons + 5 crayons = 8 crayons.
5. Bill has nine oranges. His friend has one orange. If his friend gives his orange to Bill, how many oranges will Bill have?
Show answer
Answer: 9 oranges + 1 orange = 10 oranges.
6. Jassie has four leaves. Ben has two leaves. Ben gives her all his leaves. How many leaves does Jessie have in all?
Show answer
Answer: 4 leaves + 2 leaves = 6 leaves.
Subtraction for the first and second grades
1. There were three books in total at the book shop. A customer bought one book. How many books are left?
Show answer
Answer: 3 books – 1 book = 2 books.
2. There are five pizzas in total at the pizza shop. Andy bought one pizza. How many pizzas are left?
Show answer
Answer: 5 pizzas – 1 pizza = 4 pizzas.
3. Liza had eleven stickers. She gave one of her stickers to Sarah. How many stickers does Liza have?
Show answer
Answer: 11 stickers – 1 sticker = 10 stickers.
4. Adrianna had ten stones. But then she left two stones. How many stones does Adrianna have?
Show answer
Answer: 10 stones – 2 stones = 8 stones.
5. Mary bought a big bag of candy to share with her friends. There were 20 candies in the bag. Mary gave three candies to Marissa. She also gave three candies to Kayla. How many candies were left?
Show answer
Answer: 20 candies – 3 candies – 3 candies = 14 candies.
6. Betty had a pack of 25 pencil crayons. She gave five to her friend Theresa. She gave three to her friend Mary. How many pencil crayons does Betty have left?
Show answer
Answer: 25 crayons – 5 crayons – 3 crayons = 17 crayons.
Multiplication for the 2nd grade and 3rd grade
See the simple multiplication word problems. Make sure that the kid has a concrete understanding of the meaning of multiplication before.
Bill is having his friends over for the game night. He decided to prepare snacks and games.
1. He makes mini sandwiches. If he has five friends coming over and he made three sandwiches for each of them, how many sandwiches did he make?
Show answer
Answer: 5 x 3 = 15 sandwiches.
2. He also decided to get some juice from fresh oranges. If he used two oranges per glass of juice and made six glasses of juice, how many oranges did he use?
Show answer
Answer: 2 x 6 = 12 oranges.
3. Then Bill prepared the games for his five friends. If each game takes 7 minutes to prepare and he prepared a total of four games, how many minutes did it take for Bill to prepare all the games?
Show answer
Answer: 7 x 4 = 28 minutes.
4. Bill decided to have takeout food as well. If each friend and Bill eat three slices of pizza, how many slices of pizza do they have in total?
Show answer
Answer: 6 (5 friends and Bill) x 3 slices of pizza = 18 slices of pizza.
Mike is having a party at his house to celebrate his birthday. He invited some friends and family.
1. He and his mother prepared cupcakes for dessert. Each box had 8 cupcakes, and they prepared four boxes. How many cupcakes have they prepared in the total?
Show answer
Answer: 8 x 4 = 32 cupcakes.
2. They also baked some cookies. If they baked 6 pans of cookies, and there were 7 cookies per pan, how many cookies did they bake?
Show answer
Answer: 6 x 7 = 42 cookies.
3. Mike planned to serve some cold drinks as well. If they make 7 pitchers of drinks and each pitcher can fill 5 glasses, how many glasses of drinks are they preparing?
Show answer
Answer: 7 x 5 = 35 glasses.
4. At the end of the party, Mike wants to give away some souvenirs to his 6 closest friends. If he gives 2 souvenir items for each friend, how many souvenirs does Mike prepare?
Show answer
Answer: 6 x 2 = 12 souvenirs.
Division: best for 3rd and 4th grades
1. If you have 10 books split evenly into 2 bags, how many books are in each bag?
Show answer
Answer: 10 : 2 = 5 books.
2. You have 40 tickets for the fair. Each ride costs 2 tickets. How many rides can you go on?
3. The school has $20,000 to buy new equipment. If each piece of equipment costs $100, how many pieces can the school buy in total?
Show answer
Answer: $20,000 : $100= 200.
4. Melissa has 2 packs of tennis balls for $10 in total. How much does 1 pack of tennis balls cost?
5. Jack has 25 books. He has a bookshelf with 5 shelves on it. If Jack puts the same number of books on each shelf, how many books will be on each shelf?
6. Matt is having a picnic for his family. He has 36 cookies. There are 6 people in his family. If each person gets the same number of cookies, how many cookies will each person get?
Division with remainders for fourth and fifth grades
1. Sarah sold 35 boxes of cookies. How many cases of ten boxes, plus extra boxes does Sarah need to deliver?
Show answer
Answer: 35 boxes divided by 10 boxes per case = 3 cases and 5 boxes.
2. Candies come in packages of 16. Mat ate 46 candies. How many whole packages of candies did he eat, and how many candies did he leave? 46 candies divided by 16 candies = 2 packages and 2 candies left over.
3. Mary sold 24 boxes of chocolate biscuits. How many cases of ten boxes, plus extra boxes does she need to deliver?
Show answer
Answer: 24 boxes divided by 10 boxes per case = 2 cases and four boxes.
4. Gummy bears come in packages of 25. Suzie and Tom ate 30 gummy bears. How many whole packages did they eat? How many gummy bears did they leave?
Show answer
Answer: 30 divided by 25 = 1 package they have eaten and 20 gummy bears left over.
5. Darel sold 55 ice-creams. How many cases of ten boxes, plus extra boxes does he need to deliver?
Show answer
Answer: 55 boxes divided by 10 boxes per case = 5 cases and 5 boxes.
6. Crackers come in packages of 8. Mat ate 20 crackers. How many whole packages of crackers did he eat, and how many crackers did he leave?
Show answer
Answer: 20 divided by 8 = 2 packages eaten and 4 crackers are left.
Mixed operations for the fifth grade
These math word problems involve four basic operations: addition, multiplication, subtraction, and division. They suit best for the fifth-grade schoolers.
200 planes are taking off from the airport daily. During the Christmas holidays, the airport is busier — 240 planes are taking off every day from the airport.
1. During the Christmas holidays, how many planes take off from the airport in each hour if the airport opens 12 hours daily?
Show answer
Answer: 240÷12=20 planes take off from this airport each hour during the Christmas holidays.
2. Each plane takes 220 passengers. How many passengers depart from the airport every hour during the Christmas holidays? 20 x 220 = 4400.
Show answer
Answer: 4400 passengers depart from the airport every hour.
3. Compared with a normal day, how many more passengers are departing from the airport in a day during the Christmas holidays?
Show answer
Answer: (240-200) x 220 = 8800 more passengers departing from the airport in a day during the Christmas holidays.
4. During normal days on average 650 passengers are late for their plane daily. During the Christmas holidays, 1300 passengers are late for their plane. That’s why 14 planes couldn’t take off and are delayed. How many more passengers are late for their planes during Christmas week?
Show answer
Answer: 1300 – 650 = 650 more passengers are late for their planes each day during the Christmas holidays.
5. According to the administration’s study, an additional 5 minutes of delay in the overall operation of the airport is caused for every 27 passengers that are late for their flights. What is the delay in the overall operation if there are 732 passengers late for their flights?
Show answer
Answer: 732 ÷ 27 × 5 = 136. There will be a delay of 136 minutes in the overall operation of the airport.
Extra info math problems for the fifth grade
1. Ann has 7 pairs of red socks and 8 pairs of pink socks. Her sister has 12 pairs of white socks. How many pairs of socks does Ann have?
2. Kurt spent 17 minutes doing home tasks. He took a 3-minute snack break. Then he studied for 10 more minutes. How long did Kurt study altogether?
Show answer
Answer: 17 + 10 = 27 minutes.
3. There were 15 spelling words on the test. The first schooler spelled 9 words correctly. Miguel spelled 8 words correctly. How many words did Miguel spell incorrectly?
4. In the morning, Jack gave his friend 2 gummies. His friend ate 1 of them. Later Jack gave his friend 7 more gummies. How many gummies did Jack give his friend in all?
5. Peter wants to buy 2 candy bars. They cost 8 cents, and the gum costs 5 cents. How much will Peter pay?
Finding averages for 5th grade
We need to find averages in many situations in everyday life.
1. The dog slept 8 hours on Monday, 10 hours on Tuesday, and 900 minutes on Wednesday. What was the
average number of hours the dog slept per day?
Show answer
Answer: (8+10+(900:60)) : 3 = 11 hours.
2. Jakarta can get a lot of rain in the rainy season. The rainfall during 6 days was 90 mm, 74 mm, 112 mm, 30 mm, 100 mm, and 44 mm. What was the average daily rainfall during this period?
Show answer
Answer: (90+74+112+30+100+44) : 6 = 75 mm.
3. Mary bought 4 books. The prices of the first 3 books were $30, $15, and $18. The average price she paid for the 4 books was $25 per books. How much did she pay for the 4th books?


Math & logic courses for kids
Times more complex than school, extremely fun, interactive and rewarding to keep 7-13 years old kids engaged. We’re gonna make them love math!
learn more
Ordering and number sense for the 5th grade
1. There are 135 pencils, 200 pens, 167 crayons, and 555 books in the bookshop. How would you write these numbers in ascending order?
Show answer
Answer: 135, 167, 200, 555
2. There are five carrots, one cabbage, eleven eggs, and 15 apples in the fridge. How would you write these numbers in descending order?
3. Peter has completed exercises on pages 279, 256, 264, 259, and 192. How would you write these numbers in ascending order?
Show answer
Answer: 192, 256, 259, 264, 279.
4. Mary picked 32 pants, 15 dresses, 26 pairs of socks, 10 purses. Put all these numbers in order.
5. The family bought 12 cans of tuna, 23 potatoes, 11 onions, and 33 pears. Put all these numbers in order.
Fractions for the 6th-8th grades
1. Jannet cooked 12 lemon biscuits for her daughter, Jill. She ate up 4 biscuits. What fraction of lemon biscuits did Jill eat?
Show answer
Answer: 1/3 of the lemon biscuits.
2. Guinet travels a distance of 7 miles to reach her school. The bus covers only 5 miles. Then she has to walk 2 miles to reach the school. What fraction of the distance does Guinet travel by bus?
Show answer
Answer: 5/7 of the distance
3. Bob has 24 pencils in a box. Eighteen pencils have #2 marked on them, and the 6 are marked #3. What fraction of pencils are marked #3?
Show answer
Answer: 1/4 of the pencils.
4. My mother places 15 tulips in a glass vase. It holds 6 yellow tulips and 9 red tulips. What fraction of tulips are red?
Show answer
Answer: 3/5 of the tulips.
5. Bill owns 14 pairs of socks, of which 7 pairs are white, and the rest are brown. What fraction of pairs of socks are brown?
Show answer
Answer: 1/2 of the pairs of socks.
6. Bred spotted a total of 39 birds in an aviary at the Zoo. He counted 18 macaws and 21 cockatoos. What fraction of macaws did Bred spot at the aviary?
Show answer
Answer: 6/13 of the birds.
Decimals for the 6th grade
Write in words the following decimals:
- 0,004
- 0,07
- 2,1
- 0,725
- 46,36
- 2000,19
Show answer
Answer:
- 0,004 = four thousandths.
- 0,07 = seven hundredths.
- 2,1 = two and one tenth.
- 0,725 = seven hundred twenty five thousandths.
- 46,36 = foury six and thirty six hundredths.
- 2000,19 = two thousand and nineteen hundredths.
Comparing and sequencing for the 6th grade
1. The older brother picked 42 apples at the orchard. The younger brother picked only 22 apples. How many more apples did the older brother pick?
Show answer
Answer: 42 – 22 = 20 apples more.
2. There were 16 oranges in a basket and 66 oranges in a barrel. How many fewer oranges were in the basket than were in the barrel?
Show answer
Answer: 66 – 16 = 50 fewer oranges.
3. There were 40 parrots in the flock. Some of them flew away. Then there were 25 parrots in the flock. How many parrots flew away?
Show answer
Answer: 40 – 25 = 15 parrots flew away.
4. One hundred fifty is how much greater than fifty-three?
5. On Monday, the temperature was 13°C. The next day, the temperature dropped by 8 degrees. What was the temperature on Tuesday?
6. Zoie picked 15 dandelions. Her sister picked 22 ones. How many more dandelions did her sister pick than Zoie?
Show answer
Answer: 22-15 = 7 dandelions more.
Time for the 4th grade
1. The bus was scheduled to arrive at 7:10 p.m. However, it was delayed for 45 minutes. What time was it when the bus arrived?
2. My mother starts her 7-hour work at 9:15 a.m. What time does she get off from work?
3. Jack’s walk started at 6:45 p.m. and ended at 7:25 p.m. How long did his walk last?
4. The school closes at 9:00 p.m. Today, the school’s principal left 15 minutes after the office closed, and his secretary left the office 25 minutes after he left. When did the secretary leave work?
5. Suzie arrives at school at 8:20 a.m. How much time does she need to wait before the school opens? The school opens at 8:35 a.m.
6. The class starts at 9:15 a.m.. The first bell will ring 20 minutes before the class starts. When will the first bell ring?
Money word problems for the fourth grade
1. James had $20. He bought a chocolate bar for $2.30 and a coffee cup for $5.50. How much money did he have left?
Show answer
Answer: $20.00 – $2.30 – $5.50 = $12.20. James had $12.20 left.
2. Coffee mugs cost $1.50 each. How much do 7 coffee mugs cost?
Show answer
Answer: $1.5 x 7 = $10.5.
3. The father gives $32 to his four children to share equally. How much will each of his children get?
4. Each donut costs $1.20. How much do 6 donuts cost?
Show answer
Answer: $1.20 * 6 = $7,2.
5. Bill and Bob went out for takeout food. They bought 4 hamburgers for $10. Fries cost $2 each. How much does one hamburger with fries cost?
Show answer
Answer: $10 ÷ 4 = $2.50. One hamburger costs $2.50. $2.50 + $2.00 = $4.50. One hamburger with fries costs $4.50.
6. A bottle of juice costs $2.80, and a can is $1.50. What would it cost to buy two cans of soft drinks and a bottle of juice?
Show answer
Answer: $1.50 x 2 + $2.80 = $5.80.
Measurement word problems for the 6th grade
The task is to convert the given measures to new units. It best suits the sixth-grade schoolers.
- 55 yd = ____ in.
- 43 ft = ____ yd.
- 31 in = ____ ft.
- 29 ft = ____ in.
- 72 in = ____ ft.
- 13 ft = ____ yd.
- 54 lb = ____ t.
- 26 t = ____ lb.
- 77 t = ____ lb.
- 98 lb = ____ t.
- 25 lb = ____ t.
- 30 t = ____ lb.
Show answer
Answer:
- 55 yd = 1.980 in
- 43 ft = 14 yd 1 ft
- 31 in = 2 ft 7 in
- 29 ft = 348 in
- 72 in = 6 ft
- 13 ft = 4 yd 1 ft.
- 54 lb = 0,027 t
- 26 t = 52.000 lb
- 77 t = 154.000 lb
- 98 lb = 0,049 t
- 25 lb = 0?0125 t
- 30 t = 60.000 lb.
Ratios and percentages for the 6th-8th grades
It is another area that children can find quite difficult. Let’s look at simple examples of how to find percentages and ratios.
1. A chess club has 25 members, of which 13 are males, and the rest are females. What is the ratio of males to all club members?
2. A group has 8 boys and 24 girls. What is the ratio of girls to all children?
3. A pattern has 4 red triangles for every 12 yellow triangles. What is the ratio of red triangles to all triangles?
4. An English club has 21 members, of which 13 are males, and the rest are females. What is the ratio of females to all club members?
5. Dan drew 1 heart, 1 star, and 26 circles. What is the ratio of circles to hearts?
6. Percentages of whole numbers:
- 50% of 60 = …
- 100% of 70 = …
- 90% of 70 = …
- 20% of 30 = …
- 40% of 10 = …
- 70% of 60 = …
- 100% of 20 = …
- 80% of 90 = …
Show answer
Answer:
- 50% of 60 = 30
- 100% of 70 = 70
- 90% of 70 = 63
- 20% of 30 = 6
- 40% of 10 = 4
- 70% of 60 = 42
- 100% of 20 = 20
- 80% of 90 = 72.
Probability and data relationships for the 8th grade
1. John ‘s probability of winning the game is 60%. What is the probability of John not winning the game?
2. The probability that it will rain is 70%. What is the probability that it won’t rain?
3. There is a pack of 13 cards with numbers from 1 to 13. What is the probability of picking a number 9 from the pack?
4. A bag had 4 red toy cars, 6 white cars, and 7 blue cars. When a car is picked from this bag, what is the probability of it being red or blue?
5. In a class, 22 students like orange juice, and 18 students like milk. What is the probability that a schooler likes juice?
Geometry for the 7th grade
The following task is to write out equations and find the angles. Complementary angles are two angles that sum up to 90 degrees, and supplementary angles are two angles that sum up to 180 degrees.
1. The complement of a 32° angle = …
2. The supplement of a 10° angle = …
3. The complement of a 12° angle = …
4. The supplement of a 104° angle = …
Variables/ equation word problems for the 5th grades
1. The park is 𝑥 miles away from Jack’s home. Jack had to drive to and from the beach with a total distance of 36 miles. How many miles is Jack’s home away from the park?
Show answer
Answer: 2𝑥 = 36 → 𝑥 = 18 miles.
2. Larry bought some biscuits which cost $24. He paid $x and got back $6 of change. Find x.
Show answer
Answer: x = 24 + 6 = $30.
3. Mike played with his children on the beach for 90 minutes. After they played for x minutes, he had to remind them that they would be leaving in 15 minutes. Find x.
Show answer
Answer: x = 90 – 15 = 75 minutes.
4. At 8 a.m., there were x people at the orchard. Later at noon, 27 of the people left the orchard, and there were 30 people left in the orchard. Find x.
Show answer
Answer: x = 30 + 27 = 57 people
Travel time word problems for the 5th-7th grades
1. Tony sprinted 22 miles at 4 miles per hour. How long did Tony sprint?
Show answer
Answer: 22 miles divided by 4 miles per hour = 5.5 hours.
2. Danny walked 15 miles at 3 miles per hour. How long did Danny walk?
Show answer
Answer: 15 miles divided by 3 miles per hour = 5 hours.
3. Roy sprinted 30 miles at 6 miles per hour. How long did Roy sprint?
Show answer
Answer: 30 miles divided by 6 miles per hour = 5 hours.
4. Harry wandered 5 hours to get Pam’s house. It is 20 miles from his house to hers. How fast did Harry go?
Show answer
Answer: 20 miles divided by 5 hours = 4 miles per hour.
STEM subjects for kids
STEM courses for kids ages 7-13 in physics, chemistry, math and logic in interactive game format
learn more
Free Math Word Problems Collection for Grades 1-5
The LogicLike team has collected over 500+ math problems on various topics! We provide word
problems and math puzzles designed by experienced teachers. LogicLike helps children improve
their math skills in a playfull way!

Educational platform LogicLike.com helps children to build critical
thinking, math & logic skills. Adults improve mental abilities and develop
ingenuity.
Choose Word Problems by Grade
Our team has created word math problems for grades 1-5! Choose your grade, learn math and have
fun with LogicLike!
1st Grade Math Word Problems
In first grade, an important task for students is to learn addition and subtraction. Word
problems will help them do it!
Go to Math Word
Problems for 1st Grade.
2nd Grade Math Word Problems
In second grade children learn to add and subtract more complex numbers. We offer
our own collection of word math problems for 2nd grade students to practice!
Go to Math Word
Problems for 2nd Grade.
3rd Grade Math Word Problems
In grade 3 children begin to master multiplication and division, two-step word problems, solve
time and measurement problems!
Go to Math Word
Problems for 3rd Grade.
4th Grade Math Word Problems
In 4th grade, it is very important to consolidate all your knowledge from previous years and
learn how to apply it to more difficult word problems!
Go to Math Word
Problems for 4th Grade.
5th Grade Math Word Problems
In fifth grade, children begin to learn fractions, variable equations and mixed numbers.
LogicLike will help them do just that!
Go to Math Word
Problems for 5th Grade.
Children ages 5-12 enjoy the LogicLike course in a playful way. In the meantime,
they learn to reason, develop their math and logical skills, and interest in
knowledge.
Choose Word Problems by Topic
LogicLike has made over 13 themed picks for learning important topics in math! You can solve the
best word problems for addition and subtraction, multiplication and division, fractions and
mixed numbers, and more!
Money Word Problems
Tom has 50 cents, and his mother gives him 4 quarters.
How much money does Tom have?
Sara wants to buy 14 ChocoPies. The ChocoPies cost 35 cents each.
How much money will 14 ChocoPies cost?
Michael had $9,896.00 in his checking account.
Then, he spent $3,458.00 on the account.
How much money is left in Michael’s checking account?
Mixed Addition and Subtraction Word Problems
Sam caught 4 fish in the morning. Later, he caught 1 more fish.
How many fish did Sam catch in all?
At the birthday party, there were 12 cups but 4 cups were broken.
Mom goes out and buys 10 cups.
How many cups are there after she returns?
The pirate has a chest with coins.
Inside there are 328 gold, 264 silver and 136 copper coins.
How many coins are in the chest in total?

Multi-Step (Multiple Step) Word Problems
There were 6 yellow apples and 4 red apples on the plate. We ate 7
apples.
How many apples are left on the plate?
The clown had balloons of 3 colors, 6 pieces of each color.
He gave the kids 4 balls of 2 colors.
How many balloons does the clown have left?
Mary bought 15 pounds of strawberries at $1.68 per pound.
Marion bought 14 pounds of strawberries at $1.80 per pound.
Who paid more?
Multiplication Word Problems
Jessica saw 4 dozen doves in the park.
How many doves did Jessica see?
The chef of the restaurant prepares an omelet from 3 eggs.
If the chef has 72 omelets to make, how many eggs will he need?
Brenda’s kitten weighs 3 3/5 pounds.
Oliver’s dog weighs 4 times more.
How much does Oliver’s dog weigh?
Mixed Multiplication and Division Word Problems
Each crayon costs $3.00.
How much do 18 crayons cost?
A concert hall contains 6 sections of seats with the same number of seats in
each section. If there are 768 seats, how many seats are in each section?
The online store has $ 21,000 to buy online ads.
If each ad costs $ 6, how many ads can an online store purchase in a
month?
Is this enough to get 300 ads per month for a year?
Division Word Problems
There are 3 students in the class and 21 pens.
If the pens are divided equally among the students,
how many does each student get?
Monika earned $216 babysitting in 9 months.
She earned the same amount each month.
How much did Tina earn babysitting each month?
The toy company makes Teddy bears in two sizes — big and small.
The company produced 1,620 Teddy Bears last week.
They made 11 times more small Teddies than large ones.
How many big size toys did they make?
Fraction Word Problems
Sarah made nine chocolate bars.
She put powdered sugar on three chocolate bars.
Which part of the bars now have powdered sugar?
Jessica had $200, 1/4 of this money she spent on cosmetics.
How much money did Jessica spend?
The perimeter of the triangle is 40 inches.
The first side is 3/10 of the perimeter,
the other is 3/2 of the first side.
What is the third side of the triangle?
Proportion Word Problems and Worksheets
The cinema has 400 seats, 260 of which are occupied by spectators.
Express the attendance at a percent of capacity.
Molly has 45 markers. 20% of the markers write poorly.
How many markers are bad at writing?
In an exam, Shawna secured 340 marks.
If she secured 85% makes, find the maximum marks.

Ratio Word Problems
The ratio of green and red apples in a bag is 2 : 5.
If there are only green and red apples in a bag,
what is the smallest total number of apples possible?
65 children are swimming in the pool.
There are 15 more boys than girls.
What is the ratio of boys to girls?
James gives Kathy a box of building blocks and tells her that the ratio of
red blocks to total is 3 to 19. He also tells her there are 3 times as many
yellow blocks as red, and that there are 2 more green than red.
What is the ratio of yellow blocks to green?
Dividing Decimals Word Problems
Jack paid $99 for 6 pizzas.
How much did he pay per pizza?
Mark has run a total of 84.24 miles in 32.4 days of running training.
How many miles did he run on average per day?
An Olive Oil Factory made 809.9 pounds of olive oil in 6.5 minutes.
How much oil, on average, did the factory make each minute?
Volume Word Problems
Ship container has a length of 40 feet, width 8 feet, and 9.6 feet in
height.
Find the volume of the container in cubic feet.
The volume of a cylinder is 441 cubic inches. The height of the cylinder is
9 in.
Find the radius of the cylinder to the nearest tenth of an inch.
A cylindrical hole with a diameter of 8 inches is bored through a cub 10
inches on a side. Find the surface area and volume of this solid casting.
Measurement Word Problems
Jack was 5 feet 9 inches tall last year.
He grew 7 inches in the past year.
How tall is he now?
The turkey is 18 lb 11 oz and the stuffing inside the turkey is 5 oz.
What is the total weight of the roasted turkey?
From 10g of instant coffee, 120 ml of coffee can be brewed.
In a can of instant coffee is 200 g.
How much coffee (in liters) can you make from a can?
Mila is 5 years older than her brother, but 3 times younger than her
mother.
How old is Mila and how old is her mother, if Mila’s brother is 6 years old?
In 8 years, Mary will be 3 times as old as she is today.
How old is Mary today?
Felix is twice as old as his friend Greg.
Greg is 5 years older than Rachel.
In 5 years, Felix will be three times as old as Rachel.
How old is Greg now?
Have a look at some age word
problems that the LogicLike team creates for
children and adults.
Enhance your math knowledge by practicing the Word Problems Involving Least Common Multiple for free of cost. LCM will lay a stronger foundation in learning all other similar math concepts as well increases your problem-solving ability. Refer to the Word Problems on LCM available here and get an idea of how to solve LCM Questions using various methods. Be familiar with the concept and attempt the exams on different questions framed on Least Common Multiple with utmost confidence and score well.
Also, Refer:
- Word Problems on H.C.F
- Worksheet on LCM
- Worksheet on H.C.F
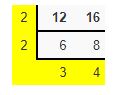
Example 1.
Find the lowest number which is exactly divisible by 12, 16
Solution: We have to find the Lcm to find the lowest number exactly divisible by 12,16.
LCM= 2 ×2 × 3 × 4=48.
Therefore, 48 is the lowest number exactly divisible by 12, 16.
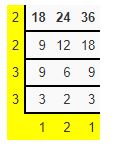
Example 2.
Find the lowest number which is less by 3 to be divided by 18, 24,36
Solution: We find LCM of 18,24,36
LCM=2 × 2 × 3 × 3 × 1 × 2 × 1 =72
Now subtract 3 from 72 to get the required number.
72-3=69
Hence, 69 is the lowest number that divides 18,24,36.
Example 3.
A shopkeeper sells chocolate Packets that contain 15 chocolate and biscuit packets that contain 9 biscuits. What is the least number of chocolates and biscuits Siri should buy so that there will be one biscuit for every chocolate?
Solution: We have to find the LCM for Knowing how many chocolates and biscuits Siri should buy.
Multiples of 15 are 15,30,45,60,75
Multiples of 9 are 9,18,27,36,45,54
The lowest common multiple is 45.
The least number of chocolates and biscuits Siri should buy is 45.
Example 4.
A teacher has to arrange 25 students in different rows. Find out how many ways he can arrange the students with the same number in each row.
Solution: We have to find all the factors of 25.
25= 1× 25, 5 × 5
Factors of 25 are 1, 5, and 25.
A Teacher can arrange students in rows of 1, 5,25.
Example 5.
Pratima attends dance classes every 6 days, singing classes every 4 days, and yoga classes every 16 days. If she does all three activities today, in how many days will she do all the three activities again on the same day?
Solution: Multiples of 4 are 4,8,12,16,20,24,28,32,36,40,44,48,52
Multiples of 6 are 6,12,18,24,30,36,42,48,54
Multiples of 16 are 16,32,48
In 48 days she will do all three on the same day.
Example 6.
Nevada goes shopping every 30 days. If she did shopping on Friday, find how many days she has to wait for shopping again on a Friday?
Solution: For finding a common multiple we have to multiply 30 days by 7 days in a week(to end up Friday again)
30 × 7=210.
Hence, Nevada has to wait for 210 days for shopping.
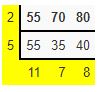
Example 7.
In an evening walk, three friends step off together. Their steps measure 55 cm, 70 cm, and 80 cm respectively. What is the minimum distance each should walk so that all can cover the same distance in complete steps?
Solution: The distance covered by each of them is the same and minimum.
We have to find the LCM of the numbers 55,70 and 80.
The LCM of 55,70,80 is 2 × 5 × 11 ×7 ×8= 6160.
Hence, the minimum distance each should walk is 6160 cm.
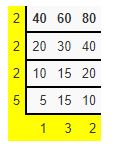
Example 8.
Find the lowest number to be more by 5 that is exactly divisible by 40,60,80.
Solution: We find LCM of 40,60,80.
LCM of 40,60,80 is 2 ×2 ×2 ×5 ×1 ×3 × 2=240.
Therefore, the required number is 240+5=245.
Example 9.
A shopkeeper sells tea shirts 24 and pants 12. What is the least number of pants and shirts Pranavi should buy so that there will be one shirt for each pair of pant?
Solution: To find the least number of pants and shirts we find LCM.
Multiples of 24 are 24,48,72,96,120….
Multiples of 12 are 12,24,36,48,60……
The least common multiple is 24.
Hence, The least number of pants and shirts Pranavi should buy is 24.
Example 10.
Jagadish has to arrange 30 brinjal plants in different rows. Find out how many ways he can arrange the brinjal plants with the same number in each row.
Solution: We have to find all the factors of 30.
30= 1× 30, 2 ×15, 3 × 10, 5 × 6
Factors of 30 are 1,2,3,5,6,10, 15 and 30.
Jagadish can arrange brinjal plants in rows of 1,2,3,5,6,10,15,30.