Does the word “and” always mean a logical (boolean) operation?
Certainly not, a quick glance at the dictionary demonstrates that the use of and is not limited to a boolean operation:
conjunction
1.0 Used to connect words of the same part of speech, clauses, or sentences, that are to be taken jointly:
bread and butter
they can read and write
a hundred and fifty1.1 Used to connect two clauses when the second refers to something that happens after the first:
he turned round and walked out1.2 Used to connect two clauses, the second of which refers to something that results from the first:
there was a flash flood and by the next morning the town was under water1.3 Connecting two identical comparatives, to emphasize a progressive change:
getting better and better1.4 Connecting two identical words, implying great duration or great extent:
I cried and cried1.5 Used to connect two identical words to indicate that things of the same name or class have different qualities:
all human conduct is determined or caused—but there are causes and causes1.6 Used to connect two numbers to indicate that they are being added together:
six and four makes ten1.7 archaic Used to connect two numbers, implying succession:
a line of men marching two and two2.0 Used to introduce an additional comment or interjection:
if it came to a choice—and this was the worst thing—she would turn her back on her parents2.1 Used to introduce a question in connection with what someone else has just said:
‘I found the letter in her bag.’ ‘And did you steam it open?’2.2 Used to introduce a statement about a new topic:
and now to the dessert3.0 informal Used after some verbs and before another verb to indicate intention, instead of ‘to’:
I would try and do what he saidODO
And is a conjunction connecting two related units, and the connection is not necessarily boolean:
… for the purpose of encouraging immigration and increasing the
trade in the products of Michigan, or …
The larger context informs of the relationship between encouraging immigration and increasing the trade:
The boards of supervisors of the several counties may levy a special tax on the taxable property within their respective counties for the purpose of creating a fund; or appropriate out of the general fund an amount to be used for advertising agricultural or industrial advantages of the state or county or any part of the state, or for
collecting, preparing or maintaining an exhibition of the products and
industries of the county at any domestic or foreign exposition, for
the purpose of encouraging immigration and increasing the trade in the
products of Michigan, or advertising the state and any portion thereof
for tourists and resorters.
Recognizing the legislative source, and the productive analysis of parallelism, the exhibition mentioned in the larger context seems to have a three-fold purpose: immigration and trade or tourism. The conjunction and seems to be «boolean» in reference to the purpose—both are included together.
It is not necessarily «boolean» in reference to outcome. At some expositions, the the exhibit may effectively encourage immigration. At some expositions, the the exhibit may effectively increase the trade. At some expositions, the the exhibit may accomplish both.
Interestingly, the or presses the and toward a boolean interpretation in reference to the purpose. By contrast with the conjunction and, the conjunction or sets the advertising part of the there-fold purpose apart as an alternative to the pair: encouraging immigration and increasing the trade.
Still and would not necessarily have a strictly boolean function in reference to the outcomes. At any exposition, the the exhibit may fulfill any combination of the listed purposes—which were linguistically presented as a single three-fold purpose.
Conclusion:
The semantic complexity of purpose, rooted in the complexity of human reasoning and interaction, transcends a simple boolean arrangement. Unless they anticipate litigation, both the average writer and the average reader can manage this complexity without the need for precise boolean logic. Though this legislative language likely anticipated litigation, it remains a matter of subjective judgement to determine the «purpose» of an exhibit.
Published on
May 2, 2022
by
Eoghan Ryan.
Revised on
November 4, 2022.
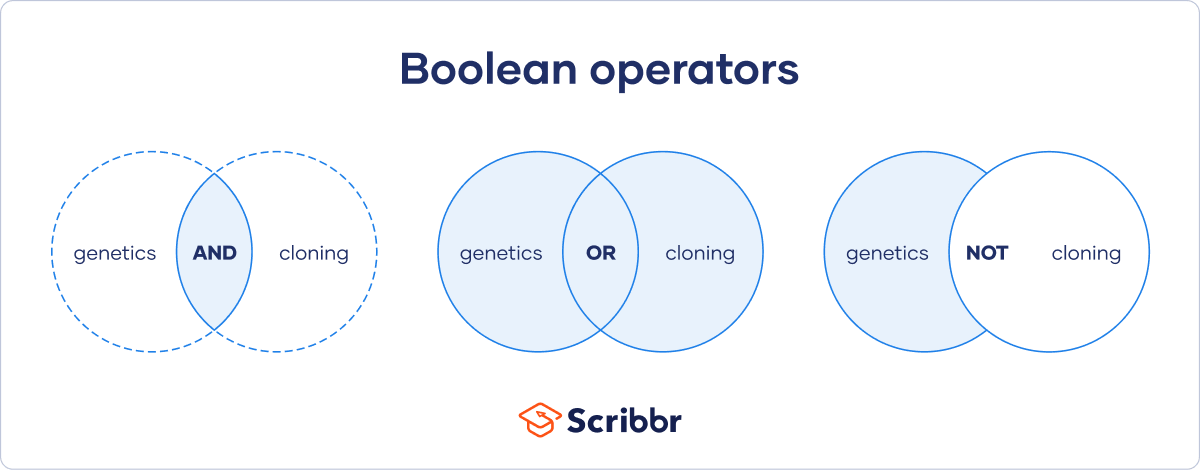
Boolean operators are words and symbols, such as AND or NOT, that let you expand or narrow your search parameters when using a database or search engine. When you search using these operators, it is known as a Boolean search.
You can use Boolean operators such as AND, OR, and NOT alongside keywords to create a Boolean string that will refine your search to find the most relevant results and sources.
How to use Boolean operators
Knowing how to use Boolean operators effectively can save you a lot of time and help you to find useful sources, determine the relevance of your research topic, and create strong research questions. It’s also very helpful when you’re working on a literature review or systematic review.
| Boolean operator | Function | Example |
|---|---|---|
| AND | Provides results that contain both or all keywords | paradigm AND syntagm |
| OR | Provides results that contain either keyword | meteor OR meteorite |
| NOT or AND NOT | Provides results that contain the first keyword but not the second | football NOT soccer |
| Quotation marks “” | Provides results with the exact phrase | “Newtonian mechanics” |
| Parentheses () | Allows you to group together keywords and control the order in which the terms will be searched | (rural OR urban) AND sociology |
| Asterisk * | Provides results that contain a variation of the keyword | Develop*
This will return results containing words such as “development,” “developer,” and “developing.” |
AND
AND will provide search results containing both or all of your keywords.
Use this when you want results that contain two or more specific keywords.
OR
OR will provide search results containing at least one of your keywords.
Use this when you want results that contain at least one (though not necessarily both) of your chosen keywords.
NOT
NOT will provide search results containing the first of your keywords but not the second. Make sure to put your keywords in the correct order when using NOT, as the search results provided will exclude the latter keyword.
Use this when you want results that contain one specific keyword but not another.
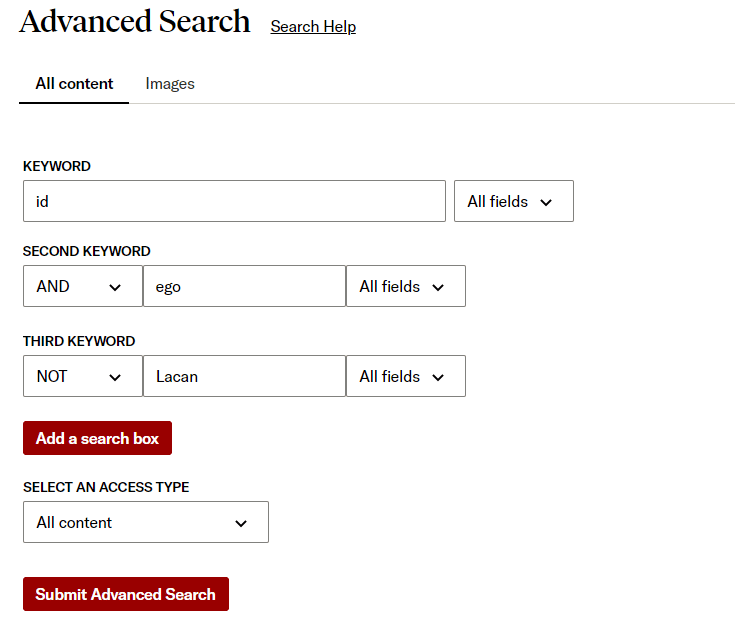
Parentheses: ()
Parentheses allow you to group together keywords and control the order in which the terms will be searched, just like in a mathematical statement. Keywords and Boolean operators within parentheses will be searched first, followed by keywords outside parentheses.
For example, the combination shown below will provide results that are initially filtered to contain at least one of “id” or “ego,” and then further refined to also include “developmental.”
You can also use more than one pair of parentheses. The search will filter results based on the innermost parenthetical keywords first, followed by the keywords in outer parentheses, and finally the keyword(s) outside parentheses.
Quotation marks: “”
Quotation marks will provide search results containing the exact keyword(s) contained within.
Use this when you want results that contain a precise keyword or keywords.
Asterisk: *
An asterisk will provide search results containing variations of a root word.
Use this when you want results that contain the keyword that you entered or other words that begin with those letters.
This will provide results including variations of the chosen word such as “formal” and “formation.”
Each database or search engine may use Boolean operators in slightly different ways. Therefore, it is important to check how Boolean operators work in the particular database or search engine you’re using.
Note: Many databases and search engines also offer an “advanced search” option that lets you choose the most relevant Boolean operators from a drop-down list, like in the example from JSTOR below.
Proximity operators
Proximity operators are similar to Boolean operators. They let you filter results based on the proximity of one keyword to another.
Proximity operators include NEAR (Nx), WITHIN (Wx), and SENTENCE.
| Proximity operator | Function | Example |
|---|---|---|
| NEAR (Nx) | Provides results that contain your chosen keywords within x words of each other, regardless of the order they occur in | Solar N5 energy will provide results in which “energy” appears within five words of the word “solar.” This will include results such as “solar energy,” and “energy produced by solar panels.” |
| WITHIN (Wx) | Provides results that contain your chosen keywords within x words of each other in the order you entered them | Solar W5 energy will provide results in which “energy” appears within five words of the word “solar” but will exclude results in which the order is reversed, such as “energy produced by solar panels.” |
| SENTENCE | Provides results in which two or more keywords occur in the same sentence | Learning SENTENCE environment will provide results in which “learning” and “environment” appear in the same sentence, such as “a supportive environment is essential to the learning process.” |
Note: Not all databases use proximity operators. Be sure to check the search operations of the database you are using.
Scribbr Citation CheckerNew
The AI-powered Citation Checker helps you avoid common mistakes such as:
- Missing commas and periods
- Incorrect usage of “et al.”
- Ampersands (&) in narrative citations
- Missing reference entries
Learn more
Frequently asked questions about Boolean operators
-
What is a Boolean search?
-
A Boolean search uses specific words and symbols known as Boolean operators (e.g., AND, OR) alongside keywords to limit or expand search results. Boolean searches allow you to:
- Prioritize keywords
- Exclude keywords
- Search exact keywords
- Search variations of your keywords
-
What are Boolean operators and how do I use them?
-
Boolean operators are specific words and symbols that you can use to expand or narrow your search parameters when using a database or search engine.
The most common Boolean operators are AND, OR, NOT or AND NOT, quotation marks “”, parentheses (), and asterisks *.
Each Boolean operator has a unique function. For example, the Boolean operator AND will provide search results containing both/all of your keywords.
-
What are proximity operators and how do I use them?
-
Proximity operators are specific words used alongside your chosen keywords that let you specify the proximity of one keyword in relation to another.
The most common proximity operators include NEAR (Nx), WITHIN (Wx), and SENTENCE.
Each proximity operator has a unique function. For example, Nx allows you to find sources that contain the specified keywords within a set number of words (x) of each other.
-
How do I search research databases efficiently?
-
When searching for sources in databases, think of specific keywords that are relevant to your topic, and consider variations on them or synonyms that might be relevant.
Once you have a clear idea of your research parameters and key terms, choose a database that is relevant to your research (e.g., Medline, JSTOR, Project MUSE).
Find out if the database has a “subject search” option. This can help to refine your search. Use Boolean operators to combine your keywords, exclude specific search terms, and search exact phrases to find the most relevant sources.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Ryan, E.
(2022, November 04). Boolean Operators | Quick Guide, Examples & Tips. Scribbr.
Retrieved April 12, 2023,
from https://www.scribbr.com/working-with-sources/boolean-operators/
Is this article helpful?
You have already voted. Thanks 
Your vote is saved 
Processing your vote…
Published on November 5, 2018
|
Last modified on December 12, 2022
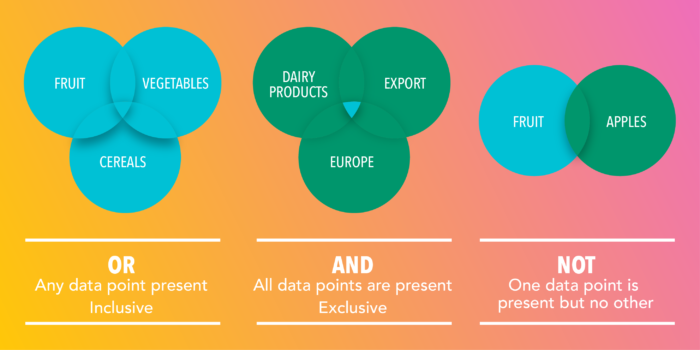
Boolean Logic is a form of algebra that is centered around three simple words known as Boolean Operators: “Or,” “And,” and “Not.” These Boolean operators are the logical conjunctions between your keywords in a search to help broaden or narrow its scope.
At the heart of a Boolean Logic expression is the idea that all values are either true or false. In other words, Boolean means using operators to compare variables against the criteria you define to determine if the variables meet them. A Boolean operation, then, is the construction of a logical expression to help carry out that function.
Within the Lotame platform, the use of Boolean Logic allows for the creation of more complex audience definitions, allowing for audiences to be built to a very specific set of definitions. This article explores the uses of individual Boolean operators and how they relate to building audiences.
An Example of “OR”
An Example of “AND”
An Example of “NOT <“
An Example of Boolean Logic at Work In Building Audiences : OR
Our first example of a Boolean operator is “OR,” which broadens your search. This operator is used to express that as long as one of two or more conditions are met, the value of a specified query is true. In computer logic, the search results will return a “true” for every variable you’re searching that meets the criteria — meaning your results will include any of the searched terms.
For example, to build an audience that encompasses anyone who enjoys Mexican, Chinese, or French Cuisine, the following audience definition would apply:
Using the “OR” operator would ensure that anyone who has shown an affinity for at least one of these cuisines will be included in the audience created.
Let’s look at a second example. Suppose your company or advertiser is a retailer of products, food, treats and remedies for dogs, cats and birds. To build this specific audience, you can use the Boolean expression “cat owners OR dog owners OR bird owners.”
This Boolean operation will yield those who have cats, those who have dogs and those who have birds. It would also include households with any combination of those three animals. Yet, the search would exclude owners of reptiles, horses and other animals, delivering only the applicable target households. Using this logic ensures your custom content only displays to the relevant pet owner audience.
An Example of Boolean Logic at Work In Building Audiences : AND
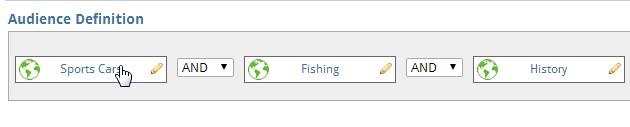
As a Boolean operator, “AND” serves to indicate that ALL specified conditions must be met in order for a query to return true. Since all variables in the search logic must be true for the results to display, you maintain more control over who sees the relevant content. This operator is valuable for eliminating audiences who aren’t likely to need or use a particular product or service because it narrows the search.
Remember you can use “AND” with more than two search variables — each condition you add must be true for the database to supply a result.
In the event that a client were building an audience and wanted to target only users who had shown an affinity for Sports Cars and Fishing and History, the following audience definition would apply:
The use of the “AND” operator means that a user must meet ALL of the specified criteria to be included in the audience; users who merely like Fishing or like only Fishing and History (etc.) will be excluded from this audience definition.
We can revisit our pet retailer as an example of this logic at work. Suppose the company has a product applying explicitly to households that own both cats and dogs, such as a smart pet door that allows dogs outside but keeps indoor cats inside.
Use the Boolean logic “cat owners AND dog owners” to build the appropriate audience to target with this product. Your results will exclude the households that don’t have both pets and those only owning birds.
An Example of Boolean Logic at Work In Building Audiences : NOT<
The “NOT” Boolean operator is used to exclude nodes from an audience definition. As it applies to the creation of an audience definition, “NOT” will exclude all users falling under the node which has been prepended by “NOT.” By nature, “NOT” narrows a search. It will exclude any content containing the words following “NOT” and preceding other operators. As a result, it transforms the “true” parts into “false” to limit the results.
In other words, the database looks for a “true” value in the information you want to omit and doesn’t report those results.
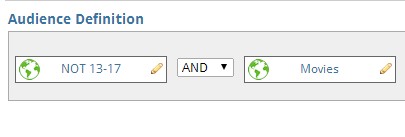
For example, to create an audience of users over the age of 18 (NOT 13-17 years of age) with a demonstrated interest in movies, the following audience definition would be used:
In this instance, the “NOT” which prepends 13-17 means that no users within this age range will be included in this audience definition. It is also worth noting that the “AND” operator is used here as well. Translated into plain English, this definition would be read as “Users who are not between ages 13 and 17 and who have an interest in movies.”
We can again see this action with the pet product retailer as an example. Imagine the company sells an all-natural flea repellent remedy that’s unsafe for use around birds. We’d want to use “NOT” to exclude households with birds. Combining it with “OR” will help us do just that. We can construct the Boolean expression to say, “cat owners OR dog owners NOT bird owners” to get the desired audience. Doing so ensures the ad or content only appears for those who could safely use the product in their homes.
When to Use Parentheses
Generally, databases give weight to “AND” first. Parentheses help you adjust for more emphasis on a specific concept by prioritizing the information within them, followed by information outside the parentheses. When you’re using both “AND” and “OR” operators, it’s generally best to enclose the “OR” items with parentheses.
For example, suppose the pet retailer is trying to build more business in Canada. To find this audience, they can use the Boolean construction “(cat owners OR dog owners OR bird owners) AND Canada.” This search would yield anyone who owns cats, dogs or birds and lives in Canada.
Users of Lotame’s Data Management Platform (DMP) use Boolean Logic to build audiences for targeted ads, content customization, and many other business applications. By understanding who your audience is, and grouping them into audience segments, you can personalize your messaging to increase engagement with your products & services.
Learn more about a DMP in this short video:
Boost Engagement With Lotame
We are a leading partner for audience analysis, giving you deeper insight into your customers and website visitors. Our technology gives you a centralized source for gathering and leveraging data to deliver more relevant content.
Want to learn more? Let’s chat. We’d love to show you a demo of our platform and how it can help your marketing work harder for you, to increase engagement and conversion rates. Fill out the form below and get in touch with us!
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Using the Python and Operator
Python has three Boolean operators, or logical operators: and, or, and not. You can use them to check if certain conditions are met before deciding the execution path your programs will follow. In this tutorial, you’ll learn about the and operator and how to use it in your code.
In this tutorial, you’ll learn how to:
- Understand the logic behind Python’s
andoperator - Build and understand Boolean and non-Boolean expressions that use the
andoperator - Use the
andoperator in Boolean contexts to decide the course of action of your programs - Use the
andoperator in non-Boolean contexts to make your code more concise
You’ll also code a few practical examples that will help you understand how to use the and operator to approach different problems in a Pythonic way. Even if you don’t use all the features of and, learning about them will allow you to write better and more accurate code.
Working With Boolean Logic in Python
Back in 1854, George Boole authored The Laws of Thought, which contains what’s known as Boolean algebra. This algebra relies on two values: true and false. It also defines a set of Boolean operations, also known as logical operations, denoted by the generic operators AND, OR, and NOT.
These Boolean values and operators are pretty helpful in programming. For example, you can construct arbitrarily complex Boolean expressions with the operators and determine their resulting truth value as true or false. You can use the truth value of Boolean expressions to decide the course of action of your programs.
In Python, the Boolean type bool is a subclass of int and can take the values True or False:
>>>
>>> issubclass(bool, int)
True
>>> help(bool)
Help on class bool in module builtins:
class bool(int)
...
>>> type(True)
<class 'bool'>
>>> type(False)
<class 'bool'>
>>> isinstance(True, int)
True
>>> isinstance(False, int)
True
>>> int(True)
1
>>> int(False)
0
As you can see in this code, Python implements bool as a subclass of int with two possible values, True and False. These values are built-in constants in Python. They’re internally implemented as integer numbers with the value 1 for True and 0 for False. Note that both True and False must be capitalized.
Along with the bool type, Python provides three Boolean operators, or logical operators, that allow you to combine Boolean expressions and objects into more elaborate expressions. Those operators are the following:
| Operator | Logical Operation |
|---|---|
and |
Conjunction |
or |
Disjunction |
not |
Negation |
With these operators, you can connect several Boolean expressions and objects to build your own expressions. Unlike other languages, Python uses English words to denote Boolean operators. These words are keywords of the language, so you can’t use them as identifiers.
In this tutorial, you’ll learn about Python’s and operator. This operator implements the logical AND operation. You’ll learn how it works and how to use it either in a Boolean or non-Boolean context.
Getting Started With Python’s and Operator
Python’s and operator takes two operands, which can be Boolean expressions, objects, or a combination. With those operands, the and operator builds more elaborate expressions. The operands in an and expression are commonly known as conditions. If both conditions are true, then the and expression returns a true result. Otherwise, it returns a false result:
>>>
>>> True and True
True
>>> False and False
False
>>> True and False
False
>>> False and True
False
These examples show that an and expression only returns True when both operands in the expressions are true. Since the and operator takes two operands to build an expression, it’s a binary operator.
The quick examples above show what’s known as the and operator’s truth table:
operand1 |
operand2 |
operand1 and operand2 |
|---|---|---|
| True | True | True |
| True | False | False |
| False | False | False |
| False | True | False |
This table summarizes the resulting truth value of a Boolean expression like operand1 and operand2. The result of the expression depends on the truth values of its operands. It’ll be true if both are true. Otherwise, it’ll be false. This is the general logic behind the and operator. However, this operator can do more than that in Python.
In the following sections, you’ll learn how to use and for building your own expressions with different types of operands.
Using Python’s and Operator With Boolean Expressions
You’ll typically use logical operators to build compound Boolean expressions, which are combinations of variables and values that produce a Boolean value as a result. In other words, Boolean expressions return True or False.
Comparisons and equality tests are common examples of this type of expression:
>>>
>>> 5 == 3 + 2
True
>>> 5 > 3
True
>>> 5 < 3
False
>>> 5 != 3
True
>>> [5, 3] == [5, 3]
True
>>> "hi" == "hello"
False
All these expressions return True or False, which means they’re Boolean expressions. You can combine them using the and keyword to create compound expressions that test two—or more–subexpressions at a time:
>>>
>>> 5 > 3 and 5 == 3 + 2
True
>>> 5 < 3 and 5 == 5
False
>>> 5 == 5 and 5 != 5
False
>>> 5 < 3 and 5 != 5
False
Here, when you combine two True expressions, you get True as a result. Any other combination returns False. From these examples, you can conclude that the syntax for creating compound Boolean expressions with the and operator is the following:
expression1 and expression2
If both subexpressions expression1 and expression2 evaluate to True, then the compound expression is True. If at least one subexpression evaluates to False, then the result is False.
There’s no limit to the number of and operators you can use when you’re building a compound expression. This means that you can combine more than two subexpressions in a single expression using several and operators:
>>>
>>> 5 > 3 and 5 == 3 + 2 and 5 != 3
True
>>> 5 < 3 and 5 == 3 and 5 != 3
False
Again, if all the subexpressions evaluate to True, then you get True. Otherwise, you get False. Especially as expressions get longer, you should keep in mind that Python evaluates the expressions sequentially from left to right.
Short-Circuiting the Evaluation
Python’s logical operators, such as and and or, use something called short-circuit evaluation, or lazy evaluation. In other words, Python evaluates the operand on the right only when it needs to.
To determine the final result of an and expression, Python starts by evaluating the left operand. If it’s false, then the whole expression is false. In this situation, there’s no need to evaluate the operand on the right. Python already knows the final result.
Having a false left operand automatically makes the whole expression false. It would be a waste of CPU time to evaluate the remaining operand. Python prevents this by short-circuiting the evaluation.
In contrast, the and operator evaluates the operand on the right only if the first operand is true. In this case, the final result depends on the right operand’s truth value. If it’s true, then the whole expression is true. Otherwise, the expression is false.
To demonstrate the short-circuiting feature, take a look at the following examples:
>>>
>>> def true_func():
... print("Running true_func()")
... return True
...
>>> def false_func():
... print("Running false_func()")
... return False
...
>>> true_func() and false_func() # Case 1
Running true_func()
Running false_func()
False
>>> false_func() and true_func() # Case 2
Running false_func()
False
>>> false_func() and false_func() # Case 3
Running false_func()
False
>>> true_func() and true_func() # Case 4
Running true_func()
Running true_func()
True
Here’s how this code works:
- Case 1: Python evaluates
true_func(), which returnsTrue. To determine the final result, Python evaluatesfalse_func()and getsFalse. You can confirm this by seeing both functions’ output. - Case 2: Python evaluates
false_func(), which returnsFalse. Python already knows that the final result isFalse, so it doesn’t evaluatetrue_func(). - Case 3: Python runs
false_func()and getsFalseas a result. It doesn’t need to evaluate the repeated function a second time. - Case 4: Python evaluates
true_func()and getsTrueas a result. It then evaluates the function again. Since both operands evaluate toTrue, the final result isTrue.
Python processes Boolean expressions from left to right. It stops when it no longer needs to evaluate any further operands or subexpressions to determine the final outcome. To sum up this concept, you should remember that if the left operand in an and expression is false, then the right operand won’t be evaluated.
Short-circuit evaluation can have a significant impact on your code’s performance. To take advantage of that, consider the following tips when you’re building and expressions:
- Place time-consuming expressions on the right of the
andkeyword. This way, the costly expression won’t run if the short-circuit rule takes effect. - Place the expression that is more likely to be false on the left of the
andkeyword. This way, it’s more likely that Python can determine if the whole expression is false by evaluating the left operand only.
Sometimes you may want to avoid lazy evaluation in a specific Boolean expression. You can do so by using the bitwise operators (&, |, ~). These operators also work in Boolean expressions, but they evaluate the operands eagerly:
>>>
>>> def true_func():
... print("Running true_func()")
... return True
...
>>> def false_func():
... print("Running false_func()")
... return False
...
>>> # Use logical and
>>> false_func() and true_func()
Running false_func()
False
>>> # Use bitwise and
>>> false_func() & true_func()
Running false_func()
Running true_func()
False
In the first expression, the and operator works lazily, as expected. It evaluates the first function, and since the result is false, it doesn’t evaluate the second function. In the second expression, however, the bitwise AND operator (&) calls both functions eagerly even though the first function returns False. Note that in both cases, the final result is False.
Even though this trick works, it’s generally discouraged. You should use bitwise operators to manipulate bits, and Boolean operators to work with Boolean values and expressions. For a deeper dive into bitwise operators, check out Bitwise Operators in Python.
Using Python’s and Operator With Common Objects
You can use the and operator to combine two Python objects in a single expression. In that situation, Python internally uses bool() to determine the truth value of the operands. As a result, you get a specific object rather than a Boolean value. You only get True or False if a given operand explicitly evaluates to True or False:
>>>
>>> 2 and 3
3
>>> 5 and 0.0
0.0
>>> [] and 3
[]
>>> 0 and {}
0
>>> False and ""
False
In these examples, the and expression returns the operand on the left if it evaluates to False. Otherwise, it returns the operand on the right. To produce these results, the and operator uses Python’s internal rules to determine an object’s truth value. The Python documentation states these rules like this:
By default, an object is considered true unless its class defines either a
__bool__()method that returnsFalseor a__len__()method that returns zero, when called with the object. Here are most of the built-in objects considered false:
- constants defined to be false:
NoneandFalse.- zero of any numeric type:
0,0.0,0j,Decimal(0),Fraction(0, 1)- empty sequences and collections:
'',(),[],{},set(),range(0)(Source)
With these rules in mind, look again at the code above. In the first example, the integer number 2 is true (nonzero), so and returns the right operand, 3. In the second example, 5 is true, so and returns the right operand even though it evaluates to False.
The next example uses an empty list ([]) as the left operand. Since empty lists evaluate to false, the and expression returns the empty list. The only case where you get True or False is the one where you use a Boolean object explicitly in the expression.
Here’s how you can summarize the behavior of the and operator when you use it with common Python objects instead of Boolean expressions. Note that Python uses the truth value of each object to determine the final result:
object1 |
object2 |
object1 and object2 |
|---|---|---|
| False | False | object1 |
| False | True | object1 |
| True | True | object2 |
| True | False | object2 |
In general, if the operands in an and expression are objects instead of Boolean expressions, then the operator returns the object on the left if it evaluates to False. Otherwise, it returns the object on the right, even when it evaluates to False.
Mixing Boolean Expressions and Objects
You can also combine Boolean expressions and common Python objects within an and expression. In that situation, the and expression still returns the left operand if it’s false, or else it returns the right operand. The returned value could be True, False, or a regular object, depending on which part of the expression provides that result:
>>>
>>> 2 < 4 and 2
2
>>> 2 and 2 < 4
True
>>> 2 < 4 and []
[]
>>> [] and 2 < 4
[]
>>> 5 > 10 and {}
False
>>> {} and 5 > 10
{}
>>> 5 > 10 and 4
False
>>> 4 and 5 > 10
False
These examples use a combination of Boolean expressions and common objects. In each pair of examples, you see that you can get either a non-Boolean object or a Boolean value, True or False. The result will depend on which part of the expression provides the final result.
Here’s a table that summarizes the behavior of the and operator when you combine Boolean expressions and common Python objects:
expression |
object |
expression and object |
|---|---|---|
True |
True | object |
True |
False | object |
False |
False | False |
False |
True | False |
To find out what’s returned, Python evaluates the Boolean expression on the left to get its Boolean value (True or False). Then Python uses its internal rules to determine the truth value of the object on the right.
As an exercise to test your understanding, you could try to rewrite this table by swapping the order of the operands in the third column to object and expression. Try to predict what will be returned in each row.
Combining Python Logical Operators
As you’ve seen earlier in this tutorial, Python provides two additional logical operators: the or operator and the not operator. You can use them along with the and operator to create more complex compound expressions. If you want to make accurate and clear expressions with multiple logical operators, then you need to consider the precedence of each operator. In other words, you need to consider the order in which Python executes them.
Python’s logical operators have low precedence when compared with other operators. However, sometimes it’s healthy to use a pair of parentheses (()) to ensure a consistent and readable result:
>>>
>>> 5 or 2 and 2 > 1
5
>>> (5 or 3) and 2 > 1
True
These examples combine the or operator and the and operator in a compound expression. Just like the and operator, the or operator uses short-circuit evaluation. Unlike and, however, the or operator stops once it finds a true operand. You can see this in the first example. Since 5 is true, the or subexpression immediately returns 5 without evaluating the rest of the expression.
In contrast, if you enclose the or subexpression in a pair of parentheses, then it works as a single true operand, and 2 > 1 gets evaluated as well. The final result is True.
The takeaway is that if you’re using multiple logical operators in a single expression, then you should consider using parentheses to make your intentions clear. This trick will also help you get the correct logical result.
Using Python’s and Operator in Boolean Contexts
Like all of Python’s Boolean operators, the and operator is especially useful in Boolean contexts. Boolean contexts are where you’ll find most of the real-world use cases of Boolean operators.
Two main structures define Boolean contexts in Python:
ifstatements let you perform conditional execution and take different courses of action based on the result of some initial conditions.whileloops let you perform conditional iteration and run repetitive tasks while a given condition is true.
These two structures are part of what you’d call control flow statements. They help you decide your programs’ execution path.
You can use Python’s and operator to construct compound Boolean expressions in both if statements and while loops.
if Statements
Boolean expressions are commonly known as conditions because they typically imply the need for meeting a given requirement. They’re pretty useful in the context of conditional statements. In Python, this type of statement starts with the if keyword and continues with a condition. A conditional statement can additionally include elif and else clauses.
Python conditional statements follow the logic of conditionals in English grammar. If the condition is true, then the if code block executes. Otherwise, the execution jumps to a different code block:
>>>
>>> a = -8
>>> if a < 0:
... print("a is negative")
... elif a > 0:
... print("a is positive")
... else:
... print("a is equal to 0")
...
a is negative
Since a holds a negative number, the condition a < 0 is true. The if code block runs, and you get the message a is negative printed on your screen. If you change the value of a to a positive number, however, then the elif block runs and Python prints a is positive. Finally, if you set a to zero, then the else code block executes. Go ahead and play with a to see what happens!
Now say you want to make sure that two conditions are met—meaning that they’re both true—before running a certain piece of code. To try this out, suppose you need to get the age of a user running your script, process that information, and display to the user their current life stage.
Fire up your favorite code editor or IDE and create the following script:
# age.py
age = int(input("Enter your age: "))
if age >= 0 and age <= 9:
print("You are a child!")
elif age > 9 and age <= 18:
print("You are an adolescent!")
elif age > 18 and age <= 65:
print("You are an adult!")
elif age > 65:
print("Golden ages!")
Here, you get the user’s age using input() and then convert it to an integer number with int(). The if clause checks if age is greater than or equal to 0. In the same clause, it checks if age is less than or equal to 9. To do this, you build an and compound Boolean expression.
The three elif clauses check other intervals to determine the life stage associated with the user’s age.
If you run this script from your command line, then you get something like this:
$ python age.py
Enter your age: 25
You are an adult!
Depending on the age you enter at the command line, the script takes one course of action or another. In this specific example, you provide an age of 25 years and get the message You are an adult! printed to your screen.
while Loops
The while loop is the second construct that can use and expressions to control a program’s execution flow. By using the and operator in the while statement header, you can test several conditions and repeat the loop’s code block for as long as all conditions are met.
Say you’re prototyping a control system for a manufacturer. The system has a critical mechanism that should work with a pressure of 500 psi or lower. If the pressure goes over 500 psi while staying under 700 psi, then the system has to run a given series of standard safety actions. For pressures greater than 700 psi, there are a whole new set of safety actions that the system must run.
To approach this problem, you can use a while loop with an and expression. Here’s a script that simulates a possible solution:
1# pressure.py
2
3from time import sleep
4from random import randint
5
6def control_pressure():
7 pressure = measure_pressure()
8 while True:
9 if pressure <= 500:
10 break
11
12 while pressure > 500 and pressure <= 700:
13 run_standard_safeties()
14 pressure = measure_pressure()
15
16 while pressure > 700:
17 run_critical_safeties()
18 pressure = measure_pressure()
19
20 print("Wow! The system is safe...")
21
22def measure_pressure():
23 pressure = randint(490, 800)
24 print(f"psi={pressure}", end="; ")
25 return pressure
26
27def run_standard_safeties():
28 print("Running standard safeties...")
29 sleep(0.2)
30
31def run_critical_safeties():
32 print("Running critical safeties...")
33 sleep(0.7)
34
35if __name__ == "__main__":
36 control_pressure()
Inside control_pressure(), you create an infinite while loop on line 8. If the system is stable and the pressure is below 500 psi, the conditional statement breaks out of the loop and the program finishes.
On line 12, the first nested while loop runs the standard safety actions while the system pressure stays between 500 psi and 700 psi. In each iteration, the loop gets a new pressure measurement to test the condition again in the next iteration. If the pressure grows beyond 700 psi, then the second loop on line 16 runs the critical safety actions.
To run this script, open up your command line and enter the following command:
$ python pressure.py
psi=756; Running critical safeties...
psi=574; Running standard safeties...
psi=723; Running critical safeties...
psi=552; Running standard safeties...
psi=500; Wow! The system is safe...
The output on your screen should be a little different from this sample output, but you can still get an idea of how the application works.
Using Python’s and Operator in Non-Boolean Contexts
The fact that and can return objects besides just True and False is an interesting feature. For example, this feature allows you to use the and operator for conditional execution. Say you need to update a flag variable if the first item in a given list is equal to a certain expected value. For this situation, you can use a conditional statement:
>>>
>>> a_list = ["expected value", "other value"]
>>> flag = False
>>> if len(a_list) > 0 and a_list[0] == "expected value":
... flag = True
...
>>> flag
True
Here, the conditional checks if the list has at least one item. If so, it checks if the first item in the list is equal to the "expected value" string. If both checks pass, then flag changes to True. You can simplify this code by taking advantage of the and operator:
>>>
>>> a_list = ["expected value", "other value"]
>>> flag = False
>>> flag = len(a_list) > 0 and a_list[0] == "expected value"
>>> flag
True
In this example, the highlighted line does all the work. It checks both conditions and makes the corresponding assignment in one go. This expression takes the and operator out of the if statement you used in the previous example, which means that you’re not working in a Boolean context any longer.
The code in the example above is more concise than the equivalent conditional statement you saw before, but it’s less readable. To properly understand this expression, you’d need to be aware of how the and operator works internally.
Putting Python’s and Operator Into Action
So far, you’ve learned how to use Python’s and operator for creating compound Boolean expressions and non-Boolean expressions. You’ve also learned how to use this logical operator in Boolean contexts like if statements and while loops.
In this section, you’ll build a few practical examples that’ll help you decide when to use the and operator. With these examples, you’ll learn how to take advantage of and for writing better and more Pythonic code.
Flattening Nested if Statements
One principle from the Zen of Python states that “Flat is better than nested.” For example, while code that has two levels of nested if statements is normal and totally okay, your code really starts to look messy and complicated when you have more than two levels of nesting.
Say you need to test if a given number is positive. Then, once you confirm that it’s positive, you need to check if the number is lower than a given positive value. If it is, you can proceed with a specific calculation using the number at hand:
>>>
>>> number = 7
>>> if number > 0:
... if number < 10:
... # Do some calculation with number...
... print("Calculation done!")
...
Calculation done!
Cool! These two nested if statements solve your problem. You first check if the number is positive and then check if it’s lower than 10. In this small example, the call to print() is a placeholder for your specific calculation, which runs only if both conditions are true.
Even though the code works, it’d be nice to make it more Pythonic by removing the nested if. How can you do that? Well, you can use the and operator to combine both conditions in a single compound condition:
>>>
>>> number = 7
>>> if number > 0 and number < 10:
... # Do some calculation with number...
... print("Calculation done!")
...
Calculation done!
Logical operators like the and operator often provide an effective way to improve your code by removing nested conditional statements. Take advantage of them whenever possible.
In this specific example, you use and to create a compound expression that checks if a number is in a given range or interval. Python provides an even better way to perform this check by chaining expressions. For example, you can write the condition above as 0 < number < 10. That’s a topic for the following section.
Checking Numeric Ranges
With a close look at the example in the section below, you can conclude that Python’s and operator is a convenient tool for checking if a specific numeric value is inside a given interval or range. For example, the following expressions check if a number x is between 0 and 10, both inclusive:
>>>
>>> x = 5
>>> x >= 0 and x <= 10
True
>>> x = 20
>>> x >= 0 and x <= 10
False
In the first expression, the and operator first checks if x is greater than or equal to 0. Since the condition is true, the and operator checks if x is lower than or equal to 10. The final result is true because the second condition is also true. This means that the number is within the desired interval.
In the second example, the first condition is true, but the second is false. The general result is false, which means the number isn’t in the target interval.
You can enclose this logic in a function and make it reusable:
>>>
>>> def is_between(number, start=0, end=10):
... return number >= start and number <= end
...
>>> is_between(5)
True
>>> is_between(20)
False
>>> is_between(20, 10, 40)
True
In this example, is_between() takes number as an argument. It also takes start and end, which define the target interval. Note that these arguments have default argument values, which means they’re optional arguments.
Your is_between() function returns the result of evaluating an and expression that checks if number is between start and end, both inclusive.
Even though using the and operator allows you to check gracefully if a number is within a given interval, there’s a more Pythonic technique to approach the same problem. In mathematics, you can write 0 < x < 10 to denote that x is between 0 and 10.
In most programming languages, this expression doesn’t make sense. In Python, however, the expression works like a charm:
>>>
>>> x = 5
>>> 0 < x < 10
True
>>> x = 20
>>> 0 < x < 10
False
In a different programming language, this expression would start by evaluating 0 < x, which is true. The next step would be to compare the true Boolean with 10, which doesn’t make much sense, so the expression fails. In Python, something different happens.
Python internally rewrites this type of expression to an equivalent and expression, such as x > 0 and x < 10. It then performs the actual evaluation. That’s why you get the correct result in the example above.
Just like you can chain several subexpressions with multiple and operators, you can also chain them without explicitly using any and operators:
>>>
>>> x = 5
>>> y = 15
>>> 0 < x < 10 < y < 20
True
>>> # Equivalent and expression
>>> 0 < x and x < 10 and 10 < y and y < 20
True
You can also use this Python trick to check if several values are equal:
>>>
>>> x = 10
>>> y = 10
>>> z = 10
>>> x == y == z
True
>>> # Equivalent and expression
>>> x == y and y == z
True
Chained comparison expressions are a nice feature, and you can write them in various ways. However, you should be careful. In some cases, the final expression can be challenging to read and understand, especially for programmers coming from languages in which this feature isn’t available.
Chaining Function Calls Conditionally
If you’ve ever worked with Bash on a Unix system, then you probably know about the command1 && command2 construct. This is a handy technique that allows you to run several commands in a chain. Each command runs if and only if the previous command was successful:
$ cd /not_a_dir && echo "Success"
bash: cd: /not_a_dir: No such file or directory
$ cd /home && echo "Success"
Success
These examples use Bash’s short-circuit AND operator (&&) to make the execution of the echo command dependent on the success of the cd command.
Since Python’s and also implements the idea of lazy evaluation, you can use it to emulate this Bash trick. For example, you can chain a series of function calls in a single and expression like the following:
func1() and func2() and func3() ... and funcN()
In this case, Python calls func1(). If the function’s return value evaluates to a true value, then Python calls func2(), and so on. If one of the functions returns a false value, then Python won’t call the rest of the functions.
Here’s an example that uses some pathlib functions to manipulate a text file:
>>>
>>> from pathlib import Path
>>> file = Path("hello.txt")
>>> file.touch()
>>> # Use a regular if statement
>>> if file.exists():
... file.write_text("Hello!")
... file.read_text()
...
6
'Hello!'
>>> # Use an and expression
>>> file.exists() and file.write_text("Hello!") and file.read_text()
'Hello!'
Nice! In a single line of code, you run three functions conditionally without the need for an if statement. In this specific example, the only visible difference is that .write_text() returns the number of bytes it wrote to the file. The interactive shell automatically displays that value to the screen. Keep in mind that this difference isn’t visible when you run the code as a script.
Conclusion
Python’s and operator allows you to construct compound Boolean expressions that you can use to decide the course of action of your programs. You can use the and operator to solve several problems both in Boolean or non-Boolean contexts. Learning about how to use the and operator properly can help you write more Pythonic code.
In this tutorial, you learned how to:
- Work with Python’s
andoperator - Build Boolean and non-Boolean expressions with Python’s
andoperator - Decide the course of action of your programs using the
andoperator in Boolean contexts - Make your code more concise using the
andoperator in non-Boolean contexts
Going through the practical examples in this tutorial can help you get a general idea of how to use the and operator to make decisions in your Python code.
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Using the Python and Operator
What is Boolean operation?
Boolean Operators are simple words (AND, OR, NOT or AND NOT) used as conjunctions to combine or exclude keywords in a search, resulting in more focused and productive results.
How are Boolean operations accessed in CAD?
To perform a Boolean operation between Solid3d objects inside AutoCAD, you can use Solid3d. BooleanOperation() on the primary Solid3d, passing in the secondary one. We want to implement commands for Unite (or Union), Intersect (Intersection) and Subtract (Subtraction).
What are the 3 types of Boolean operations?
They connect your search words together to either narrow or broaden your set of results. The three basic boolean operators are: AND, OR, and NOT.
What is Boolean function with example?
A Boolean function is a function that has n variables or entries, so it has 2n possible combinations of the variables. These functions will assume only 0 or 1 in its output. An example of a Boolean function is this, f(a,b,c) = a X b + c. These functions are implemented with the logic gates. Digital circuit of f(a,b,c)
Which one of the following is Boolean operation?
Boolean operators are the words “AND”, “OR” and “NOT”. When used in library databases (typed between your keywords) they can make each search more precise – and save you time!
What is Union in Boolean?
Essentially, Boolean Union, Difference, and Intersection are all the same operation. Just different parts of the objects are kept at the end. With Boolean Union, for example, the parts that overlap are thrown away and the rest joined together. With Intersect, it is exactly the opposite.
How many workspaces are available in AutoCAD?
How many workspaces are available in AutoCAD? Explanation: There are three workspaces available to switch between in AutoCAD. These are drafting and annotation, 3D basics and 3D modelling.
What are the 5 boolean operators?
5 Boolean Operators You Need to Know
- AND. AND will narrow your search results to include only relevant results that contain your required keywords. …
- OR. …
- NOT. …
- Quotation Marks “ “ …
- Parentheses ( ) …
- Boolean Is as Much Art as It Is Science. …
- Practice Makes Perfect.
What are the types of Boolean expressions?
A Boolean expression is a logical statement that is either TRUE or FALSE .
…
3.6 Boolean Expressions
- BOOLEAN values ( YES and NO , and their synonyms, ON and OFF , and TRUE and FALSE )
- BOOLEAN variables or formulas.
- Functions that yield BOOLEAN results.
- BOOLEAN values calculated by comparison operators.
Why are boolean operators important?
Boolean operators are the bones of any good literature search. These operators—or connecting words—tell a database how to combine search terms. Researchers use them to configure their searches to find more precise and relevant results.
What is an example of a Boolean?
A Boolean expression is any expression that has a Boolean value. For example, the comparisons 3 < 5, x < 5, x < y and Age < 16 are Boolean expressions. The comparison 3 < 5 will always give the result true, because 3 is always less than 5.
What are the 16 Boolean functions?
Table 1. Complete list of Boolean functions for a single input system
| Name of the Boolean Function | Boolean Function | Meaning |
|---|---|---|
| Transfer | (A ) | Pass value of A |
| (B ) | Pass value of B | |
| NOT | (bar{A}) | Pass negated value of A |
| (bar{B}) | Pass negated value of B |
How many Boolean functions are there?
Theorem 1.
There are 22n different Boolean functions on n Boolean variables.
Permalink
Cannot retrieve contributors at this time
CodeWars Python Solutions
Convert boolean values to strings ‘Yes’ or ‘No’.
Complete the method that takes a boolean value and return a "Yes" string for true, or a "No" string for false.
Given Code
def bool_to_word(boolean): # your code here
Solution
def bool_to_word(boolean): return "Yes" if boolean == True else "No"
See on CodeWars.com