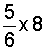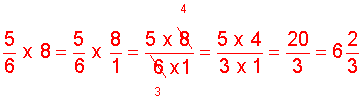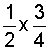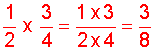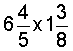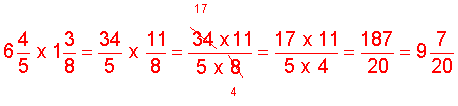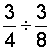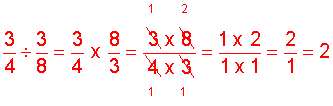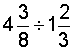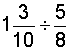Dividing fractions word problems arise in numerous situations. We will show you some examples. I recommend that you review the lesson about division of fractions before starting this lesson.
Dividing fractions word problems: a few examples
Example #1:
An Italian sausage is 8 inches long. How many pieces of sausage can be cut from the 8-inch piece of sausage if each piece is to be two-thirds of an inch?
Solution
Since you are trying to find out how many two-thirds there are in 8, it is a division of fractions problem.
You will need to divide 8 by 2/3 in order to get the answer.
8 ÷ 2/3 = 8/1 ÷ 2/3
8 ÷ 2/3 = 8/1 × 3/2
8 ÷ 2/3 = (8 × 3)/(1 × 2)
8 ÷ 2/3 = 24/2
8 ÷ 2/3 = 12
Therefore, you can make 12 pieces of sausages having a length of 2/3 inches from an 8 inches long Italian sausage.
Example #2
How many halves are there in six-fourths?
Again, since you are trying to find out how many halves there are in six-fourths, it is a division of fractions problem.
You will need to divide 6/4 by 1/2 to get the answer.
6/4 ÷ 1/2 = 6/4 × 2/1
6/4 ÷ 1/2 = (6 × 2)/(4 × 1)
6/4 ÷ 1/2 = 12/4
6/4 ÷ 1/2 = 3
Therefore, there are 3 halves in six-fourths.
Example #3:
An airplane covers 50 miles in 1/5 of an hour. How many miles can the airplane cover in 5 hours?
This problem is a combination of division and multiplication of fractions.
First, find out how many fifths (1/5) are there in 5. This is a division of fractions problem.
You will need to divide 5 by 1/5.
5 ÷ 1/5 = 5/1 ÷ 1/5
5 ÷ 1/5 = 5/1 × 5/1
5 ÷ 1/5 = (5 × 5)/(1 × 1)
5 ÷ 1/5 = 25/1
5 ÷ 1/5 = 25
Then, you need to multiply 50 by 25 to get the answer.
50 × 30 = 1250
In 5 hours, the airplane will cover 1250 miles.
Example #4
3 friends share 4/5 of a pizza. what fraction of pizza does each person get?
The amount to share is 4/5
Since the amount will be shared between 3 friends, the amount must be divided between 3 people.
So each person must get 4/5 divided by 3
(4 / 5) / 3 = (4 / 5) / (3 / 1) = 4 / 5 × 1 / 3 = (4 × 1) / (5 × 3)= 4 / 15
Each person will eat 4/15.
Indeed, 4 / 15 + 4 / 15 + 4 / 15 = 12 / 15 = 4/5 (divide 12 and 15 by 3 to get 4 / 5)
Example #4
On June 21st, there were 9/10 of a billion stars visible to the naked eye.
On December 21st, there were 4/5 of a billion stars out visible to the naked eye.
How many times more stars were there visible on June 21st than December 21st?
Set it up.
9/10 divided by 4/5 = ?
Find the reciprocal of the divisor.
9/10 × 5/4 = ?
Simplify
9/10 × 5/4 = 9/2 × 1/4
Simplify again
9/8= 1 1/8
Did you have a hard time understanding the problems above? Did you not understand them at all? Take a look at this figure !
Do you need to master fractions once and for all? Check out my book about fractions.
Have A Great Basic Math Word Problem?
Share it here with a very detailed solution!
What Other Visitors Have Said
Click below to see contributions from other visitors to this page…
Recent Articles
-
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
-
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Word problems + fractions = a lot of struggle for many students. Especially when you throw in new concepts like multiplying and dividing fractions. Those fraction word problems are always pretty tricky for my students. The first year that I taught multiplying and dividing fractions, I really had to spend some time breaking down the concepts myself in order to best help my students. On this post, I will share an anchor chart and a free word problem sort that helps my students solve these types of fraction word problems and see the difference/connection between the two.
Note: This is based on 5th grade standards and focuses only on multiplying fractions less than 1 and dividing with unit fractions and whole numbers. Click here to grab some free printables to help your students with solving word problems involving multiplying mixed numbers.
Teach Multiplying and Dividing Fractions with Models and a Context
Before even beginning with word problems, I always introduce multiplying and dividing fractions (separately) with a context/situation. And then we work through the situation and solve the problem/ answer the question using models. This really helps the students conceptually understand the operations. When students are only exposed to algorithms, they may not fully understand the operation. As a result, they will struggle with choosing the correct operations when solving word problems.
Here are my go-to introductory word problems for when I first introduce multiplying and dividing fractions (again I introduce each one separately). I prefer to use fudge for all of my introductory word problems because I love fudge, my students love it, the contexts make sense and are relatable, and it is almost an inside joke between us by the middle of the year. I also use student names or teacher names in the problems whenever possible and friendly fractions for easy modeling and visualizing.
Multiplying Fractions Introductory Word Problem: While shopping at a bakery, Ms. Findley purchased 1/2 of a pound of chocolate fudge. After dinner that night, she ate 1/4 of the chocolate fudge that she bought. How much of a pound of fudge did Ms. Findley eat?
Dividing Fractions Introductory Word Problem: Jamal’s mother made 1/3 of a pound of his favorite fudge, peanut butter caramel fudge. She divided the fudge into 4 equal containers. How much fudge did she put in each container?
How I Use the Introductory Word Problems: I write the problem on an anchor chart, gather my students at our mini-lesson area (around a large rug) and follow these steps:
- Read the word problem once (myself or a student).
- Read it again, if needed (based on the level of my students)
- Have the students retell the problem with partners in their own words.
- Have a few students share their retellings with the class.
- Focus on what the question is asking by writing the question in a sentence.
- Use models to demonstrate the situation in the problem (since these are new concepts for them, this part is heavily teacher driven, but typically I prefer student driven). The students practice with models as well. This can be paper folding models, visual representation drawings, or both — my favorite is both in the beginning.
- Translate the visual into a labeled equation (read more about labeled equations here) and answer the question.
- Discuss the answer and determine if it makes sense.
- Practice similar/same situations but with different numbers.
Reminder: I teach both of these concepts separately for about a week each.
Fraction Word Problems: Do I Divide or Multiply?
Once my students have “mastered” multiplying and dividing fractions and have seen each in a variety of contexts (through the word problems I use), they are ready to tackle both and see the connections and differences between the two. To do this, I use this anchor chart to show some of the situations and contexts that require multiplication and division of fractions. We discuss each one and how it relates back to multiplication and division.
My students then use this chart (and the printable version I provide – available for free in the next section) to support them as they solve word problems. They read the word problem and then check the chart for a matching situation.
Since it is impossible to expose students to every type of situation and context, the blurb at the end of the chart is key. The students really need to make a habit of checking to see if their answers make sense. This will help them if they choose the wrong operation.
FREE Multiplying and Dividing Fractions Word Problem Sort
In addition to the above anchor chart, we also do a word problem sort. The word problems were specifically written to match the contexts from the chart so this is a great extension of the lesson involving the anchor chart. The students read the word problems, check the chart, and then sort them accordingly. I do this activity with partners or small groups (pulling a group to work with me that may struggle based on previous assessments using exit slips), but this could also be done as a math center activity.
Click here or on the image above to download the multiplying and dividing fractions word problem sort and a printable version of the anchor chart.
My Go-To Resource for Teaching Multiplying and Dividing Fractions
The anchor chart and the sort are used after I have introduced and we have practiced both operations in isolation. I do this by using resources from my Multiplying and Dividing Fractions resource.
This resource includes:
- Teaching Posters
- Practice Printables
- Constructed Response Tasks
- and more!
Click here to purchase the Multiplying and Dividing Fractions Resource from my TPT store.
Want More Hands-On Math Activities and Centers?
More Helpful Word Problem Posts, Freebies, and Resources
Teaching Word Problems without Key Words (And What to Teach Instead)
Word Problem of the Day : FREE Starter Packs
8 Ways to Help Students Be Successful with Word Problems
Show the LOVE with Word Problems: Helping Students Answer Word Problems
Teaching Students How To Justify Answers in Math
Solving Multi-Part Word Problems
FREE Word Problem Graphic Organizers/Mats
5th Grade Word Problem of the Day TpT Resource
More Fraction Resources, Freebies, and Blog Posts:
Free Fraction Mats: I use these free downloadable fraction mats to support my students further as they add and subtract fractions with unlike denominators.
Free Fraction Pacing Guide: This blog post shares an “I Can” checklist for students and shares how I pace my 5th grade fraction skills.
Free Fraction Fun with Snacks Printables: If you can use food in your instruction, your students will love reviewing fraction operations (multiplication and division) using Twizzlers, skittles, and brownies.
4 Ways to Teach Students to Make Common Denominators: Read about the four ways I teach my students to find common denominators and grab a free printable.
Free Fraction Activities: Grab some super easy to prep fraction activities on this post.
Fraction Word Problems With Interactive Exercises
Fraction Word Problems With Interactive ExercisesExample 1: If it takes 5/6 yards of fabric to make a dress, then how many yards will it take to make 8 dresses?
Analysis: To solve this problem, we will convert the whole number to an improper fraction. Then we will multiply the two fractions.
Solution:
Answer: It will take 6 and 2/3 yards of fabric to make 8 dresses.
Example 2: Renee had a box of cupcakes, of which she gave 1/2 to her friend Juan. Juan gave 3/4 of his share to his friend Elena. What fractional part of the original box of cupcakes did Elena get?
Analysis: To solve this problem, we will multiply these two fractions.
Solution:
Answer: Elena got 3/8 of the original box of cupcakes.
Example 3: Nina’s math classroom is 6 and 4/5 meters long and 1 and 3/8 meters wide. What is the area of the classroom?
Analysis: To solve this problem, we will multiply these mixed numbers. But first we must convert each mixed number to an improper fraction.
Solution:
Answer: The area of the classroom is 9 and 7/20 square meters.
Example 4: A chocolate bar is 3/4 of an inch long. If it is divided into pieces that are 3/8 of an inch long, then how many pieces is that?
Analysis: To solve this problem, we will divide the first fraction by the second.
Solution:
Answer: 2 pieces
Example 5: An electrician has a piece of wire that is 4 and 3/8 centimeters long. She divides the wire into pieces that are 1 and 2/3 centimeters long. How many pieces does she have?
Analysis: To solve this problem, we will divide the first mixed number by the second.
Solution:
Answer: The electrician has 2 and 5/8 pieces of wire.
Example 6: A warehouse has 1 and 3/10 meters of tape. If they divide the tape onto pieces that are 5/8 meters long, then how many pieces will they have?
Analysis: To solve this problem, we will divide the first mixed number by the second. First, we will convert each mixed number into an improper fraction.
Solution:
Answer: The warehouse will have 2 and 2/25 pieces of tape.
Summary: In this lesson we learned how to solve word problems involving multiplication and division of fractions and mixed numbers.
Exercises
Directions: Subtract the mixed numbers in each exercise below. Be sure to simplify your result, if necessary. Click once in an ANSWER BOX and type in your answer; then click ENTER. After you click ENTER, a message will appear in the RESULTS BOX to indicate whether your answer is correct or incorrect. To start over, click CLEAR.
Note: To write the mixed number four and two-thirds, enter 4, a space, and then 2/3 into the form.
| 1. | One batch of cookies contains 1 and 3/4 cups of melted chocolate. How many cups of melted chocolate are needed to make 8 batches of cookies? |
| 2. | Todd drank 5/8 of a 24-ounce can of juice. Lila drank 1/3 as much juice as Todd did. How many ounces did Lila drink? |
| 3. | A rectangular area rug has a length of 3 and 2/3 feet and a width of 2 and 3/4 feet. What is the area of the rug? |
| 4. | Janet has 5 and 3/4 centimeters of licorice. She divides the licorice into pieces that are 1 and 7/8 centimeters long. How many pieces of licorice will she have? |
| 5. | A piece of wood is 15 feet long. How many 3/4-foot sections can be cut from it? |
Sign Up For Our FREE Newsletter!
Sign Up For Our FREE Newsletter!
Percentage Word Problems
This Word Problems Worksheet will produce problems that focus on division with fractions.
You have the option to select the range of denominators, as well as the types of fractions displayed.
Denominator Range
(2 — 10)
(11 — 20)
(2 — 20)
Types of Fractions
Proper Fractions
Improper Fractions
Mixed Fractions
Language for the Word Problems Worksheet
| English | German | Albanian |
| Spanish | Swedish | Italian |
| French | Turkish | Polish |
| Norwegian |
Memo Line for the Word Problems Worksheet
You may enter a message or special instruction that will appear on the bottom left corner
of the Word Problems Worksheet.
Word Problems Worksheet Answer Page
Include Word Problems Worksheet Answer Page
Now you are ready to create your Word Problems Worksheet by pressing the Create Button.
If You Experience Display Problems with Your Math Worksheet
 |
|
 |
|
 |
|
 |
|
 |
Click here for More Word Problems Worksheets
| Dividing fractions word problems | |
|---|---|
 |
|
| Description | |
| Exercise Name: | Dividing fractions word problems |
| Math Missions: | 6th grade (U.S.) Math Mission, 7th grade (U.S.) Math Mission, Arithmetic essentials Math Mission, Algebra I Math Mission |
| Types of Problems: | 3 |
The Dividing fractions word problems exercise appears under the 6th grade (U.S.) Math Mission, 7th grade (U.S.) Math Mission, Arithmetic essentials Math Mission and Algebra I Math Mission. This exercise has practice on word problems that specifically work with operations on fractions.
Types of Problems
There are three types of problems in this exercise:
- Division of fractions problem: This problem describes a word problem in which the solution can be found by dividing the two fraction provided. The user is asked to find the correct solution and writes it in the box.
Division of fractions problem
- Other order of fractions problem: This problem describes a word problem in which the solution can be found by dividing the two fraction provided but the order of division is backwards to the presentation of the fractions. The user is asked to find the correct solution and writes it in the box.
Other order of fractions problem
- Meaning of expression: This problem describes a situation and provides an expression that divides two fractions. Users are asked to select the option that best represents the meaning of the division problem presented.
Meaning of expression
Strategies
This exercise is medium to get accuracy badges because the first two types of problems can be subtle. The speed badges are medium because of the care needed to distinguish between the those first two types of problems.
- The answer to Meaning of expression can often be clear with without reading the division problem, as the situation described can lead to the answer by considering what someone would be interested in for the given problem.
- The Other order of fractions problems often concerned a container of objects with an almost ratio feel. Research has not continued to verify that this is always the case, but it should be completed soon.
Real-life Applications
- Fractions, decimals, and percents are used in many sports such as basketball to determine how many field goals the player has made over how many they attempted.
- Fractions are used in real life in many different ways, but they are most commonly used in the cooking, construction and science industries.
The exponential growth models describe the population of the indicated country, A, in millions, t years after 2006.
CanadaA=33.1e0.009tUgandaA=28.2e0.034tleft. begin{array} { l } Canadaquad { A = 33.1 e ^ { 0.009 t } } \ Ugandaquad{ A = 28.2 e ^ { 0.034 t } } end{array} right.
Use this information to determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. In 2006, Canada’s population exceeded Uganda’s by 4.9 million.