Аналог поиска решения в excel

Подбор слагаемых для нужной суммы

Не очень частый, но и не экзотический случай. На моих тренингах такой вопрос задавали не один и не два раза  Суть в том, что мы имеем конечный набор каких-то чисел, из которых надо выбрать те, что дадут в сумме заданное значение.

В реальной жизни эта задача может выглядеть по-разному.

• Например, мы выгрузили из интернет-банка все платежи, которые поступили на наш счет за последний месяц. Один из клиентов разбивает сумму своего платежа на несколько отдельных счетов и платит частями. Мы знаем общую сумму оплаты и количество счетов, но не знаем их сумм. Надо подобрать те суммы в истории платежей, которые дадут в общем заданное значение.
• У нас есть несколько рулонов стали (линолеума, бумаги…), из которых надо подобрать под заказ те, что дадут заданную длину.
• Блэкджек или в народе «очко». Надо набрать карты суммарной стоимостью максимально близкой к 21 баллу, но не превысить этот порог.

В некоторых случаях может быть известна разрешенная погрешность допуска. Она может быть как нулевой (в случае подбора счетов), так и ненулевой (в случае подбора рулонов), или ограниченной снизу или сверху (в случае блэкджека).

Давайте рассмотрим несколько способов решения такой задачи в Excel.

Способ 1. Надстройка Поиск решения (Solver)

Эта надстройка входит в стандартный набор пакета Microsoft Office вместе с Excel и предназначена, в общем случае, для решения линейных и нелинейных задач оптимизации при наличии списка ограничений. Чтобы ее подключить, необходимо:

• в Excel 2007 и новее зайти Файл — Параметры Excel — Надстройки — Перейти (File — Excel Options — Add-ins — Go)
• в Excel 2003 и старше — открыть меню Сервис — Надстройки (Tools — Add-ins)

и установить соответствующий флажок. Тогда на вкладке или в меню Данные (Data) появится нужная нам команда.

Чтобы использовать надстройку Поиск решения для нашей задачи необходимо будет слегка модернизировать наш пример, добавив к списку подбираемых сумм несколько вспомогательных ячеек и формул:

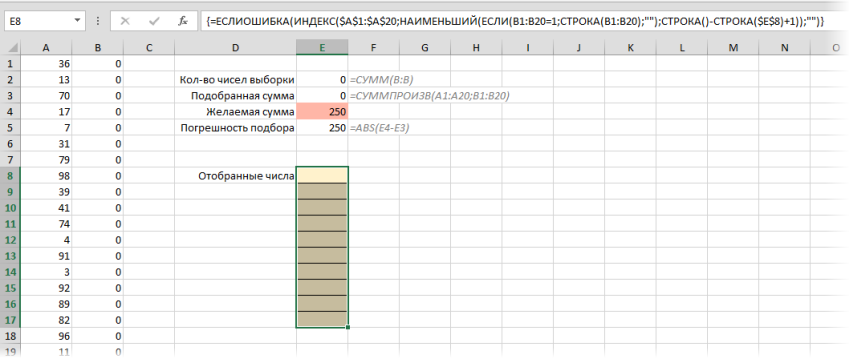
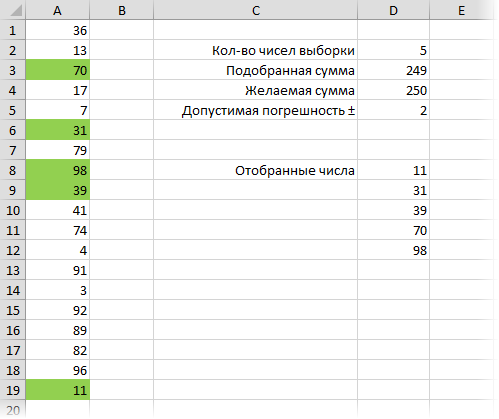
• Диапазон A1:A20 содержит наши числа, из которых мы будем выбирать нужные, чтобы «вписаться» в заданную сумму.
• Диапазон В1:B20 будет своего рода набором переключателей, т.е. будет содержать нули или единички, показывая, отбираем мы данное число в выборку или нет.
• В ячейке E2 стоит обычная автосумма всех единичек по столбцу B, подсчитывающая кол-во выбранных чисел.
• В ячейке E3 с помощью функции СУММПРОИЗВ (SUMPRODUCT) считается сумма попарных произведений ячеек из столбцов А и B (то есть A1*B1+A2*B2+A3*B3+…). Фактически, здесь подсчитывается сумма чисел из столбца А, отобранных единичками из столбца В.
• В розовую ячейку E4 пользователь вводит желаемую сумму для подбора.
• В ячейке E5 вычисляется абсолютное по модулю значение погрешности подбора с целью ее будущей минимизации.
• Все желтых ячейках Е8:E17 хотелось бы получить список отобранных чисел, т.е. тех чисел из столбца А, напротив которых в столбце В есть единички. Для этого необходимо выделить сразу все (!) желтые ячейки и в них ввести вот такую формулу массива:

=ЕСЛИОШИБКА(ИНДЕКС($A$1:$A$20;НАИМЕНЬШИЙ(ЕСЛИ(B1:B20=1;СТРОКА(B1:B20);»»);СТРОКА()-СТРОКА($E$8)+1));»»)

=IFERROR(INDEX($A$1:$A$20;SMALL(IF(B1:B20=1;ROW(B1:B20);»»);ROW()-ROW($E$8)+1));»»)

После ввода формулы ее необходимо ввести не как обычную формулу, а как формулу массива, т.е. нажать не Enter, а Ctrl+Shift+Enter. Похожая формула используется в примере о ВПР, выдающей сразу все найденные значения (а не только первое).



Теперь перейдем на вкладку (или в меню) Данные и запустим инструмент Поиск решения (Data — Solver):

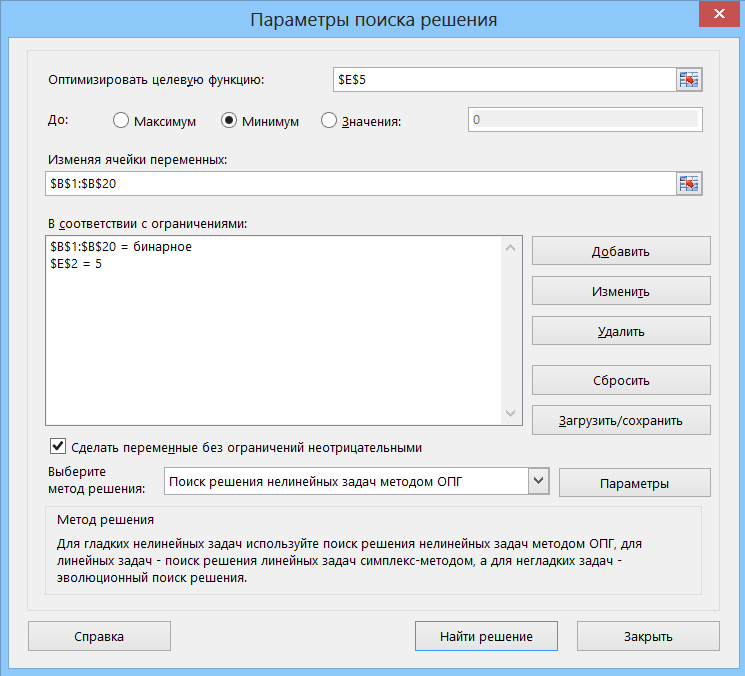
В открывшемся окне необходимо:

• Задать как целевую функцию (Target Cell) — ячейку вычисления погрешности подбора E5. Чуть ниже выбрать опцию — Минимум, т.к. мы хотим подобрать числа под заданную сумму с минимальной (а лучше даже нулевой) погрешностью.
• В качестве изменяемых ячеек переменных (Changing cells) задать диапазон столбца переключателей B1:B20.
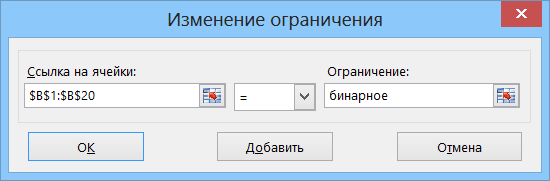
• С помощью кнопки Добавить (Add) создать дополнительное условие на то, что ячейки диапазона B1:B20 должны быть бинарными (т.е. содержать только 0 или 1):

  

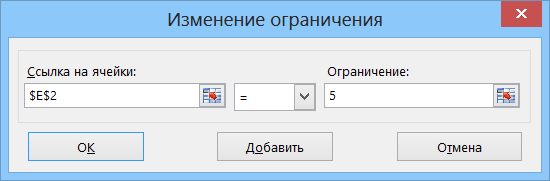
• С помощью той же кнопки, при необходимости, создать ограничение на количество чисел в выборке. Например, если мы знаем, что сумма была разбита на 5 счетов, то:

  

После ввода всех параметров и ограничений запускаем процесс подбора кнопкой Найти решение (Solve). Процесс подбора занимает от нескольких секунд до нескольких минут (в тяжелых случаях) и заканчивается появлением следующего окна:

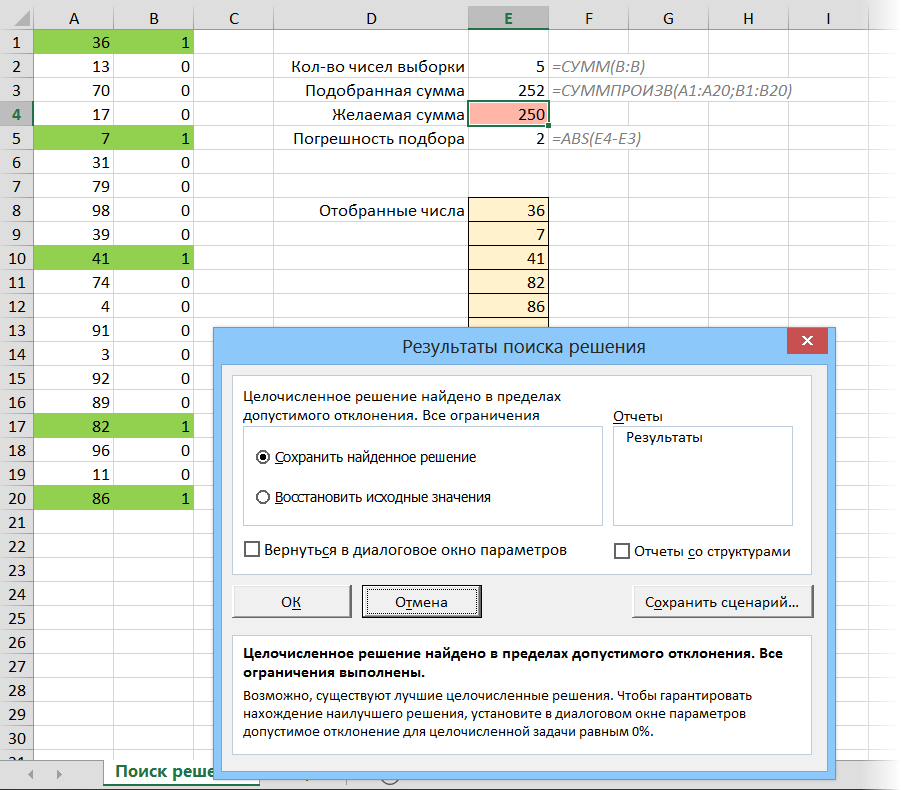
Теперь можно либо оставить найденное решение подбора (Сохранить найденное решение), либо откатиться к прежним значениям (Восстановить исходные значения).

Необходимо отметить, что для такого класса задач существует не одно, а целое множество решений, особенно, если не приравнивать жестко погрешность к нулю. Поэтому запуск Поиска решения с разными начальными данными (т.е. разными комбинациями 0 и 1 в столбце В) может приводить к разным наборам чисел в выборках в пределах заданных ограничений. Так что имеет смысл прогнать эту процедуру несколько раз, произвольно изменяя переключатели в столбце В.

Найденные комбинации можно сохранять виде сценариев (кнопка Сохранить сценарий), чтобы вернуться к нем позднее с помощью команды Данные — Анализ «что-если» — Диспетчер сценариев (Data — What-If Analysis — Scenario Manager):

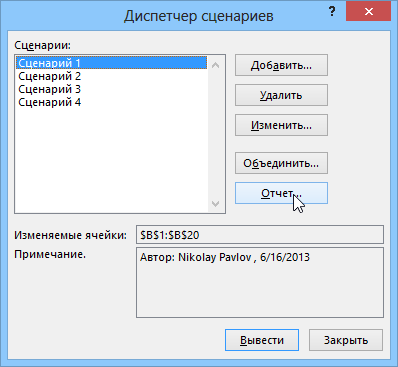
И весьма удобно будет вывести все найденные решения, сохраненные в виде сценариев, в одной сравнительной таблице с помощью кнопки Отчет (Summary):

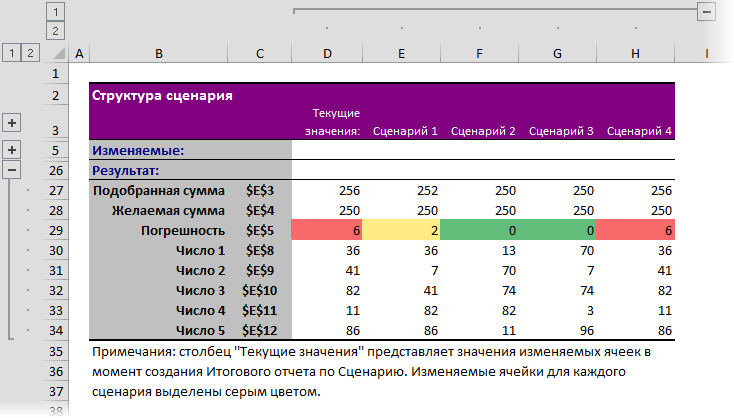
Способ 2. Макрос подбора

В этом способе всю работу делает макрос, который тупо перебирает случайные комбинации чисел, пока не наткнется на нужную сумму в пределах разрешенной погрешности. Добавлять столбец с нулями и единичками и формулы в этом случае не нужно.

Для использования макроса нажмите сочетание Alt+F11, в открывшемся окне редактора Visual Basic вставьте новый модуль через меню Insert — Module и скопируйте туда этот код:

Sub Combinator()
    Dim Data() As Variant, Selected() As Variant
    Dim goal As Double, sel_count As Integer, prec As Double
    Const LIMIT = 1000000
    
    prec = Range("D5").Value
    sel_count = Range("D2").Value
    goal = Range("D4").Value
    
    Set OutRange = Range("D8")
    Set InputRange = Range("A1", Range("A1").End(xlDown))
    input_count = InputRange.Cells.Count
    Data = InputRange.Value
    ReDim Selected(1 To sel_count) As Variant

NewTry:
    For j = 1 To sel_count
Start:
        RandomIndex = Int(Rnd * input_count + 1)
        RandomValue = Data(RandomIndex, 1)
        
        'начиная со второго элемента дополнительно проверяем, чтобы такой уже не был выбран
        If j > 1 Then
            For k = 1 To j - 1
                If Selected(k) = RandomValue Then GoTo Start
            Next k
        End If
        Selected(j) = RandomValue
    Next j
    
    If Abs(WorksheetFunction.Sum(Selected) - goal) <= prec Then
        Range("D3").Value = WorksheetFunction.Sum(Selected)
        MsgBox "Подбор завершен. Необходимая точность достигнута."
        Range(OutRange, OutRange.End(xlDown)).ClearContents
        OutRange.Resize(sel_count, 1).Value = Application.Transpose(Selected)
        Exit Sub
    Else
        iterations = iterations + 1
        If iterations > LIMIT Then
            MsgBox "Достигнут лимит попыток. Решение не найдено."
            Exit Sub
        Else
            GoTo NewTry
        End If
    End If
End Sub

Аналогично первому способу, запуская макрос несколько раз, можно получать разные наборы подходящих чисел.

P.S. Сейчас набегут энтузиасты с мехмата МГУ с криками «Тупой перебор — это неэстетично!» Да, я в курсе, что прямой перебор вариантов — это не самый оптимальный способ поиска. Да, существует много умных алгоритмов поиска решения таких задач, которые сокращают время поиска и находят нужную комбинацию заметно быстрее. Могу даже рассказать про парочку. Но мне на данном этапе существующей скорости «тупого перебора» вполне достаточно — обработка массива из 1000 ячеек идет меньше секунды. Готов подождать

Ссылки по теме

• Оптимизация бизнес-модели с помощью надстройки Поиск решения (Solver)
• Что такое макросы, куда и как вставлять код макросов на VBA

Макрос — аналог инструмента «Поиск решения»

cerber412 Дата: Вторник, 12.06.2018, 16:46 | Сообщение № 1 Группа: Проверенные Ранг: Форумчанин Сообщений: 131 Репутация: 0 ± Замечаний: 0% ± Excel 2013 Всем привет. Подскажите — как решить задачу при помощи макроса. Обычно для такого типа задач применяют инструмент «Поиск решения». Как найти коэффициент в ячейке E2, без помощи инструмента «Поиск решения» — одним лишь макросом ? Тут нюанс — нельзя подключать вообще никаких надстроек навроде Solver Add-in К сообщению приложен файл: primer1.xls (26.5 Kb)   Ответить

StoTisteg Дата: Вторник, 12.06.2018, 16:53 | Сообщение № 2 Группа: Авторы Ранг: Старожил Сообщений: 1161 Репутация: 103 ± Замечаний: 0% ± Excel 2010 cerber412, а что мешает взять да и записать тот же поиск решения макрорекордером и использовать полученный код? Интуитивно понятный код — это когда интуитивно понятно, что это код.   Ответить

cerber412 Дата: Вторник, 12.06.2018, 17:00 | Сообщение № 3 Группа: Проверенные Ранг: Форумчанин Сообщений: 131 Репутация: 0 ± Замечаний: 0% ± Excel 2013 StoTisteg, нет — для этого нужно подключать надстройку (Solver Add-in кажется). А делать этого нельзя — я же написал. Поэтому я и задаю вопрос о том как это сделать макросом.   Ответить

RAN Дата: Вторник, 12.06.2018, 18:39 | Сообщение № 4 Группа: Друзья Ранг: Экселист Сообщений: 5645 cerber412, элементарно! Напишите на VBA аналог надстройки Solver. Быть или не быть, вот в чем загвоздка!   Ответить

nilem Дата: Вторник, 12.06.2018, 19:15 | Сообщение № 5 Группа: Авторы Ранг: Старожил Сообщений: 1612 Репутация: 563 ± Замечаний: 0% ± Excel 2013, 2016 cerber412, привет Имеется в виду, что сумма премий известна. Надо только подобрать коэф-нт. Так? Яндекс.Деньги 4100159601573   Ответить

cerber412 Дата: Вторник, 12.06.2018, 20:03 | Сообщение № 6 Группа: Проверенные Ранг: Форумчанин Сообщений: 131 Репутация: 0 ± Замечаний: 0% ± Excel 2013 Имеется в виду, что сумма премий известна. Надо только подобрать коэф-нт. Так? Да   Ответить

nilem Дата: Среда, 13.06.2018, 06:39 | Сообщение № 7 Группа: Авторы Ранг: Старожил Сообщений: 1612 Репутация: 563 ± Замечаний: 0% ± Excel 2013, 2016 Как-то вот так: [vba] Код Sub ttt() Dim smOkl#, smPrem#, kf# smPrem = Application.InputBox(«Введите сумму премий», , 1000, , , , , 2) If smPrem = 0 Then Exit Sub With Range(«B2», Cells(Rows.Count, 2).End(xlUp))     smOkl = WorksheetFunction.Sum(.Value)     kf = smPrem / smOkl     .Offset(, 1).FormulaR1C1 = «=R2C5*RC[-1]» End With Range(«E2»).Value = kf End Sub [/vba] Яндекс.Деньги 4100159601573   Ответить

cerber412 Дата: Среда, 13.06.2018, 10:08 | Сообщение № 8 Группа: Проверенные Ранг: Форумчанин Сообщений: 131 Репутация: 0 ± Замечаний: 0% ± Excel 2013 nilem, ясно. Спасибо.   Ответить

   DmSk

05.04.11 — 12:26

Ищу аналог «поиска решений» EXEL на 1С 7.7. Есть исходники на си, но переписывать долго.

   1Сергей

1 — 05.04.11 — 12:27

йоксель?

   1Сергей

2 — 05.04.11 — 12:27

хотя, нет. Что за «поиск решений» я хз

   skunk

3 — 05.04.11 — 12:30

   МихаилМ

4 — 05.04.11 — 12:31

   DrZombi

5 — 05.04.11 — 12:32

(3)Еще их кличут «Анализ данных…» (Сервис -> «Анализ данных…»)…
(0)Так то это все рассчитываемо и без этих мастеров.

   Оболтус

6 — 05.04.11 — 12:32

Excel тогда уж…

   1Сергей

7 — 05.04.11 — 12:35

ни у кого не возник китайский вопрос?

   DmSk

8 — 05.04.11 — 12:43

(4) сколько примерно времени нужно чтобы в 1-го это сделать ?

   DmSk

9 — 05.04.11 — 12:44

(4) задача неясно поставлена, нужно именно прикладное решение, потому самому пыхтеть придется

   DmSk

10 — 05.04.11 — 12:45

   Denp

11 — 05.04.11 — 12:52

   Ахиллес

12 — 05.04.11 — 12:58

(11) Расшифруй. Что значит «пишите на 1с и выносите в ВК». Давно у нас в 1С компилятор встроен?

   Denp

13 — 05.04.11 — 12:59

(12) пардон. конечно, имел в виду в (11) «пишите на с++ и выносите в ВК»

   DmSk

14 — 05.04.11 — 13:06

   DmSk

15 — 05.04.11 — 13:06

написано специально для 1С

   Denp

16 — 05.04.11 — 13:07

(15) а какая задача исходно стоит? что надо оптимизировать?

   DmSk

17 — 05.04.11 — 13:13

(16) расчет состава рецепта комбикорма,
из условий,
1. что  полученное качество будет не хуже госта
2. процент вхождения каждого компонента состава в пределах от и до
3. Компоненты есть на складе, если компонента нет то есть список взаимозаменяемости компонентов

   dk

18 — 05.04.11 — 13:14

а по OLE в Excel запускать не вариант?

   Denp

19 — 05.04.11 — 13:14

(17) качество — это содержание белка?
взаимозаменяемость по условию, а не произвольная, сильно усложняет задачу

   DmSk

20 — 05.04.11 — 13:15

(18) плохой вариант

   DmSk

21 — 05.04.11 — 13:20

(19) каждый компонент (отруби и т.д.) имеет свой показетель питательной ценности, это обменная энергия, сырой протеин, клетчатка, Лизин, и т.д.
вот  в сумме  эти компоненты должны давать корм с пит ценностью, для протеина от 15 до 17% , для клетчатки до 9% и т.д.
с взаимозаменяемостью, задача вообще непонятно как стоит, ведь несколько компонентов можно заменить на один и тот же, пока буду опираться на практику, то есть на примеры решений технолога,а потом выведу метод . возможно комбинатоника пригодится

   DmSk

22 — 05.04.11 — 13:22

кроме того в формулу оптимизации цена стремится к минимуму, нужно предусмотреть чтобы можно было приготовить корм из остатков, чтобы свести конечный остаток к минимуму. так что задача классная !

   Denp

23 — 05.04.11 — 13:22

(21) а критерий оптимизации какой тогда? Стоиомсть?

   Fragster

24 — 05.04.11 — 13:24

в 1се есть какой-то анализ данных

   DmSk

25 — 05.04.11 — 13:28

(23) взависимости от выбора решения
если не нужно остатки подбивать, то стоимость -> МИн,
если нужно остатки подбить, то остатки на складе — >Мин

   DmSk

26 — 07.04.11 — 06:57

В общем компонента тупит(не находит решение), там где эксель справляется

   ASV

27 — 07.04.11 — 07:11

(26) исходные данные выложи

   DmSk

28 — 07.04.11 — 08:12

   DmSk

29 — 07.04.11 — 10:34

вот слил исходники с откомпиленным exe, тоже реализация метода, по примеру находит решение без проблем
http://hddfiles.ru/download/4915/

   DmSk

30 — 07.04.11 — 10:55

Вообщем, я так понял компонента использует метод Гомори,
ошибка в разных программах одна и таже «невозможно найти начальный базис», другими методами задача решается

   Кирпич

31 — 07.04.11 — 13:06

(0) Да тупого перебора хватит должно хватить. Даже если на 1С реализовать.

   Попытка1С

32 — 07.04.11 — 13:09

А я прям из 1с заюзал екселевский механизм поиска решений.

   ado

33 — 07.04.11 — 13:17

(8) Пара часов, если соответствующей математикой владеешь.

   Denp

34 — 07.04.11 — 13:18

(31) бугага

   Кирпич

35 — 07.04.11 — 13:38

(34) Чо ты ржешь?

   Denp

36 — 07.04.11 — 13:44

(35) какой перебор при нецелочисленной оптимизации нафих?
какая скорость перебора при нескольких переменных?
чо за фантазии?

   Кирпич

37 — 07.04.11 — 13:56

(36) Да ладна. Ничо там страшного нету.

   Eugeneer

38 — 07.04.11 — 13:57

Если бы 1С сделал свой эксель он бы быстро набрал бы популярность. Я бы точно купил.

   Denp

39 — 07.04.11 — 14:12

(37) теоретик?

   Кирпич

40 — 07.04.11 — 14:14

(39) Хуже

   DmSk

41 — 08.04.11 — 05:59

(39)(40)
если даже взять целочисленно дял каждоко компонента от 0..100, и этих компонентов будет 5,
то получим 100*100*100*100*100 = 10 000 000 000 комбинаций,
если ещё проверять ограничения их штук 8, взависимости от типа смеси.
представим что 1С за 1 секунду переберет 1000 варинатов (что врядли), получи  10 000 000 секунд, получим 115 дней

   Denp

42 — 08.04.11 — 06:39

   Кирпич

43 — 08.04.11 — 08:23

(41) Ну там можно не всё перебирать, а только то, что нужно. Автор объяснил бы поконкретнее, что именно нужно.

   Denp

44 — 08.04.11 — 08:24

(43) «можно не всё перебирать, а только то, что нужно»
гы) конгениально!) только это уже будет не «тупой перебор», как ты предлагал

   Кирпич

45 — 08.04.11 — 08:26

(44) Это будет тупой перебор того, что нужно. И не обещал я ничего. Я предположение высказал.

   DmSk

46 — 14.04.11 — 13:24

ну вот прошло 9 дней с момента поиска до реализации,
как ни странно компонента для 1С с http://www.openproj.ru/75/
не всё решала, ходя делфовый исходник в (написал прогу на дельфи) тестовые примеры выполняла. получилось, что
исходник на дельфи работает, а из компоненты не хочет.
Поскольку исходника компоненты небыло, пришлось самому писать, шаблон компоненты взял отсюда с мисты спасибо огромное всё довольно просто оказалось в создании компонент.
Далее из компоненты сделал лог, который показывал результаты, оказалось, что результаты сверхмалых величин разные (вот тут описал проблему В компоненте для 1С 7.7.на Delphi 6 получаются другие значение, чем на самом Del, перевел коэффициент погрешности в с -13 степени на -10 и всё пошло !!! Из-за того, что автор компоненты не учёл этого, пришлось изучить методику создания компоненты, + вспомнить математику, спасибо автору !

чуть позже выложу исходники , для совместимости с предыдущей компонентой все названия методов оставл прежние

Одной из самых интересных функций в программе Microsoft Excel является Поиск решения. Вместе с тем, следует отметить, что данный инструмент нельзя отнести к самым популярным среди пользователей в данном приложении. А зря. Ведь эта функция, используя исходные данные, путем перебора, находит наиболее оптимальное решение из всех имеющихся. Давайте выясним, как использовать функцию Поиск решения в программе Microsoft Excel.

Включение функции

Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.

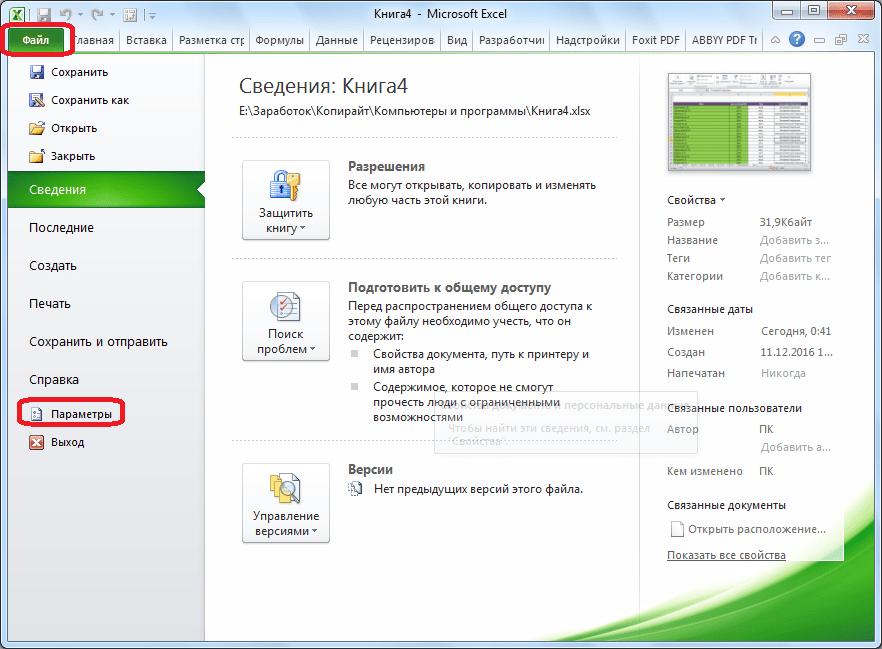
Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».

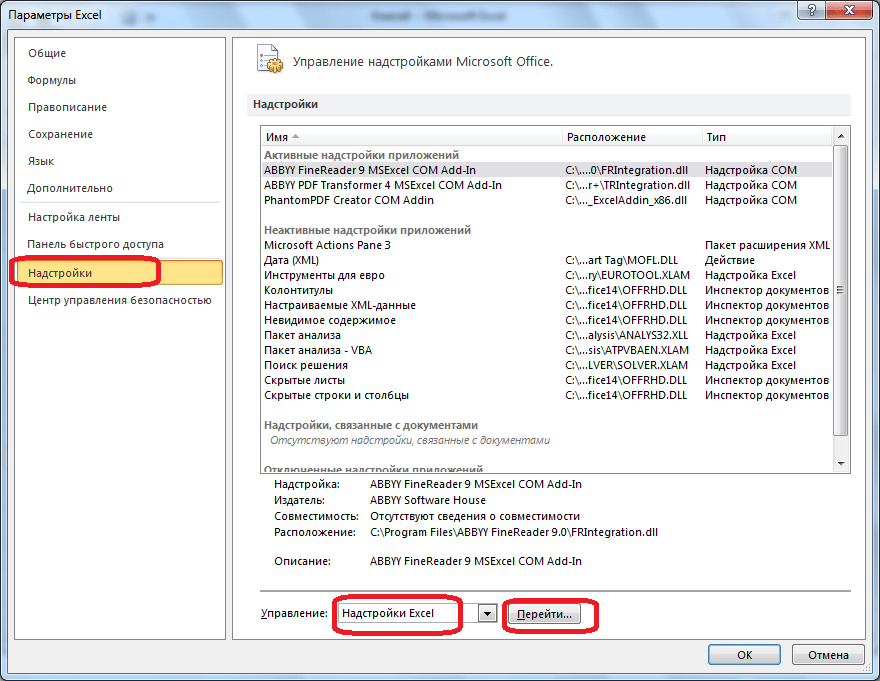
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».

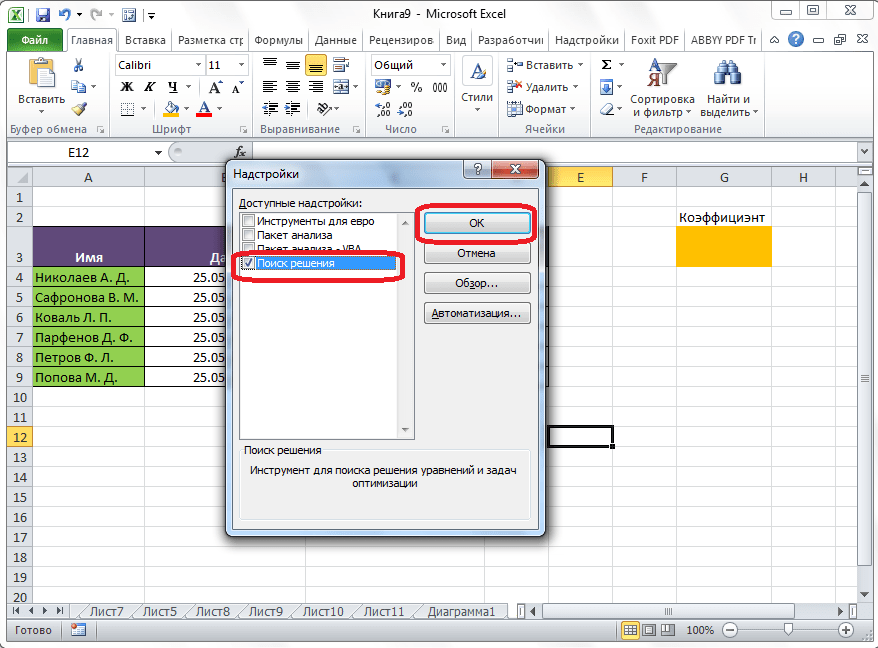
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».

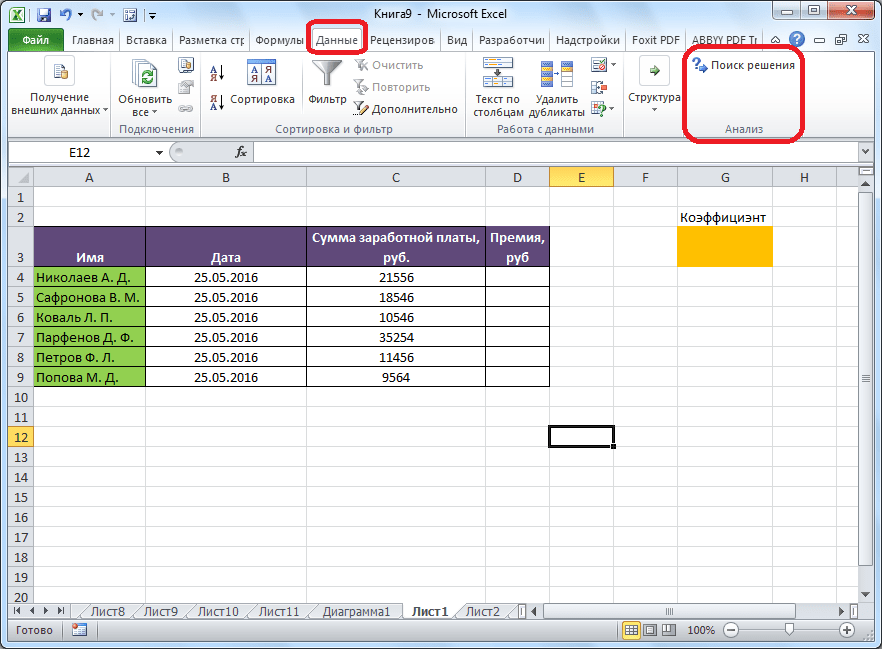
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».

Подготовка таблицы

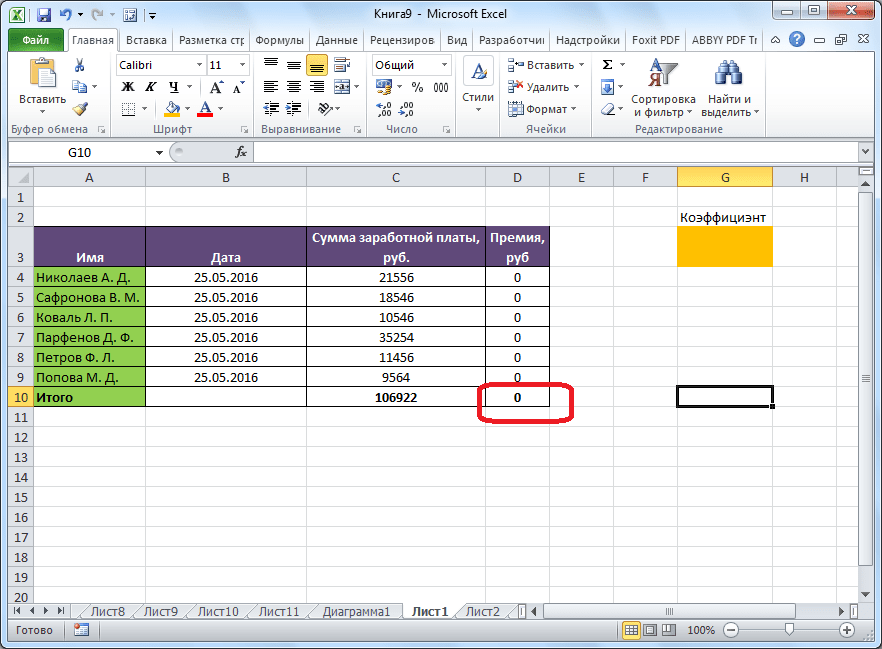
Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

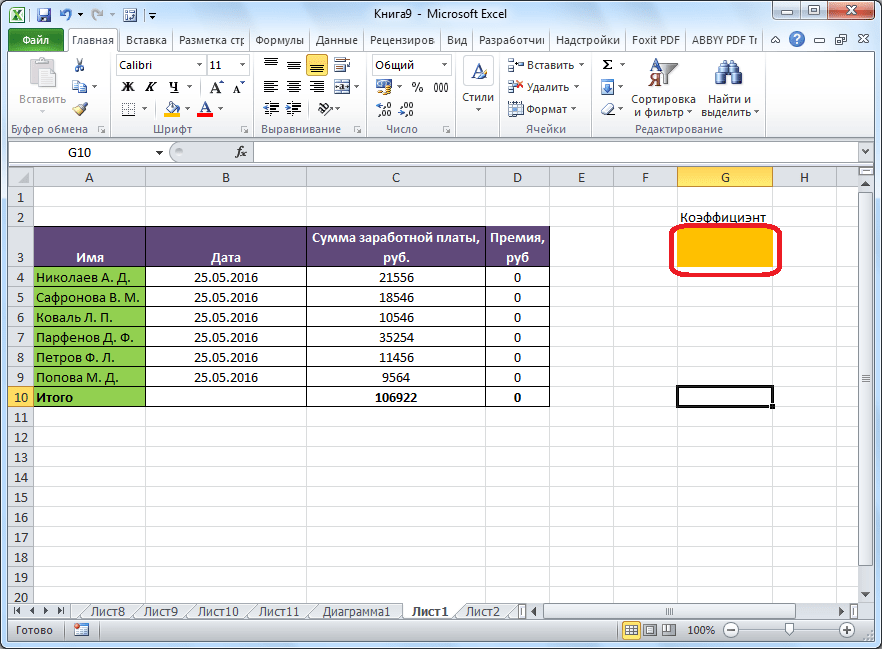
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

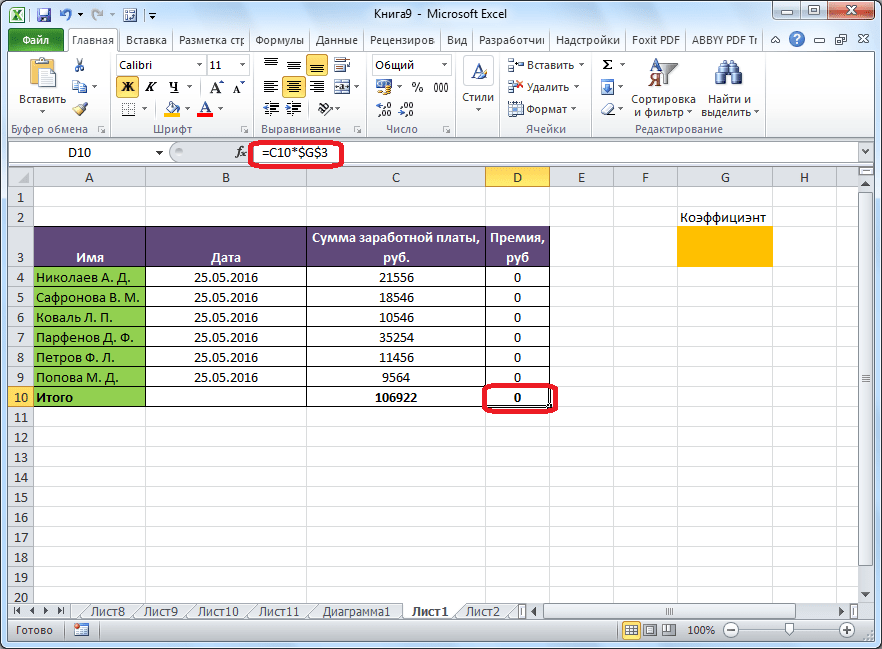
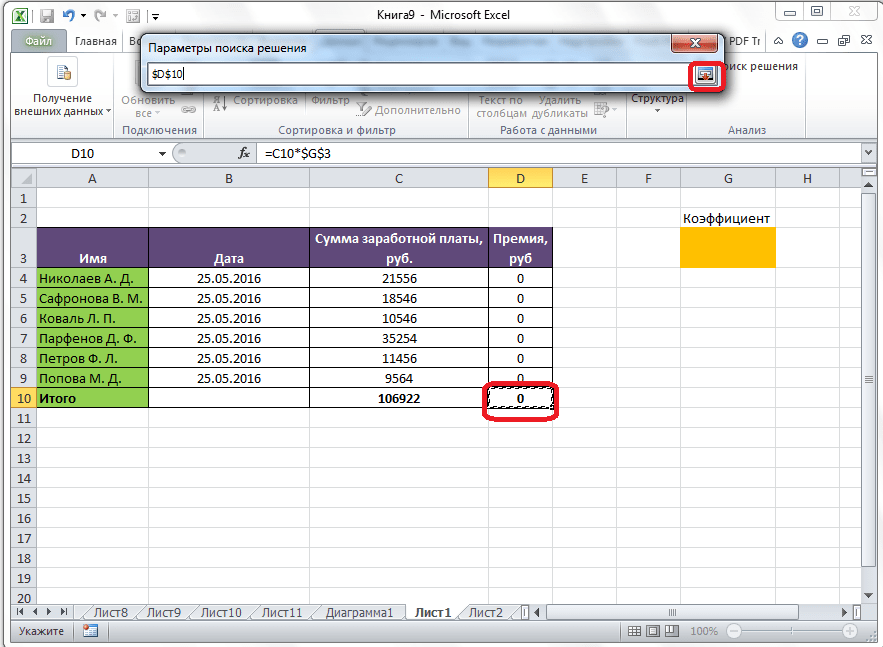
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

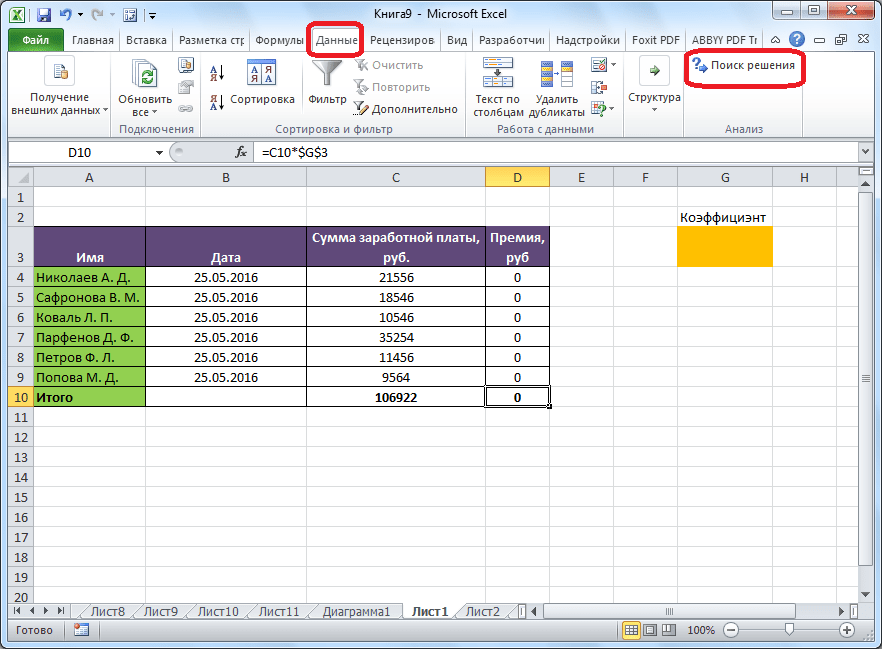
Запуск инструмента Поиск решения

После того, как таблица подготовлена, находясь во вкладке «Данные», жмем на кнопку «Поиск решения», которая расположена на ленте в блоке инструментов «Анализ».

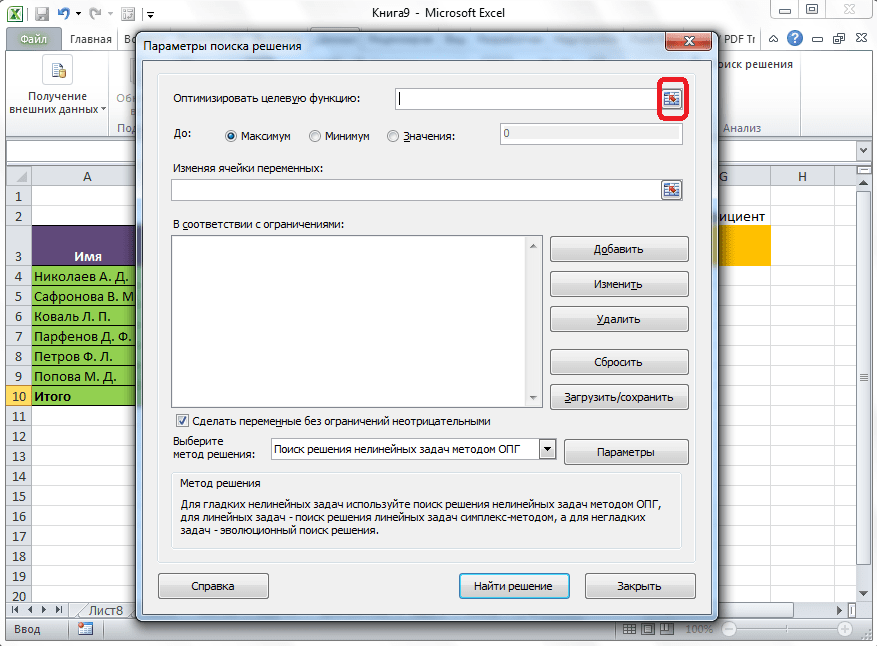
Открывается окно параметров, в которое нужно внести данные. В поле «Оптимизировать целевую функцию» нужно ввести адрес целевой ячейки, где будет располагаться общая сумма премии для всех работников. Это можно сделать либо пропечатав координаты вручную, либо кликнув на кнопку, расположенную слева от поля введения данных.

После этого, окно параметров свернется, а вы сможете выделить нужную ячейку таблицы. Затем, требуется опять нажать по той же кнопке слева от формы с введенными данными, чтобы развернуть окно параметров снова.

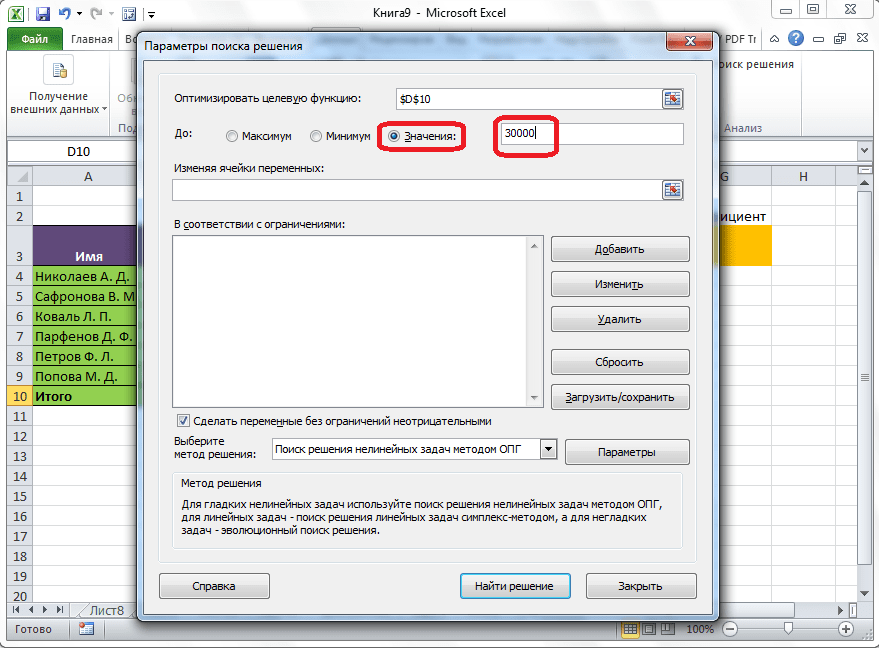
Под окном с адресом целевой ячейки, нужно установить параметры значений, которые будут находиться в ней. Это может быть максимум, минимум, или конкретное значение. В нашем случае, это будет последний вариант. Поэтому, ставим переключатель в позицию «Значения», и в поле слева от него прописываем число 30000. Как мы помним, именно это число по условиям составляет общую сумму премии для всех работников предприятия.

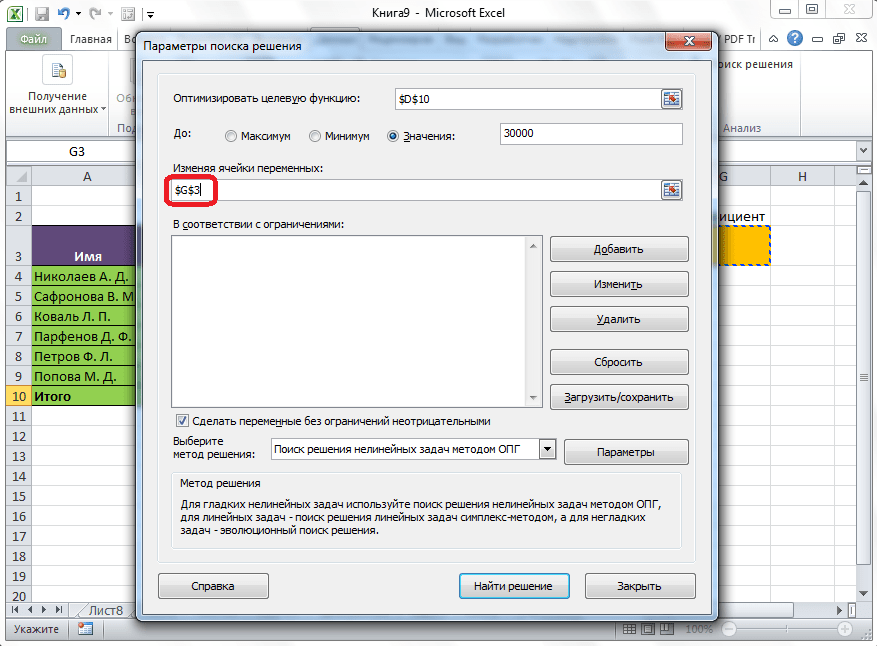
Ниже расположено поле «Изменяя ячейки переменных». Тут нужно указать адрес искомой ячейки, где, как мы помним, находится коэффициент, умножением на который основной заработной платы будет рассчитана величина премии. Адрес можно прописать теми же способами, как мы это делали для целевой ячейки.

В поле «В соответствии с ограничениями» можно выставить определенные ограничения для данных, например, сделать значения целыми или неотрицательными. Для этого, жмем на кнопку «Добавить».

После этого, открывается окно добавления ограничения. В поле «Ссылка на ячейки» прописываем адрес ячеек, относительно которых вводится ограничение. В нашем случае, это искомая ячейка с коэффициентом. Далее проставляем нужный знак: «меньше или равно», «больше или равно», «равно», «целое число», «бинарное», и т.д. В нашем случае, мы выберем знак «больше или равно», чтобы сделать коэффициент положительным числом. Соответственно, в поле «Ограничение» указываем число 0. Если мы хотим настроить ещё одно ограничение, то жмем на кнопку «Добавить». В обратном случае, жмем на кнопку «OK», чтобы сохранить введенные ограничения.

Как видим, после этого, ограничение появляется в соответствующем поле окна параметров поиска решения. Также, сделать переменные неотрицательными, можно установив галочку около соответствующего параметра чуть ниже. Желательно, чтобы установленный тут параметр не противоречил тем, которые вы прописали в ограничениях, иначе, может возникнуть конфликт.

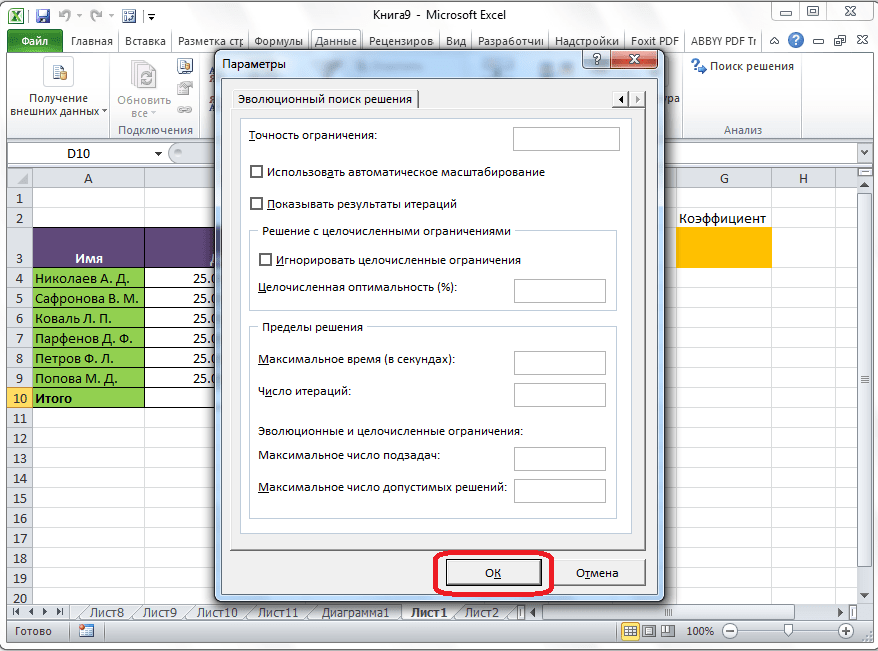
Дополнительные настройки можно задать, кликнув по кнопке «Параметры».

Здесь можно установить точность ограничения и пределы решения. Когда нужные данные введены, жмите на кнопку «OK». Но, для нашего случая, изменять эти параметры не нужно.

После того, как все настройки установлены, жмем на кнопку «Найти решение».

Далее, программа Эксель в ячейках выполняет необходимые расчеты. Одновременно с выдачей результатов, открывается окно, в котором вы можете либо сохранить найденное решение, либо восстановить исходные значения, переставив переключатель в соответствующую позицию. Независимо от выбранного варианта, установив галочку «Вернутся в диалоговое окно параметров», вы можете опять перейти к настройкам поиска решения. После того, как выставлены галочки и переключатели, жмем на кнопку «OK».

Если по какой-либо причине результаты поиска решений вас не удовлетворяют, или при их подсчете программа выдаёт ошибку, то, в таком случае, возвращаемся, описанным выше способом, в диалоговое окно параметров. Пересматриваем все введенные данные, так как возможно где-то была допущена ошибка. В случае, если ошибка найдена не была, то переходим к параметру «Выберите метод решения». Тут предоставляется возможность выбора одного из трех способов расчета: «Поиск решения нелинейных задач методом ОПГ», «Поиск решения линейных задач симплекс-методом», и «Эволюционный поиск решения». По умолчанию, используется первый метод. Пробуем решить поставленную задачу, выбрав любой другой метод. В случае неудачи, повторяем попытку, с использованием последнего метода. Алгоритм действий всё тот же, который мы описывали выше.

Как видим, функция Поиск решения представляет собой довольно интересный инструмент, который, при правильном использовании, может значительно сэкономить время пользователя на различных подсчетах. К сожалению, далеко не каждый пользователь знает о его существовании, не говоря о том, чтобы правильно уметь работать с этой надстройкой. В чем-то данный инструмент напоминает функцию «Подбор параметра…», но в то же время, имеет и существенные различия с ним.

---

Расскажи друзьям, если статья оказалась полезной:

    Видеоинструкции по использованию надстройки MulTEx

Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике

Как включить функцию “Поиск решения”

Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:

1. Открываем меню “Файл”, кликнув по соответствующему названию.
2. Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
3. Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
4. На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
5. Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.

Подготовительный этап

Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.

Итак, у нас есть данные про продаже товаров, представленные в табличном виде.

И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.

Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.

Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.

Применение функции и ее настройка

Формула готова. Теперь нужно применить саму функцию.

1. Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
2. Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
3. Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
4. Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
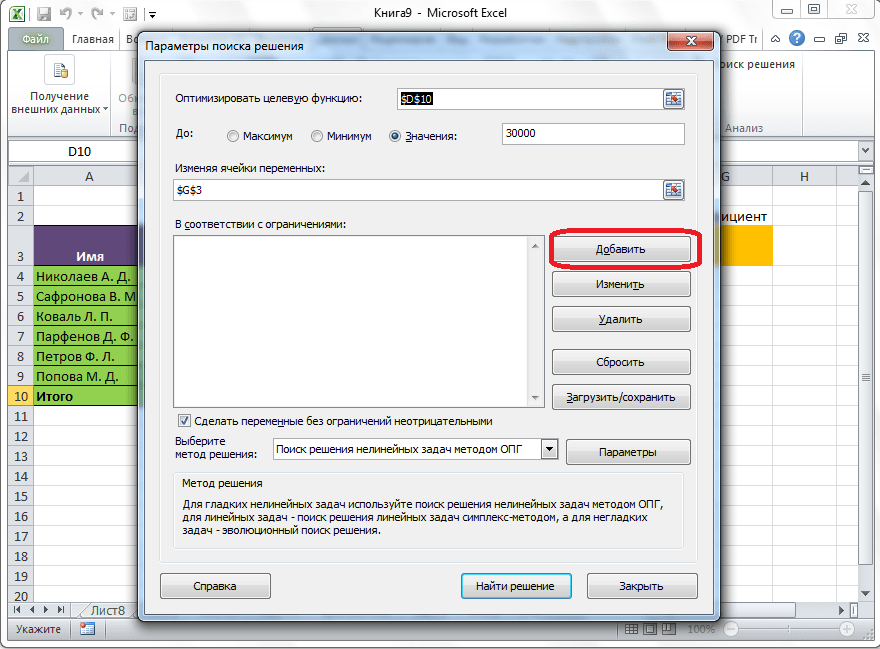
5. Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
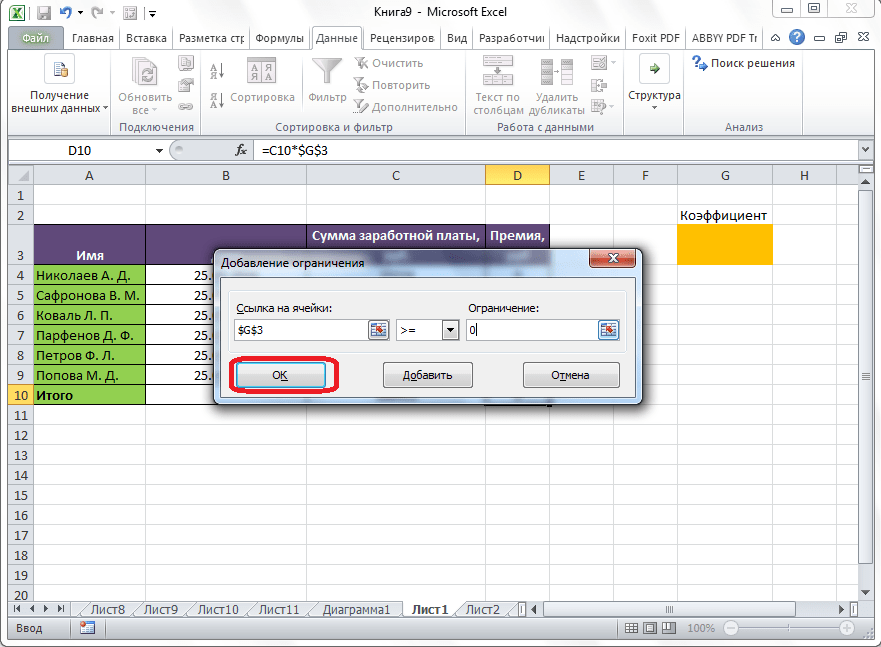
6. Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
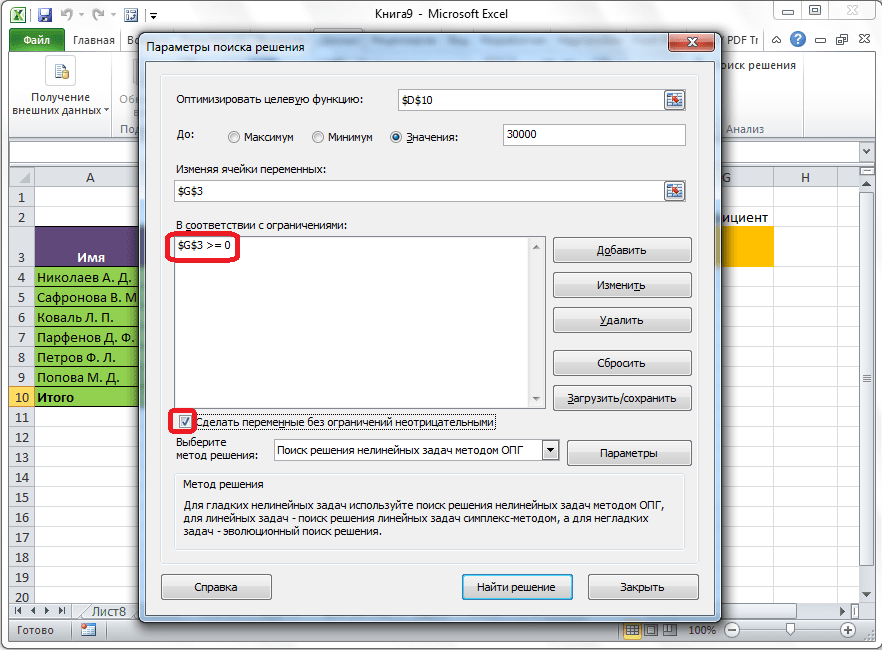
7. После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
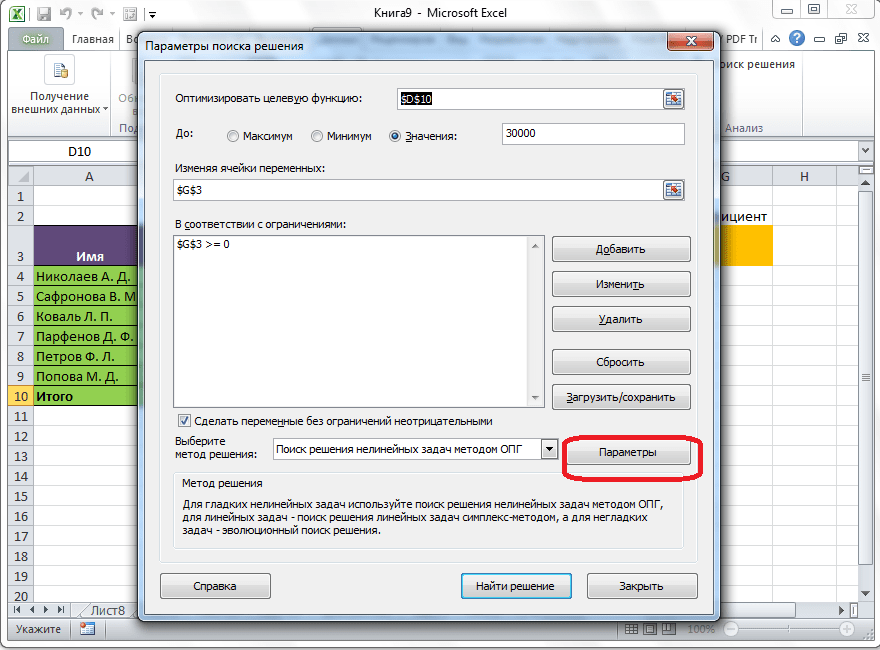
8. Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
9. В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
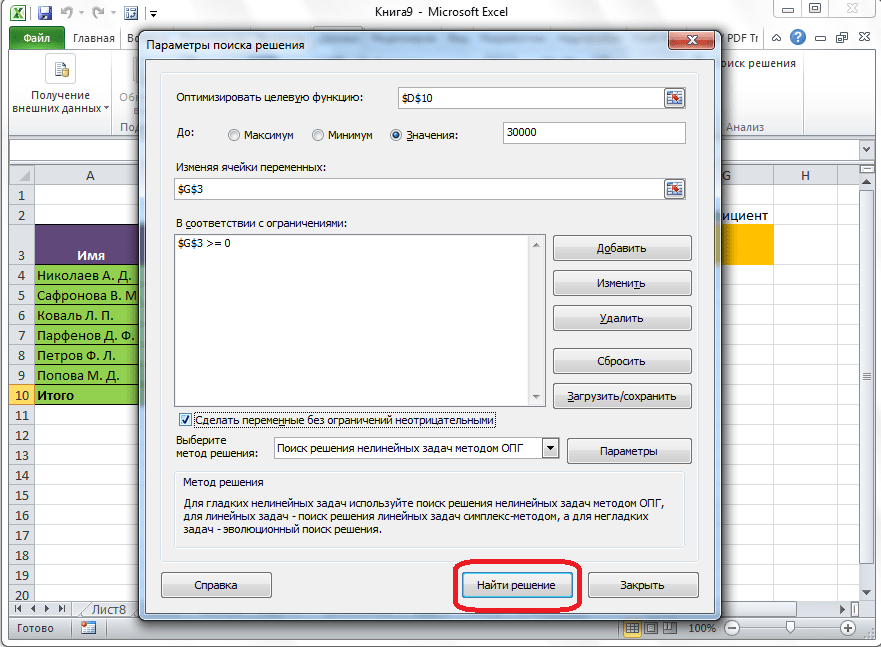
10. Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
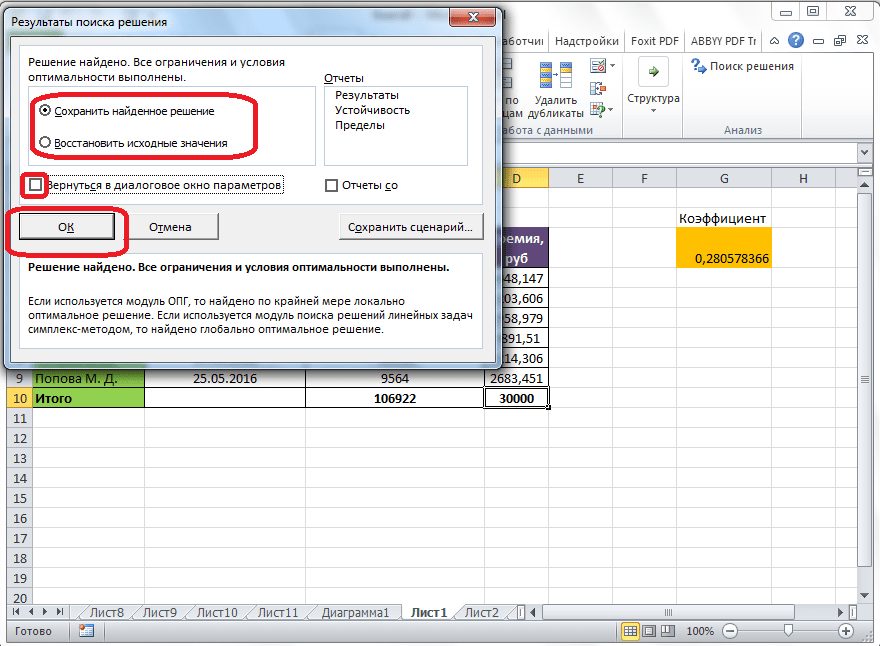
11. После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
12. Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
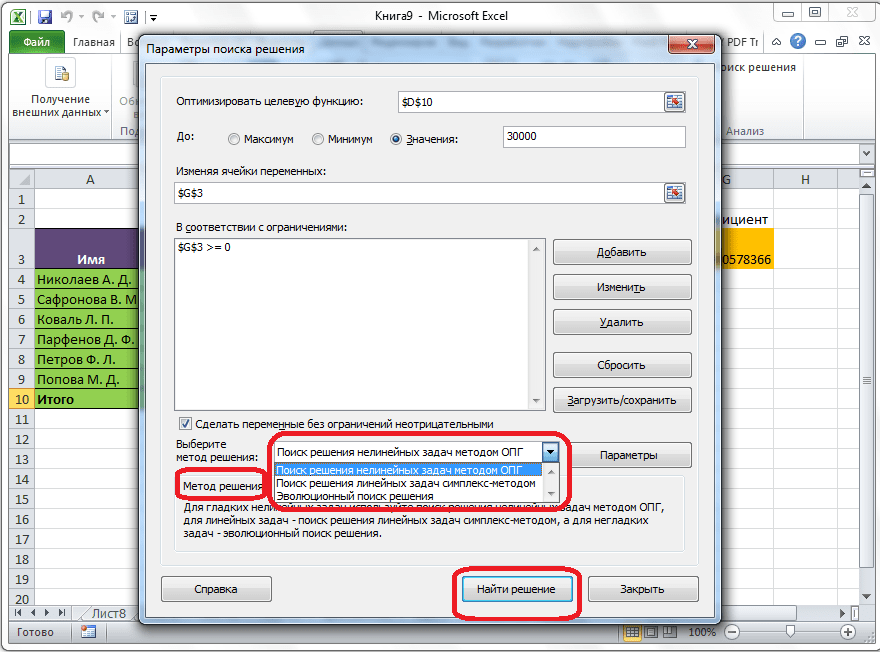
13. Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
    • Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
    • Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
    • Третий – для выполнения поставленной задачи использует эволюционный поиск.
    • В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
14. Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
15. Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
16. Теперь наша таблица полностью готова в соответствии с поставленной задачей.

Заключение

Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.