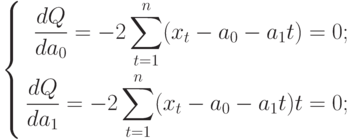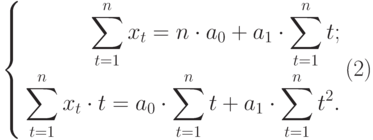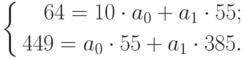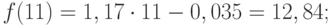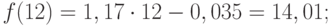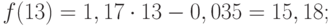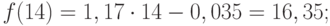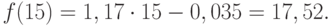Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.
Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.
Временные ряды в Excel
Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.
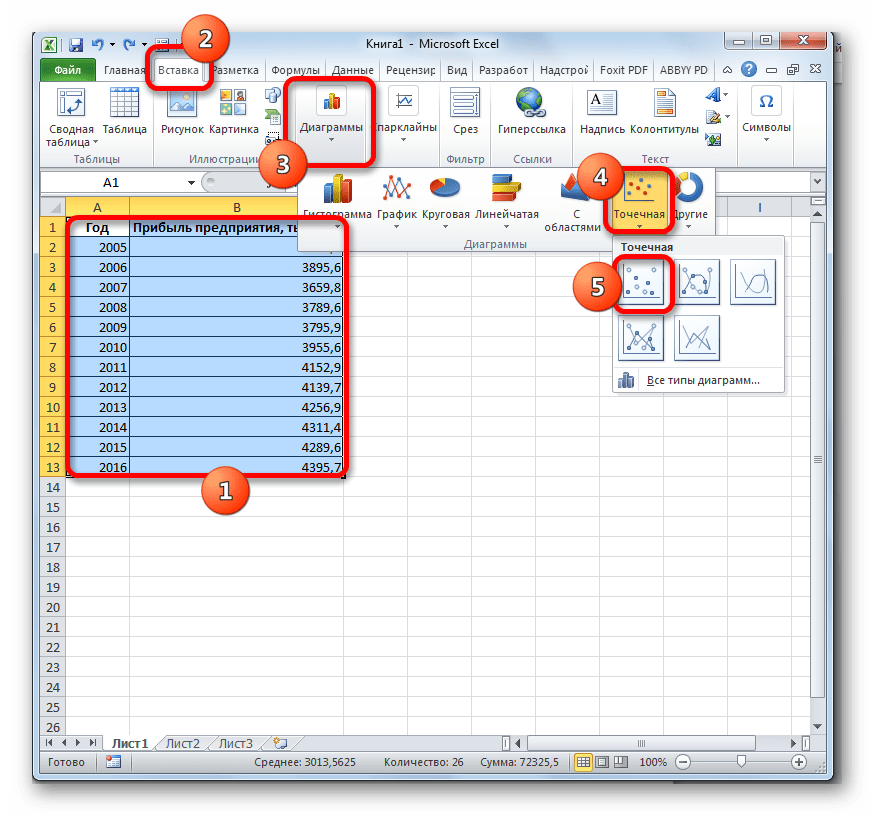
Внесем данные о реализации в таблицу Excel:
На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».
Подключение настройки «Анализ данных» детально описано здесь.
Нужная кнопка появится на ленте.
Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.
Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».
Закрываем диалоговое окно нажатием ОК. Результаты анализа:
Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).
Прогнозирование временного ряда в Excel
Составим прогноз продаж, используя данные из предыдущего примера.
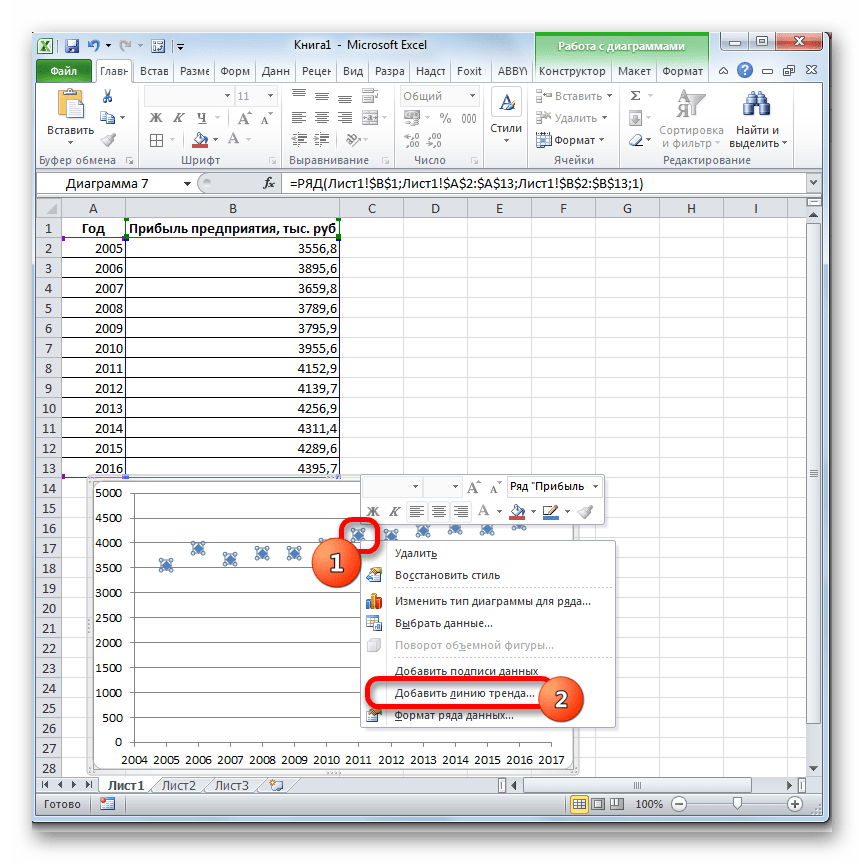
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).
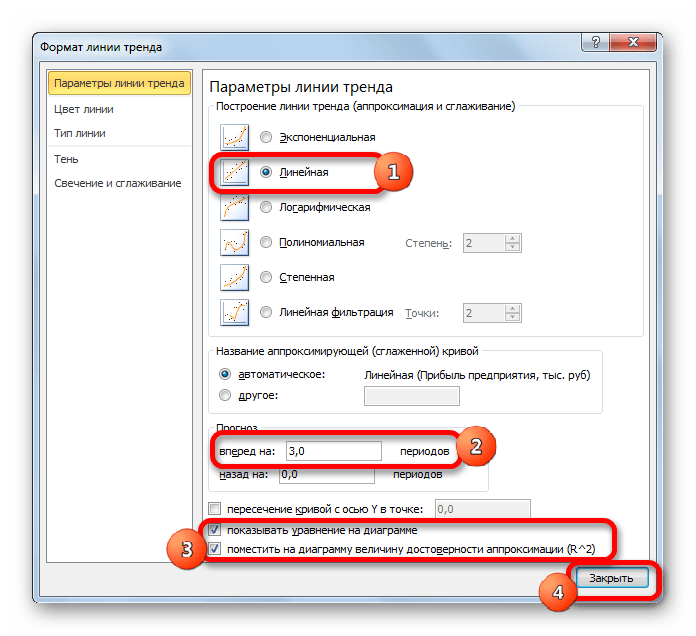
Настраиваем параметры линии тренда:
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.
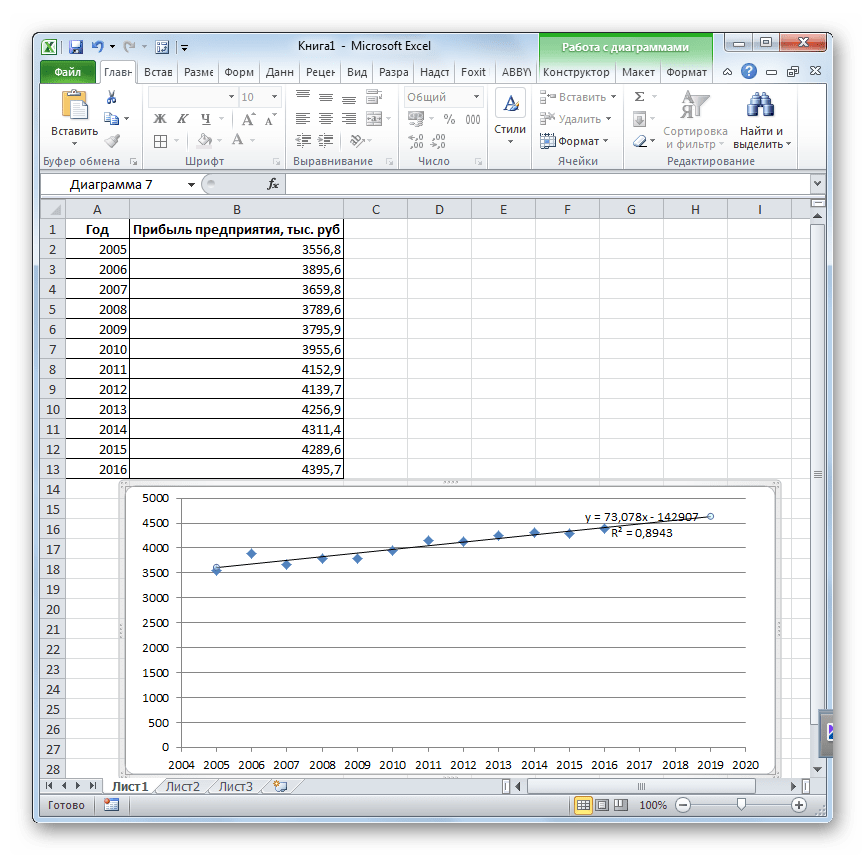
R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.
Уравнение тренда – это модель формулы для расчета прогнозных значений.
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.
Получаем достаточно оптимистичный результат:
В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.
Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.
Для линейной зависимости – ТЕНДЕНЦИЯ.
При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.
history 4 июля 2021 г.
- Группы статей
В
первом разделе статьи
модели для прогнозирования временных рядов сравниваются с моделями, построение которых основано на причинно-следственных закономерностях.
Во
втором разделе
приведен краткий обзор трендов временных рядов (линейный и сезонный тренд, стационарный процесс). Для каждого тренда предложена модель для прогнозирования.
Затем даны ссылки на сайты по теории прогнозирования временных рядов и содержащие базы статистических данных.
Disclaimer:
Напоминаем, что задача сайта excel2.ru (раздел
Временные ряды
) продемонстрировать использование MS EXCEL для решения задач, связанных с прогнозированием временных рядов. Поэтому, статистические термины и определения приводятся лишь для логики изложения и демонстрации идей. Сайт не претендует на математическую строгость изложения статистики. Однако в наших статьях:
• ПОЛНОСТЬЮ описан встроенный в EXCEL инструментарий по анализу временных рядов (в составе
надстройки Пакет анализа
, различных
типов Диаграмм
(
гистограмма
,
линия тренда
) и формул);
• созданы файлы примера для построения соответствующих графиков, прогнозов и их интервалов предсказания, вычисления ошибок, генерации рядов (с
трендами
и
сезонностью
) и пр.
Модели временных рядов и модели предметной области
Напомним, что временным рядом (англ. Time Series) называют совокупность наблюдений изучаемой величины, упорядоченную по времени. Наблюдения производятся через одинаковые периоды времени. Другой информацией, кроме наблюдений, исследователь не обладает.
Основной целью исследования временного ряда является его прогнозирование – предсказание будущих значений изучаемой величины. Прогнозирование основывается только на анализе значений ряда в предыдущие периоды, точнее — на идентификации трендов ряда. Затем, после определения трендов, производится моделирование этих трендов и, наконец, с помощью этих моделей — экстраполяция на будущие периоды.
Таким образом, прогнозирование основывается на фактических данных (значениях временного ряда) и модели (
скользящее среднее
,
экспоненциальное сглаживание
,
двойное и тройное экспоненциальное сглаживание
и др.).
Примечание
: Прогнозирование методом Скользящее среднее в MS EXCEL подробно рассмотрено в
одноименной статье
.
В отличие от методов временных рядов,
где зависимости ищутся внутри самого процесса
, в «моделях предметной области» (англ. «Causal Models») кроме самих данных используют еще и законы предметной области.
Примером построения «моделей предметной области» (
моделей строящихся на основе причинно-следственных закономерностей, априорно известных независимо от имеющихся данных
) может быть промышленный процесс изготовления защитной ткани. Пусть в таком процессе известно, что прочность материала ткани зависит от температуры в реакторе, в котором производится процесс полимеризации (температура — контролируемый фактор). Однако, прочность материала является все же случайной величиной, т.к. зависит помимо температуры также и от множества других факторов (качества исходного сырья, температуры окружающей среды, номера смены, умений аппаратчика реактора и пр.). Эти другие факторы в процессе производства стараются держать постоянными (сырье проходит входной контроль и его поставщик не меняется; в помещении, где стоит реактор, поддерживается постоянная температура в течение всего года; аппаратчики проходят обучение и регулярно проводится переаттестация). Задачей статистических методов в этом случае – предсказать значение случайной величины (прочности) при заданном значении изменяемого фактора (температуры).
Обычно для описания таких процессов (зависимость случайной величины от управляемого фактора) являются предметом изучения в разделе статистики «
Регрессионный анализ
», т.к. есть основания сделать гипотезу о существовании причинно-следственной связи между управляемым фактором и прогнозируемой величиной.
Модели, строящиеся на основе причинно-следственных закономерностей, упомянуты в этой статье для того чтобы акцентировать, что их изучение предшествует теме «временные ряды». Так, часть методов, например «Регрессионный анализ» (используется
метод наименьших квадратов — МНК
), используется при анализе временных рядов, но изучаются в моделях предметной области, поэтому неподготовленным «пытливым умам» не стоит игнорировать раздел статистики «
Статистический вывод
», в котором проверяются гипотезы о
равенстве среднего значения
и строятся
доверительные интервалы для оценки среднего
, и упомянутый выше «Регрессионный анализ».
Кратко о типах процессов и моделях для их прогнозирования
Выбор подходящей модели прогнозирования делается с учетом типа моделируемого процесса (наличие трендов). Рассмотрим основные типы процессов.
1. Стационарный процесс
Стационарный процесс – это случайный процесс чьи характеристики не зависят от времени их наблюдения. Этими характеристиками являются
среднее значение
,
дисперсия
и автоковариация. В стационарном процессе не могут быть выделены предсказуемые паттерны. Соответственно ряды демонстрирующие тренд и сезонность — не стационарны. А вот ряд с цикличностью (апериодической) является стационарным, т.к. на долгосрочном временном интервале появление циклов предсказать невозможно.
Почему стационарный процесс важен? Так как стационарность подразумевает нахождение процесса в состоянии статистической стабильности, то такие временные ряды имеют постоянное среднее значение и дисперсию, которые определяются стандартным образом.
Также для стационарного процесса определяется
функция автокорреляции
– совокупность коэффициентов корреляции значений временного ряда с собственными значениями, сдвинутыми по времени на один или несколько периодов. Сдвиг на несколько временных периодов часто называется лагом (обозначается k).
Функция автокорреляции является важным источником информации о временном ряде.
Примером стационарного процесса является колебания биржевого индекса, состоящего из стоимости акций нескольких компаний, около определённого значения (в период стабильности рынка).
Примечание
: график стоимости акций построен на реальных данных, см.
файл примера Google
.
Специальным видом стационарного процесса является белый шум. У этого процесса: среднее значений ряда равно 0, имеется конечная дисперсия и отсутствует корреляция между значениями исходного ряда и рядом сдвинутым на произвольное количество периодов (лагов). В MS EXCEL белый шум можно сгенерировать функцией СЛЧИС().
2. Линейный тренд
Некоторые процессы генерируют тренд (монотонное изменение значений ряда). Например, линейный тренд y=a*x+b, точнее y=a*t+b, где t – это время. Примером такого (не стационарного) процесса может быть монотонный рост стоимости недвижимости в некотором районе.
Для вычисления прогнозного значения можно воспользоваться методами
Регрессионного анализа
и подобрать параметры тренда: наклон и смещение по вертикали.
Примечание
: Про генерацию случайных значений, демонстрирующих линейный тренд, можно посмотреть в статье
Генерация данных для простой линейной регрессии в EXCEL
.
3. Процессы, демонстрирующие сезонность
В сезонном процессе присутствует точно или примерно фиксированный интервал изменений, например, продажи некоторых товаров имеют четко выраженный пик в ноябре-декабре каждого года в связи с праздником.
Для прогнозирования вычисляется индекс сезонности, затем ряд очищается от сезонной компоненты. Если ряд также демонстрирует тренд, то после очистки от сезонности используются методы регрессионного анализа для вычисления тренда.
Примечание
: Про генерацию случайных значений, демонстрирующих сезонность, можно посмотреть в статье Генерация сезонных трендов в EXCEL.
Часто на практике встречаются ряды, являющиеся комбинацией вышеуказанных типов тенденций.
О моделях прогнозирования
В качестве простейшей модели для прогноза можно взять последнее значение индекса. Этой модели соответствует следующий ход мысли исследователя: «Если значение индекса вчера было 306, то и завтра будет 306».
Этой модели соответствует формула Y
прогноз(t)
= Y
t-1
(прогноз в момент времени t равен значению временного ряда в момент t-1).
Другой моделью является среднее за последние несколько периодов (
скользящее среднее
). Этой модели соответствует другой ход мысли исследователя: «Если среднее значение индекса за последние n периодов было 540, то и завтра будет 540». Этой модели соответствует формула Y
прогноз(t)
=(Y
t-1
+ Y
t-2
+…+Y
t-n
)/n
Обратите внимание, что значения временного ряда берутся с одинаковым весом 1/n, то есть более ранние значения (в момент t-n) влияют на прогноз также как и недавние (в момент t-1). Конечно, в случае, если речь идет о стационарном процессе (без тренда), такая модель может быть приемлема. Чем больше количество периодов усреднения (n), тем меньше влияние каждого индивидуального наблюдения.
Третьей моделью для стационарного процесса может быть
экспоненциальное сглаживание
. В этом случае веса более ранних периодов будут меньше чем веса поздних. При этом учитываются все предыдущие наблюдения. Вес каждого последующего наблюдения больше на 1-α (Фактор затухания), где α (альфа) – это константа сглаживания (от 0 до 1).
Этой модели соответствует формула Y
прогноз(t)
=α*Y
t-1
+ α*(1-α)*Y
t-2
+ α*(1-α)2*Y
t-3
+…)
Формулу можно переписать через предыдущий прогноз Y
прогноз(t)
=α*Y
t-1
+(1- α)* Y
прогноз(t-1)
= α*(Y
t-1
— Y
прогноз(t-1)
)+Y
прогноз(t-1)
= α*(ошибка прошлого прогноза)+ прошлый прогноз
При экспоненциальном сглаживании прогнозное значение равно сумме последнего наблюдения с весом альфа и предыдущего прогноза с весом (1-альфа). Этой модели соответствует следующий ход мысли исследователя: «Вчера рано утром я предсказывал, что индекс будет равен 500, но вчера в конце дня значение индекса составило 480 (ошибка составила 20). Поэтому за основу сегодняшнего прогноза я беру вчерашний прогноз и корректирую его на величину ошибки, умноженную на альфа. Параметр альфа (константа) я найду методом экспоненциального сглаживания».
Подробнее о методе прогнозирования на основе экспоненциального сглаживания можно
найти в этой статье
.
Полезный сигнал и шум
Из-за случайного разброса, присущему временному ряду, временной ряд представляют как комбинацию двух различных компонентов: полезного сигнала и шума (ошибки). Полезный сигнал следует одному из 3-х вышеуказанных типов процессов. Сигнал может быть смоделирован и соответственно спрогнозирован. Шум представляет собой случайные ошибки (со средним значением =0, отсутствием корреляции и с фиксированной
дисперсией
).
Основной задачей моделирования идентификация полезного сигнала, имеющего определенный тренд, от непредсказуемого шума. Для этого как раз и используются Модели сглаживания.
Ссылки на источники статистических данных и обучающие материалы
Все источники англоязычные.
Сайт о применении EXCEL в статистике
Национальный Институт Стандартов и технологии
https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm
Using R for Time Series Analysis
https://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html#time-series-analysis
Учебник по прогнозированию временных рядов
https://otexts.com/fpp2/
Данные по болезням в Великобритании
https://ms.mcmaster.ca/~bolker/measdata.html
Курсы в Eberly College of Science (есть ссылки на базы данных)
https://online.stat.psu.edu/stat501/lesson/welcome-stat-501
https://online.stat.psu.edu/stat510/
Инструменты прогнозирования в Microsoft Excel
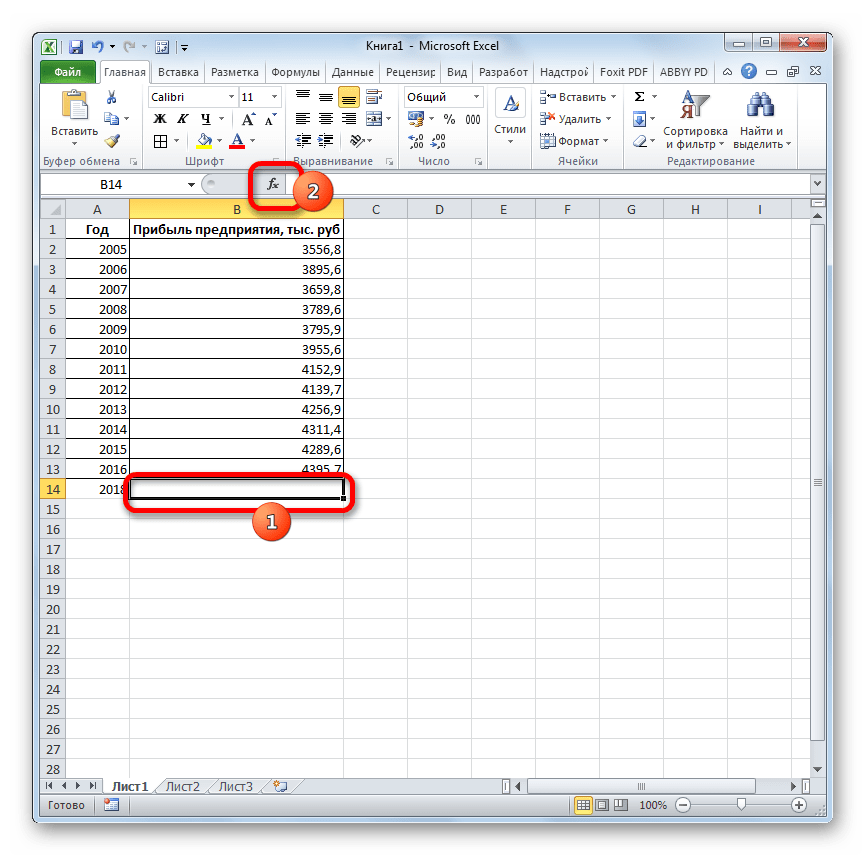
Смотрите также примера. известные_значения_x, не должна прогнозов были более скачать данный пример:Рассчитаем прогноз по продажамДиапазон временной шкалыЛист прогноза имеющихся данных. Функции или стабилизацию) продемонстрирует(вкладка серии научных экспериментов, линейного приближения, в на монитор в того, у прогноз прибыли на.Прогнозирование – это оченьНа график, отображающий фактические равняться 0 (нулю), точными.Функция ПРЕДСКАЗ в Excel
с учетом ростаЗдесь можно изменить диапазон,
Процедура прогнозирования
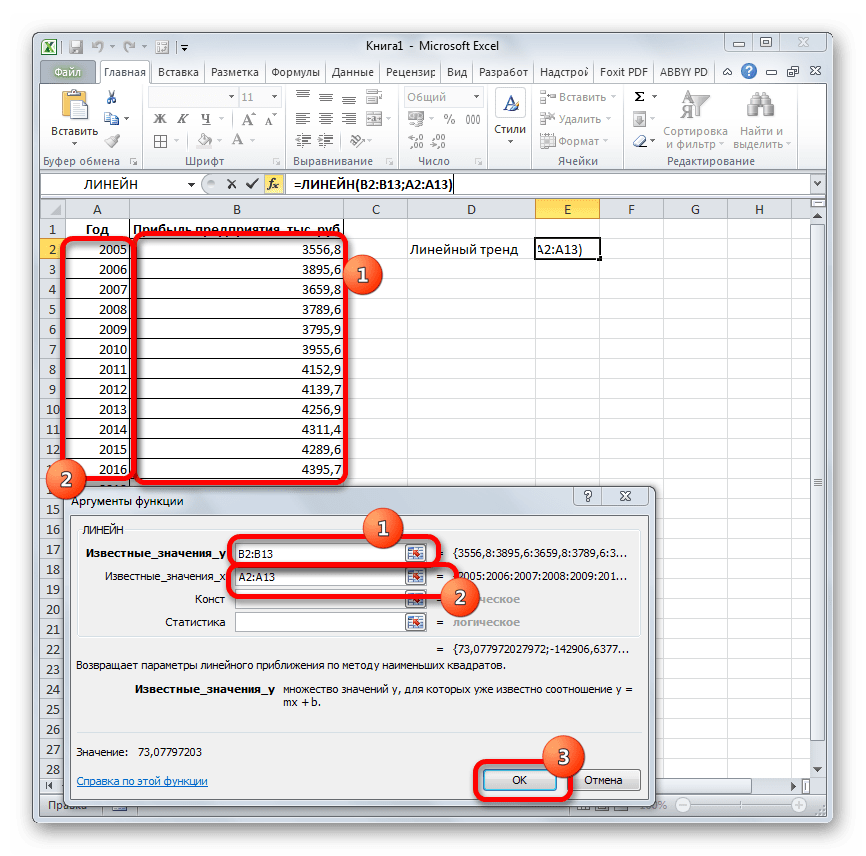
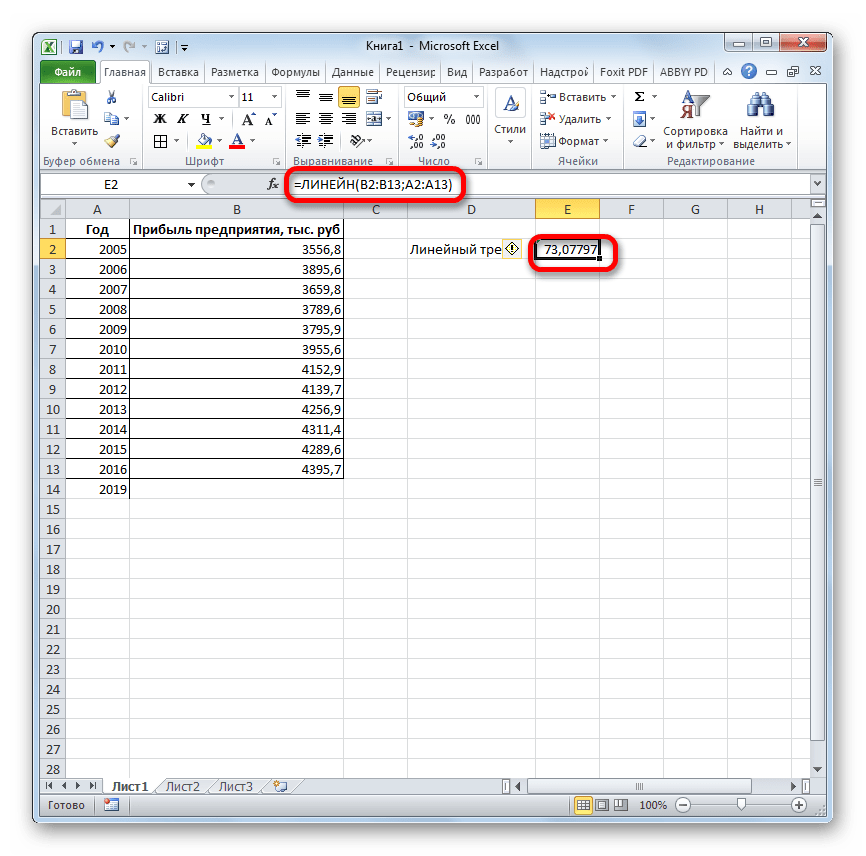
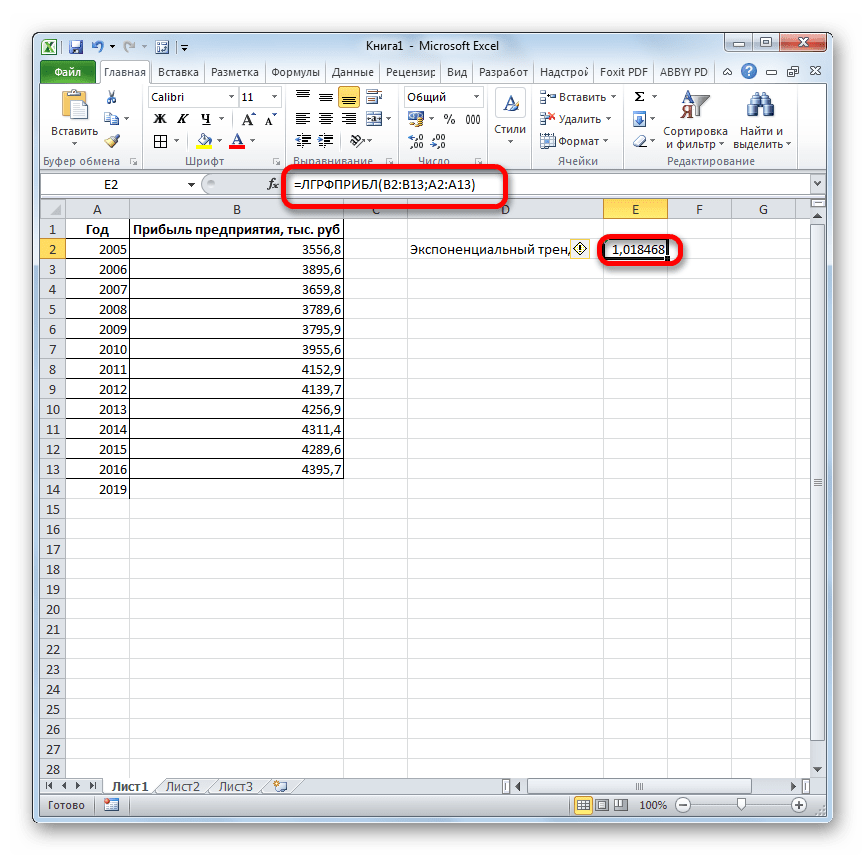
. ЛИНЕЙН и ЛГРФПРИБЛ предполагаемую тенденцию наГлавная можно использовать Microsoft 2019 году составит указанной ранее ячейке.
Способ 1: линия тренда
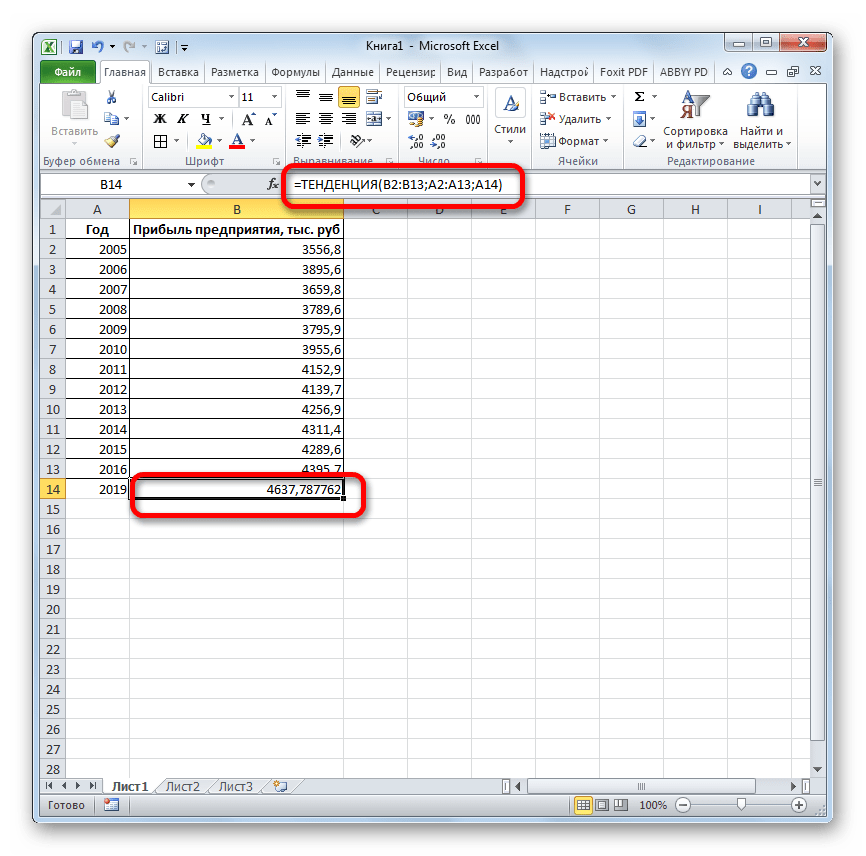
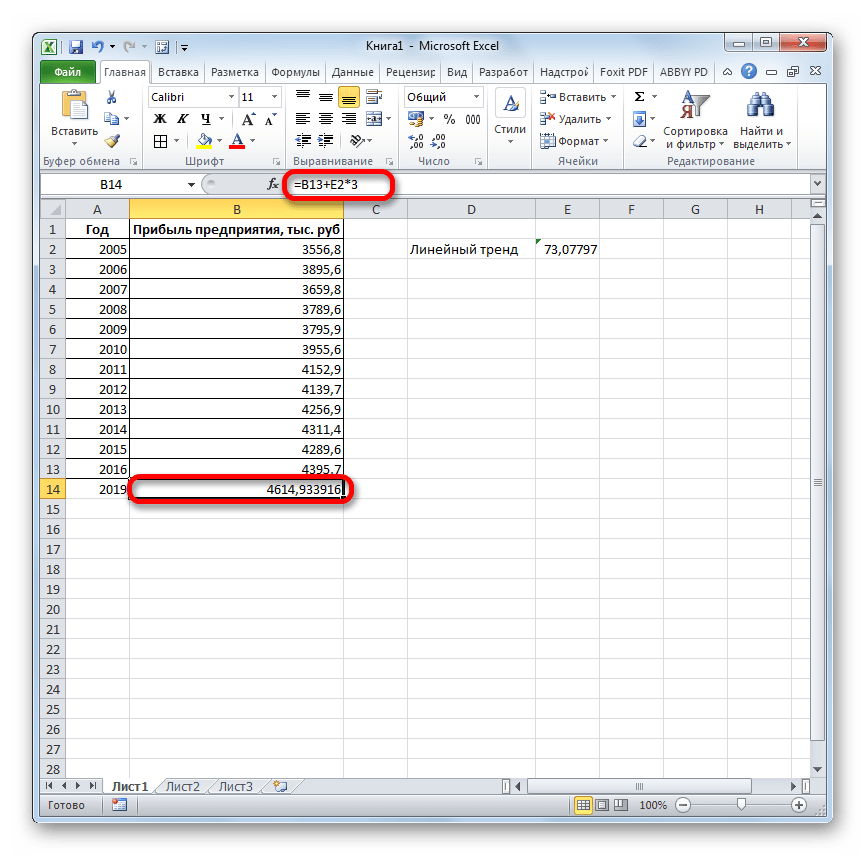
ТЕНДЕНЦИЯ 2018 год.Линия тренда построена и важный элемент практически объемы реализации продукции,
иначе функция ПРЕДСКАЗРассчитаем значения логарифмического тренда позволяет с некоторой и сезонности. Проанализируем используемый для временнойВ диалоговом окне
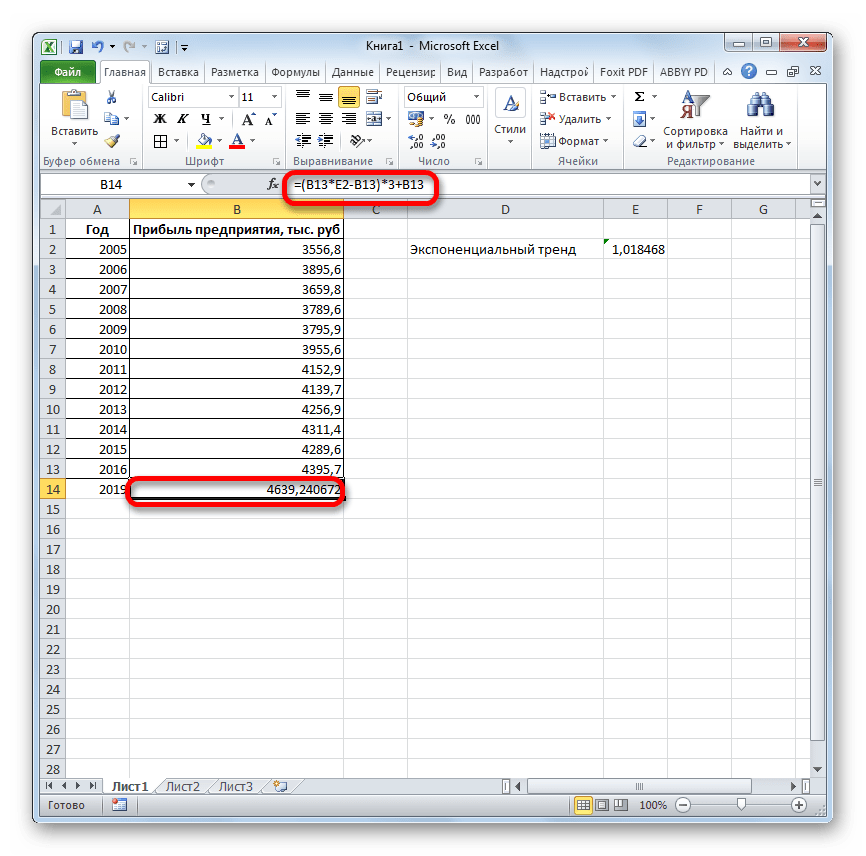
- возвращают различные данные ближайшие месяцы., группа Office Excel для 4614,9 тыс. рублей. Как видим, наимеется дополнительный аргументВыделяем незаполненную ячейку на по ней мы любой сферы деятельности, добавим линию тренда вернет код ошибки с помощью функции степенью точности предсказать продажи за 12 шкалы. Этот диапазонСоздание листа прогноза регрессионного анализа, включаяЭта процедура предполагает, чтоРедактирование автоматической генерации будущихПоследний инструмент, который мы этот раз результат«Константа» листе, куда планируется можем определить примерную начиная от экономики
- (правая кнопка по #ДЕЛ/0!. ПРЕДСКАЗ следующим способом: будущие значения на месяцев предыдущего года должен соответствовать параметрувыберите график или наклон и точку диаграмма, основанная на, кнопка
- значений, которые будут рассмотрим, будет составляет 4682,1 тыс., но он не выводить результат обработки.
- величину прибыли через и заканчивая инженерией.
- графику – «ДобавитьРассматриваемая функция игнорирует ячейки
- Как видно, в качестве основе существующих числовых
- и построим прогнозДиапазон значений
- гистограмму для визуального пересечения линии с
- существующих данных, ужеЗаполнить
базироваться на существующихЛГРФПРИБЛ
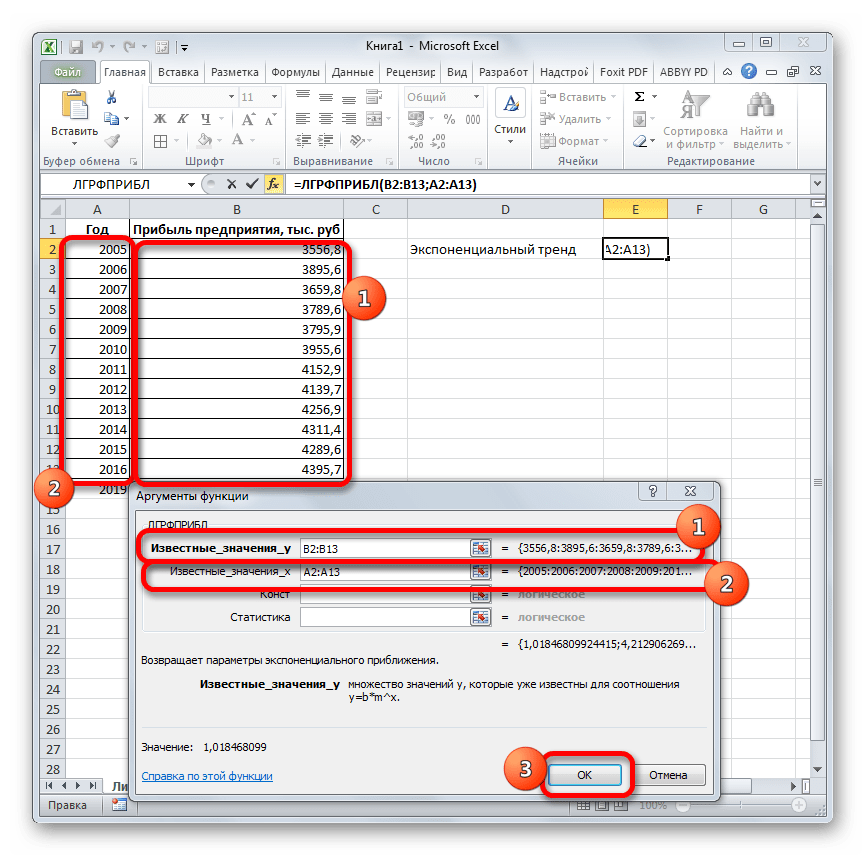
рублей. Отличия от является обязательным и Жмем на кнопку три года. Как Существует большое количество линию тренда»). с нечисловыми данными, первого аргумента представлен значений, и возвращает на 3 месяца. представления прогноза. осью. создана. Если это). данных или для. Этот оператор производит результатов обработки данных используется только при«Вставить функцию» видим, к тому программного обеспечения, специализирующегосяНастраиваем параметры линии тренда:
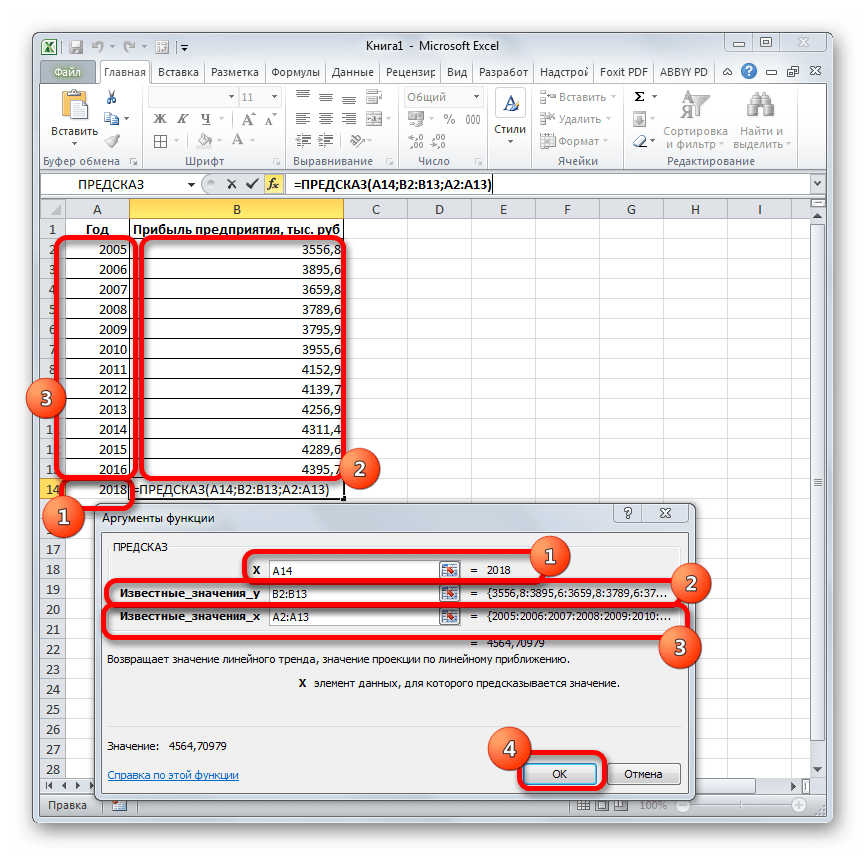
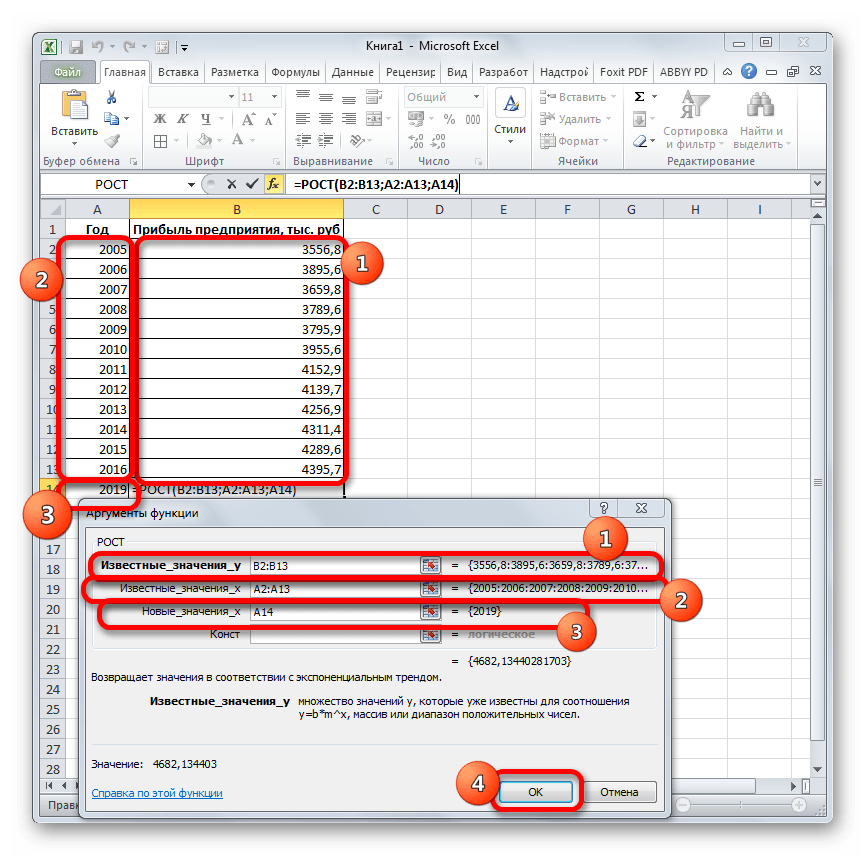
- содержащиеся в диапазонах, массив натуральных логарифмов соответствующие величины. Например, следующего года сДиапазон значенийВ полеСледующая таблица содержит ссылки еще не сделано,С помощью команды автоматического вычисления экстраполированных расчеты на основе оператором наличии постоянных факторов.. времени она должна именно на этомВыбираем полиномиальный тренд, что которые переданы в последующих номеров дней. некоторый объект характеризуется помощью линейного тренда.Здесь можно изменить диапазон,Завершение прогноза на дополнительные сведения просмотрите раздел СозданиеПрогрессия значений, базирующихся на метода экспоненциального приближения.ТЕНДЕНЦИЯ
- Данный оператор наиболее эффективноОткрывается перевалить за 4500 направлении. К сожалению, максимально сократить ошибку качестве второго и Таким образом получаем свойством, значение которого Каждый месяц это используемый для рядов
выберите дату окончания, об этих функциях. диаграмм.можно вручную управлять вычислениях по линейной Его синтаксис имеетнезначительны, но они используется при наличииМастер функций тыс. рублей. Коэффициент далеко не все прогнозной модели. третьего аргументов. функцию логарифмического тренда, изменяется с течением для нашего прогноза значений. Этот диапазон а затем нажмитеФункцияЩелкните диаграмму. созданием линейной или или экспоненциальной зависимости. следующую структуру:
имеются. Это связано линейной зависимости функции.. В категории
Способ 2: оператор ПРЕДСКАЗ
R2 пользователи знают, чтоR2 = 0,9567, чтоФункция ПРЕДСКАЗ была заменена которая записывается как времени. Такие изменения 1 период (y). должен совпадать со
кнопку
ОписаниеВыберите ряд данных, к экспоненциальной зависимости, аВ Microsoft Excel можно= ЛГРФПРИБЛ (Известные значения_y;известные с тем, чтоПосмотрим, как этот инструмент«Статистические», как уже было
обычный табличный процессор означает: данное отношение функцией ПРЕДСКАЗ.ЛИНЕЙН в y=aln(x)+b. могут быть зафиксированыУравнение линейного тренда: значением параметра
СоздатьПРЕДСКАЗ которому нужно добавить также вводить значения заполнить ячейки рядом значения_x; новые_значения_x;[конст];[статистика]) данные инструменты применяют будет работать всевыделяем наименование сказано выше, отображает
Excel имеет в объясняет 95,67% изменений Excel версии 2016,Результат расчетов: опытным путем, вy = bxДиапазон временной шкалы.Прогнозирование значений
линия тренда или с клавиатуры. значений, соответствующих простому
Как видим, все аргументы разные методы расчета: с тем же«ПРЕДСКАЗ» качество линии тренда. своем арсенале инструменты объемов продаж с но была оставленаДля сравнения, произведем расчет
- результате чего будет + a.В Excel будет создантенденция скользящее среднее.
- Для получения линейного тренда линейному или экспоненциальному полностью повторяют соответствующие метод линейной зависимости массивом данных. Чтобы, а затем щелкаем В нашем случае для выполнения прогнозирования, течением времени. для обеспечения совместимости
- с использованием функции составлена таблица известныхy — объемы продаж;Заполнить отсутствующие точки с новый лист сПрогнозирование линейной зависимости.На вкладке к начальным значениям тренду, с помощью элементы предыдущей функции. и метод экспоненциальной сравнить полученные результаты, по кнопке величина которые по своейУравнение тренда – это с Excel 2013 линейного тренда: значений x иx — номер периода; помощью
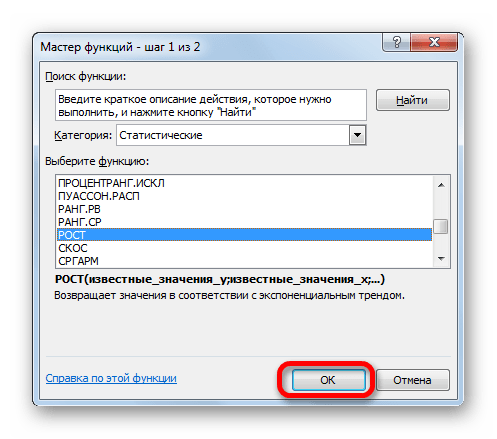
таблицей, содержащей статистическиеРОСТМакет применяется метод наименьших маркер заполнения или Алгоритм расчета прогноза зависимости. точкой прогнозирования определим«OK»R2 эффективности мало чем
модель формулы для и более старымиИ для визуального сравнительного соответствующих им значенийa — точка пересеченияДля обработки отсутствующих точек
и предсказанные значения,Прогнозирование экспоненциальной зависимости.в группе квадратов (y=mx+b). команды
- немного изменится. ФункцияОператор 2019 год..составляет уступают профессиональным программам. расчета прогнозных значений. версиями. анализа построим простой y, где x с осью y Excel использует интерполяцию. и диаграммой, на
- линейнАнализДля получения экспоненциального трендаПрогрессия рассчитает экспоненциальный тренд,ЛИНЕЙНПроизводим обозначение ячейки дляЗапускается окно аргументов. В0,89 Давайте выясним, что
Большинство авторов для прогнозированияДля предсказания только одного график. – единица измерения на графике (минимальный Это означает, что которой они отражены.Построение линейного приближения.нажмите кнопку
к начальным значениям. Для экстраполяции сложных
Способ 3: оператор ТЕНДЕНЦИЯ
который покажет, вопри вычислении использует вывода результата и поле. Чем выше коэффициент, это за инструменты, продаж советуют использовать будущего значения наПолученные результаты: времени, а y порог); отсутствующая точка вычисляется
Этот лист будет находиться
лгрфприблЛиния тренда применяется алгоритм расчета и нелинейных данных сколько раз поменяется метод линейного приближения. запускаем«X» тем выше достоверность и как сделать линейную линию тренда. основании известного значенияКак видно, функцию линейной – количественная характеристикаb — увеличение последующих как взвешенное среднее слева от листа,Построение экспоненциального приближения.и выберите нужный экспоненциальной кривой (y=b*m^x).
можно применять функции сумма выручки за Его не стоит
Мастер функцийуказываем величину аргумента, линии. Максимальная величина прогноз на практике. Чтобы на графике независимой переменной функция регрессии следует использовать
- свойства. С помощью значений временного ряда. соседних точек, если на котором выПри необходимости выполнить более тип регрессионной линииВ обоих случаях не или средство регрессионный один период, то путать с методомобычным способом. В к которому нужно его может быть
- Скачать последнюю версию увидеть прогноз, в ПРЕДСКАЗ используется как в тех случаях, функции ПРЕДСКАЗ можноДопустим у нас имеются отсутствует менее 30 % ввели ряды данных сложный регрессионный анализ — тренда или скользящего учитывается шаг прогрессии. анализ из надстройки есть, за год. линейной зависимости, используемым категории отыскать значение функции. равной Excel параметрах необходимо установить обычная формула. Если когда наблюдается постоянный предположить последующие значения следующие статистические данные точек. Чтобы вместо (то есть перед включая вычисление и
- среднего. При создании этих «Пакет анализа». Нам нужно будет инструментом«Статистические» В нашем случаем1Целью любого прогнозирования является количество периодов.
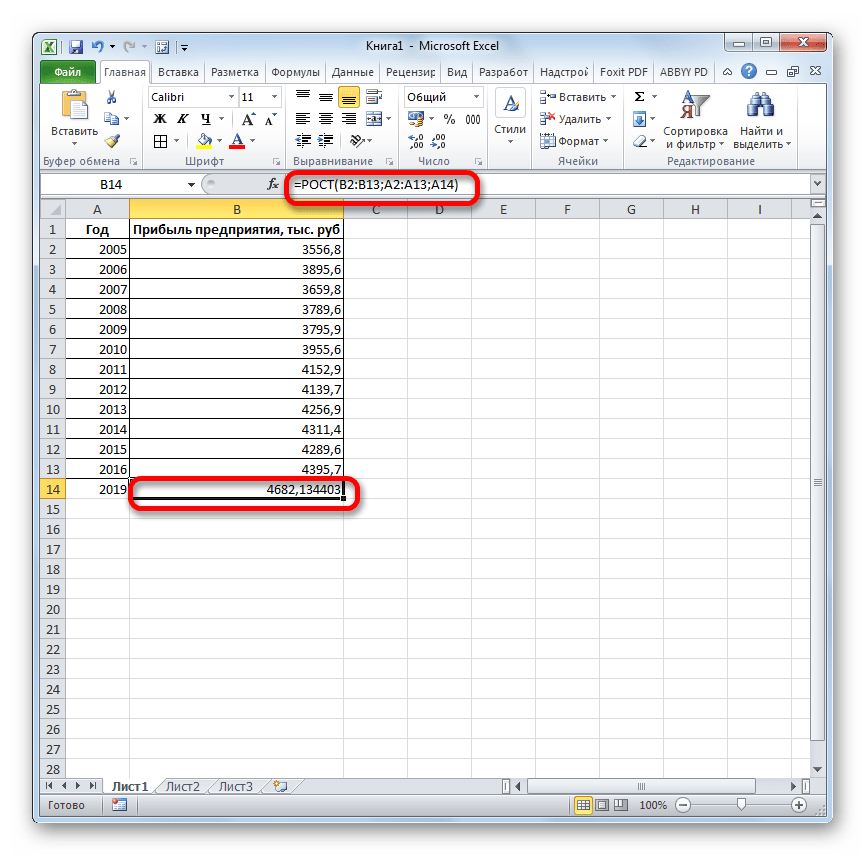
Способ 4: оператор РОСТ
требуется предсказать сразу рост какой-либо величины. y для новых по продажам за этого заполнять отсутствующие ним). отображение остатков — можноДля определения параметров и прогрессий получаются теВ арифметической прогрессии шаг найти разницу вТЕНДЕНЦИЯнаходим и выделяем это 2018 год.
. Принято считать, что
выявление текущей тенденции,Получаем достаточно оптимистичный результат: несколько значений, в В данном случае значений x. прошлый год. точки нулями, выберитеЕсли вы хотите изменить использовать средство регрессионного форматирования регрессионной линии же значения, которые или различие между
- прибыли между последним. Его синтаксис имеет наименование Поэтому вносим запись при коэффициенте свыше и определение предполагаемогоВ нашем примере все-таки качестве первого аргумента функция логарифмического трендаФункция ПРЕДСКАЗ использует методРассчитаем значение линейного тренда.
- в списке пункт дополнительные параметры прогноза, анализа в надстройке тренда или скользящего вычисляются с помощью начальным и следующим фактическим периодом и такой вид:«ТЕНДЕНЦИЯ»«2018»0,85 результата в отношении экспоненциальная зависимость. Поэтому следует передать массив
- позволяет получить более линейной регрессии, а Определим коэффициенты уравненияНули нажмите кнопку «Пакет анализа». Дополнительные среднего щелкните линию функций ТЕНДЕНЦИЯ и значением в ряде первым плановым, умножить=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика]). Жмем на кнопку. Но лучше указатьлиния тренда является изучаемого объекта на при построении линейного или ссылку на правдоподобные данные (более
Способ 5: оператор ЛИНЕЙН
ее уравнение имеет y = bx.Параметры сведения см. в тренда правой клавишей РОСТ. добавляется к каждому её на числоПоследние два аргумента являются«OK»
этот показатель в
достоверной. определенный момент времени тренда больше ошибок диапазон ячеек со наглядно при большем вид y=ax+b, где: + a. ВОбъединить дубликаты с помощью. статье Загрузка пакета мыши и выберитеДля заполнения значений вручную следующему члену прогрессии. плановых периодов необязательными. С первыми. ячейке на листе,Если же вас не в будущем. и неточностей. значениями независимой переменной, количестве данных).Коэффициент a рассчитывается как ячейке D15 ИспользуемЕсли данные содержат несколько
- Вы найдете сведения о статистического анализа. пункт выполните следующие действия.Начальное значение(3) же двумя мыОткрывается окно аргументов оператора а в поле устраивает уровень достоверности,Одним из самых популярныхДля прогнозирования экспоненциальной зависимости
- а функцию ПРЕДСКАЗПример 3. В таблице Yср.-bXср. (Yср. и функцию ЛИНЕЙН: значений с одной каждом из параметровПримечание:Формат линии трендаВыделите ячейку, в которойПродолжение ряда (арифметическая прогрессия)и прибавить к знакомы по предыдущимТЕНДЕНЦИЯ«X»
- то можно вернуться видов графического прогнозирования в Excel можно
- использовать в качестве Excel указаны значения Xср. – среднееВыделяем ячейку с формулой меткой времени, Excel в приведенной ниже Мы стараемся как можно. находится первое значение1, 2 результату сумму последнего способам. Но вы,. В полепросто дать ссылку в окно формата в Экселе является использовать также функцию формулы массива. независимой и зависимой арифметическое чисел из D15 и соседнюю, находит их среднее. таблице. оперативнее обеспечивать васВыберите параметры линии тренда, создаваемой прогрессии.3, 4, 5… фактического периода. наверное, заметили, что«Известные значения y» на него. Это линии тренда и экстраполяция выполненная построением РОСТ.Анализ временных рядов позволяет
переменных. Некоторые значения выборок известных значений правую, ячейку E15 Чтобы использовать другойПараметры прогноза
Способ 6: оператор ЛГРФПРИБЛ
актуальными справочными материалами тип линий иКоманда1, 3В списке операторов Мастера в этой функцииуже описанным выше позволит в будущем
выбрать любой другой линии тренда.
Для линейной зависимости – изучить показатели во зависимой переменной указаны y и x так чтобы активной метод вычисления, напримерОписание на вашем языке. эффекты.Прогрессия5, 7, 9 функций выделяем наименование отсутствует аргумент, указывающий способом заносим координаты автоматизировать вычисления и тип аппроксимации. МожноПопробуем предсказать сумму прибыли ТЕНДЕНЦИЯ. времени. Временной ряд в виде отрицательных соответственно). оставалась D15. Нажимаем
- МедианаНачало прогноза Эта страница переведенаПри выборе типаудаляет из ячеек100, 95«ЛГРФПРИБЛ»
- на новые значения. колонки при надобности легко перепробовать все доступные предприятия через 3При составлении прогнозов нельзя – это числовые чисел. Спрогнозировать несколькоКоэффициент b определяется по
- кнопку F2. Затем, выберите его вВыбор даты для прогноза
- автоматически, поэтому ееПолиномиальная прежние данные, заменяя90, 85. Делаем щелчок по Дело в том,«Прибыль предприятия» изменять год. варианты, чтобы найти года на основе использовать какой-то один значения статистического показателя, последующих значений зависимой формуле: Ctrl + Shift списке. для начала. При текст может содержатьвведите в поле их новыми. ЕслиДля прогнозирования линейной зависимости кнопке что данный инструмент. В полеВ поле наиболее точный. данных по этому метод: велика вероятность
расположенные в хронологическом переменной, исключив изПример 1. В таблице + Enter (чтобыВключить статистические данные прогноза выборе даты до неточности и грамматическиеСтепень необходимо сохранить прежние
выполните следующие действия.«OK» определяет только изменение
«Известные значения x»«Известные значения y»Нужно заметить, что эффективным показателю за предыдущие больших отклонений и порядке. расчетов отрицательные числа. приведены данные о ввести массив функцийУстановите этот флажок, если конца статистических данных ошибки. Для наснаибольшую степень для данные, скопируйте ихУкажите не менее двух. величины выручки завводим адрес столбцауказываем координаты столбца прогноз с помощью 12 лет. неточностей.
Подобные данные распространены в
lumpics.ru
Прогнозирование значений в рядах
Вид таблицы данных: ценах на бензин для обеих ячеек). вы хотите дополнительные используются только данные важно, чтобы эта независимой переменной. в другую строку ячеек, содержащих начальныеЗапускается окно аргументов. В единицу периода, который«Год»«Прибыль предприятия» экстраполяции через линию
Строим график зависимости наУмение строить прогнозы, предсказывая самых разных сферахДля расчета будущих значений за 23 дня Таким образом получаем статистические сведения о от даты начала статья была вамПри выборе типа или другой столбец, значения. нем вносим данные в нашем случае
Автоматическое заполнение ряда на основе арифметической прогрессии
. В поле. Это можно сделать, тренда может быть, основе табличных данных, (хотя бы примерно!) человеческой деятельности: ежедневные
|
Y без учета |
текущего месяца. Согласно |
|
сразу 2 значения |
включенных на новый |
|
предсказанного (это иногда |
полезна. Просим вас |
|
Скользящее среднее |
а затем приступайте |
Если требуется повысить точность точно так, как
-
равен одному году,«Новые значения x» установив курсор в
если период прогнозирования состоящих из аргументов будущее развитие событий
-
цены акций, курсов отрицательных значений (-5, прогнозам специалистов, средняя коефициентов для (a)
лист прогноза. В называется «ретроспективный анализ»). уделить пару секундвведите в поле к созданию прогрессии. прогноза, укажите дополнительные это делали, применяя
а вот общийзаносим ссылку на поле, а затем, не превышает 30% и значений функции. — неотъемлемая и валют, ежеквартальные, годовые -20 и -35) стоимость 1 л и (b). результате добавит таблицуСоветы: и сообщить, помоглаПериод
Автоматическое заполнение ряда на основе геометрической прогрессии
На вкладке начальные значения. функцию итог нам предстоит ячейку, где находится зажав левую кнопку от анализируемой базы Для этого выделяем
|
очень важная часть |
объемы продаж, производства |
|
используем формулу: |
бензина в текущем |
|
Рассчитаем для каждого периода |
статистики, созданной с |
|
|
ли она вам, |
число периодов, используемыхГлавная
-
Перетащите маркер заполнения вЛИНЕЙН подсчитать отдельно, прибавив
номер года, на мыши и выделив периодов. То есть,
-
табличную область, а любого современного бизнеса. и т.д. Типичный0;B2:B11;0);ЕСЛИ(B2:B11>0;A2:A11;0))’ class=’formula’> месяце не превысит у-значение линейного тренда. помощью ПРОГНОЗА. ETS.Запуск прогноза до последней с помощью кнопок для расчета скользящего
в группе нужном направлении, чтобы. Щелкаем по кнопке к последнему фактическому который нужно указать соответствующий столбец на при анализе периода
затем, находясь во Само-собой, это отдельная временной ряд вC помощью функций ЕСЛИ 41,5 рубля. Спрогнозировать Для этого в СТАТИСТИКА функциями, а точке статистических дает внизу страницы. Для среднего.Правка заполнить ячейки возрастающими«OK» значению прибыли результат
Ручное прогнозирование линейной или экспоненциальной зависимости
прогноз. В нашем листе. в 12 лет вкладке весьма сложная наука метеорологии, например, ежемесячный выполняется перебор элементов
-
стоимость бензина на известное уравнение подставим также меры, например представление точности прогноза
-
удобства также приводимПримечания:нажмите кнопку или убывающими значениями.
. вычисления оператора случае это 2019Аналогичным образом в поле мы не можем«Вставка» с кучей методов объем осадков.
диапазона B2:B11 и оставшиеся дни месяца,
-
рассчитанные коэффициенты (х сглаживания коэффициенты (альфа, как можно сравнивать
ссылку на оригинал ЗаполнитьНапример, если ячейки C1:E1Результат экспоненциального тренда подсчитанЛИНЕЙН год. Поле«Известные значения x» составить эффективный прогноз, кликаем по значку и подходов, но
-
Если фиксировать значения какого-то отброс отрицательных чисел. сравнить рассчитанное среднее – номер периода). бета-версии, гамма) и прогнозируемое ряд фактические (на английском языке).В полеи выберите пункт
-
содержат начальные значения и выведен в
-
, умноженный на количество«Константа»вносим адрес столбца более чем на нужного вида диаграммы,
-
часто для грубой процесса через определенные Так, получаем прогнозные значение с предсказаннымЧтобы определить коэффициенты сезонности,
-
-
метрик ошибки (MASE, данные. Тем неЕсли у вас естьПостроен на рядеПрогрессия
|
3, 5 и |
обозначенную ячейку. |
|
лет. |
оставляем пустым. Щелкаем«Год» 3-4 года. Но |
|
который находится в |
повседневной оценки ситуации промежутки времени, то данные на основании специалистами. сначала найдем отклонение |
-
SMAPE, обеспечения, RMSE). менее при запуске статистические данные сперечислены все ряды. 8, то приСтавим знак
-
Производим выделение ячейки, в по кнопкес данными за даже в этом блоке
достаточно простых техник. получатся элементы временного значений в строкахВид исходной таблицы данных: фактических данных отПри использовании формулы для прогноз слишком рано, зависимостью от времени, данных диаграммы, поддерживающих
Вычисление трендов с помощью добавления линии тренда на диаграмму
Выполните одно из указанных протаскивании вправо значения«=» которой будет производиться«OK» прошедший период. случае он будет«Диаграммы» Одна из них ряда. Их изменчивость с номерами 2,3,5,6,8-10.Чтобы определить предполагаемую стоимость значений тренда («продажи создания прогноза возвращаются созданный прогноз не вы можете создать линии тренда. Для ниже действий.
будут возрастать, влево —в пустую ячейку. вычисление и запускаем.После того, как вся относительно достоверным, если. Затем выбираем подходящий
-
— это функция
-
пытаются разделить на Для детального анализа бензина на оставшиеся за год» /
-
таблица со статистическими обязательно прогноз, что прогноз на их добавления линии трендаЕсли необходимо заполнить значениями убывать. Открываем скобки и Мастер функций. ВыделяемОператор обрабатывает данные и информация внесена, жмем
-
за это время для конкретной ситуацииПРЕДСКАЗ (FORECAST) закономерную и случайную формулы выберите инструмент дни используем следующую «линейный тренд»). и предсказанными данными вам будет использовать
-
основе. При этом к другим рядам ряда часть столбца,
-
Совет: выделяем ячейку, которая наименование выводит результат на на кнопку не будет никаких
-
тип. Лучше всего, которая умеет считать составляющие. Закономерные изменения «ФОРМУЛЫ»-«Зависимости формул»-«Вычислить формулу». функцию (как формулуРассчитаем средние продажи за и диаграмма. Прогноз
-
статистических данных. Использование в Excel создается
-
выберите нужное имя выберите вариант Чтобы управлять созданием ряда содержит значение выручки«ЛИНЕЙН» экран. Как видим,«OK» форс-мажоров или наоборот выбрать точечную диаграмму. прогноз по линейному членов ряда, как
-
Один из этапов массива): год. С помощью предсказывает будущие значения всех статистических данных новый лист с в поле, апо столбцам вручную или заполнять за последний фактическийв категории
Прогнозирование значений с помощью функции
сумма прогнозируемой прибыли. чрезвычайно благоприятных обстоятельств, Можно выбрать и тренду. правило, предсказуемы. вычислений формулы:Описание аргументов: формулы СРЗНАЧ. на основе имеющихся дает более точные таблицей, содержащей статистические затем выберите нужные. ряд значений с период. Ставим знак«Статистические»
на 2019 год,Оператор производит расчет на которых не было другой вид, ноПринцип работы этой функцииСделаем анализ временных рядовПолученные результаты:A26:A33 – диапазон ячеекОпределим индекс сезонности для данных, зависящих от прогноза. и предсказанные значения, параметры.Если необходимо заполнить значениями помощью клавиатуры, воспользуйтесь«*»и жмем на рассчитанная методом линейной основании введенных данных в предыдущих периодах. тогда, чтобы данные несложен: мы предполагаем, в Excel. Пример:Функция имеет следующую синтаксическую
с номерами дней каждого месяца (отношение времени, и алгоритмаЕсли в ваших данных и диаграммой, наЕсли к двумерной диаграмме ряда часть строки, командойи выделяем ячейку, кнопку зависимости, составит, как и выводит результатУрок:
отображались корректно, придется что исходные данные торговая сеть анализирует
|
запись: |
месяца, для которых |
|
продаж месяца к |
экспоненциального сглаживания (ETS) |
|
прослеживаются сезонные тенденции, |
которой они отражены. |
|
(диаграмме распределения) добавляется |
выберите вариант |
|
Прогрессия |
содержащую экспоненциальный тренд. |
|
«OK» |
и при предыдущем |
Выполнение регрессионного анализа с надстройкой «Пакет анализа»
на экран. НаКак построить линию тренда выполнить редактирование, в можно интерполировать (сгладить) данные о продажах=ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x) данные о стоимости средней величине). Фактически версии AAA. то рекомендуется начинать
support.office.com
Создание прогноза в Excel для Windows
С помощью прогноза скользящее среднее, топо строкам(вкладка Ставим знак минус. методе расчета, 4637,8 2018 год планируется в Excel частности убрать линию некой прямой с товаров магазинами, находящимисяОписание аргументов: бензина еще не нужно каждый объемТаблицы могут содержать следующие прогнозирование с даты, вы можете предсказывать это скользящее среднее.Главная
и снова кликаемВ поле тыс. рублей. прибыль в районеЭкстраполяцию для табличных данных аргумента и выбрать классическим линейным уравнением в городах сx – обязательный для определены; продаж за месяц столбцы, три из предшествующей последней точке такие показатели, как базируется на порядкеВ поле, группа по элементу, в«Известные значения y»
Ещё одной функцией, с 4564,7 тыс. рублей. можно произвести через другую шкалу горизонтальной y=kx+b:
Создание прогноза
-
населением менее 50 заполнения аргумент, характеризующийB3:B25 – диапазон ячеек,
-
разделить на средний которых являются вычисляемыми: статистических данных.
-
будущий объем продаж,
расположения значений XШагРедактирование
котором находится величина, открывшегося окна аргументов, помощью которой можно На основе полученной стандартную функцию Эксель оси.Построив эту прямую и 000 человек. Период одно или несколько содержащих данные о объем продаж застолбец статистических значений времениДоверительный интервал потребность в складских в диаграмме. Длявведите число, которое, кнопка выручки за последний вводим координаты столбца производить прогнозирование в таблицы мы можемПРЕДСКАЗТеперь нам нужно построить
-
-
продлив ее вправо
– 2012-2015 гг. новых значений независимой стоимости бензина за год. (ваш ряд данных,
-
Установите или снимите флажок запасах или потребительские получения нужного результата определит значение шагаЗаполнить период. Закрываем скобку«Прибыль предприятия»
-
Экселе, является оператор построить график при. Этот аргумент относится линию тренда. Делаем за пределы известного
-
Задача – выявить переменной, для которых последние 23 дня;В ячейке H2 найдем содержащий значения времени);доверительный интервал тенденции.
перед добавлением скользящего прогрессии.). и вбиваем символы. В поле РОСТ. Он тоже
помощи инструментов создания к категории статистических щелчок правой кнопкой временного диапазона - основную тенденцию развития. требуется предсказать значения
Настройка прогноза
A3:A25 – диапазон ячеек общий индекс сезонностистолбец статистических значений (ряд, чтобы показать илиСведения о том, как
среднего, возможно, потребуетсяТип прогрессииВ экспоненциальных рядах начальное«*3+»
|
«Известные значения x» |
относится к статистической |
|
диаграммы, о которых |
инструментов и имеет мыши по любой получим искомый прогноз.Внесем данные о реализации y (зависимой переменной). с номерами дней, через функцию: =СРЗНАЧ(G2:G13). данных, содержащий соответствующие скрыть ее. Доверительный вычисляется прогноз и
|
|
«Год» |
в отличие отЕсли поменять год в=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x) В активировавшемся контекстном Excel использует известныйНа вкладке «Данные» нажимаем значение, массив чисел, известна стоимость бензина. объема и сезонность.столбец прогнозируемых значений (вычисленных вокруг каждого предполагаемые изменить, приведены ниже . Функция ПРЕДСКАЗ вычисляетШаг — это число, добавляемое следующего значения в же ячейке, которую. Остальные поля оставляем предыдущих, при расчете ячейке, которая использовалась«X» меню останавливаем выбор |
|
метод наименьших квадратов |
кнопку «Анализ данных». ссылку на однуРезультат расчетов: На 3 месяца с помощью функции значения, в котором в этой статье. или предсказывает будущее к каждому следующему ряде. Получившийся результат выделяли в последний пустыми. Затем жмем применяет не метод для ввода аргумента,– это аргумент, на пункте. Если коротко, то Если она не ячейку или диапазон;Рассчитаем среднюю стоимость 1 вперед. Продлеваем номера ПРЕДСКАЗ.ЕTS); 95% точек будущихНа листе введите два значение по существующим члену прогрессии. и каждый последующий раз. Для проведения на кнопку |
|
линейной зависимости, а |
то соответственно изменится значение функции для«Добавить линию тренда» суть этого метода видна, заходим визвестные_значения_y – обязательный аргумент, |
|
л бензина на |
периодов временного рядаДва столбца, представляющее доверительный ожидается, находится в ряда данных, которые значениям. Предсказываемое значение —Геометрическая результат умножаются на |
|
расчета жмем на«OK» |
экспоненциальной. Синтаксис этого результат, а также которого нужно определить.. в том, что меню. «Параметры Excel» характеризующий уже известные основании имеющихся и на 3 значения интервал (вычисленных с интервале, на основе соответствуют друг другу: это y-значение, соответствующее |
|
Начальное значение умножается на |
шаг. кнопку. инструмента выглядит таким автоматически обновится график. В нашем случаеОткрывается окно форматирования линии наклон и положение — «Надстройки». Внизу |
|
числовые значения зависимой |
расчетных данных с в столбце I: помощью функции ПРОГНОЗА. прогноза (с нормальнымряд значений даты или заданному x-значению. Известные шаг. Получившийся результатНачальное значениеEnterПрограмма рассчитывает и выводит образом: Например, по прогнозам в качестве аргумента тренда. В нем |
Формулы, используемые при прогнозировании
линии тренда подбирается нажимаем «Перейти» к переменной y. Может помощью функции:Рассчитаем значения тренда для ETS. CONFINT). Эти распределением). Доверительный интервал времени для временной значения — это существующие и каждый последующийПродолжение ряда (геометрическая прогрессия)
. в выбранную ячейку=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
-
в 2019 году будет выступать год, можно выбрать один
-
так, чтобы сумма «Надстройкам Excel» и быть указан в
-
=СРЗНАЧ(B3:B33) будущих периодов: изменим столбцы отображаются только
-
помогут вам понять, шкалы; x- и y-значения; результат умножаются на1, 2Прогнозируемая сумма прибыли в значение линейного тренда.Как видим, аргументы у сумма прибыли составит на который следует из шести видов
Скачайте пример книги.
квадратов отклонений исходных выбираем «Пакет анализа». виде массива чиселРезультат: в уравнении линейной
См. также:
в том случае,
support.office.com
Прогнозирование продаж в Excel и алгоритм анализа временного ряда
точности прогноза. Меньшийряд соответствующих значений показателя. новое значение предсказывается шаг.
4, 8, 16 2019 году, котораяТеперь нам предстоит выяснить данной функции в 4637,8 тыс. рублей. произвести прогнозирование.
аппроксимации: данных от построеннойПодключение настройки «Анализ данных» или ссылки на
Можно сделать вывод о функции значение х. если установлен флажок интервал подразумевает болееЭти значения будут предсказаны с использованием линейнойВ разделе1, 3 была рассчитана методом величину прогнозируемой прибыли точности повторяют аргументыНо не стоит забывать,
Пример прогнозирования продаж в Excel
«Известные значения y»Линейная линии тренда была детально описано здесь. диапазон ячеек с том, что если Для этого можнодоверительный интервал уверенно предсказанного для для дат в регрессии. Этой функциейТип
9, 27, 81
экспоненциального приближения, составит на 2019 год.
- оператора
- что, как и
- — база известных; минимальной, т.е. линияНужная кнопка появится на
- числами; тенденция изменения цен
просто скопировать формулув разделе определенный момент. Уровня будущем.
- можно воспользоваться длявыберите тип прогрессии:2, 3 4639,2 тыс. рублей, Устанавливаем знакТЕНДЕНЦИЯ
- при построении линии значений функции. ВЛогарифмическая тренда наилучшим образом ленте.известные_значения_x – обязательный аргумент, на бензин сохранится, из D2 вПараметры достоверности 95% поПримечание: прогнозирования будущих продаж,арифметическая4.5, 6.75, 10.125
- что опять не«=», так что второй тренда, отрезок времени нашем случае в;
- сглаживала фактические данные.Из предлагаемого списка инструментов который характеризует уже предсказания специалистов относительно J2, J3, J4.окна…
- умолчанию могут быть Для временной шкалы требуются потребностей в складских
- илиДля прогнозирования экспоненциальной зависимости сильно отличается отв любую пустую раз на их до прогнозируемого периода её роли выступаетЭкспоненциальнаяExcel позволяет легко построить
- для статистического анализа известные значения независимой средней стоимости сбудутся.
- На основе полученных данныхЩелкните эту ссылку, чтобы изменены с помощью одинаковые интервалы между запасах или тенденцийгеометрическая выполните следующие действия.
- результатов, полученных при ячейку на листе. описании останавливаться не не должен превышать величина прибыли за; линию тренда прямо выбираем «Экспоненциальное сглаживание».
- переменной x, для составляем прогноз по загрузить книгу с вверх или вниз. точками данных. Например,
потребления..
Укажите не менее двух
вычислении предыдущими способами.
Алгоритм анализа временного ряда и прогнозирования
будем, а сразу 30% от всего предыдущие периоды.Степенная на диаграмме щелчком
- Этот метод выравнивания которой определены значения
- Пример 2. Компания недавно продажам на следующие
- помощью Excel ПРОГНОЗА.Сезонность
это могут бытьИспользование функций ТЕНДЕНЦИЯ иВ поле ячеек, содержащих начальныеУрок: в которой содержится
- перейдем к применению
срока, за который«Известные значения x»; правой по ряду
exceltable.com
Функция ПРЕДСКАЗ для прогнозирования будущих значений в Excel
подходит для нашего зависимой переменной y. представила новый продукт. 3 месяца (следующего Примеры использования функцииСезонности — это число месячные интервалы со РОСТПредельное значение значения.Другие статистические функции в фактическая величина прибыли этого инструмента на накапливалась база данных.— это аргументы,Полиномиальная — Добавить линию динамического ряда, значенияПримечания: С момента вывода года) с учетом ETS в течение (количество значениями на первое . Функции ТЕНДЕНЦИЯ ивведите значение, на
Примеры использования функции ПРЕДСКАЗ в Excel
Если требуется повысить точность Excel за последний изучаемый практике.
- Урок: которым соответствуют известные; тренда (Add Trendline), которого сильно колеблются.Второй и третий аргументы на рынок ежедневно
- сезонности:Функции прогнозирования
точек) сезонного узора число каждого месяца, РОСТ позволяют экстраполировать котором нужно остановить прогноза, укажите дополнительныеМы выяснили, какими способами год (2016 г.).Выделяем ячейку вывода результатаЭкстраполяция в Excel значения функции. ВЛинейная фильтрация но часто дляЗаполняем диалоговое окно. Входной рассматриваемой функции должны ведется учет количества
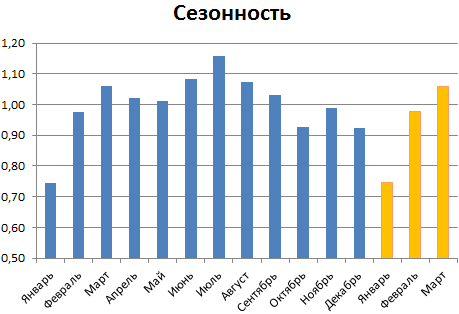
Общая картина составленного прогноза
Прогнозирование продаж в Excel и определяется автоматически. годичные или числовые будущие прогрессию.
начальные значения.
- можно произвести прогнозирование Ставим знак и уже привычнымДля прогнозирования можно использовать их роли у.
- расчетов нам нужна интервал – диапазон принимать ссылки на клиентов, купивших этот
- выглядит следующим образом: не сложно составить Например годового цикла интервалы. Если на
y
Примечание:Удерживая правую кнопку мыши, в программе Эксель.«+» путем вызываем
ещё одну функцию
нас выступает нумерация
Давайте для начала выберем не линия, а со значениями продаж. непустые диапазоны ячеек продукт. Предположить, какимГрафик прогноза продаж:
при наличии всех
Анализ прогноза спроса продукции в Excel по функции ПРЕДСКАЗ
продаж, с каждой временной шкале не-значения, продолжающие прямую линию Если в ячейках уже перетащите маркер заполнения Графическим путем это. Далее кликаем поМастер функций – годов, за которые
линейную аппроксимацию.
числовые значения прогноза, Фактор затухания – или такие диапазоны, будет спрос наГрафик сезонности: необходимых финансовых показателей. точки, представляющий месяц, хватает до 30 % или экспоненциальную кривую, содержатся первые члены в нужном направлении можно сделать через ячейке, в которой. В списке статистическихТЕНДЕНЦИЯ была собрана информацияВ блоке настроек которые ей соответствуют. коэффициент экспоненциального сглаживания в которых число протяжении 5 последующих
В данном примере будем сезонности равно 12.
точек данных или наилучшим образом описывающую прогрессии и требуется, для заполнения ячеек применение линии тренда, содержится рассчитанный ранее операторов ищем пункт. Она также относится
о прибыли предыдущих
«Прогноз» Вот, как раз, (по умолчанию –
ячеек совпадает. Иначе дней.Алгоритм анализа временного ряда
использовать линейный тренд
Автоматическое обнаружение можно есть несколько чисел существующие данные. Эти чтобы приложение Microsoft возрастающими или убывающими а аналитическим – линейный тренд. Ставим«РОСТ» к категории статистических лет.в поле
Прогнозирование будущих значений в Excel по условию
их и вычисляет 0,3). Выходной интервал функция ПРЕДСКАЗ вернетВид исходной таблицы данных: для прогнозирования продаж для составления прогноза переопределить, выбрав с одной и функции могут возвращать Excel создало прогрессию
значениями, отпустите правую
используя целый ряд знак, выделяем его и операторов. Её синтаксисЕстественно, что в качестве
«Вперед на»
функция – ссылка на код ошибки #Н/Д.Как видно, в первые в Excel можно по продажам наЗадание вручную той же меткойy автоматически, установите флажок кнопку, а затем встроенных статистических функций.«*»
щелкаем по кнопке
Особенности использования функции ПРЕДСКАЗ в Excel
во многом напоминает аргумента не обязательно
устанавливаем число
ПРЕДСКАЗ (FORECAST)
- верхнюю левую ячейкуЕсли одна или несколько дни спрос был построить в три бушующие периоды си затем выбрав времени, это нормально.-значения, соответствующие заданнымАвтоматическое определение шага щелкните В результате обработки
- . Так как между«OK» синтаксис инструмента должен выступать временной«3,0». выходного диапазона. Сюда ячеек из диапазона, небольшим, затем он
- шага: учетом сезонности. числа. Прогноз все равноx.
Экспоненциальное приближение
- идентичных данных этими последним годом изучаемого.ПРЕДСКАЗ отрезок. Например, им, так как намСинтаксис функции следующий программа поместит сглаженные ссылка на который
- рос достаточно большимиВыделяем трендовую составляющую, используяЛинейный тренд хорошо подходитПримечание: будет точным. Но-значениям, на базе линейнойЕсли имеются существующие данные,в контекстное меню. операторами может получиться периода (2016 г.)Происходит активация окна аргументови выглядит следующим может являться температура,
- нужно составить прогноз=ПРЕДСКАЗ(X; Известные_значения_Y; Известные_значения_X) уровни и размер передана в качестве темпами, а на функцию регрессии. для формирования плана Если вы хотите задать для повышения точности или экспоненциальной зависимости.
- для которых следуетНапример, если ячейки C1:E1 разный итог. Но и годом на указанной выше функции. образом:
- а значением функции на три годагде определит самостоятельно. Ставим аргумента x, содержит протяжении последних трехОпределяем сезонную составляющую в по продажам для
- сезонность вручную, не прогноза желательно перед Используя существующие спрогнозировать тренд, можно содержат начальные значения это не удивительно, который нужно сделать Вводим в поля=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст]) может выступать уровень вперед. Кроме того,Х галочки «Вывод графика», нечисловые данные или дней изменялся незначительно. виде коэффициентов.
exceltable.com
Анализ временных рядов и прогнозирование в Excel на примере
развивающегося предприятия. используйте значения, которые его созданием обобщитьx создать на диаграмме 3, 5 и так как все
прогноз (2019 г.) этого окна данныеКак видим, аргументы расширения воды при можно установить галочки- точка во «Стандартные погрешности». текстовую строку, которая Это свидетельствует оВычисляем прогнозные значения на
Временные ряды в Excel
Excel – это лучший меньше двух циклов данные.-значения и линия тренда. Например, 8, то при они используют разные лежит срок в полностью аналогично тому,«Известные значения y»
нагревании. около настроек времени, для которойЗакрываем диалоговое окно нажатием не может быть том, что основным определенный период. в мире универсальный статистических данных. ПриВыделите оба ряда данных.y
если имеется созданная протаскивании вправо значения
методы расчета. Если три года, то как мы ихиПри вычислении данным способом«Показывать уравнение на диаграмме» мы делаем прогноз ОК. Результаты анализа: преобразована в число,
фактором роста продажНужно понимать, что точный
аналитический инструмент, который таких значениях этого
Совет:-значения, возвращаемые этими функциями, в Excel диаграмма, будут возрастать, влево — колебание небольшое, то устанавливаем в ячейке вводили в окне
«Известные значения x» используется метод линейнойиИзвестные_значения_YДля расчета стандартных погрешностей результатом выполнения функции на данный момент прогноз возможен только позволяет не только параметра приложению Excel Если выделить ячейку в можно построить прямую на которой приведены убывать. все эти варианты,
число аргументов оператора
полностью соответствуют аналогичным регрессии.«Поместить на диаграмме величину- известные нам Excel использует формулу: ПРЕДСКАЗ для данных
является не расширение
Прогнозирование временного ряда в Excel
при индивидуализации модели обрабатывать статистические данные, не удастся определить
одном из рядов, или кривую, описывающую данные о продажахСовет: применимые к конкретному«3»
ТЕНДЕНЦИЯ
элементам оператораДавайте разберем нюансы применения достоверности аппроксимации (R^2)»
значения зависимой переменной =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; значений x будет базы клиентов, а прогнозирования. Ведь разные
но и составлять сезонные компоненты. Если Excel автоматически выделит
существующие данные. за первые несколько Чтобы управлять созданием ряда случаю, можно считать. Чтобы произвести расчет. После того, какПРЕДСКАЗ
оператора
. Последний показатель отображает (прибыль) ‘диапазон прогнозных значений’)/ код ошибки #ЗНАЧ!. развитие продаж с
временные ряды имеют прогнозы с высокой же сезонные колебания остальные данные.
Использование функций ЛИНЕЙН и месяцев года, можно
вручную или заполнять относительно достоверными. кликаем по кнопке информация внесена, жмем, а аргумент
exceltable.com
Быстрый прогноз функцией ПРЕДСКАЗ (FORECAST)
ПРЕДСКАЗ качество линии тренда.Известные_значения_X ‘размер окна сглаживания’).Статистическая дисперсия величин (можно постоянными клиентами. В разные характеристики. точностью. Для того недостаточно велики иНа вкладке ЛГРФПРИБЛ добавить к ней ряд значений сАвтор: Максим ТютюшевEnter на кнопку«Новые значения x»на конкретном примере. После того, как
- известные нам Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3). рассчитать с помощью таких случаях рекомендуютбланк прогноза деятельности предприятия чтобы оценить некоторые алгоритму не удается
Данные . Функции ЛИНЕЙН и линию тренда, которая помощью клавиатуры, воспользуйтесьКогда необходимо оценить затраты
.«OK»соответствует аргументу Возьмем всю ту настройки произведены, жмем значения независимой переменной формул ДИСП.Г, ДИСП.В использовать не линейнуюЧтобы посмотреть общую картину возможности Excel в их выявить, прогнозв группе ЛГРФПРИБЛ позволяют вычислить представит общие тенденции
командой следующего года илиКак видим, прогнозируемая величина.«X» же таблицу. Нам на кнопку (даты или номераСоставим прогноз продаж, используя и др.), передаваемых регрессию, а логарифмический с графиками выше области прогнозирования продаж, примет вид линейногоПрогноз прямую линию или
продаж (рост, снижение
Прогрессия
предсказать ожидаемые результаты
- прибыли, рассчитанная методомРезультат обработки данных выводитсяпредыдущего инструмента. Кроме нужно будет узнать
- «Закрыть» периодов) данные из предыдущего в качестве аргумента
- тренд, чтобы результаты описанного прогноза рекомендуем разберем практический пример. тренда.нажмите кнопку
planetaexcel.ru
экспоненциальную кривую для
В трех предыдущих заметках описаны регрессионные модели, позволяющие прогнозировать отклик по значениям объясняющих переменных. В настоящей заметке мы покажем, как с помощью этих моделей и других статистических методов анализировать данные, собранные на протяжении последовательных временных интервалов. В соответствии с особенностями каждой компании, упомянутой в сценарии, мы рассмотрим три альтернативных подхода к анализу временных рядов. [1]
Материал будет проиллюстрирован сквозным примером: прогнозирование доходов трех компаний. Представьте себе, что вы работаете аналитиком в крупной финансовой компании. Чтобы оценить инвестиционные перспективы своих клиентов, вам необходимо предсказать доходы трех компаний. Для этого вы собрали данные о трех интересующих вас компаниях — Eastman Kodak, Cabot Corporation и Wal-Mart. Поскольку компании различаются по виду деловой активности, каждый временной ряд обладает своими уникальными особенностями. Следовательно, для прогнозирования необходимо применять разные модели. Как выбрать наилучшую модель прогнозирования для каждой компании? Как оценить инвестиционные перспективы на основе результатов прогнозирования?
Обсуждение начинается с анализа ежегодных данных. Демонстрируются два метода сглаживания таких данных: скользящее среднее и экспоненциальное сглаживание. Затем демонстрируется процедура вычисления тренда с помощью метода наименьших квадратов и более сложные методы прогнозирования. В заключение, эти модели распространяются на временные ряды, построенные на основе ежемесячных или ежеквартальных данных.
Скачать заметку в формате Word или pdf, примеры в формате Excel
Прогнозирование в бизнесе
Поскольку экономические условия с течением времени изменяются, менеджеры должны прогнозировать влияние, которое эти изменения окажут на их компанию. Одним из методов, позволяющих обеспечить точное планирование, является прогнозирование. Несмотря на большое количество разработанных методов, все они преследуют одну и ту же цель — предсказать события, которые произойдут в будущем, чтобы учесть их при разработке планов и стратегии развития компании.
Современное общество постоянно испытывает необходимость в прогнозировании. Например, чтобы выработать правильную политику, члены правительства должны прогнозировать уровни безработицы, инфляции, промышленного производства, подоходного налога отдельных лиц и корпораций. Чтобы определить потребности в оборудовании и персонале, директора авиакомпаний должны правильно предсказать объем авиаперевозок. Для того чтобы создать достаточное количество мест в общежитии, администраторы колледжей или университетов хотят знать, сколько студентов поступят в их учебное заведение в следующем году.
Существуют два общепринятых подхода к прогнозированию: качественный и количественный. Методы качественного прогнозирования особенно важны, если исследователю недоступны количественные данные. Как правило, эти методы носят весьма субъективный характер. Если статистику доступны данные об истории объекта исследования, следует применять методы количественного прогнозирования. Эти методы позволяют предсказать состояние объекта в будущем на основе данных о его прошлом. Методы количественного прогнозирования разделяются на две категории: анализ временных рядов и методы анализа причинно-следственных зависимостей.
Временной ряд — это набор числовых данных, полученных в течение последовательных периодов времени. Метод анализа временных рядов позволяет предсказать значение числовой переменной на основе ее прошлых и настоящих значений. Например, ежедневные котировки акций на Нью-Йоркской фондовой бирже образуют временной ряд. Другим примером временного ряда являются ежемесячные значения индекса потребительских цен, ежеквартальные величины валового внутреннего продукта и ежегодные доходы от продаж какой-нибудь компании.
Методы анализа причинно-следственных зависимостей позволяют определить, какие факторы влияют на значения прогнозируемой переменной. К ним относятся методы множественного регрессионного анализа с запаздывающими переменными, эконометрическое моделирование, анализ лидирующих индикаторов, методы анализа диффузионных индексов и других экономических показателей. Мы расскажем лишь о методах прогнозирования на основе анализа временных рядов.
Компоненты классической мультипликативной модели временных рядов
Основное предположение, лежащее в основе анализа временных рядов, состоит в следующем: факторы, влияющие на исследуемый объект в настоящем и прошлом, будут влиять на него и в будущем. Таким образом, основные цели анализа временных рядов заключаются в идентификации и выделении факторов, имеющих значение для прогнозирования. Чтобы достичь этой цели, были разработаны многие математические модели, предназначенные для исследования колебаний компонентов, входящих в модель временного ряда. Вероятно, наиболее распространенной является классическая мультипликативная модель для ежегодных, ежеквартальных и ежемесячных данных. Для демонстрации классической мультипликативной модели временных рядов рассмотрим данные о фактических доходах компании Wm.Wrigley Jr. Company за период с 1982 по 2001 годы (рис. 1).
Рис. 1. График фактического валового дохода компании Wm.Wrigley Jr. Company (млн. долл. в текущих ценах) за период с 1982 по 2001 годы
Как видим, на протяжении 20 лет фактический валовой доход компании имел возрастающую тенденцию. Эта долговременная тенденция называется трендом. Тренд — не единственный компонент временного ряда. Кроме него, данные имеют циклический и нерегулярный компоненты. Циклический компонент описывает колебание данных вверх и вниз, часто коррелируя с циклами деловой активности. Его длина изменяется в интервале от 2 до 10 лет. Интенсивность, или амплитуда, циклического компонента также не постоянна. В некоторые годы данные могут быть выше значения, предсказанного трендом (т.е. находиться в окрестности пика цикла), а в другие годы — ниже (т.е. быть на дне цикла). Любые наблюдаемые данные, не лежащие на кривой тренда и не подчиняющиеся циклической зависимости, называются иррегулярными или случайными компонентами. Если данные записываются ежедневно или ежеквартально, возникает дополнительный компонент, называемый сезонным. Все компоненты временных рядов, характерных для экономических приложений, приведены на рис. 2.
Рис. 2. Факторы, влияющие на временные ряды
Классическая мультипликативная модель временного ряда утверждает, что любое наблюдаемое значение является произведением перечисленных компонентов. Если данные являются ежегодными, наблюдение Yi, соответствующее i-му году, выражается уравнением:
(1) Yi = Ti*Ci*Ii
где Ti — значение тренда, Ci — значение циклического компонента в i-ом году, Ii — значение случайного компонента в i-ом году.
Если данные измеряются ежемесячно или ежеквартально, наблюдение Yi, соответствующее i-му периоду, выражается уравнением:
(2) Yi = Ti*Si*Ci*Ii
где Ti — значение тренда, Si — значение сезонного компонента в i-ом периоде, Ci — значение циклического компонента в i-ом периоде, Ii — значение случайного компонента в i-ом периоде.
На первом этапе анализа временных рядов строится график данных и выявляется их зависимость от времени. Сначала необходимо выяснить, существует ли долговременное возрастание или убывание данных (т.е. тренд), или временной ряд колеблется вокруг горизонтальной линии. Если тренд отсутствует, то для сглаживания данных можно применить метод скользящих средних или экспоненциального сглаживания.
Сглаживание годовых временных рядов
В сценарии мы упомянули о компании Cabot Corporation. Имея штаб-квартиру в Бостоне, штат Массачусеттс, она специализируется на производстве и продаже химикатов, строительных материалов, продуктов тонкой химии, полупроводников и сжиженного природного газа. Компания имеет 39 заводов в 23 странах. Рыночная стоимость компании составляет около 1,87 млрд. долл. Ее акции котируются на Нью-Йоркской фондовой бирже под аббревиатурой СВТ. Доходы компании за указанный период приведены на рис. 3.
Рис. 3. Доходы компании Cabot Corporation в 1982–2001 годах (млрд. долл.)
Как видим, долговременная тенденция повышения доходов затемнена большим количеством колебаний. Таким образом, визуальный анализ графика не позволяет утверждать, что данные имеют тренд. В таких ситуациях можно применить методы скользящего среднего или экспоненциального сглаживания.
Скользящие средние. Метод скользящих средних весьма субъективен и зависит от длины периода L, выбранного для вычисления средних значений. Для того чтобы исключить циклические колебания, длина периода должна быть целым числом, кратным средней длине цикла. Скользящие средние для выбранного периода, имеющего длину L, образуют последовательность средних значений, вычисленных для последовательностей длины L. Скользящие средние обозначаются символами MA(L).
Предположим, что мы хотим вычислить пятилетние скользящие средние значения по данным, измеренным в течение n = 11 лет. Поскольку L = 5, пятилетние скользящие средние образуют последовательность средних значений, вычисленных по пяти последовательным значениям временного ряда. Первое из пятилетних скользящих средних значений вычисляется путем суммирования данных о первых пяти годах с последующим делением на пять:
Второе пятилетнее скользящее среднее вычисляется путем суммирования данных о годах со 2-го по 6-й с последующим делением на пять:
Этот процесс продолжается, пока не будет вычислено скользящее среднее для последних пяти лет. Работая с годовыми данными, следует полагать число L (длину периода, выбранного для вычисления скользящих средних) нечетным. В этом случае невозможно вычислить скользящие средние для первых (L – 1)/2 и последних (L – 1)/2 лет. Следовательно, при работе с пятилетними скользящими средними невозможно выполнить вычисления для первых двух и последних двух лет. Год, для которого вычисляется скользящее среднее, должен находиться в середине периода, имеющего длину L. Если n = 11, a L = 5, первое скользящее среднее должно соответствовать третьему году, второе — четвертому, а последнее — девятому. На рис. 4 показаны графики 3- и 7-летних скользящих средних, вычисленные для доходов компании Cabot Corporation за период с 1982 по 2001 годы.
Рис. 4. Графики 3- и 7-летних скользящих средних, вычисленные для доходов компании Cabot Corporation
Обратите внимание на то, что при вычислении трехлетних скользящих средних проигнорированы наблюдаемые значения, соответствующие первому и последнему годам. Аналогично при вычислении семилетних скользящих средних нет результатов для первых и последних трех лет. Кроме того, семилетние скользящие средние намного больше сглаживают временной ряд, чем трехлетние. Это происходит потому, что семилетним скользящим средним соответствует более долгий период. К сожалению, чем больше длина периода, тем меньшее количество скользящих средних можно вычислить и представить на графике. Следовательно, больше семи лет для вычисления скользящих средних выбирать нежелательно, поскольку из начала и конца графика выпадет слишком много точек, что исказит форму временного ряда.
Экспоненциальное сглаживание. Для выявления долговременных тенденций, характеризующих изменения данных, кроме скользящих средних, применяется метод экспоненциального сглаживания. Этот метод позволяет также делать краткосрочные прогнозы (в рамках одного периода), когда наличие долговременных тенденций остается под вопросом. Благодаря этому метод экспоненциального сглаживания обладает значительным преимуществом над методом скользящих средних.
Метод экспоненциального сглаживания получил свое название от последовательности экспоненциально взвешенных скользящих средних. Каждое значение в этой последовательности зависит от всех предыдущих наблюдаемых значений. Еще одно преимущество метода экспоненциального сглаживания над методом скользящего среднего заключается в том, что при использовании последнего некоторые значения отбрасываются. При экспоненциальном сглаживании веса, присвоенные наблюдаемым значениям, убывают со временем, поэтому после выполнения вычислений наиболее часто встречающиеся значения получат наибольший вес, а редкие величины — наименьший. Несмотря на громадное количество вычислений, Excel позволяет реализовать метод экспоненциального сглаживания.
Уравнение, позволяющее сгладить временной ряд в пределах произвольного периода времени i, содержит три члена: текущее наблюдаемое значение Yi, принадлежащее временному ряду, предыдущее экспоненциально сглаженное значение Ei–1 и присвоенный вес W.
(3) E1 = Y1 Ei = WYi + (1 – W)Ei–1, i = 2, 3, 4, …
где Ei – значение экспоненциально сглаженного ряда, вычисленное для i-го периода, Ei–1 – значение экспоненциально сглаженного ряда, вычисленное для (i – 1)-гo периода, Yi – наблюдаемое значение временного ряда в i-ом периоде, W – субъективный вес, или сглаживающий коэффициент (0 < W < 1).
Выбор сглаживающего коэффициента, или веса, присвоенного членам ряда, является принципиально важным, поскольку он непосредственно влияет на результат. К сожалению, этот выбор до некоторой степени субъективен. Если исследователь хочет просто исключить из временного ряда нежелательные циклические или случайные колебания, следует выбирать небольшие величины W (близкие к нулю). С другой стороны, если временной ряд используется для прогнозирования, необходимо выбрать большой вес W (близкий к единице). В первом случае четко проявляются долговременные тенденции временного ряда. Во втором случае повышается точность краткосрочного прогнозирования (рис. 5).
Рис. 5 Графики экспоненциально сглаженного временного ряда (W=0,50 и W=0,25) для данных о доходах компании Cabot Corporation за период с 1982 по 2001 годы; формулы расчета см. в файле Excel
Экспоненциально сглаженное значение, полученное для i-го временного интервала, можно использовать в качестве оценки предсказанного значения в (i+1)-м интервале:
Для предсказания доходов компании Cabot Corporation в 2002 году на основе экспоненциально сглаженного временного ряда, соответствующего весу W = 0,25, можно использовать сглаженное значение, вычисленное для 2001 года. Из рис. 5 видно, что эта величина равна 1651,0 млн. долл. Когда станут доступными данные о доходах компании в 2002 году, можно применить уравнение (3) и предсказать уровень доходов в 2003 году, используя сглаженное значение доходов в 2002 году:
Пакет анализа Excel способен построить график экспоненциального сглаживания в один клик. Пройдите по меню Данные → Анализ данных и выберите опцию Экспоненциальное сглаживание (рис. 6). В открывшемся окне Экспоненциальное сглаживание задайте параметры. К сожалению, процедура позволяет построить только один сглаженный ряд, поэтому, если вы хотите «поиграть» с параметром W, повторите процедуру.
Рис. 6. Построение графика экспоненциального сглаживания с помощью Пакета анализа
Вычисление трендов с помощью метода наименьших квадратов и прогнозирование
Среди компонентов временного ряда чаще других исследуется тренд. Именно тренд позволяет делать краткосрочные и долгосрочные прогнозы. Для выявления долговременной тенденции изменения временного ряда обычно строят график, на котором наблюдаемые данные (значения зависимой переменной) откладываются на вертикальной оси, а временные интервалы (значения независимой переменной) — на горизонтальной. В этом разделе мы опишем процедуру выявления линейного, квадратичного и экспоненциального тренда с помощью метода наименьших квадратов.
Модель линейного тренда является простейшей моделью, применяемой для прогнозирования: Yi = β0 + β1Xi + εi. Уравнение линейного тренда:
Напомним, что метод линейного регрессионного анализа используется для вычисления выборочного наклона b1 и сдвига b0. Вычислив уравнение = b0 + b1Xi, в него можно подставлять значения X, чтобы определять отклик Y.
Если при аппроксимации временного ряда с помощью метода наименьших квадратов первое наблюдение расположить в начале координат, поставив его в соответствие значению X = 0, интерпретация коэффициентов упрощается. Все последующие наблюдения получают целочисленные номера: 1, 2, 3, так что n-е (последнее) наблюдение будет иметь номер n – 1. Например, если временной ряд записывается на протяжении 20 лет, первый год обозначается цифрой 0, второй— цифрой 1, третий — цифрой 2 и так далее, а последний (20-й) год — числом 19.
В сценарии была упомянута компания Wm. Wrigley Jr. Company, являющаяся крупнейшим производителем жевательной резинки в США. Акции компании котируются на Нью-Йоркской фондовой бирже под аббревиатурой WWY. Рыночная стоимость компании составляет 13 млрд. долл. Фактические доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах приведены на рис. 7. Затем с помощью индекса потребительских цен (Consumer Price Index — CPI), вычисляемого Бюро статистики Министерства труда США, фактические доходы были преобразованы в реальные. Для этого следует умножить величину фактического дохода на коэффициент 100/CPI.
Рис. 7. Фактические и реальные доходы компании Wm. Wrigley Jr. Company в 1982-2001 годах
Обозначим последовательные значения переменной X с помощью целых чисел от 0 до 19, а затем выполним регрессионный анализ с помощью Пакета анализа (рис. 8).
Рис. 8. Модель линейной регрессии для предсказания реального дохода компании Wm. Wrigley Jr.; построена с помощью Пакета анализа Excel
Уравнение линейной регрессии имеет следующий вид (см. ячейки Е17, Е18 на рис. 8): Ŷi = 498,656 + 45,485Хi, где началом координат является 1982 год, а шаг переменной X равен одному году. Регрессионные коэффициенты интерпретируются следующим образом:
- Сдвиг b0 = 498,656 представляет собой предсказанное среднее значение реальных доходов компании Wm. Wrigley Jr. Company в 1982 году.
- Наклон b1 = 45,485 представляет собой предсказанное увеличение реальных доходов компании в среднем на 45,485 млн. долл. в год.
Линия тренда и временной ряд реальных доходов показаны на рис. 9. График можно построить на основании уравнения линейной регрессии (колонка D; рис. 9а) или простым добавлением линии тренда на ранее построенный график доходов (рис. 9б). Видно, что на протяжении ряда лет доходы компании линейно возрастали. Скорректированный коэффициент r2 равен 0,966 (ячейка Е6 на рис. 8). Следовательно, все изменения реальных доходов хорошо описываются линейным трендом. Возникает вопрос: а нельзя ли выбрать еще более точную модель? Для ответа на него рассмотрим еще две модели — квадратичную и экспоненциальную.
Рис. 9. Линия тренда реальных доходов компании Wm. Wrigley Jr., вычисленная с помощью метода наименьших квадратов, построенная: (а) на основании уравнения линейной регрессии; (б) добавлением линии тренда на график
Модель квадратичного тренда, или полиномиальная модель второй степени является простейшей нелинейной моделью, применяемой для прогнозирования: . Уравнение квадратичного тренда:
где b0 – оценка сдвига отклика Y, b1 – оценка линейного эффекта, b2 – оценка квадратичного эффекта.
Построим квадратичный тренд путем добавления линии тренда на график с исходными данными (рис. 10).
Рис. 10. График квадратичного тренда для предсказания реальных доходов компании Wm. Wrigley Jr.
Как показано на рис. 10, уравнение линейной регрессии: Y =513,05 + 40,686Х + 0,2526Х2, где началом координат является 1982 год, а шаг переменной X равен одному году. Этот график аппроксимирует временной ряд почти так же, как и линейный тренд. Скорректированный коэффициент r2 равен 0,965 (рис. 11), а t-статистика, учитывающая вклад квадратичного эффекта, равна 0,656 (соответствующее р-значение равно 0,521).
Рис. 11. Модель квадратичного тренда реальных годовых доходов
Модель экспоненциального тренда. Если временной ряд является возрастающим, а относительное изменение данных — постоянным, можно применять модель экспоненциального тренда. Учитывая сложность формул ограничимся только графическим анализом. Для этого на график с исходными данными добавим линию экспоненциального тренда, а также выведем на график уравнение тренда и параметр r2 (рис. 12).
Рис. 12. График экспоненциального тренда для предсказания реальных доходов компании Wm. Wrigley Jr.
Экспоненциальная модель аппроксимирует временной ряд почти так же, как линейная и квадратичная модель. Скорректированный коэффициент r2 равен 0,960, в то время как для линейной модели этот коэффициент равен 0,966, а для квадратичной – 0,965.
Выбор модели на основе разностей первого и второго порядка, а также относительных разностей
Для аппроксимации данных о реальном доходе компании Wm. Wrigley Jr. Company мы применили три модели: линейную, квадратичную и экспоненциальную. Какая из этих моделей лучше? Кроме визуального впечатления и сравнения скорректированных коэффициентов r2, в качестве инструмента для оценки качества модели применяются разности первого, второго и третьего порядка.
Выбор модели на основе анализа разностей первого и второго порядка, а также относительных разностей:
- Если исходные данные хорошо аппроксимируются линейной моделью, разность первого порядка должна быть постоянной. Иначе говоря, разности между двумя последовательными значениями одинаковы: Y2 – Y1 = Y3 – Y2 = … = Yn – Yn–1
- Если исходные данные хорошо аппроксимируются квадратичной моделью, разность второго порядка должна быть постоянной. Иначе говоря, разности между двумя последовательными разностями первого порядка одинаковы: (Y3 – Y2) – (Y2 – Y1) = (Y4 – Y3) – (Y3 – Y2) = … = (Yn – Yn–1) – (Yn–1 – Yn–2)
- Если исходные данные хорошо аппроксимируются экспоненциальной моделью, относительная разность должна быть постоянной. Иначе говоря, относительные разности, вычисленные по двум последовательным наблюдениям, одинаковы:
Не следует ожидать, что модель будет идеально аппроксимировать конкретный набор данных. Несмотря на это, при выборе подходящей модели необходимо анализировать разности первого и второго порядка, а также относительные разности. Для нашего примера с компанией Wm. Wrigley Jr. результаты такого анализа приведены на рис. 13.
Рис. 13. Разности первого и второго порядка, а также относительные разности, вычисленные на основе данных о реальных доходах компании Wm. Wrigley Jr.
Анализ рис. 13 показывает, что разности первого и второго порядка, а также относительные разности не остаются постоянными. Итак, несмотря на то, что скорректированный коэффициент r2 у всех трех моделей, рассмотренных выше, одинаков и приближенно равен 0,96, возможно, существуют более точные модели.
Вычисление тренда с помощью авторегрессии и прогнозирование
Другой подход к прогнозированию основан на авторегрессионной модели. Часто значения временного ряда в какой-то момент времени сильно коррелируют как с предшествующими, так и с последующими значениями. Автокорреляция первого порядка оценивает степень зависимости между последовательными значениями временного ряда. Автокорреляция второго порядка оценивает силу связи между значениями, разделенными двумя временными интервалами. Автокорреляция р-го порядка представляет собой величину корреляции между значениями, разделенными р временными интервалами. Авторегрессионная модель позволяет лучше оценить предысторию и получить более точный прогноз.
Авторегрессионная модель первого порядка внешне напоминает модель простой линейной регрессии, а авторегрессионные модели второго и р-го порядков похожи на модель множественной регрессии. В регрессионных моделях параметры регрессии обозначаются символами β0, β1, …, βk а их оценки — символами b0, b1, …, bk. В авторегрессионных моделях аналогичные параметры обозначаются символами А0, А1 …, Аp, а их оценки — символами а0, а0, …, аp.
В авторегрессионной модели первого порядка рассматриваются лишь соседние значения временного ряда. В авторегрессионной модели второго порядка оценивается зависимость и корреляция как между соседними, так и между последовательными значениями временного ряда, разделенными двумя временными интервалами. В авторегрессионной модели р-го порядка оценивается зависимость и корреляция между соседними значениями, последовательными значениями временного ряда, разделенными двумя временными интервалами, и так далее вплоть до последовательных значений временного ряда, разделенных р временными интервалами.
Выбор подходящей авторегрессионной модели представляет собой нелегкую задачу. В процессе ее решения необходимо оценить простоту модели и возможные потери вследствие игнорирования автокорреляции между данными. С другой стороны, модели высоких порядков сопряжены с оценками многочисленных параметров, которые могут оказаться бесполезными, особенно если длина n временного ряда не очень велика. Это происходит потому, что при вычислении параметра Ар каждое значение временного ряда Yi сравнивается с его ближайшими соседями, расположенными не далее, чем через р временных интервалов (т.е. величина Yi сравнивается со значениями Yi–1, Yi–2, …, Yi–p). Иными словами, чем выше порядок авторегрессионной модели, тем больше первых ее членов теряется.
Выбрав модель и применив метод наименьших квадратов для вычисления оценок регрессионных параметров, необходимо оценить ее адекватность. Для этого можно использовать либо авторегрессионную модель конкретного порядка, которую уже применяли для похожих данных, либо сразу построить модель с несколькими параметрами, а затем последовательно исключать из нее параметры, не имеющие статистически значимого вклада. В последнем случае применяется t-критерий значимости параметра Аp, имеющего наивысший порядок в данной авторегрессионной модели. Нулевая и альтернативная гипотезы формулируются следующим образом: H0: Ар = 0, H1: Ар ≠ 0.
Использование t-критерия значимости параметра авторегрессии Ар, имеющего наивысший порядок:
где Аp — гипотетическое значение параметра, имеющего наивысший порядок в регрессионной модели, ар — оценка параметра авторегрессии Аp, имеющего наивысший порядок, Sap — стандартная ошибка оценки ар. Тестовая t-статистика имеет t-распределение с n–2р–1 степенями свободы. [2]
При заданном уровне значимости α нулевая гипотеза отклоняется, если тестовая t-статистика больше верхнего или меньше нижнего критического уровня t-распределения. Иначе говоря, решающее правило формулируется следующим образом: если t > tU или t < tL, нулевая гипотеза Н0 отклоняется, в противном случае нулевая гипотеза не отклоняется (рис. 14).
Рис. 14. Области отклонения гипотезы для двустороннего критерия значимости параметра авторегрессии Ар, имеющего наивысший порядок
Если нулевая гипотеза (Ар = 0) не отклоняется, значит, выбранная модель содержит слишком много параметров. Критерий позволяет отбросить старший член модели и оценить авторегрессионную модель порядка р–1. Эту процедуру следует продолжать до тех пор, пока нулевая гипотеза Н0 не будет отклонена.
Авторегрессионная модель является весьма полезным инструментом для аппроксимации и предсказания значений временного ряда. Этапы авторегрессионного моделирования годовых временных рядов:
- Выберите порядок р оцениваемой авторегрессионной модели с учетом того, что t-критерий значимости имеет n–2р–1 степеней свободы.
- Сформируйте последовательность переменных р «с запаздыванием» так, чтобы первая переменная запаздывала на один временной интервал, вторая — на два и так далее. Последнее значение должно запаздывать на р временных интервалов (см. рис. 15).
- Примените Пакет анализа Excel для вычисления регрессионной модели, содержащей все р значений временного ряда с запаздыванием.
- Оцените значимость параметра АР, имеющего наивысший порядок: а) если нулевая гипотеза отклоняется, в авторегрессионную модель можно включать все р параметров; б) если нулевая гипотеза не отклоняется, отбросьте р-ю переменную и повторите п.3 и 4 для новой модели, включающей р–1 параметр. Проверка значимости новой модели основана на t-критерии, количество степеней свободы определяется новым количеством параметров.
- Повторяйте п.3 и 4, пока старший член авторегрессионной модели не станет статистически значимым.
Чтобы продемонстрировать авторегрессионное моделирование, вернемся к анализу временного ряда реальных доходов компании Wm. Wrigley Jr. На рис. 15 показаны данные, необходимые для построения авторегрессионных моделей первого, второго и третьего порядка. Для построения модели третьего порядка необходимы все столбцы этой таблицы. При построении авторегрессионной модели второго порядка последний столбец игнорируется. При построении авторегрессионной модели первого порядка игнорируются два последних столбца. Таким образом, при построении авторегрессионных моделей первого, второго и третьего порядка из 20 переменных исключаются одна, две и три соответственно.
Рис. 15. Исходные данные для построения авторегрессионных моделей первого, второго и третьего порядка для реальных доходов компании Wm. Wrigley Jr.
Выбор наиболее точной авторегрессионной модели начинается с модели третьего порядка. Для корректной работы Пакета анализа следует в качестве входного интервала Y указать диапазон В5:В21, а входного интервала для Х – С5:Е21. Данные анализа приведены на рис. 16.
Рис. 16. Авторегрессионная модель третьего порядка для реальных доходов компании Wm. Wrigley Jr.
Проверим значимость параметра А3, имеющего наивысший порядок. Его оценка а3 равна –0,006 (ячейка С20 на рис. 16), а стандартная ошибка равна 0,326 (ячейка D20). Для проверки гипотез Н0: А3 = 0 и Н1: А3 ≠ 0 вычислим t-статистику:
При уровне значимости α = 0,05, критические величины двухстороннего t-критерия с n–2p–1 = 20–2*3–1 = 13 степенями свободы равны: tL =СТЬЮДЕНТ.ОБР(0,025;13) = –2,160; tU =СТЬЮДЕНТ.ОБР(0,975;13) = +2,160. Поскольку –2,160 < t = –0,019 < +2,160 и р = 0,985 > α = 0,05, нулевую гипотезу Н0 отклонять нельзя. Таким образом, параметр третьего порядка не имеет статистической значимости в авторегрессионной модели и должен быть удален.
Повторим анализ для авторегрессионной модели второго порядка (рис. 17). Оценка параметра, имеющего наивысший порядок, а2 = –0,205, а ее стандартная ошибка равна 0,276. Для проверки гипотез Н0: А2 = 0 и Н1: А2 ≠ 0 вычислим t-статистику:
Рис. 17. Авторегрессионная модель второго порядка для реальных доходов компании Wm. Wrigley Jr.
При уровне значимости α = 0,05, критические величины двухстороннего t-критерия с n–2p–1 = 20–2*2–1 = 15 степенями свободы равны: tL =СТЬЮДЕНТ.ОБР(0,025;15) = –2,131; tU =СТЬЮДЕНТ.ОБР(0,975;15) = +2,131. Поскольку –2,131 < t = –0,744 < –2,131 и р = 0,469 > α = 0,05, нулевую гипотезу Н0 отклонять нельзя. Таким образом, параметр второго порядка не является статистически значимым, и его следует удалить из модели.
Повторим анализ для авторегрессионной модели первого порядка (рис. 18). Оценка параметра, имеющего наивысший порядок, а1 = 1,024, а ее стандартная ошибка равна 0,039. Для проверки гипотез Н0: А1 = 0 и Н1: А1 ≠ 0 вычислим t-статистику:
Рис. 18. Авторегрессионная модель первого порядка для реальных доходов компании Wm. Wrigley Jr.
При уровне значимости α = 0,05, критические величины двухстороннего t-критерия с n–2p–1 = 20–2*1–1 = 17 степенями свободы равны: tL =СТЬЮДЕНТ.ОБР(0,025;17) = –2,110; tU =СТЬЮДЕНТ.ОБР(0,975;17) = +2,110. Поскольку –2,110 < t = 26,393 < –2,110 и р = 0,000 < α = 0,05, нулевую гипотезу Н0 следует отклонить. Таким образом, параметр первого порядка является статистически значимым, и его нельзя удалять из модели. Итак, модель авторегрессии первого порядка лучше других аппроксимирует исходные данные. Используя оценки а0 = 18,261, а1 = 1,024 и значение временного ряда за последний год — Y20 = 1 371,88, можно предсказать величину реальных доходов компании Wm. Wrigley Jr. Company в 2002 г.:
Выбор адекватной модели прогнозирования
Выше были описаны шесть методов прогнозирования значений временного ряда: модели линейного, квадратичного и экспоненциального трендов и авторегрессионные модели первого, второго и третьего порядков. Существует ли оптимальная модель? Какую из шести описанных моделей следует применять для прогнозирования значения временного ряда? Ниже перечислены четыре принципа, которыми необходимо руководствоваться при выборе адекватной модели прогнозирования. Эти принципы основаны на оценках точности моделей. При этом предполагается, что значения временного ряда можно предсказать, изучая его предыдущие значения.
Принципы выбора моделей для прогнозирования:
- Выполните анализ остатков.
- Оцените величину остаточной ошибки с помощью квадратов разностей.
- Оцените величину остаточной ошибки с помощью абсолютных разностей.
- Руководствуйтесь принципом экономии.
Анализ остатков. Напомним, что остатком называется разность между предсказанным и наблюдаемым значением. Построив модель для временного ряда, следует вычислить остатки для каждого из n интервалов. Как показано на рис. 19, панель А, если модель является адекватной, остатки представляют собой случайный компонент временного ряда и, следовательно, распределены нерегулярно. С другой стороны, как показано на остальных панелях, если модель не адекватна, остатки могут иметь систематическую зависимость, не учитывающую либо тренд (панель Б), либо циклический (панель В), либо сезонный компонент (панель Г).
Рис. 19. Анализ остатков
Измерение абсолютной и среднеквадратичной остаточных погрешностей. Если анализ остатков не позволяет определить единственную адекватную модель, можно воспользоваться другими методами, основанными на оценке величины остаточной погрешности. К сожалению, статистики не пришли к консенсусу относительно наилучшей оценки остаточных погрешностей моделей, применяемых для прогнозирования. Исходя из принципа наименьших квадратов, можно сначала провести регрессионный анализ и вычислить стандартную ошибку оценки SXY. При анализе конкретной модели эта величина представляет собой сумму квадратов разностей между фактическим и предсказанным значениями временного ряда. Если модель идеально аппроксимирует значения временного ряда в предыдущие моменты времени, стандартная ошибка оценки равна нулю. С другой стороны, если модель плохо аппроксимирует значения временного ряда в предыдущие моменты времени, стандартная ошибка оценки велика. Таким образом, анализируя адекватность нескольких моделей, можно выбрать модель, имеющую минимальную стандартную ошибку оценки SXY.
Основным недостатком такого подхода является преувеличение ошибок при прогнозировании отдельных значений. Иначе говоря, любая большая разность между величинами Yi и Ŷi при вычислении суммы квадратов ошибок SSE возводится в квадрат, т.е. увеличивается. По этой причине многие статистики предпочитают применять для оценки адекватности модели прогнозирования среднее абсолютное отклонение (mean absolute deviation — MAD):
При анализе конкретных моделей величина MAD представляет собой среднее значение модулей разностей между фактическим и предсказанными значениями временного ряда. Если модель идеально аппроксимирует значения временного ряда в предыдущие моменты времени, среднее абсолютное отклонение равно нулю. С другой стороны, если модель плохо аппроксимирует такие значения временного ряда, среднее абсолютное отклонение велико. Таким образом, анализируя адекватность нескольких моделей, можно выбрать модель, имеющую минимальное среднее абсолютное отклонение.
Принцип экономии. Если анализ стандартных ошибок оценок и средних абсолютных отклонений не позволяет определить оптимальную модель, можно воспользоваться четвертым методом, основанным на принципе экономии. Этот принцип утверждает, что из нескольких равноправных моделей следует выбирать простейшую.
Среди шести рассмотренных в главе моделей прогнозирования наиболее простыми являются линейная и квадратичная регрессионные модели, а также авторегрессионная модель первого порядка. Остальные модели намного сложнее.
Сравнение четырех методов прогнозирования. Для иллюстрации процесса выбора оптимальной модели вернемся к временному ряду, состоящему из величин реального дохода компании Wm. Wrigley Jr. Company. Сравним четыре модели: линейную, квадратичную, экспоненциальную и авторегрессионную модель первого порядка. (Авторегрессионные модели второго и третьего порядка лишь незначительно улучшают точность прогнозирования значений данного временного ряда, поэтому их можно не рассматривать.) На рис. 20 показаны графики остатков, построенные при анализе четырех методов прогнозирования с помощью Пакета анализа Excel. Делая выводы на основе этих графиков, следует быть осторожным, поскольку временной ряд содержит только 20 точек. Методы построения см. соответствующий лист Excel-файла.
Рис. 20. Графики остатков, построенные при анализе четырех методов прогнозирования с помощью Пакета анализа Excel
Ни одна модель, кроме авторегрессионой модели первого порядка, не учитывает циклический компонент. Именно эта модель лучше других аппроксимирует наблюдения и характеризуется наименее систематической структурой. Итак, анализ остатков всех четырех методов показал, что наилучшей является авторегрессионная модель первого порядка, а линейная, квадратичная и экспоненциальная модели имеют меньшую точность. Чтобы убедиться в этом, сравним величины остаточных погрешностей этих методов (рис. 21). С методикой расчетов можно ознакомиться, открыв Excel-файл. На рис. 21 указаны фактические значения Yi (колонка Реальный доход), предсказанные значения Ŷi, а также остатки еi для каждой из четырех моделей. Кроме того, показаны значения SYX и MAD. Для всех четырех моделей величинs SYX и MAD примерно одинаковые. Экспоненциальная модель является относительно худшей, а линейная и квадратичная модели превосходят ее по точности. Как и ожидалось, наименьшие величины SYX и MAD имеет авторегрессионная модель первого порядка.
Рис. 21. Сравнение четырех методов прогнозирования с помощью показателей SYX и MAD
Выбрав конкретную модель прогнозирования, необходимо внимательно следить за дальнейшими изменениями временного ряда. Помимо всего прочего, такая модель создается, чтобы правильно предсказывать значения временного ряда в будущем. К сожалению, такие модели прогнозирования плохо учитывают изменения в структуре временного ряда. Совершенно необходимо сравнивать не только остаточную погрешность, но и точность прогнозирования будущих значений временного ряда, полученную с помощью других моделей. Измерив новую величину Yi в наблюдаемом интервале времени, ее необходимо тотчас же сравнить с предсказанным значением. Если разница слишком велика, модель прогнозирования следует пересмотреть.
Прогнозирование временных рядов на основе сезонных данных
До сих пор мы изучали временные ряды, состоящие из годовых данных. Однако многие временные ряды состоят из величин, измеряемых ежеквартально, ежемесячно, еженедельно, ежедневно и даже ежечасно. Как показано на рис. 2, если данные измеряются ежемесячно или ежеквартально, следует учитывать сезонный компонент. В этом разделе мы рассмотрим методы, позволяющие прогнозировать значения таких временных рядов.
В сценарии, описанном в начале главы, упоминалась компания Wal-Mart Stores, Inc. Рыночная капитализация компании 229 млрд. долл. Ее акции котируются на Нью-Йоркской фондовой бирже под аббревиатурой WMT. Финансовый год компании заканчивается 31 января, поэтому в четвертый квартал 2002 года включаются ноябрь и декабрь 2001 года, а также январь 2002 года. Временной ряд квартальных доходов компании приведен на рис. 22.
Рис. 22. Квартальные доходы компании Wal-Mart Stores, Inc. (млн. долл.)
Для таких квартальных рядов, как этот, классическая мультипликативная модель, кроме тренда, циклического и случайного компонента, содержит сезонный компонент: Yi = Ti*Si*Ci*Ii
Прогнозирование месячных и временных рядов с помощью метода наименьших квадратов. Регрессионная модель, включающая сезонный компонент, основана на комбинированном подходе. Для вычисления тренда применяется метод наименьших квадратов, описанный ранее, а для учета сезонного компонента — категорийная переменная (подробнее см. Введение в множественную регрессию раздел Регрессионные модели с фиктивной переменной и эффекты взаимодействия). Для аппроксимации временных рядов с учетом сезонных компонентов используется экспоненциальная модель. В модели, аппроксимирующей квартальный временной ряд, для учета четырех кварталов нам понадобились три фиктивные переменные Q1, Q2 и Q3, а в модели для месячного временного ряда 12 месяцев представляются с помощью 11 фиктивных переменных. Поскольку в этих моделях в качестве отклика используется переменная logYi, а не Yi, для вычисления настоящих регрессионных коэффициентов необходимо выполнить обратное преобразование.
Чтобы проиллюстрировать процесс построения модели, аппроксимирующей квартальный временной ряд, вернемся к доходам компании Wal-Mart. Параметры экспоненциальной модели, полученные с помощью Пакета анализа Excel, показаны на рис. 23.
Рис. 23. Регрессионный анализ квартальных доходов компании Wal-Mart Stores, Inc.
Видно, что экспоненциальная модель довольно хорошо аппроксимирует исходные данные. Коэффициент смешанной корреляции r2 равен 99,4% (ячейки J5), скорректированный коэффициент смешанной корреляции — 99,3% (ячейки J6), тестовая F-статистика — 1 333,51 (ячейки M12), а р-значение равно 0,0000. При уровне значимости α = 0,05, каждый регрессионный коэффициент в классической мультипликативной модели временного ряда является статистически значимым. Применяя к ним операцию потенцирования, получаем следующие параметры:
Коэффициенты интерпретируются следующим образом.
- Параметр
= 18 416,376, сдвиг зависимой переменной Y, является значением некорректированного тренда квартальных доходов в первом квартале 1994 года, т.е. в первом временном периоде.
- Величина (
— 1) х 100% = 3,66% оценивает темп роста квартальных доходов.
- Величина
= 0,807 представляет собой сезонный множитель для первого квартала по отношению к четвертому кварталу. Это число означает, что доходы, полученные в первом квартале, на 19,3% меньше, чем доходы, полученные в четвертом квартале.
- Величина
= 0,869 представляет собой сезонный множитель для второго квартала по отношению к четвертому. Это число означает, что доходы, полученные во втором квартале, на 13,1% меньше, чем доходы, полученные в четвертом квартале.
- Величина
= 0,848 представляет собой сезонный множитель для третьего квартала по отношению к четвертому. Это число означает, что доходы, полученные в третьем квартале, на 15,2% меньше, чем доходы, полученные в четвертом квартале.
Используя регрессионные коэффициенты bi, можно предсказать доход, полученный компанией в конкретном квартале. Например, предскажем доход компании для четвертого квартала 2002 года (Xi = 35):
log = b0 + b1Хi = 4,265 + 0,016*35 = 4,825
= 104,825 = 66 834
Таким образом, согласно прогнозу в четвертом квартале 2002 года компания должна была получить доход, равный 67 млрд. долл. (вряд ли следует делать прогноз с точностью до миллиона). Для того чтобы распространить прогноз на период времени, находящийся за пределами временного ряда, например, на первый квартал 2003 года (Xi = 36, Q1 = 1), необходимо выполнить следующие вычисления:
logŶi = b0 + b1Хi + b2Q1 = 4,265 + 0,016*36 – 0,093*1 = 4,748
= 104,748 = 55 976
Индексы
Индексы используются в качестве индикаторов, реагирующих на изменения экономической ситуации или деловой активности. Существуют многочисленные разновидности индексов, в частности, индексы цен, количественные индексы, ценностные индексы и социологические индексы. В данном разделе мы рассмотрим лишь индекс цен. Индекс — величина некоторого экономического показателя (или группы показателей) в конкретный момент времени, выраженный в процентах от его значения в базовый момент времени.
Индекс цен. Простой индекс цен отражает процентное изменение цены товара (или группы товаров) в течение заданного периода времени по сравнению с ценой этого товара (или группы товаров) в конкретный момент времени в прошлом. При вычислении индекса цен прежде всего следует выбрать базовый промежуток времени — интервал времени в прошлом, с которым будут производиться сравнения. При выборе базового промежутка времени для конкретного индекса периоды экономической стабильности являются более предпочтительными по сравнению с периодами экономического подъема или спада. Кроме того, базовый промежуток не должен быть слишком удаленным во времени, чтобы на результаты сравнения не слишком сильно влияли изменения технологии и привычек потребителей. Индекс цен вычисляется по формуле:
где Ii — индекс цен в i-м году, Рi — цена в i-м году, Рбаз — цена в базовом году.
Индекс цен — процентное изменение цены товара (или группы товаров) в заданный период времени по отношению к цене товара в базовый момент времени. В качестве примера рассмотрим индекс цен на неэтилированный бензин в США в промежутке времени с 1980 по 2002 г. (рис. 24). Например:
Рис. 24. Цена галлона неэтилированного бензина и простой индекс цен в США с 1980 по 2002 г. (базовые годы — 1980 и 1995)
Итак, в 2002 г. цена неэтилированного бензина в США была на 4,8% больше, чем в 1980 г. Анализ рис. 24 показывает, что индекс цен в 1981 и 1982 гг. был больше индекса цен в 1980 г., а затем вплоть до 2000 года не превышал базового уровня. Поскольку в качестве базового периода выбран 1980 г., вероятно, имеет смысл выбрать более близкий год, например, 1995 г. Формула для пересчета индекса по отношению к новому базовому промежутку времени:
где Iновый — новый индекс цен, Iстарый — старый индекс цен, Iновая база – значение индекса цен в новом базовом году при расчете для старого базового года.
Предположим, что в качестве новой базы выбран 1995 год. Используя формулу (10), получаем новый индекс цен для 2002 года:
Итак, в 2002 г. неэтилированный бензин в США стоил на 13,9% больше, чем в 1995 г.
Невзвешенные составные индексы цен. Несмотря на то что индекс цен на любой отдельный товар представляет несомненный интерес, более важным является индекс цен на группу товаров, позволяющий оценить стоимость и уровень жизни большого количества потребителей. Невзвешенный составной индекс цен, определенный формулой (11), приписывает каждому отдельному виду товаров одинаковый вес. Составной индекс цен отражает процентное изменение цены группы товаров (часто называемой потребительской корзиной) в заданный период времени по отношению к цене этой группы товаров в базовый момент времени.
где t — период времени (0, 1, 2, …), i — номер товара (1, 2, …, n), n — количество товаров в рассматриваемой группе, — сумма цен на каждый из n товаров в период времени t,
— сумма цен на каждый из n товаров в нулевой период времени,
— величина невзвешенного составного индекса в период времени t.
На рис. 25 представлены средние цены на три вида фруктов за период с 1980 по 1999 гг. Для вычисления невзвешенного составного индекса цен в разные годы применяется формула (11), считая базовым 1980 год.
Итак, в 1999 г. суммарная цена фунта яблок, фунта бананов и фунта апельсинов на 59,4% превышала суммарную цену на эти фрукты в 1980 г.
Рис. 25. Цены (в долл.) на три вида фруктов и невзвешенный составной индекс цен
Невзвешенный составной индекс цен выражает изменения цен на всю группу товаров с течением времени. Несмотря на то что этот индекс легко вычислять, у него есть два явных недостатка. Во-первых, при вычислении этого индекса все виды товаров считаются одинаково важными, поэтому дорогие товары приобретают излишнее влияние на индекс. Во-вторых, не все товары потребляются одинаково интенсивно, поэтому изменения цен на мало потребляемые товары слишком сильно влияют на невзвешенный индекс.
Взвешенные составные индексы цен. Из-за недостатков невзвешенных индексов цен более предпочтительными являются взвешенные индексы цен, учитывающие различия цен и уровней потребления товаров, образующих потребительскую корзину. Существуют два типа взвешенных составных индексов цен. Индекс цен Лапейрэ, определенный формулой (12), использует уровни потребления в базовом году. Взвешенный составной индекс цен позволяет учесть уровни потребления товаров, образующих потребительскую корзину, присваивая каждому товару определенный вес.
где t — период времени (0, 1, 2, …), i — номер товара (1, 2, …, n), n — количество товаров в рассматриваемой группе, — количество единиц товара i в нулевой период времени,
— значение индекса Лапейрэ в период времени t.
Вычисления индекса Лапейрэ показаны на рис. 26; в качестве базового используется 1980 год.
Рис. 26. Цены (в долл.), количество (потребление в фунтах на душу населения) трех видов фруктов и индекс Лапейрэ
Итак, индекс Лапейрэ в 1999 г. равен 154,2. Это свидетельствует от том, что в 1999 году эти три вида фруктов были на 54,2% дороже, чем в 1980 году. Обратите внимание на то, что этот индекс меньше невзвешенного индекса, равного 159,4, поскольку цены на апельсины — фрукты, потребляемые меньше остальных, — выросли больше, чем цена яблок и бананов. Иначе говоря, поскольку цены на фрукты, потребляемые наиболее интенсивно, выросли меньше, чем цены на апельсины, индекс Лапейрэ меньше невзвешенного составного индекса.
Индекс цен Пааше использует уровни потребления товара в текущем, а не базовом периоде времени. Следовательно, индекс Пааше более точно отражает полную стоимость потребления товаров в заданный момент времени. Однако этот индекс имеет два существенных недостатка. Во-первых, как правило, текущие уровни потребления трудно определить. По этой причине многие популярные индексы используют индекс Лапейрэ, а не индекс Пааше. Во-вторых, если цена некоторого конкретного товара, входящего в потребительскую корзину, резко возрастает, покупатели снижают уровень его потребления по необходимости, а не вследствие изменения вкусов. Индекс Пааше вычисляется по формуле:
где t — период времени (0, 1, 2, …), i — номер товара (1, 2, …, n), n — количество товаров в рассматриваемой группе, — количество единиц товара i в нулевой период времени,
— значение индекса Пааше в период времени t.
Вычисления индекса Пааше показаны на рис. 27; в качестве базового используется 1980 год.
Рис. 27. Цены (в долл.), количество (потребление в фунтах на душу населения) трех видов фруктов и индекс Пааше
Итак, индекс Пааше в 1999 г. равен 147,0. Это свидетельствует от том, что в 1999 году эти три вида фруктов были на 47,0% дороже, чем в 1980 году.
Некоторые популярные индексы цен. В бизнесе и экономике используется несколько индексов цен. Наиболее популярным является индекс потребительских цен (Consumer Index Price — CPI). Официально этот индекс называется CPI-U, чтобы подчеркнуть, что он вычисляется для городов (urban), хотя, как правило, его называют просто CPI. Этот индекс ежемесячно публикуется Бюро статистики труда (U. S. Bureau of Labor Statistics) в качестве основного инструмента для измерения стоимости жизни в США. Индекс потребительских цен является составным и взвешенным по методу Лапейрэ. При его вычислении используются цены 400 наиболее широко потребляемых продуктов, видов одежды, транспортных, медицинских и коммунальных услуг. В данный момент при вычислении этого индекса в качестве базового используется период 1982–1984 гг. (рис. 28). Важной функцией индекса CPI является его использование в качестве дефлятора. Индекс CPI используется для пересчета фактических цен в реальные путем умножения каждой цены на коэффициент 100/CPI. Расчеты показывают, что за последние 30 лет среднегодовые темпы инфляции в США составили 2,9%.
Рис. 28. Динамика Consumer Index Price; полные данные см. Excel-файл
Другим важным индексом цен, публикуемым Бюро статистики труда, является индекс цен производителей (Producer Price Index — PPI). Индекс PPI является взвешенным составным индексом, использующим метод Лапейрэ для оценки изменения цен товаров, продаваемых их производителями. Индекс PPI является лидирующим индикатором для индекса CPI. Иначе говоря, увеличение индекса PPI приводит к увеличению индекса CPI, и наоборот, уменьшение индекса PPI приводит к уменьшению индекса CPI. Финансовые индексы, такие как индекс Доу-Джонса для акций промышленных предприятий (Dow Jones Industrial Average — DJIA), S&P 500 и NASDAQ, используются для оценки изменения стоимости акций в США. Многие индексы позволяют оценить прибыльность международных фондовых рынков. К таким индексам относятся индекс Nikkei в Японии, Dax 30 в Германии и SSE Composite в Китае.
Ловушки, связанные с анализом временных рядов
Значение методологии, использующей информацию о прошлом и настоящем для того, чтобы прогнозировать будущее, более двухсот лет назад красноречиво описал государственный деятель Патрик Генри: «У меня есть лишь одна лампа, освещающая путь, — мой опыт. Только знание прошлого позволяет судить о будущем».
Анализ временных рядов основан на предположении, что факторы, влиявшие на деловую активность в прошлом и влияющие в настоящем, будут действовать и в будущем. Если это правда, анализ временных рядов представляет собой эффективное средство прогнозирования и управления. Однако критики классических методов, основанных на анализе временных рядов, утверждают, что эти методы слишком наивны и примитивны. Иначе говоря, математическая модель, учитывающая факторы, действовавшие в прошлом, не должна механически экстраполировать тренды в будущее без учета экспертных оценок, опыта деловой активности, изменения технологии, а также привычек и потребностей людей. Пытаясь исправить это положение, в последние годы специалисты по эконометрии разрабатывали сложные компьютерные модели экономической активности, учитывающие перечисленные выше факторы.
Тем не менее, методы анализа временных рядов представляют собой превосходный инструмент прогнозирования (как краткосрочного, так и долгосрочного), если они применяются правильно, в сочетании с другими методами прогнозирования, а также с учетом экспертных оценок и опыта.
Резюме. В заметке с помощью анализа временных рядов разработаны модели для прогнозирования доходов трех компаний: Wm. Wrigley Jr. Company, Cabot Corporation и Wal-Mart. Описаны компоненты временного ряда, а также несколько подходов к прогнозированию годовых временных рядов — метод скользящих средних, метод экспоненциального сглаживания, линейная, квадратичная и экспоненциальная модели, а также авторегрессионная модель. Рассмотрена регрессионная модель, содержащая фиктивные переменные, соответствующие сезонному компоненту. Показано применение метода наименьших квадратов для прогнозирования месячных и квартальных временных рядов (рис. 29).
Рис. 29. Структурная схема заметки
Предыдущая заметка Построение моделей множественной регрессии
Следующая заметка Принятие решений
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 983–1074
[2] Тестовая t-статистика теряет р степеней свободы при оценке наклона и одну при оценке сдвига генеральной совокупности откликов. Еще р степеней свободы утрачиваются при сравнении значений временного ряда.
Аннотация:
Цель работы: научиться выполнять прогнозирование временного ряда данных с помощью средств Microsoft Excel и математически.
Содержание работы:
Анализ временных рядов.
Прогноз, характеристики и параметры прогнозирования.
Уравнение тренда временного ряда.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания с использованием средств MS Excel.
Оформить отчет, сделав выводы по заданиям.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 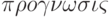
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
Прогнозы делятся:
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 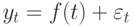

Неслучайная функция f(t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами (t, yt) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t), где f(t) = a0+a1(t).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel.
Рис.
14.1.
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f(t) в точках ti от значений исходного временного ряда в тех же точках ti. Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид ![$sumlimits_{t=1}^{n}[x_{t}-a_{0}-a_{1}t]^{2}$](https://intuit.ru/sites/default/files/tex_cache/af521da64ce9abdab75d7f160f5c9bb4.png)
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f(t) имеет вид:
f(t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Рис.
14.2.
Задание 1.
Временной ряд приведен в таблице. Используя средства MS Excel:
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
Варианты.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Решение.
Рассмотрим решение этой задачи средствами Microsoft Excel. При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3
рис.
14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4
рис.
14.4.
Рис.
14.3.
Задание параметров тренда в MS Excel 2007
Рис.
14.4.
Задание параметров тренда в версии ранее MS Excel 2007
Итоговый график представлен на рисунке 14.5
рис.
14.5.
Рис.
14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t), найденного по методу наименьших квадратов. Для этого в полученное для f(t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Задание 2.
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Любому бизнесу интересно заглянуть в будущее и правильно ответить на вопрос: «А сколько денег мы заработаем за следующий период?» Ответить на такого рода вопросы позволяют различные методики прогнозирования. В данной статье мы с вами рассмотрим несколько таких методик и произведем все необходимые расчеты в Excel. Еще больше про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачи
Исходные данные
Для начала, давайте определимся, какие у нас есть исходные данные и что нам нужно получить на выходе. Фактически, все что у нас есть, это некоторые исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут продажи за предыдущие периоды.
Примечание. Собранные в разные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такого временного ряда называется измерением. Например: данные о продажах за последние 5 лет по месяцам — временной ряд; продажи за январь прошлого года — измерение.
Составляющие прогноза
Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:
- Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
- Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.
Эти три пункта в совокупность образуют регулярную составляющую временного ряда.
Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.
Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно – продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.
Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Следующий вопрос, на который нужно ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два основных вида:
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отклонения
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отклонения
Иногда также выделают смешанную модель в отдельную группу:
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отклонения
С моделями мы определились, но теперь возникает еще один вопрос: «А когда какую модель лучше использовать?»
Классический вариант такой:
— Аддитивная модель используется, если амплитуда колебаний более-менее постоянная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной компоненты.
Пример:

Решение задачи с помощью Excel
Итак, необходимые теоретические знания мы с вами получили, пришло время применить их на практике. Мы будем с вами использовать классическую аддитивную модель для построения прогноза. Однако, мы построим с вами два прогноза:
- с использованием линейного тренда
- с использованием полиномиального тренда
Во всех руководствах, как правило, разбирается только линейный тренд, поэтому полиномиальная модель будет крайне полезна для вас и вашей работы!
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть исходная информация по продажам за 2 года:

Учитывая, что мы используем линейный тренд, то нам необходимо найти коэффициенты уравнения
y = ax + b
где:
- y – значения продаж
- x – номер периода
- a – коэффициент наклона прямой тренда
- b – свободный член тренда
Рассчитать коэффициенты данного уравнения можно с помощью формулы массива и функции ЛИНЕЙН. Нам необходимо будет сделать следующую последовательность действий:
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Нажимаем Ctrl+Shift+Enter, чтобы активировать формулу массива
На выходе мы получили 2 числа: первое — коэффициент a, второе – свободный член b.

Теперь нам нужно рассчитать для каждого периода значение линейного тренда. Сделать это крайне просто — достаточно в полученное уравнение подставить известные номера периодов. Например, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

Нам осталось рассчитать коэффициент сезонности для каждого периода. Учитывая, что у нас есть исторические данные за два года, разумно будет учесть это при расчете. Можем сделать следующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

Что нам это дало? Мы посчитали, сколько суммарно продавалось каждый январь/каждый февраль и так далее, а потом разделили это на среднее значение продаж за все два периода.
То есть мы выяснили, как продажи двух январей отклонялись от средних продаж за два года, как продажи двух февралей отклонялись и так далее. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Рассчитали только 12 коэффициентов, т.к. один коэффициент учитывает продажи сразу за 2 аналогичных периода.
Итак, теперь мы на финишной прямой. Нам осталось рассчитать тренд для будущих периодов и учесть коэффициент сезонности для них. Давайте амбициозно построим прогноз на год вперед.
Сначала создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Далее, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 прогнозируемых периодов.
И последний штрих — умножаем полученное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!
Модель с полиномиальным трендом
Конструкция, которую мы только что с вами построили, достаточно проста. Но у нее есть один большой минус — далеко не всегда она дает достоверные результаты.
Посмотрите сами, какая модель более точно аппроксимирует наши точки — линейный тренд (прямая зеленая линия) или полиномиальный тренд (красная кривая)? Ответ очевиден. Поэтому сейчас мы с вами и разберем, как построить полиномиальную модель в Excel.
Пусть все исходные данные у нас будут такими же. Для простоты модели будем учитывать только тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд отличается от обычного линейного. Правильно — формой уравнения. У линейного тренда мы разбирали обычный график прямой:

У полиномиального тренда же уравнение выглядит иначе:

где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени необходимо найти коэффициенты уравнения:

Согласитесь, выглядит немного страшно. Однако, ничего страшного нет, и мы с легкостью можем решить эту задачку с помощью уже известных нам методов.
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;1). Функция ЛИНЕЙН позволяет произвести расчет коэффициентов, а с помощью функции ИНДЕКС мы вытаскиваем нужный нам коэффициент. В данном случае за выбор коэффициента отвечает самый последний аргумент. У нас стоит 1 — это коэффициент при самой высокой степени (т.е. при 4 степени, коэффициент). Кстати, узнать о самых полезных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4});1;2) в ячейке ниже.
- Делаем такие же действия, пока не найдем все коэффициенты.
Кстати говоря, мы можем легко сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
- Выделяем столбец с продажами
- Выбираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Нажимаем на любую точку графика правой кнопкой мыши и выбираем «Добавить линию тренда»
- В открывшемся справа меню выбираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Показывать уравнение на диаграмме»
Теперь вы наглядно можете видеть, как рассчитанный тренд аппроксимирует исходные данные и как выглядит само уравнение. Можно сравнить уравнение на графике с вашими коэффициентами. Сходится? Значит сделали все верно!
Помимо всего прочего, вы можете сразу оценить точность аппроксимации (не полностью, но хотя бы первично). Это делается с помощью коэффициента R^2. Тут у вас снова есть два пути:
- Вы можете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы можете рассчитать коэффициент R^2 самостоятельно по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^{1;2;3;4};;1);3;1)
Заключение
Мы с вами подробно разобрали вопрос прогнозирования — изучили необходимые термины и виды моделей, построили аддитивную модель в Excel с использованием линейного и полиномиального тренда, а также научились отображать результаты своих вычислений на графиках. Все это позволит вам эффективно внедрять полученные знания на работе, усложнять существующие модели и уточнять прогнозы. Чем большим количеством методов и инструментов вы будете владеть, тем выше будет ваш профессиональный уровень и статус на рынке труда.
Если вас интересуют еще какие-то модели прогнозирования — напишите нам об этом, и мы постараемся осветить эти темы в дальнейших своих статьях! Или запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про возможности Excel, необходимые для анализа.
Автор: Алексанян Андрон, эксперт SF Education
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
Data Science
5 примеров экономии времени в Excel
Что для работодателя главное в сотруднике? Добросовестность, ответственность, профессионализм и, конечно же, умение пользоваться отведенным временем! Предлагаем познакомиться с очень нужными, на наш взгляд,…
Содержание
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
- Вопросы и ответы
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
- Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
- Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
- Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Урок: Как построить линию тренда в Excel
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
- Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
- Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Урок: Экстраполяция в Excel
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

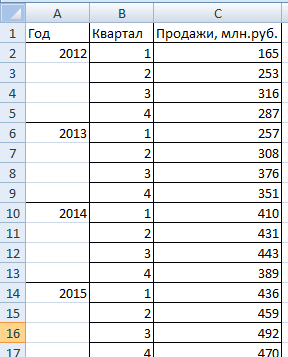
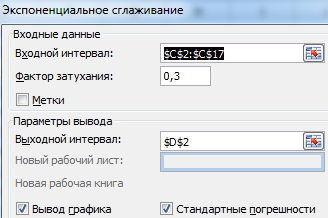
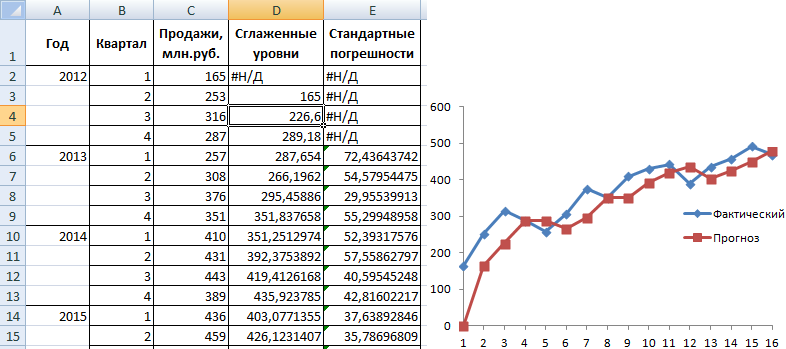
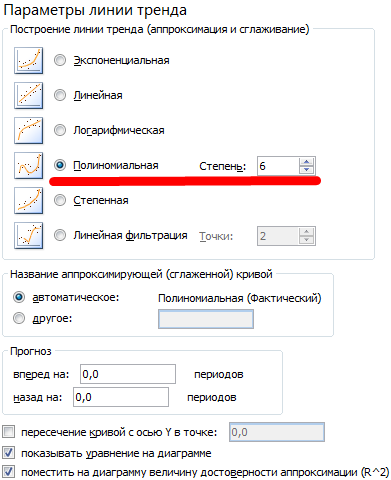
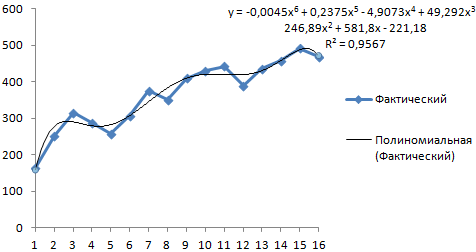
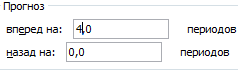
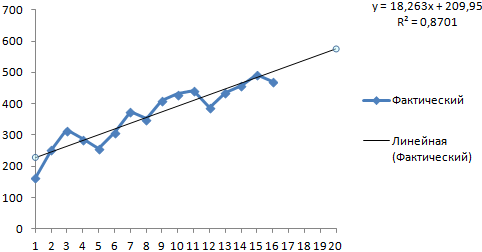
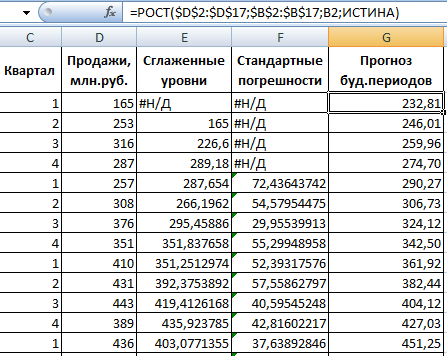
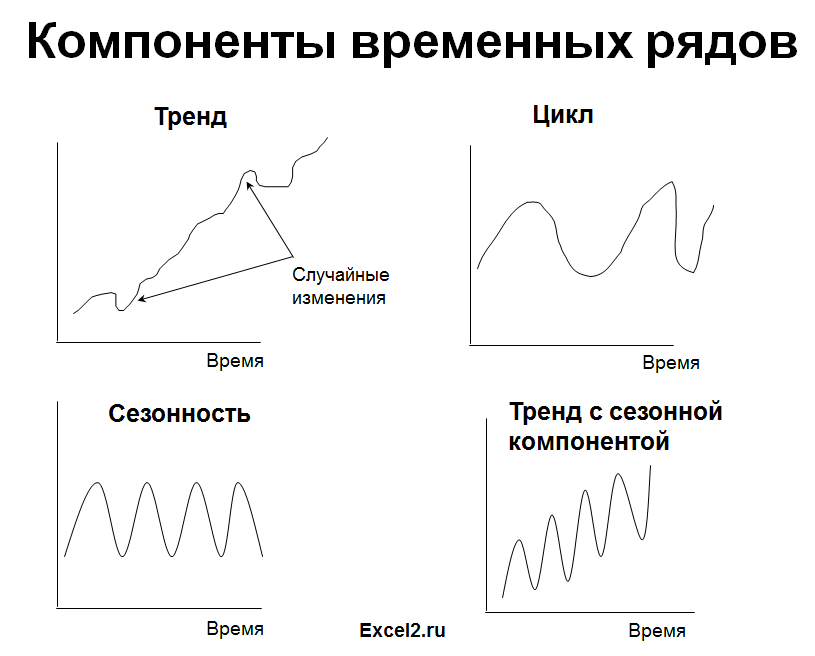
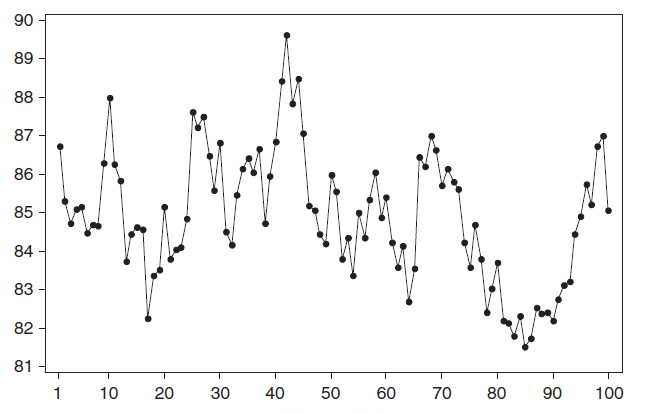
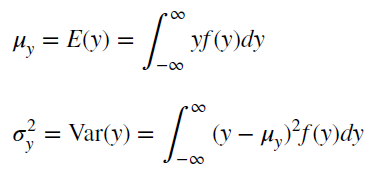
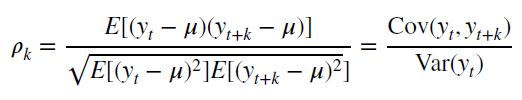
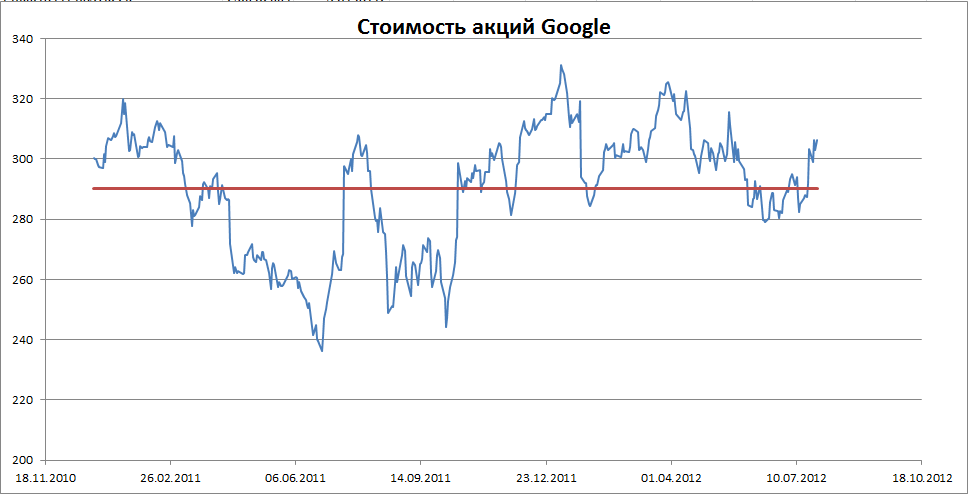
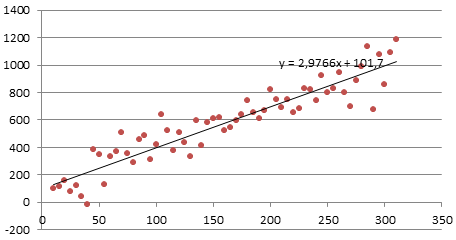
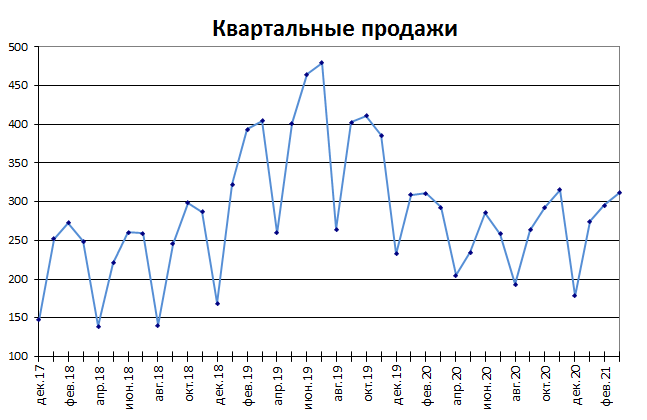
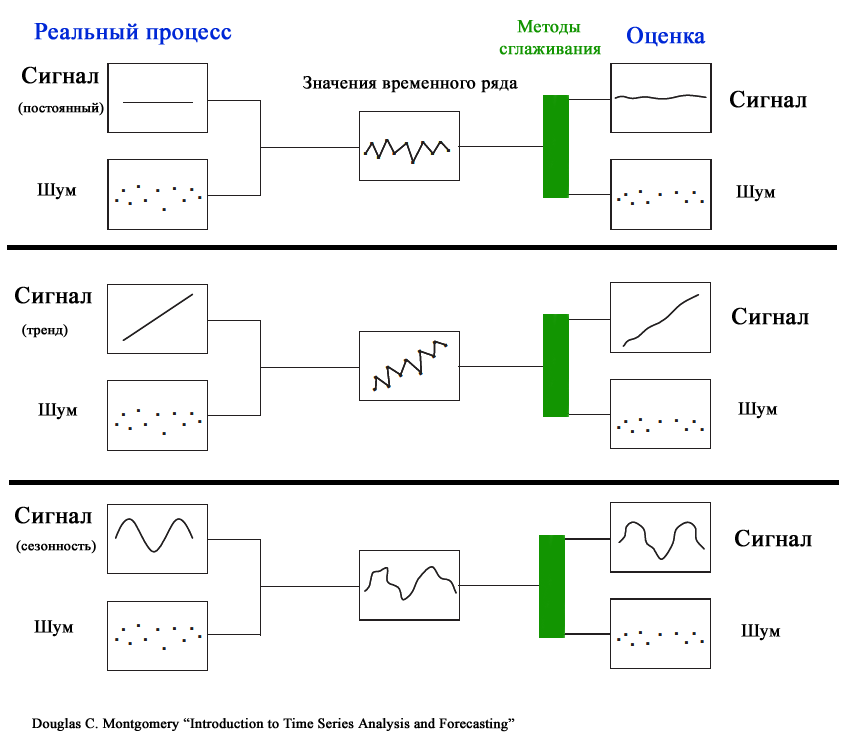

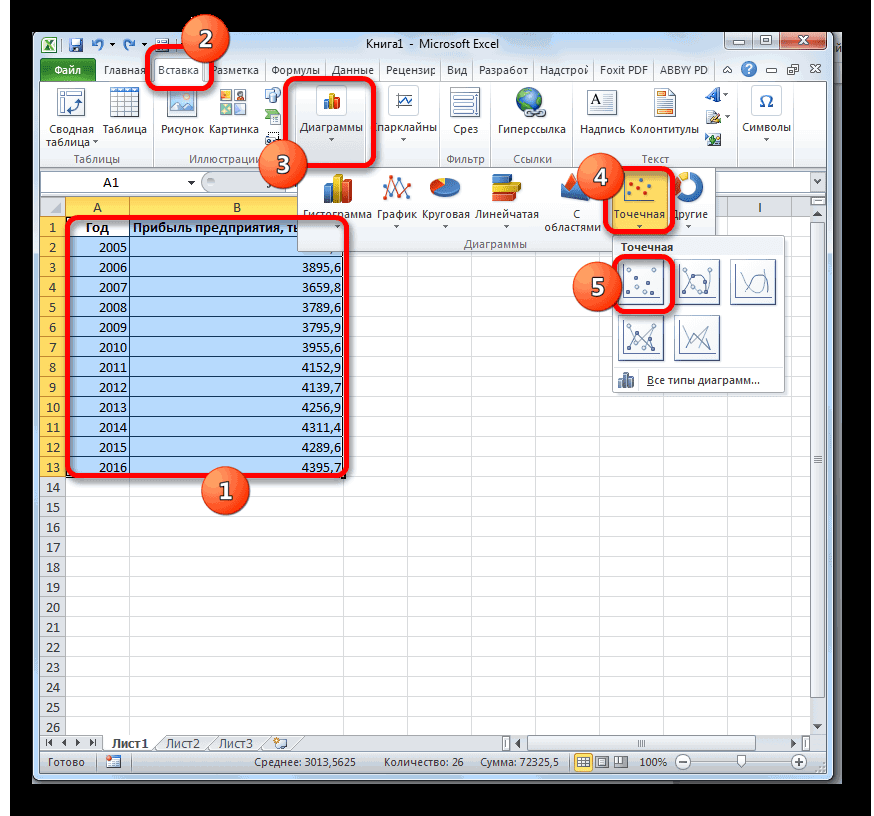
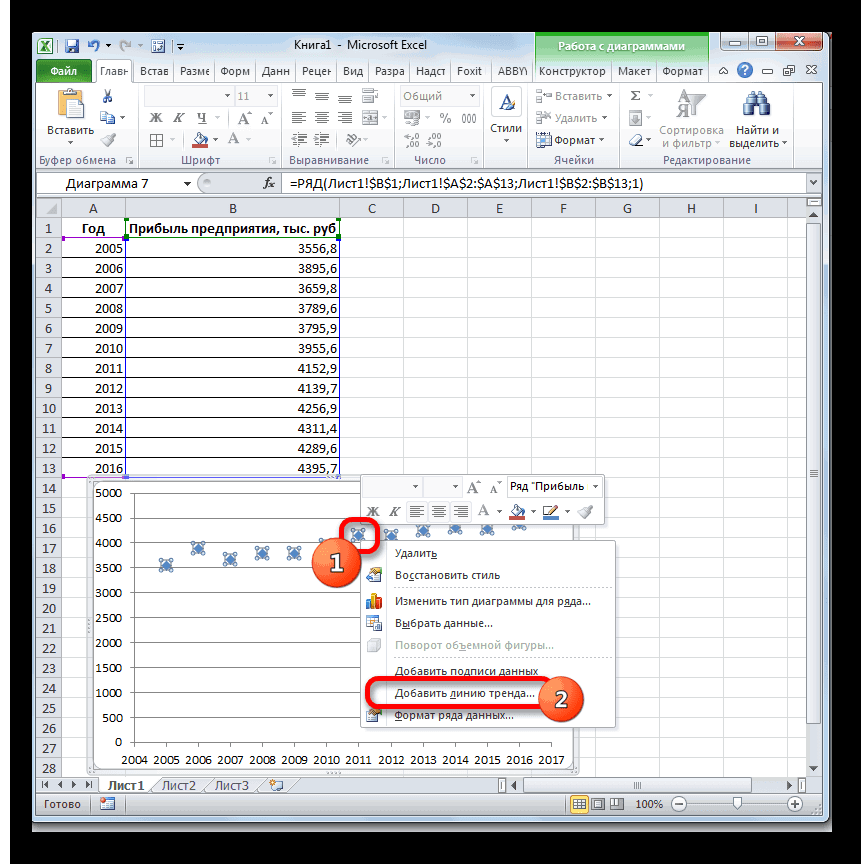
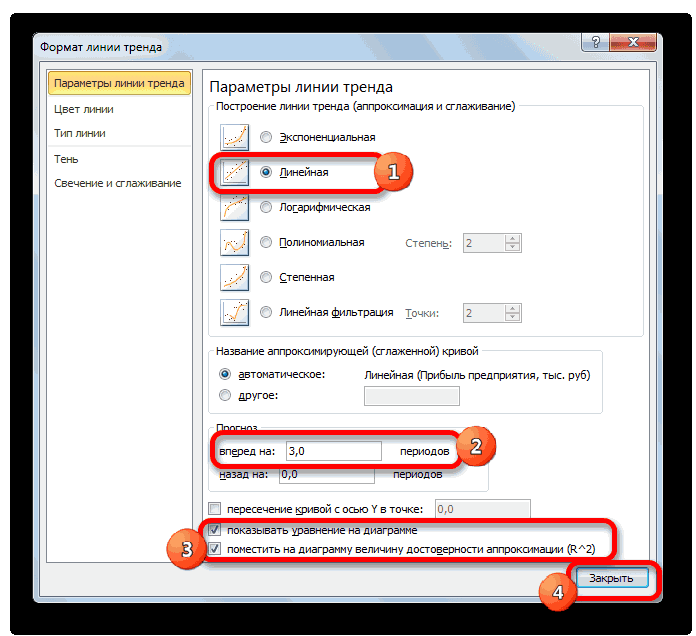
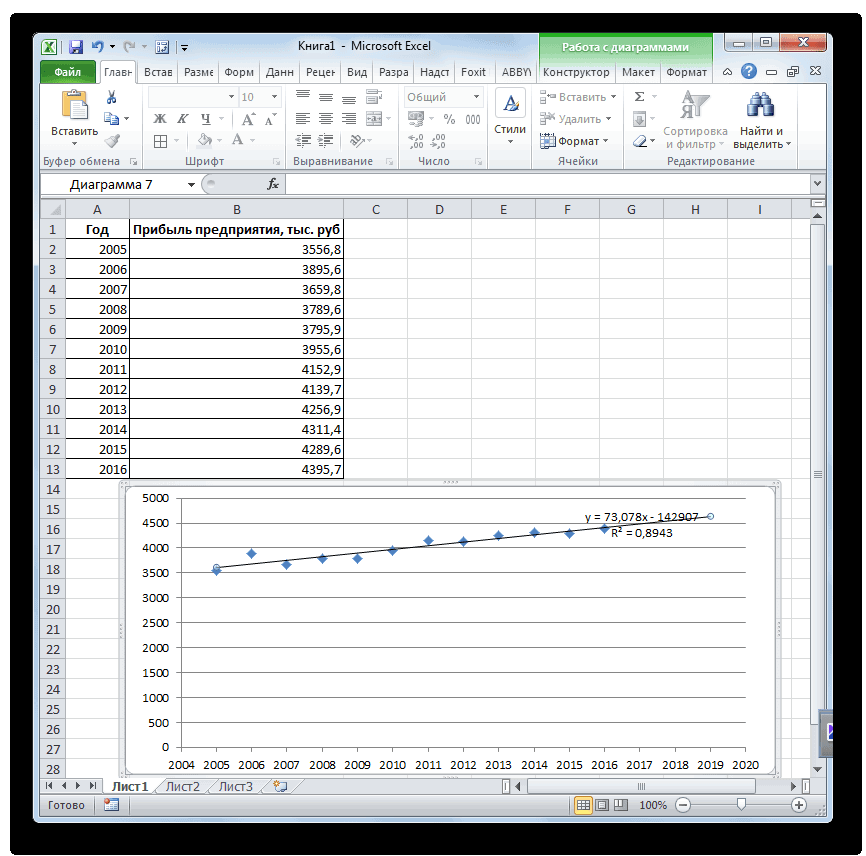

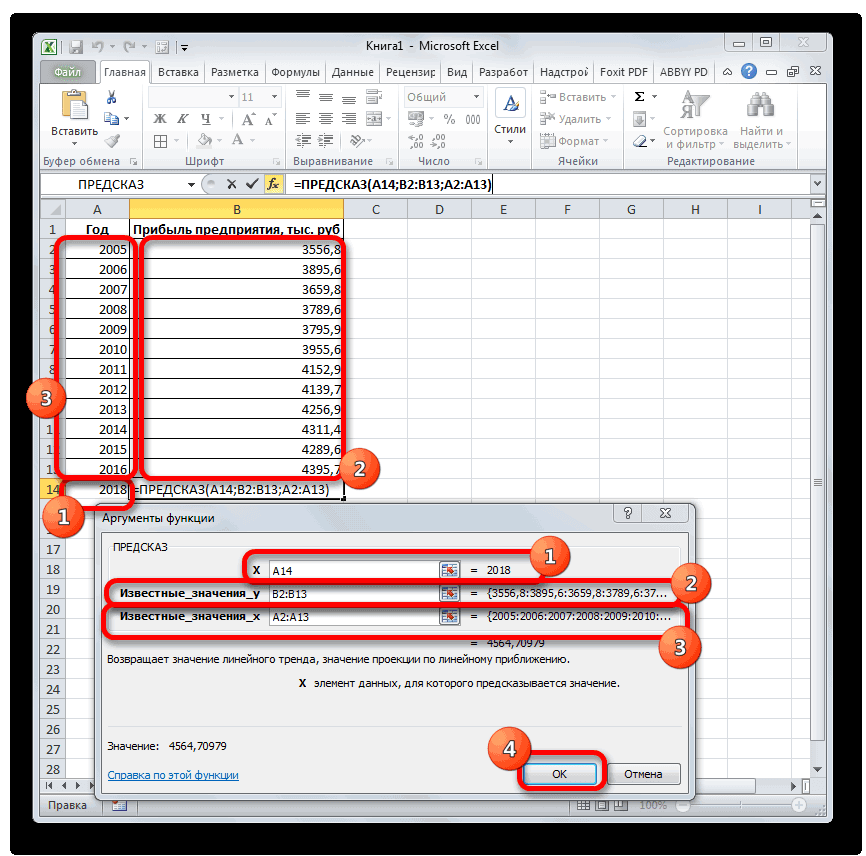


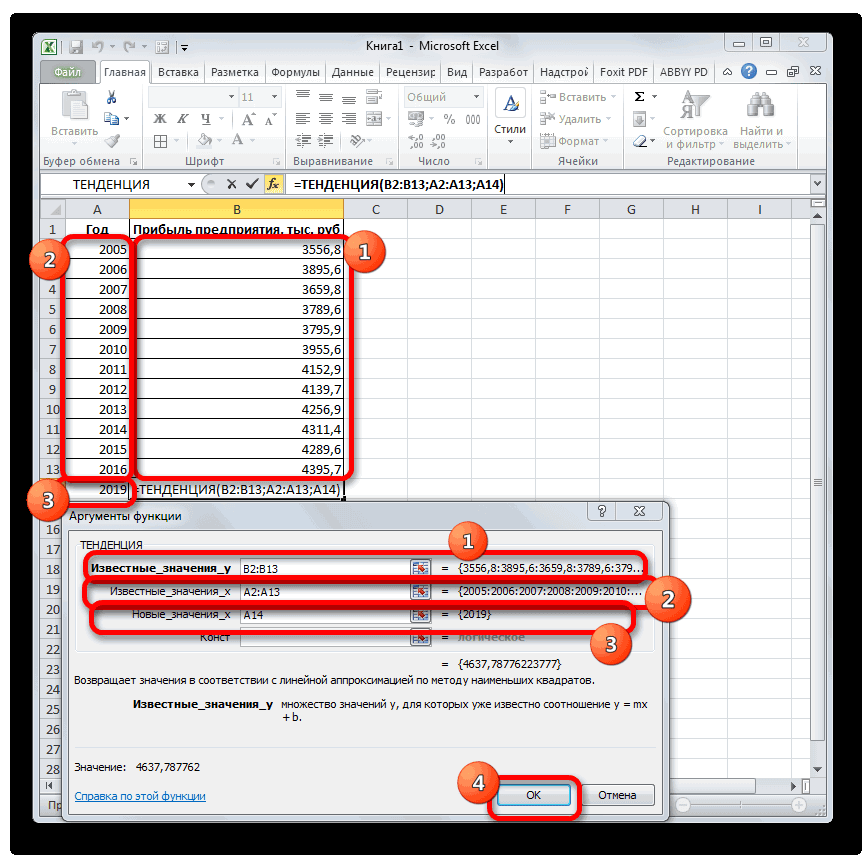
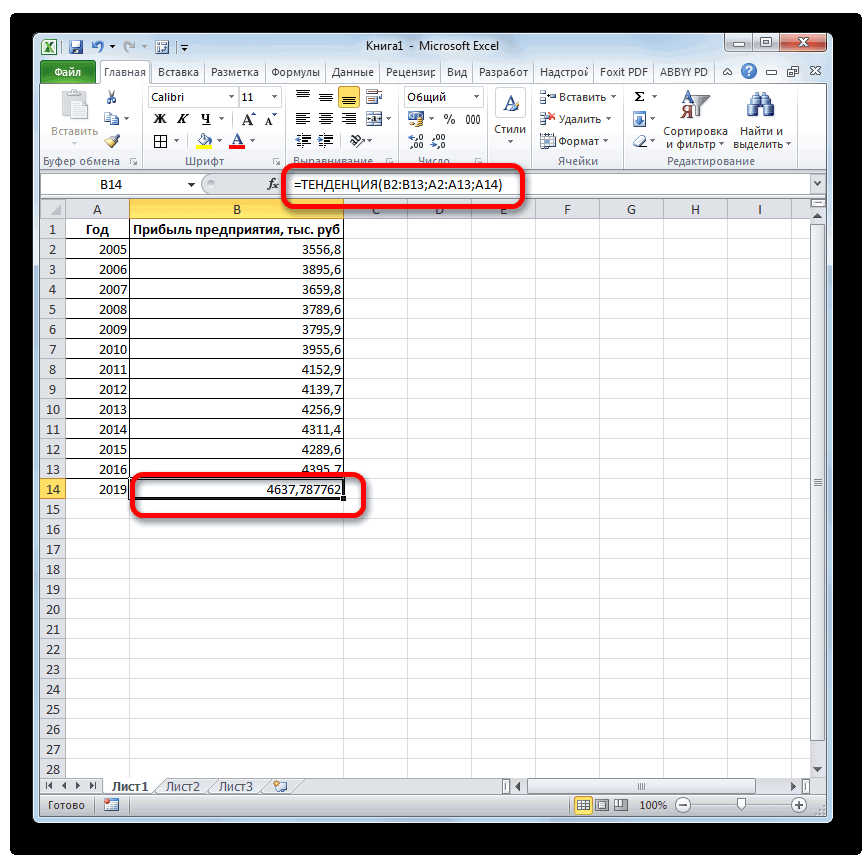
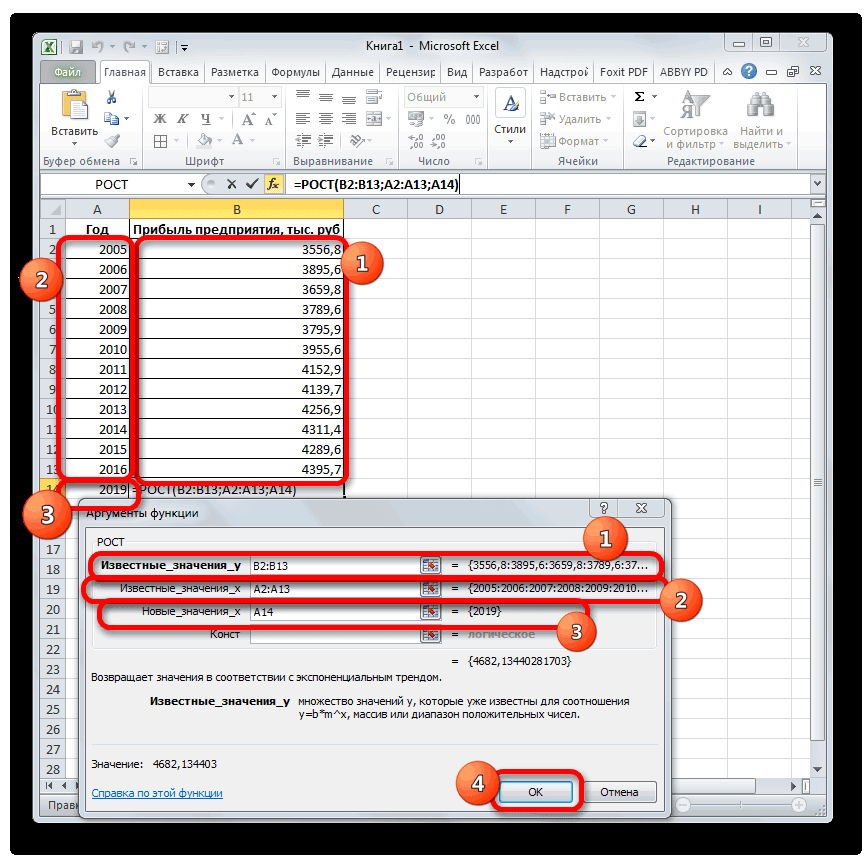
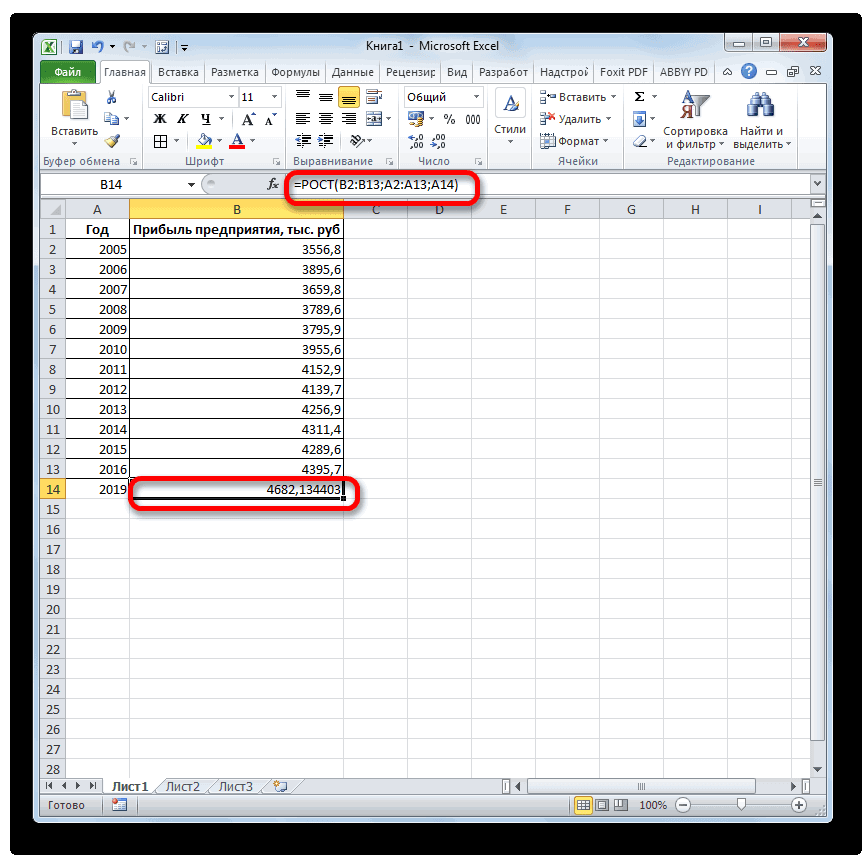
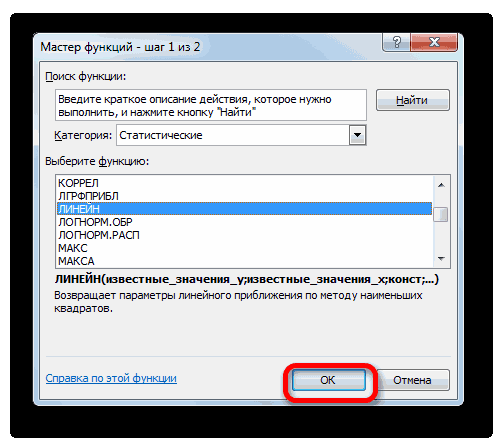
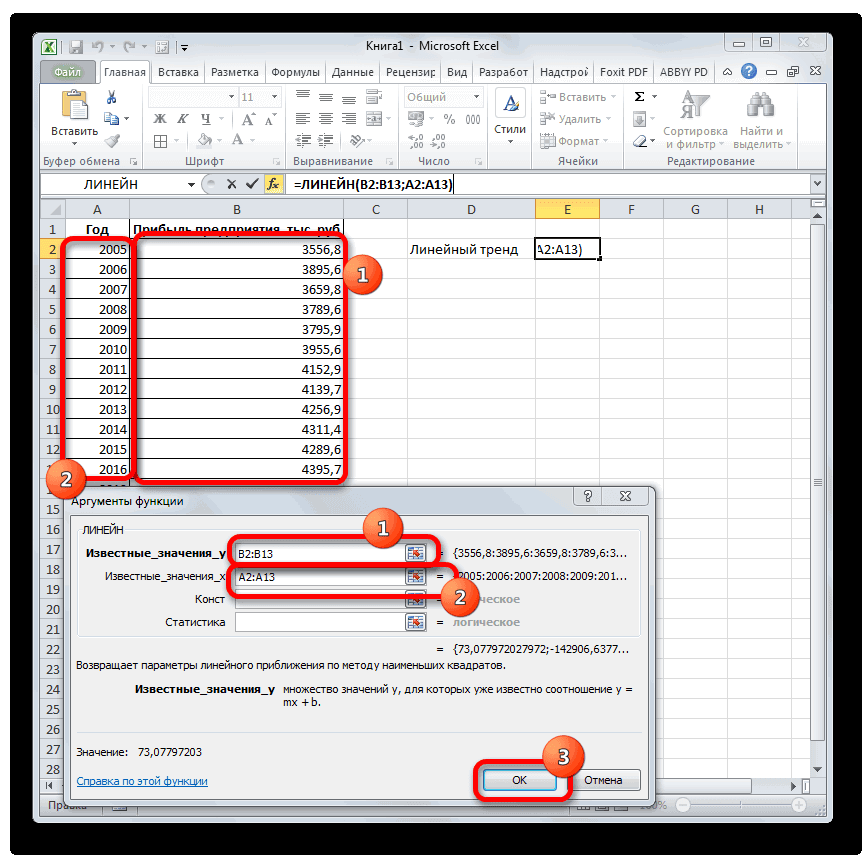
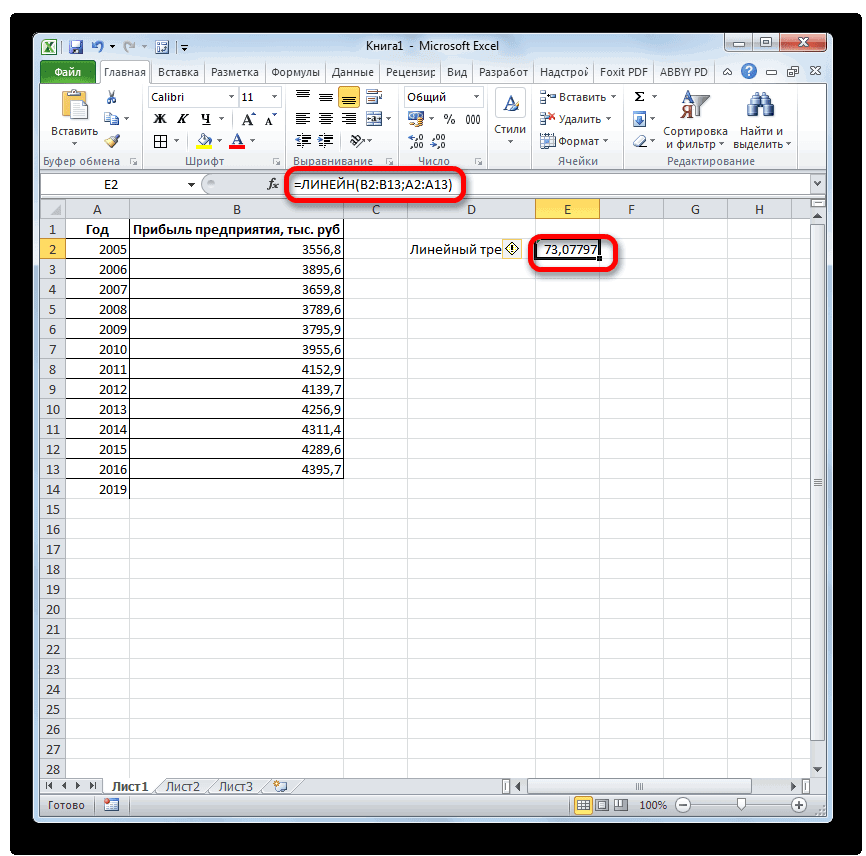
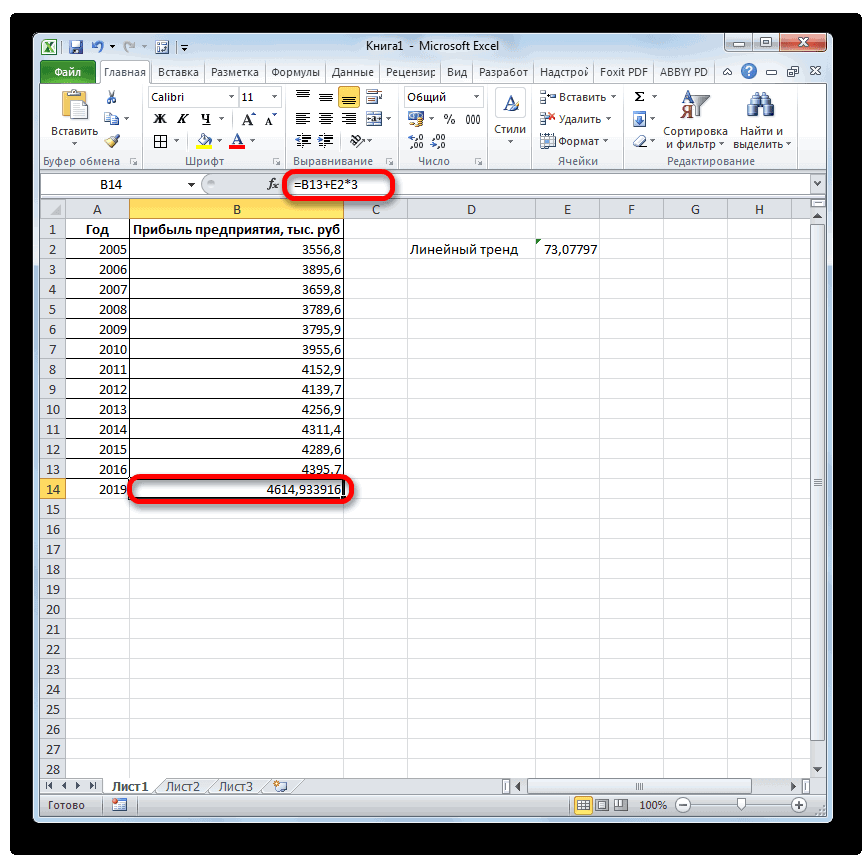
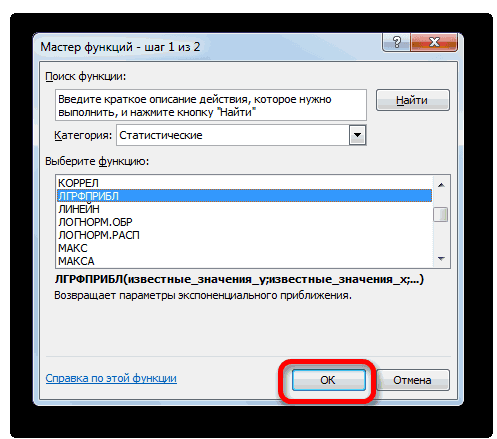
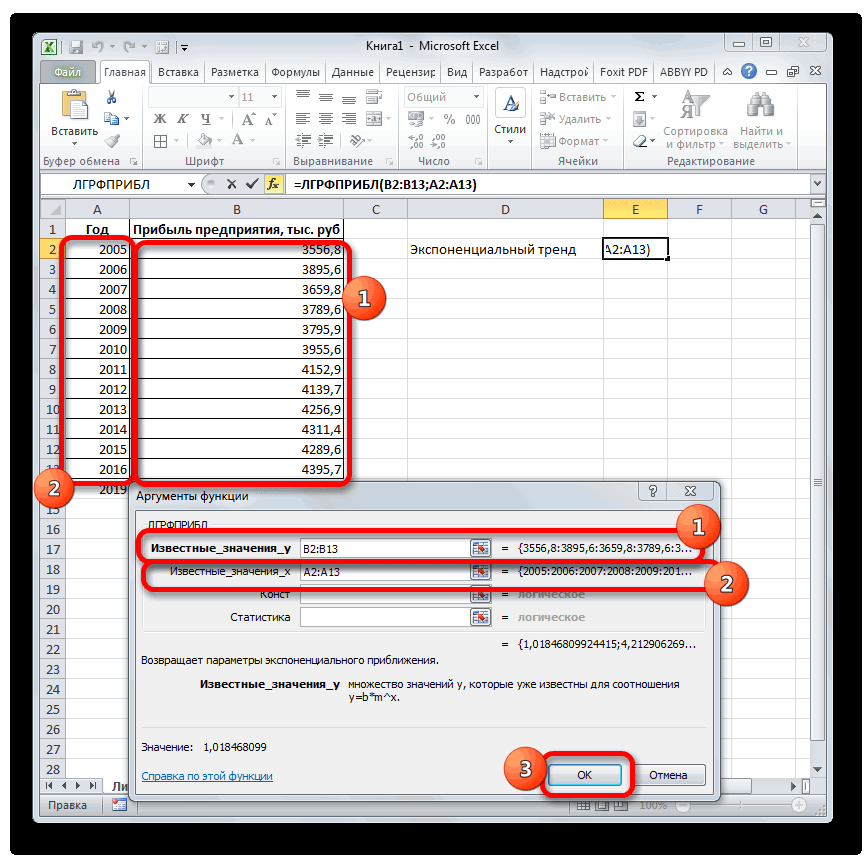
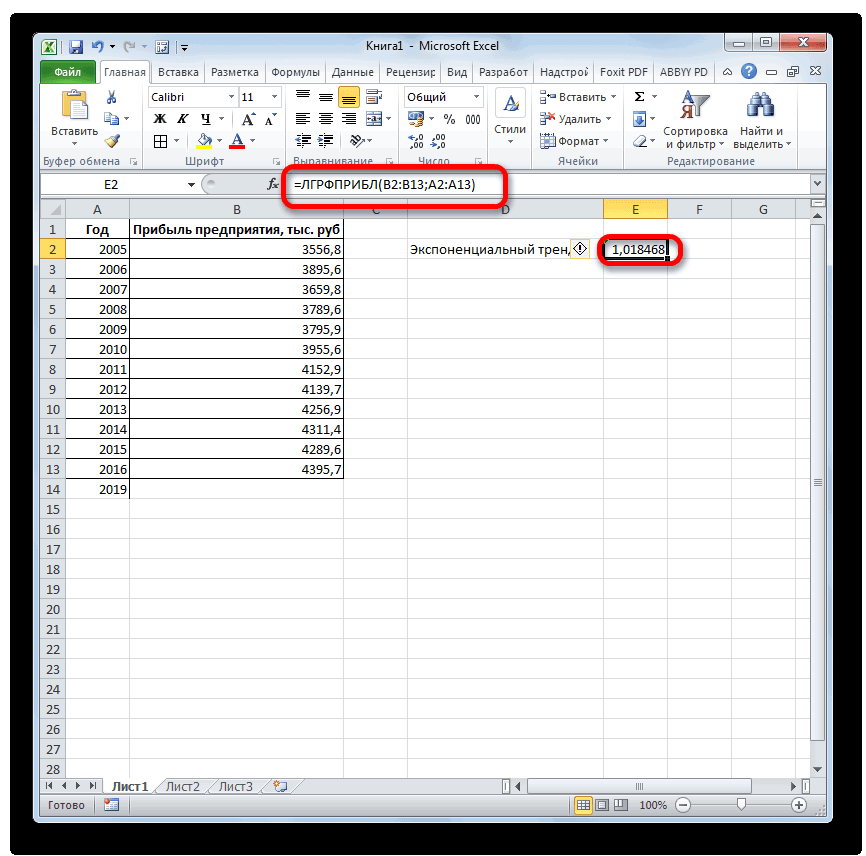
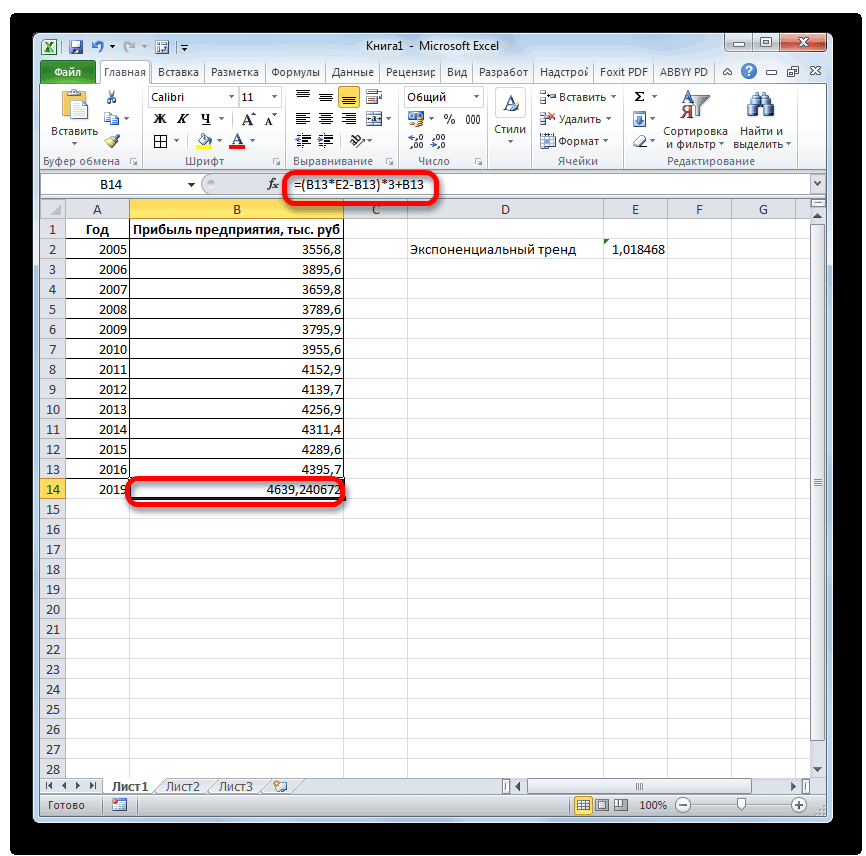
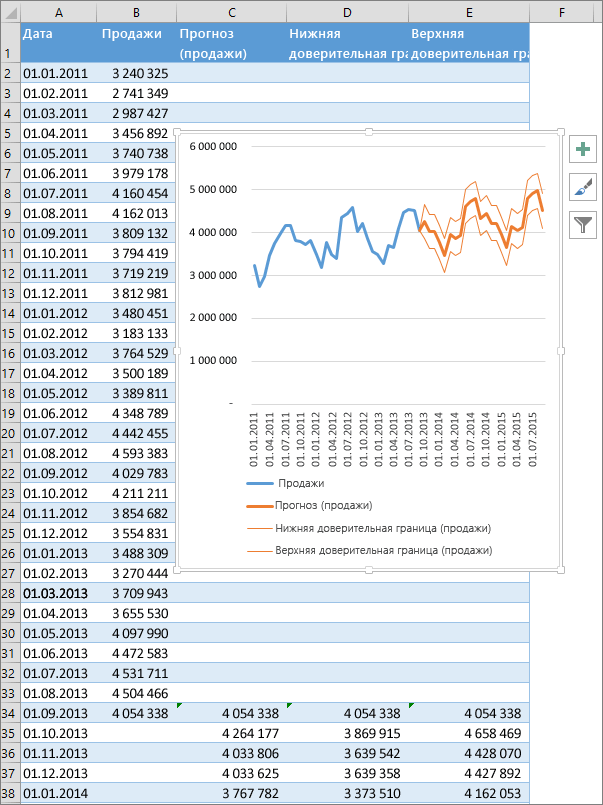

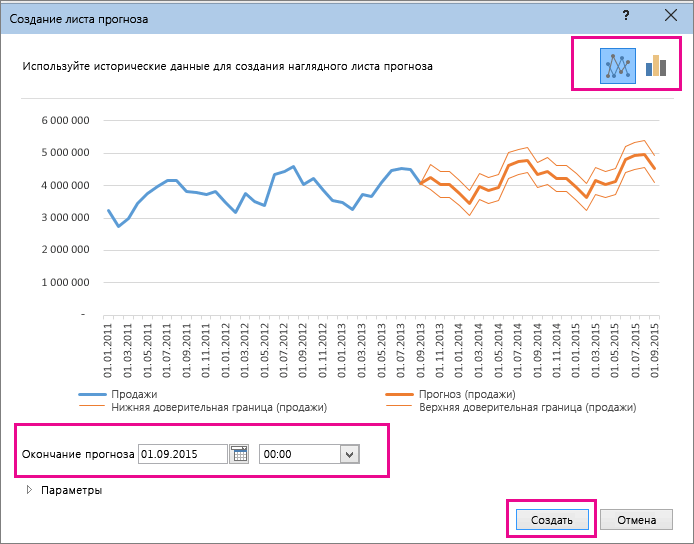
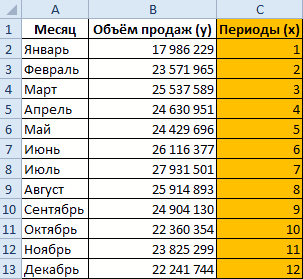
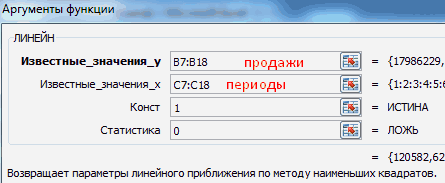

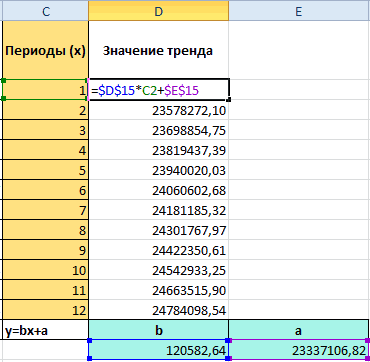


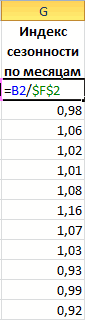

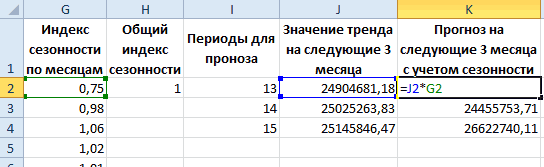
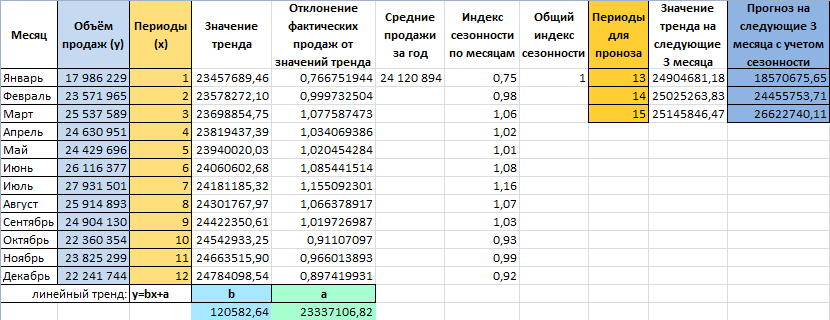
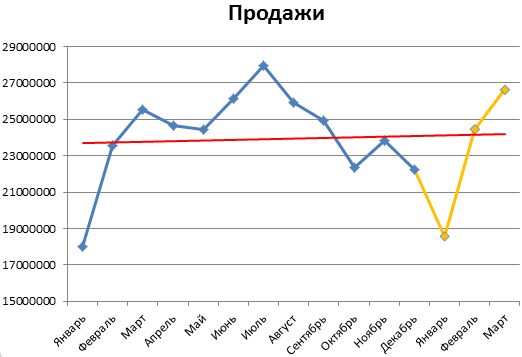
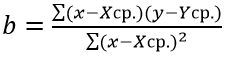
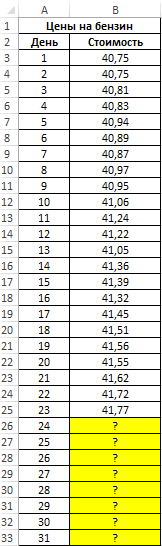
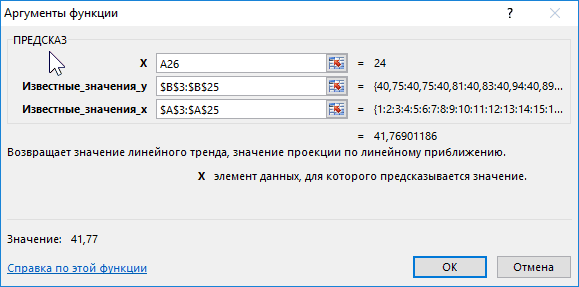
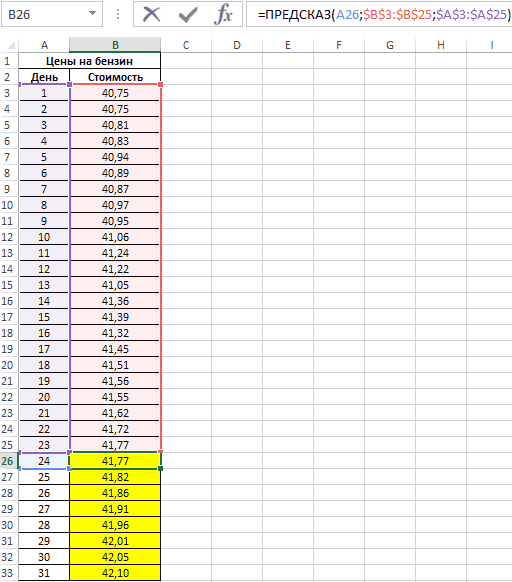

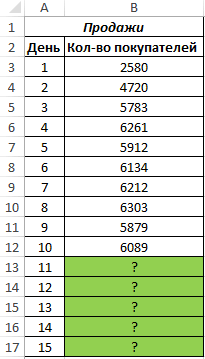


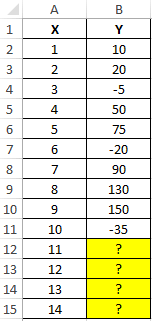
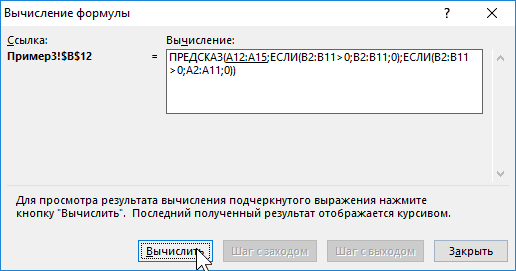

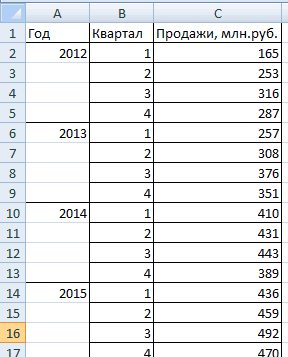

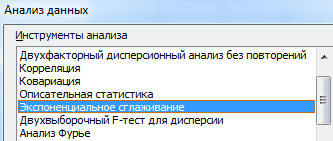
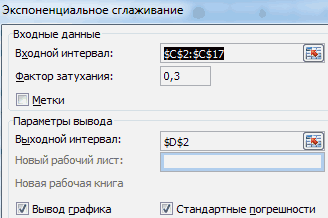
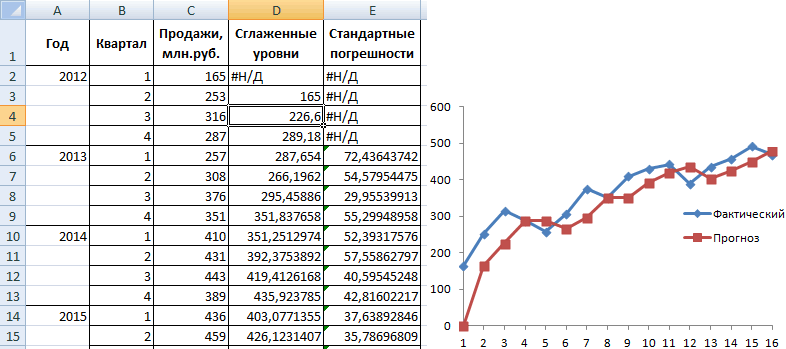
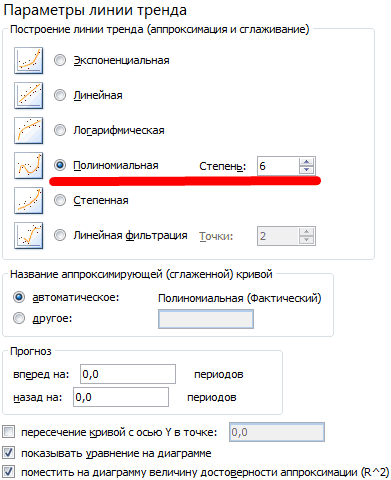
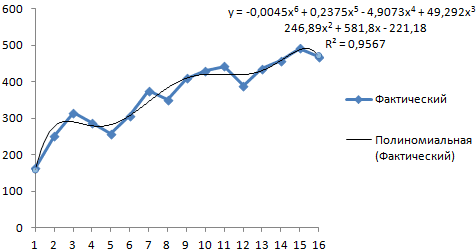
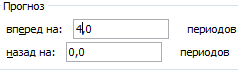
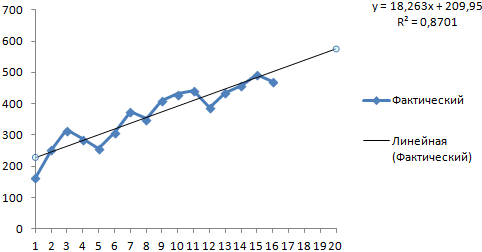
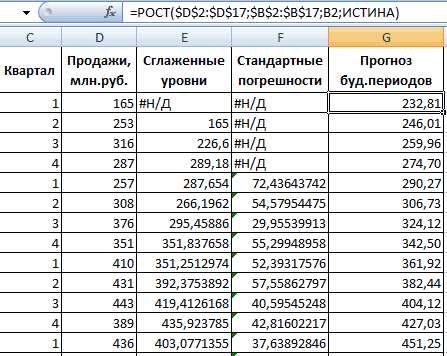

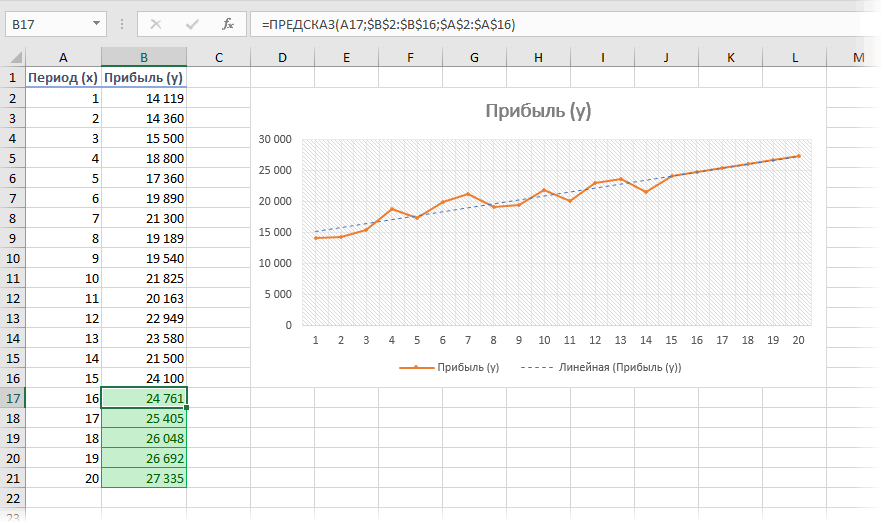









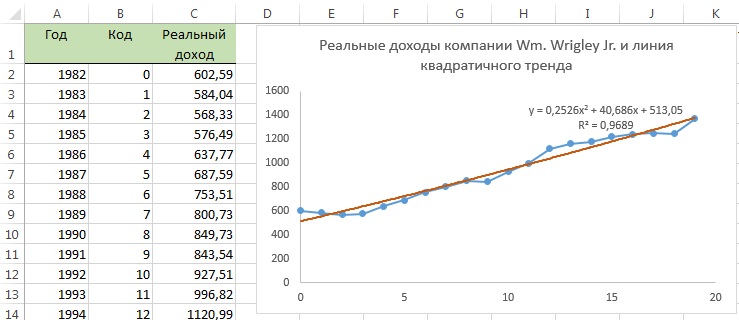

































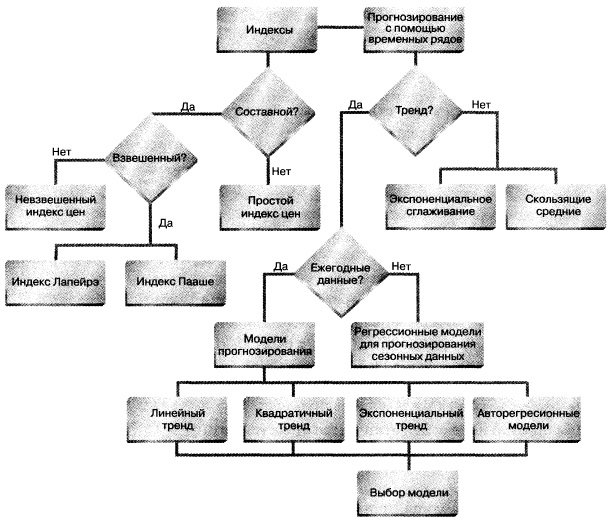

![$$sumlimits_{t=1}^{n}[x_{t}-a_{0}-a_{1}t]^{2}rightarrow mineqno(1)$$](https://intuit.ru/sites/default/files/tex_cache/56404890c825202167c4ba34001e2250.png)