Как построить вариационный ряд в Excel
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.
Построим дискретный вариационный ряд
по затратам труда на 1 ц зерна.
Открываем лист Excel,
в ячейку А1 записываем условное обозначение
результативного признака – у, а в ячейки
А2:А31 значения затрат труда на 1 ц зерна.
В ячейки В2:В3 введём наименьшее и
следующее за ним значения признака 0,7
и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем
мышью правый нижний угол выделительной
рамки и потянем вниз до значения 1,5
(наибольшее значение признака). В ячейках
В2:В10 получим варианты признака в
ранжированном порядке. Для определения
частот проделаем следующие шаги:
1.Поставим курсор в ячейку С2.
2.Выберем Вставка,
Функция.
Выберем в категории
Статистические функции
функцию Частота и
нажмём ОК.
3.В поле данных
укажем ячейки А2:А31, а в поле интервалов
В2:В10.
4.Нажмём кнопку ОК.
5.Выделим ячейки
С2:С10.
6.Нажмём F2,
а затем комбинацию клавиш Shift+Ctrl+Enter.
В ячейках С2:С10 появятся
частоты.
Вычислим накопленные
частоты, которые потребуются для
дальнейших расчётов, путём последовательного
суммирования локальных частот (нарастающим
итогом). Так, первая плюс вторая частоты
дают накопленную частоту второго
варианта (1+2=3); прибавляя к ней третью
частоту, получим накопленную частоту
третьего варианта (3+4=7) и т.д.
Скопируем полученный
в Excel
вариационный ряд и построим таблицу.
Таблица 2
Дискретный вариационный ряд распределения
затрат труда на 1 ц зерна
|
Варианты |
Частоты |
Накопленные |
|
0,7 |
1 |
1 |
|
0,8 |
2 |
3 |
|
0,9 |
4 |
7 |
|
1,0 |
5 |
12 |
|
1,1 |
6 |
18 |
|
1,2 |
4 |
22 |
|
1,3 |
3 |
25 |
|
1,4 |
3 |
28 |
|
1,5 |
2 |
30 |
Построим
полигон распределения частот с помощью
Мастера
диаграмм.
Выберем точечную диаграмму, соединим
полученные точки отрезками, а крайние
точки с осью абсцисс в точках, отстоящих
от крайних на расстоянии шага.
Р
1. Полигон распределения сельскохозяйственных
предприятий по затратам труда на 1 ц
зерна
Рассмотрим
построение интервального вариационного
ряда.
Рис. 2. Построение интервального
вариационного ряда
На
листе Excel в ячейку А1 записываем условное
обозначение факторного признака – х,
в ячейки А2:А31 – значения факторного
признака – урожайности озимой пшеницы.
Произведём сортировку данных, для чего
выделяем диапазон данных, выбираем
Данные – Сортировка и в появившемся
окне «Сортировка диапазона» указываем
«по возрастанию», нажимаем ОК. Данные
в ячейках А2:А31 расположатся в ранжированном
порядке по возрастанию признака. По
формуле Стерджесса определяем количество
групп (интервалов). Для вычисления
десятичного логарифма lg30 выбираем
Мастер функций – Математические –
LOG10. В появившемся окне в поле Число
записываем число 30, десятичный логарифм
которого необходимо найти. Нажатием ОК
получаем этот логарифм 1,477121. . Подставляя
числовые данные в формулу (1), получим
число групп (интервалов) 5,9, округляем
до 6. По формуле (2) определяем величину
интервалов – шаг с такой же точностью,
с которой даны исходные данные (в данном
случае с точностью до десятых:
(30-20)/6≈1,7. Следовательно, совокупность
надо разбить на 6 интервалов. Получаем
шаг 1,7. Озаглавим следующие столбцы в
Excel словами «Интервалы», «Частоты»,
«Накопленные частоты», «Середины
интервалов». В ячейку В2 вписываем
минимальное значение признака Хmin=20,
в ячейку В3 формулу =В2+1,7, т.е. минимальное
значение плюс шаг. Копируем эту формулу
на 5 строк вниз. В результате в этих шести
строках (В3:В8) получим верхние границы
всех интервалов. Нижними границами
интервалов будут данные в соседних
верхних ячейках, т.е. для первого интервала
нижней границей будет содержание ячейки
В2, для второго В3 и для шестого В7.
Для
расчёта частот выберем Сервис — Анализ
данных – Гистограмма и нажмём ОК. В
появившемся окне «Гистограмма» в поле
«Входной интервал» копируем исходные
данные (ячейки А2:А31), в поле «Интервал
карманов» — верхние границы интервалов
(ячейки В3:В8), в поле «Выходной интервал»
ячейки частот (С3:С8), нажимаем ОК. В ячейки
D3:D8 будут записаны частоты для всех
шести интервалов. Накопленные частоты
подсчитываем нарастающим итогом.
Для
построения диаграммы необходимо найти
середины интервалов. Для этого вводим
формулу расчёта середины интервала:
,
рассчитаем середину первого интервала.
Копируем формулу для остальных пяти
групп.
Для
построения диаграммы выделяем массив
частот и середин интервалов.
Далее в
Мастере диаграмм выбираем вид диаграммы
— гистограмму определённого вида.
Нажимаем кнопку Далее. В появившемся
окне выбираем вкладку Ряд, удаляем ряд
1, а в поле «Подписи оси х» копируем
середины интервалов. Нажимаем далее, в
появившемся окне выбираем вкладку
Заголовки. В поле «ось х (категорий)»
вписываем название факторного признака
(в данном случае урожайность, ц/га), в
поле «Ось у (значений)» вписываем частоты.
Нажимаем Далее, Готово. Появится
диаграмма, состоящая из столбиков,
отделённых друг от друга некоторым
зазором. Щёлкаем правой кнопкой мыши
на одном из столбиков диаграммы. В
раскрывающемся списке элементов щёлкаем
по кнопке Формат рядов данных. В
появившемся диалоговом окне активизируем
вкладку Параметры и в поле Ширина зазора
устанавливаем значение 0. Нажимаем ОК,
в результате чего гистограмма принимает
стандартный вид.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение рядов распределения
Любой ряд распределения характеризуется двумя элементами:
— варианта(хi) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);
— частота (ni) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:
где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
Проиллюстрируем процесс первичной обработки данных на следующих примерах.
Пример 1.1. имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.
Рис.1.5. Пример 2. Построение равноинтервального ряда
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.
Рис.1.6. Пример 2. Построение равноинтервального ряда
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Стиль и внешний вид гистограммы
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
- добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:
Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
Создание вариационного
ряда, вариационной кривой, определение среднего значения и среднеквадратичного
отклонения.
Для селекционера,
например, важно знать, сколько зерен содержит колос выведенного (выводимого) им
нового сорта пшеницы. В этой ситуации совершенно ясно, что подсчетом количества
зерен только в одном колосе не обойтись. Для определения числа зерен надо
воспользоваться достаточно большим количеством колосьев, скажем не менее сотни.
Приведем пример математической обработки результатов селекции.
Все поле
пшеницы, которое вырастил селекционер можно на математическом языке назвать
генеральной совокупностью. Подсчитать количество зерен в колосьях всей
генеральной совокупности, очевидно, не представляется возможным, но из всей
генеральной совокупности можно выбрать, скажем, сто колосьев и подсчитать
количество зерен в них. Эти сто колосьев будут называться выборкой из генеральной
совокупности, и они с определенной точностью будут отражать число зерен во всем
поле (генеральной совокупности). Чтобы по данным выборки иметь возможность
судить обо всей генеральной совокупности, она должна быть отобрана случайно.
Так в нашем случае селекционер ни в коем случае не должен отдавать предпочтение
тем или иным колосьям (по размерам, внешнему виду, месту произрастания на поле
и т.п.) в процессе их выборки. Наиболее целесообразно в данной ситуации
совершать выбор колосьев из непрозрачного мешка наугад. У всех выбранных
колосьев производится подсчет числа зерен, и результаты фиксируются в виде ряда
чисел, с которыми в дальнейшем и предстоит совершать математические действия. В
данном примере можно предложить следующую их последовательность.
2.1 Создание вариационного ряда.
Вариационным
рядом называется ранжированный в порядке возрастания или убывания ряд вариантов
с соответствующими им весами (частотами или частностями). Вариационный ряд
будет дискретным, если любые его варианты отличаются на постоянную величину, и
непрерывным, если варианты могут отличатся один от другого на сколь угодно
малую величину.
Иными словами в вариационном ряду
полученные значения располагаются в порядке их увеличения и, если значение
повторяется, то рядом записывается число его повторений. Т.е. в данном примере
по числу зерен в колосьях ряд может выглядеть так (таб. 2):
Таблица 2
|
Число зерен в колосе |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
Число колосьев |
1 |
2 |
2 |
4 |
6 |
8 |
8 |
9 |
10 |
|
Число зерен в колосе |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
|
Число колосьев |
9 |
9 |
9 |
8 |
6 |
4 |
3 |
1 |
1 |
Полученный вариационный ряд
позволяет выявить закономерности распределения колосьев по числу зерен в них.
2.2 Создание вариационной
кривой.
Закономерности распределения
можно представить более наглядно, создав вариационную кривую, называемую
полигоном (рис 3), или представить в виде столбчатой диаграммы, которая здесь
будет называться гистограммой (рис 4).
Из полученных схем уже можно наглядно судить о закономерностях
распределения.
Диаграммы
строятся при помощи «Excel»
так:
Ø Ввести в окно программы данные вариационного
ряда.
Ø Запустить «Мастер диаграмм», нажатием
кнопки 
Ø В графе «тип» выбирать или «гистограмма», или
«график».
Ø Нажать кнопку «Далее».
Ø В «шаге 2 из 4» найти строку с названием
«Диапазон» и щелкнуть по кнопке, расположенной справа от надписи и пустого
поля, при этом «Мастер диаграмм» несколько свернется.
Ø Выделить данные в окне программы (в примере это
значения в ячейках В1 – В18).
Ø Снова щелкнуть по кнопке в «Мастере диаграмм».
«Мастер» развернется. В окне «Мастера» появится эскиз гистограммы или полигона.
Ø В этом же шаге (2 из 4) щелкнуть по закладке с
надписью «Ряд».
Ø В открывшейся страничке найти строчку с надписью
«Подписи оси Х».
Ø Щелкнуть по кнопке справа от надписи и пустого
поля.
Ø Выделить значения в окне программы, которые
будут на диаграмме представляться в качестве данных оси Х. (в примере значения
в ячейках А1 – А18).
Ø Щелкнуть по кнопке в свернутом «Мастере».
Ø Щелкнуть по кнопке «Далее» (шаг 3 из 4).
Ø При необходимости, в графе «Заголовки» выполнить
подписи осей Х и Y, а
так же дать диаграмме название.
Ø Щелкнуть по кнопке далее, затем готово и в
результате получится готовая гистограмма или полигон (рис 3).
2.3 Определение среднего значения признака.
Среднее
значение ряда данных находится обычным образом. Суммируются все значения
признака и делятся на количество этих значений. Т.е. здесь общее число зерен в
100 колосках равно 2551, то среднее значение будет равно 2551/100 = 25.51.
Для определения
среднего значения признака с использованием «Excel» надо выполнить следующие шаги:
Ø Ввести в столбец А окна программы все значения
признака, в том числе и повторяющиеся. Т.е. здесь все 100 значений зерен в
колосках. Ввод можно осуществлять в любой последовательности – по возрастанию,
по убыванию или в разнобой. Введенный массив чисел лучше сохранить, так как он
пригодится для расчета отклонения.
Ø Щелкнуть в окне программы по любой пустой
ячейке. По окончании расчетов в ней появится соответствующее среднее значение.
Ø В меню «Вставка» выбрать «Функция».
Ø В появившемся списке функций выбрать функцию
«СРЗНАЧ».
Ø Щелкнуть по кнопке «ОК». Появится окно
«Аргументы функции».
Ø Щелкнуть по кнопке правее надписи «Число 1» и
поля (окно свернется).
Ø Выделить в окне программы весь числовой массив,
среднее значение которого необходимо определить.
Ø Щелчком по кнопке справа от поля с надписями
развернуть окно «Аргументы функции».
Ø Щелкнуть по кнопке «ОК». В выбранной
предварительно ячейке появится среднее значение массива чисел.
2.4 Определение среднего квадратического
отклонения.
Вариационная кривая имеет
определенную ширину. Нетрудно догадаться, что чем больше ширина вариационной
кривой, тем сильнее разброс значений относительно средней величины.
Как показано на рисунках 5 и 6 при
одном и том же среднем значении, равном 25.51, полигон первого рисунка шире
полигона второго.
Оценить
степень разброса данных относительно среднего значения можно рассчитав значение
дисперсии S2,
или среднее квадратическое отклонение S, равное корню квадратному из дисперсии. Дисперсией вариационного ряда называется
средняя арифметическая квадратов отклонений вариантов от их средней
арифметической. Значением среднего квадратического отклонения пользоваться
удобнее, так как оно выражается в тех же единицах, что и значение признака. Так
среднее квадратическое отклонение данных, представленных графически на первом
полигоне равно 3.70, а на втором полигоне 2.65. Видим, что отклонение первое
больше второго и это как раз и отражается на ширине полигона.
Алгоритм
расчета среднего квадратического отклонения
и дисперсии такой же, как и для расчета среднего арифметического
значения, только в списке функций надо выбрать «СТАНДОТКЛОН» для вычисления отклонения, или «ДИСП» для расчета дисперсии.
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, – генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» – «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.2.
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Дата добавления: 2018-11-12 ; просмотров: 1065 | Нарушение авторских прав
Вариационный ряд может быть:
– дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
– интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.

Построить вариационный ряд и полигон распределения
Решение .
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel

5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда

7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа – в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число
где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:
Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).
Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
- 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.
Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»
В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).
Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
1. Построение вариационного ряда
Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»
2. Построение группировочного статистического ряда
Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:
а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)
b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.
с) выбрать функцию ЧАСТОТА
d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101
e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.
f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.
g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).
Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.
В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).
3. Построение гистограммы группировочного статистического ряда
Теперь построим кумуляту — график накопленных относительных частот. Расположим его под гистограммой.
Кумулята — это экспериментальная оценка формы графика функции распределения. Теоретическая кривая будет красивой и гладкой — мы познакомились с ней в начале работы, обсуждая свой вариант задания. Экспериментальная оценка — ломаная линия, да ещё и с погрешностями. Эти случайные ошибки вызваны ограниченным, не бесконечным объёмом выборки. В любом случае, эти графики начинаются в нуле и постепенно растут до 100%.
Напомним, что значения накопленных частот должны быть привязаны к верхним границам интервалов — в соответствии со стандартами и здравым смыслом. Идея в том, что накопленная частота накапливается именно к концу интервала, а не к середине.
Построим график в виде ломаной линии:
Insert — Charts — Insert Scatter (X, Y) or Bubble Chart
Вставка — Диаграммы — Вставить точечную (X, Y) или пузырьковую диаграмму
Вставка графика Y (X)
Выбираем тип графика
Scatter — Scatter with Straight Lines
Точечная — Точечная с прямыми отрезками
Это просто ломаная линия без маркеров точек.
Ломаная линия
Выбираем данные для графика:
Select Data — Select Data Source — Legend Entries (Series) — Add
Выбрать данные — Выбор источника данных — Элементы легенды (ряды) — Добавить
В окне
Edit Series
Изменение ряда
выбираем следующие данные.
Столбец «иксов» — верхние границы:
Series X Values
Значения Х
Столбец «игреков» — накопленные частоты:
Series Y Values
Значения Y
Убираем заголовок диаграммы:
Chart Elements — Chart Title
Элементы диаграммы — Название диаграммы
Настраиваем цвет линии на графике.
Format Data Series — Series options — Fill & Line — Line
Формат ряда данных —Параметры ряда — Заливка и границы — Линия
Line — Solid line
Линия — Сплошная линия
Color — Black
Цвет — Чёрный
Width = 0.5 pt
Ширина — 0,5 пт
Если отрезков много, то ломаная линия выглядит как гладкая кривая.
Кумулята
Настроим числовые метки на вертикальной оси, чтобы выводились целые числа:
Format Axis — Axis Options — Number — Decimal places — 0
Формат оси — Параметры оси — Число — Число десятичных знаков — 0
Целочисленные метки
Установим диапазоны значений по осям.
Вертикальная ось — метки в процентах, а границы диапазона — числа. Поэтому пределы изменения будут от 0 до 1:
Category — Percentage
Категория — Процентный
Axis Options — Bounds
Параметры оси — Границы
Minimum — 0
Минимум — 0
Maximum — 1
Максимум — 1
Горизонтальная ось — в соответствии с интервалами группировки — от 190 до 310.
Кумулята
Подгоняем размеры графика и размещаем его под гистограммой. Можно сделать это вручную.
Если захочется особой точности, поработаем через меню параметров графика (числа условные).
Format Chart Area — Chart Options — Size & Properties — Size
Формат области диаграммы — Параметры диаграммы — Размер и свойства — Размер
Height — 1.8 in
Высота — 7,62 см
Width — 5.3 in
Ширина — 12,7 см
В английской версии пакета размеры измеряются в дюймах. В русской версии — в сантиметрах. Можем установить точные значения размеров вручную.
Размер диаграммы
Окончательно совмещаем маштаб гистограммы и кумуляты: начало первого интервала 190, конец последнего интервала 310. Положения этих двух меток на обоих графиках должны совпадать.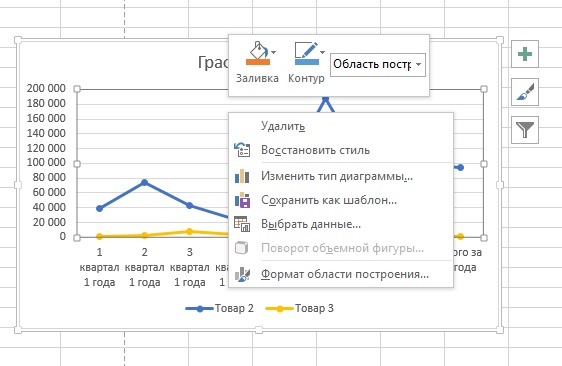
Проблемы с масштабом решаем так. Значение 190 находится в начале интервала, обозначенного 193. Значение 310 находится в конце интервала, следующего за 303.
Гистограмма и кумулята
Как построить кумуляту в excel
Как сделать кумуляту в excel по данным таблицы
Гистограмма — интервальный ряд, изображаемый столбиковой диаграммой, в которой основания столбиков, расположенные по оси абсцисс (x), являются интервалами значений варьирующего признака; а высоты столбиков — это частоты, соответствующие масштабу по оси ординат (y).
Соответственно, дискретный ряд надо преобразовать в интервальный. Для этого воспользуемся формулой Стёрджесса, чтобы определить число групп:
k = 1 + 3,322 lgN
где k — число групп, округляемое до ближайшего целого числа, а N — численность совокупности.
k = 1 + 3,322 lg150 = 1 + 3,322 2,176 = 8,229 ? 8
Можно было воспользоваться готовой таблицей оптимальных соотношений числа единиц статистической совокупности и числа групп. Значения вычислены по той же формуле Стёрджесса:
Как построить кумуляту в excel по данным таблицы
Построение вариационных рядов, графическое изображение вариационного ряда с помощью MS Office Excel
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения.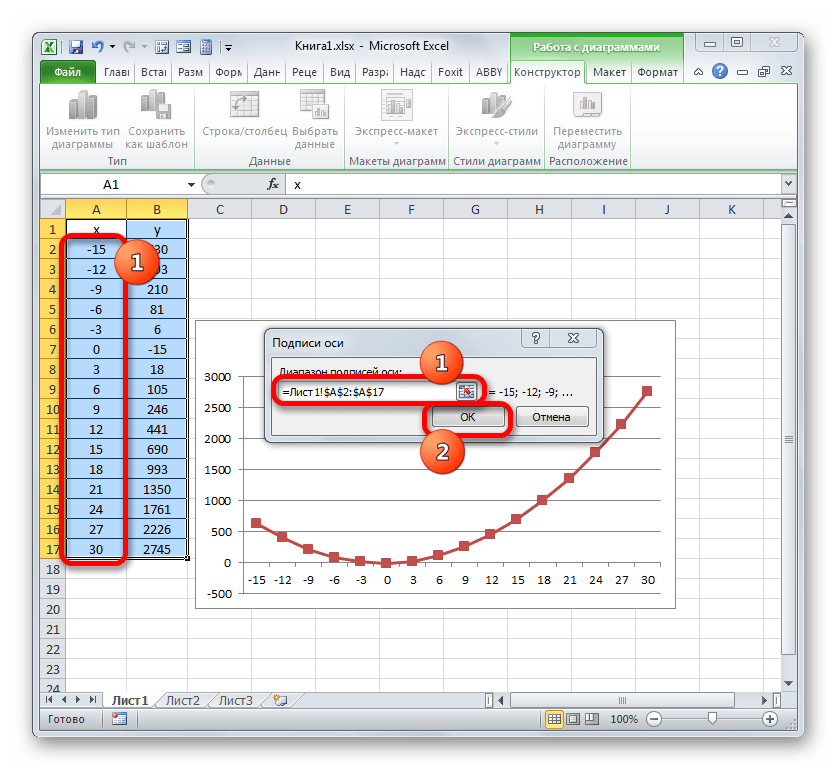
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12.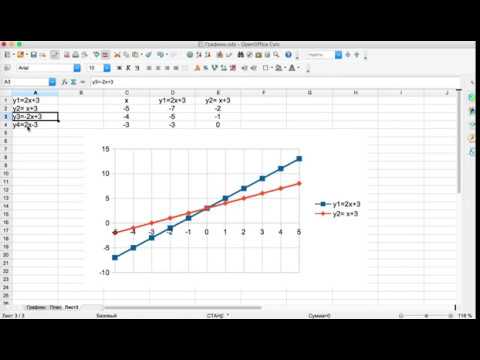
Рисунок 2.13. Полигон распределения частот
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.2.
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд.
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
Воспользуемся функцией ЧАСТОТА.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Построить гистограмму и кумуляту
Гистограмма — интервальный ряд, изображаемый столбиковой диаграммой, в которой основания столбиков, расположенные по оси абсцисс (x), являются интервалами значений варьирующего признака; а высоты столбиков — это частоты, соответствующие масштабу по оси ординат (y).
Соответственно, дискретный ряд надо преобразовать в интервальный. Для этого воспользуемся формулой Стёрджесса, чтобы определить число групп:
k = 1 + 3,322 lgN
где k — число групп, округляемое до ближайшего целого числа, а N — численность совокупности.
k = 1 + 3,322 lg150 = 1 + 3,322 2,176 = 8,229 ? 8
Можно было воспользоваться готовой таблицей оптимальных соотношений числа единиц статистической совокупности и числа групп. Значения вычислены по той же формуле Стёрджесса:
Кумулята
Теперь построим кумуляту — график накопленных относительных частот. Расположим его под гистограммой.
Кумулята — это экспериментальная оценка формы графика функции распределения. Теоретическая кривая будет красивой и гладкой — мы познакомились с ней в начале работы, обсуждая свой вариант задания. Экспериментальная оценка — ломаная линия, да ещё и с погрешностями. Эти случайные ошибки вызваны ограниченным, не бесконечным объёмом выборки.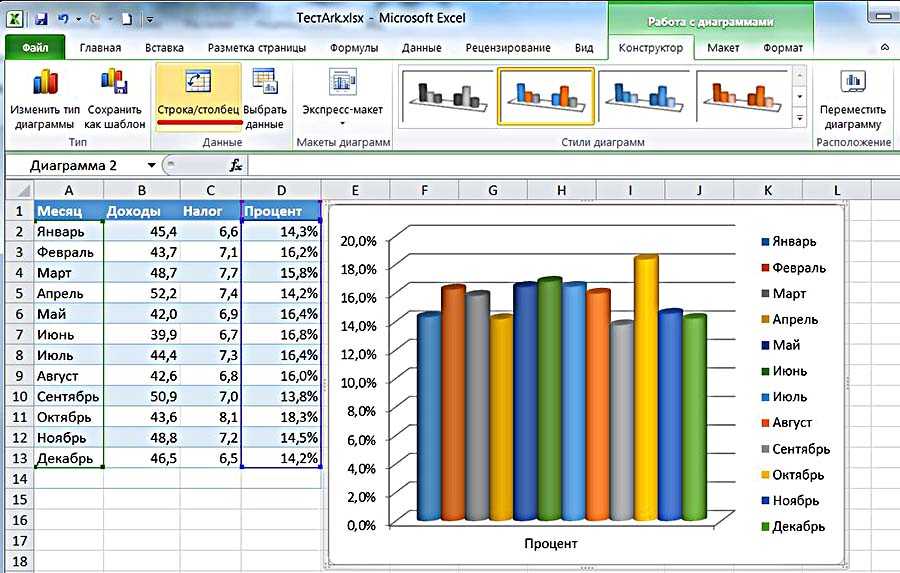
Напомним, что значения накопленных частот должны быть привязаны к верхним границам интервалов — в соответствии со стандартами и здравым смыслом. Идея в том, что накопленная частота накапливается именно к концу интервала, а не к середине.
Построим график в виде ломаной линии:
Insert — Charts — Insert Scatter (X, Y) or Bubble Chart
Вставка — Диаграммы — Вставить точечную (X, Y) или пузырьковую диаграмму
Вставка графика Y (X)
Выбираем тип графика
Scatter — Scatter with Straight Lines
Точечная — Точечная с прямыми отрезками
Это просто ломаная линия без маркеров точек.
Выбираем данные для графика:
Select Data — Select Data Source — Legend Entries (Series) — Add
Выбрать данные — Выбор источника данных — Элементы легенды (ряды) — Добавить
Edit Series
Изменение ряда
выбираем следующие данные.
Столбец «иксов» — верхние границы:
Series X Values
Значения Х
Столбец «игреков» — накопленные частоты:
Series Y Values
Значения Y
Убираем заголовок диаграммы:
Chart Elements — Chart Title
Элементы диаграммы — Название диаграммы
Настраиваем цвет линии на графике.
Format Data Series — Series options — Fill & Line — Line
Формат ряда данных —Параметры ряда — Заливка и границы — Линия
Line — Solid line
Линия — Сплошная линия
Color — Black
Цвет — Чёрный
Width = 0.5 pt
Ширина — 0,5 пт
Если отрезков много, то ломаная линия выглядит как гладкая кривая.
Настроим числовые метки на вертикальной оси, чтобы выводились целые числа:
Format Axis — Axis Options — Number — Decimal places — 0
Формат оси — Параметры оси — Число — Число десятичных знаков — 0
Установим диапазоны значений по осям.
Вертикальная ось — метки в процентах, а границы диапазона — числа. Поэтому пределы изменения будут от 0 до 1:
Category — Percentage
Категория — Процентный
Axis Options — Bounds
Параметры оси — Границы
Minimum — 0
Минимум — 0
Maximum — 1
Максимум — 1
Горизонтальная ось — в соответствии с интервалами группировки — от 190 до 310.
Подгоняем размеры графика и размещаем его под гистограммой. Можно сделать это вручную.
Если захочется особой точности, поработаем через меню параметров графика (числа условные).
Format Chart Area — Chart Options — Size & Properties — Size
Формат области диаграммы — Параметры диаграммы — Размер и свойства — Размер
Height — 1.
Высота — 7,62 см
Width — 5.3 in
Ширина — 12,7 см
В английской версии пакета размеры измеряются в дюймах. В русской версии — в сантиметрах. Можем установить точные значения размеров вручную.
Окончательно совмещаем маштаб гистограммы и кумуляты: начало первого интервала 190, конец последнего интервала 310. Положения этих двух меток на обоих графиках должны совпадать.
Проблемы с масштабом решаем так. Значение 190 находится в начале интервала, обозначенного 193. Значение 310 находится в конце интервала, следующего за 303.
Создание гистограммы
Гистограмма — это столбчатая диаграмма, которая показывает частоту повторяемости значений.
Примечание: В этой статье рассматривается только создание гистограмм. Сведения о диаграммах Парето (отсортированных гистограммах) см. в статье Создание диаграммы Парето.
Какие версии или продукты вы используете?
- Какие версии или продукты вы используете?
- Excel 2016 и более новых версиях
- Excel 2007–2013
- Outlook, PowerPoint, Word 2016
-
Выберите Вставка > Вставить диаграмму статистики > Гистограмма.
Гистограмму также можно создать с помощью вкладки Все диаграммы в разделе Рекомендуемые диаграммы.
Выделите данные.
(Это типичный пример данных для гистограммы.)
Советы:
-
На вкладках Конструктор и Формат можно настроить внешний вид диаграммы.
-
Если они не отображаются, щелкните в любом месте гистограммы, чтобы добавить на ленту область Работа с диаграммами.
-
Правой кнопкой мыши щелкните горизонтальную ось диаграммы, выберите Формат оси, а затем щелкните Параметры оси.
-
Руководствуясь приведенной ниже таблицей, вы сможете выбрать параметры, которые нужно задать в области задач Формат оси
.
Параметр
Описание
По категориям
Выберите этот вариант, если категории (горизонтальная ось) текстовые, а не числовые.
На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.
Совет: Чтобы подсчитать количество появлений текстовых строк, добавьте столбец и укажите в нем значение «1», а затем отобразите гистограмму и выберите параметр По категориям.
Автоматическая
Это вариант по умолчанию для гистограмм. Длина интервала вычисляется по формуле Скотта.
Длина интервала
Введите положительное десятичное число, задающее количество точек данных в каждом диапазоне.
Количество интервалов
Введите количество интервалов гистограммы (включая интервалы для значений, выходящих за верхнюю и нижнюю границы).
Выход за верхнюю границу интервала
Установите этот флажок, чтобы создать интервал для всех значений, превышающих значение в поле справа.
Чтобы изменить его, введите в поле другое десятичное число.
Выход за нижнюю границу интервала
Установите этот флажок, чтобы создать интервал для всех значений, не превышающих значение в поле справа. Чтобы изменить его, введите в поле другое десятичное число.
Совет: Дополнительные сведения о гистограммах и их пользе для визуализации статистических данных см. в этой записи о гисторамме, диаграммах Парето и «ящик с усами» блога группы разработчиков Excel.
Вариант «Автоматическая» (формула Скотта)
Формула Скотта минимизирует отклонение вариационного ряда на гистограмме по сравнению с набором данных, исходя из предположения о нормальном распределении данных.
Вариант «Выход за верхнюю границу интервала»
Вариант «Выход за нижнюю границу интервала»
-
Загрузите надстройку «Пакет анализа». Дополнительные сведения см.
в статье Загрузка надстройки «Пакет анализа» в Excel.
-
В один столбец на листе введите исходные данные. При необходимости добавьте в первую ячейку подпись.
Используйте количественные числовые данные, например, количество элементов или результаты тестов. Мастер гистограмм не будет работать с такими количественными числовыми данными, как идентификационные номера, введенные в виде текста.
-
В следующий столбец введите интервалы в возрастающем порядке. При необходимости добавьте в первую ячейку подпись.
Используйте собственные интервалы, поскольку они могут лучше соответствовать целям вашего анализа.
Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек.
-
Откройте вкладку Данные и выберите команду Анализ данных.
-
Выберите пункт Гистограмма и нажмите кнопку OK.
-
В разделе Ввод выполните указанные ниже действия:
-
В поле Интервал карманов введите ссылку на ячейку с диапазоном, который содержит числа интервала.
Если на листе использовались подписи столбцов, можно включать их в ссылки на ячейки.
Совет: Вместо того чтобы вводить ссылки вручную, щелкните , чтобы временно свернуть диалоговое окно, чтобы выбрать диапазоны на этом сайте. При повторном нажатии этой кнопки диалоговое окно опять разворачивается.
В поле Формировать список по диапазону введите ссылку на ячейку с диапазоном данных, который содержит исходные числа.
-
-
В группе Параметры вывода выберите местоположение выходных данных.
Гистограмму можно расположить на том же листе, новом листе в текущей книге или в новой книге.
-
Установите один или несколько флажков:
<c0>Парето (отсортированная гистограмма)</c0>. Отображает частоту данных по убыванию.
<c0><c1>Суммарный процент</c1></c0>.
Отображает суммарные проценты и добавляет в гистограмму строку суммарных процентов.
<c0><c1>Вывод диаграммы</c1></c0>.
Отображает встроенную гистограмму. -
Нажмите кнопку ОК.
Если вы хотите настроить гистограмму, вы можете изменить подписи текста и щелкнуть в любом месте гистограммы, чтобы использовать кнопки Элементы диаграммы, Стили диаграмм и Фильтр диаграммы справа от диаграммы.
-
На вкладке Вставка нажмите кнопку Диаграмма.
-
В диалоговом окне Вставка диаграммы в разделе Все диаграммы выберите пункт Гистограмма, а затем нажмите кнопку ОК.
Выделите данные.
(Это типичный пример данных для гистограммы.)
Советы:
-
Если они не отображаются, щелкните в любом месте гистограммы, чтобы добавить на ленту область Работа с диаграммами.
-
Правой кнопкой мыши щелкните горизонтальную ось диаграммы, выберите Формат оси, а затем щелкните Параметры оси.
-
Выделите данные.
(Это типичный пример данных для гистограммы.)
-
На ленте на вкладке Вставка нажмите кнопку (статистический значок) и в области Гистограммавыберите гистограмма.
Советы:
-
На вкладках Конструктор и Формат можно настроить внешний вид диаграммы.
-
Если они не отображаются, щелкните в любом месте гистограммы, чтобы добавить их на ленту.
Чтобы создать гистограмму в Excel 2011 для Mac, необходимо скачать сторонную надстройку. Дополнительные сведения см. в Excel 2011 для Mac.
В Excel Online вы можете просмотреть гистограмму (гистограмму с частотой), но не можете создать ее, так как для нее требуется надстройка Excel, не поддерживаемая в Excel в Интернете.
Если у вас есть Excel, вы можете нажать кнопку Изменить в Excel, чтобы открыть Excel на компьютере и создать гистограмму.
-
Коснитесь данных, чтобы выделить их.
-
Если вы на телефоне, коснитесь значка редактирования , чтобы отдемонстрировать ленту.
и нажмите Главная.
-
Выберите элементы Вставка > Диаграммы > Гистограмма.
При необходимости вы можете настроить элементы диаграммы.
Примечание: Эта функция доступна только при наличии подписки на Microsoft 365.. Если вы являетесь подписчиком Microsoft 365, убедитесь, что у вас установлена последняя версия Office.
Купить или попробовать Microsoft 365
-
Коснитесь данных, чтобы выделить их.
-
Выберите элементы Вставка > Диаграммы > Гистограмма.
Чтобы создать гистограмму в Excel, необходимо предоставить данные двух типов: данные, которые нужно проанализировать, и интервалы, которые представляют интервалы для измерения частоты. Данные необходимо расположить в двух столбцах на листе. Ниже приведены типы данных, которые должны содержаться в этих столбцах.
-
Введенные данные. Это данные, которые вы хотите проанализировать с помощью мастера гистограмм.
-
Числовые интервалы. Они представляют диапазоны, на основании которых мастер гистограмм проводит оценку введенных данных во время их анализа.
При использовании инструмента Гистограмма Excel количество точек данных в каждом из них. Точка данных включается в определенный интервал, если соответствующее значение больше нижней границы интервала данных и меньше верхней. Если диапазон диапазонов диапазонов Excel создается набор равномерно распределенных диапазонов между минимальным и максимальным значениями входных данных.
Результат анализа гистограммы отображается на новом листе (или в новой книге) и содержит таблицу и гистограмму, которая отражает данные этой таблицы.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Создание каскадной диаграммы
Создание диаграммы Парето
Создание диаграммы «солнечные лучи» в Office
Создание диаграммы «ящик с усами»
Создание диаграммы «дерево» в Office
Как вычислить промежуточный итог в Excel
- Промежуточный итог, также известный как кумулятивная сумма, является широко используемой функцией в образовательном и деловом мире.
- Процесс создания промежуточного итога в Excel состоит из трех простых шагов.
- Промежуточные итоги используются в розничных магазинах, на распродажах и на спортивных мероприятиях и т.д.
- Эта статья предназначена для владельцев бизнеса и профессионалов, которые хотят узнать, как создать промежуточный итог в Microsoft Excel.
Создать промежуточный итог (или накопительную сумму, как это известно в Excel) легко, как только вы освоите его. Многие владельцы бизнеса используют кумулятивные суммы для отслеживания расходов и доходов, рабочего времени сотрудников и управления запасами.
Идея промежуточного итога состоит в том, чтобы взять столбец чисел и рядом с ним показать промежуточный итог этих чисел. Вы можете использовать как положительные, так и отрицательные числа в промежуточной сумме, поэтому при желании вы можете сложить свои продажи и изъятия.
Что такое промежуточный итог?
Промежуточная сумма или кумулятивная сумма — это последовательность частичных сумм любого заданного набора данных. Промежуточный итог используется для отображения сводки данных по мере их роста с течением времени. Этот очень распространенный метод ежедневно используется студентами и профессионалами, которым поручено использовать Excel для вычисления и вычисления массива сложных данных и уравнений. Кроме того, наличие промежуточного итога может избавить вас от необходимости записывать саму последовательность, если нет необходимости знать отдельные используемые числа.
Как создать промежуточный итог в Excel
1. Начните с =СУММ. Нажмите на ячейку, с которой вы хотите, чтобы ваша промежуточная сумма начиналась. Затем выберите функцию СУММ в этой ячейке. Но вместо выделения ячеек в круглых скобках (путем перетаскивания курсора по ячейкам, которые вы хотите включить в уравнение), как если бы вы добавляли столбец чисел, вам нужно создать так называемую «абсолютную ссылку», за которой следует по «относительной ссылке». Не волнуйся; это не так сложно, как кажется. Следующий шаг описывает, как это сделать.
2. Создайте формулу промежуточного итога. В этой формуле необходимо использовать знак доллара, даже если подсчитываемые числа не являются суммами в долларах. Допустим, в нашем образце рабочей книги Excel вы хотите, чтобы совокупный итог был размещен в столбце C. В ячейке C1 вы должны ввести =СУММ($B$2:B2). Это создает необходимую относительную контрольную точку (B2) и абсолютную контрольную точку ($B$2) для вашего текущего подсчета.
Что это за ссылки? Относительные контрольные точки могут измениться при копировании и вставке формулы из одного места в другое. Например, если вы скопируете формулу на две строки вправо, относительная контрольная точка сдвинется на две строки вправо. Абсолютные опорные точки не изменяются при копировании.
3. Щелкните правый нижний угол ячейки с формулой. Затем перетащите вниз до тех пор, пока не будет применен промежуточный итог. Когда формула перетаскивается вниз, абсолютная контрольная точка $B$2 остается неизменной. Относительная контрольная точка B2 изменяется по мере того, как вы перетаскиваете курсор вниз до B3, B4, B5 и т. д.
Например, если стоимость продаж за март составляет 500 долларов США, стоимость продаж за апрель составляет 650 долларов США, а стоимость продаж за май составляет 500 долларов США. 700 долл. США, введите эти значения в столбце «Продажи». Чтобы получить промежуточную сумму, введите 500 долларов в верхнем правом столбце и используйте приведенную выше формулу для расчета промежуточной суммы. Затем вы перетащите курсор вниз, чтобы охватить продажи за апрель, май и июнь. Затем промежуточная сумма будет отображать 500, 1150 и 1850 долларов соответственно. Затем у вас будет промежуточная сумма, к которой вы сможете добавлять ежемесячные значения продаж с течением времени. Вот и все.
Как можно использовать промежуточный итог?
Хотя это вычисление может показаться немного сложным, на самом деле это довольно распространенная концепция, с которой многие из нас регулярно сталкиваются, независимо от того, используем ли мы ее. Вот некоторые примеры использования промежуточной суммы:
Операции с кассовым аппаратом.
Одним из наиболее распространенных примеров промежуточных сумм, с которыми вы регулярно сталкиваетесь, является использование кассовых аппаратов. В частности, кассовые аппараты отображают промежуточную сумму различных продуктов по мере их сканирования в систему. Кроме того, они обычно подсчитывают все транзакции, совершенные в течение дня.
В кассовом аппарате может быть предусмотрена функция отчетности, которая показывает нарастающие итоги повседневных функций в магазине, включая количество покупателей в определенное время дня и самые популярные товары за день или за все время, в зависимости от категории. Использование промежуточного итога позволяет розничным магазинам выявлять тенденции среди покупателей и улучшать свою работу.
Игровые табло.
Еще одним распространенным применением промежуточных сумм являются табло на спортивных мероприятиях. Хотя вы видите каждое очко, когда оно попадает на доску, чтобы понять, как рассчитывается конечный счет, в конце концов, окончательный счет — это единственное значение, которое имеет значение. Кроме того, игра в крикет, в частности, является отличным примером промежуточного итога. Каждый раз, когда игрок забивает ран, он добавляется к общему количеству. Таким образом, общий балл — это просто промежуточный итог или сумма прогонов.
Позиции по продажам
Если вы работаете в сфере продаж, вы, вероятно, сталкиваетесь с различными промежуточными итогами. Например, если у вас есть квота, вы можете использовать промежуточный итог, чтобы отслеживать свой прогресс, пока ваша квота не будет достигнута. Это также верно и в других отраслях, таких как телекоммуникации или банковское дело, где количество продаж, новых клиентов и проданных продуктов может быть связано с производительностью труда.
Менеджеры могут использовать эти промежуточные итоги для ежемесячной, ежеквартальной или годовой оценки производительности. Эти промежуточные итоги также могут определять реальную производительность по отношению к целевым показателям с течением времени. Затем эти данные можно использовать для устранения неполадок, которые необходимо изменить, если цели не достигнуты.
Расчеты с начала года
Одно из самых популярных применений промежуточных сумм — это расчеты с начала года. Расчет с начала года (с начала года) используется для записи определенной функции или деятельности (обычно финансовой) с определенной даты до конца года.
Например, вы можете увидеть массив расчетов за текущий год в своих платежных квитанциях. Это пример промежуточного итога, поскольку он отслеживает различные сделанные платежи и собранные налоги, чтобы дать вам окончательную сумму в конце каждого года. Эти окончательные итоги затем переносятся в формы W-2 и используются для целей налогообложения. Расчеты за текущий год также используются для расчета дохода от аренды, финансового положения бизнеса или доходности акций.
Итоги запасов
Другим распространенным применением промежуточных сумм является метод, используемый компанией для отслеживания запасов. Компании должны записывать количество проданных товаров и сравнивать это число с тем, сколько товаров у них есть на складе, так что это пример промежуточной суммы. Например, если в начале недели у вас есть на складе 1000 файлов cookie, каждая продажа будет вычитаться из общего запаса, и после каждой транзакции будет подсчитываться новая сумма.
Бухгалтерские балансы.
Если у вас есть работа, в которой используются балансовые отчеты, это также может быть примером промежуточной суммы. Балансовые отчеты также могут показать вам четкую картину любых активов и обязательств в определенный момент времени. Бухгалтерские балансы позволяют вести подробный список таких вещей, как расходы. После добавления новых элементов вы получаете новую сумму.
Балансы на банковских счетах
В выписке с банковского счета содержится подробный список того, что вносится и выплачивается каждый месяц. После каждой транзакции вы получаете новую сумму. Когда вы выходите в Интернет, чтобы просмотреть свой счет, вы увидите свой промежуточный итог.
Расход бензина
Компании, предоставляющие услуги по совместному использованию транспортных средств и службы доставки, также используют промежуточные итоги. Учитывая, что водителям часто платят за милю, промежуточная сумма позволяет отслеживать, сколько человек должен платить. Это также верно при создании электронных таблиц расходов, если вам приходится путешествовать несколько дней по работе.
Подсчет калорий
Промежуточные итоги также можно использовать для подсчета калорий в течение дня или недели. Люди, которые используют подсчет калорий, чтобы похудеть, могут использовать приложение или создать электронную таблицу, которая позволяет им вводить количество калорий каждого приема пищи, чтобы в конечном итоге рассчитать количество калорий на дни или недели. Приложение или таблица начнут с нуля калорий и создадут промежуточный итог в зависимости от того, что они едят.
Как создать промежуточный итог в Excel (кумулятивная сумма)
Что такое промежуточный итог?
Промежуточный итог в Excel (также известный как кумулятивная сумма) относится к частичной сумме набора данных. Это сумма последовательности чисел, которая обновляется каждый раз, когда к последовательности добавляется новое число.
Промежуточные итоги очень часто используются в Excel, особенно когда речь идет о ежедневных данных, таких как ежедневные продажи, ежедневный баланс банка, ежедневное потребление калорий или результаты спортивной игры. Он показывает общее количество за каждый день или месяц, в зависимости от измерений.
Как создать промежуточный итог
Существует множество способов создания промежуточного итога, в том числе с помощью простого сложения, функции СУММ и сводных таблиц.
Давайте посмотрим, как создать базовый промежуточный итог с помощью сложения, чтобы познакомить вас с его логикой.
Загрузите бесплатный файл для тренировок с текущими показателями
Используйте этот бесплатный файл Excel для тренировок вместе с учебным пособием.
Введите адрес электронной почты
Ниже приведена выписка по кредитной карте с различными расходами и кредитами в списке. Промежуточный итог помогает отслеживать доступный кредитный лимит и личные расходы. Чтобы создать промежуточный итог, нажмите D2 и введите =C2, начальный кредитный лимит, с которого нужно начать.
Учитывая, что промежуточные итоги показывают суммирование данных по мере добавления новых элементов в общий набор, чтобы сохранить изменения:
- Щелкните ячейку D3, введите =D2+C3.
Это нужно для добавления начального кредитного лимита и нового пункта — расхода от Whole Foods.
Теперь в ячейке D3 указаны кредитные лимиты после вычета расходов из Whole Foods — 49 долларов США.16.
Чтобы узнать оставшиеся доступные кредитные лимиты, перетащите формулу в D3 вниз и примените ее к остальным ячейкам в столбце D. от предыдущего значения промежуточной суммы и добавляет значение нового элемента.
Ниже приведена полная картина с промежуточным итогом, показывающим движение кредитного лимита с каждым добавленным элементом.
Как рассчитать промежуточный итог в Excel
Как упоминалось ранее, существует несколько способов расчета промежуточных сумм в Excel, в зависимости от сложности имеющейся ситуации и использования.
1. Создание промежуточного итога с помощью функции СУММ
Создание промежуточного итога с помощью функции СУММ очень похоже на простое сложение.
В ячейку D2 введите:
=СУММ(C2,D1)
Это нужно для сложения значения начального кредитного лимита и заголовка — Промежуточный итог. Заголовок сам по себе не содержит значения и при расчете будет считаться равным 0.
Это, в отличие от сложения, избавляет вас от дополнительной работы по созданию начального баланса, а затем добавлению нового элемента во вторую ячейку.
Скопируйте формулу в оставшуюся часть ячейки. Это должно выглядеть так, как показано на изображении ниже, где каждый промежуточный итог основан на предыдущих значениях.
Однако при добавлении строки в промежуточном итоге будет пробел, и пользователям нужно будет скопировать формулу и перетащить ее вниз, чтобы обновить остальные.
Аналогично, при удалении строки возникает ошибка #ССЫЛКА! показывает, что ссылка на ячейку удалена. Чтобы рассчитать промежуточный итог, скопируйте формулу из последней правильной ячейки (D5) и примените к остальным.
Функция СУММ позволяет быстро и легко вычислить промежуточную сумму. Однако, когда требуется корректировка данных (например, добавление или удаление строки), пользователям потребуется вручную настроить и повторно применить правильные формулы к ячейкам.
Если набор данных невелик и включает несколько расчетов или листов, ручная корректировка не представляет сложности. Однако, если набор данных большой с несколькими листами и ссылками на ячейки, ручная корректировка будет более сложной и может привести к ошибкам.
2. Создайте промежуточный итог с помощью функции СУММ и смешанной ссылки
Пользователи могут включать смешанные ссылки — как абсолютные, так и относительные — в формулу СУММ для расчета промежуточного итога.
В ячейку D2 введите:
=СУММ($C$2:C2)
Это блокирует ссылку на ячейку C2, поэтому суммирование всегда будет начинаться с ячейки C2.
Скопируйте формулу и перетащите ее вниз, чтобы применить к остальным ячейкам.
Как вы можете видеть ниже, промежуточный итог в ячейке D5 вычисляет сумму значений от C2 до C5.
Суммирование всегда будет начинаться с ячейки C2, так как она заблокирована знаком $ (абсолютная ссылка) и включает любые другие значения между C2 и C5 (относительная ссылка).
То же, что и функция СУММ, вставка и удаление строки приведет к ошибкам в формулах и потребует ручных корректировок.
3. Создайте промежуточный итог с помощью сводных таблиц
Сводные таблицы — это мощная функция Excel, позволяющая упорядочивать, обобщать и анализировать таблицы. Он обычно используется для сортировки, группировки, вычисления суммы, усреднения или подсчета значений. Сводная таблица также может подсчитывать промежуточные итоги.
В новой электронной таблице создайте сводную таблицу, используя тот же набор данных.
- Под строками добавьте дату и описание
- В разделе «Значения» дважды укажите движение.
Это сделано для того, чтобы в столбце C были показаны ежедневные промежуточные итоги и итоги движения. А столбец D — сумма движения 2 будет изменен, чтобы показать промежуточный итог позже.
Для удобства просмотра сводная таблица показана в форме схемы ниже.
В полях сводной таблицы щелкните правой кнопкой мыши сумму движения 2, чтобы получить доступ к выбору меню. Щелкните Параметры поля значений .
Появится диалоговое окно «Настройки поля значения». Здесь можно сделать много чего.
Сначала измените название на «Нарастающий итог», чтобы различать его.
Выберите вкладку — Показать значения как и в раскрывающемся списке найдите Промежуточный итог В , чтобы значения отображались как Промежуточный итог. В Базовом поле выберите — Дата, так как промежуточный итог будет выполняться на основе дат. Нажмите «ОК».
Теперь в сводной таблице отображается промежуточная сумма движения кредита по датам. Метка поля также обновляется до промежуточного итога.
В этом примере промежуточные итоги отображаются вверху каждой группы. Вы можете изменить его в конце каждой группы, если это лучше соответствует вашим привычкам.
На вкладке «Дизайн» найдите «Промежуточные итоги», затем нажмите «Показать все промежуточные итоги внизу группы».
Теперь сводная таблица отображает всю информацию в упорядоченном виде, детализируя действия по датам, а также итоги движения кредита и промежуточный итог по датам.
Если есть какие-либо изменения в исходных данных, будь то добавление или удаление строки, просто нажмите «Обновить», и таблица автоматически отобразит изменения.
Не существует идеального способа создания промежуточных сумм в Excel. Все три метода дают одинаковые результаты, и у каждого есть свои плюсы и минусы. Это зависит от сложности набора данных и имеющихся расчетов.
Различия в Windows и Mac
Шаги, необходимые для выполнения промежуточного итога в Windows и Mac, одинаковы.
Сводка
Промежуточные итоги в Excel (также называемые совокупной суммой) полезны для отслеживания прогресса и изменений с течением времени, особенно когда из набора данных поступают новые данные или удаляются старые данные. Обычно он используется для отслеживания моделей продаж, банковского баланса, потребления калорий, платы за коммунальные услуги и результатов спортивных игр.
Существует несколько способов создания промежуточных итогов в Excel, каждый из которых имеет свои плюсы и минусы. Важно учитывать свои потребности и просматривать набор данных, прежде чем выбрать наиболее эффективный метод расчета промежуточной суммы в Excel.
Что дальше?
Попробуйте курс GoSkills Microsoft Excel — базовый и продвинутый сегодня, чтобы улучшить свои навыки работы с Excel!
Повысьте уровень своих навыков работы с Excel
Станьте сертифицированным мастером Excel с небольшими курсами GoSkills
Начать бесплатную пробную версию
5 простых способов подсчета промежуточного итога в Excel (накопительная сумма)
Расчет промежуточного итога с табличными данными
Если у вас есть табличные данные (т. е. таблица в Excel, которая не преобразована в таблицу Excel), вы можете использовать несколько простых формул для расчета промежуточных итогов.
Использование оператора сложения
Предположим, у вас есть данные о продажах по датам и вы хотите рассчитать промежуточную сумму в столбце C.
Ниже приведены шаги для этого.
Шаг 1 — В ячейке C2, которая является первой ячейкой, где вы хотите промежуточный итог, введите
= B2
Это просто даст те же значения продаж в ячейке B2.
Шаг 2 – В ячейку C3 введите следующую формулу:
=C2+B3
Шаг 3 – Примените формулу ко всему столбцу. Вы можете использовать маркер заполнения, чтобы выбрать и перетащить его, или просто скопировать и вставить ячейку C3 во все оставшиеся ячейки (что автоматически скорректирует ссылку и даст правильный результат).
Это даст вам результат, как показано ниже.
Это очень простой метод, который хорошо работает в большинстве случаев.
Логика проста – каждая ячейка берет значение над ней (которое представляет собой совокупную сумму до предыдущей даты) и добавляет значение в соседней ячейке (которое является стоимостью продажи за этот день).
Есть только один недостаток — если вы удалите любую из существующих строк в этом наборе данных, все ячейки ниже вернут ошибку ссылки (#ССЫЛКА!)
Если это возможно с вашим набором данных, используйте следующий метод, использующий формулу СУММ
Использование СУММ с частично заблокированной ссылкой на ячейку
Предположим, у вас есть данные о продажах по датам и вы хотите рассчитать промежуточную сумму в столбце C.
Ниже приведена формула СУММ, которая даст вам промежуточный итог.
=СУММ($B$2:B2)
Позвольте мне объяснить, как работает эта формула.
В приведенной выше формуле СУММ я использовал ссылку для добавления как $B$2:B2
- $B$2 — это абсолютная ссылка, что означает, что когда я копирую ту же формулу в ячейках ниже, эта ссылка не собирается меняться.
Таким образом, при копировании формулы в ячейку ниже формула изменится на SUM($B$2:B3)
- B2 — это вторая часть ссылки, которая является относительной ссылкой, что означает, что она будет меняться по мере копирования. формулу вниз или вправо. Таким образом, при копировании формулы в ячейку ниже это значение станет B3
Читайте также: Абсолютные, относительные и смешанные ссылки на ячейки в Excel итоги.Расчет промежуточного итога в таблице Excel
При работе с табличными данными в Excel рекомендуется преобразовать их в таблицу Excel. Это значительно упрощает управление данными, а также упрощает использование таких инструментов, как Power Query и Power Pivot.
Работа с таблицами Excel имеет такие преимущества, как структурированные ссылки (что упрощает обращение к данным в таблице и использование их в формулах) и автоматическую корректировку ссылок при добавлении или удалении данных из таблицы.
Хотя вы все еще можете использовать приведенную выше формулу, которую я показал вам в таблице Excel, позвольте мне показать вам несколько лучших способов сделать это.
![]()
Предположим, у вас есть таблица Excel, как показано ниже, и вы хотите рассчитать промежуточный итог в столбце C.
Ниже приведена формула, которая сделает это:
=СУММ(Данные о продажах[[#Заголовки],[Продажа]]:[@Продажа])Приведенная выше формула может показаться длинной, но вы не надо писать самому. то, что вы видите в формуле суммы, называется структурированными ссылками, что является эффективным способом Excel ссылаться на определенные точки данных в таблице Excel.
Например, SalesData[[#Headers],[Sale]] относится к заголовку Sale в таблице SalesData (SalesData — это имя таблицы Excel, которое я дал при создании таблицы)
И [@Sale] относится к значению в ячейке в той же строке столбца «Продажа».
Я только что объяснил это здесь для вашего понимания, но даже если вы ничего не знаете о структурированных ссылках, вы все равно можете легко создать эту формулу.
Ниже приведены шаги для этого:
- В ячейку C2 введите =СУММ(
- Выберите ячейку B1, которая является заголовком столбца с продажной стоимостью.
Вы можете использовать мышь или клавиши со стрелками. Вы заметите, что Excel автоматически вводит структурированную ссылку для этой ячейки
- Добавьте : (двоеточие)
- Выберите ячейку B2. Excel снова автоматически вставит структурированную ссылку для ячейки
- . Закройте скобку и нажмите Enter
. Вы также заметите, что вам не нужно копировать формулу во весь столбец, таблица Excel автоматически сделает это за вас.
Еще одна замечательная особенность этого метода заключается в том, что если вы добавите новую запись в этот набор данных, таблица Excel автоматически рассчитает промежуточную сумму для всех новых записей.
Хотя мы включили заголовок столбца в нашу формулу, помните, что формула будет игнорировать текст заголовка и учитывать только данные в столбце
Расчет промежуточного итога с помощью Power Query сводится к подключению к базам данных, извлечению данных из нескольких источников и их преобразованию перед помещением в Excel.
![]()
Если вы уже работаете с Power Query, было бы более эффективно добавлять промежуточные итоги во время преобразования данных в самом редакторе Power Query (вместо того, чтобы сначала получать данные в Excel, а затем добавлять промежуточные итоги с помощью любого из вышеупомянутые методы, описанные выше).
Хотя в Power Query нет встроенной функции для добавления промежуточных сумм (а хотелось бы, чтобы она была), вы все равно можете сделать это, используя простую формулу.
Предположим, у вас есть таблица Excel, как показано ниже, и вы хотите добавить промежуточные итоги к этим данным:
Ниже приведены шаги для этого:
- Выберите любую ячейку в таблице Excel
- Щелкните Данные
- На вкладке «Получить и преобразовать» щелкните значок «Из таблицы/диапазона». Это откроет таблицу в редакторе Power Query 9.0004
- [Необязательно] Если ваш столбец «Дата» еще не отсортирован, щелкните значок фильтра в столбце «Дата», а затем нажмите «Сортировать по возрастанию».
![]()
- Перейдите на вкладку «Добавить столбец» в редакторе Power Query. щелкните раскрывающийся список Столбец индекса (нажимайте не на значок столбца индекса, а на маленькую черную наклонную стрелку рядом с ним, чтобы отобразить дополнительные параметры)
- Щелкните параметр «От 1». Это добавит новый индексный столбец, который будет начинаться с единицы и вводить числа, увеличивающиеся на 1 во всем столбце
- Щелкните значок «Пользовательский столбец» (который также находится на вкладке «Добавить столбец»)
- В открывшемся диалоговом окне пользовательского столбца введите имя нового столбца. в этом примере я буду использовать имя «Нарастающая сумма»
- В поле формулы «Пользовательский столбец» введите следующую формулу: ))
- Убедитесь, что в нижней части диалогового окна установлен флажок «Синтаксические ошибки не обнаружены»
- Нажмите ОК. Это добавит новый столбец промежуточной суммы
- Удалить столбец индекса
- Щелкните вкладку «Файл», а затем щелкните «Закрыть и загрузить».
текущие итоги.
Теперь, если вы думаете, что это слишком много шагов по сравнению с предыдущими методами использования простых формул, вы правы.
Если у вас уже есть набор данных и все, что вам нужно сделать, это добавить промежуточные итоги, лучше не использовать Power Query.
Использование Power Query имеет смысл, когда вам нужно извлечь данные из базы данных или объединить данные из нескольких разных книг, а также в процессе добавить к ним промежуточные итоги.
Кроме того, после того, как вы выполните эту автоматизацию с помощью Power Query, в следующий раз, когда ваш набор данных изменится, вам не нужно делать это снова, вы можете просто обновить запрос, и он даст вам результат на основе нового набора данных.
Как это работает?
Теперь позвольте мне быстро объяснить, что происходит в этом методе.
Первое, что мы делаем в редакторе Power Query, — вставляем индексный столбец, начиная с единицы и увеличивая его на единицу по мере продвижения вниз по ячейкам.
![]()
Мы делаем это, потому что нам нужно использовать этот столбец при вычислении промежуточного итога в другом столбце, который мы вставляем на следующем шаге.
Затем мы вставляем пользовательский столбец и используем приведенную ниже формулу
List.Sum(List.Range(#"Added Index"[Sale],0,[Index]))Это формула List.Sum, которая дать вам сумму диапазона, который указан в нем.
И этот диапазон указывается с помощью функции List.Range.
Функция List.Range дает указанный диапазон в столбце продажи в качестве выходных данных, и этот диапазон изменяется в зависимости от значения индекса. Например, для первой записи диапазон будет просто первой стоимостью продажи. И по мере того, как вы спускаетесь по ячейкам, этот диапазон будет расширяться.
Итак, для первой ячейки. List.Sum даст вам только сумму первой стоимости продажи, а для второй ячейки — сумму первых двух значений продажи и так далее.
Хотя этот метод работает хорошо, он очень медленно работает с большими наборами данных — тысячами строк.
Если вы имеете дело с большим набором данных и хотите добавить к нему промежуточные итоги, ознакомьтесь с этим руководством, в котором показаны другие более быстрые методы.
Расчет промежуточного итога на основе критериев
До сих пор мы видели примеры, в которых мы вычисляли промежуточный итог для всех значений в столбце.
Но могут быть случаи, когда вы хотите рассчитать промежуточную сумму для определенных записей.
Например, ниже у меня есть набор данных, и я хочу рассчитать промежуточную сумму для принтеров и сканеров отдельно в двух разных столбцах.
Это можно сделать с помощью формулы СУММЕСЛИ, которая вычисляет промежуточный итог, проверяя выполнение указанного условия.
Ниже приведена формула, которая сделает это для столбцов принтеров:
=СУММЕСЛИ($C$2:C2,$D$1,$B$2:B2)Аналогичным образом, чтобы вычислить промежуточный итог для сканеров, используйте следующую формулу:
=СУММЕСЛИ($C$2:C2,$E$1,$B$2:B2)В приведенных выше формулах я использовал СУММЕСЛИ, что дало бы мне сумму в диапазоне при соблюдении указанных критериев.
.
Формула принимает три аргумента:
- диапазон : это диапазон критериев, который будет проверяться на соответствие заданным критериям
- критерии : это критерии, которые будут проверяться только в том случае, если этот критерий выполняется тогда значения в третьем аргументе, который является диапазоном суммы, будут добавлены
- [sum_range] : это диапазон суммы, из которого значения будут добавлены, если критерии соблюдены , чтобы по мере продвижения вниз по ячейкам диапазон продолжал расширяться. Это позволяет нам учитывать и добавлять значения только до этого диапазона (отсюда промежуточные итоги).
В этой формуле я использовал столбец заголовка (принтер и сканер) в качестве критерия. вы также можете жестко закодировать критерии, если заголовки столбцов не совпадают с текстом критериев.
Если вам необходимо проверить несколько условий, вы можете использовать формулу СУММЕСЛИМН.
![]()
Промежуточный итог в сводных таблицах
Если вы хотите добавить промежуточные итоги в результат сводной таблицы, вы можете легко сделать это, используя встроенную функцию сводных таблиц.
Предположим, у вас есть сводная таблица, как показано ниже, где у меня есть дата в одном столбце и стоимость продажи в другом столбце.
Ниже приведены шаги по добавлению дополнительного столбца, в котором будет отображаться промежуточная сумма продаж по дате:
- Перетащите поле «Продажа» в область «Значение».
- Это добавит еще один столбец со значениями продаж.
- Щелкните параметр «Сумма продажи2» в области «Значение».
- Щелкните параметр «Параметры поля значения». «Промежуточные итоги»
- Щелкните вкладку «Показать значение как»
- В раскрывающемся списке «Показать значение как» выберите параметр «Промежуточный итог в»
- В параметрах базового поля убедитесь, что выбрана дата
- Нажмите «ОК».
![]()
No related posts.
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт





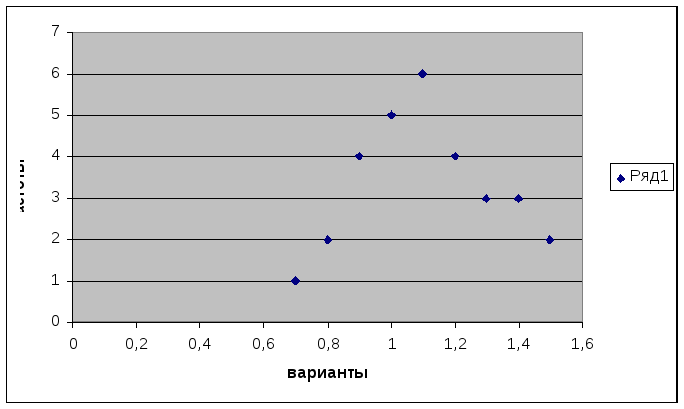























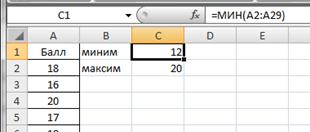
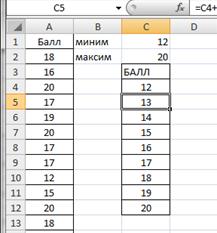
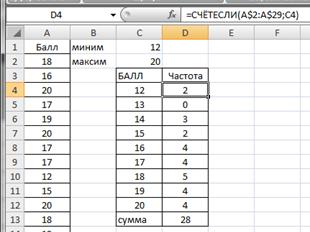
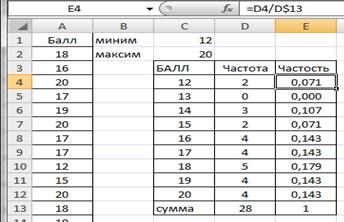
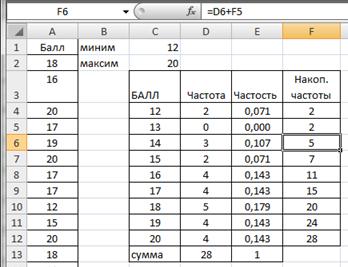
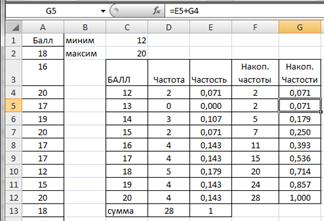

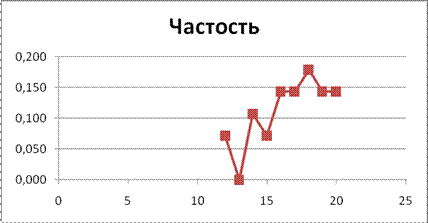
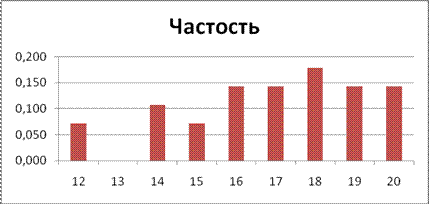

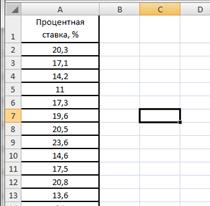

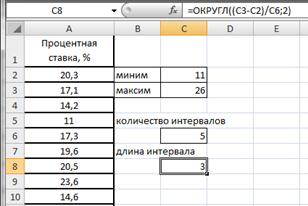
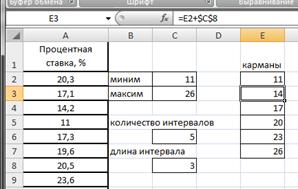
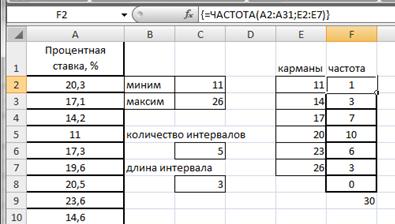
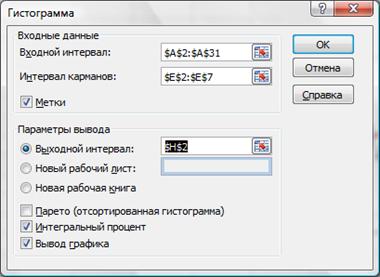
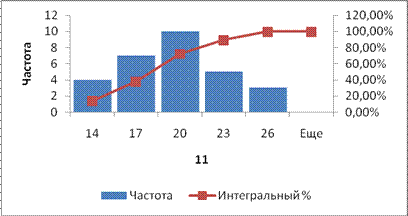








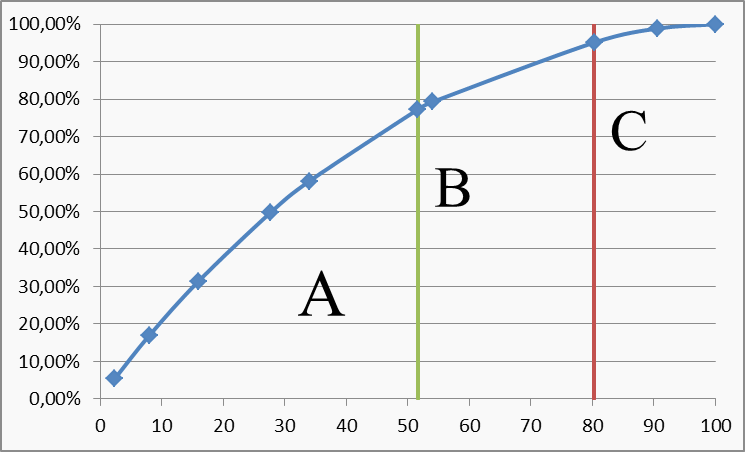
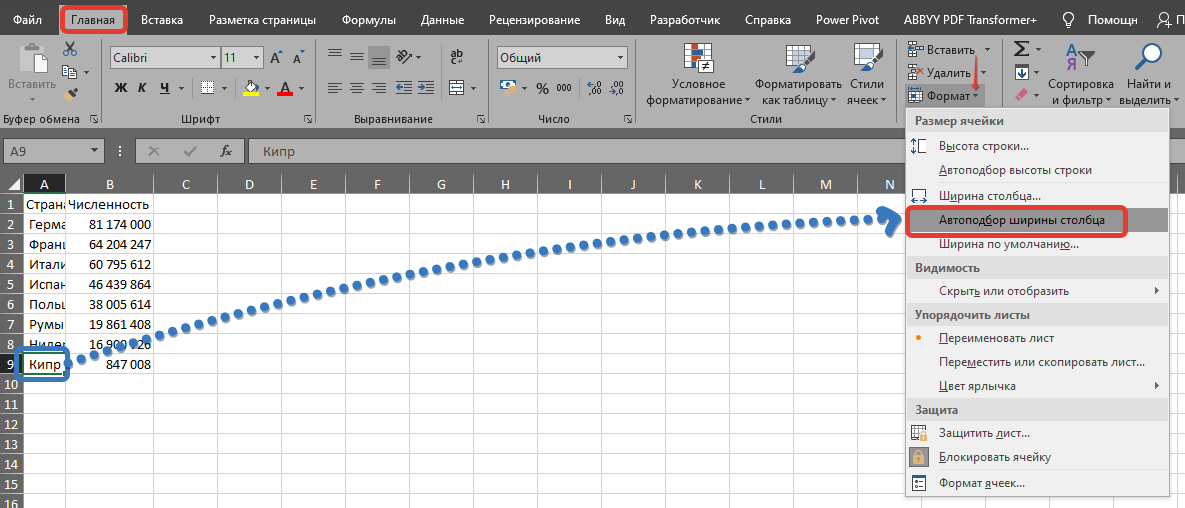
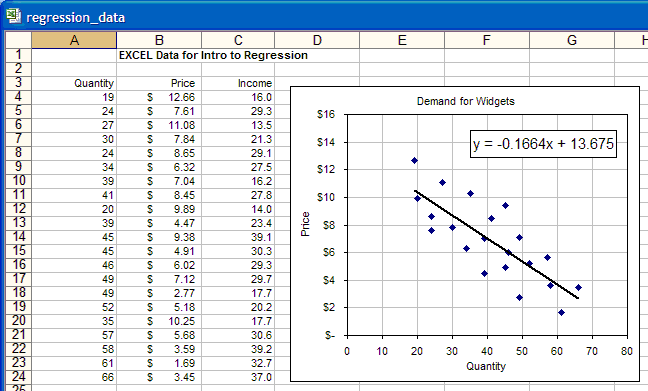 На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.
На гистограмме одинаковые категории будут сгруппированы, а значения на оси значений — просуммированы.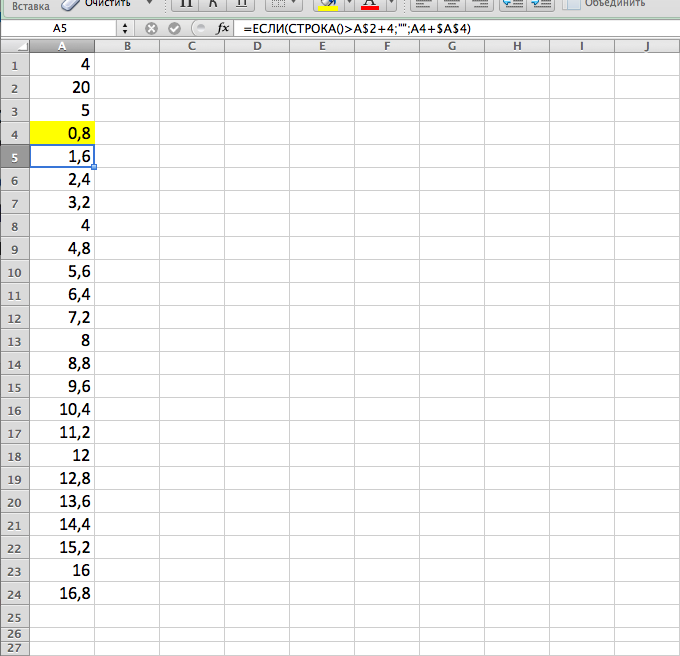
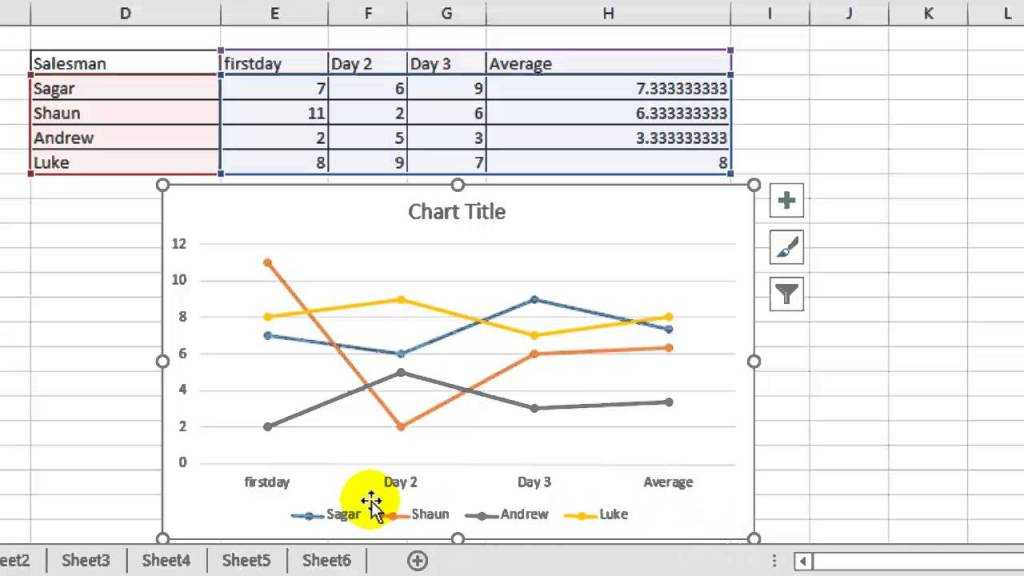 Чтобы изменить его, введите в поле другое десятичное число.
Чтобы изменить его, введите в поле другое десятичное число. в статье Загрузка надстройки «Пакет анализа» в Excel.
в статье Загрузка надстройки «Пакет анализа» в Excel. Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек.
Если вы не введете их, мастер гистограмм создаст равномерно распределенные интервалы, используя минимальное и максимальное значение во введенном диапазоне в качестве начальной и конечной точек.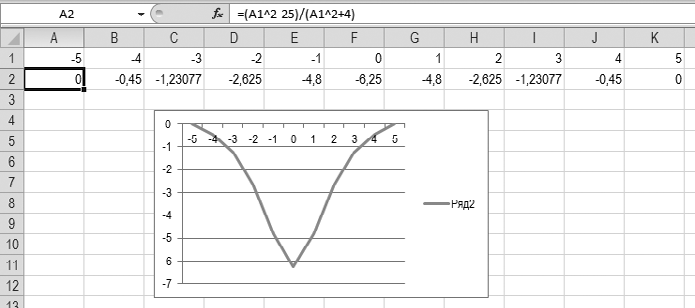

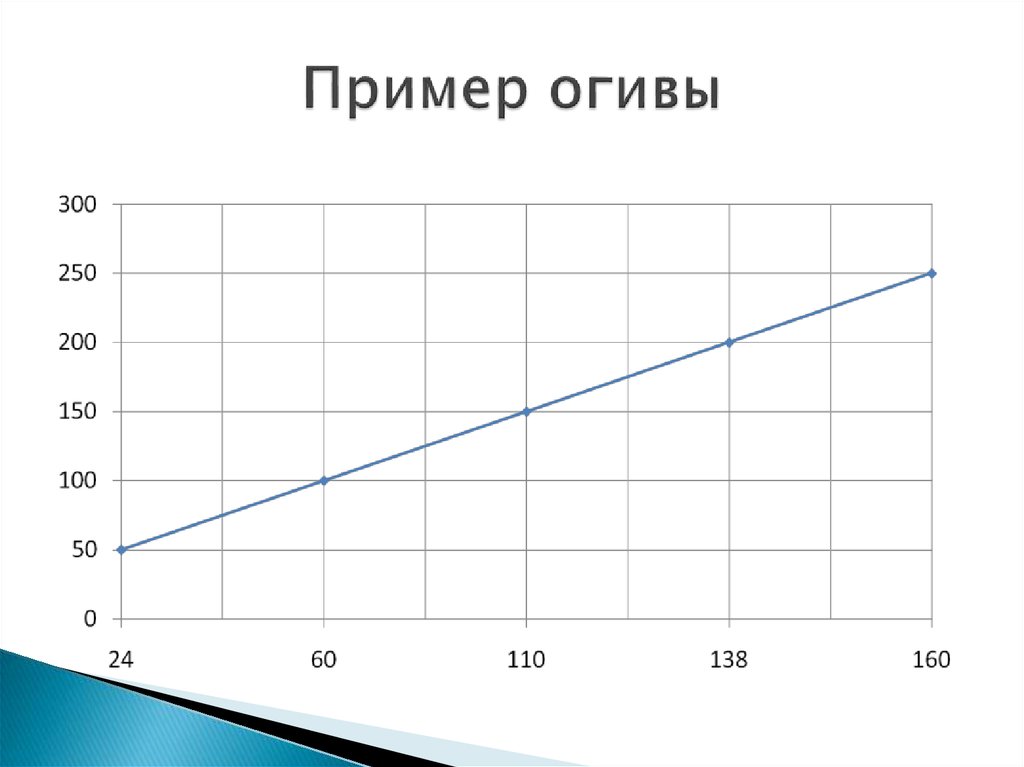 и нажмите Главная.
и нажмите Главная.