Анализ социологических данных в excel

В ходе проведения массовых социологических опросов перед исследователями нередко возникает проблема, связанная с обработкой больших совокупностей полученных данных и их преобразованием из рукописного вида в электронный, машиночитаемый формат.

К сожалению, практически все специализированные программы для обработки социологической информации (SPSS, Statistica, Vortex, PolyAnalyst и др.) распространяются на коммерческой основе, предъявляют серьезные требования к техническим характеристикам персональных компьютеров и зачастую не имеют русифицированного файла помощи.

В связи с этим возрастает необходимость обращения к программному обеспечению, имеющемуся на большинстве современных ЭВМ и позволяющему решать различные задачи необходимые социологу-практику.  Одной из таковых программ является Microsoft Office Excel (Excel).

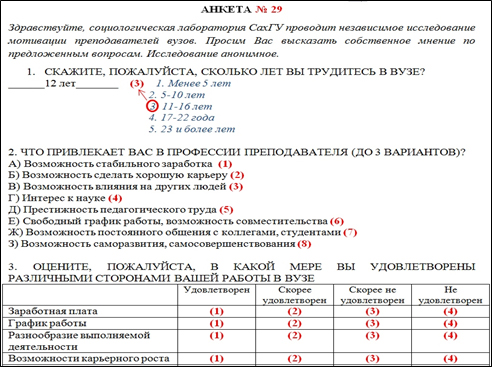
Обработка первичной социологической информации полученной в ходе опроса происходит в Excel в несколько этапов.На первом этапе необходимо пронумеровать все анкеты подлежащие анализу, для постоянного контроля ввода данных и возможности их своевременного корректирования. Далее необходимо «закрыть» все открытые вопросы анкеты, объединив ответы респондентов в группы [1, с. 434-437].Так, при ответе на открытый вопрос «Сколько лет Вы трудитесь в вузе?» человек может указать точный стаж, который социолог для удобства анализа отнесет в группы: «менее 5 лет», «5-10 лет», «11-16 лет», «17-22 года», «23 и более лет» (рис.1, вопрос 1).

Рис. 1 Фрагмент анкеты

Когда все открытые вопросы анкеты приведены в «закрытый» вид, следует присвоить числовой код каждому варианту ответа в каждом вопросе, то есть закодировать его. Если вопрос задан в виде таблицы (рис 1, вопрос 3), то при его анализе необходимо каждую строку ответа кодировать как отдельный вопрос. Ведь, по сути, каждый вопрос таблицы задается респонденту как отдельный: «Насколько Вы удовлетворены заработной платой?», «Насколько Вы удовлетворены графиком работы?» и т.д. Если же респондент пропустил вопрос или не смог ответить на него, то код отсутствию ответа не присваивается.

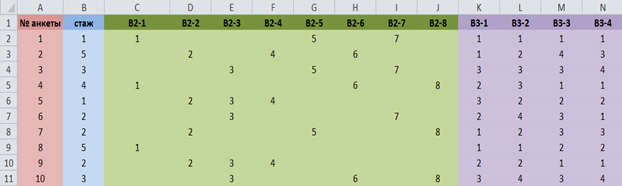
На втором этапе происходит формирование базы данных социологического опроса в Excel.

В первый столбец матрицы необходимо внести номера анкет, а в первую строку – краткие формулировки вопросов или их номера. Таким образом, каждой строке матрицы соответствует одна анкета, а каждому столбцу – один вопрос или подвопрос (рис. 2).

Рис. 2. Фрагмент базы данных социологического опроса в Excel

Поскольку во втором вопросе анкеты (рис.1) респондент может выбрать несколько вариантов, вопрос необходимо разбить на колонки по числу вариантов ответа (подвопросы).

При обработке вопроса заданного в виде таблицы, следует разбивать его на подвопросы по количеству строк.

Затем в матрицу вносятся данные всех анкет в соответствии с ранее произведенным кодированием.

Таким образом, согласно нашей матрице, респондент заполнивший анкету № 2, имеющий стаж работы более 23 лет, выбрал в качестве ответов на второй вопрос варианты №2, 4, 6 (возможность сделать хорошую карьеру, интерес к науке, свободный график работы и возможность совместительства). Он же удовлетворен заработной платой; скорее удовлетворен графиком работы; не удовлетворен разнообразием выполняемой деятельности; скорее не удовлетворен возможностями карьерного роста.

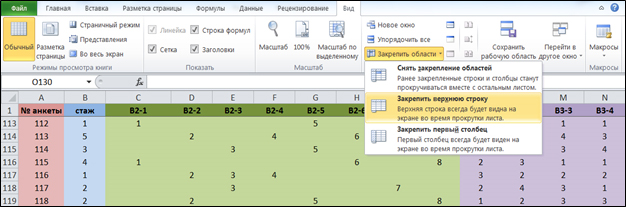
Для удобства формирования базы данных социологического опроса рекомендуется закреплять первую строку матрицы (вкладка «Вид» → «Закрепить области» → «Закрепить верхнюю строку») (рис. 3), что позволит всегда видеть заголовок таблицы.

Рис. 3 Матрица данных с закрепленным заголовком

Кроме того, если в анкете присутствует значительное количество вопросов, требующих разбивки в матрице данных, эти вопросы желательно выделять одним цветом (щелчок левой кнопкой мыши по столбцу выделяет его, далее во вкладке «Главная» выбираем «Заливка» и необходимый цвет).

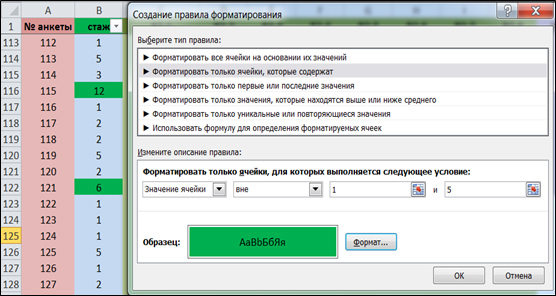
На третьем этапе  исследователем должен быть осуществлен поиск и устранение ввода ошибочных значений. Реализуется такая процедура с помощью функции «Условное форматирование», она позволяет выделить цветом все ячейки, содержащие ошибку. Согласно нашей кодировке в вопросе № 1 в матрице данных могут присутствовать только значения 1-5. Все иные цифры являются ошибочными и должны быть исправлены. Для поиска иных значений в вопросе №1 выделим его щелчком мыши. Далее перейдем во вкладку «Главная» → «Условное форматирование» → «Создать правило». В открывшемся окне отметим «Форматировать только ячейки, которые содержат» в полях раздела «Форматировать только ячейки, для которых выполняется следующее условие», выберем «значение ячейки», «вне», «1», «5». Затем выберем требуемый формат, например фон. При нажатии кнопки «OK», Excel выделит зеленым ошибочные значения. (Рис. 4).

 Рис. 4. Поиск ошибок ввода данных

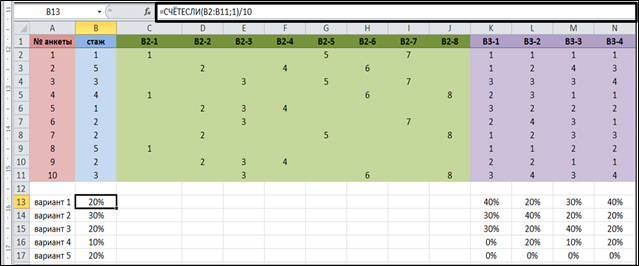
На четвертом этапе происходит непосредственная обработка социологической информации. Для подсчета процентного распределения ответов на вопросы, предполагающие только один ответ, необходимо пользоваться функцией «СЧЕТЕСЛИ». Для этого под таблицей, в столбце «№ анкеты» прописываем номера вариантов ответа на вопросы. Во втором столбце прописываем формулу (рис. 5). В нашем примере формула подсчета первого варианта ответа на вопрос о стаже работы будет иметь следующий вид:

=СЧЁТЕСЛИ(B2:B11;1)/10, где

B2:B11- столбец, в котором находятся интересующие нас ответы;

1 – номер варианта ответа, процент которого необходимо посчитать;

10 – общее количество анкет.

Для подсчета второго варианта, формула приобретет значение: =СЧЁТЕСЛИ(B2:B11;2)/10. Полученное число необходимо перевести в процентный формат: вкладка «Главная» → «Процентный формат».

Когда все варианты ответа в первом столбце просчитаны, формулу можно растянуть вправо для подсчета процентов по всем вопросам, предполагающим один ответ.

Рис. 5 Подсчет процентного распределения ответов на вопросы, предполагающие один вариант

Если вопрос предполагает множественный ответ, то расчет процентного соотношения ответов рассчитывается следующим образом: сначала необходимо узнать, сколько всего ответов дали респонденты при ответе на вопрос. Для этого воспользуемся счетом заполненных ячеек, с помощью формулы: =СЧЁТЗ(C2:J11), где C2:J11- диапазон столбцов, в которых находятся интересующие нас ответы.

Далее применим формулу использованную ранее. Для подсчета процентного распределения первого варианта ответа во втором вопросе анкеты, формула будет иметь вид:

=СЧЁТЕСЛИ(C2:C11;1)/27, где

C2:C11 – диапазон столбцов, в которых находятся интересующие нас ответы;

1- номер варианта ответа, процент которого необходимо посчитать;

27 – сумма всех ответов на вопрос № 2. (Рис.6)

Рис. 6 Подсчет процентного распределения ответов на вопрос, предполагающий множественный ответ.

Если в ходе исследования социологу необходимо определить связь между признаками, например, выяснить, сколько респондентов со стажем работы от 5 до 10 лет полностью удовлетворены заработной платой (столбец В3-1), необходимо пользоваться формулой вида:

=СЧЁТЕСЛИМН(B2:B11;2;K2:K11;1)/СЧЁТЕСЛИ(B2:B11;2), где

B2:B11 – диапазон столбцов, в которых находятся ответы о стаже работы;

2 – код ответа, обозначающий стаж работы от 5 до 10 лет;

K2:K11- диапазон столбцов, в которых находятся ответы об удовлетворенностью заработной платой;

1 – код ответа, обозначающий полную удовлетворенность заработной платой.

Таким образом, с помощью программы MS Excel, социолог может в сжатые сроки базовый анализ данных, интерпретировать значительные числовые массивы, полученные в ходе эмпирических исследований. Высокая адаптивность и простота работы, легкость экспорта данных, как между пользователями, так и между другими программными продуктами, позволяет реализовать на практике любой метод количественных исследований и решить большую часть задач, встречающихся в работе социолога.

Библиографический список

1. Рабочая книга социолога / под ред. Г.В. Осипова. Изд. 4-е, стереотипное. – М.: КомКнига, 2006. – 480 с.

---

Количество просмотров публикации: Please wait

Все статьи автора «Чуднова Ольга Владимировна»

Базовый анализ статистических данных можно проводить и в распространенной системе MS Excel или
ее бесплатных аналогах, таких как Open Office или online редакторах типа Google Docs.

Первоначально результаты опросов должны быть оцифрованы в виде таблицы в столбцах которой представлены
ответы на вопросы, а в строках результаты анкет. Такой вариант представления данных соответсвует
реляционным базам данных.

Для начала найдем распределение ответов при помощи функций СУММ, ЕСЛИ,
СУММЕСЛИ, СУММЕСЛИМН, СЧЕТЕСЛИи СЧЕТЕСЛИМН.

Описание функций Excel

• СУММ(Диапазон) — функция для нахождения суммы значений указанного диапазона.
  Пример: =СУММ(B2:B25).
• ЕСЛИ(это истинно, то сделать это, в противном случае сделать что-то еще). У функции ЕСЛИ
  возможны два результата. Первый результат возвращается в случае, если сравнение истинно,
  второй — если сравнение ложно. Пример: =ЕСЛИ(E2=»Да»;1;2).
• СУММЕСЛИ(Диапазон;Условие) — функция для нахождения суммы значений указанного диапазона,
  соответствующие указанному условию.
  Пример: =СУММЕСЛИ(B2:B25;»>35″).
  Есть возможность разделения диапазонов сравнения и суммирования, для этого диапазон суммирования указывается
  в качестве третьего параметра: =СУММЕСЛИ(D2:D5; «Теле2»; B2:B5) суммирует только те значения
  из диапазона B2:B5, для которых соответствующие значения из диапазона D2:D5 равны «Теле2».
• Функция СУММЕСЛИМН(диапазон_суммирования; диапазон_условия1; условие1) похожа на второй вариант
  использования функции СУММЕСЛИ(диапазон_условия;Условие;диапазон_суммирования), только диапазон
  суммирования и диапазон условия переставлены местами.
  Кроме этого есть возможность указания нескольких диапазонов условий СУММЕСЛИМН(диапазон_суммирования;
  диапазон_условия1; условие1; диапазон_условия2; условие2; …). Можно ввести до 127 пар диапазонов и
  условий.
  Пример: =СУММЕСЛИМН(B2:B9; D2:D9; «=М*»; C2:C9; «м») найдет сумму возрастов мужчин, оператор которых
  начинатеся на букву М.
• Функции СЧЕТЕСЛИ и СЧЕТЕСЛИМН аналогичны функциям СУММЕСЛИ и
  СУММЕСЛИМН, только они ничего не суммируют, а просто считают количество ячеек, удовлетворяющих
  условиям.
  Примеры: =СЧЁТЕСЛИ(C2:C10;$C$2) считает число мужчин.
  =СЧЁТЕСЛИ(F2:F5;»<>»&$F$10) считает число анкет с графиком не равным «Свободный».
  Знак амперсанда (&) объединяет оператор сравнения «<>» (не равно) и значение в ячейке $F$10,
  в результате чего получается формула =СЧЁТЕСЛИ(F2:F5;»<>Свободный»).

На представленном рисунке приведен пример подсчета мужских и женских анкет. Аналогично можно
проанализировать и другие дихотомические (т.е. принимающие одно из двух значений) параметры.

В приведенном примере только два дихотомических параметра: пол и замужество. Их можно проверить
на зависимость. Для этого подсчитаем «Коэффициент контингенции Пирсона»

[r_a = frac{ad-bc}{sqrt{(a+b)(c+d)(a+c)(b+d)}}, ]

где (a), (b), (c), (d) — элементы четырехпольной корреляционной таблицы, в которой представлены частоты или количество
совместных событий.

	Событие 1
Событие 2	(a)	(b)	(a+b)
(c)	(d)	(c+d)
	(a+c)	(b+d)

Например, если за «событие 1» принять пол (м,ж), а за «событие 2» — замужество (да, нет), то (a) — это количество женатых мужчин,
(b) — количество замужних женщин, (c) — количество неженатых мужчин, (d) — количество незамужних женщин.

В рассматриваемом примере Коээффициент контингенции Пирсона получился равным -0,29778. Если взглянуть
на шкалу Чедокка, то видим, что имеется слабая обратная зависимость между параметрами.

Коэффициент	0,1 — 0,3	0,3 — 0,5	0,5 — 0,7	0,7 — 0,9	0,9 — 0,99
Характеристика зависимости	Слабая	Умеренная	Заметная	Высокая	Весьма высокая

Найдем ошибку коэффициента корреляции по формуле:

[m_{r_a} = frac{1-|r_a|}{sqrt{n-1}}]

Она составила 0,100318. Ниже приведена таблица с исходными данными:

Номер	Возраст	Пол	Оператор	Женат/За мужем	График работы
1	20	м	Другое	Да	Свободный
2	22	ж	Мегафон	Да	Нет
3	32	м	Мегафон	Нет	Плавающий
4	35	м	Мегафон	Да	Неделя
5	21	м	Мегафон	Нет	Неделя
6	40	ж	Теле2	Нет	Неделя
7	37	ж	Мегафон	Нет	Плавающий
8	23	м	Теле2	Нет	Нет
9	33	ж	Теле2	Нет	Свободный
10	25	м	Билайн	Нет	Свободный
11	23	м	Билайн	Нет	Неделя
12	35	м	Билайн	Да	Неделя
13	34	ж	МТС	Да	Нет
14	36	ж	Теле2	Да	Неделя
15	19	м	Билайн	Да	Нет
16	23	ж	МТС	Нет	Свободный
17	27	ж	Билайн	Да	Плавающий
18	38	ж	Билайн	Нет	Неделя
19	41	ж	Теле2	Да	Неделя
20	33	ж	МТС	Да	Неделя
21	29	ж	Билайн	Нет	Свободный
22	20	м	МТС	Да	Плавающий
23	24	м	Теле2	Нет	Плавающий
24	28	ж	Билайн	Нет	Неделя
25	31	м	МТС	Нет	Неделя
26	37	ж	Билайн	Да	Нет
27	35	м	Билайн	Нет	Свободный
28	34	ж	Теле2	Да	Неделя
29	33	м	МТС	Нет	Неделя
30	32	ж	Билайн	Да	Свободный
31	40	ж	Теле2	Нет	Неделя
32	25	м	Мегафон	Да	Плавающий
33	28	ж	Мегафон	Да	Плавающий
34	20	м	МТС	Нет	Нет
35	23	ж	Билайн	Да	Плавающий
36	37	м	Мегафон	Нет	Неделя
37	41	ж	Теле2	Нет	Неделя
38	40	ж	Мегафон	Да	Плавающий
39	31	ж	Мегафон	Да	Свободный
40	25	ж	Другое	Да	Нет
41	31	ж	МТС	Да	Неделя
42	39	ж	Теле2	Да	Неделя
43	19	м	Мегафон	Да	Нет
44	21	м	Теле2	Нет	Свободный
45	34	м	Мегафон	Да	Неделя
46	22	ж	Мегафон	Да	График
47	28	ж	Билайн	Да	График
48	29	ж	МТС	Да	График
49	38	ж	Мегафон	Да	График
50	39	ж	Теле2	Да	Плавающий

1. Методы статистического анализа в Ms Excel для анализа социологических данных

2. Среднее арифметическое

Среднее арифметическое
набора чисел определяется как
их сумма, деленная на их
количество.

3. Медиана

Медиа́на (от лат. mediāna — середина) 50-й
перцентиль или квантиль 0,5 — статистика,
которая делит ранжированную совокупность
(вариационный ряд выборки) на две равные
части: 50 % «нижних» членов ряда данных будут
иметь значение признака не больше, чем
медиана, а «верхние» 50 % — значения признака
не меньше, чем медиана.
В Excel функция Медиана

4. Стандартное отклонение

Стандартное отклонение показывает, как
распределены значения относительно среднего в
выборке
Если количество элементов в выборке превышает 30,
то знаменатель дроби под корнем принимает
значение n-1. Иначе используется n.
В Excel функция Стандоткл (количество элементов в
выборке более 30)

5. Пример. Количество участников в общественном мероприятии

6. Пример:

7. Пошагово вычисление стандартного отклонения:

Пошагово
вычисление
стандартног
о отклонения:
ВЫЧИСЛЯЕМ СРЕДНЕЕ
АРИФМЕТИЧЕСКОЕ
ВЫБОРКИ ДАННЫХ
ОТНИМАЕМ ЭТО СРЕДНЕЕ
ОТ КАЖДОГО ЭЛЕМЕНТА
ВЫБОРКИ
ВСЕ ПОЛУЧЕННЫЕ РАЗНИЦЫ
ВОЗВОДИМ В КВАДРАТ
СУММИРУЕМ ВСЕ
ПОЛУЧЕННЫЕ КВАДРАТЫ
ДЕЛИМ ПОЛУЧЕННУЮ
СУММУ НА КОЛИЧЕСТВО
ЭЛЕМЕНТОВ В ВЫБОРКЕ
(ИЛИ НА N-1, ЕСЛИ N>30)
ВЫЧИСЛЯЕМ КВАДРАТНЫЙ
КОРЕНЬ ИЗ ПОЛУЧЕННОГО
ЧАСТНОГО (ИМЕНУЕМОГО
ДИСПЕРСИЕЙ)

8. Дисперсия

Мера рассеивания, отклонения от среднего.

9. Ранги и ранжирование

Рангом наблюдения называют тот номер, который
получит это наблюдение в упорядоченной
совокупности всех данных — после их упорядочения
по определенному правилу (например, от меньших
значений к большим или наоборот).

10. Пример

6, 17, 14,5, 12
Процедура перехода от совокупности наблюдений к
последовательности их рангов называется ранжированием.
Результат ранжирования называется ранжировкой.
2, 5, 4, 1, 3

11. Коэффициент корреляции

Корреляция измеряет мощность
и направление связи между x и y.

12.

13.

Коэффициент корреляции

14.

Коэффициент корреляции

Для
автоматизации математической обработки
результатов социологического исследования,
использовались электронные таблицы
(Excel)
и специализированные программы(SPSS).

Для
проверки первой гипотезы «если
положительные личностные качества
преподавателя будут на высоком уровне,
то отношение студентов к преподавателю
будет объективным».
требуется
выяснить тесноту связи с помощью
коэффициента корреляции.

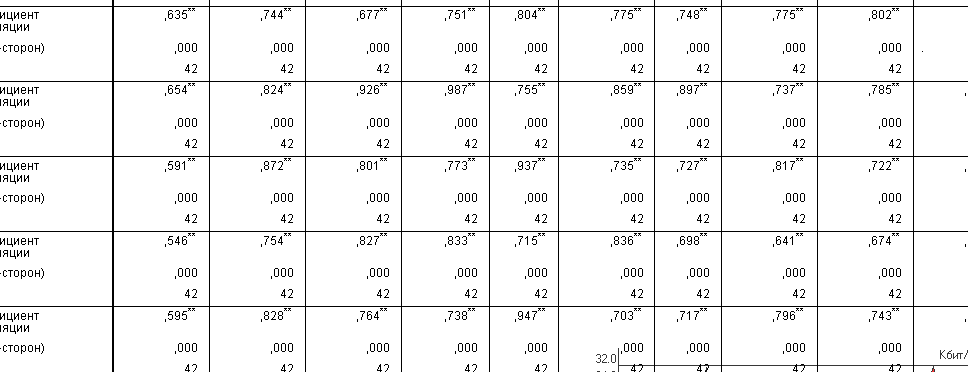
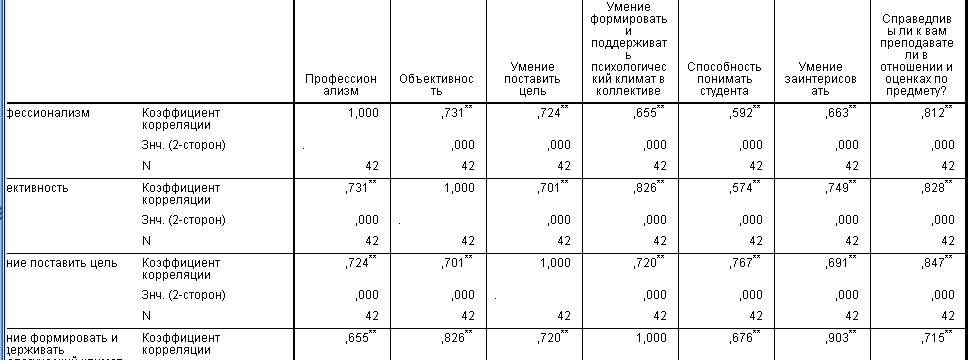
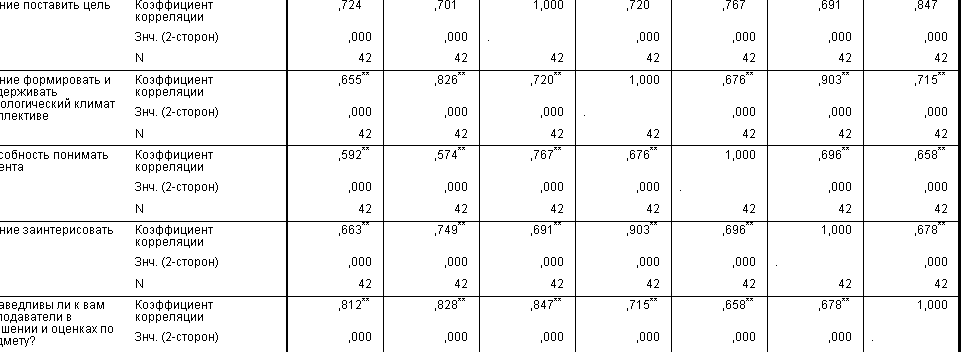
Рис
5. Корреляционная связь.

Вывод:
корреляционная связь между личностными
качествами преподавателя отмечена (**)
– корреляция высокой значимости на
уровне 0.01двусторонняя. Выдвинутая
гипотеза подтверждается.

Для
проверки второй гипотезы «Если
профессиональные качества преподавателя
будут на высоком уровне, то отношение
студентов к преподавателю будет
объективным». Необходимо выяснить
тесноту связи с помощью коэффициента
Кендалла.

Рис
6. Корреляционная связь(коэффициент
Кендалла).

Вывод:
корреляционная связь между профессиональными
качествами преподавателя отмечена (**)
– корреляция высокой значимости на
уровне 0.01 двусторонняя. Выдвинутая
гипотеза подтверждается.

Для
проверки третьей гипотезы «Общие и
индивидуальные характеристики
преподавателя влияют на отношение
студентов к преподавателю». Требуется
выяснить тесноту связи посредствам
коэффициента Спирмена.

Рис
7. Корреляционная связь индивидуальных
характеристик и общих.

Вывод:
корреляционная связь между индивидуальными
и общими качествами преподавателя
отмечена (**) – корреляция высокой
значимости на уровне 0.01 двусторонняя.
Выдвинутая гипотеза подтверждается.

Рис
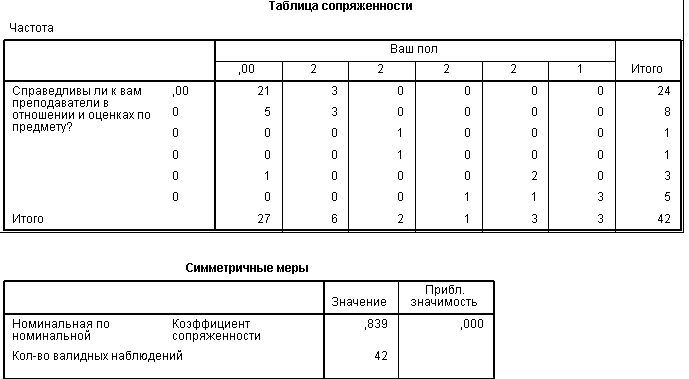
8. Таблица сопряженности

Рис
9. Таблица сопряженности.

Рис
10.

Из
рисунка видно, что такое качество как
доброжелательность преподавателей
находится на высоком уровне.

Рис
11.

Рис
12. ( 10, 11) Гистограммы в SPSS.

Рис
13. Диаграмма в Excel.

3.3. Сравнительный анализ использования Excel и spss на разных этапах обработки социологических данных.

В
нашей курсовой работе были использованы
программный продукты Excel и SPSS. Они
использовались совместно и в этом
разделе мы проанализируем преимущества
и недостатки этих двух программ.

Большим
преимуществом программного продукта
SPSS является простота в освоении. В SPSS
есть широкий спектр аналитических
функций и статистических методов,
благодаря которым работа с данными
становится простой и легкой , позволяющий
проводить практически любые операции
по анализу данных.

Преимущества:
структурированная организация данных,
наличие в файлах данных полной информации,
включающей в себя как собственно данные
(ответы на вопросы), так и тексты вопросов
, вариантов ответов , а также информации
и типах вопросов, их размерности и т.д.

Недостатки:
ограниченные возможности проведения
нестандартных видов анализа, неудобство
при вводе данных непосредственно сразу
в программный продукт, так как варианты
ответа и данные находятся на разных
рабочих листах.

Мы
выполнили логический анализ в программном
продукте SPSS при помощи коэффициента
Спирмена, Кендалла и таблицы сопряженности.
Это не занимало больших усилий, так как
SPSS имеет большое количество функций
для статистического анализа и все
подсчеты производились автоматически.
Также он сразу помечал значимые
корреляционные связи. «Excel –
это широко распространенная компьютерная
программа. Нужна она для проведения
расчетов, составления таблиц и диаграмм,
вычисления простых и сложных функций»¹⁰.

В
программном продукте Excel для построения
таблиц сопряженности надо было вбивать
несколько формул. Это занимало много
времени и места на рабочем листе.

ЗАКЛЮЧЕНИЕ

В
современном образовании возрастает
роль преподавателя, расширяется диапазон
его психологического и педагогического
воздействия на учащихся. Преподаватель
уже не может быть только проводником
знаний и информации, он должен быть
педагогом, психологом, психотерапевтом.
От этого во многом зависит успешность
его педагогической деятельности и
авторитет.

В
ходе работы исследования над темой
«отношение студентов к преподавателям»
нами были выдвинуты гипотезы, в которых
мы предположили, что личностные,
профессиональные, общие и индивидуальные
качества преподавателя влияют на
отношение студентов к преподавателям.

Для
подтверждения гипотез нами были проведены
статистические расчеты полученных
данных, входе анкетирования студентов
ФИиСТех группы СОЦ-11 в количестве
тридцати двух человек.

Исходя
из результатов, можно сделать вывод,
что студенты в основном дают положительную
оценку, тем качествам, которые исследовались
у преподавателей.

СПИСОК
ЛИТЕРАТУРЫ

1.Социология,
К.Габдуллина, Е.Раисов, Алматы, 2005, стр.126

2.
Социология, под ред. В.Н.Лавриненко,
Москва 2002, 349стр.

3.
Социология. Основы общей теории ,ред.
Г.В.Осипов, Л.Н.Москвичев, москва 2003, 735.

4.Социология.
Основы общей теории, ред. Г.В.Осипов,
Л.Н.Москвичев, москва 2003, 810

5.
Социология, Ю.Г.Волков, В.И.Добреньков,
В.Н.Нечипуренко, А.В.Попов, Москва, 2003,
стр. 78

6.Социология,
К.Габдуллина, Е.Раисов, Алматы, 2005, стр.
128

7.Социология,
К.Габдуллина, Е.Раисов, Алматы, 2005, стр.
150

8.
Горшков
М.К. Прикладная социология: методология
и методы: интерактивное учебное пособие./
М.К. Горшков, Ф.Э. Шереги. – М.: Институт
социологии РАН,2011.

9.
Новикова С.С. Социология: история, основы,
институционализация в России. Глава
4. Виды и формы связей в социальной
системе.

10.
Электронная
библиотека. – Режим доступа:
http://www.bibliofond.ru/view.aspx?id=465141

11.
Режим
доступа: http://ru.wikipedia.org/

12.
http://ru.wikipedia.org/wiki/Microsoft_Excel

1
Электронная библиотека. – Режим доступа:
http://www.bibliofond.ru/view.aspx?id=465141

2
Википедия. Режим доступа:
http://ru.wikipedia.org/

3
Режим доступа: http://ru.wikipedia.org/

4
Новикова С.С. Социология: история,
основы, иннституционализация в России.
Глава 4. ВИДЫ И ФОРМЫ СВЯЗЕЙ В СОЦИАЛЬНОЙ
СИСТЕМЕ.

5
Горшков М.К. Прикладная социология:
методология и методы: интерактивное
учебное пособие./ М.К. Горшков, Ф.Э.
Шереги. – М.: Институт социологии
РАН,2011. – С.

6
Режим доступа: http://ru.wikipedia.

7
Социология. Режим доступа:
http://vsempomogu.ru/sociolog/301-10.html

8
Горшков М.К. Прикладная социология:
методология и методы: интерактивное
учебное пособие./ М.К. Горшков, Ф.Э.
Шереги. – М.: Институт социологии
РАН,2011. – С.

9
«социология», К.Габдуллина, Е.Раисов,
Алматы, 2005, стр. 150

10
http://ru.wikipedia.org/wiki/Microsoft_Excel

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #