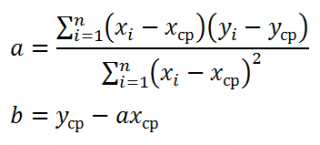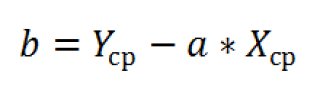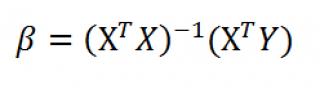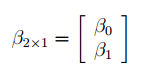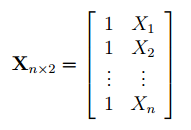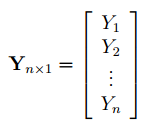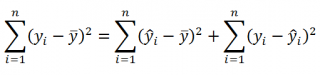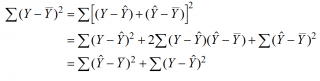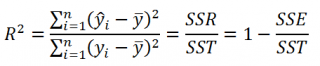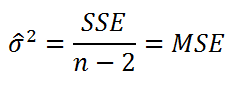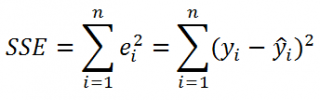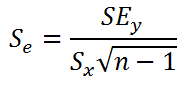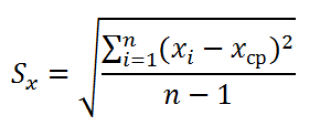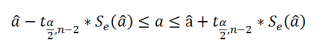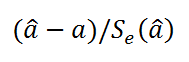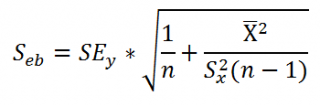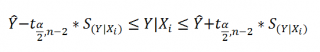Информация воспринимается легче, если представлена наглядно. Один из способов презентации отчетов, планов, показателей и другого вида делового материала – графики и диаграммы. В аналитике это незаменимые инструменты.
Построить график в Excel по данным таблицы можно несколькими способами. Каждый из них обладает своими преимуществами и недостатками для конкретной ситуации. Рассмотрим все по порядку.
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
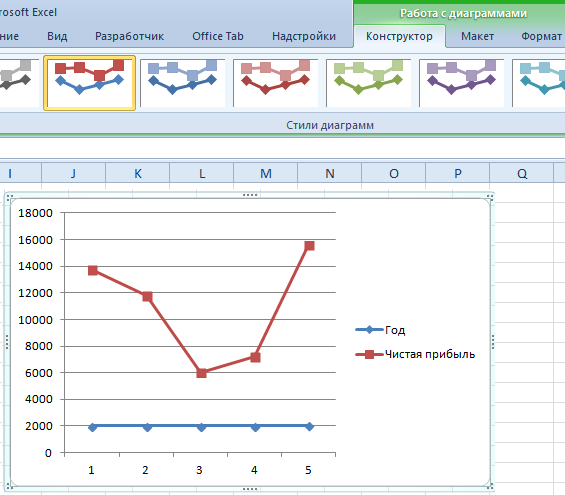
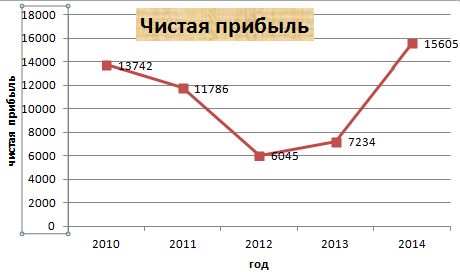
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
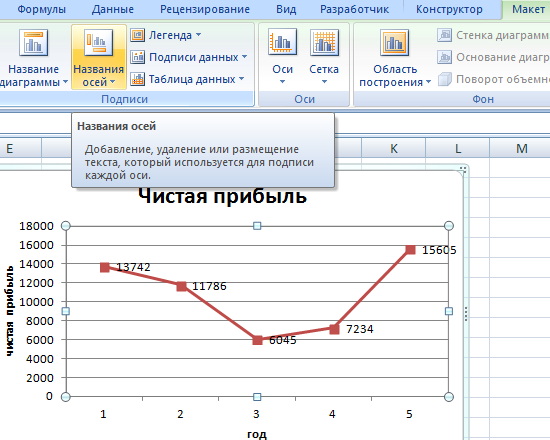
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
График с двумя и более кривыми
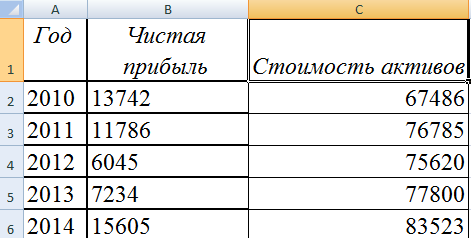
Допустим, нам нужно показать не только чистую прибыль, но и стоимость активов. Данных стало больше:
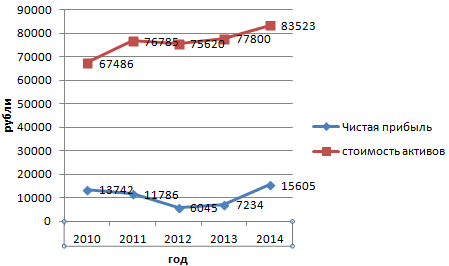
Но принцип построения остался прежним. Только теперь есть смысл оставить легенду. Так как у нас 2 кривые.
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
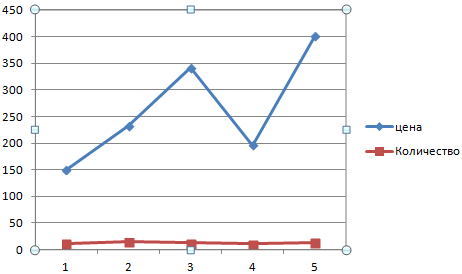
Сначала строим график так, будто у нас одинаковые единицы измерения.
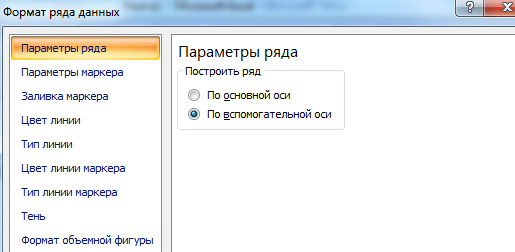
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
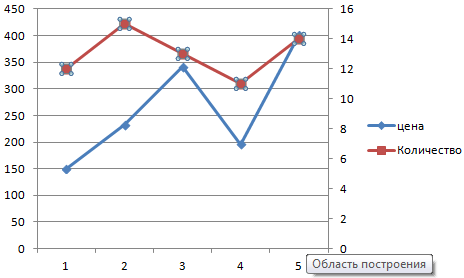
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
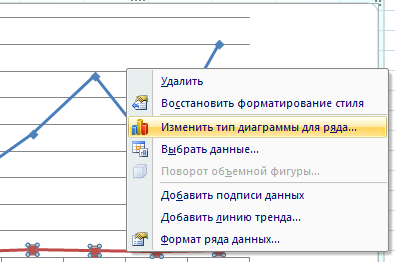
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Строим график функций в Excel
Вся работа состоит из двух этапов:
- Создание таблицы с данными.
- Построение графика.
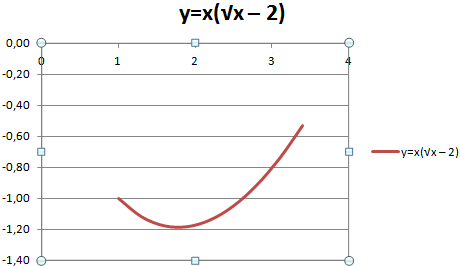
Пример: y=x(√x – 2). Шаг – 0,3.
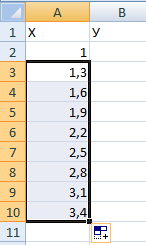
Составляем таблицу. Первый столбец – значения Х. Используем формулы. Значение первой ячейки – 1. Второй: = (имя первой ячейки) + 0,3. Выделяем правый нижний угол ячейки с формулой – тянем вниз столько, сколько нужно.
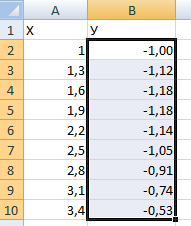
В столбце У прописываем формулу для расчета функции. В нашем примере: =A2*(КОРЕНЬ(A2)-2). Нажимаем «Ввод». Excel посчитал значение. «Размножаем» формулу по всему столбцу (потянув за правый нижний угол ячейки). Таблица с данными готова.
Переходим на новый лист (можно остаться и на этом – поставить курсор в свободную ячейку). «Вставка» — «Диаграмма» — «Точечная». Выбираем понравившийся тип. Щелкаем по области диаграммы правой кнопкой мыши – «Выбрать данные».
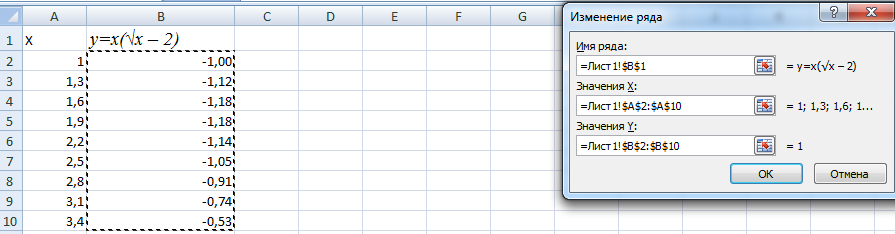
Выделяем значения Х (первый столбец). И нажимаем «Добавить». Открывается окно «Изменение ряда». Задаем имя ряда – функция. Значения Х – первый столбец таблицы с данными. Значения У – второй.
Жмем ОК и любуемся результатом.
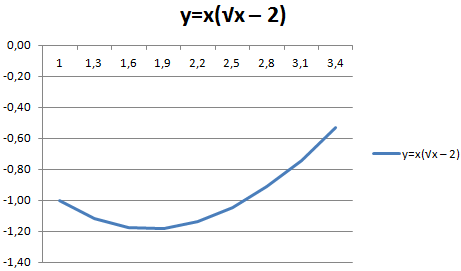
С осью У все в порядке. На оси Х нет значений. Проставлены только номера точек. Это нужно исправить. Необходимо подписать оси графика в excel. Правая кнопка мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». И выделяем диапазон с нужными значениями (в таблице с данными). График становится таким, каким должен быть.
Наложение и комбинирование графиков
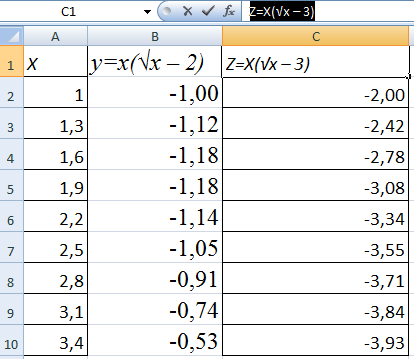
Построить два графика в Excel не представляет никакой сложности. Совместим на одном поле два графика функций в Excel. Добавим к предыдущей Z=X(√x – 3). Таблица с данными:
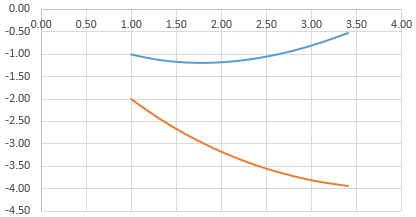
Выделяем данные и вставляем в поле диаграммы. Если что-то не так (не те названия рядов, неправильно отразились цифры на оси), редактируем через вкладку «Выбрать данные».
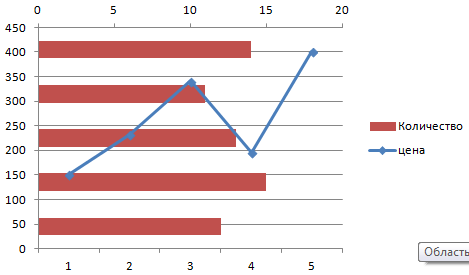
А вот наши 2 графика функций в одном поле.
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
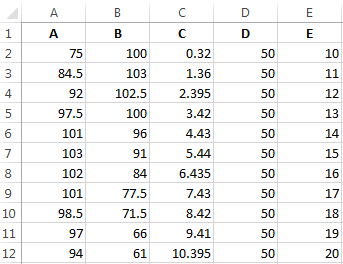
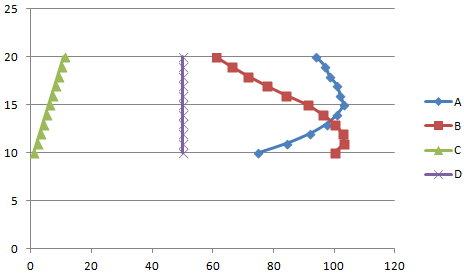
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
Скачать все примеры графиков
Готовые примеры графиков и диаграмм в Excel скачать:
Как сделать шаблон, дашборд, диаграмму или график для создания красивого отчета удобного для визуального анализа в Excel? Выбирайте примеры диаграмм с графиками для интерактивной визуализации данных с умных таблиц Excel и используйте их для быстрого принятия правильных решений. Бесплатно скачивайте готовые шаблоны динамических диаграмм для использования их в дашбордах, отчетах или презентациях.
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Вы можете отображать свои отчеты анализа данных в Excel несколькими способами. Однако если результаты анализа данных можно визуализировать в виде диаграмм, которые выделяют заметные точки в данных, ваша аудитория может быстро понять, что вы хотите спроецировать в данные. Это также оставляет хорошее влияние на ваш стиль презентации.
В этой главе вы узнаете, как использовать диаграммы Excel и функции форматирования Excel на диаграммах, которые позволяют с акцентом представлять результаты анализа данных.
Визуализация данных с помощью диаграмм
В Excel диаграммы используются для графического представления любого набора данных. Диаграмма – это визуальное представление данных, в котором данные представлены такими символами, как столбцы на линейчатой диаграмме или линии на линейной диаграмме. Excel предоставляет вам множество типов диаграмм, и вы можете выбрать тот, который подходит вашим данным, или вы можете использовать опцию Excel Recommended Charts, чтобы просмотреть диаграммы, настроенные для ваших данных, и выбрать один из них.
Обратитесь к учебным таблицам Excel для получения дополнительной информации о типах диаграмм.
В этой главе вы познакомитесь с различными методами, которые вы можете использовать с диаграммами Excel, чтобы более эффективно освещать результаты анализа данных.
Создание комбинационных диаграмм
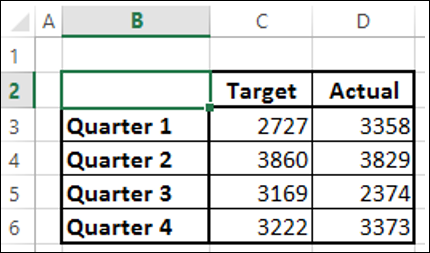
Предположим, у вас есть целевая и фактическая прибыль за 2015-2016 финансовый год, которую вы получили из разных регионов.
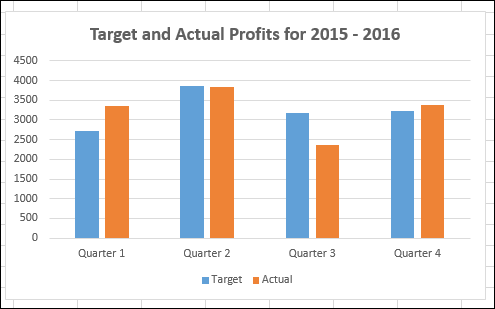
Мы создадим кластеризованную диаграмму столбцов для этих результатов.
Как вы заметили, трудно быстро визуализировать сравнение между целями и фактическими значениями на этом графике. Это не оказывает реального влияния на ваши результаты.
Лучший способ различения двух типов данных для сравнения значений – использование комбинированных диаграмм. В Excel 2013 и вышеприведенных версиях вы можете использовать комбинированные диаграммы для той же цели.
Используйте вертикальные столбцы для целевых значений и линию с маркерами для фактических значений.
- Перейдите на вкладку «ДИЗАЙН» под вкладкой «ИНСТРУМЕНТЫ ДИАГРАММ» на ленте.
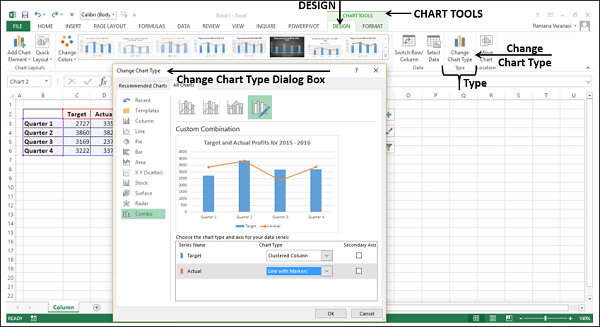
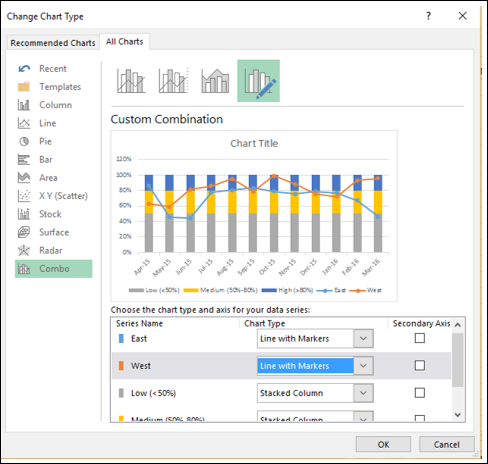
- Нажмите Изменить тип диаграммы в группе Тип. Откроется диалоговое окно «Изменить тип диаграммы».
-
Нажмите Combo.
-
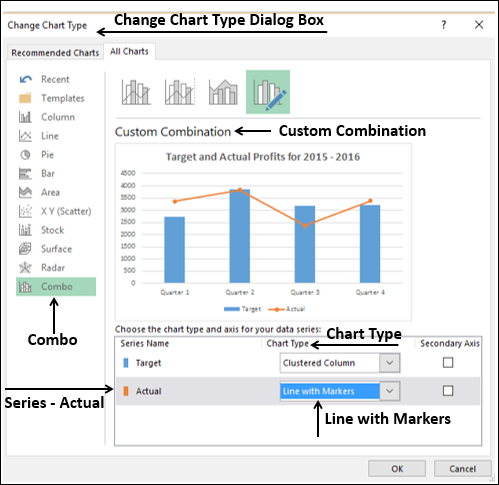
Измените Тип диаграммы для серии Фактическая на Линия с маркерами. Предварительный просмотр отображается в разделе «Пользовательская комбинация».
-
Нажмите ОК.
Нажмите Combo.
Измените Тип диаграммы для серии Фактическая на Линия с маркерами. Предварительный просмотр отображается в разделе «Пользовательская комбинация».
Нажмите ОК.
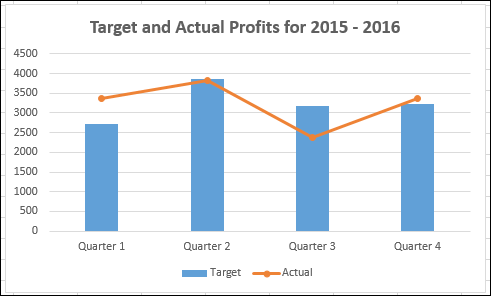
Ваша индивидуальная комбинационная таблица будет отображена.
Как видно из диаграммы, целевые значения указаны в столбцах, а фактические значения отмечены вдоль линии. Визуализация данных стала лучше, поскольку она также показывает тенденцию ваших результатов.
Однако этот тип представления не работает, когда диапазоны данных двух ваших значений данных значительно различаются.
Создание комбинированной диаграммы со вторичной осью
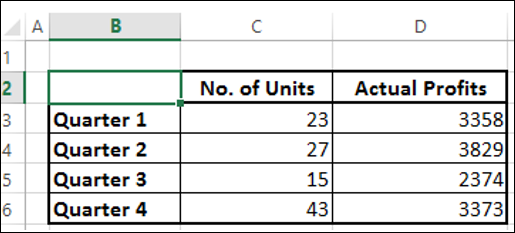
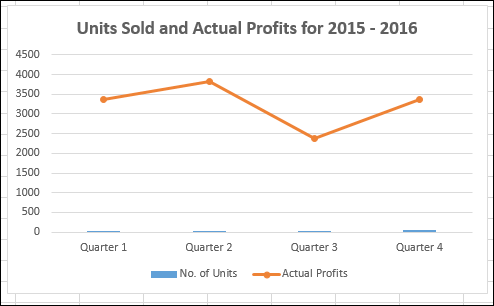
Предположим, у вас есть данные о количестве отгруженных единиц вашего продукта и о фактической прибыли за финансовый год 2015-2016, которую вы получили из разных регионов.
Если вы используете ту же комбинацию, что и раньше, вы получите следующее –
На диаграмме данные о количестве единиц не видны, поскольку диапазоны данных значительно различаются.
В таких случаях вы можете создать комбинированную диаграмму со вторичной осью, чтобы основная ось отображала один диапазон, а вторичная ось отображала другой.
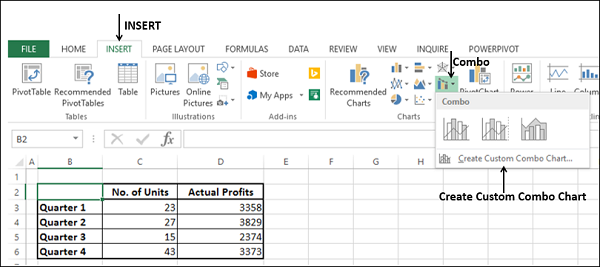
- Нажмите вкладку INSERT.
- Нажмите Combo в группе диаграмм.
- Нажмите Create Custom Combo Chart из выпадающего списка.
Появится диалоговое окно «Вставка диаграммы» с выделенным списком.
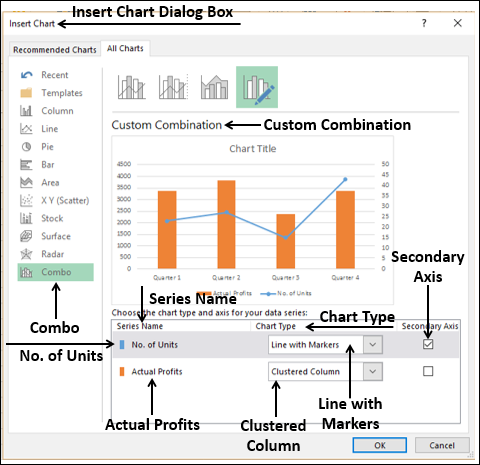
Для Типа диаграммы выберите –
-
Линия с маркерами для серии № единиц
-
Кластерный столбец для фактической прибыли серии
-
Установите флажок «Вторичная ось» справа от номера серии и нажмите «ОК».
Предварительный просмотр вашей диаграммы появится под Custom Combination.
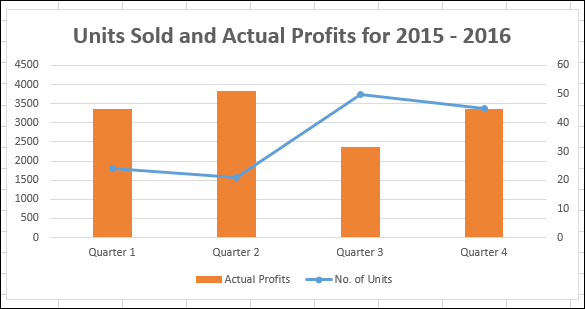
Ваша комбо-диаграмма отображается с Secondary Axis.
Вы можете наблюдать значения для фактической прибыли на первичной оси и значения для количества единиц на вторичной оси.
Значительное наблюдение на приведенном выше графике относится к 3 кварталу, где количество проданных единиц больше, но фактическая полученная прибыль меньше. Вероятно, это может быть отнесено на расходы по продвижению, которые были понесены для увеличения продаж. Ситуация улучшается в четвертом квартале, с небольшим снижением продаж и значительным увеличением фактической прибыли.
Различающие серии и оси категорий
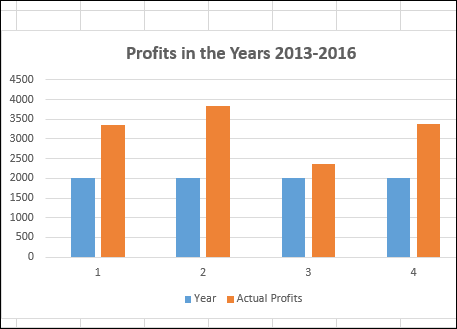
Предположим, вы хотите спроектировать фактическую прибыль, полученную в 2013-2016 годах.
Создайте кластеризованный столбец для этих данных.
Как вы заметили, визуализация данных неэффективна, так как годы не отображаются. Вы можете преодолеть это, изменив год на категорию.
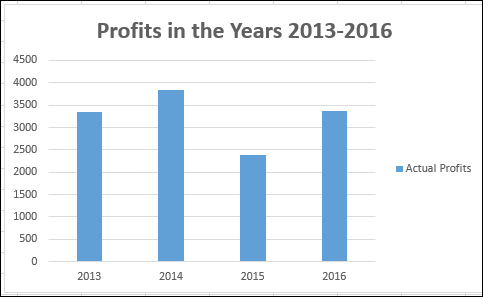
Удалить заголовок года в диапазоне данных.
Теперь год считается категорией, а не серией. Ваша диаграмма выглядит следующим образом –
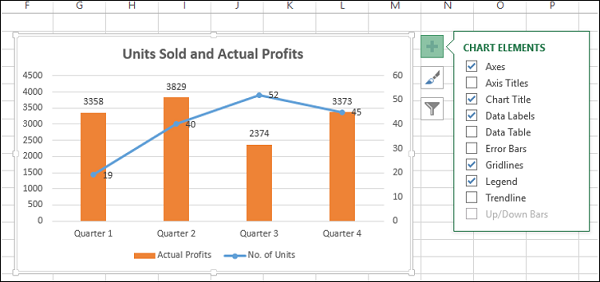
Элементы диаграммы и стили диаграммы
Элементы диаграммы дают больше описания вашим диаграммам, помогая тем самым визуализировать ваши данные более осмысленно.
- Нажмите на диаграмму
Три кнопки появляются рядом с правым верхним углом графика –
Для подробного объяснения этого обратитесь к учебнику Excel Charts.
- Нажмите Элементы диаграммы.
- Нажмите Метки данных.
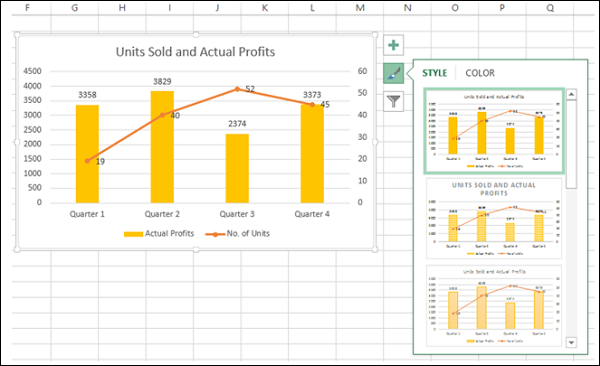
- Нажмите Стили диаграммы
- Выберите стиль и цвет, которые соответствуют вашим данным.
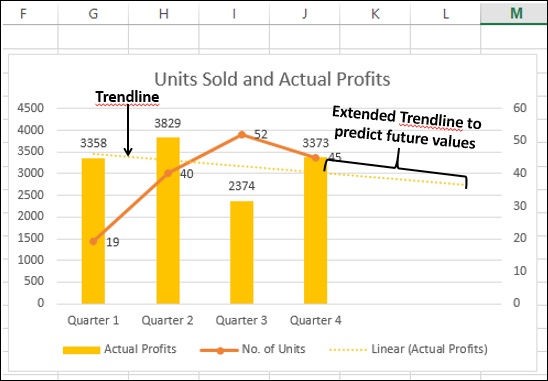
Вы можете использовать Trendline для графического отображения трендов в данных. Вы можете расширить линию тренда на графике за пределы фактических данных, чтобы предсказать будущие значения.
Метки данных
Excel 2013 и более поздние версии предоставляют различные варианты отображения меток данных. Вы можете выбрать одну метку данных, отформатировать ее так, как вам нравится, а затем использовать текущую метку клонирования, чтобы скопировать форматирование в остальные метки данных на диаграмме.
Метки данных в диаграмме могут иметь эффекты, различающиеся по форме и размеру.
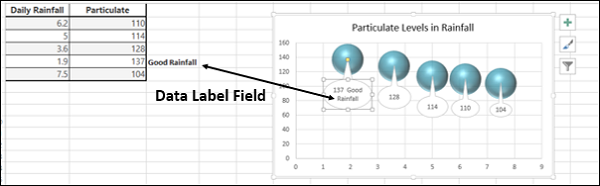
Также возможно отобразить содержимое ячейки как часть метки данных с полем «Вставить метку данных».
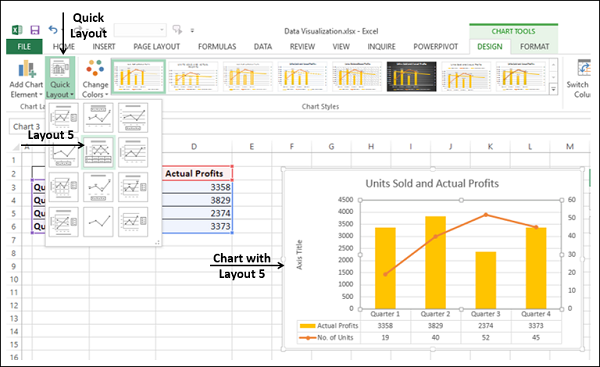
Быстрый макет
Вы можете использовать быструю компоновку, чтобы быстро изменить общую компоновку диаграммы, выбрав один из предопределенных вариантов компоновки.
- Нажмите на график.
- Перейдите на вкладку «ДИЗАЙН» под «ИНСТРУМЕНТЫ»
- Нажмите Быстрый макет.
Различные возможные макеты будут отображаться. При перемещении по параметрам макета макет диаграммы меняется на этот конкретный параметр.
Выберите макет, который вам нравится. Диаграмма будет отображаться с выбранным макетом.
Использование изображений в столбчатых диаграммах
Вы можете сделать больший акцент на своем представлении данных, используя изображение вместо столбцов.
-
Нажмите на столбец на диаграмме столбца.
-
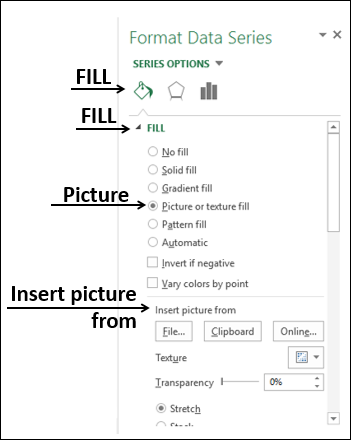
В Серии данных формата нажмите Заполнить.
-
Выберите изображение.
-
В разделе «Вставить картинку из» укажите имя файла или, если необходимо, буфер обмена, если вы ранее скопировали изображение.
Нажмите на столбец на диаграмме столбца.
В Серии данных формата нажмите Заполнить.
Выберите изображение.
В разделе «Вставить картинку из» укажите имя файла или, если необходимо, буфер обмена, если вы ранее скопировали изображение.
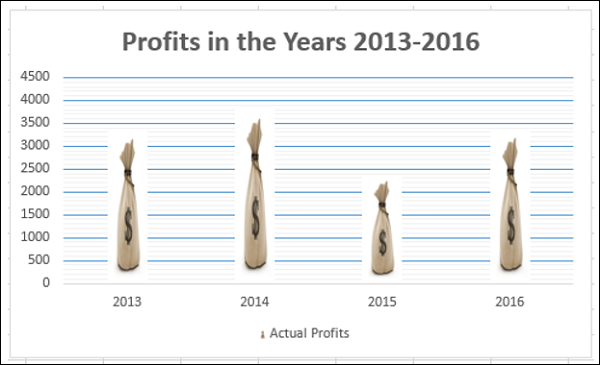
Выбранная вами картинка появится вместо столбцов на диаграмме.
Диаграмма группы
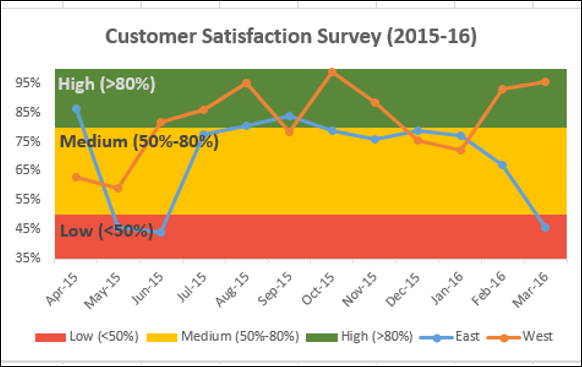
Возможно, вам придется представить результаты опроса клиентов продукта из разных регионов. Band Chart подходит для этой цели. Полосная диаграмма – это линейная диаграмма с добавленной заштрихованной областью для отображения верхней и нижней границ групп данных.
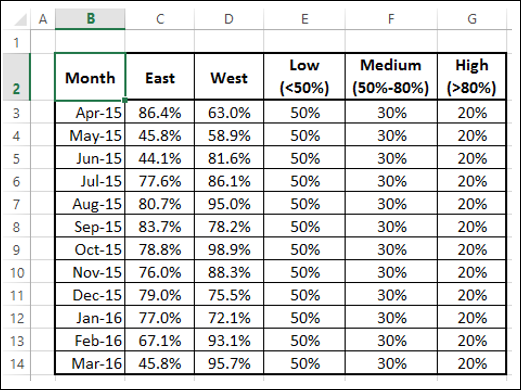
Предположим, ваши результаты опроса клиентов из восточных и западных регионов, по месяцам, –
Здесь в данных <50% – Низкий, 50% – 80% – Средний,> 80% – Высокий.
С помощью Band Chart вы можете отобразить результаты своего опроса следующим образом –
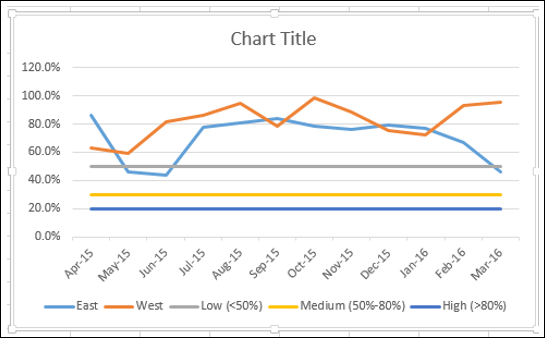
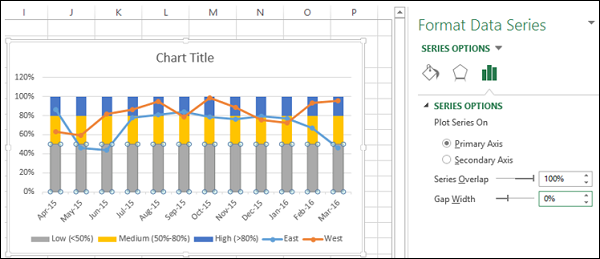
Создайте линейную диаграмму из ваших данных.
Измените тип диаграммы на –
- Ряды Востока и Запада с линией маркеров.
- Низкий, средний и высокий ряд в столбец с накоплением.
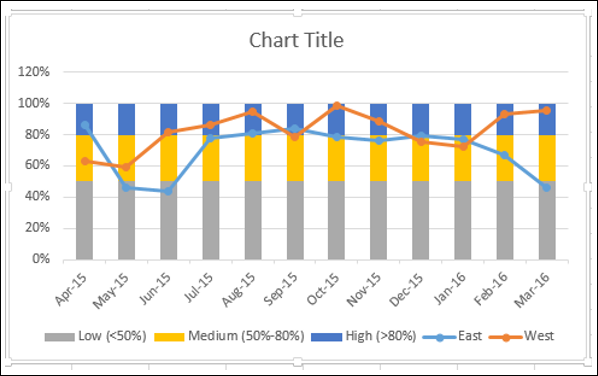
Ваша диаграмма выглядит следующим образом.
- Нажмите на один из столбцов.
- Измените ширину промежутка до 0% в формате Data Series.
Вы получите группы вместо столбцов.
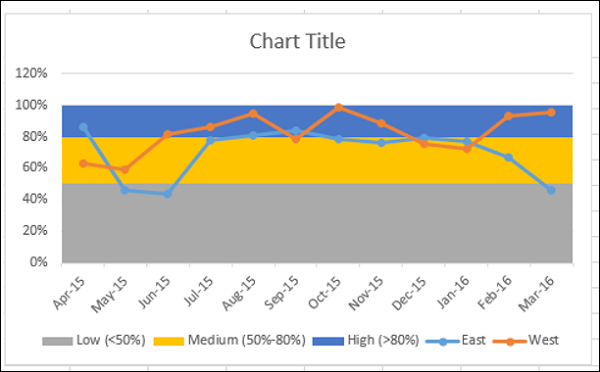
Чтобы сделать диаграмму более презентабельной –
- Добавить заголовок диаграммы.
- Отрегулируйте диапазон вертикальной оси.
- Измените цвета полос на Зеленый-Желтый-Красный.
- Добавьте ярлыки в группы.
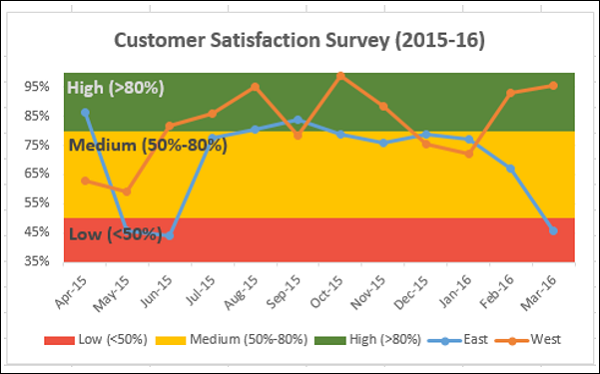
Конечным результатом является диаграмма полос с определенными границами и результаты опроса, представленные по полосам. Из графика можно быстро и четко определить, что, хотя результаты опроса для региона Запад являются удовлетворительными, результаты для региона Восток в последнем квартале сократились и требуют внимания.
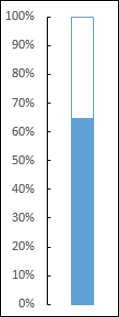
Диаграмма термометра
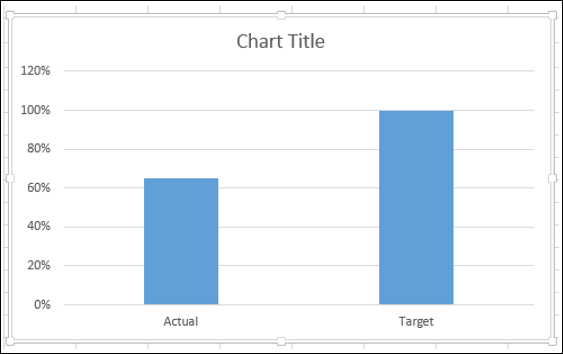
Когда вам нужно представить целевое значение и фактическое значение, вы можете легко создать диаграмму термометра в Excel, которая четко показывает эти значения.
С помощью диаграммы термометра вы можете отобразить ваши данные следующим образом –
Расположите ваши данные, как показано ниже –
- Выберите данные.
- Создайте диаграмму кластерных столбцов.
Как вы заметили, правая колонка является Target.
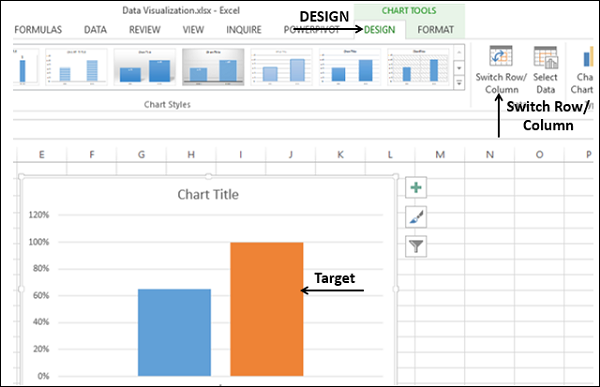
- Нажмите на столбец в диаграмме.
- Нажмите на переключатель строки / столбца на ленте.
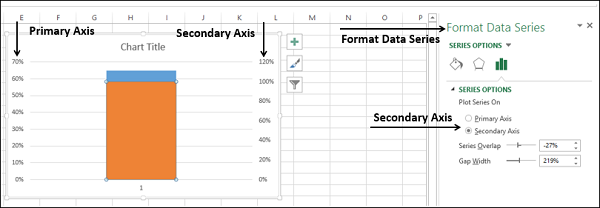
- Щелкните правой кнопкой мыши на целевой колонке.
- Нажмите на Формат данных серии.
- Нажмите на Вторичную Ось.
Как вы наблюдаете, у Первичной Оси и Вторичной Оси есть разные диапазоны.
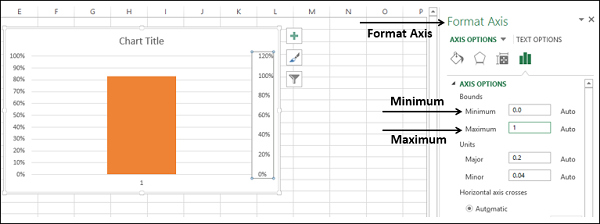
- Щелкните правой кнопкой мыши по основной оси.
- В параметрах Оси формата в разделе Границы введите 0 для минимума и 1 для максимума.
- Повторите то же самое для Вторичной Оси.
Первичная и вторичная оси будут установлены в 0% – 100%. Целевая колонка скрывает фактическую колонку.
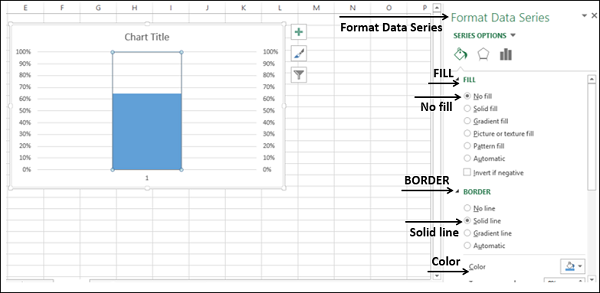
- Щелкните правой кнопкой мыши видимый столбец (Target)
- В Серии форматирования данных выберите
- Не заполнять для FILL
- Сплошная линия для ГРАНИЦЫ
- Синий для цвета
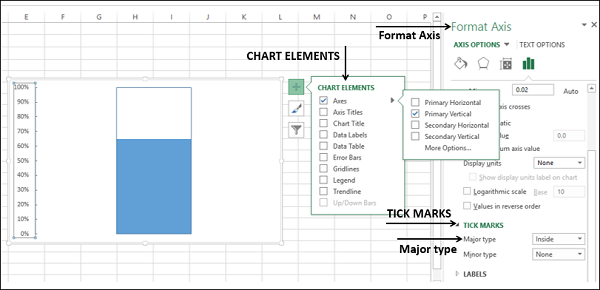
- В элементах диаграммы отмените выбор
- Ось → Первичная Горизонтальная
- Ось → Вторичная Вертикаль
- Сетки
- Заголовок диаграммы
- На графике щелкните правой кнопкой мыши на Первичной вертикальной оси
- В опциях формата оси нажмите на метки
- Для основного типа выберите Внутри
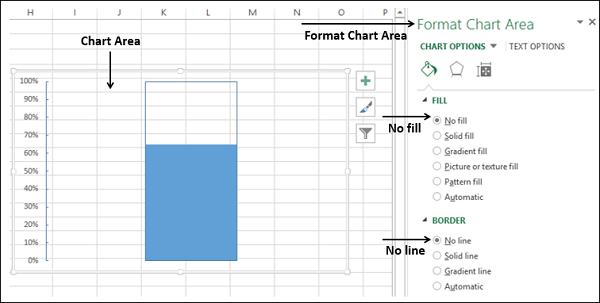
- Щелкните правой кнопкой мыши на Chart Area.
- В опциях Формат области диаграммы выберите
- Не заполнять для FILL
- Нет линии для границы
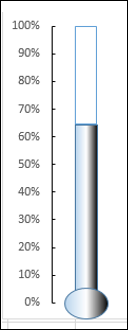
Измените размер области диаграммы, чтобы получить форму термометра.
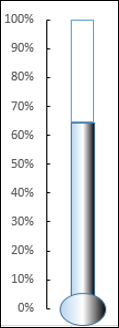
Вы получили свой график термометра с фактическим значением по сравнению с целевым показанным значением. Вы можете сделать эту диаграмму термометра более впечатляющей с некоторым форматированием.
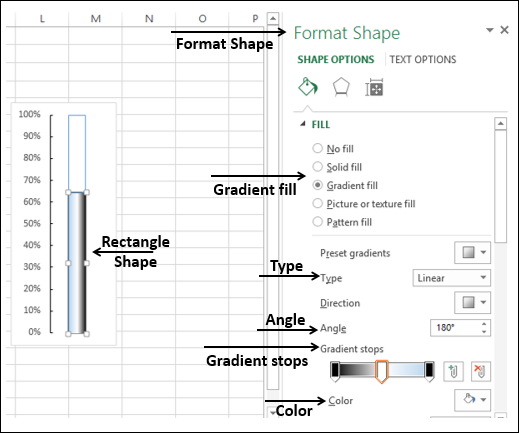
- Вставьте прямоугольник, накладывая синюю прямоугольную часть на диаграмме.
- В параметрах формата формы выберите –
- Градиентная заливка для FILL
- Линейный для Типа
- 180 0 для угла
- Установите градиентные остановки на 0%, 50% и 100%.
- Для градиента останавливается на 0% и 100%, выберите черный цвет.
- Для градиента на 50% выберите белый цвет.
- Вставьте овальную форму внизу.
- Форматировать фигуру с теми же параметрами.
Результатом является таблица термометров, с которой мы начали.
Диаграмма Ганта
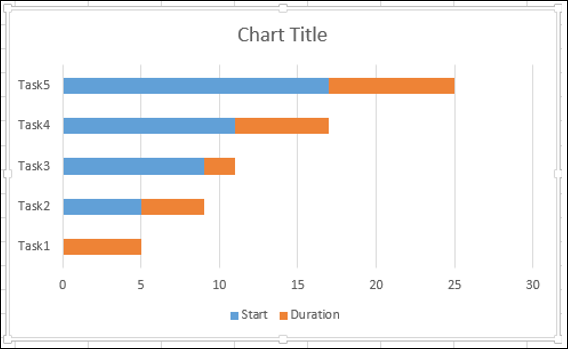
Диаграмма Ганта – это диаграмма, на которой ряд горизонтальных линий показывает объем работы, выполненной в определенные периоды времени, относительно объема работы, запланированного на эти периоды.
В Excel вы можете создать диаграмму Ганта, настроив тип диаграммы с накоплением, чтобы она отображала задачи, продолжительность и иерархию задач. Диаграмма Ганта в Excel обычно использует дни как единицу времени по горизонтальной оси.
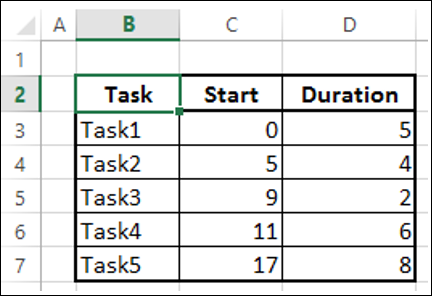
Рассмотрим следующие данные, где столбец –
- Задача представляет Задачи в проекте
- Начало представляет количество дней с даты начала проекта
- Длительность представляет продолжительность задачи
Обратите внимание, что начало любой задачи – это начало предыдущей задачи + продолжительность. Это тот случай, когда задачи находятся в иерархии.
- Выберите данные.
- Создать столбчатую диаграмму с накоплением.
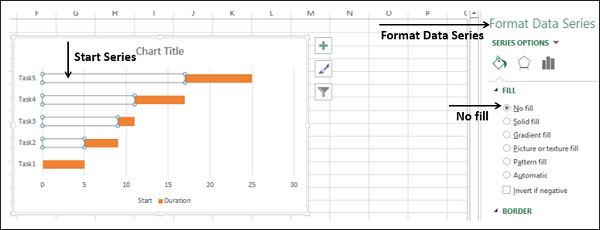
- Щелкните правой кнопкой мыши на Start Series.
- В параметрах «Форматировать ряд данных» выберите «Не заполнять».
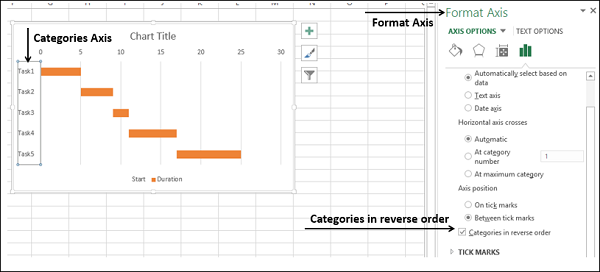
- Щелкните правой кнопкой мыши по оси категорий.
- В параметрах формата оси выберите Категории в обратном порядке.
- В элементах диаграммы отмените выбор
- легенда
- Сетки
- Отформатируйте горизонтальную ось, чтобы
- Отрегулируйте диапазон
- Основные отметки тика с интервалом в 5 дней
- Незначительные отметки тика с интервалом в 1 день
- Формат Data Series, чтобы он выглядел впечатляюще
- Дайте название диаграммы
Водопад Chart
Waterfall Chart – один из самых популярных инструментов визуализации, используемых в малых и крупных компаниях. Графики водопадов идеально подходят для того, чтобы показать, как вы достигли чистой стоимости, такой как чистый доход, путем разбивки совокупного эффекта положительных и отрицательных взносов.
Excel 2016 предоставляет тип диаграммы водопада. Если вы используете более ранние версии Excel, вы все равно можете создать диаграмму водопадов с помощью столбчатой диаграммы с накоплением.
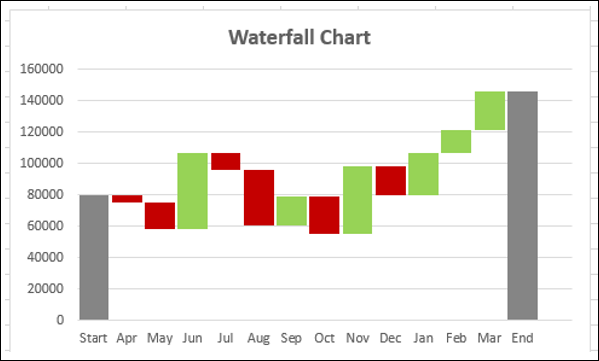
Столбцы имеют цветовую кодировку, так что вы можете быстро отличить положительные от отрицательных чисел. Столбцы начальных и конечных значений начинаются с горизонтальной оси, а промежуточные значения являются плавающими столбцами. Из-за этого взгляда, Карты Водопада также называют Мостовыми картами.
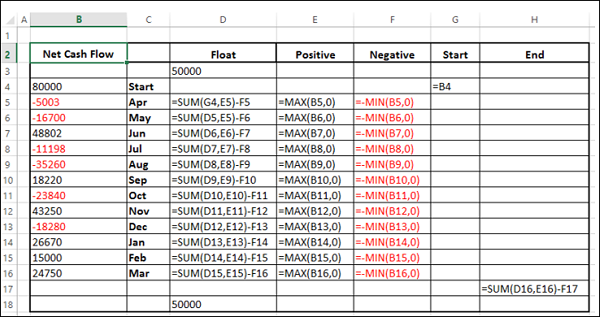
Рассмотрим следующие данные.
-
Подготовьте данные для диаграммы водопада
-
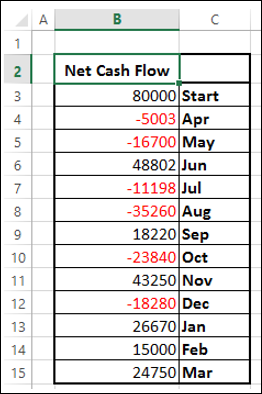
Убедитесь, что столбец «Чистый денежный поток» находится слева от столбца «Месяцы» (это потому, что этот столбец не будет включен при создании диаграммы)
-
Добавьте 2 столбца – Увеличение и Уменьшение для положительных и отрицательных денежных потоков соответственно
-
Добавить столбец Start – первый столбец в диаграмме с начальным значением в Net Cash Flow
-
Добавить столбец Конец – последний столбец на графике с конечным значением в Чистом денежном потоке
-
Добавить столбец с плавающей точкой, поддерживающий промежуточные столбцы.
-
Вычислите значения для этих столбцов следующим образом
Подготовьте данные для диаграммы водопада
Убедитесь, что столбец «Чистый денежный поток» находится слева от столбца «Месяцы» (это потому, что этот столбец не будет включен при создании диаграммы)
Добавьте 2 столбца – Увеличение и Уменьшение для положительных и отрицательных денежных потоков соответственно
Добавить столбец Start – первый столбец в диаграмме с начальным значением в Net Cash Flow
Добавить столбец Конец – последний столбец на графике с конечным значением в Чистом денежном потоке
Добавить столбец с плавающей точкой, поддерживающий промежуточные столбцы.
Вычислите значения для этих столбцов следующим образом
-
В столбце Float вставьте строку в начале и в конце. Разместите n произвольное значение 50000. Это просто, чтобы иметь некоторое пространство слева и справа от графика.
В столбце Float вставьте строку в начале и в конце. Разместите n произвольное значение 50000. Это просто, чтобы иметь некоторое пространство слева и справа от графика.
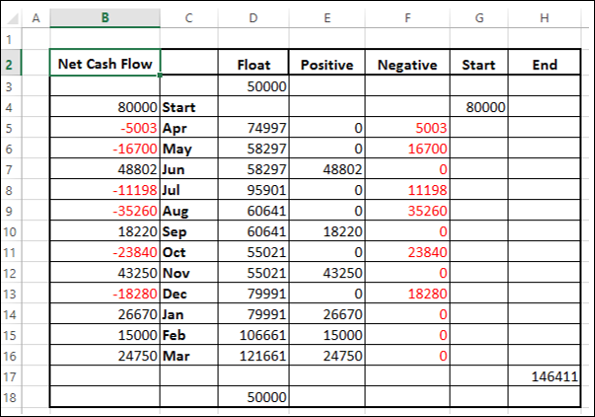
Данные будут следующими.
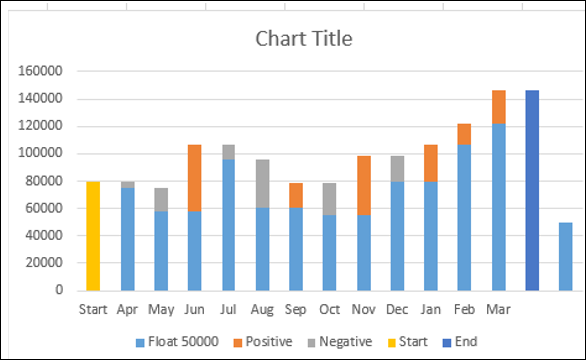
- Выберите ячейки C2: H18 (столбец Исключить чистый денежный поток)
- Создать столбчатую диаграмму с накоплением
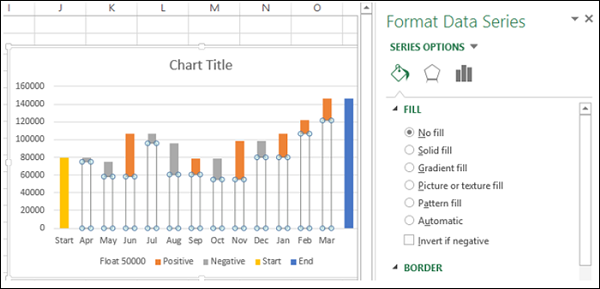
- Щелкните правой кнопкой мыши на Float Series.
- Нажмите Формат данных серии.
- В параметрах «Форматировать ряд данных» выберите «Не заполнять».
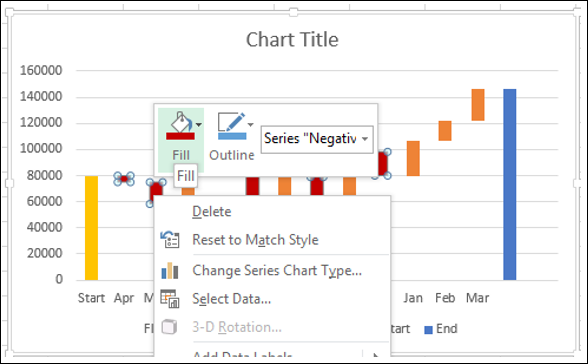
- Щелкните правой кнопкой мыши на Negative Series.
- Выберите Fill Color как Red.
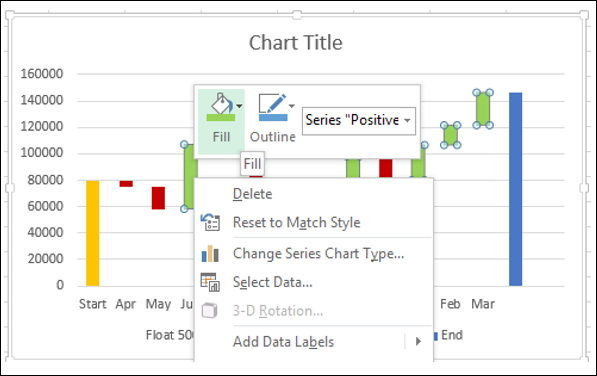
- Щелкните правой кнопкой мыши на Positive Series.
- Выберите Fill Color как Зеленый.
- Щелкните правой кнопкой мыши на Start Series.
- Выберите Цвет заливки как Серый.
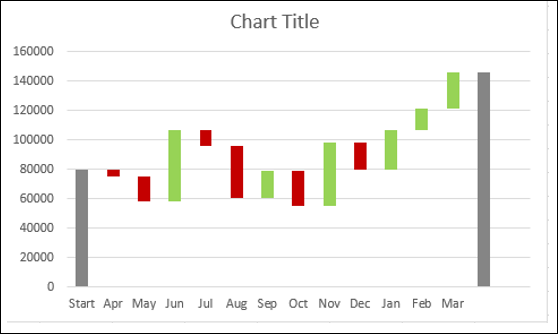
- Щелкните правой кнопкой мыши по Конец серии.
- Выберите Цвет заливки как Серый.
- Удалить легенду.
- Щелкните правой кнопкой мыши на любой серии
- В параметрах «Форматировать ряд данных» выберите «Ширина зазора» как 10% в разделе «Параметры ряда».
Дайте название диаграммы. Диаграмма водопада будет отображаться.
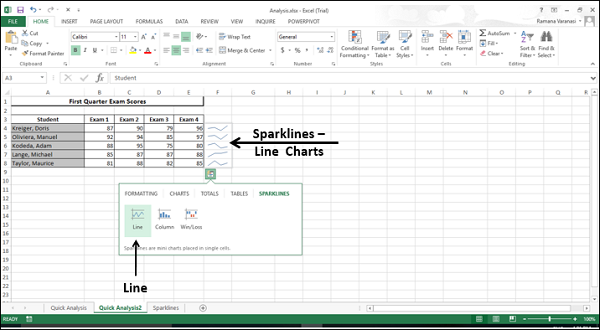
Sparklines
Спарклайны – это крошечные диаграммы, помещенные в отдельные ячейки, каждая из которых представляет собой строку данных в вашем выделении. Они обеспечивают быстрый способ увидеть тенденции.
Вы можете добавить Sparklines с помощью инструмента Quick Analysis.
- Выберите данные, для которых вы хотите добавить Sparklines.
- Держите пустой столбец справа от данных для Спарклайнов.
Кнопка быстрого анализа 
-
Нажмите на Быстрый анализ
кнопка. Появится панель быстрого анализа с различными параметрами.
Нажмите на Быстрый анализ 
Нажмите ИСКРЫ . Отображаемые параметры диаграммы основаны на данных и могут отличаться.
Нажмите Линия . Линейная диаграмма для каждой строки отображается в столбце справа от данных.
сводные диаграммы
Сводные диаграммы используются для графического суммирования данных и изучения сложных данных.
Сводная диаграмма отображает ряды данных, категории и оси диаграммы так же, как стандартная диаграмма. Кроме того, он также предоставляет вам интерактивные элементы управления фильтрацией прямо на графике, чтобы вы могли быстро проанализировать подмножество ваших данных.
Сводные диаграммы полезны, когда у вас есть данные в огромной сводной таблице или во многих сложных данных рабочего листа, которые содержат текст и числа. Сводная диаграмма может помочь вам разобраться в этих данных.
Вы можете создать сводную диаграмму из
- Сводная таблица.
- Таблица данных как отдельная без сводной таблицы.
Сводная диаграмма из сводной таблицы
Чтобы создать сводную диаграмму, выполните следующие действия:
- Нажмите на сводную таблицу.
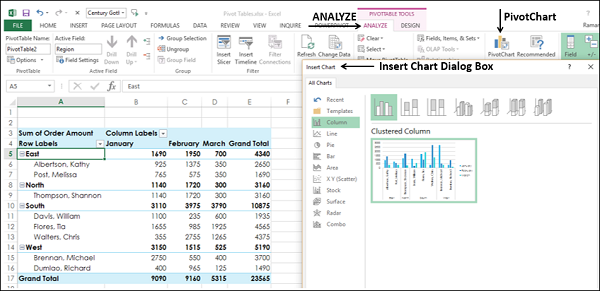
- Нажмите АНАЛИЗ в разделе СРЕДСТВА СЧЕТА на ленте.
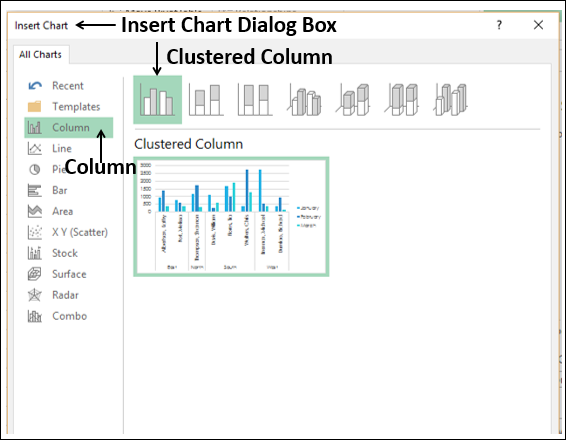
- Нажмите на сводную диаграмму. Откроется диалоговое окно «Вставка диаграммы».
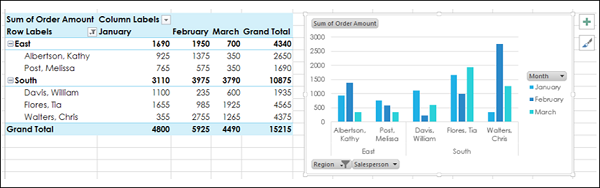
Выберите Clustered Column из опции Column.
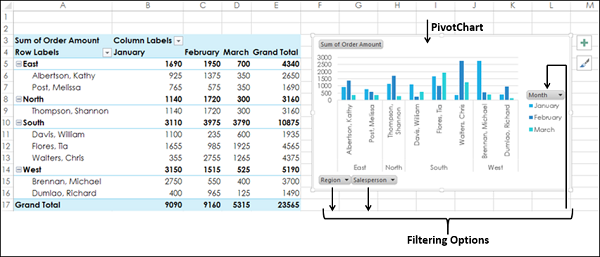
Нажмите ОК. Сводная диаграмма отображается.
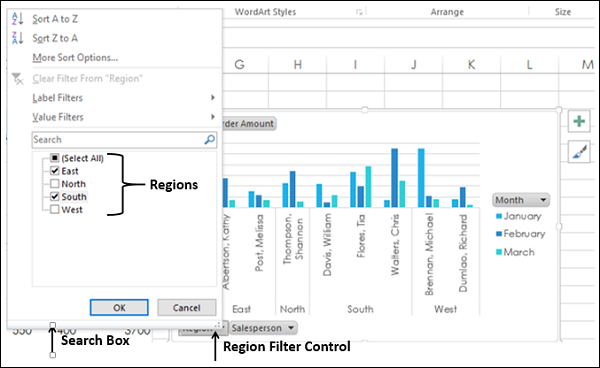
Сводная диаграмма имеет три фильтра – Регион, Продавец и Месяц.
-
Нажмите «Регион управления фильтром». Появится окно поиска со списком всех регионов. Флажки отображаются рядом с регионами.
-
Выберите Восток и Юг.
Нажмите «Регион управления фильтром». Появится окно поиска со списком всех регионов. Флажки отображаются рядом с регионами.
Выберите Восток и Юг.
Отфильтрованные данные отображаются как в сводной диаграмме, так и в сводной таблице.
Сводная диаграмма без сводной таблицы
Вы можете создать отдельную сводную диаграмму, не создавая сводную таблицу.
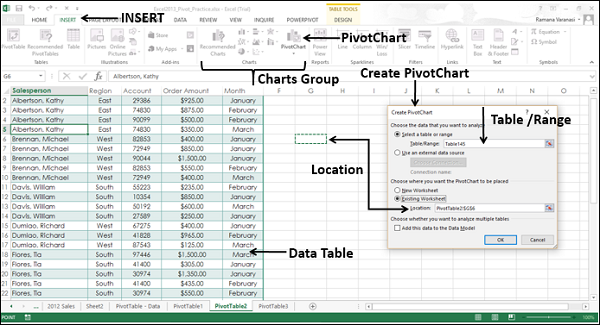
- Нажмите Таблица данных.
- Нажмите вкладку Вставка.
- Нажмите Сводная диаграмма в группе Графики. Откроется окно «Создание сводной диаграммы».
- Выберите таблицу / диапазон.
- Выберите место, где вы хотите разместить сводную диаграмму.
Вы можете выбрать ячейку в самом существующем рабочем листе или в новом рабочем листе. Нажмите ОК.
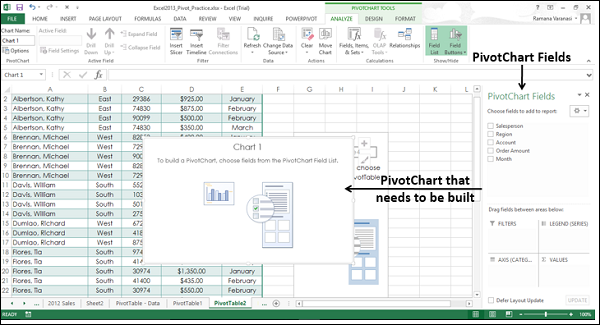
Пустая сводная диаграмма и пустая сводная таблица появляются вместе со списком полей сводной диаграммы для построения сводной диаграммы.
-
Выберите поля, которые будут добавлены в сводную диаграмму
-
Расположите поля, перетащив их в ФИЛЬТРЫ, ЛЕГЕНДЫ (СЕРИЯ), ОСЬ (КАТЕГОРИИ) и ЦЕННОСТИ
-
Используйте элементы управления фильтра на сводной диаграмме, чтобы выбрать данные для размещения на сводной диаграмме.
Выберите поля, которые будут добавлены в сводную диаграмму
Расположите поля, перетащив их в ФИЛЬТРЫ, ЛЕГЕНДЫ (СЕРИЯ), ОСЬ (КАТЕГОРИИ) и ЦЕННОСТИ
Используйте элементы управления фильтра на сводной диаграмме, чтобы выбрать данные для размещения на сводной диаграмме.
Excel автоматически создаст связанную сводную таблицу.
Советы, которые следует прочитать до начала работы
-
Позвольте приложению Excel выбрать для вас сводную таблицу Чтобы быстро отбирать данные, которые вы хотите проанализировать в Excel, сначала нужно выбрать с помощью макета Excel для ваших данных.
-
Анализ данных в нескольких таблицах
Вы можете анализировать данные из двух таблиц в отчете Excel, даже если не используете Power Pivot. Функция модели данных встроена в Excel. Просто добавьте данные в несколько таблиц в Excel а затем создайте связи между ними на листе таблицы или Power View. Готово! Теперь у вас есть модель данных, которая добавляет больше энергии для анализа данных. -
Наносите данные непосредственно на интерактивную сводную диаграмму В Excel можно создать автономный (автономный) сводная диаграмма, который позволяет взаимодействовать с данными и фильтровать их прямо на диаграмме.
-
Использовать все Power Pivot и Power View Если у вас установлен Office профессиональный плюс, попробуйте воспользоваться преимуществами этих мощных надстройок:
-
Встроенной модели данных может быть достаточно для анализа содержимого нескольких таблиц, однако Power Pivot позволяет создать более сложную модель в отдельном окне Power Pivot. Прежде чем приступать к работе, ознакомьтесь с различиями.
-
Надстройка Power View позволяет превратить данные Power Pivot (или любую другую информацию в таблице Excel) в многофункциональный интерактивный отчет, имеющий профессиональный вид. Чтобы начать, просто нажмите кнопку Power View на вкладке Вставка.
-
Создание и создание сводная диаграмма
|
Создание сводной таблицы для анализа данных на листе |
Принимайте более обоснованные бизнес-решения на основе данных в отчетах сводных таблиц, на которые можно взглянуть под разным углом. Excel поможет вам приступить к работе, порекомендовав модель, оптимальную для имеющихся данных. |
|---|---|
|
Создание сводной таблицы для анализа внешних данных |
Если данные, которые требуется обработать, хранятся в другом файле за пределами Excel (например, в базе данных Access или в файле куба OLAP), вы можете подключиться к этому источнику внешних данных и проанализировать их в отчете сводной таблицы. |
|
Создание сводной таблицы для анализа данных в нескольких таблицах |
Если вы хотите проанализировать данные в нескольких таблицах, это можно сделать в Excel. Узнайте о различных способах создания связей между несколькими таблицами в отчете таблицы для мощного анализа данных. В этом Excel создается модель данных. |
|
Учебник. Импорт данных в Excel и создание модели данных |
Прежде чем приступать к самостоятельной работе, воспользуйтесь инструкциями, приведенными в этом учебнике. Они помогут вам создать в Excel учебную сводную таблицу, которая объединяет информацию из нескольких таблиц в общую модель данных. |
|
Упорядочение полей сводной таблицы с помощью списка полей |
Создав сводную таблицу на основе данных листа, внешних данных или информации из нескольких таблиц, воспользуйтесь списком полей, который позволяет добавлять, упорядочивать и удалять поля в отчете сводной таблицы. |
|
Создание сводной диаграммы |
Чтобы провести наглядную презентацию, создайте сводную диаграмму с интерактивными элементами фильтрации, позволяющими анализировать отдельные подмножества исходных данных. Приложение Excel даже может порекомендовать вам подходящую сводную диаграмму. Если вам необходима просто интерактивная диаграмма, создавать для этого сводную таблицу не требуется. |
|
Удаление сводной таблицы |
Если требуется удалить сводную таблицу, перед нажатием клавиши DELETE необходимо выделить всю таблицу, которая может содержать довольно много данных. В этой статье рассказывается, как быстро выделить всю сводную таблицу. |
Изменение формата вашей скайп-формы
|
Разработка макета и формата сводной таблицы |
После создания сводной таблицы и добавления в нее полей можно изменить макет данных, чтобы информацию было удобнее просматривать и изучать. Чтобы мгновенно сменить макет данных, достаточно выбрать другой макет отчета. |
|---|---|
|
Изменение стиля сводной таблицы |
Если вам не нравится, как выглядит созданная вами сводная таблица, попробуйте выбрать другой стиль. Например, если в ней много данных, лучше включить чередование строк или столбцов, чтобы информацию было проще просматривать, либо выделить важные сведения. |
Отображение сведений сводной таблицы
|
Сортировка данных в сводной таблице |
Сортировка помогает упорядочивать большие объемы данных в сводных таблицах, чтобы упростить поиск объектов анализа. Данные можно отсортировать в алфавитном порядке, по убыванию или возрастанию. |
|---|---|
|
Фильтрация данных в сводной таблице |
Чтобы провести более подробный анализ определенного подмножества исходных данных сводной таблицы, их можно отфильтровать. Сделать это можно несколькими способами. Например, можно добавить один или несколько срезов, которые позволяют быстро и эффективно фильтровать информацию. |
|
Группировка и отмена группировки данных в отчете сводной таблицы |
Группировка позволяет выделить для анализа определенное подмножество данных сводной таблицы. |
|
Изучение данных сводной таблицы на разных уровнях |
Переход на разные уровни при больших объемах данных в иерархии сводной таблицы всегда занимал много времени, включая многочисленные операции развертывания, свертывания и фильтрации. В Excel новая функция «Быстрое изучение» позволяет детализтировать данные в кубе OLAP или иерархии на основе модели данных для анализа данных на разных уровнях. Эта функция позволяет переходить к нужным сведениям и действует как фильтр при их детализации. Соответствующая кнопка отображается при выборе элемента в поле. |
|
Создание временной шкалы сводной таблицы для фильтрации дат |
Вместо создания фильтров для отображения данных в сводной таблице теперь можно воспользоваться временной шкалой. Ее можно добавить в сводную таблицу, а затем с ее помощью осуществлять фильтрацию по времени и переходить к различным периодам. |
Расчет значений сводной таблицы
|
Добавление промежуточных итогов в сводную таблицу |
Промежуточные итоги в сводных таблицах вычисляются автоматически и отображаются по умолчанию. Если итогов не видно, их можно добавить. Кроме того, вы можете узнать, как рассчитывать процентные величины для промежуточных итогов, а также скрывать промежуточные и общие итоги, чтобы удалить их из таблицы. |
|---|---|
|
Сведение данных в сводной таблице |
Для сведения данных в сводных таблицах предназначены функции расчета суммы, количества и среднего значения. Функции сведения недоступны в сводных таблицах на базе источников данных OLAP. |
Изменение и обновление данных сводной таблицы
|
Изменение исходных данных сводной таблицы |
После создания сводной таблицы может потребоваться изменить исходные данные для анализа (например, добавить или исключить те или иные сведения). |
|---|---|
|
Обновление данных в сводной таблице |
Если сводная таблица подключена к внешним данным, ее необходимо периодически обновлять, чтобы информация в таблице оставалась актуальной. |
Использование богатых возможностей Power Pivot
|
Power Pivot: мощные средства анализа и моделирования данных в Excel |
Если вы уже установили Office профессиональный плюс, запустите надстройку Power Pivot, которая поставляется вместе с Excel для проведения мощного анализа данных. После этого вы сможете создавать сложные модели данных в окне Power Pivot. |
|---|---|
|
Учебник. Импорт данных в Excel и создание модели данных |
В этом учебнике рассказано, как импортировать сразу несколько таблиц с данными. Во второй его части описывается работа с моделью данных в окне Power Pivot. |
|
Получение данных с помощью надстройки PowerPivot |
Вместо импорта данных или подключения к ним в Excel можно воспользоваться быстрой и эффективной альтернативой: импортом реляционных данных в окне Power Pivot. |
|
Создание связи между двумя таблицами |
Расширить возможности анализа данных помогают связи между таблицами, которые содержат сходную информацию (например, одинаковые поля с идентификаторами). Связи позволяют создавать отчеты сводных таблиц, использующие поля из каждой таблицы, даже если они происходят из разных источников. |
|
Вычисления в Power Pivot |
Для решения задач, связанных с анализом и моделированием данных в Power Pivot, можно использовать возможности вычисления, такие как функция автосуммирования, вычисляемые столбцы и формулы вычисляемых полей, а также настраиваемые формулы на языке выражений анализа данных (DAX). |
|
Добавление ключевых показателей эффективности в сводную таблицу |
С помощью Power Pivot можно создавать ключевые показатели эффективности и добавлять их в сводные таблицы. |
|
Оптимизация модели данных для отчетов Power View |
В этом учебнике показано, как вносить изменения в модель данных для улучшения отчетов Power View. |
Анализ данных с помощью Power View
|
Power View: исследование, визуализация и представление данных |
Надстройка Power View, которая входит в состав Office профессиональный плюс, позволяет создавать интерактивные диаграммы и другие наглядные объекты на отдельных листах Power View, напоминающих панели мониторинга, которые можно представить всем заинтересованным лицам. В конце учебника: импорт данных в Excel и Создание модели данных вы найдете полезные инструкции по оптимизации Power Pivot данных для Power View. |
|---|---|
|
Примеры использования Power View и Power Pivot |
Из этих видеороликов вы узнаете, каких результатов можно добиться с помощью надстройки Power View, функции которой дополняются возможностями Power Pivot. |
Excel – это эффективный инструмент для статистической обработки данных. И определение корреляций является очень важной составляющей этого процесса. Программа имеет весь необходимый инструментарий для осуществления расчетов такого плана. Сегодня мы более детально разберемся, что нам нужно для осуществления анализа этого типа.
Содержание
- Что представляет собой корреляционный анализ
- Корреляционный анализ в Excel — 2 способа
- Как рассчитать коэффициент корреляции
- Способ 1. Определение корреляции с помощью Мастера Функций
- Способ 2. Вычисление корреляции с помощью пакета анализа
- Как построить поле корреляции в Excel
- Диаграмма рассеивания. Поле корреляции
Что представляет собой корреляционный анализ
Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.
Для определения зависимости используется другой тип анализа, который называется регрессионным.
Величина, определяющая степень выраженности взаимосвязи, называется коэффициентом корреляции. Это единственная величина, которая рассчитывается корреляционным анализом по сравнению с регрессионным. Возможные вариации коэффициента корреляции могут быть в пределах от -1 до 1. Если это число положительное, взаимосвязь между динамикой изменения значений прямая. Если же отрицательное, то увеличение числа 1 приводит к аналогичному уменьшению числа 2. Если число меньше единицы по модулю, то корреляция неполная. Например, увеличение числа 1 на единицу приводит к увеличению числа 2 на 0,5. В таком случае коэффициент корреляции составляет 0,5. Если же коэффициент корреляции составляет 0, то взаимосвязи между двумя переменными нет.
Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:
- Количество человек, которые стали утопленниками в бассейнах, четко коррелирует с количеством фильмов, в которых Николас Кейдж был актером.
- Количество съеденной моцареллы и количество человек, которые получили докторскую степень, также коррелирует на протяжении 2000-2009 годов. Наверно, действительно, моцарелла как-то влияет на мозг и стимулирует желание совершать научные открытия.
- Почти во всех случаях средний возраст женщин, которые получили статус «Мисс Америка» коррелирует с количеством людей, которые погибли от нахождения в горячем паре.
- Число людей, которое погибло в результате дорожно-транспортного происшествия, четко коррелирует с количеством сметаны, которое съедают люди.
- Мало кто знает, что чем больше курятины человек ест, тем больше сырой нефти импортируется в мире. Правда, это тоже пример ложной корреляции. Кстати, импорт сырой нефти родом из Норвегии тесно связано с количеством людей, которые погибли в результате столкновения автомобиля с поездом. Причем в этом случае корреляция почти 100 процентов.
- А еще маргарин негативно влияет на статистику разводов. Чем больше людей, которые проживали в штате Мэн, потребляли маргарина, тем выше была частота разводов. Правда, здесь еще может быть рациональное зерно. Ведь частота потребления маргарина имеет обратную корреляцию с экономическим положением в семье. В свою очередь, плохое экономическое положение в семье имеет непосредственную связь с количеством разводов. И это уже доказано научно. Так что кто знает, может, эта корреляция и не является такой ложной. Правда, никто этого не перепроверял.
- Количество денег, которое правительство США тратит на развитие науки, космоса и технологий, имеет тесную связь с количеством самоубийств, проведенных в форме повешения или удушения.
Ну и наконец, еще один пример ложной корреляции – чем больше сыра люди едят, тем больше людей умирает из-за того, что они запутываются в своих простынях.
Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.
Корреляционный анализ в Excel — 2 способа
Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.
Как рассчитать коэффициент корреляции
Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.
Способ 1. Определение корреляции с помощью Мастера Функций
Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:
- С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций.
- Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке.
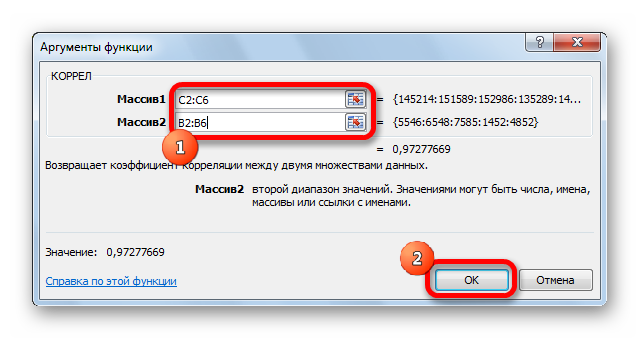
- Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон.
- После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.
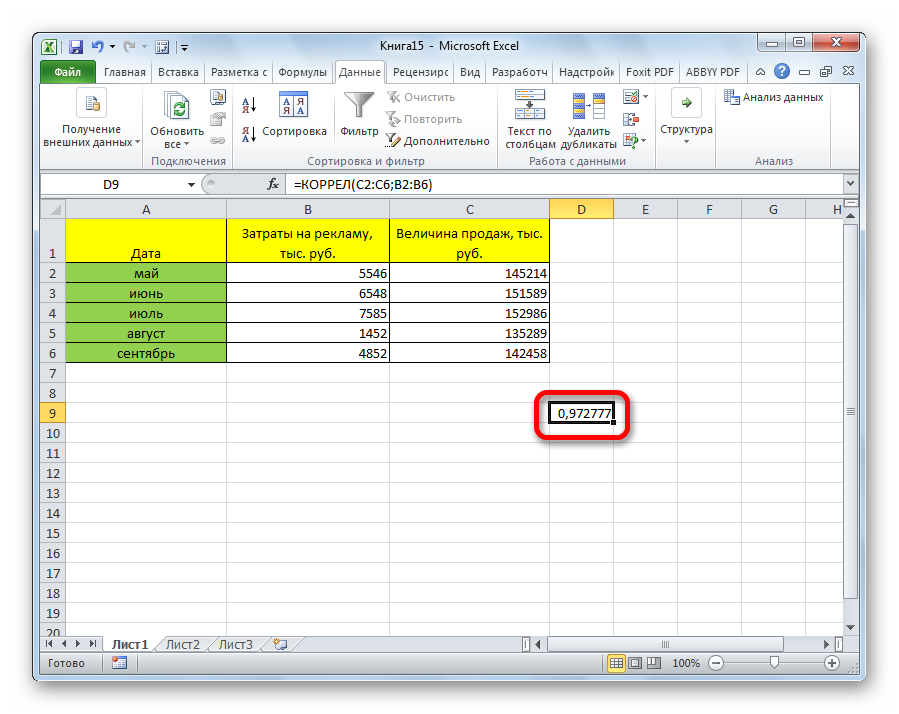
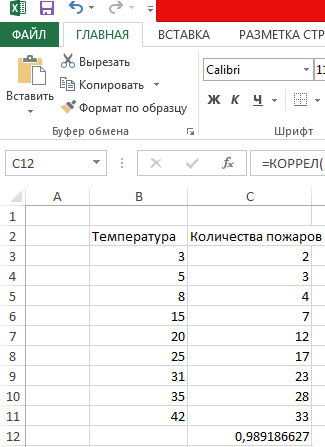
После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.
Способ 2. Вычисление корреляции с помощью пакета анализа
Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:
- Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная».
- После этого открываем раздел с настройками.
- В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи.
- Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений.
- Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК».
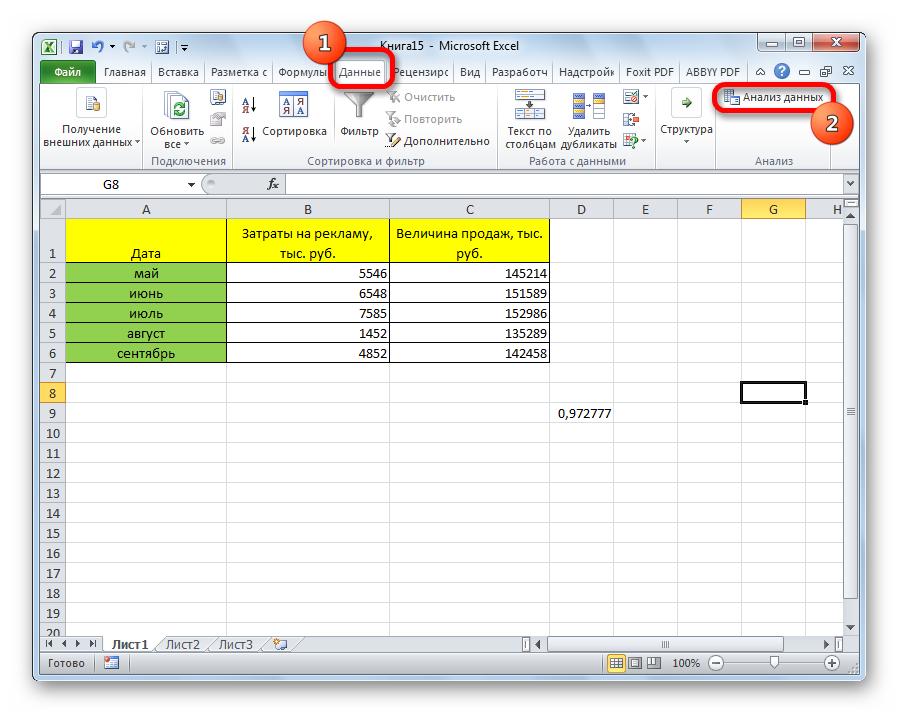
Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее.
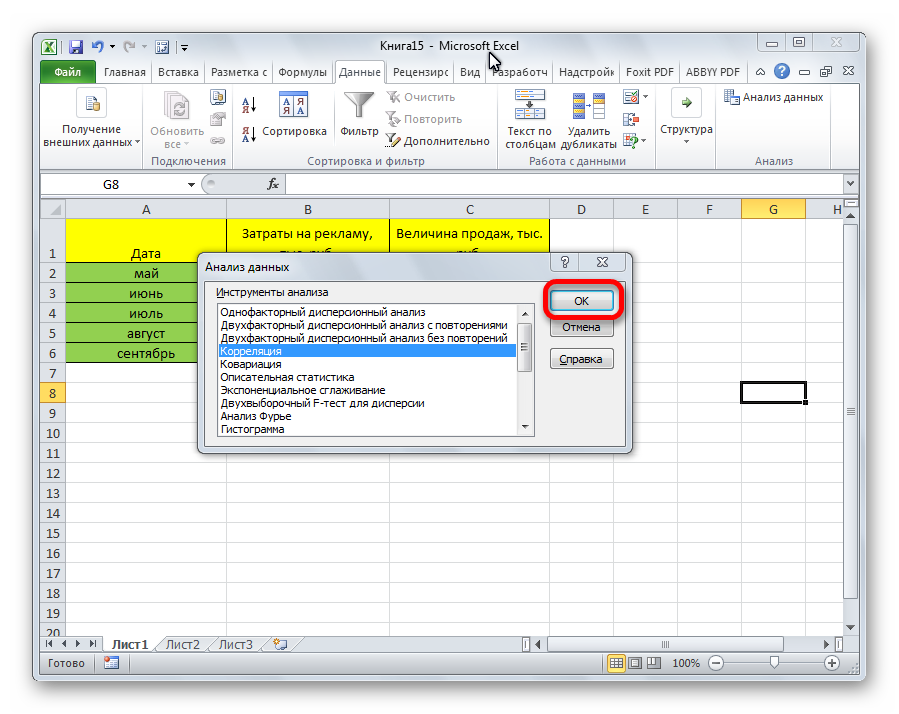
Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК».
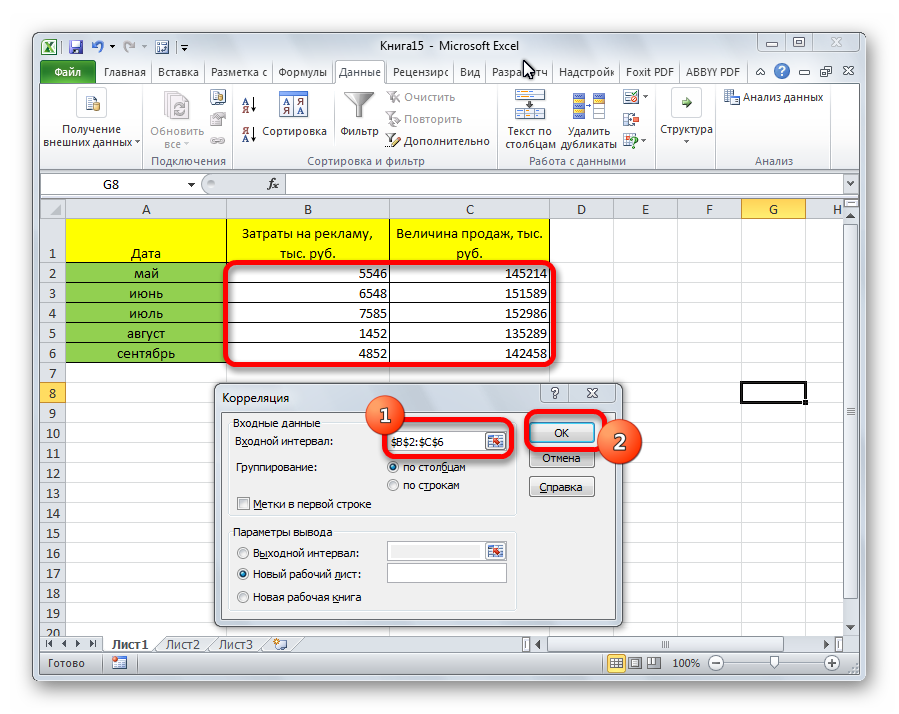
Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».
Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».
В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».
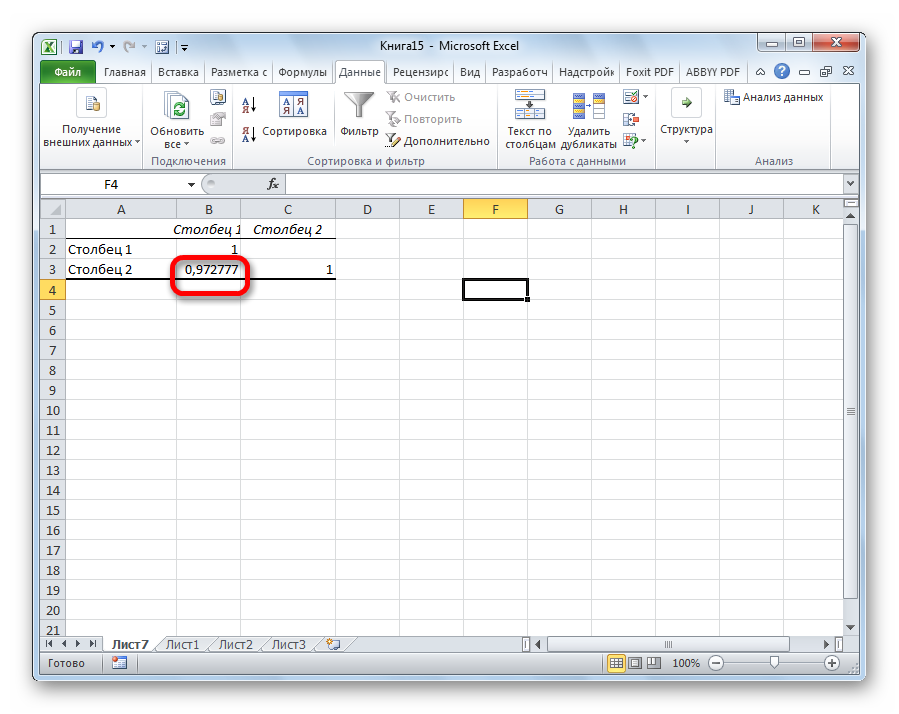
Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.
Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.
Как построить поле корреляции в Excel
Итак, давайте теперь разберемся, как построить поле корреляции. Для начала нужно разобраться, что это вообще такое. Под корреляционным полем подразумевается фактически график корреляции. Главное требование к такой диаграмме – каждая точка должна соответствовать единице совокупности. Поле корреляции поможет установить более глубокие связи и проанализировать данные более качественно. Для начала нам нужно найти коэффициент корреляции между двумя диапазонами, используя функцию КОРРЕЛ.
После того, как мы это сделали, мы теперь можем сделать поле корреляции. Для этого выполняем следующие действия:
- Переходим во вкладку «Вставка» и там находим вариант диаграммы «точечный график».
- После того, как мы его добавили, нажимаем по будущему полю корреляции правой кнопкой мыши и вызываем контекстное меню. Далее нажимаем на «Выбрать данные».
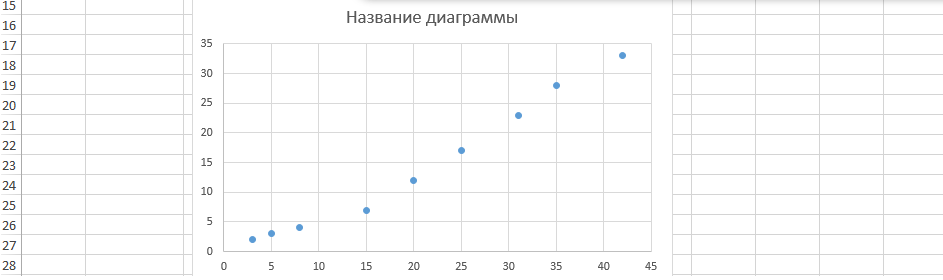
- Далее выбираем наш диапазон в качестве источника данных. После этого подтверждаем свои действия нажатием клавиши ОК. Все остальные действия программа выполнит самостоятельно.
Этот график можно построить не только на основе корреляции, определенной через функцию КОРРЕЛ.
Диаграмма рассеивания. Поле корреляции
До сих пор часть пользователей сидит на старой версии Word. Как построить корреляционное поле в этом случае? Для этого существует специальный инструмент, который называется мастером диаграмм. Найти его можно на панели инструментов по специфическому изображению диаграммы. Если навести на эту иконку мышкой, то появится всплывающая подсказка, которая поможет нам убедиться в том, что это действительно мастер диаграмм.
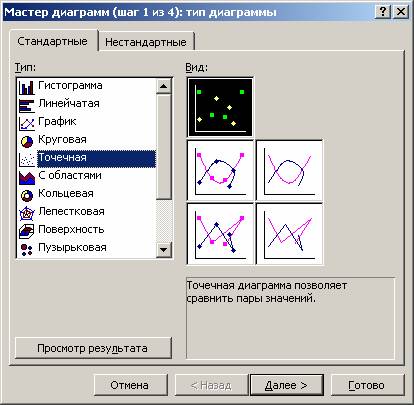
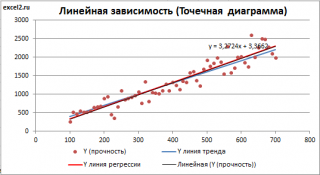
После этого появится диалоговое окно, в котором нам надо выбрать точечный тип диаграммы. Видим, что логика действий в старых версиях офисного пакета в целом остается той же самой, просто немного другой интерфейс. Немного правее мы можем увидеть, как будет выглядеть точечная диаграмма и выбрать подходящий вид, а также прочитать описание этого типа диаграммы. После этого нажимаем на кнопку «Далее».
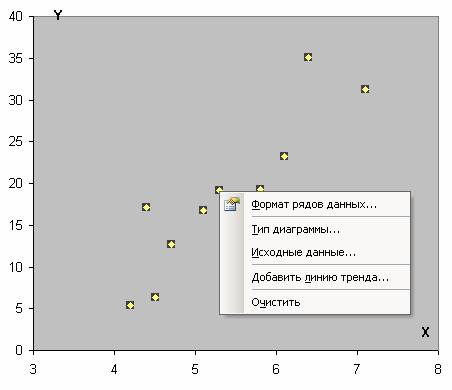
Затем выбираем диапазон данных, и наша линия появляется. После этого можно добавить линию регрессии к графику. Для этого необходимо сделать клик правой кнопкой мыши по одной из точек и в появившемся перечне найти «Добавить линию тренда» и сделать клик по этому пункту.
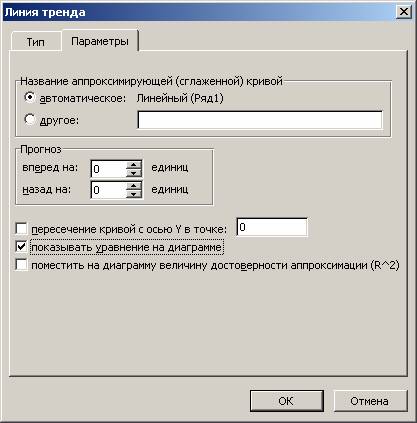
Далее выставляем настройки. Нас интересует тип «Линейная», а в окне параметров нужно поставить флажок «Показывать уравнение на диаграмме».
После подтверждения действий у нас появится что-то типа такого графика.
Как видим, возможных вариантов построения может быть огромное количество.
Оцените качество статьи. Нам важно ваше мнение:
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
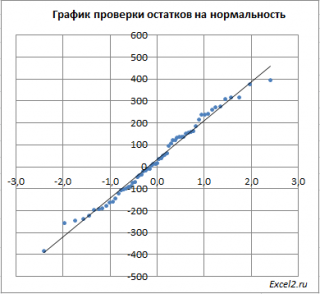
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12765 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
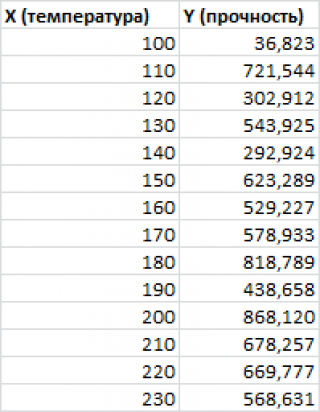
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
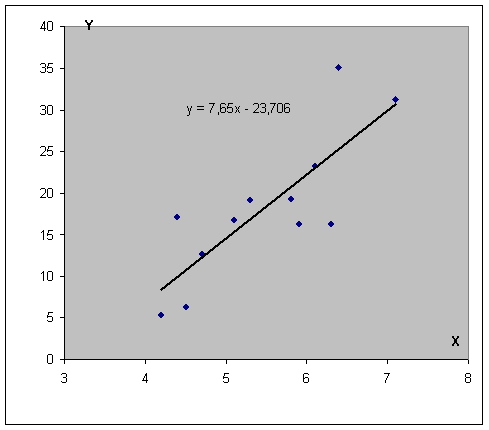
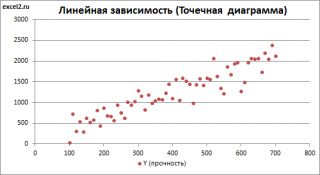
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
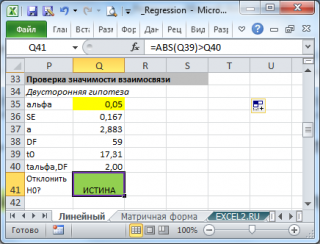
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
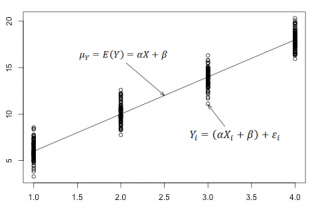
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
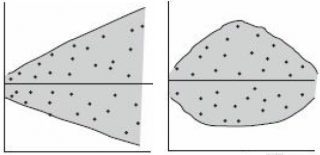
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
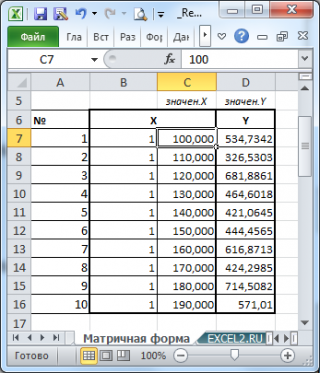
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
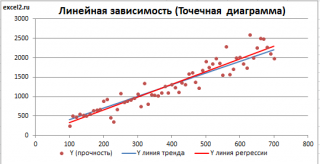
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
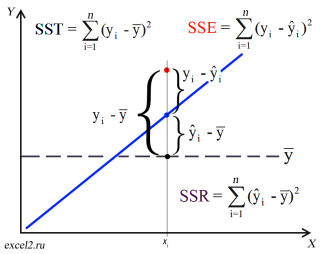
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
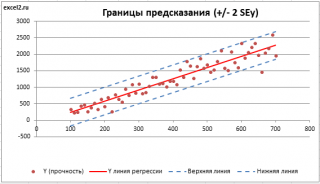
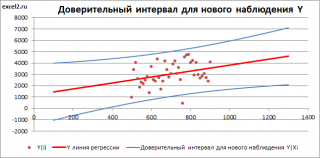
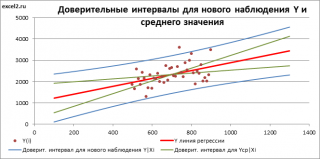
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
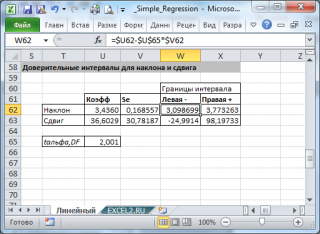
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Как построить график в Excel по уравнению
Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.
Что это такое
График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.
А нужно ли это
Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.
Как построить график уравнения регрессии в Excel
Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.
Подготовительные работы
Перед использованием функции активируйте Пакет анализа. Перейдите: 
Выберите раздел: 
Далее: 
Прокрутите окно вниз, выберите: 
Отметьте пункт: 
Открыв раздел «Данные», появится кнопка «Анализ».
Как пользоваться
Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите: 
Выберите: 
Отобразится окно настроек, где входной интервал:
- Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
- Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».
Анализ
Нажав кнопку «ОК», отобразится результат. 
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.
Как построить график квадратного уравнения в Excel
График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].
- Составьте таблицу как на скриншоте;
- В третьей строке указываем коэффициенты и их значения;
- Пятая — диапазон значений;
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;


При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите: 
Поместите график в свободное место на листе.
Как построить график линейного уравнения
Функция имеет вид: y=kx+b. Построим в интервале [-4;4].
- В таблицу прописываем значение постоянных величин. Строка три;
- Строка 5. Вводим диапазон значений;
- Ячейка В6. Прописываем формулу.


График — прямая линия.
Вывод
Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.
источники:
http://excel2.ru/articles/prostaya-lineynaya-regressiya-v-ms-excel
http://public-pc.com/kak-postroit-grafik-v-excel-po-uravneniyu/