Процессы в сфере финансов всегда взаимосвязаны – один фактор зависит от другого и меняется вместе с ним. Отследить эти изменения и понять, чего стоит ожидать в будущем, возможно с помощью функций Excel и табличных методов.
Содержание
- Получение нескольких результатов с помощью таблицы данных
- Общие сведения
- Базовые сведения о таблицах данных
- Создание таблицы данных с одной переменной
- Добавление формулы в таблицу данных с одной переменной
- Создание таблицы данных с двумя переменными
- Ускорение вычислений для листов, содержащих таблицы данных
- Другие инструменты для выполнения анализа чувствительности
- Анализ чувствительности инвестиционного проекта в Excel
- Метод анализа чувствительности в сфере инвестиций
- Формула
- Пример анализа чувствительности инвестиционного проекта в Excel
- Анализ чувствительности инвестиций при помощи таблицы данных
- Факторный и дисперсионный анализ в Excel с автоматизацией подсчетов
- Дисперсионный анализ в Excel
- Факторный анализ в Excel: пример
- Двухфакторный дисперсионный анализ в Excel
- Заключение
Получение нескольких результатов с помощью таблицы данных
Возможности таблиц данных представляют собой элементы анализа «что если» – его нередко проводят через Microsoft Excel. Это второе название анализа чувствительности.
Общие сведения
Таблица данных – это тип диапазона ячеек, с помощью которого можно решать возникающие проблемы путем изменения значений в некоторых ячейках. Ее составляют, когда необходимо следить за изменениями компонентов формулы и получать обновления результатов, согласно этим изменениям. Выясним, как применять таблички данных в исследованиях, и каких видов они бывают.
Базовые сведения о таблицах данных
Существует два вида таблиц данных, они различаются по количеству компонентов. Составлять таблицу нужно с ориентацией на количество значений, которые нужно проверить с ее помощью.
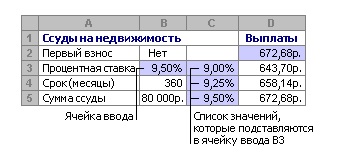
Специалисты статистики применяют таблицу с одной переменной, когда в одном или нескольких выражениях есть только одна переменная, которая может повлиять на изменение их результата. К примеру, ее часто используют в связке с функцией ПЛТ. Формула предназначена для расчета суммы регулярного платежа и учитывает установленную в договоре процентную ставку. При подобных вычислениях переменные записывают в одну колонку, а результаты вычислений в другую. Пример таблички данных с 1 переменной:
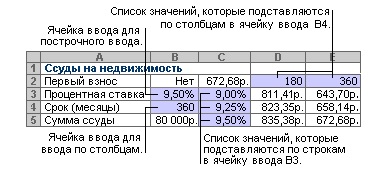
Далее рассмотрим таблички с 2 переменными. Они применяются в тех случаях, когда на изменение какого-либо показателя влияют два фактора. Две переменные могут оказаться в другой таблице, связанной с займом, – с ее помощью можно выявить оптимальный срок выплаты и сумму ежемесячного платежа. В таком расчете тоже нужно использовать функцию ПЛТ. Пример таблички с 2 переменными:
Создание таблицы данных с одной переменной
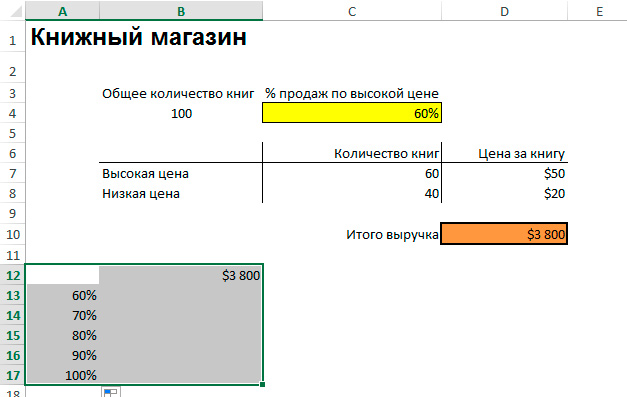
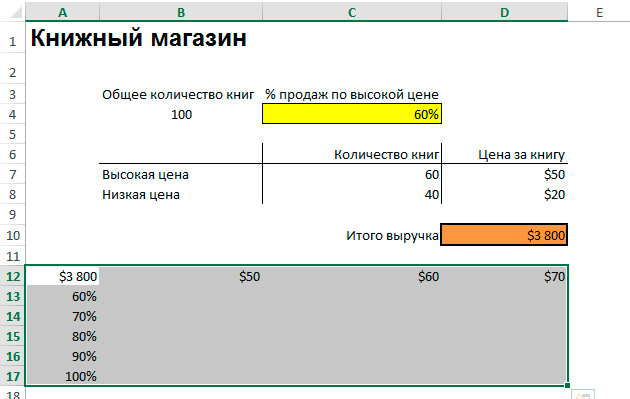
Рассмотрим метод анализа на примере небольшого книжного магазина, где всего 100 книг в наличии. Часть из них можно продать дороже (50$), остальные обойдутся покупателям дешевле (20$). Рассчитан общий доход с продажи всех товаров – владелец решил, что продаст по высокой цене 60% книг. Необходимо выяснить, как вырастет выручка, если повысить цену на больший объем товара – 70% и так далее.
Обратите внимание! Общую выручку обязательно нужно считать с помощью формулы, иначе не получится составить таблицу данных.
- Выбираем свободную ячейку в отдалении от края листа и записываем в ней формулу: =Ячейка общей выручки. Например, если доход записан в ячейке С14 (указано случайное обозначение), необходимо написать так: =С14.
- Записываем проценты объема товара в столбец слева от этой ячейки – не под ней, это очень важно.
- Выделяем диапазон ячеек, где располагается столбец процентов и ссылка на общий доход.
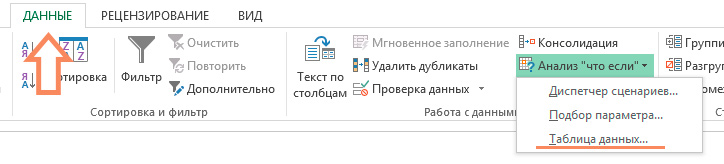
- Находим на вкладке «Данные» пункт «Анализ «что если»» и кликаем по нему – в открывшемся меню нужно выбрать опцию «Таблица данных».
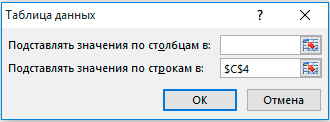
- Откроется небольшое окно, где необходимо указать ячейку с процентом изначально проданных по высокой цене книг в графе «Подставлять значения по строкам в…». Этот шаг делают для того, чтобы делать перерасчет общей выручки с учетом возрастающего процента.
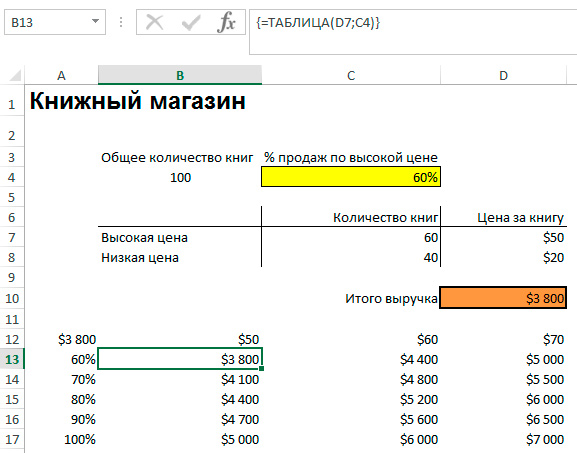
После нажатия кнопки «ОК» в окне, где вводились данные для составления таблицы, в строках появятся результаты вычислений.
Добавление формулы в таблицу данных с одной переменной
Из таблицы, которая помогала рассчитывать действие только с одной переменной, можно сделать усложненный инструмент анализа, добавив дополнительную формулу. Ее необходимо вписать рядом с уже существующей формулой – например, если таблица ориентирована по строкам, вписываем выражение в ячейку справа от уже существующего. Когда установлена ориентация по столбцам, записываем новую формулу под старой. Далее следует действовать по алгоритму:
- Вновь выделяем диапазон ячеек, но теперь он должен включать новую формулу.
- Открываем меню анализа «что если» и выбираем «Таблицу данных».
- Добавляем новую формулу в соответствующее поле по строчкам или по столбикам в зависимости от ориентации таблички.
Создание таблицы данных с двумя переменными
Начало составления такой таблицы немного отличается – нужно поместить ссылку на общую выручку над значениями процентов. Далее выполняем эти шаги:
- Записать варианты цены в одну строку со ссылкой на доход – каждой цене одна ячейка.
- Выделить диапазон ячеек.
- Открыть окно таблицы данных, как при составлении таблички с одной переменной – через вкладку «Данные» на панели инструментов.
- Подставить в графу «Подставлять значения по столбцам в…» ячейку с начальной высокой ценой.
- Добавить в графу «Подставлять значения по строкам в…» ячейку с начальным процентом продаж дорогих книг и нажать «ОК».
В результате вся табличка заполнена суммами возможного дохода с разными условиями продажи товара.
Ускорение вычислений для листов, содержащих таблицы данных
Если требуются быстрые вычисления в табличке данных, не запускающие пересчет книги целиком, можно выполнить несколько действий для ускорения процесса.
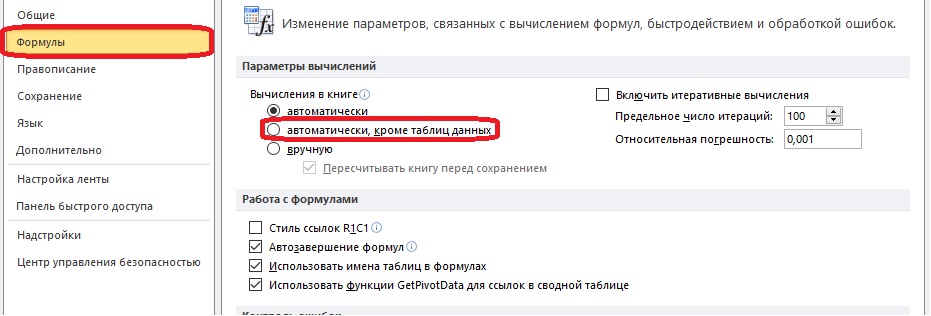
- Открываем окно параметров, выбираем пункт «Формулы» в меню справа.
- Выбираем пункт «Автоматически, кроме таблиц данных» в разделе «Вычисления в книге».
- Выполним пересчет результатов в табличке вручную. Для этого нужно выделить формулы и нажать клавишу F
Другие инструменты для выполнения анализа чувствительности
В программе есть и другие инструменты, помогающие выполнять анализ чувствительности. Они автоматизируют некоторые действия, которые в ином случае пришлось бы выполнять вручную.
- Функция «Подбор параметра» подойдет, если известен нужный результат, и требуется узнать входное значение переменной для получения такого результата.
- «Поиск решения» – это надстройка для решения задач. Необходимо установить ограничения и указать на них, после чего система найдет ответ. Решение определяется путем изменения значений.
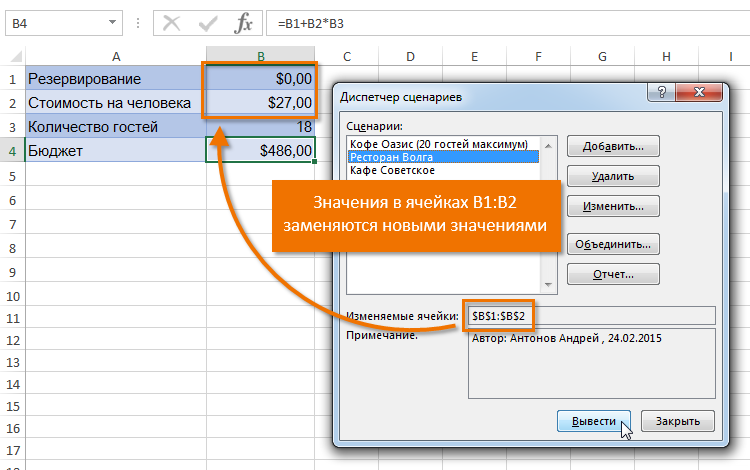
- Анализ чувствительности можно провести с помощью диспетчера сценариев. Этот инструмент находится в меню анализа «что если» на вкладке «Данные». Он подставляет значения в несколько ячеек – количество может достигать 32-х. Диспетчер сравнивает эти значения, и пользователю не придется менять их вручную. Пример применения диспетчера сценариев:
Анализ чувствительности инвестиционного проекта в Excel
Анализ «что если» оказывается особенно полезным в ситуациях, где требуется прогнозирование – например, в сфере инвестиций. Аналитики применяют этот метод, чтобы выяснить, как будет меняться стоимость акций компании в результате изменения некоторых факторов.
Метод анализа чувствительности в сфере инвестиций
При анализе «что если» используют перебор – ручной или автоматический. Известен диапазон значений, и они по очереди подставляются в формулу. В итоге получается набор значений. Из них выбирают подходящую цифру. Рассмотрим четыре показателя, по которым ведется анализ чувствительности в сфере финансов:
- Чистая приведенная стоимость – вычисляется путем вычитания размера вложения из объема доходов.
- Внутренняя норма доходности/прибыли – указывает, какую прибыль требуется получить с вложения за год.
- Коэффициент окупаемости – отношение всей прибыли к начальному вложению.
- Дисконтированный индекс прибыли – указывает на эффективность инвестиции.
Формула
Чувствительность вложения можно вычислить с помощью этой формулы: Изменение выходного параметра в % / Изменение входного параметра в %.
Выходным и входным параметром могут быть величины, описанные ранее.
- Необходимо узнать результат при стандартных условиях.
- Заменяем одну из переменных и следим за изменениями результата.
- Вычисляем процентное изменение обоих параметров относительно установленных условий.
- Вставляем полученные проценты в формулу и определяем чувствительность.
Пример анализа чувствительности инвестиционного проекта в Excel
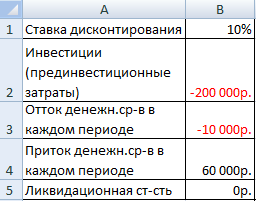
Для лучшего понимания методики анализа необходим пример. Проанализируем проект с такими известными данными:
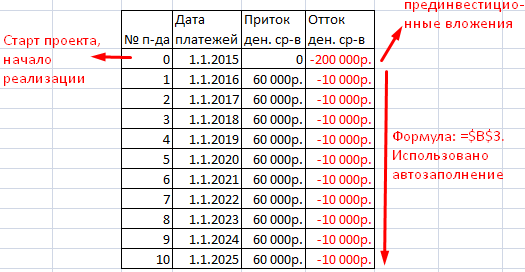
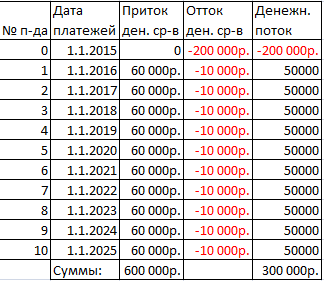
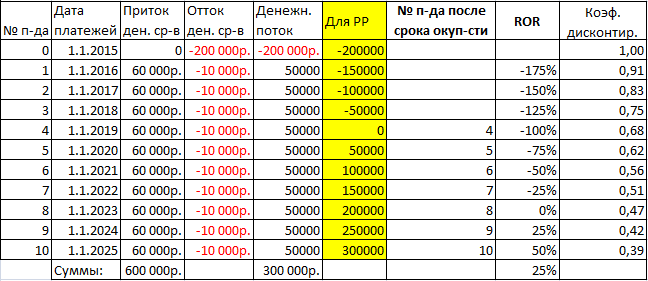
- Заполним таблицу, чтобы анализировать проект по ней.
- Вычисляем денежный поток с помощью функции СМЕЩ. На начальном этапе поток равен вложениям. Далее применяем формулу: =ЕСЛИ(СМЕЩ(Номер;1;)=2;СУММ(Приток 1:Отток 1); СУММ(Приток 1:Отток 1)+$B$5)
Обозначения ячеек в формуле могут быть другими, это зависит от размещения таблицы. В конце прибавляется значение из начальных данных – ликвидационная стоимость.
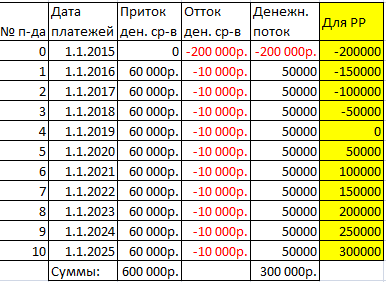
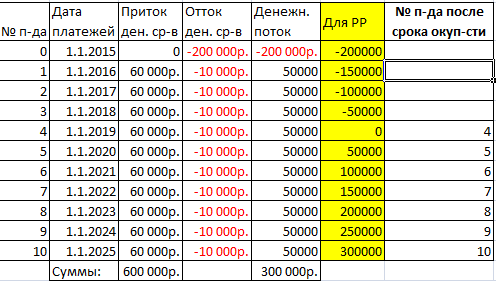
- Определяем срок, за который проект окупится. Для начального периода используем эту формулу: =СУММЕСЛИ(G7:G17;»<0″). Диапазон ячеек – это столбец денежного потока. На дальнейших периодах применим эту формулу: =Начальный период+ЕСЛИ(Первый д.поток>0; Первый д.поток;0). Проект оказывается в точке безубыточности за 4 года.
- Создаем столбец для номеров тех периодов, когда проект окупается.
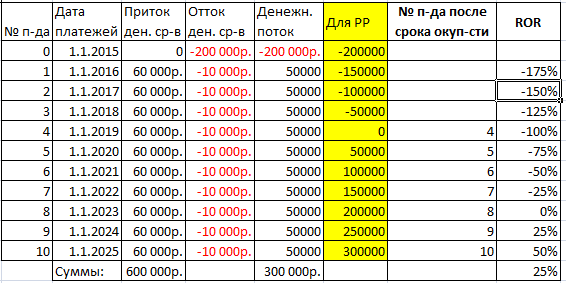
- Вычисляем рентабельность вложений. Необходимо составить выражение, где прибыль в конкретном отрезке времени делится на начальные вложения.
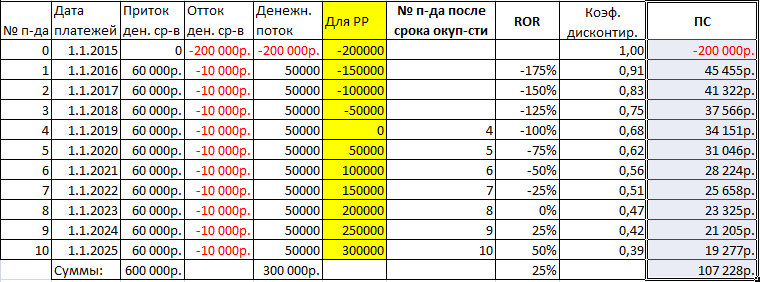
- Определяем коэффициент дисконтирования по этой формуле: =1/(1+Ставка диск.%) ^Номер.
- Вычислим приведенную стоимость с помощью умножения – денежный поток умножается на коэффициент дисконтирования.
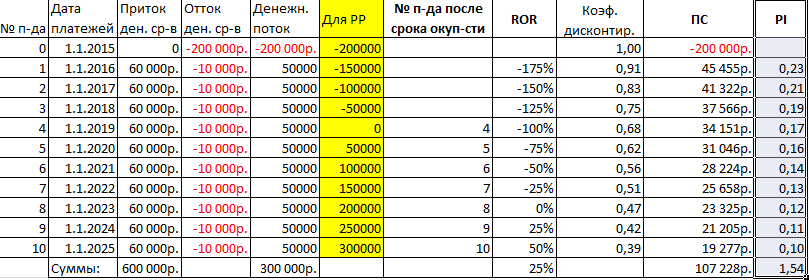
- Рассчитаем PI (индекс рентабельности). Приведенная стоимость в отрезке времени делится на вложения в начале развития проекта.
- Определим внутреннюю норму прибыли с помощью функции ВСД: =ВСД(Диапазон денежного потока).
Анализ чувствительности инвестиций при помощи таблицы данных
Для анализа проектов в сфере инвестирования лучше подходят другие способы, нежели таблица данных. У многих пользователей возникает путаница при составлении формулы. Чтобы выяснить зависимость одного фактора от изменений в других, нужно выбрать правильные ячейки ввода вычислений и для считывания данных.
Факторный и дисперсионный анализ в Excel с автоматизацией подсчетов
Еще одна типология анализа чувствительности – факторный и дисперсионный анализ. Первый тип определяет связь между числами, второй выявляет зависимость одной переменной от других.
Дисперсионный анализ в Excel
Цель подобного анализа – разделить изменчивость величины на три компонента:
- Изменчивость в результате влияния других значений.
- Изменения из-за взаимосвязи влияющих на него значений.
- Случайные изменения.
Выполним дисперсионный анализ через надстройку Excel «Анализ данных». Если она не включена, ее можно подключить в параметрах.
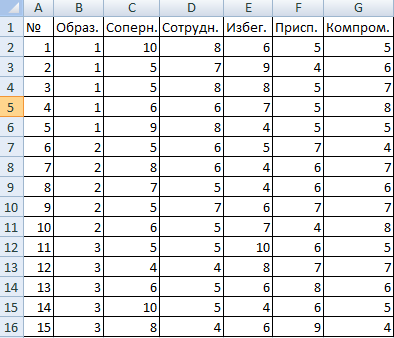
Начальная таблица должна соответствовать двум правилам: на каждую величину приходится один столбец, и данные в нем располагаются по возрастанию или по убыванию. Необходимо проверить влияние уровня образования на поведение в конфликте.
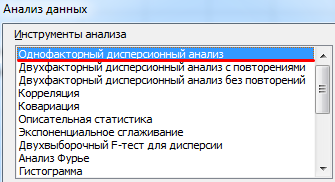
- Находим во вкладке «Данные» инструмент «Анализ данных» и открываем его окно. В списке нужно выбрать однофакторный дисперсионный анализ.
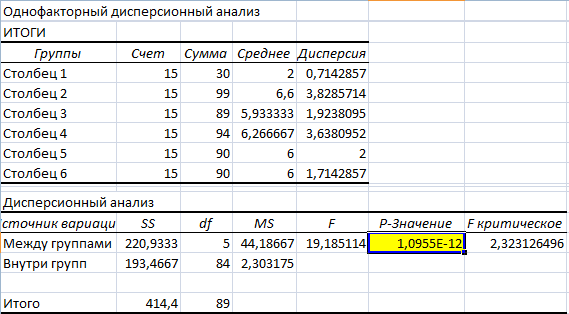
- Заполняем строки диалогового окна. Входной интервал – все ячейки без учета шапки и номеров. Группируем по столбцам. Выводим результаты на новый лист.
Поскольку значение в желтой ячейке больше единицы, можно считать предположение неверным – зависимости между образованием и поведением в конфликте нет.
Факторный анализ в Excel: пример
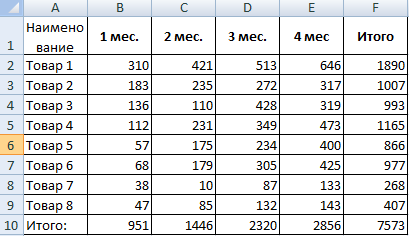
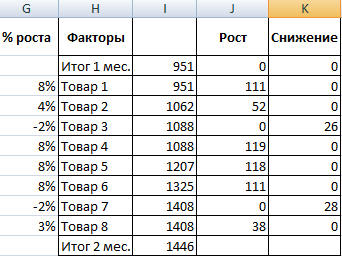
Проанализируем взаимосвязь данных в сфере продаж – необходимо выявить популярные и непопулярные товары. Начальная информация:
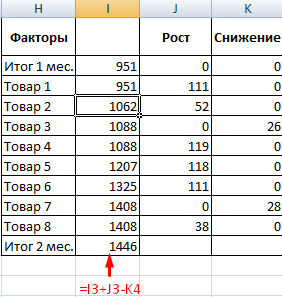
- Нужно выяснить, на какие товары больше всего вырос спрос в течение второго месяца. Составляем новую таблицу для определения роста и снижения спроса. Рост рассчитывается по этой формуле: =ЕСЛИ((Спрос 2-Спрос 1)>0; Спрос 2- Спрос 1;0). Формула снижения: =ЕСЛИ(Рост=0; Спрос 1- Спрос 2;0).
- Подсчитаем рост спроса на товары в процентах: =ЕСЛИ(Рост/Итог 2 =0;Снижение/Итог 2; Рост/Итог 2).
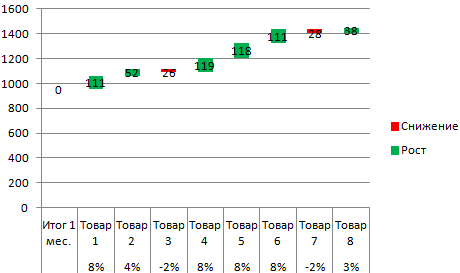
- Составим диаграмму для наглядности – выделяем диапазон ячеек и создаем гистограмму через вкладку «Вставка». В настройках нужно убрать заливку, это можно сделать через инструмент «Формат ряда данных».
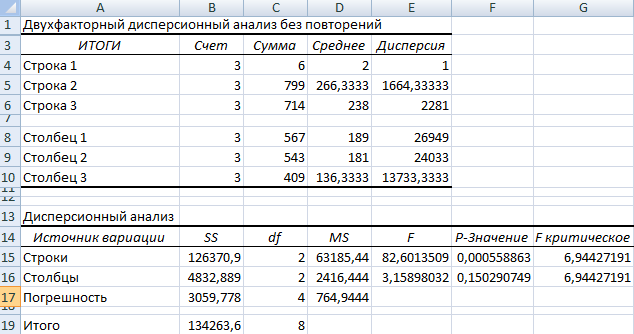
Двухфакторный дисперсионный анализ в Excel
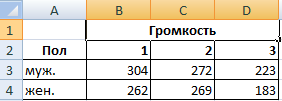
Дисперсионный анализ проводят с несколькими переменными. Рассмотрим это на примере: нужно выяснить, как быстро проявляется реакция на звук разной громкости у мужчин и женщин.
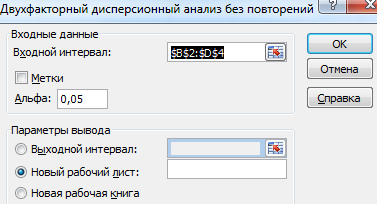
- Открываем «Анализ данных», в списке нужно найти двухфакторный дисперсионный анализ без повторений.
- Входной интервал – ячейки, где содержатся данные (без шапки). Выводим результаты на новый лист и жмем «ОК».
Показатель F больше, чем F-критическое – это означает, что пол влияет на скорость реакции на звук.
Заключение
В данной статье был подробно рассмотрен анализ чувствительности в табличном процессоре Excel, благодаря чему каждый пользователь сможет разобраться в методах его применения.
Оцените качество статьи. Нам важно ваше мнение:
28
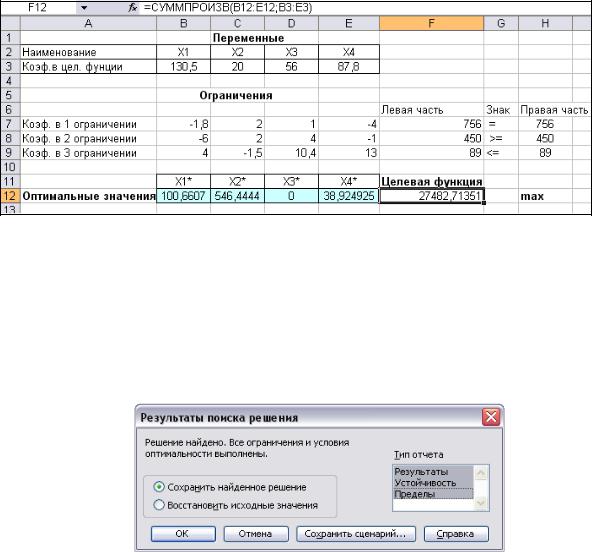
Рис. 1.10. Экранная форма задачи (1.1) после получения решения
Для анализа полученного оптимального решения в MS Excel предусмотрены три типа отчетов: отчет по результатам, устойчивости и пределам.
Проведем анализ чувствительности задачи (1.1). Для этого необходимо после запуска в Excel задачи на решение в окне Результаты поиска решения выделить с помощью мыши три типа отчетов: Результаты, Устойчивость и Пределы (рис. 1.11).
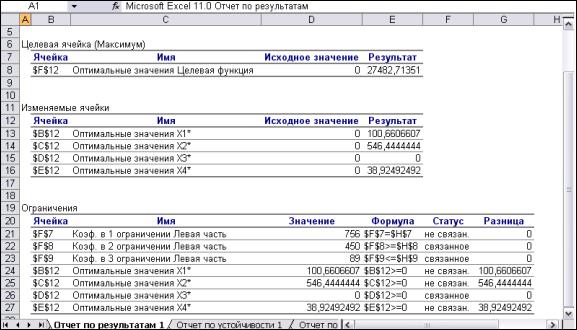
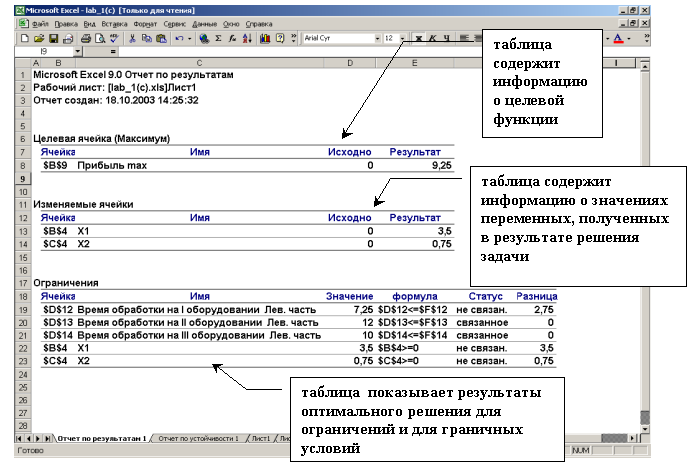
Рис. 1.11. Типы отчетов Отчет по результатам. Отчет по результатам состоит из трех таблиц (рис.1.12):
1)таблица 1 содержит информацию о целевой функции;
2)таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
3)таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для ограничений в столбце Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в столбце Значение приведены величины использованного ресурса.
29
Рис. 1.12. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе Статус соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан.».
Для граничных условий (строки 24-27 на рис. 1.12) в графе Разница показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения целевой функции.
Так, если на ресурс наложено ограничение типа ≥, то в графе Разница дается количество ресурса, на которое была превышена минимально необходимая норма.
Если на ресурс наложено ограничение типа ≤, то в графе Разница дается количество ресурса, которое не используется при реализации оптимального решения.
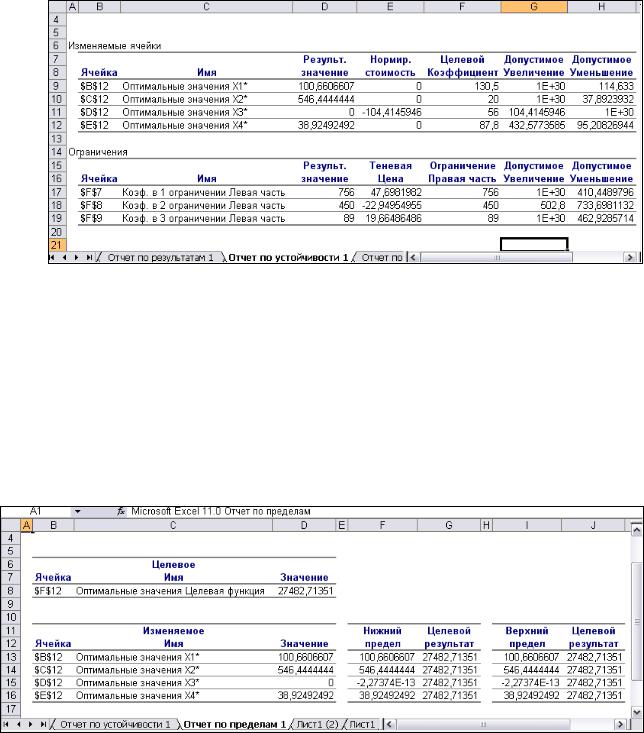
Отчет по устойчивости. Отчет по устойчивости состоит из двух таблиц (рис.1.13). Таблица 1 содержит информацию, относящуюся к переменным:
—результирующие значения переменных;
—нормированная стоимость, т.е. дополнительные двойственные переменные, которые показывает, на сколько изменяется целевая функция при принудительном включении единицы этой переменной в оптимальное решение;
—коэффициенты целевой функции;
—допустимые значения приращения коэффициентов целевой функции, при которых сохраняется первоначальное оптимальное решение.
30
Рис. 1.13. Отчет по устойчивости Таблица 2 (рис. 1.13) содержит информацию, относящуюся к ограничениям:
—величина использованных ресурсов в колонке Результ. значение;
—теневые цены, т.е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу. Теневая цена рассчитывается только для дефицитных ресурсов;
—значения приращения ресурсов, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
Отчет по пределам. В отчете пределам (рис. 1.14) показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.
Рис. 1.14. Отчет по пределам
1.4. Двойственная задача линейного программирования
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче.
|
Прямая задача |
Двойственная задача |
|
Целевая функция |
Целевая функция |
|
L(X )= c1x1 + c2 x2 +… + cn xn → max (min), |
F(Z )=b1z1 +b2 z2 +…+bm zm →min (max), |

31
|
при ограничениях |
||||||||||||||||||
|
a |
x |
+a |
x |
2 |
+…+a |
x |
n |
≤(≥,=)b |
, |
|||||||||
|
11 1 |
12 |
1n |
1 |
|||||||||||||||
|
a21x1 +a22 x2 +…+a2n xn |
≤(≥,=)b2 , |
|||||||||||||||||
|
… |
||||||||||||||||||
|
a |
x |
+a |
m2 |
x |
2 |
+…+a |
mn |
x |
n |
≤ |
(≥,=)b |
, |
||||||
|
m1 1 |
m |
|||||||||||||||||
|
x |
j |
≥ |
0 (j =1,…,n). |
|||||||||||||||
|
при ограничениях |
|||||||||||||||||||
|
a |
z |
+a |
21 |
z |
2 |
+…+a |
m1 |
z |
m |
≤(≥,=)c |
, |
||||||||
|
11 |
1 |
1 |
|||||||||||||||||
|
a12 z1 +a22 z2 +…+am2 zm ≤(≥,=)c2 , |
|||||||||||||||||||
|
… |
|||||||||||||||||||
|
a |
z |
+a |
2n |
z |
2 |
+…+a |
mn |
z |
m |
≤ (≥,=)c |
n |
, |
|||||||
|
1n |
1 |
||||||||||||||||||
|
z |
i |
≥ 0 (i =1,…,m). |
|||||||||||||||||
Рассмотрим задачу линейного программирования (1.1):
L (X )=130,5x1 +20x2 +56x3 +87,8x4 →max;−1,8x1 +2x2 + x3 −4x4 =756,
−6x1 +2x2 +4x3 − x4 ≥ 450,
4x 1−1,5x2 +10,4x3 +13x4 ≤89,x j ≥0; j =1,4.
|
В сформулированной задаче |
неравенство −6x1 +2x2 +4x3 − x4 ≥ 450 эквивалентно |
|
|
неравенству |
6x1 −2x2 −4x3 + x4 |
≤ 450 , а равенство −1,8x1 +2x2 + x3 −4x4 =756 можно |
|
представить |
как два неравенства: |
−1,8x1 +2x2 + x3 −4x4 ≤756 и 1,8x1 −2x2 − x3 +4x4 ≤−756. |
Таким образом, рассматриваемую задачу линейного программирования можно представить в виде (1.4):
|
L (X )=130,5x1 +20x2 +56x3 +87,8x4 |
→max; |
||||||||||||||||||||
|
−1,8x |
+2x |
2 |
+ x |
3 |
−4x |
4 |
≤756, |
||||||||||||||
|
1 |
|||||||||||||||||||||
|
1,8x1 − |
2x2 − x3 +4x4 ≤ −756 |
(1.4). |
|||||||||||||||||||
|
−2x2 −4x3 + x4 |
≤ −450, |
||||||||||||||||||||
|
6x1 |
|||||||||||||||||||||
|
4x |
1 |
− |
1,5x |
2 |
+ |
10,4x |
3 |
+13x |
4 |
≤89, |
|||||||||||
|
j =1,4. |
|||||||||||||||||||||
|
x j ≥0; |
|||||||||||||||||||||
|
Поэтому двойственная задача имеет следующий вид (1.5): |
|||||||||||||||||||||
|
F (Z )=756z1 −756z2 −450z3 +89z4 |
→min; |
||||||||||||||||||||
|
−1,8z1 +1,8z2 +6z3 +4z4 |
≥130,5, |
||||||||||||||||||||
|
2z2 −2z3 −1,5z4 ≥ 20 |
|||||||||||||||||||||
|
2z1 − |
(1.5) |
||||||||||||||||||||
|
− z |
2 −4z3 +10,4z4 |
≥56 |
|||||||||||||||||||
|
z1 |
|||||||||||||||||||||
|
− |
4z |
1 |
+4z |
2 |
+ x |
3 |
+13z |
4 |
≥ |
87,8, |
|||||||||||
|
≥0; i =1,4. |
|||||||||||||||||||||
|
zi |
Схема формирования двойственной задачи приведена на рисунке 1.15. Коэффициенты прямой целевой функции становятся правой частью ограничений. Правая часть ограничений становится коэффициентами новой целевой функции. Матрица коэффициентов ограничений транспонируется.

32
Рис. 1.15. Схема формирования двойственной задачи Ввод зависимостей для двойственной задачи показан на рисунке 1.16.
Рис. 1.16. Ввод зависимостей для двойственной задачи Левая часть ограничений представляет собой произведение матрицы коэффициентов
ограничений на вектор переменных. Целевая функция записывается как произведение транспонированного вектора коэффициентов целевой функции на вектор переменных.
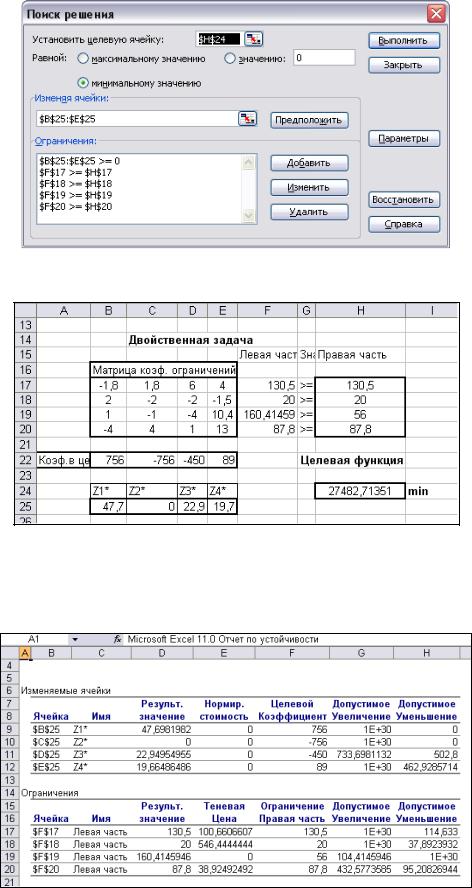
Ограничения приведены на рисунке 1.17 в окне Поиск решения. Это положительность переменных и то, что вектор левой части ограничений должен быть больше вектора из правой части. Для целевой ячейки устанавливаем флажок минимизации.
33
Рис. 1.17. Окно Поиск решения с ограничениями для двойственной задачи Результаты решения двойственной задачи приведены на рисунке 1.18.
Рис. 1.18. Решение для двойственной задачи Открыв отчет по устойчивости (рис. 1.19), можно увидеть новые двойственные
оценки (в столбце Теневая цена) и убедиться, что значения переменных при решении задачи на максимизацию становятся двойственными оценками при задаче на минимизацию, и наоборот (сравните с рисунком 1. 13).
Рис. 1.19. Отчет по устойчивости для двойственной задачи
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анализ оптимального решения на чувствительность в Excel
Задание 1. Проведем анализ чувствительности задачи о производстве двух видов продукции из лабораторной работы №1.
Для этого:
1. Откройте из папки МАТ_МОД файл lab_2(а).
2. Снова запустите задачу на решение (Сервис / Поиск решения) и в окне «Результаты поиска решения» выделите с помощью мыши два типа отчетов: «Результаты» и «Устойчивость» (Рис. 1).
Рис. 1. Выделение типов отчетов, требуемых для анализа чувствительности

3. Проанализируйте первый полученный отчет — «Отчет по результатам 1» (Рис. 2).
Рис. 2. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе «Статус» («Состояние») соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан». В графе «Значение» приведены величины использованного ресурса.
Для граничных условий в графе «Разница» показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ.
Если на ресурс наложено ограничение типа 
Если на ресурс наложено ограничение типа 
Так, анализ строки 19 (Рис. 2) отчета по результатам для задачи о выпуске продукции показывает, что время обработки на I оборудовании составило 7,25 ч. Неизрасходованным остается 2,75 ч из общего фонда времени, отведенного на обработку продукции на I оборудовании. Из этого следует, что запас недефицитного ресурса “Фонд времени работы на I оборудовании” можно уменьшить на 2,75 ч и это никак не повлияет на оптимальное решение. Отсюда следует, что количество рабочих, обслуживающих I оборудование, можно уменьшить или перевести их на выпуск другой продукции. Ресурсы время работы на II и III оборудовании являются дефицитными.
На основании проведенного анализа можно сделать вывод о том, что существуют причины (ограничения), не позволяющие предприятию выпускать большее количество (в кг) продукции и получать большую прибыль. Проанализировать эти причины позволяет отчет по устойчивости.
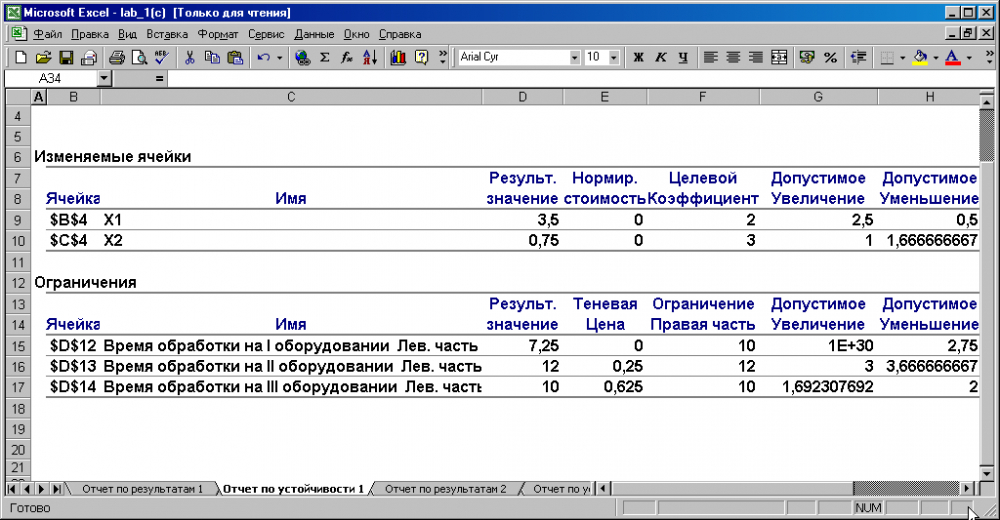
4. Проанализируйте второй полученный отчет — «Отчет по устойчивости 1».
Отчет по устойчивости состоит из двух таблиц «Изменяемые ячейки» и «Ограничения» (Рис. 3).
Таблица «Изменяемые ячейки» содержит информацию», относящуюся к переменным:
- Результат решения задачи можно увидеть в столбце «Результ. значение».
Рис. 3. Отчет по устойчивости
- Нормированная стоимость показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение.
- Коэффициенты ЦФ.
- Предельные значения приращения целевых коэффициентов
(столбцы «Допустимое Увеличение» и «Допустимое Уменьшение»), при которых сохраняется первоначальное оптимальное решение.
Например, допустимое увеличение цены на продукт А равно 2,5 тыс.руб./кг, а допустимое уменьшение – 0,5 тыс.руб./кг. Это означает, что если цена на продукт А возрастет более чем на 2,5 тыс.руб./кг., например станет равной 5 тыс.руб./кг., то оптимальное решение изменится: станет целесообразным выпуск А. И если его цена будет снижена до 1 тыс.руб./кг., то оптимальное решение также измениться: выгоднее будет увеличить выпуск продукта B. А вот если цена на продукт станет равна 4 тыс.руб./кг. или 1,8 тыс.руб./кг, то оптимальное решение не измениться.
Задание 2. Убедитесь в этом самостоятельно, для этого:
1. Увеличьте цену на продукт А – установите 4 тыс.руб./кг (в ячейку 7 внесите 4) и осуществите поиск решения с предоставлением отчетов.
2. Уменьшите цену на продукт А – установите 1,8 тыс.руб./кг и осуществите поиск решения с предоставлением отчетов.

3. Увеличьте цену на продукт А – установите 5 тыс.руб./кг и осуществите поиск решения с предоставлением отчетов.

4. Уменьшите цену на продукт А – установите 1 тыс.руб./кг и осуществите поиск решения с предоставлением отчетов.

5. Сохраните файл с полученными отчетами в своей папке с текущим именем.
Таблица «Ограничения» содержит информацию, относящуюся к ограничениям.
- Величина использованных ресурсов содержится в колонке «Результ. значение».
- Предельные значения приращения ресурсов
содержатся в столбцах «Допустимое Уменьшение» и «Допустимое Увеличение».
В графе «Допустимое Уменьшение» показывается:

В графе «Допустимое Увеличение» показывается:
Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан выше (напоминаем, что в нашем случае только один ресурс не является дефицитным – время работы I оборудования). Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие предприятию выпускать больший, чем в оптимальном решении, объем продукции и получать более высокую прибыль. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы “Время обработки на II оборудовании” и “Время обработки на III оборудовании”. Поскольку знак ограничений этих ресурсов имеет вид 
Задание 3. Убедитесь в этом самостоятельно, для этого снова откройте файл lab_2(а) из папки МАТ_МОД и поэкспериментируйте с исходными данными о фонде рабочего времени оборудования:
1. Увеличьте фонд рабочего времени для оборудования – установите 14 часов (в ячейку 13 внесите 14) и осуществите поиск решения с предоставлением отчетов.
2. Установите исходное значение фонда времени для оборудования (12 часов) и увеличьте фонд рабочего времени для оборудования – установите 11 часов (в ячейку 14 внесите 11), осуществите поиск решения с предоставлением отчетов.

3. Фонд рабочего времени для II оборудования – установите 16 часов, для III оборудования – установите исходное значение 10 часов и осуществите поиск решения с предоставлением отчетов.
4. Фонд рабочего времени для II оборудования – установите исходное значение 12 часов, для III оборудования – установите значение 14 часов и осуществите поиск решения с предоставлением отчетов.

5. Сохраните файл с полученными отчетами с именем lab_2(b) в своей папке.
- Ценность дополнительной единицы i-го ресурса («Теневая цена») рассчитывается только для дефицитных ресурсов.
После того как мы установили, что увеличение фонда рабочего времени оборудования II и III приведет к новым планам выпуска, обеспечивающим более высокую прибыль, возникает следующий вопрос. Что выгоднее в первую очередь увеличивать фонд рабочего времени для II оборудования или для III оборудования? Ответ на этот вопрос дает графа «Теневая цена». Для II оборудования она равна 0,25 тыс. руб./кг., а для III оборудования – 0,625 тыс.руб./кг. Отсюда вывод: в первую очередь выгодно увеличивать фонд рабочего времени для III оборудования.
Задание 4.
1. Постройте математическую модели для следующей задачи ЛП и найдите ее оптимальное решение средствами.
Предприятие выпускает телевизоры, стереосистемы и акустические системы, используя общий склад комплектующих. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий для получения наибольшей прибыли. Общее количество запасов комплектующих, расход (шт.) на изготовление единицы изделия и прибыль от реализации единицы каждого представлены в таблице 1.
Таблица 1. Исходные данные
Если Вы все сделали правильно, то Вы должны получить оптимальное решение, которое приведено на Рис. 4.
Рис. 4. Оптимальное решение
1. Проведите анализ оптимального решения данной задачи на чувствительность.
2. Переименуйте «Лист 2» в «Выводы» и разместите на нем результаты анализа:
- опишите, какие комплектующие являются дефицитными, недефицитными;
- нормированная стоимость для акустических систем отлична от нуля, объясните экономический смысл данного явления;
- укажите, насколько возможно увеличить (уменьшить) прибыль от продажи телевизоров, чтобы выпуск бытовой техники не изменился;
- измениться ли оптимальное решение, если прибыль от реализации стереосистем будет равна 70 руб, 35 руб (в случае положительного ответа, необходимо указать новое решение);
- укажите, при какой прибыли выгодно будет выпускать акустические системы;
- укажите, насколько можно уменьшить запасы шасси, кинескопов, блоков питания на складе, чтобы не было излишек;
- укажите, насколько необходимо увеличить запасы динамиков и электронных плат, чтобы увеличить выпуск бытовой техники и повысить общую прибыль;
- укажите, запасы какого ресурса выгоднее всего увеличить: динамиков или электронных плат и почему.
3. Сохраните файл с полученными отчетами с именем lab_2(с).

1) Оптимальное решение задачи ЛП, полученное для конкретной экономической ситуации, после ее изменения может оказаться непригодным или неоптимальным. Анализ чувствительности задачи ЛП, а именно того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение, позволяет увидеть перспективы и возможные варианты решения в изменившейся ситуации.
2) Создание отчетов:
- Сервис / Поиск решения;
- в окне «Результаты поиска решения» выделите с помощью мыши два типа отчетов: «Результаты» и «Устойчивость».
Теоретическая часть
Контрольные задания
Для анализа полученного оптимального решения в MS Excel предусмотрены три типа отчетов: отчет по результатам, устойчивости и пределам.
Проведем анализ чувствительности задачи (2.1). Для этого необходимо после запуска в Excel задачи на решениев окне Результаты поиска решения выделить с помощью мыши три типа отчетов: Результаты, Устойчивость и Пределы (рис. 3.1).
Рис. 3.1. Типы отчетов
Отчет по результатам.Отчет по результатам состоит из трех таблиц (рис. 3.2):
1) таблица 1 содержит информацию о целевой функции;
2) таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
3) таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для ограничений в столбце Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в столбце Значение приведены величины использованного ресурса.

Рис. 3.2. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе Статуссоответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан.».
Для граничных условий (строки 24-27 на рис. 3.2) в графе Разница показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения целевой функции.
Так, если на ресурс наложено ограничение типа
, то в графе Разница дается количество ресурса, на которое была превышена минимально необходимая норма.
Если на ресурс наложено ограничение типа
, то в графе Разница дается количество ресурса, которое не используется при реализации оптимального решения.
Отчет по устойчивости. Отчет по устойчивости состоит из двух таблиц (рис.3.3).
Таблица 1 содержит информацию, относящуюся к переменным:
результирующие значения переменных;
нормированная стоимость, т.е. дополнительные двойственные переменные, которые показывает, на сколько изменяется целевая функция при принудительном включении единицы этой переменной в оптимальное решение;
коэффициенты целевой функции;
допустимые значения приращения коэффициентов целевой функции, при которых сохраняется первоначальное оптимальное решение.

Рис. 3.3. Отчет по устойчивости
Таблица 2 (рис. 3.3) содержит информацию, относящуюся к ограничениям:
величина использованных ресурсовв колонке Результ. значение;
теневые цены, т.е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу. Теневая цена рассчитывается только для дефицитных ресурсов;
значения приращения ресурсов, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
Отчет по пределам. В отчете пределам (рис. 3.4) показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.

Рис. 3.4. Отчет по пределам
Двойственная задача линейного программирования
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче.
Лекция 4 Анализ чувствительности решения задачи линейного программирования
Похожие статьи:
- Карьерные решения: анализ и воображение
- Пример решения задачи, решаемой с использованием пакета ms excel.
- Градиентный метод решения задачи нелинейного планирования.
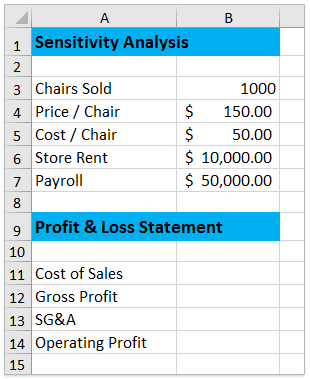
Допустим, у вас есть магазин стульев и вы продали стулья, как показано на скриншоте ниже. Теперь вы хотите проанализировать, как цена и объем продаж одновременно влияют на прибыль этого магазина, чтобы вы могли скорректировать свою стратегию продаж для получения большей прибыли. Собственно, анализ чувствительности может решить вашу проблему.
Проведите анализ чувствительности с помощью таблицы данных в Excel
Проведите анализ чувствительности с помощью таблицы данных в Excel
Этот метод будет применять функцию таблицы данных для анализа чувствительности в Excel. Пожалуйста, сделайте следующее:
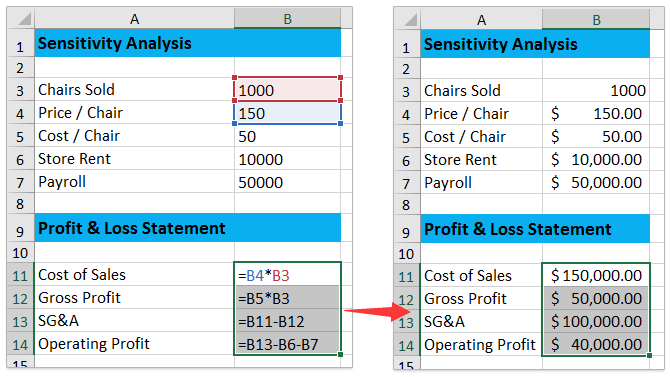
1. Завершите таблицу отчета о прибылях и убытках, как показано на скриншоте ниже:
(1) В ячейке B11 введите формулу = B4 * B3;
(2) В ячейке B12 введите формулу = B5 * B3;
(3) В ячейке B13 введите формулу = B11-B12;
(4) В ячейке B14 введите формулу = B13-B6-B7.
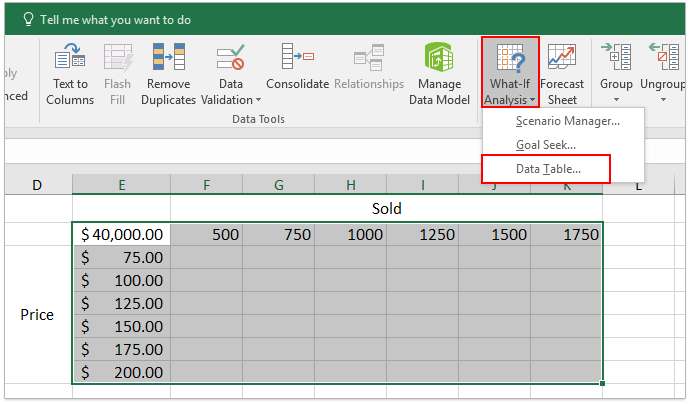
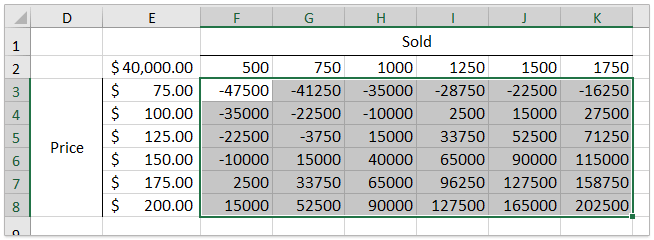
2. Подготовьте таблицу анализа чувствительности, как показано на скриншоте ниже:
(1) В диапазоне F2: K2 введите объемы продаж от 500 до 1750;
(2) В диапазоне E3: E8 введите цены от 75 до 200;
(3) В ячейке E2 введите формулу = B14
3. Выберите Range E2: K8 и нажмите Данные > Что-Анализ > Таблица данных. Смотрите скриншот:
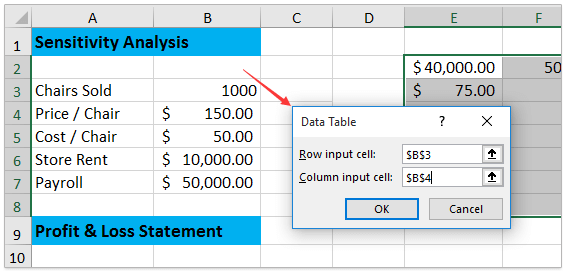
4. В появившемся диалоговом окне Таблица данных, пожалуйста (1) в Ячейка ввода строки в поле укажите ячейку с объемом продаж стульев (в моем случае B3), (2) в Ячейка ввода столбца укажите ячейку с ценой стула (в моем случае B4), а затем (3) нажмите OK кнопка. Смотрите скриншот:
5. Теперь таблица анализа чувствительности создана, как показано на скриншоте ниже.
Вы можете легко узнать, как изменяется прибыль при изменении объема продаж и цен. Например, если вы продали 750 стульев по цене 125.00 долларов, прибыль изменится до -3750.00 долларов; тогда как когда вы продали 1500 стульев по цене 100.00 долларов, прибыль изменилась до 15000.00 долларов.
Статьи по теме:
Лучшие инструменты для работы в офисе
Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%
- Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
- Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
- Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
- Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
- Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
- Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
- Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
- Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
- Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.
Вкладка Office: интерфейс с вкладками в Office и упрощение работы
- Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
- Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
- Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!
Комментарии (4)
Оценок пока нет. Оцените первым!






 (столбцы «Допустимое Увеличение» и «Допустимое Уменьшение»), при которых сохраняется первоначальное оптимальное решение.
(столбцы «Допустимое Увеличение» и «Допустимое Уменьшение»), при которых сохраняется первоначальное оптимальное решение.  содержатся в столбцах «Допустимое Уменьшение» и «Допустимое Увеличение».
содержатся в столбцах «Допустимое Уменьшение» и «Допустимое Увеличение».