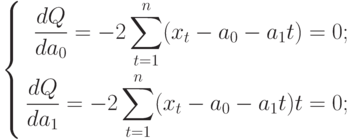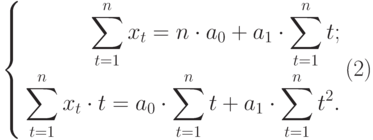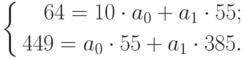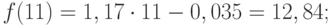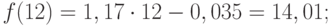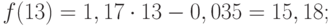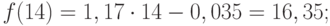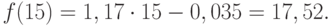Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.
Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.
Временные ряды в Excel
Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.
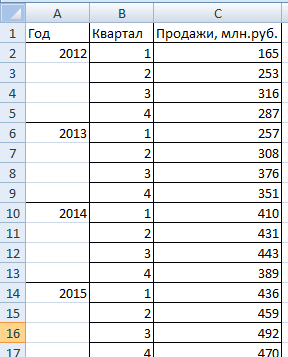
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.
Внесем данные о реализации в таблицу Excel:
На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».
Подключение настройки «Анализ данных» детально описано здесь.
Нужная кнопка появится на ленте.
Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.
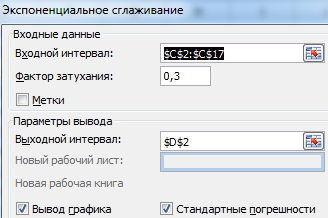
Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».
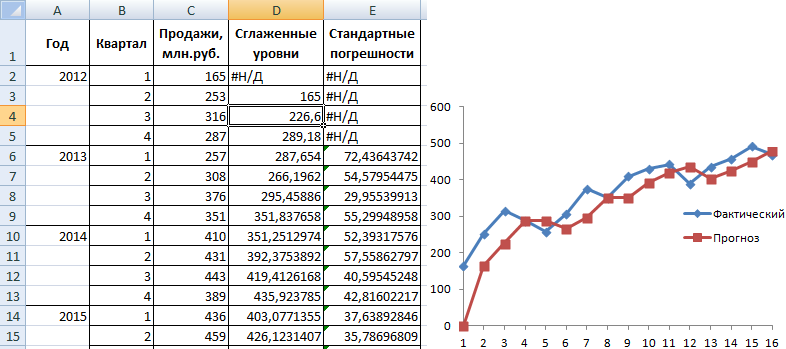
Закрываем диалоговое окно нажатием ОК. Результаты анализа:
Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).
Прогнозирование временного ряда в Excel
Составим прогноз продаж, используя данные из предыдущего примера.
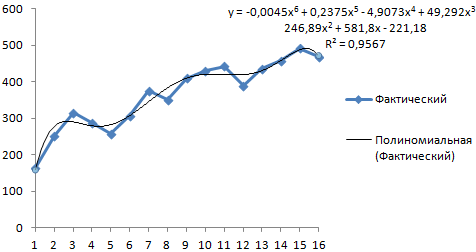
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).
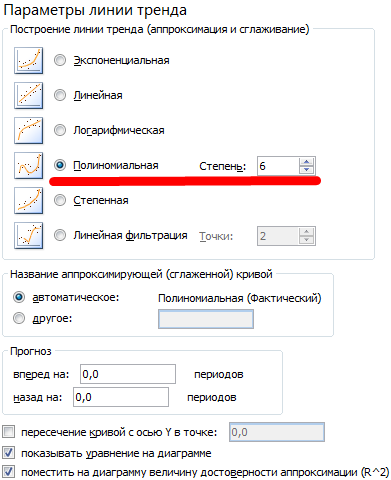
Настраиваем параметры линии тренда:
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.
R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.
Уравнение тренда – это модель формулы для расчета прогнозных значений.
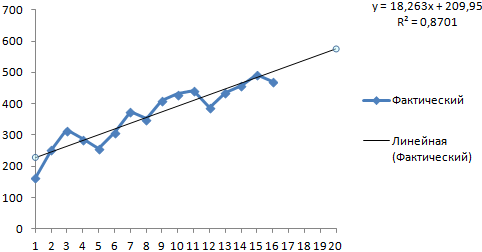
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.
Получаем достаточно оптимистичный результат:
В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.
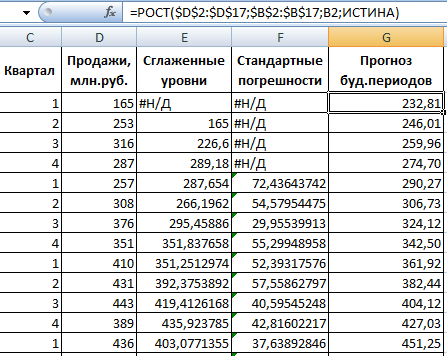
Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.
Для линейной зависимости – ТЕНДЕНЦИЯ.
При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.
Статистический
анализ динамических рядов в MS Excel
Показатели динамики
При изучении изменений
какого-либо явления во времени составляется
динамический ряд. Динамическим рядом
называется совокупность однородных
статистических величин, показывающих
изменение какого-либо явления на
протяжении определенного промежутка
времени.
Величины, составляющие
динамический ряд, называются уровнями
ряда. Уровни динамического ряда могут
быть представлены:
-
абсолютными
величинами; -
относительными
величинами (в том числе показателями
интенсивными, экстенсивными, соотношения); -
средними
величинами.
Динамические ряды
бывают двух видов:
-
Моментный
динамический ряд состоит из величин,
характеризующих явление на какой-то
определенный момент (дату). Например,
каждый уровень может характеризовать
численность населения, численность
врачей и т.д. на конец какого-то года. -
Интервальный
динамический ряд состоит из величин,
характеризующих явление за определенный
промежуток времени (интервал). Например,
каждый уровень такого ряда может
характеризовать смертность, рождаемость,
заболеваемость, среднегодовую занятость
койки за какой-то год.
Рассмотрим пример
интервального динамического ряда.
Проанализируем демографическую
обстановку в Приморском крае.
Основными параметрами,
по которым определяется демографическая
обстановка в стране, являются рождаемость
и смертность. Исходя из того, какой будет
демография России, руководство страны
сможет сформировать социально-экономическую
политику, которой в дальнейшем государство
будет придерживаться. Демографические
успехи и провалы напрямую влияют на то,
как российское общество будет развиваться
и какой путь выберет для этого. Качество
жизни россиян, экономическая обстановка
в стране, ее обороноспособность,
социальная и политическая устойчивость
в мире – все это зависит от того, как в
государстве происходит развитие и
формирование трудовых ресурсов.
Соответственно, ресурсы эти должны быть
откуда-то взяты, именно поэтому важность
грамотного формирования демографической
политики возрастает в разы.
Заходим на сайт
«Территориальный орган Федеральной
службы государственной статистики по
Приморскому краю» по ссылке
http://primstat.gks.ru/.
Далее открываем
раздел официальной статистики «Население»
и переходим на закладку «Число
родившихся».
В открывшемся окне
формируем таблицу за все последние
года. Данные копируем на рабочий лист
Microsoft
Excel.
С помощью MS Excel необходимо провести
анализ полученного ряда динамики.
Для облегчения анализа
статистического материала, полученные
показатели изображают графически. Под
графиками понимают условные изображения
числовых величин и их соотношений при
помощи различных линий, поверхностей
и т.п.
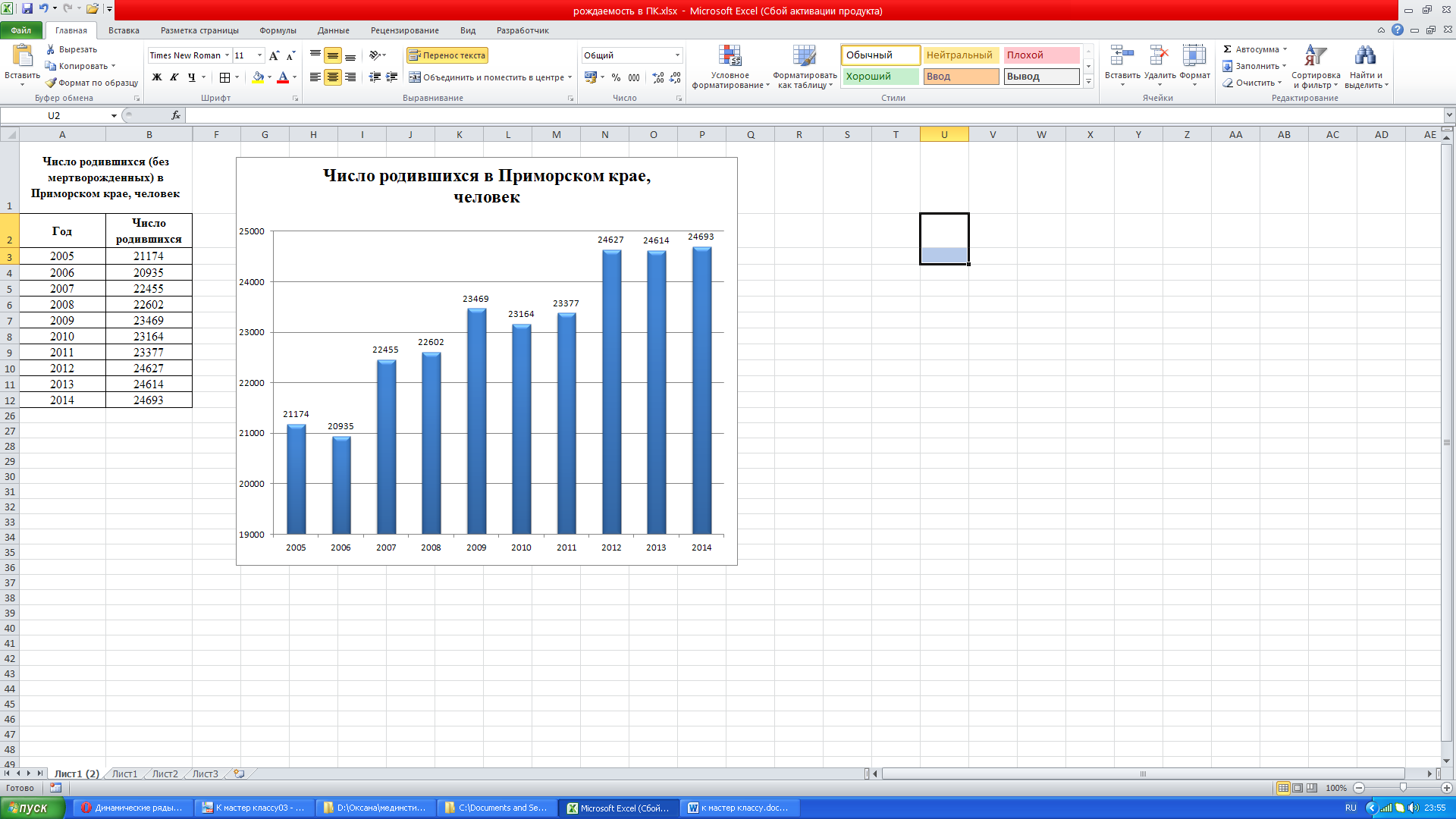
Данный ряд динамики
можно изобразить графически. Наиболее
распространенным видом графического
изображения является гистограмма. В MS
Excel заходим на вкладку Вставка
диаграмма
гистограмма.
Методы медицинской
статистики позволяют измерять размеры
изменений, которые состоялись на
протяжении определенного периода
времени, и количественно охарактеризовать
направленность их развития. С данной
целью используют следующие показатели:
абсолютный прирост, темп роста, темп
прироста.
• Абсолютный
прирост (убыль)
– разность между последующим и предыдущим
уровнем. Измеряется в тех же единицах,
в которых представлены уровни ряда.
• Показатель
роста (убыли)
– отношение каждого последующего уровня
к предыдущему, принятому за 100%. Он
показывает сколько % от предыдущего
уровня составляет последующий уровень.
• Темп
прироста (убыли)
– отношение абсолютного прироста
(убыли) каждого последующего уровня к
предыдущему уровню, принятому за 100%. Он
показывает, на сколько % увеличился
(снизился) последующий уровень по
сравнению с предыдущим и поэтому может
быть рассчитан по формуле:
темп прироста = темп
роста – 100%.
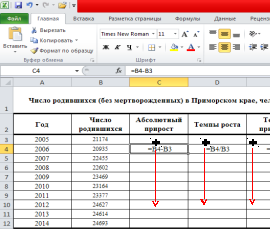
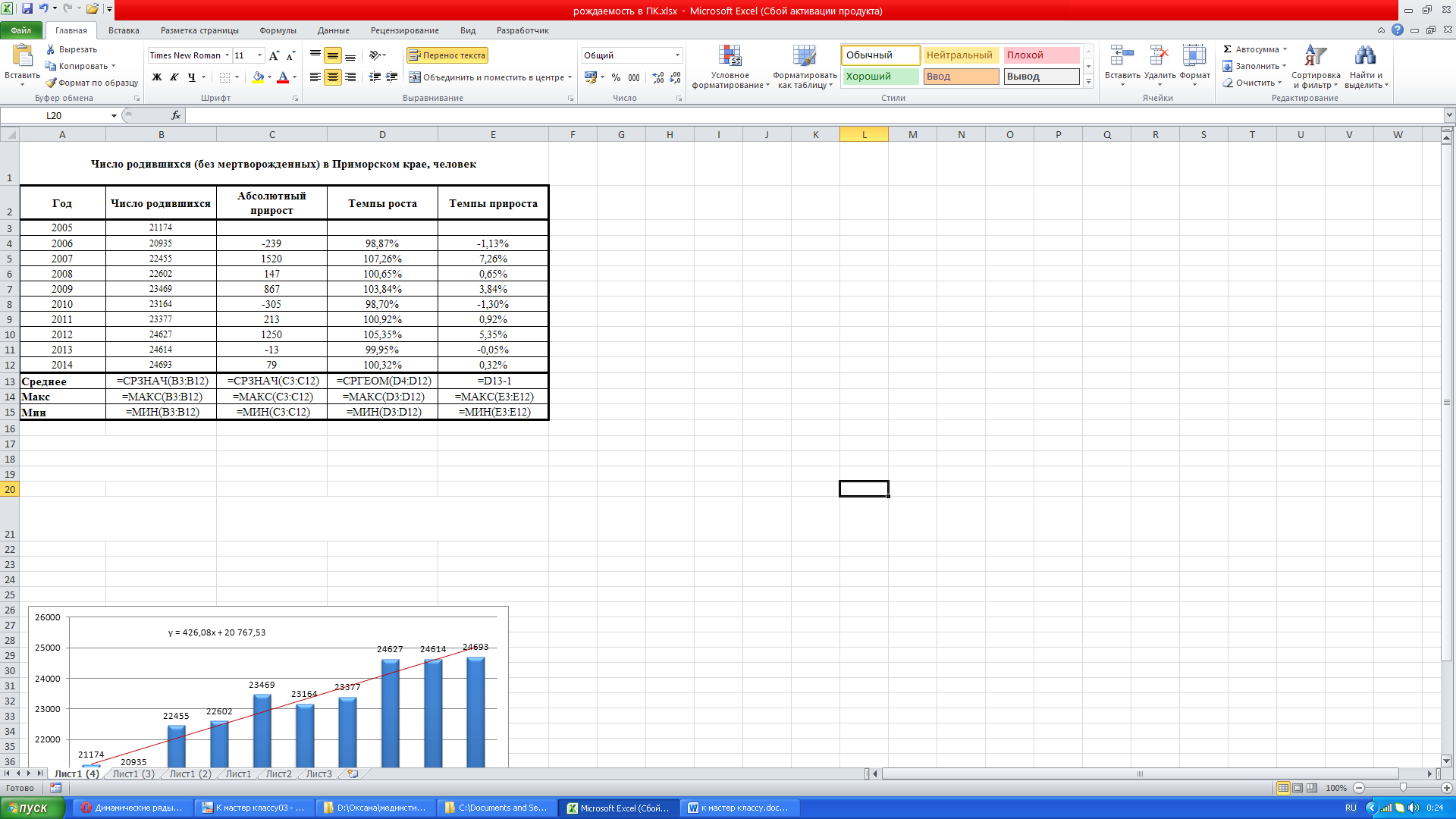
Рассчитаем
данные показатели. Формулы представлены
на рисунке ниже. Темпы роста и прироста
являются относительными показателями,
поэтому ячейки в столбце D
и E
переводим в процентный формат.
Для характеристики
динамики изучаемого явления за
продолжительный период рассчитывают
группу средних показателей динамики.
Можно выделить две категории показателей
в этой группе:
-
средние
уровни ряда; -
средние
показатели изменения уровней ряда.
Для нахождения
среднего уровня ряда воспользуемся
формулой в MS Excel =СРЗНАЧ. Этой же формулой
можно рассчитать и средний абсолютный
прирост (средний показатель изменения
уровня ряда). Эти два показателя
рассчитываются по формуле простой
средней арифметической.
Для того, чтобы
рассчитать средний темп роста, применяется
формула средней геометрической =СРГЕОМ.
Средний темп прироста
вычисляется вычитанием из среднего
темпа роста 100% или 1 (1 и 100% для MS Excel
равнозначные значения, разница только
в формате представления).
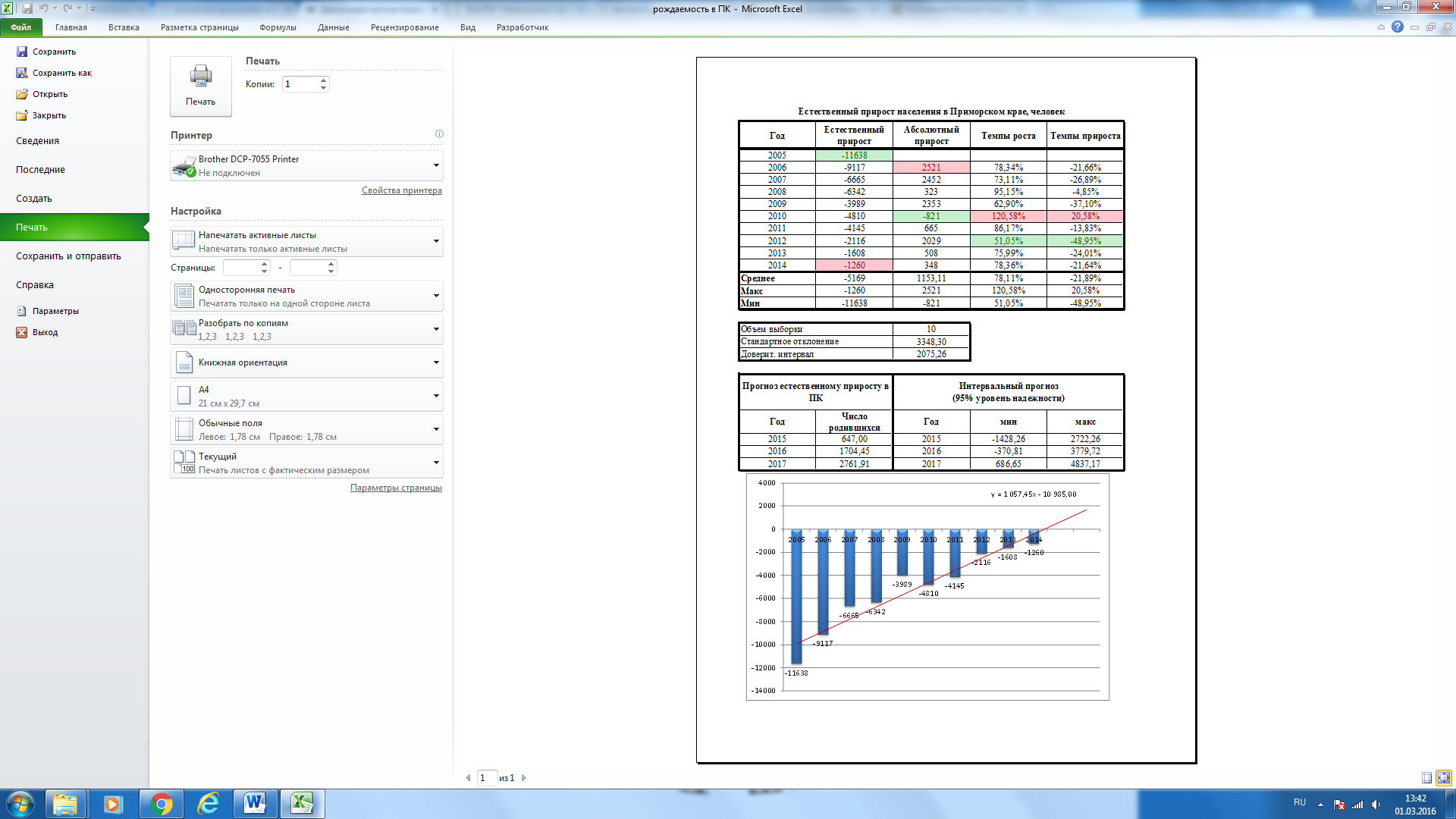
Помимо средних
показателей определим года с максимальными
и минимальными показателями рождаемости
в Приморском крае.
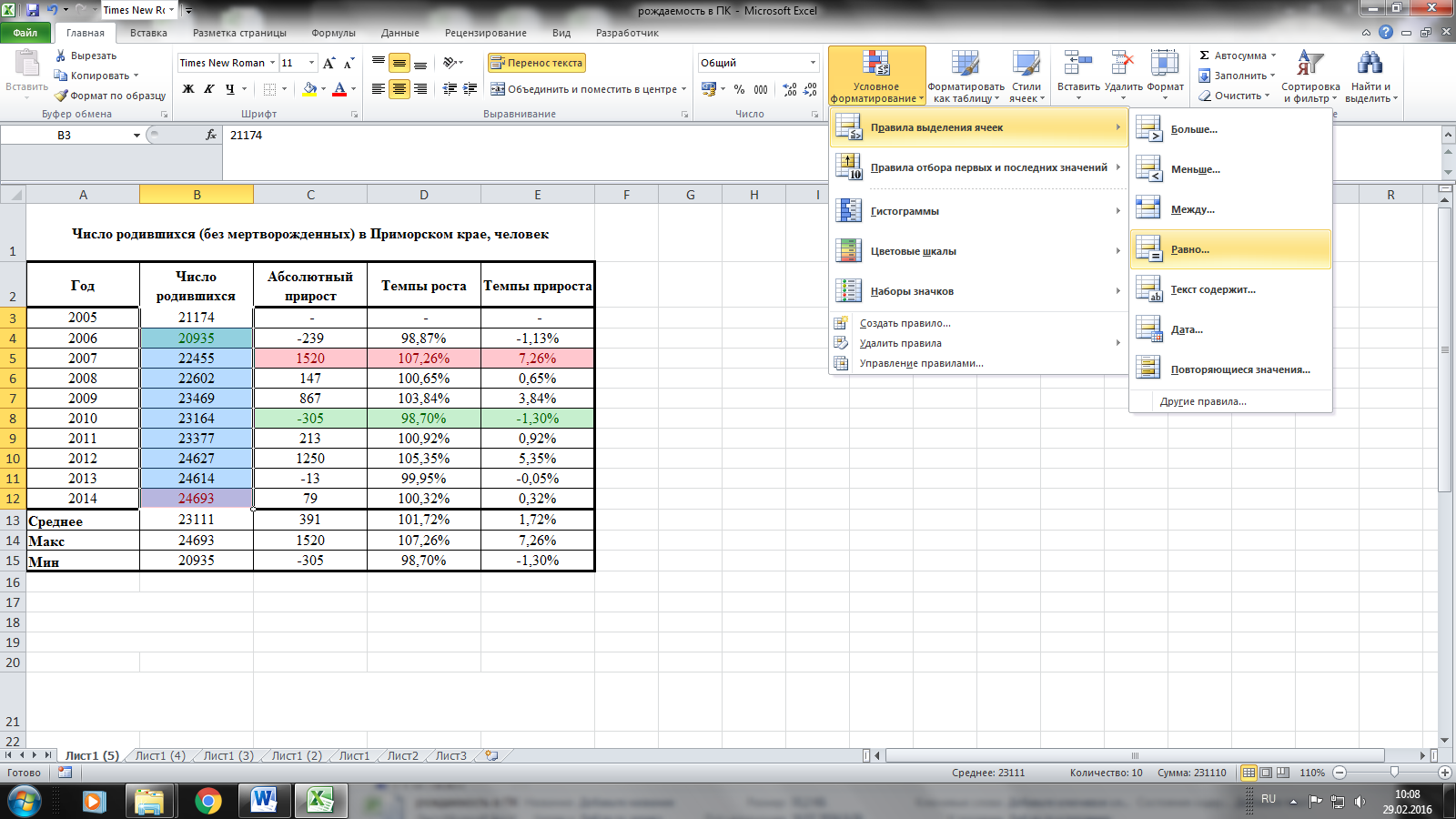
С помощью условного
форматирования можно выделить года,
когда наблюдались максимальные и
минимальные показатели в динамике
рождаемости. В 2014 году достигнут самый
высокий показатель рождаемости за
последние 10 лет, а минимальное число
родившихся за этот период зафиксировано
в 2006 году. Максимальные приросты
наблюдались в 2007 году. В 2010 году наблюдался
отрицательный рост или убыль, это
свидетельствует о том, что в этом году
родилось меньше детей чем в предыдущем.
Показатель «среднее»
в столбце «Число родившихся» означает,
что в Приморском крае ежегодно рождается
в среднем 23111 детей. Средний абсолютный
прирост свидетельствует о том, что
ежегодно в нашем регионе появляется на
свет на 391 малышей больше чем в предыдущем
году. В процентном соотношении ежегодный
прирост рождаемости составляет в среднем
1,72%. Демографические показатели в
Приморском крае демонстрируют повышение
рождаемости, но остается открытым вопрос
– за счет чего произошли эти положительные
изменения. Имеют ли они этнические и
конфессиональные корни или обусловлено
материальными факторами (экономическим
благополучием региона)?
Выявление тенденции
(тренда) в рядах динамики.
Тренд — это закономерность
описывающая подъем или падение показателя
в динамике. Если изобразить любой
динамический ряд на графике, часто
выделяется определенный угол – кривая
либо постепенно идет на увеличение или
на уменьшение, в таких случаях принято
говорить, что ряд динамики имеет тенденцию
(к росту или падению соответственно).
Если же построить
модель, описывающую это явление, то
получается довольно простой и очень
удобный инструмент для прогнозирования,
не требующий каких-либо сложных вычислений
или временных затрат на проверку
значимости или адекватности влияющих
факторов.
Итак, что же собой
представляет тренд как модель? Это
совокупность расчетных коэффициентов
уравнения, которые выражают регрессионную
зависимость показателя (Y) от изменения
времени (t). То есть, это точно такая же
регрессия, только влияющим фактором
здесь выступает именно показатель
времени.
Для графического
анализа данных на диаграмме можно
воспользоваться построением линии
тренда. Такая линия тренда позволяет
построить сглаженную кривую, графическое
представление которой более ясно
показывает существующую закономерность
в развитии данных.
В этом примере
продолжим использовать один и тот же
динамический ряд – уровень рождаемости
в Приморском крае в периоде с 2005-го по
2014-й гг.
На построенной ранее
гистограмме выделяем столбцы правой
кнопкой мыши и из появившегося контекстного
меню выбираем пункт «Добавить линию
тренда».
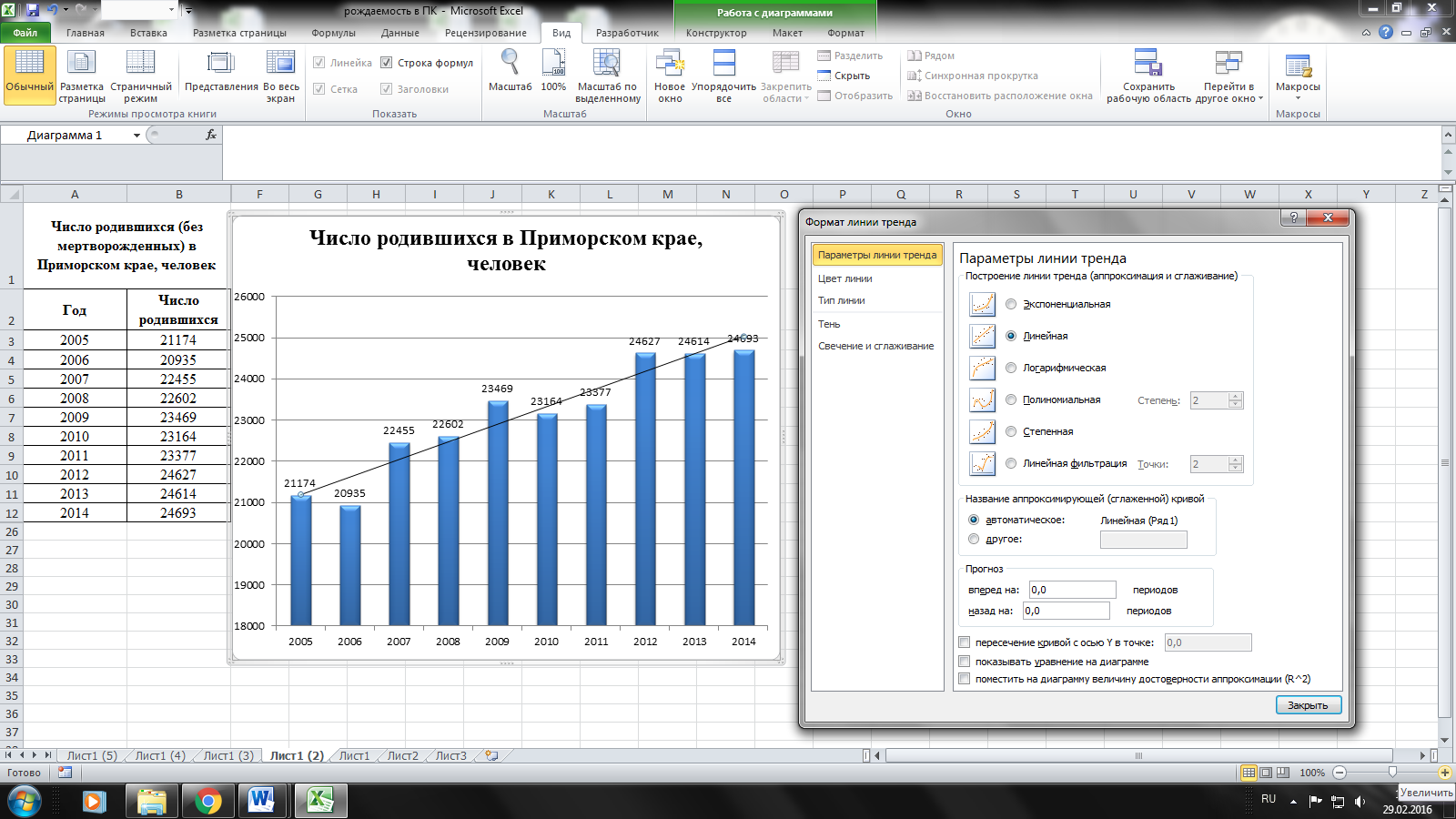
Откроется окошко для
настройки параметров построения линии
тренда, где среди типов моделей выбираем
«Линейная», ставим галочку напротив
пункта «Показывать уравнение на
диаграмме», этого будет достаточно,
чтобы на графике отобразилась уже
построенная линия тренда, а также
математический вариант отображения
модели в виде готового уравнения. Если
интересует отображение на графике
прогноза, чтобы визуально оценить отрыв
исследуемого показателя, указываем в
поле «Прогноз» вперед на количество
интересующих периодов. Отображаемое
уравнение линейного тренда это и есть
непосредственно сама модель, которую
можно использовать, в качестве формулы,
чтобы получить расчетные значения по
модели и соответственно точные значения
прогноза (прогноз, отображаемый на
графике, оценить можно лишь приблизительно).
Уравнение линейного
тренда более точно можно определить с
помощью формулы =ЛИНЕЙН или с помощью
надстройки «Анализ данных»
«Регрессия».
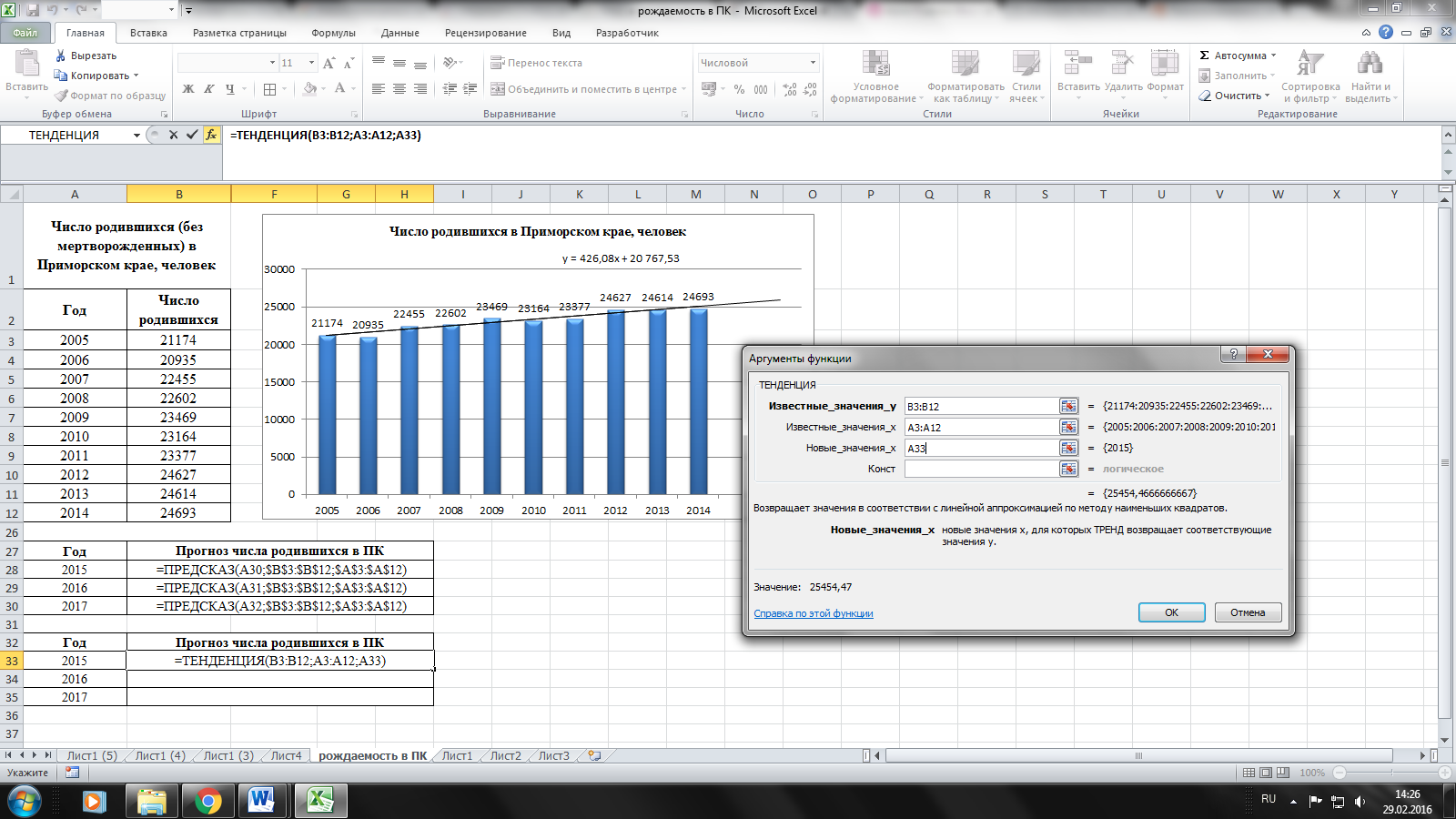
Чтобы получить
прогноз, можно воспользоваться функциями
=ПРЕДСКАЗ или =ТЕНДЕНЦИЯ. Эти функции
как раз и выдают уже готовое рассчитанное
прогнозное значение по линейному тренду
на основе известных исходных данных.
Полученные результаты в формулах должны
совпадать, т.к. используется одна и та
же линейная модель и суть данных функций
целиком и полностью идентичны, разница
лишь в порядке прописывания исходных
данных в формуле.
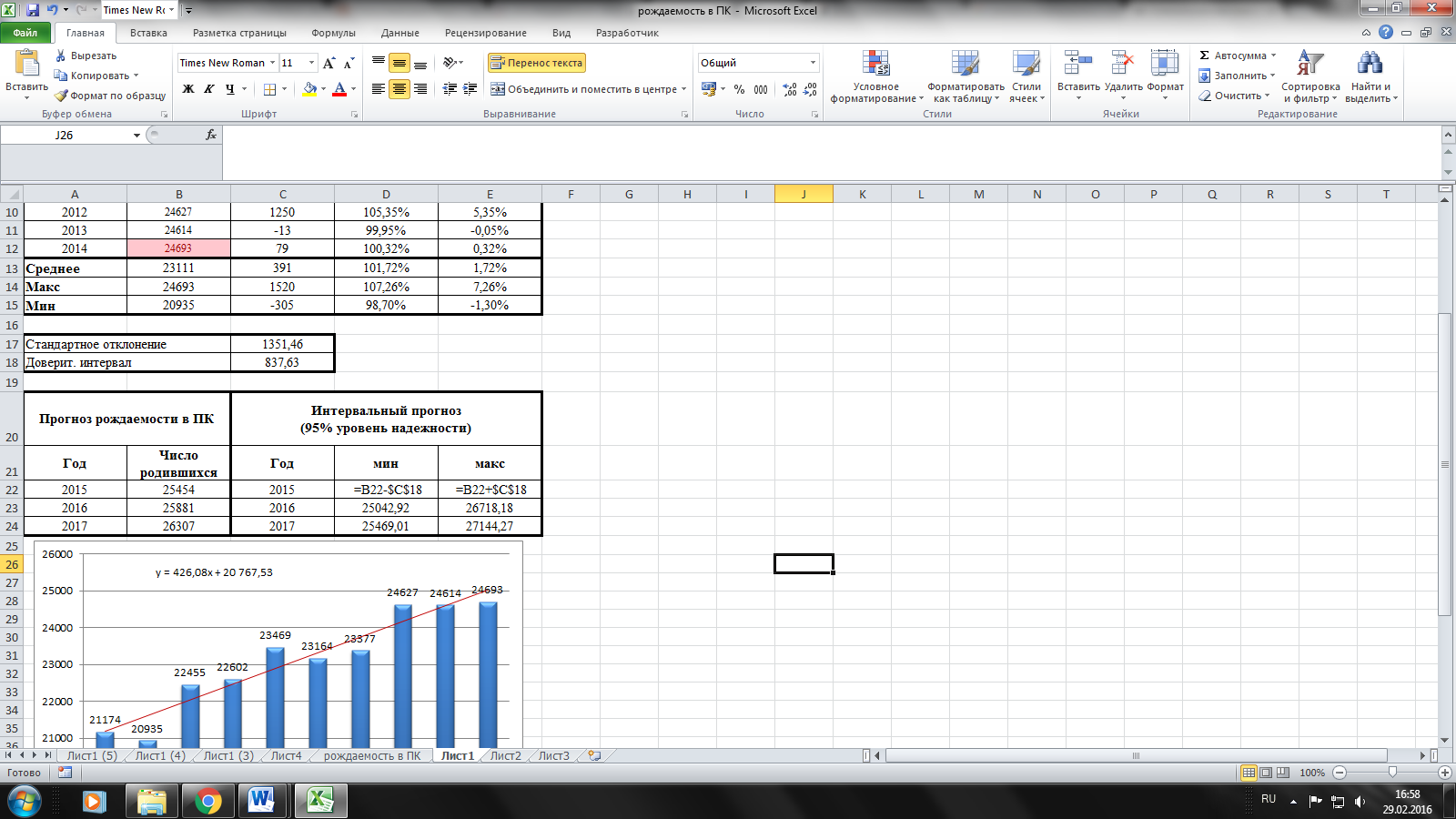
По нашим прогнозным
оценкам ожидается положительная динамика
и предвидится рост
показателей рождаемости в Приморском
крае. В 2015 году – 25 454, в 2016 – 25 881 и в 2017
– 26 307 детей.
Прогноз, полученный
подстановкой в уравнение регрессии (в
нашем случае линейный тренд) ожидаемого
значения фактора, называют точечным
прогнозом. Вероятность точной реализации
такого прогноза крайне мала. Необходимо
сопроводить его значением средней
ошибкой прогноза или доверительным
интервалом прогноза с достаточно большой
вероятностью. Интервальный
прогноз заключается в построении
доверительного интервала прогноза,
т.е. верхней и нижней границы интервала,
содержащего точную величину для
прогнозного значения. Доверительный
интервал всегда определяется с заданной
вероятностью, соответствующей принятому
значению уровня значимости α (типичные
значения «альфа-уровня» – 0,05, 0,01 и
0,001).
Предварительно
вычисляется стандартная ошибка прогноза
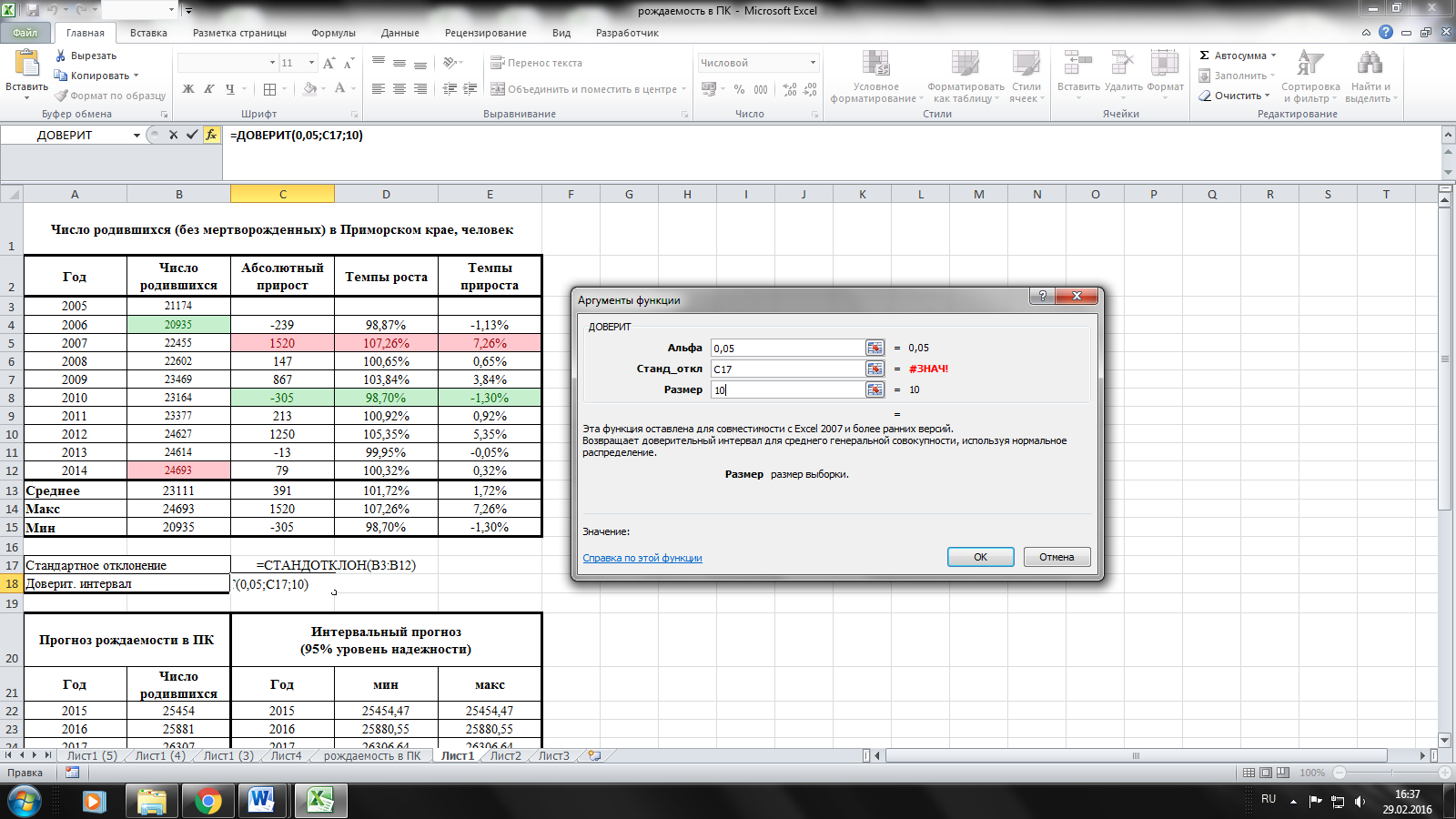
по формуле =СТАНДОТКЛОН.
Затем вычисляем
доверительный интервал по формуле
=ДОВЕРИТ. Уровень значимости примем
стандартное значение 0,05. В поле «размер»
ставим значение 10, т.к. имеем данные за
10 лет. Если данных по годам будет больше
или меньше, соответственно ставим в
«размер» число, равное количеству лет.
Можно использовать формулу =СЧЕТ для
подсчета данных в динамическом ряду.
Далее строим нижнюю
и верхнюю границы прогнозного интервала,
вычитая и прибавляя соответственно к
точечному прогнозу полученное значение
функции ДОВЕРИТ.
Несмотря на рост
показателей, уровень рождаемости в
течение многих лет не обеспечивает
простого воспроизводства населения в
Приморском крае. Поэтому необходимы
дальнейшие и эффективные меры
социально-экономического и собственно
демографического характера для приведения
уровня воспроизводства населения в
соответствие с общественной необходимостью.
Изменение репродуктивных установок
населения, повышение потребности в
детях – задача-максимум, глобальная
цель политики в области рождаемости,
для достижения которой необходимо
длительное время. Ближайшая задача
состоит в расширенном воспроизводстве
здоровых поколений, улучшении условий
реализации репродуктивных установок.
Автоматизация
расчетов
В
предыдущей работе исследование
динамического ряда по рождаемости в
Приморском крае было полностью
автоматизировано. Поэтому целесообразно
использовать данный лист MS
Excel
как шаблон. Создадим копию данного листа
в этой же книге Excel
и присвоим ему новое имя «Смертность».
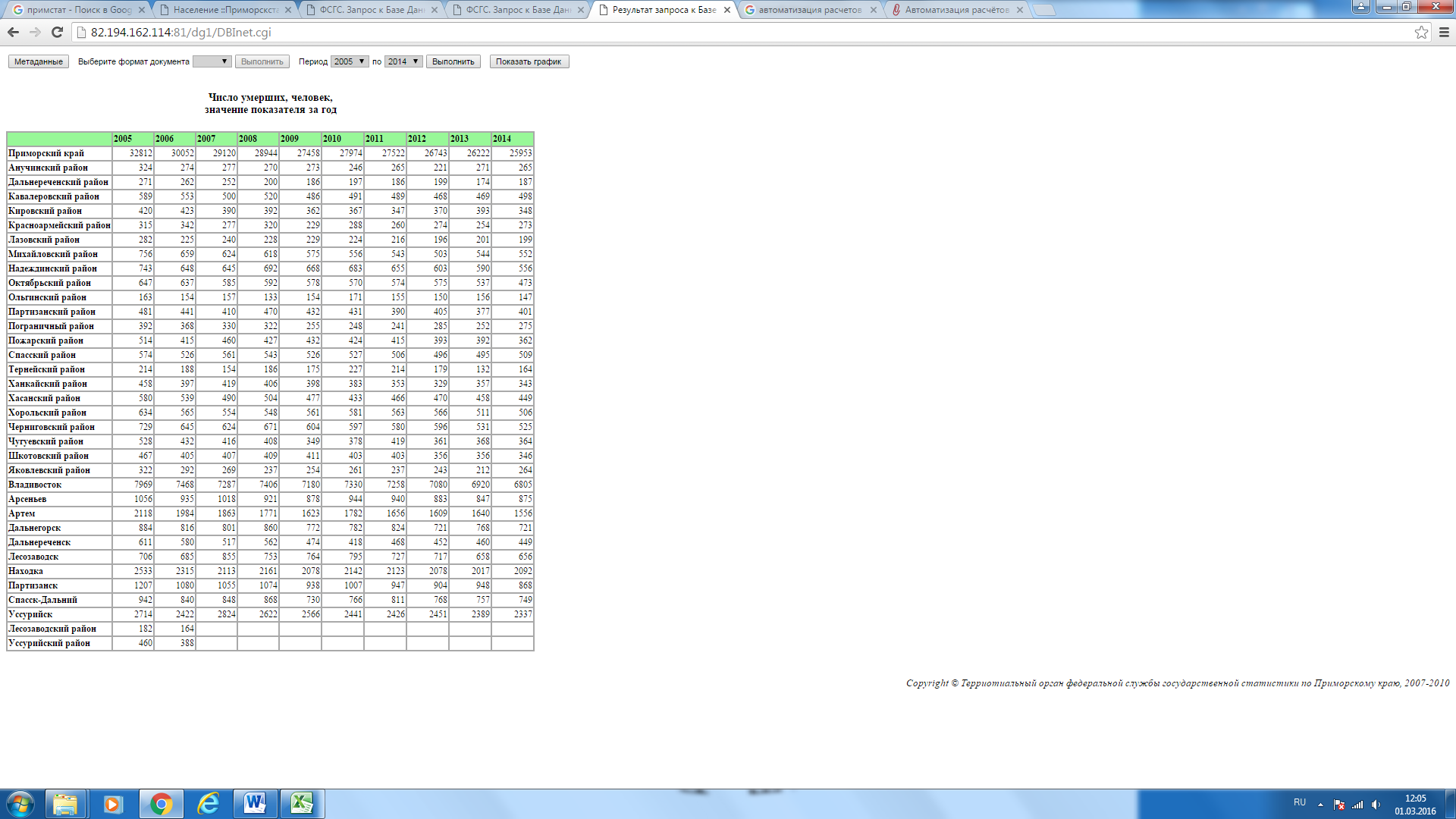
Заходим на сайт
«Территориальный орган Федеральной
службы государственной статистики по
Приморскому краю». Из раздела официальной
статистики «Население» переходим на
закладку «Число умерших».
Копируем верхнюю строку данных по
Приморскому краю и вставляем в столбец
данных по рождаемости, переименовывая
столбец в «Число умерших» и ячейку
«Прогноз рождаемости в ПК» в ячейку
«Прогноз смертности в ПК». С помощью
созданного шаблона MS
Excel автоматически выполнил
все рассчеты для анализа данного
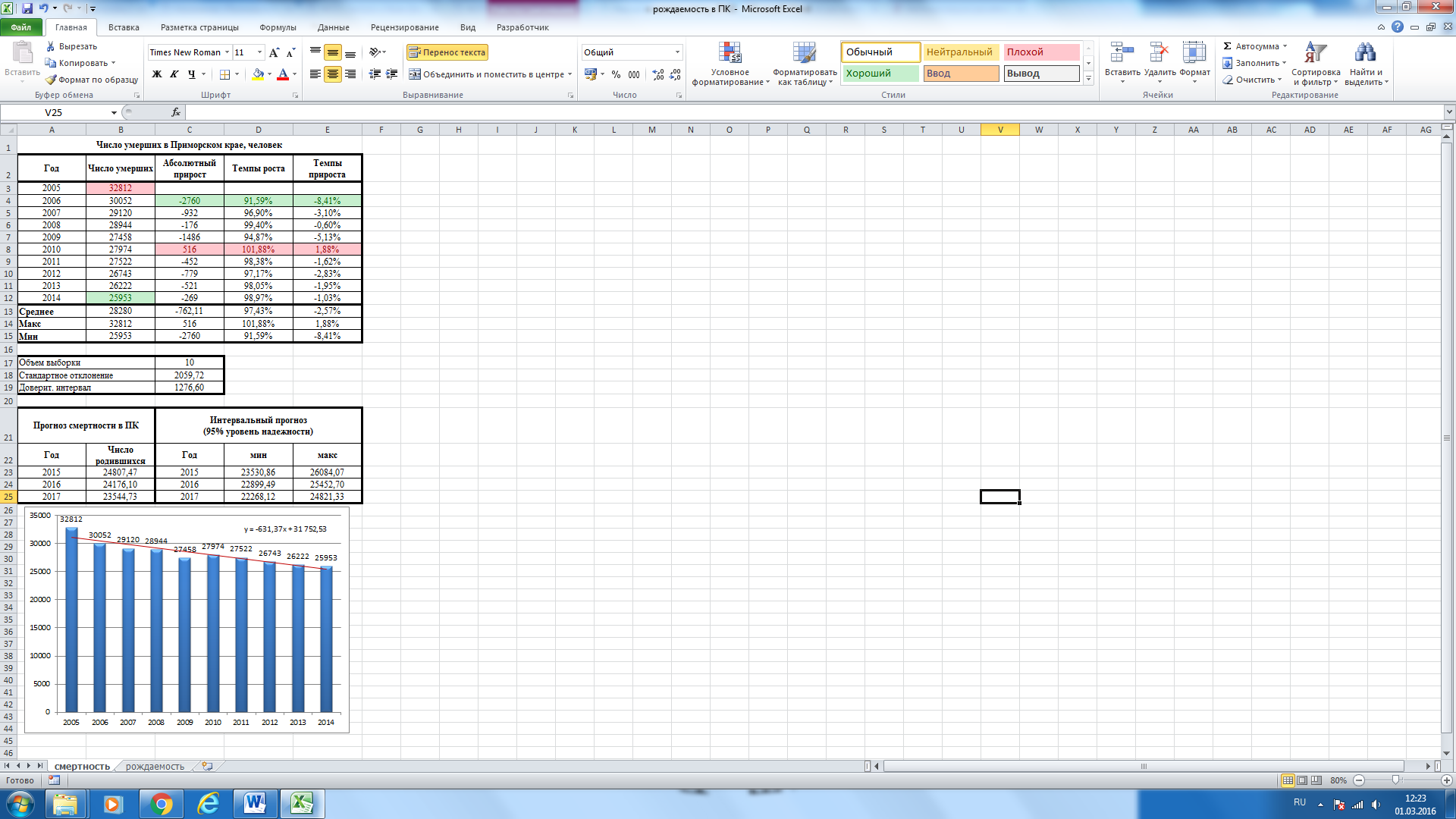
динамического ряда. Можно отметить, что
тенденция смертности в ПК в отличие от
рождаемости за последние 10 лет идет на
убыль. (Полученные показатели
проанализировать самостоятельно).
Одним из главных
демографических показателей является
естественный прирост населения. Это
разница между количеством родившихся
и количеством умерших за определенный
период времени. Проанализируем эти
показатели в Приморском крае за последние
10 лет.
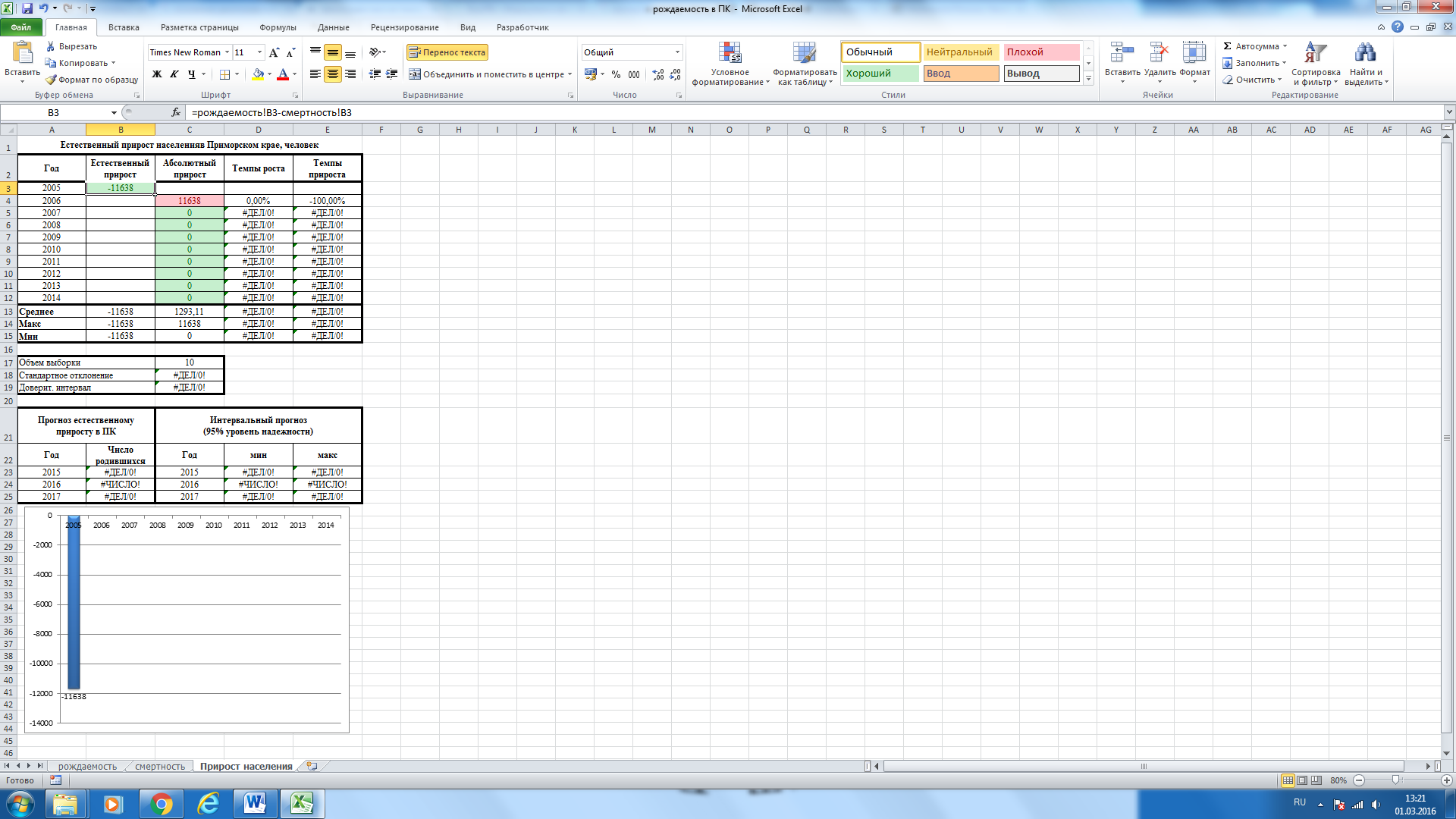
Создадим еще одну
копию шаблонного листа в MS
Excel
и присвоим имя «Прирост населения».
Переименуем столбец B
(ячейка B2)
в «Естественный прирост», а ячейку A21
в «Прогноз по естественному приросту».
Ячейку B3
заменим формулой разности ячеек B3
из листа «рождаемость» и «смертность».
Не смотря на положительную динамику по
рождаемости и смертности в Приморском
крае до 2015 года наблюдалась естественная
убыль населения. За последние 10 лет в
среднем на 5 169 человек уменьшается
количество населения в Приморье. Самым
убыточным оказался первый год нашего
исследования – 2005 г., а самым оптимистичным
– последний 2014 год . По сложившейся
тенденции происходит сокращение
естественной убыли российского населения
и показатели 2015 с последующими годами
должны быть хотя бы неотрицательними.
13
Сравнение показателей в таблице за определенный период – одна из популярных задач, которая стоит перед пользователями Microsoft Excel. Чаще всего это осуществляется путем вывода вспомогательного столбца, где значения указаны в процентах, и сразу становится понятно, насколько сильной была позитивная или негативная динамика.
В этой статье я на простом примере предлагаю разобраться с соответствующим оформлением таблицы.
Предварительные действия
Сначала понадобится подготовить таблицу, чтобы кроме ввода функций далее от вас ничего не требовалось. Выберите два общих значения, которые будете сравнивать. Если это должна быть, например, месячная выручка, сначала сделайте сводную таблицу по дням и ссылайтесь на нее при создании общей суммы. Выведите два значения, динамику между которыми нужно сравнивать, чтобы перейти далее. На изображении ниже показан самый простой пример подходящей таблицы.
Создайте вспомогательный столбец для вывода процентов. Введите для него совершенно любое удобное для вас название и задайте визуальное оформление в соответствии со стилем основной таблицы.
Сейчас стоит учитывать, что тип ячейки, в которой будут отображаться проценты, является общим. При расчетах в таком случае появится очень большое значение в виде обычного числа. Поэтому понадобится изменить формат ячеек, чтобы проценты выводились корректно.
-
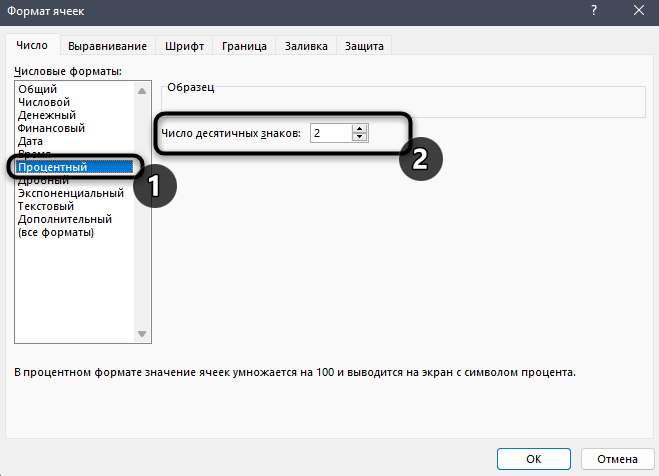
Для этого выделите необходимые ячейки и щелкните по любой из них правой кнопкой мыши. Из контекстного меню выберите пункт «Формат ячеек».
-
Отобразится отдельное окно, в котором будет выбрана вкладка «Число». На ней выберите «Процентный» и определите количество знаков после запятой или оставьте его по умолчанию. После этого сохраните новый формат ячейки.
На этом подготовительные действия завершены, поэтому можно приступить к заполнению формул и вычислении положительной или негативной динамики.
Комьюнити теперь в Телеграм
Подпишитесь и будьте в курсе последних IT-новостей
Подписаться
Создание формулы отслеживания динамики роста
В следующей инструкции я постараюсь наглядно описать каждое действие при написании функции, чтобы вы понимали, какие значения берутся, как они сравниваются и что получается в итоге. Если вы сделали таблицу такого же формата, как и в примере, достаточно будет выполнить точно такие же действия, чтобы отследить динамику роста в процентах.
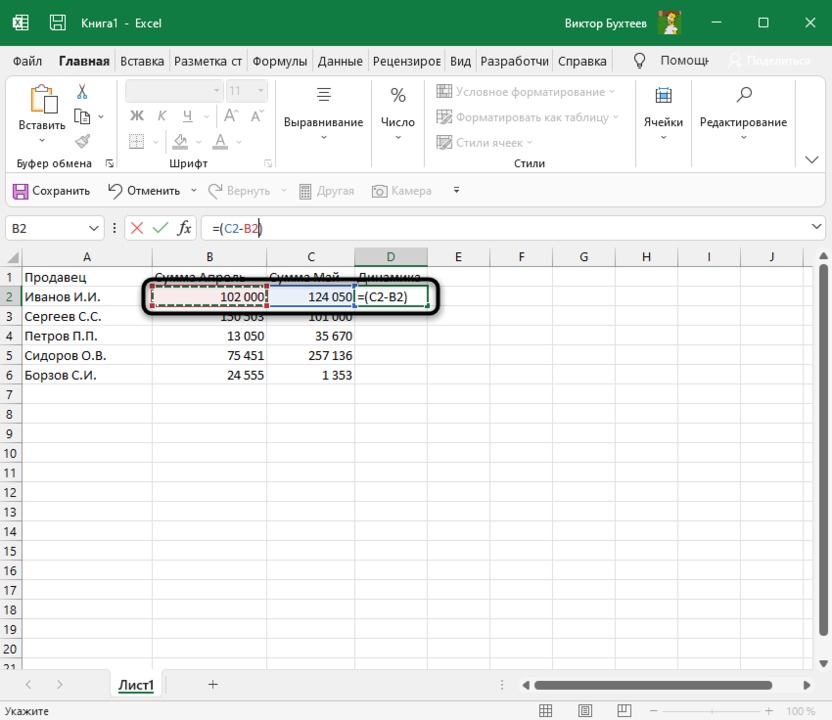
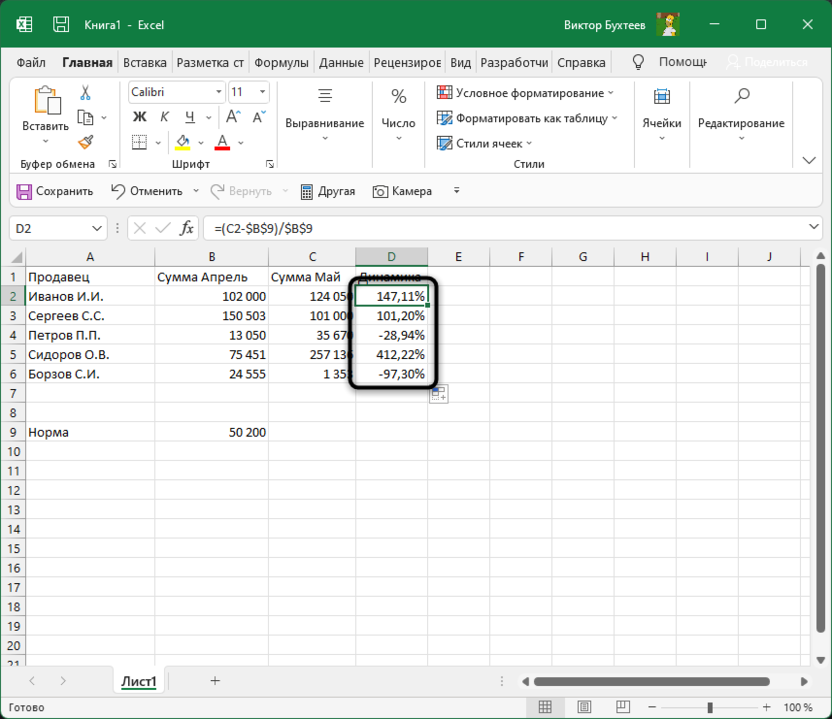
-
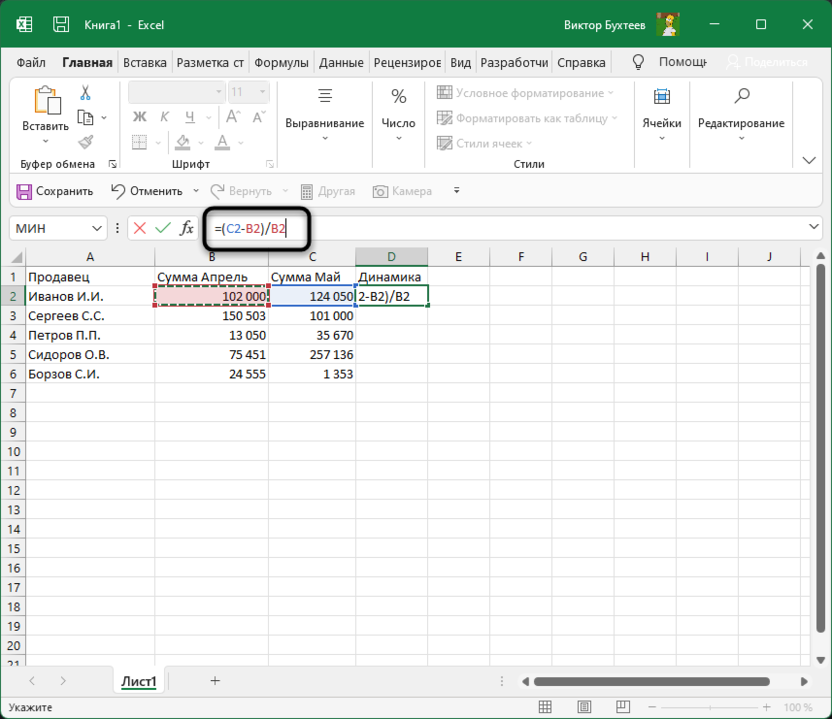
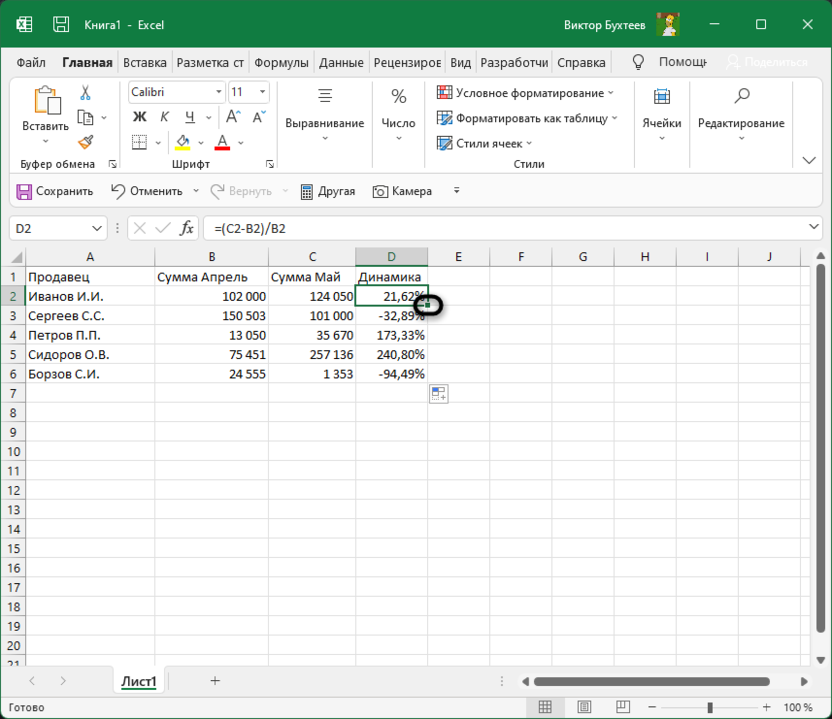
Выделите ячейку, где должны выводиться проценты и напишите первую часть формулы =(C2 — B2). Это поможет определить разницу между суммами за два разных месяца. Соответственно, если номера ячеек в вашей таблице другие, замените их, отняв сумму второго значения от первого.
-
После скобок добавьте /B2, чтобы разделить это все на сумму первого значения, то есть на 100%, если говорить о стандартных математических операциях с процентами.
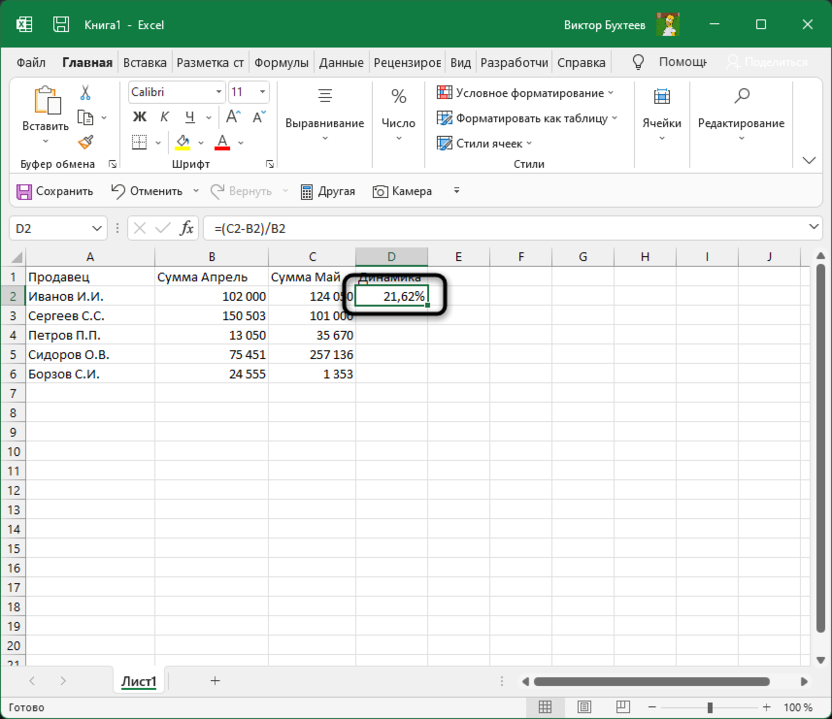
-
Нажмите Enter и посмотрите на результат. В моем случае сумма за первый месяц была 102 000, за второй — 124 000, а разница – 22 000. Получается, динамика роста является положительной и равняется 21,62%. У вас значение будет другим, в соответствии с суммами в таблице.
-
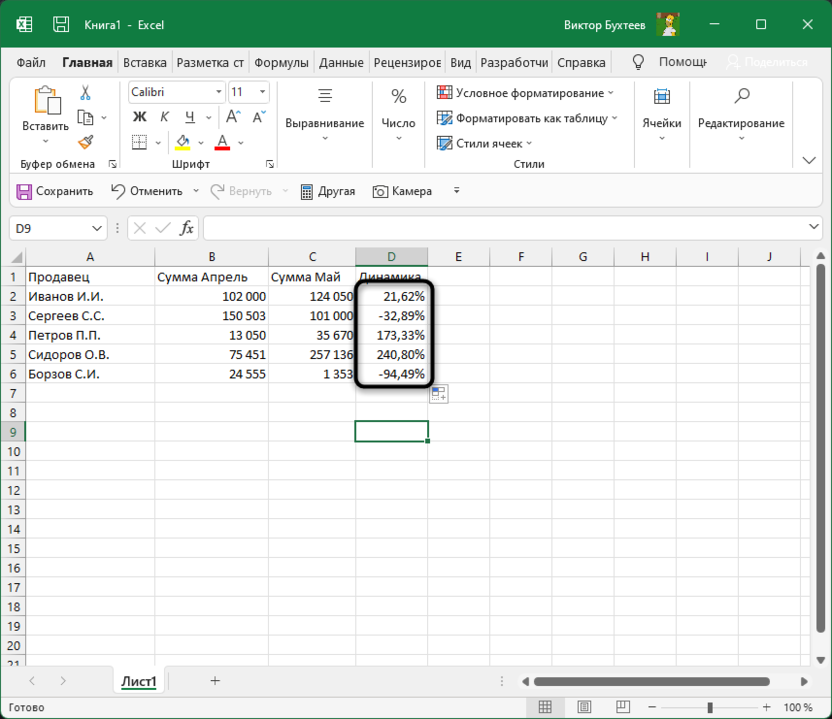
Если далее в таблице должно происходить такое же сравнение значений и вывод процентов, просто зажмите левой кнопкой мыши правый угол текущей ячейки и растяните ее вниз.
-
В итоге таблица сама заполнится, и на экране появится список всех процентов, характеризующих положительную или отрицательную динамику роста.
Далее ничего вас не ограничивает, вы можете сравнивать показатели бесконечное количество раз. Отнимать и добавлять проценты, чтобы понять общую сумму изменений и заниматься дальнейшим взаимодействием с электронной таблицей для своих целей.
Формула отслеживания динамики роста по норме
Иногда расчеты подразумевают наличие нормы, то есть средневзвешенной суммы, которая является оптимальной. Вы можете использовать только это значение, чтобы сравнить его с другими показателями и вычислить проценты. Давайте наглядно разберемся с изменениями, которые вносятся в этом типе расчетов.
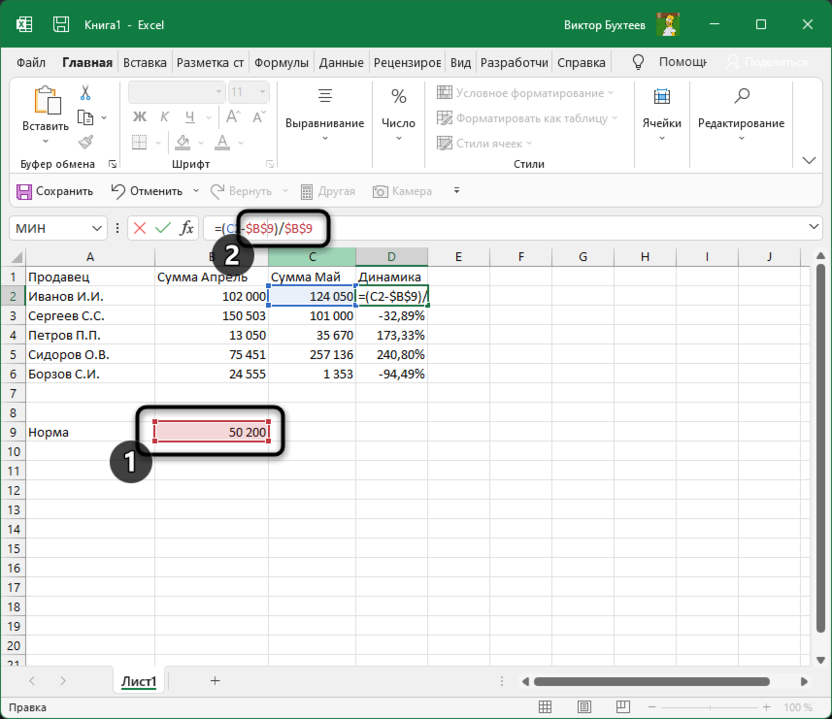
-
Найдите ту ячейку, где будет указана норма. Если ее еще нет, создайте и введите необходимое число. Формула будет немного отличаться от предыдущей. Вам нужно в качестве первого значения как раз и задать эту ячейку, полностью закрепив ее при помощи знаков $.
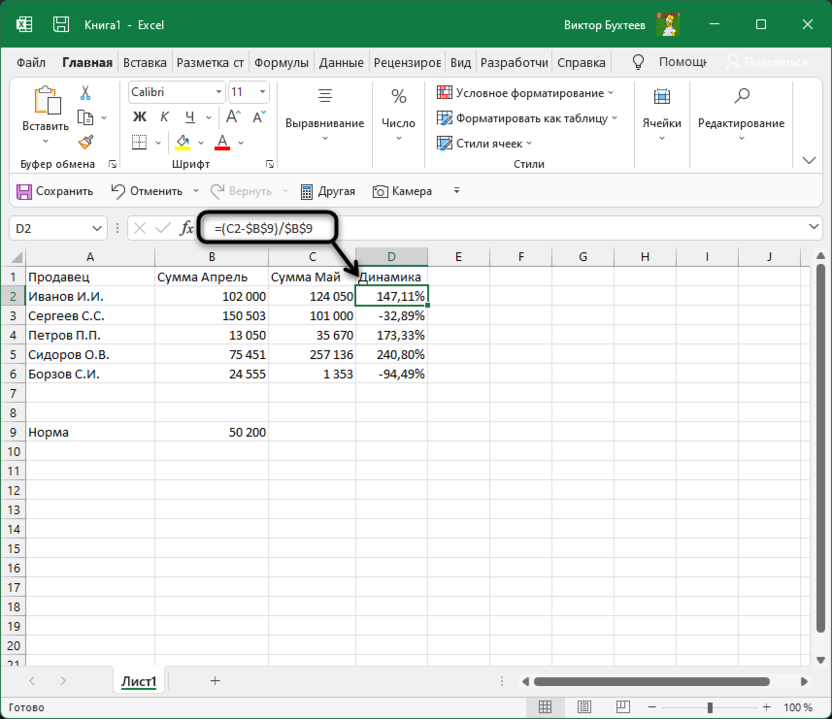
-
Больше никаких изменений вводить не нужно, достаточно нажать Enter, чтобы ознакомиться с результатом.
-
При растягивании формула тоже будет считаться корректно, поскольку ранее вы полностью закрепили одну ячейку.
В этом случае формула обретает вид =(C2-$B$9)/$B$9, где $B$9 – номер той самой закрепленной ячейки, а C2 – сумма второго месяца, от которой и отнимается норма для вычисления процентов.
На основе созданной таблицы вы можете добавлять наглядный график, визуально демонстрирующий динамику роста. Детальнее о его создании рассказано в другой моей статье по ссылке ниже.
Подробнее: Как создать диаграмму темпов роста в Microsoft Excel
Анализ интенсивности динамики
Цель – получение навыков расчета показателей динамики в MS Excel.
Задание – с помощью MS Excel необходимо провести анализ рядов динамики, дать экономическую интерпретацию экономических показателей.
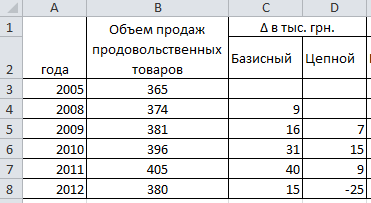
Для проведения маркетингового исследования необходимо проанализировать объем продаж продовольственных товаров в динамике.
Обсяг продажу продовольчих товарів
|
Год |
2005 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
Объем продаж продовольственных товаров, тыс. грн. |
365,00 |
374,00 |
381,00 |
396,00 |
405,00 |
380,00 |
Необходимо рассчитать все показатели динамического ряда(база сравнения — 2005 г), среднегодовые темпы роста и прироста по периодам:
1.2005-2008
2.2008-2012
3.2005-2012
Создадим нужную нам таблицу в MS Excel.
Определим абсолютные приросты. В ячейке С4 введем формулу =B4-$B$3 и растянем формулу на весь столбец.
В ячейку D5 (для 2005 года невозможно рассчитать цепным способом абсолютный прирост, потому что нет предыдущего периода – 2004 года ) используем формулу =B5-B4 и тоже растягиваем на весь столбец. Ниже представлены результаты расчета:
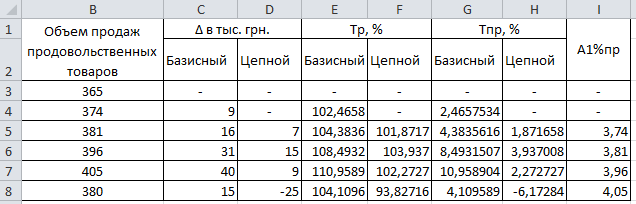
Определим темп роста:
В ячейке Е4 вводим формулу вводим формулу =B4/$B$3*100, растягиваем формулу на весь столбец.
В ячейке F5 (для 2005 года темп роста, как и абсолютный, невозможно рассчитать цепным способом, потому что нет предыдущего периода – 2004 года) вводим формулу =B5/B4*100 и растягиваем на весь столбец.
Определим темп прироста:
В ячейке G4 вводим формулу =E4-100 и растягиваем на весь столбец.
В ячейке H5 вводим формулу =F5-100 и тоже растягиваем формулу на весь столбец.
Определим абсолютное значение 1% прироста:
В ячейке I5 вводим формулу =B4/100. Растягиваем формулу на весь столбец. Внизу представлены результаты вычислений:
Определим средние показатели динамики.
Определение среднего уровня ряда. Так как у нас есть пропущенные уровни ряда, то средний уровень ряда целесообразно рассчитывать за период 2008-2012 годов. В ячейке В10 выбираем встроенную функцию СРЗНАЧ и выбираем нужный нам диапазон.
Найдем средний абсолютный прирост – в ячейке В11 введем формулу =(B8-B3)/8.
Найдем средний темп роста.
1. 2005-2008
В ячейке В14 вводим формулу =(B4/B3)^(1/3).
2. 2008-2012
Базисным способом – в ячейке В16 вводим формулу =(B8/B4)^(1/4).
Цепным способом – в ячейке B17 вводим формулу =((F5/100)*(F6/100)*(F7/100)*(F8/100))^(1/4).
3. 2005-2012
Базисным способом – в ячейку В19 вводим формулу =(B8/B3)^(1/7).
Цепным способом – по формуле средней геометрической взвешенной: в ячейке В20 вводим формулу =((B14)^3*(B16)^4)^(1/7).
Найдем средний темп прироста
1. 2005-2008: в ячейке С14 вводим формулу =(B14-1)*100.
2. 2008-2012: в ячейке С16 вводим формулу =(B16-1)*100.
3. 2005-2012: в ячейке С20 вводим формулу =(B20-1)*100.
Результаты проведенных расчетов представлены ниже:
Таким образом на протяжении 2005-2008 годов наблюдалось постоянный рост объемов инвестиций, только в 2012 году объем инвестиций снизился по сравнению с 2011 годом на 25 тысяч гривен (по сравнению с 2005 годом увеличился на 15 тысяч гривен). Темп роста в 2012 году, рассчитанный базисным способом составляет 104,11%, что означает увеличение объема производства на 4,11%. Цепной темп прироста показал уменьшение объема производства по сравнению с 2011 годом на 6,17%. В 1
% прироста в 2012 году вмещалось 405 гривен. В период 2005-2012 объем инвестиций ежегодно увеличивался в среднем на 1875 гривен или на 0,58%.
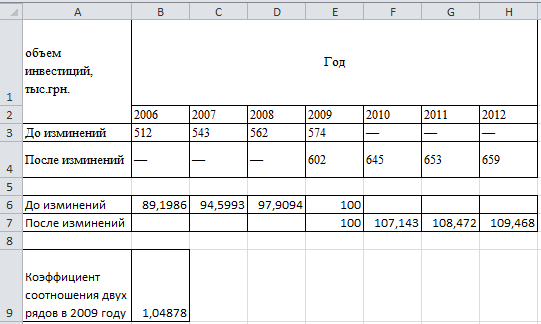
Есть данные про объем инвестиций в маркетинговую компанию, в составе которой произошли изменения. Необходимо проанализировать объем инвестиций в период 2006-2012 годов.
Обсяг інвестицій в компанію
|
Объем инвестиций, тыс. грн. |
Год |
||||||
|
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
|
|
До изменений |
512 |
543 |
562 |
574 |
— |
— |
— |
|
После изменений |
— |
— |
— |
602 |
645 |
653 |
659 |
Для этого задания существует два способа решения.
1 способ решения задания – выражения ряда динамики с помощью относительных показателей, взяв за базу период, в котором произошли изменения. Базой сравнения будет 2009 год.
В ячейке В6 вводим формулу =B3/$E$3*100. Растягиваем эту формулу до ячейки Е6.
В ячейке Н7 вводим формулу =H4/$E$4*100. Растягиваем эту формулу до ячейки Е7.
2 способ – перерасчет абсолютных показателей.
Для этого определяем в 2009 году коэффициент соотношения уровней двух рядов:
В ячейке B9 вводим формулу =E4/E3.
Перемножаем на этот коэффициент уровни первого ряда и получаем их соотношение с уровнями второго ряда.
2009 год – в ячейке В11 вводим формулу =B3*$B$9 и растягиваем эту формулу до ячейки D11.
Тогда получаем сравнительный ряд динамики объема производства в рамках концерна.
Ниже представлены полученные при вычислениях данные:
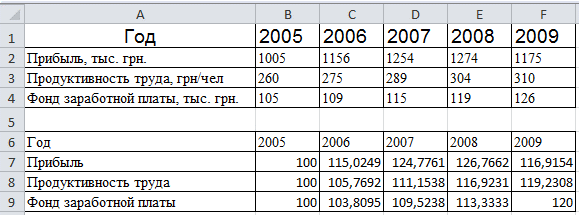
Для формирования маркетинговой стратегии необходимо провести динамический анализ выхода продукции предприятия А и основных факторов интенсивности производства за 2005-2009 года.
|
Год |
2005 |
2006 |
2007 |
2008 |
2009 |
|
Прибыль, тыс. Грн.. |
1005 |
1156 |
1254 |
1274 |
1175 |
|
Продуктивность труда, грн./чел. |
260 |
275 |
289 |
304 |
310 |
|
Фонд заработной платы, тыс.грн. |
105 |
109 |
115 |
119 |
126 |
Необходимо привести ряды динамики к одной основе, к общей базе сравнения.
Введем данные в диапазоне ячеек A1:F4.
Нужно осуществить сравнительный анализ трех представленных рядов динамики, используя их приведение к одной основе.
Приведем сравнительные ряды к одной основе, определив относительные уровни рядов: базисные темпы роста с постоянной базой сравнения – уровни за 2005 год:
В ячейке В7 вводим формулу =B2/$B$2*100, растягиваем эту формулу до ячейки F7.
В ячейке В8 вводим формулу =B3/$B$3*100, растягиваем эту формулу до ячейки F8.
В ячейке В9 вводим формулу =B4/$B$4*100, растягиваем эту формулу до ячейки F9.
Полученные данные в процентах приведены ниже:
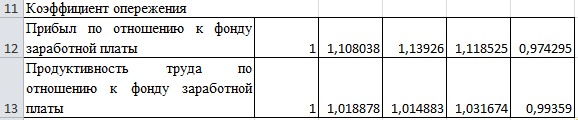
Рассчитаем коэффициент опережения:
В ячейке В12 введем формулу =B7/B$9, растянем эту формулу до ячейки F12.
В ячейке В13 вводим формулу =B7/B$9, растягиваем эту формулу до ячейки F13.
Ниже представлены данные, полученные при вычислении:
Анализ таблиц приводит к таким выводам:
Сравнение темпов роста фонду заработной платы, прибыли и продуктивности труда говорят о опережающих темпах роста факторов результативности производства (в 1,16- 1,26 раз) по сравнению с темпами роста фонда заработной платы (ы 1,13 раз) на протяжении 2005-2008 годов и отстающий темп роста указанных показателей от фонда заработной платы в 2009 году. Это означает, что на предприятии до 2008 года имеет место позитивная динамика роста показателей результативности производства по сравнению к вложенным средствам в рабочую силу, но в 2009 году эта тенденция изменилась, что может объясняться кризисными явлениями в экономике, неэффективностью управления, непредсказуемыми затратами предприятия.
Увеличение прибыли по сравнению с увеличением фонда заработной платы составляло в относительном выражении 1.12 (1,2677:1,1333) в2008 году и 0,97 (1,1692:120,00) в 2009 году. Рост продуктивности труда по сравнению с ростом фонду заработной платы – 1,03 (1,1692:1,1333) в 2008 году и 0,99 (1,1923:120,00) в 2009 году.
Таким образом, темп роста факторов результативности производства (прибыльность, продуктивность труда) в 2009 году отставали от темпов роста фонда заработной платы. Это должно насторожить руководство и заставить принять все возможные меры для исправления ситуации в обратное направление.
0
Концентрация, дифференциация и подобность распределения |
Описание курса
| Статистические индексы. Индексный метод анализа
Аннотация:
Цель работы: научиться выполнять прогнозирование временного ряда данных с помощью средств Microsoft Excel и математически.
Содержание работы:
Анализ временных рядов.
Прогноз, характеристики и параметры прогнозирования.
Уравнение тренда временного ряда.
Порядок выполнения работы:
Изучить методические указания.
Выполнить задания с использованием средств MS Excel.
Оформить отчет, сделав выводы по заданиям.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Анализ временных рядов
Временной ряд (или ряд динамики) – это упорядоченная по времени последовательность значений некоторой произвольной переменной величины. Тем самым, временной ряд существенным образом отличается от простой выборки данных. Каждое отдельное значение данной переменной называется отсчётом (уровнем элементов) временного ряда.
Временные ряды состоят из двух элементов:
- периода времени, за который или по состоянию на который приводятся числовые значения;
- числовых значений того или иного показателя, называемых уровнями ряда.
Временные ряды классифицируются по следующим признакам:
- по форме представления уровней: ряды абсолютных показателей, относительных показателей, средних величин;
- по количеству показателей, когда определяются уровни в каждый момент времени: одномерные и многомерные временные ряды;
- по характеру временного параметра: моментные и интервальные временные ряды. В моментных временных рядах уровни характеризуют значения показателя по состоянию на определенные моменты времени. В интервальных рядах уровни характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. Отдельные же уровни моментного ряда абсолютных величин содержат элементы повторного счета. Это делает бессмысленным суммирование уровней моментных рядов;
- по расстоянию между датами и интервалами времени выделяют равноотстоящие – когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами и неполные (неравноотстоящие) – когда принцип равных интервалов не соблюдается;
- по наличию пропущенных значений: полные и неполные временные ряды. Временные ряды бывают детерминированными и случайными: первые получают на основе значений некоторой неслучайной функции (ряд последовательных данных о количестве дней в месяцах); вторые есть результат реализации некоторой случайной величины;
- в зависимости от наличия основной тенденции выделяют стационарные ряды – в которых среднее значение и дисперсия постоянны и нестационарные – содержащие основную тенденцию развития.
Временные ряды, как правило, возникают в результате измерения некоторого показателя. Это могут быть как показатели (характеристики) технических систем, так и показатели природных, социальных, экономических и других систем (например, погодные данные). Типичным примером временного ряда можно назвать биржевой курс, при анализе которого пытаются определить основное направление развития (тенденцию или тренда).
Анализ временных рядов – совокупность математико-статистических методов анализа, предназначенных для выявления структуры временных рядов и для их прогнозирования. Сюда относятся, в частности, методы регрессионного анализа. Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое является источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений.
Прогноз, характеристики и параметры прогнозирования
Прогноз (от греч. 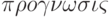
Прогнозирование, разработка прогноза; в узком значении – специальное научное исследование конкретных перспектив развития какого-либо процесса.
Прогнозы делятся:
- по срокам: краткосрочные, среднесрочные, долгосрочные;
- по масштабу: личные, на уровне предприятия (организации), местные, региональные, отраслевые, мировые (глобальные).
К основным методам прогнозирования относятся:
- статистические методы;
- экспертные оценки (метод Дельфи);
- моделирование.
Прогноз – обоснованное суждение о возможном состоянии объекта в будущем или альтернативных путях и сроках достижения этих состояний. Прогнозирование – процесс разработки прогноза. Этап прогнозирования – часть процесса разработки прогнозов, характеризующаяся своими задачами, методами и результатами. Деление на этапы связано со спецификой построения систематизированного описания объекта прогнозирования, сбора данных, с построением модели, верификацией прогноза.
Прием прогнозирования – одна или несколько математических или логических операций, направленных на получение конкретного результата в процессе разработки прогноза. В качестве приема могут выступать сглаживание динамического ряда, определение компетентности эксперта, вычисление средневзвешенного значения оценок экспертов и т. д.
Модель прогнозирования – модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта прогнозирования в будущем и (или) путях и сроках их осуществления.
Метод прогнозирования – способ исследования объекта прогнозирования, направленный на разработку прогноза. Методы прогнозирования являются основанием для методик прогнозирования.
Методика прогнозирования – совокупность специальных правил и приемов (одного или нескольких методов) разработки прогнозов.
Прогнозирующая система – система методов и средств их реализации, функционирующая в соответствии с основными принципами прогнозирования. Средствами реализации являются экспертная группа, совокупность программ и т. д. Прогнозирующие системы могут быть автоматизированными и неавтоматизированными.
Прогнозный вариант – один из прогнозов, составляющих группу возможных прогнозов.
Объект прогнозирования – процесс, система, или явление, о состоянии которого даётся прогноз.
Характеристика объекта прогнозирования – качественное или количественное отражение какого-либо свойства объекта прогнозирования.
Переменная объекта прогнозирования – количественная характеристика объекта прогнозирования, которая является или принимается за изменяемую в течение периода основания и (или) периода упреждения прогноза.
Период основания прогноза – промежуток времени, за который используют информацию для разработки прогноза. Этот промежуток времени называют также периодом предыстории.
Период упреждения прогноза – промежуток времени, на который разрабатывается прогноз.
Прогнозный горизонт – максимально возможный период упреждения прогноза заданной точности.
Точность прогноза – оценка доверительного интервала прогноза для заданной вероятности его осуществления.
Достоверность прогноза – оценка вероятности осуществления прогноза для заданного доверительного интервала.
Ошибка прогноза – апостериорная величина отклонения прогноза от действительного состояния объекта.
Источник ошибки прогноза – фактор, способный привести к появлению ошибки прогноза. Различают источники регулярных и нерегулярных ошибок.
Верификация прогноза – оценка достоверности и точности или обоснованности прогноза.
Статистические методы прогнозирования – научная и учебная дисциплина, к основным задачам которой относятся разработка, изучение и применение современных математико-статистических методов прогнозирования на основе объективных данных; развитие теории и практики вероятностно-статистического моделирования экспертных методов прогнозирования; методов прогнозирования в условиях риска и комбинированных методов прогнозирования с использованием совместно экономико-математических и эконометрических (как математико-статистических, так и экспертных) моделей. Научной базой статистических методов прогнозирования является прикладная статистика и теория принятия решений.
Простейшие методы восстановления используемых для прогнозирования зависимостей исходят из заданного временного ряда, т. е. функции, определённой в конечном числе точек на оси времени. Временной ряд при этом часто рассматривается в рамках той или иной вероятностной модели, вводятся другие факторы (независимые переменные), помимо времени, например, объем денежной массы. Временной ряд может быть многомерным. Основные решаемые задачи – интерполяция и экстраполяция. Метод наименьших квадратов в простейшем случае (линейная функция от одного фактора) был разработан К. Гауссом в 1794–1795 гг. Могут оказаться полезными предварительные преобразования переменных, например, логарифмирование. Наиболее часто используется метод наименьших квадратов при нескольких факторах.
Оценивание точности прогноза (в частности, с помощью доверительных интервалов) – необходимая часть процедуры прогнозирования. Обычно используют вероятностно-статистические модели восстановления зависимости, например, строят наилучший прогноз по методу максимального правдоподобия. Разработаны параметрические (обычно на основе модели нормальных ошибок) и непараметрические оценки точности прогноза и доверительные границы для него (на основе Центральной Предельной Теоремы теории вероятностей). Применяются также эвристические приемы, не основанные на вероятностно-статистической теории: метод скользящих средних, метод экспоненциального сглаживания.
Многомерная регрессия, в том числе с использованием непараметрических оценок плотности распределения – основной на настоящий момент статистический аппарат прогнозирования. Нереалистическое предположение о нормальности погрешностей измерений и отклонений от линии (поверхности) регрессии использовать не обязательно; однако для отказа от предположения нормальности необходимо опереться на иной математический аппарат, основанный на многомерной Центральной Предельной Теореме теории вероятностей, технологии линеаризации и наследования сходимости. Он позволяет проводить точечное и интервальное оценивание параметров, проверять значимость их отличия от 0 в непараметрической постановке, строить доверительные границы для прогноза.
Уравнение тренда временного ряда
Рассматривая временной ряд как множество результатов наблюдений изучаемого процесса, проводимых последовательно во времени, в качестве основных целей исследования временных рядов можно выделить: выявление и анализ характерного изменения параметра у, оценка возможного изменения параметра в будущем (прогноз).
Значения временного ряда можно представить в виде: 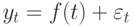

Неслучайная функция f(t) называется трендом. Тренд отражает характерное изменение (тенденцию) yt за некоторый промежуток времени. На практике в качестве тренда выбирают несколько возможных теоретических или эмпирических моделей. Могут быть выбраны, например, линейная, параболическая, логарифмическая, показательная функции. Для выявления типа модели на координатную плоскость наносят точки с координатами (t, yt) и по характеру расположения точек делают вывод о виде уравнения тренда. Для получения уравнения тренда применяют различные методы: сглаживание с помощью скользящей средней, метод наименьших квадратов и другие.
Уравнение тренда линейного вида будем искать в виде yt=f(t), где f(t) = a0+a1(t).
Пример 1. Имеется временной ряд:
| ti | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| xti | 2 | 1 | 4 | 4 | 6 | 8 | 7 | 9 | 12 | 11 |
Построим график xti во времени. Добавим на графике линию тренда исходных значений ряда. При этом, щелкнув правой кнопкой мыши по линии тренда, можно вызвать контекстное меню «Формат линии тренда», а в нем поставить флажок «показывать уравнение на диаграмме», тогда на диаграмме высветится уравнение линии тренда, вычисленное встроенными возможностями Excel.
Рис.
14.1.
Чтобы определить уравнение тренда, необходимо найти значения коэффициентов а0 и а1. Эти коэффициенты следует определять, исходя из условия минимального отклонения значений функции f(t) в точках ti от значений исходного временного ряда в тех же точках ti. Это условие можно записать в виде (на основе метода наименьших квадратов):
где n – количество значений временного ряда.
Для того, чтобы найти значения а0 и а1, необходимо иметь систему из двух уравнений. Эти уравнения можно получить, используя условие равенства нулю производной функции в точках её экстремума. В нашем случае эта функция имеет вид ![$sumlimits_{t=1}^{n}[x_{t}-a_{0}-a_{1}t]^{2}$](https://intuit.ru/sites/default/files/tex_cache/af521da64ce9abdab75d7f160f5c9bb4.png)
Полученная система может быть преобразована (математически) в систему так называемых нормальных уравнений. При этом уравнения примут вид:
Теперь необходимо решить преобразованную систему уравнений относительно а0 и а1. Однако предварительно следует составить и заполнить вспомогательную таблицу:
Подставив значения n = 10 в систему уравнений (2), получим
Решив систему уравнений относительно а0 и а1, получим а0 = -0,035, а1 = 1,17. Тогда функция тренда заданного временного ряда f(t) имеет вид:
f(t) = -0,035 + 1,17t.
Изобразим полученную функцию на графике.
Рис.
14.2.
Задание 1.
Временной ряд приведен в таблице. Используя средства MS Excel:
- построить график временного ряда;
- добавить линию тренда и ее уравнение;
- найти уравнение тренда методом наименьших квадратов, сравнить уравнения (выше на графике и полученное);
- построить график временного ряда и полученной функции тренда в одной системе координат.
Варианты.
1. Реализация аспирина по аптеке (у.е.) за последние 7 недель приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 3,2 | 3,3 | 2,9 | 2,2 | 1,6 | 1,5 | 1,2 |
2. Динамика потребления молочных продуктов (у.е.) по району за последние 7 месяцев:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| хti | 30 | 29 | 27 | 24 | 25 | 24 | 23 |
3. Динамика числа работников, занятых в одной из торговых сетей города за последние 8 лет приведена в таблице:
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 280 | 361 | 384 | 452 | 433 | 401 | 512 | 497 |
4. Динамика потребления сульфаниламидных препаратов в клинике по годам (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 14 | 21 | 29 | 33 | 38 | 44 | 46 | 50 |
5. Динамика продаж однокомнатных квартир в городе за последние 8 лет (тыс. ед.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| уt | 39 | 40 | 36 | 34 | 36 | 37 | 33 | 35 |
6. Динамика потребления антибиотиков в клинике (тыс. упаковок):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 10 | 17 | 18 | 13 | 17 | 21 | 25 | 29 |
7. Динамика производства хлебобулочных изделий на хлебозаводе (тонн):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 510 | 502 | 564 | 680 | 523 | 642 | 728 | 665 |
8. Динамика потребления противовирусных препаратов по аптечной сети в начале эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 36 | 42 | 34 | 38 | 12 | 32 | 26 | 20 |
9. Динамика потребления противовирусных препаратов по аптечной сети в конце эпидемии гриппа (тыс. единиц):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 46 | 52 | 44 | 48 | 32 | 42 | 36 | 30 |
10. Динамика потребления витаминов по аптечной сети в весенний период (с марта по апрель) в разные годы (у.е.):
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| хti | 0,9 | 1,7 | 1,5 | 1,7 | 1,5 | 2,1 | 2,5 | 3,6 |
Пример 2. Используя данные примера 1, приведенного выше, вычислить точечный прогноз исходного временного ряда на 5 шагов вперед.
Исходя из условия задачи, необходимо определить точечную оценку прогноза для t = 11, 12, 13, 14, 15, где t в данном случае – шаг упреждения.
Решение.
Рассмотрим решение этой задачи средствами Microsoft Excel. При решении данной задачи следует так же, как и в примере 1, ввести исходные данные. Выделив данные, построить точечный график, щелкнув правой кнопкой мыши по ряду данных, вызвать контекстное меню и выбрать «Добавить линию тренда».
Щелкнув правой кнопкой мыши по линии тренда, вызвать контекстное меню, выбрать «Формат линии тренда», в окне Параметры линии тренда указать прогноз на 5 периодов и поставить флажок в окошке «Показывать уравнение на диаграмме (рис. 14.3
рис.
14.3.). В версии Excel ранее 2007 окно диалога представлено на рисунке 14.4
рис.
14.4.
Рис.
14.3.
Задание параметров тренда в MS Excel 2007
Рис.
14.4.
Задание параметров тренда в версии ранее MS Excel 2007
Итоговый график представлен на рисунке 14.5
рис.
14.5.
Рис.
14.5.
Значения прогноза для 11, 12, 13, 14 и 15 уровней получим, используя функцию ПРЕДСКАЗ( ). Данная функция позволяет получить значения прогноза линейного тренда. Вычисленные значения: 12,87, 14,04, 15,22, 16,39, 17,57.
Значения точечного прогноза для исходного временного ряда на 5 шагов вперед можно вычислить и с помощью уравнения функции тренда f(t), найденного по методу наименьших квадратов. Для этого в полученное для f(t) выражение необходимо подставить значения t = 11, 12, 13, 14, 15. В результате получим (эти значения следует рассчитать, сформировав формулу в табличном процессоре MS Excel):
Сравнивая результаты точечных прогнозных оценок, полученных разными способами, выявляем, что данные отличаются незначительно, таким образом, в любом из способов расчета присутствует определенная погрешность (ошибка) прогноза (
Задание 2.
Используя значения временного ряда Задания 1 согласно вашего варианта, вычислить точечный прогноз на 4 шага вперед. Продлить линию тренда на 4 прогнозных значения, вывести уравнение тренда, определить эти значения с помощью функции ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(), а также по выражению функции тренда f(t), полученному по методу наименьших квадратов в Задании 1. Сравнить полученные результаты.




![$$sumlimits_{t=1}^{n}[x_{t}-a_{0}-a_{1}t]^{2}rightarrow mineqno(1)$$](https://intuit.ru/sites/default/files/tex_cache/56404890c825202167c4ba34001e2250.png)