Чтобы проанализировать изменчивость признака под воздействием контролируемых переменных, применяется дисперсионный метод.
Для изучения связи между значениями – факторный метод. Рассмотрим подробнее аналитические инструменты: факторный, дисперсионный и двухфакторный дисперсионный метод оценки изменчивости.
Дисперсионный анализ в Excel
Условно цель дисперсионного метода можно сформулировать так: вычленить из общей вариативности параметра 3 частные вариативности:
- 1 – определенную действием каждого из изучаемых значений;
- 2 – продиктованную взаимосвязью между исследуемыми значениями;
- 3 – случайную, продиктованную всеми неучтенными обстоятельствами.
В программе Microsoft Excel дисперсионный анализ можно выполнить с помощью инструмента «Анализ данных» (вкладка «Данные» — «Анализ»). Это надстройка табличного процессора. Если надстройка недоступна, нужно открыть «Параметры Excel» и включить настройку для анализа.
Работа начинается с оформления таблицы. Правила:
- В каждом столбце должны быть значения одного исследуемого фактора.
- Столбцы расположить по возрастанию/убыванию величины исследуемого параметра.
Рассмотрим дисперсионный анализ в Excel на примере.
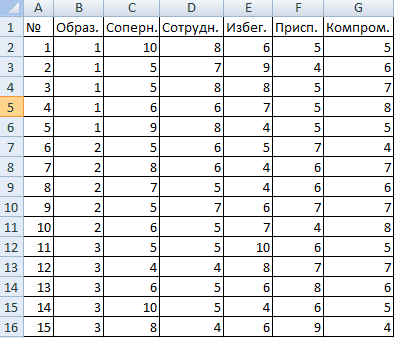
Психолог фирмы проанализировал с помощью специальной методики стратегии поведения сотрудников в конфликтной ситуации. Предполагается, что на поведение влияет уровень образования (1 – среднее, 2 – среднее специальное, 3 – высшее).
Внесем данные в таблицу Excel:
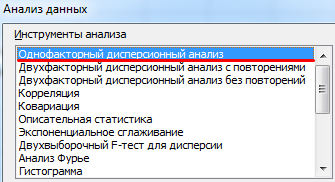
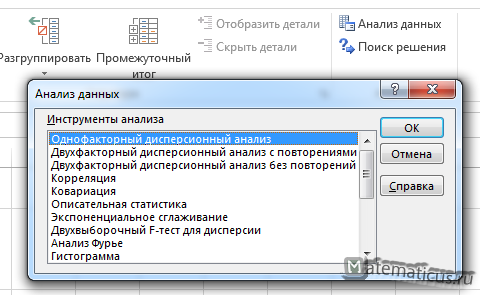
- Открываем диалоговое окно нашего аналитического инструмента. В раскрывшемся списке выбираем «Однофакторный дисперсионный анализ» и нажимаем ОК.
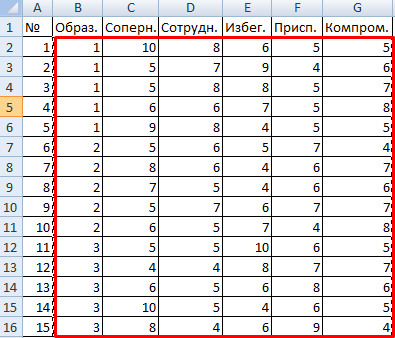
- В поле «Входной интервал» ввести ссылку на диапазон ячеек, содержащихся во всех столбцах таблицы.
- «Группирование» назначить по столбцам.
- «Параметры вывода» — новый рабочий лист. Если нужно указать выходной диапазон на имеющемся листе, то переключатель ставим в положение «Выходной интервал» и ссылаемся на левую верхнюю ячейку диапазона для выводимых данных. Размеры определятся автоматически.
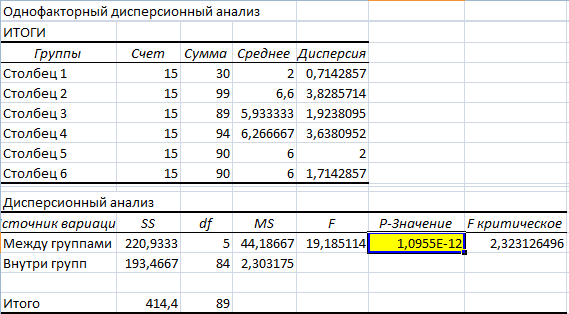
- Результаты анализа выводятся на отдельный лист (в нашем примере).
Значимый параметр залит желтым цветом. Так как Р-Значение между группами больше 1, критерий Фишера нельзя считать значимым. Следовательно, поведение в конфликтной ситуации не зависит от уровня образования.
Факторный анализ в Excel: пример
Факторным называют многомерный анализ взаимосвязей между значениями переменных. С помощью данного метода можно решить важнейшие задачи:
- всесторонне описать измеряемый объект (причем емко, компактно);
- выявить скрытые переменные значения, определяющие наличие линейных статистических корреляций;
- классифицировать переменные (определить взаимосвязи между ними);
- сократить число необходимых переменных.
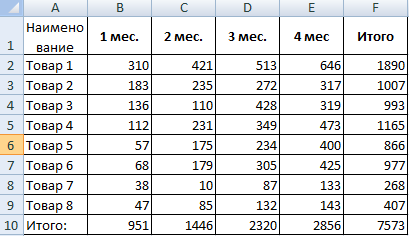
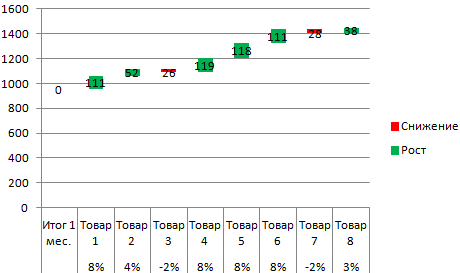
Рассмотрим на примере проведение факторного анализа. Допустим, нам известны продажи каких-либо товаров за последние 4 месяца. Необходимо проанализировать, какие наименования пользуются спросом, а какие нет.
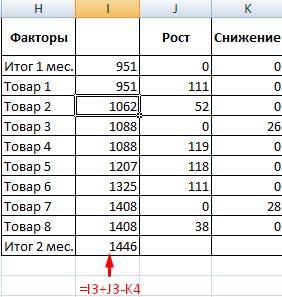
- Посмотрим, за счет, каких наименований произошел основной рост по итогам второго месяца. Если продажи какого-то товара выросли, положительная дельта – в столбец «Рост». Отрицательная – «Снижение». Формула в Excel для «роста»: =ЕСЛИ((C2-B2)>0;C2-B2;0), где С2-В2 – разница между 2 и 1 месяцем. Формула для «снижения»: =ЕСЛИ(J3=0;B2-C2;0), где J3 – ссылка на ячейку слева («Рост»). Во втором столбце – сумма предыдущего значения и предыдущего роста за вычетом текущего снижения.
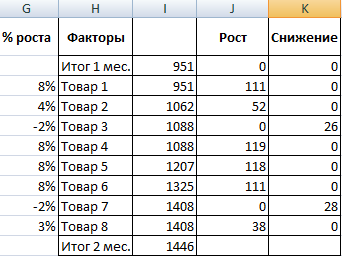
- Рассчитаем процент роста по каждому наименованию товара. Формула: =ЕСЛИ(J3/$I$11=0;-K3/$I$11;J3/$I$11). Где J3/$I$11 – отношение «роста» к итогу за 2 месяц, ;-K3/$I$11 – отношение «снижения» к итогу за 2 месяц.
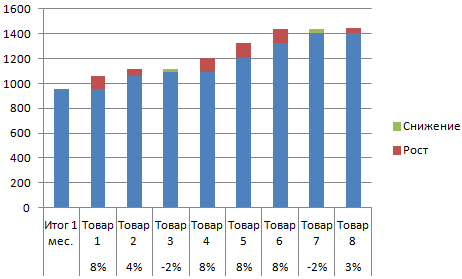
- Выделяем область данных для построения диаграммы. Переходим на вкладку «Вставка» — «Гистограмма».
- Поработаем с подписями и цветами. Уберем накопительный итог через «Формат ряда данных» — «Заливка» («Нет заливки»). С помощью данного инструментария меняем цвет для «снижения» и «роста».
Теперь наглядно видно, продажи какого товара дают основной рост.
Двухфакторный дисперсионный анализ в Excel
Показывает, как влияет два фактора на изменение значения случайной величины. Рассмотрим двухфакторный дисперсионный анализ в Excel на примере.
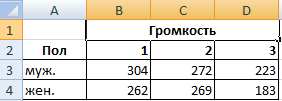
Задача. Группе мужчин и женщин предъявляли звук разной громкости: 1 – 10 дБ, 2 – 30 дБ, 3 – 50 дБ. Время ответа фиксировали в миллисекундах. Необходимо определить, влияет ли пол на реакцию; влияет ли громкость на реакцию.
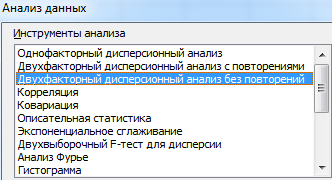
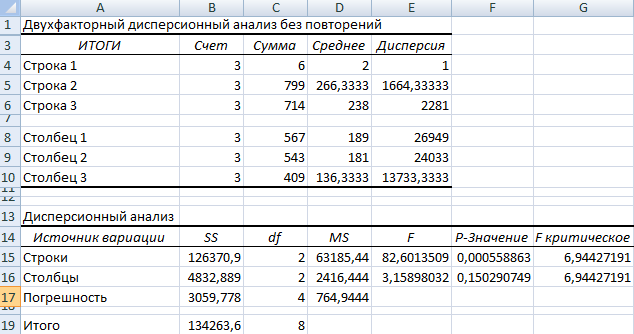
- Переходим на вкладку «Данные» — «Анализ данных» Выбираем из списка «Двухфакторный дисперсионный анализ без повторений».
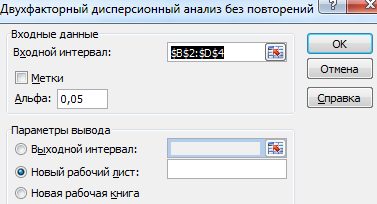
- Заполняем поля. В диапазон должны войти только числовые значения.
- Результат анализа выводится на новый лист (как было задано).
Та как F-статистики (столбец «F») для фактора «Пол» больше критического уровня F-распределения (столбец «F-критическое»), данный фактор имеет влияние на анализируемый параметр (время реакции на звук).
Скачать пример факторного и дисперсионного анализа
скачать факторный анализ отклонений
скачать пример 2
Для фактора «Громкость»: 3,16 < 6,94. Следовательно, данный фактор не влияет на время ответа.
Для примера также прилагаем факторный анализ отклонений в маржинальном доходе.
17 авг. 2022 г.
читать 3 мин
Однофакторный дисперсионный анализ («дисперсионный анализ») используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более независимых групп.
В этом руководстве объясняется, как выполнить однофакторный дисперсионный анализ в Excel.
Пример. Однофакторный дисперсионный анализ в Excel
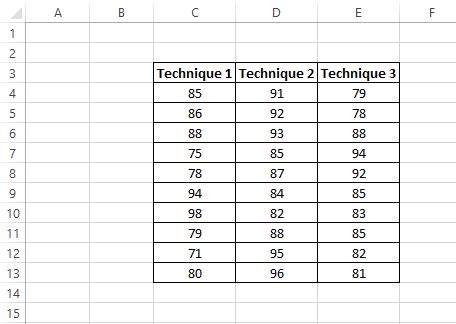
Предположим, исследователь набирает 30 студентов для участия в исследовании. Студентам случайным образом назначают использовать один из трех методов обучения в течение следующих трех недель для подготовки к экзамену. По истечении трех недель все студенты сдают одинаковый тест.
Ниже представлены результаты тестов учащихся:
Исследователь хочет выполнить однофакторный дисперсионный анализ, чтобы определить, одинаковы ли средние баллы для всех трех групп.
Чтобы выполнить однофакторный дисперсионный анализ в Excel, перейдите на вкладку « Данные », затем щелкните параметр «Анализ данных» в группе « Анализ ».
Если вы не видите опцию Анализ данных , вам сначала нужно загрузить бесплатный пакет инструментов анализа .
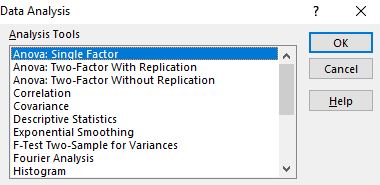
После того, как вы нажмете на нее, появится окно с различными параметрами инструментов анализа. Выберите Anova: Single Factor , затем нажмите OK .
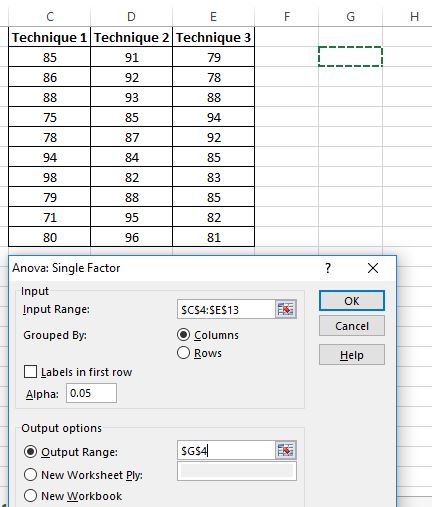
Появится новое окно с запросом Input Range.Вы можете либо перетащить рамку вокруг ваших данных, либо вручную ввести диапазон данных. В этом случае наши данные находятся в ячейках C4:E13 .
Затем выберите альфа -уровень для теста. По умолчанию это число равно 0,05. В этом случае я оставлю значение 0,05.
Наконец, выберите ячейку для выходного диапазона , в которой появятся результаты однофакторного дисперсионного анализа. В этом случае я выбираю ячейку G4 .
После того, как вы нажмете OK , появится результат однофакторного дисперсионного анализа:
Односторонний вывод ANOVA в Excel Интерпретация вывода
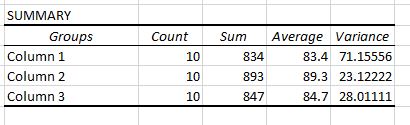
В выводе показаны две таблицы. Первая представляет собой сводную таблицу, в которой показано количество тестовых баллов в каждой группе, сумма тестовых баллов, среднее значение тестов и дисперсия тестовых баллов.
Напомним, что однофакторный дисперсионный анализ используется для определения наличия или отсутствия статистически значимой разницы между средними значениями трех или более групп.
Из этой первой таблицы мы видим, что средний балл для каждой из трех групп отличается, но чтобы узнать, являются ли эти различия статистически значимыми, нам нужно взглянуть на вторую таблицу.
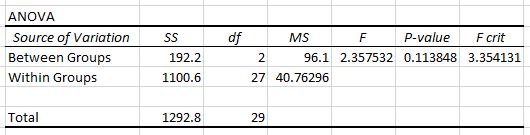
Вторая таблица показывает статистику теста F, критическое значение F и значение p:
В этом случае статистика F-теста равна 2,3575 , а критическое значение F равно 3,3541.Поскольку статистика F-теста меньше критического значения F, у нас нет достаточных доказательств, чтобы отклонить нулевую гипотезу о том, что средние значения для трех групп равны.
Это означает, что у нас нет достаточных доказательств того, что между тремя методами обучения есть разница в результатах тестов.
Мы могли бы также использовать p-значение , чтобы прийти к такому же выводу. В этом случае p-значение равно 0,1138 , что больше, чем альфа-уровень 0,05 .
Это означает, что у нас нет достаточных доказательств, чтобы отвергнуть нулевую гипотезу о том, что средние значения для трех групп равны.
Примечание. В тех случаях, когда вы отвергаете нулевую гипотезу, вы можете выполнить апостериорный тест Тьюки-Крамера, чтобы точно определить, какие средние значения групп различаются.
Однофакторный дисперсионный анализ изучает влияния одного фактора на анализируемый признак.
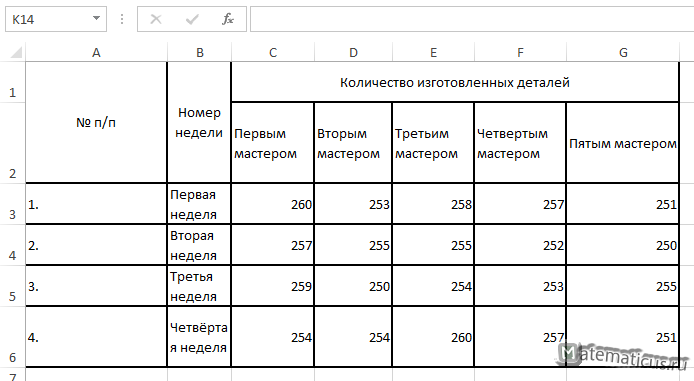
В таблицы приведены статистические данные по количеству изготовленных деталей на заводе каждым мастером в течение каждой недели.
Необходимо выяснить зависимость количества изготовленных деталей от производительности мастера. Уровень значимости равен α=0.05.
| № п/п | Номер недели | Количество изготовленных деталей | ||||
| Первым мастером | Вторым мастером | Третьим мастером | Четвертым мастером | Пятым мастером | ||
| 1. | Первая неделя | 260 | 253 | 258 | 257 | 251 |
| 2. | Вторая неделя | 257 | 255 | 255 | 252 | 250 |
| 3. | Третья неделя | 259 | 250 | 254 | 253 | 255 |
| 4. | Четвёртая неделя | 254 | 254 | 260 | 257 | 251 |
Решение
Переходим на вкладку Данные -> Анализ данных. Выбираем однофакторный дисперсионный анализ и жмём Ок.
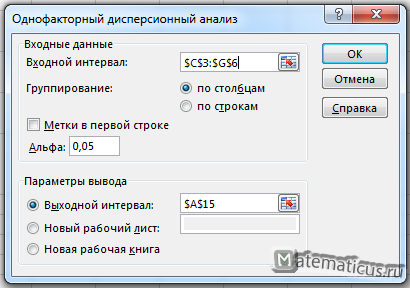
Появляется окно, здесь во входном интервале выбираем диапазон данный в нашей таблицы в нашем случае это диапазон ячеек $C$3:$G$6, альфа ставим 0,05 (обычно в Excel данная величина стоит по умолчанию) и в выходном интервале указываем произвольную ячейку на листе Excel, где желаете, чтобы отобразился результат, далее Ок.
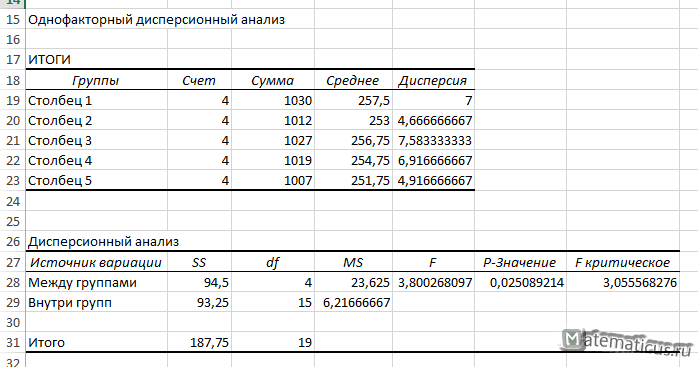
В результате получим решение в виде таблицы.
| Однофакторный дисперсионный анализ | ||||||
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| Столбец 1 | 4 | 1030 | 257,5 | 7 | ||
| Столбец 2 | 4 | 1012 | 253 | 4,666666667 | ||
| Столбец 3 | 4 | 1027 | 256,75 | 7,583333333 | ||
| Столбец 4 | 4 | 1019 | 254,75 | 6,916666667 | ||
| Столбец 5 | 4 | 1007 | 251,75 | 4,916666667 | ||
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 94,5 | 4 | 23,625 | 3,800268097 | 0,025089214 | 3,055568276 |
| Внутри групп | 93,25 | 15 | 6,21666667 | |||
| Итого | 187,75 | 19 |
Из таблицы значения F-критерия равно Fнабл=3.8, а Fкрит=3, правосторонний интервал (3; +∞) Fнабл>Fкрит, отсюда следует, что Fнабл лежит в этом интервале, следовательно, нулевую гипотезу H0 о равенстве групповых матожиданий — отвергаем, следовательно фактор — количества изготовленных деталей зависит от признака — производительности мастера.
Найдём выборочный коэффициент детерминации:
${R^2} = frac{{frac{{94,5}}{{20}}}}{{frac{{187,75}}{{20}}}} approx 0,5$
Этот показатель говорит о том, что около половины еженедельного количества изготовленных деталей мастерами связано с номером недели.
7262
В
программе MS
Excel для
статистического анализа данных имеется
надстройка «Пакет
анализа«,
которая позволяет проводить дисперсионный
анализ следующих видов:
-
однофакторный
дисперсионный анализ, -
двухфакторный
дисперсионный анализ без повторений, -
двухфакторный
дисперсионный анализ с повторениями.
-
Однофакторный дисперсионный анализ.
Условием применения
такого анализа является повторность
данных.
Например:
Необходимо оценить влияние условий и
характера труда (в данном случае профиля
цеха) на заболеваемость рабочих острым
и хроническим гастритом. Повторность
данных – обеспечена наблюдением за
работниками предприятий, схожими по
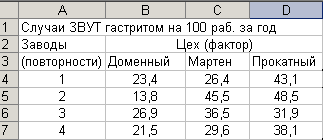
профилю. Исходные данные представлены
в таблице ():
Согласно
таблице исследуемый фактор имеет 3
уровня: доменный, мартеновский и прокатный
цеха. В каждой группе имеется только по
4 наблюдения – 1,2,3,4 заводы, которые
рассматриваются как повторности
наблюдений.
Рисунок 100.
Исходные данные однофакторного комплекса
Для
решения задачи в MS
Excel:
1.Сформируйте
таблицу с исходными данными ().
2.Выберите
<Пакет
анализа>
из меню <Сервис>.
3.В
соответствии с условиями задачи выберите
в появившемся диалоговом окне метод
«Однофакторный
дисперсионный анализ»
и нажмите кнопку [OK].
4.В
окне «Однофакторный
дисперсионный анализ»
установите для входных данных следующие
параметры:
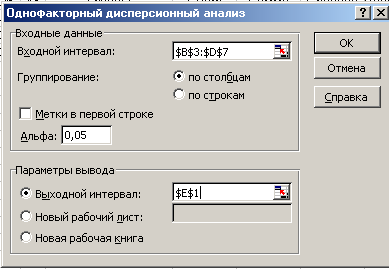
-
входной
интервал ($B$4:$D$7), -
метки
(выбранный нами входной диапазон не
содержит метки, то есть названий строк
и столбцов), -
альфа
(уровень значимости =0,05).
5.Для
параметров вывода установите переключатель
в положение
«Выходной интервал»
и укажите клетку с координатой (Е1).
6.После
завершения настройки параметров нажмите
кнопку [OK].
Диалоговое
окно с заполненными исходными параметрами
должно выглядеть следующим образом
Рисунок
101. Окно исходных параметров однофакторного
дисперсионного комплекса
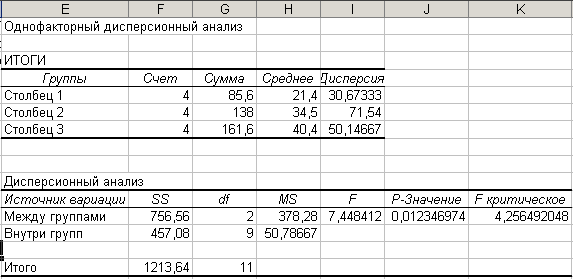
Результаты
дисперсионного анализа будут состоять
из двух таблиц. В первой таблице для
каждого столбца исходной таблицы, в
которых располагаются анализируемые
группы, приведены числовые параметры:
количество чисел (счет), суммы по столбцам,
средние дисперсии по столбцам.
Рисунок
102. Результаты анализа однофакторного
комплекса
Во
второй части результатов MS
Excel использует
следующие обозначения:
-
SS
— сумма квадратов, -
df
— степени свободы, -
MS
— средний квадрат (дисперсия), -
F
— F-статистика Фишера (фактическое
значение), -
p-значение
– общая значимость результатов
дисперсионного анализа данных,
расположенных по столбцам; -
F-критическое
— критическое значение F-статистики
(Фишера) при заданном ранее p=0,05.
Таким
образом, сумма квадратов, обусловленная
влиянием исследуемого фактора
(межгрупповая сумма), равна 756,56 Остаточная
сумма квадратов (внутригрупповая) равна
457,08. Соответствующие дисперсии
межгрупповая (для исследуемого фактора)
— 378,28. , остаточная, внутригрупповая —
55,79.
Основной
вывод
из полученных результатов заключается
в следующем:
Есть
основания отвергать нулевую гипотезу
об отсутствии влияния рассмотренного
фактора (условия и характер работы в
разных цехах) на заболеваемость рабочих
гастритом: т.к. выполняется неравенство
FFкр.,
при котором величина значимости Р
= 0,012. Для отрицания нулевой гипотезы
она должна быть не более 0,05.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

If you are working on statistical analysis and, more specifically, undertaking a variation analysis, there is a tool available through add-ins that should help make the process much easier. Regardless of how complex the research you are working with, the ANOVA tool is simple and user friendly. Here we will briefly take a look at the tool and walk through the steps involved in using it.
If you are interested in learning more about Excel’s advanced analytical capabilities, you might be interested in an online advanced Excel course.
Understanding ANOVA in Excel
The ANOVA function in Excel is the analytical tool used for variance analysis. A form of hypothesis testing, it will determine whether two or more factors have the same mean. Currently, it has three different variations depending on the test you want to perform: Single factor, two-factor with replication and two factor without replication.
Single-factor: This offers a test on data of two or more samples. With it, you can test the hypothesis that each of the samples is drawn from the same underlying probability distribution against the hypothesis that the underlying probability distribution is not the same.
If you are working with only two samples, note that Excel gives you an alternative called T-Test, which is built in to its regular set of functions. If you would like to understand how this and other standard functions operate in Excel, you can take an online course in advanced Excel.
two-factor with replication: when you have two factors on which the variance depends and you are collecting multiple data points for a specified condition, you will want to use this option.
two-factor without replication: When variance depends on two factors and you are collecting a single dat point for a specified condition, you will use this test.
This tutorial assumes that you are familiar with these statistical concepts and will focus on explaining how to use Excel to help you run the tests. If, however, you need to brush up on concepts in statistics, you can take an online introduction to statistics that should serve as a refresher.
Enable the Analysis Toolpak
The ANOVA function is part of an add-in for Excel, so if you haven’t already, you will need to enable the Excel Analysis Toolpak before you can use it. In addition to ANOVA, this add-in for Excel will give you access to a number of helpful tools for running statistical analysis in your workbooks. If you would like to dive in and understand the power of Excel for working with statistics, you can take a course on Excel’s statistical functions.
Here are instructions for enabling the toolpak in Excel 2010. Depending on the version you are using, the method may vary slightly. So if this does not work for you, you should be able to search for another method or find it on Office.com
1. Go to the file menu
2. Select Options
3. From the options menu, select add-ins from the left column
4. At the bottom of the menu, you will see a label that says “Manage:” followed by a drop-down box. Make sure Excel add-ins is selected from that drop-down and click Go.
5. Another menu will appear, showing you the available add-ins. Check the box next to Analysis Toolpak, and click OK
If the Analysis toolpak is not listed, click browse to locate it. If the program tells you it isn’t installed, click Yes to install it.
You should now have the Analysis Toolpak enabled. To verify, click on the data tab from the main ribbon. You should see a data analysis option on the right. If you click on that Anova should be among the first options available.
Running ANOVA
Now that you have the Analysis toolpak enabled, you have what you need to complete the test.
Running the ANOVA function
To start with the Anova function, open the workbook containing the data you want to run the test on. Then, follow these steps:
1. click in a cell on your spreadsheet where your output will begin. The results, of course, will cover a range of cells.
2. Click on the Data tab from the main ribbon and select data analysis, which should be in the analysis menu on the right.
3. Select the appropriate Anova test from the options in the Data Analysis menu.
4. The function’s menu will pop up. Start by putting in the range containing the data to be analyzed. If you click the button to the right of the text box (containing a red arrow) you can select your cell range by clicking and dragging.
5. Select the number of rows each sample contains.
6. Specify the alpha (the default 0.05 represents a 95% confidence interval.
7. Specify the output range. Again, you can click the button to the right of the text box to click and drag. All you really need to consider here is where the first cell of the results will be located. You do not need to indicate the exact number of rows and columns for the result. Note that the output will be contained in a range of 7 columns by 30 rows.
You now have your result. All that’s left is interpreting it! If you are a little bit fuzzy on what the numbers mean, don’t worry, you have resources available to help out. In fact you can take an online course that includes a walkthrough of ANOVA and its results.
Hopefully, your test has run smoothly and produced a useable outcome.