Анализ данных моделирование бизнеса microsoft excel - Word и Excel

Время на прочтение
5 мин

Количество просмотров 8.5K

Привет, Хаброжители! Уэйн Винстон научит вас быстро анализировать данные, принимать решения, подводить итоги, составлять отчеты, обрабатывать данные и строить аналитические модели в Microsoft Excel 2019 и Office 365. В новом шестом издании вас ждут более 800 бизнес-задач, основанных на реальных ситуациях, а также обсуждение новых инструментов и функций. Где бы вы ни работали — в крупной корпорации, небольшой компании, государственной или некоммерческой структуре, — это поможет вам увеличить прибыль, снизить издержки или эффективно управлять производством. Прочитав эту книгу, вы сможете cпрогнозировать результаты выборов, научитесь определять точки безубыточности, рассчитывать вероятность выигрыша в кости или победы любимой команды в турнире. Хотите обогнать конкурентов? Решайте в Excel реальные задачи!

Инструмент Получить и преобразовать данные

Обсуждаемые вопросы

Как загрузить актуальный курс биткойна и сделать так, чтобы эти данные обновлялись каждый день?

Как загрузить цифры текущего населения городов США?

Бизнес-аналитикам нередко нужен простой способ импортировать в Excel данные из интернета, текстового файла, базы данных или другого источника. Эти данные нужно упорядочить или обработать. Наконец, импортированные данные должны обновляться, не отставать от изменений в их источнике. В этой главе мы познакомим читателя с потрясающими возможностями инструмента Excel 2019 «Получить и преобразовать данные» (Get & Transform), который позволяет аналитикам эффективно импортировать, по-новому упорядочивать и преобразовывать данные. Как видно из рис. 40.1, начиная с Excel 2016 инструмент «Получить и преобразовать данные» находится непосредственно на вкладке Данные (Data).

Как показано на рис. 40.2 и 40.3, нажав на кнопку Получить данные (Get Data), вы увидите подробный список источников данных, поддерживаемых инструментом Получить и преобразовать данные.

По причине ограниченности печатных площадей мы остановимся только на применении инструмента «Получить и преобразовать» к данным, добытым из интернета: как их импортировать, упорядочивать и преобразовывать.

Ответы на вопросы

Как загрузить актуальный курс биткойна и сделать так, чтобы эти данные обновлялись каждый день?

Многие люди завороженно наблюдают за ежедневными вариациями в стоимости биткойна. В этой главе мы покажем, как импортировать свежие ежедневные курсы биткойна в Excel. Наш рабочий лист будет отражать курс биткойна за последние 100 дней. Данные можно будет в любой момент обновить, чтобы отразить самые свежие.

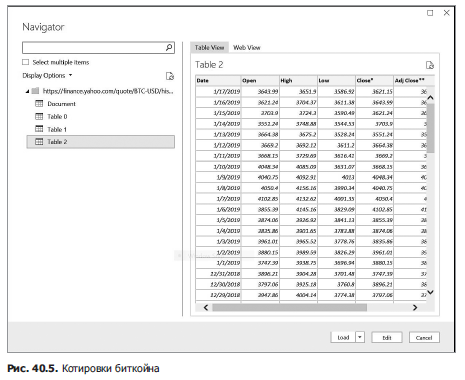
Для начала нам нужен веб-адрес, по которому находятся ежедневные курсы биткоийа. К счастью, эти сведения есть на Yahoo Finance. Нужный нам URL — finance.yahoo.com/quote/BTC-USD/history. Если вам нужны сведения по акциям (например, «Microsoft»), просто замените текст после /quote условным биржевым обозначением (тикером). Например, цены на акции «Microsoft» можно импортировать с адреса finance.yahoo.com/quote/MSFT/history. В пустой книге Excel нажмите Получить данные (Get Data) на вкладке Данные (Data), в разделе Получить и преобразовать данные (Get & Transform) на ленте и выберите Из других источников (Other Sources). Выбрав Из Интернета (From Web), заполните диалоговое окно, как показано на рис. 40.4. Вот вы и создали поисковый запрос! Нажав OK, вы увидите список всех таблиц, содержащихся по указанному веб-адресу (рис. 40.5). Щелкнув по таблице 2 (Table 2), вы увидите предпросмотр того, что будет импортировано. В нашем случае таблица 2 содержит необходимую информацию о курсе биткойна.

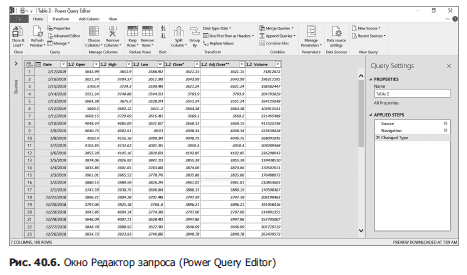
Теперь, если хотите, можете выбрать Загрузить (Load) и сразу же загрузить данные в свою книгу. Мы же, однако, вместо этого решили упорядочить импортируемые данные иным образом, поэтому выбираем Преобразовать данные (Edit), что вызывает окно Редактор Power Query (Power Query Editor), представленное на рис. 40.6.

Допустим, вам нужно импортировать только столбцы Дата (Date) и Скорректированная цена закрытия (Adj Close). Тогда с помощью клавиши Control мы выделяем столбцы, которые хотим удалить. Щелкнув правой кнопкой мыши, выберите Удалить столбцы (Remove Columns), и у вас останутся только столбцы Дата (Date) и Скорректированная цена закрытия (Adj Close). Или, предположим, вам также надо импортировать неделю года. Для этого сначала выполните щелчок правой кнопкой мышки по столбцу Дата (Date) и выберите Создать дубликат столбца (Duplicate Column). Выполнив на нем щелчок правой кнопкой мышки, выбираем Переименовать (Rename) и переименовываем дубликат столбца с датами именем Неделя года (Week of Year).

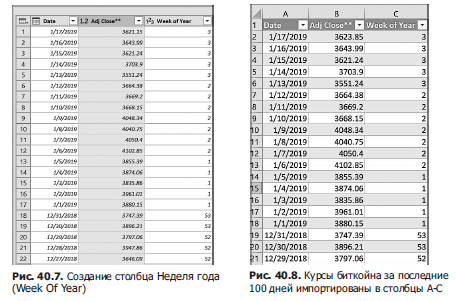
Выделив столбец Неделя года (Week Of Year), выберите из контекстного меню Преобразование (Transform), затем Неделя (Week) и Неделя года (Week Of Year). Как видим на рис. 40.7, теперь у нас есть столбец Неделя года (Week Of Year).

Теперь мы готовы импортировать нужные нам данные в Excel. Просто выберите Закрыть и загрузить (Close And Load) на вкладке Главная (Home). Вы увидите курс биткойна за 100 последние дней, как показано на рис. 40.8 и в файле Bitcoinquery.xlsx.

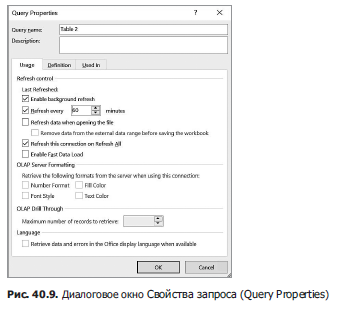
Чтобы в любой момент обновить данные, просто поместите курсор в ячейку внутри импортированных данных, выполните щелчок правой кнопкой мышки и выберите Обновить (Refresh). Если вы хотите, чтобы информация обновлялась через заданные промежутки времени или при каждом открытии файла, то выберите Обновить все (Refresh All) на вкладке Данные (Data), в группе Запросы и подключения (Queries and Con nections), выберите Запросы и подключения и затем на появившейся панели в Запросах щелкните по Table 2 и из контекстного меню выберите Свойства…. Теперь в диалоговом окне Свойства запроса (Query Properties) вы можете настроить параметры его обновления. Как показано на рис. 40.9, мы задали период обновления — каждые 60 минут.

Как загрузить цифры текущего населения городов США?

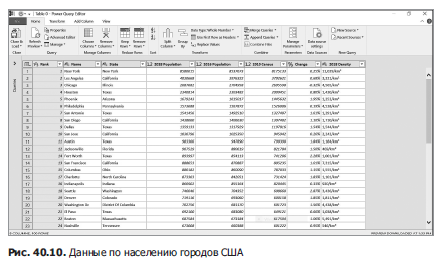
Допустим, вы хотите импортировать в Excel население 100 крупнейших городов США. Необходимые сведения содержатся на сайте worldpopulationreview.com/us-cities. Применяя тот же метод, что мы использовали для загрузки курсов биткойна, мы выбрали Таблицу 0 (Table 0) и получили результаты, представленные на рис. 40.10.

Предположим, мы хотим, чтобы город и штат находились в одном столбце, а население каждого города — в другом. Также предположим, что иные сведения нам не нужны, и мы не хотим их импортировать. Чтобы добиться этого, нажимаем Преобразование (Transform), удалим с помощью клавиши Control последние четыре столбца. Затем выбираем столбцы Город (City) и Штат (State). Выбираем Объединить столбцы (Merge Columns) из контекстного меню и выбираем запятую в качестве символа-разделителя между городом и штатом. Переименование получившегося столбца предложено выполнить здесь же — называем его Город и штат (City and state). Теперь из меню Файл (File) мы сможем загрузить требующиеся нам данные и поисковый запрос в файл UScityquery.xlsx. Конечный результат представлен на рис. 40.11.

Если вы хотите увидеть, из каких шагов состояло выполнение нашего интернет-запроса, поместите курсор в ячейку внутри импортированных данных и выберите Запрос (Query) в правой части меню ленты. Щелкнув Редактировать (Edit) в правой части экрана, вы увидите шаги, которые потребовались для реализации вашего запроса (рис. 40.12). Панель Параметры запроса также, как правило, отображается сама — где мы видим Примененные шаги. Разумеется, выбрав Закрыть и загрузить (Close And Load), вы вернетесь к книге Excel.

» Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для Хаброжителей скидка 25% по купону — Microsoft Excel

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.

Источник

УЭЙН ВИНСТОН

БИЗНЕС — МОДЕЛИРОВАНИЕ
И АНАЛИЗ ДАННЫХ
Р ЕШЕНИЕ

АКТУАЛЬНЫХ ЗАДАЧ С ПОМОЩЬЮ

Microsoft
Excel
6-Е ИЗДАНИЕ

2021

ББК 32.973.23-018.2
УДК 004.67
В49

Винстон Уэйн
В49

Бизнес-моделирование и анализ данных. Решение актуальных задач с помощью
Microsoft Excel. 6-е издание. — СПб.: Питер, 2021. — 944 с.: ил. — (Серия «IT для
бизнеса»).
ISBN 978-5-4461-1446-7
Уэйн Винстон научит вас быстро анализировать данные, принимать решения, подводить итоги,
составлять отчеты, обрабатывать данные и строить аналитические модели в Microsoft Excel 2019
и Ofﬁce 365. В новом шестом издании вас ждут более 800 бизнес-задач, основанных на реальных
ситуациях, а также обсуждение новых инструментов и функций. Где бы вы ни работали — в крупной
корпорации, небольшой компании, государственной или некоммерческой структуре, — это поможет
вам увеличить прибыль, снизить издержки или эффективно управлять производством.
Прочитав эту книгу, вы сможете cпрогнозировать результаты выборов, научитесь определять точки
безубыточности, рассчитывать вероятность выигрыша в кости или победы любимой команды в турнире.
Хотите обогнать конкурентов? Решайте в Excel реальные задачи!

16+ (В соответствии с Федеральным законом от 29 декабря 2010 г. № 436-ФЗ.)
ББК 32.973.23-018.2
УДК 004.67
Права на издание получены по соглашению с Pearson Education Inc. Все права защищены. Никакая часть данной
книги не может быть воспроизведена в к акой бы то ни был о форме без письменного разрешения владельцев
авторских прав.
Информация, содержащаяся в данной книге, получена из источников, рассматриваемых издательством как надежные. Тем не менее, имея в виду в озможные человеческие или технические ошибки, издательство не может
гарантировать абсолютную точность и полноту приводимых сведений и не несет ответственности за возможные
ошибки, связанные с использованием книги. Издательство не несет ответственности за доступность материалов,
ссылки на которые вы можете найти в этой книге. На момент подготовки книги к изданию все ссылки на интернетресурсы были действующими.

ISBN 978-1509305889 англ.
ISBN 978-5-4461-1446-7

© 2019 by Pearson Education, Inc.
© Перевод на русский язык ООО Издательство «Питер», 2021
© Издание на русском языке, оформление ООО Издательство
«Питер», 2021
© Серия «IT для бизнеса», 2021

Оглавление

Об а вторе …………………………………………………………………………………………….. 16
Введение …………………………………………………………………………………………….. 17
Новое в этом издании ………………………………………………………………….. 18
Что необходимо знать для работы с книгой …………………………………….. 19
Как работать с книгой ………………………………………………………………….. 19
Сопроводительный сайт ……………………………………………………………….. 20
Благодарности ……………………………………………………………………………. 20
Поддержка и обратная связь…………………………………………………………. 21
От издательства………………………………………………………………………….. 21
Глава 1

Основы моделирования в электронных таблицах …………………… 22
Ответы на вопросы ……………………………………………………………………… 22
Задания …………………………………………………………………………………….. 30

Глава 2

Имена диапазонов ………………………………………………………………… 31
Как создать именованный диапазон? ……………………………………………… 31
Ответы на вопросы ……………………………………………………………………… 36
Задания …………………………………………………………………………………….. 41

Глава 3

Функции поиска ……………………………………………………………………. 43
Синтаксис функций поиска …………………………………………………………… 43
Ответы на вопросы ……………………………………………………………………… 44
Задания …………………………………………………………………………………….. 48

Глава 4

Функция ИНДЕКС ………………………………………………………………….. 51
Синтаксис функции ИНДЕКС …………………………………………………………. 51
Ответы на вопросы ……………………………………………………………………… 51
Задания …………………………………………………………………………………….. 53

Глава 5

Функция ПОИСКПОЗ ……………………………………………………………… 54
Ответы на вопросы ……………………………………………………………………… 56
Задания …………………………………………………………………………………….. 60

Оглавление

Глава 6

Текстовые функции и инструмент Мгновенное заполнение …….. 61
Синтаксис текстовых функций ………………………………………………………. 62
Ответы на вопросы ……………………………………………………………………… 66
Задания …………………………………………………………………………………….. 77

Глава 7

Даты и функции работы с датами ………………………………………….. 80
Ответы на вопросы ……………………………………………………………………… 81
Задания …………………………………………………………………………………….. 86

Глава 8

Оценка инвестиций по чистой приведенной стоимости …………… 89
Ответы на вопросы ……………………………………………………………………… 90
Задания …………………………………………………………………………………….. 94

Глава 9

Внутренняя ставка доходности ……………………………………………… 96
Ответы на вопросы ……………………………………………………………………… 97
Задания …………………………………………………………………………………… 102

Глава 10

Еще несколько финансовых функций Excel ………………………….. 104
Ответы на вопросы ……………………………………………………………………. 104
Задания …………………………………………………………………………………… 114

Глава 11

Циклические ссылки …………………………………………………………… 119
Ответы на вопросы ……………………………………………………………………. 119
Задания …………………………………………………………………………………… 122

Глава 12

Функции ЕСЛИ, ЕСЛИОШИБКА, ЕСЛИМН, ВЫБОР и ПЕРЕКЛЮЧ … 125
Ответы на вопросы ……………………………………………………………………. 126
Задания …………………………………………………………………………………… 145

Глава 13

Время и функции времени …………………………………………………… 151
Ответы на вопросы ……………………………………………………………………. 151
Задания …………………………………………………………………………………… 157

Глава 14

Команда Специальная вставка …………………………………………….. 158
Ответы на вопросы ……………………………………………………………………. 158
Задания …………………………………………………………………………………… 164

Глава 15

Трехмерные формулы и гиперссылки ………………………………….. 165
Ответы на вопросы ……………………………………………………………………. 165
Задания …………………………………………………………………………………… 169

Оглавление

Глава 16

Инструменты проверки зависимостей и надстройка Inquire ….. 170
Ответы на вопросы ……………………………………………………………………. 173
Задания …………………………………………………………………………………… 181

Глава 17

Анализ чувствительности с помощью таблиц данных …………… 182
Ответы на вопросы ……………………………………………………………………. 183
Задания …………………………………………………………………………………… 191

Глава 18

Инструмент Подбор параметра …………………………………………….. 195
Ответы на вопросы ……………………………………………………………………. 196
Задания …………………………………………………………………………………… 198

Глава 19

Анализ чувствительности с помощью Диспетчера сценариев… 201
Ответ на вопрос ………………………………………………………………………… 201
Задания …………………………………………………………………………………… 206

Глава 20

Функции СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СЧЁТ, СЧЁТЗ
и СЧИТАТЬПУСТОТЫ ……………………………………………………………. 207
Ответы на вопросы ……………………………………………………………………. 209
Задания …………………………………………………………………………………… 213

Глава 21

Функции СУММЕСЛИ, СРЗНАЧЕСЛИ, СУММЕСЛИМН,
СРЗНАЧЕСЛИМН, МАКСЕСЛИ и МИНЕСЛИ ……………………………… 215
Ответы на вопросы ……………………………………………………………………. 217
Задания …………………………………………………………………………………… 221

Глава 22

Функция СМЕЩ …………………………………………………………………… 223
Ответы на вопросы ……………………………………………………………………. 224
Задания …………………………………………………………………………………… 235

Глава 23

Функция ДВССЫЛ ……………………………………………………………….. 238
Ответы на вопросы ……………………………………………………………………. 239
Задания …………………………………………………………………………………… 248

Глава 24

Условное форматирование ………………………………………………….. 249
Ответы на вопросы ……………………………………………………………………. 251
Задания …………………………………………………………………………………… 276

Глава 25

Сортировка в Excel ………………………………………………………………. 281
Ответы на вопросы ……………………………………………………………………. 281
Задания …………………………………………………………………………………… 289

Оглавление

Глава 2 6

Таблицы ……………………………………………………………………………… 291
Ответы на вопросы ……………………………………………………………………. 291
Задания …………………………………………………………………………………… 305

Глава 27

Счетчики, полосы прокрутки, переключатели, флажки,
группы и поля со списками ………………………………………………….. 307
Ответы на вопросы ……………………………………………………………………. 308
Задания …………………………………………………………………………………… 318

Глава 28

Революция в аналитике ………………………………………………………. 320
Ответы на вопросы ……………………………………………………………………. 320

Глава 29

Введение в оптимизацию с надстройкой Поиск решения ………. 326
Задания …………………………………………………………………………………… 330

Глава 30

Поиск решения при определении оптимального
ассортимента продукции……………………………………………………… 331
Ответы на вопросы ……………………………………………………………………. 331
Задания …………………………………………………………………………………… 341

Глава 31

Поиск решения при планировании расписания работы
сотрудников ……………………………………………………………………….. 344
Ответ на вопрос ………………………………………………………………………… 344
Задания …………………………………………………………………………………… 347

Глава 32

Поиск решения для задач транспортировки и распределения ….349
Ответ на вопрос ………………………………………………………………………… 349
Задания …………………………………………………………………………………… 352

Глава 33

Поиск решения для бюджетирования капиталовложений …….. 355
Ответ на вопрос ………………………………………………………………………… 355
Задания …………………………………………………………………………………… 360

Глава 34

Поиск решения при финансовом планировании …………………… 363
Ответы на вопросы ……………………………………………………………………. 364
Задания …………………………………………………………………………………… 368

Глава 35

Поиск решения при оценке спортивных команд …………………… 370
Ответ на вопрос ………………………………………………………………………… 371
Задания …………………………………………………………………………………… 374

Оглавление

Глава 36

Расположение складов по методу ОПГ с несколькими
начальными точками и согласно эволюционному
поиску решения ………………………………………………………………….. 376
Метод ОПГ с несколькими начальными точками и эволюционный
поиск решения ………………………………………………………………………….. 376
Ответы на вопросы ……………………………………………………………………. 381
Задания …………………………………………………………………………………… 385

Глава 37

Штрафы и эволюционный поиск решения ……………………………. 386
Ответы на вопросы ……………………………………………………………………. 386
Задания …………………………………………………………………………………… 390

Глава 38

Задача коммивояжера…………………………………………………………. 393
Ответы на вопросы ……………………………………………………………………. 393
Задания …………………………………………………………………………………… 396

Глава 39

Импорт данных из текстового файла или документа …………….. 398
Ответ на вопрос ………………………………………………………………………… 398
Задания …………………………………………………………………………………… 403

Глава 40

Инструмент Получить и преобразовать данные ……………………. 404
Ответы на вопросы ……………………………………………………………………. 405
Задания …………………………………………………………………………………… 410

Глава 41

Типы данных «Акции» и «География» …………………………………. 411
Ответы на вопросы ……………………………………………………………………. 411
Задания …………………………………………………………………………………… 415

Глава 42

Проверка достоверности данных …………………………………………. 416
Ответы на вопросы ……………………………………………………………………. 416
Задания …………………………………………………………………………………… 422

Глава 43

Обобщение данных на гистограммах и диаграммах Парето ….. 425
Ответы на вопросы ……………………………………………………………………. 425
Задания …………………………………………………………………………………… 437

Глава 44

Обобщение данных с помощью описательной статистики …….. 439
Ответы на вопросы ……………………………………………………………………. 440
Задания …………………………………………………………………………………… 457

Глава 45

Сводные таблицы и срезы для описания данных ………………….. 460
Ответы на вопросы ……………………………………………………………………. 461
Задания …………………………………………………………………………………… 505

10
Глава 46

Оглавление

Модель данных …………………………………………………………………… 509
Ответы на вопросы ……………………………………………………………………. 509
Задания …………………………………………………………………………………… 516

Глава 47

Power Pivot …………………………………………………………………………. 517
Ответы на вопросы ……………………………………………………………………. 518
Задания …………………………………………………………………………………… 531

Глава 48

2D-картограммы и 3D-карты Power Map ………………………………. 532
Ответы на вопросы ……………………………………………………………………. 532
Задания …………………………………………………………………………………… 543

Глава 49

Спарклайны ………………………………………………………………………… 544
Ответы на вопросы ……………………………………………………………………. 544
Задания …………………………………………………………………………………… 548

Глава 50

Обработка данных с помощью статистических функций
для баз данных …………………………………………………………………… 549
Ответы на вопросы ……………………………………………………………………. 551
Задания …………………………………………………………………………………… 556

Глава 51

Фильтрация данных и удаление дубликатов ………………………… 558
Ответы на вопросы ……………………………………………………………………. 560
Задания …………………………………………………………………………………… 572

Глава 52

Консолидация данных …………………………………………………………. 573
Ответ на вопрос ………………………………………………………………………… 573
Задания …………………………………………………………………………………… 577

Глава 53

Создание промежуточных итогов ………………………………………… 578
Ответы на вопросы ……………………………………………………………………. 578
Задания …………………………………………………………………………………… 582

Глава 54

Приемы работы с диаграммами …………………………………………… 583
Ответы на вопросы ……………………………………………………………………. 584
Задания …………………………………………………………………………………… 622

Глава 55

Оценка линейных зависимостей ………………………………………….. 625
Ответы на вопросы ……………………………………………………………………. 627
Задания …………………………………………………………………………………… 632

Оглавление

Глава 56

Моделирование экспоненциального роста……………………………. 634
Ответ на вопрос ………………………………………………………………………… 635
Задания …………………………………………………………………………………… 637

Глава 57

Степенная кривая ……………………………………………………………….. 638
Ответ на вопрос ………………………………………………………………………… 640
Задания …………………………………………………………………………………… 643

Глава 58

Представление зависимостей с помощью корреляции ………….. 645
Ответ на вопрос ………………………………………………………………………… 647
Задания …………………………………………………………………………………… 650

Глава 59

Введение во множественную регрессию ………………………………. 652
Ответы на вопросы ……………………………………………………………………. 652

Глава 60

Включение качественных факторов во множественную
регрессию …………………………………………………………………………… 659
Ответы на вопросы ……………………………………………………………………. 659

Глава 61

Моделирование нелинейных характеристик и взаимосвязей … 670
Ответы на вопросы ……………………………………………………………………. 670
Задания к главам 59–61 ……………………………………………………………… 674

Глава 62

Однофакторный дисперсионный анализ ………………………………. 678
Ответы на вопросы ……………………………………………………………………. 679
Задания …………………………………………………………………………………… 683

Глава 63

Рандомизированные блоки и двухфакторный
дисперсионный анализ ……………………………………………………….. 684
Ответы на вопросы ……………………………………………………………………. 685
Задания …………………………………………………………………………………… 693

Глава 64

Скользящие средние для временных рядов………………………….. 694
Ответ на вопрос ………………………………………………………………………… 694
Задание …………………………………………………………………………………… 696

Глава 65

Метод Винтерса и Лист прогноза………………………………………….. 697
Характеристики временных рядов ………………………………………………… 697
Определение параметров …………………………………………………………… 698
Определение начальных параметров для метода Винтерса ………………. 698
Вычисление сглаживающих постоянных………………………………………… 699

Оглавление

Инструмент Excel Лист прогноза ………………………………………………….. 701
Задания …………………………………………………………………………………… 704
Глава 66

Метод прогнозирования «по отношению
к скользящему среднему» …………………………………………………… 705
Ответы на вопросы ……………………………………………………………………. 705
Задание …………………………………………………………………………………… 708

Глава 67

Прогноз для особых случаев ……………………………………………….. 709
Ответы на вопросы ……………………………………………………………………. 709
Задания …………………………………………………………………………………… 717

Глава 68

Введение в теорию вероятности ………………………………………….. 718
Ответы на вопросы ……………………………………………………………………. 718
Задания …………………………………………………………………………………… 725

Глава 69

Введение в случайные величины …………………………………………. 728
Ответы на вопросы ……………………………………………………………………. 728
Задания …………………………………………………………………………………… 732

Глава 70

Биномиальные, гипергеометрические и отрицательные
биномиальные случайные величины …………………………………… 733
Ответы на вопросы ……………………………………………………………………. 734
Задания …………………………………………………………………………………… 740

Глава 71

Пуассоновская и экспоненциальная случайные величины ……. 742
Ответы на вопросы ……………………………………………………………………. 742
Задания …………………………………………………………………………………… 745

Глава 72

Нормальная случайная величина и Z-оценка ……………………….. 747
Ответы на вопросы ……………………………………………………………………. 747
Задания …………………………………………………………………………………… 755

Глава 73

Распределение Вейбулла и бета-распределение:
моделирование надежности механизмов
и продолжительности работы ……………………………………………… 758
Ответы на вопросы ……………………………………………………………………. 758
Задания …………………………………………………………………………………… 763

Глава 74

Создание вероятностных высказываний на основе прогнозов . 764
Ответы на вопросы ……………………………………………………………………. 765
Задания …………………………………………………………………………………… 767

Оглавление

Глава 75

Логарифмически нормальная случайная величина
в моделировании курса акций ……………………………………………… 768
Ответы на вопросы ……………………………………………………………………. 768
Задания …………………………………………………………………………………… 772

Глава 76

Импорт в Excel истории торгов (загрузка биржевых данных) … 773
Ответы на вопросы ……………………………………………………………………. 773
Задания …………………………………………………………………………………… 776

Глава 77

Введение в моделирование по методу Монте-Карло……………… 777
Ответы на вопросы ……………………………………………………………………. 777
Задания …………………………………………………………………………………… 786

Глава 78

Вычисление оптимальной цены предложения ……………………… 788
Ответы на вопросы ……………………………………………………………………. 788
Задания …………………………………………………………………………………… 792

Глава 79

Моделирование цен на акции и распределения средств
между а ктивами ………………………………………………………………….. 794
Ответы на вопросы ……………………………………………………………………. 795
Задания …………………………………………………………………………………… 803

Глава 80

Развлечения и игры: моделирование вероятностей
для азартных игр и спортивных соревнований …………………….. 804
Ответы на вопросы ……………………………………………………………………. 804
Задания …………………………………………………………………………………… 811

Глава 81

Анализ данных с помощью повторной выборки ……………………. 813
Ответ на вопрос ………………………………………………………………………… 813
Задания …………………………………………………………………………………… 816

Глава 82

Ценообразование опционов…………………………………………………. 818
Ответы на вопросы ……………………………………………………………………. 818
Задания …………………………………………………………………………………… 830

Глава 83

Определение потребительской ценности ……………………………… 833
Ответы на вопросы ……………………………………………………………………. 833
Задания …………………………………………………………………………………… 837

Глава 84

Оптимальный размер заказа в модели управления запасами… 839
Ответы на вопросы ……………………………………………………………………. 839
Задания …………………………………………………………………………………… 843

Оглавление

Глава 85

Построение моделей управления запасами
для неопределенного спроса ……………………………………………….. 844
Ответы на вопросы ……………………………………………………………………. 845
Задания …………………………………………………………………………………… 850

Глава 86

Теория массового обслуживания (теория очередей) …………….. 851
Ответы на вопросы ……………………………………………………………………. 851
Задания …………………………………………………………………………………… 856

Глава 87

Оценка кривой спроса …………………………………………………………. 858
Ответы на вопросы ……………………………………………………………………. 858
Задания …………………………………………………………………………………… 862

Глава 88

Ценообразование продуктов с сопутствующими товарами ……. 863
Ответ на вопрос ………………………………………………………………………… 863
Задания …………………………………………………………………………………… 866

Глава 89

Ценообразование продуктов с помощью субъективно
определяемого спроса…………………………………………………………. 868
Ответы на вопросы ……………………………………………………………………. 868
Задания …………………………………………………………………………………… 871

Глава 90

Нелинейное ценообразование ……………………………………………… 874
Ответы на вопросы ……………………………………………………………………. 874
Задания …………………………………………………………………………………… 882

Глава 91

Формулы массива и функции, возвращающие массив ………….. 883
Ответы на вопросы ……………………………………………………………………. 884
Задания …………………………………………………………………………………… 903

Глава 92

Запись макросов …………………………………………………………………. 907
Ответы на вопросы ……………………………………………………………………. 907
Задания …………………………………………………………………………………… 918

Глава 93

Продвинутый анализ чувствительности ……………………………….. 919
Ответ на вопрос ………………………………………………………………………… 919
Задания …………………………………………………………………………………… 921

Вивиан, Джен и Грегу.
Вы замечательные, и я вас очень люблю!

Об авторе

Уэйн Л. Винстон — почетный профессор Школы бизнеса Kelley
School of Business при Университете Индианы. Он также преподавал в У ниверситете Хьюстона и У эйк-Форест. Он получил
свыше 40 наград для преподавателей, обучил работе в Excel и моделированию в среде Excel множество бизнес-аналитиков из
компаний, входящих в F ortune 500, бухгалтерских фирм, армии
и флота США. Двукратный чемпион игры Jeopardy! и соавтор системы мониторинга игроков, применяемой Марком К убаном
и командой НБА «Даллас Мэверикс».

Введение
Работаете ли вы в крупной корпорации, в небольшой компании, в правительственной или некоммерческой структуре — если вы читаете эту книгу, то, скорее всего,
вы используете Microsoft для выполнения своих повседневных задач. Возможно,
вы занимаетесь тем, что подводите итоги, составляете отчеты и анализируете данные. Или же вы строите аналитические модели, призванные помочь работодателю
увеличить прибыль, снизить издержки или эффективно управлять операциями.
Начиная с 1999 г. я обучил продуктивному использованию программы Microsoft
Excel тысячи аналитиков в таких организациях, как Abbott Labs, консалтинговая
компания Booz Allen Hamilton, Bristol-Myers Squibb, Broadcom, Cisco Systems,
Deloitte Consulting, Drugstore.com, eBay , Eli Lilly, Ford, General Electric, General
Motors, Intel, Microsoft, MGM Hotels Morgan Stanley, NCR, Owens Corning, Pfizer,
Proctor & Gamble, PWC, Schlumberger, Tellabs, 3M, Армия США, Министерство
обороны США, Военно-морской флот США и Verizon. Студенты часто говорят
мне, что инструменты и методы, которые они освоили на занятиях, сэкономили
им массу рабочего времени благодаря тому, что важные бизнес-задачи теперь анализируются быстрее и рациональнее.
Методы решения многих бизнес-задач, которые описаны в этой книге, я использую и сам, когда консультирую компании. Например, мы с Excel помогли менеджерам баскетбольных команд НБА «Даллас Мэверикс» и «Нью-Йорк Никербокерс» оценить судейство, игроков и позиции игроков на поле. Последние 20 лет
я также веду занятия по бизнес-моделированию и анализу данных в Excel для
студентов, обучающихся по программам MBA в Школе бизнеса Kelley School
of Business при У ниверситете Индианы, в Бауэровском колледже бизнеса Bauer
College of Business при Университете Хьюстона и в Уэйк-Форест. (Мой преподавательский опыт подтвержден более чем 45 наградами для преподавателей, включая шесть наград Школы для преподавателей программ MBA.) Хочу заметить, что
95% студентов MBA из Университета Индианы выбрали мой курс моделирования
в электронных таблицах, который даже не входит в обязательную программу.
В этой книге я попытался изложить этот популярный курс так, чтобы его мог пройти каждый. Эта книга научит вас более эффективной работе в Excel, и вот почему:
Материалы протестированы на тысячах аналитиков из компаний, входящих
в Fortune 500, и правительственных организаций.
Книга написана в разговорном стиле. Я считаю, что такой стиль позволяет перенести дух успешной работы в аудитории на печатные страницы.
Для обучения я использую задания, упрощающие освоение концепций. В заданиях разбираются реальные ситуации, часто встречающиеся на практике.
Многие задания основаны на вопросах, которые задавали мне работники компаний, входящих в Fortune 500.

ВВЕДЕНИЕ

Я даю все инструкции, необходимые для изучения моих методов работы в Excel.
Вы будете читать мои пояснения и отслеживать процесс решения по примерам
листов Excel. Кроме того, я разместил файлы шаблонов для заданий на сопроводительном сайте книги ( MicrosoftPressStore.com/Excel2019DataAnalysis/downloads).
Вы можете использовать эти шаблоны для работы прямо в Excel и самостоятельно выполнить все задания.
Как правило, главы невелики по размеру и посвящены чему-то одному.Я старался
сделать так, чтобы каждую главу можно было освоить за два часа. Вопросы в начале каждой главы дадут вам общее представление о тех проблемах, которые вы
будете в состоянии разрешить после освоения темы данной главы.
Помимо формул Excel вы безболезненно освоите некоторые важные разделы математики. Например, вы познакомитесь со статистическими методами, прогнозированием, моделями оптимизации, моделированием по методу Монте-Карло, построением моделей управления запасами и теорией очередей. Также вы получите
представление о таких новшествах в деловом мышлении, как реальные опционы,
потребительская ценность и математические модели ценообразования.
В конце каждой главы я поместил список практических задач (всего их более 800),
с которыми вы можете работать самостоятельно. Многие задачи основаны на реальных ситуациях, с которыми имеют дело бизнес-аналитики компаний из списка
Fortune 500. Эти задачи помогут до конца понять изложенный в главе материал.
Ответы к задачам находятся на сопроводительном сайте книги.
И, самое главное, обучение прежде всего должно доставлять удовольствие. Прочитав эту книгу, вы узнаете, как прогнозировать президентские выборы в США, как
определить точки безубыточности для футбольных матчей, как вычислить вероятность выигрыша в кости и вероятность победы определенной команды в турнире
Национальной ассоциации студенческого спорта (NCAA). Благодаря подобным
интересным примерам вы получите множество интересных и важных сведений
о том, как решать бизнес-задачи с использованием Excel.
ПРИМЕЧАНИЕ
Для работы с этой книгой необходимо иметь программу Microsoft Excel 2019 или
Office 365. Однако для большей части книги будет вполне достаточно Excel 2013 или
2016. Предыдущие издания этой книги можно использовать с программами Excel 2003,
Excel 2007 или Excel 2010.

Новое в этом издании
В это издание книги внесены следующие изменения:
Добавлена новая глава (глава 40) об инструменте «Получить и преобразовать
данные» (Get&Transform).
Добавлена новая глава (глава 41) о новых типах данных — «География» и «Акции».
Обсуждение шести новых функций, входящих в Office 365, —
МАКСЕСЛИ, МИНЕСЛИ, СМЕЩ, ОЪЕДИНИТЬ и СЦЕП.

ЕСЛИМН,

Введение

Обсуждение (в главе 6) функции ТЕКСТ.
Обсуждение (в главе 48) картограмм и 3D-карт Power Map.
Обсуждение (в главе 65) инструмента «Лист прогноза».
Обсуждение (в главе 12) функции ВЫБОР.
Обсуждение (в главе 76) загрузки данных по различным акциям одновременно.
Обсуждение (в главе 93) продвинутого анализа чувствительности.

Что необходимо знать для работы с книгой
Для выполнения описанных в книге заданий вам не нужно знать Excel досконально. В принципе, достаточно уметь выполнять два ключевых действия.
Вводить формулы. Формулы всегда начинаются со знака равенства (=). Следует также знать знаки основных математических операторов. Например, звездочка (*) используется для умножения, слеш (/) — для деления, а знак вставки
(^) — для возведения в степень.
Работать со ссылками на ячейки. Важно помнить, что при копировании формулы, содержащей ссылку на ячейку , оформленную как $A$4 (для создания
абсолютной ссылки используется знак доллара), там, куда вы скопируете формулу, формула будет продолжать ссылаться на ячейку A4. При копировании
формулы с такой ссылкой, как $A4 (смешанная ссылка), номер столбца останется прежним, а номер строки изменится. И, наконец, при копировании формулы со ссылкой вида A4 (относительная ссылка) изменится и номер строки,
и номер столбца ячейки, ссылку на которую содержит формула.
Эти понятия подробно описаны в главе 1.

Как работать с книгой
Для выполнения заданий, представленных в книге, вы можете выбрать один из
двух подходов.
Можно открыть файл шаблона, соответствующий изучаемому заданию, и шаг
за шагом выполнять задания по мере прочтения книги. Вы удивитесь, насколько легким окажется процесс обучения и как много всего вы сможете узнать
и запомнить. Именно такой подход я использую при обучении студентов.
Вместо того чтобы работать с шаблоном, можно читать пояснения в книге
к окончательному варианту каждого файла с примером.

Сопроводительный сайт
У этой книги есть сопроводительный сайт, на котором предоставлен доступ ко всем
используемым в заданиях файлам (на сайт выложены как окончательные варианты
книг Excel, так и исходные шаблоны, с которыми можно работать самостоятельно).

ВВЕДЕНИЕ

Книги Excel и шаблоны лежат в папках, названных поглавно. К заданиям, которые
помещены в конце каждой главы, есть файлы примеров и ответы. Каждому файлу
с ответами присвоено имя, по которому его можно легко идентифицировать. Например, файл с ответом на задание 2 к главе 10 называется s10_2.xlsx.
Для работы с заданиями необходимо скопировать файлы примеров на свой компьютер. Эти файлы и другие данные вы можете скачать по адресу:
MicrosoftPressStore.com/Excel2019DataAnalysis/downloads

Для загрузки файлов откройте страницу в браузере и следуйте инструкции.

Благодарности
Я бесконечно благодарен Дженнифер Скуг (Jennifer Skoog) и Норму Т
онине
(Norm Tonina), которые поверили в меня и первыми пригласили вести занятия
по Excel для Microsoft Finance. В частности, Дженнифер помогла мне составить
план и методику занятий, на основе которых написана книга. Кейт Ланге (Keith
Lange) из компании Eli Lilly, Пэт Китинг (Pat Keating) и Дуг Хопп (Doug Hoppe)
из корпорации Cisco Systems, а также Дэннис Фуллер (Dennis Fuller) из армии
США помогли мне прояснить мое понимание того, как следует преподавать анализ и моделирование данных.
Редакторы проекта Рик и Шарлотта К уген (Rick and Charlotte Kughen) — превосходно справились с копированием и редактурой рукописи. Выпускающий редактор Лоретта Йейтс (Loretta Yates) буквально нянчилась с проектом до самого
его успешного завершения, а еще она сразу же отвечает на письма! Также я благодарен своим слушателям из организаций, где преподавал, и студентам из Школы
бизнеса Kelley School of Business при У ниверситете Индианы и из Бауэровского
колледжа бизнеса Bauer College of Business при Университете Хьюстона. Они научили меня таким вещам об Excel, которые я сам не знал.
Алекс Блантон (Alex Blanton), ранее работавший в Microsoft Press, горячо приветствовал этот проект с самого начала и разделял мою точку зрения на создание
текста в непринужденном стиле, ориентированного на бизнес-аналитиков.
И наконец, моя любимая талантливая жена Вивиан (Vivian) и мои замечательные
дети, Дженнифер (Jennifer) и Грегори (Gregory), мирились с тем, что я проводил
долгие часы в выходные дни за клавиатурой.

Поддержка и обратная связь
Ниже вы найдете информацию об опечатках, клиентской поддержке и о том, куда
направлять ваши отзывы и предложения.

Контакты
Давайте продолжим наше общение. Twitter: http://twitter.com/MicrosoftPress.

Введение

Найденные опечатки и поддержка
Мы приложили все усилия к тому , чтобы информация в книге и на сопроводительном сайте была точной и правильной.
Сведения о найденных опечатках и соответствующих исправлениях печатаются
на этой странице (на английском языке):
MicrosoftPressStore.com/Excel2019DataAnalysis/errata

Если вы найдете какую-нибудь новую ошибку , пожалуйста, сообщите нам о ней
через эту же страницу.
Если вам требуется дополнительная помощь, напишите в клиентский отдел
«Microsoft Press Book» на электронный адрес microsoftpresscs@pearson.com.
Пожалуйста, обратите внимание, что по указанным выше адресам не предлагается
поддержка программных и аппаратных продуктов Microsoft, поэтому за таковой
вам следует обращаться сюда: http://support.microsoft.com.

От издательства
Ваши замечания, предложения, вопросы отправляйте по адресу
(издательство «Питер», компьютерная редакция).

comp@piter.com

Мы будем рады узнать ваше мнение!
На веб-сайте издательства www.piter.com вы найдете подробную информацию о наших книгах. Когда мы только начинали перевод книги, перед нами встала сложная
задача: подготовить книгу таким образом, чтобы ей могли пользоваться владельцы как английской, так и русской версии Excel. У большинства пользователей
в России и других странах СНГ установлена русская версия Excel, однако многие
интернациональные компании используют только английские версии Excel, поэтому все команды, формулы, функции и элементы интерфейса даются на двух
языках.
В книге сохранены авторские скриншоты интерфейса, так как большая их часть
показывает процесс решения авторских задач. Перевод элементов интерфейса
дается в тексте, в скобках сохранены оригинальные названия, английские названия функций приводятся в начале глав, далее по тексту идет только русское
название.
Обратите внимание: в английской версии Excel десятичные дроби отделяются от
целого числа точкой, в русской версии — запятой. Числа с точкой не воспринимаются в русскоязычных версиях Excel, как числовой формат . В файлах для самостоятельной работы используются числа с точкой.
Задачи для самостоятельной работы можно скачать по адресу: MicrosoftPressStore.
com/Excel2019DataAnalysis/downloads.

ГЛ А В А 1

Основы моделирования
в электронных таблицах

Обсуждаемые вопросы
Как эффективно определить понедельные выплаты всех моих сотрудников?
Как эффективно определить, сколько пекарня должна каждому из своих поставщиков?
Как оценить, какое количество посетителей будет иметь новый фитнес-клуб через 10 лет?
Как правильно задавать порядок выполнения операций в Excel?
Как определить влияние на прибыль изменения в цене и себестоимости единицы
товара для кофейни по соседству?

Мой друг Деннис Фуллер сказал как-то: «Электронная таблица для бизнес-аналитика — это то же, что холст для художника». Никто из нас не может написать
шедевр, подобный «Звездной ночи» Ван Г ога, но, зная Excel, мы можем начать
с чистого листа электронной таблицы и создать свой собственный шедевр, моделирующий виртуально любую ситуацию. Для многих барьером к овладению Excel
является понимание того, как в Excel работают формулы. В этой главе мы разберем несколько различных простых моделей таблиц, которые помогут вам перейти
к созданию сложных моделей в Excel.

Ответы на вопросы
?

Как эффективно определить понедельные выплаты всех моих сотрудников?

В файле Wagestemp.xlsx (в папке Templates), показанном на рис. 1.1, заданы количество отработанных часов и почасовая оплата нескольких сотрудников. Необходимо определить выплату каждому сотруднику, а также общую сумму отработанных
часов и среднюю почасовую оплату.
Для вычисления недельной зарплаты сотрудника Luka необходимо перемножить
значения в ячейках C4 и D4. Для этого в ячейку E4 вы помещаете формулу =C4*D4.

Основы моделирования в электронных таблицах

Рис. 1.1. Расчет недельной платежной ведомости

Для вычисления зарплаты Terry можно было бы перейти в ячейку E5 и ввести формулу =C5*D5, но можно воспользоваться командой Excel Копировать (Copy), что
позволит легко вычислить недельную зарплату каждого сотрудника, будь их хоть
миллион. (Excel 2007 и более поздние версии поддерживают 1 048 576 строк!) Просто перейдите в ячейку E4 и нажмите Ctrl+C для копирования формулы. Затем выделите диапазон E5:E11, или примените комбинацию Ctrl+V, или нажмите Enter, чтобы
применить эту формулу к диапазону E5:E11. Кроме того, вы можете скопировать
формулу из E4 в диапазон E5:E11, наведя курсор на маленький квадратик в нижнем
правом углу ячейки E4, и, после того как курсор изменит свой вид на тонкое черное
перекрестье, нажать левую кнопку мыши и перетащить нужную формулу в диапазон E5:E11. В каждой ячейке, куда скопирована формула, Excel перемножит два значения слева от этой ячейки в столбце E. Отметьте, что мы будем часто использовать
функцию Excel Ф.ТЕКСТ (FORMULATEXT) (появившуюся в Excel 2013), чтобы текст
формул был виден в электронной таблице. Например, если ввести в ячейке F4 формулу =FORMULATEXT(E4), то в ней отобразится формула из E4.
Кроме того, вы можете вычислить в ячейке C12 (вы можете это увидеть в файле
Wagesfinal.xlsx) общую сумму отработанных часов за неделю с помощью формулы
=SUM(C4:C11). В ячейке E14 я вычислил среднюю зарплату работника по формуле
=СРЗНАЧ(E4:E11) .

Как эффективно определить, сколько пекарня должна каждому из своих
поставщиков?

В файле Bakery1temp.xlsx задана цена за фунт, которую пекарня платит каждому из
шести поставщиков сахара, масла и муки. Нам нужно узнать сумму , которая выплачивается каждому поставщику сахара, муки и масла. Также нам нужно определить суммарную выплату.

ГЛАВА 1

Как показано на рис. 1.2, в ячейке E23 мы вычисляем сумму, выплаченную за сахар
поставщику Supplier 1, умножая стоимость фунта сахара, запрошенную Supplier 1,
на количество сахара, закупленного у этого поставщика. Для этого мы используем
формулу =E5*E14.
Чтобы вычислить сумму, выплаченную каждому поставщику за каждый продукт,
мы можем воспользоваться любым из приведенных далее способов:
Выделите ячейку E23 и, нажав Ctrl+C, выберите диапазон E23:G28, а затем нажмите Ctrl+V.
Выделите ячейку E23 и, нажав Ctrl+C, выберите диапазон E23:G28, а затем нажмите Enter.
Выделите ячейку E23 и, после того как вид курсора изменится на перекрестье,
перетащите формулу в F23:G23. Затем перетащите диапазон E23:G23 в E24:G28.

Рис. 1.2. Вычисление выплат пекарни: цены у поставщиков различаются

Чтобы найти сумму, выплаченную каждому из поставщиков, введите в H23 формулу =СУММ(E23:G23) и скопируйте эту формулу в
H24:H28. Введя формулу
= СУММ(E23:E28) в ячейку E29 и скопировав эту формулу в F29:H29, вы получите
общую сумму, выплаченную за каждый продукт.
Более быстрый способ задать эти суммы — это выбрать диапазон H23:H28 и (с нажатой клавишей Ctrl) выбрать диапазон E30:G30. Затем просто нажмите кнопку

Основы моделирования в электронных таблицах

Сумма (AutoSum, значок Σ) в группе Редактирование (Editing) на вкладке Главная
(Home), как показано на рис. 1.3.

Рис. 1.3. Использование кнопки AutoSum для суммирования группы чисел

Команда Сумма выбирает (не всегда верно, так что будьте внимательны!) диапазон
ячеек, которые вы хотите просуммировать, чтобы заполнить выделенные ячейки.
Сумма может сэкономить вам пять секунд времени!
В файле Bakery2temp.xlsx, изображенном на рис. 1.4, мы исходим из предположения, что все поставщики запрашивают одинаковую цену на каждый из продуктов.
Снова вычислите сумму, выплаченную каждому из поставщиков за каждый продукт, и общую сумму, которую пекарня выплатит каждому поставщику.

Рис. 1.4. Вычисление выплат пекарни: цены у поставщиков одинаковые

Действуя, как предлагалось ранее, неискушенный читатель может ввести в ячейку E23 формулу =E12*E14 и скопировать эту формулу в диапазон E23:G28. К сожалению, в строках от 24 до 28 ссылки на строки и 12, и 14 будут изменяться. При
копировании этой формулы мы хотели бы, чтобы ссылка на строку 14 менялась,
а на 12 — нет, потому что нам нужно брать цену каждого продукта из строки 12.

ГЛАВА 1

Чтобы этого добиться, мы помещаем перед 12 знак $. Это называется абсолютной
адресацией или блокированием строки. Когда в формуле перед номером строки
стоит знак доллара и эта формула копируется, номер строки останется неизменным. Поэтому мы вводим в ячейку E23 формулу =E$12*E14.
Простой способ добавить знак доллара — использовать клавишуF4. Если вы выделите часть формулы и будете несколько раз нажимать F4, Excel циклически добавит сначала знак доллара к строке и к столбцу, затем только к строке, затем только
к столбцу, а затем совсем уберет знак доллара.

Как оценить, какое количество посетителей будет иметь новый фитнесклуб через 10 лет?

Ответ вы найдете в файле Chapter1customer.xlsx, приведенном на рис. 1.5. Т еперь
нам требуется создать модель с чистого листа. Модели в электронных таблицах
содержат исходные данные или предположения, которые мы используем, чтобы
вычислить требуемые выходные значения. В базовой исходной модели оценки посетителей нам необходимы три исходных значения:
Число посетителей, посещающих клуб, на начало года 1 (Year 1).
Коэффициент оттока клиентов: доля посетителей на начало года (не считая
новых посетителей), которые перестают посещать клуб, каждый год.
Число новых посетителей, приходящих каждый год.

Рис. 1.5. Прогнозирование числа посетителей с помощью построения модели
с входными и выходными значениями

Мы ввели значения этих исходных данных в ячейки C2:C4. Важно следить, чтобы
исходные данные в электронной таблице были отделены от выходных значений

Основы моделирования в электронных таблицах

и никогда не программировались формулами Excel. Отделение в электронной
таблице исходных данных от выходных значений позволяет легко определять, как
изменение в исходных данных влияет на выходные значения.
В строках 8–17 рассчитывается количество посетителей на конец года путем сложения количества новых посетителей с количеством посетителей в начале года за
вычетом посетителей, которые перестают посещать клуб. В ячейках С2:С4 содержатся входные значения этой таблицы. Ключевыми отношениями нашей модели
оценки числа посетителей являются следующие:
(Посетители на конец года t (End Year t Customers)) = (Посетители на начало года t (Start Year t Customers)) + (Новые посетители года t (New Year t
Customers)) – (Переставшие ходить (Year Customer quits)).
(Посетители на начало года 1 (Start Year 1 Customers)) = значение в ячейке C2.
Другим ключом к решению этой задачи является понимание того, что нам нужно
отслеживать в течение каждого года:
число посетителей на начало года;
новые посетители, приходящие каждый год;
посетители, перестающие ходить;
число посетителей на конец года.
В ячейке C8 мы вычисляем начальное число посетителей в первый год (Year 1) по
формуле =C2. Затем в столбце D мы повторно вводим число новых посетителей
для каждого года, копируя значение из D8 в D9:D17 с помощью формулы =$C$3
или C$3.
Обратите внимание, что цифре 3 должен предшествовать знак доллара; в противном случае при копировании формулы из ячейки D8 обращение к 3 изменится, что приведет к неверным резуль татам. Перед символом C знак доллара
можно как вставлять, так и не вставлять, так как мы не копируем эту формулу
в другой столбец.
Число посетителей, перестающих посещать клуб каждый год, — это число посетителей в начале года, умноженное на коэффициент оттока клиентов. Поэтому
в столбце E мы вычисляем количество посетителей, отсеивающихся каждый год,
копируя из E8 в E9:E18 формулу =$C$4*C8 или C$4*C8. Отметьте, что здесь перед
цифрой 8 мы не используем знак доллара, потому что при копировании мы хотим,
чтобы 8 изменялась на 9, 10 и т. д.
Количество посетителей на конец каждого года вычисляется как сумма посетителей на начало этого года плюс новые клиенты, из которой вычитается количество
покинувших клуб клиентов. Скопировав из F8 в F9:F18 формулу =C8+D8-F8, мы
вычисляем число посетителей на конец каждого года.
Для годов 2–10 число клиентов на начало года равно числу клиентов в конце прошлого года, поэтому копируем из C9 в C10:C17 формулу =F8. Мы получим (не пере-

ГЛАВА 1

живайте по поводу дробных чисел), что через 10 лет в нашем фитнес-клубе будет
около 127 посетителей.
Проницательный читатель может возразить, что на самом деле мы не знаем коэффициента оттока клиентов и количества новых посетителей каждый год. Это действительно так. Мы должны выполнить анализ чувствительности, чтобы выяснить,
как изменения числа новых клиентов и коэффициента ежегодного оттока клиентов
меняют конечное число посетителей 10-го года. В главе 17 мы изучим, как использовать таблицы данных для выполнения такого анализа чувствительности.

Как правильно задавать порядок выполнения операций в Excel?

Сложные формулы в Excel часто содержат множество сложных математических
операций, таких как возведение в степень, умножение и деление. При вычислении
формул Excel следует правилам выполнения математических операций:
Сначала выполняются операции в скобках.
Затем выполняются все возведения в степень, следуя слева направо.
Затем выполняются все умножения и деления, следуя слева направо.
После этого выполняются все сложения и вычитания, следуя слева направо.
Например, Excel будет вычислять формулу =3+6*(5+4)/3–7 в следующем порядке.
3+6 × 9/3 – 7 (скобки сняты).
3 + 54/3 – 7 (умножение).
3 + 18 – 7 (деление).
21 – 7 (суммирование).
14 (вычитание).
Или, например, предположим, нам нужно извлечь квадратный корень из значения
ежегодного процентного роста продаж наших продуктов (см. файл PEMDAStemp .xlsx
и рис. 1.6).

Рис. 1.6. Пример применения порядка выполнения операций

В F4 мы ввели правильную формулу, =((E4-D4)/D4)^0.5, и скопировали ее в F5:F6.
Эта формула заставляет Excel вычислить процентную долю (выраженную в виде
дроби) роста продаж (.5) и затем извлечь квадратный корень. Окончательное значение .707 (квадратный корень из .5) правильно. Обратите внимание: знак ^ (находится на клавиатуре на цифре 6) — это знак возведения в степень.

Основы моделирования в электронных таблицах

В G4 мы ввели неправильную формулу, =(E4-D4)/D4^.5.
По этой формуле сначала вычисляется E4-D4 = 50, а затем извлекается квадратный
корень из D4 (10). После этого конечный (неверный) резуль тат такой: 50/10 = 5.

Как определить влияние на прибыль изменения в цене и себестоимости
единицы товара для кофейни по соседству?

Ключом к пониманию того, как изменение цены влияет на прибыль, является
правильная оценка кривой спроса. Кривая спроса показывает , как изменения
в цене меняют спрос на продукт . Давайте предположим, что дневной спрос на
кофе в кофейне составляет 100-15*Цена в долларах. (См. главы 87–89, где подробнее рассматривается оценка кривой спроса.) В файле Coffee.xlsx (рис. 1.7)
показано, как дневная прибыль зависит от того, как меняются себестоимость
и цена чашки кофе.

Рис. 1.7. Зависимость спроса от цены и себестоимости

Мы исходим из предположения, что себестоимость чашки кофе варьируется между $0,50 и $2,00, а цена чашки кофе варьируется между $2,00 и $5,00. Чтобы определить прибыль для каждой комбинации цена/себестоимость, нам потребуется
ввести в F10 формулу =($F$5-$F$4*F$9)*(F$9-$E10) и скопировать эту формулу из
F10 в F10:L13.
Ссылки на F5 и F4 — абсолютные, так как нам нужно, чтобы ни строка, ни столбец не менялись при копировании формулы.
Ссылка на цену (ячейка F9) требует использования знака доллара (или блокирования строки), так как нам всегда требуется, чтобы цена бралась из строки 9.
Ссылка на себестоимость (E10) требует, чтобы перед буквой столбца стоял
знак доллара, так как нам всегда требуется, чтобы себестоимость бралась из
столбца E.

ГЛАВА 1

Мы получим, например, что если себестоимость равна $1,50, а мы продаем чашку
за $4,00, наша прибыль составит $100: (100 – 4*15)*(4 – 1,5) = $100.
Заметьте, что для каждого значения себестоимости цена, при которой прибыль
максимальна, выделяется желтым фоном. В главе 24 вы узнаете, как использовать
условное форматирование для создания такого стильного выделения.

Задания
1. Проводя занятия, я дал пять домашних заданий, каждое оценив в 25 баллов,
и три теста, оценив каждый в 100 баллов. Я вычисляю итоговую оценку студента, присваивая весовой коэффициент в 75% для тестов и 25% для домашних заданий. Создайте таблицу для вычисления итоговой оценки студента,
которая позволит вам изменять весовой коэффициент , присвоенный тестам.
2. Индекс массы тела человека (ИМТ , BMI) вычисляется так: BMI=703*Weight/
Height2. Создайте таблицу вычисления ИМТ человека.
3. Последовательность Фибоначчи определяется следующим образом: F0 = 0, Fx
= 1, а для n больше 1 — FN+X = FN + Fn–1. Создайте таблицу для вычисления
последовательности Фибоначчи. Покажите, что для больших значений N отношение последовательных чисел Фибоначчи стремится к золотому сечению
(1,62).
4. Знаменитый эффект бабочки утверждает, что если бабочка взмахнет крыльями на Таити, это маленькое событие может вызвать ураган в Т ехасе. Предположим, что погода во время t всегда имеет значение между 0 и 1 и управляется
выражением xt+1 = 4 × xt × (1–xt). Для xt = 0,3 и xt = 0,3000001 вычислите x1, x2,
… x50. Как ваши вычисления иллюстрируют эффект бабочки?
5. Зарыбление озера оценивается в настоящее время в 12 230 особей. Каждый
год коэффициент рождений у рыб равен 1,2, а коэффициент смертей равен
0,7. Покажите, что если улов каждый год будет составлять 6115 особей, количество рыбы в озере будет оставаться постоянным.
6. Коэффициент Джини обычно используется для измерения расслоения общества по уровню годового дохода. Если доходы n человек перечислены по возрастанию (x1= наименьший доход, xn = наибольший доход), то коэффициент
Джини вычисляется по формуле:

Создайте таблицу, определяющую коэффициент Джини для группы из пяти человек.

ГЛАВА 2

Имена диапазонов

Обсуждаемые вопросы
Необходимо вычислить общий объем продаж в штатах Аризона, Калифорния,
Монтана, Нью-Йорк и Нью-Джерси. Можно ли для вычисления общего объема продаж воспользоваться формулой AZ+CA+MT+NY+NJ вместо формулы
СУММ(A21:A25) и получить правильный ответ?
Для чего нужна формула СРЗНАЧ(A:A)?
Чем различаются имена с областью действия «книга» и «лист»?
Мне начинают нравиться имена диапазонов. Я стал использовать имена диапазонов во многих книгах, которые я создаю в офисе. Однако эти имена не появляются в формулах. Как добиться отображения недавно созданных имен диапазонов
в ранее созданных формулах?
Каким образом можно вставить список имен всех диапазонов (и представляемых
ими ячеек) в лист?
Предполагаемый годовой доход вычисляется как кратный прошлогоднему доходу. Может ли формула выглядеть как (1+прирост)*предыдущий_год?
Для каждого дня недели даны почасовая оплата и количество отработанных часов. Можно ли вычислить итоговую сумму оплаты за каждый день по формуле
почасовая_оплата*часы?

Возможно, вам доводилось работать с листами, в которых использовалась, например, формула =СУММ(A5000:A5049). В этом случае вам приходилось догадываться,
что находится в ячейках A5000:A5049. Если в ячейках A5000:A5049 содержатся объемы продаж по всем штатам США, не кажется ли вам формула=СУММ(USSales) более понятной? В данной главе рассказывается, как присваивать имена отдельным
ячейкам и диапазонам ячеек, а также вставлять имена диапазонов в формулы.

Как создать именованный диапазон?
Создать именованный диапазон можно тремя способами:
ввести имя диапазона в поле Имя (Name);
выбрать на вкладке Формулы (Formulas) в группе Определенные имена (Deﬁned
Names) инструмент Создать из выделенного (Create from Selection);

ГЛАВА 2

выбрать на вкладке Формулы (Formulas) в группе Определенные имена (Deﬁned
Names) инструментов Присвоить имя (Deﬁne Name) или Диспетчер имен (Name
Manager).

Создание имени диапазона в поле Имя
Поле Имя (Name) (рис. 2.1) находится прямо над меткой столбца A, слева от поля
Строка формул (Formula bar). Для создания имени диапазона выделите ячейку или
диапазон ячеек, которым требуется присвоить имя, затем перейдите в поле Имя
(Name) и введите имя диапазона. Имя диапазона создастся, когда вы нажмете Enter.
При нажатии в поле Имя (Name) на стрелку появятся имена диапазонов, которые
есть в текущей книге. Клавиша F3 открывает диалоговое окноВставка имени (Paste
Name) с именами всех диапазонов. Если выбрать в полеИмя (Name) имя диапазона,
то все ячейки, соответствующие этому диапазону , отметятся автоматически. Так
вы можете убедиться, что правильно выбрали ячейку или диапазон ячеек для указанного имени. Имена диапазонов не чувствительны к регистру букв.
Скажем, нам нужно присвоить ячейке F3 имя east, а ячейке F4 — имя west (см.
рис. 2.2 и файл Eastwestempt.xlsx). Выделите ячейку F3, введите east в поле Имя
(Name) и нажмите Enter. Выделите ячейку F4, введите west в поле Имя (Name) и нажмите Enter. Теперь в какой-нибудь другой ячейке для ссылки на ячейкуF3 можно
указывать =east, а не =F3. То есть вместо любой ссылки east в формуле будет автоматически подставлено значение из ячейки F3.

Рис. 2.1. Можно создать имя диапазона,
выбрав диапазон ячеек, который вы хотите
назвать, и введя имя в поле Имя

Рис. 2.2. Присвоение ячейкам F3 и F4
имен east и west

Предположим, необходимо присвоить имя data прямоугольному диапазону ячеек
(например, A1:B4). Выделите диапазон ячеек A1:B4, введите data в поле Имя (Name)
и нажмите Enter . Теперь мы можем вычислить среднее значение содержимого
ячеек A1:B4 с помощью функции СРЗНАЧ (AVERAGE) по формуле =СРЗНАЧ(data) (см.
файл Data.xlsx и рис. 2.3).
Иногда требуется присвоить имя диапазону ячеек, состоящему из нескольких несмежных прямоугольных диапазонов. Например, на рис. 2.4 и в файле
Noncontigtemp.xlsx показан диапазон с именем noncontig, состоящий из ячеек B3:C4,
E6:G7 и B10:C10. Выделите любой из трех прямоугольников (здесь B3:C4). С нажатым Ctrl выделите оставшиеся два диапазона ( E6:G7 и B10:C10). Отпустите Ctrl,
введите noncontig в поле Имя (Name) и нажмите Enter. Теперь в любой формуле имя

Имена диапазонов

noncontig указывает на содержимое ячеек B3:C4, E6:G7 и B10:C10. Например, введя формулу =СРЗНАЧ(noncontig) в ячейку E11, мы получим значение 4,75 (сумма
12 чисел в заданном диапазоне равна 57 и 57/12 = 4,75).

Рис. 2.3. Присвоение диапазону A1:B4 имени data

Рис. 2.4. Присвоение имени несмежному диапазону ячеек

Создание имен с помощью инструмента Создать
из выделенного
На листе Statestemp.xlsx указаны мартовские продажи для каждого из 50 штатов
США. На рис. 2.5 вы видите фрагмент этих данных. Требуется присвоить каждой
ячейке в диапазоне B6:B55 правильную двухбуквенную аббревиатуру — сокращенное название штата. Сначала выделите диапазон A6:B55 и на вкладке Формулы
(Formulas) в группе Определенные имена (Defined Names) выберите Создать из выделенного (Create from Selection), как показано на рис. 2.6, а затем в открывшемся
диалоговом окне установите флажок В столбце слева (Left column) (рис. 2.7) и нажмите OK.
Теперь имена в первом столбце выделенного диапазона связаны с ячейками во
втором столбце выделенного диапазона. Таким образом, ячейке B6 присвоено имя
диапазона AL, ячейке B7 — AK и т. д. Мы бы устали создавать имена таких диапазонов с помощью поля Имя (Name)! Нажмите на стрелку в поле Имя (Name) и убедитесь, что все имена диапазонов созданы.

ГЛАВА 2

Рис. 2.5. После присвоения имен ячейкам, содержащим продажи и сокращенные названия
штатов, при ссылке на ячейку вместо буквы столбца и номера строки можно использовать
соответствующее сокращенное название

Рис. 2.6. Выберите Создать
из выделенного

Рис. 2.7. Установите флажок в столбце
слева

Создание имен диапазонов с помощью инструмента
Присвоить имя
Откроем диалоговое окно Создание имени (New Name), показанное на рис. 2.8. Для
этого на вкладке Формулы (Formulas) в группе Определенные имена (Defined Names)
нажмите Присвоить имя (Define Name) в меню, показанном на рис. 2.6.
Предположим, нам нужно присвоить имя range1 (в именах диапазонов регистр букв
не учитывается) диапазону ячеек A2:B7. Введите range1 в поле Имя (Name) и выделите диапазон или введите =A2:B7 в поле Диапазон (Refers To). Диалоговое окно Создание имени (New Name) должно выглядеть так, как на рис. 2.9. Нажмите OK.
Нажав на стрелку раскрывающегося списка в поле Область (Scope), вы можете выбрать строку Книга (Workbook) или любой лист в книге, указав тем самым область

Имена диапазонов

действия имени. Более подробно этот вопрос обсуждается далее в этой главе,
а пока выберите область действия по умолчанию — Книга (Workbook). Кроме того,
к любым именам диапазонов можно добавить комментарии.

Рис. 2.8. Диалоговое окно Создание имени
до задания каких-либо имен

Рис. 2.9. Диалоговое окно Создание имени
при создании имени диапазона

Диспетчер имен
Если теперь вы нажмете на стрелку в поле Имя (Name), то увидите в раскрывающемся списке имя range1 (и все остальные созданные ранее диапазоны).
В Microsoft Excel 2019 есть простой способ изменения или удаления имен диапазонов. На вкладке Формулы (Formulas) выберите группу Определенные имена
(Defined Names) и откройте Диспетчер имен (Name Manager), показанный на рис. 2.6.
Появится список имен всех диапазонов. Например, так выглядит диалоговое окно
Диспетчер имен (Name Manager) для файла States.xlsx (рис. 2.10).
Для изменения имени диапазона дважды щелкните кнопкой мыши на имени этого
диапазона или выделите его и нажмите кнопку Изменить (Edit). После этого можно
изменить не только имя диапазона, но и его область действия, а также поменять
ячейки в диапазоне.
Чтобы удалить некоторое подмножество имен диапазонов, выделите имена диапазонов: если имена диапазонов идут последовательно, выделите первое имя
в группе имен, которую требуется удалить, затем, удерживая Shift, выделите последнее имя в группе. Если требуемые имена не следуют друг за другом, можно
выделить любое из имен, которое необходимо удалить, а далее, удерживая Ctrl,
выделить остальные требуемые имена диапазонов. Затем нажмите кнопку Удалить (Delete).
Теперь рассмотрим несколько конкретных примеров использования имен диапазонов.

ГЛАВА 2

Рис. 2.10. Диалоговое окно Диспетчер имен для файла States.xlsx

Ответы на вопросы
Необходимо вычислить общий объем продаж в штатах Аризона, Калифорния, Монтана, Нью-Йорк и Нью-Джерси. Можно ли для вычисления общего объема продаж воспользоваться формулой AZ+CA+MT+NY+NJ вместо
формулы СУММ(A21:A25) и получить правильный ответ?

Вернемся к файлу States.xlsx, в котором двухбуквенные аббревиатуры были присвоены как имена диапазонов соответствующим объемам продаж. Для вычисления общего объема продаж в Алабаме, на Аляске, в Аризоне и в Арканзасе можно
воспользоваться формулой =СУММ(B6:B9). Однако если указать ячейки B6, B7, B8
и B9, формула будет выглядеть так: =AL+AK+AZ+AR. Последняя запись, конечно,
гораздо нагляднее.
В качестве другого примера использования имен диапазонов рассмотрим файл
Historicalinvesttemp.xlsx (рис. 2.11), в котором содержится годовая процентная доходность акций, казначейских векселей и облигаций. (На этом рисунке часть
строк скрыта; данные заканчиваются в строке 89.)
Выделите диапазон ячеек B1:D89 и на вкладке Формулы (Formulas) в группе Определенные имена (Defined Names) выберите Создать из выделенного (Create from
Selection). В этом примере имена диапазона указаны В строке выше (Top row). Диа-

Имена диапазонов

пазон B2:B89 получает имя Акции (Stocks), диапазон C2:C89 — имя Векселя (Tbills)
и диапазон D2:D89 — имя Облигации (Bonds10). Затем введите в ячейке =СРЗНАЧ(,
но перед тем как вводить диапазон, можно нажать F3, и откроется диалоговое
окно Вставка имени (Paste Name), показанное на рис. 2.12.

Рис. 2.11. Ретроспективные данные
по инвестициям

Рис. 2.12. Добавление имени диапазона
в формулу в диалоговом окне Вставка имени

Теперь в окне Вставка имени (Paste Name) выберите из списка имя Акции и нажмите
OK. После ввода закрывающей скобки в формуле =СРЗНАЧ(Акции) автоматически
будет рассчитано среднее значение доходности акций ( 11,41 %). Прелесть этого
подхода состоит в в том, что даже не помня точно, где находятся данные, можно
работать с данными о доходности акций в любом месте книги!
Было бы упущением с моей стороны не упомянуть о такой интересной возможности Microsoft Excel 2019, как автозавершение формул (AutoComplete). После
ввода =СРЗНАЧ(В автоматически появится список диапазонов и функций, имена
которых начинаются с В. Для завершения ввода имени диапазона дважды щелкните на имени Векселя, и затем вам останется только ввести закрывающую скобку.

Для чего нужна формула СРЗНАЧ(A:A)?

При использовании в формуле имени столбца (в форматеA:A, C:C и т. д.) весь столбец обрабатывается в Excel как именованный диапазон. Например, по формуле
=СРЗНАЧ(A:A) вычисляется среднее значение всех чисел в столбце A. Использование имени диапазона для целого столбца очень эффективно при частом вводе
новых данных в столбец. Например, если столбец A содержит данные о ежемесячных продажах продукта, то новые данные добавляются каждый месяц, и по такой
формуле вычисляется актуальное среднее значение ежемесячных продаж. Однако

ГЛАВА 2

будьте осторожны: если ввести формулу =СРЗНАЧ(A:A) в столбец A, то появится сообщение о циклической ссылке, так как значение в ячейке, содержащей формулу
расчета среднего, будет зависеть от ячейки, содержащей среднее значение. Способ
разрешения циклических ссылок приведен в главе 11. Аналогично по формуле
=СРЗНАЧ(1:1) рассчитывается среднее значение всех чисел в строке 1.

Чем различаются имена с областью действия «книга» и «лист»?

Понять различие вам поможет файл Sheetnames.xlsx. При создании имен с помощью поля Имя (Name) областью действия имен по умолчанию становится Книга.
Предположим, что с помощью поля Имя (Name) имя sales присвоено диапазону
ячеек E4:E6 на листе Лист3, и эти ячейки содержат числа 1, 2 и 4 соответственно.
Если мы введем формулу =СУММ(sales) на любом листе, то получим 7, так как областью действия созданных в поле Имя (Name) имен является книга. То есть если
в любом месте книги указано имя sales (областью действия которого является вся
книга), то оно указывает на ячейки E4:E6 на листе Лист3.
Теперь введите числа 4, 5, 6 в ячейки E4:E6 на листе Лист1 и 3, 4, 5 в ячейки E4:E6
на листе Лист2. Откройте окно Диспетчер имен (Name Manager), присвойте имя jam
ячейкам E4:E6 на Лист1 и определите область действия этого имени как Лист1. Перейдите на Лист2, откройте окно Диспетчер имен, присвойте имя jam ячейкам E4:E6
и определите область действия этого имени как Лист2. Диалоговое окно Диспетчер
имен теперь будет выглядеть как на рис. 2.13.

Рис. 2.13. Имена на уровне листа и на уровне книги в диалоговом окне Диспетчер имен

Имена диапазонов

Что произойдет, если ввести формулу =СУММ(jam) на каждом из трех листов? На
листе Лист1 будут просуммированы значения ячеек E4:E6. Так как в этих ячейках
содержатся числа 4, 5 и 6, получится 15. На листе Лист2 также будут просуммированы значения ячеек E4:E6, что в сумме даст 3 + 4 + 5 = 12. Однако на листе Лист3
вычисление по формуле =СУММ(jam) вызовет ошибку #ИМЯ?, поскольку на этом
листе отсутствует диапазон с именем jam. Если где-либо на листе Лист3 ввести
формулу =СУММ(Лист2!jam), Excel распознает имя на уровне листа, которое представляет диапазон ячеек E4:E6 листа Лист2, и в результате получится 3 + 4 + 5 = 12.
То есть если вы указываете перед именем диапазона нужное имя листа с восклицательным знаком (!), Excel обращается к диапазону на другом листе.
Мне начинают нравиться имена диапазонов. Я стал определять имена диапазонов во многих книгах, которые я создаю в офисе. Однако эти имена не
появляются в формулах. Как добиться отображения недавно созданных имен
диапазонов в ранее созданных формулах?

Рассмотрим файл Applynames.xlsx и рис. 2.14.

Рис. 2.14. Новые имена диапазонов в старых формулах

В ячейке F3 на листе Лист1 указана цена продукта, а в ячейке F4 — потребность
в продукте =10000–300*F3. Ячейки F5 и F6 содержат себестоимость единицы продукции и постоянные затраты соответственно. Прибыль вычисляется в ячейкеF7
по формуле =F4*(F3–F5)–F6. В диапазон E3:E7 введены новые имена. Выделите
диапазон E3:F7, затем присвойте ячейкам следующие имена: ячейке F3 — цена,
ячейке F4 — потребность, ячейке F5 — себестоимость, ячейке F6 — затраты и ячейке F7 — прибыль. Для этого на вкладке Формулы (Formulas) используйте Создать
из выделенного (Create from Selection) и флажок в столбце слева (Left column). Теперь имена созданных диапазонов необходимо отобразить в формулах ячеек F4
и F7. Для этого выделите диапазон, для которого они создаются (в данном случае F4:F7). Затем на вкладке Формулы (Formulas) в группе Определенные имена
(Defined Names) нажмите стрелку Присвоить имя (Define Name) и выберите инструмент Применить имена (Apply Names). Выделите в окне имена, которые требуется
применить, и нажмите OK. Обратите внимание, что в ячейке F4 теперь находится
формула =10000–300*цена, а в ячейке F7 формула =потребность*(цена–себестоимость)–затраты, что и требовалось.

ГЛАВА 2

Если вам нужно применить имена диапазонов ко всему листу, выделите его кнопкой Выделить все (Select All) на пересечении заголовков столбцов и строк.

Каким образом можно вставить список имен всех диапазонов (и представляемых ими ячеек) в лист?

Нажмите F3. Откроется окно Вставка имени (Paste Name). Теперь нажмите кнопку
Все имена (Paste List) — см. рис. 2.12. На листе, начиная с текущей ячейки, появится
список имен диапазонов и соответствующих им ячеек.

Предполагаемый годовой доход вычисляется как кратный прошлогоднему
доходу. Может ли формула выглядеть как (1+прирост)*предыдущий_год?

Решение этой проблемы ищите в файле Last year.xlsx. Как показано на рис. 2.15,
требуется вычислить доходы за 2014–2021 гг. с приростом 10% в год, начиная с базового уровня $300 млн в 2014 г.
В поле Имя (Name) присвойте ячейке B3 имя прирост. А теперь самое интересное!
Переместите курсор в ячейку B7 и на вкладке Формулы (Formulas) в группе Определенные имена (Defined Names) выберите Присвоить имя (Define Name) — откроется
диалоговое окно Редактировать имя (Edit Name). Введите в него данные, как показано на рис. 2.16; на рисунке видно, как, при положении курсора в ячейке B7, мы можем создать имя предыдущий_год, которое всегда будет ссылаться на ячейку ровно
на одну строку выше текущей.

Рис. 2.15. Создание имени диапазона
для предыдущего года

Рис. 2.16. Создание имени диапазона
для подсчета продаж предыдущего года

Поскольку мы сейчас на ячейке B7, Excel интерпретирует имя диапазона как указывающее на ячейку, находящуюся над текущей ячейкой. Конечно, это не сработает, если в ссылке на ячейку B6 останется знак доллара. Т еперь если мы введем
в ячейку B7 формулу =предыдущий_год*(1+прирост) и скопируем ее в диапазон

Имена диапазонов

B8:B13, каждая ячейка будет содержать нужную нам формулу , по которой содержимое ячейки, находящейся над активной, будет умножаться на 1,1.

Для каждого дня недели даны почасовая оплата и количество отработанных часов. Можно ли вычислить итоговую сумму оплаты за каждый день
по формуле почасовая_оплата*часы?

Как показано на рис. 2.17 (см. файл Namedrows.xlsx), строка 12 содержит данные
о почасовой оплате по дням недели, а строка 13 — количество отработанных часов
за каждый день.

Рис. 2.17. Использование имен диапазонов для ссылки на различные строки

Выберите строку 12 (щелкнув на 12) и в поле Имя (Name) введите имя почасовая_
оплата. Выберите строку 13 и введите в поле Имя (Name) имя часы. Если теперь
в ячейку F14 ввести формулу =почасовая_оплата*часы и скопировать эту формулу
в диапазон G14:L14, то в каждом столбце появится произведение двух множителей — почасовой оплаты и отработанных часов.

Замечания
В Excel нельзя использовать буквы r и c в качестве имен диапазонов.
Если вы используете Создать из выделенного (Create from Selection), пробелы
в созданном имени автоматически будут заменены на подчеркивание ( _). Например, имя Product 1 будет создано как Product_1.
Имена диапазонов не могут начинаться с цифр или выглядеть как ссылка на
ячейку. Например, нельзя использовать имена 3Q и A4. Поскольку Excel поддерживает более 16 000 столбцов, такие имена, как cat1, являются недопустимыми, поскольку существует ячейка CAT1. Если вы попробуете присвоить
ячейке имя CAT1, появится сообщение о том, что вы ввели недопустимое имя.
Возможно, самый наилучший вариант — назвать ячейку cat1_.
Единственные символы, которые можно использовать в именах диапазонов,
это точка (.) и подчеркивание (_).

Задания
1. Файл Stock.xlsx содержит данные о ежемесячной доходности акций General
Motors и Microsoft. Присвойте имена диапазонам, содержащим ежемесячную

ГЛАВА 2

доходность для каждой акции, и вычислите среднемесячную доходность каждой акции.
2. Создайте новую пустую книгу и присвойте имя Red диапазону, содержащему
ячейки A1:B3 и A6:B8.
3. Если задать широту и долготу любых двух городов, в файле Citydistances.xlsx
будет вычислено расстояние между этими двумя городами. Определите имена диапазонов для широты и долготы каждого города и проверь те, чтобы эти
имена отображались в формуле для расчета расстояния.
4. Файл Sharedata.xlsx содержит количество акций ( shares) для каждого вида акций и цену одной акции ( price). Вычислите стоимость акций каждого вида по
формуле =shares*price.
5. Создайте имя диапазона для расчета среднего значения продаж за последние
пять лет. Предполагается, что годовые продажи перечислены в единственном
столбце.

ГЛАВА 3

Функции поиска

Обсуждаемые вопросы
Как создать формулу для вычисления налоговых ставок на основе дохода?
Как посмотреть цену продукта по идентификатору продукта?
Допустим, что цена продукта изменяется со временем. Известна дата продажи
продукта. Как создать формулу для вычисления цены продукта?

Синтаксис функций поиска
Функция поиска в Excel позволяет просматривать значения в диапазонах на листах книги. В Microsoft Excel 2016 доступен как вертикальный (с помощью функции ВПР), так и горизонтальный просмотр (с помощью функции ГПР). При вертикальном просмотре операция поиска начинается с первого столбца диапазона.
При горизонтальном просмотре поиск начинается с первой строки диапазона.
Я сосредоточусь на функции ВПР, поскольку в большинстве формул используется
вертикальный просмотр.

Синтаксис функции ВПР
Ниже приведен синтаксис функции ВПР (VLOOKUP). В квадратных скобках ( [ ])
указаны необязательные аргументы.
ВПР(искомое_значение;таблица;номер_столбца;[интервальный_просмотр])

искомое_значение (lookup_value) — значение для поиска в первом столбце таблицы;
таблица (table_range) — диапазон таблицы. В него входит первый столбец, в котором выполняется поиск искомого значения, и любые другие столбцы, в которых требуется просмотреть результаты расчетов по формулам;
номер_столбца (column_index) — номер столбца в таблице, из которого функция
поиска возвращает значение;
интервальный_просмотр (range_lookup) является необязательным аргументом.
Он устанавливает точное или приблизительное совпадение. Если значение интервальный_просмотр равно ИСТИНА или опущено, первый столбец диапазона
таблицы должен быть отсортирован по возрастанию. Если значение интерваль-

ГЛАВА 3
ный_просмотр равно ИСТИНА или опущено и в первом столбце таблицы найдено точное совпадение, Excel основывает поиск на табличной строке, в которой
найдено точное совпадение. Если значение интервальный_просмотр равно ИСТИНА
или опущено и нет точного совпадения, то поиск основывается на наибольшем
значении в первом столбце, не превышающем искомое значение. Если значение
интервальный_просмотр равно ЛОЖЬ и в первом столбце таблицы найдено точное совпадение, поиск основывается на табличной строке, в которой найдено
точное совпадение. Если точного совпадения нет , Excel выдает сообщение об
ошибке #Н/Д (недоступно). В главе 12 вы узнаете, как использовать функцию
ЕСЛИОШИБКА (IFERROR), чтобы Excel не выдавал подобной ошибки ( #Н/Д). Обратите внимание, что значение 1 для аргумента интервальный_просмотр эквивалентно значению ИСТИНА, а значение 0 эквивалентно значению ЛОЖЬ.

Синтаксис функции ГПР
Функция ГПР (HLOOKUP) ищет значение в первой строке (а не в первом столбце)
таблицы. Для функции ГПР используйте синтаксис функции ВПР, только поменяйте номер_столбца на номер_строки.
Теперь рассмотрим несколько интересных примеров с использованием функций
поиска.

Ответы на вопросы
?

Как создать формулу для вычисления налоговых ставок на основе дохода?

Вот как работает функция ВПР с первым столбцом таблицы, состоящим из чисел,
отсортированных по возрастанию. Допустим, налоговая ставка зависит от дохода,
как показано в таблице.
Уровень доходов

Налоговая ставка

$0–$9999

15%

$10 000–$29 999

30%

$30 000–$99 999

34%

$100 000 и выше

40%

Как создать формулу для расчета налоговой ставки см. в файле
рис. 3.1.

Lookup.xlsx и на

Сначала в диапазон ячеек D6:E9 мы ввели соответствующие данные (налоговые
ставки и точки прерывания). Таблице D6:E9 присвоено имя lookup. Рекомендуется
всегда присваивать имена ячейкам, используемым в качестве диапазона таблицы.

Функции поиска

Рис. 3.1. Функция поиска для расчета налоговой ставки.
Числа в первом столбце таблицы отсортированы по возрастанию

Тогда нам не нужно помнить точное местонахождение таблицы, а при копировании любой формулы, включающей функцию поиска, диапазон поиска всегда будет правильным. Затем для демонстрации работы функции поиска я вввел
в диапазон D13:D17 значения доходов. Налоговая ставка для уровней доходов,
указанных в диапазоне D13:D17, была рассчитана путем копирования формулы
=ВПР(D13;Lookup;2;ИСТИНА) из E13 в E14:E17.
Проверьте, как работает поиск в ячейках E13:E17. Обратите внимание, что ответ
всегда берется из второго столбца таблицы, поскольку в формуле указан номер
столбца 2.
В D13 доход, равный -1000, вызвал ошибку #Н/Д, поскольку такая сумма меньше самого низкого уровня доходов в первом столбце таблицы. Если вам нужно
связать налоговую ставку 15% с доходом –$1000, замените 0 в ячейке D6 числом, не большим -1000.
В D14 доход в $30 000 точно совпадает со значением в первом столбце таблицы,
поэтому функция возвращает значение ставки 34%.
В D15 доход в $29 000 не имеет точного совпадения в первом столбце таблицы. Это означает, что функция поиска остановилась на самом большом числе в первом столбце таблицы, не превышающем $29 000; в данном случае это
$10 000. Функция возвратила налоговую ставку из второго столбца таблицы,
соответствующую $10 000, то есть 30%.
В D16 доход в $98 000 не имеет точного совпадения в первом столбце таблицы.
Функция поиска остановилась на самом большом числе в первом столбце таб-

ГЛАВА 3

лицы, не превышающем $98 000. Она возвратила налоговую ставку из второго
столбца таблицы, соответствующую $30 000, то есть 34%.
В D17 доход в $104 000 не имеет точного совпадения в первом столбце таблицы. Функция поиска остановилась на самом большом числе в первом столбце
таблицы, не превышающем $104 000, что означает возврат налоговой ставки из
второго столбца таблицы, соответствующей $100 000, то есть 40%.
В F13:F17 я изменил значение аргумента интервальный_просмотр с ИСТИНА на ЛОЖЬ,
и скопировал из ячейки F13 в F14:F17 формулу =ВПР(D13;Lookup;2;ЛОЖЬ). Ячейка F14 по-прежнему содержит налоговую ставку 34%, поскольку в первом столбце
таблицы имеется точное совпадение — 30000. Во всех других ячейках F13:F17 Excel
выдал ошибку #Н/Д, поскольку уровни дохода в этих ячейках не имеют точного
совпадения в первом столбце таблицы.

Как посмотреть цену продукта по идентификатору продукта?

Нередко бывает так, что числа в первом столбце не отсортированы по возрастанию. Например, там могут быть перечислены идентификаторы продуктов или
имена сотрудников. Из своей практики я знаю, что тысячи финансовых аналитиков не умеют пользоваться функцией поиска, если в первом столбце числа не
указаны в возрастающем порядке. Здесь нужно помнить только одно простое правило: для аргумента интервальный_просмотр указывайте значение ЛОЖЬ.
Например, файл Lookup.xlsx (рис. 3.2) содержит цену для пяти продуктов, указанных по идентификаторам. Каким создать формулу , которая по идентификатору
продукта выдавала бы цену продукта?

Рис. 3.2. Поиск цен по идентификаторам продуктов. Если таблица не отсортирована
по возрастанию, укажите в формуле значение ЛОЖЬ для последнего аргумента
функции поиска

Многие ввели бы в ячейку I18 формулу =ВПР(H18;Lookup2;2). Но, если вы опустите четвертый аргумент (интервальный_просмотр), предполагается, что его значение

Функции поиска

равно ИСТИНА. Тогда будет возвращена неправильная цена (3,50), поскольку идентификаторы продуктов в таблице Lookup2 (ячейки H11:I15) перечислены не в алфавитном порядке. Если ввести в ячейку I18 формулу =ВПР(H18;Lookup2;2;ЛОЖЬ),
цена будет возвращена правильная (5,20).
Для поиска зарплаты сотрудника по его фамилии или идентификационному номеру укажите значение ЛОЖЬ в формуле аналогичным образом.
Кстати, на рис. 3.2 видно, что столбцы A–G скрыты. Чтобы скрыть нужные столбцы, сначала выделите их. Затем на вкладке Главная (Home) в группе Ячейки (Cells)
раскройте список Формат (Format), в Видимость (Visibility) выберите Скрыть или отобразить (Hide & Unhide) и затем Скрыть столбцы (Hide Columns).

Допустим, что цена продукта изменяется со временем. Известна дата продажи продукта. Как создать формулу для вычисления цены продукта?

Допустим, цена продукта зависит от даты его продажи. Каким образом можно написать для формулы функцию поиска правильной цены продукта? Например, для
следующей таблицы?
Дата продажи

Цена

Январь–апрель 2005 г.

$98

Май–июль 2005 г.

$105

Август–декабрь 2005 г.

$112

Напишите формулу для определения правильной цены продукта для любой из
дат продажи продукта в 2005 г . Для разнообразия воспользуйтесь функцией ГПР.
Даты изменения цены приведены в первой строке таблицы (см. файл Datelookup.
xlsx и рис. 3.3).

Рис. 3.3. Функция ГПР для определения цены,
изменяющейся в зависимости от даты продажи

ГЛАВА 3

Я скопировал формулу =ГПР(B8,lookup,2,ИСТИНА) из C8 в C9:C11. Формула пытается сравнить даты из столбца B с первой строкой диапазона B2:D3. Для любой даты
между 01.01.05 и 30.04.05 функция поиска выбирает 01.01.05 и возвращает значение цены из B3; для любой даты между 01.05.05 и 31.07.05 функция поиска выбирает 1 мая и возвращает значение цены из C3; и для любой даты после 01.08.05
выбирается 1 августа и возвращается значение цены из D3.

Задания
1. В файле Hr.xlsx указаны идентификационные номера, оклады и стаж работников. Создайте формулу для поиска зарплаты работника по идентификационному коду. Создайте еще одну формулу, находящую стаж работника по его
идентификационному коду.
2. В файле Assign.xlsx работники распределены по четырем группам. Т акже там
указано, насколько данный работник пригоден для работы в каждой группе
(по шкале от 0 до 10). Напишите формулу, которая вычисляет, насколько пригоден каждый работник для группы, в которую его назначили.
3. Вы подумываете о рекламе продуктов Microsoft на спортивном канале. Чем
больше рекламных объявлений вы покупаете, тем ниже цена одного объявления (см. таблицу ниже).
Количество рекламных объявлений

Цена одного рекламного объявления

1–5

$12 000

6–10

$11 000

11–20

$10 000

21 и более

$9000

Например, при покупке 8 рекламных объявлений за одно объявление придется выложить $11 000, а при покупке 14 объявлений — $10 000. Напишите
формулу, рассчитывающую общие затраты для любого количества рекламных
объявлений.
4. Вы подумываете о рекламе продуктов Microsoft в популярной музыкальной
телепрограмме. За первую группу рекламных объявлений вы платите фиксированную сумму, но если вы покупаете больше рекламных объявлений, цена
за каждое объявление снижается (см. таблицу ниже).
Количество рекламных объявлений

Цена одного рекламного объявления

1–5

$12 000

6–10

$11 000

11–20

$10 000

21 и более

$9000

Функции поиска

Например, при покупке 8 рекламных объявлений первые 5 объявлений обойдутся в $12 000 каждое, а оставшиеся — по $11 000. При покупке 14 объявлений первые 5 стоят $12 000, следующие 5 по $11 000 и оставшиеся 4 по
$10 000. Напишите формулу расчета общих затрат на покупку любого количества объявлений. Подсказка: вам потребуются минимум три столбца в таблице и две функции поиска в формуле.
5. В следующей таблице приведены ежегодные процентные ставки по предоставляемым банком кредитам на 1, 5, 10 и 30 лет.
Срок кредитования, лет

Процентная ставка, %

Если кредит в банке взят на любой срок от 1 до 30 лет
, не указанный в таблице,
процентная ставка рассчитывается путем интерполяции между ставками, указанными в таблице. Например, если кредит взят на 15 лет, процентная ставка
определяется по формуле:
.
Напишите формулу расчета процентной ставки по кредиту для любого срока
от 1 года до 30 лет.
6. Расстояние между двумя городами США (Аляску и Г авайи не учитываем)
можно вычислить приблизительно по следующей формуле:

В файле Citydata.xlsx приведен список городов США с шириной и долготой.
Создайте таблицу, вычисляющую расстояние между любыми двумя городами
из данного списка.
7. На первом листе книги Pinevalley.xlsx указаны зарплаты сотрудников Университета Pine Valley, на втором листе указан их возраст, на третьем — стаж работы. Создайте четвертый лист , содержащий зарплату, возраст и стаж каждого
сотрудника.
8. В файле Lookupmultiplecolumns.xlsx приведены данные продаж в магазине электроники. Имя продавца будет введено в B17. Создайте формулу Excel, которую можно скопировать из C17 в D17:F17 и которая извлекает данные о том,
сколько этот продавец продал радиотоваров, в C17, телевизоров — в D17, принтеров — в E17 и CD — в F17.

ГЛАВА 3

9. В файле Grades.xlsx приведены экзаменационные оценки студентов. Допустим,
соотношение баллов и оценок следующее (см. табл.).
Баллы

Оценка

Ниже 60

60–69

70–79

80–89

90 и выше

При помощи формулы Excel определите оценку каждого студента по баллам.
10. В файле Employees.xlsx вы найдете рейтинг (по шкале от 0 до 10), присвоенный
каждым из 35 сотрудников трем заданиям. В файле также указаны задания,
выданные каждому сотруднику. С помощью формулы определите рейтинг ,
который каждый сотрудник присвоил назначенному ему заданию.
11. Допустим, что за один доллар дают 1000 иен, 5 песо или 0,7 евро. Создайте
электронную таблицу, в которую можно ввести сумму в долларах США, указать валюту и затем перевести введенную сумму в указанную валюту.
12. В файле Qb2013.xlsx содержится статистика по квотербэкам (QB) национальной футбольной лиги за сезон 2013 г . Напишите в ячейках J2 и K2 формулы,
возвращающие количество забитых мячей и перехватов мяча конкретного нападающего, когда вы вводите его имя в ячейке I2.
13. Файл NBAplayers.xlsx содержит данные о возрасте и заработной плате нескольких игроков НБА. Введите формулы в ячейках J5:K50, которые возвращают
возраст и зарплату каждого игрока.
14. В столбце F файла Hardware.xlsx содержатся коды хозтоваров, а в столбце G —
цены этих товаров. В столбцах M–O перечислены количество и цена, по которой магазин хозтоваров закупил различные товары. Определите общую стоимость закупок магазина хозтоваров.

ГЛАВА 4

Функция ИНДЕКС

Обсуждаемые вопросы
У меня есть список расстояний между различными городами США. Как должна
выглядеть функция, возвращающая расстояние между Сиэтлом и Майами?
Можно ли создать формулу со ссылкой на весь столбец, содержащий сведения
о расстоянии между Сиэтлом и другими городами?

Синтаксис функции ИНДЕКС
Функция ИНДЕКС (INDEX) возвращает содержимое ячейки в указанной строке
и указанном столбце внутри массива чисел. Наиболее часто для функции ИНДЕКС
используется следующий синтаксис:
ИНДЕКС(массив;номер_строки;номер_столбца)

Например, формула =ИНДЕКС(A1:D12;2;3) возвращает содержимое ячейки во второй строке третьего столбца массива A1:D12. Это ячейка C2.

Ответы на вопросы
У меня есть список расстояний между различными городами США. Как
должна выглядеть функция, возвращающая расстояние между Сиэтлом
и Майами?

В файле Index.xlsx (рис. 4.1) содержатся данные о расстоянии между восемью городами США. Диапазону C10:J17 с этими данными присвоено имя Distances.
Допустим, вы хотите ввести в ячейку расстояние между Бостоном и Денвером.
Поскольку расстояния от Бостона до других городов перечислены в первой строке массива Distances, а расстояния до Денвера указаны в четвертом столбце массива, формула выглядит так: =ИНДЕКС(distances;1;4). В результате Бостон и Денвер
разделяет 1991 миля. Аналогично расстояние (гораздо более значительное) между Сиэтлом и Майами можно узнать по формуле =ИНДЕКС(distances;6;8). Сиэтл
и Майами разделяют 3389 миль.

ГЛАВА 4

Рис. 4.1. Использование функции ИНДЕКС для определения расстояния между городами

Представьте, что футбольная команда из Сиэтла отправляется в турне, в котором они проводят игры в Финиксе, Лос-Анджелесе, Денвере, Далласе и Чикаго.
В конце выездной серии игр команда возвращается в Сиэтл. Легко ли подсчитать,
сколько миль они проедут в течение турне? Как показано на рис. 4.2, следует просто перечислить города в порядке посещения ( 8-7-5-4-3-2-8), начиная и заканчивая Сиэтлом, и скопировать формулу =ИНДЕКС(distances;C21;C22) в ячейки с D21
по D26. Формула в ячейке D21 определяет расстояние между Сиэтлом и Финиксом (город номер 7), формула в ячейке D22 — расстояние между Финиксом и ЛосАнджелесом и т. д. Всего команда проедет 7112 миль. И просто забавы ради покажите с помощью функции ИНДЕКС, что команда «Майами Хит» путешествует за
сезон больше любой другой команды НБА.

Рис. 4.2. Расстояния для турне футбольной команды из Сиэтла

Можно ли создать формулу со ссылкой на весь столбец, содержащий сведения о расстоянии между Сиэтлом и другими городами?

Функция ИНДЕКС позволяет сослаться на всю строку или весь столбец какого-либо массива. Если установить значение 0 для номера строки, то функция ИНДЕКС

Функция ИНДЕКС

будет ссылаться на указанный столбец. А если установить 0 для номера столбца,
то функция ИНДЕКС ссылается на указанную строку . Предположим, необходимо
определить суммарное расстояние между всеми перечисленными городами и Сиэтлом. Можно ввести любую из следующих формул:
=СУММ(ИНДЕКС(distances;8;0))
=СУММ(ИНДЕКС(distances;0;8))

В первой формуле суммируются числа в восьмой строке (строка
17) массива
Distances; во второй формуле суммируются числа в восьмом столбце (столбец J)
массива Distances. И в том, и в другом случае суммарное расстояние от Сиэтла до
других городов и от этих городов до Сиэтла составляет 15 221 миль (см. рис. 4.1).

Задания
1. С помощью функции ИНДЕКС определите расстояние между Лос-Анджелесом
и Финиксом, а также расстояние между Денвером и Майами.
2. С помощью функции ИНДЕКС вычислите суммарное расстояние от Далласа до
других городов, перечисленных на рис. 4.1.
3. Джерри Джонс с командой «Далласские Ковбои» отправляются в путешествие на машине в Чикаго, Денвер, Лос-Анджелес, Финикс и Сиэтл. Сколько
миль им предстоит проехать?
4. В файле Product.xlsx содержатся данные о продаже шести продуктов по месяцам. С помощью функции ИНДЕКС покажите продажи продукта 2 за март. Используйте функцию ИНДЕКС для подсчета общего объема продаж за апрель.
5. В файле Nbadistances.xlsx показаны расстояния между любыми двумя спортивными аренами НБА. Допустим, вы находитесь в Атланте и вам нужно посетить арены в указанном порядке и затем вернуться в Атланту. Какое расстояние вы проедете?
6. Используйте функцию ИНДЕКС для решения задания 10 из главы 3. Вернемся
к этому заданию: в файле Employees.xlsx вы найдете рейтинг (по шкале от 0 до
10), присвоенный каждым из 35 сотрудников трем заданиям. В файле также
указаны задания, выданные каждому сотруднику. С помощью формулы определите рейтинг, который каждый сотрудник присвоил назначенному ему заданию.

ГЛ А В А 5

Функция ПОИСКПОЗ
Обсуждаемые вопросы
Как создать формулу, возвращающую объем продаж какого-либо продукта за
определенный месяц, если даны ежемесячные продажи для нескольких продуктов? Например, сколько продукта 2 было продано за июнь?
Как создать формулу, определяющую бейсболиста с самой высокой зарплатой,
если дан список зарплат игроков? А бейсболиста с пятой по величине зарплатой?
Как создать формулу, определяющую период окупаемости для первоначальных
инвестиционных вложений, если известны ежегодные денежные потоки от реализации инвестиционного проекта?

Предположим, что у вас есть лист с 5000 имен в 5000 строках. Необходимо найти имя John Doe, про которое известно, что оно встречается в списке только один
раз. Хотите узнать формулу, возвращающую номер строки, содержащей искомое
имя? Функция ПОИСКПОЗ (MATCH) позволяет найти первое вхождение заданной
текстовой строки или числа в пределах указанного массива. Используйте функцию ПОИСКПОЗ вместо функции поиска, если вам нужно найти положение числа
в диапазоне, а не значение в определенной ячейке. Синтаксис функцииПОИСКПОЗ:
ПОИСКПОЗ(искомое_значение;просматриваемый_массив;[тип_сопоставления])

В приведенном далее пояснении предполагается, что все ячейки массива расположены в одном и том же столбце. Здесь:
искомое_значение (lookup_value) — это значение, с которым сопоставляются значения просматриваемого массива;
просматриваемый_массив (lookup_range) — это диапазон, который просматривается для сопоставления с искомым значением. Просматриваемый массив должен быть либо строкой либо столбцом;
тип_сопоставления (match_type) = 1 — просматриваемый диапазон должен состоять из чисел, отсортированных по возрастанию. Функция ПОИСКПОЗ возвращает позицию строки в просматриваемом массиве (по отношению к верхней
части массива), которая содержит наибольшее значение в массиве, превышающее искомое значение или равное ему;
тип_сопоставления = –1 — просматриваемый диапазон должен состоять из чисел, отсортированных по убыванию. Функция ПОИСКПОЗ возвращает позицию
строки в просматриваемом массиве (по отношению к верхней части массива),

Функция ПОИСКПОЗ

которая содержит последнее значение в массиве, превышающее искомое значение или равное ему;
тип_сопоставления = 0 — возвращает местоположение строки в просматриваемом диапазоне, содержащей первое точное соответствие искомому значению.
(В главе 20 рассматривается поиск второго или третьего совпадения.) Если
точного соответствия не существует и тип сопоставления равен 0, появляется
сообщение об ошибке #Н/Д. Обычно в функции ПОИСКПОЗ указывают тип_сопоставления = 0, но если этот аргумент не задан, считается, что тип_сопоставления = 1. Указывайте тип_сопоставления = 0, если содержимое ячеек просматриваемого массива не отсортировано. Такая ситуация возникает чаще всего.
В файле Matchex.xlsx (рис. 5.1) представлены три примера синтаксиса функции
ПОИСКПОЗ.

Рис. 5.1. Определение положения значения в диапазоне с помощью функции ПОИСКПОЗ

В ячейке B13 формула =ПОИСКПОЗ(«Бостон»;B4:B11;0) возвращает значение 1, поскольку значение Бостон содержится в первой строке диапазона B4:B11. Текстовые значения должны быть заключены в кавычки ( » «). В ячейке B14 формула
=ПОИСКПОЗ(«Финикс»;B4:B11;0) возвращает значение 7, поскольку ячейка B10
(седьмая ячейка в диапазоне B4:B11) является первой ячейкой в просматриваемом диапазоне, значение которой совпадает с Финикс. В ячейке E12 формула
=ПОИСКПОЗ(0;E4:E11;1) возвращает значение 4, так как последнее число, не превышающее 0 в диапазоне E4:E11, находится в ячейке E7 (четвертой ячейке в просматриваемом массиве). В ячейке G12 формула =ПОИСКПОЗ(-4;G4:G11;-1) возвращает
значение 7, поскольку последнее число в диапазоне G4:G11, превышающее или
равное -4, находится в ячейке G10 (седьмой ячейке в просматриваемом массиве).
Функция ПОИСКПОЗ работает и с неточными совпадениями. Например, в ячейке
B15 формула =ПОИСКПОЗ(«Фин*»;B4:B11;0) возвращает значение 7. Звездочка обрабатывается как подстановочный знак, следовательно, в диапазонеB4:B11 выпол-

ГЛАВА 5

няется поиск первой текстовой строки, начинающейся с символов Фин. Кстати,
этот же прием работает и для функции поиска. Например, в задании по поиску
цены в главе 3 формула =ВПР(«x*»;lookup2;2) возвратит цену продукта X212 (4,80).
Если просматриваемый массив содержится в строке, функция возвращает относительную позицию первого совпадения в массиве, двигаясь слева направо. Как
я покажу далее, функция ПОИСКПОЗ особенно эффективна в сочетании с другими
функциями Excel, такими как ВПР, ИНДЕКС и МАКС (MAX).

Ответы на вопросы
Как создать формулу, возвращающую объем продаж какого-либо продукта за определенный месяц, если даны ежемесячные продажи для нескольких продуктов? Например, сколько продукта 2 было продано за июнь?

В файле Productlookup.xlsx (рис. 5.2) указаны объемы продаж с января по июнь для
четырех фигурок НБА. Как создать формулу, которая вычисляла бы продажи конкретного продукта за определенный месяц? Хитрый прием, который нам поможет, — использование одной функции ПОИСКПОЗ для поиска строки с указанным
продуктом и другой функции ПОИСКПОЗ для поиска столбца с заданным месяцем.
Затем вы можете применить функцию ИНДЕКС для возврата объема продаж продукта за этот месяц.

Рис. 5.2. Функция ПОИСКПОЗ может использоваться в сочетании
с функциями ИНДЕКС и ВПР

В диапазоне B4:G7 с именем Sales содержатся данные об объемах продаж кукол.
Продукт, данные о котором требуется найти, указан в ячейкеA10, а месяц — в ячейке
B10. В ячейку C10 введена формула =ПОИСКПОЗ(A10;A4:A7;0) для определения номера строки в диапазоне Sales с данными по кукле Kobe. Далее в ячейке D10 находится формула =ПОИСКПОЗ(B10;B3:G3;0) для определения номера столбца в диапазоне
Sales с данными по продажам за июнь. Теперь, когда номера строки и столбца, в кото-

Функция ПОИСКПОЗ

рых содержатся требуемые данные по продажам, известны, можно воспользоваться
формулой =ИНДЕКС(Sales;C10;D10) в ячейке E10 для получения требуемых данных.
Для получения дополнительной информации о функции ИНДЕКС см. главу 4.
Как создать формулу, определяющую бейсболиста с самой высокой зарплатой, если дан список зарплат игроков? А бейсболиста с пятой по величине зарплатой?

В файле Baseball.xlsx (рис. 5.3) перечислены зарплаты, выплаченные 401 ведущим
игрокам бейсбольной лиги в течение сезона 2001 г. Данные по зарплате не отсортированы. Требуется составить формулу, возвращающую имя игрока с самой высокой зарплатой, а также имя игрока с пятой по величине зарплатой.
Для поиска игрока с самой высокой зарплатой выполните следующее:
1. С помощью функции МАКС определите значение самой высокой зарплаты.
2. С помощью функции ПОИСКПОЗ определите строку, содержащую имя игрока
с самой высокой зарплатой.
3. С помощью функции ВПР (обрабатывающей строку данных с зарплатой игрока) найдите имя игрока.
Данные о зарплатах игроков содержатся в диапазоне C12:C412 с именем Salaries.
Диапазон, указанный в функции ВПР (диапазон A12:C412), называется Lookup.

Рис. 5.3. Поиск и отображение самого большого значения
в списке с помощью функций МАКС, ПОИСКПОЗ и ВПР

ГЛАВА 5

В ячейке C9 по формуле =MAКС(salaries) найдите самую высокую зарплату (22 млн
долларов). Затем в ячейке C8 по формуле =ПОИСКПОЗ(C9;Salaries;0) определите номер игрока с самой высокой зарплатой. Так как зарплаты не отсортированы ни по
возрастанию, ни по убыванию, используется аргумент тип_сопоставления = 0. Самую высокую зарплату имеет игрок с номером 345. Наконец, в ячейке C6 по формуле =ВПР(C8;Lookup;2) найдите имя игрока во втором столбце диапазона Lookup.
Неудивительно, что самым высокооплачиваемым игроком в 2001 г. был Алекс Родригес (Alex Rodriguez).
Для поиска имени игрока с пятой по величине зарплатой необходима функция поиска пятого по величине числа в массиве. Эту работу выполнит функция НАИБОЛЬШИЙ (LARGE). Ее синтаксис: НАИБОЛЬШИЙ(массив,k). В таком виде
она возвращает k-е по величине число в диапазоне. Т аким образом, формула
=НАИБОЛЬШИЙ(salaries;5) в ячейке D9 дает пятую по величине зарплату (12,6 млн
долларов). Действуя по описанному выше алгоритму, вы обнаружите, что игроком
с пятой по величине зарплатой был Дерек Джетер (Derek Jeter). (Буквы dl перед
его именем указывают, что в начале сезона Джетер был в списке травмированных
игроков.) Функция НАИМЕНЬШИЙ (SMALL) в формуле =НАИМЕНЬШИЙ(salaries;5)
служит для поиска пятой снизу по величине зарплаты.
Как создать формулу, определяющую период окупаемости для первоначальных инвестиционных вложений, если известны ежегодные денежные
потоки от реализации инвестиционного проекта?

В файле Payback.xlsx (рис. 5.4) показаны прогнозируемые денежные потоки для
инвестиционного проекта в следующие 15 лет. Предположим, что в нулевой период потребовался отток денежных средств в размере 100 млн долларов. За первый
год проект вызвал приток денежных средств в размере 14 млн долларов. Ожидается, что денежные потоки будут расти на 10% в год. Сколько лет пройдет, прежде
чем инвестиции в проект окупятся?
Количество лет, необходимых для возврата первоначальных инвестиционных затрат на проект, называется периодом окупаемости. В высокотехнологичных отраслях период окупаемости часто используется для ранжирования инвестиционных
проектов. (В главе 8 показано, что использование периода окупаемости как меры
качества инвестиционных проектов является некорректным, поскольку при этом
игнорируется изменение стоимости денег во времени.) В данный момент, однако,
сосредоточимся на способе определения периода окупаемости для этой упрощенной инвестиционной модели.
Для определения периода окупаемости проекта выполните следующее:
1. В столбце B вычислите денежный поток для каждого года.
2. В столбце C вычислите суммарный денежный поток для каждого года.
Теперь с помощью функции ПОИСКПОЗ (укажите тип_сопоставления равным 1)
определите номер строки первого года с положительным значением суммарного
денежного потока. Это вычисление позволит получить период окупаемости.

Функция ПОИСКПОЗ

Рис. 5.4. Вычисление периода окупаемости инвестиций с помощью функции ПОИСКПОЗ

Ячейкам диапазона B1:B3 присвоены имена, соответствующие тексту в ячейках A1:A3. Денежный поток в нулевой период, а именно начальные инвестиции
со знаком «минус», введены в ячейку B5. Денежный приток первого года указан
в ячейке B6. Денежные потоки со второго года по пятнадцатый вычисляются путем копирования формулы =B6*(1+прирост) из ячейки B7 в ячейки B8:B20.
При расчете суммарного денежного потока для нулевого периода используйте
формулу из ячейки B5 в ячейке C5. Для последующих лет суммарный денежный
поток можно вычислить по формуле:
суммарный_поток_за_год t = (суммарный_поток_за_год t – 1) + поток_за_год t.

Для реализации этого отношения скопируйте формулу
в ячейки C7:C20.

=C5+B6 из ячейки C6

Для расчета периода окупаемости с помощью функции ПОИСКПОЗ (укажите тип_
сопоставления равным 1) вычислите последнюю строку диапазона C5:C20, содержащую значение меньше 0. Этот расчет всегда дает период окупаемости. Если
последней строкой в C5:C20, содержащей отрицательное значение, является шестая строка в диапазоне (год 5), то седьмое значение соответствует суммарному
денежному потоку первого года, когда проект начнет приносить прибыль. Поскольку отсчет идет с нулевого года, проект окупится на шестой год. Т аким образом, формула =ПОИСКПОЗ(0;C5:C20;1) в ячейке E2 дает срок окупаемости (6 лет).
Если какие-либо денежные потоки после нулевого периода имеют отрицательное
значение, этот метод работать не будет и выдаст сообщение об ошибке, потому

ГЛАВА 5

что в этом случае диапазон суммарных денежных потоков не будет отсортирован
по возрастанию. Используя функцию ЕСЛИОШИБКА (IFERROR) (представленную
в главе 12), вы можете обеспечить выдачу в ячейке E2 текстового сообщения (например «Срок окупаемости не может быть найден»), если не удается вычислить
срок окупаемости.

Задания
1. Воспользуйтесь данными о расстояниях между городами США в файле Index.
xlsx и напишите формулу с функцией ПОИСКПОЗ для определения (на основе
названий городов) расстояния между любыми двумя городами.
2. В файле Matchtype1.xlsx перечислены суммы 30 сделок в хронологическом порядке. Напишите формулу для определения первой сделки, после которой общий объем сделок превысил $10 000.
3. В файле Matchthemax.xlsx содержатся идентификационные коды продуктов
и показатели продаж в штуках для 265 продуктов. С помощью формулы
с функцией ПОИСКПОЗ определите идентификационный код продукта с наибольшим показателем продаж.
4. В файле Buslist.xlsx содержатся интервалы времени (в минутах) между автобусами на пересечении 45-й улицы и Парк-авеню в Нью-Йорке. Напишите
формулу расчета времени ожидания пассажиром автобуса для любого времени прихода пассажира на остановку (отсчет от первого автобуса). Например,
если бы вы пришли на остановку , начиная с настоящего момента, через 12,4
минуты, а автобусы прибыли бы, начиная с настоящего момента, через 5 минут и через 21 минуту, вам пришлось бы ждать автобус 21 – 12,4 = 8,6 минуты.
5. В файле Salesdata.xlsx находятся данные о количестве компьютеров, проданных каждым продавцом. Напишите формулу , возвращающую количество
проданного товара указанным продавцом.
6. Предположим, что функция ВПР была удалена из Excel. Объясните, как ее
можно заменить с помощью функций ПОИСКПОЗ и ИНДЕКС.
7. В файле Baseballproblem7.xlsx приведены статистики по бейсбольным командам высшей лиги. Вы будете вводить имя команды в ячейку I2 и статистику
в ячейку J2. Напишите формулу в ячейке K2, возвращающую значение этой
статистики для выбранной команды.
8. В файле Footballproblem8.xlsx приведены показатели по нападающим НФЛ. Допустим, мы ввели имя нападающего в ячейку G3 и показатель в ячейку H3. Напишите формулу, возвращающую в ячейке I3 значение показателя для этого
игрока.

ГЛАВА 6

Текстовые функции и инструмент
Мгновенное заполнение
Обсуждаемые вопросы
У меня есть лист, каждая ячейка которого содержит описание продукта, идентификатор продукта и цену продукта. Как поместить все описания в столбец A, все
идентификаторы в столбец B и все цены в столбец C?
Каждый день я получаю данные о совокупных продажах в США, которые вычисляются в одной ячейке как сумма продаж на востоке, севере и юге. Как мне
извлечь продажи на востоке, севере и юге в отдельные ячейки?
В конце каждого семестра студенты оценивают мою преподавательскую деятельность по шкале от 1 до 7 баллов. Мне известно, сколько студентов выставили тот
или иной балл. Как создать гистограмму оценки качества преподавания?
Числовые данные были загружены из интернета или из базы данных. При попытке использовать их в вычислениях появляется ошибка #ЗНАЧ!. Как решить
эту проблему?
Текстовые функции — вещь хорошая, но есть ли простой способ (без них) извлечь имена и фамилии из данных, создать список адресов электронной почты
из списка имен или выполнить другие стандартные операции с текстовыми данными?
Что такое символы Unicode?
Чем новая функция ОБЪЕДИНИТЬ лучше старой функции СЦЕПИТЬ (или &)?
Мне нравятся текстовые функции, а как пользоваться функцией Excel ТЕКСТ?

Когда кто-нибудь посылает вам данные или вы скачиваете их из интернета, они
часто имеют не тот формат, что вам нужен. Например, даты и объемы продаж, которые должны находиться в отдельных ячейках, в скачанных данных по продажам могут быть вместе в одной ячейке. Как привести данные в нужный формат?
Для этого нужно научиться пользоваться текстовыми функциями Microsoft Excel.
В этой главе я расскажу вам, как пользоваться следующими текстовыми функциями Excel:
ЛЕВСИМВ (LEFT);
ПРАВСИМВ (RIGHT);
ПСТР (MID);

ЗАМЕНИТЬ (REPLACE);
ЗНАЧЕН (VALUE);
ПРОПИСН (UPPER);

ГЛАВА 6

СЖПРОБЕЛЫ (TRIM);
ДЛСТР (LEN);
НАЙТИ (FIND);
ПОИСК (SEARCH);
ПОВТОР (REPT);
СЦЕПИТЬ (CONCATENATE);

СТРОЧН (LOWER);
ПРОПНАЧ (PROPER);
СИМВОЛ (CHAR);
ПЕЧСИМВ (CLEAN);
ПОДСТАВИТЬ (SUBSTITUTE);
ОБЪЕДИНИТЬ (TEXTJOIN).

Также я продемонстрирую вам, как пользоваться новым инструментом Мгновенное заполнение (Flash Fill), позволяющим, как по волшебству, мгновенно придавать
вашим данным желаемый вид. Наконец, вы узнаете о доступном в Excel 2019 обширном наборе символов Unicode.

Синтаксис текстовых функций
Файл Textfunctions.xlsx (рис. 6.1) содержит примеры текстовых функций. Начнем
с небольшого обзора каждой функции, а затем рассмотрим их применение для решения конкретных задач. Затем мы научимся комбинировать функции для более
сложной обработки данных.

Рис. 6.1. Примеры использования текстовых функций

Функция ЛЕВСИМВ
Функция ЛЕВСИМВ(текст,k) возвращает первые k символов текстовой строки. Например, формула =ЛЕВСИМВ(A3;4) в ячейке C3 возвращает значение Regg.

Текстовые функции и инструмент Мгновенное заполнение

Функция ПРАВСИМВ
Функция ПРАВСИМВ(текст,k) возвращает последние k символов текстовой строки.
Например, формула =ПРАВСИМВ(A3;4) в ячейке C4 возвращает значение ller.

Функция ПСТР
Функция ПСТР(текст,k,m) возвращает m символов текстовой строки, начиная с k-го
символа. Например, формула =ПСТР(A3;2;5) в ячейке C8 возвращает символы 2–6
из ячейки A3; результат равен eggie.

Функция СЖПРОБЕЛЫ
Функция СЖПРОБЕЛЫ(текст) удаляет все пробелы из текстовой строки, за исключением одиночных пробелов между словами. Например, в ячейке
C5 формула
=СЖПРОБЕЛЫ(A3) удаляет два из трех пробелов между Reggie и Miller и возвращает результат Reggie Miller. Функция СЖПРОБЕЛЫ также удаляет пробелы в начале
и конце содержимого ячейки.

Функция ДЛСТР
Функция ДЛСТР(текст) возвращает количество символов в текстовой строке
(с пробелами). Например, в ячейке C6 формула =ДЛСТР(A3) возвращает значение
15, поскольку в ячейке A315 символов. В ячейке C7 формула =ДЛСТР(C5) возвращает значение 13. Так как в ячейке C5 убрано два пробела, в ней на два символа
меньше, чем в исходном тексте в ячейке A3.

Функции НАЙТИ и ПОИСК
Функция НАЙТИ(искомый_текст;просматриваемый_текст;k) возвращает позицию
первого символа искомого текста в просматриваемом тексте. Параметр k указывает начальную позицию поиска. Функция НАЙТИ учитывает регистр. Синтаксис
функции ПОИСК аналогичен синтаксису функции НАЙТИ, но не учитывает регистр.
Например, формула =НАЙТИ(«r»;A3;1) в ячейке C10 возвращает значение 15 — позицию первой строчной буквы r в текстовой строке Reggie Miller. (Заглавная R игнорируется, так как функция НАЙТИ учитывает регистр.) Формула =ПОИСК(«r»;A3;1)
в ячейке C11 возвращает 1, потому что функция ПОИСК сопоставляет символ r
=НАЙТИ(» «;A3;1)
с символом как нижнего, так и верхнего регистра. Формула
в ячейке C9 возвращает 7, поскольку первым пробелом в строке Reggie Miller является седьмой символ.

Функция ПОВТОР
Функция ПОВТОР используется для повторения текстовой строки указанное
число раз. Синтаксис функции:
ПОВТОР(текст;число_повторений). Например,
ПОВТОР(«|»,3) дает в результате |||.

ГЛАВА 6

Функции СЦЕПИТЬ и &
Функция СЦЕПИТЬ(текст1;текст2;…;текст30) предназначена для объединения максимум 30 текстовых строк в одну строку. Вместо функции СЦЕПИТЬ можно воспользоваться оператором &. Например, формула =A1&» «&B1 в ячейке C12 возвращает
строку Reggie Miller. Формула =СЦЕПИТЬ(A1;» «;B1) в ячейке D12 дает тот же результат.

Функция ОБЪЕДИНИТЬ
Функция ОБЪЕДИНИТЬ соединяет текст из нескольких диапазонов и/или строк
и содержит заданный вами символ-разделитель между текстовыми значениями, которые предстоит объединить. Если символом-разделителем является пустая текстовая строка, то эта функция эффективно сцепит диапазоны. Функция
ОБЪЕДИНИТЬ имеется только в Office 365. Синтаксис ее следующий:
ОБЪЕДИНИТЬ(разделитель; игнорировать пустые; текст1; [текст2], …).

Символ-разделитель должен быть указан обязательно, он отделяет выбранные
фрагменты текста друг от друга. Параметр «игнорировать пустые» также обязателен, и если он имеет значение ИСТИНА, то будут игнорироваться пустые ячейки.
Функция ОБЪЕДИНИТЬ нужна, если требуется сцепить текст , который должен разделяться одним и тем же символом-разделителем. Например, потребуется функция
ОБЪЕДИНИТЬ, если вы хотите объединить текст из 10 ячеек так, чтобы фрагменты отделяла запятая. Функция ОБЪЕДИНИТЬ позволяет не включать запятую после упоминания каждой ячейки, как это было бы в формуле с функцией СЦЕПИТЬ или с &.
Подробный пример с применением функции ОБЪЕДИНИТЬ дан ниже в этой главе.

Функция ТЕКСТ
Функция ТЕКСТ позволяет вам изменять форматирование внешнего вида чисел
или даты за счет применения специальных кодов. Синтаксис функции ТЕКСТ следующий: ТЕКСТ (форматируемое значение; «желаемый код форматирования»). Ниже
в этой главе даны примеры применения функции ТЕКСТ и правильных кодов форматирования.

Функция ЗАМЕНИТЬ
Функция ЗАМЕНИТЬ(старый_текст;k;m;новый_текст) заменяет новым текстом
m символов в старом тексте начиная с
k-го символа. Например, формула
=ЗАМЕНИТЬ(A3;3;2;»nn») в ячейке C13 заменяет третий и четвертый символы ( gg)
в ячейке A3 символами nn. В результате получается Rennie Miller.

Функция ЗНАЧЕН
Функция ЗНАЧЕН(текст) преобразует текстовую строку , представляющую число,
в число. Например, формула =ЗНАЧЕН(A15) в ячейке B15 преобразует текстовую

Текстовые функции и инструмент Мгновенное заполнение

строку 31 из ячейки A15 в числовое значение 31. Значение 31 в ячейке A15 можно
распознать как текст, поскольку оно выровнено по левому краю. Аналогично значение 31 в ячейке B15 можно идентифицировать как число по выравниванию по
правому краю.

Функции ПРОПИСН, СТРОЧН и ПРОПНАЧ
Функция ПРОПИСН(текст) меняет в строке текст все буквы на прописные. Например, в ячейке C17 по формуле =ПРОПИСН(C16) все символы преобразуются в прописные и получается REGGIE MILLER. В ячейке C16 по формуле =СТРОЧН(C12) все
прописные буквы заменяются строчными и получается
reggie miller. Наконец,
в ячейке C18 по формуле =ПРОПНАЧ(C17) восстанавливается правильный регистр,
и в результате получается Reggie Miller.

Функция СИМВОЛ
Функция СИМВОЛ(число) возвращает (для числа от 1 до 255) символ ASCII с указанным номером. Например, СИМВОЛ(65) дает в результате A, СИМВОЛ(66) дает B,
и так далее. Список символов ASCII вы найдете в файле ASCIIcharacters.xlsx. Часть
списка представлена на рис. 6.2.

Рис. 6.2. Часть списка символов ASCII

ГЛАВА 6

Функция ПЕЧСИМВ
Если вы посмотрите в файл ASCIIcharacters.xlsx, то заметите, что отдельные символы, такие как символ под номером 10 (перевод строки), являются невидимыми.
Функция ПЕЧСИМВ удаляет из ячейки некоторые (но не все) невидимые символы
ASCII. Например, функция ПЕЧСИМВ не удалит СИМВОЛ(160), являющийся неразрывным пробелом. Как удалить такие проблематичные символы, какСИМВОЛ(160),
мы рассмотрим далее в этой главе.

Функция ПОДСТАВИТЬ
Функция ПОДСТАВИТЬ заменяет в ячейке указанный текст , если местоположение
текста неизвестно. Синтаксис функции ПОДСТАВИТЬ: ПОДСТАВИТЬ(ячейка;старый_
текст;новый_текст;[номер_вхождения]).

Последний аргумент является необязательным. Если он опущен, то каждое вхождение старого текста в ячейке заменяется новым текстом. Если последний аргумент присутствует (например, его значение равно n), тогда только n-е вхождение
старого текста заменится новым текстом. Чтобы вы поняли, как работает функция
ПОДСТАВИТЬ, допустим, что мы хотим заменить пробелы в ячейкеC17 звездочками.
Сначала введите формулу =ПОДСТАВИТЬ(D17;» «;»*») в ячейку C19. Каждый пробел будет заменен звездочкой ( *), и в резуль тате получится I*LOVE*EXCEL*2019!.
При вводе в ячейку C20 формулы =ПОДСТАВИТЬ(D17;» «;»*»;3) произойдет замена
на * только третьего пробела, и получится I LOVE EXCEL*2019!.

Ответы на вопросы
Текстовые функции очень эффективны при решении многих актуальных задач,
над которыми бьются бывшие студенты, ныне работающие в крупных корпорациях. Часто для решения проблемы нужно всего лишь объединить несколько текстовых функций в одну формулу.
У меня есть лист , каждая ячейка которого содержит описание продукта,
идентификатор продукта и цену продукта. Как поместить все описания
в столбец A, все идентификаторы в столбец B и все цены в столбец C?

В этом примере идентификатор продукта всегда определяется первыми 12 символами, а цена всегда указана в последних 8 символах (с двумя пробелами после
каждой цены). В решении (см. файл Lenora.xlsx и рис. 6.4) используются функции
ЛЕВСИМВ, ПРАВСИМВ, ПСТР, ЗНАЧЕН, СЖПРОБЕЛЫ, ДЛСТР и СЦЕПИТЬ.
Начать хорошо всегда с удаления лишних пробелов. Для этого скопируйте формулу =СЖПРОБЕЛЫ(A4) из ячейки B4 в ячейки B5:B12. Единственными удаленными пробелами в столбце A оказались пробелы после каждой цены. У бедитесь
в этом, поставив курсор в ячейку A4 и нажав < F2> для редактирования ячейки.

Текстовые функции и инструмент Мгновенное заполнение

В конце ячейки вы увидите два пустых символа. Результат применения функции
СЖПРОБЕЛЫ показан на рис. 6.3 в столбце B. Мы знаем, что функция СЖПРОБЕЛЫ
удалила два дополнительных пробела в конце ячейки, по длине строк после применения формул =ДЛСТР(A4) и =ДЛСТР(B4). Проверьте себя: в ячейке A4 должно
быть 52 символа, а в ячейке B4 — 50 символов.

Рис. 6.3. Удаление лишних пробелов с помощью функции СЖПРОБЕЛЫ

Для получения идентификатора продукта нам надо извлечь 12 крайних слева символов из столбца B. Скопируйте формулу =ЛЕВСИМВ(B4;12) из ячейки C4 в ячейки
C5:C12. Эта формула извлечет 12 первых символов из ячейки B4 и последующих
ячеек и сформирует код продукта (рис. 6.4).

Рис. 6.4. Извлечение кода, цены и описания продукта из текстовой строки с помощью
текстовых функций

Для извлечения цен, про которые известно, что они находятся в последних шести
цифрах каждой ячейки, нам нужно извлечь шесть крайних справа символов из
каждой ячейки. Я скопировал формулу =ЗНАЧЕН(ПРАВСИМВ(B4;6)) из ячейки D4
в ячейки D5:D12. Я использовал функцию ЗНАЧЕН для преобразования извлеченного текста в числовое значение. Без этого преобразования математические операции над ценами в дальнейшем будут невозможны.
Для извлечения описания продукта придется попотеть сильнее. Изучив данные,
вы увидите, что если начать извлечение с тринадцатого символа и продолжать до
тех пор, пока не останется шесть символов до конца ячейки, можно получить требуемые данные. Эту работу выполнит формула =ПСТР(B4;13;ДЛСТР(B4)-6-12), скопированная из ячейки E4 в ячейки E5:E12. Функция ДЛСТР(B4) возвращает общее

ГЛАВА 6

количество символов в сжатой строке. Формула ПСТР начинает обработку с тринадцатого символа и извлекает количество символов, равное общему количеству
минус 12 начальных (код продукта) и минус 6 конечных символов (цена продукта). После операции отбрасывания ненужных символов остаются только символы
описания продукта.
Теперь предположим, что у вас есть следующее: идентификатор продукта в столбце C, цена продукта в столбце D и описание продукта в столбце E. Можно ли соединить эти значения и восстановить первоначальный текст?
Текстовые строки можно объединить с помощью функции СЦЕПИТЬ. Копирование
формулы =СЦЕПИТЬ(C4;E4;D4) из ячейки F4 в ячейки F5:F12 восстановит исходный
(без лишних пробелов) текст (см. рис. 6.4).
Объединение начинается с идентификатора продукта в ячейке C4, затем добавляется описание продукта из ячейки E4 и в конце присоединяется цена из ячейки D4.
Вы восстановили текст, описывающий каждый компьютер! Объединить строки
также можно при помощи знака &. Исходный текст в одной ячейке может восстановить формула =C4&E4&D4. Обратите внимание, что ячейка E4 содержит один
пробел до и после описания продукта. Если бы эти пробелы отсутствовали, можно
было бы воспользоваться для их вставки формулой =C4&» «&E4&» «&D4. Пробел
между кавычками означает вставку пробела.
Если идентификатор продукта не всегда состоит из 12 символов, такой метод извлечения информации не годится. В таком случае можно извлечь код продукта,
применив функцию НАЙТИ для обнаружения позиции первого пробела. Далее следует применить функцию ЛЕВСИМВ для извлечения всех символов слева от пробела. Этот подход показан на примере в следующем разделе.
Если цена не всегда состоит из шести символов, извлечь ее будет сложнее. (См.
в задании 15 пример извлечения последнего слова текстовой строки.)
Каждый день я получаю данные о совокупных продажах в США, которые
вычисляются в одной ячейке как сумма продаж на востоке, севере и юге.
Как мне извлечь продажи на востоке, севере и юге в отдельные ячейки?

Этот вопрос прислала мне сотрудница финансового отдела компании Microsoft.
Каждый день она получала лист , содержащий такие формулы, как =50+200+400,
=5+124+1025, и другие им подобные. Ей нужно было извлечь каждое число в ячейку соответствующего столбца. Например, необходимо было первое число (продажи на востоке) извлечь в ячейку столбца C, второе число (продажи на севере) —
в столбец D и третье число (продажи на юге) — в столбец E. Задача непростая, так
как мы не знаем точную позицию символов, с которых начинаются второе и третье числа в каждой ячейке. В ячейке A3 данные продаж на севере начинается с четвертого символа. В ячейке A4 — с третьего символа.
Данные для этого примера вы найдете в файле Salesstripping.xlsx (рис. 6.5). Позицию
данных продаж для различных регионов можно определить следующим образом:

Текстовые функции и инструмент Мгновенное заполнение

продажи на востоке представлены символами слева от первого знака «+»;
продажи на севере представлены символами между первым и вторым знаками «+»;
продажи на юге представлены символами справа от второго знака «+».

Рис. 6.5. Использование функций НАЙТИ, ЛЕВСИМВ, ДЛСТР и ПСТР для извлечения
региональных продаж в отдельные ячейки

Задача легко решается комбинированием функций
и ПСТР.

НАЙТИ, ЛЕВСИМВ, ДЛСТР

Используйте команды редактирования для замены всех знаков равенства
(=) пробелами. Для этого выделите диапазон A3:A6. Затем на вкладке Главная
(Home) в группе Редактирование (Editing) кликните на Найти и выделить (Find &
Select), а затем на Заменить… (Replace). В поле Найти (Find What) введите знак
равенства, а в поле Заменить на (Replace With) введите пробел. Затем нажмите
кнопку Заменить все (Replace All). Замена знаков равенства на пробелы преобразует формулу в текст.
Примените функцию НАЙТИ для определения позиции обоих знаков «+» в каждой ячейке.
Начните с поиска позиции первого знака «+» для каждого фрагмента данных. Для
этого скопируйте формулу =НАЙТИ(«+»;A3;1) из ячейки B3 в ячейки B4:B6. Поиск
второго знака «+» начните с символа, следующего за первым знаком «+», скопировав формулу =НАЙТИ(«+»;A3;B3+1) из ячейки C3 в ячейки C4:C6.
Для извлечения данных продаж на востоке примените функциюЛЕВСИМВ (извлечь
все символы слева от первого знака «+»), скопировав формулу=ЛЕВСИМВ(A3;B3-1)
из ячейки D3 в ячейки D4:D6. Для извлечения продаж на севере примените функцию ПСТР и извлеките все символы между двумя знаками «+». Начните с символа, следующего за первым знаком «+», и извлеките количество символов,
равное (позиция_второго_знака_плюс) – (позиция_первого_знака_плюс) -1. Если не

ГЛАВА 6

учесть -1, в результат попадет второй знак «+». (Проверь те это самостоятельно.)
Таким образом, для извлечения данных продаж на севере скопируйте формулу
=ПСТР(A3;B3+1;C3-B3-1) из ячейки E3 в ячейки E4:E6.
Для извлечения данных продаж на юге необходимо извлечь все символы справа от второго знака «+», применив функцию ПРАВСИМВ. Число таких символов
равно (общее_число_символов_в_ячейке) – (позиция_второго_знака_плюс). Общее
число символов для каждой ячейки вычислите, скопировав формулу =ДЛСТР(A3)
из ячейки F3 в ячейки F4:F6. Наконец, данные продаж на юге можно получить, скопировав формулу =ПРАВСИМВ(A3;F3-C3) из ячейки G3 в ячейки G4:G6.

Извлечение данных с помощью Мастера распределения
текста по столбцам
Есть простой способ извлечь данные по продажам на востоке, севере и юге (и другие аналогичные данные) без применения текстовых функций. Выделите ячейки A3:A6 и затем на вкладке Данные (Data) в группе Работа с данными (Data Tools)
кликните на Текст по столбцам (Text To Columns). Выберите формат С разделителями
(Delimited), нажмите Далее (Next) и заполните данные в диалоговом окне, как показано на рис. 6.6.

Рис. 6.6. Мастер распределения текста по столбцам

Если мы выберем знак «+» в качестве символа-разделителя, то распределим текст
каждой ячейки по столбцам в соответствии с вхождениями знака «+». Разделителями также могут служить знак табуляции, точка с запятой, запятая и пробел. Теперь
нажмите Далее (Next), выберите левый верхний угол целевого диапазона (в примере
я выбрал ячейку A8) и нажмите Готово (Finish). Результат представлен на рис. 6.7.

Рис. 6.7. Результат работы Мастера распределения текста по столбцам

Текстовые функции и инструмент Мгновенное заполнение

В конце каждого семестра студенты оценивают мою преподавательскую
деятельность по шкале от 1 до 7 баллов. Мне известно, сколько студентов
выставили тот или иной балл. Как создать гистограмму оценки качества преподавания?

В файле Repeatedhisto.xlsx находятся оценки моей преподавательской деятельности (по шкале от 1 до 7 баллов). Два человека поставили 1 балл, три человека — 2 балла и т. д. График, обобщающий эти данные, можно построить с помощью
функции ПОВТОР.
Скопируйте формулу =ПОВТОР(«|»;C4) из ячейки D4 в ячейки D5:D10. По этой формуле символы «|» извлекаются в столбец D в количестве, соответствующем значениям в столбце C. На рис. 6.8 ясно виден перевес хороших оценок (6 и 7 баллов)
над плохими (1 и 2 балла). Повторение символа « |» позволяет имитировать гистограмму. Другие вопросы создания гистограмм в Excel обсуждаются в главе 43
«Обобщение данных на гистограммах и диаграммах Парето».

Рис. 6.8. Создание графика с помощью функции ПОВТОР

Числовые данные были загружены из интернета или из базы данных. При
попытке использовать их в вычислениях появляется ошибка #ЗНАЧ!. Как
решить эту проблему?

В файле Cleanexample.xlsx (рис. 6.9) непечатаемые СИМВОЛ(10) и СИМВОЛ(160)
вставлены перед числом 33 в ячейках E5 и H6 соответственно. В ячейках E8
и H8 мы применили функцию ЗНАЧЕН, попытавшись преобразовать содержимое ячеек E5 и H6 в числа, но получили ошибку #ЗНАЧ!, которая говорит нам
о том, что Excel не понимает , что должен обрабатывать содержимое ячеек как
числа. В ячейке E11 находится содержимое ячейки E5, очищенное по формуле
=ПЕЧСИМВ(E5). В ячейке E12 находится числовое значение 33, то есть после того
как СИМВОЛ(10) был удален, содержимое ячейки было обработано по формуле
=ЗНАЧЕН(E11) без ошибок.
В ячейке H10 мы попытались очистить содержимое ячейки H6 с помощью формулы =ПЕЧСИМВ(H6). В ячейке H11 после применения формулы =ЗНАЧЕН(H10) получена ошибка, так как функция ПЕЧСИМВ не удалила СИМВОЛ(160). Для устранения ошибки необходимо СИМВОЛ(160) заменить пробелом с помощью функции

ГЛАВА 6

ПОДСТАВИТЬ. В ячейку H14 запишите формулу =НАЙТИ(СИМВОЛ(160);H10) и убедитесь, что символ СИМВОЛ(160) присутствует в ячейке H10: он стоит на первом месте
в ячейке. Если применение функции НАЙТИ вызовет ошибку, значит, СИМВОЛ(160)
в ячейке отсутствует. В ячейке H15 все вхождения этого непечатаемого символа
заменяются пробелом с помощью формулы =ПОДСТАВИТЬ(H6;СИМВОЛ(160);» «).
В ячейке H16 формула =ЗНАЧЕН(H15) дает в результате число 33. Таким образом,
теперь над содержимым ячейки H15 можно производить математические операции.

Рис. 6.9. Удаление непечатаемых символов с помощью функций ПЕЧСИМВ и ПОДСТАВИТЬ

Текстовые функции — вещь хорошая, но есть ли простой способ (без них)
извлечь имена и фамилии из данных, создать список адресов электронной
почты из списка имен или выполнить другие стандартные операции с текстовыми данными?

Инструмент Мгновенное заполнение (Flash Fill; впервые появился в Excel 2013)
использует современные технологии распознавания образов, позволяя моделировать множество задач, ранее выполнявшихся с помощью текстовых функций.
Файл Flashfill.xlsx демонстрирует применение инструмента Мгновенное заполнение
в следующих примерах:
извлечение имен и фамилий (на листе First And Last);
создание адресов электронной почты для университета UXYZ University путем добавления @UXYZ.edu к фамилии сотрудника (на листе Email);
извлечение сумм в долларах и центах из списка цен (на листе Dollars And Cents).

Текстовые функции и инструмент Мгновенное заполнение

Для использования инструмента Мгновенное заполнение выделите столбец рядом
с данными. В первой ячейке, соответствующей имеющимся данным, введите пример того, чем требуется заполнить остальные ячейки. Как правило, если нажать
Enter и затем Ctrl+E, инструмент Мгновенное заполнение автоматически правильно
заполнит оставшиеся ячейки. Однако иногда для получения безошибочного результата приходится ввести несколько примеров.
Как показано на рис. 6.10, мы собираемся извлечь имена и фамилии сотрудников в столбцы E и F. Напечатайте Tricia в ячейке E6 листа First and Last и нажмите
Enter. Затем нажмите Ctrl+E, и ячейки E7:E13 автоматически заполнятся именами
сотрудников. Аналогично, если напечатать Lopez в ячейке F6, нажать Enter и затем
Ctrl+E, инструмент Мгновенное заполнение запишет фамилии сотрудников в ячейки F7:F13.

Рис. 6.10. Автоматический ввод имен и фамилий

Как показано на рис. 6.11, мы собираемся создать email-адрес для каждого сотрудника, добавив к его фамилии @UXYZ.edu. Напечатайте Lopez@UXYZ.edu в ячейке E6
листа email. Далее нажмите Enter, а затем Ctrl+E, и инструмент Мгновенное заполнение автоматически создаст email-адреса в диапазоне E7:E13.
Как показано на рис. 6.12, мы собираемся извлечь сумму в долларах и центах из
ячеек D6:D11 столбца с ценами на листе Dollars and Cents. Для начала введите 6
в ячейку E6 и нажмите Enter. После того как вы нажмите Ctrl+E, верное количество
долларов будет вставлено в ячейки E7:E11. Аналогично после ввода 56 в ячейку F6
и нажатия Enter и затем Ctrl+E инструмент Мгновенное заполнение заполнит ячейки F7:F11 верным количеством центов.
Инструмент Мгновенное заполнение может работать с ошибками, особенно на слабо согласованных данных. Кроме того (в отличие от формул, в том числе с текстовыми функциями), результаты работы инструмента Мгновенное заполнение не
являются динамическими и не обновляются при изменении исходных данных.
Инструмент Мгновенное заполнение можно отключить: на вкладке Файл (File) выберите Параметры (Options). Затем выберите раздел Дополнительно (Advanced)

ГЛАВА 6

и в диа логовом окне Дополнительные параметры для работы с Excel в разделе Параметры правки (Editing Options) снимите флажок Автоматически выполнять мгновенное
заполнение (Automatically Flash Fill).

Рис. 6.11. Создание email-адресов
с помощью инструмента Мгновенное
заполнение

Рис. 6.12. Извлечение суммы в долларах
и центах с помощью инструмента Мгновенное
заполнение

Что такое символы Unicode?

Набор символов Unicode содержит около 120 000 символов, включая множество
символов, используемых в научной литературе, и символы из других языков.

Рис. 6.13. Примеры использования функций UNICODE и UNICH

Текстовые функции и инструмент Мгновенное заполнение

Каждому символу Unicode соответствует числовой код. (Подробное описание
Unicode вы можете найти по адресу http://www.alanwood.net/unicode/.)
Например, символы греческого алфавита (важные для носителей греческого языка и для ученых!) имеют коды в районе 900 (см. файл Unicodefinal.xlsx и рис. 6.13).
Найти символ, соответствующий кодовому значению, можно с помощью функции ЮНИСИМВ(кодовое_значение) (UNICHAR(code number)). Например, формула
=ЮНИСИМВ(F67) вернет греческий символ µ, так как кодовое значение для µ — 956.
Узнать кодовое значение символа можно, используя функцию UNICODE(символ).
Так, формула =UNICODE(G67) вернет кодовое значение для µ (956).

Чем новая функция ОБЪЕДИНИТЬ лучше старой функции СЦЕПИТЬ
(или &)?

В файле Textjoinfinal.xlsx (рис. 6.14) продемонстрировано использование новой
функции ОБЪЕДИНИТЬ (TEXTJOIN). Нам нужно поместить в одну ячейку в виде скомбинированные данные, разделенные пробелами, из диапазона ячеекH2:L2. В ячейке
M2 это проделано с помощью устаревшей функции Concatenate, по формуле =H2&»
«&I2&» «&K2&» «&L2. В ячейке G2 применена формула =TEXTJOIN(» «;ИСТИНА;H2:L2)
с тем же результатом. Первый аргумент функции » » гарантирует разделение данных из ячеек H2:L2 пробелами. Второй аргумент, ИСТИНА, обеспечивает игнорирование пустых ячеек (в нашем случае это J2). В ячейку G3 мы ввели формулу
=TEXTJOIN(» «;ЛОЖЬ;H3:L3). Результат отличается только включением пробела из
пустой ячейки J3 в нашу цепочку. Преимущество функции ОБЪЕДИНИТЬ опять
проявляется и в отсутствии необходимости повторять символ-разделитель.

Рис. 6.14. Пример использования функции ОБЪЕДИНИТЬ

Мне нравятся текстовые функции, а как пользоваться функцией Excel
ТЕКСТ?

Допустим, вы работаете в отделе кадров, и вам принесли имена и даты рождения
сотрудников (рис. 6.15). По каждому сотруднику вы хотите записать фразу типа
«Джен родилась 14 октября 1988 г.». В ячейке F14 мы попробовали сделать это
с помощью формулы D3&» was born on «&E3. А программа нам отвечает: «Джен
родилась 32430-го». Это число дней, минувших с 1 января 1900 г. для даты 14 октября 1988 г. То есть проблема в том, что при конкатенации Excel выбирает неверный формат. Вот когда нас выручит функция ТЕКСТ. Если вы знаете правильный
код форматирования (а именно мм/дд/гггг), вы просто изменяете формулу следу-

ГЛАВА 6

ющим образом: D3&» was born on » & ТЕКСТ(E3,»мм/дд/гггг»), и — вуаля! Формат правильный.

Рис. 6.15. Пример использования функции ТЕКСТ

А как найти правильный формат? Просто перейдите в ячейку, где нужен правильный формат (например, E3), и нажмите CTRL+F1, чтобы открыть диалоговое окно
Формат ячеек (Format Cells). Выберите вкладку Число (Number) и затем Все форматы (Custom). Вы увидите экран со всякими сложными значками, показанный на
рис. 6.16. Просто скопируйте нужный код из поля Тип (Type) (в данном случае, мм/
дд/гггг) и вставьте этот код, заключенный в кавычки, как аргументфункции ТЕКСТ.

Рис. 6.16. Выбрав Все форматы, можно найти формат любого типа

Текстовые функции и инструмент Мгновенное заполнение

Как показано в диапазоне ячеек D8:G10, с помощью правильного формата вы можете извлечь название месяца или дня недели из даты.
«ммм» возвращает сокращенное название месяца.
«мммм» возвращает полное название месяца.
«ддд» возвращает сокращенное название дня недели.
«дддд» возвращает полное название дня недели.

Задания
1. В ячейках B3:B6 файла Showbiz.xlsx содержатся фиктивные адреса некоторых
знаменитостей. С помощью текстовых функций извлеките имена в один столбец, а адреса — в другой.
2. В файле IDprice.xlsx находятся идентификаторы продуктов вместе с ценами.
Используя текстовые функции, извлеките идентификаторы и цены в разные
столбцы. Затем примените Распределение текста по столбцам (Convert Text To
Columns) на вкладке Данные (Data) для достижения той же цели.
3. В файле Quarterlygnpdata.xlsx хранятся квартальные данные по ВНП США
(в млрд долларов). Распределите эти данные по трем столбцам следующим
образом: в первый столбец извлеките год, во второй — номер квартала и в третий — ВНП.
4. В файле Textstylesdata.xlsx хранится информация о фасоне, цвете и размере
различных рубашек. Например, первая рубашка имеет фасон 100 (указанный
цифрами между двоеточием и дефисом), цвет 65 и размер L. Используя текстовые функции, извлеките в разные столбцы фасон, цвет и размер для каждой рубашки.
5. В файле Emailproblem.xlsx даны имена и фамилии новых сотрудников Microsoft.
Для создания email-адреса каждому сотруднику возьмите первую букву его
имени, фамилию сотрудника и в конце добавь те @microsoft.com. Используйте
текстовые функции для эффективного создания адресов.
6. В файле Lineupdata.xlsx хранится число минут , сыгранных составами из пяти
игроков. (Например, первый состав сыграл 10,4 минуты.) С помощью текстовых функций преобразуйте эти данные в форму, пригодную для вычислений;
например, преобразуйте 10.4m в число 10,4.
7. В файле Reversenames.xlsx содержатся имена, вторые имена или инициалы
и фамилии нескольких людей. Преобразуйте эти имена следующим образом:
сначала фамилия, за ней запятая, затем имя и второе имя. Например, преобразуйте Gregory William Winston в Winston, Gregory William.
8. В файле Incomefrequency.xlsx находится распределение стартовых зарплат выпускников MBA колледжа F aber College. Обобщите эти данные с помощью
частотного графа.

ГЛАВА 6

9. Вспомните, что СИМВОЛ(65) дает в результате букву A, СИМВОЛ(66) — букву B
и т. д. Воспользовавшись этими знаниями, создайте книгу , заполнив ячейки
B1:B26 последовательностью букв A, B, C и так далее до Z.
10. В файле Capitalizeﬁrstletter.xlsx содержатся названия различных песен и фразы,
например, The rain in Spain falls mainly in the plain. Убедитесь, что каждое название
песни начинается с прописной буквы.
11. В файле Ageofmachine.xlsx хранятся данные в следующем виде:
S/N: 160768, vib roller, 84″ smooth drum, canopy Auction: 6/2–4/2005 in Montgomery,
Alabama

Это записи о покупках автомобиля. Определите год каждой покупки.
12. При скачивании корпоративных данных с сайта Security and Exchange Commission’s EDGAR полученные данные часто выглядят следующим образом:
денежные средства и их эквиваленты: $31 848, $31 881.

Как эффективно извлечь денежные средства и их эквиваленты для каждой
компании?
13. В файле Lookuptwocolumns.xlsx хранятся данные о модели, годе выпуска и цене
для ряда автомобилей. Напишите формулу, позволяющую по введенной модели и году выпуска автомобиля получить его цену.
14. В файле Moviedata.xlsx хранятся названия фильмов, за которыми следует количество DVD-копий, проданных в местном видеомагазине. Извлеките из этих
данных названия всех фильмов.
15. В файле Moviedata.xlsx хранятся названия фильмов, за которыми следует количество DVD-копий, проданных в местном видеомагазине. Для каждого фильма извлеките из данных количество проданных копий. Подсказка: возможно,
потребуется функция ПОДСТАВИТЬ. Ее синтаксис: ПОДСТАВИТЬ(ячейка;старый_
текст;новый_текст;[номер_вхождения]).
Если номер вхождения опущен, то каждое вхождение старого текста в ячейке заменяется новым текстом. Если номер вхождения указан, то только это
вхождение старого текста заменяется новым текстом. Например, функция ПОДСТАВИТЬ(A4;1;2) заменит каждую 1 в ячейке A4 на 2, а функция
ПОДСТАВИТЬ(A4;1;2;3) заменит только третье вхождение 1 в ячейке A4 на 2.
16. В файле Problem16data.xlsx хранится информация о людях, заполнивших рекламный опросник с пятью вариантами ответов (1 = скорее всего, не куплю, …,
5 = скорее всего, куплю). Обобщите эти данные графически с помощью символа «*». Для более наглядного представления на вкладке Главная (Home) откройте в группе Выравнивание (Alignment) раскрывающийся список Ориентация
(Orientation) и сделайте текст вертикальным. Затем щелкните правой кнопкой
мыши по номеру строки и увеличьте высоту строки. Наконец, в группе Выравнивание (Alignment) выберите Перенести текст (Wrap Text), чтобы сделать текст
вашего графика вертикальным.

Текстовые функции и инструмент Мгновенное заполнение

17. В файле Problem17data.xlsx содержатся имена (в виде Mr. John Doe). Используя текстовые функции, извлеките обращение (Mr . или Mrs.) и первое имя
каждого человека в отдельные столбцы.
18. В файле Weirddata.xlsx находятся три числа, импортированные с веб-сайта.
Сложив числа, убедитесь в некорректности результата. Измените данные таким образом, чтобы функция СУММ дала правильный резуль тат. Подсказка:
воспользуйтесь функцией НАЙТИ для поиска невидимого символа!
19. Используя Мгновенное заполнение, запишите имена в файле Flashﬁlltemplate.xlsx
(в папке Templates) строчными буквами.
20. Используя Мгновенное заполнение, извлеките число из каждой строки в файле
Movienumbers.xlsx.
21. Для данных в файле Movienumbers.xlsx создайте столбец и с помощью инструмента Мгновенное заполнение поместите в него фразу: The number in the title of
this movie is… и число для каждого названия фильма.
22. В каждой строке файла Problem22data.xlsx указано название города, штата и население города. Используя текстовые функции, извлеките название штата
в отдельный столбец.
23. В файле Problem23data.xlsx строка представляет имя квотербека (QB), его рейтинг и количество резуль тативных передач. Используя текстовые функции,
извлеките для каждого игрока количество результативных передач.
24. В каждой строке файла Problem24data.xlsx содержится индекс города, его название, штат (везде Texas!), широта и долгота. С помощью формул извлеките
из всех строк название города. Можете оттолкнуться от того факта, что индекс
всегда состоит из пяти символов. Подсказка: функция FIND чувствительна
к регистру.
25. В каждой строке файла Problem25data.xlsx между дефисом и запятой указано
число забитых квотербеком мячей. Примените текстовые функции для извлечения числа забитых мячей для каждого квотербека.
26. В файле Problem26data.xlsx содержатся сведения о 2000 крупнейших компаний
мира. Если в ячейку B3 вводится целое число от 1 до 2000, то ячейка C3 должна возвратить предложение типа «Доход компании, занимающей место № 1
по доходу, равен $328.21». Примените функцию ТЕКСТ, чтобы обеспечить правильный формат суммы в долларах.

ГЛ А В А 7

Даты и функции работы с датами
Обсуждаемые вопросы
Когда я ввожу даты в Excel, то часто получаю число, например 37625, а не дату
вида 04.01.2003. Что делать?
Как с помощью формулы автоматически отобразить сегодняшнюю дату?
Как определить дату через 50 рабочих дней после другой даты? Как исключить
праздничные дни?
Как определить количество рабочих дней между двумя датами?
На листе Excel введено 500 дат. Какие формулы нужны, чтобы извлечь из каждой
даты месяц, год, день месяца и день недели?
У меня есть значения года, месяца и дня. Существует ли простой способ восстановления фактической даты?
У меня бизнес по купле-продаже автомобилей. Для некоторых автомобилей известны даты покупки и продажи. Каким образом можно определить, сколько месяцев эти автомобили пробыли на стоянке?
Как поместить в лист статичную (неизменяемую) дату?

Для иллюстрации наиболее часто использующихся форматов в Microsoft
Excel 2019 предположим, что сегодня 4 января 2004 г. Эту дату можно ввести, например, следующим образом:
4/1/20041;
4-янв-2004;
4 янв 2004;
4/1/04;
04.01.2004.
Если год указан двумя последними цифрами, и это цифры 30 и больше, то Excel
предполагает, что это год XX века; если цифры меньше 30, считается, что они относятся к XXI веку. Например, 1/1/29 будет означать 1 января 2029 г., а 1/1/30 будет обработано как 1 января 1930 г . Год, определяющий обработку даты как даты
в XXI веке, увеличивается на единицу каждый год.
1

В русифицированной версии Microsoft Excel 2019 используется формат день-месяцгод. — Примеч. пер.

Даты и функции работы с датами

Ответы на вопросы
?

Когда я ввожу даты в Excel, то часто получаю число, например 37625, а не
дату вида 04.01.2003. Что делать?

То, как Excel обрабатывает даты, иногда сбивает с толку новичков. Важно понимать, что в Excel есть два формата отображения дат: день-месяц-год и числовой
формат. Дата в числовом формате, например 37625, — это целое положительное
число, равное количеству дней между заданной датой и 1 января 1900 г. При подсчете учитывается как текущая дата, так и 1 января 1900 г. Например, в Excel дата
3 января 1900 г. в формате числа отображается как число 3. Таким образом, считается, что промежуток между 1 января 1900 г. и 3 января 1900 г. (включая оба этих
дня) составляет три дня.
ПРИМЕЧАНИЕ
Excel считает, что 1900 г. был високосным, то есть содержал 366 дней. В действительности в нем было 365 дней. Занимательную информацию о происхождении этой
ошибки можно прочитать здесь: www.joelonsoftware.com/items/2006/06/16.html.

На рис. 7.1 показан лист serial format в файле Dates.xlsx. Допустим, даты в ячейках
D5:D14 даны в числовом формате. Например, значение 37622 в ячейке D5 указывает на дату, приходящуюся на 37 622-й день после 1 января 1900 г . (включая 1 января 1900 г. и сам 37 622-й день). Скопируйте даты в числовом формате в ячейки E5:E14 для отображения в формате день-месяц-год. Выделите диапазон ячеек
E5:E14, щелкните правой кнопкой мыши по выделенной области и выберите в контекстном меню Формат ячеек… (Format Cells). Кстати, диалоговое окно Формат ячеек
(Format Cells) можно открыть в любое время, нажав Ctrl+1. Из списка, показанного
на рис. 7.2, выберите формат Дата (Date) и Тип (Type). Даты в ячейках E5:E14 отобразятся в формате день-месяц-год (рис. 7.1). Если нужно перевести даты в числовой формат, выделите ячейки E5:E14, щелкните правой кнопкой мыши по выделенной области и выберите Формат ячеек… | Общий (Format Cells | General).

Рис. 7.1. Преобразование дат из формата десятичного числа
в формат день-месяц-год с помощью команды Формат ячеек

ГЛАВА 7

Простая замена формата даты в ячейке на общий формат приведет к отображению даты в числовом формате. Можно воспользоваться другим способом и применить функцию ДАТАЗНАЧ (DATEVALUE) с датой, заключенной в кавычки. Например, в файле Dates.xlsx на листе date format в ячейке I5 находится формула
=ДАТАЗНАЧ(«4/1/2003»). В результате ее вычисления получается 37625, что соответствует дате в числовом формате для 4 января 2003 г.

Рис. 7.2. Переформатирование даты в формате десятичного числа в формат день-месяцгод в диалоговом окне Формат ячеек

Как с помощью формулы автоматически отобразить сегодняшнюю дату?

Пример отображения сегодняшней даты с помощью функции СЕГОДНЯ (TODAY)
приведен в ячейке C13 на листе date format (рис. 7.3). Введите в ячейку формулу
=СЕГОДНЯ(). Этот скриншот был сделан 15 июня 2016 г.

Как определить дату через 50 рабочих дней после другой даты? Как исключить праздничные дни?

Для этого примените функцию РАБДЕНЬ (WORKDAY). Синтаксис этой функции:
РАБДЕНЬ(нач_дата;#число_дней;[праздники]). Функция РАБДЕНЬ отображает дату
через столько рабочих дней (рабочий день — это не выходной день) после заданной начальной даты, сколько указано значением аргумента
#число_дней.
Аргумент праздники является необязательным и позволяет исключить из расчета любые даты, указанные в диапазоне ячеек. Т
аким образом, по формуле
=РАБДЕНЬ(C14;50) в ячейке D14 листа date format пятидесятым рабочим днем по-

Даты и функции работы с датами

сле 03.01.2003 является 14 марта 2003 г . Если необходимо учесть праздники
День Мартина Лютера Кинга и День независимости, измените формулу на следующую: =РАБДЕНЬ(C14;50;F17:F18) (она приведена в ячейке E14). В этом случае
20.01.2003 не будет учтено, и пятидесятым рабочим днем после 03.01.2003 станет 17 марта 2003 г . Обратите внимание, что вместо ссылки на даты праздников
в других ячейках можно ввести даты в формулу , указав каждый праздник в числовом формате, заключенном в фигурные скобки ( { }). Например, в формуле
=РАБДЕНЬ(38500;10;{38600;38680;38711}) для подсчета десятого рабочего дня после даты с номером 38 500 исключены праздники День труда, День благодарения
и Рождество в 2005 г.

Рис. 7.3. Примеры использования функций обработки дат

В Microsoft Excel 2010 появилась функция РАБДЕНЬ.МЕЖД (WORKDAY.INTL), позволяющая выбрать собственное определение рабочего дня. Синтаксис этой функции: РАБДЕНЬ.МЕЖД(нач_дата;число_дней;выходные;[праздники]). Для определения выходного дня используется третий аргумент. Коды, приведенные в таблице
ниже, определяют как выходные следующие дни:
Код

Выходные дни

Код

Выходные дни

1 или аргумент опущен

суббота, воскресенье

только воскресенье

воскресенье, понедельник

только понедельник

понедельник, вторник

только вторник

вторник, среда

только среда

среда, четверг

только четверг

четверг, пятница

только пятница

пятница, суббота

только суббота

ГЛАВА 7

Например, в файле Dates.xlsx на листе date format в ячейке C27 по формуле
=РАБДЕНЬ.МЕЖД(C23;100;2) вычислена дата сотого рабочего дня после 14.03.2011
с воскресеньем и понедельником в качестве выходных дней (рис. 7.4). В ячейке C28 по формуле =РАБДЕНЬ.МЕЖД(C23;100;11) вычислена дата сотого рабочего
дня после 14.03.2011 для случая, когда выходным является только воскресенье.
Кроме того, выходные дни можно определить с помощью строки из семи единиц и нулей; единица означает выходной день, и первая позиция в строке соответствует понедельнику, вторая — вторнику и т . д. Таким образом, в ячейках D26
и D27 предыдущие резуль таты продублированы с помощью формул = РАБДЕНЬ.
МЕЖД(C23;100;»1000001″) и =РАБДЕНЬ.МЕЖД(C23;100;»0000001″), соответственно.

Рис. 7.4. Примеры использования функций для международных дат

Как определить количество рабочих дней между двумя датами?

Нам потребуется функция ЧИСТРАБДНИ (NETWORKDAYS). Синтаксис этой функции:
ЧИСТРАБДНИ(нач_дата;кон_дата;[праздники]), где праздники (holidays) — необязательный аргумент, указывающий диапазон ячеек с датами, считающимися праздниками. Функция ЧИСТРАБДНИ возвращает количество рабочих дней между начальной
и конечной датами, исключая выходные дни и все указанные праздники. В качестве
иллюстрации работы функции ЧИСТРАБДНИ рассмотрим ячейку C18 на листе date
format файла Dates.xlsx с формулой =ЧИСТРАБДНИ(C14;C15). По этой формуле рассчитывается количество рабочих дней между 03.01.2003 и 04.08.2003, которое составляет 152 дня. В ячейке C17 по формуле =ЧИСТРАБДНИ(C14;C15;F17:F18) вычисляется
количество рабочих дней между 03.01.2003 и 04.08.2003, исключая День Мартина
Лютера Кинга и День независимости. В результате получается 152 – 2 = 150.
В Microsoft Excel 2010 появилась функция ЧИСТРАБДНИ.МЕЖД (NETWORKDAYS.
INTL). Аналогично функции РАБДЕНЬ.МЕЖД, функция ЧИСТРАБДНИ.МЕЖД позволяет задать собственное определение выходных дней. Например, в файле Dates.
xlsx на листе date format в ячейке C31 по формуле =ЧИСТРАБДНИ.МЕЖД(C23;C24;2)
вычисляется количество рабочих дней ( 373) между 14.03.2011 и 16.08.2012

Даты и функции работы с датами

для случая, когда выходными днями являются воскресенье и понедельник
(рис. 7.4). В ячейке D31 те же вычисления выполнены по формуле =ЧИСТРАБДНИ.
МЕЖД(C23;C24;»1000001″).

На листе Excel введено 500 дат. Какие формулы нужны, чтобы извлечь из
каждой даты месяц, год, день месяца и день недели?

В файле Dates.xlsx на листе date format (см. рис. 7.3) в диапазоне ячеек B5:B10 указано несколько дат. В ячейке B5 и ячейках B7:B9 я использовал четыре формата
для отображения даты 4 января 2003 г . В столбцах D:G я поместил извлеченные
год, месяц, день месяца и день недели для каждой даты. Г од из каждой даты я извлек, применив функцию ГОД (YEAR) — я скопировал формулу =ГОД(B5) из ячейки
D5 в ячейки D6:D10. Номер месяца (1 — январь, 2 — февраль и т . д.) из каждой
даты я извлек с помощью функции МЕСЯЦ (MONTH) путем копирования формулы =МЕСЯЦ(B5) из ячейки E5 в ячейки E6:E10. День месяца был извлечен с помощью функции ДЕНЬ (DAY) путем копирования формулы =ДЕНЬ(B5) из ячейки F5
в ячейки F6:F10. Наконец, день недели для каждой даты был извлечен с помощью
функции ДЕНЬНЕД (WEEKDAY) путем копирования формулы =ДЕНЬНЕД(B5;1) из
ячейки G5 в ячейки G6:G10. Обратите внимание: региональные настройки (не для
США) могут потребовать внесения в пример некоторых изменений.
Если значение последнего аргумента функции ДЕНЬНЕД равно 1, то 1 — это воскресенье, 2 — понедельник и т. д. Если это значение равно 2, то 1 — это понедельник,
2 — вторник и т. д. Если значение равно 3, 0 — это понедельник, 1 — вторник и т. д.

У меня есть значения года, месяца и дня. Существу ет ли простой способ
восстановления фактической даты?

Функция ДАТА (DATE) с аргументами ДАТА(год;месяц;день) возвращает дату для
указанного года, месяца и дня. На листе date format я восстановил исходные даты,
скопировав формулу =ДАТА(D5;E5;F5) из ячейки H5 в ячейки H6:H10.
У меня бизнес по купле-продаже автомобилей. Для некоторых автомобилей известны даты покупки и продажи. Каким образом можно определить,
сколько месяцев эти автомобили пробыли на стоянке?

Количество полных лет, месяцев или дней между двумя датами можно определить с помощью функции РАЗНДАТ (DATEDIF). В файле Datedif.xlsx (рис. 7.5) приведен пример покупки автомобиля 15 октября 2016 г. и его последующей продажи
10 апреля 2018 г. Сколько полных лет, месяцев или дней стоял на парковке этот
автомобиль? Синтаксис функции: РАЗНДАТ(нач_дата,кон_дата,единицы_времени).
Если для аргумента единицы_времени указать значение «y», функция возвратит
количество полных лет между начальной и конечной датами. Если указать значение «m», функция возвратит количество полных месяцев, а если указать значение
«d», то будет получено количество полных дней между двумя указанными датами. Таким образом, ввод формулы =РАЗНДАТ(D4;D5;»y») в ячейку D6 показывает,
что машина хранилась один полный год. Ввод формулы =РАЗНДАТ(D4;D5;»m»)

ГЛАВА 7

в ячейку D7 дает результат: 17 полных месяцев. Введенная в ячейку D8 формула
=РАЗНДАТ(D4;D5;»d») возвращает число 543 — число полных дней. Кстати, функция РАЗНДАТ отсутствует в списке мастера функций.

Рис. 7.5. Результат применения функции РАЗНДАТ

Как поместить в лист статичную (неизменяемую) дату?

Ввод в ячейке функции =СЕГОДНЯ() всегда возвращает сегодняшнюю дату . При
создании книги нам может потребоваться, чтобы в книге всегда отображалась дата
ее создания. Комбинация клавиш Ctrl+; (точка с запятой) поместит сегодняшнюю
дату в ячейку, но в отличие от функции =СЕГОДНЯ(), эта дата больше меняться
не будет. Книга, представленная на рис. 7.6 (см. файл Staticdate.xls), была создана
11 июня 2018 г., и эта дата всегда будет отображаться в ячейке F6.

Рис. 7.6. Cоздание статичной даты с помощью комбинации Ctrl+;

Задания
1. Как выглядит дата 25 января 2006 г. в числовом формате?
2. Как выглядит дата 14 февраля 1950 г. в числовом формате?
3. Какой фактической дате соответствует дата 4526?
4. Какой фактической дате соответствует дата 45 000?
5. Определите день, который приходится на 74-й рабочий день после сегодняшней даты (включая праздники).

Даты и функции работы с датами

6. Определите день, который приходится на 74-й рабочий день после сегодняшней даты (включая праздники, но исключая Рождество, Новый год и День независимости).
7. Сколько рабочих дней (включая праздники) между 10 июля 2005 г. и 15 августа 2006 г.?
8. Сколько рабочих дней (включая праздники, но исключая Рождество, Новый
год и День независимости) между 10 июля 2005 г. и 15 августа 2006 г.?
В файле Datep.xlsx содержится несколько сотен дат . Используйте этот файл для
выполнения следующей группы заданий.
1. Определите месяц, год, день месяца и день недели для каждой даты.
2. Представьте каждую дату в числовом формате.
3. Проект стартует 4 декабря 2005 г . Он включает этапы 1, 2 и 3. Этап 2 может
начаться на следующий день после завершения этапа 1. Этап 3 может начаться на следующий день после завершения этапа 2. Создайте лист , на котором
входными данными является продолжительность (в днях) всех трех этапов
проекта, а выходными данными — месяц и год, в которые завершится каждый
этап.
4. Допустим, вы приобрели акции 29 июля 2005 г . и продали их 30 декабря
2005 г. Фондовая биржа закрыта в День труда, на Рождество и в День благодарения1. Создайте список рабочих дней фондового рынка в тот период, когда
вы владели акциями.
5. В файле Machinedates.xlsx содержатся даты покупки и продажи нескольких автомобилей. Определите, сколько месяцев и лет автомобили провели на стоянке.
6. Для любой даты найдите способ вычисления дня недели первого числа месяца, на который приходится эта дата.
7. Для любой даты найдите способ вычисления последнего дня месяца, на
который приходится дата. Подсказка: как ни удивительно, но формула
=ДАТА(2005;13;1) возвращает 01.01.2006.
8. Как для любой даты вычислить ее порядковый номер от начала года? Например, каким по счету днем года является 15 апреля 2020 г.? Подсказка: формула =ДАТА(2020;1;0) возвращает порядковый номер для нулевого дня в январе
2020 г., который в Excel обрабатывается как 31 декабря 2019 г.
9. Во Фредонии выходными днями являются вторник и среда. Какой дате соответствует день через 200 рабочих дней после 03.05.2013?
10. В стране Нижняя Амперия выходными днями являются пятница и суббота.
Кроме того, праздничным днем считается День святого Валентина. Сколько
рабочих дней там между 10 января 2014 г. и 31 мая 2015 г.?
1

Разумеется, вы можете использовать другие праздничные даты, например 4 ноября —
День народного единства. — Примеч. ред.

ГЛАВА 7

11. Первым кварталом каждого года является январь — март , вторым кварталом — апрель — июнь и т. д. Напишите формулу, которая возвращает первый
день квартала для указанной даты.
12. Для кварталов из задания 11 напишите формулу расчета последнего дня предыдущего квартала для любой указанной даты.
13. Создайте таблицу, в которой можно указать дату рождения и получить фактический возраст.
14. День памяти всегда приходится на последний понедельник мая. Создайте таблицу, в которой можно указать год и получить дату Дня памяти.
15. Создайте таблицу, в которой всегда перечислены следующие 50 рабочих дней
(праздники не учитываются, и дни с понедельника по пятницу считаются рабочими днями).
16. Грег Уинстон работает на федеральное правительство, и в 2016 году у него
было 10 выходных в государственные праздники. (Посмотрите даты этих
праздников в интернете.) В каждую не приходящуюся на праздник пятницу
Грег также выходной, равно как и в выходные дни, начиная с 8 января 2016 г .
Создайте список всех рабочих дней Грега в 2016 г.

ГЛАВА 8

Оценка инвестиций по чистой
приведенной стоимости

Обсуждаемые вопросы
Что такое чистая приведенная стоимость (ЧПС)?
Как работать с функцией ЧПС в Excel?
Как рассчитать ЧПС, если денежные потоки приходят в начале или середине
года?
Как рассчитать ЧПС, если денежные потоки приходят через неравные промежутки времени?

Рассмотрим на примере два инвестиционных проекта, денежные потоки которых
представлены в файле NPV.xlsx и на рис. 8.1.

Рис. 8.1. Для оценки этих двух инвестиций необходимо рассчитать
чистую приведенную стоимость

ГЛАВА 8

Инвестиционный проект 1 требует расходов в размере $10 000 сегодня
и $14 000 через два года. Через год эта инвестиция принесет $24 000.
Инвестиционный проект 2 требует расходов в размере $6000 сегодня и $1000
через два года. Через год эта инвестиция принесет $8000.
Какой из проектов представляет собой лучшее вложение средств? Совокупный денежный поток для первого проекта равен $0, в то время как второй проект принесет
$1000. На первый взгляд, второй инвестиционный проект более эффективен, но не
будем спешить с выводами. Большая часть расходов на первый проект будет через
два года, в то время как большая часть расходов по второму проекту придется на
настоящий момент. Один доллар через два года кажется не такой большой тратой,
как один доллар сегодня, так что, вполне возможно, первый инвестиционный проект окажется более привлекательным. Для оценки привлекательности инвестиций
необходимо сравнить стоимости денежных потоков, полученные в разные моменты
времени. Вот где пригодится понятие чистой приведенной стоимости.

Ответы на вопросы
?

Что такое чистая приведенная стоимость (ЧПС)?

Чистая приведенная стоимость (ЧПС) потока денежных средств, полученная
в разные моменты времени, — это просто стоимость, измеренная в текущих долларах. Допустим, у вас есть один доллар, и вы инвестируете этот доллар под годовую
процентную ставку r процентов. За первый год этот доллар вырастет до 1 + r долларов, за второй год до (1 + r)2 долларов и т. д. В некотором роде можно сказать,
что один доллар сегодня эквивалентен 1 + r долларам через год и (1 + r)2 долларам
через два года. В целом один доллар сегодня эквивалентен (1 + r)n долларам через
n лет. Эти расчеты можно записать следующим уравнением:
1 доллар сегодня = (1 + r)n долларов через n лет.
Если разделить обе части этого уравнения на (1 +r)n, получим следующий результат:

Этот результат показывает, как рассчитать ЧПС (в текущих долларах) для любой
последовательности денежных потоков. Любой денежный поток можно конвертировать в текущие доллары путем умножения стоимости денежного потока через
n лет (n может быть дробью) на

Далее для вычисления ЧПС инвестиционного проекта сложите стоимости денежных потоков (в текущих долларах). Пусть r равно 0,2. ЧПС для данных инвестиционных проектов можно рассчитать следующим образом:

Оценка инвестиций по чистой приведенной стоимости

По критерию ЧПС первая инвестиция превосходит вторую. Хотя совокупный денежный поток для второго проекта превышает совокупный денежный поток первого проекта, ЧПС первого проекта больше, поскольку большая часть отрицательного денежного потока первого проекта приходит позже, а критерий ЧПС придает
меньший вес денежным потокам, приходящим позже. Если годовая процентная
ставка r составляет 0,02%, то ЧПС второй инвестиции будет больше, поскольку
при малых значениях r более поздние денежные потоки дисконтируются не так
сильно, и ЧПС будет соответствовать ранжированию инвестиций по совокупному
денежному потоку.
ПРИМЕЧАНИЕ
Я выбрал процентную ставку r = 0,2 случайным образом во избежание обсуждения
способов определения подходящего значения r. Чтобы понимать все аспекты определения нужного значения r, необходимо минимум год посвятить изучению управления
финансами. Нужное значение r, используемое при расчете ЧПС, часто называют стоимостью капитала компании. Достаточно сказать, что в большинстве американских
компаний годовая стоимость капитала составляет от 0,1 (10%) до 0,2 (20%). Если
годовая процентная ставка выбирается в соответствии с общепринятой финансовой
практикой, проекты с ЧПС > 0 увеличивают стоимость компании, а проекты с ЧПС < 0
ее уменьшают, в то время как проекты с ЧПС = 0 не изменяют стоимость компании.
Компания должна (если располагает неограниченным инвестиционным капиталом)
инвестировать в каждый доступный инвестиционный проект с положительной ЧПС.

Для определения ЧПС первой инвестиции в Excel я присвоил диапазону с процентной ставкой (ячейке C3) имя r_. (Если вы попытаетесь присвоить ячейке
имя r, Excel преобразует его в r_, см. главу 2.) Затем я скопировал денежный поток нулевого периода из C5 в C7. ЧПС для первого и второго годов я определил,
скопировав формулу =D5/(1+r_)^D$4 из D7 в E7. Символ вставки (^) означает возведение в степень. В ячейке A5 я вычислил ЧПС первой инвестиции, сложив ЧПС
первого проекта для каждого года по формуле =СУММ(C7:E7). Для определения
ЧПС второй инвестиции я скопировал формулы из C7:E7 в C8:E8 и из A5 в A6.

Как работать с функцией ЧПС в Excel?

Синтаксис функции ЧПС (NPV) в Excel: ЧПС(ставка;диапазон_ячеек). Эта функция
определяет ЧПС по заданной ставке для денежных потоков в указанном диапазоне ячеек. При расчете подразумевается, что первый денежный поток отстоит на
один период от настоящего момента. То есть для определения ЧПС первой инвестиции нельзя применить формулу =ЧПС(r_;C5:E5). Вместо этого по ней (в ячей-

ГЛАВА 8

ке C14) я рассчитал ЧПС следующих денежных потоков: для –$10 000 через год
от настоящего момента, для $24 000 через два года и для –$14 000 через три года.
Назовем это значение приведенной стоимостью на конец года. ЧПС первого инвестиционного проекта на конец года равна $231,48. Для расчета фактической ЧПС
первого проекта с учетом денежных потоков в начале года нужно ввести формулу
=C7+ЧПС(r_;D5:E5) в ячейку C11. По этой формуле денежный отток в нулевой период вообще не учитывается (что правильно, поскольку денежный отток в нулевой период уже выражен в текущих долларах), и сначала денежный поток в ячейке
D5 умножается на 1/1,2, а затем денежный поток в ячейкеE5 умножается на 1/1,22.
Формула в ячейке C11 вычисляет корректную ЧПС первой инвестиции, а именно
$277,78.

Как рассчитать ЧПС, если денежные потоки приходят в начале или середине года?

Чтобы применить функцию ЧПС для расчета чистой приведенной стоимости проекта, денежные потоки которого всегда приходятся на начало года, можно воспользоваться подходом, который я описал для определения ЧПС первой инвестиции.
Отделите денежный поток первого года и примените функцию ЧПС к оставшимся
денежным потокам. Или учтите то, что для любого n-го года $1, полученный в начале n-го года, эквивалентен $(1 + r) в конце n-го года. Помните: в течение года
доллар вырастет в 1 + r раз. Таким образом, если умножить результат, полученный
с помощью функции ЧПС, на 1 + r, можно конвертировать ЧПС последовательности денежных потоков на конец года в ЧПС последовательности денежных потоков на начало года. Т о есть ЧПС первой инвестиции рассчитывается по формуле =(1+r_)*C14 (см. ячейку D11). Конечно, вы снова получите $277,78. Т еперь
допустим, что денежные потоки инвестиционного проекта приходят в середине
каждого года. Для организации, которая получает ежемесячные взносы в рамках
подписки, можно приблизительно считать 12 месячных взносов, полученных за
указанный год, единовременной суммой, полученной в середине года. Каким образом с помощью функции ЧПС можно определить ЧПС последовательности
долларов, полуденежных потоков в середине года? Для любого n-го года
ченных в конце n-го года, эквивалентны $1, полученному в середине n-го года,
поскольку за полгода $1 вырастет в
раз.
Если предположить, что денежные потоки для первой инвестиции приходят в середине года, можно рассчитать ЧПС первого проекта на середину года в ячейке
C17 по формуле =КОРЕНЬ(1+r_)*C14. ЧПС равна $253,58.

Как рассчитать ЧПС, если денежные потоки приходят через неравные
промежутки времени?

Деньги часто поступают нерегулярно, что усложняет расчет ЧПС или внутренней
ставки доходности (ВСД) этих потоков. К счастью, на помощь нам спешит такая
функция Excel, как ЧИСТНЗ (XNPV), вычисляющая ЧПС денежных потоков, спланированных через неравные промежутки времени.

Оценка инвестиций по чистой приведенной стоимости

Для функции ЧИСТНЗ используется синтаксис ЧИСТНЗ(ставка;значения;даты). Первая дата должна быть самой ранней, а остальные даты не обязательно указывать
в хронологическом порядке. Функция ЧИСТНЗ вычисляет ЧПС заданных денежных потоков при условии, что текущая дата является первой датой последовательности. Например, если первой указана дата 08.04.13, то ЧПС рассчитывается
в стоимости доллара на 8 апреля 2013 г.
Работа функции ЧИСТНЗ показана в примере на листе NPV as of first date в файле
XNPV.xlsx (см. также рис. 8.2). Допустим, 8 апреля 2015 г . было выплачено $900.
Позже были получены следующие суммы:
$300 15 августа 2015 г.;
$400 15 января 2016 г.;
$200 25 июня 2016 г.;
$100 3 июля 2016 г.
Если годовая процентная ставка составляет 10%, то какова величина ЧПС этих денежных потоков? Введите даты (в формате дат Excel) в D3:D7 и денежные потоки
в E3:E7. После ввода формулы =ЧИСТНЗ(A9;E3:E7;D3:D7) в ячейку D11 будет рассчитана ЧПС проекта в стоимости доллара на 8 апреля 2015 г., поскольку это первая дата
в списке. ЧПС этого проекта в стоимости доллара на 8 апреля 2015 г. равна $28,64.

Рис. 8.2. Функция ЧИСТНЗ в действии

Функция ЧИСТНЗ выполняет следующие вычисления:
1. Вычисляет количество лет после 8 апреля 2015 г., через которое наступит каждая дата в списке (см. столбец F). Например, 15 августа наступит через 0,3534
года после 8 апреля.
2. Дисконтирует денежные потоки по ставке
Например, денежный поток 15 августа 2015 г
(1+0.1)^3534.

1/(1+ставка)^количество_лет.

. дисконтируется по ставке:

3. Суммирует совокупные денежные потоки в ячейке E11: (стоимость денежных
потоков)*(коэффициент дисконтирования).

ГЛАВА 8

Допустим, сегодня 8 июля 2013 г . Как вычислить ЧПС инвестиции в текущих
долларах? Просто добавьте строку с текущей датой и нулевой денежный поток
и включите эту строку в диапазон для функцииЧИСТНЗ. (См. рис. 8.3 и лист today.)
ЧПС проекта в текущих долларах составляет $106,99.

Рис. 8.3. Конвертация ЧПС в текущие доллары

Если денежный поток останется пустым, функция ЧПС проигнорирует и денежный поток, и период, а функция ЧИСТНЗ возвратит ошибку #ЧИСЛО!.

Задания
1. Игрок НБА получает бонус за подписание контракта в размере $1 000 000
сейчас и $2 000 000 через год, через два года и через три года. Предполагая, что
r = 0,10, и игнорируя налоги, стал бы он богаче, если бы получил $6 000 000
сразу?
2. Ниже приведены денежные потоки проекта:
Сегодня

Через год

Через два года

Через три года

–$4 млн

$4 млн

–$3 млн

Если стоимость капитала компании составляет 15%, не стоит ли ей отказаться
от этой инвестиции?
3. Через месяц клиент будет платить своему интернет-провайдеру $25 в месяц
в течение последующих пяти лет. При условии что все годовые доходы поступают в середине года, рассчитайте ЧПС этих доходов. Примите r = 0,15.
4. Через месяц клиент будет платить своему интернет-провайдеру $25 в месяц
в течение последующих пяти лет . При условии что все месячные доходы поступают в начале месяца, воспользуйтесь функцией ЧИСТНЗ для получения
точного значения ЧПС этих доходов. Примите r = 0,15.

Оценка инвестиций по чистой приведенной стоимости

5. Рассмотрите денежные потоки за четыре года в нижеследующей таблице.
Определите ЧПС этих денежных потоков, если r = 0,15 и денежные потоки
приходят в конце года.
Год

–$600

$550

–$680

$1000

6. Рассмотрите следующие денежные потоки:
Дата

Денежный поток

15.12.01

–$1000

11.01.02

$300

07.04.03

$600

15.07.04

$925

Если сегодня 1 ноября 2001 г. и r = 0,15, какова ЧПС этих потоков?
7. После получения MBA студент начнет получать с 1 сентября 2005 г. $80 000
в год. Он рассчитывает на ежегодное увеличение оклада на 5%, пока не выйдет
на пенсию 1 сентября 2035 г. При условии, что стоимость капитала составляет
8% в год, определите совокупную приведенную стоимость его заработка до
уплаты налогов.
8. Рассмотрим 30-летнюю облигацию с выплатой $50 в конце года с первого года
по 29-й и выплатой $1050 в конце 30-го года. Если дисконтная ставка составляет 5% в год, какая цена является справедливой за эту облигацию?

ГЛ А В А 9

Внутренняя ставка доходности

Обсуждаемые вопросы
Как вычислить внутреннюю ставку доходности денежных потоков?
Всегда ли проект имеет единственное значение ВСД?
Существуют ли условия, гарантирующие единственное значение ВСД проекта?
Если единственное значение ВСД имеют два проекта, как можно использовать
значение ВСД для этих проектов?
Как вычислить ВСД для нерегулярно поступающих денежных потоков?
Что такое модифицированная внутренняя ставка доходности (МВСД) и как она
рассчитывается?

Чистая приведенная стоимость (ЧПС) последовательности денежных потоков зависит от используемой процентной ставки (r). Например, анализ денежных потоков первого и второго проектов (см. листIRR в файле IRR.xlsx и рис. 9.1) показывает,
что при r = 0,2 ЧПС второго проекта больше, чем первого, а при r = 0,01 наоборот.
При использовании ЧПС для ранжирования инвестиций резуль тат может зависеть от процентной ставки. Человеку свойственно стремление свести все в жизни
к единственному показателю. ВСД проекта — это процентная ставка, при которой

Рис. 9.1. Пример использования функции ВСД

Внутренняя ставка доходности

величина ЧПС проекта равна 0. Если проект имеет единственное значение ВСД,
то у такой ВСД точная трактовка. Например, если ВСД проекта равна 15%, то годовая норма прибыли на вложенные денежные средства составит 15%. В упомянутом примере ВСД первого проекта равна 47,5%. То есть $400, вложенные в первый
год, дадут годовую норму прибыли 47,5%. Но иногда проект имеет несколько ВСД
или даже ни одной ВСД. В этих случаях говорить о ВСД проекта не имеет смысла.

Ответы на вопросы
?

Как вычислить внутреннюю ставку доходности денежных потоков?

Внутренняя ставка доходности вычисляется с помощью функции ВСД (IRR). Синтаксис функции ВСД: ВСД(диапазон_денежных_потоков;[предположение]), где предположение является необязательным аргументом. Если предполагаемое значение
для ВСД проекта не указано, Excel начинает вычисления с предположения, что
значение ВСД проекта равно 10%, и затем значение ВСД изменяется до тех пор,
пока не будет найдена процентная ставка, при которой ЧПС проекта равна 0 (это
и есть ВСД проекта). Если процентная ставка, при которой ЧПС проекта равна 0,
не найдена, возвращается ошибка #ЧИСЛО!. Я ввел в ячейке B5 листа IRR файла
IRR.xlsx формулу =ВСД(C2:I2) для расчета ВСД первого проекта. В резуль тате получилось 47,5%. Таким образом, ЧПС первого проекта равна 0 при годовой процентной ставке 47,5. Аналогично ВСД второго проекта равна 80,1%.
Даже если функция ВСД найдет значение ВСД, у проекта может оказаться несколько ВСД. Чтобы это выяснить, можно варьировать начальное предположение
о величине ВСД проекта (например, от –90% до 90%). Предположение о величине
ВСД первого проекта можно варьировать, скопировав формулу=ВСД($C$2:$I$2;A8)
из B8 в B9:B17. Поскольку при всех предположениях о величине ВСД первого проекта в результате получается 47,5%, можно с уверенностью сказать, что первый
проект имеет единственную ВСД, и она равна 47,5%. Аналогично можно утверждать, что второй проект имеет единственную ВСД 80,1%.

Всегда ли проект имеет единственное значение ВСД?

В файле IRR.xlsx на листе Multiple IRR и на рис. 9.2 показано, что у третьего проекта
(с денежными потоками –20, 82, –60, 2) имеется два значения ВСД. Предположение о величине ВСД третьего проекта варьировалось от –90% до 90% путем копирования формулы =ВСД($B$4:$E$4;B8) из ячейки C8 в ячейки C9:C17.
Если предполагаемая величина ВСД не больше 30%, то ВСД проекта равна –9,6%.
Для других предполагаемых величин ВСД проекта равна 216,1%. Для обеих этих
процентных ставок ЧПС третьего проекта нулевая.
В файле IRR.xlsx на листе No IRR (рис. 9.3) показано, что вне зависимости от предположений о величине ВСД четвертого проекта в результате всегда возвращается
ошибка #ЧИСЛО!. Это означает, что четвертый проект не имеет ВСД.

ГЛАВА 9

Рис. 9.2. Проект имеет несколько значений ВСД

Если у проекта несколько ВСД или же она отсутствует , понятие ВСД теряет
смысл. Однако несмотря на эту проблему , многие компании все еще используют
ВСД в качестве основного инструмента ранжирования инвестиций.

Рис. 9.3. У этого проекта значение ВСД отсутствует

Внутренняя ставка доходности

Существуют ли условия, гарантирующие единственное значение ВСД проекта?

Если в последовательности денежных потоков проекта происходит только одна
смена знака, проект гарантированно имеет одно значение ВСД. Например, у второго проекта в ячейках C3:I3 на листе IRR последовательность знаков денежных
потоков такая: – + + + + +. Смена знака происходит только один раз (между первым и вторым годом), поэтому у второго проекта должно быть только одно значение ВСД. Последовательность знаков денежных потоков у третьего проекта
в ячейках B4:E4 на листе Multiple IRR такова: – + – +. Поскольку знак денежных
потоков меняется три раза, единственное значение ВСД не гарантировано. У четвертого проекта в ячейках B5:D5 на листе No IRR знаки денежных потоков ( + – +)
меняются два раза, в этом случае единственное значение ВСД также не гарантируется. Большинство проектов капиталовложений (таких как строительство завода)
начинается с отрицательного денежного потока, за которым следуют положительные денежные потоки. Следовательно, большинство проектов капиталовложений
должно иметь единственное значение ВСД.

Если единственное значение ВСД имеют два проекта, как можно использовать значение ВСД для этих проектов?

Если у проекта единственное значение ВСД, то можно утверждать, что проект
увеличивает стоимость компании тогда и только тогда, когда ВСД проекта превышает годовую стоимость капитала. Например, если стоимость капитала компании
составляет 15%, оба проекта, и первый, и второй, увеличат ее стоимость.
Допустим, что к рассмотрению представлены два проекта (у обоих проектов значение ВСД единственное), но выбрать нужно только один. Кажется, что следует
выбрать проект, значение ВСД которого больше. Но принятое на основании этого
решение может оказаться неверным, что продемонстрировано на рис. 9.4 и в файле
IRR.xlsx на листе Which Project. ВСД пятого проекта 40%, а шестого — 50%. Если проекты ранжируются на основе ВСД и нужно выбрать только один проект , наверное,
будет выбран шестой проект. Вспомните, что ЧПС проекта измеряет величину стоимости, которую проект добавляет компании. Очевидно, что пятый проект имеет
(практически для любой стоимости капитала) значение ЧПС больше, чем шестой.
Следовательно, если требуется выбрать один проект, то это должен быть пятый проект. Основываться только на ВСД опасно, поскольку игнорируется масштаб проекта. Несмотря на то что шестой проект превосходит пятый по доходности на каждый
вложенный доллар, благодаря масштабности пятый проект более ценен для компании. ВСД не отражает масштаба проекта, а ЧПС — отражает.

Рис. 9.4. Оценка на основе ВСД может привести к выбору не самого выгодного проекта

100

ГЛАВА 9

Как вычислить ВСД для нерегулярно поступающих денежных потоков?

Денежные потоки приходятся на реальные даты, а не только на начало или
конец года. ВСД для нерегулярных дат вычисляется с помощью функции
ЧИСТВНДОХ (XIRR). Синтаксис функции
ЧИСТВНДОХ: ЧИСТВНДОХ(денежные_
потоки;даты;[предположение]). Функция ЧИСТВНДОХ (XIRR) определяет ВСД последовательности денежных потоков, имеющих место в любом наборе нерегулярных
дат. Как и в случае с функцией ВСД, аргумент предположение является необязательным. См. пример использования функции ЧИСТВНДОХ на рис. 9.5 и в файле
IRR.xlsx на листе XIRR.

Рис. 9.5. Пример использования функция ЧИСТВНДОХ

Расчет по формуле =ЧИСТВНДОХ(F4:F7;E4:E7) в ячейке D9 показывает, что ВСД
седьмого проекта равна –48,69%.

Что такое модифицированная внутренняя ставка доходности (МВСД)
и как она рассчитывается?

Во многих случаях ставка, по которой компания занимает средства, отличается
от ставки, по которой компания реинвестирует средства. При расчете ВСД неявно предполагается, что обе эти ставки равны ВСД. Если известны фактическая
ставка займа и ставка реинвестирования, то мы можем, применив функцию МВСД
(MIRR), рассчитать ставку дисконтирования, при которой ЧПС всех денежных потоков (включая погашение займа и реинвестирование поступлений по займу с заданной ставкой) нулевая. Синтаксис функции МВСД: МВСД(значения_денежных_
потоков;ставка_финансирования; ставка_реинвестирования). К счастью, значение
МВСД всегда единственное. На рис. 9.6 и в файле IRR.xlsx на листе MIRR представлен пример использования функции МВСД. Допустим, вы заняли $120 000 и получили следующие денежные потоки: первый год — $39 000; второй год — $30 000;
третий год — $21 000; четвертый год — $37 000; пятый год — $46 000. Скажем, вы
взяли заем под 10% годовых, а реинвестировали прибыль под 12% годовых.
Введите эти значения на листе MIRR в ячейки E7:E12 и рассчитайте МВСД в ячейке D15 по формуле =МВСД(E7:E12;E3,E4). Таким образом, МВСД этого проекта составляет 12,61%. В ячейке D16 вычислена фактическая ВСД — 13,07%.

Внутренняя ставка доходности

101

Рис. 9.6. Пример использования функции МВСД

Для людей с математическим складом ума в файлеMIRR.xlsx (рис. 9.7) представлен
детальный расчет МВСД. Как видим, денежный поток отрицателен в периоды 0-й
и 1-й и положителен во 2-й и 3-й периоды. Во-первых, обратите внимание, что
если вы инвестируете x $ в 0-й период и инвестиция приносит y/ $ в 3-й период, то
ВСД такой простой инвестиции равна (y/x)1/3 – 1. В данном случае мы рассчитываем х как нынешнюю стоимость отрицательного денежного потока (ориентируясь

Рис. 9.7. Расчет МВСД

102

ГЛАВА 9

на ставку по займу) в первый период, а (y — как будущую стоимость (ориентируясь на ставку реинвестирования) положительного денежного потока в последний
период. И тогда выражением для МВСД инвестиции является (y/x)1/3 – 1.
В заключение обращу ваше внимание на то, что при пустом денежном потоке
функция ВСД игнорирует и денежный поток, и период и возвращает сообщение
об ошибке #ЧИСЛО!.

Задания
1. Вычислите все виды ВСД для следующего ряда денежных потоков:
Год 1

Год 2

Год 3

Год 4

Год 5

Год 6

Год 7

–$10 000

$8000

$1500

–$1500

2. Рассмотрите проект с приведенными ниже денежными потоками. Определите
ВСД проекта. Если годовая стоимость капитала составляет 20%, следует ли
браться за этот проект?
Год 1

Год 2

Год 3

–$4000

$2000

$4000

3. Найдите все виды ВСД для следующего проекта:
Год 1

Год 2

Год 3

$100

–$300

$250

4. Найдите все виды ВСД для проекта с заданными денежными потоками, приходящимися на перечисленные даты:
10.01.2003 10.07.2003 25.05.2004 18.07.2004 20.03.2005 01.04.2005 10.01.2006

–$1000

$900

$800

$700

$500

$350

5. Рассмотрите следующие два проекта при условии, что стоимость капитала
компании составляет 15%. Найдите ВСД и ЧПС каждого проекта. Какие проекты увеличат стоимость компании? Если бы компания могла выбрать только
один проект, какой проект ей следовало бы выбрать?
Год 1

Год 2

Год 3

Год 4

Проект 1

–$40

$130

$19

$26

Проект 2

–$80

$36

Внутренняя ставка доходности

103

6. Двадцатипятилетняя Мэг Прайор намерена инвестировать $10 000 в свой
пенсионный фонд в начале каждого года в течение следующих 40 лет . Допустим, в течение следующих 30 лет Мэг заработает 15% на своей инвестиции,
а в последние 10 лет перед выходом на пенсию ее инвестиция будет приносить
5%. Определите ВСД, связанную с ее инвестицией, и ее окончательное положение при выходе на пенсию. Будет ли значение ВСД единственным? Как бы
вы интерпретировали единственное значение ВСД?
7. Попробуйте объяснить, почему шестой проект (см. в файле IRR.xlsx лист Which
Project) имеет ВСД, равную 50%.
8. Исследуйте проект со следующими денежными потоками:
Год 1

Год 2

Год 3

–$70 000

$12 000

$15 000

Попытайтесь найти ВСД этого проекта без предположений. Какая при этом
возникает проблема? Какова ВСД этого проекта? Имеет ли проект единственное значение ВСД?
9. Для денежного потока в задании 1 при условии, что можно взять кредит под
12% годовых и инвестировать прибыль под 15% годовых, вычислите МВСД
проекта.
10. Допустим, что за облигацию из задания 9 в главе 8 («Оценка инвестиций по
чистой приведенной стоимости») сегодня уплачено $1000. Какова величина
ВСД облигации? ВСД облигации часто называют доходностью облигации.

ГЛ А В А 10

Еще несколько финансовых
функций Excel

Обсуждаемые вопросы
Вы покупаете копировальный аппарат. Как лучше поступить: заплатить $11 000
сразу или выплачивать по $3000 в год в течение пяти лет?
В конце каждого года в течение следующих 40 лет я собираюсь инвестировать
по $2000 в год вплоть до выхода на пенсию и зарабатывать 8% в год на своих
инвестициях. Какую сумму я получу при выходе на пенсию?
Я занял $10 000 на срок 10 месяцев под 8% годовых. Каковы мои ежемесячные
платежи? Каковы ежемесячные выплаты по основной сумме и по процентам?
Я собираюсь занять $80 000 и вносить ежемесячные платежи в течение 10 лет.
Максимальный ежемесячный платеж, который я могу себе позволить, составляет
$1000. На какую максимальную процентную ставку я могу рассчитывать?
Если я возьму взаймы $100 000 под 8% годовых и буду вносить платежи в размере $10 000 в год, через сколько лет я выплачу кредит?
Я дипломированный бухгалтер и часто работаю со сложными методами оценки
амортизации оборудования. Имеются ли в Excel функции для расчета амортизации?

При кредите на покупку автомобиля или жилья всегда возникают сомнения относительно выгодности заключаемой сделки. При откладывании денег в пенсионный период всегда любопытно, насколько велики окажутся сбережения. Подобные финансовые вопросы постоянно возникают в повседневной работе и личной
жизни. Ответы на них дает изучение и применение следующих функций Microsoft
Excel: ПС (PV), БС (FV), ПЛТ (PMT), ОСПЛТ (PPMT), ПРПЛТ (IPMT), ОБЩДОХОД
(CUMPRINC), ОБЩПЛАТ (CUMIPMT), СТАВКА (RATE) и КПЕР (NPER).

Ответы на вопросы
?

Вы покупаете копировальный аппарат . Как лучше поступить: заплатить
$11 000 сразу или выплачивать по $3000 в год в течение пяти лет?

Нам нужно оценить ежегодные выплаты в размере $3000 в год. Допустим, стоимость капитала составляет 12% в год. Мы можем воспользоваться функцией
ЧПС, но функция ПС (PV) в Excel позволяет решить задачу гораздо быстрее. По-

Еще несколько финансовых функций Excel

105

ток денежных средств, состоящий из периодических, равных по сумме платежей
(или поступлений), называется аннуитетом. Если предположить, что процентная
ставка за период постоянна, аннуитет можно рассчитать с помощью функции ПС.
Она возвращает приведенную стоимость (в долларах на сегодняшний день) для
серии будущих периодических платежей при условии, что платежи и процентная
ставка постоянны. Синтаксис функции ПС: ПС(ставка;#кпер[;плт][;бс][;тип]), где
плт, бс и тип являются необязательными аргументами.
ПРИМЕЧАНИЕ
При работе с финансовыми функциями Excel используются следующие соглашения
по знакам для аргументов плт (платеж) и бс (будущая стоимость): полученные суммы
указываются со знаком «+», а выплаченные — со знаком «–».

ставка — процентная ставка за период. Например, если кредит берется под 6%
годовых, а период равен одному году, то ставка = 0,06. Если период равен одному месяцу, то ставка = 0,06/12 = 0,005.
#кпер — число периодов аннуитета. Для примера с копировальным аппаратом
#кпер = 5. Если вы платите за копировальный аппарат каждый месяц в течение
пяти лет, то #кпер = 60. Разумеется, значение аргумента ставка должно соответствовать количеству периодов #кпер. Если значение #кпер указано в месяцах,
то необходимо использовать ежемесячную процентную ставку; если в годах —
годовую.
плт — выплата, производимая в каждый период. Для примера с копировальным
аппаратом плт = -$3000. Выплаты указываются со знаком «–», а прибыль — со
знаком «+». В вызове функции должен присутствовать по крайней мере один
из аргументов, плт или бс.
бс — остаток денежных средств (или будущая стоимость) после последнего
платежа. Для примера с копировальным аппаратом бс = 0. Например, если
желаемый остаток средств после последнего платежа равен $500, то бс = $500.
Если в конце последнего периода требуется внести дополнительный платеж
в размере $500, то бс = –$500. Если аргумент бс опущен, то его значение считается равным 0.
тип — число 0 или 1, указывающее, когда производится выплата. Если тип опущен или равен 0, выплаты производятся в конце каждого периода. Еслитип = 1,
выплаты производятся в начале каждого периода. Обратите внимание, что во
всех функциях, описанных в данной главе, вместо 1 можно указать ИСТИНА,
а вместо 0 — ЛОЖЬ.
Решение задачи о копировальном аппарате показано на рис. 10.1. (См. лист
в файле Excelfinfunctions.xlsx.)

Приведенная (к текущему моменту) стоимость платежа в размере $3000 в конце
каждого года в течение пяти лет со стоимостью капитала 12% рассчитана в ячейке B3 по формуле =ПС(0,12;5;-3000;0;0). Получившийся результат равен $10 814,33.

106

ГЛАВА 10

Рис. 10.1. Применение функции ПС

Последние два аргумента можно опустить и по формуле =ПС(0,12;5;-3000) получить тот же самый резуль тат. Таким образом, выгоднее платить частями, чем отдать $11 000 сразу.
Если вы платите за копировальный аппарат по $3000 в начале каждого года
B4 по формуле
в течение пяти лет , ЧПС платежей будет вычислена в ячейке
=ПС(0,12;5;-3000;0;1). Таким образом, изменяя значение последнего аргумента с 0
на 1, вы переносите расчеты с конца года на его начало. В этом случае ЧПС будет
равна $12 112,05. Следовательно, выгоднее заплатить $11 000 сразу,чем осуществлять платежи в начале года.
Теперь предположим, что вы платите по $3000 в конце каждого года и необходимо
включить дополнительный платеж в размере $500 в конце последнего (пятого)
года. Для этого случая стоимость всех платежей рассчитана в ячейке B5 с включением будущего платежа в размере $500 в формулу =ПС(0,12;5;-3000;-500;0). Обратите внимание: денежные потоки $3000 и $500 имеют отрицательные знаки,
поскольку денежные средства выплачиваются. Приведенная стоимость для всех
выплат составляет $11 098,04.
В конце каждого года в течение следующих 40 лет я собираюсь инвестировать по $2000 в год вплоть до выхода на пенсию и зарабатывать 8% в год на
своих инвестициях. Какую сумму я получу при выходе на пенсию?

В этом случае речь идет о будущей стоимости аннуитета (через 40 лет), а не о стоимости в долларах на сегодняшний день. Это задача для функции БС (будущая
стоимость). Функция БС (FV) возвращает будущую стоимость инвестиции при условии, что периодические платежи и процентная ставка постоянны. Синтаксис
функции БС: БС(ставка;#кпер;плт;[пс];[тип]), где плт, пс и тип являются необязательными аргументами.

Еще несколько финансовых функций Excel

107

ставка — процентная ставка за период. В данном случае ставка = 0,08.
#кпер — количество периодов в будущем, для которых требуется вычислить
будущую стоимость. #кпер также означает количество периодов выплаты аннуитета. В данном случае #кпер = 40.
плт =
плт — выплата, осуществляемая в каждый период. В данном случае
–$2000. Знак «–» показывает, что мы кладем деньги на счет. Если этот аргумент
опущен, то аргумент пс является обязательным.

пс — сумма денежных средств (в текущих долларах), которую вы взяли в долг
сейчас. В данном случае пс равно $0. Если вы сегодня взяли взаймы у кого-либо $10 000, то пс равна $10 000, потому что кредитор дал вам $10 000 и вы их
получили. Если у вас сегодня было $10 000 в банке, то пс равна –$10 000, потому
что вы положили на свой счет в банке $10 000. Если аргумент пс опущен, то по
умолчанию его значение равно 0.
тип — число 0 или 1, обозначающее, когда производятся выплаты или когда
денежные средства кладутся на депозит. Если тип = 0 или аргумент тип опущен,
выплаты производятся или денежные средства кладутся на депозит в конце периода. В данном примере значение тип равно 0 или опущено. Если значение
тип = 1, выплаты производятся или денежные средства кладутся на депозит
в начале периода.
В файле Excelfinfunctions.xlsx на листе FV (рис. 10.2) я ввел в ячейку B3 формулу
=БС(0,08;40;-2000) и узнал, что через 40 лет сбережения составят $518 113,04. Обратите внимание, что для ежегодного платежа необходимо ввести отрицательное
значение, потому что $2000 будут положены на ваш счет. Тот же результат можно
получить, указав в формуле =БС(0,08;40;-2000;0;0) два последних необязательных
аргумента.

Рис. 10.2. Применение функции БС

108

ГЛАВА 10

Если депозит вносится в начале каждого года в течение 40 лет, то по формуле
=БС(0,08;40;-2000;0;1) в ячейке B4 можно рассчитать результат 40-летних накоплений: $559 562,08.
Наконец, предположим, что в дополнение к вкладу, составляющему $2000 в конце
года в течение 40 лет, вы изначально положили на счет $30 000. Если вложения
приносят 8% в год, какая денежная сумма окажется на вашем счету к моменту выхода на пенсию через 40 лет?
БС для аргумента бс значение
Ответ можно получить, установив в функции
–$30 000. Знак «–» означает , что вы сделали депозит в размере $30 000. В ячейке B5 по формуле =БС(0,08;40;-2000;-30000;0) вычислена будущая стоимость —
$1 169 848,68.

Я занял $10 000 на срок 10 месяцев под 8% годовых. Каковы мои ежемесячные платежи? Каковы ежемесячные выплаты по основной сумме и по
процентам?

Функция ПЛТ (PMT) возвращает сумму периодических платежей по кредиту при
условии, что платежи и процентная ставка постоянны. Синтаксис функции ПЛТ:
ПЛТ(ставка;#кпер;пс;[бс];[тип]), где бс и тип являются необязательными аргументами.
ставка — процентная ставка по кредиту за период. В данном примере в качестве
периода укажите месяц, тогда ставка будет равна 0,08/12 = 0,006666667.
#кпер — число выплат. В данном случае #кпер = 10.
пс — приведенная стоимость всех платежей. Иначе говоря, пс — это сумма кредита. В данном случае пс = $10 000. Значение пс имеет знак «+», поскольку вы
получаете $10 000.
бс — окончательный баланс ссуды после последнего платежа. В данном случае бс = 0. Если аргумент бс опущен, то его значение принимается равным 0.
Допустим, вы взяли «шаровой» кредит , по которому платите в конце каждого месяца, а в конце срока гасите кредит , внеся большой одноразовый платеж
в размере $1000. Тогда значение бс равно –$1000. Значение бс отрицательное,
поскольку платите вы.
тип — число 0 или 1, показывающее, когда должны быть выплаты. Если этот
аргумент равен 0 или опущен, выплаты производятся в конце периода. Если
вы собираетесь делать платеж в конце месяца, укажите для аргумента тип значение 0 или ничего не указывайте. Если значение тип равно 1, выплаты производятся или деньги кладутся на хранение в начале периода.
В файле Excelfinfunctions.xlsx на листе PMT в ячейке G1 я вычислил по формуле
=-ПЛТ(0,08/12;10;10000;0;0) ежемесячный платеж по 10-месячному кредиту на
сумму $10 000 под 8% годовых и с внесением платежа в конце месяца (рис. 10.3).
Ежемесячный платеж составляет $1037,03. Функция ПЛТ возвращает отрицательное значение, поскольку производятся платежи компании-кредитору.

Еще несколько финансовых функций Excel

109

Рис. 10.3. Примеры использования функций ПЛТ, ОСПЛТ, ПРПЛТ, ОБЩДОХОД и ОБЩПЛАТ

По необходимости вы можете применить функции ПРПЛТ (IPMT) и ОСПЛТ (PPMT),
чтобы рассчитать выплачиваемые проценты и сумму ежемесячного основного
платежа (это называется погашением основной суммы) отдельно.
Вычислите, сколько процентов вы платите каждый месяц, применив функцию
ПРПЛТ. Синтаксис функции: ПРПЛТ(ставка;период;#кпер;пс;[бс];[тип]), где бс и тип
являются необязательными аргументами. Аргумент период указывает номер перио-

да, для которого вычисляется процент. Остальные аргументы аналогичны аргументам функции ПЛТ. Размер ежемесячного платежа в счет погашения основной суммы
можно определить с помощью функции ОСПЛТ. Синтаксис функции: ОСПЛТ(ставка;
период;#кпер;пс; [бс]; [тип]). Все аргументы этой функции аналогичны аргументам
функции ПРПЛТ. Чтобы вычислить размер ежемесячного платежа в счет погашения
основной суммы, скопируйте формулу =-ОСПЛТ(0,08/12;C6;10;10000;0;0) из ячейки F6 в ячейки F7:F16. Например, за первый месяц выплачивается только $970,37
в счет погашения основной суммы. Как и ожидалось, размер основного платежа растет каждый месяц. Знак «–» необходим, поскольку основная сумма выплачивается
компании-кредитору, и функция ОСПЛТ возвратит отрицательное число. Сумму,
ежемесячно выплачиваемую по процентам, вы можете вычислить, скопировав формулу =-ПРПЛТ(0,08/12;C6;10;10000;0;0) из ячейки G6 в ячейки G7:G16. Например, за
первый месяц необходимо заплатить по процентам $66,67. Естественно, выплачиваемая по процентам сумма каждый месяц уменьшается.

110

ГЛАВА 10

Обратите внимание, что каждый месяц (платеж по процентам) + (платеж в счет погашения основной суммы) = (ежемесячный платеж). Иногда из общей суммы в результате округления исчезает один цент.
С помощью соотношения (остаток на конец месяца t) = (остаток на начало месяца
t) — (платеж в счет погашения основной суммы за месяц t) можно рассчитать в столбце H остаток на конец каждого месяца. Обратите внимание, что остаток на начало
первого месяца равен $10 000. В столбце D я создал остаток на начало каждого месяца с помощью соотношения (для t =2, 3,…10) (остаток на начало месяца t) = (остаток на конец месяца t–1). Естественно, остаток на конец десятого месяца равен $0
(ячейка H15), как и должно быть. Выплаты по процентам за каждый месяц можно
вычислить как (проценты за месяц t) = (процентная ставка) × (остаток на начало месяца t). Например, выплаты по процентам за третий месяц составят 0,0066667 ×
× 8052,80 = $53,69.
Очевидно, что ЧПС всех платежей равна точно $10 000. Я проверил это в ячейке D17, применив формулу =ЧПС(0,08/12;E6:E15). В ячейке D17 приведена формула
=ЧПС(E1;E6:E15), а в ячейке E1 — формула =0,08/12 (см. рис. 10.3).
Если платежи производятся в начале каждого месяца, размер каждого такого платежа можно вычислить в ячейке D19 по формуле =-ПЛТ(0,08/12;10;10000;0;1). Замена последнего аргумента на 1 перемещает платеж в начало месяца. Поскольку
кредитор получает деньги раньше, размер ежемесячного платежа в этом случае
меньше, чем при выплате в конце месяца. При выплате в начале месяца ежемесячный платеж составляет $1030,16.
Наконец, предположим, что в конце десятимесячного периода требуется произвести большой одноразовый платеж в размере $1000. Если ежемесячные платежи
отнесены на конец месяца, то размер такого ежемесячного платежа рассчитан по
формуле =-ПЛТ(0,08/12;10;10000;-1000;0) в ячейке D20. В этом случае ежемесячный
платеж равен $940. Он меньше исходного ежемесячного платежа, выплачиваемого в размере $1037,03 в конце месяца, поскольку $1000 кредита не выплачивается
с ежемесячными платежами.

Функции ОБЩДОХОД и ОБЩПЛАТ
Часто требуется собрать кумулятивные данные о выплатах по процентам или выплатам в счет основной суммы за несколько периодов. С функциями ОБЩДОХОД
(CUMPRINC) и ОБЩПЛАТ (CUMIPMT) это проще пареной репы.
Функция ОБЩДОХОД вычисляет выплаты в погашение основной суммы между двумя заданными периодами (включая эти периоды). Синтаксис функции
ОБЩДОХОД: ОБЩДОХОД(ставка;#кпер;пс;нач_период;кон_период;тип). Аргументы
ставка, #кпер, пс и тип аналогичны описанным ранее аргументам.
Функция ОБЩПЛАТ возвращает проценты, выплачиваемые между двумя периодами (включая эти периоды). Синтаксис функции: ОБЩПЛАТ(ставка;#кпер;пс;нач_
период;кон_период;тип). Аргументы функции аналогичны описанным ранее

Еще несколько финансовых функций Excel

111

аргументам. Например, на листе PMT в ячейке F19 я вычислил по формуле
=ОБЩПЛАТ(0,08/12;10;10000;2;4;0) сумму процентов, выплачиваемых со второго по четвертый месяц ($161,01). В ячейке G19 я вычислил по формуле ОБЩДОХОД(0,08/12;10;10000;2;4;0) выплаты в погашение основной суммы со второго по
четвертый месяц ($2950,08).
Я собираюсь занять $80 000 и вносить ежемесячные платежи в течение
10 лет. Максимальный ежемесячный платеж, который я могу себе позволить, составляет $1000. На какую максимальную процентную ставку я могу
рассчитывать?

Функция СТАВКА (RATE) рассчитает для вас процентную ставку , если известны
сумма кредита, продолжительность кредита и размер регулярных выплат . Синтаксис функции: СТАВКА(#кпер;плт;пс;[бс];[тип];[прогноз]), где бс, тип и прогноз
являются необязательными аргументами. Аргументы #кпер, плт, пс, бс и тип аналогичны ранее описанным аргументам. Аргумент прогноз указывает предполагаемый размер ставки. Как правило, аргумент прогноз можно опустить. На листе
Rate (в файле Excelfinfunctions.xlsx) в ячейке D9 я рассчитал по формуле =СТАВКА(120;-1000;80000;0;0) размер ежемесячной ставки — 0,7241%. Предполагается,
что выплаты производятся в конце каждого месяца (рис. 10.4).

Рис. 10.4. Пример с функцией СТАВКА

Правильно ли рассчитана ставка, можно проверить в ячейке
D15 по формуле
=ПС(0,007241;120;-1000;0;0). Результат $80 000,08 говорит о том, что выплаты по
$1000 в конце каждого месяца в течение 120 месяцев имеют текущую стоимость
$80 000,08.
Если вы готовы выплатить единовременно $10 000 в 120-м месяце, то формула
=СТАВКА(120;-1000;80000;-10000;0;0) в ячейке D12 рассчитает вам максимальную

процентную ставку, что вы можете себе позволить. В этом случае она будет равна
0,818%.

112

ГЛАВА 10

Если я возьму взаймы $100 000 под 8% годовых и буду вносить платежи
в размере $10 000 в год, через сколько лет я выплачу кредит?

Если известны сумма кредита, размер платежа по периодам и процентная ставка, то
количество периодов, необходимых для погашения ссуды, можно рассчитать с помощью функции КПЕР (NPER). Синтаксис функции: КПЕР(ставка;плт;пс;[бс];[тип]),
где бс и тип являются необязательными аргументами.
Если мы вносим платеж в конце года, то по формуле=КПЕР(0,08;-10000;100000;0;0)
в ячейке D7 листа Nper (в файле Excelfinfunctions.xlsx) получим 20,91 года (рис. 10.5).
Таким образом, для выплаты кредита двадцати лет недостаточно, а за двадцать
один год возникнет небольшая переплата. Проверим вычисления с помощью
функции ПС в ячейках D10 и D11 и увидим, что в случае платежей по $10 000 в год
в течение 20 лет будет возвращено $98 181,47, а в случае платежей по $10 000 в течение 21 года будет возвращено $100 168,03.
Допустим, вы собираетесь внести единовременный платеж в размере $40 000 в заключительный период оплаты. Через сколько лет будет возвращен кредит? Расчет
по формуле =КПЕР(0,08;-10000;100000;-40000;0) в ячейке D14 показывает, что срок
погашения кредита составит 15,90 года. Таким образом, для оплаты кредита 15 лет
недостаточно, а за 16 лет возникнет небольшая переплата по кредиту.

Рис. 10.5. Пример с функцией КПЕР

Я дипломированный бухгалтер и часто работаю со сложными методами
расчета амортизации оборудования. Имеются ли в Excel функции для расчета амортизации?

Амортизация — это снижение стоимости долгосрочных активов вследствие их использования или устаревания. Чаще всего используются следующие три метода
расчета амортизации:

Еще несколько финансовых функций Excel

113

равномерная (линейная) амортизация, функция АПЛ (SLN);
амортизация по сумме числа лет срока полезного использования (амортизация
суммы лет), функция АСЧ (SYD);
Метод двойного уменьшения остатка (двойной регрессии), функция
(DDB).

ДДОБ

Пусть стоимость нового оборудования составляет $15 000, а его остаточная стоимость после пяти лет эксплуатации определена в $3000. Как различные методы
расчета амортизации распределяют $15 000 – $3000 = $12 000 по пяти годам эксплуатации?
Метод линейной амортизации просто ежегодно уменьшает стоимость оборудования на фиксированную сумму (в данном случае $12 000/5 = $2400).
Если срок полезного использования определен в N лет, метод амортизации
суммы лет определяет отчисления за год 1 по формуле: (начальная_стоимость –
остаточная_стоимость) × (5 – 1 + 1)/( N × (N+1)/2). (N × (N+1)/2) — это сумма чисел 1, 2, …, N. В нашем примере к году 1 относится 5/15 полного износа,
к году 2 — 4/15 и т. д.
начальная_стоимость – на Если мы определяем балансовую стоимость как
численный_износ, то для износа в течение N лет эксплуатации метод двойного уменьшения остатка вычисляет износ за год по формуле: 2 × балансовая_
стоимость/N. В нашем примере N = 5. Поэтому за каждый год амортизация
должна составлять 40% балансовой стоимости. К сожалению, метод двойного
уменьшения остатка может не позволить точно распределить сумму , равную
(начальная_стоимость — остаточная_стоимость), на амортизационные расходы.
В таких случаях метод двойного уменьшения остатка подстраивает амортизацию за последние несколько лет так, чтобы общая амортизация была равнастоимость – остаточная_стоимость. В нашем примере метод двойного уменьшения
остатка распределяет 0,4×15 000 = $6000 на год 1, 0,4 ×9000 = $3600 на год 2
и 0,4× (5400) = $2160 на год 3. Если отнести амортизацию 0,4 × (3240) = $1296
на год 4, полная амортизация превысит $12 000. Поэтому амортизация за год 4
составит 12 000 – (6000+ 3600 + 2160) = $240 долларов, а за год 5 будет равна 0.

Excel предлагает функции для каждого из этих типов расчета амортизации:
Для равномерной амортизации функция АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации), вычисляет ежегодную амортизацию.
АСЧ(нач_стоимость;ост_
Для метода амортизации по сумме лет функция
стоимость;время_эксплуатации;период) вычисляет амортизацию за указанный
период.

Для метода двойного уменьшения остатка функция ДДОБ(нач_стоимость;ост_
стоимость;время_эксплуатации;период;[коэффициент]) вычисляет амортизацию
за указанный период.
После создания имен диапазонов для ячеек C2:C4 на основании диапазона B2:B4
(как показано на рис. 10.6 и в файле Depreciationexamples.xlsx) мы можем вычис-

114

ГЛАВА 10

лить амортизацию с использованием каждого из этих трех методов следующим
образом:
Вычислить линейную амортизацию, скопировав из ячейки E8 в F8:J8 формулы = АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации) (=SLN(Cost,Salvage_
Value,Years)).
Вычислить амортизацию по сумме лет, скопировав из ячейки E9 в F9:J9 формулы =АСЧ(нач_стоимость;ост_стоимость;время_эксплуатации;период) (=SYD(Cost,
Salvage_value,Years,E7)).
Вычислить амортизацию по методу двойного уменьшения остатка, скопировав
из ячейки E10 в F10:J10 формулы =ДДОБ(нач_стоимость;ост_стоимость;время_
эксплуатации;период) (=DDB(Cost,Salvage_value,Years,E7)).
Обратите внимание, что методы АСЧ и ДДОБ переносят большую часть амортизации на первые годы эксплуатации.

Рис. 10.6. Примеры функций Excel для расчета амортизации

Задания
Все платежи производятся в конце периода, если не указано иное.
1. Вы только что выиграли в лотерею. В конце каждого года в течение следующих 20 лет вы будете получать по $50 000. Если стоимость капитала составляет 10% в год, какова текущая стоимость выигрыша?
2. Перпетуитет — это бессрочный аннуитет. Если при сдаче дома в аренду я получаю в начале каждого года $14 000, какова стоимость этого перпетуитета?
Допустим, что стоимость капитала равна 10% в год. Подсказка: воспользуйтесь функцией ПС, и пусть периодов будет много!
3. У меня положено $250 000 на банковский счет . В конце каждого года в течение следующих 20 лет я буду снимать по $15 000. Если я зарабатываю 8% в год
на своем вложении, сколько денег у меня будет через 20 лет?
4. Я буду класть в банк $2000 в месяц (в конце каждого месяца) в течение следующих 10 лет. Мои вложения принесут мне 0,8% в месяц. Через 10 лет я хотел
бы получить 1 млн долл. Сколько денег я должен внести сейчас?

Еще несколько финансовых функций Excel

115

5. Игрок футбольной премьер-лиги будет получать 15 млн долл. в конце каждого года в течение следующих семи лет. На своих вложениях он может заработать 6% в год. Какова текущая стоимость его будущих доходов?
6. В конце каждого года в течение следующих 20 лет я буду получать следующие
суммы:
Годы

Сумма

1–5

$200

6–10

$300

11–20

$400

Найдите с помощью функции ПС текущую стоимость денежных потоков при
условии, что стоимость капитала составляет 10%. Подсказка: начните с вычисления стоимости получения $400 в течение 20 лет, а затем вычтите стоимость получения $100 в течение 10 лет и т. д.
7. Вы взяли ипотеку на 30 лет в размере $200 000 под 10% годовых. Вычислите
ежемесячный платеж, ежемесячные выплаты по процентам и ежемесячные
выплаты в счет погашения основной суммы при условии, что выплаты производятся в конце месяца.
8. Выполните задание 7 при условии, что выплаты производятся в начале месяца.
9. С помощью функции БС определите накопленную стоимость для $100 в течение трех лет при 7% годовых.
10. У вас есть обязательство выплатить $1 000 000 через 10 лет. Стоимость капитала составляет 10% в год. Какую сумму следует откладывать в конце каждого
года в течение 10 лет для выполнения этого обязательства?
11. Вы планируете купить новый автомобиль за $50 000. Вам предложили две
схемы оплаты:
• 10%-ная скидка на продажную цену автомобиля и далее 60 ежемесячных
платежей со ставкой 9% в год;
• скидка на продажную цену автомобиля отсутствует; 60 ежемесячных платежей со ставкой 2% в год.
Если годовая стоимость вашего капитала составляет 9%, какая схема оплаты
выгоднее? Считается, что все платежи производятся в конце месяца.
12. У меня $10 000 на банковском счете. В начале каждого года в течение следующих 20 лет я буду класть на счет $4000 под 6% годовых. Сколько денег у меня
будет через 20 лет?
13. В случае «шаровой» ипотеки необходимо погасить часть кредита в течение
определенного периода, а затем произвести единовременный платеж остав-

116

ГЛАВА 10

шегося кредита. Предположим, вы взяли «шаровой» ипотечный кредит в размере $400 000 сроком на 20 лет с процентной ставкой 0,5% в месяц. Выплаты
в конце каждого месяца в течение 20 лет должны погасить $300 000 из вашего
кредита, затем вы должны выплатить остальные $100 000. Вычислите свои
ежемесячные платежи по этому кредиту.
14. Когда вы берете ипотеку с регулируемой процентной ставкой, ежемесячные
выплаты привязаны к индексу ставок (например, к ставкам векселей казначейства США). Допустим, что вы взяли ипотеку размером $60 000 с регулируемой процентной ставкой на 30 лет (360 ежемесячных платежей). Первые
12 платежей регулируются по текущей ставке векселей казначейства 8%. Со
второго по пятый годы ежемесячные платежи устанавливаются по ежемесячной ставке векселей казначейства на начало года плюс 2%. Ставки векселей
казначейства на начало годов со второго по пятый представлены ниже:
Начало года

Ставка векселей казначейства, %

Вычислите ежемесячные платежи с первого по пятый годы и остаток на конец
периода для каждого года.
15. Предположим, что вы взяли кредит под 14,4% годовых и выплачиваете его
ежемесячно. Если вы пропустили четыре платежа подряд, сколько вам придется выплатить в следующий раз?
16. Через 10 лет вы намерены поменять станок на новый, стоимость которого оцениваете приблизительно в $80 000. При условии, что ежегодно можно заработать 8% на вкладе, сколько денег необходимо откладывать в конце каждого
года для покрытия стоимости нового станка?
17. При покупке мотоцикла вы платите $1500 сразу и $182,50 ежемесячно в течение трех лет. Если годовая процентная ставка составляет 18%, какова была
первоначальная стоимость мотоцикла?
18. Пусть годовая процентная ставка равна 10%. Вы платите $200 каждый месяц
в течение двух лет, $300 каждый месяц в течение года и $400 каждый месяц
в течение двух лет. Какова текущая стоимость всех платежей?
19. Вы собираетесь вкладывать $500 в конце каждого шестимесячного периода
в течение пяти лет . Если через пять лет необходимо накопить $6000, какой
должна быть годовая норма прибыли по вкладу?
20. Я собираюсь взять кредит в размере $2000 и выплачивать его ежеквартально
в течение двух лет. Годовая процентная ставка равна 24%. Каков размер каждого платежа?

Еще несколько финансовых функций Excel

117

21. Я взял в кредит $15 000. Мне предстоит выполнить 48 ежемесячных платежей, и годовая процентная ставка равна 9%. Какова общая сумма выплачиваемых процентов по кредиту?
22. Я собираюсь взять кредит в размере $5000 и планирую погасить его за 36 месяцев, осуществляя платежи каждый месяц. Годовая процентная ставка равна
16,5%. Через год я дополнительно выплачу $500 и сокращу срок кредита до
двух лет в общей сложности. Каким будет мой ежемесячный платеж в течение
второго года действия кредита?
23. При ипотеке с переменной ставкой ежемесячные выплаты зависят от процентных ставок в начале каждого года. Вы взяли $60 000 в ипотеку на 30 лет.
В первый год ежемесячные платежи рассчитываются, исходя из текущей годовой ставки векселей казначейства 9%. Со второго по пятый годы ежемесячные платежи базируются на перечисленных далее годовых ставках векселей
казначейства +2%.
• второй год: 10%;
• третий год: 13%;
• четвертый год: 15%;
• пятый год: 10%.
Проблема в том, что для ипотек с переменной ставкой существует положение,
гарантирующее, что ежемесячные платежи могут расти год от года максимум
на 7,5%. Для компенсации кредитору этого условия заемщик регулирует остаток на конец периода в конце каждого года, исходя из разницы между тем, что
заемщик фактически заплатил, и тем, что он должен был заплатить. Рассчитайте ежемесячные платежи с первого по пятый годы ипотеки.
24. Вы можете выбрать: получать ли $8000 ежегодно, начиная с 62 лет и до конца
жизни, или получать $10 000 ежегодно, начиная с 65 лет и до конца жизни.
Если можно заработать 8% в год на вкладах, какой выбор будет правильным?
25. Вы только что выиграли в лотерею и будете получать $50 000 ежегодно в течение 20 лет. При какой процентной ставке эти выплаты будут эквивалентны
получению $500 000 единовременно?
26. Имеется облигация с купонной выплатой в размере $50 в конце каждого года
в течение 30 лет и выплатой номинальной стоимости в размере $1000 через
30 лет. Если денежные потоки дисконтируются по годовой ставке 6%, какая
цена за облигацию будет справедливой?
27. Вы взяли $100 000 в ипотеку на 40 лет с ежемесячными выплатами. Г одовая
процентная ставка составляет 16%. Сколько вы выплатите за время ипотеки?
Какую сумму останется выплатить за четыре года до окончания ипотеки?
28. Мне необходимо занять $12 000. Я могу выплачивать $500 в месяц, а годовая
процентная ставка составляет 4,5%. Сколько месяцев потребуется для погашения кредита?

118

ГЛАВА 10

29. Вы собираетесь взять кредит в размере $50 000 на 180 месяцев. Годовая процентная ставка по кредиту зависит от вашего кредитного балла следующим
образом:
Кредитный балл

Годовая процентная ставка, %

740–750

8,15

720–739

8,45

700–719

8,95

670–699

9,725

640–669

11,225

620–639

12,475

Напишите формулу зависимости ежемесячных платежей от кредитного балла.
30. Вы собираетесь взять автокредит в размере $40 000. Нужно вычислить ежемесячные платежи и итоговые проценты, выплачиваемые для следующих ситуаций:
• кредит на 48 месяцев под 6,85% годовых;
• кредит на 60 месяцев под 6,59% годовых.
31. Допустим, есть станок, который стоит $50 000 и остаточная стоимость которого после десятилетнего износа составит $5000. Вычислите в течение каждого года равномерную амортизацию, амортизацию по сумме числа лет срока
полезного использования и амортизацию по методу двойного уменьшения
остатка.

Г Л А В А 11

Циклические ссылки

Обсуждаемые вопросы
Я часто получаю в Excel сообщение о циклической ссылке. Означает ли это, что
я сделал ошибку?
Как исправить циклическую ссылку?

Если в Microsoft Excel 2019 появляется сообщение о циклической ссылке в книге,
это означает, что между двумя или более ячейками книги образовался замкнутый
контур — петля, или зависимость. Например, циклическая ссылка возникает, если
значение в ячейке A1 оказывает влияние на значение в ячейке D3, значение в ячейке D3 влияет на значение в ячейке F6, а значение в ячейке F6 влияет на значение
в ячейке A1. На рис. 11.1 представлена схема возникновения циклической ссылки.

Рис. 11.1. Возникновение циклической ссылки

Как вы скоро увидите, для устранения циклических ссылок в книге следует выбрать на левой панели вкладки Файл (File) команду Параметры (Options), а затем выбрать группу параметров Формулы (Formulas) и установить флажок Включить итеративные вычисления (Enable Iterative Calculation) в разделе Параметры вычислений
(Calculation Options).

Ответы на вопросы
?

Я часто получаю в Excel сообщение о циклической ссылке. Означает ли
это, что я сделал ошибку?

Циклическая ссылка обычно образуется на логически непротиворечивом листе,
на котором несколько ячеек связаны между собой так, как показано на рис. 11.1.

120

ГЛАВА 11

Рассмотрим элементарный пример, не имеющий простого решения в Excel без
создания циклической ссылки.
Небольшая компания с доходом $1500 и расходами $1000 собирается потратить
10% своей чистой прибыли на благотворительность. Ставка налога составляет
40%. Сколько денежных средств пойдет на благотворительность? Решение этой
задачи представлено в файле Circular.xlsx на листе Sheet1, показанном на рис. 11.2.

Рис. 11.2. Циклическая ссылка может возникнуть при расчете налогов

Я начал с того, что присвоил ячейкам
D3:D8 соответствующие имена в ячейках C3:C8. В ячейки D3:D5 я ввел размер доходов, налоговой ставки и расходов
компании. Для расчета суммы пожертвования, равной 10% от прибыли после
уплаты налогов, я ввел формулу =0,1*после_уплаты_налогов в ячейку D6. Затем
я рассчитал прибыль до уплаты налогов в ячейке D7, вычтя расходы и пожертвование из дохода по формуле =доход – издержки – благотворительность. Наконец,
я вычислил прибыль после уплаты налогов в ячейке D8 по формуле =(1 – налоговая_ставка)*до_уплаты_налогов.
Excel сообщает о циклической ссылке в ячейке D8 (в левом нижнем углу файла
Circular. xlsx). В чем дело?

1. Размер пожертвования (ячейка D6) влияет на размер прибыли до уплаты налогов (ячейка D7).
2. Размер прибыли до уплаты налогов (ячейка D7) влияет на размер прибыли
после уплаты налогов (ячейка D8).
3. Размер прибыли после уплаты налогов (ячейка D8) влияет на размер пожертвования.
Итак, образовалась петля D6-D7-D8-D6 (показана стрелками на рис. 11.2), вызвавшая сообщение о циклической ссылке. Лист является логически непротиворечивым; все было сделано правильно. Тем не менее, как видно по рис. 11.2, Excel неправильно рассчитывает величину взноса на благотворительность.

Как исправить циклическую ссылку?

Исправление циклических ссылок не представляет затруднений. Просто перейдите на вкладку Файл (File) в левой части ленты Excel, выберите
Параметры

Циклические ссылки

121

(Options) и затем Параметры Excel (Excel Options). На левой панели окна выберите
группу параметров Формулы (Formulas) и установите флажок Включить итеративные
вычисления (Enable iterative calculation) в разделе Параметры вычислений (Calculation
Options), как показано на рис. 11.3.

Рис. 11.3. Разрешение циклических ссылок с помощью флажка Включить
итеративные вычисления

После установки флажка Включить итеративные вычисления (Enable iterative
calculation) программа Excel распознает порожденную циклической ссылкой систему трех уравнений с тремя неизвестными:
благотворительность=0,1*(после_уплаты_налогов)
до_уплаты_налогов=доход – издержки – благотворительность
после_уплаты_налогов=(1 – налоговая_ставка)*(до_уплаты_налогов)

Тремя неизвестными являются благотворительность, до_уплаты_налогов и после_
уплаты_ налогов. После установки флажка Включить итеративные вычисления (Enable
iterative calculation) Excel выполняет итерации (опыт работы с циклическими ссылками показывает, что потребуется 100 итераций) для поиска решения всех уравнений, порожденных циклической ссылкой. От итерации к итерации значения неизвестных изменяются по сложной математической процедуре (по методу итераций
Гаусса — Зейделя). Excel завершает процесс, если изменение значения в любой

122

ГЛАВА 11

ячейке листа от итерации к итерации меньше, чем значение, указанное в поле Относительная погрешность (Maximum Change). По умолчанию оно равно 0,001. При
необходимости значение относительной погрешности можно уменьшить, например, до 0,000001. Если его не уменьшить, Excel может, например, присвоить ячейке со значением 5 значение 5,001, что будет неточно. Кроме того, для некоторых
сложных листов на разрешение циклической ссылки может потребоваться более
100 итераций. Однако в рассматриваемом примере зацикливание было разрешено
практически мгновенно (рис. 11.4).

Рис. 11.4. Разрешение циклической ссылки методом итераций

Размер пожертвования в размере $28,30 в точности соответствует 10% от прибыли после уплаты налогов ($283,01). Значения во всех остальных ячейках теперь
рассчитываются правильно.
Обратите внимание, что метод итераций в Excel гарантированно работает только
при решении линейных уравнений. В остальных случаях решение не гарантируется. В примере с налогами разрешение циклических ссылок потребовало решения
системы линейных уравнений, поэтому Excel выдал правильный ответ.
Вот еще один пример циклической ссылки. В любой формуле Excel можно обратиться по имени к целому столбцу или к целой строке. Например, по формуле
=СРЗНАЧ(B:B) рассчитывается средняя величина значений в столбце B. Формула
=СРЗНАЧ(1:1) вычисляет среднюю величину в строке 1. Это удобно, когда в столбец или строку постоянно добавляются новые данные (например, данные ежемесячных продаж). По этой формуле всегда вычисляется средний объем продаж,
и ее не требуется изменять. Проблема заключается в том, что если ввести эту
формулу в столбец или строку , на которую она ссылается, то, конечно, создастся циклическая ссылка. Подобные циклические ссылки мгновенно исправляются
установкой флажка Включить итеративные вычисления (Enable iterative calculation).

Задания
1. Компания получила прибыль $60 000 до выплаты бонусов сотрудникам
и уплаты налога штата и федерального налога. Компания выплачивает со-

Циклические ссылки

123

трудникам бонус в размере 5% от прибыли после уплаты налогов. Налог штата составляет 5% от прибыли (после выплаты бонусов). Федеральный налог
составляет 40% от прибыли (после выплаты бонусов и уплаты налога штата).
Вычислите суммы, выплаченные в виде бонусов, налога штата и федерального налога.
2. 1 января 2002 г. у меня было $500. В конце каждого месяца я получаю 2% со
своих денег. Проценты за каждый месяц вычисляются от среднего значения
баланса на начало и на конец месяца. Сколько денег у меня будет через 12 месяцев?
3. Мой самолет летит по следующему маршруту: Хьюстон — Лос-Анджелес —
Сиэтл — Миннеаполис — Хьюстон. На каждом отрезке путешествия расход топлива (в милях на галлон) равен 40 – 0,02*(средний расход топлива для
маршрута). Здесь средний расход топлива для маршрута равен 0,5*(начальное
количество топлива для маршрута + конечное количество топлива для маршрута).
Полет начинается в Хьюстоне с 1000 галлонов топлива. Дальность полета на
каждом отрезке приведена ниже:
Отрезок

Мили

Хьюстон — Лос-Анджелес

1200

Лос-Анджелес — Сиэтл

1100

Сиэтл — Миннеаполис

1500

Миннеаполис — Хьюстон

1400

Сколько галлонов топлива останется по возвращении в Хьюстон?
4. Распространенным методом распределения затрат для вспомогательных подразделений является метод взаимного распределения затрат. Этот метод может
быть реализован с помощью циклических ссылок. Предположим,что в компании Widgetco есть два вспомогательных подразделения: бухгалтерия и отдел
консалтинга. Кроме того, в компании есть два производственных подразделения: отдел 1 и отдел 2. Компания приняла решение распределить $600 000 затрат бухгалтерии и $116 000 затрат отдела консалтинга между подразделениями компании. Далее указаны соотношения затрат между подразделениями:
Бухгалтерия

Консалтинг

Отдел 1

Отдел 2

Процент бухгалтерской работы, выполненной для других подразделений
компании

Процент консультационной работы,
выполненной для других подразделений компании

124

ГЛАВА 11

Какая часть затрат бухгалтерии и отдела консалтинга должна быть распределена между другими подразделениями компании? Необходимо определить
две величины: совокупные затраты, присвоенные бухгалтерии, и совокупные
затраты, присвоенные отделу консалтинга. Совокупные затраты, присвоенные бухгалтерии, равны $600 000+0,1*(совокупные затраты, присвоенные отделу консалтинга), поскольку 10% всей консалтинговой работы было выполнено
для бухгалтерии.
Аналогичное уравнение можно написать для совокупных затрат, присвоенных
отделу консалтинга. Теперь вы сможете правильно рассчитать распределение
затрат бухгалтерии и отдела консалтинга между другими подразделениями
компании.
5. Мы начали год с $200 и в течение года получили еще $100. Мы также получили в конце года 10% прибыли на основе баланса на начало года. Мы закончили
год с $320. Вычислите баланс на конец года, если проценты начисляются в зависимости от среднего значения баланса на начало и на конец года.

Г Л А В А 12

Функции ЕСЛИ, ЕСЛИОШИБКА,
ЕСЛИМН, ВЫБОР и ПЕРЕКЛЮЧ

Обсуждаемые вопросы
При заказе 500 единиц продукции необходимо заплатить $3,00 за единицу продукции. При заказе от 501 до 1200 единиц цена за единицу падает до $2,70. При заказе от 1201 до 2000 единиц стоимость единицы продукции составляет $2,30. При
заказе свыше 2000 единиц — $2,00. Как написать формулу, выражающую затраты
на приобретение как функцию количества приобретенных единиц продукции?
Я купил 100 акций по цене $55 за акцию. Для хеджирования риска снижения
стоимости акций я купил 60 шестимесячных европейских пут-опционов. Каждый
опцион имеет цену исполнения $45 и стоит $5 долларов. Как разработать таблицу, в которой указана процентная доходность моего инвестиционного портфеля
через шесть месяцев для ряда возможных будущих цен?
Многие аналитики фондового рынка считают, что торговые правила для торговли
по скользящим средним могут опережать рынок. Общее рекомендуемое правило
для торговли по скользящим средним гласит: покупай, когда цена акции превысит
средний показатель за последние 15 месяцев, и продавай, когда цена акции упадет ниже среднего показателя за последние 15 месяцев. Как это торговое правило
может быть сформулировано для биржевого индекса Standard&Poor’s 500 (S&P)?
В игре в кости брошены две кубика. Если сумма чисел при первом броске равна
2, 3 или 12 — вы проиграли. Если сумма чисел при первом броске равна 7 или
11 — вы выиграли. Во всех остальных случаях игра продолжается. Как создать
формулу, определяющую состояние игры после первого броска?
В большинстве гипотетических финансовых отчетов в качестве средства уравновешивания активов и обязательств используются денежные средства. Я знаю,
что более реалистично использовать для этого долгосрочные обязательства. Как
настроить гипотетический отчет с долгосрочными обязательствами в качестве
средства уравновешивания?
При копировании формулы с функцией ВПР для вычисления зарплаты сотрудников я получаю множество сообщений об ошибке #Н/Д. Затем при расчете
средней зарплаты сотрудников я не могу получить числовой ответ из-за ошибки
#Н/Д. Можно ли заменить ошибки #Н/Д пробелом и рассчитать, таким образом,
среднюю зарплату?
Лист содержит ежеквартальные доходы компании Walmart. Как вычислить доход
за каждый год и внести его в строку, содержащую продажи в первом квартале
соответствующего года?

126

ГЛАВА 12

Формула с функцией ЕСЛИ может оказаться довольно длинной. Сколько вложенных функций ЕСЛИ можно поместить в ячейку? Каково максимально допустимое
количество символов в формуле Excel?
Вложенные функции ЕСЛИ могут оказаться слишком длинными и сложными. Как
новая функция ЕСЛИМН облегчает написание вложенных функций ЕСЛИ?
Как работает функция ВЫБОР?
Как работает новая функция ПЕРЕКЛЮЧ?

Перечисленные выше проблемы на первый взгляд имеют мало общего (или
вообще не имеют). Т ем не менее, создание в Microsoft Excel 2019 модели для
каждой из этих ситуаций требует применить функцию ЕСЛИ (IF). Функция ЕСЛИ
(и новая функция ЕСЛИМН) — вероятно, самые распространенные функции
в Excel. С ее помощью можно проверять условия для значений и формул, подражая (в какой-то степени) условной логике языков программирования, таких
как C, C++ и Java.
Первым аргументом функции ЕСЛИ является условие, например A1>10. Если условие истинно, функция возвращает первое из двух приведенных в ней значений;
в противном случае возвращается второе значение. Самый простой способ показать эффективность функций ЕСЛИ — это применить их в ответах на все вопросы
данной главы.

Ответы на вопросы
При заказе 500 единиц продукции необходимо заплатить $3,00 за единицу
продукции. При заказе от 501 до 1200 единиц цена за единицу падает до
$2,70. При заказе от 1201 до 2000 единиц стоимость единицы продукции составляет $2,30. При заказе свыше 2000 единиц — $2,00. Как написать формулу, выражающую затраты на приобретение как функцию количества приобретенных
единиц продукции?

Решение этой задачи можно найти на листе Quantity Discount в файле Ifstatement.
xlsx. Этот лист показан на рис. 12.1.
Пусть в ячейке A9 содержится объем заказа. Стоимость заказа как функцию от
объема заказа можно вычислить, реализовав следующую логику:
если значение в ячейке A9 меньше или равно 500, стоимость заказа равна 3*A9;
если значение в ячейке A9 больше или равно 501 и меньше 1200, стоимость заказа равна 2,70*A9;
если значение в ячейке A9 больше или равно 1201 и меньше 2000, стоимость
заказа равна 2,30*A9;
если значение в ячейке A9 больше 2000, стоимость заказа равна 2*A9.

Функции ЕСЛИ, ЕСЛИОШИБКА, ЕСЛИМН, ВЫБОР и ПЕРЕКЛЮЧ

127

Рис. 12.1. Моделирование оптовых скидок с помощью функции ЕСЛИ

Сперва присвоим имена из ячеек A2:A4 ячейкам B2:B4 и имена из ячеек D2:D5 ячейкам C2:C5. Затем реализуем указанную выше логику в ячейкеB9 в следующей формуле:
=ЕСЛИ(A9=4 необходимо заключить в кавычки, поскольку комбинация символов «больше или равно» ( >=), как
и комбинация , обрабатывается как текст. Как видно из рис. 20.3, дольше четырех минут звучало 477 песен.

Сколько песен длились дольше, чем средняя продолжительность звучания
песен из списка?

Для ответа на этот вопрос сначала вычислите среднюю продолжительность
звучания песен по формуле =СРЗНАЧ(Минуты) в ячейке G5. Затем в ячейке C17
подсчитайте число песен с продолжительностью звучания больше средней по
формуле =СЧЁТЕСЛИ(Минуты;»>»&G5). Символ & используется для ссылки в критерии на другую ячейку (в данном случае, G5). Как видно из того же рисунка,
дольше среднего звучали 477 песен, что соответствует числу песен, звучавших
не менее четырех минут. Эти результаты совпадают, поскольку подразумевается,
что продолжительность звучания каждой песни является целым числом. Таким
образом, если песня звучала не меньше 3,48 минут, значит, она звучала не меньше 4 минут.

Функции СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СЧЁТ, СЧЁТЗ и СЧИТАТЬПУСТОТЫ

211

Сколько песен было исполнено певцами, фамилии которых начинаются
с S?

Для ответа на этот вопрос воспользуйтесь в критерии подстановочным знаком
«*». Звездочка означает любую последовательность символов. Т аким образом,
по формуле =СЧЁТЕСЛИ(Исполнитель;»S*») в ячейке C18 подсчитываются все песни, исполненные певцами, чьи фамилии начинаются с S. (В критериях регистр не
учитывается.) Певцы, фамилии которых начинаются с S, исполнили 232 песни.
Это просто общее число песен, исполненных Брюсом Спрингстином и Бритни
Спирс (103 + 129 = 232).

Сколько песен было исполнено певцами, фамилии которых состоят из шести букв?

Для этой задачи следует воспользоваться подстановочным знаком « ?», который
означает любой символ. Следовательно, число песен, исполненных певцами с фамилиями из шести букв, можно вычислить в ячейке C19 по формуле =СЧЁТЕСЛИ
(Исполнитель;»??????»). В результате получится 243 песни. (У двух исполнителей
фамилии состоят из шести букв у Бритни Спирс и у Эминема, которые в сумме
исполнили 243 песни (129 + 114 = 243).)

Сколько песен прозвучало после 15 июня 2005 г.?

В критериях, используемых в функциях СЧЁТЕСЛИ, даты обрабатываются на основе порядкового номера. (Более поздняя дата считается больше, чем более ранняя
дата.) В ячейке C20 по формуле =СЧЁТЕСЛИ(Дата;»>15/6/2005″) подсчитано, что после 15 июня 2005 г. прозвучало 98 песен.

Сколько песен прозвучало до 2009 г.?

Здесь критерий должен учесть все даты до 31 декабря 2008 .гвключительно. Я ввел
в ячейку C21 формулу =СЧЁТЕСЛИ(Дата;»=100″). В таких сдел-

ках Джен продала помады на $3583. Для сделок с помадой на сумму менее $100
результат вычислен в ячейке B25 по формуле =СУММЕСЛИМН(Доллары;Имя;»Jen»;
Продукт;»lipstick»;Доллары;»=1/1/2004″; Дата; «»&T10 позволяет задать условие попадания значения в сумму в зависимости от содержимого ячейки T10. Таким образом, формула =БДСУМ(data,5,S6:T7)
вычислит общую выручку от продаж Бетси в транзакциях, в которых сумма
была больше, чем некое значение в ячейке T10.

Рис. 50.5. Использование знака & при задании условия

У меня есть база со следующими данными для каждой сделки: выручка,
дата продажи и идентификационный код продукта. Как быстро извлечь
сумму выручки для сделки по заданной дате продажи и идентификационному
коду?

Файл Dget.xlsx (рис. 50.6) содержит базу данных с суммами выручки, датами продаж и идентификационными кодами продуктов для ряда сделок. Если известна
дата сделки и идентификационный код продукта, каким образом можно найти
сумму выручки? Проще всего воспользоваться функцией БИЗВЛЕЧЬ (DGET). Синтаксис функции: БИЗВЛЕЧЬ(база_данных;поле;условия). При заданном диапазоне
для базы данных и заданном значении для поля в базе данных (отсчет столбцов

556

ГЛАВА 50

выполняется слева направо в пределах диапазона) функция БИЗВЛЕЧЬ возвращает
содержимое заданного столбца в записи базы данных, удовлетворяющей критериям. Если ни одна запись не удовлетворяет критериям, функция БИЗВЛЕЧЬ возвращает сообщение об ошибке #ЗНАЧ!. Если критериям удовлетворяет несколько
записей, функция БИЗВЛЕЧЬ возвращает сообщение об ошибке #ЧИСЛО!.
Пусть вам нужно извлечь выручку для сделки с идентификационным кодом продукта 62426, имевшей место 9/1/2006 (9 января). Допустим, с этим
продуктом в указанный день была проведена только одна сделка. Формула
=БИЗВЛЕЧЬ(B7:D28;1;G5:H6), введенная в ячейку G9, дает результат $169. Обратите
внимание, что для аргумента поле было указано значение 1, поскольку столбец
Выручка является первым столбцом базы данных (занимающей диапазон B7:D28).
Поиск сделки с кодом продукта 62426 и датой совершения 9/1/2006 обеспечивает
диапазон условий G5:H6.

Рис. 50.6. Применение функции БИЗВЛЕЧЬ

Задания
1. Сколько блеска для губ продала Зарет в 2004 и 2005 г . (используйте данные
из файла Makeupdb.xlsx)?
2. Создайте таблицу данных, содержащую общую выручку и количество проданных единиц продукции для каждого продавца.
3. Сколько блеска для губ продала Коллин не в регионе Запад?

Обработка данных с помощью статистических функций для баз данных

557

4. На основе данных в файле Makeupdb.xlsx создайте таблицу данных, показывающую среднюю выручку за единицу продукции для каждого продавца для
сделок, где средняя цена за единицу продукции превысила $3,30.
5. На основе данных в файле Sales.xlsx определите следующее:
• общий объем продаж в регионе Средний Запад;
• общий объем продаж для Хизер в регионе Восток;
• общий объем продаж для Хизер и для региона Восток;
• общий объем продаж в регионе Восток для Хизер или для Джона;
• число сделок в регионе Восток;
• число сделок с продажами выше среднего;
• общий объем продаж не в регионе Средний Запад.
6. Файл Housepricedata.xlsx содержит следующую информацию для ряда домов:
• площадь в кв. футах;
• цена;
• количество ванных комнат;
• количество спален.
На основе этой информации ответьте на следующие вопросы:
• Какова средняя цена для всех домов с общим количеством ванных комнат
и спален не меньше шести?
• Сколько домов с общим количеством спален и ванных комнат не более
пяти продано более чем за $300 000?
• Сколько домов имеют как минимум три ванные комнаты, но общее количество спален и ванных комнат в них не превышает шести?
• Какова максимальная цена дома площадью не более 3000 кв. футов и общим количеством спален и ванных комнат не более шести? (Подсказка:
для решения задачи используйте функцию ДМАКС.)
7. Файл Deciles.xlsx содержит данные о невыплаченных остатках для 20 счетов.
С помощью функций для баз данных вычислите невыплаченные остатки по
счетам для каждого дециля.

ГЛ А В А 51

Фильтрация данных
и удаление дубликатов

Обсуждаемые вопросы
Joolas — небольшая компания, производящая косметику. Менеджеры компании хранят
данные обо всех сделках на листе Microsoft Excel. Иногда им необходимо извлечь или
отфильтровать подмножество данных о продажах. Например, на основе этих данных
требуется ответить на следующие вопросы:
Как определить все сделки Джен по продаже помады в регионе Восток?
Как определить все сделки Кики и Коллин по продаже помады и туши в регионе
Восток или Юг?
Как скопировать все сделки Кики и Коллин по продаже помады и туши в регионе
Восток или Юг на другой лист?
Как очистить фильтры в столбце или базе данных?
Как определить все сделки по продаже более 90 единиц продукции и более чем
на $280?
Как определить все сделки, заключенные в 2005 и 2006 г.?
Как определить все сделки, заключенные в последние три месяца 2005 г. и в первые три месяца 2006 г.?
Как определить все сделки, заключенные продавцами, имена которых начинаются с C?
Как определить все сделки, для которых ячейка с названием продукта окрашена
в красный цвет?
Как определить все сделки среди 30 сделок с максимальной выручкой, в которых
продавцами были Халлаган или Джен?
Как быстро получить полный список продавцов?
Как просмотреть все комбинации «продавец — продукт — регион», встречающиеся в базе данных?
Если данные изменились, как повторно применить тот же самый фильтр?
Как извлечь все сделки по продаже основы под макияж, заключенные Эмили
и Джен за первые шесть месяцев 2005 г., в которых средняя цена единицы продукции составила больше $3,20?

Фильтрация данных и удаление дубликатов

559

Microsoft Excel 2019 обладает возможностями филь трации для определения любого подмножества данных. Кроме того, Excel позволяет быстро удалить дублирующиеся записи с листа. Данные для работы находятся в файле Makeupfiltertemp.
xlsx в папке Templates. Для 1891 сделки в этом файле (часть сделок представлена на
рис. 51.1) хранятся следующие данные:
номер сделки;
имя продавца;
дата сделки;
продаваемый продукт;
количество единиц проданной продукции;
сумма сделки в долларах;
место сделки.

Рис. 51.1. Данные сделок по продаже косметики

Далее любой прямоугольный диапазон ячеек с заголовками в первой строке каждого столбца называется базой данных. Каждый столбец (с C по I) базы данных
(диапазон ячеек C4:I1894) называется полем. Каждая строка базы данных, содержащая данные, называется записью. (Таким образом, записи базы данных хранятся в диапазоне C4:I1894.) Первая строка каждого поля должна содержать имя
поля. Например, поле в столбце F имеет имя Продукт. Для идентификации подмножества записей можно обратиться с запросом к базе данных при помощи автофильтра Excel (AutoFilter) и И-условий. То есть вы можете использовать запросы

560

ГЛАВА 51

в форме «Найти все записи, в которых поле 1 удовлетворяет определенным условиям, и поле 2 удовлетворяет определенным условиям, и поле 3 удовлетворяет
определенным условиям». Возможности автофильтра Excel демонстрируются на
примерах в данной главе.

Ответы на вопросы
?

Как определить все сделки Джен по продаже помады в регионе Восток?

Для начала установите курсор в какую-нибудь ячейку базы данных и на вкладке
Данные (Data) ленты Excel в группе Сортировка и фильтр (Sort & Filter) выберите
Фильтр (Filter). Как показано на рис. 51.2, теперь у каждого столбца базы данных
в строке заголовка появилась стрелка раскрывающегося списка (см. лист Data).

Рис. 51.2. Стрелки раскрывающегося списка фильтрации

Данные можно отфильтровать, используя раскрывающиеся списки.
Откройте список в столбце Имя (рис. 51.3). В нем можно было бы выбрать элемент
Текстовые фильтры (Text Filters), позволяющий фильтровать данные на основе характеристик имен сотрудников (подробнее об этом далее). Но сейчас необходимо
обработать данные для Джен (Jen), поэтому сначала снимите флажок ( Выделить
все) (Select All), установите флажок для Джен и нажмите кнопку OK.
Теперь видны только те записи, где Джен была продавцом. Далее в столбце Продукт установите флажок для помады (lipstick). В столбце Регион установите флажок

Фильтрация данных и удаление дубликатов

561

для региона Восток (East). Теперь видны только сделки Джен по продаже помады в регионе Восток (см. рис. 51.4 и лист Lipstick Jen East в файле Makeupfilter.xlsx).
Обратите внимание, что в столбцах, где были установлены условия филь трации,
стрелка заменилась на воронку.

Рис. 51.3. Условия фильтрации для столбца Имя

Рис. 51.4. Сделки Джен по продаже помады в регионе Восток

Как определить все сделки Кики и Коллин по продаже помады и туши в регионе Восток или Юг?

Просто выберите в столбце Имя Cici и Colleen, в столбце Продукт — lipstick и mascara
и в столбце Регион — East и South. Записи, отвечающие этим условиям, показаны на
рис. 51.5. (См. лист Cici Colleen Lipstick And Masc.)

562

ГЛАВА 51

Рис. 51.5. Сделки Кики и Коллин по продаже помады и туши в регионе Восток или Юг

Как скопировать все сделки Кики и Коллин по продаже помады и туши
в регионе Восток или Юг на другой лист?

Выделите все отфильтрованные ячейки на листе Cici Colleen lipstick and mascara
и скопируйте их на пустой лист. (В новом листе в заголовках столбцов настройки фильтров исчезнут, и может потребоваться сделать шире столбец E, содержащий даты.) Для создания пустого листа в книге щелкните правой кнопкой
мыши по ярлычку любого листа, выберите Вставить (Insert) и нажмите OK (или
щелкните знак + справа от последнего листа). Лист Visible Cells Copied содержит
записи о сделках Кики и Коллин по продаже помады и туши в восточном и южном регионах.

Как очистить фильтры в столбце или базе данных?

Для удаления всех филь тров на вкладке Данные (Data) нажмите кнопку Фильтр
(Filter). Для удаления фильтра из столбца щелкните по значку воронки возле нужного столбца и выберите Удалить фильтр из столбца (при этом сбрасываются только результаты фильтрации, но не удаляется кнопка фильтра).

Как определить все сделки по продаже более 90 единиц продукции и более
чем на $280?

Для включения фильтрации на вкладке Данные (Data) в группе Сортировка и фильтр
(Sort & Filter) нажмите кнопку Фильтр (Filter). Затем щелкните на стрелке раскрывающегося списка в столбце Количество (рис. 51.6).

Фильтрация данных и удаление дубликатов

563

В этом списке можно указать любое подмножество числовых значений (например, все сделки, в которых фигурировали –10 или –8 единиц продукции). Здесь
выбран список Числовые фильтры (Number Filters), который показан на рис. 51.7.

Рис. 51.6. Параметры фильтрации
для столбца с числовыми значениями

Рис. 51.7. Список Числовые фильтры

Большая часть этого списка не требует разъяснения. Выберите Больше (Greater
Than) и заполните диалоговое окно Пользовательский автофильтр (Custom AutoFilter),
как показано на рис. 51.8.

Рис. 51.8. Выбор всех записей с количеством проданных единиц продукции больше 90

Затем в столбце Сумма аналогичным образом выберите только те записи, сумма
в которых превышает $280. Выберите Числовые фильтры (Number Filters), больше
(Greater Than), введите 280 и нажмите OK. На листе останутся записи, показанные
на рис. 51.9. (См. лист Sales>90 units dollars>$280.) Обратите внимание, что во всех
записях проданных единиц продукции больше 90 и сумма превышает $280.

564

ГЛАВА 51

Рис. 51.9. Сделки по продаже более 90 единиц продукции на сумму свыше $280

Как определить все сделки, заключенные в 2005 или 2006 г.?

После включения фильтрации кнопкой Фильтр (Filter) щелкните на стрелке раскрывающегося списка в столбце Дата для отображения списка, показанного на
рис. 51.10.

Рис. 51.10. Параметры фильтрации для столбца Дата

После установки флажков для 2005 и 2006 г . останутся только записи, включающие продажи в 2005 и 2006 гг . (рис. 51.11, лист Sales In 2005 And 2006 слева от
предыдущих листов).

Фильтрация данных и удаление дубликатов

565

Рис. 51.11. Данные о продажах в 2005 и 2006 г.

Кроме того, в раскрывающемся списке можно выбрать элемент Фильтры по дате
(Date Filters) и просмотреть список параметров (рис. 51.12).

Рис. 51.12. Параметры фильтрации по дате

566

ГЛАВА 51

Большинство этих параметров филь трации также не требует пояснений. Параметр Настраиваемый фильтр (Custom Filter) позволяет выбрать в качестве условий
фильтрации любой диапазон дат.

Как определить все сделки, заключенные в последние три месяца 2005 г .
и в первые три месяца 2006 г.?

Откройте в столбце Дата раскрывающийся список (см. рис. 51.10). Откройте список месяцев, щелкнув по знаку + слева от обозначения соответствующего года.
Выберите месяцы с октября по декабрь 2005 г. и с января по март 2006 г. для отображения всех продаж за этот период. (См. рис. 51.13 и лист Filter By Months.)

Рис. 51.13. Продажи с октября по декабрь 2005 г. и с января по март 2006 г.

Как определить все сделки, заключенные продавцами, имена которых начинаются с C?

Щелкните по стрелке раскрывающегося списка столбца Имя и выберите в нем элемент Текстовые фильтры (Text Filters). В появившемся меню выберите Начинается с

Рис. 51.14. Диалоговое окно Пользовательский автофильтр
для выбора всех записей, в которых имя продавца начинается с C

Фильтрация данных и удаление дубликатов

567

(Begins With) и заполните диалоговое окно Пользовательский автофильтр (Custom
AutoFilter), как показано на рис. 51.14.

Как определить все сделки, для которых ячейка с названием продукта
окрашена в красный цвет?

Щелкните по стрелке раскрывающегося списка столбца Продукт и выберите в нем
элемент Фильтр по цвету (Filter By Color). Затем выберите цвет, используемый как
фильтр (рис. 51.15). На рис. 51.16 показаны только те записи, в которых ячейка
с названием продукта окрашена в красный цвет (см. лист Filter By Color).

Рис. 51.15. Диалоговое окно для фильтрации по цвету ячейки

Рис. 51.16. Все записи, в которых ячейка с названием продукта окрашена в красный цвет

Как определить все сделки среди 30 сделок с максимальной выручкой,
в которых продавцами были Халлаган или Джен?

Нажмите кнопку Фильтр (Filter), щелкните по стрелке раскрывающегося списка
в столбце Имя и установите флажки для Халлаган (Hallagan) и Джен (Jen). Щелкните по стрелке раскрывающегося списка в столбце Сумма и выберите Числовые
фильтры (Number Filters). В списке выберите Первые 10 (Top 10) и заполните диалоговое окно (рис. 51.17), заменив значение 10 на 30. В результате все записи
будут отфильтрованы и останутся только 30 записей для сделок с наибольшими

568

ГЛАВА 51

значениями выручки, в которых продавцами были Джен или Халлаган. (См. результаты на рис. 51.18 и на листе Top 30 $s With Hallagan Or Jen). Следует отметить,
что из первых по сумме 30 сделок только в пяти продавцами были Халлаган
и Джен. Аналогичным образом можно выбрать показ наибольших 5% от количества элементов, наименьших 20% от количества элементов и т . д. для любых
числовых столбцов.

Рис. 51.17. Диалоговое окно
для выбора 30 первых записей
по значению суммы

Рис. 51.18. Тридцать первых сделок
по значению суммы, в которых продавцами были
Халлаган или Джен

Как быстро получить полный список продавцов?

Мы хотим получить список всех продавцов без повторения имен. На вкладке Данные (Data) в группе Работа с данными выберите Удалить дубликаты (Remove
Duplicates). Появится диалоговое окно Удалить дубликаты (Remove Duplicates), показанное на рис. 51.19. Сначала нажмите кнопку Снять выделение (Unselect All), затем
установите флажок только для столбца Имя и нажмите OK. После фильтрования
останутся только первые записи, включающие имя каждого продавца. См. результаты на рис. 51.20 и на листе Name Duplicates Removed.

Рис. 51.19. Диалоговое окно Удалить дубликаты для столбца Имя

ВАЖНО!
Поскольку при удалении дубликатов удаляется часть данных, рекомендуется перед
этим сделать копию данных.

Фильтрация данных и удаление дубликатов

569

Рис. 51.20. Список имен продавцов

Как просмотреть все комбинации «продавец — продукт — регион», встречающиеся в базе данных?

Здесь снова требуется начать с удаления дубликатов на вкладке Данные (Data).
Заполните диалоговое окно Удалить дубликаты (Remove Duplicates), как показано на
рис. 51.21 (нажмите кнопку Снять выделение (Unselect All), установите флажки для
столбцов Имя, Продукт и Регион и нажмите OK).

Рис. 51.21. Поиск уникальных комбинаций
«продавец — продукт — регион»

На рис. 51.22 представлены первые записи для каждой комбинации «продавец —
продукт — регион», встречающейся в базе данных. (См. лист Unique Name Product
Location.) Всего получается 180 уникальных комбинаций. Как видите, двадцатая
запись отсутствует, поскольку она относится к сделке Зарет (Zaret) с блеском для
губ (lip gloss) в регионе Средний Запад (Midwest), а пятая запись уже включает такую
комбинацию.

570

ГЛАВА 51

Рис. 51.22. Список уникальных комбинаций «продавец — продукт — регион»

Если данные изменились, как повторно применить тот же самый фильтр?

Щелкните правой кнопкой мыши на любой ячейке в резуль татах фильтрования
и в группе Сортировка и фильтр (Sort & Filter) укажите на Фильтр (Filter) и щелкните
по значку Повторить (Reapply). В отфильтрованных данных отразятся любые изменения данных.
Как извлечь все сделки по продаже основы под макияж, заключенные
Эмили и Джен за первые шесть месяцев 2005 г ., в которых средняя цена
единицы продукции составила больше $3,20?

Автофильтр (даже настраиваемый) ограничен И-запросами по столбцам. Это
означает, например, что поиск всех сделок Джен с помадой за 2005 г. и сделок Зарет с основой под макияж за 2004 г. невозможен. Для выполнения более сложных
запросов, подобных этому, необходимо использовать Расширенный фильтр. Для
него задают диапазон условий, определяющий записи, которые требуется извлечь.
(Этот процесс подробно описан в главе 50 «Обработка данных с помощью статистических функций для баз данных».) После этого указывают диапазон, в который
будут помещены извлеченные записи. Для определения всех сделок с основой под
макияж (foundation) за первые шесть месяцев 2005 г., в которых продавцами были
Эмили и Джен и в которых средняя цена единицы продукции составила больше
$3,20, можно задать диапазон условий, показанный в ячейках O4:S6 на рис. 51.23.
(См. лист Jen+Emilee в файле Advancedfilter.xlsx.)
В ячейки R5 и R6 я ввел формулу =(L5/K5)>3,2. Вспомните из главы 50, что такая формула является вычисляемым условием, по которому помечается каждая

Фильтрация данных и удаление дубликатов

571

Рис. 51.23. Диапазон условий для расширенного фильтра

строка со средней ценой за единицу продукции больше $3,20. Т акже напомню,
что заголовок для вычисляемого условия не должен быть именем поля. Я указал заголовок Цена. Согласно условиям, в диапазоне O5:S5 помечаются все записи для сделок, в которых продавцом является Джен, дата приходится на период
между 1/1/2005 и 30/6/2005, проданным продуктом является основа под макияж,
а средняя цена за единицу продукции составляет больше $3,20. Т аким образом,
помечаются именно те записи, которые требуются. Напомню, что условия в разных строках объединяются оператором ИЛИ.
Теперь выберите любую ячейку в базе данных и на вкладке Данные (Data) в группе
Сортировка и фильтр (Sort & Filter) на вкладке Данные (Data) щелкните по значку
Дополнительно (Advanced, значок воронки с карандашиком). Заполните диалоговое
окно Расширенный фильтр (Advanced Filter) и нажмите OK — рис. 51.24.

Рис. 51.24. Диалоговое окно Расширенный фильтр

Согласно этим данным, из базы данных (в диапазоне G4:M1895) должны быть извлечены все записи, которые удовлетворяют условиям в O4:S6. Эти записи должны быть скопированы в диапазон, левым верхним углом которого является ячейка O14. Извлеченные записи представлены в диапазоне ячеек O14:U18. Указанным
условиям соответствуют только четыре записи (см. рис. 51.25 и лист Jen+Emilee.)

Рис. 51.25. Результаты работы расширенного фильтра

572

ГЛАВА 51

Если в диалоговом окне Расширенный фильтр (Advanced Filter) установить флажок
Только уникальные записи (Unique records only), дублирующиеся записи не будут извлечены. Например, если бы Джен провела еще одну сделку с основой под макияж
в регионе Восток 19 марта 2005 г. для одной единицы продукции на сумму $4,88,
была бы извлечена запись только по одной сделке.

Задания
1. Используя файл Makeupﬁltertemp.xlsx (для этого и всех следующих заданий),
найдите все сделки Халлаган (Hallagan) по продаже подводки для глаз в регионе Запад.
2. Найдите все сделки, входящие в 5% наиболее крупных сделок по количеству
проданных единиц продукции.
3. Найдите первые 20 наиболее доходных сделок, включающих продажи основы
под макияж (foundation).
4. Найдите все сделки за 2004 г. по продаже не менее 60 единиц продукции, для
которых цена за единицу продукции составила максимум $3,10.
5. Найдите все сделки с основой под макияж ( foundation) за первые три месяца
2004 г., в которых цена за единицу продукции была выше средней цены, полученной за основу под макияж, за весь период.
6. Найдите все сделки Зарет (Zaret) или Бетси (Betsy) по продаже помады (lipstick)
или основы под макияж.
7. Найдите все уникальные комбинации «продукт — продавец».
8. Найдите 30 самых крупных сделок (по количеству единиц продукции) по
продаже блеска для губ (lip gloss) или туши (mascara) в 2005 г.
9. Найдите все сделки Джен (Jen) с 10 августа по 15 сентября 2005 г.
10. Найдите все сделки Коллин (Colleen) по продаже помады (lipstick), в которых
количество проданных единиц продукции больше, чем среднее количество
единиц продукции в сделках по продаже помады.
11. Найдите все уникальные комбинации «имя — продукт — регион», встречающиеся в сделках за первые три месяца 2006 г.
12. Найдите все записи, в которых ячейка с названием продукта окрашена в желтый цвет.

Г Л А В А 52

Консолидация данных

Обсуждаемый вопрос
Компания продает продукцию в нескольких регионах США. В каждом регионе
хранятся записи о количестве проданных единиц продукции в январе, феврале
и марте. Существует ли простой способ создания мастер-книги, в которой постоянно объединяются продажи для всех регионов и проводится подсчет общей
суммы выручки для каждого продукта, проданного в США в течение каждого
месяца?

Бизнес-аналитики часто получают листы с одними и теми же обобщенными
данными (таким как ежемесячные продажи продукции) из различных филиалов или регионов. Аналитику , как правило, приходится объединять или консолидировать эту информацию в одной книге Microsoft Excel для определения
общей прибыльности компании. Для этой цели можно создать из нескольких
диапазонов консолидации сводные таблицы, но существует другой, редко используемый способ — инструмент Консолидация (Consolidate) на вкладке Данные
(Data) в группе Работа с данными (Data Tools). С его помощью можно обеспечить
автоматическое отражение на объединенном листе изменений, произошедших
на отдельных листах.

Ответ на вопрос
Компания продает продукцию в нескольких регионах США. В каждом регионе хранятся записи о количестве проданных единиц продукции в январе, феврале и марте. Существу ет ли простой способ создания мастер-книги,
в которой постоянно объединяются продажи для всех регионов и проводится
подсчет общей суммы выручки для каждого продукта, проданного в США в течение каждого месяца?

Файл East.xlsx (рис. 52.1) содержит данные о ежемесячных продажах продуктов
A–H в восточных штатах США за январь, февраль и март . Аналогично файл West.
xlsx (рис. 52.2) содержит данные о ежемесячных продажах продуктов A–H в западных штатах США за январь, февраль и март . Необходимо создать объединенный
лист, в котором были бы сведены в таблицу общие объемы продаж для каждого
продукта за месяц.

574

ГЛАВА 52

Рис. 52.1. Продажи в регионе Восток с января
по март

Рис. 52.2. Продажи в регионе Запад
с января по март

Перед применением инструмента Консолидация (Consolidate) полезно просмотреть
оба листа вместе на экране. Для этого откройте обе книги и на вкладке Вид (View)
в группе Окно (Window) щелкните по значку Рядом (View Side By Side). Экран должен выглядеть, как на рис. 52.3. Теперь откройте пустой лист, щелкните на Упорядочить все (Arrange All) и выберите Рядом (Tiled).
На пустом листе на вкладке Данные (Data) в группе Работа с данными (Data Tools)
выберите инструмент Консолидация (Consolidate). Откроется диалоговое окно Консолидация (Consolidate), показанное на рис. 52.4.
Для объединения данных из регионов Восток и Запад на новом пустом листе в диалоговом окне Консолидация (Consolidate) в поле Ссылка (Reference) по очереди выберите диапазоны, которые требуется объединить. После выбора каждого диапазона нажмите Добавить (Add). Флажки Подписи верхней строки (Top row) и Значения
левого столбца (Left column), установленные в разделе Использовать в качестве имени
(Use labels in), позволят убедиться в том, что объединяются выделенные диапазоны путем просмотра меток в верхней строке и левом столбце каждого диапазона.
Флажок Создавать связи с исходными данными (Create links to source data) обеспечивает отображение изменений в выделенных диапазонах на объединенном листе.
В раскрывающемся списке Функция (Function) выберите Сумма (Sum), поскольку
требуется сложить объемы продаж каждого продукта за месяц. С помощью функции Количество (Count) можно посчитать количество сделок для каждого продукта
в каждом месяце, а с помощью функции Максимум (Max) определить самую крупную сделку для каждого продукта в каждом месяце. Диалоговое окно Консолидация (Consolidate) должно быть заполнено так, как на рис. 52.5.

Консолидация данных

575

Рис. 52.3. Продажи в регионах Восток и Запад на одном экране

Рис. 52.4. Диалоговое окно Консолидация

Когда вы нажмете OK, новый лист будет выглядеть так, как на рис. 52.6. (См. файл
Eastandwestconsolidated.xlsx.) Видно, что в феврале было продано 1317 единиц продукта A, в январе — 597 единиц продукта F и т. д.
Теперь в ячейке C2 файла East.xlsx измените объем продаж продукта A в феврале с 263 на 363. Обратите внимание, что на объединенном листе значение объема

576

ГЛАВА 52

Рис. 52.5. Диалоговое окно Консолидация, заполненное данными

Рис. 52.6. Данные об общих объемах продаж после консолидации

продаж продукта A в феврале также увеличилось на 100 единиц (с 1317 до 1417).
Это изменение произошло из-за того, что мы установили флажок Создавать связи
с исходными данными (Create links to source data) в диалоговом окне Консолидация
(Consolidate). Кстати, если щелкнуть по цифре 2 в левом верхнем углу объединенного листа, можно увидеть, как в Excel для выполнения консолидации были
сгруппированы данные. Результат содержится в файле Eastandwestconsolidated.xlsx.
Разумеется, вы можете объединить данные с разных листов и при помощи сводных таблиц с несколькими диапазонами консолидации (см. главу 45 «Сводные таблицы и срезы для описания данных») или при помощи модели данных (глава 46
«Модель данных»).
Если вам приходится часто загружать в исходную книгу (в данном примере East.
xlsx и West.xlsx) новые данные, рекомендуется диапазонам с данными присвоить
имена, как таблицам. Тогда новые данные будут автоматически включаться в консолидацию. Или можно под текущим набором данных выделить несколько пустых строк. После заполнения пустых строк новыми данными они будут учтены
при консолидации. Третий вариант — преобразовать диапазоны данных в динамические диапазоны (см. главу 22 «Функция СМЕЩ»).

Консолидация данных

577

Задания
Эти задания по файлам Jancon.xlsx и Febcon.xlsx. Каждый файл содержит проданный продукт, показатели продаж в единицах продукции и выручку в долларах для
сделок за месяц.
1. Создайте объединенный лист, на котором определен общий показатель продаж в единицах продукции и общая выручка в долларах для каждого продукта
по регионам.
2. Создайте объединенный лист, на котором за первый квартал по регионам для
каждого продукта определяется самая крупная сделка с точки зрения выручки и количества проданных единиц продукции.

ГЛ А В А 53

Создание промежуточных итогов

Обсуждаемые вопросы
Существует ли быстрый способ настроить лист для вычисления общей выручки
и количества проданных единиц продукции по регионам?
Как можно при этом получить разбивку продаж по продавцам в каждом регионе?

Joolas — небольшая компания по производству косметики. Для каждой сделки она
отслеживает имя продавца, место совершения сделки, проданный продукт , количество проданных единиц товара и выручку . Руководству компании необходимо
получить ответы на вопросы, приведенные выше.
В Microsoft Excel для получения срезов данных можно использовать сводные таблицы. Однако зачастую требуется просто обработать список или базу данных
в виде списка. Например, в базе данных по продажам необходимо суммировать
выручку по регионам, по продуктам и по продавцам. Если отсортировать список
Промежуточный итог
по столбцу с нужными данными, с помощью инструмента
(Subtotal) можно создать в списке подытог. Например, если базу данных косметических товаров отсортировать по регионам, то можно вычислить общую выручку и количество проданных единиц продукции для каждого региона и поместить
промежуточные данные непосредственно под последней строкой для соответствующего региона. Или еще один пример. После сортировки базы данных по продукту можно с помощью инструмента Промежуточный итог (Subtotal) вычислить общую выручку и количество проданных единиц продукции для каждого продукта
и вывести промежуточные данные под строкой, в которой изменяется продукт .
Переходим к рассмотрению конкретных примеров.

Ответы на вопросы
?

Существует ли быстрый способ настроить лист для вычисления общей выручки и количества проданных единиц продукции по регионам?

Данные к этому примеру находятся в файле Makeupsubtotals.xlsx. На рис. 53.1 показана часть данных после сортировки списка по столбцу Регион (Location).
Для вычисления выручки и количества проданных единиц продукции по регионам установите курсор в пределах базы данных и затем на вкладке Данные (Data)

Создание промежуточных итогов

579

в группе Структура (Outline) выберите инструмент Промежуточный итог (Subtotal).
Диалоговое окно Промежуточные итоги (Subtotal) заполните, как на рис. 53.2.

Рис. 53.1. После сортировки списка по значениям в конкретном столбце можно быстро
создать промежуточные итоги для соответствующих данных

Рис. 53.2. Диалоговое окно Промежуточные итоги

В списке При каждом изменении в (At each change in) выберите столбец Регион для
создания промежуточных итогов в каждой точке, в которой значение в этом столбце изменяется, то есть происходит переход к другому региону. В списке Операция
(Use function) выберите Сумма (Sum) для итогов по каждому региону на основе любого набора столбцов. Выберите в списке Добавить итоги по (Add subtotal to) столб-

580

ГЛАВА 53

цы Количество и Сумма для промежуточных итогов по этим столбцам. Флажок
Заменить текущие итоги (Replace current subtotals) позволяет Excel удалять любые
ранее вычисленные промежуточные итоги. Поскольку таковые в данном примере
еще не созданы, для нас флажок не важен. Если установлен флажок Конец страницы между группами (Page break between groups), каждый раз после промежуточных
итогов автоматически будет вставлен разрыв страницы. При включенном флажке Итоги под данными (Summary below data) промежуточные итоги располагаются
под данными. Если этот флажок не активен, промежуточные итоги создаются
над теми данными, которые использовались для вычислений. Кнопка Убрать все
(Remove All) удаляет все промежуточные итоги из списка.
На рис. 53.3 приведен пример промежуточных итогов. Как видите, в регионе Восток (East) было продано 18 818 единиц продукции на сумму $57 372,09.

Рис. 53.3. Промежуточные итоги для региона Восток

Обратите внимание, что в левом верхнем углу окна (см. рис. 53.3) появились
кнопки с числами 1, 2 и 3. Если нажать кнопку с наибольшим числом (в данном
случае 3), то на листе останутся и данные, и итоги. Если нажать кнопку 2, то появятся промежуточные итоги по регионам, как на рис. 53.4. Если нажать кнопку 1,
то появится общий итог, как на рис. 53.5. Таким образом, меньшее число соответствует меньшему уровню детализации.

Рис. 53.4. При создании промежуточных итогов добавляются кнопки для отображения
различных уровней детализации

Создание промежуточных итогов

581

Рис. 53.5. Общий итог без детализации

Как можно при этом получить разбивку продаж по продавцам в каждом
регионе?

Если хотите, вы можете представить итоговые суммы во вложенном виде. Другими словами, можно получить разбивку продаж по каждому продавцу в каждом
регионе или даже разбивку по количеству проданных продуктов для каждого продавца в каждом регионе. (См. файл Nestedsubtotals.xlsx.) Для демонстрации вложенных промежуточных итогов создадим разбивку продаж по каждому продавцу
в каждом регионе.
Прежде всего, надо отсортировать данные по столбцу Регион, затем по столбцу
Имя. Получится разбивка для каждого продавца по количеству проданных единиц
товара и по выручке в каждом регионе. Если отсортировать сначала по Имя, а затем по Регион, получится разбивка по количеству проданных единиц товара и по
выручке для каждого продавца по регионам. После сортировки данных выполните действия, аналогичные описанным ранее, и создайте промежуточные итоги по
регионам. Снова выберите инструмент Промежуточный итог (Subtotal) и заполните
диалоговое окно, как на рис. 53.6.

Рис. 53.6. Создание вложенных промежуточных итогов

Теперь нам нужна разбивка по столбцу Имя. Снимите флажок Заменить текущие
итоги (Replace current subtotals) для гарантии того, что разбивка по регионам не будет замещена. Как видно из рис. 53.7, теперь появилась разбивка продаж по каждому продавцу в каждом регионе.

582

ГЛАВА 53

Рис. 53.7. Вложенные промежуточные итоги

Задания
Данные к заданиям находятся в файле Makeupsubtotals.xlsx. Используя инструмент
Промежуточный итог (Subtotal), выполните следующие расчеты:
1. Найдите количество проданных единиц продукции и выручку для каждого
продавца.
2. Найдите количество сделок по каждому продукту.
3. Найдите самую крупную сделку (с точки зрения выручки) для каждого продукта.
4. Найдите среднюю сумму в долларах для сделки по регионам.
5. Покажите разбивку проданных единиц продукции и выручки для каждого
продавца, которая представляла бы резуль таты для каждого продукта по регионам.

Г Л А В А 54

Приемы работы с диаграммами

Обсуждаемые вопросы
Как создать комбинированную диаграмму?
Как создать вспомогательную ось?
Как обработать недостающие данные?
Как показать скрытые данные на диаграмме?
Как с помощью картинок сделать гистограмму интереснее?
Я отобразил данные о ежегодных продажах в виде гистограммы, но годы как
метки столбиков не отображаются. Где ошибка?
Как включить метки данных и таблицу данных в диаграмму?
Как поместить в диаграмму метки данных на основе содержимого ячеек?
Как отследить эффективность отдела сбыта по продажам за определенный период?
Как создать ленточную диаграмму для проверки наличия запасов?
Как сохранить диаграмму в качестве шаблона?
Как с помощью диаграммы «термометр» отобразить прогресс?
Как создать на диаграмме динамические метки?
Как с помощью флажков указать, какие ряды данных требуется отобразить на
диаграмме?
Как с помощью списка обеспечить выбор ряда данных для отображения на диаграмме?
Как создать диаграмму Ганта?
Как создать диаграмму на основе отсортированных данных?
Как создать гистограмму, которая при добавлении новых данных обновлялась бы
автоматически?
Как добавить условные цвета в диаграмму?
Как с помощью диаграммы «водопад» отследить приближение объемов продаж
к плану или разложить компоненты продажной цены?

584

ГЛАВА 54

Как с помощью функции ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ и таблицы
Excel создать динамические информационные панели?
Как вставить в диаграмму вертикальную линию для разделения производительности до и после слияния?
Как с помощью лепестковой диаграммы отобразить различия баскетболистов
в силе, скорости и прыгучести?
Известно, что изменение двух переменных можно представить с помощью точечной диаграммы. А как представить изменение трех переменных с помощью
пузырьковой диаграммы?
Как создать диаграмму «водопад»?
Как используются для обобщения иерархических данных диаграммы «дерево»
и «солнечные лучи»?
Что такое диаграмма типа «воронка»?
Как отразить в диаграмме свежую динамику по интересующим меня акциям?

Древняя китайская пословица гласит: «Одна картина стоит тысячи слов». В Excel
можно создавать великолепные диаграммы, и в данной главе я дам вам множество
советов и рекомендаций. Только помните, что в этой сфере в Microsoft Excel произошли значительные изменения (в лучшую сторону!) по сравнению с версиями
до 2013 года.

Ответы на вопросы
?

Как создать комбинированную диаграмму?

В файле Combinationstemp.xlsx содержатся данные о фактических и плановых
продажах с января по июль. Вы хотите создать диаграмму , отображающую фактические и плановые продажи за каждый месяц. Сначала выделите диапазон
F5:H12 и на вкладке Вставка (Insert) в списке Гистограмма или линейчатая диаграмма
(Insert Column Or Bar Chart) выберите первую 2D-гистограмму (с группировкой) —
рис. 54.1.
Использование двух столбиков не позволяет сразу увидеть различия между фактическими и плановыми продажами, поэтому я предпочел создать комбинированную диаграмму, в которой один ряд данных представлен как линия, а другой —
как столбики. Для создания такой диаграммы щелкните правой кнопкой мыши
по любому ряду и выберите Изменить тип диаграммы (Change Chart Type). Выберите
в левой панели Комбинированная (Combo) и затем — первый вариант ( Гистограмма
с группировкой и график), как на рис. 54.2. Появится комбинированная диаграмма
(рис. 54.3).

Приемы работы с диаграммами

Рис. 54.1. Гистограмма фактических и плановых продаж

Рис. 54.2. Выбор комбинированной диаграммы

Рис. 54.3. Комбинированная диаграмма

585

586

ГЛАВА 54

Как создать вспомогательную ось?

При составлении диаграммы для двух величин с различной амплитудой часто
применяется вспомогательная ось, призванная повысить наглядность диаграммы.
Для примера рассмотрим рис. 54.6 (см. файл Secondaryaxis.xlsx), на котором показаны ежемесячная выручка и количество проданных единиц продукции. Если
представить эти данные на единственной оси y, значения ежемесячной выручки
будут едва различимы. Для решения этой проблемы сначала выделите диапазон
D7:F16, затем выберите на вкладке Вставка (Insert) Вставить комбинированную диаграмму (Combo Chart) (рис. 54.4) и затем первый в списке вариант выбора, Гистограмма с группировкой и график (Clustered Column-Line). Заполните диалоговое окно,
как на рис. 54.5: в дополнение параметрам по умолчанию установите флажок Вспомогательная ось (Secondary Axis) для ряда Выручка (Revenue) и нажмите OK.

Рис. 54.4. Значок Вставить комбинированную диаграмму

Рис. 54.5. Создание комбинированной диаграммы со вспомогательной осью

В получившейся диаграмме (рис. 54.6) выручка суммируется на вспомогательной
оси (на вертикальной оси справа) в виде графика. Как видите, ежемесячная выручка и количество проданных единиц продукции изменяются практически синхронно.

Приемы работы с диаграммами

587

Рис. 54.6. Итоговая выручка на вспомогательной оси

Как обработать недостающие данные?

Нередко случается так, что в некоторых строках таблицы не хватает данных. Excel
предоставляет три способа составления диаграмм с недостающими данными:
обработка данных как нулевых значений;
обработка данных как пустых значений (пропуски);
замена недостающей точки данных линией, соединяющей соседние точки данных.
Для примера рассмотрим файл Missingdata.xlsx, содержащий почасовые значения
температуры, но часть из них отсутствует . После представления данных в виде
графика щелкните правой кнопкой мыши на графике и выберите команду
Выбрать данные (Select Data). В появившемся диалоговом окне Выбрать источник данных (Select Data Source) нажмите Скрытые и пустые ячейки (Hidden And Empty Cells).
Откроется диалоговое окно Настройка скрытых и пустых ячеек (Hidden and Empty Cell
Settings), показанное на рис. 54.7.

Рис. 54.7. Диалоговое окно Настройка скрытых и пустых ячеек

Установите переключатель Показывать пустые ячейки как в положение линию
(Connect data points with line). Затем с помощью контекстного меню измените тип
диаграммы и выберите График с маркерами (Line Graph with Dots and Lines). Полу-

588

ГЛАВА 54

чившийся график представлен на рис. 54.8. На нем легко отличить недостающие
данные, поскольку для них маркеры отсутствуют.

Рис. 54.8. Недостающие данные заменены линиями

Как показать скрытые данные на диаграмме?

Довольно часто приходится создавать диаграммы для ежедневных продаж
и фильтровать данные в таблице. В такой ситуации Excel может сделать две вещи:
либо продолжать показывать все данные на диаграмме, либо показывать только
отфильтрованные данные. В файле Hidden.xlsx находятся данные о ежедневных
продажах продукта в течение года. Данные, представленные в виде графика, показаны на рис. 54.9.

Рис. 54.9. Диаграмма ежедневных продаж продукта

Если щелкнуть по графику правой кнопкой мыши, затем по Выбрать данные (Select
Data) и в окне Настройка скрытых и пустых ячеек (Hidden and Empty Cell Settings) (см. рис.
54.7) включить флажок Показывать данные в скрытых строках и столбцах (Show data in

Приемы работы с диаграммами

589

hidden rows and columns), на диаграмме будут представлены все точки данных даже

после фильтрования данных. Например, на рис. 54.10 данные отфиль трованы для
показа только декабрьских продаж, но на графике по-прежнему представлены ежедневные продажи за весь год. Если флажок Показывать данные в скрытых строках
и столбцах не активен, на диаграмме будут видны только декабрьские продажи.

Рис. 54.10. Данные отфильтрованы, а точки на диаграмме — нет

Как с помощью картинок сделать гистограмму интереснее?

Как правило, амплитуда продаж продукции обобщается как скучные столбцы или
полосы, где высота столбцов или ширина полос пропорциональна продажам продукции. Разве не было бы интереснее представить итоги в виде картинки с продуктом, масштабированной пропорционально фактическим продажам? Для иллюстрации этой идеи рассмотрим данные в файле Picturegraph.xlsx и рис. 54.11.
Допустим, вы продаете книги.
Сначала выделите диапазон C5:D8. На вкладке Вставка (Insert) щелкните Гистограмма или линейчатая диаграмма (Insert Column Or Bar Chart) и выберите первую
2D-гистограмму (с группировкой). Затем щелкните правой кнопкой мыши по
любому столбику. Выберите в контекстном меню Заливка (Fill) и затем Рисунок
(Picture). Откроется диалоговое окно, представленное на рис. 54.12. Введите книги (books) в поле Поиск изображений Bing (Bing Image Search) и нажмите Enter. Появится множество картинок с книгами. Выбрав книгу , нажмите Вставить (Insert).
Картинка будет вставлена в диаграмму (см. рис. 54.11). Высота книг пропорциональна фактическим продажам.
Возможно, будет лучше сделать так, чтобы вместо одной книги продажи отображались стопками книг, где одна книга равна 1000 проданных экземпляров. На листе
stack and stretch (рис. 54.14) создана как раз такая диаграмма. Чтобы изменить диаграмму, где одна книга отображает месячные продажи, щелкните правой кнопкой

590

ГЛАВА 54

Рис. 54.11. Объемы продаж книг в виде изображений книг

Рис. 54.12. Диалоговое окно Вставка картинок

Рис. 54.13. Изменение диаграммы так, чтобы одна книга отражала 1000 экземпляров

Приемы работы с диаграммами

591

мыши по любой книге и выберите Формат ряда данных (Format Data Series). Как
показано на рис. 54.13, выбираем Заливка (Fill) (первый значок слева) и изменяем
выбор с Растянуть (Stretch) на Размножить (Stack), а точнее — Размножить в масштабе
(Stack and Scale with), и устанавливаем масштаб (Units/Picture) 1000 единиц = 1 книга.

Рис. 54.14. Теперь одна книга отражает 1000 экземпляров

Я отобразил данные о ежегодных продажах в виде гистограммы, но годы
как метки столбиков не отображаются. Где ошибка?

В файле Categorylabel.xlsx (рис. 54.15) содержатся данные о ежегодных продажах
продукта за 2007–2010 гг . В гистограмме, созданной на основе диапазона D5:E9,

Рис. 54.15. Отсутствие метки позволяет придать гистограмме правильный вид

592

ГЛАВА 54

на оси x годы не указаны, поскольку Excel думает, будто я хочу, чтобы год обрабатывался как ряд данных. Если убрать метку категории Год в левом верхнем углу
исходного диапазона и выбрать в качестве данных для гистограммы диапазон
D20:E24, то на гистограмме появится ось x для годов.

Как включить метки данных и таблицу данных в диаграмму?

Часто нам нужно вставить метки данных рядом со столбиками или полосами или
сделать красивую таблицу данных под диаграммой. Рассмотрим этот процесс на
примере файла Labelsandtables.xlsx. В нем хранятся продажи за текущий месяц
по четырем группам продуктов. Сначала создадим на основе этих данных гистограмму и поместим метки, содержащие имена продуктов и фактические продажи, над столбиками. Для этого создайте обычную гистограмму , затем выберите
столбик с данными на гистограмме и выберите Добавить элемент диаграммы (Add
Chart Element) на появившейся вкладке Конструктор (Chart Tools Design). Щелкните стрелку справа от Метки данных (Data Labels), затем Дополнительные параметры
подписей данных (More Data Label Options). В панели Формат подписей данных (Format
Data Labels) заполните раздел Параметры подписи (Label Options), как показано на
рис. 54.16. Появится диаграмма, представленная на рис. 54.17.
Теперь я покажу, как поместить таблицу данных, обобщающую продажи, под диаграмму. Просто выделите любую часть диаграммы и затем нажмите Добавить элемент диаграммы на вкладке Конструктор. Затем выберите Таблица данных (Data Tables)
и вариант Без легенды (No Legend Keys). Диаграмма примет вид, как на рис. 54.18.

Рис. 54.16. Параметры, необходимые для настройки
показа имен групп и объемов продаж в отдельных строках

Приемы работы с диаграммами

593

Рис. 54.17. В гистограмму включены имена групп и объемы продаж

Рис. 54.18. Продажи обобщены в таблице данных

Для просмотра дополнительных возможностей щелкните на треугольнике раскрывающегося списка справа от флажка Таблица данных (Data Table).

Как поместить в диаграмму метки данных на основе содержимого ячеек?

Начиная с Excel 2013 можно помещать в диаграммы метки данных непосредственно из ячеек. В качестве примера рассмотрим файл Labelsfromcells.xlsx, представленный на рис. 54.19.
Сначала выделите ячейки H5:I10 и на вкладке Вставка (Insert) выберите первый вариант для точечной диаграммы. Значок Точечная или пузырьковая диаграмма (Insert
Scatter (X, Y) Or Bubble Chart) расположен рядом со значком круговой диаграммы.
Появится точечная диаграмма, как на рис. 54.19, но без меток городов. Для создания
меток городов выделите диаграмму, на вкладке Конструктор (Работа с диаграммами)
(Design) в раскрывающемся списке Добавить элемент диаграммы (Add Chart Element)

594

ГЛАВА 54

Рис. 54.19. Точечная диаграмма с метками из ячеек

выберите Метки данных (Data Labels) и затем Дополнительные параметры подписей
данных (More Data Label Options). На панели Формат подписей данных (Format Data
Labels) снимите флажок Значения Y (Y Value), установите флажок значения из ячеек
(Value from Cells) и укажите диапазон G6:G10 для вставки меток городов в диаграмму, как показано на рис. 54.19.

Как отследить эффективность отдела сбыта по продажам за определенный
период?

В файле Salestracker.xlsx представлены ежемесячные продажи для каждого сотрудника отдела продаж с января по май (рис. 54.20).

Рис. 54.20. Данные о ежемесячных продажах

Приемы работы с диаграммами

595

Вы хотите использовать значки (стрелку вверх, вниз, вправо) для отслеживания изменения ранга продавцов от месяца к месяцу (ранг повысился, понизился,
остался прежним). Для этой цели можно было бы выбрать набор значков Excel
(см. главу 24 «Условное форматирование»), но тогда пришлось бы вставлять набор
значков для каждого месяца, что довольно трудоемко. Гораздо эффективнее (но не
так эстетично) создать эти значки путем ввода буквы h для стрелки вверх, i для
стрелки вниз и g для стрелки вправо. Если затем изменить шрифт на Wingdings 3,
появятся требуемые стрелки, поскольку буквы алфавита в W ingdings 3 соответствуют символам, показанным на рис. 54.21.

Рис. 54.21. Соответствие между буквами и символами Wingdings 3

Для создания значков, показанных на рис. 54.22, предпримите следующее:
1. Скопируйте формулу =РАНГ(E6;E$6:E$20;0) из J6 в J6:N20 для вычисления ранга каждого продавца в каждом месяце.
2. Скопируйте формулу =ЕСЛИ(K6J6;»i»;»g»)) из O6 в O7:R20.
В ячейках появится буква h, если ранг продавца повысился, буква i, если понизился, и буква g, если остался прежним.
3. После изменения в диапазоне O6:R20 шрифта на Wingdings 3 появятся стрелки, как на рис. 54.22.
Преимущество такого подхода в том, что вы можете применить функцию
(IF) для быстрого создания критериев выбора соответствующего значка.

ЕСЛИ

596

ГЛАВА 54

Рис. 54.22. Значки, использованные для оценки эффективности продавцов

Как создать ленточную диаграмму для проверки наличия запасов?

Довольно часто требуется отслеживать количественные величины (запасы, наличные денежные средства, количество аварий) и определять, остается ли отслеживаемая величина в границах между историческим максимумом и минимумом.
Ленточная диаграмма — полезный инструмент для отслеживания изменений с течением времени. Пример ленточной диаграммы приведен на рис. 54.23. (См. файл
Bandchart.xlsx.)

Рис. 54.23. Ленточная диаграмма для отслеживания запасов

Приемы работы с диаграммами

597

Для создания ленточной диаграммы выполните следующее:
Введите нижнюю границу запаса (5) в ячейку B2 и верхнюю границу (25)
в ячейку B3.
В строке 5 введите нижнюю границу для каждого месяца, скопировав формулу
=$B$2 из B5 в C5:G5.
Скопируйте формулу =$B$3-$B$2 из B6 в C6:G6 для вычисления разницы между
верхней и нижней границами. Назовем эту строку Верхняя граница, поскольку
при построении диаграммы именно эта строка будет использоваться для создания линии, представляющей верхнюю границу запаса в 25 единиц.
Выделите диапазон A4:G7 и на вкладке Вставка (Insert) в группе Диаграммы
(Chart) выберите График или диаграмма с областями (Insert Line Or Area Chart)
и затем С накоплением (Stacked Column), это второй вариант среди 2D-диаграмм
с областями. Измените название диаграммы на Ленточная диаграмма.
Щелкните правой кнопкой мыши по ряду Значения (зеленая полоса), выберите
в контекстном меню Изменить тип диаграммы для ряда (Change Series Chart Type).
В открывшемся диалоговом окне под заголовком Выберите тип диаграммы и ось
для рядов данных: (Choose The Chart Type And Axis For Your Data Series) для ряда
Верхняя граница выберите Заливка (Area), первый вариант в соответствующем
разделе. Для ряда Значения выберите График, первый вариант в разделе графиков. Нажмите OK.
Щелкните правой кнопкой мыши по ряду Нижняя граница на диаграмме и выберите Заливка (Fill). В меню Заливка (Fill) выберите Нет заливки (No Fill).
Полученная ленточная диаграмма показывает, что запас с трудом удается удерживать между требуемыми верхней и нижней границами.

Как сохранить диаграмму в качестве шаблона?

Я только что создал прекрасную ленточную диаграмму.Возможно, вы думаете, что
теперь каждый раз придется повторять вышеописанные шаги для того же результата. Если так, то вы ошиблись. Можно сохранить ленточную (или любую другую)
диаграмму как шаблон и менять настройки диаграммы в любое время. В качестве
примера откройте файл Bandchart.xlsx, щелкните правой кнопкой мыши по диаграмме, выберите Сохранить как шаблон (Save As Template) и присвойте диаграмме
любое имя (например, Band). Предположим, вам нужна ленточная диаграмма для
месяцев с января по март. Выделите диапазон данных A4:D7 и на вкладке Вставка
(Insert) в группе Диаграммы (Chart) щелкните по стрелке в правом нижнем углу. На
вкладке Все диаграммы (All Charts) выберите Шаблоны (Templates). Найдите требуемый шаблон диаграммы, нажмите OK, и готово!

Как с помощью диаграммы «термометр» отобразить прогресс?

Диаграмма «термометр» показывает такие величины, как выручка, в виде
столбика, отображающего плановое значение. Получившаяся диаграмма (на

598

ГЛАВА 54

рис. 54.24 и в файле Thermometer.xlsx) напоминает термометр, отсюда и идет ее
название.

Рис. 54.24. Диаграмма «термометр»

Для создания диаграммы «термометр» выполните следующее:
Выделите диапазон A1:H3 и на вкладке Вставка (Insert) в группе Диаграммы
(Chart) выберите 2D-диаграмму Гистограмма с группировкой (Clustered Column).
Щелкните правой кнопкой мыши по ряду Выручка на диаграмме (синий столбик) и выберите команду Формат ряда данных (Format Data Series). Выберите По
вспомогательной оси (Secondary Axis).
В той же панели Формат ряда данных (Format Data Series) (ряд Выручка выделен)
установите в поле Перекрытие рядов (Overlap) значение 0% и в поле Боковой зазор (Gap Width) значение 261%.
Щелкните правой кнопкой мыши по ряду План (красный столбик) и установите в поле Перекрытие рядов (Overlap) значение 0% и в поле Боковой зазор (Gap
Width) значение 48%.
Теперь диаграмма выглядит, как на рис. 54.24. При необходимости ширину бокового зазора можно отрегулировать. У меньшение бокового зазора для ряда План,
например, сделает красные столбики шире; увеличение бокового зазора для ряда
Выручка сделает синие столбики уже.

Как создать на диаграмме динамические метки?

Вероятно, многим приходилось иметь дело с диаграммами Excel, в которых при
изменении данных метки на диаграммах не менялись. Т акая ситуация часто привносит путаницу. Давайте научимся связывать метки рядов и названия диаграммы
с ячейками на листе. (См. файл DynamicLabels.xlsx и рис. 54.25.) Предположим, что
вам нужно создать диаграмму для прогнозируемого ВВП в США и Китае. Название диаграммы должно содержать год, в который Китай догонит США по ВВП,

Приемы работы с диаграммами

599

а названия рядов — ежегодные темпы роста для каждой страны. В ячейках C5 и C8
текущие расчетные значения темпов роста — 3% для ВВП США и 10% для ВВП
Китая — можно изменить.

Рис. 54.25. Создание динамических меток

Основная идея в том, чтобы связать названия диаграммы и метки с ячейками, которые изменяются при изменении темпов роста. Для этого сделайте следующее:
Скопируйте формулу =ЕСЛИ(D7>=D4;1;0) из D10 в E10:R10, которая даст в результате 1, если ВВП Китая окажется не меньше ВВП США.
В ячейке C14 определите год, когда Китай догонит США по ВВП, по формуле
=ЕСЛИОШИБКА(ПОИСКПОЗ(1;D10:R10;0);»none»). Обратите внимание, что если
Китай никогда не догонит США по ВВП, формула возвратит «none».
В ячейке C17 создайте желаемое название диаграммы по формуле
=ЕСЛИ(C14=»none»;»США опережает Китай по ВВП»;»Китай догнал США по ВВП на
«&ТЕКСТ(C14;»0″)&» году»). Обратите внимание, что если Китай никогда не догонит США по ВВП, то диаграмма будет называться «США опережает Китай по
ВВП». В противном случае название диаграммы привязывается к ячейке C14 та-

ким образом, что в него входит год, на который Китай догонит США по ВВП.
«0» в функции ТЕКСТ гарантирует, что значение для года будет отформатировано как целое число.
В ячейке C18 создайте название для ряда данных ВВП США по формуле =»США
(темпы роста «&ТЕКСТ(C5;»0,0%»)&»)». Часть текстовой функции «0,0%» гарантирует, что значение для темпов роста будет отформатировано в процентах.
В ячейке C19 создайте название для ряда данных ВВП Китая по формуле =»Китай
(темпы роста «&ТЕКСТ(C8;»0,0%»)&»)».
Теперь все готово для создания диаграммы с динамическими метками.

600

ГЛАВА 54

Удерживая Ctrl, выделите несмежные диапазоны ячеекC2:R2, C4:R4 и C7:R7 и создайте точечную диаграмму с гладкими кривыми: на вкладкеВставка (Insert) выберите Точечная или пузырьковая диаграмма (Insert Scatter (X, Y) Or Bubble Chart)
и затем Точечная с гладкими кривыми (Scatter With Smooth Lines) (третий вариант).
На вкладке Конструктор (Design) выберите Добавить элемент диаграммы (Add
Chart Element) и Название диаграммы по центру (Centered Overlay Title). В строке
формул введите знак равенства ( =), затем выберите C17 и нажмите Enter. На
диаграмме появится название с динамической меткой.
Выделите ряд данных 1 (ряд ВВП США), щелкните правой кнопкой мыши и выберите Выбрать данные (Select Data). Нажмите Изменить (Edit) и заполните диалоговое окно Изменение ряда (Edit Series), как на рис. 54.26: введите в поле Имя
ряда (Series Name) =’Dynamic labels’!$C$18, оставьте остальные значения по умолчанию и нажмите OK в обоих диалоговых окнах.

Рис. 54.26. Создание динамической метки ряда

Это связь метки ряда ВВП США с ячейкой C18, в которой содержится значение годовых темпов роста. Аналогичным образом создайте связь метки ряда ВВП Китая
с ячейкой C19. Диаграмма с динамическими метками готова.

Как с помощью флажков указать, какие ряды данных требуется отобразить на диаграмме?

В главе 27 «Счетчики, полосы прокрутки, переключатели, флажки, группы и поля
со списками» как вы, возможно, помните, мы научились переключать в ячейке
с помощью флажка значения ЛОЖЬ и ИСТИНА. Оказалось, если Excel видит в ячейке ошибку #Н/Д, то точка на диаграмме не создается. Поэтому если требуется не
включать в диаграмму какой-либо ряд данных, просто создайте формулу с функцией ЕСЛИ для записи в этот ряд данных ошибки #Н/Д после того, как с помощью
флажка в ячейке установлено значение ЛОЖЬ. См. пример на рис. 54.27.
Откройте файл Checkbox.xlsx. Сначала методами, описанными в главе 27, создайте
два флажка: один для управления рядом данных 2010, а другой для управления
рядом данных 2011. Флажок 2010 управляет содержимым ячейки B1, а флажок
2011 — содержимым ячейки C1. Исходные данные находятся в диапазоне E6:L7.
Формула =ЕСЛИ($B$1;F6;НД()), скопированная из F10 в F10:L11, дает в резуль тате либо исходные данные соответствующего года, если для этого года флажок

Приемы работы с диаграммами

601

Рис. 54.27. Флажки для управления представлением данных на диаграмме

установлен, либо ошибку #Н/Д, если для этого года флажок года снят. Теперь выберите диапазон E9:L11 в качестве исходных данных для построения диаграммы
График с маркерами (Line With Markers) — четвертый график в разделе 2D-графиков.
Сброс флажка с номером года скроет на графике данные за этот год, а установка
флажка с номером года представит на графике соответствующие данные.

Как с помощью списка обеспечить выбор ряда данных для отображения на
диаграмме?

На листе (см. файл Listbox.xlsx) содержатся данные о продажах за 2007–2011 гг .
в регионах Восток, Запад, Средний Запад и Юг. Вам нужен простой способ управления включением рядов данных в диаграмму . Такой способ предоставляет список (см. главу 27). Сначала на вкладке Разработчик (Developer) в группе Элементы
управления (Form Controls) в списке Вставить (Insert) выберите элемент управления формы Список (List Box) — пятый значок в верхнем ряду . Поместите список
на лист, щелкните правой кнопкой мыши и выберите
Формат объекта (Format
Control). В поле Формировать список по диапазону (Input Range) выберите диапазон
$A$14:$A$17 и в поле Связь с ячейкой (Cell Link) ячейку $H$2. Теперь, умно используя функцию ИНДЕКС, вы можете использовать ячейку H2 для управления рядами
данных, которые нужно включить в диаграмму (рис. 54.28).
Скопируйте формулу =ИНДЕКС($H$16:$K$21;G7;$H$2) из I7 в I8:I10 для извлечения
правильного ряда данных. Например, в списке, показанном на рис. 54.28, выбран
регион Восток. Это помещает в ячейку H2 значение 1. Функция ИНДЕКС возвращает первый столбец данных (столбец H), что и требовалось. Теперь выделите диапазон H7:Y11 и создайте точечную диаграмму с гладкими кривыми. Вы увидите, что

602

ГЛАВА 54

после щелчка на конкретном регионе из списка диаграмма построится на основе
правильного ряда данных.

Рис. 54.28. Список для управления включением рядов данных в диаграмму

Как создать диаграмму Ганта?

Часто для проекта требуется завершение ряда других проектов. На диаграмме Ганта показывается время начала каждого проекта. На рис. 54.29 (см. файл

Рис. 54.29. Диаграмма Ганта

Приемы работы с диаграммами

603

Gantt.xlsx) представлена диаграмма Ганта для проекта, состоящего из пяти задач.

Для создания такой диаграммы выполните следующее:
Выберите диапазон F3:H8 и создайте 2D-гистограмму с накоплением (второй
вариант).
Щелкните правой кнопкой мыши по ряду Начало, выберите Заливка (Fill) и Нет
заливки (No Fill), чтобы скрыть ряд Начало.
Щелкните правой кнопкой мыши по вертикальной оси и выберите Формат оси
(Format Axis). Затем установите флажок Обратный порядок категорий (Categories
In Reverse Order), обеспечивающий Задаче 1 первое место в списке.

Как создать диаграмму на основе отсортированных данных?

Пусть имеются объемы продаж в нескольких штатах (рис. 54.30 и файл
Sortedgraphx.
xlsx). Вы хотите построить диаграмму с перечислением штатов в порядке убывания объемов продаж (рис. 54.31). Перед созданием диаграммы необходимо реорганизовать данные в столбцах J–L и отсортировать данные продаж в порядке убывания.

Рис. 54.30. Данные продаж для отсортированной диаграммы

Для этого сделайте следующее:
Скопируйте формулу =РАНГ(F9;$F$9:$F$23;0) из G9 в G10:G23 для вычисления
ранга продаж в каждом штате. Например, ранг Нью-Йорка ( NY) равен шести.
Обратите внимание, что в Кентукки (KY), Алабаме (Ala) и Аризоне (Ari) объемы
продаж одинаковые. Для сортировки штатов в порядке убывания продаж необходимо связать с каждым штатом уникальный ранг.
Скопируйте формулу =G9+СЧЁТЕСЛИ($G$8:G8;G9) из H9 в H10:H23 для создания
уникального ранга каждого штата путем увеличения ранга штата, имеющего
связанный ранг, каждый раз, когда встречается связанный ранг.

604

ГЛАВА 54

Скопируйте формулу =ИНДЕКС(E$9:E$23;ПОИСКПОЗ($J9;$H$9:$H$23;0);1) из K9
в K10:L23 для сортировки штатов и продаж на основе объемов продаж по убыванию.
Теперь создайте гистограмму на основе диапазона K9:L23, как на рис. 54.31
(выберите Гистограмма с группировкой (Clustered Column) в группе Диаграммы
(Charts)).

Рис. 54.31. Объемы продаж отсортированы по убыванию

Как создать гистограмму, которая при добавлении новых данных обновлялась бы автоматически?

В главе 43 «Обобщение данных на гистограммах и диаграммах Парето» вы научились создавать гистограммы с помощью надстройки Анализ данных (Data Analysis).
К сожалению, гистограммы, созданные с помощью пакета анализа, при изменении
или добавлении данных не обновляются. Для того чтобы диаграммы автоматически подстраивались под изменения в исходных данных, нужно преобразовать данные в таблицу Excel. (См. пример в файле Dynamichistograms.xlsx и на рис. 54.32.)
Столбец E содержит зарплаты игроков НБА в миллионах долларов в сезоне 2003–
2004 гг. Сначала выделите диапазон E5:E446 и преобразуйте его в таблицу . Введите бин-диапазоны для гистограммы в ячейки H7:H28. Обратите внимание, что
в строке 28 вычисляется количество игроков с зарплатой свыше $20 млн. Т еперь
воспользуемся функцией ЧАСТОТА (FREQUENCY) для вычисления того, сколько
зарплат попадают в каждый бин-диапазон. Функция ЧАСТОТА (см. главу 91 «Формулы массива и функции, возвращающие массив») является функцией, возвращающей массив результатов. Для ее использования сначала необходимо выбрать
диапазон, который заполнит функция (в данном примере I7:I28), затем ввести
формулу с функцией ЧАСТОТА и нажать Ctrl+Shift+Enter. После выбора диапазона I7:I28 введите формулу =ЧАСТОТА(E6:E446;H7:H27) и нажмите Ctrl+Shift+Enter.
В ячейку I7 Excel введет количество игроков (0) с зарплатой менее или равной 0,
в ячейку I8 — количество игроков с зарплатой > 0 и 19 и 20 млн долл. (0). Для создания динамической гистограммы выберите диапазон H7:I28 и вставьте гистограмму (выберите Гистограмма с группировкой (Clustered Column) в группе Диаграммы
(Charts)). Мы получили динамическую гистограмму, которая будет обновляться
автоматически после изменения вводных данных. Для доказательства обновления гистограммы добавьте несколько зарплат в 30 млн долл. в столбце E (ряд 447
и больше). В правой части диаграммы появится новый столбец.

Как добавить условные цвета в диаграмму?

Допустим, вы создаете диаграмму фактических и плановых продаж для каждого
месяца. При этом вы хотите выделить месяцы, в которых фактические продажи
составили 90% и больше от плановых, синим цветом; месяцы, в которых фактические продажи составили 75% и меньше — зеленым цветом; а остальные месяцы —
красным цветом. В файле Condcolors.xlsx (рис. 54.33) показано, как это делается.
Хитрость создания такой диаграммы заключается в размещении данных для каждого цвета в отдельной строке (см. строки 19–21).
1. Сначала поместите продажи, которые требуется выделить синим, в строку 19,
скопировав формулу =ЕСЛИ(F13/F14>F15;F13/F14;» «) из F19 в G19:M19.
2. Затем поместите продажи, которые требуется выделить красным цветом, в строку 20, скопировав формулу =ЕСЛИ(И(G13/G14>G16;G13/G14G16; G13/G14 0. При этом наклон степенной кривой зависит от значения b следующим образом:
для b > 1 y возрастает при увеличении x, и наклон степенной кривой увеличивается при увеличении x;
для 0 < b < 1 y возрастает при увеличении x, и наклон степенной кривой уменьшается при увеличении x;
для b = 1 степенная кривая представляет собой прямую линию;
для b < 0 y убывает при увеличении x, и степенная кривая выпрямляется при
увеличении x.
Далее я приведу примеры различных зависимостей, которые можно смоделировать с помощью степенной кривой. Эти примеры находятся в файлеPowerexamples.
xlsx.
Диаграмма для прогнозируемой общей себестоимости продукции как функции
количества произведенной продукции показана на рис. 57.1. Обратите внимание, что b = 2. Как я уже говорил, для этого значения b себестоимость продукции
растет с количеством произведенной продукции. Наклон становится круче, что
указывает на рост себестоимости каждой дополнительно произведенной единицы
продукции. Такая зависимость может возникнуть из-за сверхурочных, оплата которых выше, чем оплата обычного рабочего времени.
Если вы пытаетесь понять, как объемы продаж зависят от расходов на рекламу, то
можете обнаружить кривую, представленную на рис. 57.2.
Здесь b = 0,5 (то есть между 0 и 1). Если значение b находится в этом интервале, по мере увеличения расходов на рекламу объем продаж увеличивается, но
с уменьшающейся скоростью. Таким образом, степенная кривая позволяет смоде-

Степенная кривая

639

лировать закон убывающей доходности: каждый дополнительно потраченный на
рекламу доллар приносит меньше прибыли.

Рис. 57.1. Прогнозируемая себестоимость как функция
количества произведенной продукции

Рис. 57.2. Объем продаж как функция расходов на рекламу

Когда вы пытаетесь спрогнозировать время, необходимое для производства последней единицы продукции, на основании количества продукции, произведенной на сегодняшний день, то полезной часто оказывается точечная диаграмма,
показана на рис. 57.3.
Здесь b = –0,1. Поскольку b меньше 0, время, необходимое для производства каждой единицы продукции, уменьшается, но скорость уменьшения, то есть скорость
«обучения», снижается. Эта зависимость означает, что сначала при производстве
продукции идет значительная экономия рабочего времени по мере накопления
рабочих навыков. Однако при последующем производстве этой продукции рабочее время экономится все меньше. Зависимость между общим количеством произведенной продукции и временем, необходимым для производства единицы про-

640

ГЛАВА 57

дукции, называется кривой обучения, или кривой опыта. Степенная кривая имеет
следующие свойства.

Рис. 57.3. Время, необходимое для производства единицы продукции,
как функция совокупного количества продукции

Свойство 1. Если x увеличивается на 1%, y увеличивается примерно на b%.
Свойство 2. Каждый раз, когда x удваивается, y увеличивается на тот же процент.
Допустим, спрос на продукт в зависимости от цены можно смоделировать как
1000*(Цена)–2. Тогда свойство 1 подразумевает, что 1%-ное увеличение цены снизит спрос (независимо от величины цены) на 2%. В этом случае показатель степени b (без минуса) называется коэффициентом эластичности. Коэффициент
эластичности рассматривается в главе 87 «Оценка кривой спроса». Т еперь, исходя из вышеизложенного, посмотрим, как подобрать степенную кривую к данным.

Ответ на вопрос
Моя компания наращивает производство. Можно ли смоделировать зависимость между количеством произведенной продукции и временем, необходимым для производства одной единицы продукции?

В файле Fax.xlsx содержатся данные о количестве произведенных факсов и себестоимости (в долларах 1982 г .) производства «последнего» факса для каждого года. Например, в 1983 г . было произведено 70 000 факсов, и себестоимость
производства «последнего» факса составила $3416. Данные представлены на
рис. 57.4.
Поскольку кривая обучения прогнозирует либо себестоимость, либо время,
затрачиваемое на производство единицы продукции, на основе данных об об-

Степенная кривая

641

щем количестве продукции, в столбце C вычисляется общее количество факсов, произведенных к концу каждого года. В ячейке C4 ссылка на ячейку B4
показывает количество факсов, произведенных в 1982 г . Скопировав формулу
=СУММ($B$4:B4) из C5 в C6:C10, я вычислил общий объем производства к концу
каждого года.

Рис. 57.4. Данные, на основе которых строится кривая обучения
для производства факсов

Теперь можно создать точечную диаграмму с совокупным количеством произведенной продукции по оси x и себестоимостью единицы продукции по оси y. После
создания диаграммы щелкните на одной из точек данных (точки данных отображаются синим цветом), а затем щелкните правой кнопкой мыши и выберите Добавить линию тренда (Add Trendline). В диалоговом окне Формат линии тренда (Format
Trendline) установите переключатель в положение Степенная (Power) и отметьте
флажки Показывать уравнение на диаграмме (Display Equation on chart) и поместить
на диаграмму величину достоверности аппроксимации (R^2) (Display R-Squared value
on chart). Диаграмма с такими параметрами показана на рис. 57.5. Нарисованная
кривая представляет собой степенную кривую, больше всего соответствующую
данным.
Степенная кривая позволяет прогнозировать себестоимость производства факса
следующим образом:
себестоимость производства факса = 65 259*(совокупное количество)–0,2533.

Обратите внимание, что большая часть точек данных находится возле подобранной степенной кривой и что значение R2 близко к 1, то есть степенная кривая подогнана должным образом.
Скопируйте формулу =65259*C4^-0,2533 из ячейки E4 в E5:E10 и вычислите прогнозируемую себестоимость последнего факса, произведенного в конце каждого
года. (Знак вставки «^», который находится на клавише «6», означает возведение
в степень.)

642

ГЛАВА 57

Рис. 57.5. Кривая обучения для производства факсов

Если вы установили, что в 1989 г. было произведено 1 000 000 факсов, то, сначала
подсчитав в ячейке C11 общий объем производства к концу 1989 г. (2 744 000 шт.),
вы можете скопировать уравнение прогноза в ячейку E11 и получить себестоимость последнего произведенного в 1989 г. факса — $1526,85.
Напомню 2-е свойство степенной кривой: каждый раз, когда x удваивается, y увеличивается на тот же процент . Введите удвоенный объем производства в 1988 г .
в ячейку C12 и скопируйте формулу из E10 в E12. Оказывается, удвоение объема
производства снижает прогнозируемую себестоимость до 83,9% от предыдущего значения (1436,83/1712,60). Поэтому текущая кривая обучения называется
84%-ной кривой обучения. Каждый раз при удвоении объема производства трудовые затраты на производство факса уменьшаются на 16,1%.
Если кривая становится круче, данным может соответствовать не только степенная кривая, но и экспоненциальная. И какая же из них больше подходит к данным? В большинстве случаев ответ получить просто: сравните на глаз кривые
и выберите ту, которая кажется более подходящей. Для более точной оценки можно вычислить сумму квадратичных ошибок для каждой кривой (сложив квадраты
разности значений на кривой и фактических значений для каждой точки данных)
и выбрать кривую с меньшей суммой квадратичных ошибок.
Кривая обучения была изобретена в 1936 г. на базе военно-воздушных сил РайтПаттерсон (Wright-Patterson Air Force Base ) в Дейтоне, штат Огайо, когда было
установлено, что каждый раз при удвоении совокупного количества произведенных самолетов время, затраченное на производство одного самолета, уменьшалось примерно на 15%.
В «Википедии» можно найти оценки кривой обучения для различных отраслей
промышленности:
авиационно-космическая промышленность: 85%;
судостроение: 80–85%;
сложные станки, для новых моделей: 75–85%;

Степенная кривая

643

повторяющееся производство электроники: 90–95%;
повторяющиеся производственные операции или штамповочные операции:
90–95%;
повторяющиеся электромонтажные работы: 75–85%;
повторяющиеся сварочные работы: 90%;
сырье: 93–96%;
покупные детали: 85–88%.

Задания
1. На основе примера по производству факсов смоделируйте зависимость между общим объемом производства и общей себестоимостью произведенной
продукции.
2. На основе примера по производству факсов смоделируйте зависимость между общим объемом производства и средней себестоимостью одного факса.
3. Коммерческий директор считает, что общий объем продаж продукта зависит
от цены так, как показано в таблице ниже. Определите зависимость между
ценой и спросом, а также прогнозируемым спросом для цены $46. На сколько
процентов уменьшается спрос при увеличении цены на 1%?
Цена

Спрос

$30,00

300

$40,00

200

$50,00

110

$60,00

4. Бренд-менеджер нового лекарственного препарата считает, что годовой объем
продаж препарата является функцией количества рекламных звонков (см. таблицу). Определите объем продаж препарата, если врачам сделано 80 000 рекламных звонков.
Коммерческие звонки

Количество проданного препарата

50 000

25 000

100 000

52 000

150 000

68 000

200 000

77 000

644

ГЛАВА 57

5. Время, затрачиваемое на производство каждого из первых десяти самолетов,
приведено в следующей таблице.
Самолет

Часы

1000

800

730

630

600

560

500

510

Определите общее количество часов, необходимое для производства следующих
десяти самолетов.

Г Л А В А 58

Представление зависимостей
с помощью корреляции

Обсуждаемый вопрос
Каким образом связаны ежемесячные доходы от акций Microsoft, GE, Intel, GM
и Cisco?

Кривые тренда помогают понять, как две переменные связаны между собой. Однако мы часто имеем дело более чем с двумя переменными. Вычисление корреляции между любыми парами переменных позволяет увидеть совместное движение
вверх и вниз значений нескольких переменных.
Корреляция (обычно обозначаемая r) между двумя переменными (назовем их x
и y) — это мера степени линейной зависимости между x и y. Коэффициент корреляции между любыми двумя переменными всегда лежит в интервале от –1 до +1.
При этом важна не столько точная формула вычисления коэффициента корреляции между двумя переменными, сколько возможность интерпретации корреляции переменных.
Коэффициент корреляции, близкий +1, означает , что между x и y имеется сильная положительная линейная зависимость. Т о есть если x больше среднего, то y
также имеет тенденцию превышать среднее, и если x меньше среднего, y также,
как правило, будет меньше среднего. Если для точек данных подбирается прямая
линия, то это будет прямая линия с положительным угловым коэффициентом, хорошо соответствующая точкам данных. Например, для данных, представленных
на рис. 58.1 (x — количество произведенной продукции, а y — ежемесячная себестоимость продукции), коэффициент корреляции между x и y равен +0,9. (Для
рис. 58.1–58.3 см. файл Correlationexamples.xlsx.)
Коэффициент корреляции, близкий –1, означает наличие между x и y сильной
отрицательной линейной зависимости, то есть если x больше среднего, y, скорее
всего, меньше среднего, и если x меньше среднего, y имеет тенденцию превышать
среднее. Если для данных подбирается прямая линия, то она имеет отрицательный угловой коэффициент и хорошо соответствует точкам данных. Например,
для данных, представленных на рис. 58.2, коэффициент корреляции между x и y
равен –0,9.

646

ГЛАВА 58

Рис. 58.1. Коэффициент корреляции, близкий +1, указывает
на сильную положительную линейную зависимость двух переменных

Рис. 58.2. Коэффициент корреляции, близкий –1,
указывает на сильную отрицательную линейную зависимость двух переменных

Коэффициент корреляции, приблизительно равный 0, свидетельствует о слабой
линейной зависимости между x и y. Другими словами, на основании информации о том, больше x или меньше среднего, невозможно предположить, больше y
своего среднего или меньше. На рис. 58.3 показан график зависимости объемов
продаж в штуках ( y) от опыта продаж в годах ( x). Опыт продаж в годах и объем
продаж в штуках имеют коэффициент корреляции 0,003. Для этого набора данных
средний опыт равен 10 годам. Как видите, у продавцов со стажем более 10 лет
объемы продаж могут быть низкими или высокими. Также можно отметить, что
у продавцов со стажем менее 10 лет объемы продаж также могут быть низкими
либо высокими. Несмотря на то что между годами опыта и объемами продаж существует незначительная линейная зависимость или линейная зависимость вовсе
отсутствует, между годами опыта и объемами продаж имеется сильная нелинейная зависимость (см. подобранную кривую). Коэффициент корреляции не является мерой степени нелинейной зависимости.

Представление зависимостей с помощью корреляции

647

Рис. 58.3. Коэффициент корреляции, близкий 0,
указывает на слабую линейную зависимость между двумя переменными

Ответ на вопрос
?

Каким образом связаны ежемесячные доходы от акций Microsoft, GE,
Intel, GM и Cisco?

В файле Stockcorrel.xlsx (рис. 58.4) содержатся ежемесячные доходы от акций
Microsoft, GE, Intel, GM и Cisco за 1990-е гг. Вы можете использовать корреляции,
чтобы попытаться понять, как связаны между собой движения этих акций.
Для нахождения корреляции (лист Initial Correlation Matrix) между каждой парой
акций на вкладке Данные (Data) в группе Анализ (Analysis) сначала выберите Анализ данных (Data Analysis), а затем в списке — инструмент Корреляция (Correlation).
(Перед использованием этого инструмента необходимо установить пакет анализа. Для этого выберите вкладку ФАЙЛ (File), нажмите Параметры (Options) и затем
выберите Надстройки (Add-Ins) в левой панели. В списке Управление (Manage) выберите Надстройки Excel (Excel Add-Ins) и нажмите Перейти (Go). В открывшемся
диалоговом окне установите флажок Пакет анализа (Analysis ToolPak) и нажмите
OK. Примеры и подробные инструкции см. в главах 43 «Обобщение данных на
гистограммах и диаграммах Парето» и 44 «Обобщение данных с помощью описательной статистики».) Нажмите OK и заполните диалоговое окно Корреляция
(Correlation), как на рис. 58.5.
Самый простой способ задать исходный диапазон состоит в следующем: выберите
левый верхний угол диапазона ( B51), нажмите Ctrl+Shift+→, а затем Ctrl+Shift+↓.
Первая строка диапазона исходных данных содержит метки, поэтому установите
флажок Метки в первой строке (Labels in first row). Введите ячейку H52 как левую
верхнюю ячейку диапазона выходных данных и нажмите OK. Полученный результат представлен на рис. 58.6.
Например, коэффициент корреляции между акциями Cisco и Microsoft составляет
0,513, а коэффициент корреляции между акциями GM и Microsoft — 0,069. Анализ

648

ГЛАВА 58

Рис. 58.4. Ежемесячный доход от акций за 1990-е гг.

Рис. 58.5. Диалоговое окно Корреляция

Рис. 58.6. Корреляционные связи между доходами от акций

показывает, что доходы от акций Cisco, Intel и Microsoft наиболее тесно связаны
между собой. Поскольку коэффициент корреляции между каждой парой этих акций приблизительно равен 0,5, эти акции демонстрируют умеренную положительную зависимость. Другими словами, если одни акции приносят доход выше средне-

Представление зависимостей с помощью корреляции

649

го, вполне вероятно (но необязательно), что другие акции также принесут доход
выше среднего. Поскольку доходы от акций Cisco, Intel и Microsoft тесно связаны
с капиталовложениями в технологии, их довольно сильная корреляция не является
неожиданной. Из рисунка видно, что ежемесячные доходы от акций Microsoft и GM
практически не коррелируют. То есть если акции Microsoft поднимутся выше обычного, это не поможет нам узнать, «выступят» ли акции GM лучше или хуже. Опять
же это неудивительно, поскольку GM не является высокотехнологичной компанией и поэтому более восприимчива к колебания делового цикла.

Заполнение корреляционной матрицы
Как вы видите в этом примере, Excel оставил некоторые ячейки корреляционной
матрицы пустыми. Например, коэффициент корреляции между акциями Microsoft
и GE (равный коэффициенту корреляции между акциями GE и Microsoft) опущен. Если вы хотите заполнить всю корреляционную матрицу, выделите матрицу,
щелкните правой кнопкой мыши и выберите команду Копировать (Copy). Щелкните правой кнопкой мыши по свободной части листа и выберите Специальная вставка (Paste Special). В диалоговом окне Специальная вставка (Paste Special) установите
флажок Транспонировать (Transpose). Строки и столбцы данных поменяются местами. Теперь выделите транспонированную матрицу, щелкните правой кнопкой
мыши и выберите команду Копировать (Copy). Выделите исходную корреляционную матрицу, щелкните правой кнопкой мыши и снова выберите Специальная
вставка (Paste Special). В диалоговом окне Специальная вставка (Paste Special) установите флажок Пропускать пустые ячейки (Skip Blanks) и нажмите OK. Транспонированные данные будут скопированы в исходную матрицу, за исключением пустых
ячеек. Полная корреляционная матрица показана на рис. 58.7.

Рис. 58.7. Полная корреляционная матрица

650

ГЛАВА 58

Функция КОРРЕЛ
В качестве альтернативы инструменту Корреляция (Correlation) из пакета анализа
можно использовать функцию КОРРЕЛ (CORREL). Например, введя в ячейку I49
формулу =КОРРЕЛ(E52:E181;F52:F181) (на листе Complete Matrix), мы также получим коэффициент корреляции ежемесячного дохода от акций Cisco (показанного
в столбце F) и дохода от акций GM (показанного в столбце E), равный 0,159.

Связь между коэффициентом корреляции и R2
В главе 55 «Оценка линейных зависимостей» вы вычислили значение R2 для количества произведенной продукции и ежемесячных эксплуатационных расходов — 0,688. Как это значение связано с коэффициентом корреляции количества
произведенной продукции и ежемесячных эксплуатационных расходов? Корреляционные связи между двумя наборами данных — это просто следующая формула для линии тренда:

В этой формуле вы выбираете знак перед квадратным корнем такой же, как знак
наклона линии тренда. Таким образом, коэффициент корреляции количества произведенной продукции и ежемесячных эксплуатационных расходов для данных
из главы 53 равен

Корреляция и регрессия к среднему
Возможно, вам знакомо выражение «регрессия к среднему». По сути оно означает, что прогнозируемое значение зависимой переменной будет в некотором смысле ближе к среднему значению этой переменной, чем независимая переменная.
Пусть вам требуется спрогнозировать зависимую переменную y по независимой
переменной x. Если x равно k стандартных отклонений от среднего, прогнозом для
y будет rk стандартных отклонений от среднего. (Здесь r — коэффициент корреляции между x и y.) Поскольку значение r находится в пределах между –1 и +1,
это означает, что y имеет меньшее стандартное отклонение от среднего, чем x. Это
истинное определение регрессии к среднему . Интересное применение регрессии
к среднему см. в задании 5.

Задания
Данные к заданиям 1–3 находятся в файле Ch56data.xlsx.
1. На листе Problem 1 указано количество автомобилей, каждый день запаркованных как на открытой, так и закрытой автостоянке возле школы У ниверсите-

Представление зависимостей с помощью корреляции

651

та Индианы. Вычислите коэффициент корреляции и объясните корреляцию
между количеством автомобилей, запаркованных на открытой и закрытой
стоянках.
2. На листе Problem 2 указаны ежедневные объемы продаж (в долларах) для лазерных принтеров, картриджей и канцелярских товаров. Вычислите коэффициенты корреляции и объясните корреляцию между этими величинами.
3. На листе Problem 3 указаны годовые доходы по акциям, казначейским векселям и облигациям. Вычислите коэффициенты корреляции и объясните корреляцию между годовыми доходами по этим трем классам инвестиций.
И еще два задания.
4. Файл Dow.xlsx содержит ежемесячные данные о доходах по 30 акциям, входящим в индекс Доу — Джонса. Найдите коэффициенты корреляции для всех
акций. Затем для каждого пакета акций с помощью условного форматирования выделите три пакета, наиболее сильно коррелирующих с ним. (Разумеется, корреляция пакета с самим собой не должна быть выделена.)
5. Команды НФЛ проводят 16 игр за регулярный сезон. Допустим, стандартное
отклонение от количества выигранных игр для всех команд равно 2, и коэффициент корреляции между количеством выигранных командой игр в двух
подряд идущих сезонах равен 0,5. Если команда ведет в регулярном сезоне со
счетом 12:4, каков наилучший прогноз для количества игр, которые команда
выиграет в следующем сезоне?

ГЛ А В А 59

Введение во множественную
регрессию

Обсуждаемые вопросы
Завод выпускает три продукта. Как спрогнозировать эксплуатационные расходы
завода на основе количества произведенной продукции?
Насколько точны мои прогнозы ежемесячных расходов на основе количества
произведенной продукции?
Множественную регрессию можно запустить командой Анализ данных. Существует ли способ запустить регрессионный анализ без этой команды и поместить результаты регрессии на тот же лист, где находятся данные?

Ответы на вопросы
?

Завод выпускает три продукта. Как спрогнозировать эксплуатационные
расходы завода на основе количества произведенной продукции?

В главах 56–58 я описал, как в Microsoft Excel с помощью кривой тренда спрогнозировать одну переменную (y, или зависимую переменную) по другой переменной
(x, или независимой переменной). Однако довольно часто бывает так, что значение
зависимой переменной нужно предсказать на основе нескольких независимых
переменных (x1, x2, …, xn). В таких случаях оценить зависимость можно либо с помощью инструмента Регрессия в пакете Excel Анализ данных (Data Analysis), либо
с помощью функции ЛИНЕЙН (LINEST).
Множественная регрессия предполагает, что зависимость между y и x1, x2, …, xn
имеет следующий вид:
y = константа + B1x1 + B2x2 + … + Bnxn.
Excel вычисляет значения константа, B1, B2, …, Bn для составления наиболее точного (в смысле минимизации суммы квадратичных ошибок) прогноза по этому
уравнению. Работа множественной регрессии продемонстрирована в следующем
примере.
Лист Data в файле Mrcostest.xlsx (рис. 59.1) содержит эксплуатационные расходы
завода за 19 месяцев, а также количество произведенного продукта A, продукта B
и продукта C в каждом месяце.

Введение во множественную регрессию

653

Рис. 59.1. Данные для прогноза по ежемесячным эксплуатационным расходам

Требуется найти лучший прогноз для ежемесячных эксплуатационных расходов
в следующем виде (называемом Вид 1):
ежемесячные эксплуатационные расходы = константа + B1*(количество A) +
+ B2*(количество B) + B3*(количество C).
Анализ данных (Data Analysis) в Excel позволяет найти уравнение вида, наиболее точно соответствующее данным. На вкладке Данные (Data) в группе Анализ (Analysis)
щелкните на Анализ данных (Data Analysis) и затем выберите инструмент Регрессия
(Regression). Заполните диалоговое окно Регрессия (Regression), как на рис. 59.2.

Рис. 59.2. Диалоговое окно Регрессия

654

ГЛАВА 59

Входной интервал Y (B3:B22 в этом примере) содержит зависимую переменную
или данные (включая метку Расходы), которые требуется предсказать.
Входной интервал X (C3:E22) содержит данные или независимые переменные
(включая метки Количество A, Количество B и Количество C), которые требуется
использовать в прогнозе. В Excel установлено ограничение — 15 независимых
переменных, которые должны находиться в смежных столбцах.
Поскольку оба входных интервала X и Y включают метки, я установил флажок
Метки (Labels).
Я выбрал поместить выходные данные на новый лист с именем Регрессия.
При установленном флажке Остатки (Residuals) для каждого наблюдения вычисляется прогноз (по уравнению Вида 1) и остатки, равные разности между
фактическими и прогнозируемыми расходами.
ПРИМЕЧАНИЕ
Если Пакет анализа (Analysis ToolPak) еще не установлен, на вкладке Файл (File) выберите команду Параметры (Options) и затем Надстройки (Add-Ins). В списке Управление (Manage) выберите Надстройки Excel (Excel Add-ins) и нажмите Перейти (Go).
Установите флажок Пакет анализа (Analysis ToolPak) и нажмите OK.

Нажав OK в диалоговом окне Регрессия (Regression), на листе Регрессия появятся
выходные данные, показанные на рис. 59.3 и 59.4.

Рис. 59.3. Первоначальный вывод итогов множественной регрессии

Какое уравнение прогноза самое лучшее? В столбце
Коэффициенты (ячейки
B16:B20) показано, что наилучшим уравнением Вида 1, по которому можно прогнозировать ежемесячные эксплуатационные расходы, является следующее:

Введение во множественную регрессию

655

прогнозируемые расходы = 35102,90 + 2,07*(количество A) + 4,18*(количество B) +
+ 4,79*(количество C).

Рис. 59.4. Первоначальный вывод остатков множественной регрессии

Возникает вопрос: какие независимые переменные полезны для прогноза ежемесячных эксплуатационных расходов? В конце концов, если в качестве независимой переменной выбрать количество игр, выигранных командой «Сиэтл Маринерс» за месяц, можно ожидать, что эта переменная окажет небольшое влияние
на прогноз ежемесячных эксплуатационных расходов. При запуске регрессионного анализа каждая независимая переменная имеет p-значение между 0 и 1.
Любая независимая переменная с p-значением (см. ячейки E16:E20), меньшим
или равным 0,05, считается приемлемой для прогноза зависимой переменной.
Таким образом, чем меньше p-значение, тем выше прогностическая способность
независимой переменной. Здесь три независимых переменных имеют следующие p-значения: 0,23 (для количества произведенного продукта A), 0,025 (для
продукта B) и 0,017 (для продукта C). Эти p-значения можно интерпретировать
следующим образом.
Если вы используете показатели B и C для предсказания ежемесячных эксплуатационных расходов, то получаете 77%-ную вероятность (1 – 0,23), что показатель A увеличит прогностическую силу.
Если вы используете показатели A и C для предсказания ежемесячных эксплуатационных расходов, то получаете 97,5%-ную вероятность (1 – 0,025), что
показатель B увеличит прогностическую силу.
Если вы используете показатели A и B для предсказания ежемесячных эксплуатационных расходов, то получаете 98,3%-ную вероятность (1 – 0,17), что
показатель C увеличит прогностическую силу.

656

ГЛАВА 59

p-значения показывают, что показатель A незначительно увеличивает прогностическую силу для продуктов B и C. Т о есть если количество продуктов B и C известно, ежемесячные эксплуатационные расходы можно предсказать почти с той
же точностью, что и в случае включения A в качестве независимой переменной.
Следовательно, показатель A как независимую переменную можно удалить и использовать для прогноза только показатели B и C. Скопируйте данные на лист
Столбец A удален и удалите столбец Количество A (столбец C). Измените параметр
Входной интервал X (C3:D22) — см. рис. 59.2. На новом листе, например с именем
Без столбца А, появятся результаты регрессии (рис. 59.5 и 59.6).

Рис. 59.5. Вывод итогов множественной регрессии без показателя A
как независимой переменной

Рис. 59.6. Вывод остатка без показателя A как независимой переменной

Как видите, показатели B и C имеют очень низкие p-значения (0,002 и 0,007 соответственно). Эти значения показывают , что обе независимые переменные об-

Введение во множественную регрессию

657

ладают значительной прогностической силой. Новые коэффициенты в столбце B
позволяют прогнозировать ежемесячные эксплуатационные расходы с помощью
следующего уравнения:
прогнозируемые ежемесячные эксплуатационные расходы = 35475,3 + 5,32*(показатель B) + 5,42*(показатель C).

Насколько точны мои прогнозы ежемесячных расходов на основе количества произведенной продукции?

В выходных данных регрессии в ячейкеB5 листа Без столбца А (см. рис. 59.5) значение R2 равно 0,61. Такое R2 означает, что вместе показатели B и C объясняют 61%
отклонений в ежемесячных эксплуатационных расходах. Обратите внимание, что
в первоначальной регрессии, включавшей показатель A в качестве независимой
переменной, R2 было равно 0,65. То есть добавление показателя A как независимой переменной объясняет только 4% отклонений в ежемесячных эксплуатационных расходах. Такая незначительная разница согласуется с решением удалить
показатель A из списка независимых переменных.
В выходных данных регрессии в ячейке B7 листа Без столбца А стандартная
ошибка для регрессии с показателями B и C в качестве независимых переменных равна 1274. Можно ожидать, что примерно 68% множественных регрессионных прогнозов будут точными в пределах одной стандартной ошибки и 95%
прогнозов будет точным в пределах двух стандартных ошибок. Любой прогноз,
отличающийся от фактического значения более чем на две стандартные ошибки,
считается выбросом. Таким образом, если прогнозируемые эксплуатационные
расходы по ошибке превышают $2548 (2 × 1274), такое наблюдение следует считать выбросом.
В части выходных данных с остатками, показанной ранее на рис. 59.6, для каждого
наблюдения приведены предсказанные расходы и остатки, эквивалентные разности фактических и предсказанных расходов. Например, для первого наблюдения
предсказанные расходы составляют $43 381,10. Остаток $1057,95 означает , что
прогноз был ниже фактических расходов на $1057,95.
Множественную регрессию можно запу стить командой Анализ данных.
Существует ли способ запустить регрессионный анализ без этой команды
и поместить результаты регрессии на тот же лист, где находятся данные?

Для вставки результатов регрессионного анализа прямо в книгу можно применить функцию Excel ЛИНЕЙН (LINEST). При наличии m независимых переменных
начните с выделения пустого диапазона ячеек, состоящего из пяти строк и m + 1
столбцов, где будут храниться резуль таты работы функции ЛИНЕЙН. Для этой
цели на листе Столбец A удален я использовал диапазон F5:H9.
Синтаксис функции: ЛИНЕЙН(известные_значения_Y; известные_значения_X; ИСТИНА; ИСТИНА). Если указать для третьего аргумента ЛОЖЬ, Excel решит уравнение
без свободного члена. Если указать ЛОЖЬ для четвертого аргумента, многие вы-

658

ГЛАВА 59

числения регрессионного анализа будут опущены, и функция ЛИНЕЙН возвратит
только уравнение множественной регрессии.
Выделите на листе Столбец A удален диапазон необходимого размера (в данном
примере F5:H9) и введите формулу =ЛИНЕЙН(B4:B22; C4:D22; ИСТИНА; ИСТИНА).
В этот момент не нажимайте Enter! Поскольку функция ЛИНЕЙН является функцией, возвращающей массив, для правильной работы функции нажмите
Enter,
удерживая Ctrl+Shift. В выделенном диапазоне появятся резуль таты, показанные
на рис. 59.7. (См. лист Столбец A удален.)

Рис. 59.7. Множественная регрессия с функцией ЛИНЕЙН

В строке 5 вы найдете уравнение прогноза (коэффициенты читаются справа налево, начиная с начальной ординаты):
прогнозируемые ежемесячные расходы = 35 475,3 + 5,32*(показатель B) +
+ 5,43*(показатель C).

Строка 6 содержит стандартные ошибки для каждого вычисленного коэффициента, но они не слишком важны. Ячейка F7 содержит значение R2 — 0,61, а в ячейке G7 находится стандартная ошибка регрессии — 1274. Строки 8 и 9 содержат
менее важную информацию (F-статистику, степени свободы, сумму квадратов регрессии и сумму квадратов остатков).
ПРИМЕЧАНИЕ
Задания по множественной регрессии находятся в конце главы 61 «Моделирование
нелинейных характеристик и взаимосвязей».

Г Л А В А 60

Включение качественных
факторов во множественную
регрессию

Обсуждаемые вопросы
Как предсказать квартальные продажи автомобилей в США?
Как предсказать президентские выборы в США?
Какая функция Excel позволяет составить прогноз по уравнению множественной
регрессии?

В первом примере с использованием множественной регрессии (глава 59) ежемесячные эксплуатационные расходы завода были спрогнозированы на основе
объемов производства каждого продукта. Поскольку объемы производства можно
подсчитать точно, объемы A, B и C возможно использовать как независимые количественные переменные. Однако во многих ситуациях независимые переменные
быстро определить количественно невозможно. В данной главе мы посмотрим,
как можно включить качественные факторы (например, сезонность, половую принадлежность, политическую партию) во множественный регрессионный анализ.

Ответы на вопросы
?

Как предсказать квартальные продажи автомобилей в США?

Допустим, вы хотите спрогнозировать квартальные продажи автомобилей в США
с целью определить влияние квартала года на объемы продаж. Мы будем пользоваться данными из файла Autotemp.xlsx на листе Data (рис. 60.1). Объемы продаж
указаны в тысячах штук, а ВНП — в миллиардах долларов.
Можно было бы попытаться определить независимую переменную как 1 для первого квартала, 2 для второго квартала и т. д. К сожалению, при таком подходе четвертый квартал превосходил бы по эффективности первый квартал в четыре раза,
что не может быть правдой. Квартал года — это независимая качественная переменная. При моделировании независимой качественной переменной вы создаете
независимую переменную, называемую фиктивной переменной, для всех возможных значений качественной переменной, кроме одного. (Невключаемое значение

660

ГЛАВА 60

выбирается произвольным образом. В данном примере я предпочел опустить четвертый квартал.) Фиктивные переменные показывают, какое значение качественной переменной имеет место.

Рис. 60.1. Данные о продажах автомобилей

Таким образом, фиктивные переменные для первого, второго и третьего кварталов
обладают следующими свойствами:
фиктивная переменная для первого квартала равна 1, если квартал является
первым кварталом, и равна 0 в противном случае;
фиктивная переменная для второго квартала равна 1, если квартал является
вторым кварталом, и равна 0 в противном случае;
фиктивная переменная для третьего квартала равна 1, если квартал является
третьим кварталом, и равна 0 в противном случае.
Наблюдения для четвертого квартала будут идентифицироваться по тому факту ,
что фиктивные переменные для кварталов с первого по третий равны 0. Т еперь
понятно, почему не нужна фиктивная переменная для четвертого квартала. Если
включить в регрессию фиктивную переменную для четвертого квартала как независимую, Excel возвратит сообщение об ошибке, поскольку если между любым
набором независимых переменных существует точная линейная зависимость, то
в ходе множественной регрессии Excel должен выполнить математический эквивалент деления на 0 (что невозможно). Если в этом примере включить фиктивную

Включение качественных факторов во множественную регрессию

661

переменную для четвертого квартала, каждая точка данных будет удовлетворять
следующей точной линейной зависимости:
(фиктивная переменная 1) + (фиктивная переменная 2) + (фиктивная переменная 3) +
+ (фиктивная переменная 4) = 1.

ПРИМЕЧАНИЕ
Точная линейная зависимость возникает в случае, если существуют константы c0, c1,
…, cN, такие, что для каждой точки данных c0 + c1x1 + c2x2 + … + cNxN = 0. Здесь x1,
…, xN — значения независимых переменных.

Чтобы создать фиктивную переменную для первого квартала, я скопировал формулу =ЕСЛИ(B12=1;1;0) из G12 в G13:G42. Эта формула помещает в столбец G значение 1, если квартал является первым кварталом, и 0 в противоположном случае. Аналогичным образом я создал фиктивные переменные для второго квартала
(в H12:H42) и третьего (в I12:I42). Результаты показаны на рис. 60.2.

Рис. 60.2. Фиктивные переменные для определения квартала,
в котором произошла продажа

В дополнение к сезонности мы хотим использовать макроэкономические переменные, такие как ВНП (в миллиардах долларов 1986 года), процентные ставки
и уровень безработицы, для прогнозирования продаж автомобилей. Допустим,
вы пытаетесь оценить продажи за второй квартал 1979 г . Поскольку значения

662

ГЛАВА 60

для ВНП, процентной ставки и уровня безработицы на начало второго квартала
в 1979 г. неизвестны, прогнозировать объемы продаж второго квартала 1979 г. на
основе этих величин невозможно. Вместо них для прогнозирования продаж следует использовать значения ВНП, процентной ставки и уровня безработицы с отставанием на один квартал. Например, скопируйте формулу =D11 из J12 в J12:L42
для создания значения с отставанием для ВНП, первой независимой макроэкономической переменной. Диапазон J12:L12 содержит ВНП, уровень безработицы
и процентную ставку для первого квартала 1979 г . (Когда для прогнозирования
зависимой переменной используются значения независимых переменных (или
переменных) с отставанием, независимые переменные называются лаговыми независимыми переменными.)
Теперь можно запустить множественную регрессию. На вкладкеДанные (Data) выберите Анализ данных (Data Analysis). (Необходимо установить пакет Анализ данных.
Инструкции см. в главе 42.) В диалоговом окне Анализ данных (Data Analysis) выберите Регрессия (Regression). Укажите C11:C42 как Входной интервал Y (Input Y Range)
и G11:L42 как Входной интервал X (Input X Range), установите флажок Метки (Labels),
так как строка 11 содержит метки, и флажок Остатки (Residuals). Введите имя нового листа и нажмите OK для получения выходных данных (см. лист Regression
и рис. 60.3–60.5).

Рис. 60.3. Итоги регрессии и таблица дисперсионного анализа для продаж автомобилей

На рис. 60.4 показано, что уравнение (уравнение 1) для прогноза квартальных
продаж автомобилей должно иметь вид:
прогнозируемые квартальные продажи = 3154,7 + 156,833*Q1 + 379,784*Q2 +
+ 203,036*Q3 + 0,174*(ВНП с отставанием в млрд долл.) – 93,83*(уровень
безработицы с отставанием) – 73,91*(процентная ставка с отставанием).

Включение качественных факторов во множественную регрессию

663

Кроме того, из рис. 60.4 видно, что p-значение каждой независимой переменной
не превышает 0,15. На основании этого можно сделать вывод, что все независимые переменные имеют значимое влияние на квартальные продажи автомобилей.
Все коэффициенты в уравнении регрессии интерпретируютсяceteris paribus — при
прочих равных условиях (то есть каждый коэффициент независимой переменной
оказывает влияние после устранения влияния всех других переменных уравнения
регрессии).

Рис. 60.4. Информация о коэффициентах регрессии для продаж автомобилей

Вот пояснения к каждому коэффициенту.
Увеличение в предыдущем квартале ВНП на 1 млрд долларов повышает квартальные продажи автомобилей на 174 шт.
Увеличение в предыдущем квартале уровня безработицы на 1% уменьшает
квартальные продажи автомобилей на 93 832 шт.
Увеличение в предыдущем квартале процентной ставки на 1% уменьшает квартальные продажи на 73 917 шт.
При интерпретации коэффициентов фиктивных переменных следует осознавать,
что они говорят вам о влиянии сезонности на значения, но не говорят о самих качественных переменных. Данные, приведенные на рис. 60.4, можно интерпретировать следующим образом:
продажи первого квартала превышают продажи четвертого квартала на
156 833 шт.;
продажи второго квартала превышают продажи четвертого квартала на
379 784 шт.;
продажи третьего квартала превышают продажи четвертого квартала на
203 036 шт.
Оказалось, что продажи автомобилей выше всего во втором квартале (апрель —
июнь; возврат налогов и наступающее лето) и ниже всего в четвертом квартале
(октябрь — декабрь; зачем покупать новую машину, если посыпание улиц солью
повредит ее?).
На основании рис. 60.3 можно сделать несколько выводов.
Изменение независимых переменных (макроэкономических факторов и сезонности) объясняет 78% изменений зависимой переменной (квартальных продаж).

664

ГЛАВА 60

Стандартная ошибка регрессии составляет 190 524 автомобиля. Можно ожидать, что приблизительно 68% прогнозов дано с точностью до 190 524 шт
.
и примерно 95% прогнозов — с точностью до 381 048 шт. (2 × 190 524).
Для подбора коэффициентов уравнения регрессии использовано 31 наблюдение.
Единственной величиной, представляющей интерес в таблице дисперсионного
анализа на рис. 60.3, является Значимость F (0,00000068). Эта мера подразумевает,
что только в 6,8 случая на 10 000 000 все вместе взятые независимые переменные
непригодны для прогнозирования продаж автомобилей. Таким образом, вы можете быть уверены в том, что независимые переменные пригодны для прогнозирования квартальных продаж. (Подробнее модель дисперсионного анализа (ANOVA;
analysis of variance) представлена в главах 62 и 63.)
Рисунок 60.5 показывает предсказанные продажи и остатки для каждого наблюдения. Например, для второго квартала 1979 г. (первое наблюдение) предсказанные
по уравнению 1 продажи составляют 2728,6 тысячи, а остаток равен 181 411 шт .
(2910 – 2728,6). Обратите внимание, что остатки не превышают 381 000 по абсолютной величине, то есть выбросы отсутствуют.

Рис. 60.5. Остатки для данных продаж автомобилей

Как предсказать президентские выборы в США?

Когда Джеймса Карвилла, советника президента, спросили о том, какие факторы влияют на президентские выборы, он ответил: «Это экономика, дурачок».

Включение качественных факторов во множественную регрессию

665

Экономист Йельского университета Рой Фэйр показал, что Карвилл был прав
в своем убеждении, что состояние экономики сильно влияет на результаты президентских выборов. В качестве зависимой переменной (см. в файле President16.
xlsx лист Data, показанный на рис. 60.6) Фэйр для каждых выборов (с 1916 по
2012 г.) использовал процент голосов, набранных партией, находящейся у власти, с учетом голосования за две партии (без голосов за кандидатов других партий). Для выборов 2016 г. были взяты данные на 2 июля 2016 г., представленные
Фэйром на его веб-сайте. Фэйр попытался предсказать процент голосов правящей партии при голосовании за две партии с помощью следующих независимых
переменных.
Партия у власти. В исходных данных 1 обозначает республиканскую партию
у власти, а 0 — демократическую.
Рост ВНП в процентах в течение первых девяти месяцев года выборов.
Абсолютное значение уровня инфляции в течение первых девяти месяцев
года выборов. Абсолютное значение используется потому, что плох как положительный, так и отрицательный уровень инфляции.
Количество кварталов за последние четыре года, в течение которых наблюдался сильный экономический рост. Сильный экономический рост определяется как ежегодный рост на уровне не менее 3,2%.

Рис. 60.6. Данные президентских выборов

666

ГЛАВА 60

Время пребывания правящей партии у власти. Фэир обозначает один срок
пребывания у власти как 0, два срока как 1, три срока как 1,25, четыре срока
как 1,5 и не менее пяти сроков как 1,75. Это определение подразумевает , что
каждый срок после первого срока пребывания у власти имеет меньше влияния
на результаты выборов, чем первый срок.
Выборы в военное время. Выборы в 1920 г. (Первая мировая война), в 1944 г.
(Вторая мировая война) и в 1948 г. (Вторая мировая война еще не закончилась
в 1945 г.) были определены как выборы в военное время. (Выборы, состоявшиеся во время вьетнамской войны, не считались выборами в военное время.)
В годы войны переменные, связанные с темпами экономического роста и инфляции, признаны неуместными, и для них установлено значение 0.
Действующий президент баллотиру ется на переизбрание. В этом случае
переменная устанавливается в 1; в противном случае она устанавливается в 0.
В 1976 г. Джеральд Форд не считался президентом, баллотирующимся на переизбрание, поскольку он не был избран ни президентом, ни вице-президентом.
Теперь попытаемся на основе данных о выборах с 1916 по 2004 г. составить уравнение множественной регрессии для предсказания резуль татов будущих президентских выборов. Данные о выборах в 2008–2016 гг . были сохранены в качестве
точек проверки достоверности. При подборе уравнения регрессии к данным всегда
желательно иметь какие-либо данные для проверки уравнения регрессии. Так мы
определим, может ли уравнение предсказать непредставленные данные. Любой инструмент прогнозирования, недостаточно хорошо предсказывающий данные, которые были ему недоступны, не следует использовать для прогнозирования будущего.
Для запуска регрессии на вкладке Данные (Data) в группе Анализ (Analysis) выберите Анализ данных (Data Analysis) и затем инструмент Регрессия (Regression). Здесь
как Входной интервал Y (Input Y Range) указаны ячейки C6:C29 и как Входной интервал X (Input X Range) — ячейки E6:L29. Установлен флажок Метки (Labels), так как
строка 6 содержит метки, и флажок Остатки (Residuals). Результаты представлены
справа от данных на листе Data и на рис. 60.7 (начиная с ячейки N14).
Как видно из рис. 60.7, все независимые переменные (если округлить коэффициент для военного времени до 0,10) имеют p-значения не больше 0,10, и все переменные должны быть применены в прогнозах. По данным из раздела коэффициентов
на рис. 60.7 можно определить, что наилучшим уравнением для прогнозирования
результатов выборов является следующее уравнение (уравнение 2):
прогнозируемый процент в президентских выборах = 43,36 + 0,69*рост_ВНП –
– 0,57*абс.уровень_инфляции + 1,1*кварталы_с_ростом – 2,91*время_у_власти +
+ 5,16*республиканцы + 6,34*военное_время + 3,93*президент_баллотируется.

Коэффициенты независимых переменных можно интерпретировать следующим
образом (после устранения влияния всех остальных независимых переменных):
1%-ное увеличение годовых темпов роста ВНП в год выборов означает прибавку 0,69% голосов для правящей партии;

Включение качественных факторов во множественную регрессию

667

Рис. 60.7. Выходные данные регрессии для прогнозирования результатов президентских
выборов

1%-ное отклонение от идеала (нулевой инфляции) означает потерю 0,57% голосов для правящей партии;
каждый квартал с высоким экономическим ростом во время президентского
срока увеличивает долю его голосов на 1,1%;
по отношению к первому сроку пребывания у власти второй срок уменьшает долю голосов за правящую партию на 2,91%, и каждый последующий срок
уменьшает долю голосов еще на 0,25 × (2,91%) = 0,73%;
республиканцы имеют преимущество в 5,16% над демократами;
если США находится в состоянии войны, к прогнозу доли голосов за правящую партию добавляется 6,34%;
если президент баллотируется на переизбрание, необходимо добавить 3,93%
к прогнозу доли голосов за действующего президента.
Остатки согласно уравнению для президентских выборов можно увидеть на
рис. 60.8.
Значение в ячейке O18 показывает, что регрессия объясняет 88,9% отклонений
в доле голосов за партию у власти. Стандартная ошибка 2,72% показывает, что
приблизительно 95% прогноза должно находиться в пределах 2 × 2,72 = 5,44%.
Поскольку допустимый предел погрешности при опросе в день президентских выборов составляет приблизительно 3%, просто удивительно, насколько хорошо работает модель, даже не учитывающая качества кандидатов! Как видно изрис. 60.8,
единственный выброс был в 1992 г. на выборах Буш — Клинтон, в которых Клинтон набрал на 5,41% голосов больше, чем ожидалось. Это может быть связано
с тем, что Клинтон умел хорошо подать себя.

668

ГЛАВА 60

Рис. 60.8. Остатки согласно уравнению для президентских выборов

Какая функция Excel позволяет составить прогноз по уравнению множественной регрессии?

Довольно утомительно делать прогнозы по уравнению 2, но можно упростить
получение прогнозов из множественной регрессии с помощью функции Excel
ТЕНДЕНЦИЯ (TREND). Для этого даже не требуется запускать регрессию с помощью
команды Анализ данных (Data Analysis).
Для иллюстрации работы функции ТЕНДЕНЦИЯ прогнозирование выборов с 1916
по 2016 г. описано с использованием только данных для выборов с 1916 по 2004 г.
См. лист Trend Function и рис. 60.9. Сначала выделите диапазон ячеек (в этом примере L7:L32), куда должны быть помещены прогнозы. Установите курсор в первую ячейку этого диапазона (ячейку L7) и введите формулу =ТЕНДЕНЦИЯ(C7:C29;
E7:K29; E7:K32; ИСТИНА). Затем нажмите Ctrl+Shift+Enter. Выбор строк 7–29 в первых двух аргументах функции ТЕНДЕНЦИЯ обеспечивает построение уравнения
регрессии на основе данных по 1916–2004 гг.
На рис. 60.9 в ячейках L7:L32 представлен сгенерированный прогноз резуль татов
выборов. Обратите внимание, что в 2008 г . партия у власти (республиканцы) получила на 1,8% меньше, чем по прогнозу; в 2012 г. правящие демократы получили
на 3,0% больше, чем по прогнозу . Хотя результаты опросов и оценки экспертов
предсказывали Х. Клинтон безоговорочную победу в 2016 г., наша модель говорила, что Клинтон получит на голосовании только 45%. В реальности она получила
51% на двухэтапном народном голосовании на прямых выборах!

Включение качественных факторов во множественную регрессию

669

Рис. 60.9. Прогноз для всех прошедших выборов

Функция ТЕНДЕНЦИЯ является функцией, возвращающей массив. Более подробное обсуждение этих функций см. в главе 91 «Формулы массива и функции, возвращающие массив». А здесь приведена некоторая базовая информация о функциях, возвращающих массив.
Перед определением функции, возвращающей массив, необходимо определить
диапазон ячеек, в который будет размещен результат работы этой функции.
Для выполнения вычислений необходимо нажать не Enter, а сочетание клавиш
Ctrl+Shift+Enter, завершающее ввод функции, возвращающей массив.
После ввода функции, возвращающей массив, при выборе какой-либо ячейки
из тех, в которых размещены резуль таты этой функции, вы увидите в строке
формул формулу в фигурных скобках. Эти скобки указывают на то, что результат в этой ячейке получен в резуль тате работы функции, возвращающей
массив.
Никакие данные из диапазона, созданные функцией, возвращающей массив,
не могут быть изменены.
Задания по множественной регрессии приведены в конце главы 61.

ГЛ А В А 61

Моделирование нелинейных
характеристик и взаимосвязей

Обсуждаемые вопросы
Когда говорят, что независимая переменная оказывает нелинейное воздействие
на зависимую переменную, что это означает?
Когда говорят, что между воздействиями двух независимых переменных на зависимую переменную существует взаимосвязь, что это означает?
Как выполнить проверку на наличие нелинейности и взаимосвязи в регрессии?

Ответы на вопросы
?

Когда говорят, что независимая переменная оказывает нелинейное воздействие на зависимую переменную, что это означает?

Зачастую независимая переменная воздействует на зависимую переменную нелинейным образом. Например, при прогнозе продаж продукта по уравнению вида
Продажи = 500 – 10 × Цена цена влияет на объем продаж линейно. Это уравнение
показывает, что при повышении цены на единицу (для любого уровня цен) объем продаж уменьшается на 10 единиц. Если соотношение между объемом продаж
и ценой определяется уравнением Продажи = 500 + 4 × Цена – 0,40 × Цена2, цена
и объем продаж связаны нелинейно. Как показано на рис. 61.1, чем больше повышается цена, тем сильнее падает спрос (см. листNonlinearity в файле Interactions.xlsx).

Рис. 61.1. Нелинейная зависимость между спросом и ценой

Моделирование нелинейных характеристик и взаимосвязей

671

Коротко говоря, если изменение зависимой переменной, вызванное изменением
на единицу независимой переменной, не является константой, между независимой и зависимой переменными имеется нелинейная зависимость.

Когда говорят, что между воздействиями двух независимых переменных
на зависимую переменную существует взаимосвязь, что это означает?

Если влияние одной независимой переменной на зависимую переменную зависит
от значения другой независимой переменной, можно сказать, что две независимые
переменные проявляют взаимосвязь. Рассмотрим для примера прогноз продаж в зависимости от цены и суммы, затраченной на рекламу . Если эффект от изменения
расходов на рекламу значим при низкой цене и незначим при высокой цене, цена
и расходы на рекламу проявляют взаимосвязь. Если эффект от изменения расходов
на рекламу одинаков при любой цене, затраты на рекламу и цена не связаны.

Как выполнить проверку на наличие нелинейности и взаимосвязи в регрессии?

Чтобы проверить, имеет ли независимая переменная нелинейный эффект на зависимую переменную, просто добавьте в уравнение регрессии член, равный квадрату независимой переменной. Если квадратный член имеет небольшое p-значение
(меньше 0,15), это доказывает наличие нелинейной зависимости.
Для проверки наличия взаимосвязи между двумя независимыми переменными
добавьте в уравнение регрессии член, равный произведению независимых переменных. Если член имеет небольшое p-значение (меньше 0,15), это является доказательством взаимосвязи.
Чтобы вы лучше поняли, я попытаюсь определить, как половая принадлежность
и опыт влияют на размер оклада в небольшой производственной компании. Для
каждого сотрудника в базе хранятся приведенные ниже данные. Информацию см.
на листе Data в файле Interactions.xlsx (рис. 61.2).
Годовая зарплата (в тысячах долларов).
Опыт работы на производстве (в годах).
Пол (1 — женский, 0 — мужской).
Используем эти данные, чтобы спрогнозировать зарплату (зависимую переменную) в зависимости от опыта (Exp) и от пола (Gender). Для проверки нелинейности
влияния опыта на зарплату я добавил член Опыт в квадрате, скопировав формулу
=B2^2 из D2 в D3:D98. На листе Data замените D2 формулой =B2^2. Затем скопируйте D2 в D3:D98. Для проверки наличия значимого взаимодействия между опытом и полом я добавил член Опыт*Пол, скопировав формулу =B2*C2 из E2 в E3:E98.
Замените E2 на формулу =B2*C2. В диалоговом окне Регрессия (Regression) я указал
A1:A98 как Входной интервал Y (Input Y Range) и B1:E98 как Входной интервал X (Input
X Range). Установив флажок Метки (Labels) и нажав OK, я запустил регрессионный
анализ и получил результаты, как на рис. 61.3.

672

ГЛАВА 61

Рис. 61.2. Данные для прогнозирования зарплаты в зависимости от пола и опыта

Рис. 61.3. Результаты регрессии для теста на нелинейность и взаимодействие

Как видно из рисунка, пол не является значимым ( p-значение для него больше
0,15). Все остальные независимые переменные — значимые (т. е. имеют p-значение
не больше 0,15). Не оказывающую влияние переменную пола можно удалить из
независимых переменных. Для этого я скопировал данные на новый лист с именем FinalRegression, щелкнул правой кнопкой мыши на вкладке листа, выбралПереместить или скопировать (Move Or Copy) и в диалоговом окне установил флажок

Моделирование нелинейных характеристик и взаимосвязей

673

Создать копию (Create A Copy). После удаления столбца Пол можно получить результаты регрессии, как на листе FinalRegression и на рис. 61.4.

Рис. 61.4. Результаты регрессии после удаления незначимой переменной Пол

Теперь все независимые переменные являются значимыми (имеют p-значение не
больше 0,15). Следовательно, можно предсказать зарплату (в тысячах долларов)
по следующему уравнению (уравнение 3):
прогнозируемая зарплата = 59,06 + 0,78*(опыт) – 0,033*(опыт2) – 2,07*(опыт*пол).

Отрицательный член (опыт2) показывает, что каждый дополнительный год опыта
все меньше влияет на зарплату. То есть опыт оказывает нелинейное воздействие
на зарплату. Фактически эта модель говорит о том, что после 13 лет работы каждый дополнительный год опыта на самом деле уменьшает зарплату.
Напомню, что переменная Пол равна 1 для женщин и 0 для мужчин. После подстановки 1 в уравнение 3 зарплату для женщин можно спрогнозировать следующим
образом:
прогнозируемая зарплата = 59,06 + 0,78*(опыт) – 0,033*(опыт2) – 2,07(опыт*1) =
= 59,06 – 0,033*(опыт2) – 1,29*(опыт).

Для мужчин (после подстановки пол=0) получится следующее уравнение:
прогнозируемая зарплата = 59,06 + 0,78*(опыт) – 0,033*(опыт2) – 2,07(опыт*0) =
= 59,06 + 0,78*(опыт) – 0,033*(опыт2).

Таким образом, взаимосвязь между полом и опытом показывает , что каждый
дополнительный год опыта работы приносит женщинам выгоды в среднем на
0,78 – (–1,29) = $2070 меньше, чем мужчинам. Это указывает на несправедливое
отношение к женщинам.

674

ГЛАВА 61

Задания к главам 59–61
Компания Fizzy Drugs должна оптимизировать размер выработки от важного химического процесса. Компания считает , что количество произведенной продукции в фунтах при каждом запуске процесса зависит от размера используемого
резервуара, давления и температуры. Привлеченные к решению задачи ученые
полагают, что влияние одной переменной может зависеть от значений других
переменных. Резервуар должен иметь объем 1,3–1,5 м 3, кроме того, необходимо
поддерживать давление между 4 и 4,5 мм рт . ст. и температуру 22–30 °C. У ченые
провели эксперименты для нижних и верхних уровней трех контрольных переменных, результаты которых представлены в файле Fizzy.xlsx. Используйте данные
из этого файла для ответа на задания 1–3.
1. Определите связь между количеством продукции, объемом резервуара, температурой и давлением.
2. Рассмотрите взаимосвязь между давлением, объемом резервуара и температурой.
3. Какие значения температуры и давления и какой объем резервуара вы бы рекомендовали?
Еще несколько заданий по множественной регрессии.
4. В супермаркете Mr. D’s в течение 12 недель подряд проводились наблюдения
за продажами (количество покупок) консервированных томатов. (См. файл
Grocery.xlsx.) Каждую неделю отслеживались следующие данные.
• Во все ли тележки была положена реклама консервированных томатов?
• Каждому ли покупателю был вручен скидочный купон на консервированные томаты?
• Была ли снижена цена (нет, на 1 или 2 цента)?
На основе этих данных определите, как перечисленные факторы влияют на
продажи. Предскажите продажи консервированных томатов для недели, на
которой в тележки были положены рекламные листовки, покупателям предлагался купон и цена на томаты была снижена на 1 цент.
5. В файле Countryregion.xlsx для нескольких слаборазвитых стран/регионов содержатся следующие данные:
• детская смертность;
• уровень грамотности взрослого населения;
• процент учеников, закончивших начальную школу;
• ВНП на душу населения.
Исходя из этих данных, создайте уравнение для прогнозирования детской
смертности. Имеются ли в этом наборе данных выбросы? Проинтерпретируйте коэффициенты полученного уравнения. В пределах каких значений 95%
прогнозов по детской смертности должны быть точными?

Моделирование нелинейных характеристик и взаимосвязей

675

6. В файле Baseball96.xlsx содержатся следующие данные: засчитанные пробежки, одинарные, двойные, тройные удары, хоум-раны, кражи базы и уолки для
каждой команды Главной лиги бейсбола в сезоне 1996 г . На основе этих данных определите влияние одиночных и двойных ударов, а также других действий на пробежки.
7. В файле Cardata.xlsx приведена следующая информация для 392 моделей автомобилей:
• количество цилиндров;
• объем двигателя;
• мощность в лошадиных силах;
• вес;
• разгон;
• количество миль на галлон горючего.
Определите уравнение для прогнозирования количества миль на галлон горючего. Почему все независимые переменные не являются значимыми?
8. В файле Priceads.xlsx находятся данные о еженедельных объемах продаж продукта, а также о цене продукта и расходах на рекламу. Объясните, как реклама
и цена продукта влияют на объемы продаж.
9. Файл Teams.xlsx содержит следующие данные: засчитанные пробежки, хитбай-питчи, уолки, одиночные, двойные, тройные удары и хоум-раны для
команд Главной лиги бейсбола в сезонах 2000–2006 гг.
• Исходя из этих данных, постройте модель, предсказывающую на основе
статистики ударов, сколько очков получит команда за пробежки.
• Насколько точно эта модель предсказывает количество засчитанных пробежек для команды за сезон?
• Предположим, что команда имеет положительный остаток, превышающий
в три раза стандартную ошибку регрессии. Что могло привести к такому
результату?
10. Процент занятия базы (OBP) вычисляется как (хит-бай-питч + уолк + хит)/
(выход на биту + хит-бай-питч + уолк + сакрифайс флай). Процент мощности
отбивания (SLG) равен количеству баз (хоум-ран дает очки за четыре базы,
тройной удар — за три, двойной удар — за две и одинарный — за одну), деленному на количество выходов на биту. В файле OPSslug.xlsx содержится информация об ударах для команд Главной лиги в сезонах 2000–2006 гг.
На основе этих данных создайте модель для прогнозирования засчитанных
пробежек по OBP и SLG команды.
• Какую из моделей, эту или модель из задания 9, можно порекомендовать
для прогнозирования засчитанных пробежек?
• Как с помощью этой модели можно определить способность к отбиванию
у отдельных игроков?

676

ГЛАВА 61

• Почему можно отнестись скептически к вычислению с помощью этой модели способности к отбиванию у такого действительно великого хиттера,
как Альберт Пухолс (Albert Pujols) из «Сент-Луис Кардиналс»?
11. Файл NFLinfo.xlsx содержит следующие данные для команд НФЛ в сезонах
2003–2006 гг.:
• Margin (преимущество) — количество очков, на которое команда опережает своего соперника;
• NYP/A — набранные ярды относительно попыток выполнить пас;
• YR/A — набранные ярды относительно попыток выполнить вынос;
• DNYP/A — набранные противником ярды относительно попыток выполнить пас;
• DYR/A — набранные противником ярды относительно попыток выполнить вынос;
• TO — перехваты, выполненные командой;
• DTO — перехваты, выполненные командой противника.
Показывают ли эти данные, что больше влияет на успех команды: эффективный пас или вынос?
В какое количество очков приблизительно обходится команде перехват мяча?
Многие футбольные болельщики считают, что для организации паса необходим эффективный вынос. Соответствуют ли данные такой точке зрения?
12. В файле Qbinfo.xlsx перечислены рейтинги знаменитых квотербеков НФЛ
в сезоне 2009 г. Рейтинг квотербеков основан на проценте завершенных пасов;
проценте пасов, приведших к тачдаунам; процентах набранных ярдов относительно попыток выполнить пас и проценте перехваченных пасов.
• Создайте формулу прогнозирования рейтинга квотербека на основе его
статистики за сезон.
• Насколько точны прогнозы?
13. В файле Problem13data.xlsx приведены еженедельные данные о продаже печенья в супермаркете. Кроме того, приведены еженедельные данные для каждого продукта о наличии скидки и/или о его рекламной выкладке. Объясните,
как цена и рекламная выкладка влияют на продажи печенья. Между какими
значениями, _____ и _____, должны находиться объемы продаж с точностью
95% в неделю, когда продукт находится на рекламной выкладке и цена на него
снижена?
14. Фармкомпании требуется определить, как давление, температура и размер
резервуара влияют на объем выхода нового лекарства. Даны значения выхода
для нескольких партий этого нового лекарства, а также давление, температура
и размер резервуара для каждой партии. Определите уравнение, объясняющее, как эти факторы влияют на выход. Если процесс проходит при высоком

Моделирование нелинейных характеристик и взаимосвязей

677

давлении, низкой температуре и в большом резервуаре, можно с вероятностью 95% утверждать, что выход будет между _____ и _____. Можете игнорировать нелинейности и взаимодействия.
15. В файле Problem15data.xsls приведены данные о количестве открыток, проданных аптекой в течение нескольких кварталов, и средняя цена за открытки
в течение квартала. Определите, как цена и сезонность влияют на продажу
открыток. Если в четвертом квартале вы продаете открытки по цене 4 доллара
за штуку, то с вероятностью в 95% будет продано от _____ до _____ открыток.
16. В файле Problem16data.xlsx приведены данные о количестве круассанов с миндальным кремом, продаваемых в кондитерской каждый день. Для каждого дня
приведены данные о том, был ли день солнечный или пасмурный. Создайте
уравнение, прогнозирующее ежедневные продажи круассанов. Объясните,
как погода и день недели влияют на продажи. В пасмурный выходной день
можно с вероятностью в 95% утверждать, что продажи будут в интервале между _____ и _____.

ГЛ А В А 62

Однофакторный дисперсионный
анализ

Обсуждаемые вопросы
Владелец издательства, публикующего компьютерную литературу, хочет знать,
влияет ли на продажи местоположение стенда с книгами в отделе компьютерной
литературы в книжных магазинах. В частности, имеет ли значение, в какой зоне
отдела компьютерной литературы (передней, задней или средней) находится
стенд с книгами?
Если я определяю, имеют ли популяции значимо различные средние значения,
почему метод называется дисперсионным анализом?
Как применить результаты однофакторного дисперсионного анализа для прогнозирования?

Аналитики данных часто имеют дело с данными о нескольких группах людей или
предметов и стараются определить, различаются ли данные о группах на значимую величину. Вот несколько примеров:
Есть ли значимое различие в длительности, на которую четыре врача оставляют своих пациенток в больнице после родов?
Зависит ли количество производимого нового препарата от размера резервуара, в котором он производится (большой, маленький или средний)?
Было ли вызвано падение давления после приема одного из четырех препаратов?
Если вы пытаетесь определить, являются ли средние значения для нескольких
наборов данных, зависящих от одного фактора, значимо различными, следует
воспользоваться однофакторным дисперсионным анализом. В перечисленных
примерах к таким факторам относятся врачи, размер резервуара и препараты соответственно. При анализе данных можно выбрать одну из двух гипотез.
Нулевую гипотезу, согласно которой средние значения всех групп идентичны.
Альтернативную гипотезу, согласно которой между средними значениями
групп имеется статистически значимое различие.
Для проверки этих гипотез в Microsoft Excel есть инструмент Однофакторный дисперсионный анализ (Anova: Single Factor), который выбирается в диалоговом окне

Однофакторный дисперсионный анализ

679

Анализ данных (Data Analysis). Если вычисленное p-значение окажется небольшим
(как правило, не больше 0,15), можно сделать вывод, что верна альтернативная гипотеза (средние значения значимо различны). Если p-значение больше 0,15, верна
нулевая гипотеза (генеральные совокупности имеют одинаковые средние значения). Давайте рассмотрим пример.

Ответы на вопросы
Владелец издательства, публикующего компьютерную литературу , хочет
знать, влияет ли на продажи местоположение стенда с книгами в отделе
компьютерной литературы в книжных магазинах. В частности, имеет ли значение, в какой зоне отдела компьютерной литературы (передней, задней или
средней) находится стенд с книгами?

Издательству необходимо знать, лучше ли продаются книги в зависимости от
того, выставлены ли они на стенде в передней, задней или средней зоне отдела
компьютерной литературы. В 12 магазинах были отслежены еженедельные продажи (в сотнях штук). В пяти магазинах стенды были установлены в передней зоне
отдела, в четырех магазинах — в задней зоне и в трех магазинах — в средней. Полученные объемы продаж представлены на листе Signif в файле Onewayanovatemp.xlsx
(рис. 62.1). Указывают ли данные на значимость местоположения стенда или нет?

Рис. 62.1. Данные о продажах книг

Допустим, во всех 12 магазинах одинаковая структура продаж и они приблизительно одинаковые по площади. Это предположение позволяет воспользоваться
однофакторным дисперсионным анализом, поскольку в таком случае можно считать, что на продажи влияет не более одного фактора (а именно положение стенда
с книгами в отделе компьютерной литературы). (Если бы магазины были разных
размеров, данные пришлось бы анализировать с помощью двухфакторного дисперсионного анализа, рассматриваемого в главе 63 «Рандомизированные блоки
и двухфакторный дисперсионный анализ».)
Для анализа данных на вкладке Данные (Data) щелкните на кнопке Анализ данных (Data Analysis) и выберите инструмент Однофакторный дисперсионный анализ
(Anova: Single Factor). Заполните диалоговое окно, как на рис. 62.2.

680

ГЛАВА 62

Рис. 62.2. Диалоговое окно Однофакторный дисперсионный анализ

Я использовал следующие конфигурации:
данные для входного интервала, включая метки, находятся в ячейках B3:D8;
выбран флажок Метки в первой строке (Labels in ﬁrst row), поскольку первая
строка входного интервала содержит метки;
я установил переключатель в положение по столбцам (Columns), поскольку данные объединены в столбцы;
я указал ячейку C12 как левую верхнюю ячейку выходного интервала ( Output
Range);
выбор значения Альфа (Alpha) несуществен. Можно оставить значение по умолчанию.
После нажатия OK появятся результаты, показанные на рис. 62.3.

Рис. 62.3. Результаты однофакторного дисперсионного анализа

В ячейках F16:F18 вы видите средний объем продаж в зависимости от местоположения стенда. Когда стенд располагается в передней зоне отдела компьютерной

Однофакторный дисперсионный анализ

681

литературы, средний объем продаж составляет 900 шт .; когда он располагается
в задней зоне отдела, то средний объем продаж равен 1400 шт .; когда он располагается в средней зоне, средний объем продаж составляет 1100 шт . Поскольку
p-значение, равное 0,003 (в ячейке H23), меньше 0,15, можно сделать вывод, что
эти средние значения значимо различны.

Если я определяю, имеют ли популяции значимо различные средние значения, почему метод называется дисперсионным анализом?

Предположим, что данные о продаже книг — это данные на листе Insig в файле
Onewayanovatemp.xlsx (рис. 62.4). Если вы запустите однофакторный дисперсионный анализ для этих данных, то получите результаты, представленные на рис. 62.5.

Рис. 62.4. Данные о продажах, для которых принята нулевая гипотеза

Рис. 62.5. Результаты дисперсионного анализа, для которых принята нулевая гипотеза

Обратите внимание, что средний объем продаж для каждой зоны отдела точно такой же, как раньше. Тем не менее p-значение, равное 0,66, показывает, что следует
принять нулевую гипотезу и сделать вывод об отсутствии влияния размещения
стенда в отделе компьютерной литературы на объемы продаж. Причина такого
странного результата в том, что во втором наборе данных вариация в объемах продаж для каждого положения стенда в секции более значительна. В первом наборе
данных, например, вариация в объемах продаж, когда стенд находится в передней

682

ГЛАВА 62

зоне отдела, составляет от 700 до 1100 книг , в то время как во втором наборе вариация в объемах продаж для стенда в той же зоне составляет от 200 до 2000 книг.
Вариация продаж для каждого местоположения стенда измеряется суммой квадратов отклонений от среднего для данных внутри групп. Эта мера приведена
в ячейке D24 в первом наборе данных и в ячейке F24 во втором. В первом наборе
данных сумма квадратов отклонений от среднего для данных внутри групп равна
22, в то время как во втором наборе данных сумма квадратов внутри групп равна
574! Такая большая вариация точек данных для каждого местоположения стенда
маскирует вариацию между самими группами (положениями стенда), и для второго набора данных нет возможности заключить, что разница между объемами
продаж для разных положений стенда значима.

Как применить результаты однофакторного дисперсионного анализа для
прогнозирования?

Если между средними значениями по каждой группе есть значимая вариация,
наилучшим прогнозом для каждой группы будет среднее значение по этой группе.
Следовательно, для первого набора данных можно предсказать следующее:
объем продаж для стенда в передней зоне отдела компьютерной литературы
составит 900 книг в неделю;
объем продаж для стенда в задней зоне отдела компьютерной литературы составит 1400 книг в неделю;
объем продаж для стенда в средней зоне отдела компьютерной литературы составит 1100 книг в неделю.
Если значимая вариация отсутствует, наилучшим прогнозом для каждого наблюдения будет просто общее среднее. Таким образом, для второго набора данных
можно предсказать, что еженедельные продажи составят 1117 книг, независимо от
того, где расположен стенд.
Так же можно оценить точность прогнозов. Средним квадратичным отклонением
прогноза по результатам однофакторного дисперсионного анализа является корень квадратный из среднего квадратичного (MS) внутри групп. Как показано на
рис. 62.3, среднее квадратичное отклонение прогноза для первого набора данных
составляет 1,56 (см. лист Signif). Это означает, что следует ожидать, например, следующих результатов:
для 68% недель, в течение которых книги будут находиться в переднейзоне отдела компьютерной литературы, объем продаж составит от 900 – 156 = 744 до
900 + 156 = 1056 книг;
для 95% недель, в течение которых книги будут находиться в передней зоне
отдела компьютерной литературы, объем продаж составит от 900 – 2 × (156) =
= 588 до 900 + 2 × (156) = 1212 книг.

Однофакторный дисперсионный анализ

683

Задания
Данные к этим заданиям находятся в файле Chapter62data.xlsx.
1. Для пациентов четырех кардиологов известно количество дней, в течение которых пациенты оставались в больнице после операции на открытом сердце.
• Существуют ли доказательства того, что врачи проводят различную политику выписки из лечебного учреждения?
• В течение скольких дней пациент первого кардиолога будет оставаться
в больнице с вероятностью 95%?
2. Лекарственный препарат может быть изготовлен в термостате с рабочей температурой 400, 300 или 200 градусов. Дано количество полученного препарата
в фунтах для различных партий, изготовленных при разных температурах.
• Влияет ли температура на объем выработки препарата?
• Каков интервал в фунтах, в котором с вероятностью 95% окажется выработка продукта из термостата с рабочей температурой 200 градусов?
• Если считать, что давление внутри корпуса также влияет на резуль тативность процесса, остается ли анализ надежным?

ГЛ А В А 63

Рандомизированные
блоки и двухфакторный
дисперсионный анализ

Обсуждаемые вопросы
Я пытаюсь проанализировать эффективность отдела продаж. Проблема в том,
что кроме эффективности самого торгового представителя сумма его продаж зависит от региона, в который он назначен. Как можно включить в анализ распределение продавцов по регионам?
Как предсказать объем продаж на основе информации о торговых представителях и регионах? Насколько точными окажутся прогнозы?
Как определить, влияют ли на продажи видеоигр изменение цены и расходов на
рекламу? Как определить, значимо ли взаимодействие цены и рекламы?
Как интерпретировать влияние цены и рекламы на продажи при отсутствии значимого взаимодействия между ценой и рекламой?

Во многих наборах данных на зависимую переменную могут оказывать влияние
два фактора. В следующей таблице приведено несколько подобных примеров.
Факторы

Зависимая переменная

Продавец и назначенный регион

Объем продаж

Цена продукта и расходы на рекламу

Объем продаж

Температура и давление

Выход продукции

Хирург и марка используемого стента

Здоровье пациента после операции на открытом сердце

Если на зависимую переменную могут повлиять два фактора, то для определения
фактора, оказывающего значительное влияние на зависимую переменную (если это
имеет место), вы можете использовать либо анализ с рандомизированными блоками, либо двухфакторный дисперсионный анализ с повторениями. Кроме того, двухфакторный дисперсионный анализ позволяет определить, проявляют ли два фактора значимое взаимодействие. Допустим, вам необходимо спрогнозировать объем

Рандомизированные блоки и двухфакторный дисперсионный анализ

685

продаж в зависимости от цены продукта и рекламного бюджета. Цена и реклама
значимо влияют друг на друга, если эффект от рекламы зависит от цены продукта.
В модели с рандомизированными блоками каждая возможная комбинация факторов наблюдается только один раз. Вы не можете проверить взаимодействие в рандомизированном блочном плане. В модели двухфакторного дисперсионного анализа каждая комбинация факторов наблюдается одинаковое число раз (назовем
его k). Для проверки взаимодействия k должно быть больше 1. В модели двухфакторного дисперсионного анализа проверить взаимодействие не составляет труда.

Ответы на вопросы
Я пытаюсь проанализировать эффективность отдела продаж. Проблема
в том, что кроме эффективности самого торгового представителя сумма
его продаж зависит от региона, в который он назначен. Как можно включить
в анализ распределение продавцов по регионам?

Пусть необходимо определить, как продавец и регион продаж, в который он назначен, влияют на объемы продаж продукта. Допустим, каждый из четырех торговых представителей провел в каждом из пяти регионов один месяц. Полученные в результате объемы продаж приведены на листе Randomized Blocks в файле
Twowayanova.xlsx (рис. 63.1). Например, первый представитель продал за месяц
20 единиц продукции, когда работал в регионе 4.

Рис. 63.1. Данные для примера с рандомизированными блоками

Эта модель называется двухфакторным дисперсионным анализом без повторений,
так как на объем продаж могут оказывать влияние два фактора (регион и торговый
представитель) при наличии единственного наблюдения для каждой комбинации «представитель — регион». Т акже эта модель называется рандомизированным
блочным планом, поскольку в ней можно рандомизировать (в хронологическом порядке) распределение представителей по регионам. Другими словами, необходимо убедиться, что месяц, в течение которого представитель 1 работал в регионе 1,
с одинаковой вероятностью может быть первым, вторым, третьим, четвертым или
пятым месяцем. Есть надежда, что такая рандомизация уменьшает влияние временного периода на анализ (предположительно, со временем квалификация торгового
представителя повышается); и в каком-то смысле «блокируется» влияние выбора
региона на результат при попытке сравнения торговых представителей.

686

ГЛАВА 63

Для анализа этих данных в Microsoft Excel на вкладкеДанные (Data) выберите Анализ данных (Data Analysis) и затем инструмент Двухфакторный дисперсионный анализ без повторений (Anova: Two-Factor Without Replication). (Необходимо установить
пакет Анализ данных. Инструкции см. в главе 44 «Обобщение данных с помощью
описательной статистики».) Заполните диалоговое окно, как на рис. 63.2.

Рис. 63.2. Диалоговое окно Двухфакторный дисперсионный анализ
без повторений для настройки модели с рандомизированными блоками

Я использовал следующую информацию:
входной интервал находится в ячейках C5:G10;
я выбрал флажок Метки (Labels), поскольку первая строка входного интервала
содержит метки;
я ввел B12 как левую верхнюю ячейку выходного интервала;
выбор значения Альфа (Alpha) несущественен. Можно оставить значение по
умолчанию.

Рис. 63.3. Выходные данные рандомизированного блочного плана

Рандомизированные блоки и двухфакторный дисперсионный анализ

687

Результат анализа представлен на рис. 63.3. (Резуль таты в ячейках G12:G24 созданы не с помощью инструмента Excel Анализ данных. Как я ввел формулы в эти
ячейки, объясню далее в этой главе.)
Оказывает ли фактор в строках (регионы) или фактор в столбцах (торговые представители) значимый эффект на продажи, можно определить поp-значению. Если
p-значение для фактора небольшое (меньше 0,15), фактор оказывает значимый
эффект на продажи. Оба p-значения, для строк (0,0000974) и для столбцов(0,024),
меньше 0,15, поэтому и регион, и представитель оказывают существенное влияние
на продажи.

Как предсказать объем продаж на основе информации о торговых представителях и регионах? Насколько точными окажутся прогнозы?

Как предсказать объемы продаж продукта? Продажи за месяц можно предсказать
по следующему уравнению 1:
прогнозируемый объем продаж = общее_среднее + (влияние_представителя) + (влияние_региона).

В этом уравнении (влияние_представителя) равно 0, если фактор «торговый представитель» не значимый. Если он значимый, (влияние_представителя) равно среднему значению для данного представителя минус общее среднее. Аналогично,
(влияние_региона) равно 0, если фактор «регион» не значимый. Если он значимый,
(влияние_региона) равно среднему значению для данного региона минус общее
среднее.
G12 по формуле =СРЗНАЧ(D6:G10).
Я вычислил общее среднее (17,6) в ячейке
Влияние представителей и регионов вычисляется путем копирования формулы
=E15-$G$12 из ячейки G15 в G16:G24. В качестве примера вы можете вычислить
прогнозируемые продажи представителя 4 в регионе 2 как 17,6 – 2,85 + 3,6 = 18,35.
Это значение вычислено в ячейке D38 (рис. 63.4) по формуле =G12+G16+G24. Если
бы влияние региона было значимо, а влияние представителя незначимо, прогнозируемые продажи для представителя 4 в регионе 2 составили бы 17,6 – 2,85 = 14,75.

Рис. 63.4. Прогноз объема продаж для представителя 4 в регионе 2

Как и в однофакторном дисперсионном анализе, стандартное отклонение ошибок
прогноза равно корню квадратному из среднеквадратичной погрешности, показанной в ячейке E31. Стандартное отклонение вычислено в ячейке E32 по формуле
=КОРЕНЬ(E31). Таким образом, можно быть на 95% уверенным в том, что если пред-

688

ГЛАВА 63

ставитель 4 будет назначен в регион 2, ежемесячные объемы продаж составят от
18,35 – 2 × 3,99 = 10,37 до 18,35 + 2 × 3,99 = 26,33. Эти границы вычислены в ячейках D39 и D40 по формулам =$D$38-2*$E$32 и =$D$38+2*$E$32, соответственно.
Как определить, влияют ли на продажи видеоигр изменение цены и расходов на рекламу? Как определить, значимо ли взаимодействие цены
и рекламы?

Если для каждой комбинации факторов в строках и столбцах имеется более одного наблюдения, воспользуйтесь двухфакторным дисперсионным анализом с повторениями. Для выполнения такого анализа Excel требует , чтобы число наблюдений для каждой комбинации факторов в строках и столбцах было одинаковым.
В дополнение к проверке значимости факторов в строках и столбцах можно также проверить значимость их взаимодействия. Например, если необходимо определить, как цена и расходы на рекламу влияют на объемы продаж, взаимосвязь
между ценой и расходами на рекламу означает , что эффект от изменения стоимости рекламы будет зависеть от уровня цены (или, что то же самое, эффект от
изменения цены будет зависеть от стоимости рекламы). Отсутствие взаимодействия между ценой и рекламой означает, что эффект от изменения цены не будет
зависеть от стоимости рекламы.
В качестве примера для двухфакторного дисперсионного анализа с повторениями определим, как цена и стоимость рекламы влияют на ежемесячные продажи
видеоигры. В файле Twowayanova.xlsx на листе Two Way ANOVA No Interaction находятся данные, представленные на рис. 63.5. Например, за три месяца, в течение
которых расходы на рекламу были низкими, а цена — средней, было продано 21,
20 и 16 единиц продукции.

Рис. 63.5. Данные о продажах видеоигры; нет взаимодействия между факторами

Обратите внимание, что для каждой комбинации «цена — реклама» имеется ровно
по три наблюдения. В ячейке D1 по формуле =СРЗНАЧ(D4:F12) я вычислил общее
среднее (25,037) для всех наблюдений. В ячейкахG4, G7 и G10 я вычислил эффекты
для каждого уровня расходов. Например, эффект от низкого уровня расходов на

Рандомизированные блоки и двухфакторный дисперсионный анализ

689

рекламу равен среднему значению для низкого уровня расходов на рекламу минус
общее среднее. Эффект от низкого уровня расходов на рекламу (-5,59) я вычислил
в ячейке G4 по формуле =СРЗНАЧ(D4:F6)-$D$1. Аналогичным образом, я вычислил
эффекты для каждого уровня цены, скопировав формулу =СРЗНАЧ(D4:D12)-$D$1
из D13 в E13:F13.
Для анализа этих данных на вкладке Данные (Data) выберите Анализ данных (Data
Analysis) и затем в диалоговом окнеАнализ данных (Data Analysis) — инструмент Двухфакторный дисперсионный анализ с повторениями (Anova: Two-Factor With Replication).
Заполните диалоговое окно, как на рис. 63.6.

Рис. 63.6. Диалоговое окно Двухфакторный дисперсионный анализ с повторениями для
запуска анализа с повторениями

Для анализа я указал следующую информацию.
Входные данные, включая метки, находятся в диапазоне C3:F12. В Excel в двухфакторном дисперсионном анализе с повторениями для каждого уровня эффекта требуются метки в первой строке каждого столбца входного интервала.
Таким образом, в ячейки D3:F3 я ввел Низкая, Средняя и Высокая (цена). В Excel
также требуются метки для каждого уровня эффекта в первом столбце входного интервала. Эти метки должны находиться в строках, отмечающих начало
данных для каждого уровня. Таким образом, метки, соответствующие низкому,
среднему и высокому уровню расходов на рекламу, следует разместить в ячейках C4, C7 и C10.
В поле Число строк для выборки (Rows Per Sample) я ввел 3, поскольку для каждой комбинации «цена — реклама» имеется три повторения.
Для левой верхней ячейки выходного интервала я указал B14.
Затем я нажал OK. Единственно важной частью выходных данных является таблица дисперсионного анализа, показанная на рис. 63.7.
Как и в случае с рандомизированными блоками, влияние (включая взаимодействие) значимо, если p-значение меньше 0,15. Здесь Выборка (строка с данными
о воздействии рекламы, Sample) и Цена (показанная в строке с меткой Столбцы,
Columns) являются высокозначимыми, а значимое взаимодействие отсутствует .

690

ГЛАВА 63

Рис. 63.7. Выходные данные двухфакторного дисперсионного анализа
с повторениями; взаимодействия между факторами нет

(p-значение для взаимодействия, Interaction, равно 0,79!). Таким образом, можно
заключить, что цена и реклама влияют на объем продаж, и воздействие рекламы
на объем продаж не зависит от уровня цены. На рис. 63.8 приведена диаграмма
среднего объема продаж для каждой комбинации «цена — реклама». Как видите, цена и реклама не проявляют значимого взаимодействия. (См. лист Graph No
Interaction.)

Рис. 63.8. Взаимодействие между ценой и рекламой в этом наборе данных отсутствует

Обратите внимание, что по мере повышения расходов на рекламу средние объемы продаж увеличиваются примерно с одинаковой скоростью, независимо от
низкого, среднего или высокого уровня цены. В принципе, можно распознать отсутствие взаимодействия по тому факту, что линии для всех уровней цены почти
параллельны.

Как интерпретировать влияние цены и рекламы на продажи при отсутствии
значимого взаимодействия между ценой и рекламой?

В отсутствие значимого взаимодействия можно прогнозировать объемы продаж
в двухфакторном дисперсионном анализе с повторениями так же, как в двухфакторном дисперсионном анализе без повторений по следующему уравнению (уравнение 2):
прогнозируемый объем продаж = общее среднее + [строка или эффект рекламы (если
значимо)] + [столбец или эффект цены (если значимо)].

Рандомизированные блоки и двухфакторный дисперсионный анализ

691

В этом анализе предполагается, что цена и реклама являются единственными
факторами, влияющими на объем продаж. Если продажи имеют ярко выраженный сезонный характер, в анализ необходимо включить сезонность. (Сезонность
рассматривается в главах 65 «Метод Винтерса и лист прогноза» и 67 «Прогноз для
особых случаев».) Например, если цена высокая, а уровень расходов на рекламу
средний, прогнозируемый объем продаж составит 25,037 + (–1,814) + (–8,704) =
= 14,52. (См. ячейку E54 на рис. 63.9, на котором снова представлен лист Two Way
ANOVA No Interaction.) На рис. 63.5 было показано, что общее среднее равно 25,037,
эффект от среднего уровня расходов на рекламу равен –1,814 и эффект от высокой цены равен –8,704.

Рис. 63.9. Прогноз для объема продаж при высокой цене и среднем уровне рекламы

Стандартное отклонение ошибок прогноза равно корню квадратному из среднеквадратичной погрешности:

С вероятностью 95% прогноз будет точен в пределах 10,92 единицы. Другими словами, можно быть на 95% уверенным, что объем продаж в течение месяца при высокой цене и среднем уровне расходов на рекламу составит от 3,60 до 25,43 единицы.
На листе Two Way ANOVA with Interaction я заменил данные из предыдущего примера
данными, показанными на рис. 63.10. После выполнения двухфакторного дисперсионного анализа с повторениями я получил результаты, как на рис. 63.11.
В этом наборе данных
p-значение для взаимодействия равно 0,001. Если
p-значение для взаимодействия небольшое (меньше 0,15), можно даже не проверять p-значения для факторов в строке и столбце. Прогнозируемый объем продаж
для любой комбинации цены и уровня расходов на рекламу равен среднему трех
наблюдений, включающих эту комбинацию цены и уровня расходов на рекламу .
Например, наилучший прогноз для объема продаж в течение месяца при высоком
уровне расходов на рекламу и средней цене равен:

692

ГЛАВА 63

Рис. 63.10. Данные продаж при взаимодействии цены и рекламы

Рис. 63.11. Выходные данные для двухфакторного дисперсионного анализа
с повторениями

Стандартное отклонение ошибок прогноза также равно корню квадратному из
среднеквадратичной погрешности:

Таким образом, прогноз для объема продаж с вероятностью 95% окажется точным
в пределах 8,26 единицы.
На рис. 63.12 показано, почему эти данные проявляют значимое взаимодействие
цены и расходов на рекламу. Для низкой и средней цены повышение расходов на
рекламу приводит к повышению среднего объема продаж, но если цена высокая,
повышение расходов на рекламу не оказывает влияния на средний объем продаж.
Это объясняет, почему нельзя использовать уравнение 2 для предсказания продаж при наличии значимого взаимодействия. В конце концов, как можно говорить
о влиянии рекламы, когда влияние рекламы зависит от цены?
Главное, что можно сказать об этом графике, — серии данных не параллельны. Это
говорит о том, что для различных уровней цен изменение расходов на рекламу
имеет различное воздействие на объем продаж.

Рандомизированные блоки и двухфакторный дисперсионный анализ

693

Рис. 63.12. В этом наборе данных цена и уровень рекламы проявляют значимое
взаимодействие

Задания
Данные к заданиям 1–3 находятся в файле Ch63.xlsx.
1. Считается, что давление (высокое, среднее или низкое) и температура (высокая, средняя или низкая) влияют на объем выработки. Приняв это за основу,
решите следующие задачи.
• Исходя из данных на листе Problem 1, определите, как температура и/или
давление влияют на объем выработки.
• В каком диапазоне с вероятностью 95% находится объем выработки при
высоком давлении и низкой температуре?
2. Вам нужно определить, как конкретный торговый представитель и количество рекламных звонков врачу (один, три и пять) влияют на сумму (в тысячах
долларов), на которую каждый врач выписывает ваш лекарственный препарат. Исходя из данных на листе Problem 2, найдите ответы на следующие вопросы:
• Как представитель и количество звонков влияют на объем продаж?
• Если представитель 3 сделал пять звонков врачу, то вы на 95% уверены, что
врач выпишет рецепты вашего препарата всего на какую сумму?
3. Ответьте на вопросы к заданию 2, используя данные на листе Problem 2.
4. Файл Coupondata.xlsx содержит информацию о продажах арахисового масла
в течение нескольких недель, когда покупателям выдавался (или не выдавался) купон и когда реклама была (или не была) напечатана в воскресной газете.
Опишите, как купон и реклама влияют на продажи арахисового масла.

ГЛ А В А 64

Скользящие средние
для временных рядов

Обсуждаемый вопрос
Я пытаюсь проанализировать тенденцию роста ежеквартальных доходов Amazon.
com с 1996 г. Объем продаж в четвертом квартале в США обычно больше (из-за
Рождества), чем объем продаж в первом квартале следующего года. Эта закономерность затемняет тенденцию к росту продаж. Как отобразить тенденцию
к росту доходов графически?

Ответ на вопрос
Я пытаюсь проанализировать тенденцию роста ежеквартальных доходов
Amazon.com с 1996 г. Объем продаж в четвертом квартале в США обычно
больше (из-за Рождества), чем объем продаж в первом квартале следующего
года. Эта закономерность затемняет тенденцию к росту продаж. Как отобразить тенденцию к росту доходов графически?

Данные временных рядов просто отображают одну и ту же величину , измеренную в разные моменты времени. Например, данные в файле Amazon.com.xlsx, часть
которых показана на рис. 64.1, отображают временной ряд для ежеквартальных
доходов в миллионах долларов для Amazon.com. Данные охватывают временной
интервал от четвертого квартала 1995 г. до третьего квартала 2017 г.
Для построения диаграммы этого временного ряда выделите диапазон E4:F93, который содержит номер квартала (от 1 до 89) и ежеквартальные доходы Amazon.
com (в миллионах долларов). Затем на вкладке Вставка (Insert) в группе Диаграммы
(Chart) выберите Точечная или пузырьковая диаграмма (Insert Scatter (X, Y) Or Bubble
Chart) и затем второй тип точечной диаграммы —
Точечная с гладкими кривыми
и маркерами (Scatter With Smooth Lines And Markers). Диаграмма временного ряда
показана на рис. 64.2.
Вы видите, что наблюдается тенденция к росту доходов, но тот факт, что из-за доходов в четвертом квартале доходы в первых трех кварталах каждого года кажутся
небольшими, затрудняет ее отслеживание. Поскольку в году четыре квартала, было
бы неплохо отобразить на диаграмме средние доходы за предыдущие четыре квартала. Это называется скользящей средней для четырех периодов . Использование

Скользящие средние для временных рядов

695

Рис. 64.1. Ежеквартальные доходы от продаж Amazon.com

Рис. 64.2. Временной ряд ежеквартальных доходов Amazon.com

скользящей средней за четыре квартала сглаживает влияние сезонных колебаний, поскольку в каждое среднее будет входить по одной точке данных из каждого
квартала. Такая диаграмма называется графиком скользящей средней, так как нанесенные на диаграмму средние значения «скользят» во времени. Графики скользящей средней также сглаживают случайные изменения, что позволяет получить
более полное представление о том, что происходит с данными.

696

ГЛАВА 64

Для построения графика скользящей средней ежеквартальных доходов необходимо изменить диаграмму. Выделите диаграмму и щелкните на какой-либо точке
данных, чтобы все точки стали синего цвета. Щелкните на точке правой кнопкой
мыши и выберите Добавить линию тренда (Add Trendline), затем установите переключатель в положение Линейная фильтрация (Moving Average) и выберите в списке
Период (Period) значение 4. На диаграмму добавится кривая скользящей средней за
четыре квартала (рис. 64.3, файл Amazon.com.xlsx).

Рис. 64.3. Кривая скользящей средней за четыре квартала

Для каждого квартала ставится точка со значением среднего для текущего и трех
предыдущих кварталов. Очевидно, что для скользящей средней за четыре квартала
соответствующая кривая начинается с четвертой точки данных. Кривая скользящей средней ясно показывает, что доходы Amazon.com имеют устойчивую тенденцию к повышению. Кроме того, наклон скользящей средней за четыре квартала
увеличивается. По всей вероятности, наклон этого графика скользящей средней со
временем выровняется, в результате чего график будет выглядеть как S-образная
кривая. Инструмент Excel Кривая тренда (Trend Curve) не подбирает S-образные
кривые, но для подбора к данным S-образных кривых в Microsoft Excel 2016
можно использовать инструмент Поиск решения (Solver). Подбор S-образных кривых к данным см. в книге У эйна Винстона «Анализ рынков» (Wayne L. Winston.
Marketing Analytics, Wiley, 2014).

Задание
Файл Ch62data.xlsx содержит квартальные доходы GM, Ford и GE. Постройте кривую скользящей средней за четыре квартала для доходов каждой компании. Что
вы узнали по каждой кривой тренда?

Г Л А В А 65

Метод Винтерса и Лист прогноза

Часто требуется предсказать будущие значения временн ˆого ряда, такие как ежемесячные расходы или ежемесячная выручка от продукта. Как правило, это непросто, поскольку характеристики любого временнˆого ряда постоянно меняются.
В большинстве случаев для прогнозирования будущих значений временного ряда
лучше всего подходят методы сглаживания или адаптивные методы. В этой главе я опишу самый эффективный метод сглаживания — метод Винтерса (предложенный Петером Винтерсом (Peter Winters) и Чарльзом Хольтом (Charles Holt)).
Я также покажу вам, как пользоваться чудесным инструментом Excel Лист прогноза (добавленным в Excel 2016).
Чтобы вы поняли, как работает метод Винтерса, я использую его для прогнозирования ежемесячного объема строительства нового жилья в США. Объем строительства нового жилья — это просто количество новых домов, которые начали
строиться в течение месяца. Начнем с описания трех ключевых характеристик
временных рядов.

Характеристики временных рядов
Поведение большинства временных рядов можно объяснить тремя характеристиками: база, тренд и сезонность.
База ряда описывает текущий уровень ряда в отсутствие какой-либо сезонности. Например, предположим, что базовый уровень объема строительства нового жилья в США равен 160 000 домов. В этом случае, если текущий месяц
был средним месяцем относительно других месяцев года, можно считать, что
объем нового строительства составит 160 000 домов.
Тренд временного ряда — это процентное увеличение базы за период. Т аким
образом, тренд 1,02 означает, что, согласно оценке, объем нового строительства
увеличивается на 2% каждый месяц. Тренд 0,97 означает, что, согласно оценке,
объем нового строительства уменьшается на 3% каждый месяц.
Сезонность (индекс сезонности) для периода говорит нам, насколько больше
или меньше типичного ожидаемый ежемесячный объем нового строительства.
Например, если индекс сезонности декабря составляет 0,8, то декабрьский объем нового строительства на 20% меньше типичного ежемесячного объема. Если
индекс сезонности июня составляет 1,3, то июньский объем нового строительства на 30% больше типичного ежемесячного объема.

698

ГЛАВА 65

Определение параметров
На основе всех данных, полученных в результате наблюдения в течение месяца t,
вычисляются следующие представляющие интерес величины:
Lt — уровень ряда;
Tt — тренд ряда;
St — индекс сезонности для текущего месяца.
Ключом к методу Винтерса являются следующие три уравнения, с помощью которых обновляются величины Lt, Tt и St. В следующих формулах alp, bet и gam — это
сглаживающие постоянные. Значения этих постоянных выбираются с целью оптимизации прогнозов. В следующих формулах c равно числу периодов в сезонном
цикле (например, c = 12 месяцев), а xt равно наблюдаемому значению временного
ряда в момент t.
Формула 1: Lt = alp(xt/st – c) + (1 – alp)(Lt – 1 × Tt – 1).
Формула 2: Tt= bet(Lt/Lt – 1) + (1 – bet)Tt – 1.
Формула 3: St = gam(xt/Lt) + (1 – gam)St – c.
Формула 1 показывает, что новая оценка базы равна взвешенному среднему текущего наблюдения (с исключенной сезонной составляющей) и база предыдущего
периода обновлена в соответствии с последней оценкой тренда. Формула 2 показывает, что новая оценка тренда равна взвешенному среднему отношения текущей
базы к базе предыдущего периода (это текущая оценка тренда) плюс тренд предыдущего периода. Формула 3 показывает, что обновленная оценка индекса сезонности вычисляется как взвешенное среднее оценки индекса сезонности, основанного
на текущем периоде, плюс предыдущая оценка. Обратите внимание, что б ˆольшие
значения параметров сглаживания придают больший вес текущему наблюдению.
Ft, k можно определить как прогноз F после периода t для периода t + k. Таким образом, Ft, k = Lt(Tt)k St + k – c (формула 4).
По этой формуле сначала с помощью текущей оценки тренда обновляется база
на k периодов вперед. Затем получившаяся в результате оценка базы для периода
t + k корректируется соответствующим индексом сезонности.

Определение начальных параметров
для метода Винтерса
Для запуска метода Винтерса необходимы начальные оценки базы, тренда и индексов сезонности ряда. В качестве начальных данных для метода Винтерса я использовал ежемесячные объемы строительства нового жилья за 1986 и 1987 г
.
Затем я выбрал параметры сглаживания для оптимизации прогнозов на месяц
вперед для 1988–1996 гг. (рис. 65.1 и файл House2.xlsx).

Метод Винтерса и Лист прогноза

699

Рис. 65.1. Определение начальных параметров для метода Винтерса

Далее я выполнил следующие шаги.
Шаг 1. Я вычислил, например, январский индекс сезонности как среднее январских объемов строительства нового жилья для 1986 и 1987 г., деленное на
средние ежемесячные объемы для 1986 и 1987 г . Таким образом, скопировав
формулу =СРЗНАЧ(B2;B14)/СРЗНАЧ($B$2:$B$25) из G14 в G15:G25, я получил расчетные индексы сезонности. Например, январский индекс равен 0,75, а июньский — 1,17.
Шаг 2. Для вычисления среднего ежемесячного тренда я разделил средний
объем для 1987 г. на средний объем для 1986 г . и возвел в одну двенадцатую.
Я вычислил тренд в ячейке J3 (и скопировал в D25) по формуле =(J1/J2)^(1/12).
Шаг 3. База ряда вычисляется как декабрьское значение для 1987 г. с исключенной сезонной составляющей. Я вычислил базу в ячейке C25 по формуле
=(B25/G25).

Вычисление сглаживающих постоянных
Теперь мы готовы вычислить сглаживающие постоянные. В столбце C обновляется база ряда, в столбце D — тренд ряда и в столбце G — индексы сезонности.
В столбце E я вычислил прогноз для следующего месяца и в столбце F — абсолютную процентную ошибку для каждого месяца. Наконец, я использовал Поиск

700

ГЛАВА 65

решения (Solver) для выбора значений сглаживающих постоянных, минимизирующих сумму абсолютных процентных ошибок. Вот как я это сделал.

Шаг 1. В ячейки G11:I11 я ввел пробные значения (от 0 до 1) для сглаживающих постоянных.
Шаг 2. В ячейках C26:C119 я вычислил по формуле 1 обновленные уровни ряда,
скопировав формулу =alp*(B26/G14)+(1-alp)*(C25*D25) из C26 в C27:C119.
Шаг 3. В ячейках D26:D119 я обновил по формуле 2 тренд ряда, скопировав
формулу =bet*(C26/C25)+(1-bet)*D25 из D26 в D27:D119.
Шаг 4. В ячейках G26:G119 я обновил по формуле 3 индексы сезонности, скопировав формулу =gam*(B26/C26)+(1-gam)*G14 из G26 в G27:G119.
Шаг 5. В ячейках E26:E119 я вычислил по формуле 4 прогноз для текущего месяца, скопировав формулу =(C25*D25)*G14 из E26 в E27:E119.
Шаг 6. В ячейках F26:F119 я вычислил абсолютную процентную ошибку для
каждого месяца, скопировав формулу =ABS(B26-E26)/B26 из F26 в F27:F119.
Шаг 7. В ячейке F21 я вычислил среднюю абсолютную процентную ошибку
для 1988–1996 гг. по формуле =СРЗНАЧ(F26:F119).
Шаг 8. Наконец, я щелкнул на Поиск решения (Solver) на вкладке Данные (Data),
чтобы определить значения сглаживающих постоянных, минимизирующие
среднюю абсолютную процентную ошибку. Диалоговое окно Параметры поиска
решения (Solver Parameters) показано на рис. 65.2. Поиск решения (Solver) рассмотрен в главах 29–38.

Рис. 65.2. Диалоговое окно Параметры поиска решения для модели Винтерса

Метод Винтерса и Лист прогноза

701

ПРИМЕЧАНИЕ
Для активации надстройки Поиск решения (Solver) на вкладке Файл (File) выберите
команду Параметры (Options), затем среди параметров Excel выберите раздел Надстройки (Add-Ins). В нижней части диалогового окна в раскрывающемся списке Управление (Manage) выберите Надстройки Excel (Excel Add-Ins) и нажмите Перейти (Go).
В диалоговом окне Надстройки (Add-Ins) установите флажок Поиск решения (Solver
Add-In) и нажмите OK. На вкладке Данные (Data) в группе Анализ (Analysis) появится
кнопка Поиск решения (Solver). Подробную информацию см. в главе 29 «Введение
в оптимизацию с надстройкой Поиск решения».

Я использовал сглаживающие постоянные ( G11:I11) для минимизации средней абсолютной процентной ошибки (ячейка F21). Инструмент Поиск решения
(Solver) обеспечивает поиск оптимальной комбинации сглаживающих постоянных. Сглаживающие постоянные должны находиться в пределах от 0 до 1. Здесь
средняя абсолютная процентная ошибка минимизируется при alp = 0,50, bet = 0,01
и gam = 0,27. Возможно, значения сглаживающих постоянных будут слегка различаться, но значение средней абсолютной процентной ошибки должно быть близко
к 7,3%. В этом примере есть много комбинаций сглаживающих постоянных, которые дают прогнозы практически с одинаковой средней абсолютной процентной
ошибкой. Мой прогноз на месяц вперед ошибочен в среднем на 7,3%.

Замечания
Вместо выбора сглаживающих постоянных для оптимизации ошибок прогноза
вперед на один период можно было бы, например, выбрать оптимизацию средней абсолютной процентной ошибки прогнозирования общих объемов строительства для следующих шести месяцев.
Если в конце месяца t требуется предсказать объемы продаж для следующих
четырех кварталов, можно просто сложить Ft, 1 + Ft, 2 + Ft, 3 + Ft, 4. При необходимости можно выбрать сглаживающие постоянные для минимизации абсолютной процентной ошибки прогнозирования объемов продаж для следующих нескольких лет.

Инструмент Excel Лист прогноза
В инструменте Лист прогноза, впервые добавленном в Excel 2016, применяется
обобщение метода Винтерса. Он позволяет просто выдавать прогнозы для данных
типа временного ряда. Вы также получаете доверительные интервалы для каждого
прогноза. Чтобы воспользоваться Листом прогноза, вы должны поместить данные
в книгу с расширением *.xlsx (НЕ *.xls). В файле Airlinetemp.xlsx содержатся сведения о количестве тысяч пассажиро-миль налета на линиях США в 2001–2017 гг .
Воспользуемся данными за 2001–2016 гг. (рис. 65.3), чтобы спрогнозировать, каким будет месячный налет на пассажирских линиях в 2017 г . Сначала поместите

702

ГЛАВА 65

курсор в любое место в таблице данных (столбцыA и B), с помощью которых будет
делаться прогноз на 2017 г. Затем на вкладке Данные (Data) щелкните значок Лист
прогноза (Forecast Sheet) в группе Прогноз (Forecast). На диаграмме предпросмотра
в диалоговом окне Создание листа прогноза (Create Forecast Sheet) (рис. 65.4) выбираем 1 декабря 2017 г. как Конец периода прогноза (Forecast End). Эта диаграмма
отражает имеющиеся данные, а красным показан период прогноза для каждого
месяца. В данном случае мы видим текущий прогноз и верхний и нижний пределы 95-процентного доверительного интервала для каждого прогноза. Например, для января 2017 г. прогнозируется 70 249 426,22 мили, и мы уверены на 95%,
что реальные пассажиро-мили в январе 2017 г . будут лежать в диапазоне между
66 497 179,856 и 74 001 672,59 мили. Чтобы создать Лист прогноза, показывающий
прогнозы и доверительный интервал для требуемого периода, просто нажмите на
кнопку Создать (Create) в диалоговом окне Создать лист прогноза (Create Forecast
Sheet). На отдельном листе появятся результаты, представленные на рис. 65.5.

Рис. 65.3. Данные о пассажиро-милях

Для получения прогноза и 95%-ных доверительных интервалов на каждый месяц
также возможно применить функции Excel (см. файл Airlinemiles.xlsx и рис. 65.6).
Скопировав формулу =ПРЕДСКАЗ.ETS(A197;$B$5:$B$196;$A$5:$A$196;1;1) из D197
в D198:D208, вы получите прогноз на каждый месяц 2017 г . на основе данных за
2016-й. Первая «1» позволяет Excel автоматически определить интервал сезонности (12 месяцев в данном случае), а вторая «1» означает , что нужно применить
линейную интерполяцию между точками имеющихся данных для замещения любых недостающих данных.

Метод Винтерса и Лист прогноза

703

Рис. 65.4. В диалоговом окне Создать лист прогноза на диаграмме предпросмотра
отражены как имеющиеся данные, так и прогноз, а также верхняя и нижняя границы
95%-ного доверительного интервала для данного прогноза

Рис. 65.5. Доверительные интервалы и прогнозы пассажиро-миль в 2017 г.

Скопировав формулу =D197-ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ (A197;$B$5:$B$196;$A$5:
$A$196;0.95;12) из E197 в E198:E208, получаем нижнюю границу 95%-ного доверительного интервала для прогноза каждого месяца. Аргументы функции ПРЕДСКАЗ.
ЕTS.ДОВИНТЕРВАЛ (FORECAST.ETX.CONFINT) говорят программе о том, что нужно
использовать 12-месячный интервал сезонности и данные 2016 г . для расчета половины ширины 95%-ного доверительного интервала для прогноза каждого меся-

704

ГЛАВА 65

ца. В столбце F применена точно такая же формула, как и в столбце E, только знак
«минус» заменен на «плюс», чтобы получить верхнюю границу 95%-ного доверительного интервала для пассажиро-миль каждого месяца. Как показано в столбце G на рис. 65.6, средняя абсолютная процентная ошибка для наших прогнозов на
2017 г. составляет всего лишь 1,5%.

Рис. 65.6. Применение функций Excel для создания прогнозов и границ доверительного
интервала в 2017 г.

Задания
Данные для всех заданий находятся в файле Quarterly.xlsx.
1. С помощью метода Винтерса спрогнозируйте доходы Apple на один квартал
вперед.
2. С помощью метода Винтерса спрогнозируйте доходы Amazon.com на один
квартал вперед.
3. С помощью метода Винтерса спрогнозируйте доходы Home Depot на один
квартал вперед.
4. С помощью метода Винтерса спрогнозируйте суммарный доход Home Depot
для следующих двух кварталов.
5. Спрогнозируйте пассажиро-мили за 2016 г . на основе данных 2015 г . с помощью Листа прогноза. Рассчитайте среднюю абсолютную процентную ошибку
для ваших прогнозов.

Г Л А В А 66

Метод прогнозирования
«по отношению
к скользящему среднему»

Обсуждаемые вопросы
Что такое тренд временного ряда?
Как определить индексы сезонности для временного ряда?
Существует ли простой способ включить тренд и сезонность в прогнозирование
будущих продаж продукта?

Часто для прогнозирования будущих ежеквартальных доходов корпорации или
ежемесячных объемов продаж продукта требуется простой точный метод. Для таких ситуаций подходит точный и простой в использовании метод прогнозирования «по отношению к скользящему среднему».
В файле Ratioma.xlsx вы найдете данные о продажах продукта за 20 кварталов
(см. на рис. 66.1 строки 5–24). Т ребуется предсказать объемы продаж в следующих четырех кварталах (кварталы 21–24). Этот временной ряд характеризуется
трендом и индексом сезонности.

Ответы на вопросы
?

Что такое тренд временного ряда?

Например, тренд 10 единиц продукции за квартал означает, что объем продаж увеличивается на 10 единиц продукции за квартал, а тренд –5 единиц продукции за
квартал означает, что объем продаж имеет тенденцию к снижению на 5 единиц
в квартал. Мультипликативный тренд 1,04 означает , что продажи возрастают на
4 % за квартал; мультипликативный тренд 0,94 означает, что продажи снижаются
на 6% за квартал. В главе 65 «Метод Винтерса и Лист прогноза» мы как раз имели
дело с мультипликативным трендом; в настоящей главе мы рассматриваем аддитивный тренд.

706

ГЛАВА 66

Как определить индексы сезонности для временнˆого ряда?

Известно, что компания W almart ожидает большого роста продаж в четвертом
квартале года (благодаря праздникам). Если это не учесть, трудно составить точный прогноз квартальных доходов компании W almart. Более полно представить
модель продаж компании позволяют индексы сезонности. Квартальные индексы
сезонности для доходов Walmart:
квартал 1 (январь — март): 0,90;
квартал 2 (апрель — июнь): 0,98;
квартал 3 (июль — сентябрь): 0,96;
квартал 4 (октябрь — декабрь): 1,16.
Эти индексы означают , например, что объем продаж в четвертом квартале, как
правило, на 16% выше, чем объем продаж для квартала в среднем.
Среднее для
индексов сезонности должно быть равно 1.
Проверьте свое понимание материала, ответив на следующий вопрос: если объем
продаж компании Walmart в четвертом квартале 2013 г . составил 200 млрд долларов, а в первом квартале 2014 г. — 180 млрд долларов, идут ли дела в компании
Walmart лучше или хуже? Ключом к ответу на вопрос является устранение влияния сезонных изменений на объемы продаж и выражение объема продаж для каждого квартала относительно «среднего» квартала. Например, объем продаж в четвертом квартале 2013 г. эквивалентен продажам на сумму 200/1,16 = 172,4 млрд
долларов в «среднем» квартале, а объем продаж в первом квартале 2014 г . эквивалентен продажам на сумму 180/0,9 = 200 млрд долларов в «среднем» квартале. Таким образом, несмотря на то что фактический объем продаж в компании
Walmart снизился на 10%, по всей видимости, объем продаж увеличивается на
(200/172,4) – 1 = 16% за квартал. Этот простой пример показывает , насколько
важны индексы сезонности компании или продукта.

Существует ли простой способ включить тренд и сезонность в прогнозирование будущих продаж продукта?

Теперь давайте прибегнем к простому методу прогнозирования «по отношению
к скользящему среднему». Этот метод позволяет быстро вычислить тренд и индексы сезонности временного ряда и упрощает прогнозирование будущих значений временного ряда. Результаты моего ответа на вопрос — на рис. 66.1 и в файле
Ratioma.xlsx.
Начнем с оценки уровня ряда с исключенной сезонной составляющей для каждого
периода (с использованием центрированных скользящих средних). Затем к оценкам с исключенной сезонной составляющей (в столбцеG) подберем линию тренда.
Далее определим индекс сезонности для каждого квартала. Наконец, вычислим
будущий уровень ряда путем экстраполяции линии тренда и затем спрогнозируем
объемы продаж путем включения сезонной составляющей в оценку линии тренда.
Ниже описаны подробные шаги.

Метод прогнозирования «по отношению к скользящему среднему»

707

Рис. 66.1. Данные для прогнозирования по «отношению к скользящему среднему»

Вычисление скользящих средних. Сначала для каждого квартала вычислите скользящее среднее за четыре квартала (четыре квартала устраняют сезонность) путем усреднения значений предыдущего квартала, текущего квартала
и двух следующих кварталов. Для этого скопируйте формулу =СРЗНАЧ(E5:E8)
из F6 в F7:F22. Например, для второго квартала скользящее среднее равно
0,25 × (24 + 44 + 61 + 79) = 52.
Вычисление центрированных скользящих средних. Скользящее среднее для
второго квартала центрируется кварталом 2,5, а скользящее среднее для третьего квартала — кварталом 3,5. У среднение этих двух скользящих средних
дает центрированное скользящее среднее, оценивающее уровень процесса
в конце третьего квартала. Скопируйте формулу =СРЗНАЧ(F6:F7) из G7 в G8:G22
для вычисления уровня ряда в каждом периоде — без сезонности!
Подбор линии тренда к центрированным скользящим средним. С помощью
центрированных скользящих средних подберите линию тренда для оценки будущего уровня ряда.
В ячейке F1 я использовал формулу =НАКЛОН(G7:G22;B7:B22) для нахождения
наклона линии тренда, а в ячейкеF2 по формуле =ОТРЕЗОК(G7:G22;B7:B22) я вычислил начальную ординату линии тренда. Теперь можно рассчитать уровень
ряда в квартале t как 6,94t + 30,17. Скопируйте формулу =intercept+slope*B23 из
G25 в G26:G28 для вычисления уровня ряда в 21-м квартале и далее.

708

ГЛАВА 66

Вычисление индексов сезонности. Напомню, что индекс сезонности для квартала, например 2,0, означает, что объем продаж в этом квартале в два раза превышает объем продаж для «среднего» квартала, а индекс сезонности 0,5 для
квартала означает, что объем продаж в этом квартале составляет половину
от объема продаж «среднего» квартала. Для определения индексов сезонности сначала вычислим отношение фактических продаж к центрированному
скользящему среднему для каждого квартала. Для этого скопируйте формулу
=E7/G7 из ячейки H7 в H8:H22. Как видите, для каждого первого квартала продажи составили 71, 77, 90 и 89% от среднего, поэтому индекс сезонности для первого квартала можно вычислить как среднее для этих четырех величин (82%).
Для вычисления начальной оценки индексов сезонности скопируйте формулу
=СЗНАЧЕСЛИ($D$7:$D$22;J3;$H$7:$H$22) из ячейки K3 в K4:K6. Эта формула усредняет четыре оценки, имеющиеся для индекса сезонности первого квартала.
К сожалению, полученные индексы сезонности не равны в среднем 1. Для
обеспечения этого условия скопируйте формулу =K3/СРЗНАЧ($K$3:$K$6) из L3
в L4:L6.
Прогнозирование продаж для кварталов 21–24. Для создания прогноза продаж в каждом будущем квартале просто умножьте вычисленный уровень ряда
для каждого квартала (из столбца G) на соответствующий индекс сезонности.
Вычислите окончательный прогноз для кварталов 21–24, скопировав формулу
=ВПР(D25;season;3)*G25 из ячейки I25 в I26:I28.
Если тренд ряда недавно изменился, можно оценить его на основе самых последних данных. Например, можно получить новую оценку тренда с помощью центрированных скользящих средних для кварталов 13–18 по формуле
=НАКЛОН(G17:G22;B17:B22). В результате предполагаемый тренд составит 8,09 единицы за квартал. Если требуется предсказать продажи, например, в квартале 22, то
для оценки уровня ряда в квартале 22 необходимо добавить 4*(8,09) к последнему
имеющемуся центрированному скользящему среднему (160,13) для квартала 18.
Затем результат следует умножить на индекс сезонности второго квартала (0,933)
и получить окончательный прогноз для объема продаж в этом квартале: (160,13 +
+ 4 × 8,09) × 0,933 = 179,6 единицы.

Задание
В файле Walmartdata.xlsx содержатся данные о квартальных доходах W almart за
1994–2009 гг. Используйте метод «по отношению к скользящему среднему» для
прогнозирования доходов за третий и четвертый кварталы 2009 г . и за первый
и второй кварталы 2010 г. На основе данных за 53–60-й кварталы создайте оценку
тренда, которую будете использовать в прогнозах.

Г Л А В А 67

Прогноз для особых случаев

Обсуждаемые вопросы
Как определить, влияют ли конкретные факторы на поток клиентов?
Как оценить точность прогноза?
Как проверить, являются ли ошибки прогноза случайными?

Для студенческого проекта в начале 1990-х гг. (то есть до эры прямых депозитов)
я вместе со студентами пытался спрогнозировать количество клиентов, ежедневно посещающих филиал Eastland Plaza Branch кредитного союза У ниверситета
Индианы. Благодаря встречам с директором филиала были выявлены следующие
факторы, влияющие на количество клиентов:
месяц года;
день недели;
день выдачи зарплаты профессорско-преподавательскому составу или служебному персоналу;
день до или после праздничного дня.

Ответы на вопросы
?

Как определить, влияют ли конкретные факторы на поток клиентов?

Собранные данные находятся на листе Original в файле Creditunion.xlsx (рис. 67.1).
Если на основе этих данных выполнить регрессионный анализ с фиктивными переменными (см. главу 60 «Включение качественных факторов во множественную
регрессию»), то зависимой переменной будет количество обслуживаемых каждый
день клиентов (данные в столбце E). Кроме того, потребуется 19 независимых переменных:
одиннадцать для вычисления месяца (12 месяцев минус 1);
четыре для вычисления дня недели (5 рабочих дней минус 1);
две для вычисления типа дня выплаты ежемесячной зарплаты;
две для вычисления дня, следующего за праздничным днем, и дня, предшествующего праздничному дню.

710

ГЛАВА 67

Но в Microsoft Excel допускается только 15 независимых переменных, поэтому
у нас проблема.

Рис. 67.1. Данные для прогноза потока клиентов в кредитном союзе

Если регрессионная модель прогнозирования требует более 15 независимых переменных, то вычислить коэффициенты независимых переменных можно с помощью инструмента Excel Поиск решения (Solver). Кроме того, в Excel можно вычислить значения R2 между прогнозируемым и фактическим трафиками клиентов
и значение стандартного отклонения для ошибок прогнозирования. Для анализа
этих данных (рис. 67.2) я создал уравнение прогноза, использовав таблицу поиска дня недели, месяца и других факторов. Затем я применил инструмент Поиск
решения (Solver) для выбора коэффициентов каждого уровня каждого фактора,
дающих минимальную сумму квадратичных ошибок. (Ошибка для каждого дня
равна разности между фактическим и прогнозируемым количеством клиентов.)
Рассмотрим пример подробно.
Начнем с создания индикаторных переменных (в столбцах G–J) для дня выплаты зарплаты персоналу (SP), дня выплаты зарплаты преподавателям (F AC), дня
перед праздником (BH) и дня после праздника (AH) — см. рис. 67.1. Например,
значение 1, введенное в ячейки G4, H4 и J4, указывает, что 2 января было днем
выплаты зарплаты персоналу, днем выплаты зарплаты преподавателям и днем после праздника. В ячейке I4 стоит 0, показывающий, что 2 января — не день перед
праздником.
Прогноз определяется постоянной (которая позволяет центрировать прогнозы
для повышения точности) и влиянием каждого дня недели, каждого месяца, дня

Прогноз для особых случаев

711

выплаты зарплаты персоналу, дня выплаты зарплаты преподавателям, дня перед
праздником и дня после праздника. Я ввел пробные значения для всех этих параметров (изменяемые ячейки инструмента Поиск решения) в диапазон ячеек O4:O26,
показанный на рис. 67.2. Затем Поиск решения выберет значения, при которых модель наилучшим образом соответствует данным. Для каждого дня прогноз по количеству клиентов будет дан на основании следующего уравнения:
прогнозируемое количество клиентов = постоянная + (влияние месяца) + (влияние
дня недели) + (влияние дня выплаты з/п персоналу, если есть) + (влияние дня выплаты з/п преподавателям, если есть) + (влияние дня перед праздником, если есть) +
+ (влияние дня после праздника, если есть).

С помощью этой модели вы можете вычислить прогноз ежедневного количества
клиентов, скопировав из K4 в K5:K257 следующую формулу:
=$O$26+ВПР(B4;$N$14:$O$25;2)+ВПР(D4;$N$4:$O$8;2)+G4*$O$9+H4*$O$10+
+I4*$O$11+J4*$O$12.

В ячейке O26 вычисляется постоянный член. Функция ВПР(B4;$N$14:$O$25;2)
возвращает коэффициент влияния для текущего месяца, а функция
ВПР(D4;$N$4:$O$8;2) — коэффициент влияния дня недели для текущей недели.
Часть формулы G4*$O$9+H4*$O$10+I4*$O$11+J4*$O$12 вычисляет влияние, если
текущий день отмечен как SP, FAC, BH или AH.
Скопировав формулу =(E4-K4)^2 из L4 в L5:L257, я вычислил квадратичную ошибку для каждого дня. Затем в ячейке L2 я вычислил сумму квадратичных ошибок
по формуле =СУММ(L4:L257).

Рис. 67.2. Изменяемые ячейки и прогнозы по клиентам

712

ГЛАВА 67

В ячейке R4 я рассчитал среднее значение для изменяемых ячеек дня недели по
формуле =СРЗНАЧ(O4:O8), а в ячейке R5 — среднее значение для изменяемых ячеек
месяца по формуле =СРЗНАЧ(O14:O25). Позже я приму среднее влияние дня месяца и дня недели равным нулю; это гарантирует , что для месяца или дня недели с положительным влиянием количество клиентов будет больше, чем среднее
количество клиентов, а для месяца или дня недели с отрицательным влиянием
количество клиентов будет меньше среднего.
Вы можете использовать настройки инструмента Поиск решения (Solver), указанные на рис. 67.3, для выбора параметров прогнозирования, минимизирующих
сумму квадратов ошибок. Для этого на вкладке Данные (Data) в группе Анализ
(Analyze) щелкните Поиск решения (Solver).
ПРИМЕЧАНИЕ
Для установки надстройки Поиск решения (Solver) на вкладке Файл (File) выберите
команду Параметры (Options), затем среди параметров Excel выберите раздел Надстройки (Add-Ins). В нижней части диалогового окна в раскрывающемся списке Управление (Manage) выберите Надстройки Excel (Excel Add-Ins) и нажмите Перейти (Go).
В диалоговом окне Надстройки (Add-Ins) установите флажок Поиск решения (Solver
Add-In) и нажмите OK. На вкладке Данные (Data) в группе Анализ (Analysis) появится
кнопка Поиск решения (Solver). Подробную информацию см. в главе 29 «Введение
в оптимизацию с надстройкой Поиск решения».

Рис. 67.3. Диалоговое окно Параметры поиска решения
для определения параметров прогнозирования

Прогноз для особых случаев

713

В модели поиска решения коэффициенты для месяца, дня недели, BH, AH, SP ,
FAC и постоянная изменяются в целях минимизации суммы квадратов ошибок.
Можно также наложить ограничение (равенство нулю) на средние значения влияния дня недели и дня месяца. После этого Поиск решения (Solver) выдаст результаты, показанные на рис. 67.2. Например, самым загруженным днем недели является пятница, а самым загруженным месяцем — июнь. День выплаты зарплаты
персоналу увеличивает прогнозируемое значение (при прочих равных условиях,
на латыни — ceteris paribus) на 397 клиентов.

Как оценить точность прогноза?

J1 значение R2
Чтобы оценить точность прогноза, вычислите в ячейке
между прогнозируемым и фактическим числом клиентов по формуле
=КВПИРСОН(E4:E257;K4:K257). Функция КВПИРСОН (RSQ) вычисляет процент фактического изменения количества клиентов, который объясняется моделью прогнозирования. Здесь независимые переменные объясняют 77% ежедневной вариации количества клиентов.

Вычислите ошибку для каждого дня в столбце M, скопировав формулу =E4-K4 из
M4 в M5:M257. Достаточно хорошее приближение к стандартной погрешности прогноза дает стандартное отклонение ошибок. Это значение вычисляется в ячейке
M1 по формуле =СТАНДОТКЛОН(M4:M257). Таким образом, приблизительно 68%

прогнозов верны с точностью до 163 клиентов, 95% прогнозов — с точностью до
326 клиентов и т. д.
Попробуем найти выбросы. Напомню, что наблюдение является выбросом,
если абсолютное значение ошибки прогноза превышает в два раза стандартную
ошибку регрессии. Выделите диапазон M4:M257 (выделите ячейку M4 и нажмите
Ctrl+Shift+↓) и затем на вкладке Главная (Home) в списке Условное форматирование
(Conditional Formatting) выберите Создать правило (New Rule). В диалоговом окне
Создание правила форматирования (New Formatting Rule) щелкните на типе Использовать формулу для определения форматируемых ячеек (Use a formula to determine
which cells to format). Заполните описание правила, как показано на рис. 67.4.
(Подробнее об условном форматировании см. в главе 24 «Условное форматирование».)
После выбора формата с красным шрифтом любая ошибка, абсолютное значение
которой в два раза превышает стандартное отклонение ошибок, будет отображена
красным цветом. Как видите, модель часто занижает число клиентов для первых
трех дней месяца. Также на второй неделе марта (весенние каникулы) модель завышает прогнозы, а за день до весенних каникул прогноз значительно занижен.
Чтобы это устранить, я добавил на листе 1st Three Days (файл Creditunion.xlsx) изменяемые ячейки для каждого из первых трех дней месяца, для весенних каникул
и для дня перед весенними каникулами. В ячейки O26:O30 для этих новых эффектов я добавил пробные значения. Я включил эффект от первых трех дней месяца,
скопировав из ячейки K4 в K5:K257 следующую формулу:

714

ГЛАВА 67

=$O$25+ВПР(B4;$N$13:$O$24;2)+ВПР(D4;$N$4:$O$8;2)+G4*$O$9+H4*$O$10+
+I4*$O$11+J4*$O$12+ ЕСЛИ(C4=1;$O$26;ЕСЛИ(C4=2;$O$27;ЕСЛИ(C4=3;$O$28;0))).

Рис. 67.4. Условное форматирование для обнаружения выбросов в прогнозе

Эффект от первых трех дней месяца вычисляет часть
ЕСЛИ(C4=1;$O$26; ЕСЛИ
(C4=2; $O$27;ЕСЛИ(C4=3;$O$28;0))). В ячейки K52:K57 я вручную ввел коэффициенты для весенних каникул. Например, в ячейке K52 я добавил к формуле +O29,
а в ячейки K53:K57 я добавил +O30.
Включив в диалоговом окне Параметры поиска решения (Solver Parameters) новые
изменяемые ячейки, я получил резуль таты, показанные на рис. 67.5. Обратите
внимание, что для первых трех дней месяца количество клиентов возросло (вероятно, благодаря поддержке правительства и чекам от социальной защиты),
а в весенние каникулы количество клиентов снизилось. Кроме того, как видно из
рис. 67.5, точность прогнозирования также улучшилась. Значение R2 (рассчитанное при помощи функции КВПИРСОН (RSQ) в ячейке J1) повысилось до 87%, а стандартная ошибка уменьшилась до 122 клиентов.
Ошибки прогноза для недели с 24 по 31 декабря показывают (рис. 67.6), что модель значительно завышает прогноз количества клиентов для дней на этой неделе. Она также занижает прогнозируемое число клиентов для недели перед Рождеством. Дальнейшее изучение ошибок прогноза (часто называемых остатками)
привело к следующим выводам.
День благодарения отличается от обычных праздников тем, что в день после
него кредитный союз загружен работой намного меньше, чем ожидалось.

Прогноз для особых случаев

715

Рис. 67.5. Параметры прогнозирования и прогнозы, включающие весенние каникулы
и первые три дня месяца

Накануне Страстной пятницы сотрудники действительно сильно загружены,
так как многие уезжают из города на Пасху.
День уплаты налогов (16 апреля) также является более загруженным днем, чем
ожидалось.
Неделя перед началом осеннего семестра в Университете Индианы (последняя
неделя августа) не загружена, вероятно, потому, что многие сотрудники и преподаватели берут летом отпуск.
На листе Christmas week я добавил изменяемые ячейки для учета этих факторов.
После добавления новых параметров как изменяемых ячеек я снова запустил

Рис. 67.6. Ошибки для рождественской недели

716

ГЛАВА 67

Поиск решения. Результаты представлены на рис. 67.7. Значение R2 повысилось до

92%, а стандартная ошибка снизилась до 98,61 клиента! Обратите внимание, что
из-за влияния недели после Рождества ежедневное число клиентов снизилось на
359, в день перед Днем благодарения добавилось 607 клиентов, в день после Дня
благодарения количество клиентов уменьшилось на 161 человека и т. д.

Рис. 67.7. Окончательные параметры прогноза

Обратите также внимание, насколько усовершенствовалась модель прогнозирования при использовании выбросов. Если выбросы имеют нечто общее (как, например, первые три дня месяца), включите в качестве независимой переменной
обобщающий фактор, и ошибка прогноза снизится.

Как проверить, являются ли ошибки прогноза случайными?

Хороший метод прогнозирования должен создавать случайные ошибки прогноза,
или остатки. Под случайными ошибками я понимаю ошибки, которые не носят закономерного характера. Если ошибки прогноза случайны, знак ошибок должен
меняться (с плюса на минус или с минуса на плюс) примерно в половине случаев.
Таким образом, широко применяемым тестом для оценки случайности ошибок
прогноза является проверка перемены знака ошибок. Для n наблюдений неслучайность ошибок имеет место, если перемен знака меньше, чем

Прогноз для особых случаев

717

или больше, чем

На листе Christmas week (см. рис. 67.7) я определил число перемен знака в остатках,
скопировав формулу =ЕСЛИ(M5*M4 0, мы получаем, что
P (Дождь_в_выходные) < 1, то есть необязательно в выходные будет дождь
(кроме как в Сиэтле).
В качестве второго примера на правило сложения рассмотрим броски двух кубиков. Какова вероятность, что хотя бы на одном из них выпадет 4? Если событие
A = на_первом_кубике_4, а B = на_втором_кубике_4, мы получаем P (A) = 1/6,
P (B) = 1/6 и P (A И B) = 1/36. Тогда:
P (на_первом_или_на_втором_кубике_4) = (1/6) + (1/6) – (1/36) = 11/36.

Введение в теорию вероятности

721

Что такое независимые события?

Два события, A и B, являются независимыми, если наступление одного из них не
изменяет вероятность наступления другого. Следовательно, два события A и B
являются независимыми тогда и только тогда, когда P (A И B) = P (A)*P(B). Для
случая более двух событий строгое определение независимости событий выходит
за рамки нашего рассмотрения, но если n событий A1, A2, …, An являются независимыми, верно следующее:
P (A1 И A2 И , … An) = P (A1)*P (A2),… *P (An –1)*P (An).
Следующие два «интуитивных» примера должны прояснить определение независимых событий:
Пусть событие A = Индекс_Доу – Джонса_вырастет_в_2021 г ., а событие
B = Houston_Texans_выиграют_Суперкубок_в_2021 г. Наступление одного из
этих событий не изменяет вероятность наступления другого, поэтому эти события являются независимыми.
Пусть событие A = Chicago_Cubs_выиграют_Мировую_серию_2021,
а B = Houston_Astros_выиграют_Мировую_серию_2021. Ясно, что если наступит событие A, то вероятность события B падает до 0, поэтому события A
и B не являются независимыми. Также ясно, что события A и B не могут быть
и взаимоисключающими, и независимыми (см. задание 6).
А вот примеры для закрепления понимания концепции независимых событий.
Предположим, вы подбрасываете монету ибросаете кубик. Какова вероятность
того, что монета упадет вверх орлом и что на кубике выпадет 6 очков? Если
определить событие A = монета упадет вверх орлом, а B = на кубике выпадет 6,
то очевидно, что события A и B независимые. Так как P (A) = 1/2 и P (B) = 1/6,
то P(монета упадет вверх орлом И на кубике выпадет 6) = (1/2)*(1/6) = 1/12.
Предположим, из колоды случайным образом выбрана карта. Вы выбрали
одну карту. Являются ли независимыми события, что вытащена карта масти
пик И что вытащен туз? Пусть событие A = масть карты пика, а B = вытащен
туз. Так как в колоде из 52 карт 13 пик и 4 туза, P (A) = 13/52 и P (B) = 4/52. Также одна карта в колоде и туз, и пика (туз пик), поэтому P (пика И туз) = 1/52.
Поскольку P (пика)*P (туз) = (13/52)*(4/52) = 1/52, мы получаем, что A и B
независимые события.
Теперь предположим, что перед вытаскиванием карты мы убрали из колоды
двойку пик. Остаются ли после этого независимыми события A и B? Теперь
P (A) = 12/51, P (B) = 4/51, а P (A И B) = 1/51. Так как (12/51)*(4/51) не равно
(1/51), события A и B не являются независимыми.
Наконец, предположим, вы бросаете три кубика. Какова вероятность, что выпадет хоть одна шестерка? Пусть событие Ai = на кубике i не выпало 6. Тогда
P (Ai) = 1 — (1/6) = 5/6. Тогда по правилу дополнений мы получаем:
P (по крайней мере 1 шестерка) = 1 – P (0 шестерок).

722

ГЛАВА 68

Так как последовательные броски кубика являются независимыми событиями,
P (0 шестерок) = P (A1)*P (A2)*P (A3) = (5/6)3 = 125/216. Следовательно, мы
получим:
P (по крайней мере 1 шестерка) = 1 – (125/216) = 91/216 = 0,42.

Что такое условная вероятность?

Часто требуется узнать, как наступление одного события изменяет вероятность
наступления другого события. Формально мы записываем условную вероятность
наступления события B, если известно, что событие A уже произошло, как P (B|A).
Эта запись читается как «вероятность наступления события B при условии, что событие A уже произошло». P (B | A) может быть вычислено из следующего уравнения:

Это уравнение удобно переписать в виде P (A И B) = P (A)*P(B|A) или P (A И B) =
= P (B)*P (A|B).
События A и B являются независимыми тогда и только тогда, когдаP (B|A) = P (B).
Следующие два примера раскрывают смысл условной вероятности:
Предположим, вы бросаете два кубика. Определим событие A = выпала хотя
бы 1 шестерка, а B = сумма очков на двух кубиках равна 10. Какова P (B|A)?
P (A и B) = 2/36 и P (A) = 1 – P(нет шестерок) = 1 – (5/6) 2 = 11/36. Следовательно, получим:
P (B|A) = (2/36)/(11/36) = 2/11.
Предположим, вы вытянули туза из колоды карт. Если теперь вы вытягиваете
вторую карту, какова вероятность, что это тоже будет туз? Определим событие
A = первая карта туз, а B = вторая карта туз. После изъятия из колоды первой
карты (туза) колода содержит 51 карту и 3 туза, поэтому P (B|A) = 3/51 = 1/17.

Что такое формула полной вероятности?

Формула полной вероятности связана с вычислением вероятности события путем
сложения вероятностей нескольких взаимоисключающих событий. Иногда требуется вычислить вероятность события, находящегося в зависимости от других
событий. Например, предположим, что 5% подержанных машин пострадали во
время наводнения и 80% этих машин впоследствии имеют проблемы с двигателем. Также предположим, что 10% машин, которые не пострадали во время наводнения, впоследствии имеют проблемы с двигателем. Какова вероятность того,
что произвольно выбранный автомобиль будет иметь проблемы с двигателем?
Решая эту задачу, определим событие ПД = машина впоследствии имеет проблемы с двигателем, НВ = машина пострадала от наводнения. Т еперь событие ПД

Введение в теорию вероятности

723

можно разложить на два взаимоисключающих события: «машина, пострадавшая
от наводнения, имеет проблемы с двигателем» и «машина, не пострадавшая от наводнения, имеет проблемы с двигателем» и отразить это в следующей формуле:
P (ПД) = P (ПД И НВ) + P (ПД И не НВ) = P (ПД | НВ)*P (НВ) +
+ P (ПД |НЕ НВ)*P (НЕ НВ) = (0,80)*(0,05)+(0,10)*(0,95) = 0,135.
Также вы можете создать таблицу сопряженности признаков, в которой отражаются все возможности. Ниже представлен вариант таблицы сопряженности:
Проблемы с двигателем

Нет проблем с двигателем

НВ

0,04

0,01

не НВ

0,095

0,855

Числа в столбец Нет проблем с двигателем добавлены для демонстрации, какие слагаемые в первой строке дадут 0,05 и какие во второй дадут 0,95.

Что такое теорема Байеса?

После того как вы разобрались с условной вероятностью и формулой полной вероятности, несложно понять суть теоремы Байеса. Во многих ситуациях мы пытаемся оценить вероятность различных состояний окружающего мира. Со временем
мы получаем информацию, которая меняет наши вероятностные оценки. Например, представим себе 40-летнюю женщину без факторов риска заболевания раком
молочной железы. Состояние окружающего мира можно определить событиями
C = женщина имеет заболевание раком и NC = женщина не имеет заболевания
раком. Без какой-либо дополнительной информации вероятности этих событий
(известные как априорные вероятности) равны P (C) = 0,004 и P (NC) = 0,996.
Теперь мы получаем дополнительную информацию (результаты маммографии),
которая меняет наши оценки априорных вероятностей. Предположим, маммография выдает положительный (+) результат. Для изменения наших оценок вероятностей нам необходимо знать вероятность положительного резуль тата теста для
каждого из состояний мира. Вероятности положительного резуль тата теста составляют P (+|C) = 0,80 и P ((+|NC) = 0,10. Теперь нам требуется изменить априорную вероятность рака (0,004) после получения положительного результата теста.
Эта новая вероятность (P (C|+) называется апостериорной вероятностью. Применяя определение условной вероятности и правило полной вероятности, получаем:

Возможно, это удивительно, но даже после положительного резуль тата теста существует только маленькая вероятность (слава богу!), что эта женщина имеет заболевание раком. Из-за того что большинство женщин не больны раком молочной

724

ГЛАВА 68

железы, многие из их маммографий дадут ложные положительные резуль таты.
Другой способ убедиться в этом — взглянуть на типичную выборку из 10 000 женщин. Таблица сопряженности признаков показывает , что для 10 000 женщин заболевание и его отсутствие разделятся следующим образом:

Рис. 68.1. Интуитивное объяснение примера с маммографией

В случае положительного результата теста мы получаем в столбце F 1028 женщин.
Следовательно, при положительном результате теста для женщины вероятность
заболевания раком равна 32/1028 = 0,031.
В качестве последнего примера теоремы Байеса рассмотрим решение парадокса
Монти Холла, представленного Мэрилин Вос Савант (Marilyn Vos Savant) в ее
колонке «Спросите Мэрилин» в журнале Parade.
За одной из трех дверей находится машина, а за двумядругими — коза. Я выбираю
дверь (например, дверь 1). После этого Монти Холл (ведущий передачи «Давайте
заключим сделку)» открывает дверь (дверь 2 или дверь 3), за которой находится
коза. После этого вам предлагают поменять выбор двери. Сделаете ли вы это?
Предположим, Монти открыл дверь 2. Вот относящиеся к этой проблеме события:
Состояния мира — это события D1, D2, D3, отражающие, что машина находится за дверью i.
Определим, что S1, S2, S3 — события; Монти говорит , что машина находится
за дверью i.
Нам известны априорные вероятности P (D1) = P (D2) = P (D3) = 1/3.
Имеются следующие вероятности: P (S3|D1) = 1/2, P (S2|D1) = 1/2, P (S3|D2) = 1
и P (S2|D3) = 1.
Мы знаем, что машина находится или за дверью 3, или за дверью 1. Применяя
теорему Байеса, мы получаем следующее:

.
Следовательно, P(D1|S2) = 1 – (2/3) = 1/3. Значит, мы должны изменить наш выбор на дверь 3!

Введение в теорию вероятности

725

ПРИМЕЧАНИЕ
Ответы на задания этой главы находятся в файле Word, а не Excel. См. файл Chapter68_
answers.docx в папке с ответами к главе 68.

Задания
1. Найдите вероятность каждой возможной суммы очков при броске двух кубиков.
2. При бросании трех кубиков определите вероятность выпадения в сумме 9 очков.
3. В Carver High School 20% студентов играют в бейсбол и 15% — в баскетбол.
Пять процентов играет и в то и в другое. Какая часть студентов играет в бейсбол или в баскетбол?
4. Пусть событие A = на кубике выпало четное число очков, а B = на кубике выпало одно или два очка. Являются ли события A и B независимыми?
5. Являются ли события A и не A взаимоисключающими?
6. Могут ли взаимоисключающие события быть независимыми?
7. При игре в крэпс вы бросаете два кубика. Сумма очков 7 или 11 при первом
броске приносит победу. Какова вероятность победы при первом броске?
8. Вы вытаскиваете из колоды две карты (без возвращения). Какова вероятность, что это будет две трефы?
9. На колесо рулетки нанесены числа 0, 00, 1, 2, …, 36. Предположим, что при
каждом из 25 пусков рулетки вы ставили на 00. Какова вероятность, что вы
выиграли хотя бы раз из этих 25 пусков?
10. Предположим, что 10% взрослых людей смотрят шоу «Холостяк» (
The
Bachelor). Предположим, что 80% аудитории этого сериала составляют женщины и что мужчины составляют половину всех взрослых. Вычислите вероятность, что данная женщина или мужчина является зрителем этого сериала.
11. Какая доля мужчин и женщин смотрит шоу The Bachelor?
12. В примере с машинами, пострадавшими от наводнения, вам говорится, что машина имеет проблемы с двигателем. Какова вероятность, что машина до этого
пострадала от наводнения?
13. В комоде два выдвижных ящика. В каждом ящике лежат две монеты; известно, что в одном ящике находятся две золотые монеты, а в другом — одна золотая и одна серебряная. Вы случайным образом выбираете ящик и вытаскиваете монету. Выбранная монета золотая. Какова вероятность, что оставшаяся
в ящике монета тоже золотая?

726

ГЛАВА 68

14. 85% всех такси синего цвета, а остальные зеленого. Было определено, что такси, которое попало в аварию и водитель после этого скрылся, было зеленым.
Люди определяют верно цвет такси в 80% случаев. При опросе большая часть
студентов Стэнфордского университета утверждала, что вероятность того,
что такси действительно было зеленым, равна 80%. Вы согласны с этим?
15. В урне находится девять шаров. На каждом из шаров написан номер от 1 до 9.
Вытащите два шара (с возвращением). Какова вероятность, что вы вытащите
шар с одним и тем же номером?
16. Бросьте кубик и пусть событие A = выпало нечетное число очков, аB = выпало
число ≥ 4. Найдите P(A|B).
17. Каждый из двух механизмов работает с вероятностью 0,9. Работа или сбой
механизмов происходят независимо. Если механизмы подключены последовательно, для работы системы требуется, чтобы работали оба механизма.Если
механизмы подключены параллельно, для работы системы требуется, чтобы
работал хотя бы один механизм. Какова вероятность, что система работает ,
при последовательном и при параллельном подключении?
18. Следующая таблица представляет статистику по приему мужчин и женщин
в большой американский университет. Общее число мест для приема приведено в скобках, число принятых — вне скобок. Можно видеть, что процент принятых мужчин выше, чем процент принятых женщин. На основании применения
статистики обоснуйте, есть ли в университете дискриминация женщин.
Мужчины

Женщины

Простые специальности

864 (1386)

106 (133)

Сложные специальности

334 (1306)

451 (1702)

19. Компания имеет производство в Хьюстоне и в Далласе. Семьдесят процентов
сотрудников работает в Хьюстоне, а 30% — в Далласе. Каждый год 3% хьюстонских и 5% далласских сотрудников получают травмы. Если случайным
образом выбрать сотрудника, получившего в прошлом году травму, какова вероятность, что он работает в Хьюстоне?
20. Студентка МБА изучает финансы и маркетинг . Предположим, эта студентка
имеет 90%-ную вероятность получения оценки A по финансам и 80%-ную вероятность получения оценки A по маркетингу. Если ее успешность в каждом
из курсов не зависит от успешности в другом, какова вероятность, что она получит хотя бы одну оценку A?
21. В вазе находится четыре красных и три синих шара. Из вазы вынимаются два
шара (без возвращения). Известно, что второй шар синий. Какова вероятность, что первый шар синий?
22. Предположим, вы бросаете два кубика. Пусть событие A = на первом кубике
выпало 3, а B = сумма очков на двух кубиках равна 8. Являются ли события A
и B независимыми?

Введение в теорию вероятности

727

23. Среди страхователей страховой компании 80% являются высокорисковыми
и 20% — низкорисковыми. Предположим, никто не получает более одной
травмы в год. Также предположим, что 10% высокорисковых и 3% низкорисковых людей получают травму в течение года. Если вы случайным образом
выбрали страхователя, получившего травму в прошлом году, какова вероятность того, что он относится к высокорисковым страхователям?
24. В ежегодном турнире университетских команд первого дивизиона по баскетболу есть четыре команды, которые могут с вероятностью 3% победить команду с первым номером посева. До начала чемпионата определите вероятность того, что хотя бы одна команда с 16-м номером посева обыграет команду
с 1-м номером посева.
25. Предположим, один из 1000 людей является лжецом (неспособен говорить
правду). Также предположим, что точность детектора лжи составляет 98%.
Это означает, что если человек лжет , есть 98%-ная вероятность, что детектор
укажет, что этот человек лжет. Кроме того, если человек не лжет, есть 98%-ная
вероятность, что детектор укажет , что этот человек не лжет . Если детектор
лжи показывает, что человек лжет, какова вероятность того, что человек действительно лжет?
26. После броска двух кубиков определим событие A = сумма очков является четным числом, а B = на первом кубике выпало пять очков. Являются ли события A и B независимыми?
27. В 40% недель супермаркет снижает цену на макароны и сыр. В 20% недель супермаркет выставляет макароны и сыр на рекламных стойках, и в 15% недель
супермаркет снижает цену на макароны и сыр и выставляет макароны и сыр
на рекламных стойках. В какой доле недель макароны и сыр находятся на распродаже или на рекламных стойках?
28. Известно, что из колоды вытащены две карты, и обе черви. Какова вероятность того, что первая карта была двойка червей?
29. В ящике лежат два нормальных четвертака и один четвертак, у которого с двух
сторон орел. С закрытыми глазами вы вытаскиваете одну монету , ваш друг
подбрасывает ее и говорит , что она упала орлом вверх. Какова вероятность
того, что вы выбрали монету с двумя орлами?
30. Вы бросаете два кубика. Пусть событие A = сумма очков равна 10, а B = на
первом кубике выпало нечетное число очков. Являются ли события A и B независимыми?
31. Среди страхователей страховой компании 20% являются высокорисковыми,
40% — низкорисковыми и 40% — среднерисковыми. Среди низкорисковых
страхователей 2% получают травмы в течение года, среди среднерисковых —
4%, а среди высокорисковых — 20%. Если страхователь получил травму в течение года, какова вероятность того, что он относится к высокорисковым
страхователям?

ГЛ А В А 69

Введение в случайные величины
Обсуждаемые вопросы
Что такое случайная величина?
Что такое дискретная случайная величина?
Что такое среднее, дисперсия и стандартное отклонение случайной величины?
Что такое непрерывная случайная величина?
Что такое функция плотности вероятности?
Что такое независимые случайные величины?

В современном мире мы уверены только в том, что ни в чем не можем быть уверены. В следующих девяти главах я покажу вам несколько эффективных методов
включения неопределенности в бизнес-модели. Ключом к моделированию неопределенности является умение использовать случайные величины.

Ответы на вопросы
?

Что такое случайная величина?

Любая ситуация, исход которой не определен, называется экспериментом. Значение
случайной величины основывается на (неопределенном) резуль тате эксперимента.
Например, бросок двух кубиков является экспериментом, и случайная величина может быть определена как сумма очков, выпавших на каждом кубике. В этом примере
случайная величина могла быть равна 2, 3 и т . д. до 12. В качестве другого примера
можно привести эксперимент с продажей новой игровой приставки, для которой
случайная величина может быть определена как доля рынка этого нового продукта.

Что такое дискретная случайная величина?

Случайная величина дискретна, если она может принимать конечное число возможных значений. Вот несколько примеров дискретных случайных величин:
число потенциальных конкурентов;
число тузов, выпавших в пятикарточном покере;
количество дорожно-транспортных происшествий (надеюсь, 0!) в год;
число точек на игральной кости;

Введение в случайные величины

729

число штрафных бросков из 12, выполненных баскетболистом Кевином Дюрантом за игру.

Что такое среднее, дисперсия и стандартное отклонение случайной величины?

В главе 44 «Обобщение данных с помощью описательной статистики» обсуждались среднее, дисперсия и стандартное отклонение для множества данных. В сущности, среднее случайной величины (обозначаемое как µ) — это среднее значение,
которое можно было бы ожидать при многократном выполнении эксперимента.
Среднее случайной величины часто называют математическим ожиданием случайной величины. Дисперсия случайной величины (обозначаемая как s2) — это
среднее значение квадрата отклонения случайной величины от среднего, которое
можно было бы ожидать при многократном выполнении эксперимента. Стандартное отклонение случайной величины (обозначаемое как σ) — это просто корень
квадратный из ее дисперсии. Как и для множеств данных, среднее случайной величины является суммарным показателем для типичного значения случайной
величины, а дисперсия и стандартное отклонение оценивают разброс случайной
величины вокруг ее среднего.
В качестве примера вычисления среднего, дисперсии и стандартного отклонения
случайной величины рассмотрим предполагаемые доходы на фондовой бирже
в следующем году, регулируемые следующими вероятностями:
Вероятность

Доход на фондовой бирже

0,40

+20%

0,30

–20%

Выполненные вручную расчеты показывают следующее:
µ = 0,40 × (0,20) + 0,30 × (0,00) + 0,30 × (–0,20) = 0,02, или 2%;
s2 = 0,4 × (0,20 – 0,02) × 2 + 0,30 × (0,0 – 0,02) × 2 + 0,30 × (–0,20 – 0,02) × 2 =
= 0,0276.
Тогда σ = 0,166, или 16,6%.
Эти расчеты я проверил в файле Meanvariance.xlsx (рис. 69.1).
C9 по формуле
Среднее для дохода на фондовой бирже я вычислил в ячейке
=СУММПРОИЗВ(B4:B6;C4:C6). В этой формуле каждое значение случайной величи-

ны умножается на его вероятность, и затем произведения суммируются.
Для вычисления дисперсии дохода я определил квадрат отклонения каждого
=(B4-$C$9)^2
значения случайной величины от среднего, скопировав формулу
из D4 в D5:D6. Затем в ячейке C10 я вычислил дисперсию дохода как среднее

730

ГЛАВА 69

Рис. 69.1. Вычисление среднего, стандартного отклонения
и дисперсии случайной величины

квадратов отклонений по формуле =СУММПРОИЗВ(C4:C6;D4:D6). Наконец, в ячейке
C11 я вычислил стандартное отклонение дохода на фондовой бирже по формуле
=КОРЕНЬ(C10).

Что такое непрерывная случайная величина?

Непрерывная случайная величина — это случайная величина, которая может принимать очень большое или фактически бесконечное число значений, включающее
все значения на некотором интервале. Вот несколько примеров непрерывных случайных величин:
цена акции Microsoft через год, начиная с этого момента;
доля рынка для нового продукта;
объем рынка для нового продукта;
стоимость разработки нового продукта;
вес новорожденного;
чей-либо IQ;
процент трехочковых бросков Дирка Новицки в следующем сезоне.

Что такое функция плотности вероятности?

Дискретная случайная величина может быть задана набором значений и вероятностью появления каждого значения случайной величины. Поскольку непрерывная
случайная величина может принимать бесконечное число значений, вероятность
появления каждого значения непрерывной случайной величины перечислить
невозможно. Непрерывная случайная величина полностью описывается своей
функцией плотности вероятности . Например, функция плотности вероятности
для IQ случайно выбранного человека показана на рис. 69.2.
Функция плотности вероятности (ФПВ) обладает несколькими свойствами.
Значение ФПВ всегда больше или равно 0.
Площадь под ФПВ равна 1.

Введение в случайные величины

731

Рис. 69.2. Функция плотности вероятности для IQ

Высота ФПВ для значения x случайной величины пропорциональна вероятности того, что случайная величина примет значение в окрестностях x. Например, высота ФПВ для IQ = 83 составляет около половины высоты ФПВ для
IQ = 100. Это говорит о том, что вероятность для IQ ниже 83 приблизительно
в два раза меньше, чем вероятность для IQ около 100. Кроме того, поскольку
пик плотности приходится на значение 100, значение IQ, приблизительно равное 100, наиболее вероятно.
Вероятность того, что непрерывная случайная величина принимает диапазон
значений, равна соответствующей площади под графиком функции плотности.
Например, доля людей с IQ от 80 до 100 просто равна площади под графиком
функции плотности от 80 до 100.
Следует отметить, что дискретная случайная величина, принимающая много
значений, часто моделируется непрерывной случайной величиной (см. главу 72 «Нормальная случайная величина и Z-оценка»). Например, несмотря
на то что количество пакетов молока, продаваемых за день в небольшом продуктовом магазине, дискретно, гораздо удобнее моделировать эту дискретную
случайную величину как непрерывную.

Что такое независимые случайные величины?

Множество случайных величин независимо, если знание значений любого его
подмножества ничего не говорит о значениях других случайных величин. Например, число игр, выигранных за год футбольной командой Университета Индианы,
не зависит от процентного дохода по акциям Microsoft за тот же год. Знание о том,
что дела у Индианы идут хорошо, не изменит взгляд на то, как провела год компания Microsoft.

732

ГЛАВА 69

Однако доходы по акциям Microsoft и Intel не являются независимыми. Если говорят о высоком доходе по акциям Microsoft в каком-либо году , то, по всей вероятности, продажи компьютеров в этом году также были значительными, что,
очевидно, свидетельствует и о неплохом годе для Intel.

Задания
1. Определите, являются ли следующие случайные величины дискретными или
непрерывными:
• число игр, которые «Сиэтл Сихокс» выиграет в следующем сезоне;
• число, которое выпадет после остановки колеса рулетки;
• объем продаж планшетных ПК в следующем году;
• срок службы лампочки до того, как она перегорит.
2. Вычислите среднее, дисперсию и стандартное отклонение для числа очков
при броске кубика.
3. Определите, являются ли следующие переменные независимыми:
• ежедневная температура и продажи мороженого в магазине;
• масть и достоинство карты, вытащенной из колоды;
• инфляция и доход на фондовой бирже;
• изменившаяся цена модели автомобиля и количество проданных автомобилей.
4. Текущая цена акции компании составляет $20. Компания является объектом
для поглощения. Если поглощение пройдет успешно, цена акции повысится
до $30. Если поглощения не будет, цена акции упадет до $12. Определите диапазон значений для вероятности успешного поглощения, благодаря которому
целесообразно приобрести акции сегодня. Предположим, что цель заключается в получении максимальной ожидаемой прибыли. Подсказка: используйте
инструмент Подбор параметра (Goal Seek), рассмотренный в главе 18 «Инструмент Подбор параметра».
5. При вращении колеса рулетки возможными исходами являются номера секторов 0, 00, 1, 2, …, 36. Если ставить на какой-либо сектор, то можно выиграть
$35, если выпадет этот сектор, или проиграть $1 в противном случае. Каково
среднее значение и стандартное отклонение выигрыша при однократном запуске рулетки?
6. В настоящий момент акции торгуются по $40. Через месяц с 60%-ной вероятностью цена акций удвоится, и с 40%-ной вероятностью цена акции упадет на
50%. Через месяц вы собираетесь продать акции. Найдите среднее значение
и стандартное отклонение вашего дохода (в долларах).
7. Вы поставили в рулетке на нечет. Если выпадет нечетное число, вы выигрываете $1, а если нет, вы проигрываете $1. Найдите среднее значение и стандартное отклонение вашего дохода.

Г Л А В А 70

Биномиальные,
гипергеометрические
и отрицательные биномиальные
случайные величины

Обсуждаемые вопросы
Что такое биномиальная случайная величина?
Как с помощью функций БИНОМ.РАСП и БИНОМ.РАСП.ДИАП вычислить вероятности биномиального распределения?
Если одинаковое количество людей предпочитает кока-колу пепси-коле и наоборот, и у 100 человек спросили, предпочитают ли они кока-колу пепси-коле, какова вероятность того, что ровно 60 человек предпочитают кока-колу пепси-коле,
и вероятность того, что от 40 до 60 человек предпочитают кока-колу пепси-коле?
Из всех лифтовых направляющих, производимых компанией, 3% считаются дефектными. Компания собирается отгрузить клиенту партию из 10 000 направляющих. Перед приемкой партии клиент случайным образом отбирает 100 направляющих и проверяет на наличие дефектов. Если дефекты обнаружатся не более
чем у двух направляющих, клиент примет партию. Как определить вероятность
приемки партии?
Авиакомпаниям не нравятся рейсы с незанятыми местами. Предположим, что
в среднем 95% всех купивших билет регистрируются на рейс. Если авиакомпания
продает 105 билетов на 100-местный рейс, какова вероятность того, что произойдет избыточное бронирование рейса?
В кафе Village Deli ежедневно приходит на ланч 1000 клиентов. В среднем 20%
клиентов заказывают особый вегетарианский сэндвич. Эти сэндвичи готовят заранее. Сколько сэндвичей необходимо приготовить, если вероятность их нехватки должна быть равна 5%?
Что такое гипергеометрическая случайная величина?
Что такое отрицательная биномиальная случайная величина?

734

ГЛАВА 70

Ответы на вопросы
?

Что такое биномиальная случайная величина?

Биномиальная случайная величина — это дискретная случайная величина, используемая для вычисления вероятностей при выполнении следующих трех условий:
проводится n независимых испытаний;
каждое испытание приводит к одному из двух исходов: благоприятному либо
неблагоприятному;
в каждом испытании вероятность благоприятного исхода ( p) остается постоянной.
В такой ситуации для вычисления вероятностей, связанных с числом благоприятных исходов в заданном числе испытаний, может быть использована биномиальная случайная величина. Пусть x — случайная величина, обозначающая число
благоприятных исходов в n независимых испытаниях, когда вероятность благоприятного исхода в каждом испытании равна p. Вот несколько примеров, в которых биномиальная случайная величина релевантна.
Кока-кола или пепси-кола. Пусть одинаковое количество людей предпочитает кока-колу пепси-коле и наоборот. У 100 человек спросили, предпочитают ли
они кока-колу пепси-коле. Требуется узнать вероятность того, что 60 человек
предпочитают кока-колу пепси-коле, и вероятность того, что от 40 до 60 человек предпочитают кока-колу пепси-коле. В этой ситуации биномиальная случайная величина определяется следующим образом:
• испытание: опрос отдельных лиц;
• благоприятный исход: предпочтение отдано кока-коле;
• p = 0,50;
• n = 100.
Пусть x — количество человек из выборки, предпочитающих кока-колу. Необходимо определить вероятность того, что x = 60 и 40 d x d 60.
Направляющие для лифтов. Из всех лифтовых направляющих, производимых
компанией, 3% считаются дефектными. Компания собирается отгрузить клиенту партию из 10 000 направляющих. Перед приемкой партии клиент случайным образом отбирает 100 направляющих и проверяет на наличие дефектов.
Если дефекты обнаружатся не более чем у двух направляющих, клиент примет
партию. Необходимо определить вероятность того, что партия будет принята.
Биномиальная случайная величина определяется следующим образом:
• испытание: осмотр выбранной направляющей;
• благоприятный исход: направляющая имеет дефекты;

Биномиальные, гипергеометрические и отрицательные случайные величины

735

• p = 0,03;
• n = 100.
Пусть x — число дефектных направляющих в выборке. Т ребуется найти вероятность того, что x d 2.
Избыточное бронирование в авиакомпании. Авиакомпаниям не нравятся
рейсы с незанятыми местами. Предположим, что в среднем 95% всех купивших билет регистрируются на рейс. Если авиакомпания продает 105 билетов
на 100-местный рейс, какова вероятность того, что произойдет избыточное
бронирование рейса?
Биномиальная случайная величина определяется следующим образом:
• испытание: отдельные владельцы билетов;
• благоприятный исход: регистрация владельца билета;
• p = 0,95;
• n = 105.
Пусть x — число зарегистрировавшихся на рейс владельцев билетов. Необходимо найти вероятность того, что x t 101.

Как с помощью функции БИНОМ.РАСП и БИНОМ.РАСП.ДИАП вычислить вероятности биномиального распределения?

Microsoft Excel включает функции БИНОМ.РАСП (BINOM.DIST) и БИНОМ.РАСП.ДИАП
(BINOM.DIST.RANGE), с помощью которых можно вычислить вероятности биномиального распределения. Если требуется вычислить вероятность не более x благоприятных исходов для биномиальной случайной величины при n испытаниях с вероятностью благоприятного исхода p, просто введите формулу =БИНОМ.
РАСП(x;n;p;1). Если требуется вычислить вероятность ровно x благоприятных исходов для биномиальной случайной величины при n испытаниях с вероятностью
благоприятного исхода p, введите формулу =БИНОМ.РАСП(x;n;p;0). Ввод значения 1 в качестве последнего аргумента функции БИНОМ.РАСП приводит к выводу
накопленной вероятности; ввод значения 0 приводит к расчету функции распределения масс для любого частного значения. (Обратите внимание, что в качестве
последнего аргумента вместо 1 можно указать значение ИСТИНА, а вместо значения 0 — ЛОЖЬ.)
Функция БИНОМ.РАСП.ДИАП(n;p;s1;s2) вычисляет вероятность получения от s1 до
s2 (включительно) благоприятных исходов при n независимых испытаниях с вероятностью благоприятного исхода p в каждом испытании.
Далее приведены примеры вычисления вероятностей, о которых шла речь
выше в главе, с помощью функции БИНОМ.РАСП. Данные и анализ см. в файле
Binomialexamples.xlsx, показанном на рис. 70.1.

736

ГЛАВА 70

Если одинаковое количество людей предпочитает кока-колу пепси-коле
и наоборот, и у 100 человек спросили, предпочитают ли они кока-колу пепси-коле, какова вероятность того, что ровно 60 человек предпочитают кока-колу пепси-коле, и вероятность того, что от 40 до 60 человек предпочитают кокаколу пепси-коле?

Здесь n = 100 и p = 0,5. Требуется найти вероятность того, что x = 60, и вероятность
того, что 40 d x d 60, где x — это количество человек, предпочитающих кока-колу
пепси-коле. Сначала найдем вероятность того, что x = 60, введя в ячейку C4 формулу =БИНОМ.РАСП(60;100;0,5;0). Результат — 0,011.

Рис. 70.1. Использование биномиальной случайной величины

Чтобы применить функцию БИНОМ.РАСП для вычисления вероятности для
40 d x d 60, следует заметить, что эта вероятность равна вероятности дляx d 60 минус вероятность для x d 39. Таким образом, получить вероятность того, что от 40
до 60 человек предпочитают кока-колу, можно по формуле в ячейке C5: =БИНОМ.
РАСП(60;100;0,5;1)-БИНОМ.РАСП(39;100;0,5;1). Результат — 0,9648. Итак, если кокаколу и пепси-колу предпочитают в равной степени, маловероятно, что в выборке
из 100 человек кока-кола или пепси-кола будет иметь преимущество более 10%.
Если выборка из 100 человек показывает 10%-ное преимущество кока-колы или
пепси-колы, то возникают сомнения в том, что кока-колу и пепси-колу предпочитают в равной степени. Т а же вероятность вычислена в ячейке E5 по формуле
= БИНОМ.РАСП.ДИАП(100;0,5;40;60).
Из всех лифтовых направляющих, производимых компанией, 3% считаются дефектными. Компания собирается отгрузить клиенту партию из 10 000
направляющих. Перед приемкой партии клиент случайным образом отбирает
100 направляющих и проверяет на наличие дефектов. Если дефекты обнаружатся не более чем у двух направляющих, клиент примет партию. Как определить вероятность приемки партии?

Если x — число дефектных направляющих в партии, это биномиальная случайная
величина с n = 100 и p = 0,03. Необходимо найти вероятность того, что x d 2. Вве-

Биномиальные, гипергеометрические и отрицательные случайные величины

737

дите формулу =БИНОМ.РАСП(2;100;0,03;1) в ячейку C8. Результат — 0,42. Таким образом, партия будет принята в 42% случаев. Та же вероятность вычислена в ячейке
E7 по формуле = БИНОМ.РАСП.ДИАП(100;0,03;0;2).
В реальности вероятность благоприятного исхода не равна ровно 3% в каждом испытании. Например, если первые 10 направляющих имеют дефекты, вероятность
того, что следующая направляющая тоже имеет дефекты, снижается до 290/9990;
если первые 10 направляющих не имеют дефектов, вероятность того, что следующая направляющая дефектная — 300/9990. Следовательно, вероятность благоприятного исхода в одиннадцатом испытании зависит от вероятности благоприятного исхода в одном из первых 10 испытаний. Несмотря на это, биномиальная
случайная величина может быть использована в качестве приближения, если выборка сделана и объем выборки составляет менее 10% от генеральной совокупности. Здесь генеральная совокупность — 10 000 и объем выборки — 100. Точные
вероятности, связанные с выборкой из конечной совокупности, могут быть вычислены с помощью гипергеометрической случайной величины , рассматриваемой
далее в этой главе.
Авиакомпаниям не нравятся рейсы с незанятыми местами. Предположим,
что в среднем 95% всех купивших билет регистрируются на рейс. Если
авиакомпания продает 105 билетов на 100-местный рейс, какова вероятность
того, что произойдет избыточное бронирование рейса?

Пусть x — число обладателей билетов, зарегистрировавшихся на рейс. Здесь
n = 105 и p = 0,95. Требуется найти вероятность того, что x t 101. Обратите внимание, вероятность того, что x t 101, равна 1 минус вероятность того, что x d 100.
Таким образом, для вычисления вероятности избыточного бронирования рейса
введите в ячейку C10 формулу =1-БИНОМ.РАСП(100;105;0,95;1). Результат 0,392
означает, что вероятность избыточного бронирования равна 39,2%. Т а же вероятность вычислена в ячейке E10 по формуле =БИНОМ.РАСП.ДИАП(105;0,95;101;105).
В кафе Village Deli ежедневно приходит на ланч 1000 клиентов. В среднем
20% клиентов заказывают особый вегетарианский сэндвич. Эти сэндвичи
готовят заранее. Сколько сэндвичей необходимо приготовить, если вероятность их нехватки должна быть равна 5%?

Начиная с Microsoft Excel 2013 функция БИНОМ.ОБР (BINOM.INV) с синтаксисом
БИНОМ.ОБР(число_испытаний; вероятность_успеха; альфа) определяет наименьшее
число x, для которого вероятность не более x благоприятных исходов равна, по
меньшей мере, альфа. В более ранних версиях Excel резуль таты, аналогичные результатам функции БИНОМ.ОБР, давала функция КРИТБИНОМ (CRITBINOM) с синтаксисом КРИТБИНОМ(число_испытаний; вероятность_успеха; альфа). В этом примере число испытаний равно 1000, вероятность успеха — 0,2 и альфа — 0,95. Как
показано на рис. 70.2, если в кафе приготовят 221 сэндвич, вероятность того, что
закажут не более 221 сэндвича, равна, по меньшей мере, 0,95. Вероятность того,
что потребуется не больше 220 сэндвичей, составляет менее 0,95.

738

ГЛАВА 70

Рис. 70.2. Пример с функцией БИНОМ.ОБР

Что такое гипергеометрическая случайная величина?

Гипергеометрическая случайная величина определяет, например, такую ситуацию:
в урне находится N шаров;
каждый шар относится к одному из двух типов (благоприятный или неблагоприятный исход);
в урне s благоприятных исходов;
из урны взята выборка объемом n шаров.
Давайте посмотрим на пример в файле Hypergeom.dist.xlsx (рис. 70.3). В формуле
=ГИПЕРГЕОМ.РАСП(x;n;s;N;0) функция ГИПЕРГЕОМ.РАСП (HYPERGEOM.DIST) вычисляет вероятность x благоприятных исходов, если выбрано n шаров из урны, содержащей N шаров, из которых s помечены как благоприятный исход. В формуле
=ГИПЕРГЕОМ.РАСП(x;n;s;N;1) вычисляется вероятность не более x благоприятных
исходов, если взято n шаров из урны, содержащей N шаров, из которых s помечены
как благоприятный исход. (Как и в случае с функцией БИНОМ.РАСП, вместо значения 1 можно указать ИСТИНА, а вместо 0 — ЛОЖЬ.)
Например, предположим, что 40 компаниями из списка F
ortune 500 руководят женщины. Пятьсот главных директоров являются аналогом шаров в урне
(N = 500), а 40 женщин представляют s благоприятных исходов в урне. Формула
=ГИПЕРГЕОМ.РАСП(C8;объем_выборки; женщины_в_ген.совокупности; объем_ген.совокупности; 0), скопированная из D8 в D9:D18, дает вероятность того, что в выборке

из 10 компаний из списка Fortune 500 женщины возглавляют 0, 1, 2, …, 10 компаний. Здесь объем_выборки = 10, женщины_в_ген.совокупности = 40 и объем_ген.совокупности = 500. Вместо значения в формуле 0 можно ввести FALSE.

Биномиальные, гипергеометрические и отрицательные случайные величины

739

Благоприятным исходом является факт, что директором является женщина. Для
выборки из 10 компаний, например, вероятность отсутствия в выборке женщиндиректоров равна 0,431. Кстати, эту вероятность можно приблизительно вычислить по формуле =БИНОМ.РАСП(0;10;0,08;0), получив в резуль тате 0,434, что
очень близко к истинному значению вероятности 0,431. В ячейке F10 по формуле
=ГИПЕРГЕОМ.РАСП(2; объем_выборки; женщины_в_ген.совокупности; объем_ген.совокупности; ИСТИНА) вычислена вероятность того, что не более 2 человек в выборке

из 10 человек являются женщинами. Таким образом, вероятность того, что директорами окажутся не более двух женщин, равна 96,2%. Разумеется, такой же результат можно было получить, сложив значения в выделенных ячейках ( D8:D10).

Рис. 70.3. Гипергеометрическая случайная величина

Что такое отрицательная биномиальная случайная величина?

Отрицательная биномиальная случайная величина применима к тем же ситуациям, что и биномиальная случайная величина, но отрицательная биномиальная
случайная величина дает вероятность f неблагоприятных исходов до s-го благоприятного исхода. Таким образом, формула =ОТРБИНОМ.РАСП(f;s;p;0) вычисляет
вероятность того, что будет достигнуто ровно f неблагоприятных исходов до s-го
благоприятного исхода, если вероятность благоприятного исхода равнаp для всех
испытаний. А формула =ОТРБИНОМ.РАСП(f;s;p;1) вычисляет вероятность того, что
не более f неблагоприятных исходов будет достигнуто до s-го благоприятного
исхода, если вероятность благоприятного исхода равна p для всех испытаний.
Возьмем для примера бейсбольную команду, выигрывающую 40% игр (см. файл
Negbinom.dist.xlsx и рис. 70.4). Формула =ОТРБИНОМ.РАСП(D9;2;0,4;ЛОЖЬ), скопированная из E9 в E34, дает вероятность для 0, 1, 2, …, 25 неблагоприятных исходов перед вторым благоприятным. Здесь благоприятный исход эквивалентен
выигрышу. Например, с вероятностью 19,2% команда проиграет одну игру до
того, как выиграет две игры. В ячейке G10 я использовал формулу =ОТРБИНОМ.
РАСП(3;2;0,4;ИСТИНА) для вычисления вероятности того, что команда потерпит не
более трех поражений до того, как выиграет две игры (0,663). Конечно, тот же
самый результат можно было получить, просто сложив значения в выделенных
ячейках (E9:E12).

740

ГЛАВА 70

Рис. 70.4. Отрицательная биномиальная случайная величина

Задания
1. Допустим, в среднем 4% всех дисководов для компакт-дисков, получаемых
компьютерной компанией, имеют дефекты. Компания придерживается следующей политики: выбирает 50 дисководов из каждой партии и принимает
партию, если ни один из выбранных дисководов не имеет дефектов. На основе
этой информации определите следующее:
• Какая часть партий будет принята?
• Какая часть партий будет принята, если политика компании изменится
следующим образом: партия принимается при наличии в выборке только
одного дисковода с дефектами?
• Какова вероятность того, что выборка объемом 50 дисководов содержит, по
меньшей мере, 10 дисководов с дефектами?
2. На основе данных об избыточном бронировании в авиакомпании:
• определите, как изменяется вероятность избыточного бронирования при
изменении количества проданных билетов со 100 до 115. Подсказка: используйте однонаправленную таблицу данных;
• покажите, как изменяется вероятность избыточного бронирования при изменении количества проданных билетов со 100 до 115 и изменении вероятности регистрации владельцев билетов от 80 до 95%. Подсказка: используйте двунаправленную таблицу данных.
3. Пусть каждый год заданный открытый фонд имеет 50%-ный шанс превзойти
фондовый индекс Standard&Poor’s 500 Stock Index (индекс S&P 500). Како-

Биномиальные, гипергеометрические и отрицательные случайные величины

741

ва вероятность того, что в группе из 100 открытых фондов, по меньшей мере,
10 фондов превзойдут индекс S&P 500 в течение как минимум 8 лет из 10?
4. Профессиональный баскетболист Стив Нэш забивает штрафные броски с вероятностью 90%. Ответьте на следующие вопросы:
• Какова вероятность непопадания мяча в корзину более 15 раз при выполнении 100 штрафных бросков?
• Насколько хорошо Стив Нэш пробивал бы штрафные броски, если бы он
попадал в корзину меньше 90 раз из 100 с вероятностью только 5%? Подсказка: используйте инструмент Подбор параметра (Goal Seek) в опциях Анализ «что, если» (What-If Analysis).
5. При тестировании на экстрасенсорное восприятие участников просят определить фигуру на карте из 25-карточной колоды. В колоде 5 фигур и 5 карт
с каждой фигурой. Какой можно сделать вывод, если участник правильно
определил фигуру на 12 картах?
6. Допустим, в группе из 100 человек 20 заболели гриппом, а 80 — нет. Если выбрать 30 человек случайным образом, какова вероятность того, что среди них
окажется, по меньшей мере, 10 человек, заболевших гриппом?
7. Учащийся продает журналы в поддержку школьного благотворительного
фонда. Существует 20%-ная вероятность покупки журнала в данном доме.
Необходимо продать пять журналов. Определите вероятность необходимости
посещения 5, 6, 7, …, 100 домов для продажи пяти журналов.
8. Проверьте с помощью функции БИНОМ.РАСП правильность ответа с использованием функции БИНОМ.ОБР для примера с кафе Village Deli.
9. В XVII веке французские математики Пьер Фермá и Блез Паскаль, пытаясь решить «задачу об очках», смогли сформулировать положения современной теории вероятностей. Поясним на простом примере: пусть Паскаль и Ферма по очереди бросают монету. Ферма выигрывает очко, если выпадает орел, а Паскаль
выигрывает, если выпадает решка. Если Паскаль впереди со счетом 8:7 и игрок,
первым набравший 10 очков, выигрывает, каковы шансы Паскаля на выигрыш?
10. Допустим, если клуб «Хьюстон Астрос» играет с клубом «Нью-Йорк Янкиз»,
«Астрос» имеет 35%-ную вероятность победы в игре. Если «Астрос» играет
с «Янкиз» 10 раз, какова вероятность, что «Астрос» выиграет не менее половины игр?
11. Результативность моих штрафных бросков составляет 55%. Если я сделаю
400 бросков, какова вероятность, что я попаду от 200 до 300 раз (включительно)?
12. Предположим, 10% степлеров неисправны. Если было продано 60 степлеров,
какова вероятность, что не менее 10 из них неисправны?
13. На производстве имеется пять сборочных линий. Каждая линия остановлена
(не работает) p процентов времени. Каким должно быть p, чтобы с вероятностью 95% по меньшей мере одна линия работала?

ГЛ А В А 71

Пуассоновская
и экспоненциальная
случайные величины

Обсуждаемые вопросы
Что такое пуассоновская случайная величина?
Как вычислить распределение пуассоновской случайной величины?
Если количество клиентов, обращающихся в банк, описывается пуассоновской
случайной величиной, какая случайная величина определяет время между обращениями?

Ответы на вопросы
?

Что такое пуассоновская случайная величина?

Пуассоновская случайная величина — это дискретная случайная величина, применяемая для описания вероятностей в ситуациях, в которых события (такие как
обращение клиентов в банк или размещение заказов на продукт) имеют малую
вероятность возникновения в короткий промежуток времени. Точнее говоря,
в короткий промежуток времени, обозначаемый как t, произойдет одно событие
или ни одного события, и вероятность одного события, происходящего в короткий промежуток времени длиной t (для некоторого λ), определяется λt. Здесь λ —
среднее число событий в единицу времени.
Ситуации, к которым применима пуассоновская случайная величина:
количество единиц продукта, требуемое в течение месяца;
количество смертей в год от удара копытом в прусской армии;
количество ДТП для одного водителя в год;
количество экземпляров «Где находится душа», заказанное сегодня на Amazon.
com;
количество исков о компенсации ущерба, поданных сотрудниками компании
в этом месяце;

Пуассоновская и экспоненциальная случайные величины

743

количество дефектов в 100 ярдах струны. (Здесь 1 ярд струны играет роль времени.)

Как вычислить распределение пуассоновской случайной величины?

Для вычисления распределения пуассоновской случайной величины в Excel можно воспользоваться функцией ПУАССОН.РАСП (POISSON.DIST). В версиях Excel,
предшествующих Excel 2013, пуассоновское распределение можно получить с помощью функции ПУАССОН (POISSON). Просто помните, что в промежуток времени t среднее значение пуассоновской случайной величины равно t. Синтаксис
функции ПУАССОН.РАСП:
функция ПУАССОН.РАСП(x;лямбда;ИСТИНА_или_1) вычисляет вероятность того,
что пуассоновская случайная величина со средним значением, равным лямбда,
не больше x;
функция ПУАССОН.РАСП(x;лямбда;ЛОЖЬ_или_0) вычисляет вероятность того,
что пуассоновская случайная величина со средним значением, равным лямбда,
равна x.
Вот несколько примеров вычисления пуассоновской случайной величины. Эти
примеры вы найдете в файле Poisson.xlsx (рис. 71.1).

Рис. 71.1. Использование пуассоновской случайной величины

Допустим, в мою консалтинговую фирму звонят 30 раз в час. Для двухчасового
периода необходимо определить следующее:
вероятность того, что за следующие два часа поступит ровно 60 звонков;
вероятность того, что количество звонков за следующие два часа не превысит 60;
вероятность того, что за следующие два часа будет получено от 50 до 100
звонков.
Среднее количество звонков за двухчасовой период равно 60. В ячейке C4 я вычислил по формуле =ПУАССОН.РАСП(60;C2;ЛОЖЬ) вероятность (0,05) 60 звонков
в следующие два часа. В ячейке C5 по формуле =ПУАССОН.РАСП(60;C2;1) я нашел
вероятность (0,534) получения не более 60 звонков за два часа. В ячейке
C6 по
формуле =ПУАССОН.РАСП(100;C2;ИСТИНА)-ПУАССОН.РАСП(49;C2;ИСТИНА) я рассчитал вероятность (0,916) получения от 50 до 100 звонков за два часа.

744

ГЛАВА 71

ПРИМЕЧАНИЕ
В качестве аргумента любой функции Excel вместо значения ИСТИНА всегда можно
указать значение 1.

Если количество клиентов, обращающихся в банк, описывается пуассоновской случайной величиной, какая случайная величина определяет время между обращениями?

Время между обращениями может быть любым, поэтому время между обращениями представляет собой непрерывную случайную величину . Если среднее число
обращений λ происходит за единицу времени, время между обращениями соответствует экспоненциальной случайной величине с плотностью распределения
вероятностей f(t) =λе–λt (при t ≥ 0).
Эта случайная переменная имеет среднее значение, равное 1/λ. График экспоненциальной функции плотности вероятности (ФПВ) для λ = 30 показан на рис. 71.2.
Density в файле
Вы найдете диаграмму и данные для этого примера на листе
Exponentialdist.xlsx.

Рис. 71.2. Экспоненциальная функция распределения плотности вероятностей

В главе 69 «Введение в случайные величины» говорилось о том, что для непрерывной случайной величины значение ФПВ в точке x отражает вероятность, с которой случайная величина примет значение в окрестностях точки x. Как видно
из рис. 71.2, чрезвычайно короткое время между обращениями в банк (например,
меньше 0,05 ч) весьма вероятно, а для более длительных промежутков времени
значение функции резко падает.

Пуассоновская и экспоненциальная случайные величины

745

Даже если среднее время между обращениями составляет 1/30 = 0,033 ч, существует вероятность, что время между обращениями составит не более 0,20 ч. Функция
ЭКСП.РАСП (EXPON.DIST) в формуле =ЭКСП.РАСП(x;1/среднее;ИСТИНА_или_1) дает
вероятность того, что экспоненциальная случайная величина с заданным средним
примет значение не больше x. Таким образом, второй аргумент функции ЭКСП.
РАСП — это интенсивность возникновения событий. Например, для вычисления
вероятности, с которой время между обращениями составит 5, 10 или 15 минут ,
скопируйте формулу =1-ЭКСП.РАСП(C5;$D$2;ИСТИНА) из ячейки D5 в D7. В более
ранних версиях Excel такой же резуль тат, как функция ЭКСП.РАСП, дает функция
ЭКСПРАСП (EXPONDIST).
Обратите внимание, что сначала я преобразовал минуты в часы (5 минут = 1/12 часа и т. д.). Кроме того, среднее время между обращениями составляет 0,033 ч, поэтому я ввел в формулу значение 1/среднее = 1/0,033 = 30, то есть количество
обращений в единицу времени (рис. 71.3 и лист Computation).

Рис. 71.3. Вычисление экспоненциального распределения

Задания
1. В пабе «У Ника» в Блумингтоне, штат Индиана, посетители заказывают
в среднем 40 кружек пива в час.
• Какова вероятность заказа не менее 100 кружек за два часа?
• Какова вероятность того, что время между заказами составит не более 30
секунд?
2. Предположим, что подростки-водители попадают в среднем в 0,3 ДТП в год.
• Какова вероятность, что подросток попадет не более чем в одно ДТП в течение года?
• Какова вероятность того, что время между ДТП составит не более шести
месяцев?

746

ГЛАВА 71

3. Я следующий в очереди в ресторане быстрого питания, в котором покупатели образуют одну очередь, и время обслуживания покупателя соответствует
экспоненциальному распределению со средним значением 3 минуты. Какова
вероятность ожидания обслуживания не менее 5 минут?
4. С 1900 г. доля игр без хитов среди всех игр Высшей бейсбольной лиги составила 0,00124. Команда играет 162 игры за сезон. Какова вероятность того, что
команда сыграет не менее двух игр без хитов за сезон?
5. В кофейню в среднем заходит 80 посетителей в час. Какова вероятность того,
что за двухчасовой период зайдет не менее 150 посетителей?
6. Какая почасовая посещаемость кофейни обеспечит вероятность, равную 0,5,
того, что не менее 150 посетителей посетит кофейню в течение трех часов?

Г Л А В А 72

Нормальная случайная величина
и Z-оценка
Обсуждаемые вопросы
Каковы свойства нормальной случайной величины?
Как в Excel найти распределение нормальной случайной величины?
Как в Excel найти процентили для нормальных случайных величин?
Почему нормальная случайная величина соответствует многим реальным ситуациям?
Что такое Z-оценка?

Ответы на вопросы
?

Каковы свойства нормальной случайной величины?

Из главы 69 «Введение в случайные величины» вы узнали, как использовать непрерывные случайные величины для моделирования следующих величин:
цена акций Microsoft через год, начиная с этого момента;
доля рынка для нового продукта;
объем рынка для нового продукта;
стоимость разработки нового продукта;
вес новорожденного ребенка;
чей-либо IQ.
Напомню, что если дискретная случайная величина (такая как объем продаж бигмаков за 2025 г.) может принимать много возможных значений, ее можно также аппроксимировать с помощью непрерывной случайной величины. Как описано в главе
69, любая непрерывная случайная величина X характеризуется функцией плотности
вероятностей (ФПВ). ФПВ непрерывной случайной величины является неотрицательной функцией со следующими свойствами (a и b — произвольные числа):
площадь под кривой распределения вероятностей равна 1;
вероятность X < a равна вероятности X d a. Эта вероятность представлена площадью под кривой распределения вероятностей слева от a;

748

ГЛАВА 72

вероятность X > b равна вероятности X t b. Эта вероятность представлена площадью под кривой распределения вероятностей справа от b;
вероятность a < X < b равна вероятности a d X d b. Эта вероятность равна площади под кривой распределения вероятностей между a и b.
Таким образом, вероятность численно равна площади под кривой распределения
вероятностей непрерывной случайной величины. Кроме того, чем больше значение плотности в точке X, тем больше вероятность того, что случайная величина
примет значение в окрестностях X. Например, если значение плотности распределения вероятностей случайной величины в точке 20 в два раза больше значения
плотности распределения вероятностей случайной величины в точке 5, то случайная величина в два раза вероятнее примет значение около 20, чем около 5.
Для непрерывной случайной величины вероятность того, что X равно какому-либо значению, всегда равна 0. Например, некоторые люди имеют рост от 5,99999
до 6,00001 фута, но ни у одного человека рост не может быть ровно 6 футов. Это
объясняет, почему в вероятностных высказываниях можно заменить знак «спрос;произведено-спрос;0) вычисляются затраты на ликвидацию. Наконец, в ячейке C11 прибыль вычислена как выручка – общ_переменные_затраты – общ_затраты_на_ликвидацию.
Было бы неплохо, если бы можно было не напрягаясь нажать F9 множество раз
(например, тысячу) для каждого объема производства, а также подсчета ожидаемой прибыли для каждого объема. В этой ситуации на помощь приходит двунаправленная таблица данных. (О таблицах данных см. в главе 17 «Анализ чув-

Введение в моделирование по методу Монте-Карло

783

ствительности с помощью таблиц данных».) Т аблица данных для этого примера
представлена на рис. 77.5.

Рис. 77.5. Двунаправленная таблица данных для моделирования примера
с поздравительными открытками

В ячейках A16:A1015 я ввел номера от 1 до 1000 (соответствующие тысяче испытаний). Простой способ это сделать — ввести 1 в ячейку A16, затем выделить
ячейку, на вкладке Главная (Home) в группе Редактирование (Editing) открыть список Заполнить (Fill) и выбрать Прогрессия (Series). В открывшемся диалоговом окне
Прогрессия (Series), показанном на рис. 77.6, укажите для шага значение 1, а для
предельного значения — 1000. У становите переключатель Расположение (Series
In Area) в положение по столбцам (Columns) и нажмите OK. В столбец A, начиная
с ячейки A16, будут введены числа от 1 до 1000.
Введите в ячейки B15:E15 возможные объемы производства (10 000, 20 000, 40 000,
69 000). Для каждого номера испытаний (от 1 до 1000) и каждого объема производства необходимо вычислить прибыль. У кажите ссылку на формулу для прибыли (вычисляемую в ячейке C11) в левой верхней ячейке таблицы данных (A15)
путем ввода =profit (ячейке C11 было присвоено имя profit).
Теперь можно запустить в Excel моделирование тысячи испытаний для спроса при каждом объеме производства. Выделите таблицу ( A15:E1015) и затем на
вкладке Данные (Data) в группе Прогноз (Forecast) в списке Анализ «что, если» (What

784

ГЛАВА 77

Рис. 77.6. Диалоговое окно Прогрессия для ввода номеров испытаний от 1 до 1000

If Analysis) выберите Таблица данных (Data Table). Установите двунаправленную
таблицу, выбрав объем производства (ячейку C1) в поле Подставлять значения по
столбцам в (Row Input Cell) и любую пустую ячейку (здесь выбрана ячейка I14)
в поле Подставлять значения по строкам в (Column Input Cell). Теперь нажмите кнопку
OK для моделирования в Excel одной тысячи значений спроса для каждого объема
производства.

Чтобы понять, почему это работает , рассмотрим значения, помещенные с помощью таблицы данных в ячейки C16:C1015. Для каждой из этих ячеек при подстановке по столбцам используется значение 20 000 из ячейки C1. Для ячейки C16
при подстановке по строкам в пустую ячейку помещается значение 1, и случайное
число в ячейке C2 пересчитывается. Затем в ячейку C16 записывается соответствующая прибыль. Далее для подстановки по строкам в пустую ячейку записывается
значение 2, и случайное число в ячейке C2 пересчитывается еще раз. Соответствующая прибыль записывается в ячейку C17.
Скопировав формулу =СРЗНАЧ(B16:B1015) из ячейки B13 в C13:E13, вы можете вычислить среднюю смоделированную прибыль для каждого объема производства.
Скопировав формулу =СТАНДОТКЛОН.В(B16:B1015) из ячейки B14 в C14:E14, вы можете вычислить стандартное отклонение смоделированной прибыли для каждого
объема производства. Каждый раз при нажатии F9 для каждого объема производства моделируется 1000 итераций спроса. Для объема производства 40 000 открыток всегда в резуль тате получается самая высокая ожидаемая прибыль, поэтому
такой объем производства, по-видимому, является правильным решением.

Влияние риска на решение
Если вы произведете 20 000 открыток вместо 40 000, ожидаемая прибыль снизится примерно на 22%, но и риск (судя по стандартному отклонению прибыли)

Введение в моделирование по методу Монте-Карло

785

снизится почти на 73%. Следовательно, при общем нерасположении к риску правильным решением будет отпечатать 20 000 открыток. Между прочим, производство 10 000 открыток всегда имеет стандартное отклонение 0, поскольку 10 000
открыток будут проданы в любом случае, без остатков.
ПРИМЕЧАНИЕ
В файле Valentine.xlsx установлен параметр Автоматически, кроме таблиц данных
(Automatic Except For Tables). Он выбирается на вкладке Формулы (Formulas) в группе
Вычисление (Calculation) в списке Параметры вычислений (Calculation). Этот параметр
допускает перерасчет таблиц данных только при нажатии F9, что целесообразно,
поскольку при вводе какой-либо информации на лист перерасчет больших таблиц
данных замедляет работу. Обратите внимание, что в этом примере при каждом нажатии F9 средняя прибыль изменяется. Это происходит потому, что спрос для каждого объема производства генерируется с помощью другой последовательности из
1000 случайных чисел.

Доверительный интервал для средней прибыли
В такой ситуации естественно задать вопрос: в какой интервал с вероятностью
95% попадает истинная средняя прибыль? Этот интервал называется 95%-ным
доверительным интервалом для средней прибыли. 95%-ный доверительный интервал для среднего значения любого конечного результата моделирования вычисляется по следующей формуле:

В ячейке J11 по формуле =D13-1,96*D14/КОРЕНЬ(1000) я вычислил нижний предел 95%-ного доверительного интервала для средней прибыли при производстве
40 000 календарей. В ячейке J12 я вычислил верхний предел 95%-ного доверительного интервала по формуле =D13+1,96*D14/КОРЕНЬ(1000). Результаты вычислений
показаны на рис. 77.7.

Рис. 77.7. 95%-ный доверительный интервал для средней прибыли при производстве
40 000 календарей

С вероятностью 95% при производстве 40 000 календарей средняя прибыль составит от $55 076 до $61 008.

786

ГЛАВА 77

Задания
1. Автодилер считает, что спрос на модели 2015 г. распределяется по нормальному закону со средним значением 200 и стандартным отклонением 30. Он
приобретает Envoy за $25 000 и продает за $40 000. Половину автомобилей, не
проданных по полной цене, можно продать по $30 000. Дилер рассматривает
варианты заказа на 200, 220, 240, 269, 280 или 300 штук. Сколько автомобилей
он должен заказать?
2. Магазин пытается определить, сколько экземпляров журнала People необходимо заказывать каждую неделю. Владелец считает, что спрос на журнал соответствует следующей дискретной случайной величине:
Спрос

Вероятность

0,10

0,20

0,30

0,25

0,15

Магазин платит за каждый экземпляр $1,00 и продает его по $1,95. Каждый
непроданный экземпляр может быть возвращен за $0,50. Сколько экземпляров журнала еженедельно должен заказывать магазин?
3. Ваш супермаркет пытается определить, сколько мясных рулетов требуется
изготовить в кулинарии в понедельник. Спрос на рулеты по понедельникам
имеет нормальное распределение со средним, равным 100, и стандартным отклонением, равным 20. Себестоимость производства мясного рулета составляет $2,00, а продаете вы его за $7,00. У тилизация не проданного до конца
дня рулета стоит $0,60. Если возможно производить только 100, 110, 120 или
130 рулетов, какое их количество стоит произвести?
4. Спрос по понедельникам на круассаны с миндальным кремом соответствует
нормальному распределению со средним, равным 100, и стандартным отклонением, равным 25. Себестоимость круассана — $1,00, а продажная цена —
$4,00. Непроданные круассаны должны быть утилизированы по цене $0,40
за штуку. Кондитерская может производить 80, 100, 120 или 140 круассанов.
С помощью метода Монте-Карло определите объем производства, обеспечивающий для кондитерской максимальную прибыль.
5. Спрос на капустный салат (в фунтах) по воскресеньям соответствует нормальному распределению со средним, равным 500, и стандартным отклонением, равным 100. Себестоимость фунта капустного салата — $3,00, а продажная
цена — $8,00. В конце дня остатки салата выбрасываются. Исходя из уровней

Введение в моделирование по методу Монте-Карло

787

производства в 500, 520, 540, 560, 580 или 600 фунтов, определите объем производства, обеспечивающий максимальную прибыль.
6. Компания — производитель поздравительных открыток пытается определить, сколько выпустить открыток ко Дню святого Валентина. Стоимость
печати x открыток вычисляется по формуле: $2 млн + 0,70 x. То есть печать
1 млн открыток стоит $2,7 млн. Спрос на открытки следует нормальному распределению со средним, равным 2 млн, и стандартным отклонением, равным
400 000. Открытки продаются по цене $4,00, а остатки — по $0,05. Какой из
возможных объемов производства — 2,4; 2,6; 2,8; 3 или 3,2 млн — обеспечит
максимальную прибыль компании?

ГЛ А В А 78

Вычисление оптимальной цены
предложения

Обсуждаемые вопросы
Как смоделировать случайную величину с биномиальным распределением?
Как определить, должна ли непрерывная случайная величина моделироваться
как нормальная случайная величина?
Как с помощью моделирования определить оптимальную тендерную заявку для
проекта строительства?

Когда вы вступаете с конкурентами в борьбу за проект , двумя основными источниками неопределенности являются количество конкурентов и цены, предлагаемые каждым конкурентом. При высокой цене предложения можно заработать на
проекте много денег, но самих проектов будет мало. При низкой цене предложения проектов будет немало, но денег каждый проект принесет немного. Оптимальная цена предложения находится где-то посередине. Удобным инструментом для
определения цены предложения, максимально увеличивающей предполагаемую
прибыль, является моделирование по методу Монте-Карло.

Ответы на вопросы
?

Как смоделировать случайную величину с биномиальным распределением?

Формула =БИНОМ.ОБР(n;p;СЛЧИС()) моделирует количество благоприятных исходов в n независимых испытаниях, каждое из которых имеет вероятность благоприятного исхода, равную p. Как объяснялось в главе 77 «Введение в моделирование по
методу Монте-Карло», функция СЛЧИС (RAND) генерирует число, с равной вероятностью принимающее любое значение от 0 до 1. В файле Binomialsim.xlsx (рис. 78.1)
показано, что при нажатии F9 формула =БИНОМ.ОБР(100;0,9;D3), введенная в ячейку C3, моделирует число штрафных бросков, выполняемых Стивом Нэшем (с вероятностью 90% забивающим штрафные в НБА) в 100 попытках. Формула =БИНОМ.
ОБР(100;0,5;D4) в ячейке C4 моделирует количество выпавших орлов при подбрасывании монеты 100 раз. В ячейке C5 формула =БИНОМ.ОБР(3;0,4;D5) моделирует количество конкурентов, появившихся на рынке в течение года, при трех возможных
участниках рынка и 40%-ной вероятности для каждого конкурента выйти на рынок.
Разумеется, в ячейки D3:D5 я ввел формулу =СЛЧИС().

Вычисление оптимальной цены предложения

789

Рис. 78.1. Моделирование случайной величины с биномиальным распределением

Как определить, должна ли непрерывная случайная величина моделироваться как нормальная случайная величина?

Допустим, вы считаете, что наиболее вероятная тендерная заявка конкурента составляет $50 000. Напомню, что нормальная ФПВ является симметричной относительно среднего значения. Следовательно, для определения возможности применения нормальной случайной величины в моделировании цены предложения
конкурента необходимо проверить симметрию относительно среднего значения
цены предложения. Если цена предложения конкурента проявляет симметрию
относительно среднего значения $50 000, цены предложения $40 000 и $60 000,
$45 000 и $55 000 и т. д., должны быть приблизительно одинаково вероятны. Если
предположение о симметрии выглядит разумным, то цену предложения каждого
конкурента можно смоделировать как нормальную случайную величину со средним значением $50 000.
Как оценить стандартное отклонение цены предложения каждого конкурента?
Напомню, что согласно правилу из главы 44 «Обобщение данных с помощью описательной статистики», наборы данных с симметричными гистограммами имеют примерно 95% данных в пределах двух стандартных отклонений от среднего
значения. Аналогично нормальная случайная величина с вероятностью 95% находится в пределах двух стандартных отклонений от своего среднего значения.
Предположим, что с вероятностью 95% цена предложения конкурента составляет
от $30 000 до $70 000. Это означает , что 2 × (стандартное отклонение цены предложения конкурента) равно $20 000 или стандартное отклонение цены предложения конкурента равно $10 000.
Если предположение о симметрии разумно, цену предложения конкурента можно смоделировать с помощью формулы =НОРМ.ОБР(СЛЧИС(); 50000; 10000). (О моделировании нормальных случайных величин с помощью функции
НОРМ.ОБР
см. главу 77.)

790

ГЛАВА 78

Кроме того, нормальное распределение имеет нулевые асимметрию и эксцесс.
Если вы по достаточно большой выборке получаете, что асимметрия и/или эксцесс в абсолютном выражении больше 1, то маловероятно, что данные соответствуют нормальному распределению.

Как с помощью моделирования определить оптимальную тендерную заявку для проекта строительства?

Предположим, что вы участвуете в тендере на проект строительства, который
обойдется вам в $25 000. Подготовка тендерной заявки стоит $1000. У вас имеется шесть потенциальных конкурентов, и вы подсчитали, что с вероятностью 50%
каждый конкурент примет участие в тендере. Если конкурент подает тендерную
заявку, то цена его предложения следует закону нормального распределения со
средним значением $50 000 и стандартным отклонением $10 000. Предположим
также, что вы подготавливаете заявки только с ценой, кратной $5000. Какова
должна быть цена вашего предложения для получения максимальной ожидаемой прибыли? Напомню, что выигрывает самая низкая тендерная заявка! Данные
к этой задаче находятся в файле Bidsim.xlsx (рис. 78.2 и 78.3).

Рис. 78.2. Модель цены предложения

Ваша стратегия должна быть следующей.
Сгенерируйте количество конкурентов.
Для каждого потенциального конкурента, который действительно подает заявку, смоделируйте предложение с помощью нормальной случайной величины.
Если потенциальный конкурент не подает заявку, назначьте для него большую
цену предложения (например, $100 000), которая гарантирует ему поражение.

Вычисление оптимальной цены предложения

791

Рис. 78.3. Таблица данных для моделирования цены предложения

Определите, является ли цена вашего предложения самой низкой.
Если вы предлагаете самую низкую цену, то получите прибыль, равную предложению минус стоимость проекта минус $1000 (стоимость заявки). Если цена
вашего предложения не самая низкая, то вы теряете $1000 — стоимость заявки.
Для моделирования каждой возможной цены предложения (например, $30 000,
$35 000, …, $60 000) 1000 раз используйте двунаправленную таблицу данных
и затем выберите цену предложения с наибольшей ожидаемой прибылью.
Сначала я присвоил имена из ячеек D1:D4 ячейкам E1:E4. В ячейке E3 я определил количество конкурентов по формуле =БИНОМ.ОБР(6;0,5;F3). Ячейка
F3 содержит формулу =СЛЧИС(). Затем я определил, какой из потенциальных конкурентов действительно подает заявку , скопировав формулу =ЕСЛИ
(D90;С4;С5). В ячейку
G6 вводится победитель второй игры по формуле =ЕСЛИ(E8>0;С8;С9).
Для моделирования результата игры за чемпионский титул я ввел в ячейку H5 случайное число. Скопировав формулу =ВПР(G5;$C$4:$D$9;2;ЛОЖЬ) из I5 в I6, я получил рейтинг каждой команды в чемпионской игре. Затем в ячейке J5 я вычислил
результат финала (с позиции первой указанной команды в ячейке G5) по формуле
=НОРМ.ОБР(H5;I5-I6;10). Наконец, в ячейке K5 определен фактический чемпион по
формуле =ЕСЛИ(J5>0;G5;G6).
Теперь я могу использовать однонаправленную таблицу данных для моделирования Финала Четырех 2000 раз. Смоделированные победители указаны в диапазоне M12:M2011. Формула =СЧЁТЕСЛИ($M$12:$M$2011;J12)/2000, скопированная из
K12 в K13:K15, вычисляет прогнозируемую вероятность победы каждой команды:
23% для «Канзаса», 53% для «Вилла-новы», 22% для «Мичигана» и 15% для «Лойолы». Эти вероятности могут быть переведены в букмекерские ставки по следующей формуле:

Например, ставки на проигрыш «Канзаса» составляют 3,33 к 1:
(1 – 0,23) / 0,23 = 3,333.
То есть если вы поставили на победу «Канзаса» $1, и букмекер заплатил $3,33,
то ставка справедливая. Разумеется, букмекер слегка понизит ставки, чтобы не
остаться без заработка. (См. задание 6 в конце главы.)
Эта методика может быть легко расширена до моделирования всего турнира Национальной студенческой спортивной ассоциации. Просто используйте утверждения ЕСЛИ для обеспечения продвижения каждого победителя и функции ВПР для
нахождения рейтинга каждой команды. Моделирование сезона 2003 г. см. в файле
Ncaa2003.xlsx. Анализ отдавал команде Сиракузского университета (действительному чемпиону) победу с вероятностью 4% на старте соревнований.
На этом листе я использовал примечания к работе, показанные на рис. 80.4. Вот
несколько советов по использованию примечаний.
Для вставки примечания в ячейку сначала выделите ячейку . На вкладке Рецензирование (Review) в группе Примечания (Comments) выберите Создать примечание (New Comment) и введите текст примечания. Вы увидите небольшую
красную отметку в правом верхнем углу ячейки с примечанием.
Для редактирования примечания щелкните правой кнопкой мыши на ячейке
и выберите команду Изменить примечание (Edit Comment).

Развлечения и игры: моделирование вероятностей для азартных игр

811

Чтобы примечание всегда было видимым, щелкните на ячейке правой кнопкой мыши и выберите Показать или скрыть примечание (Show/Hide Comments).
Если отображаемое примечание необходимо скрыть, выберите Скрыть примечание (Hide Comment). Оно будет отображаться только при наведении курсора на
ячейку с примечанием.
Если вы хотите распечатать примечания, на вкладке Разметка страницы (Page
Layout) щелкните на кнопке вызова диалогового окна Параметры страницы (Page
Setup) — на маленьком значке в правом нижнем углу группы. В открывшемся
диалоговом окне на вкладке Лист (Sheet, в разделе Печать) в поле со списком
Примечания (Comments) можно указать, должны ли примечания быть напечатаны так, как на листе, или внизу листа. Нажмите OK для сохранения настроек.

Рис. 80.4. Показ примечаний на листе

Задания
1. В комнате находится 30 человек. Какова вероятность того, что по крайней
мере двое из них родились в один день?
2. Какова вероятность собрать одну пару в пятикарточном дро-покере?
3. Какова вероятность собрать две пары в пятикарточном дро-покере?
4. В игре кено перемешивают 80 шаров (пронумерованных от 1 до 80) и затем
случайным образом вытаскивают 20 шаров. Перед вытаскиванием 20 шаров
игрок выбирает 10 различных номеров. Если вытащено хотя бы пять шаров
с этими номерами, игрок выигрывает. Какова вероятность выигрыша?
5. Для финала НБА 2003 года рейтинговая система (см. главу 35) поставила клуб
«Сан-Антонио Спёрс» на три очка выше клуба «Нью-Джерси Нетс». Команды
играют до четырех побед. Первые две игры проводятся в Сан-Антонио, следу-

812

ГЛАВА 80

ющие три игры — в Нью-Джерси и две последние игры запланированы в СанАнтонио. Какова вероятность того, что «Сан-Антонио» выиграет серию?
6. Какие ставки на победу «Канзаса» в Финале Четырех должен предложить букмекер, если хочет заработать в среднем 10 центов с каждого доллара ставки?
7. Какова вероятность собрать флэш (пять карт одной масти) в пятикарточном
дро-покере?
8. Если палочку длиной 1 дюйм сломать в двух случайно выбранных местах, то
получится три маленькие палочки. Какова вероятность того, что из них можно составить треугольник?
9. Предположим, что каждый хитер в бейсбольной команде может с вероятностью 50% выполнить хоумран и с вероятностью 50% выбить в аут . Сколько
в среднем перебежек заработает эта команда в одном иннинге?
10. Кэти и Тэйлор подбрасывают монету 100 раз. Каждый раз, когда выпадает
орел, Кэти платит Т эйлору $1; каждый раз, когда выпадает решка, Т эйлор
платит Кэти $2. Какова вероятность того, что Т эйлор ни разу не будет в выигрыше?
11. Вы подбрасываете правильную монету 20 раз. Оцените вероятность того, что
вы выбросите не менее четырех орлов подряд.
12. В начале 2015 года вы вложили $100, купив акции. Каждый год с вероятностью 60% стоимость акций растет на 50%, с вероятностью 20% стоимость
акций растет на 10% и с вероятностью 20% стоимость акций падает на 50%.
Какова вероятность, что до начала 2065 г. стоимость вашего актива достигнет
(хотя бы раз) $10 000?
13. При игре в блэкджек дилер берет карты, пока сумма очков на них не будет
больше или равна 16. После этого он останавливается. Предположим, туз считается за 1 очко, а валет, дама и король — за 10. Если дилер вытаскивает карты
с возвратом, какова вероятность, что общая сумма очков будет 19, 20 или 21?
14. Вы собираетесь бросать кубик 50 раз. Если выпадает четное число очков, вам
выплачивается столько долларов, сколько очков выпало на кубике. Если выпало нечетное число очков, вы теряете $1. Какова вероятность того, что ваш
выигрыш в какой-то момент будет не менее $75?
15. Возьмем три колоды карт . Первая колода содержит 10 карт: 3 двойки, 4 пятерки и 3 девятки. Вторая колода содержит четыре карты с числами от 1 до 4.
Колода 3 содержит шесть карт с числами от 1 до 6. Грегори вытаскивает одну
карту из колоды 1, Тэйлор вытаскивает одну карту из колоды 2 и одну карту
из колоды 3. Какова вероятность того, что на карте Грегори число больше, чем
сумма чисел на двух картах Тэйлора?

Г Л А В А 81

Анализ данных с помощью
повторной выборки

Обсуждаемый вопрос
Девять партий продукции производятся при высокой температуре, а семь партий — при низкой. Какова вероятность того, что выход продукта выше при высокой температуре?

Аналитикам данных часто приходится решать следующие задачи:
Какова вероятность того, что новая методика обучения повысит успеваемость
учащихся?
Какова вероятность того, что аспирин снижает частоту инфарктов?
Какова вероятность того, что машина 1 является самой производительной из
трех машин?
Анализировать подобные данные позволяет простой, но эффективный метод, известный как повторная выборка. Для получения статистических выводов с использованием повторной выборки данные генерируются множество раз путем
выборки с возвращением. Выборка с возвращением означает , что одна и та же
точка данных может быть выбрана несколько раз. Затем на основе резуль татов
повторной выборки делаются выводы. Ключевым инструментом для реализации повторной выборки является функция СЛУЧМЕЖДУ (RANDBETWEEN). Формула =СЛУЧМЕЖДУ(a;b) дает с равной вероятностью любое целое число между a и b
(включительно). Например, формула =СЛУЧМЕЖДУ(1;9) с равной вероятностью
даст в результате одно из чисел от 1 до 9 (включительно).

Ответ на вопрос
Девять партий продукции производятся при высокой температуре, а семь
партий — при низкой. Какова вероятность того, что выход продукта выше
при высокой температуре?

В файле Resampleyield.xlsx (рис. 81.1) содержатся данные о выходе продукта для
девяти партий, произведенных при высокой температуре, и для семи партий, произведенных при низкой температуре.

814

ГЛАВА 81

Средний выход продукта при высокой температуре составляет 39,74; средний выход продукта при низкой температуре — 32,27. Однако эта разница не доказывает,
что средний выход продукта при высокой температуре превосходит средний выход продукта при низкой температуре. На основе данных выборки необходимо
узнать вероятность того, что выход продукта при высокой температуре выше, чем
при низкой. Для ответа на этот вопрос можно сгенерировать случайным образом
девять целых чисел от 1 до 9, что дает повторную выборку выхода продукта при
высокой температуре. Например, если сгенерировано случайное число 4, в повторно выбранные данные для выхода годной продукции при высокой температуре будет включено значение 41,40 и т. д. Затем случайным образом генерируются
семь целых чисел от 1 до 7, с помощью которых создается повторная выборка для
выхода продукта при низкой температуре. Далее для повторно выбранных данных
проверяется, превосходит ли средний выход продукта, произведенного при высокой температуре, средний выход продукта, произведенного при низкой температуре. И, наконец, с помощью таблицы данных этот процесс повторяется несколько
сотен раз. (Я повторил 400 раз.) В повторно выбранных данных доля случаев, когда средний выход продукта при высокой температуре превосходит средний выход продукта при низкой температуре, оценивает вероятность того, что процесс
производства при высокой температуре эффективнее процесса производства при
низкой температуре.

Рис. 81.1. Выход продукта при высокой и низкой температуре

Сначала сгенерируйте повторную выборку данных для высокой температуры,
скопировав формулу =СЛУЧМЕЖДУ(1;9) из ячейки C16 в C17:C24, как показано на
рис. 81.2. Исходные наблюдения могут быть выбраны несколько раз или не выбраны ни разу. Скопируйте формулу =ВПР(C16;lookup;2) из ячейки D16 в D17:D24
(lookup — это имя диапазона ячеек C4:E13) для генерации выходов продукта, соответствующих случайной повторной выборке данных. Далее сгенерируйте повторную выборку из данных о выходе продукта при низкой температуре. Скопируйте
формулу =СЛУЧМЕЖДУ(1;7) из E16 в E17:E22 для генерации повторной выборки из
семи случайных чисел для получения наблюдений на основе исходных данных

Анализ данных с помощью повторной выборки

815

о выходе продукта при низкой температуре. Для повторного выбора семи выходов
продукта при низкой температуре скопируйте формулу =ВПР(E16;lookup;3) из F16
в F17:F22.

Рис. 81.2. Реализация повторной выборки

В ячейке D26 я вычислил для повторно выбранных данных средний выход при высокой температуре по формуле =СРЗНАЧ(D16:D24). Аналогично в ячейке F26 я вычислил средний выход для низкой температуры по формуле =СРЗНАЧ(F16:F22).
В ячейке D29 по формуле =ЕСЛИ(D26>F26;1;0) я определил для повторно выбранных данных, превосходит ли средний выход продукта при высокой температуре
средний выход продукта при низкой температуре.
Провести повторную выборку 400 раз можно с помощью однонаправленной таблицы данных. Я поместил номера итераций от 1 до 400 в ячейки C32:431. О том,
как быстро создать список номеров итераций с помощью команды Заполнить (Fill)
и диалогового окна Прогрессия (Series), см. в главе 77 «Введение в моделирование
по методу Монте-Карло». Я ввел в ячейку D31 =D29 и создал формулу, записывающую в выходную ячейку таблицы данных то, превосходит ли средний выход
продукта при высокой температуре средний выход продукта при низкой температуре. Выделите таблицу ( C31:D431), затем на вкладке Данные (Data) в группе
Прогноз (Forecast) в списке Анализ «что, если» (What If Analysis) выберите Таблица
данных (Data Table). Укажите в поле Подставлять значения по строкам в (Column Input
Cell) любую пустую ячейку. Теперь Excel выполнит повторную выборку 400 раз.

816

ГЛАВА 81

Каждая итерация со значением 1 указывает, что в повторной выборке средний выход продукта выше при высокой температуре. Каждая итерация со значением 0
указывает, что в повторной выборке средний выход продукта выше при низкой
температуре. В ячейке F31 по формуле =СРЗНАЧ(D32:D431) я определил долю случаев, когда средний выход продукта выше при высокой температуре. На рис. 78.2
применение повторной выборки показывает, что с вероятностью 94% средний выход продукта при высокой температуре выше, чем при низкой. Разумеется, при
нажатии F9 будет сгенерирован другой набор из 400 повторных выборок, который
даст немного другую оценку вероятности того, что средний выход продукта при
высокой температуре выше, чем при низкой.

Задания
1. Тестируется новое лекарство от гриппа. Из 24 больных гриппом пациентов,
получивших новое лекарство, 20 почувствовали себя лучше, а 4 — хуже. Из
9 больных гриппом пациентов, получивших плацебо, 6 почувствовали себя
лучше, а 3 — хуже. Какова вероятность того, что лекарство эффективнее плацебо?
2. С восьмью рабочими была проведена беседа о вреде повышенного холестерина. У каждого рабочего до беседы и через какое-то время после нее был проверен уровень холестерина. Результаты проверки приведены в таблице. Какова
вероятность того, что рабочие стали питаться правильнее после беседы и их
уровень холестерина снизился?
Холестерин до беседы

Холестерин после беседы

220

210

195

198

250

210

200

199

220

224

260

212

175

179

198

184

3. Бета для акции — это значение наклона наилучшей подобранной линии, используемой для прогнозирования ежемесячного дохода от акции по ежемесячному доходу, приведенному в индексе Standard&Poor (S&P) 500. Бета
больше 1 показывает, что цикличность цены акции выше, чем цикличность
цен на рынке, а бета меньше 1 показывает, что цикличность цены акции ниже,

Анализ данных с помощью повторной выборки

817

чем цикличность цен на рынке. Файл Betaresampling.xlsx содержит данные более чем за 12 лет о ежемесячном доходе по акциям Microsoft (MSFT), Pfizer
(PFE) и другим акциям, а также индекс S&P 500. Исходя из этих данных,
определите вероятность того, что бета для Microsoft ниже беты для Pfizer. При
оценке беты для каждой итерации повторной выборки воспользуйтесь функцией НАКЛОН (SLOPE).
4. В файле Lawdata.xlsx даны баллы юридического теста LSAT и средний бал GPA
для 15 студентов юридической школы. На основе этих данных определите,
в каких пределах находится корреляция между баллами LSA T и GPA с вероятностью 95%?

ГЛ А В А 82

Ценообразование опционов
Обсуждаемые вопросы
Что такое колл-опцион и пут-опцион?
В чем разница между американским и европейским опционами?
Как выглядят выигрыши по европейским колл- и пут-опционам, если рассматривать их как функцию курса акций на дату исполнения?
Какими параметрами определяется цена опциона?
Как оценить волатильность акций на основе исторических данных?
Как реализовать в Excel формулу Блэка — Шоулза?
Как изменение ключевых параметров изменяет цену колл- и пут-опционов?
Как оценить волатильность акций по формуле Блэка — Шоулза?
В мои точные формулы ценообразования опционов никто не должен вносить изменения. Как защитить формулы на листе от изменений?
Как с помощью ценообразования опционов компания может принимать лучшие
инвестиционные решения?

В начале1970-х гг. экономисты Фишер Блэк (Fischer Black), Майрон Шоулз (Myron
Scholes) и Роберт Мертон (Robert Merton) вывели формулу ценообразования опционов Блэка — Шоулза, которая позволяет получить оценку европейских колл- и путопционов. За свою работу Шоулз и Мертон были удостоены Нобелевской премии по
экономике в 1997 г. (Блэк умер до 1997 г., а Нобелевская премия не присуждается посмертно.) Их научный труд произвел революцию в области корпоративных финансов. В этой главе я расскажу об основных положениях их важной научной работы.
ПРИМЕЧАНИЕ
Превосходное формальное исследование опционов см. в книге: David G. Luenberger,
Investment Science, 2nd ed. — Oxford University Press, 2013.

Ответы на вопросы
?

Что такое колл-опцион и пут-опцион?

Колл-опцион дает владельцу опциона право купить акцию по
цене исполнения.
Пут-опцион дает владельцу опциона право продать акцию по цене исполнения.

Ценообразование опционов

819

В чем разница между американским и европейским опционами?

Американский опцион может быть исполнен не позднее даты, известной как дата
исполнения (часто называемая датой истечения срока действия опциона). Европейский опцион может быть исполнен только в дату исполнения.

Как выглядят выигрыши по европейским колл- и пут-опционам, если рассматривать их как функцию курса акций на дату исполнения?

Давайте рассмотрим денежные потоки для шестимесячного европейского коллопциона на акции IBM с ценой исполнения $110. Пусть P — это курс акций IBM
через шесть месяцев. Прибыль от колл-опциона на эти акции составит $0, если
P d 110, и (P – 110), если P > 110. Если P меньше $110, владелец опциона может
не исполнять опцион. Если P больше $110, владелец может исполнить опцион,
купив акции по $110 и немедленно продав их поP, и тем самым получить прибыль
(P – 110). На рис. 82.1 представлена прибыль от этого колл-опциона. Коротко говоря, колл-опцион платит $1 за каждый доллар, на который курс акций превышает
цену исполнения. Прибыль от колл-опциона можно записать как max(0, P – 110).
Обратите внимание, что график колл-опциона на рис. 82.1 (см. лист Call в файле
Optionfigures.xlsx) имеет наклон 0 для значений P меньше цены исполнения. Наклон графика равен 1 для значений P больше цены исполнения.

Рис. 82.1. Денежные потоки колл-опциона

Можно показать, что если акции не приносят дивидендов, нецелесообразно исполнять американский колл-опцион досрочно. Таким образом, цена американского и европейского колл-опционов для акций, по которым не выплачиваются
дивиденды, одинакова.

820

ГЛАВА 82

Теперь рассмотрим денежные потоки для шестимесячного европейского путопциона на акции IBM с ценой исполнения $110. Пусть P — курс акций IBM через шесть месяцев. Прибыль от пут-опциона составит $0, если P t 110, и (P – 110),
если P < 110. Для P меньше $110 владелец опциона может купить акции заP и сразу продать их за $110 и тем самым получить прибыль (110 – P). Если P больше
$110, покупать акции по P и продавать за $110 невыгодно, так что владелец может
не исполнять опцион для продажи акций по $110.
На рис. 82.2 показана прибыль от этого пут-опциона (см. лист
Put в файле
Optionfigures.xlsx). Коротко говоря, пут-опцион платит $1 за каждый доллар, на
который курс акций ниже цены исполнения опциона. Прибыль от пут-опциона
можно записать как max(0, 110 – P). Обратите внимание, что график пут-опциона
имеет наклон –1 для значений P меньше цены исполнения и 0 для значений P
больше цены исполнения.

Рис. 82.2. Денежные потоки пут-опциона

Американский пут-опцион может быть исполнен досрочно, поэтому денежные
потоки для американского пут-опциона нельзя определить без знания цены акций
в период до даты истечения срока действия опциона.

Какими параметрами определяется цена опциона?

В модели ценообразования опционов Блэка — Шоулза Блэк, Шоулз и Мертон показали, что цена колл- и пут-опциона зависит от следующих параметров:
Текущая цена акций.
Цена исполнения опциона.

Ценообразование опционов

821

Время (в годах) до истечения срока действия опциона (называемое сроком опциона).
Процентная ставка (в год с учетом сложных процентов) на безрисковые инвестиции (как правило, в казначейские векселя) в течение всего срока инвестирования. Эта ставка называется безрисковой ставкой. Например, если
трехмесячные казначейские векселя приносят 5% дохода, безрисковая ставка
вычисляется как ln(1 + 0,05). (Взятие логарифма преобразует простую процентную ставку в ставку с учетом сложных процентов.) Сложные проценты
означают, что в каждый момент времени проценты приносят проценты.
Годовая ставка (в процентах от курса акций), по которой выплачиваются дивиденды. Если акции приносят каждый год 2% от своей стоимости в качестве
дивидендов, ставка дивиденда составляет 0,02.
Волатильность (нестабильность) акций (измеряемая на ежегодной основе).
Годовая волатильность, например 30%, означает, что (приближенно) стандартное отклонение относительного годичного изменения курса акций составит
примерно 30%. Во время пузыря доткомов в конце 1990-х гг. волатильность акций многих интернет-компаний превышала 100%. Мы рассмотрим два способа
вычисления этого важного параметра.
В формуле ценообразования Блэка — Шоулза курс акций должен соответствовать логарифмически нормальной случайной величине (подробнее о ней см.
в главе 75 «Логарифмически нормальная случайная величина в моделировании
курса акций»).

Как оценить волатильность акций на основе исторических данных?

Для оценки волатильности акций на основе данных о ежемесячной доходности
акций нужно предпринять следующее.
Определить ежемесячную доходность акций за несколько лет.
Определить для каждого месяца ln(1 + ежемесячный доход).
Определить стандартное отклонение для ln(1 + ежемесячный доход). Это вычисление дает ежемесячную волатильность.
Умножить ежемесячную волатильность на квадратный корень из 12 для преобразования ежемесячной волатильности в годовую.
Эта процедура проиллюстрирована в файле Dellvol.xlsx, где я вычисляю годовую
волатильность акций Dell на основе ежемесячных цен в период с августа 1988 .гпо
май 2001 г. (См. рис. 82.3, на котором часть строк скрыта.)
Скопируйте формулу =(B2-B3)/B3 из C2 в C3:C154 для вычисления ежемесячной
доходности акций Dell. Затем скопируйте формулу =1+C2 из D2 в D3:D154. Далее
вычислите ln(1 + ежемесячный доход) для каждого месяца, скопировав формулу
=LN(D2) из E2 в E3:E154, и вычислите ежемесячную волатильность в ячейке H3 по
формуле =СТАНДОТКЛОН.В(E2:E154). Наконец, вычислите годовую волатильность

822

ГЛАВА 82

акций Dell по формуле =КОРЕНЬ(12)*H3. Годовая волатильность акций Dell составляет 57,8%.

Рис. 82.3. Вычисление исторической волатильности акций Dell

Как реализовать в Excel формулу Блэка — Шоулза?

Для применения формулы Блэка — Шоулза в Microsoft Excel необходимо ввести
значения для следующих параметров:
S — текущий курс акций;
t — срок опциона (в годах);
X — цена исполнения;
r — годовая безрисковая ставка (предполагается, что эта ставка постоянно вычисляется с учетом сложных процентов);
σ — годовая волатильность акций;
y — процент от стоимости акций, выплачиваемый в виде дивидендов.
С учетом этих входных значений цена европейского колл-опциона по формуле
Блэка — Шоулза вычисляется следующим образом. Определим d1 и d2:

Тогда цена колл-опциона C определяется по формуле:

Ценообразование опционов

823

Здесь N(x) — вероятность того, что нормальная случайная величина со средним
значением 0 и стандартным отклонением σ, равным 1, меньше или равна x. Например, N(–1) = 0,16, N(0) = 0,5, N(1) = 0,84 и N(1,96) = 0,975. Нормальная случайная величина со средним значением 0 и стандартным отклонением 1 называется
нормированной случайной величиной, распределенной по нормальному закону. Нормальное интегральное распределение вычисляется с помощью функции НОРМ.
СТ.РАСП (NORM.S.DIST). Формула =НОРМ.СТ.РАСП(x;ИСТИНА_или_1) возвращает
вероятность того, что нормированная случайная величина, распределенная по
нормальному закону, меньше или равна x. Например, формула =НОРМ.СТ.РАСП(-1;
ИСТИНА), введенная в ячейку, дает в результате 0,16. Это значение показывает, что
нормальная случайная величина со средним значением 0 и стандартным отклонением 1 с вероятностью 16% примет значение менее –1.
Цену европейского пут-опциона P можно записать как:

В файле Bstemp.xlsx (рис. 82.4) я создал шаблон, вычисляющий цену для европейских колл- и пут-опционов. Введите значения параметров в B5:B10 и получите
цену европейского колл-опциона в D13, а цену европейского пут-опциона в D14.

Рис. 82.4. Определение цены европейских колл- и пут-опционов

ПРИМЕЧАНИЕ
Определение цены американских опционов в этой книге не рассматривается. Заинтересованные читатели должны обратиться к превосходному учебнику Луенбергера
Investment Science.

В качестве примера предположим, что акции Cisco сегодня продаются по $20 и вы
выпустили семилетний европейский колл-опцион. Пусть годовая волатильность

824

ГЛАВА 82

акций Cisco равна 50%, и безрисковая ставка в течение семилетнего периода исчисляется исходя из 5% в год. С учетом сложных процентов она преобразуется
в ln(1 + 0,05) = 0,04879. Cisco не выплачивает дивиденды, так что годовая ставка дивиденда равна 0. Цена колл-опциона составляет $10,64. Семилетний путопцион с ценой исполнения $24 будет стоить $7,69.

Как изменение ключевых параметров изменяет цену колл- и пут-опционов?

Как правило, влияние изменения входного параметра на цену колл- или путопциона соответствует влиянию, указанному в следующей таблице:
Европейский
колл-опцион

Европейский
пут-опцион

Американский
колл-опцион

Американский
пут-опцион

Курс акций

–

Цена исполнения

–

Срок опциона

Волатильность

Безрисковая ставка

–

Дивиденды

–

Параметр

Повышение сегодняшнего курса акций всегда повышает цену колл-опциона
и снижает цену пут-опциона.
Повышение цены исполнения всегда повышает цену пут-опциона и снижает
цену колл-опциона.
Увеличение срока опциона всегда повышает цену американского
опциона.
В случае выплаты дивидендов увеличение срока опциона может либо повысить, либо понизить цену европейского опциона.
Увеличение волатильности всегда повышает цену опциона.
Повышение безрисковой ставки повышает цену колл-опциона, поскольку более высокие ставки, как правило, увеличивают темпы роста курса акций (что
хорошо для колл-опциона). Эта ситуация более чем уравновешивает тот факт,
что из-за более высокой процентной ставки прибыль от опциона уменьшается.
Повышение безрисковой ставки всегда понижает цену пут-опциона, поскольку более высокие темпы роста курса акций, как правило, наносят ущерб путопциону, и будущая прибыль от пут-опциона уменьшается.
Дивиденды, как правило, снижают темпы роста курса акций, поэтому увеличение дивидендов снижает цену колл-опциона и повышает цену пут-опциона.
Используя однонаправленные и двунаправленные таблицы данных, вы можете
при необходимости исследовать конкретные эффекты меняющихся параметров
на цену колл- и пут-опционов (о работе с таблицами данных см. в главе 17 «Анализ чувствительности с помощью таблиц данных»).

Ценообразование опционов

825

Как оценить волатильность акций по формуле Блэка — Шоулза?

Ранее в этой главе я показал, как на основе исторических данных оценить годовую волатильность акций. Проблема с оценкой исторической волатильности состоит в том, что анализ представляет собой взгляд в прошлое. А нам нужен взгляд
в будущее. Подход на основе подразумеваемой волатильности просто оценивает
волатильность акций как значение волатильности, при котором цена по формуле Блэка — Шоулза соответствует рыночной цене опциона. Коротко говоря, подразумеваемая волатильность получает значение волатильности, подразумеваемое
рыночной ценой опциона.
Инструмент Подбор параметра (Goal Seek) с описанными ранее входными параметрами позволяет легко и быстро вычислить подразумеваемую волатильность.
22 июля 2003 г . акции Cisco торговались по $18,43 за штуку . В октябре 2003 г .
колл-опцион с ценой исполнения $17,50 продавался за $1,85. Срок действия этого
опциона истекал 18 октября (89 дней спустя). Таким образом, срок действия опциона составил 89/365 = 0,2438 года. Cisco не выплачивает дивиденды. Пусть ставка
для казначейских векселей составляет 5% и соответствующая безрисковая ставка
равна ln(1 + 0,05) = 0,04879. Для определения волатильности акций Cisco, которая
подразумевается ценой опциона, введите в ячейки B5:B10 файла Ciscoimpvol.xlsx параметры, как показано на рис. 82.5.

Рис. 82.5. Использование подразумеваемой волатильности
для вычисления волатильности акций Cisco

Далее в диалоговом окне Подбор параметра (Goal Seek), показанном на рис. 82.6,
определите волатильность (значение в ячейке B10), при которой цена опциона (формула в D13) достигнет $1,85. На вкладке Данные (Data) в группе Прогноз
(Forecast) выберите в опциях Анализ «что, если» (What-If Analysis) инструмент Подбор параметра (Goal Seek).

826

ГЛАВА 82

Рис. 82.6. Настройки в диалоговом окне Подбор параметра
для поиска подразумеваемой волатильности

Как показано на рис. 82.5, этот опцион подразумевает годовую волатильность для
Cisco в размере 34%.
ПРИМЕЧАНИЕ
На сайте https://finance.yahoo.com вы найдете оценки волатильности любых акций.

В мои точные формулы ценообразования опционов никто не должен вносить изменения. Как защитить формулы на листе от изменений?

Я вполне уверен, что не один раз бывало так, что вы посылали сотруднику файл
со своими расчетами, а тот менял выстраданные вами формулы. Нужно уметь защитить лист таким образом, чтобы другие пользователи могли только вводить
данные, но не менять формулы на нем. Посмотрим, как защитить все формулы в шаблоне Блэка — Шоулза на следующем примере. (См. файлы Bstemp.xlsx
и Bstempprotected.xlsx.)
Начнем с разблокировки всех ячеек на листе, а затем заблокируем ячейки, которые хотим защитить. Сначала щелкните на сером треугольнике в левом верхнем
углу листа, где пересекаются заголовки строк и столбцов. После щелчка по этому
треугольнику любые изменения формата будут применены на всем листе. Например, если выбрать полужирный шрифт, во всех ячейках листа будет использоваться полужирный шрифт.
После выделения всего листа на вкладке Главная (Home) в группе Шрифт (Font)
щелкните на маленьком значке вызова диалогового окна с параметрами шрифта.
Откроется диалоговое окно Формат ячеек (Format Cells), показанное на рис. 82.7. На
вкладке Защита (Protection) снимите флажок Защищаемая ячейка (Locked) и нажмите OK. Теперь все ячейки на листе разблокированы. Это означает , что даже если
лист защищен, к ячейкам можно получить доступ.
F5, открывающую
Далее выделите все формулы на листе. Для этого нажмите
диалоговое окно Переход (Go To). Нажмите Выделить (Special), выберите Формулы
(Formulas) и нажмите OK. Снова откройте диалоговое окно Формат ячеек (Format

Ценообразование опционов

827

Рис. 82.7. Диалоговое окно Формат ячеек

Cells) и на вкладке Защита (Protection) установите флажок Защищаемая ячейка
(Locked). Теперь этот флажок блокирует все формулы.

Рис. 82.8. Обеспечение доступа пользователей к незаблокированным ячейкам

828

ГЛАВА 82

Теперь вы можете защитить лист , что предотвратит изменение формул другими
пользователями. На вкладке Рецензирование (Review) в группе Изменения (Changes)
выберите Защитить лист (Protect Sheet). В диалоговом окне Защита листа (Protect
Sheet) установите флажок выделение незаблокированных ячеек (Select Unlocked
Cells) — рис. 82.8 — и нажмите OK. Это позволит пользователям шаблона выделять
незаблокированные ячейки, но не формулы.
Теперь вы не сможете увидеть или изменить содержимое любой формулы. Попробуйте испортить какую-либо формулу! Получившийся защищенный лист сохранен в файле Bstempprotected.xlsx.

Как с помощью ценообразования опционов компания может принимать
лучшие инвестиционные решения?

Ценообразование опционов можно использовать для улучшения бюджетирования
капиталовложений или процесса принятия финансовых решений. Использование
ценообразования опционов для оценки фактических инвестиционных проектов
называется реальными опционами. Идею реальных опционов приписывают Джуди Левен (Judy Lewent), в прошлом финансовому директору Merck. По сути, реальные опционы позволяют назначить явную цену для управленческой гибкости,
которую часто упускают из вида при традиционном бюджетировании капиталовложений. Концепция реальных опционов демонстрируется на следующих двух
примерах.
ПРИМЕЧАНИЕ
Для получения подробной информации о реальных опционах см. книгу Д. Луенбергера.

Пусть вы — владелец нефтяной скважины. Сегодня ваше наилучшее предположение заключается в том, что из скважины можно добыть нефти на $50 млн.
Через 5 лет (оставаясь владельцем скважины) вам предстоит принять решение
о разработке этой нефтяной скважины, которая обойдется вам в $70 млн. Один
рисковый нефтяник готов купить скважину сегодня за $10 млн. Следует ли продать скважину?
Конечно, цена нефти через 5 лет может вырасти. Даже если предположить, что цена
нефти будет расти на 5% в год, через 5 лет нефть будет стоить всего $63,81 млн.
Традиционное бюджетирование капиталовложений говорит, что нефть обесценится, поскольку стоимость ее разработки превышает стоимость нефти в скважине. Но
не торопитесь — через 5 лет цена нефти в скважине будет другой, так как многие
факторы (такие как мировая цена на нефть) могут измениться. Существует вероятность, что через 5 лет нефть будет стоить не меньше $70 млн. Если через 5 лет нефть
будет стоить $80 млн, разработка скважины через 5 лет принесет $10 млн прибыли.
По сути, вы владеете пятилетним европейским колл-опционом на эту скважину ,
так как прибыль от скважины через 5 лет такая же, как прибыль от европейского колл-опциона с курсом акций $50 млн, ценой исполнения $70 млн и сроком

Ценообразование опционов

829

опциона 5 лет. Можно предположить, что годовая волатильность подобна волатильности акций типичной нефтяной компании (например, 30%). Если использовать ставку по казначейскому векселю 5%, соответствующую безрисковой ставке
4,879%, в файле Oilwell.xlsx (рис. 82.9) можно определить, что цена такого коллопциона составляет $11,47 млн. Из этого следует , что вы не должны продавать
скважину за $10 млн.
Конечно, фактическая волатильность для этой нефтяной скважины неизвестна.
Поэтому с помощью однонаправленной таблицы данных определим, как цена
опциона зависит от оценки волатильности (см. рис. 82.9). Как видите, пока волатильность скважины составляет по меньшей мере 27%, «опцион» на нефтяную
скважину стоит более $10 млн.

Рис. 82.9. Реальный опцион на нефтяную скважину

В качестве второго примера рассмотрим биотехнологическую компанию, разрабатывающую лекарственный препарат для фармацевтической фирмы. В биотехнологической компании в настоящее время предполагают , что цена разрабатываемого препарата составляет $50 млн. Безусловно, цена препарата со временем
может снизиться. Для защиты от падения цены биотехнологической компании
требуется, чтобы препарат через 5 лет имел гарантированную цену $50 млн. Если
страховая компания собирается подписать такое обязательство, какая справедливая цена должна быть назначена?

830

ГЛАВА 82

По сути, биотехнологическая компания просит заплатить ей $1 млн за каждый
$1 млн, на который цена препарата упадет ниже $50 млн, через 5 лет . Это эквивалентно пятилетнему пут-опциону на цену препарата. Предположим, что ставка
по казначейскому векселю составляет 5% и годовая волатильность для акций сопоставимых компаний равна 40% (см. файл Drugabandon.xlsx, показанный на рис.
82.10), тогда цена этого опциона — $10,51 млн. Такой тип опциона часто называют
опционом на отказ от проекта , но он эквивалентен пут-опциону . (На рис. 82.10
однонаправленная таблица данных показывает , как цена опциона отказа от проекта зависит от предполагаемой волатильности, составляющей 30–45% от цены
препарата.)

Рис. 82.10. Вычисление опциона отказа от проекта

Задания
1. На основе данных о ежемесячной доходности акций в файлеVolatility.xlsx определите оценки годовой волатильности для акций Intel, Microsoft и GE.
2. Сегодня акции продаются по $42. Г одовая волатильность акций составляет
40%, а годовая безрисковая ставка равна 10%.
• Какова справедливая цена шестимесячного европейского колл-опциона
с ценой исполнения $40?

Ценообразование опционов

831

• Насколько текущая цена акций должна вырасти, чтобы покупатель коллопциона достиг безубыточности через шесть месяцев?
• Какова справедливая цена для шестимесячного европейского пут-опциона
с ценой исполнения $40?
• Насколько текущая цена акций должна снизиться, чтобы покупатель путопциона достиг безубыточности через шесть месяцев?
• При каком уровне волатильности 40-долларовый колл-опцион будет продаваться за $6? Подсказка: воспользуйтесь инструментом Подбор параметра (Goal Seek).
3. 25 сентября 2000 г . акции JDS Uniphase продавались по $106,81. В этот же
день 100-долларовый европейский пут-опцион, срок действия которого истекал 20 января 2001 г., продавался за $11,875. На основе этой информации вычислите подразумеваемую волатильность для акций JDS Uniphase. Используйте 5%-ную ставку по казначейскому векселю.
4. 9 августа 2002 г. акции Microsoft продавались по $48,58. Тридцатипятидолларовый европейский колл-опцион, срок действия которого истекал 17 января
2003 г., продавался за $13,85. На основе этой информации вычислите подразумеваемую волатильность для акций Microsoft. Используйте 4%-ную ставку по
казначейскому векселю.
5. Есть опцион на покупку нового самолета через три года за $25 млн. По вашим
оценкам текущая цена самолета составляет $21 млн. Г одовая волатильность
цены самолета — 25%, безрисковая ставка равна 5%. Сколько стоит опцион на
покупку самолета?
6. Текущая цена меди составляет 95 центов за фунт. Годовая волатильность для
цен на медь равна 20%, безрисковая ставка — 5%. Через год имеется возможность потратить $1,25 млн на добычу 8 млн фунтов меди. Медь может быть
продана через год. Добыча фунта меди из недр обходится в 85 центов. Выгодна ли инвестиция в медь при таких условиях?
7. У вас есть авторские права на биотехнологический лекарственный препарат .
Наилучшая оценка текущей цены на эти права составляет $50 млн. Пусть годовая волатильность биотехнологических компаний составляет 90% и безрисковая ставка равна 5%. Какова цена опциона на продажу прав на лекарственный препарат за $40 млн через пять лет от текущего момента?
8. В компании Merck обсуждается вопрос о том, стоит ли инвестировать в новый
биотехнологический проект. По оценкам компании стоимость проекта составляет –$56 млн. Инвестирование в новый проект даcт компании Merck возможность поучаствовать в более крупном технологическом проекте, который
будет доступен через 4 года. Если Merck не примет участие в новом проекте,
она не сможет получить более крупный проект . Для более крупного проекта
через 4 года, начиная с текущего момента, потребуется $1,5 млрд. В настоящее

832

ГЛАВА 82

время Merck оценивает чистую приведенную стоимость (ЧПС) денежных потоков для более крупного проекта в $597 млн. Если безрисковая ставка равна
10% и годовая волатильность для более крупного проекта составляет 35%, как
должна поступить компания Merck? (С этой задачи началось применение реальных опционов!)
9. Разработайте лист со следующими входными данными для расчета годовой
прибыли:
• ежегодные постоянные затраты;
• себестоимость единицы продукции;
• цена за единицу продукции;
• годовой спрос = 10 000 – 100 × (цена).
Защитите ячейки, в которых вычисляется годовой спрос и годовая прибыль.

Г Л А В А 83

Определение потребительской
ценности

Обсуждаемые вопросы
Компания, работающая с кредитными картами, в настоящее время имеет коэффициент удержания клиентов, равный 80. Насколько возрастет прибыльность
компании, если коэффициент удержания клиентов повысится до 90% и выше?
Междугородная телефонная компания предоставляет клиентам конкурентов бонус при смене компании. Насколько значительным должен быть бонус?

Многие компании недооценивают своих клиентов. При оценке клиента компания
должна учитывать чистую приведенную стоимость (ЧПС) для долгосрочной прибыли, которую принесет клиент. (О чистой приведенной стоимости см. в главе 8
«Оценка инвестиций по чистой приведенной стоимости».) Из-за отказа от учета
долгосрочной значимости клиента компании часто принимают неправильные решения. Например, компания может сократить отдел обслуживания клиентов на
10%, чтобы сэкономить $1 млн, но из-за снижения качества обслуживания потерять гораздо больше $1 млн в потребительской ценности, когда клиент переведет
свой бизнес в другое место. Это, в свою очередь, приведет к снижению прибыли
компании. Способы определения потребительской ценности рассматриваются на
следующих двух примерах.

Ответы на вопросы
Компания, работающая с кредитными картами, в настоящее время имеет
коэффициент удержания клиентов, равный 80. Насколько возрастет прибыльность компании, если коэффициент удержания клиентов повысится до
90% и выше?

Этот пример основан на книге Фредерика Райхельда «Эффект лояльности»1. Данные к примеру вы найдете в файле Loyalty.xlsx (рис. 83.1). Райхельд оценивает прибыльность клиента — держателя кредитной карты на основе количества лет , в течение которых клиент является держателем карты. Например, в течение первого
1

Frederick Reichheld. The Loyalty Effect. — Harvard Business School Press, 2001.

834

ГЛАВА 83

года держатель карты приносит прибыль –$40, вследствие затрат на привлечение
клиента и на создание клиентского счета. В течение каждого последующего года
прибыль, приносимая клиентом, растет, и клиент, являющийся держателем карты
20 лет и больше, приносит прибыль $161 в год.
Кредитная компания хочет определить, как потребительская ценность зависит от
коэффициента удержания клиентов. В настоящее время коэффициент удержания
клиентов составляет 80%. Это означает , что в конце каждого года 20% (1 – 0,80)
всех клиентов не возобновляют свои карты. (Эти 20% клиентов могут быть названы годовым коэффициентом «текучести» клиентов.) Кредитной компании необходимо определить долгосрочную ценность клиента для следующих значений
коэффициента удержания клиентов: 80, 85, 90, 95 и 99%.

Рис. 83.1. Ценность клиентов — держателей кредитных карт

Для определения долговременной ценности клиента начнем, например, с когорты из 100 клиентов. (Когорта — это группа лиц, имеющих общий статистический
фактор. Размер группы, 100 человек, был выбран произвольно, но круглые числа
позволяют легче следить за ходом анализа.) Затем для каждого года определим,
сколько клиентов остается клиентами компании, по формуле (клиенты для года t +
+ 1) = (коэффициент удержания клиентов) × (клиенты для года t). Будем считать, что
клиенты уходят только в конце года. Затем с помощью функции ЧПС (NPV) определим общую ЧПС (с учетом 15%-ной учетной ставки), полученную от исходной
когорты из 100 клиентов. 15%-ная учетная ставка означает , что $1, заработанный
через год от текущего момента, стоит так же, как $1,00/$1,15, заработанный сей-

Определение потребительской ценности

835

час. Разделив это число на количество клиентов в исходной когорте (100), получим ценность отдельного клиента.
Прежде всего я присвоил имена, указанные в диапазонеB6:B7, ячейкам C6:C7. Затем я ввел исходное количество клиентов (100) в ячейку C9. Затем скопировал
формулу =коэфф_сохран_клиентов*C9 из C10 в C11:C38 для вычисления количества клиентов, оставшихся на следующий год. Например, на год 2 осталось 80
клиентов.
Я вычислил прибыль, приносимую каждый год, умножив количество оставшихся
клиентов на прибыль от каждого клиента. Для этого скопируйте формулу =C9*B9
из ячейки D9 в D10:D38. В ячейке E4 я вычислил среднюю ЧПС, полученную с отдельного клиента, по формуле =(1+процентная_ставка)*ЧПС(процентная_ставка;
D9:D38)/100. Допустим, денежные потоки рассчитываются на начало года и годовая учетная ставка равна 15%. Часть формулы ЧПС(процентная_ставка;D9:D38)/100
вычисляет среднюю ЧПС, полученную от отдельного клиента, для денежных потоков на конец года. ЧПС для денежных потоков на конец года преобразуются
в ЧПС для денежных потоков на начало года путем умножения на ( 1+процентная_ставка).
При коэффициенте удержания клиентов 80% ценность среднего клиента составляет $141,72. Чтобы определить, как ценность отдельного клиента варьирует
вместе с изменением годового коэффициента удержания клиентов, я использовал однонаправленную таблицу данных. В ячейки F9:F13 я ввел соответствующие годовые коэффициенты удержания клиентов. В ячейку G8 я ввел формулу
=E4, по которой с помощью таблицы будет рассчитываться ЧПС для отдельного клиента. Затем я выделил табличный диапазон ( F8:G13) и на вкладке Данные
(Data) в списке Анализ «что, если» (What If Analysis) выбрал Таблица данных (Data
Table). Указав ячейку C6 в поле Подставлять значения по строкам в (Column Input
Cell), я получил расчеты прибыли, показанные ранее на рис. 83.1. Обратите внимание, что повышение коэффициента удержания клиентов с 80 до 90% почти
удваивает ценность каждого клиента, то есть крайне важно обращаться с такими клиентами вежливо и не экономить пенни на их обслуживании. Осознание
ценности клиента дает большинству компаний преимущество и позволяет повысить прибыль.
Междугородная телефонная компания предоставляет клиентам конкурентов бонус при смене компании. Насколько значительным должен быть
бонус?

Междугородная телефонная компания, клиенты которой тратят в среднем $400
в год, получает 10% прибыли с каждого потраченного доллара. В конце каждого
года 50% клиентов компании переходят к конкурентам и 30% клиентов конкурентов без какого-либо привлечения переходят в эту компанию. Компания рассматривает вопрос о предоставлении клиентам конкурентов одноразового бонуса
для смены компании. Насколько значительным может быть стимул без убытка
для компании?

836

ГЛАВА 83

Ключом к решению этой проблемы (см. файл Phoneloyalty.xlsx и рис. 83.2) является
внимательное изучение ЧПС при наличии двух условий:
Условие 1. Сто клиентов вначале подключаются к конкурентам.
Условие 2. Компания платит 100 клиентам конкурентов определенную сумму
за переход.
Для отслеживания каждой ситуации в течение определенного времени (например, в течение 20 лет) можно с помощью инструментаПодбор параметра (Goal Seek)
определить сумму x в долларах (выплачиваемую клиенту за переход в компанию),
которая нивелирует влияние на прибыль следующих условий:
Условие 1. Компания платит каждому из 100 нелояльных клиентов x долларов
за переход.
Условие 2. Рынок состоит из 100 нелояльных клиентов.
Пусть анализ начинается 30 июня 2014 г . и клиенты меняют компанию не чаще
одного раза в год. Присвойте имена, указанные в ячейках A2:A6, ячейкам B2:B6.
Ключевым шагом анализа является понимание того, что (клиенты компании в год t
+ 1) = 0,3 × (клиенты конкурентов в год t) + 0,5 × (клиенты компании в год t). Аналогично (клиенты конкурентов в год t + 1) = 0,7 × (клиенты конкурентов в год t) + 0,5 ×
(клиенты компании в год t).

Рис. 83.2. Анализ бонуса для телефонной компании

В ячейку D9 (клиенты компании) я ввел 100 и 0 в ячейку E9 (клиенты конкурентов). Такое распределение клиентов соответствует ситуации сразу после того, как

Определение потребительской ценности

837

бонус был предложен 100 клиентам. Предположим, что клиенты, получившие
бонус, должны оставаться клиентами компании, по крайней мере, один год. Скопировав формулу =(1-вероятность_ухода)*D9+вероятность_прихода*E9 из ячейки
D10 в D11:D28, я вычислил количество клиентов в каждом году. (На рис. 83.2 данные для 2022–2029 гг. скрыты.) Количество клиентов конкурентов в каждом году
я вычислил по формуле =вероятность_ухода*D9+(1-вероятность_прихода)*E9, скопировав ее из E10 в E11:E28.
В ячейке F9 я вычислил прибыль, полученную за первый год, по формуле
=D9*годовая_выручка*коэфф_прибыльности-бонус*100. Обратите внимание, что
из прибыли я вычел сумму, выплаченную 100 клиентам за переход от конкурентов. Для вычисления прибыли в последующие годы я скопировал формулу
=D10*годовая_выручка*коэфф_прибыльности из F10 в F11:F28. В ячейке D5 вычислена ЧПС прибыли, связанная с бонусом, по формуле =ЧИСТНЗ(0,1;F9:F28;B9:B28).
(Функция ЧИСТНЗ (XNPV) рассматривается в главе 8.)
Аналогичным образом в ячейках G8:I28 я вычислил прибыль, полученную для
случая, когда 100 клиентов первоначально были подключены к конкурентам.
30 июня 2014 г. 30 из этих 100 клиентов перешли в компанию (даже без бонуса).
В ячейке F2 я вычислил разницу между ЧПС с бонусом и ЧПС без бонуса.
Наконец, с помощью инструмента Подбор параметра (Goal Seek) я варьировал размер бонуса (ячейка B2) так, чтобы значение ячейки F2 стало равно 0. Диалоговое
окно Подбор параметра (Goal Seek) показано на рис. 82.3. ЧПС для двух ситуаций
одинакова, если размер бонуса составляет $34,22. Таким образом, компания могла
бы предоставлять клиентам бонус до $34,22 за переход и по-прежнему иметь повышенную прибыль.

Рис. 83.3. Диалоговое окно Подбор параметра для определения
максимального размера бонуса, повышающего прибыльность

Задания
1. Компания Whirlswim Appliance рассматривает возможность предоставить
всем клиентам бесплатное техническое обслуживание для каждого проданного видеомагнитофона (такие существовали до того, как кино стали снимать на

838

ГЛАВА 83

цифру). По оценкам компании, за каждый проданный видеомагнитофон придется платить в среднем $2,50 (стоимость в сегодняшних долларах). Рынок
состоит из 72 000 потребителей, последняя покупка которых была в компании
Whirlswim, и 86 000 потребителей, которые последний раз покупали у конкурентов. В указанном году 40% всех потребителей приобрели видеомагнитофоны. Если последняя покупка потребителя была в Whirlswim, с вероятностью 60% его следующая покупка также будет в Whirlswim. Если последняя
покупка была не в Whirlswim, с вероятностью 30% следующая покупка будет
в Whirlswim. Покупка в текущем году дает прибыль $20. Вклад в прибыль от
покупателя (и расходы на техническое обслуживание для каждого покупателя) растет на 5% в год. Коэффициент дисконтирования для прибыли (относительно 30-летнего горизонта) составляет 10% в год.
Предположим, что компания предоставляет бесплатное техническое обслуживание. Если последняя покупка клиента была в Whirlswim, вероятность
того, что в следующий раз он опять купит в Whirlswim, увеличится на неизвестную величину в пределах от 0 до 10%. Аналогично, если компания предоставляет бесплатное техническое обслуживание и последняя покупка клиента была не в Whirlswim, вероятность того, что следующая покупка будет
в Whirlswim, увеличится на неизвестную величину в пределах от 0 до 10%.
Следует ли компании Whirlswim предлагать клиентам бесплатное техническое обслуживание?
2. Супермаркет Mr. D пытается определить, следует ли предоставить потребителям карту клиента. В настоящее время 30% всех покупателей лояльны к супермаркету. Лояльный клиент покупает в Mr . D в 80% случаев. Нелояльный
к Mr. D клиент покупает в этом супермаркете в 10% случаев. Стандартный покупатель тратит $150 в неделю, и супермаркет Mr. D работает из 4% прибыли.
Карта клиента обойдется супермаркету Mr . D в среднем в $0,01 на каждый
потраченный доллар. Вы считаете, что доля лояльных к Mr . D покупателей
увеличится на неизвестную величину в пределах от 2 до 10%. Вы также считаете, что доля случаев, когда лояльный клиент покупает в Mr. D, увеличится
на неизвестную величину в пределах от 2 до 12%. Следует ли супермаркету
Mr. D предоставлять потребителям карту клиента? Следует ли супермаркету
Mr. D предоставлять карту, если прибыль составляет 8%, а не 4%?

Г Л А В А 84

Оптимальный размер заказа
в модели управления запасами

Обсуждаемые вопросы
Магазин электроники продает 10 000 смартфонов в год. Каждый раз при закупке
смартфонов магазин несет расходы в размере $10 за закупку. Магазин платит
$100 за каждый смартфон, и стоимость хранения смартфона на складе в течение
года составляет $20. Когда магазин закупает смартфоны, какого размера должна
быть закупка?
Завод производит 10 000 серверов в год. Себестоимость производства каждого
сервера составляет $2000. Стоимость запуска производства партии серверов составляет $200, а стоимость хранения сервера на складе в течение года — $500.
При необходимости завод может производить 25 000 серверов в год. Каким должен быть размер партии при производстве серверов?

Когда магазин заказывает один и тот же товар многократно, естественным образом возникает вопрос: какое количество товара магазин должен заказывать каждый раз? Если магазин закажет слишком много, его ждут непомерные затраты на
хранение запасов. Если магазин закажет слишком мало товара, возникнут затраты
на повторные заказы. Г де-то должна пролегать золотая середина, которая минимизирует годовые затраты на хранение запасов и на заказы.
С такой же позиции рассмотрим ситуацию с заводом, производящим продукцию
партиями. Какой размер партии минимизирует годовые затраты на хранение и на
запуск производства партии продукции? В данной главе на двух примерах показано, как формула оптимального размера заказа (предложенная в 1913 г. Ф. Харрисом (F. Harris) из Westinghouse Corporation) позволяет ответить на эти вопросы.

Ответы на вопросы
Магазин электроники продает 10 000 смартфонов в год. Каждый раз при
закупке смартфонов магазин несет расходы в размере $10 за закупку. Магазин платит $100 за каждый смартфон, и стоимость хранения смартфона на
складе в течение года составляет $20. Когда магазин закупает смартфоны, какого размера должна быть закупка?

840

ГЛАВА 84

Размер заказа на поставку, минимизирующий годовые затраты на хранение и заказы на поставку, можно определить, если известны следующие параметры:
K — затраты на закупки;
h — затраты на хранение единицы продукции в течение года;
D — годовой спрос на продукт.
Работа с этими параметрами представлена в файлеEoq.xlsx на листе EOQ (рис. 84.1).

Рис. 84.1. Шаблон для вычисления оптимального размера заказа (EOQ)

Пусть q — размер заказа на поставку, тогда годовые затраты на хранение продукции равны 0,5qh. (Назовем это уравнение уравнением 1.) В уравнении 1 мы приняли средний уровень запасов (0,5q) равным половине от максимального уровня
запасов. Чтобы убедиться, что средний уровень запасов равен 0,5q, можно вычислить средний уровень запасов для цикла (периода времени между поставкой заказов). В начале цикла закупка прибывает, и уровень запасов равен q. В конце цикла
все распродано, и уровень запасов равен 0. Поскольку спрос постоянен, средний
уровень запасов в течение цикла просто равен среднему для 0 иq, или 0,5q. Максимальный уровень запасов равен q, так как подразумевается, что следующий заказ
поступает в тот момент, когда уровень запасов снижается до 0.
Поскольку в год делается D/q заказов на поставку, годовые затраты на заказы равны (D/q) × K. (Я назвал это уравнение уравнением 2.) С помощью инструмента
Поиск решения (Solver) можно показать, что годовая сумма затрат на хранение и заказы минимальна для значения q, равного оптимальному размеру заказа (EOQ),
который вычисляется по следующей формуле (уравнение 3):

Эта формула показывает:
увеличение спроса или затрат на заказы увеличивает EOQ;
увеличение затрат на хранение уменьшает EOQ.

Оптимальный размер заказа в модели управления запасами

841

В файле Eoq.xlsx я использовал уравнение 3, чтобы определить EOQ в ячейкеC5 по
формуле =SQRT(2*K*D/h). Годовые затраты на хранение я определил в ячейкеC6 по
уравнению 1 и, соответственно, формуле =0,5*EOQ*h. Годовые затраты на заказы
в ячейке C7 вычислены по уравнению 2. Обратите внимание, что для оптимального размера заказа EOQ годовые затраты на заказы всегда равны годовым затратам
на хранение. В ячейке C8 я определил общие годовые затраты (без учета стоимости приобретения, которая не зависит от стратегии закупок) по формуле =C6+C7.
Конечно, можно воспользоваться однонаправленной или двунаправленной таблицей данных, чтобы определить чувствительность EOQ и различных затрат к изменению K, h и D. В данном примере K = $10, D = 10 000 смартфонов в год иh = $20 за
хранение одного смартфона. После ввода этих значений в ячейки C2:C4 получим
следующее:
размер каждого заказа должен составлять 100 смартфонов;
и годовые затраты на хранение, и затраты на заказы составляют $1000. Для оптимального размера заказа годовые затраты на хранение всегда равны годовым
затратам на заказы;
общие годовые затраты (без учета затрат на приобретение) составляют $2000.
При работе с EOQ необходимо учитывать следующее.
Наличие оптовых скидок лишает нахождение EOQ смысла, поскольку в таком
случае годовые затраты на приобретение зависят от размера заказа.
EOQ предполагает, что спрос равномерен в течение года. Оптимальный размер заказа не следует использовать для продуктов, на которые есть сезонный
спрос.
Предполагается, что годовые затраты на хранение, как правило, составляют
10–40% от затрат на приобретение единицы продукции.
Лист EOQ Protected в файле Eoq.xlsx — это защищенная версия листа EOQ. Когда
лист защищен, изменения в формулы внести невозможно. (О том, как защитить лист, см. в главе 82 «Ценообразование опционов».)
ПРИМЕЧАНИЕ
О построении моделей управления запасами см. в книге Уэйна Винстона (Wayne L.
Winston. Operations Research: Applications and Algorithms. — Duxbury Press, 2007).

Завод производит 10 000 серверов в год. Себестоимость производства каждого сервера составляет $2000. Стоимость запу ска производства партии
серверов составляет $200, а стоимость хранения сервера на складе в течение
года — $500. При необходимости завод может производить 25 000 серверов
в год. Каким должен быть размер партии при производстве серверов?

Модель EOQ предполагает, что по запросу закупка прибывает моментально. Когда компания производит продукт, а не закупает его, заказ на изготовление не мо-

842

ГЛАВА 84

жет быть исполнен мгновенно. В таких ситуациях нужно определить не размер
заказа, минимизирующий затраты, а размер партии, минимизирующий затраты.
Когда компания производит продукцию, а не закупает ее, размер партии, сводящей затраты к минимуму, зависит от следующих параметров:
K — затраты на запуск производства партии продукта;
h — затраты на хранение единицы продукции в запасе в течение года;
D — годовой спрос на продукт;
R — годовой показатель производства продукта. Например, производственная
мощность IBM составляет 25 000 серверов в год.
Пусть q — размер каждой партии продукта, тогда годовые затраты на хранение
равны 0,5 × (q/R) × (R – D) × h. (Я назвал это уравнение уравнением 4.) У равнение 4 имеет такой вид, потому что производство каждой партии продолжаетсяq/R
лет и во время производственного цикла запас увеличивается как R – D. Максимальный уровень запасов, который имеет место после завершения производства
партии, можно вычислить как ( q/R) × (R – D). Таким образом, средний уровень
запасов равен 0,5 × (q/R) × (R – D).
Поскольку в год производится D/q партий, годовые затраты на запуск производства равны KD/q (я назвал это уравнением 5). С помощью инструмента Excel
Поиск решения (Solver) можно показать, что размер партии, минимизирующий годовые затраты на запуск производства и на хранение, можно вычислить по следующему уравнению (я назвал его уравнением 6). Эта модель называется оптимальным размером партии (EOB):

Исходя из этой формулы можно определить следующее:
увеличение K или D увеличивает EOB;
увеличение h или R уменьшает EOB.
В файле Contrateeoq.xlsx на листе Cont Rate EOQ я создал шаблон для вычисления
EOB, годовых затрат на запуск производства и затрат на хранение. Этот лист показан на рис. 84.2.
Для этого примера K = $200, h = $500, D = 10 000 единиц в год и R = 25 000 единиц
в год. После ввода значений этих параметров в ячейки C2:C5 получим следующее.
Размер партии, минимизирующий затраты, составляет 115,47 сервера. Т аким
образом, компания должна производить партию из 115 или 116 серверов.
Годовые затраты на хранение и на
запуск производства составляют по
$17 320,51. Как и в предыдущем случае, для оптимального размера партии годовые затраты на хранение всегда равны годовым затратам на запуск производства.

Оптимальный размер заказа в модели управления запасами

843

Рис. 84.2. Шаблон для вычисления EOB

Общие годовые затраты (без учета переменных затрат на производство) составляют 34 641,02 доллара.
В год нужно производить 86,6 партии.
При работе с EOB необходимо учитывать следующее.
Если переменные затраты на производство единицы продукции зависят от размера партии, модель EOB является недействительной.
Модель EOB предполагает, что спрос относительно постоянен в течение года.
Эту модель не следует использовать для продукции, на которую есть сезонный
спрос.
Предполагается, что годовые затраты на хранение, как правило, составляют
10–40% от затрат на производство единицы продукции.
Лист Protected в файле Contrateeoq.xlsx — это защищенная версия листа
О том, как защитить лист, см. в главе 82.

EOB.

Задания
1. Магазин бытовой техники продает плазменные телевизоры. Г одовой спрос
оценивается в 1000 единиц. Стоимость хранения одного телевизора в течение
года составляет $500, а стоимость закупки телевизоров — $400.
• Сколько телевизоров следует заказывать в одной закупке?
• Сколько закупок в год нужно сделать?
• Каковы годовые затраты на хранение телевизоров и закупку?
2. Компания Waterford Crystal может произвести до 100 кувшинов для чая со
льдом в день. Допустим, завод работает 250 дней в году и годовой спрос составляет 20 000 кувшинов. Стоимость хранения кувшина в течение года составляет $10, а стоимость запуска производства кувшинов — $40.
• Каков рекомендуемый размер партии кувшинов?
• Сколько партий в год нужно произвести?
• Каковы годовые затраты на производство и хранение кувшинов?

ГЛ А В А 85

Построение моделей управления
запасами для неопределенного
спроса

Обсуждаемые вопросы
При каком уровне запасов следует делать закупку, если необходимо минимизировать годовые затраты, связанные с дефицитом, хранением и закупками?
Что означает термин «95%-ный уровень обслуживания»?

В главе 84 «Оптимальный размер заказа в модели управления запасами» мы узнали, как вычислять оптимальный размер заказа на поставку и оптимальный размер партии товара. В примерах подразумевалось, что спрос на продукт постоянен.
Таким образом, если годовой спрос составляет, например, 1200 единиц в год, ежемесячный спрос равен 100 единицам. Пока спрос держится на постоянном уровне, оптимальный размер заказа является достаточно хорошим приближением для
размера заказа, минимизирующего затраты.
В действительности спрос в любой период времени не определен, поэтому возникает естественный вопрос, до какой величины может понизиться уровень запасов, прежде чем потребуется следующая закупка. Уровень запасов, при котором
возникает необходимость в закупке, называется точкой заказа. Очевидно, что высокая точка заказа снизит потери от дефицита и увеличит затраты на хранение.
Аналогично низкая точка заказа увеличит потери от дефицита и снизит затраты
на хранение. В некой промежуточной точке заказа сумма потерь от дефицита и затрат на хранение будет минимальной. В первом примере этой главы показано, как
определить точку заказа, минимизирующую затраты, связанные с дефицитом, закупкой и хранением, на основе двух следующих предположений.
Каждая недостающая единица продукции является невыполненным заказом
клиента, и компания несет потери от дефицита CB. Эти потери в первую очередь являются мерой неудовлетворенности клиента, вызванной задержкой
в получении заказа.
Каждая недостающая единица продукции приводит к упущенной продаже,
и компания несет потери CLS > CB. Потери упущенной продажи включают прибыль, не полученную вследствие упущенной продажи, а также потери от дефицита CB.

Построение моделей управления запасами для неопределенного спроса

845

Второй пример показывает, как определить оптимальную точку заказа на основе
уровня обслуживания. Например, 95%-ный уровень обслуживания означает , что
точка заказа устанавливается на уровне, обеспечивающем в среднем удовлетворение 95% всех клиентов в срок. Как правило, стоимость потерь от дефицита и в случае невыполненного заказа, и в случае упущенной продажи определить трудно.
По этой причине в большинстве компаний устанавливают точки заказа на основе
уровня обслуживания.

Ответы на вопросы
При каком уровне запасов следу ет делать закупку, если необходимо минимизировать годовые затраты, связанные с дефицитом, хранением и закупками?

Как указано в главе 84, EOQ зависит от следующих параметров:
K — затраты на закупки;
h — затраты на хранение одной единицы продукции в запасе в течение года;
D — годовой спрос на продукт . Поскольку теперь спрос точно не известен,
пусть D обозначает ожидаемый годовой спрос на продукт.

Невыполненный заказ
Данные для этого примера находятся в файлеReorderpoint_backorder.xlsx (рис. 85.1).
Сначала предположим, что каждый дефицит приводит к отложенному заказу .
Другими словами, дефицит не приводит к потере спроса. Также подразумевается,
что каждая недостающая единица продукции приводит к потерям от дефицита CB.

Рис. 85.1. Определение точки закупки для случая отсрочки
выполнения заказа из-за дефицита

846

ГЛАВА 85

В этом случае точка заказа зависит от следующих величин:
EOQ — оптимальный размер заказа (закупаемое каждый раз количество);
K — затраты на закупку;
h — годовые затраты на хранение единицы продукции;
D — среднегодовой спрос;
SOC — потери от недостающей единицы продукции;
annsig — стандартное отклонение годового спроса;
meanLT — средний срок выполнения заказа, то есть среднее время между размещением и получением заказа;
sigmaLT — стандартное отклонение срока выполнения заказа.
Предположим, магазин пытается определить оптимальную стратегию хранения
для заказанных миксеров. Он располагает следующей информацией:
заказ на поставку миксеров обходится в $50;
хранение миксера на складе в течение года обходится в $10;
в среднем магазин продает 1000 миксеров в год;
все клиенты, которые пытаются приобрести миксеры, когда склад опустел, возвращаются позже и покупают миксеры после новой поставки. Магазин штрафуют на $20 за каждую единицу дефицита;
годовой спрос на миксеры (на основе исторических данных) имеет стандартное отклонение 40,8;
срок выполнения отложенного заказа всегда составляет две недели (0,038 года),
со стандартным отклонением 0.
После ввода K, h и D в ячейки C2:C4 в ячейке C5 вычисляется оптимальный размер заказа (100 миксеров). После ввода значений SOC, annsig, meanLT и sigmaLT
в ячейки C7:C10 в ячейке C14 вычисляется точка заказа, минимизирующая ожидаемые годовые затраты, связанные с хранением и дефицитом (51,63 миксера).
Таким образом, магазин должен закупать 100 миксеров, как только запасы понизятся до 51,62 (или 52) миксера.
Безопасный уровень запаса, связанный с заданной точкой заказа, равен (точка заказа) – (средний спрос за срок выполнения заказа).

Универмаг поддерживает безопасный уровень запаса в 51,62 – 38,46 = 13,16 миксера (вычислен в ячейке C15). По сути, безопасный запас всегда находится на
складе, что приводит к дополнительным затратам на хранение. Но при этом высокий безопасный уровень запаса уменьшает затраты, связанные с дефицитом.

Упущенные продажи
Теперь предположим, что каждый дефицит приводит к упущенной продаже. Потери, связанные с упущенными продажами, как правило, оцениваются как штраф

Построение моделей управления запасами для неопределенного спроса

847

за невыполненный заказ плюс прибыль, связанная с проданной единицей продукции. Пусть магазин получает $20 прибыли от продажи каждого миксера. Т огда
потери от дефицита для случая упущенной продажи составляют $40 ($20 упущенной прибыли + $20 штрафа за дефицит).

Рис. 85.2. Определение точки заказа для случая упущенной продажи

В файле Reorderpoint_lostsales.xlsx (рис. 85.2) вы видите мои расчеты точки заказа для случая упущенной продажи. Введя потери от упущенной продажи ($40)
в ячейку C7, я нашел, что оптимальная политика хранения состоит в том, чтобы закупать по 100 миксеров и делать новую закупку, когда запасы снижаются до 54,23
миксера. Безопасный уровень запаса составляет 15,77 миксера, и спрос на миксеры не будет удовлетворен на 2,4%. Обратите внимание, что предположение об
упущенной продаже увеличило точку заказа и уменьшило вероятность дефицита.
Это произошло потому, что из-за увеличения потерь от дефицита (с $20 до $40)
магазин прилагает больше усилий для избегания дефицита.
Увеличение неопределенности значительно повышает точку заказа. Например,
для случая упущенной продажи, если стандартное отклонение для срока выполнения заказа составляет одну неделю (0,019 года), а не 0, точка закупки повышается до 79,50 миксера, а безопасный запас увеличивается более чем в два раза по
сравнению с тем случаем, когда срок исполнения заказа был точно известен.

Что означает термин «95%-ный уровень обслуживания»?

Как было сказано ранее в этой главе, 95%-ный уровень обслуживания означает
удовлетворение 95% спроса в срок. Поскольку оценить штраф из-за дефицита и/
или штраф от упущенной продажи достаточно трудно, многие компании устанавливают безопасный уровень запаса в зависимости от уровня обслуживания.
В файле Servicelevelreorder.xlsx (рис. 85.3) точку заказа можно определить в соответствии с любым желаемым уровнем обслуживания.

848

ГЛАВА 85

Рис. 85.3. Определение точки заказа в соответствии с уровнем обслуживания

В качестве примера возьмем аптеку, которая пытается определить оптимальную
стратегию хранения лекарства. Аптека должна удовлетворять 95% спроса на лекарственный препарат в срок. Для расчета важны следующие параметры:
заказ на поставку лекарства стоит $50;
затраты на хранение единицы препарата на складе в течение года составляют
$10;
среднегодовой спрос на препарат составляет 1000 единиц;
стандартное отклонение годового спроса составляет 69,28 единицы;
время, затрачиваемое на выполнение заказа, всегда равно одному месяцу
(0,083 года).
Введите в ячейку C1 требуемый уровень обслуживания (0,95), а в ячейки C2:C4
и C7:C9 остальные параметры. Для определения точки заказа, соответствующей
желаемому уровню обслуживания, на вкладке Данные (Data) в группе Анализ (Data
Analysis) выберите Поиск решения (Solver).
ПРИМЕЧАНИЕ
Для установки надстройки Поиск решения (Solver) на вкладке Файл (File) выберите
команду Параметры (Options), затем среди параметров Excel выберите раздел Надстройки (Add-Ins). В нижней части диалогового окна нажмите Перейти (Go). В диалоговом окне Надстройки (Add-Ins) установите флажок Поиск решения (Solver Add-In)
и нажмите OK.

В модели поиска решения (рис. 85.4) точка заказа подбирается до тех пор, пока
процент удовлетворения спроса в срок не будет соответствовать желаемому уровню обслуживания. Нажмите Параметры (Options) и на вкладке Поиск решения нелинейных задач методом ОПР (GRG Nonlinear) включите флажок Использовать несколько

Построение моделей управления запасами для неопределенного спроса

849

начальных точек (Multistart) — см. главу 36 «Расположение складов по методу ОПГ

с несколькими начальными точками и согласно эволюционному поиску решения». Затем установите для точки заказа нижнюю границу 0,001 (чтобы точке заказа не присвоилось отрицательное значение) и верхнюю границу 10 000 (достаточно произвольно). Если инструмент Поиск решения (Solver) превысит верхнюю
границу, мы ее передвинем. Как показано на рис. 85.3, аптека должна заказывать
по 100 единиц лекарства каждый раз, когда уровень запаса падает до 90,23 единицы. Эта точка заказа соответствует безопасному уровню запаса 6,90 единицы.

Рис. 85.4. Диалоговое окно Параметры поиска решения
для определения точки заказа при 95%-ном уровне обслуживания

В таблице ниже приведены точки заказа и безопасные уровни запаса, соответствующие уровням обслуживания от 80 до 99%.
Уровень обслуживания, %

Точка заказа,
единицы продукции

Безопасный запас,
единицы продукции

65,34

–17,99

71,85

–11,48

79,57

–3,76

90,23

6,90

108,44

25,11

850

ГЛАВА 85

Обратите внимание, что при повышении уровня обслуживания с 80 до 99% точка
заказа увеличивается почти на 67%! Т акже следует отметить, что 90%-ный уровень обслуживания может быть достигнут при точке заказа, меньшей чем средний
спрос за время выполнения заказа (см. ячейку C10 на рис. 85.3). 90%-ный уровень
обслуживания приводит к отрицательному безопасному уровню запаса. Это возможно, поскольку дефицит возникает только во время выполнения заказа, а время выполнения заказа охватывает небольшую часть года.

Задания
В заданиях 1 и 2 предполагается, что в ресторане подается в среднем 5000 бутылок вина в год. Стандартное отклонение годового спроса на вино составляет 1000
бутылок. Ежегодные затраты на хранение бутылки вина составляют $1. Закупка
вина обходится в $10 и доставка вина в среднем занимает три недели (со стандартным отклонением в одну неделю):
1. Предположим, когда в ресторане заканчивается вино, он получает штраф $5
как результат потери репутации. Также ресторан получает прибыль в размере $2 за каждую бутылку вина. Определите оптимальную политику закупки
вина.
2. Определите политику хранения вина, которая дает 99%-ный уровень обслуживания.
3. Политику определения точки заказа часто называют политикой двух бункеров1. Как может быть реализована политика определения точки заказа, если
для хранения запасов используются два бункера?

До использования компьютерных информационных систем запасы хранили в двух бункерах. В одном — количество запасов, равное точке заказа, в другом — остальные запасы.
Запасы берутся из последнего до тех пор, пока не закончатся, что служит сигналом для
следующего заказа на поставку. — Примеч. ред.

Г Л А В А 86

Теория массового обслуживания
(теория очередей)

Обсуждаемые вопросы
Какие факторы влияют на длину очереди и время, проведенное клиентами в очереди?
Какие условия должны выполняться, чтобы можно было анализировать среднее
количество присутствующих клиентов или среднее время, проведенное клиентом
в очереди?
Почему изменчивость снижает производительность системы очередей?
Можно ли быстро определить среднее время прохождения через систему контроля безопасности в аэропорту или среднее время ожидания в очереди в банке?

Какие условия следует сформулировать, прежде чем приступать к анализу
среднего числа посетителей или среднего времени, проводимого в очереди?
По необъяснимому недоразумению, все мы тратим много времени в очередях,
и, как скоро будет показано, небольшое увеличение пропускной способности
в обслуживании часто может значительно сократить очередь. При ведении бизнеса важно гарантировать, что ваши клиенты не тратят слишком много времени
на ожидание. Поэтому деловые люди должны знать теорию очередей, обычно
называемую теорией массового обслуживания. В этой главе показано, как определить пропускную способность, необходимую для высокого качества обслуживания.

Ответы на вопросы
?

Какие факторы влияют на длину очереди и время, проведенное клиентами
в очереди?

В этой главе рассматриваются проблемы очередей, в которых все прибывающие
клиенты ждут первого освободившегося специалиста в одной очереди. Эта модель дает довольно точное представление о распространенных ситуациях, когда
вы ждете своей очереди в банке, на почте или при контроле безопасности в аэропорту. Кстати, идея формирования одной очереди возникла примерно в 1970 г .,

852

ГЛАВА 86

когда в банковских и почтовых отделениях осознали, что хотя ожидание в одной
очереди не уменьшает среднее время ожидания для клиентов, оно снижает изменчивость времени, проводимого клиентами в очереди, что создает более справедливую систему.
На время, которое клиенты проводят в очереди, влияют три фактора.
Количество специалистов. Очевидно, что чем больше специалистов, тем меньше времени в среднем проводят клиенты в очереди и меньше людей в среднем
стоит в очереди.
Среднее и стандартное отклонение времени между прибытиями клиентов.
Время между прибытиями клиентов называется временным интервалом между прибытиями. Если средний временной интервал между прибытиями увеличивается, количество прибытий уменьшается, что приводит к более короткой очереди и меньшему времени, проведенному клиентом в очереди. Как вы
вскоре увидите, увеличение стандартного отклонения временного интервала
между прибытиями увеличивает среднее время, проведенное клиентом в очереди, и среднее количество присутствующих клиентов.
Среднее значение и стандартное отклонение времени, необходимого для
обслуживания клиента. Если среднее время обслуживания увеличивается, то
повышается среднее время, проведенное клиентом в системе массового обслуживания, и количество присутствующих клиентов. У величение стандартного
отклонения времени обслуживания увеличивает среднее время, проведенное
клиентом в системе массового обслуживания, и среднее количество присутствующих клиентов.
Какие условия должны выполняться, чтобы можно было анализировать
среднее количество присутствующих клиентов или среднее время, проведенное клиентом в очереди?

При анализе времени ожидания клиентов в очередях математики говорят о характеристиках устойчивого состояния системы. Устойчивое состояние подразумевает, что система работает в течение длительного времени. Если говорить более конкретно, аналитикам необходимо выяснить значения следующих величин
в устойчивом состоянии:
W — среднее время, проведенное клиентом в системе;
Wq — среднее время ожидания в очереди до обслуживания;
L — среднее количество клиентов, присутствующих в системе;
Lq — среднее количество клиентов, ожидающих в очереди.
При этом всегда справедливы равенства: L = (1/среднее время между прибытиями) × W и Lq = (1/среднее время между прибытиями) × Wq.
Для корректного обсуждения устойчивого состояния системы очередей должно
иметь место следующее.

Теория массового обслуживания (теория очередей)

853

Среднее значение и стандартное отклонение времени между прибытиями
и времени обслуживания мало изменяются с течением времени. С технической
точки зрения это означает, что распределение для времени между прибытиями
и времени обслуживания является постоянным во времени.
(1/среднее время обслуживания) × (количество специалистов) > (1/(среднее
время между прибытиями)). Это уравнение 1.
По сути, если уравнение 1 выполняется, за час можно обслужить больше клиентов, чем число новоприбывших. Например, если среднее время обслуживания составляет 2 минуты (или 1/30 часа) и среднее время между прибытиями составляет
1 минуту (или 1/60 часа), из уравнения 1 следует, что 30 × (количество специалистов) > 60 или что для устойчивого состояния системы количество специалистов
должно быть больше или равно 3. Если клиенты не обслуживаются быстрее, чем
прибывают новые, в конце концов накапливается отставание, которое никогда не
будет наверстано, что приведет к бесконечной очереди.

Почему изменчивость снижает производительность системы очередей?

Чтобы понять, почему изменчивость снижает производительность системы очередей, рассмотрим систему с одним специалистом, в которой клиенты прибывают
каждые 2 минуты и время обслуживания также всегда составляет 2 минуты. В такой системе никогда не будет больше одного клиента. Т еперь предположим, что
клиенты прибывают каждые 2 минуты, но половина всего времени обслуживания составляет 0,5 минуты, а другая половина — 3,5 минуты. Даже если прибытия
полностью предсказуемы, неопределенность во времени обслуживания означает ,
что, в конце концов, специалист перестанет справляться и сформируется очередь.
Например, если на обслуживание каждого из первых четырех клиентов уйдет
3,5 минуты, через 12 минут в очереди будут ожидать четыре клиента (см. табл.).
Время,
минуты

Событие

Находится в системе после события,
кол-во человек

Прибытие

Обслуживание завершено

Прибытие

Обслуживание завершено

Прибытие

Обслуживание завершено

Прибытие

3,5

10,5
12

854

ГЛАВА 86

Можно ли быстро определить среднее время прохождения через систему
контроля безопасности в аэропорту или среднее время ожидания в очереди в банке?

На листе Model в файле Queuingtemplate.xlsx находится шаблон, который вы можете использовать для определения приблизительных значений L, W, Lq и Wq (как
правило, в пределах 10% от их истинных значений). Этот лист представлен на
рис. 86.1.

Рис. 86.1. Шаблон для системы очередей

Когда вы введете следующие данные в шаблон, он вычислит значения Wq, Lq, W
и L. Параметры в ячейках B6:B9 могут быть легко рассчитаны на основе данных на
листе Queuing Data.
Количество специалистов (ячейка B5).
Среднее время между прибытиями (ячейка B6).
Среднее время обслуживания (ячейка B7).
Стандартное отклонение времени между прибытиями (ячейка B8).
Стандартное отклонение времени обслуживания (ячейка B9).
А теперь — пример шаблона в действии. Вам нужно определить, как рабочие характеристики системы безопасности в аэропорту в рабочее время с 9:00 до 17:00
зависят от количества сотрудников. На листе Queuing Data в файле Queuingtemplate.
xlsx (рис. 86.2) в таблице приведено время между прибытиями и время обслуживания. (Часть строк данных скрыта.)
Скопировав формулу =СРЗНАЧ(B4:B62) из ячейки B1 в C1, вы найдете среднее
время между прибытиями (12,864 с) и среднее время обслуживания (77,102 с).

Теория массового обслуживания (теория очередей)

855

Рис. 86.2. Время между прибытиями и время обслуживания для примера
с системой контроля безопасности аэропорта

Поскольку среднее время обслуживания почти в шесть раз больше среднего времени между прибытиями, для обеспечения устойчивого состояния требуется
минимум шесть сотрудников. Скопировав формулу =СТАНДОТКЛОН.В(B4:B62) из
ячейки B2 в C2, вы определите стандартное отклонение времени между прибытиями (4,439 с) и стандартное отклонение времени обслуживания (48,051 с).
Вернемся к шаблону системы очередей на листе Model. Когда вы введете полученные значения в ячейки B6:B9 и 6 специалистов в ячейку B5, то выясните, что катастрофа неизбежна. В устойчивом состоянии системы в очереди будут находиться
около 236 человек (ячейка B19). Возможно, вам приходилось оказываться в такой
ситуации в аэропорту.
Чтобы определить, как изменение числа сотрудников влияет на производительность системы, я воспользовался однонаправленной таблицей данных (рис. 86.3).
В ячейки F9:F13 я ввел предположительное число сотрудников (от 6 до 10). Для
вычисления L я ввел в ячейку G8 формулу =B19, а для вычисления W — в ячейку H8 формулу =B18. Выделил таблицу ( F8:H13) и затем на вкладке Данные (Data)
в группе Прогноз (Forecast) в списке Анализ «что, если» (What If Analysis) выбрал
Таблица данных (Data Table). После выбора ячейки B5 (количество сотрудников)
в поле Подставлять значения по строкам в (Column Input Cell) я получил таблицу, как
на рис. 86.3. Обратите внимание, что добавление всего лишь одного сотрудника
к исходным шести уменьшает ожидаемое количество клиентов в очереди с 236 до
7. Добавление седьмого сотрудника уменьшает среднее время нахождения клиента в системе с 3038 с (50,6 мин) до 89 с (1,5 минуты). Этот пример показывает ,
что небольшое увеличение пропускной способности может значительно повысить
производительность системы очередей.

856

ГЛАВА 86

Рис. 86.3. Анализ чувствительности для системы контроля безопасности аэропорта

В ячейках F16:K22 я использовал двунаправленную таблицу данных для исследования чувствительности среднего времени, проведенного клиентом в системе (W),
к изменению количества сотрудников и изменению
стандартного отклонения
времени обслуживания. Укажите в поле Подставлять значения по столбцам в (Row
Input Cell) ячейку B5, а в поле Подставлять значения по строкам в (Column Input Cell)
ячейку B9. Если работают семь сотрудников, увеличение стандартного отклонения времени обслуживания с 40 до 90 с приводит к увеличению на 29% среднего
времени, проведенного клиентом в системе (с 86,2 до 111,8 с).
ПРИМЕЧАНИЕ
Читатели, заинтересованные в более широком обсуждении теории массового обслуживания, могут обратиться к книге Уэйна Винстона (Wayne L. Winston. Operations
Research: Applications and Algorithms. — Duxbury Press, 2007).

Задания
В банке работают шесть операционистов. Выполните задания 1–4 на основе следующей информации:
среднее время обслуживания составляет 1 минуту;
среднее время между прибытиями составляет 25 секунд;
стандартное отклонение времени обслуживания составляет 1 минуту;
стандартное отклонение времени между прибытиями составляет 10 секунд.

Теория массового обслуживания (теория очередей)

857

Выполните задания:
1. Определите среднее время ожидания клиента в очереди.
2. Сколько клиентов в среднем присутствуют в очереди?
3. Рекомендовали бы вы подключить к работе дополнительных операционистов?
4. Допустим, работа операциониста стоит $20 в час, а время клиента банк оценивает в $15 в час. Сколько операционистов должно работать в банке?
5. На пятом этаже бизнес-школы работают 30 женщин. Каждая женщина посещает туалет три раза в день (офис работает с 8:00 до 17:00) и проводит в туалете каждый раз в среднем 180 секунд со стандартным отклонением 90 секунд.
Предположим, что стандартное отклонение времени между посещениями туалета составляет 5 минут . Сколько кабинок вы бы порекомендовали установить в туалете?

ГЛ А В А 87

Оценка кривой спроса

Обсуждаемые вопросы
Что необходимо знать при назначении цены продукта?
Что такое эластичность спроса?
Существует ли простой способ оценить кривую спроса?
Каким образом кривая спроса показывает готовность покупателя платить за продукт?

В любом бизнесе необходимо определить цену для каждого продукта. Оценить
продукт адекватно достаточно сложно. В главах 88 «Ценообразование продуктов
с сопутствующими товарами» и 89 «Ценообразование продуктов с помощью субъективно определяемого спроса» я опишу несколько простых моделей, помогающих назначить цену на продукт, максимально увеличивающую его прибыльность.
Для более полного представления о ценообразовании см. прекрасную книгу Роберта Долана и Германа Саймона1.

Ответы на вопросы
?

Что необходимо знать при назначении цены продукта?

Возьмем такой продукт, как шоколадный батончик. Для определения цены, приносящей максимальную прибыль, необходимо знать две вещи:
переменные затраты на производство каждой единицы продукции (я назвал
эту величину UC);
кривую спроса на продукт. Кривая спроса показывает количество единиц продукта, на которое будет спрос, в зависимости от конкретной цены. Таким образом, если назначить цену единицы продукции $ p, то по кривой спроса можно
определить число D(p), эквивалентное количеству единиц продукции, которое
будет востребовано по цене $p. Безусловно, кривая спроса постоянно меняется
и нередко зависит от факторов, находящихся вне контроля компании (таких
как состояние экономики и цены конкурентов).
1

Robert J. Dolan, Hermann Simon. Power Pricing. — Free Press, 1997.

Оценка кривой спроса

859

Если значение UC и кривая спроса известны, прибыль, соответствующая цене
в $p, просто равна (p – UC) × D(p). Если известно уравнение для D(p), вычисляющее количество востребованного продукта для каждой цены, можно с помощью
инструмента Поиск решения (Solver) найти цену, обеспечивающую максимальную
прибыль, как будет показано в главах 88 и 89.

Что такое эластичность спроса?

В соответствии с кривой спроса ценовая эластичность спроса — это процентное сокращение спроса в результате повышения цены на 1%. Если эластичность выше 1%,
спрос является эластичным по цене. Когда спрос эластичен по цене, снижение цены
увеличивает выручку. Если эластичность меньше 1%, спрос является неэластичным
по цене. Когда спрос неэластичен по цене, снижение цены снижает выручку . Далее
приведены отслеженные оценки эластичности спроса на некоторые продукты.
Соль — 0,1 (крайне неэластичный).
Кофе — 0,25 (неэластичный).
Гонорары адвокатов — 0,4 (неэластичный).
Телевизоры — 1,2 (незначительно эластичный).
Ресторанная еда — 2,3 (эластичный).
Поездки за границу — 4,0 (очень эластичный).
Например, снижение стоимости поездки за границу на 1% приводит к увеличению спроса на такие поездки на 4%.

Существует ли простой способ оценить кривую спроса?

Пусть q — величина спроса на продукт. Для оценки кривой спроса наиболее часто
используются две формы.
Линейная кривая спроса. В этом случае спрос выражается линейным соотношением вида q = a – bp. Например, q = 10 – p — линейная кривая спроса. (Здесь
a и b могут быть определены по методу, который я описываю далее в этой главе.) Если кривая спроса линейна, эластичность постоянно меняется.
Степенная кривая спроса. В этой ситуации кривая спроса описывается степенной кривой вида q = apb, где b < 0 (см. главу 57 «Степенная кривая»). Как
и в предыдущем случае, a и b можно определить по методу, который я описываю далее в этой главе. Уравнение q = 100p – 2 является примером степенной
кривой спроса. Если спрос соответствует степенной кривой, эластичность равна –b для любой цены. Таким образом, для кривой спроса q = 100p – 2 ценовая
эластичность спроса всегда равна 2.
Предположим, что кривая спроса на продукт соответствует линейной или степенной кривой спроса. Если известна текущая цена и спрос на продукт , а также
ценовая эластичность спроса, определить кривую спроса для продукта проще простого. Вот два примера.

860

ГЛАВА 87

Пусть в настоящее время продукт продается за $100, и спрос на него составляет
500 единиц. Ценовая эластичность спроса для продукта равна 2. Предположим,
что кривая спроса является линейной. Необходимо определить уравнение кривой
спроса. Решение находится в файле Linearfit.xlsx (рис. 87.1).

Рис. 87.1. Подбор линейной кривой спроса

Если заданы две точки, то через них можно провести только одну прямую. Для
кривой спроса действительно известны две точки, и первая из них — p = 100
и q = 500. Поскольку эластичность спроса равна 2, повышение цены на 1% приводит к уменьшению спроса на 2%. Следовательно, если p = 101 (повышение на 1%),
спрос падает на 2% от 500 (10 единиц) до 490. Таким образом, p = 101 и q = 490 —
это вторая точка кривой спроса. Т еперь с помощью линии тренда в Excel можно
найти прямую линию, проходящую через точки (100,500) и (101,490).
Начнем с ввода этих точек в ячейки D5:E6, как показано на рис. 87.1. Затем выделите диапазон D4:E6 и на вкладке Вставка (Insert) в группе Диаграммы (Charts)
выберите Точечная или пузырьковая диаграмма (Insert Scatter (X, Y) Or Bubble Chart)
и затем последний тип точечной диаграммы — Точечная диаграмма с прямыми отрезками и маркерами (Scatter With Straight Lines). График получился с положительным наклоном. То есть повышение цены ведет к повышению спроса, а это неверно.
Проблема в следующем: при наличии только двух точек данных Excel предполагает, что точки данных, по которым строится график, находятся в отдельных столбцах, а не в отдельных строках. В подтверждение того, что отдельные точки находятся в разных строках, щелкните в области диаграммы и затем в секции Работа
с диаграммами (Chart Tools) откройте вкладку Конструктор (Design). На этой вкладке в группе Данные (Data) выберите Строка/столбец (Switch Row/Column). Обрати-

Оценка кривой спроса

861

те внимание, что после нажатия Выбрать данные (Select Data) можно изменить исходные данные, на основе которых создается диаграмма. Теперь щелкните правой
кнопкой мыши на одной из точек, выберите Добавить линию тренда (Add Trendline),
затем установите переключатель в положение Линейная (Linear) и отметьте флажок Показывать уравнение на диаграмме (Display Equation On Chart). Появится прямолинейный график, а также уравнение прямой (вверху справа от графика), как
показано на рис. 87.1. Т ак как x равен цене, а y — спросу, уравнение для кривой
спроса имеет вид q = 1500 – 10p. Это уравнение означает, что каждое повышение
цены на $1 приводит к потере 10 единиц спроса. Разумеется, спрос не может быть
линейным для всех значений цены, поскольку для больших значений p линейная
кривая спроса приведет к негативному спросу. Однако для цен, близких к текущей
цене, линейная кривая спроса является достаточно хорошим приближением к истинной кривой спроса на продукт.
Для второго примера давайте снова предположим, что в настоящее время продукт
продается за $100 и спрос на него составляет 500 единиц. Ценовая эластичность
спроса для продукта равна 2. Теперь подберем к этим данным степенную кривую
спроса. См. файл Powerfit.xlsx и рис. 87.2.

Рис. 87.2. Степенная кривая спроса

Введите в ячейку E3 пробное значение a. Затем в ячейку D5 введите текущую цену
$100. Так как эластичность спроса равна 2, кривая спроса имеет вид q = ap–2, где
a неизвестно. В ячейку E5 введите спрос для цены $100, соответствующий зна-

862

ГЛАВА 87

чению a в ячейке E3 по формуле =a*D5^-2. Теперь с помощью инструмента Подбор параметра (Goal Seek) (см. главу 18) определите значение a, при котором спрос
для цены $100 составляет 500 единиц. У становите в ячейке E5 значение 500, изменив ячейку E3. Оказывается, спросу в 500 единиц при цене $100 соответствует
а, равное 5 000 000. Т аким образом, кривая спроса (графически представленная
на рис. 87.2) описывается уравнением q = 5000000 p–2. Для любой цены ценовая
эластичность спроса на этой кривой равна 2.

Каким образом кривая спроса показывает готовность покупателя платить
за продукт?

Вы пытаетесь продать ПО крупной корпорации. Пусть q — это количество копий ПО, которое требуется компании, а p — цена ПО. Вы вычислили, что кривая
спроса на ПО описывается уравнением q = 400 – p. Очевидно, что клиент хотел
бы платить меньше за каждую дополнительную копию ПО. В этой кривой спроса
заключена информация о том, сколько компания готова платить за каждую копию
ПО. Эта информация является ключевой для максимального увеличения прибыльности продаж.
Перепишем уравнение кривой спроса как p = 400 – q. Таким образом, если q = 1,
p = $399 и т. д. Теперь попытаемся определить ценность, которую клиент придает
каждой из первых двух копий ПО. Предположим, что клиент прагматичен, то есть
будет покупать копию ПО тогда и только тогда, когда ценность этой копии превысит запрошенную цену. При цене $400 спрос равен 0, так что первая копия не
может стоить $400. Однако при цене $399 образуется спрос на одну копию ПО.
Следовательно, первая копия ПО должна стоить где-то между $399 и $400. Аналогично, вторую копию ПО клиент за $399 не купит . Однако при цене $398 клиент покупает две копии, то есть клиент покупает вторую копию. Следовательно,
потребительская ценность второй копии лежит где-то между $399 и $398.
Можно показать, что наилучшим приближением стоимости i-й единицы продукта, покупаемой клиентом, является цена, при которой спрос равен i – 0,5. Например, если установить для q значение 0,5, то стоимость первой копии равна
400 – 0,5 = $399,50. Аналогично, если установить q = 1,5, стоимость второй копии
равна 400 – 1,5 = $398,50.

Задания
1. Вы оценили изобретенную вами настольную игру в $60 и продали 3000 экземпляров за последний год. Известно, что ценовая эластичность для настольных
игр равна 3. На этой основе определите линейную и степенную кривые спроса.
2. Для каждого ответа из задания 1 определите потребительскую стоимость
двухтысячного экземпляра игры.

Г Л А В А 88

Ценообразование продуктов
с сопутствующими товарами

Обсуждаемый вопрос
Как покупка клиентами вместе с бритвенным станком лезвий способствует установлению максимально увеличивающей прибыль цены на бритву?

Покупка некоторых потребительских товаров часто приводит к покупке сопутствующих товаров, или товаров принудительного ассортимента. В следующей таблице приведено несколько примеров таких покупок.
Первичная покупка

Сопутствующий товар

Бритвенный станок

Лезвия

Мужской костюм

Рубашка и/или галстук

Компьютер

Руководство по программному обеспечению

Игровая приставка

Видеоигра

Кривую спроса для первичного продукта можно легко определить с помощью методов, описанных в главе 87 «Оценка кривой спроса». Затем вы можете использовать Поиск решения (Solver) и рассчитать цену первичного продукта, максимизирующую сумму прибылей, полученных от исходного и сопутствующего товаров.
Следующий пример демонстрирует, как проводится такой анализ.

Ответ на вопрос
?

Как покупка клиентами вместе с бритвенным станком лезвий способствует
установлению максимально увеличивающей прибыль цены на бритву?

Пусть в настоящее время вы берете за бритвенный станок $5,00 и продаете 6 млн
бритвенных станков. Предположим, что переменные затраты на производство одного станка составляют $2,00. Наконец, допустим, что ценовая эластичность спроса на бритвенные станки равна 2. Какую цену следует назначить на станок?
Предположим (ошибочно), что покупатели бритвенных станков не покупают
лезвия. Кривая спроса (в случае линейной кривой спроса) показана на рис. 88.1.

864

ГЛАВА 88

(См. данные и диаграмму на листе No Blades в файле Razorsandblades.xlsx.) Двумя
точками на кривой спроса являются цена = $5,00, спрос = 6 млн бритв и цена =
= 5,05 (увеличенная на 1%), спрос = 5,88 млн (на 2% меньше 6 млн). После создания диаграммы и вставки линейной линии тренда можно, как показано в главе 87
«Оценка кривой спроса», найти уравнение кривой спроса: y = 18 – 2,4x. Поскольку x — это цена, а y — спрос, уравнение кривой спроса на бритвенные станки можно записать в следующем виде: спрос (в млн) = 18 – 2,4(цена).

Рис. 88.1. Определение цены на бритвенные станки, максимизирующей прибыль

Я связал имена в ячейках C6 и C9:C11 с ячейками D6 и D9:D11 соответственно. Затем я ввел пробную цену в ячейку D9 и определил спрос для этой цены в ячейке D10 по формуле =18-2,4*цена. Далее я определил в ячейке D11 прибыль от бритвенных станков по формуле =спрос*(цена-себестоимость_бритвы).
Затем я применил Поиск решения (Solver) со вкладки Данные (Data) для определения цены, максимизирующей прибыль. Диалоговое окно Параметры поиска решения (Solver Parameters) показано на рис. 88.2.
ПРИМЕЧАНИЕ
Если вы еще не установили надстройку Поиск решения (Solver), на вкладке Файл (File)
выберите команду Параметры (Options), затем среди параметров Excel выберите раздел Надстройки (Add-Ins). В нижней части диалогового окна нажмите Перейти (Go).
В диалоговом окне Надстройки (Add-Ins) установите флажок Поиск решения (Solver
Add-In) и нажмите OK.

Я максимизировал прибыль (ячейка D11), изменив цену (ячейка D9). Эта модель
нелинейная, поскольку в целевой ячейке перемножаются две величины — спрос
и (цена-себестоимость_бритвы), каждая из которых зависит от значения в изменяемой ячейке. Инструмент Поиск решения (Solver) выполнит поиск цены за бритвен-

Ценообразование продуктов с сопутствующими товарами

865

ный станок, максимизирующей прибыль, и получит $4,75. (Максимальная прибыль составляет $18,15 млн.)
Теперь предположим, что покупатель бритвенного станка приобретает в среднем
50 лезвий и каждое купленное лезвие приносит прибыль $0,15. Каким образом

Рис. 88.2. Диалоговое окно Параметры поиска решения для поиска цены бритвы,
максимизирующей прибыль

Рис. 88.3. Цена на станки с включенной прибылью от лезвий

866

ГЛАВА 88

должна измениться цена, назначаемая на бритвенный станок? Предположим, что
цена на бритвенный станок фиксированная. (В задании 3 в конце этой главы цена
станка меняется.) Анализ этой ситуации представлен на листеBlades и на рис. 88.3.
На вкладке Формулы (Formulas) в группе Определенные имена (Defined Names) я выбрал Создать из выделенного (Create From Selection) для присвоения имен из ячеек
C6:C11 ячейкам D6:D11. (Например, ячейка D10 называется Demand (спрос).)
ПРИМЕЧАНИЕ
Внимательные читатели помнят, что ячейка D10 на листе No Blades также носит имя
«спрос». Что сделает Excel, если вы укажете имя Спрос в формуле? Он просто использует ячейку с именем Спрос на текущем листе. Другими словами, если указано
имя Спрос на листе Blades, Excel обращается к ячейке D10 на этом листе, а не к ячейке
D10 на листе No Blades.

В ячейки D7 и D8 я ввел соответствующие данные о лезвиях. В ячейку D9 я ввел
пробное значение цены бритвенного станка и в ячейке D10 вычислил спрос по
формуле =18-2,4*цена. Далее в ячейке D11 по формуле =спрос*(цена-себестоимость_
бритвы)+спрос*лезвия_для_бритвы*прибыль_от_лезвия я вычислил общую прибыль от бритвенных станков и лезвий. Обратите внимание, что часть формулы
спрос*лезвия_для_бритвы*прибыль_от_лезвия вычисляет прибыль от лезвий.
Диалоговое окно Параметры поиска решения (Solver Parameters) выглядит так же,
как было показано на рис. 88.2. Изменяйте цену для получения максимальной
прибыли. Безусловно, теперь формула прибыли включает прибыль, полученную
от лезвий. Решение показывает, что прибыль максимальна при цене всего лишь
$1,00 (половина переменных затрат!) за бритвенный станок. Такая цена является
результатом получения большой прибыли от лезвий. Намного выгоднее продать
бритвенные станки множеству клиентов, даже если вы теряете по $1 на каждом
проданном станке. Многие компании не понимают важность прибыли от сопутствующих товаров. Они завышают цену на первичный продукт и лишают себя
возможности получить максимальную общую прибыль.

Задания
Во всех заданиях предполагается линейная кривая спроса.
1. Определите цену игровой приставки, максимизирующую прибыль. В настоящее время на приставку назначена цена $180, и объем продаж составляет
2 млн приставок в год. Стоимость производства приставки — $150, и ценовая
эластичность спроса на приставку равна 3. Какую цену следует назначить на
приставку?
2. Теперь предположим, что покупатель игровой приставки покупает в среднем
10 видеоигр, и прибыль от каждой игры составляет $10. Какова правильная
цена на игровую приставку?

Ценообразование продуктов с сопутствующими товарами

867

3. Предположим, что в примере с бритвами и лезвиями стоимость производства
лезвия составляет $0,20. Если за лезвие назначена цена $0,35, клиент покупает в среднем 50 лезвий. Пусть ценовая эластичность спроса на лезвия равна 3.
Какую цену следует назначить на станок и на лезвие?
4. Кинотеатр может обслужить 8000 зрителей в неделю. Спрос, текущая цена
и эластичность для продаж билетов, попкорна, лимонада и конфет приведены
на рис. 88.4. Кинотеатр оставляет себе 45% выручки от билетов. Даны также
себестоимость билета, продаж попкорна, продаж конфет и продаж лимонада.
Каким образом кинотеатр может получить максимальную прибыль при условии линейной кривой спроса? Спрос на продукты питания — это доля клиентов, покупающих указанные продукты. См. данные на рис. 88.4.

Рис. 88.4. Данные к заданию 4

5. Лекарства, отпускаемые по рецепту , производятся в США и продаются по
всему миру. Производство каждой единицы лекарственного препарата стоит
$60. На немецком рынке препарат продается по 150 евро. Текущий обменный
курс составляет 0,667 доллара США за евро. Т екущий спрос на препарат составляет 100 единиц, а расчетная эластичность равна 2,5. Определите соответствующую продажную цену (в евро) на препарат при условии линейной
кривой спроса.
6. Предположим, спрос на костюмы в магазине мужской одежды соответствует
линейной кривой, эластичность цены равна 5. При текущей цене в $500 продается 60 костюмов в неделю. Себестоимость костюма составляет $200. Предположим, к костюму клиент покупает два галстука и одну рубашку. Прибыль
от продажи галстука составляет $15, а от продажи рубашки — $25. Какую
цену на костюм должен установить магазин?
7. В настоящее время региональный агент по продаже спортивных автомобилей
продает за год 200 машин по цене $150 000. Дилерская цена закупки автомобиля составляет $60 000. Предположим, за время эксплуатации автомобиля
дилер зарабатывает $25 000 на его обслуживании. Г одовой спрос на автомобили следует линейной кривой с эластичностью 4. Какую цену на автомобиль
должен установить дилер, чтобы получить максимальную прибыль от продаж
и обслуживания?

ГЛ А В А 89

Ценообразование продуктов
с помощью субъективно
определяемого спроса

Обсуждаемые вопросы
Иногда ценовая эластичность продукта неизвестна. Или невозможно определить,
какая из кривых спроса, линейная или степенная, является релевантной. Можно
ли все равно оценить кривую спроса и воспользоваться инструментом Поиск решения, чтобы определить цену, максимизирующую прибыль?
Как небольшой аптеке определить цену на помаду, максимизирующую прибыль?

Ответы на вопросы
Иногда ценовая эластичность продукта неизвестна. Или невозможно определить, какая из кривых спроса, линейная или степенная, является релевантной. Можно ли все равно оценить кривую спроса и воспользоваться инструментом Поиск решения, чтобы определить цену , максимизирующую прибыль?

Если ценовая эластичность для продукта неизвестна или если невозможно выбрать, на линейную или на степенную кривую спроса полагаться, эффективным
способом определения кривой спроса является выявление самой низкой и самой
высокой разумной цены. Затем следует оценить спрос на продукт при высокой,
низкой и промежуточной цене. При наличии этих трех точек на кривой спроса на
продукт можно с помощью линии тренда в Microsoft Excel подобрать квадратическую кривую спроса по следующей формуле (уравнение 1):
спрос= a(цена)2 +b(цена)+c.
Для любых трех указанных точек на кривой спроса существуют значения a, b и c,
при которых уравнение 1 точно соответствует трем указанным точкам. Поскольку
уравнение 1 соответствует трем точкам на кривой спроса, по-видимому , разумно
предположить, что уравнение даст точное представление о спросе и для других цен.
Затем вы можете использовать уравнение 1 и инструмент Поиск решения (Solver),
чтобы определить максимальную прибыль по формуле(цена-себестоимость)*спрос.
В следующем примере показано, как это сделать.

Ценообразование продуктов с помощью субъективно определяемого спроса

Как небольшой аптеке определить цену на помаду
прибыль?

869

, максимизирующую

Предположим, что аптека приобретает помаду за $0,90 за штуку. Для помады рассматривается цена от $1,50 до $2,50. В аптеке полагают , что при цене $1,50 будет продаваться 60 штук в неделю (см. рис. 89.1 и файл Lipstickprice.xlsx), при цене
$2,00 — 51 штука в неделю и при цене $2,50 — 20 штук в неделю. Какую цену на
помаду должна назначить аптека?

Рис. 89.1. Модель ценообразования на помаду

Начните с ввода в ячейки E3:F6 трех точек, по которым будет строиться кривая
спроса. Выделите ячейки E3:F6, на вкладке Вставка (Insert) в группе Диаграммы
(Charts) выберите Точечная или пузырьковая диаграмма (Insert Scatter (X, Y) Or Bubble
Chart) и затем выберите первый тип точечной диаграммы (Scatter). Затем щелкните правой кнопкой мыши на точке данных и в контекстном меню выберите Добавить линию тренда (Add Trendline). В диалоговом окне Формат линии тренда (Format
Trendline), показанном на рис. 89.2, установите переключатель в положение Полиномиальная (Polynomial) и в поле со списком Степень (Order) выберите значение 2
(для получения квадратичной кривой по уравнению 1). У становите флажок Показывать уравнение на диаграмме (Display Equation on chart).
Появится диаграмма, показанная на рис. 89.1. У равнение вычисленной кривой
спроса (уравнение 2):
спрос = –44 × цена2 +136 × цена – 45.

870

ГЛАВА 89

Рис. 89.2. Диалоговое окно Формат линии тренда для полиномиальной кривой спроса

Далее введите пробное значение цены в ячейкуI2. В ячейке I3 в соответствии с уравнением 2 вычислите спрос на продукт по формуле
=-44*цена^2+136*цена-45. (Ячейке
I2 присвоено имя цена.) Потом в ячейке I4 по формуле =-спрос*(цена-себестоимость)
вычислите еженедельную прибыль от продаж помады. (Ячейке E2 присвоено имя
себестоимость, а ячейке I3 — имя спрос.) Затем с помощью инструмента Поиск решения (Solver) определите цену, приносящую максимальную прибыль. Диалоговое
окно Параметры поиска решения (Solver Parameters) показано на рис. 89.3. Обратите
внимание, что цена ограничена самой низкой и самой высокой ценой (от $1,50 до
$2,50). Если так не сделать, квадратичная кривая спроса может пойти вверх, и тогда
получится, что более высокая цена приводит к более высокому спросу . Такой результат не имеет смысла, поэтому цену необходимо ограничить.
Итак, аптека должна назначить на помаду цену $2,04. Такая цена приведет к продаже 49,4 штуки в неделю и еженедельной прибыли $56,24.
Подход к ценообразованию, изложенный в этой главе, не требует знания концепции эластичности спроса. Инструмент Поиск решения по умолчанию рассматривает эластичность для каждой цены, когда определяет цену , максимизирующую
прибыль. Такой подход легко может быть применен в организациях, продающих
тысячи разных продуктов. Единственные данные, которые требуется указать для
каждого продукта,— это себестоимость и три точки на кривой спроса.

Ценообразование продуктов с помощью субъективно определяемого спроса

871

Рис. 89.3. Диалоговое окно Параметры поиска решения
для вычисления цены на помаду

Задания
1. Предположим, что производство одной игровой приставки стоит $250. Рассматривается цена от $200 до $400. Предполагаемый спрос на игровые приставки представлен в таблице:
Цена

Спрос (в млн)

$200

$300

0,9

$400

0,2

Какую цену следует назначить на игровую приставку?
2. Для выполнения этого задания возьмите данные о спросе из задания 1. Каждый владелец игровой приставки покупает в среднем 10 видеоигр. Прибыль
от каждой видеоигры составляет $10. Какую цену следует назначить на игровую приставку?

872

ГЛАВА 89

3. Необходимо определить правильную цену на новый еженедельный журнал.
Переменные затраты на печать и распространение экземпляра журнала составляют $0,50. Рассматривается цена от $0,50 до $1,30 за экземпляр. Расчетные еженедельные продажи журнала представлены в таблице:
Цена

Спрос (в млн)

$0,50

$0,90

1,2

$1,30

0,3

В дополнение к выручке от продаж журнала можно получить по $30 за каждую проданную 1000 экземпляров каждой из 20 страниц рекламы, размещаемой в еженедельнике. Какую цену следует назначить на журнал?
4. Аптеке требуется определить, какую цену установить на шоколадный батончик. Аптека платит за каждый батончик 60 центов и планирует продавать их
по цене от $1 до $2 за штуку . Предположительный спрос, соответствующий
трем уровням цены, приведен в таблице ниже. Какую цену на батончик следует установить?
Цена

Спрос

$1,00

$1,50

$2,00

5. Магазин женской одежды закупает костюмы по $200 за штуку. Спрос за неделю оценивается следующим образом:
Цена

Спрос

250

300

350

Предположим, что каждая женщина, приобретая костюм, дополнительно покупает аксессуаров на $80, 50% от которых составляют прибыль магазина. Какую цену на костюм должен назначить магазин?
6. Подписчики рекомендательной службы получают доступ к рекомендациям
о местных поставщиках услуг, таких как врачи, сантехники и т. д. Предполагается, что число новых подписчиков, подключающихся к службе ежемесячно,
зависит от стоимости подписки следующим образом:

Ценообразование продуктов с помощью субъективно определяемого спроса

Цена

Спрос

$10

20 000

$20

15 000

$30

6000

873

Предположим, что каждый подписчик остается таковым в течение года. Кроме
платы за подписку, прибыль приносит щелчок подписчика по рекламному объявлению. Средний подписчик просматривает 10 рекламных объявлений в год.
Какая цена подписки будет приносить максимальную прибыль?
7. Число струйных принтеров, продаваемых магазином электроники в неделю,
оценивается следующей зависимостью от цены:
Цена

Спрос

$70

128

$100

$130

Магазин платит за каждый струйный принтер $50. В среднем каждый, кто покупает принтер, покупает 10 картриджей, на каждом из которых магазин зарабатывает $8. Какая цена на принтер обеспечит максимальную общую прибыль?

ГЛ А В А 90

Нелинейное ценообразование

Обсуждаемые вопросы
Что такое линейное ценообразование?
Что такое нелинейное ценообразование?
Что такое объединение в набор и как оно может повысить прибыльность?
Как составить план нелинейного ценообразования с максимальной прибылью?

Ответы на вопросы
?

Что такое линейное ценообразование?

В главах 88 «Ценообразование продуктов с сопутствующими товарами» и 89 «Ценообразование продуктов с помощью субъективно определяемого спроса» показано, как определить цену продукта, максимизирующую прибыль. Однако
в примерах к этим главам подразумевается, что независимо от количества единиц
приобретаемого товара покупатель платит одну и ту же сумму за каждую единицу.
Такая модель известна как линейное ценообразование, поскольку стоимость покупки x единиц товара является прямолинейной функцией x, а именно:
стоимость x единиц товара = (цена единицы товара) × x.
В этой главе показано, что нелинейное ценообразование зачастую может значительно увеличить прибыль компании.

Что такое нелинейное ценообразование?

Нелинейная схема ценообразования просто означает , что стоимость покупки x
единиц товара не является прямолинейной функцией x. С нелинейными стратегиями ценообразования сталкивался каждый. Вот два примера.
Скидка за количество. Первые пять единиц товара могут стоить по $20,
а остальные единицы — по $12. Скидки за количество, как правило, предоставляются компаниями, продающими компьютеры и компьютерный софт .
Пример стоимости покупки x единиц товара показан на листе nonlinear pricing
examples в файле Nlp.xlsx и на рис. 90.1. Обратите внимание, что график имеет
наклон 20 для пяти и менее единиц товара и наклон 12 для большего количества приобретенных единиц товара.

Нелинейное ценообразование

875

Рис. 90.1. План стоимости со скидкой на количество

Двухчастный тариф. При вступлении в загородный клуб обычно платят фиксированный взнос, а затем взнос за каждую игру в гольф. Предположим, что
загородный клуб взимает членский взнос в размере $500 в год и $20 долларов
за каждую игру. Такой тип стратегии ценообразования называется двухчастным тарифом. Стоимость покупки заданного количества игр для такой политики ценообразования показана на рис. 90.2. Как и в предыдущем случае, см.
лист nonlinear pricing examples в файле Nlp.xlsx. Обратите внимание, что график
имеет наклон 520 от нуля до одной приобретенной единицы и наклон 20 для
большего количества приобретенных единиц. Прямая линия должна всегда

Рис. 90.2. Стоимость при двухчастном тарифе

876

ГЛАВА 90

иметь одинаковый наклон, а двухчастный тариф, как видно из рисунка, является нелинейным.

Что такое объединение в набор и как оно может повысить прибыльность?

При объединении в набор клиенту предлагается купить набор продуктов по цене
меньшей, чем сумма цен входящих в него продуктов. Для анализа феномена объединения в набор необходимо понять, как рациональный потребитель принимает
решения. Для каждой возможной комбинации продуктов рациональный потребитель определяет для себя ценность того, что продается, и вычитает из нее реальную
стоимость покупки. Эта разница называется потребительской выгодой. Рациональный потребитель не купит ничего, если потребительская выгода для каждого доступного варианта является отрицательной. В противном случае потребитель покупает комбинацию продуктов, имеющую самую большую потребительскую выгоду .
Так как же объединение в набор может повысить прибыльность? Предположим,
что вы продаете компьютеры и принтеры двум клиентам. Ценность, которую каждый клиент придает компьютеру и принтеру, представлена в таблице:
Клиент

Ценность компьютера

Ценность принтера

$1000

$500

$1000

Если компьютер и принтер предлагаются к продаже только по отдельности, то, назначив цену $1000 на принтер и на компьютер, вы продадите один принтер и один
компьютер и получите $2000 выручки. Т еперь предположим, что вы предлагаете
такой набор: компьютер и принтер за $1500. Каждый клиент купит и компьютер,
и принтер, и вы получите $3000 выручки. При объединении в набор компьютера и принтера можно извлечь больше выгоды из общей потребительской ценности. Объединение в набор действует эффективнее, если корреляция для потребительской ценности продуктов, включенных в набор, является отрицательной.
В приведенном примере корреляция между ценностью продуктов отрицательная,
поскольку клиент, который высоко оценивает принтер, дает низкую оценку компьютеру, а клиент, для которого принтер малоценен, высоко оценивает компьютер.
Когда вы идете в парк развлечений, например в Диснейленд, вы не покупаете билет на каждый аттракцион. Вместо этого вы покупаете билет на вход в парк. Это
пример чистого объединения в набор, поскольку потребитель не имеет возможности заплатить за подмножество предлагаемых продуктов. Такой подход уменьшает очереди (представьте очередь на каждый аттракцион) и приводит к дополнительной прибыли.
Чтобы понять причину увеличения прибыльности от объединения в набор, предположим, что имеется только один клиент , и количество аттракционов, которые
клиент собирается посетить, определяется следующей кривой спроса: (количество
аттракционов) = 20 – 2 × (цена аттракциона). Из главы 87 «Оценка кривой спроса»

Нелинейное ценообразование

877

вы знаете, что ценность, которую клиент придает i-му аттракциону, является ценой,
при которой спрос равен i – 0,5. Таким образом, i – 0,5 = 20 – 2× (ценность аттракциона i) или (ценность аттракциона i) = 10,25 – (i/2). Первый аттракцион стоит $9,75,
второй аттракцион — $9,25 и т. д. до двадцатого аттракциона, который стоит $0,25.
Предположим, что за аттракцион назначена постоянная цена и переменные затраты составляют $2 за аттракцион. Требуется найти схему линейного ценообразования с максимальной прибылью. Вычисление максимизирующей прибыль цены за
аттракцион показано на листе OnePrice в файле Nlp.xlsx и на рис. 90.3.

Рис. 90.3. Схема линейного ценообразования с максимальной прибылью

Я связал имена в ячейках C8:C10 с ячейками D8:D10. Затем я ввел пробное значение цены в ячейку D8 и вычислил количество приобретенных билетов на аттракционы в ячейке D9 по формуле =20-(2*D8). Прибыль вычислена в ячейке D12
по формуле =спрос*(цена-себестоимость). Затем я применил Поиск решения (Solver)
и нашел максимум значения в ячейке D12 (прибыль), изменив ячейку D8 (цена).
Цена в $6 приведет к покупке восьми билетов на аттракционы, что позволит получить максимальную прибыль в $32.
Теперь представим, что наш парк — Диснейленд, который предлагает только набор из 20 билетов на аттракционы. У становим цену, равную сумме потребительской ценности для каждого аттракциона: (9,75 + 9,25 + … + 0,75 + 0,25 = $100,00).
Потребительская ценность всех 20 аттракционов составляет $100,00, поэтому
клиент купит входной билет в парк за $100,00. Полученная прибыль составит
100,00 – 2,00 × (20) = $60,00, что почти в два раза превышает прибыль при линейном ценообразовании.

Как составить план нелинейного ценообразования с максимальной прибылью?

В этом разделе я покажу, как определить план ценообразования для двухчастного тарифа с максимальной прибылью на примере парка развлечений. Выполните
следующие шаги:
Предложите пробные значения для фиксированного взноса и цены за билет на
аттракцион.
Определите ценность каждого аттракциона для клиента: ценность аттракциона i = 10 – 0,5(i – 0,5) = 10,25 – 0,5i.

878

ГЛАВА 90

Определите общую ценность покупки i билетов на аттракционы.
Определите цену для i билетов на аттракционы: (фиксированный взнос) + i ×
× (цена за билет на аттракцион).
Определите потребительскую выгоду для покупки i билетов на аттракционы:
(ценность i аттракционов) – (цена i билетов на аттракционы).
Определите максимальную потребительскую выгоду.
Определите количество приобретенных единиц. Если максимальная потребительская выгода отрицательная, это количество равно нулю. В противном случае используйте функцию ПОИСКПОЗ (MATCH) и найдите количество единиц,
приносящее максимальную выгоду.
С помощью функции ВПР (VLOOKUP) найдите выручку, соответствующую количеству приобретенных единиц.
Вычислите прибыль как (выручка – затраты).
Используйте двунаправленную таблицу данных для определения фиксированного взноса и цены для билета на аттракцион, которые приносят максимальную прибыль.
Рассмотрим лист two-part tariff в файле Nlp.xlsx и рис. 90.4.
Сначала я назначил ячейке F2 имя фикс_взнос, а ячейке F3 — имя цена_аттр. В ячейки F2 и F3 я ввел пробные значения для фиксированного взноса и цены за билет
на аттракцион. Затем я определил ценность, которую клиент придает каждому
аттракциону, скопировав формулу =10,25-(D6/2) из ячейки E6 в E7:E25. Оказалось,
что клиент оценивает первый аттракцион в $9,75,второй аттракцион — в $9,25 и т. д.
Для вычисления общей ценности первых i аттракционов я скопировал формулу
=СУММ($E$6:E6) из F6 в F7:F25. Эта формула суммирует все значения в столбце E
из текущей строки и над ней. Скопировав формулу =фикс_взнос+цена_аттр*D6 из
G6 в G7:G25, я вычислил цену за i аттракционов. Например, цена пяти билетов на

аттракционы — $68,50.
Напомню, что потребительская выгода для i аттракционов равна (ценность i аттракционов) – (стоимость i билетов на аттракционы). Скопировав формулу
=F6-G6 из ячейки H6 в ячейки H7:H25, я вычислил потребительскую выгоду от покупки билетов на любое количество аттракционов. Например, потребительская
выгода от билетов на пять аттракционов равна –$24,75, что является следствием
большого фиксированного взноса.
В ячейке H4 я вычислил максимальную потребительскую выгоду по формуле
=МАКС(H6:H25). Помните, что если максимальная потребительская выгода отрицательная, у вас ничего не купят. В противном случае клиент приобретет то количество единиц предлагаемой продукции, которое дает максимальную потребительскую прибыль. Следовательно, я ввел в ячейку I1 формулу =ЕСЛИ(H4>=0;ПОИСК
ПОЗ(H4;H6:H25;0);0) и узнал количество приобретенных билетов на аттракционы
(в данном случае, 15). Обратите внимание, что функция ПОИСКПОЗ (MATCH) воз-

Нелинейное ценообразование

879

Рис. 90.4. Определение оптимального двухчастного тарифа

вращает число строк, на которое необходимо сдвинуться вниз в диапазоне H6:H24,
чтобы найти первое совпадение со значением максимальной выгоды.
Теперь я присвою диапазону D5:G25 имя lookup. Тогда в четвертом столбце этого
диапазона я смогу найти общую выручку на основе количества приобретенных
билетов на аттракционы (которое уже вычислено в ячейкеI1). Общая выручка вычисляется в ячейке I2 по формуле =ЕСЛИ(I1=0;0;ВПР(I1;lookup;4)). Обратите внимание, что если билеты не были приобретены, то выручка отсутствует. В ячейке I3
по формуле =I1*C3 я вычислил общую себестоимость катания на аттракционах
для приобретенного количества билетов. В ячейке J6 по формуле =I2-I3 я вычислил прибыль как выручку минус расходы.
Теперь я могу использовать двунаправленную таблицу данных, чтобы определить
комбинацию фиксированного взноса и цены билета на аттракцион, максимизирующую прибыль. Таблица данных показана на рис. 90.5. (Многие строки и столбцы скрыты.) При настройке таблицы данных я изменял фиксированный взнос
от $10,00 до $60,00 (ячейки K10:K60), а цену билета — от $0,50 до $5,00 (ячейки
L9:BE9). Прибыль пересчитана в ячейке K9 по формуле =J6.
Я выделил табличный диапазон (ячейки K9:BE60) и затем на вкладке Данные (Data)
в группе Прогноз (Forecast) в списке Анализ «что, если» (What If Analysis) выбрал
Таблица данных (Data Table). В поле Подставлять значения по строкам в (Column Input
Cell) я указал ячейку F2 (фиксированный взнос), а в поле Подставлять значения по
столбцам в (Row Input Cell) — ячейку F3 (цена билета на аттракцион). После нажа-

880

ГЛАВА 90

тия OK в диалоговом окне Таблица данных (Table) вычислится прибыль по каждой
комбинации фиксированного взноса и цены билета на аттракцион, представленной в таблице.

Рис. 90.5. Двунаправленная таблица для вычисления оптимального двухчастного тарифа

Для выделения цветом двухчастного тарифа, максимизирующего прибыль, я применил Условное форматирование, выделив диапазон L10:BE60. На вкладке Главная
(Home) в группе Стили (Styles) я щелкнул на Условное форматирование (Conditional
Formatting). Далее выбрал Правила отбора первых и последних значений (Top/Bottom
Rules) и Первые 10 элементов (Top 10 Items). Для форматирования только максимальной прибыли замените в диалоговом окне 10 на 1. Здесь фиксированный
взнос $56,00 и цена билета на аттракцион $2,50 дают прибыль $63,50, что почти
в два раза превышает прибыль при линейном ценообразовании. Фиксированный
взнос $59,00 и цена билета $2,30 также дают прибыль $63,50.
Поскольку план ценообразования со скидкой на количество включает выбор трех
переменных (отсечка, высокая и низкая цена), невозможно определить план со
скидкой на количество, максимизирующий прибыль, с помощью таблицы данных.
Можно подумать, что для определения стратегии ценообразования со скидкой на
количество, максимизирующей прибыль, следует взять модель поиска решения
(с изменяющимися ячейками, в которых находятся значения отсечки, высокой
и низкой цены). До Excel 2010 Поиск решения (Solver) не всегда верно находил
корректные решения, если значение в целевой ячейке вычислялось по формулам,

Нелинейное ценообразование

881

содержащим функции ЕСЛИ (IF). В Microsoft Excel 2019 эта проблема полностью
устранена. В файле Qd.xlsx (рис. 90.6) я использовал эволюционный метод поиска
решения, чтобы найти план со скидкой на количество, максимизирующий прибыль. Предположим, что все единицы продукции, приобретенные до отсечки (отсечка), проданы по высокой цене ( высок_цена), а остальные единицы — по низкой
цене (низк_цена). Единственное изменение внесено в столбецG. После присвоения
ячейкам F1:F3 имен в ячейках E1:E3 я вычислил сумму, которую клиент уплатит за
любое количество единиц продукции, скопировав формулу =ЕСЛИ(D6=2;

Формулы массива и функции, возвращающие массив

889

ЗНАЧЕН(ПСТР(A4:A11;2;1));0))}. По этой формуле любое целое число из одной циф-

ры заменяется значением 0, и в результате получается правильная сумма.

Существует ли способ просмотра двух списков имен и поиска имен, встречающихся в обоих списках?

В файле Arrays.xlsx на листе Matching Names хранятся два списка имен (в столбцах D
и E), как показано на рис. 91.5. Т ребуется определить, какие имена из списка 1
встречаются также и в списке 2. Для решения задачи выделите диапазон C5:C28
и введите формулу массива {=ПОИСКПОЗ(D5:D28;E5:E28;0)} в ячейку C5. Эта формула относится ко всему диапазону C5:C28. В ячейке C5 формула проверяет, имеет
ли имя в ячейке D5 совпадения в столбце E. Если таковое существует, возвращается позиция первого совпадения в диапазоне E5:E28. Если такового не существует,
возвращается сообщение об ошибке #Н/Д (недоступно). Аналогично в ячейке C6
формула проверяет, имеет ли совпадение второе имя из списка 1. Как видно из
рисунка, например, имя Artest не встречается в списке 2, а имя Harrington встречается (первое совпадение находится во второй ячейке диапазона E5:E28).

Рис. 91.5. Поиск совпадений в двух списках

Чтобы записать в ячейку значение Да для каждого имени из списка 1, встречающегося в списке 2, и Нет для противоположного случая, выделите диапазон ячеек B5:B28 и введите в ячейку B5 формулу массива {=ЕСЛИ(ЕОШИБКА(C5:C28);»Не
т»;»Да»)}. По этой формуле для каждой ячейки в C5:C28, содержащей сообщение
об ошибке #Н/Д, записывается Нет и для всех ячеек с числовыми значениями за-

890

ГЛАВА 91

писывается Да. Обратите внимание, что формула =ЕОШИБКА(x) дает в результате
ИСТИНА, если в x имеется ошибка, и ЛОЖЬ в противном случае.

Как написать формулу, вычисляющую среднее значение для чисел в списке, которые больше или равны медиане списка?

В файле Arrays.xlsx на листе Average Those > Median (рис. 91.6) диапазон D5:D785
(с именем Prices) содержит список цен. Требуется получить среднее значение для
всех цен, которые не уступают медиане цены. В ячейке F2 я вычислил медиану по
формуле =МЕДИАНА(prices). В ячейке F3 я вычислил среднее значение чисел, которые больше или равны медиане, по формуле =СУММЕСЛИ(prices; «>=»&F2; prices)/
СЧЁТЕСЛИ(prices;»>=»&F2). Эта формула суммирует все цены, по меньшей мере, не
уступающие значению медианы (243), и затем делит сумму на число цен, не уступающих значению медианы. Среднее значение для всех цен, которые не меньше
медианы цены, составляет $324,30.

Рис. 91.6. Среднее значение для цен, которые не меньше медианы цены

Более простой подход — выделить ячейку F6 и ввести формулу массива {=СРЗНАЧ
(ЕСЛИ(prices>=МЕДИАНА(prices);prices;»»))}. Эта формула создает массив, содержащий цену, если цена больше или равна медиане цены, или пробел в противном случае. Вычисление среднего значения для этого массива дает требуемый
результат.

У небольшой компании декоративной косметики имеется база данных по
продажам, в которой указан продавец, количество проданных единиц про-

Формулы массива и функции, возвращающие массив

891

дукции и сумма в долларах для каждой сделки. Мне известно, что для обобщения этих данных подойдут статистические функции или функции СЧЁТЕСЛИМН (COUNTIFS), СУММЕСЛИМН (SUMIFS) и СРЗНА
ЧЕСЛИМН
(AVERAGEIFS). Но могу ли я использовать также функции, возвращающие
массив, чтобы обобщить эти данные и ответить на вопросы типа: сколько единиц косметики продал продавец, или сколько помады было продано, или сколько единиц косметики было продано определенным продавцом?
В файле Makeuparray.xlsx хранится список 1900 торговых сделок компании декоративной косметики. Для каждой сделки указаны номер сделки, продавец, дата
сделки, проданный продукт, количество проданных единиц продукции и объем
продаж в долларах. Часть данных представлена на рис. 91.7.

Рис. 91.7. База данных компании декоративной косметики

Эти данные можно обобщить с помощью статистических функций для баз данных, описанных в главе 50 «Обработка данных с помощью статистических функций для баз данных», или с помощью функцийСЧЁТЕСЛИМН (COUNTIFS) и СУММЕСЛИМН (SUMIFS). (См. главы 20 и 21.) Как будет показано в этом разделе, простую
и эффективную альтернативу этим функциям составляют функции, возвращающие массив.
Сколько единиц косметики продала Джен?
На этот вопрос легко ответить с помощью функции СУММЕСЛИ (SUMIF). На указанном листе диапазону
J5:J1904 присвойте имя Имя, а диапазону M5:M1904 — имя Количество. В ячейку E7 введите формулу =СУММЕСЛИ(Имя;»Jen»;Количество) для суммирования

892

ГЛАВА 91

всех единиц продукции, проданных Джен (Jen). Всего Джен продала 9537 единиц косметики. Также ответ на этот вопрос можно получить, если ввести формулу массива {=СУММ(ЕСЛИ(J5:J1904=»Jen»;M5:M1904;0))} в ячейку E6. Эта формула создает массив, содержащий количество проданных единиц косметики
в сделках Джен и 0 для всех остальных сделок. Т аким образом, суммирование
элементов этого массива также дает в резуль тате количество единиц товара,
проданных Джен, — 9537 (рис. 91.8).

Рис. 91.8. Суммирование данных с помощью формул массива

Сколько помады продала Джен? Для решения этой задачи необходим критерий обработки только двух столбцов ( Имя и Продукт). Ответ можно получить
в ячейке F7 по формуле =БДСУММ(J4:N1904;4;E9:F10) со статистической функцией для баз данных. Формула показыает, что Джен продала 1299 штук помады.
На этот вопрос можно также ответить с помощью формулы массива {=СУММ
((J5:J1904=»Jen»)*(L5:L1904=»lipstick»)*M5:M1904)}, введенной в ячейку F6.
Для понимания этой формулы необходимо немного знать булеву алгебру. Для
части формулы ( J5:J1904=»Jen») создается булев массив. Для каждой ячейки
в J5:J1904, содержащей Jen, в массив включается значение ИСТИНА, а для каждой ячейки в J5:J1904, которая не содержит Jen, в массив включается значение
ЛОЖЬ. Аналогично, для части формулы (L5:L1904=»lipstick») также создается булев массив, в котором значения ИСТИНА соответствуют каждой ячейке в диапазоне, содержащей lipstick, а значение ЛОЖЬ соответствует каждой ячейке, не
содержащей lipstick. При перемножении булевых массивов создается еще один
массив по следующим правилам:

Формулы массива и функции, возвращающие массив

893

• ИСТИНА*ИСТИНА = 1;
• ИСТИНА*ЛОЖЬ = 0;
• ЛОЖЬ*ИСТИНА = 0;
• ЛОЖЬ*ЛОЖЬ = 0.
Коротко говоря, перемножение булевых массивов имитирует оператор И. При
умножении произведения булевых массивов на значения в диапазонеM5:M1904
создается новый массив. В любой строке, где Джен продавала помаду, этот массив содержит количество проданной помады. Во всех остальных строках этого
массива содержится значение 0. Сумма элементов этого массива дает общее
количество помады, проданной Джен (1299 шт.).
Сколько единиц продукции было продано Джен и сколько всего было продано помады? В ячейке G7 я использовал статистическую функцию для баз данных =БДСУММ(J4:N1904;4;E12:F14) и вычислил, что единицы продукции, проданные Джен, и проданная помада в сумме составили 17 061 штуку
. В ячейке G6
я вычислил сумму для количества продукции, проданной Джен, и количества
проданной помады по формуле массива {СУММ(ЕСЛИ((J5:J1904=»jen»)+(L5:L1904
=»lipstick»);1;0)*M5:M1904)}.
Опять же часть формулы (J5:J1904=»jen»)+(L5:L1904=»lipstick») создает два булевых массива. Первый массив содержит значения ИСТИНА тогда и только тогда,
когда продавцом является Джен (в формуле регистр символов не учитывается). Второй массив содержит значения ИСТИНА тогда и только тогда, когда проданный продукт является помадой (lipstick). Булевы массивы складываются по
следующим правилам:
• ЛОЖЬ + ИСТИНА = 1;
• ИСТИНА + ИСТИНА = 1;
• ИСТИНА + ЛОЖЬ = 1;
• ЛОЖЬ + ЛОЖЬ = 0.
Коротко говоря, сложение булевых массивов имитирует оператор ИЛИ. Таким
образом, эта формула создает массив, в котором для каждой строки, где Джен
является продавцом или помада является проданным продуктом, количество
проданных единиц продукции умножается на 1. Во всех остальных строках количество проданных единиц продукции умножается на 0. Результат тот же, что
и со статистической функцией для баз данных (17 061).
Как просуммировать количество единиц каждого продукта, проданного
каждым продавцом? Формулы массива легко дают ответы на такие вопросы.
Сначала составьте список продавцов в диапазоне ячеек A17:A25 и список названий продуктов в диапазоне ячеек B16:F16. Затем в ячейку B17 введите формулу
массива {СУММ(($J$5:$J$1904=$A17)*($L$5:$L$1904=B$16)*$M$5:$M$1904)}.

894

ГЛАВА 91

Эта формула вычисляет только количество подводки для глаз ( eyeliner), проданной Эшли ( Ashley), — 1920 штук. Скопировав эту формулу в C17:F17, я вычислю поштучное количество каждого товара, проданного Эшли. Затем я скопирую формулу из C17:F17 в C18:C25 и вычислю поштучное количество каждого товара, проданного каждым продавцом. Обратите внимание, что я добавил
знак доллара к A в ссылке на ячейку A17 для получения имени соответствующего продавца и знак доллара к 16 в ссылке на ячейку B16 для получения соответствующего продукта.
ПРИМЕЧАНИЕ
Внимательные читатели могут спросить, почему бы просто не выделить формулу в B17
и попытаться скопировать ее за один шаг? Напомню, что невозможно скопировать
формулу массива в диапазон, содержащий и пустые ячейки, и формулы массива.
Вот почему необходимо сначала скопировать формулу из B17 в C17:F17, а затем уже
перетащить ее вниз для завершения таблицы.

Чтобы лучше понять эти формулы, нажмите Вычислить формулу (Evaluate Formula)
и повторно щелкайте по Вычислить (Evaluate), чтобы понять, как Excel рассчитывает по этой формуле конечный результат.

Что такое массив констант и для чего он нужен?

Можно создать собственные массивы и применять их в формулах массива. Для этого заключите значения элементов массива в фигурные скобки { }. Кроме того, текст
необходимо указывать в кавычках ( » «). В качестве элементов массива можно также включать логические значения ИСТИНА или ЛОЖЬ. В массивы констант нельзя
включать формулы или символы, такие как знак доллара или запятая.
В качестве примера использования массива констант рассмотрим лист

Creating

Powers в файле Arrays.xlsx (рис. 91.9).

Рис. 91.9. Возведение объемов продаж во вторую, третью и четвертую степень

На этом листе даны объемы продаж за шесть месяцев, и для каждого месяца требуется создать вторую, третью и четвертую степень объемов продаж. Сначала выделите диапазон D4:F9, в который будут помещены резуль таты вычислений. Введите формулу массива {=C4:C9^{2,3,4}} в ячейку D4. По этой формуле в диапазоне

Формулы массива и функции, возвращающие массив

895

D4:D9 каждое значение из диапазона C4:C9 возводится в квадрат. В диапазоне ячеек E4:E9 по этой формуле каждое значение из C4:C9 возводится в куб. Наконец,
в диапазоне ячеек F4:F9 каждое число из диапазона C4:C9 возводится в четвертую
степень. Массив констант {2, 3, 4} необходим для перебора значений степени.

Как изменить формулу массива?

Допустим, формула массива создает резуль таты во многих ячейках, а вам необходимо изменить, переместить или удалить результаты. Отдельный элемент массива изменить невозможно. Чтобы изменить формулу массива, сначала выделите
все ячейки диапазона массива. Затем выделите одну ячейку в массиве. Нажав F2,
вы сможете внести изменения в эту ячейку . После внесения изменений нажмите
Ctrl+Shift+Enter для применения изменений. Теперь весь массив обновится.

Как оценить тренд и сезонность выручки для магазина игрушек по заданной квартальной выручке?

В файле Toysrustrend.xlsx (рис. 91.10) содержатся данные о квартальной выручке
(в миллионах долларов) магазина игрушек за 1997–2002 гг. Я хочу оценить квартальную тенденцию выручки, а также сезонность, связанную с каждым кварталом
(первый квартал: январь — март; второй квартал: апрель — июнь; третий квартал:
июль — сентябрь; четвертый квартал: октябрь — декабрь). Например, тенденция
1% за квартал означает, что продажи повысились на 1% за квартал. Индекс сезонности 0,80 для первого квартала, например, означает, что продажи за первый квартал составляют приблизительно 80% от продаж среднего квартала.

Рис. 91.10. Оценка тренда и сезонности для выручки магазина игрушек

896

ГЛАВА 91

В решении задачи нам поможет функция ЛГРФПРИБЛ (LOGEST). Допустим, вы хотите предсказать переменную y по независимым переменным x1, x2, …, xn, и полагаете, что для некоторых значений a, b1, b2, …, bn отношение между y и x1, x2, …, xn
задается уравнением y = a(b1)x1(b2)x2···(bn)xn. (Назовем его уравнением 1.)
Функция ЛГРФПРИБЛ (LOGEST) используется для определений значений a, b1, b2,
…, bn, наилучшим образом приближающих это уравнение к наблюдаемым данным.
Для использования функции ЛГРФПРИБЛ в целях вычисления тренда и сезонности
нужно иметь в виду следующее:
y равен квартальной выручке;
x1 равен номеру квартала. (В хронологическом порядке: текущий квартал —
это первый квартал, следующий квартал — второй квартал и т. д.);
x2 равен 1, если квартал является первым кварталом года, и 0 в противном случае;
x3 равен 1, если квартал является вторым кварталом года, и 0 в противном случае;
x4 равен 1, если квартал является третьим кварталом года, и 0 в противном случае.
Необходимо выбрать один квартал для исключения из модели. (Я произвольно выбрал четвертый квартал.) Этот подход аналогичен подходу с фиктивными
переменными из главы 60. Теперь модель оценки выглядит следующим образом:
y = a(b1)x1(b2)x2…(b3)x3(b4)x4. После того как функция ЛГРФПРИБЛ определит значения a, b1, b2, b3 и b4, больше всего соответствующие набору данных, эти значения можно будет интерпретировать следующим образом:
a — константа для масштабирования прогнозов;
b1 — константа, представляющая среднее поквартальное процентное увеличение продаж в магазине игрушек;
b2 — константа, измеряющая отношение продаж в первом квартале к продажам
в опущенном (четвертом) квартале;
b3 — константа, измеряющая отношение продаж во втором квартале к продажам в опущенном квартале;
b4 — константа, измеряющая отношение продаж в третьем квартале к продажам в опущенном квартале.
Сначала в ячейках G6:I27 я создал фиктивные переменные для кварталов 1–3,
скопировав формулу =ЕСЛИ($D6=G$4;1;0) из G6 в G6:I27. Напомню, что четвертый
квартал также определен в Excel, поскольку для четвертого квартала все три фиктивных переменных имеют значение 0, и поэтому нет необходимости заводить для
него фиктивную переменную.
Теперь я выделил диапазон K6:O6, потому что хочу, чтобы рассчитанные функцией ЛГРФПРИБЛ коэффициенты были помещены в него. Константа a займет самую

Формулы массива и функции, возвращающие массив

897

правую ячейку, за ней последуют коэффициенты в соответствии с независимыми
переменными. Таким образом, рядом с константой окажется коэффициент тренда,
затем коэффициент для квартала 1 и т. д.
Функция ЛГРФПРИБЛ имеет синтаксис: ЛГРФПРИБЛ(известные_значения_y; известные_значения_x; ИСТИНА; ИСТИНА). После ввода в ячейку K6 формулы массива
{=ЛГРФПРИБЛ(E6:E27;F6:I27;ИСТИНА;ИСТИНА)} будут рассчитаны коэффициенты, показанные на рис. 91.10. Уравнение прогноза квартальной выручки (в млн)
имеет вид:
4219,57 × 1,0086номер_кварт × 0,435К1_макет × 0,426К2_макет × 0,468К3_макет.
В первом квартале коэффициент К1_макет равен 1, а коэффициенты для второго
и третьего кварталов равны 0. (Напомню, что любое число, возведенное в нулевую
степень, равно 1.) Таким образом, прогнозируемая выручка для первого квартала
составляет 4219,57 × 1,00860086номер_кварт × (0,435).
Во втором квартале коэффициенты К1_макет и К3_макет равны 0, а коэффициент
К2_макет равен 1. Прогнозируемая выручка для этого квартала равна 4219,57
×
× 1,0086номер_кварт × 0,426. В третьем квартале коэффициенты К1_макет и К2_макет
равны 0, а коэффициент К3_макет равен 1. Прогнозируемая выручка для этого
квартала составляет 4219,57 × 1,0086номер_кварт × 0,468. Наконец, в четвертом квартале коэффициенты К1_макет, К2_макет и К3_макет равны 0. Прогнозируемая выручка для этого квартала составляет 4219,57 × 1,0086номер_кварт.
Таким образом, по оценкам квартальная тенденция к росту доходов составляет
0,9% (около 3,6% в год). После корректировки тренда получаем:
выручка за квартал 1 в среднем составляет 43,5% от выручки за квартал 4;
выручка за квартал 2 в среднем составляет 42,6% от выручки за квартал 4;
выручка за квартал 3 в среднем составляет 46,8% от выручки за квартал 4.
Для вычисления индекса сезонности по каждому кварталу присвойте опущенному кварталу значение 1 и найдите весовой коэффициент для среднего квартала по
следующей формуле (см. ячейку K2 на рис. 91.10):

Затем можно вычислить относительный индекс сезонности для кварталов 1–3,
скопировав формулу =K6/$K$2 из K4 в L4:M4. Сезонность для квартала 4 вычисляется в ячейке M2 по формуле =1/K2. После корректировки тренда получаем:
объем продаж в квартале 1 составляет 75% от объема продаж в типичном квартале;
объем продаж в квартале 2 составляет 73% от объема продаж в типичном квартале;

898

ГЛАВА 91

объем продаж в квартале 3 составляет 80% от объема продаж в типичном квартале;
объем продаж в квартале 4 составляет 172% от объема продаж в типичном
квартале.
Пусть вам необходимо подготовить прогноз на каждый квартал в соответствии
с подобранным уравнением (уравнение 1). Вы можете использовать для этого
функцию РОСТ (GROWTH), возвращающую массив. Ее синтаксис: РОСТ(известные_
значения_y; известные_значения_x;новые_значения_x;ИСТИНА). Эта функция возвращает прогнозы для новых значений x, когда уравнение 1 подогнано к данным,
содержащимся в диапазонах с известными значениями y и x. Выделите диапазон
J6:J27 и введите в ячейкуJ6 формулу массива{=РОСТ(E6:E27;F6:I27;F6:I27;ИСТИНА)}.
Формула сгенерирует прогнозы по уравнению 1 для выручки в каждом квартале.
Например, прогноз на квартал 4 1997 г. по уравнению 1 составил $4,366 млрд.

Как вычислить медианный размер сделки в каждой стране по заданному
списку сделок в различных странах?

В файле Medians.xlsx (рис. 91.11) содержатся данные о выручке по сделкам компании во Франции, США и Канаде. Здесь необходимо вычислить медианный размер
сделки в каждой стране. Предположим, например, что вам нужно вычислить медианный размер сделки в США. Простой способ это сделать — создать массив, содержащий только данные по США, заменив остальные данные пустым значением.
Далее вычислите медиану этого нового массива. Присвойте имя Страна столбцу C
и имя Выручка столбцу D, затем в ячейку G5 введите формулу массива {=МЕДИАНА
(ЕСЛИ(Страна=F5;Выручка;»»))} для замещения выручки в каждой строке, содержащей сделку, совершенную не в США, пустым значением и для вычисления

Рис. 91.11. Вычисление медианного размера сделок в каждой стране

Формулы массива и функции, возвращающие массив

медианного размера сделок в США ($6376,50). Формула, скопированная из
в G6:G7, вычисляет медианный размер сделки для Канады и Франции.

899
G5

Имеются данные о торговых сделках с разбивкой по продавцам, продуктам
и местоположению. Как определить стандартное отклонение проданных
единиц продукции для каждого сочетания «продавец — продукт — регион»?

Файл Stdevif.xlsx содержит 456 сделок по продаже косметики. (См. рис. 91.12.)
Для каждой сделки известны продавец, количество проданных единиц продукции, продукт и местоположение. Необходимо определить для каждого сочетания
«продавец — продукт — регион» стандартное отклонение проданных единиц продукции для соответствующих транзакций. Сначала на вкладке Формулы (Formulas)
в группе Определенные имена (Defined Names) выберите Создать из выделенного
(Create From Selection) для присвоения имен столбцам данных. Затем скопируйте
данные на новый лист ( Sheet2) и выберите для создания всех уникальных комбинаций «продавец — продукт — регион» инструмент Удалить дубликаты (Remove
Duplicates) на вкладке Данные (Data) в группе Работа с данными (Data Tools). Вставьте эти комбинации в диапазон ячеек L6:N51 (снова на листе Sheet1). Затем скопируйте формулу массива {=СТАНДОТКЛОН(ЕСЛИ(Имя=L7; ЕСЛИ(Продукт=M7;
ЕСЛИ(Регион=N7;Кол_во))))} из ячейки O7 в O8:O51. Эта формула сначала создаст
массив из единиц (если Имя в ячейке равно Ashley) и нулей (если Имя в ячейке не
равно Ashley). Затем массив из единиц и нулей для продукта mascara (тушь) и наконец — массив из единиц и нулей для региона East. Затем эти массивы перемножаются, в результате давая массив, соответствующий строкам, в которых Ashley
продавала mascara в регионе East. Этот последний массив из единиц и нулей умножается на столбец Кол_во (Units), и вы получаете все объемы продаж туши в сделках Ashley в регионе East. Функция СТАНДОТКЛОН возвращает стандартное отклонение (29,2) проданных единиц во всех сделках Ashley по продаже туши в регионе
East. Копирование этой формулы в ячейки O8:O51 дает все требуемые стандартные отклонения. Чтобы лучше понять эту формулу, вы можете применить инструмент Вычислить формулу (Evaluate Formula) на вкладке Формулы (Formulas) в группе
Зависимости формул (Formula Auditing).
Как применить функцию СУММПРОИЗВ (SUMPRODUCT) взамен условного
счета, условного суммирования и условного определения среднего наравне с формулами массивов?

Функцию СУММПРОИЗВ мы использовали с главы 30 «Поиск решения при определении оптимального ассортимента продукции» для решения многих задач на
оптимизацию. Как показано в файле Sumproductstricks.xlsx, функция СУММПРОИЗВ
может применяться и для имитации многих расчетов, выполняемых с помощью
массивов, условного счета и условного суммирования. Как показано на рис. 91.13,
допустим, имеются объемы продаж компьютерных чипов по разным странам.
Продемонстрируем теперь на нескольких примерах скрытую мощь функции
СУММПРОИЗВ.

900

ГЛАВА 91

Рис. 91.12. Вычисление стандартных отклонений на срезах данных

Рис. 91.13. Объемы продаж компьютерных чипов

Формулы массива и функции, возвращающие массив

901

Для скольких сделок фактические доходы оказались меньше, чем заложенные в бюджет (прогнозные)?

В ячейке G3 видно (рис. 91.14), что по формуле=СУММПРОИЗВ(—(D2:D208 (Add).
4. Щелкнув кнопку Изменить… (Modify) (справа внизу), вы можете настроить
расположение значка, используемого для запуска макроса, чтобы он отображался последним в панели быстрого доступа. Нажмите OK в диалоговом окне
Изменение кнопки (Modify Button) и в диалоговом окне Параметры Excel (Excel
Options).
5. Если вы выделите диапазон ячеек, щелчок на значке, который вы добавили на
панель быстрого доступа, запустит на выполнение макрос redbold.

Рис. 92.7. Назначение макроса кнопке

Рис. 92.8. Кнопка запуска макроса redbold

914

ГЛАВА 92

Рис. 92.9. Выбор макроса redbold для добавления в панель быстрого доступа

Как при записи макросов использовать относительные ссылки?

Предположим, вам требуется ввести свое имя в заданную ячейку и текущую дату
в соседнюю справа от нее ячейку.
Сначала создадим макрос, всегда помещающий ваше имя в ячейку A1, а текущую
дату — в ячейку B1. (См. файл Namedatemacro.xlsm.)
1. На вкладке Разработчик (Developer) выберите Запись макроса (Record Macro), назовите макрос Namedatea1 и присвойте ему сочетание клавишCtrl+Shift+A. Нажмите OK, чтобы закрыть диалоговое окно Запись макроса.
2. Перейдите в ячейку A1 и введите свое имя, затем перейдите в ячейку B1 и введите формулу =TODAY(), которая всегда возвращает текущую дату.
3. Нажмите Остановить запись (Stop Recording).
4. Для проверки работы макроса перейдите в какую-либо ячейку и введите сочетание клавиш Ctrl+Shift+A. Вы увидите, что введенное вами имя появится в ячейке A1, а текущая дата в ячейке B1. Теперь выберите Изменить (Edit)
в диалоговом окне Макрос (Macro), и вы увидите код VBA, приведенный на
рис. 92.10.

Запись макросов

915

Рис. 92.10. Макрос, помещающий имя в ячейку A1 и текущую дату в ячейку B1

Просмотрев код, вы увидите, что сначала Excel выбирает ячейку A1. Она становится активной, и Excel вводит Wayne в текущую активную ячейку (A1). Потом он
перемещается в ячейку B1 и вводит в нее формулу =TODAY().
Так как при записи макроса не было изменено перемещение курсора, Excel затем
перемещает курсор на одну ячейку вниз, в ячейку B2. Если удалить из макроса
строку Range(«B2»).Select и перезапустить выполнение макроса, вы увидите, что
макрос завершит работу в ячейке B1, а не B2. Этот простой пример показывает
возможности редактирования кода макроса. Теперь предположим, что вам нужно
иметь возможность выбрать любую ячейку , чтобы ввести в нее свое имя и чтобы текущая дата отображалась в соседней справа от нее ячейке. Это означает , что
макрос должен содержать относительные ссылки. Для этого выберите опцию Относительные ссылки (Use Relative References) в группе Код (Code) на вкладке Разработчик (Developer), как показано на рис. 92.11.

Рис. 92.11. Включение режима относительных ссылок

916

ГЛАВА 92

После включения режима относительных ссылок макрос не будет содержать явных ссылок на ячейки, кроме тех, которые были выбраны до записи макроса. При
выполнении этого макроса все вводы будут выполняться относительно текущей
активной ячейки. Для создания макроса, который пишет ваше имя в выделенной
ячейке и помещает текущую дату в соседней с ней справа ячейке, выполните следующие действия. (См. файл Namedaterelative.xlsm.)
1. Откройте новую книгу и переместитесь в произвольную ячейку (например, H5).
2. Перейдите на вкладку Разработчик (Developer), включите режим Относительные
ссылки (Use Relative References) в группе Код (Code).
3. Выберите Запись макроса (Record Macro) и присвойте макросу имя Имядатаотносит. Щелкните OK.
4. Введите свое имя в активной ячейке (в H5).
5. Переместитесь на одну ячейку вправо, в I5, и введите формулу =TODAY().
6. Дважды щелкните на заголовке столбца I, чтобы его ширина вмещала дату.
7. Щелкните Остановить запись (Stop Recording).
8. Создайте кнопку для запуска макроса, как было описано ранее.
9. Перейдите в некоторую ячейку листа и запустите макрос. Вы увидите свое
имя в выбранной ячейке и текущую дату в соседней с ней справа. В завершение выполнения макроса курсор переместится на одну ячейку вниз от даты.
Если вам нужно, чтобы этого не происходило, отредактируйте макрос, удалив
инструкцию, перемещающую курсор от ячейки с датой вниз.
Код VBA для этого макроса приведен на рис. 92.12.

Рис. 92.12. Код VBA, помещающий в произвольную ячейку ваше имя и рядом текущую дату

Запись макросов

917

Далее приведены описания всех использованных в макросе инструкций:
Sub Namedaterelative(). Макрос начинается с инструкции Sub, содержащей
имя макроса.
‘ Namedaterelative Macro. Инструкции, начинающиеся с одиночной прямой
кавычки (‘), являются комментариями и не исполняются. Данная инструкция — комментарий, определяющий имя макроса.
ActiveCell.FormulaR1C1 = «Wayne». Эта инструкция вставляет текст Wayne1
в выбранную перед запуском макроса ячейку.
ActiveCell.Offset(0, 1).Range(«A1»).Select. Эта инструкция перемещает
курсор на одну ячейку вправо от текущей ячейки. Обратите внимание на использование Offset, сходное с использованием функции СМЕЩ (OFFSET), о которой рассказывалось в главе 22.
ActiveCell.FormulaR1C1 = «=TODAY()». Эта инструкция вводит текущую
дату в активную ячейку, которая находится на один столбец правее ячейки, содержащей ваше имя.
ActiveCell.Offset(1, 0).Range(«A1»).Select. Эта инструкция перемещает
курсор на одну ячейку вниз от ячейки с текущей датой. Если удалить эту инструкцию из макроса, активной ячейкой после завершения работы макроса будет ячейка, содержащая текущую дату.
ActiveCell.Columns(«A:A»).EntireColumn.EntireColumn.AutoFit. Инструкция подбирает ширину столбца, содержащего дату , чтобы дата отображалась
полностью.
End Sub. Инструкция End Sub отмечает конец макроса.

Как записать макрос, фильтрующий сводную таблицу так, чтобы отображались только данные о 20 основных клиентах?

Файл Ptcustomerstemp.xlsx (в папке Template) содержит сводную таблицу из главы 45 «Сводные таблицы и срезы для описания данных», в которой собраны
продажи по 100 клиентам. Мы создадим макрос, который при щелчке кнопкой
отфильтрует сводную таблицу и выведет данные о 20 основных клиентах. Выполните следующие шаги:
1. На вкладке Разработчик (Developer) в группе Код (Code) выберите Запись макроса (Record Macro). В открывшемся диалоговом окне присвойте макросу имя
Topcustomers. Щелкните OK, чтобы начать запись.
2. Перейдите в ячейку A4 и, нажав на стрелку , открывающую меню, выберите
Фильтры по значению (Value ﬁlters).
3. Выберите Первые 10 (Top 10). Затем в диалоговом окне Фильтр «Первые 10» (Top
10 Filter (Customer)) измените значение 10 на 20, чтобы задать филь тр на отображение первых 20 клиентов. Щелкните OK.
1

В вашем макросе в этой инструкции будет ваш текст. — Примеч. пер.

918

ГЛАВА 92

4. Нажмите Остановить запись (Stop Recording).
5. Создайте кнопку для запуска макроса. При запуске макроса будут отображаться только данные по первым 20 клиентам. Для проверки работы готового
макроса откройте файл Ptcustomers.xlsm из папки Practice Files, сбросьте значение фильтра в ячейке A4 и нажмите кнопку Top20.
Вы можете теперь записать макрос, восстанавливающий исходную сводную таблицу. (См. задание 4.)

Задания
1. Игроков команды MБA зовут Уэйн, Тейлор, Бритни и Кэти. Создайте макрос,
вводящий имена игроков в ячейки A1:D1.
2. Измените макрос из задания 1 так, чтобы имена игроков вводились в одной
строке, начиная с произвольно заданной ячейки.
3. Создайте макрос, размещающий толстую красную границу вокруг любого набора выделенных ячеек.
4. Для примера сводной таблицы из файла Ptcustomers.xlsm создайте макрос,
сбрасывающий любые фильтры на данные по клиентам.
5. Создайте макрос, который будет форматировать начертание любого выделенного диапазона ячеек как полужирный курсив.
6. Сочетание клавиш Ctrl+A выделяет все ячейки на текущем листе. Используйте
этот факт при создании макроса, который гарантированно отформатирует все
ячейки листа начертанием полужирный курсив.
7. Часто требуется зафиксировать резуль таты в некотором диапазоне, вычисленные по формулам, и заменить формулы значениями. Создайте макрос, который, основываясь на выделенной ячейке, будет находить наибольший диапазон ячеек, содержащий текущую ячейку , и преобразовывать все формулы
в значения. Подсказка: Ctrl+Shift+* выделит требуемый диапазон. Протестируйте макрос, введя в лист набор функций =СЛЧИС() (RAND).
8. Создайте макрос, который выделяет желтым цветом столбец данных целиком. Этот макрос должен работать для любого количества строк в столбце.
Подсказка: используйте сочетание клавиш Ctrl+Shift+↓.

Г Л А В А 93

Продвинутый анализ
чувствительности
Обсуждаемый вопрос
В электронной таблице много исходных параметров, поэтому двунаправленная
таблица данных в этом случае неприемлема для анализа чувствительности. Как
же мне все-таки провести анализ чувствительности?

Ответ на вопрос
В электронной таблице много исходных параметров, поэтому двунаправленная таблица данных в этом случае неприемлема для анализа чувствительности. Как же мне все-таки провести анализ чувствительности?

В файле Spiderplottemplate.xlsx (рис. 93.1) содержится расчет чистой приведенной
стоимости (ЧПС/NPV) после уплаты налогов от нового продукта на основе базовых исходных параметров в ячейках D6:D13. Нужно построить график, показы-

Рис. 93.1. ЧПС нового продукта

920

ГЛАВА 93

вающий изменение ЧПС, когда все исходные параметры, за исключением одного,
остаются на уровне своих базовых значений, а значение оставшегося исходного
параметра изменяется в диапазоне от –40% до +40% от его базового значения.
Хитрость в том, чтобы все-таки использовать двунаправленную таблицу, указав
ячейку Е4 в поле Подставлять значения по строкам (Row input cell), что позволяет
определить процентное изменение исходного параметра, и ячейку Е3 в поле Подставлять значения по столбцам (Column input cell) для выбора исходного параметра
(на основании меток в диапазоне ячеек A6:A13).
Скопировав из C6 в C7:C13 следующую формулу =ЕСЛИ(A6=Change;D6*(1+
+percentage);D6), мы можем быть уверены, что таблица данных, представленная на
рис. 93.2, рассчитывает ЧПС, когда значение каждого исходного параметра варьирует в пределах 40% от его базового значения. Например, в ячейке R26 мы видим,
что если рост базовых продаж сократится на 20%, а все другие исходные параметры останутся на базовом уровне, то ЧПС упадет до 34925,57 доллара.

Рис. 93.2. Таблица данных для анализа чувствительности

Рис. 93.3. «Паукограмма»

Продвинутый анализ чувствительности

921

Таблица данных с ячейкой E4 для подстановки значений по строкам и E3 для подстановки значений по столбцам отражает изменение ЧПС при изменении каждого исходного параметра в диапазоне 40% от его базового значения.
Скопировав результаты из таблицы данных в диапазон P23:X31 и имена исходных
параметров в диапазон O24:O31, мы можем построить линейную диаграмму, комбинирующую все данные из таблицы, представленную на рис. 93.3 (также называемую «паукограммой», spiderplot).

Задания
1. Измените пример, приведенный в главе, чтобы создать «паукограмму», отражающую изменения значения каждого исходного параметра в диапазоне 80%
от базового значения (с шагом в 20%).
2. В файле Customers.xlsx содержится расчет числа клиентов на конец десятого
года на основании трех входных параметров: число клиентов на начало года,
ежегодное количество новых клиентов и коэффициент оттока (учитывающий
уход постоянных клиентов). Постройте «паукограмму», показывающую, как
варьирует число клиентов на конец десятого года при изменении каждого исходного параметра в диапазоне до 40% от его базового уровня.

Список вопросов

Стр.

Глава 1. Основы моделирования в электронных таблицах

Как эффективно определить понедельные выплаты всех моих сотрудников?

Как эффективно определить, сколько пекарня должна каждому из своих поставщиков?

Как оценить, какое количество посетителей будет иметь новый фитнес-клуб через 10 лет?

Как правильно задавать порядок выполнения операций в Excel?

Как определить влияние на прибыль изменения в цене и себестоимости единицы товара для кофейни по соседству?
Глава 2. Имена диапазонов

Необходимо вычислить общий объем продаж в штатах Аризона, Калифорния, Монтана, НьюЙорк и Нью-Джерси. Можно ли для вычисления общего объема продаж воспользоваться формулой AZ+CA+MT+NY+NJ вместо формулы СУММ(A21:A25) и получить правильный ответ?

Для чего нужна формула СРЗНАЧ(A:A)?

Чем различаются имена с областью действия «книга» и «лист»?

Мне начинают нравиться имена диапазонов. Я стал определять имена диапазонов во многих книгах, которые я создаю в офисе. Однако эти имена не появляются в формулах. Как добиться отображения недавно созданных имен диапазонов в ранее созданных формулах?

Каким образом можно вставить список имен всех диапазонов (и представляемых ими ячеек)
в лист?

Предполагаемый годовой доход вычисляется как кратный прошлогоднему доходу . Может ли
формула выглядеть как (1+прирост)*предыдущий_год?

Для каждого дня недели даны почасовая оплата и количество отработанных часов. Можно ли
вычислить итоговую сумму оплаты за каждый день по формуле почасовая_оплата*часы?
Глава 3. Функции поиска

Как создать формулу для вычисления налоговых ставок на основе дохода?

Как посмотреть цену продукта по идентификатору продукта?

Допустим, что цена продукта изменяется со временем. Известна дата продажи продукта. Как создать формулу для вычисления цены продукта?
Глава 4. Функция Индекс

У меня есть список расстояний между различными городами США. Как должна выглядеть функция, возвращающая расстояние между Сиэтлом и Майами?

Можно ли создать формулу со ссылкой на весь столбец, содержащий сведения о расстоянии
между Сиэтлом и другими городами?

Список вопросов

923

Глава 5. Функция ПОИСКПОЗ
56

Как создать формулу, возвращающую объем продаж какого-либо продукта за определенный месяц, если даны ежемесячные продажи для нескольких продуктов? Например, сколько продукта 2
было продано за июнь?

Как создать формулу, определяющую бейсболиста с самой высокой зарплатой, если дан список
зарплат игроков? А бейсболиста с пятой по величине зарплатой?

Как создать формулу, определяющую период окупаемости для первоначальных инвестиционных
вложений, если известны ежегодные денежные потоки от реализации инвестиционного проекта?
Глава 6. Текстовые функции и инструмент Мгновенное заполнение

У меня есть лист, каждая ячейка которого содержит описание продукта, идентификатор продукта и цену продукта. Как поместить все описания в столбец A, все идентификаторы в столбец B
и все цены в столбец C?

Каждый день я получаю данные о совокупных продажах в США, которые вычисляются в одной
ячейке как сумма продаж на востоке, севере и юге. Как мне извлечь продажи на востоке, севере
и юге в отдельные ячейки?

В конце каждого семестра студенты оценивают мою преподавательскую деятельность по шкале
от 1 до 7 баллов. Мне известно, сколько студентов выставили тот или иной балл. Как создать
гистограмму оценки качества преподавания?

Числовые данные были загружены из интернета или из базы данных. При попытке использовать
их в вычислениях появляется ошибка #ЗНАЧ!. Как решить эту проблему?

Текстовые функции — вещь хорошая, но есть ли простой способ (без них) извлечь имена и фамилии из данных, создать список адресов электронной почты из списка имен или выполнить другие
стандартные операции с текстовыми данными?

Что такое символы Unicode?

Чем новая функция ОБЪЕДИНИТЬ лучше старой функции СЦЕПИТЬ (или &)?

Мне нравятся текстовые функции, а как пользоваться функцией Excel ТЕКСТ?
Глава 7. Даты и функции работы с датами

Когда я ввожу даты в Excel, то часто получаю число, например 37625, а не дату вида 04.01.2003.
Что делать?

Как с помощью формулы автоматически отобразить сегодняшнюю дату?

Как определить дату через 50 рабочих дней после другой даты? Как исключить праздничные дни?

Как определить количество рабочих дней между двумя датами?

На листе Excel введено 500 дат. Какие формулы нужны, чтобы извлечь из каждой даты месяц,
год, день месяца и день недели?

У меня есть значения года, месяца и дня. Существует ли простой способ восстановления фактической даты?

У меня бизнес по купле-продаже автомобилей. Для некоторых автомобилей известны даты покупки и продажи. Каким образом можно определить, сколько месяцев эти автомобили пробыли
на стоянке?

Как поместить в лист статичную (неизменяемую) дату?
Глава 8. Оценка инвестиций по чистой приведенной стоимости

Что такое чистая приведенная стоимость (ЧПС)?

Как работать с функцией ЧПС в Excel?

924

Список вопросов

Как рассчитать ЧПС, если денежные потоки приходят в начале или середине года?

Как рассчитать ЧПС, если денежные потоки приходят через неравные промежутки времени?
Глава 9. Внутренняя ставка доходности

Как вычислить внутреннюю ставку доходности денежных потоков?

Всегда ли проект имеет единственное значение ВСД?

Существуют ли условия, гарантирующие единственное значение ВСД проекта?

Если единственное значение ВСД имеют два проекта, как можно использовать значение ВСД
для этих проектов?

100 Как вычислить ВСД для нерегулярно поступающих денежных потоков?
100 Что такое модифицированная внутренняя ставка доходности (МВСД) и как она рассчитывается?
Глава 10. Еще несколько финансовых функций Excel
104 Вы покупаете копировальный аппарат . Как лучше поступить: заплатить $11 000 сразу или выплачивать по $3000 в год в течение пяти лет?
106 В конце каждого года в течение следующих 40 лет я собираюсь инвестировать по $2000 в год
вплоть до выхода на пенсию и зарабатывать 8% в год на своих инвестициях. Какую сумму я получу при выходе на пенсию?
108 Я занял $10 000 на срок 10 месяцев под 8% годовых. Каковы мои ежемесячные платежи? Каковы
ежемесячные выплаты по основной сумме и по процентам?
111 Я собираюсь занять $80 000 и вносить ежемесячные платежи в течение 10 лет . Максимальный
ежемесячный платеж, который я могу себе позволить, составляет $1000. На какую максимальную процентную ставку я могу рассчитывать?
112 Если я возьму взаймы $100 000 под 8% годовых и буду вносить платежи в размере $10 000 в год,
через сколько лет я выплачу кредит?
112 Я дипломированный бухгалтер и часто работаю со сложными методами расчета амортизации
оборудования. Имеются ли в Excel функции для расчета амортизации?
Глава 11. Циклические ссылки
119 Я часто получаю в Excel сообщение о циклической ссылке. Означает ли это, что я сделал
ошибку?
120 Как исправить циклическую ссылку?
Глава 12. Функции ЕСЛИ, ЕСЛИОШИБКА, ЕСЛИМН, ВЫБОР и ПЕРЕКЛЮЧ
126 При заказе 500 единиц продукции необходимо заплатить $3,00 за единицу продукции. При заказе от 501 до 1200 единиц цена за единицу падает до $2,70. При заказе от 1201 до 2000 единиц
стоимость единицы продукции составляет $2,30. При заказе свыше 2000 единиц — $2,00. Как
написать формулу, выражающую затраты на приобретение как функцию количества приобретенных единиц продукции?
127 Я купил 100 акций по цене $55 за акцию. Для хеджирования риска снижения стоимости акций
я купил 60 шестимесячных европейских пут-опционов. Каждый опцион имеет цену исполнения
$45 и стоит $5 долларов. Как разработать таблицу , в которой указана процентная доходность
моего инвестиционного портфеля через шесть месяцев для ряда возможных будущих цен?
129 Многие аналитики фондового рынка считают, что торговые правила для торговли по скользящим
средним могут опережать рынок. Общее рекомендуемое правило для торговли по сколь зящим
средним гласит: покупай, когда цена акции превысит средний показатель за последние 15 меся-

Список вопросов

925

цев, и продавай, когда цена акции упадет ниже среднего показателя за последние 15 месяцев. Как
это торговое правило может быть сформулировано для биржевого индекса Standard&Poor’s 500
(S&P)?
132 В игре в кости брошены две кубика. Если сумма чисел при первом броске равна 2, 3 или 12 — вы
проиграли. Если сумма чисел при первом броске равна 7 или 11 — вы выиграли. Во всех остальных случаях игра продолжается. Как создать формулу , определяющую состояние игры после
первого броска?
132 В большинстве гипотетических финансовых отчетов в качестве средства уравновешивания активов и обязательств используются денежные средства. Я знаю, что более реалистично использовать для этого долгосрочные обязательства. Как настроить гипотетический отчет с долгосрочными обязательствами в качестве средства уравновешивания?
137 При копировании формулы с функцией ВПР для вычисления зарплаты сотрудников я получаю
множество сообщений об ошибке #Н/Д. Затем при расчете средней зарплаты сотрудников я не
могу получить числовой ответ из-за ошибки #Н/Д. Можно ли заменить ошибки #Н/Д пробелом
и рассчитать, таким образом, среднюю зарплату?
140 Лист содержит ежеквартальные доходы компании Walmart. Как вычислить доход за каждый год
и внести его в строку, содержащую продажи в первом квартале соответствующего года?
141 Формула с функцией ЕСЛИ может оказаться довольно длинной. Сколько вложенных функций ЕСЛИ можно поместить в ячейку? Каково максимально допустимое количество символов
в формуле Excel?
141 Вложенные функции ЕСЛИ могут оказаться слишком длинными и сложными. Как новая функция ЕСЛИМН облегчает написание вложенных функций ЕСЛИ?
142 Как работает функция ВЫБОР?
144 Как работает новая функция ПЕРЕКЛЮЧ?
Глава 13. Время и функции времени
151 Как указать время в Excel?
152 Как указать время и дату в одной ячейке?
152 Как в Excel обрабатываются значения времени?
153 Как отобразить на листе текущее время?
154 Как создать значения времени с помощью функции ВРЕМЯ?
154 Как использовать функцию ВРЕМЗНА Ч для преобразования строки из текстового формата
в формат времени?
154 Как извлечь часы, минуты и секунды из заданного значения времени?
154 Как определить, сколько часов отработал сотрудник, если известно время начала и окончания
работы?
155 Я суммирую общее время, отработанное сотрудником, но у меня никогда не получается больше
24 часов. Где ошибка?
155 Как создать последовательность равномерно распределенных временных интервалов?
156 Как поместить в книгу статичное временное значение?
Глава 14. Команда Специальная вставка
158 Как переместить результаты расчетов (но не формулы) в другую часть листа?
160 В столбце имеется список имен. Как поместить список в строку вместо столбца?
161 Я скачал с сайта в Excel процентные ставки по казначейским векселям США. В полученных данных отображается 5, если процентная ставка составляет 5%, 8 — если процентная ставка состав-

926

Список вопросов
ляет 8%, и т . д. Как быстро разделить все резуль таты на 100, чтобы, например, пятипроцентная
ставка отображалась как 0,05?
Глава 15. Трехмерные формулы и гиперссылки

165 Существует ли простой способ создания многостраничной книги, в которой все листы имеют
одинаковую структуру? Можно ли создать формулы со ссылками на ячейки, расположенные на
разных листах?
167 Я работаю с 200-страничной книгой. Как организовать простую навигацию по страницам?
Глава 16. Инструменты проверки зависимостей и надстройка Inquire
173 Я только что получил лист с 5000 строк, на котором вычисляется чистая приведенная стоимость
(ЧПС) нового автомобиля. На этом листе мой финансовый аналитик сделал предположение
о годовом проценте роста цены продукта. Каких ячеек на листе касается это предположение?
175 Мне кажется, что мой финансовый аналитик сделал ошибку при вычислении прибыли до уплаты
налогов за первый год. Какие ячейки на модели листа использовались в этом расчете?
177 Как инструменты проверки зависимостей работают с данными на нескольких листах или в нескольких книгах?
178 Что такое надстройка Inquire и как ее установить?
178 Как применить надстройку Inquire для сравнения книг?
179 Как применить надстройку Inquire для анализа структуры книги?
179 Как применить надстройку Inquire для анализа связей между листами и книгами?
180 Как применить надстройку Inquire для анализа влияющих и зависимых ячеек для конкретной
ячейки?
180 Как с помощью Inquire очистить ячейку от избыточного форматирования?
Глава 17. Анализ чувствительности с помощью таблиц данных
183 Я подумываю открыть магазин в местном торговом центре и продавать натуральный лимонад.
Я хотел бы знать до открытия магазина, как прибыль, доход и переменные затраты будут зависеть от цены и себестоимости единицы продукции.
187 Я собираюсь построить новый дом. Сумма кредита (с периодом погашения 15 лет) зависит от
цены, по которой я продам свой нынешний дом. Я также не уверен в годовой процентной ставке,
которую я получу по завершении процесса продажи. Можно ли определить, как ежемесячные
платежи будут зависеть от суммы кредита и годовой процентной ставки?
188 Крупная интернет-компания подумывает о покупке еще одного магазина. Т екущий годовой доход от этого магазина составляет $100 млн, а расходы — $150 млн. Текущие прогнозы показывают, что доходы магазина ежегодно растут на 25%, а расходы — на 5%. Известно, однако, что
прогнозы могут быть ошибочными, и хотелось бы знать с учетом различных предположений о годовом росте доходов и расходов, через сколько лет магазин начнет приносить прибыль.
190 Как создать диаграмму на основе таблицы данных?
Глава 18. Инструмент Подбор параметра
196 Сколько стаканов лимонада в год по определенной цене должен продать магазин для достижения
безубыточности?
196 Мы собираемся выплатить ипотеку за 15 лет . Годовая процентная ставка составляет 6%. Банк
сообщил, что максимальный ежемесячный платеж для нас составляет $2000. Какую сумму мы
можем взять в кредит?

Список вопросов

927

197 Мне всегда плохо давались сюжетные задачи по алгебре в средней школе. Может ли Excel упростить решение таких задач?
Глава 19. Анализ чувствительности с помощью Диспетчера сценариев
201 Я хочу создать для компании наиболее благоприятный, наименее благоприятный и наиболее
вероятный сценарии продаж модели автомобиля, изменяя значения объема продаж за год 1, годового роста продаж и розничной цены в год 1. В таблице данных для анализа чувствительности
можно изменять только один или два исходных параметра, поэтому для решения этой задачи
таблица данных не подходит . Существует ли в Excel другой инструмент , который при анализе
чувствительности позволяет изменять более двух параметров?
Глава 20. Функции СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СЧЁТ, СЧЁТЗ и СЧИТАТЬПУСТОТЫ
209 Сколько песен исполнил каждый певец?
210 Сколько песен было исполнено не Эминемом?
210 Сколько песен длились не меньше четырех минут?
210 Сколько песен длились дольше, чем средняя продолжительность звучания песен из списка?
211 Сколько песен было исполнено певцами, фамилии которых начинаются с S?
211 Сколько песен было исполнено певцами, фамилии которых состоят из шести букв?
211 Сколько песен прозвучало после 15 июня 2005 г.?
211 Сколько песен прозвучало до 2009 г.?
211 Сколько было исполнено песен, длящихся ровно четыре минуты?
211 Сколько песен, длящихся ровно четыре минуты, было исполнено Брюсом Спрингстином?
212 Сколько песен, длящихся от трех до четырех минут, было исполнено Мадонной?
212 Как подсчитать в диапазоне количество ячеек, содержащих числа?
212 Как подсчитать количество пустых ячеек в диапазоне?
212 Как подсчитать количество непустых ячеек в диапазоне?
Глава 21. Функции СУММЕСЛИ, СРЗНАЧЕСЛИ, СУММЕСЛИМН, СРЗНАЧЕСЛИМН,
МАКСЕСЛИ и МИНЕСЛИ
217 Каков объем продаж в долларах для каждого продавца?
217 Сколько единиц товара было возвращено?
218 Каков объем продаж в долларах начиная с 2005 г.?
218 Сколько штук блеска для губ было продано? Какова выручка от продажи блеска для губ?
219 Каков объем продаж в долларах для всех продавцов, за исключением Джен?
219 Каково среднее количество единиц проданного товара по всем сделкам, совершенным конкретным продавцом?
219 Каков объем продаж помады в долларах у Джен?
219 Каково среднее количество проданной помады (в единицах товара) по всем продажам, совершенным Зарет?
219 Каково среднее количество проданной помады (в единицах товара) по всем сделкам, совершенным Зарет, для сделок по крайней мере с 50 единицами товара?
219 Каков объем продаж помады в долларах повсем сделкам, совершенным конкретным продавцом, для
сделок на сумму свыше $100? Каков объем продаж в долларах для сделок на сумму менее $100?
220 Может ли Excel искать максимумы и минимумы по условию?

928

Список вопросов
Глава 22. Функция СМЕЩ

224 Как создать ссылку на диапазон ячеек, который отстоит от ячейки или другого диапазона на заданное количество строк и столбцов?
225 Как можно выполнить операцию поиска при помощи крайнего правого столбца таблицы вместо
крайнего левого?
226 Я часто скачиваю данные о продажах программных продуктов, сгруппированные по странам/регионам. Я должен отслеживать для Ирана выручку, затраты и количество проданных программных продуктов, но данные по Ирану не всегда находятся в одной и той же части листа. Можно ли
создать формулу, в которой выручка, затраты и количество проданных программных продуктов
выбираются всегда правильно?
227 Каждый разрабатываемый компанией препарат проходит три этапа разработки. У меня есть список затрат по месяцам на каждый препарат, и я знаю продолжительность в месяцах каждого этапа
разработки. Можно ли создать формулу, вычисляющую общие затраты для каждого препарата на
каждом этапе разработки?
228 Я владелец небольшого видеопроката. На рабочем листе мой бухгалтер указал названия всех
фильмов и количество копий на складе. К сожалению, он объединил информацию для каждого
фильма в одной ячейке. Как мне переписать данные о количестве копий на складе для каждого
фильма в отдельную ячейку?
230 Как работает в Excel инструмент Вычислить формулу?
231 Как написать формулу, всегда возвращающую последнее число в столбце?
231 Как создать диапазон, автоматически включающий новые данные?
233 Я ежемесячно составляю диаграммы по объемам продаж в штуках для продукта компании. Каждый месяц я загружаю новые данные. Хорошо бы диаграммы обновлялись автоматически. Есть
ли простой способ добиться этого?
Глава 23. Функция ДВССЫЛ
239 Мои формулы на листе часто содержат ссылки на ячейки, или диапазоны ячеек, или на то и другое. Вместо замены ссылок в формулах можно ли поместить эти ссылки в собственные ячейки
и быстро заменять в них ссылки без изменения базовых формул?
240 На каждом листе книги в ячейке D1 записываются ежемесячные продажи продукта. Можно
ли написать и скопировать формулу для записи продаж продукта за каждый месяц на одном
листе?
241 Предположим, что я суммирую значения в диапазоне A5:A10 по формуле =СУММ(A5:A10).
Если я вставлю пустую строку где-либо между строками 5 и 10, моя формула будет автоматически обновлена до =СУММ(A5:A11). Каким образом следует составить формулу , которая при
вставке пустой строки между строками 5 и 10 по-прежнему суммировала бы стоимости в исходном диапазоне A5:A10?
243 Как с помощью функции ДВССЫЛ обеспечить интерпретацию части формулы в качестве имени
диапазона?
244 Книга содержит продажи по каждому продукту компании в разных странах и регионах, и каждый
континент отображен на отдельном листе. Как объединить эти данные на одном листе?
245 Как составить список всех листов в книге?
246 Моя книга содержит множество листов. Можно ли легко составить оглавление с гиперссылками
так, чтобы была связь со всеми листами в книге?
Глава 24. Условное форматирование
251 Как можно визуально отобразить, связаны ли последние температурные данные с глобальным
потеплением?

Список вопросов

929

253 Как работают правила выделения ячеек в условном форматировании?
254 Как можно проверить и настроить созданные правила?
256 Как работают гистограммы?
259 Как работают цветовые шкалы?
261 Как работают наборы значков?
264 Как применить цветовой код к ежемесячной доходности акций для отображения каждого удачного месяца одним цветом, а каждого неудачного — другим?
267 При поступлении данных о ежеквартальных доходах корпорации как можно выделить одним
цветом кварталы, в которых доходы увеличились по сравнению с предыдущим кварталом, и другим цветом кварталы, в которых доходы снизились по сравнению с предыдущим кварталом?
270 Как в заданном списке дат выделить цветом даты, приходящиеся на выходные дни?
272 Наш тренер по баскетболу присвоил каждому игроку рейтинг от 1 до 10 на основе способностей
игрока к игре в защите, нападении или в качестве центрового. Можно ли создать лист, визуально
демонстрирующий способность каждого игрока играть на позиции, на которую его поставили?
273 Для чего нужны флажки «Остановить, если истина» (Stop If True) в диалоговом окне «Управление правилами» (Manage Rules)?
275 Как с помощью инструмента Формат по образцу скопировать условный формат?
Глава 25. Сортировка в Excel
281 Как можно отсортировать данные торговых сделок сначала по продавцам, потом по продуктам,
по количеству проданных единиц товара и в хронологическом порядке от самых старых до самых
новых?
285 Мне всегда хотелось отсортировать данные на основе цвета ячеек или цвета шрифта. Возможно
ли это в Excel 2016?
286 Мне нравятся большие наборы значков, описанные в главе 24. Можно ли отсортировать данные
на основе значков в ячейке?
286 На листе имеется столбец, в котором указан месяц для каждой продажи. При сортировке по этому столбцу я получаю первым или первый месяц по алфавиту, или последний. Как можно отсортировать данные по этому столбцу в хронологическом порядке, то есть сначала получить сделки
за январь, затем за февраль и т. д.?
287 Можно ли отсортировать данные без диалогового окна Сортировка (Sort)?
288 Мне часто требуется напечатать список городов, в которых моя компания имеет служебные подразделения. Имеется ли возможность создать свой список, а потом при вводе только первого
города из списка и перетаскивании курсора вниз автоматически заполнить ячейки остальными
городами из этого списка?
Глава 26. Таблицы
291 Я указал на листе количество проданных единиц товара и общую выручку для каждого продавца,
и теперь легко могу вычислить среднюю цену единицы товара для каждого продавца. Как создать
формат, который при вводе новых данных копировался бы автоматически? Кроме того, существует ли простой способ автоматически скопировать формулы при добавлении новых данных?
296 Я ввел в книгу цены на природный газ за несколько лет и создал подходящую линейную диаграмму, отображающую ежемесячное изменение цен. Можно ли добиться, чтобы при добавлении
новой информации о ценах диаграмма обновлялась автоматически?
297 Для каждой торговой сделки указаны продавец, дата, продукт , место продажи и объем продажи. Можно ли подсчитать, например, общий объем продаж помады на Востоке для Джен или
Коллин?

930

Список вопросов

300 Как срезы (добавлены в Microsoft Excel 2013) позволяют выполнить срез данных в таблице
Excel?
302 Как сослаться на фрагмент таблицы в других частях листа?
304 Применяются ли условные форматы автоматически к новым данным, добавляемым в таблицу?
Глава 27. Счетчики, полосы прокрутки, переключатели, флажки, группы и поля
со списками
308 Мне необходимо запустить анализ чувствительности с множеством ключевых исходных данных, таких как объем продаж за первый год, годовой рост продаж, цена реализации в первый год
и себестоимость единицы товара. Каким образом можно быстро изменить эти исходные данные
и сразу отследить влияние такого изменения, например, на расчет ЧПС?
313 Как создать простой флажок, с помощью которого можно было бы включать и отключать условное форматирование?
316 Как создать лист, который позволит персоналу, занятому в цепочке поставок, одним нажатием
кнопки назначить высокую, низкую или среднюю цену продукта?
317 Как предоставить пользователю простой способ ввода дня недели без необходимости набирать
какой-либо текст?
Глава 28. Революция в аналитике
320 Что такое аналитика?
320 Что такое прогнозная аналитика?
321 Что такое предписывающая аналитика?
322 Почему значение аналитики возрастает?
322 Насколько важна аналитика для вашей организации?
323 Что необходимо знать для проведения анализа?
323 Какие трудности могут возникнуть при осуществлении анализа?
325 Какие тенденции будут влиять на развитие аналитики?
Глава 30. Поиск решения при определении оптимального ассортимента
продукции
331 Как определить ежемесячный ассортимент продукции, максимизирущий прибыльность?
340 Всегда ли модель поиска решения имеет решение?
341 Что означает выдаваемый моделью поиска решения ответ «Значения ячейки целевой функции
не сходятся»?
Глава 31. Поиск решения при планировании расписания работы сотрудников
344 Каким спланировать рабочее расписание сотрудников для удовлетворения потребности в рабочей силе?
Глава 32. Поиск решения для задач транспортировки и распределения
349 Как фармацевтическая компания может определить, где следует производить препараты и откуда их лучше отгружать заказчикам?
Глава 33. Поиск решения для бюджетирования капиталовложений
355 Как с помощью инструмента Поиск решения компания может определить, какой из проектов ей
следует принять к реализации?

Список вопросов

931

Глава 34. Поиск решения при финансовом планировании
364 Можно ли с помощью инструмента Поиск решения проверить точность функции ПЛТ или определить ипотечные платежи с плавающей процентной ставкой?
366 Можно ли с помощью инструмента Поиск решения определить, сколько денег нужно отложить
до выхода на пенсию?
Глава 35. Поиск решения при оценке спортивных команд
371 Как можно с помощью Excel распределить очки для команд НФЛ?
Глава 36. Расположение складов по методу ОПГ с несколькими начальными
точками и согласно эволюционному поиску решения
381 В каком месте в США транспортная интернет-компания должна расположить единственный
склад для минимизации суммарной протяженности транспортировки пакетов?
383 В каком месте в США транспортная интернет-компания должна расположить два склада для
минимизации суммарной протяженности транспортировки пакетов?
Глава 37. Штрафы и эволюционный поиск решения
386 Что является ключом к успешному использованию эволюционного поиска решения?
387 Каким образом с помощью эволюционного поиска решения можно распределить 80 сотрудников
финансового отдела Microsoft по четырем рабочим группам?
Глава 38. Задача коммивояжера
393 Как с помощью Excel решать задачи упорядочения?
394 Как с помощью Excel решить задачу коммивояжера?
Глава 39. Импорт данных из текстового файла или документа
398 Как импортировать данные из текстового файла в Excel для анализа?
Глава 40. Инструмент Получить и преобразовать данные
405 Как загрузить актуальный курс биткойна и сделать так, чтобы эти данные обновлялись каждый
день?
409 Как загрузить цифры текущего населения городов США?
Глава 41. Типы данных «Акции» и «География»
411 Какие географические сведения можно использовать в формулах Excel?
414 Какие показатели деятельности корпораций можно использовать в формулах Excel?
Глава 42. Проверка достоверности данных
416 Я ввожу результаты профессиональных баскетбольных матчей в Excel. Я знаю, что команда набирает от 50 до 200 очков за игру . Один раз я ввел 1000 очков вместо 100, что привело к неправильным результатам анализа. Существует ли в Excel способ предотвращения ошибок такого
типа?
418 Я ввожу даты и суммы деловых расходов на следующий год. В начале года я часто по ошибке ввожу в поле даты предыдущий год. Могут ли настройки Excel предотвратить ошибки такого типа?
419 Я ввожу длинный список чисел. Могу ли я получить в Excel предупреждение, если введу нечисловое значение?

932

Список вопросов

420 Мой помощник при вводе многочисленных торговых сделок должен вводить сокращенные названия штатов. Можно ли создать список сокращенных названий штатов для сведения к минимуму ошибок ввода неправильных сокращений?
Глава 43. Обобщение данных на гистограммах и диаграммах Парето
425 Говорят, одна картина стоит тысячи слов. Как с помощью Excel можно создать изображение (называемое гистограммой), которое обобщает значения в наборе данных?
432 Каковы самые распространенные типы гистограмм?
434 Что можно узнать, сравнивая гистограммы для разных наборов данных?
435 Как создать диаграмму Парето?
Глава 44. Обобщение данных с помощью описательной статистики
440 Как определяется типичное значение набора данных?
444 Как измерить, насколько набор данных отклонился от своего типичного значения?
445 Как среднее значение и стандартное отклонение характеризуют набор данных?
447 Как с помощью описательной статистики сравнить наборы данных?
447 Как для заданной точки данных можно найти величину ее процентиля в наборе данных? Например, как найти девяностый процентиль набора данных?
449 Как найти второе наибольшее или второе наименьшее число в наборе данных?
450 Как можно ранжировать числа в наборе данных?
450 Что такое урезанное среднее набора данных?
451 Существует ли быстрый способ получить для выбранного диапазона ячеек различные статистики, описывающие данные в этих ячейках?
451 Почему финансовые аналитики часто определяют средний доход по акциям с помощью среднего
геометрического?
453 Как использовать ящики с усами (boxplots) для характеристики и сравнения наборов данных?
Глава 45. Сводные таблицы и срезы для описания данных
461 Что такое сводная таблица?
462 Как с помощью сводной таблицы обобщить данные о продажах товаров в нескольких продуктовых магазинах?
466 Какие макеты сводных таблиц доступны в Microsoft Excel 2019?
467 Почему сводные таблицы называются сводными?
468 Как быстро изменить формат в сводной таблице?
468 Как свернуть и развернуть поля?
469 Как сортировать и фильтровать поля сводной таблицы?
473 Как обобщить данные в сводной таблице с помощью сводной диаграммы?
474 Для чего предназначена область ФИЛЬТРЫ в сводной таблице?
474 Как работают срезы сводной таблицы?
475 Как добавить пустые строки или скрыть промежуточные итоги в сводной таблице?
476 Как применить к сводной таблице Условное форматирование?
477 Как обновить вычисления при добавлении новых данных?

Список вопросов

933

478 Я работаю в небольшой турфирме и должен разослать проспект о ней потенциальным клиентам. Мой бюджет ограничен, поэтому послать проспект необходимо тем людям, которые больше
остальных тратят денег на путешествия. У меня есть случайная выборка из 925 человек, о которых известна следующая информация: возраст, пол и количество денег, потраченных на путешествия за прошлый год. Как с помощью этих данных определить влияние пола и возраста на расходы на путешествия? Какие выводы можно сделать о типе потенциального клиента, которому
следует отправить проспект по почте?
483 Я провожу маркетинговое исследование автомобилей-универсалов. Мне необходимо определить, какие факторы влияют на вероятность покупки семьей автомобиля-универсала. У меня
есть большая выборка семей с информацией об их размере (большая или нет) и доходе (высокий
или низкий). Как определить влияние размера семьи и семейного дохода на вероятность покупки
автомобиля-универсала?
485 Я работаю в компании, продающей микрочипы по всему миру. Ежемесячно я получаю данные
о фактических и прогнозируемых объемах продаж чипа 1, чипа 2 и чипа 3 в Канаде, Франции
и США. Я также получаю расхождение, или разницу , между фактической выручкой и выручкой, заложенной в бюджет. Для каждого месяца и каждой комбинации страны и продукта мне
нужно отобразить следующие данные: фактическая выручка, выручка, заложенная в бюджет ,
фактическое расхождение, фактическая выручка как процент от годового дохода и расхождение как процент от выручки, заложенной в бюджет . Каким образом можно отобразить эту информацию?
488 Что такое вычисляемое поле?
490 Что использовать: фильтр отчета или срез?
491 Как сгруппировать элементы в сводной таблице?
492 Что такое вычисляемый объект?
494 Что такое детализация?
494 Мне часто приходится использовать конкретные данные в сводной таблице для вычисления прибыли, например апрельских продаж чипа 1 во Франции. К сожалению, при добавлении новых
данных в сводную таблицу эти перемещаются. Существует ли в Excel функция, позволяющая
всегда извлекать из сводной таблицы объем апрельских продаж чипа 1 во Франции?
497 Как применить временную шкалу для обобщения данных за разные периоды времени?
498 Как с помощью сводной таблицы получить нарастающий итог общего объема продаж для каждого периода года?
499 Как с помощью сводной таблицы сравнить объем продаж за месяц с объемом продаж за тот же
месяц предыдущего года?
500 Как создать сводную таблицу на основе данных из нескольких местоположений?
503 Как создать сводную таблицу на основе уже имеющейся сводной таблицы?
504 Как использовать фильтр отчета для создания нескольких сводных таблиц?
505 Как быстро изменить настройки для сводной таблицы по умолчанию?
Глава 46. Модель данных
509 Что представляет собой инструмент Модель данных и зачем он нужен?
510 Как добавить данные в модель данных?
511 Как удалить данные из модели данных?
511 Как создать связь в модели данных?
512 Как с помощью модели данных создать сводную таблицу?
513 Как добавить новые данные в модель данных?

934

Список вопросов

513 Как с помощью модели данных создать новую сводную таблицу?
514 Как изменять и удалять связи?
514 Как работает функция Число различных элементов (DISTINCT COUNT)?
Глава 47. Power Pivot
518 Как загрузить данные в Power Pivot?
522 Как с помощью Power Pivot создать сводную таблицу?
523 Как использовать срезы с Power Pivot?
524 Что такое функции DAX и вычисляемые столбцы?
525 Как работает функция RELATED?
530 Как работает функция CALCULATE и что такое вычисляемая мера?
Глава 48. 2D-картограммы и 3D-карты Power Map
532 Как создать двумерную картограмму?
536 Как создать 3D-карту Power Map?
538 Как применить фильтр к карте Power Map?
538 Как изменить способ отображения данных на карте Power Map?
539 Как с помощью временной шкалы анимировать карту Power Map?
541 Можно ли обобщить данные с карты Power Map двумерной диаграммой?
542 Как создать карту Power Map, содержащую круговые диаграммы с подписями?
542 Как убедиться, что на карте Power Map правильно отображены геоточки?
Глава 49. Спарклайны
544 Как графически отобразить ежедневные расчеты с клиентами для каждого филиала банка в одной ячейке?
545 Как изменять спарклайны?
547 Как обобщить серию из побед и поражений команд НФЛ в одной ячейке?
548 Обновляются ли спарклайны автоматически при добавлении новых данных?
Глава 50. Обработка данных с помощью статистических функций
для баз данных
551 На какую сумму продала блеск для губ Джен?
552 Каково среднее количество проданной помады для каждой сделки Джен в регионе Восток?
552 На какую общую сумму было продано косметики либо продавцом Эмили, либо в регионе Восток?
552 На какую сумму продали помаду Коллин и Зарет в регионе Восток?
552 Сколько сделок с помадой было совершено не в регионе Восток?
553 На какую сумму продала помаду Джен в 2004 г.?
553 Сколько единиц косметики было продано по цене не менее $3,20?
554 Какова общая сумма выручки для каждого косметического товара, реализованного каждым продавцом?
555 Какие приемы применяются при создании диапазона условий?

Список вопросов

935

555 У меня есть база со следующими данными для каждой сделки: выручка, дата продажи и идентификационный код продукта. Как быстро извлечь сумму выручки для сделки по заданной дате
продажи и идентификационному коду?
Глава 51. Фильтрация данных и удаление дубликатов
560 Как определить все сделки Джен по продаже помады в регионе Восток?
561 Как определить все сделки Кики и Коллин по продаже помады и туши в регионе Восток или Юг?
562 Как скопировать все сделки Кики и Коллин по продаже помады и туши в регионе Восток или Юг
на другой лист?
562 Как очистить фильтры в столбце или базе данных?
562 Как определить все сделки по продаже более 90 единиц продукции и более чем на $280?
564 Как определить все сделки, заключенные в 2005 или 2006 г.?
566 Как определить все сделки, заключенные в последние три месяца 2005 г . и в первые три месяца
2006 г.?
566 Как определить все сделки, заключенные продавцами, имена которых начинаются с C?
567 Как определить все сделки, для которых ячейка с названием продукта окрашена в красный цвет?
567 Как определить все сделки среди 30 сделок с максимальной выручкой, в которых продавцами
были Халлаган или Джен?
568 Как быстро получить полный список продавцов?
569 Как просмотреть все комбинации «продавец — продукт — регион», встречающиеся в базе данных?
570 Если данные изменились, как повторно применить тот же самый фильтр?
570 Как извлечь все сделки по продаже основы под макияж, заключенные Эмили и Джен за первые
шесть месяцев 2005 г., в которых средняя цена единицы продукции составила больше $3,20?
Глава 52. Консолидация данных
573 Компания продает продукцию в нескольких регионах США. В каждом регионе хранятся записи
о количестве проданных единиц продукции в январе, феврале и марте. Существует ли простой
способ создания мастер-книги, в которой постоянно объединяются продажи для всех регионов
и проводится подсчет общей суммы выручки для каждого продукта, проданного в США в течение каждого месяца?
Глава 53. Создание промежуточных итогов
578 Существует ли быстрый способ настроить лист для вычисления общей выручки и количества
проданных единиц продукции по регионам?
581 Как можно при этом получить разбивку продаж по продавцам в каждом регионе?
Глава 54. Приемы работы с диаграммами
584 Как создать комбинированную диаграмму?
586 Как создать вспомогательную ось?
587 Как обработать недостающие данные?
588 Как показать скрытые данные на диаграмме?
589 Как с помощью картинок сделать гистограмму интереснее?
591 Я отобразил данные о ежегодных продажах в виде гистограммы, но годы как метки столбиков не
отображаются. Где ошибка?
592 Как включить метки данных и таблицу данных в диаграмму?

936

Список вопросов

593 Как поместить в диаграмму метки данных на основе содержимого ячеек?
594 Как отследить эффективность отдела сбыта по продажам за определенный период?
596 Как создать ленточную диаграмму для проверки наличия запасов?
597 Как сохранить диаграмму в качестве шаблона?
597 Как с помощью диаграммы «термометр» отобразить прогресс?
598 Как создать на диаграмме динамические метки?
600 Как с помощью флажков указать, какие ряды данных требуется отобразить на диаграмме?
601 Как с помощью списка обеспечить выбор ряда данных для отображения на диаграмме?
602 Как создать диаграмму Ганта?
603 Как создать диаграмму на основе отсортированных данных?
604 Как создать гистограмму, которая при добавлении новых данных обновлялась бы автоматически?
605 Как добавить условные цвета в диаграмму?
606 Как с помощью диаграммы «водопад» отследить приближение объемов продаж к плану или разложить компоненты продажной цены?
608 Как с помощью функции ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ и таблицы Excel создать динамические информационные панели?
611 Как вставить в диаграмму вертикальную линию для разделения производительности до и после
слияния?
611 Как с помощью лепестковой диаграммы отобразить различия баскетболистов в силе, скорости
и прыгучести?
612 Известно, что изменение двух переменных можно представить с помощью точечной диаграммы.
А как представить изменение трех переменных с помощью пузырьковой диаграммы?
613 Как создать диаграмму «водопад»?
616 Как используются для обобщения иерархических данных диаграммы «дерево» и «солнечные
лучи»?
619 Что такое диаграмма типа «воронка»?
619 Как отразить в диаграмме свежую динамику по интересующим меня акциям?
Глава 55. Оценка линейных зависимостей
627 Как определить зависимость между ежемесячным производством и ежемесячными эксплуатационными расходами?
630 Насколько точно эта зависимость объясняет ежемесячные колебания эксплуатационных расходов предприятия?
630 Насколько точны мои прогнозы?
631 Какие функции при оценке линейной зависимости позволяют получить угловой коэффициент
и начальную ординату прямой, точнее всего соответствующие данным?
Глава 56. Моделирование экспоненциального роста
635 Как моделировать рост доходов компании с течением времени?
Глава 57. Степенная кривая
640 Моя компания наращивает производство. Можно ли смоделировать зависимость между количеством произведенной продукции и временем, необходимым для производства одной единицы
продукции?

Список вопросов

937

Глава 58. Представление зависимостей с помощью корреляции
647 Каким образом связаны ежемесячные доходы от акций Microsoft, GE, Intel, GM и Cisco?
Глава 59. Введение во множественную регрессию
652 Завод выпускает три продукта. Как спрогнозировать эксплуатационные расходы завода на основе количества произведенной продукции?
657 Насколько точны мои прогнозы ежемесячных расходов на основе количества произведенной
продукции?
657 Множественную регрессию можно запустить командой Анализ данных. Существует ли способ
запустить регрессионный анализ без этой команды и поместить резуль таты регрессии на тот же
лист, где находятся данные?
Глава 60. Включение качественных факторов во множественную регрессию
659 Как предсказать квартальные продажи автомобилей в США?
664 Как предсказать президентские выборы в США?
668 Какая функция Excel позволяет составить прогноз по уравнению множественной регрессии?
Глава 61. Моделирование нелинейных характеристик и взаимосвязей
670 Когда говорят, что независимая переменная оказывает нелинейное воздействие на зависимую
переменную, что это означает?
671 Когда говорят, что между воздействиями двух независимых переменных на зависимую переменную существует взаимосвязь, что это означает?
671 Как выполнить проверку на наличие нелинейности и взаимосвязи в регрессии?
Глава 62. Однофакторный дисперсионный анализ
679 Владелец издательства, публикующего компьютерную литературу, хочет знать, влияет ли на продажи местоположение стенда с книгами в отделе компьютерной литературы в книжных магазинах. В частности, имеет ли значение, в какой зоне отдела компьютерной литературы (передней,
задней или средней) находится стенд с книгами?
681 Если я определяю, имеют ли популяции значимо различные средние значения, почему метод называется дисперсионным анализом?
682 Как применить результаты однофакторного дисперсионного анализа для прогнозирования?
Глава 63. Рандомизированные блоки и двухфакторный дисперсионный анализ
685 Я пытаюсь проанализировать эффективность отдела продаж. Проблема в том, что кроме эффективности самого торгового представителя сумма его продаж зависит от региона, в который он
назначен. Как можно включить в анализ распределение продавцов по регионам?
687 Как предсказать объем продаж на основе информации о торговых представителях и регионах?
Насколько точными окажутся прогнозы?
688 Как определить, влияют ли на продажи видеоигр изменение цены и расходов на рекламу? Как
определить, значимо ли взаимодействие цены и рекламы?
690 Как интерпретировать влияние цены и рекламы на продажи при отсутствии значимого взаимодействия между ценой и рекламой?
Глава 64. Скользящие средние для временных рядов
694 Я пытаюсь проанализировать тенденцию роста ежеквартальных доходов Amazon.com с 1996 г .
Объем продаж в четвертом квартале в США обычно больше (из-за Рождества), чем объем про-

938

Список вопросов
даж в первом квартале следующего года. Эта закономерность затемняет тенденцию к росту продаж. Как отобразить тенденцию к росту доходов графически?
Глава 66. Метод прогнозирования «по отношению
к скользящему среднему»

705 Что такое тренд временного ряда?
706 Как определить индексы сезонности для временного ряда?
706 Существует ли простой способ включить тренд и сезонность в прогнозирование будущих продаж
продукта?
Глава 67. Прогноз для особых случаев
709 Как определить, влияют ли конкретные факторы на поток клиентов?
713 Как оценить точность прогноза?
716 Как проверить, являются ли ошибки прогноза случайными?
Глава 68. Введение в теорию вероятности
718 Что такое эксперимент, выборочное пространство и событие?
719 Каковы аксиомы, которым должны удовлетворять вероятности наступления событий?
719 Что такое правило дополнений?
720 Что такое взаимоисключающие события?
720 Что такое правило сложения вероятностей?
721 Что такое независимые события?
722 Что такое условная вероятность?
722 Что такое формула полной вероятности?
723 Что такое теорема Байеса?
Глава 69. Введение в случайные величины
728 Что такое случайная величина?
728 Что такое дискретная случайная величина?
729 Что такое среднее, дисперсия и стандартное отклонение случайной величины?
730 Что такое непрерывная случайная величина?
730 Что такое функция плотности вероятности?
731 Что такое независимые случайные величины?
Глава 70. Биномиальные, гипергеометрические и отрицательные
биномиальные случайные величины
734 Что такое биномиальная случайная величина?
735 Как с помощью функции БИНОМ.РАСП и БИНОМ.РАСП.ДИАП вычислить вероятности биномиального распределения?
736 Если одинаковое количество людей предпочитает кока-колу пепси-коле и наоборот , и у 100 человек спросили, предпочитают ли они кока-колу пепси-коле, какова вероятность того, что ровно
60 человек предпочитают кока-колу пепси-коле, и вероятность того, что от 40 до 60 человек предпочитают кока-колу пепси-коле?

Список вопросов

939

736 Из всех лифтовых направляющих, производимых компанией, 3% считаются дефектными. Компания собирается отгрузить клиенту партию из 10 000 направляющих. Перед приемкой партии
клиент случайным образом отбирает 100 направляющих и проверяет на наличие дефектов. Если
дефекты обнаружатся не более чем у двух направляющих, клиент примет партию. Как определить вероятность приемки партии?
737 Авиакомпаниям не нравятся рейсы с незанятыми местами. Предположим, что в среднем 95% всех
купивших билет регистрируются на рейс. Если авиакомпания продает 105 билетов на 100-местный рейс, какова вероятность того, что произойдет избыточное бронирование рейса?
737 В кафе Village Deli ежедневно приходит на ланч 1000 клиентов. В среднем 20% клиентов заказывают особый вегетарианский сэндвич. Эти сэндвичи готовят заранее. Сколько сэндвичей необходимо приготовить, если вероятность их нехватки должна быть равна 5%?
738 Что такое гипергеометрическая случайная величина?
739 Что такое отрицательная биномиальная случайная величина?
Глава 71. Пуассоновская и экспоненциальная случайные величины
742 Что такое пуассоновская случайная величина?
743 Как вычислить распределение пуассоновской случайной величины?
744 Если количество клиентов, обращающихся в банк, описывается пуассоновской случайной величиной, какая случайная величина определяет время между обращениями?
Глава 72. Нормальная случайная величина и Z-оценка
747 Каковы свойства нормальной случайной величины?
750 Как в Excel найти распределение нормальной случайной величины?
751 Как в Excel найти процентили для нормальных случайных величин?
752 Почему нормальная случайная величина соответствует многим реальным ситуациям?
754 Что такое Z-оценка?
Глава 73. Распределение Вейбулла и бета-распределение: моделирование
надежности механизмов и продолжительности работы
758 Как оценить вероятность безотказной работы станка в течение не менее 20 часов?
761 Как оценить вероятность того, что продолжительность работ по монтажу перегородки из гипсокартона в здании составит более 200 часов?
Глава 74. Создание вероятностных высказываний на основе прогнозов
765 На основании чего вычисляются прогнозы?
766 Фармацевтическая компания планирует продать в следующем году 60 млн единиц препарата. Какова вероятность того, что в следующем году будет продано более 65 млн единиц этого препарата?
Глава 75. Логарифмически нормальная случайная величина в моделировании
курса акций
768 Что такое логарифмически нормальная случайная величина?
769 По какой причине курс акций ведет себя подобно случайной величине с логарифмически нормальным распределением?
769 Как смоделировать будущий курс любых акций как логарифмически нормальную случайную величину?

940

Список вопросов

771 Как вычислить вероятность того, что курс акций Microsoft превысит $130 через шесть месяцев?
771 Как вычислить вероятность того, что курс акций Microsoft не превысит $90 через шесть месяцев?
771 Как вычислить средний курс акций Microsoft через шесть месяцев?
Глава 76. Импорт в Excel истории торгов (загрузка биржевых данных)
773 Как просто импортировать ретроспективные биржевые данные в Excel?
775 Как рассчитать годовую доходность по моему портфелю акций?
Глава 77. Введение в моделирование по методу Монте-Карло
777 Где применяется моделирование по методу Монте-Карло?
778 Что происходит при вводе в ячейку формулы =СЛЧИС()?
779 Как моделируют значения дискретной случайной величины?
780 Как моделируют значения нормальной случайной величины?
781 Как компания — производитель поздравительных открыток может определить, сколько открыток следует произвести?
Глава 78. Вычисление оптимальной цены предложения
788 Как смоделировать случайную величину с биномиальным распределением?
789 Как определить, должна ли непрерывная случайная величина моделироваться как нормальная
случайная величина?
790 Как с помощью моделирования определить оптимальную тендерную заявку для проекта строительства?
Глава 79. Моделирование цен на акции и распределения средств
между активами
795 Я недавно купил 100 акций компании GE. Какова вероятность того, что в течение следующего
года эта инвестиция принесет доход более 10%?
798 Я пытаюсь распределить свой инвестиционный портфель между акциями, казначейскими векселями и облигациями. Какое распределение средств между активами в рамках пятилетнего горизонта планирования принесет ожидаемый доход не менее 8% и минимизирует риск?
Глава 80. Развлечения и игры: моделирование вероятностей для азартных игр
и спортивных соревнований
804 Какова вероятность выиграть в крэпс?
806 Какова вероятность получить «тройку» в пятикарточном дро-покере?
808 Какова вероятность выигрыша в Финале Четырех 2018 г . для каждой баскетбольной команды
Национальной студенческой спортивной ассоциации?
Глава 81. Анализ данных с помощью повторной выборки
813 Девять партий продукции производятся при высокой температуре, а семь партий — при низкой.
Какова вероятность того, что выход продукта выше при высокой температуре?
Глава 82. Ценообразование опционов
818 Что такое колл-опцион и пут-опцион?
819 В чем разница между американским и европейским опционами?

Список вопросов

941

819 Как выглядят выигрыши по европейским колл- и пут-опционам, если рассматривать их как
функцию курса акций на дату исполнения?
820 Какими параметрами определяется цена опциона?
821 Как оценить волатильность акций на основе исторических данных?
822 Как реализовать в Excel формулу Блэка — Шоулза?
824 Как изменение ключевых параметров изменяет цену колл- и пут-опционов?
825 Как оценить волатильность акций по формуле Блэка — Шоулза?
826 В мои точные формулы ценообразования опционов никто не должен вносить изменения. Как
защитить формулы на листе от изменений?
828 Как с помощью ценообразования опционов компания может принимать лучшие инвестиционные решения?
Глава 83. Определение потребительской ценности
833 Компания, работающая с кредитными картами, в настоящее время имеет коэффициент удержания клиентов, равный 80. Насколько возрастет прибыльность компании, если коэффициент
удержания клиентов повысится до 90% и выше?
835 Междугородная телефонная компания предоставляет клиентам конкурентов бонус при смене
компании. Насколько значительным должен быть бонус?
Глава 84. Оптимальный размер заказа в модели управления запасами
839 Магазин электроники продает 10 000 смартфонов в год. Каждый раз при закупке смартфонов магазин несет расходы в размере $10 за закупку. Магазин платит $100 за каждый смартфон, и стоимость хранения смартфона на складе в течение года составляет $20. Когда магазин закупает
смартфоны, какого размера должна быть закупка?
841 Завод производит 10 000 серверов в год. Себестоимость производства каждого сервера составляет $2000. Стоимость запуска производства партии серверов составляет $200, а стоимость хранения сервера на складе в течение года — $500. При необходимости завод может производить
25 000 серверов в год. Каким должен быть размер партии при производстве серверов?
Глава 85. Построение моделей управления запасами
для неопределенного спроса
845 При каком уровне запасов следует делать закупку , если необходимо минимизировать годовые
затраты, связанные с дефицитом, хранением и закупками?
847 Что означает термин «95%-ный уровень обслуживания»?
Глава 86. Теория массового обслуживания (теория очередей)
851 Какие факторы влияют на длину очереди и время, проведенное клиентами в очереди?
852 Какие условия должны выполняться, чтобы можно было анализировать среднее количество присутствующих клиентов или среднее время, проведенное клиентом в очереди?
853 Почему изменчивость снижает производительность системы очередей?
854 Можно ли быстро определить среднее время прохождения через систему контроля безопасности
в аэропорту или среднее время ожидания в очереди в банке?
Глава 87. Оценка кривой спроса
858 Что необходимо знать при назначении цены продукта?
859 Что такое эластичность спроса?

942

Список вопросов

859 Существует ли простой способ оценить кривую спроса?
862 Каким образом кривая спроса показывает готовность покупателя платить за продукт?
Глава 88. Ценообразование продуктов с сопутствующими товарами
863 Как покупка клиентами вместе с бритвенным станком лезвий способствует установлению максимально увеличивающей прибыль цены на бритву?
Глава 89. Ценообразование продуктов с помощью субъективно определяемого
спроса
868 Иногда ценовая эластичность продукта неизвестна. Или невозможно определить, какая из кривых спроса, линейная или степенная, является релевантной. Можно ли все равно оценить кривую спроса и воспользоваться инструментом Поиск решения, чтобы определить цену , максимизирующую прибыль?
869 Как небольшой аптеке определить цену на помаду, максимизирующую прибыль?
Глава 90. Нелинейное ценообразование
874 Что такое линейное ценообразование?
874 Что такое нелинейное ценообразование?
876 Что такое объединение в набор и как оно может повысить прибыльность?
877 Как составить план нелинейного ценообразования с максимальной прибылью?
Глава 91. Формулы массива и функции, возвращающие массив
884 Что такое формула массива?
885 Как интерпретировать формулы, такие как =(D2:D7)*(E2:E7) и =СУММ(D2:D7*E2:E7)?
886 Имеется список имен в столбце. Имена в списке часто меняются. Существует ли простой способ
перенести имена в одну строку так, чтобы изменения в исходном столбце отражались бы в этой
новой строке?
886 Имеется список ежемесячных доходов по акциям. Существует ли способ определить количество
значений доходов, попадающих в интервалы от –30 до –20%, от –10 до 0% и т. д., которые обновлялись бы автоматически при изменении исходных данных?
888 Как написать формулу, суммирующую вторые цифры из списка целых чисел?
889 Существует ли способ просмотра двух списков имен и поиска имен, встречающихся в обоих списках?
890 Как написать формулу, вычисляющую среднее значение для чисел в списке, которые больше или
равны медиане списка?
890 У небольшой компании декоративной косметики имеется база данных по продажам, в которой
указан продавец, количество проданных единиц продукции и сумма в долларах для каждой
сделки. Мне известно, что для обобщения этих данных подойдут статистические функции или
функции СЧЁТЕСЛИМН (COUNTIFS), СУММЕСЛИМН (SUMIFS) и СРЗНА ЧЕСЛИМН
(AVERAGEIFS). Но могу ли я использовать также функции, возвращающие массив, чтобы обобщить эти данные и ответить на вопросы типа: сколько единиц косметики продал продавец, или
сколько помады было продано, или сколько единиц косметики было продано определенным продавцом?
894 Что такое массив констант и для чего он нужен?
895 Как изменить формулу массива?
895 Как оценить тренд и сезонность выручки для магазина игрушек по заданной квартальной выручке?

Список вопросов

943

898 Как вычислить медианный размер сделки в каждой стране по заданному списку сделок в различных странах?
899 Имеются данные о торговых сделках с разбивкой по продавцам, продуктам и местоположению.
Как определить стандартное отклонение проданных единиц продукции для каждого сочетания
«продавец — продукт — регион»?
899 Как применить функцию СУММПРОИЗВ (SUMPRODUCT) взамен условного счета, условного суммирования и условного определения среднего наравне с формулами массивов?
901 Для скольких сделок фактические доходы оказались меньше, чем заложенные в бюджет (прогнозные)?
901 У скольких сделок доход меньше заложенного в бюджет, с разбиением по типу чипа?
901 Сколько сделок происходит в конкретных странах?
901 Каков общий доход от каждого чипа?
901 Рассчитайте общий доход для каждой комбинации страны и чипа.
902 Рассчитайте общий доход в каждой стране.
Глава 92. Запись макросов
907 Что такое макрос?
907 Как используется вкладка Разработчик (Developer) при записи и запуске макросов?
908 Как записать макрос?
910 Как записать макрос, применяющий требуемый формат к произвольному диапазону ячеек?
912 Как запустить макрос?
914 Как при записи макросов использовать относительные ссылки?
917 Как записать макрос, филь трующий сводную таблицу так, чтобы отображались только данные
о 20 основных клиентах?
Глава 93. Продвинутый анализ чувствительности
919 В электронной таблице много исходных параметров, поэтому двунаправленная таблица данных
в этом случае неприемлема для анализа чувствительности. Как же мне все-таки провести анализ
чувствительности?

Уэйн Винстон
Бизнес-моделирование и анализ данных.
Решение актуальных задач с помощью Microsoft Excel
6-е издание
Перевела с английского Ю. Бочина

Заведующая редакцией
Ю. Сергиенко
Руководитель проекта
Н. Римицан
Ведущий редактор
К. Тульцева
Художественный редактор
В. Мостипан
Корректор
М. Молчанова, Н. Сидорова, Г. Шкатова
Верстка
Л. Егорова

Изготовлено в России. Изготовитель: ООО «Прогресс книга».
Место нахождения и фактический адрес: 194044, Россия, г. Санкт-Петербург,
Б. Сампсониевский пр., д. 29А, пом. 52. Тел.: +78127037373.
Дата изготовления: 12.2020. Наименование: книжная продукция. Срок годности: не ограничен.
Налоговая льгота — общероссийский классификатор продукции ОК 034-2014, 58.11.12 — Книги печатные
профессиональные, технические и научные.
Импортер в Беларусь: ООО «ПИТЕР М», 220020, РБ, г. Минск, ул. Тимирязева, д. 121/3, к. 214, тел./факс: 208 80 01.
Подписано в печать 25.11.20. Формат 70×100/16. Бумага офсетная. Усл. п. л. 76,110. Тираж 1000. Заказ 0000.

Источник

Бизнес-моделирование и анализ данных. Решение актуальных задач с помощью Microsoft Excel — 2833633 — 1

ID товара

2833633

Год издания

2021

ISBN

978-5-4461-1446-7

Количество страниц

944

Размер

24.1×17.1×4.7

Тип обложки

Твердый переплёт

Тираж

1000

Вес, г

1322

Возрастные ограничения

16+

Уэйн Винстон научит вас быстро анализировать данные, принимать решения, подводить итоги, составлять отчеты, обрабатывать данные и строить аналитические модели в Microsoft Excel 2019 и Office 365. В новом шестом издании вас ждут более 800 бизнес-задач, основанных на реальных ситуациях, а также обсуждение новых инструментов и функций. Где бы вы ни работали — в крупной корпорации, небольшой компании, государственной или некоммерческой структуре, — это поможет вам увеличить прибыль, снизить издержки или эффективно управлять производством.
Прочитав эту книгу, вы сможете cпрогнозировать результаты выборов, научитесь определять точки безубыточности, рассчитывать вероятность выигрыша в кости или победы любимой команды в турнире.
Хотите обогнать конкурентов? Решайте в Excel реальные задачи!

Питер

Как получить бонусы за отзыв о товаре

Сделайте заказ в интернет-магазине

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать
неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в
первой десятке.

Правила начисления бонусов

Интересно, сложно, много ошибок в формулах

Книга «Бизнес-моделирование и анализ данных. Решение актуальных задач с помощью Microsoft Excel» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Уэйн Винстон
«Бизнес-моделирование и анализ данных. Решение актуальных задач с помощью Microsoft Excel» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.

Источник

Эта книга может быть полезна, как начинающим, так и более опытным пользователям. Она – не полное руководство по Excel, а освещает избранные темы. По какому принципу автор отбирал эти темы, для меня осталось загадкой. Но затронутые темы описаны интересно, глубоко, с разнообразными практическими примерами (естественно, американскими :)). Представлены новейшие инструменты Excel, появившиеся в версиях 2010 и 2013 гг. Рассмотрены функции ИНДЕКС, ПОИСПОЗ, ВПР, СУММЕСЛИ, СМЕЩ, ДВССЫЛ и многие другие. Рассказывается о множественной регрессии, экспоненциальном сглаживании, статистических функциях, функциях даты и времени. Рассмотрено построение наглядных диаграмм, решение сложных задач оптимизации, имитационное моделирование по методу Монте-Карло.

Винстон Уэйн Л. Microsoft Excel 2013. Анализ данных и бизнес-моделирование. – М.: Издательство «Русская редакция»; СПб.: «БХВ-Петербург», 2015. – 864 с. [1]

Скачать содержание (оглавление) в формате Word или pdf

Купить цифровую книгу в ЛитРес

Содержание

Глава 1. Имена диапазонов

Глава 2. Функции поиска

Глава 3. Функция Индекс

Глава 4. Функция ПОИСКПОЗ

Глава 5. Текстовые функции

Глава 6. Даты и функции даты

Глава 7. Оценка инвестиций по чистой приведенной стоимости

Глава 8. Внутренняя ставка доходности

Глава 9. Еще несколько финансовых функций Excel

Глава 10. Циклические ссылки

Глава 11. Функция ЕСЛИ

Глава 12. Время и функции времени

Глава 13. Команда Специальная вставка

Глава 14. Трехмерные формулы

Глава 15. Инструменты проверки зависимостей и надстройка Inquire

Глава 16. Анализ чувствительности с помощью таблиц данных

Глава 17. Инструмент Подбор параметра

Глава 18. Анализ чувствительности с помощью Диспетчера сценариев

Глава 19. Функции СЧЁТЕСЛИ, СЧЁТЕСЛИМН, СЧЁТ, СЧЁТЗ и СЧИТАТЬПУСТОТЫ

Глава 20. Функции СУММЕСЛИ, СРЗНАЧЕСЛИ, СУММЕСЛИМН и СРЗНАЧЕСЛИМН

Глава 21. Функция СМЕЩ

Глава 22. Функция ДВССЫЛ

Глава 23. Условное форматирование

Глава 24. Сортировка в Excel

Глава 25. Таблицы

Глава 26. Счетчики, полосы прокрутки, переключатели, флажки, группы и поля со списками

Глава 27. Революция в аналитике

Глава 28. Введение в оптимизацию с надстройкой Поиск решения

Глава 29. Поиск решения при определении оптимального ассортимента продукции

Глава 30. Поиск решения при планировании расписания работы сотрудников

Глава 31. Поиск решения для задач транспортировки и распределения

Глава 32. Поиск решения для бюджетирования капиталовложений

Глава 33. Поиск решения при финансовом планировании

Глава 34. Поиск решения при оценке спортивных команд

Глава 35. Расположение складов по методу ОПГ с несколькими начальными точками и согласно эволюционному поиску решения

Глава 36. Штрафы и эволюционный поиск решения

Глава 37. Задача коммивояжера

Глава 38. Импорт данных из текстового файла или документа

Глава 39. Импорт данных из сети Интернет

Глава 40. Проверка достоверности данных

Глава 41. Обобщение данных на гистограммах

Глава 42. Обобщение данных с помощью описательной статистики

Глава 43. Сводные таблицы и срезы для описания данных

Глава 44. Модель данных

Глава 45. PowerPivot

Глава 46. Power View

Глава 47. Спарклайны

Глава 48. Обработка данных с помощью статистических функций для баз данных

Глава 49. Фильтрация данных и удаление дубликатов

Глава 50. Консолидация данных

Глава 51. Создание промежуточных итогов

Глава 52. Приемы работы с диаграммами

Глава 53. Оценка линейных зависимостей

Глава 54. Моделирование экспоненциального роста

Глава 55. Степенная кривая

Глава 56. Представление зависимостей с помощью корреляции

Глава 57. Введение во множественную регрессию

Глава 58. Включение качественных факторов во множественную регрессию

Глава 59. Моделирование нелинейных характеристик и взаимосвязей

Глава 60. Однофакторный дисперсионный анализ

Глава 61. Рандомизированные блоки и двухфакторный дисперсионный анализ

Глава 62. Скользящие средние для временных рядов

Глава 63. Метод Винтерса

Глава 64. Метод прогнозирования «по отношению к скользящему среднему»

Глава 65. Прогноз для особых случаев

Глава 66. Введение в случайные величины

Глава 67. Биномиальные и гипергеометрические случайные величины

Глава 68. Пуассоновская и экспоненциальная случайные величины

Глава 69. Нормальная случайная величина

Глава 70. Распределение Вейбулла и бета-распределение: моделирование надежности механизмов и продолжительности работы

Глава 71. Создание вероятностных высказываний на основе прогнозов

Глава 72. Логарифмически нормальная случайная величина в моделировании курса акции

Глава 73. Введение в моделирование по методу Монте-Карло

Глава 74. Вычисление оптимальной цены предложения

Глава 75. Моделирование цен на акции и распределения средств между активами

Глава 76. Игры: моделирование вероятностей для азартных игр и спортивных соревнований

Глава 77. Анализ данных с помощью повторной выборки

Глава 78. Ценообразование опционов

Глава 79. Определение ценности клиента

Глава 80. Оптимальный размер заказа в модели управления запасами

Глава 81. Построение моделей управления запасами для неопределенного спроса

Глава 82. Теория массового обслуживания (теория очередей)

Глава 83. Оценка кривой спроса

Глава 84. Ценообразование продуктов с сопутствующими товарами

Глава 85. Ценообразование продуктов с помощью субъективно определяемого спроса

Глава 86. Нелинейное ценообразование

Глава 87. Функции и формулы массива

Для работы с книгой доступны файлы на английском языке: http://aka.ms/Excel2013Data/files. Я брал их за основу при подготовке заметок.

[1] Я также читал более раннее издание. Уэйн Л. Винстон. Microsoft Excel. Анализ данных и построение бизнес-моделей. 2005 г. Настоящее издание я приобрел в цифровом виде. На момент публикации заметки бумажная книга, похоже, еще не вышла из печати.

Источник

Описание

Рассматриваются реальные ситуации, на которых автор подробно знакомит с методами работы в программе Excel, применяемыми при постановке задач и получении ответов на широкий круг вопросов, связанных с анализом данных и бизнес-моделированием. Помимо материала по использованию формул Excel, изложены основы статистики, прогнозирования, оптимизационных моделей, моделирования методом Монте-Карло, моделей управления запасами и теории очередей. Рассматриваются современные экономические концепции, такие как реальные опционы, ценность клиента и математические модели ценообразования. В конце каждой главы приводятся практические задачи для самостоятельной работы (всего более 500). Прилагаемый компакт-диск содержит файлы примеров к каждой главе, файлы-шаблоны и заготовки для примеров, приведенных в книге, а также электронную версию книги на английском языке в формате PDF….

Дополнительные файлы скачать: Зеркало1
Дополнительные файлы скачать (Chrome): Зеркало2

Источник