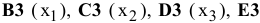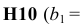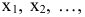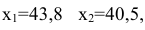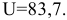
28
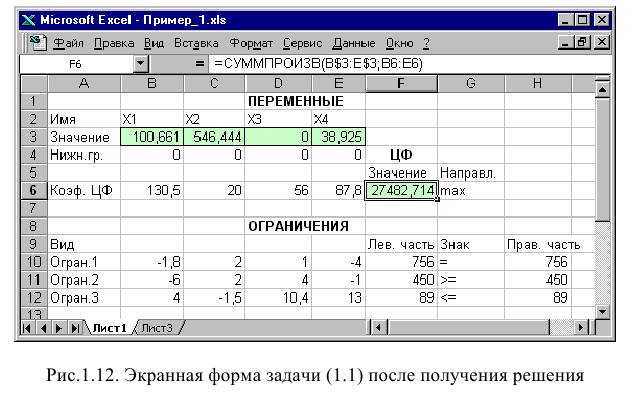
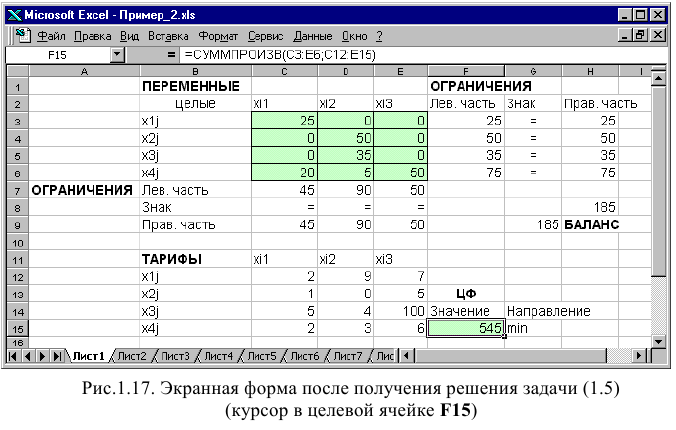
Рис. 1.10. Экранная форма задачи (1.1) после получения решения
Для анализа полученного оптимального решения в MS Excel предусмотрены три типа отчетов: отчет по результатам, устойчивости и пределам.
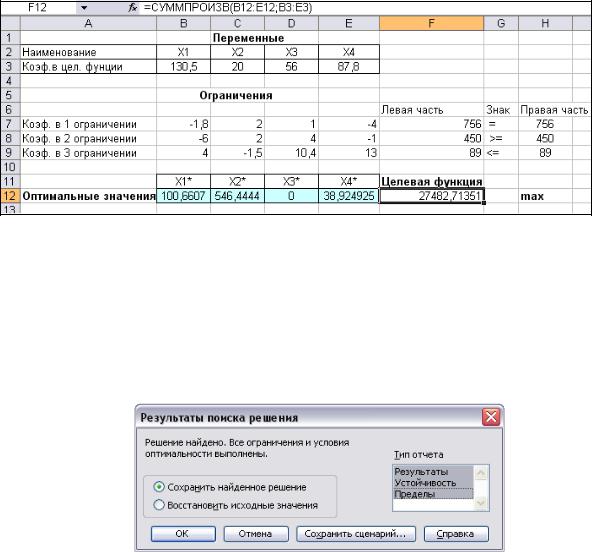
Проведем анализ чувствительности задачи (1.1). Для этого необходимо после запуска в Excel задачи на решение в окне Результаты поиска решения выделить с помощью мыши три типа отчетов: Результаты, Устойчивость и Пределы (рис. 1.11).
Рис. 1.11. Типы отчетов Отчет по результатам. Отчет по результатам состоит из трех таблиц (рис.1.12):
1)таблица 1 содержит информацию о целевой функции;
2)таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
3)таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для ограничений в столбце Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в столбце Значение приведены величины использованного ресурса.
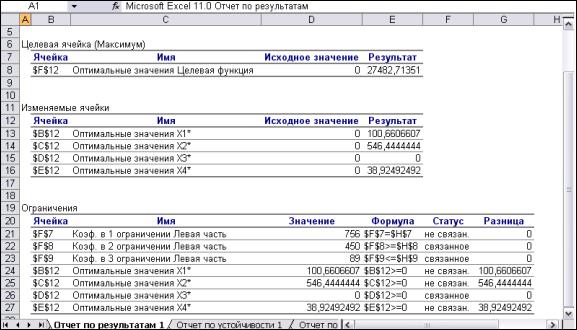
29
Рис. 1.12. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе Статус соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан.».
Для граничных условий (строки 24-27 на рис. 1.12) в графе Разница показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения целевой функции.
Так, если на ресурс наложено ограничение типа ≥, то в графе Разница дается количество ресурса, на которое была превышена минимально необходимая норма.
Если на ресурс наложено ограничение типа ≤, то в графе Разница дается количество ресурса, которое не используется при реализации оптимального решения.
Отчет по устойчивости. Отчет по устойчивости состоит из двух таблиц (рис.1.13). Таблица 1 содержит информацию, относящуюся к переменным:
—результирующие значения переменных;
—нормированная стоимость, т.е. дополнительные двойственные переменные, которые показывает, на сколько изменяется целевая функция при принудительном включении единицы этой переменной в оптимальное решение;
—коэффициенты целевой функции;
—допустимые значения приращения коэффициентов целевой функции, при которых сохраняется первоначальное оптимальное решение.
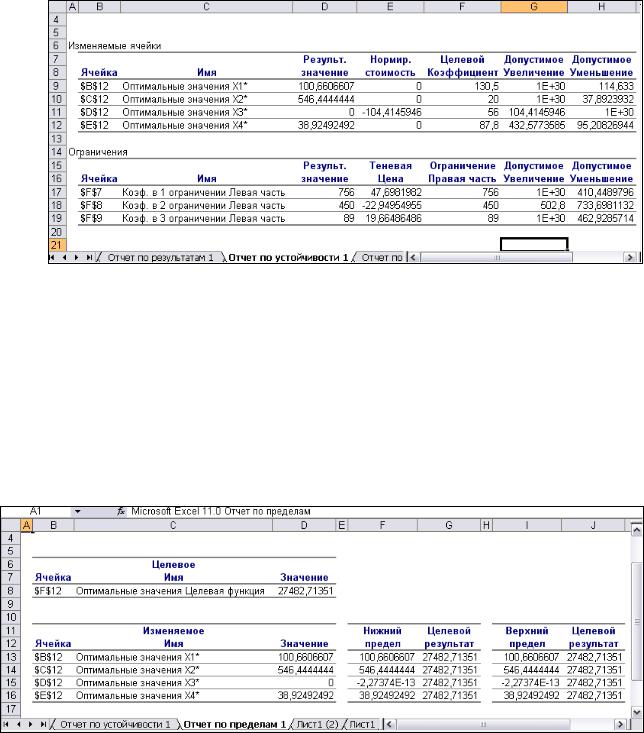
30
Рис. 1.13. Отчет по устойчивости Таблица 2 (рис. 1.13) содержит информацию, относящуюся к ограничениям:
—величина использованных ресурсов в колонке Результ. значение;
—теневые цены, т.е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу. Теневая цена рассчитывается только для дефицитных ресурсов;
—значения приращения ресурсов, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
Отчет по пределам. В отчете пределам (рис. 1.14) показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.
Рис. 1.14. Отчет по пределам
1.4. Двойственная задача линейного программирования
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче.
|
Прямая задача |
Двойственная задача |
|
Целевая функция |
Целевая функция |
|
L(X )= c1x1 + c2 x2 +… + cn xn → max (min), |
F(Z )=b1z1 +b2 z2 +…+bm zm →min (max), |
31
|
при ограничениях |
||||||||||||||||||
|
a |
x |
+a |
x |
2 |
+…+a |
x |
n |
≤(≥,=)b |
, |
|||||||||
|
11 1 |
12 |
1n |
1 |
|||||||||||||||
|
a21x1 +a22 x2 +…+a2n xn |
≤(≥,=)b2 , |
|||||||||||||||||
|
… |
||||||||||||||||||
|
a |
x |
+a |
m2 |
x |
2 |
+…+a |
mn |
x |
n |
≤ |
(≥,=)b |
, |
||||||
|
m1 1 |
m |
|||||||||||||||||
|
x |
j |
≥ |
0 (j =1,…,n). |
|||||||||||||||
|
при ограничениях |
|||||||||||||||||||
|
a |
z |
+a |
21 |
z |
2 |
+…+a |
m1 |
z |
m |
≤(≥,=)c |
, |
||||||||
|
11 |
1 |
1 |
|||||||||||||||||
|
a12 z1 +a22 z2 +…+am2 zm ≤(≥,=)c2 , |
|||||||||||||||||||
|
… |
|||||||||||||||||||
|
a |
z |
+a |
2n |
z |
2 |
+…+a |
mn |
z |
m |
≤ (≥,=)c |
n |
, |
|||||||
|
1n |
1 |
||||||||||||||||||
|
z |
i |
≥ 0 (i =1,…,m). |
|||||||||||||||||
Рассмотрим задачу линейного программирования (1.1):
L (X )=130,5x1 +20x2 +56x3 +87,8x4 →max;−1,8x1 +2x2 + x3 −4x4 =756,
−6x1 +2x2 +4x3 − x4 ≥ 450,
4x 1−1,5x2 +10,4x3 +13x4 ≤89,x j ≥0; j =1,4.
|
В сформулированной задаче |
неравенство −6x1 +2x2 +4x3 − x4 ≥ 450 эквивалентно |
|
|
неравенству |
6x1 −2x2 −4x3 + x4 |
≤ 450 , а равенство −1,8x1 +2x2 + x3 −4x4 =756 можно |
|
представить |
как два неравенства: |
−1,8x1 +2x2 + x3 −4x4 ≤756 и 1,8x1 −2x2 − x3 +4x4 ≤−756. |
Таким образом, рассматриваемую задачу линейного программирования можно представить в виде (1.4):
|
L (X )=130,5x1 +20x2 +56x3 +87,8x4 |
→max; |
||||||||||||||||||||
|
−1,8x |
+2x |
2 |
+ x |
3 |
−4x |
4 |
≤756, |
||||||||||||||
|
1 |
|||||||||||||||||||||
|
1,8x1 − |
2x2 − x3 +4x4 ≤ −756 |
(1.4). |
|||||||||||||||||||
|
−2x2 −4x3 + x4 |
≤ −450, |
||||||||||||||||||||
|
6x1 |
|||||||||||||||||||||
|
4x |
1 |
− |
1,5x |
2 |
+ |
10,4x |
3 |
+13x |
4 |
≤89, |
|||||||||||
|
j =1,4. |
|||||||||||||||||||||
|
x j ≥0; |
|||||||||||||||||||||
|
Поэтому двойственная задача имеет следующий вид (1.5): |
|||||||||||||||||||||
|
F (Z )=756z1 −756z2 −450z3 +89z4 |
→min; |
||||||||||||||||||||
|
−1,8z1 +1,8z2 +6z3 +4z4 |
≥130,5, |
||||||||||||||||||||
|
2z2 −2z3 −1,5z4 ≥ 20 |
|||||||||||||||||||||
|
2z1 − |
(1.5) |
||||||||||||||||||||
|
− z |
2 −4z3 +10,4z4 |
≥56 |
|||||||||||||||||||
|
z1 |
|||||||||||||||||||||
|
− |
4z |
1 |
+4z |
2 |
+ x |
3 |
+13z |
4 |
≥ |
87,8, |
|||||||||||
|
≥0; i =1,4. |
|||||||||||||||||||||
|
zi |
Схема формирования двойственной задачи приведена на рисунке 1.15. Коэффициенты прямой целевой функции становятся правой частью ограничений. Правая часть ограничений становится коэффициентами новой целевой функции. Матрица коэффициентов ограничений транспонируется.
32
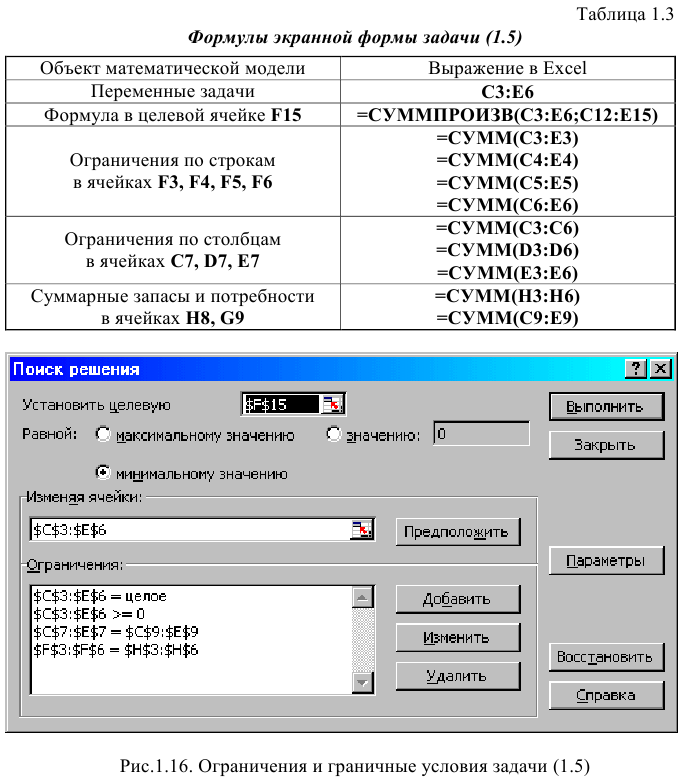
Рис. 1.15. Схема формирования двойственной задачи Ввод зависимостей для двойственной задачи показан на рисунке 1.16.
Рис. 1.16. Ввод зависимостей для двойственной задачи Левая часть ограничений представляет собой произведение матрицы коэффициентов
ограничений на вектор переменных. Целевая функция записывается как произведение транспонированного вектора коэффициентов целевой функции на вектор переменных.
Ограничения приведены на рисунке 1.17 в окне Поиск решения. Это положительность переменных и то, что вектор левой части ограничений должен быть больше вектора из правой части. Для целевой ячейки устанавливаем флажок минимизации.
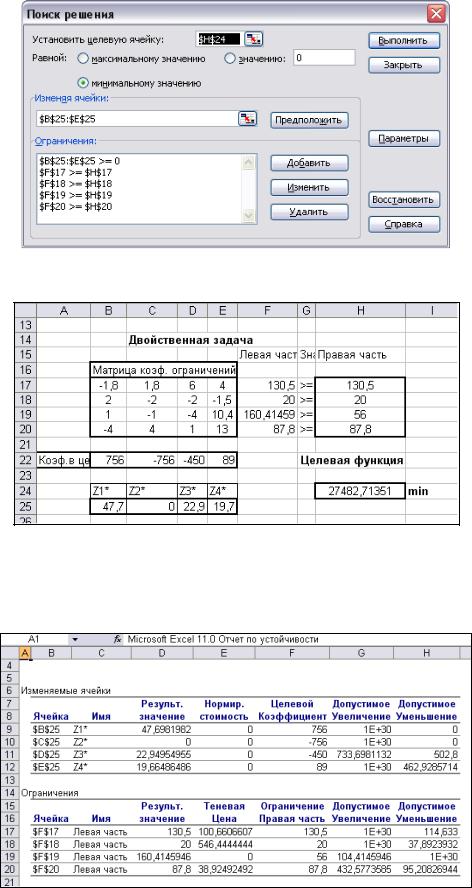
33
Рис. 1.17. Окно Поиск решения с ограничениями для двойственной задачи Результаты решения двойственной задачи приведены на рисунке 1.18.
Рис. 1.18. Решение для двойственной задачи Открыв отчет по устойчивости (рис. 1.19), можно увидеть новые двойственные
оценки (в столбце Теневая цена) и убедиться, что значения переменных при решении задачи на максимизацию становятся двойственными оценками при задаче на минимизацию, и наоборот (сравните с рисунком 1. 13).
Рис. 1.19. Отчет по устойчивости для двойственной задачи
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Анализ оптимального решения на чувствительность в Excel
Задание 1. Проведем анализ чувствительности задачи о производстве двух видов продукции из лабораторной работы №1.
Для этого:
1. Откройте из папки МАТ_МОД файл lab_2(а).
2. Снова запустите задачу на решение (Сервис / Поиск решения) и в окне «Результаты поиска решения» выделите с помощью мыши два типа отчетов: «Результаты» и «Устойчивость» (Рис. 1).
Рис. 1. Выделение типов отчетов, требуемых для анализа чувствительности
Обратите внимание: для задач с целочисленными переменными возможно создать только отчет по результатам.
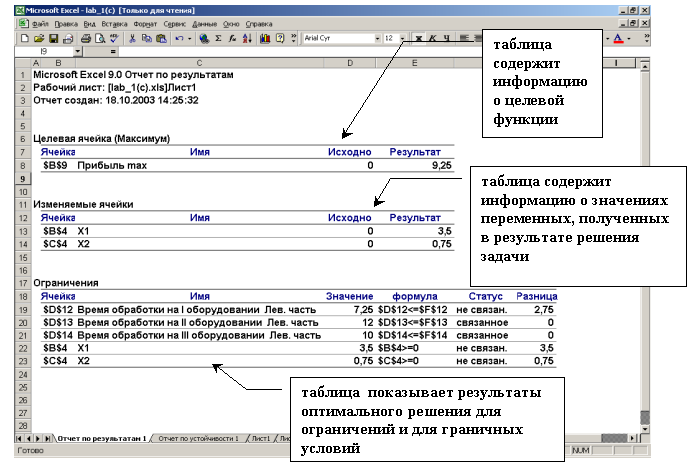
3. Проанализируйте первый полученный отчет — «Отчет по результатам 1» (Рис. 2).
Рис. 2. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе «Статус» («Состояние») соответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан». В графе «Значение» приведены величины использованного ресурса.
Для граничных условий в графе «Разница» показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения ЦФ.
Если на ресурс наложено ограничение типа 
, то в графе «Разница» дается количество ресурса, на которое была превышена минимально необходимая норма.
Если на ресурс наложено ограничение типа 
, то в графе «Разница» дается количество ресурса, которое не используется при реализации оптимального решения.
Так, анализ строки 19 (Рис. 2) отчета по результатам для задачи о выпуске продукции показывает, что время обработки на I оборудовании составило 7,25 ч. Неизрасходованным остается 2,75 ч из общего фонда времени, отведенного на обработку продукции на I оборудовании. Из этого следует, что запас недефицитного ресурса “Фонд времени работы на I оборудовании” можно уменьшить на 2,75 ч и это никак не повлияет на оптимальное решение. Отсюда следует, что количество рабочих, обслуживающих I оборудование, можно уменьшить или перевести их на выпуск другой продукции. Ресурсы время работы на II и III оборудовании являются дефицитными.
На основании проведенного анализа можно сделать вывод о том, что существуют причины (ограничения), не позволяющие предприятию выпускать большее количество (в кг) продукции и получать большую прибыль. Проанализировать эти причины позволяет отчет по устойчивости.
4. Проанализируйте второй полученный отчет — «Отчет по устойчивости 1».
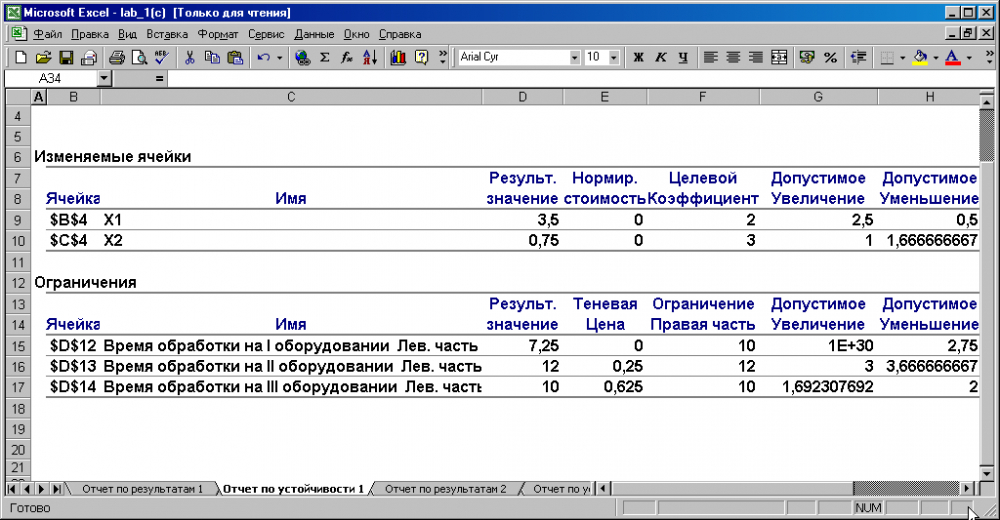
Отчет по устойчивости состоит из двух таблиц «Изменяемые ячейки» и «Ограничения» (Рис. 3).
Таблица «Изменяемые ячейки» содержит информацию», относящуюся к переменным:
- Результат решения задачи можно увидеть в столбце «Результ. значение».
Рис. 3. Отчет по устойчивости
- Нормированная стоимость показывает, на сколько изменится значение ЦФ в случае принудительного включения единицы этой продукции в оптимальное решение.
- Коэффициенты ЦФ.
- Предельные значения приращения целевых коэффициентов
(столбцы «Допустимое Увеличение» и «Допустимое Уменьшение»), при которых сохраняется первоначальное оптимальное решение.
(столбцы «Допустимое Увеличение» и «Допустимое Уменьшение»), при которых сохраняется первоначальное оптимальное решение. Например, допустимое увеличение цены на продукт А равно 2,5 тыс.руб./кг, а допустимое уменьшение – 0,5 тыс.руб./кг. Это означает, что если цена на продукт А возрастет более чем на 2,5 тыс.руб./кг., например станет равной 5 тыс.руб./кг., то оптимальное решение изменится: станет целесообразным выпуск А. И если его цена будет снижена до 1 тыс.руб./кг., то оптимальное решение также измениться: выгоднее будет увеличить выпуск продукта B. А вот если цена на продукт станет равна 4 тыс.руб./кг. или 1,8 тыс.руб./кг, то оптимальное решение не измениться.
Задание 2. Убедитесь в этом самостоятельно, для этого:
1. Увеличьте цену на продукт А – установите 4 тыс.руб./кг (в ячейку 7 внесите 4) и осуществите поиск решения с предоставлением отчетов.
2. Уменьшите цену на продукт А – установите 1,8 тыс.руб./кг и осуществите поиск решения с предоставлением отчетов.
Обратите внимание, что в обоих случаях оптимальное решение не изменилось.
3. Увеличьте цену на продукт А – установите 5 тыс.руб./кг и осуществите поиск решения с предоставлением отчетов.
Обратите внимание, что оптимальное решение изменилось: целесообразно стало выпускать 4 кг продукта A и не выпускать продукт B.
4. Уменьшите цену на продукт А – установите 1 тыс.руб./кг и осуществите поиск решения с предоставлением отчетов.
Обратите внимание, что оптимальное решение изменилось: целесообразно стало выпускать продукт A и продукт B в равных количествах.
5. Сохраните файл с полученными отчетами в своей папке с текущим именем.
Таблица «Ограничения» содержит информацию, относящуюся к ограничениям.
- Величина использованных ресурсов содержится в колонке «Результ. значение».
- Предельные значения приращения ресурсов содержатся в столбцах «Допустимое Уменьшение» и «Допустимое Увеличение».
содержатся в столбцах «Допустимое Уменьшение» и «Допустимое Увеличение». В графе «Допустимое Уменьшение» показывается:
При этом при таких изменениях количества ресурса, оптимальное решение остается прежним.
В графе «Допустимое Увеличение» показывается:
Рассмотрим анализ дефицитных ресурсов, так как анализ недефицитных ресурсов был дан выше (напоминаем, что в нашем случае только один ресурс не является дефицитным – время работы I оборудования). Анализируя отчет по результатам, мы установили, что существуют причины (ограничения), не позволяющие предприятию выпускать больший, чем в оптимальном решении, объем продукции и получать более высокую прибыль. В рассматриваемой задаче такими ограничениями являются дефицитные ресурсы “Время обработки на II оборудовании” и “Время обработки на III оборудовании”. Поскольку знак ограничений этих ресурсов имеет вид 
, то возникает вопрос, на сколько максимально должен возрасти фонд времени работы этих оборудований, чтобы обеспечить увеличение выпуска продукции. Ответ на этот вопрос показан в графе «Допустимое Увеличение». Фонд времени работы II оборудования имеет смысл увеличить самое большее на 3 часа, а III оборудования самое большее на 1,69 часа. Это приведет к новым оптимальным решениям, увеличивающим прибыль по сравнению с найденным. Дальнейшее увеличение фонда времени работы оборудования II и III сверх указанных пределов не будет больше улучшать решение, т.к. уже другие ресурсы станут дефицитными.
Задание 3. Убедитесь в этом самостоятельно, для этого снова откройте файл lab_2(а) из папки МАТ_МОД и поэкспериментируйте с исходными данными о фонде рабочего времени оборудования:
1. Увеличьте фонд рабочего времени для оборудования – установите 14 часов (в ячейку 13 внесите 14) и осуществите поиск решения с предоставлением отчетов.
2. Установите исходное значение фонда времени для оборудования (12 часов) и увеличьте фонд рабочего времени для оборудования – установите 11 часов (в ячейку 14 внесите 11), осуществите поиск решения с предоставлением отчетов.
Обратите внимание, что в обоих случаях оптимальное решение изменилось и повысилась прибыль, но ресурс – фонд времени для оборудования I не стал дефицитным.
3. Фонд рабочего времени для II оборудования – установите 16 часов, для III оборудования – установите исходное значение 10 часов и осуществите поиск решения с предоставлением отчетов.
4. Фонд рабочего времени для II оборудования – установите исходное значение 12 часов, для III оборудования – установите значение 14 часов и осуществите поиск решения с предоставлением отчетов.
Обратите внимание, что в этих случаях оптимальное решение изменилось, но ресурс – фонд времени для оборудования I стал дефицитным.
5. Сохраните файл с полученными отчетами с именем lab_2(b) в своей папке.
- Ценность дополнительной единицы i-го ресурса («Теневая цена») рассчитывается только для дефицитных ресурсов.
После того как мы установили, что увеличение фонда рабочего времени оборудования II и III приведет к новым планам выпуска, обеспечивающим более высокую прибыль, возникает следующий вопрос. Что выгоднее в первую очередь увеличивать фонд рабочего времени для II оборудования или для III оборудования? Ответ на этот вопрос дает графа «Теневая цена». Для II оборудования она равна 0,25 тыс. руб./кг., а для III оборудования – 0,625 тыс.руб./кг. Отсюда вывод: в первую очередь выгодно увеличивать фонд рабочего времени для III оборудования.
Задание 4.
1. Постройте математическую модели для следующей задачи ЛП и найдите ее оптимальное решение средствами.
Предприятие выпускает телевизоры, стереосистемы и акустические системы, используя общий склад комплектующих. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий для получения наибольшей прибыли. Общее количество запасов комплектующих, расход (шт.) на изготовление единицы изделия и прибыль от реализации единицы каждого представлены в таблице 1.
Таблица 1. Исходные данные
Если Вы все сделали правильно, то Вы должны получить оптимальное решение, которое приведено на Рис. 4.
Рис. 4. Оптимальное решение
1. Проведите анализ оптимального решения данной задачи на чувствительность.
2. Переименуйте «Лист 2» в «Выводы» и разместите на нем результаты анализа:
- опишите, какие комплектующие являются дефицитными, недефицитными;
- нормированная стоимость для акустических систем отлична от нуля, объясните экономический смысл данного явления;
- укажите, насколько возможно увеличить (уменьшить) прибыль от продажи телевизоров, чтобы выпуск бытовой техники не изменился;
- измениться ли оптимальное решение, если прибыль от реализации стереосистем будет равна 70 руб, 35 руб (в случае положительного ответа, необходимо указать новое решение);
- укажите, при какой прибыли выгодно будет выпускать акустические системы;
- укажите, насколько можно уменьшить запасы шасси, кинескопов, блоков питания на складе, чтобы не было излишек;
- укажите, насколько необходимо увеличить запасы динамиков и электронных плат, чтобы увеличить выпуск бытовой техники и повысить общую прибыль;
- укажите, запасы какого ресурса выгоднее всего увеличить: динамиков или электронных плат и почему.
3. Сохраните файл с полученными отчетами с именем lab_2(с).
Резюме:
1) Оптимальное решение задачи ЛП, полученное для конкретной экономической ситуации, после ее изменения может оказаться непригодным или неоптимальным. Анализ чувствительности задачи ЛП, а именно того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение, позволяет увидеть перспективы и возможные варианты решения в изменившейся ситуации.
2) Создание отчетов:
- Сервис / Поиск решения;
- в окне «Результаты поиска решения» выделите с помощью мыши два типа отчетов: «Результаты» и «Устойчивость».
Теоретическая часть
Контрольные задания
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
16 * х1 + 4 * х2 ≤ 400
6 * х1 + 6 * х2 ≤ 240
х2 ≥ 12
х1 ≥ 0
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
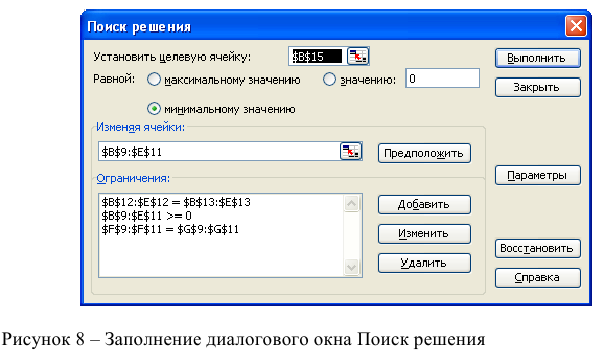
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
Рис. 8. Увеличение погрешности вычислений
Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
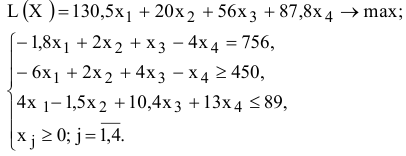
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
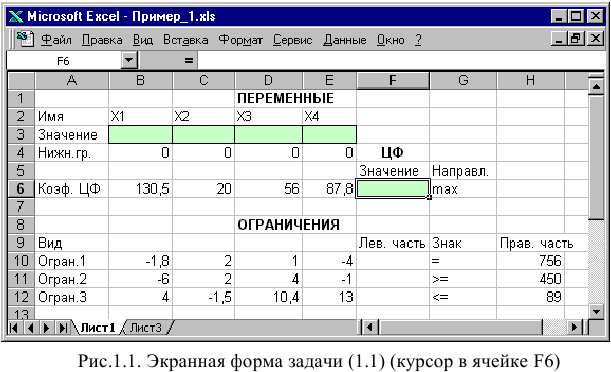
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 
, коэффициентам ЦФ соответствуют ячейки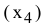
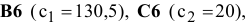
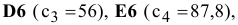
правым частям ограничений соответствуют ячейки
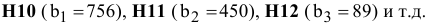
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
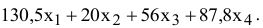
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
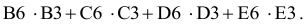
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
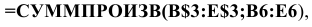
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
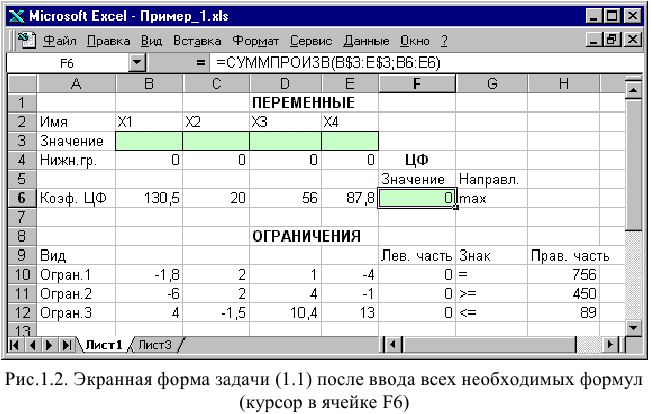
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «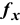
» на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
• курсор в поле F6;
• нажав кнопку ««, вызовите окно «Мастер функций — шаг 1 из 2»;
• выберите в окне «Категория» категорию «Математические»;
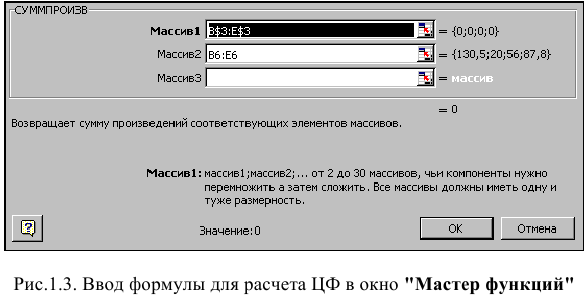
• в окне «Функция» выберите функцию СУММПРОИЗВ;
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.
Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).
Задание ЦФ
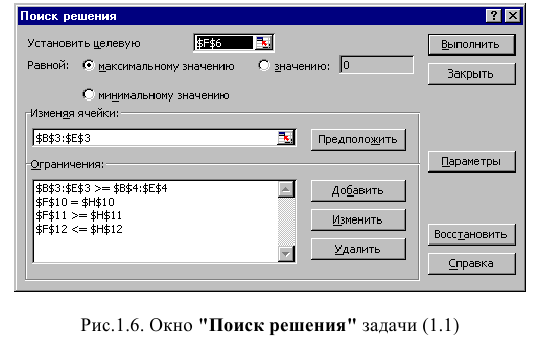
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
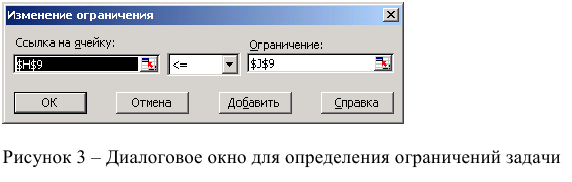
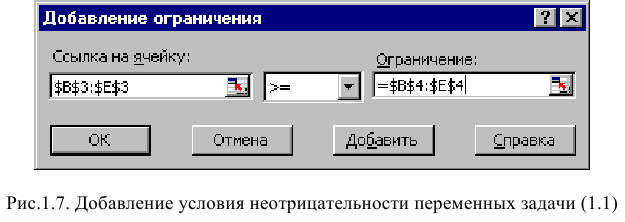
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Задание знаков ограничений <. >, =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
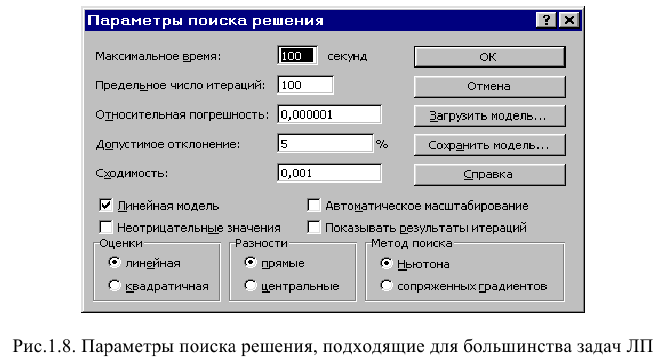
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
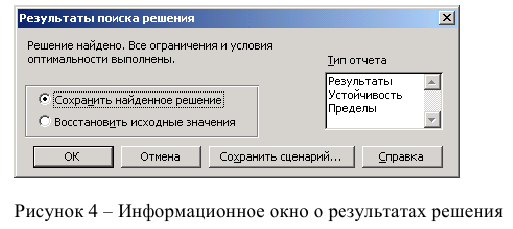
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.
Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
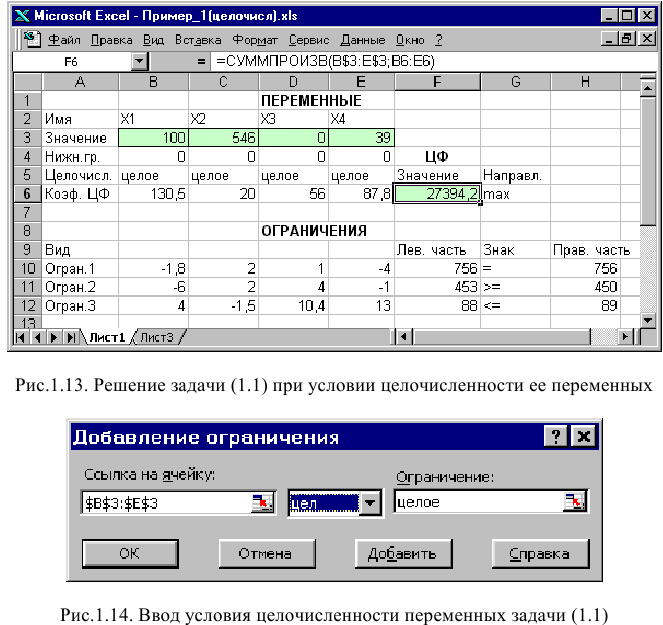
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
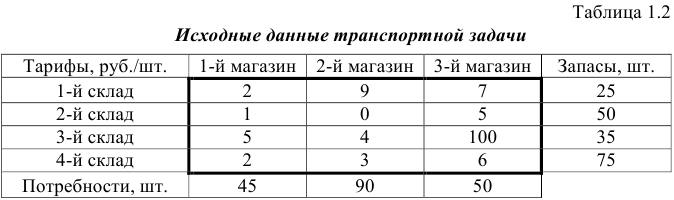
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
Целевая функция и ограничения данной задачи имеют вид
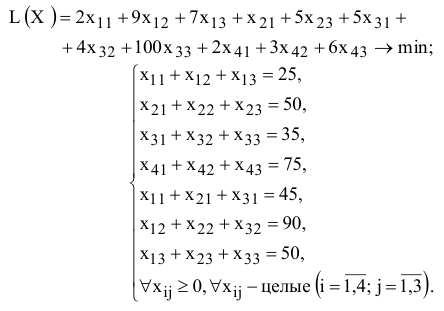
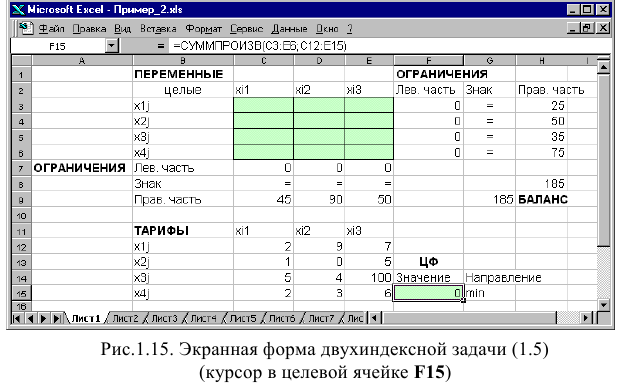
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные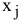 
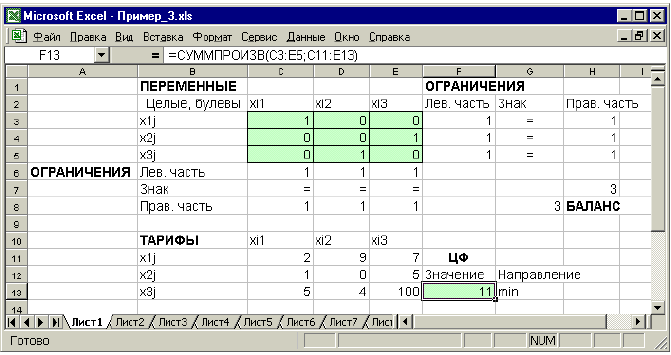
могут принимать только одно из двух значений: 0 или 1. Такие переменные в честь предложившего их английского математика Джорджа Буля называют булевыми. На рис. 1.18 представлена экранная форма с решением некоторой двухиндексной задачи с булевыми переменными.
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
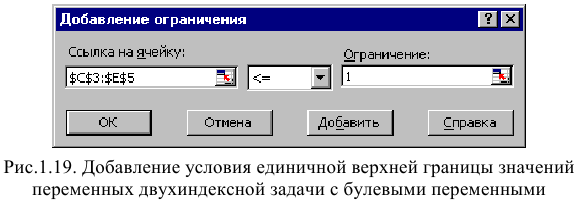
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
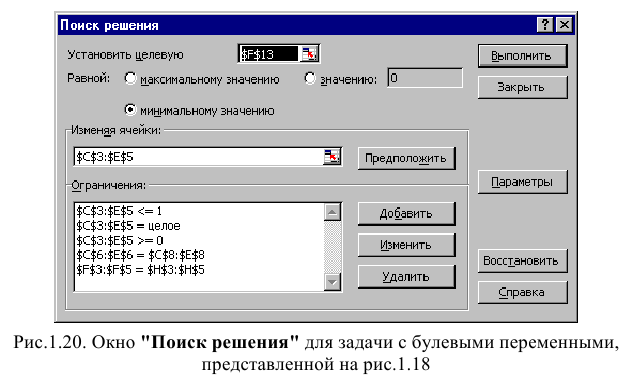
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Одноиндексные ЗЛП
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
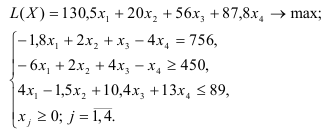
- Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
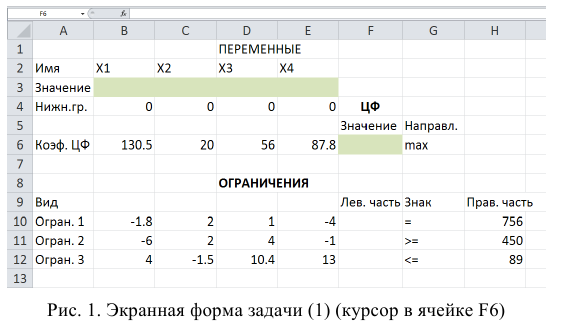
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
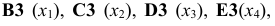
коэффициентам ЦФ соответствуют ячейки
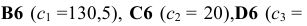
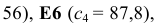
правым частям ограничений соответствуют ячейки
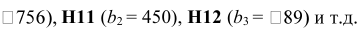
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
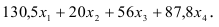
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
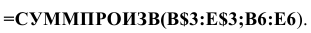
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
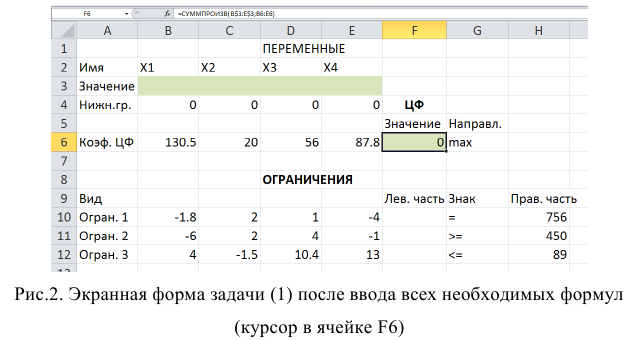
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
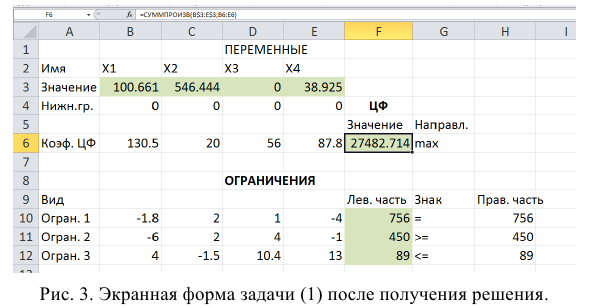
Целочисленное программирование
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
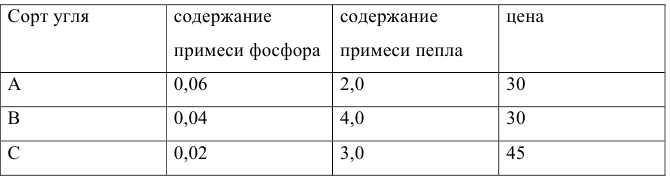
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
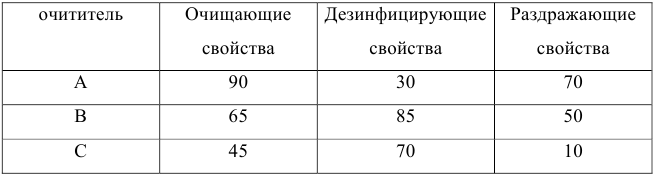
Составим математическую модель задачи. Пусть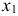 
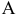
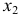
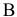
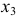
— доля очистителя 
в конечном продукте, 
— доля очистителя 
в конечном продукте, 
— доля очистителя 
в конечном продукте.
Целевая функция: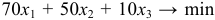 
(т.е. минимизируем раздражающее воздействие на кожу конечного продукта).
Ограничения:
Решение задачи с помощью MS Excel.
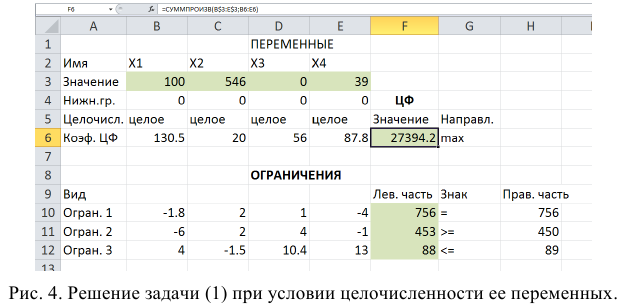
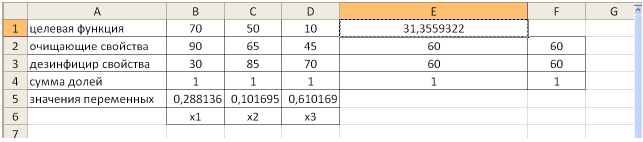
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
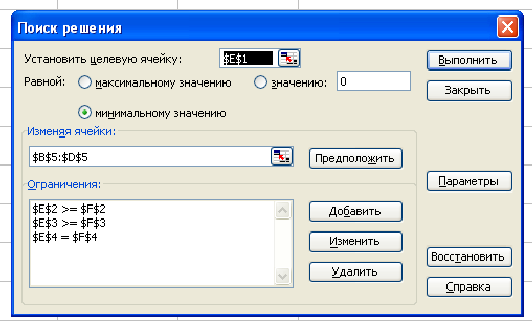
«Поиск решения».
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
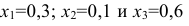
(т.е. очистители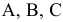 
нужно брать в долях 30%, 10% и 60% соответственно).
Задача 2.
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 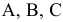по следующим ценам (за тонну):
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
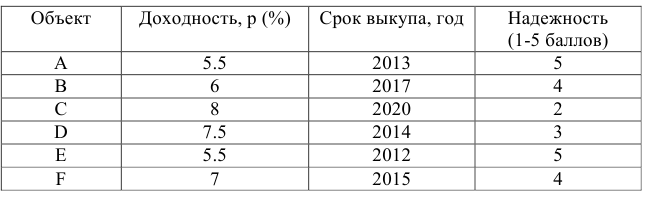
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: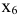 
.
Прибыль, которую получит инвестор, задается целевой функцией:
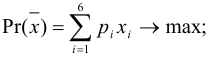
Сформируем ограничения:
Ограничения на суммарный объем активов —
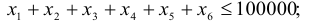
Ограничение на размер доли каждого актива
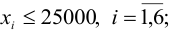
Необходимость долгосрочного инвестирования (например, более 3 лет)
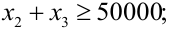
Учет необходимости снижения риска —
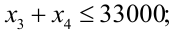
Естественное экономическое ограничение — неотрицательность искомых переменных —
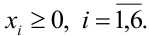
Для решения задачи выполним следующие шаги.
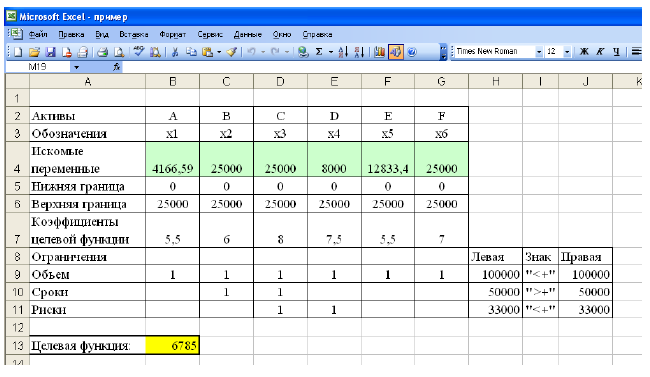
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
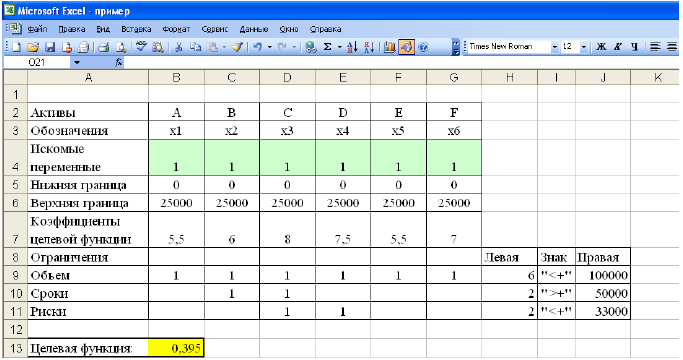
Рисунок 1 — Исходные данные для решения ЗЛП
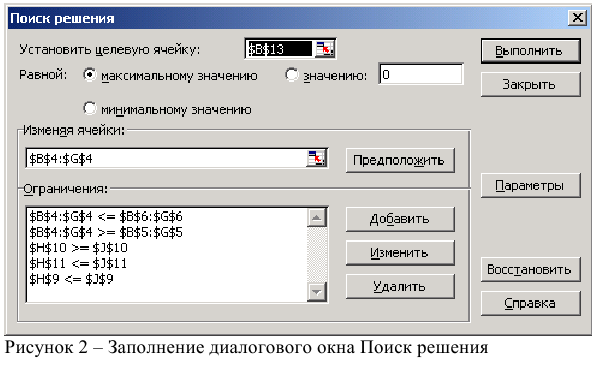
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
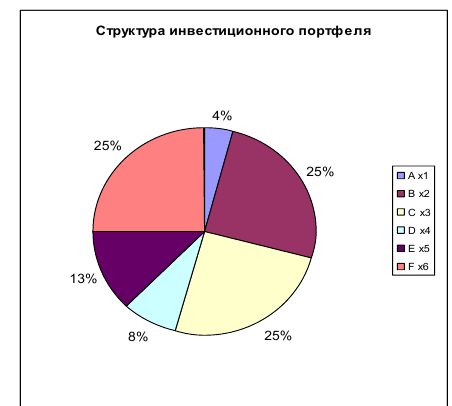
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
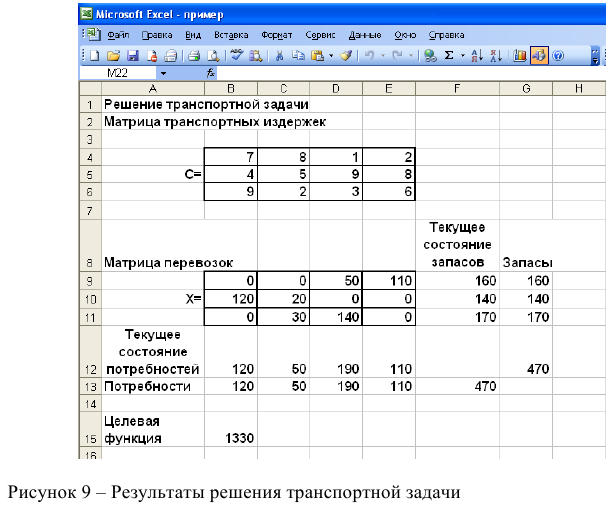
Технология решения транспортной задачи
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
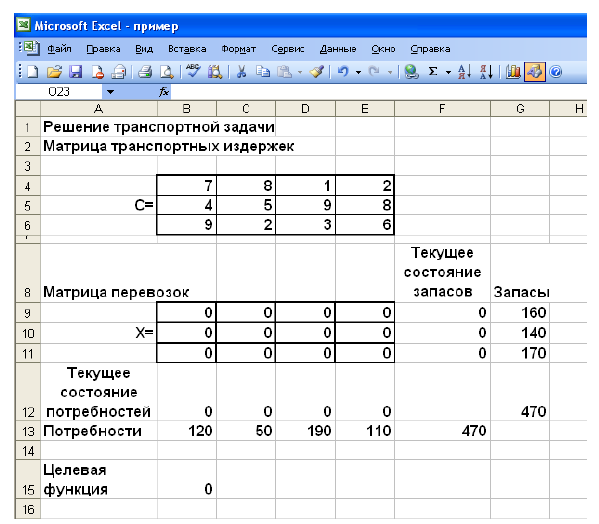
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности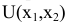 
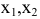
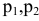
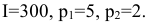
на товары 
, ценах 
и
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
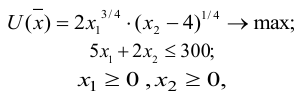
где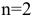 
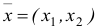
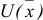
— число потребляемых товаров или благ, 
— потребительский набор, 
— функция полезности потребителя.
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
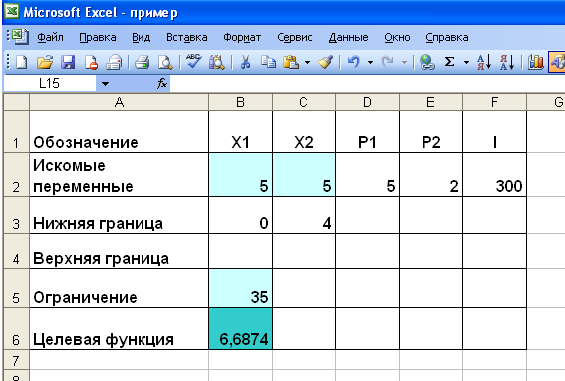
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
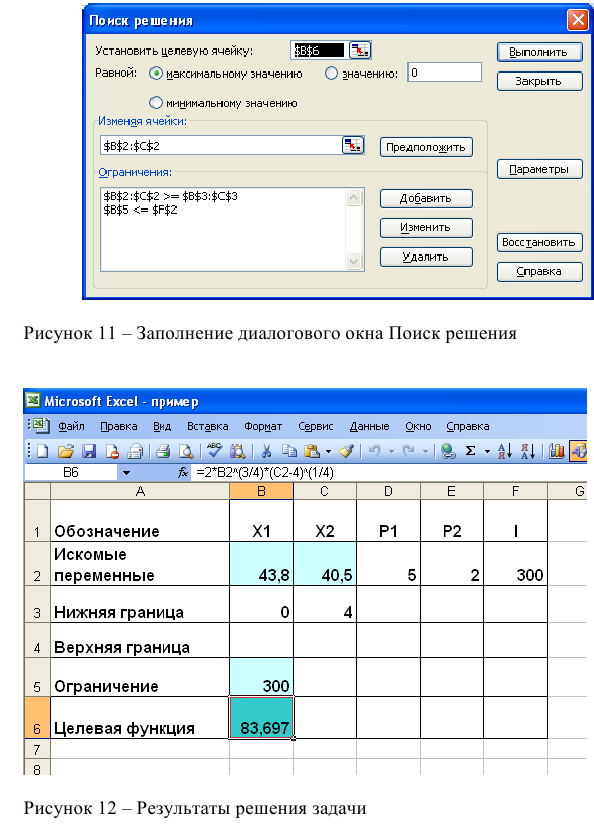
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
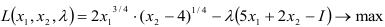
Найдем точки экстремума функции Лагранжа.
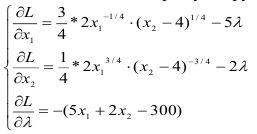
Приравняем каждое уравнение к 0:
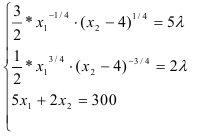
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
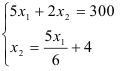
Подставим второе уравнение в первое и построим аналитические функции спроса:
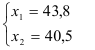
Максимальное значение функции полезности-
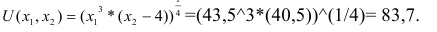
Решением задачи потребительского выбора будет набор 
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию
Лабораторная работа №1
Тема: Решение задач линейного программирования и анализ чувствительности с помощью MS Excel.
Цель: Изучить возможности надстройки Поиск решения пакета MS Excel для решения однокритериальных задач теории принятия решений.
Порядок выполнения работы:
- Изучение теории и примера.
- Построение математической модели проблемы в виде задачи линейного программирования.
- Решение задачи с использованием надстройки Поиск решения пакета MS Excel.
- Анализ чувствительности решения с использованием сценариев.
- Составление отчёта по лабораторной работе, в котором представляется:
- формулировка индивидуального задания;
- математическая модель и пояснение к её построению;
- снимок экрана монитора, содержащий табличную модель задачи, снимки отчетов по результатам, устойчивости и пределам, а также снимок отчета по сценариям с содержательными пояснениями к ним;
- выводы по лабораторной работе.
Теория
Процесс принятия управленческого решения можно представить как последовательность выполнения следующих действий (этапов выработки решения).
I. Анализ ситуации и формализация исходной проблемы. На этом этапе надо просто четко сформулировать проблему, понять и сформулировать цели, которые хочется достичь в виде решения проблемы. Другими словами, надо поставить проблему, четко определить цели, возможные решения и факторы, влияющие на решение проблемы. Часто результат этого этапа представляют в виде формальной модели проблемы (пока записанной обычным языком), где были бы собраны воедино цели, решения и факторы и где бы присутствовала основа для формализации отношений между ними.
II. Построение математической модели, т. е. перевод формальной модели, построенной на предыдущем этапе, на язык математических отношений.
III. Анализ математической модели и получение математического решения проблемы. На этом этапе анализируется построенная математическая модель, проверяется адекватность модели и находится решение математической задачи, вытекающей из этой модели. Если для решения математической задачи используется вычислительная техника, то предварительно строится также компьютерная модель задачи. Обычно этот этап наиболее простой из всех этапов процесса принятия решения, поскольку здесь, как правило, используются известные и апробированные алгоритмы решения математических задач.
IV. Анализ математического решения проблемы и формирование управленческого решения. На этом этапе анализируется полученное математическое решение (выполняется так называемый анализ чувствительности), и затем на основе этого математического решения формируется управленческое решение.
После выполнения этих этапов следует этап реализации принятого решения.
I. Рассмотрим первый этап процесса принятия решения: анализ проблемы и формализация исходной проблемы. Этот этап можно рассматривать как первую стадию перехода от реального мира к компьютерному представлению проблемы.
На данном этапе надо четко сформулировать свою проблему, понять и сформулировать цели, которые хочется достичь в виде решения проблемы. Другими словами, надо четко поставить проблему. Поэтому на данном этапе на простом русском языке надо
♦ сформулировать проблему, по возможности максимально четко;
♦ сформулировать цели, которые должны быть достигнуты в результате реализации найденного решения;
♦ указать, что считать решением проблемы (решение должно гарантировать достижение целей);
♦ выявить и описать возможности достижения целей;
♦ выявить и описать факторы, от которых может зависеть решение проблемы;
♦ выявить и описать ограничения, препятствующие достижению целей;
♦ описать возможные альтернативные способы решения проблемы.
Эти пункты и составляют формальную модель проблемы. Таким образом, формальная модель — это просто четкое описание вашей проблемы, в котором необходимо выделить перечисленные пункты.
Пусть некий лакокрасочный завод «Олимп», в связи с изменившейся конъюнктурой рынка хочет разработать новый производственный план для выпуска краски типов А и Б, не трогая пока производство другой продукции. Допустим, что «Олимп» имеет месячный цикл производства. Таким образом, нужно определить, сколько в месяц следует производить краски типа А и сколько — типа Б. Ответ вроде бы простой: чем больше, тем лучше, конечно, с учетом производственных возможностей. Итак, вот первая цель — увеличить до максимума производство как продукции А, так и продукции Б. Допустим, производственные мощности позволяют выпускать в месяц суммарно 500 т краски всех типов. Вот появилось первое ограничение — общее количество краски типов А и Б не должно превышать 500 т.
Как видно, первую цель достичь можно, однако проблема остается плохо поставленной, поскольку дает неоднозначное решение. Поэтому вспомним, что всякое производство должно приносить прибыль. Теперь можно сформулировать вторую цель — производственный план должен приносить максимальную прибыль. Пусть одна тонна краски А приносит в среднем 2000 руб. прибыли, а одна тонна краски Б — 2500 руб. Здесь величины удельной прибыли (т.е. прибыли на одну тонну краски) являются факторами, которые влияют на конечную цель.
На этом шаге мы сделали огромное упрощение реальной ситуации, т. к. удельная прибыль любого производимого изделия зависит от многих факторов (конъюнктуры рынка, стоимости исходных материалов, себестоимости производства, уровня рентабельности и т. д.) и не является величиной постоянной даже на протяжении относительно небольшого временного промежутка. Тем более сложно предсказать и трудоемко подсчитать ее значение на будущий более-менее продолжительный период времени. Можно только оценить будущую удельную прибыль, да и то с определенной степенью точности. Пусть в нашем примере получены оценки будущей удельной прибыли производства краски типа А: от 1500 до 2300 руб., а краски типа Б: от 2100 до 3000 руб. Приведенные выше величины удельных прибылей 2000 и 2500 руб. являются наиболее вероятными ожидаемыми значениями. Далее именно эти величины примем за значения удельных прибылей, а возможные последствия от их неточного задания рассмотрим при проведении анализа полученного решения.
Очевидно, что для достижения второй цели надо производить только краску типа Б и забыть о краске типа А. Однако отдел маркетинга требует, чтобы краски типа А производилось не менее 200 т в месяц, поскольку есть договоры на такое количество, а краску типа Б нельзя производить более 150 т, поскольку большее количество трудно реализовать. Итак, имеем еще два ограничения: произведенное количество краски А должно быть не меньше 200 т, а краски Б — не более 150 т.
При таких ограничениях даже начальник производства составит план: надо производить 350 т краски А и 150 т краски Б. Этот план учитывает только ограничения по производственным мощностям и маркетинговые ограничения. Но для производства любой продукции нужны еще исходные материалы. Пусть на изготовление красок А и Б необходимо сырье трех видов согласно следующей таблице.
| Краска А, кг | Краска Б, кг | Месячный запас, т | |
| Сырье 1 | 50 | 100 | 50 |
| Сырье 2 | 70 | 80 | 30 |
| Сырье 3 | 40 | 70 | 25 |
В этой таблице показано, сколько и какого сырья необходимо для производства одной тонны краски А и одной тонны краски Б, а также величины месячных запасов этого сырья. Очевидно, что общее количество сырья, используемого для производства краски, не должно превышать их месячные запасы. Таким образом, имеем еще три ограничения — по одному для каждого типа сырья. С учетом этих ограничений производственный план «на пальцах» уже не подсчитаешь.
Здесь сделано еще одно существенное упрощение реальной ситуации — реальный процесс производства чего бы то ни было зависит не только от наличия исходных материалов, необходимых для создания конечного продукта, но и от многих других факторов: наличия достаточных производственных мощностей, наличия рабочей силы, периодичности поступления исходных материалов, качества этих материалов и т.д. Здесь эти факторы отброшены, оставлены только ограничения на сырье трех видов. При этом сделано еще одно неявное допущение, что другие компоненты, необходимые для производства краски, имеются в достаточном количестве и не влияют на объемы производства.
Итак, что же мы имеем после небольшого анализа проблемы.
♦ Постановка проблемы: разработать производственный план, который максимизировал бы прибыль с учетом всех видов ограничений.
♦ Цель: максимизировать прибыль.
♦ Решение: количество тонн краски А и Б, производимых в месяц.
♦ Факторы, от которых зависит решение: значения удельной прибыли каждого типа краски, предельное число производимой краски, предельные числа производимых красок типов А и Б (маркетинговые ограничения), количества сырья (необходимых для производства одной тонны краски), значения запасов сырья (всего 14 факторов).
♦ Факторы, влияющие на прибыль: все перечисленные факторы, кроме значений количества сырья, необходимого для производства одной тонны краски. (Считаем, что на рецептуру красок мы влиять не можем.)
♦ Ограничения: на предельное общее количество производимой краски, на предельные количества производимых красок А и Б в отдельности, на предельные количества используемого сырья (всего 6 ограничений).
Мы выделили факторы, влияющие на прибыль отдельно, чтобы в дальнейшем провести анализ чувствительности решения именно по этим факторам.
И еще одно замечание: при такой размытой постановке исходной проблемы можно сформулировать много разных целей. Например, можно составить производственный план, который бы минимизировал себестоимость продукции. Можно сформулировать более сложные цели (что обычно имеет место в реальных ситуациях), например, максимизировать прибыль и одновременно минимизировать использование каких-то исходных материалов, которые являются дорогими или дефицитными. При этом в зависимости от сформулированных целей могут выделяться разные факторы, влияющие на эти цели, и могут формироваться разные ограничения. В нашем примере мы ограничимся сформулированной целью максимизации прибыли.
II. Построение математической модели означает перевод формальной модели, построенной на предыдущем этапе, на четкий язык математических отношений. Математическая модель должна содержать три основных компонента.
1. Переменные, значения которых необходимо вычислить (это переменные решения из формальной модели).
2. Целевая функция — это цель, записанная математически в виде функции от переменных. Обязательно указывается, что необходимо сделать с этой функцией для решения проблемы: найти ее максимум, минимум или конкретное заданное значение.
3. Ограничения — записанные математически ограничения из формальной модели.
Если определены переменные, то построение целевой функции и ограничений обычно не вызывает затруднений, поскольку на предыдущем этане и цель и ограничения уже формулировались с привязкой к переменным решения.
В нашем примере обозначим через х1 и х2 переменные, которые определяют месячные объемы производства краски (в тоннах) типа А и Б соответственно. Напомним, что 1 тонна краски А приносит прибыль 2000 руб., а 1 тонна краски Б — 2500 руб. Тогда суммарная прибыль z при производстве х1 тонн краски А и х2 тонн краски Б составит
z = 2000*х1 + 2500*х2 (руб.)
Это и есть целевая функция, которую необходимо максимизировать.
Теперь запишем ограничения. Первое ограничение говорит о том, что суммарный объем производства краски обоих типов не должен превышать 500 т. Это запишется так: х1 + х2 500. Маркетинговые ограничения записываются просто: х1 200 и х2 150. Теперь надо записать ограничения па сырье. Напомним, что сырья 1 на производство 1 т краски А расходуется 0,05 т (50 кг) и 0,1 т (100 кг) на производство 1 т краски Б. Таким образом, всего на производство x1, тонн краски А и x2 тонн краски Б потребуется 0,05*х1 + 0,1*х2 тонн сырья 1. Эта величина не должна превышать 50 т. Отсюда получаем ограничение: 0,05*х1 + 0,1*х2 50. Подобным способом получаем еще два ограничения на сырье 2 и сырье 3: 0,07*x1 + 0,08*x2 30 и 0,04*x1 + 0,07*x2 25. Еще одно неявное ограничение состоит в том, что переменные х1 и х2 должны быть неотрицательными (если не вдаваться в мистику, то отрицательные объемы производства физически просто невозможны). Это ограничение называется условием неотрицательности переменных и записывается так: х1 0 и х2 0. Однако заметим, что условие неотрицательности для переменной х1 здесь излишне, поскольку имеем более сильное ограничение х1 200. Поэтому неравенство х1 0 исключаем из списка ограничений.
Обратите особое внимание на то, что размерности всех переменных и параметров должны быть согласованы. Поэтому в нашем примере удельные расходы сырья переведены из килограммов в тонны, поскольку переменные измеряются в тоннах.
Обычно ограничение записывают таким образом, чтобы в левой части неравенства находилось выражение с переменными, а в правой части неравенства — только числа. Тогда левую часть неравенства называют функцией ограничения.
Окончательно математическая модель нашей проблемы запишется следующим образом:
максимизировать z = 2000*х1 + 2500*х2 при выполнении ограничений
х1 + х2 500,
х1 200,
х2 150,
0,05*х1 + 0,1*х2 50,
0,07*x1 + 0,08*x2 30,
0,04*x1 + 0,07*x2 25,
х2 0.
Любое решение (т.е. пара значений переменных х1 и х2), удовлетворяющее всем ограничениям модели, называется допустимым. В нашем примере решение х1 = 200 и х2 = 150 будет допустимым, поскольку не нарушает ни одного ограничения, включая условия неотрицательности. Чтобы убедиться в этом, надо подставить значения х1 = 200 и х2 = 150 в левые части ограничений, выполнить вычисления и проверить, что ни одно неравенство не нарушается. Значение целевой функции при этом решении будет равно z = 2000*200 + 2500*150 = 775 000 (руб.).
Итак, математическая модель построена, осталось найти решение модели. Для выполнения этого дела мы привлечем программу электронных таблиц Excel, а еще точнее — надстройку Поиск решения.
Для анализа полученного оптимального решения в MS Excel предусмотрены три типа отчетов: отчет по результатам, устойчивости и пределам.
Проведем анализ чувствительности задачи (2.1). Для этого необходимо после запуска в Excel задачи на решениев окне Результаты поиска решения выделить с помощью мыши три типа отчетов: Результаты, Устойчивость и Пределы (рис. 3.1).
Рис. 3.1. Типы отчетов
Отчет по результатам.Отчет по результатам состоит из трех таблиц (рис. 3.2):
1) таблица 1 содержит информацию о целевой функции;
2) таблица 2 содержит информацию о значениях переменных, полученных в результате решения задачи;
3) таблица 3 показывает результаты оптимального решения для ограничений и для граничных условий.
Для ограничений в столбце Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в столбце Значение приведены величины использованного ресурса.
Рис. 3.2. Лист отчета по результатам
Если ресурс используется полностью (то есть ресурс дефицитный), то в графе Статуссоответствующее ограничение указывается как «связанное»; при неполном использовании ресурса (то есть ресурс недефицитный) в этой графе указывается «не связан.».
Для граничных условий (строки 24-27 на рис. 3.2) в графе Разница показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Таблица 3 отчета по результатам дает информацию для анализа возможного изменения запасов недефицитных ресурсов при сохранении полученного оптимального значения целевой функции.
Так, если на ресурс наложено ограничение типа
, то в графе Разница дается количество ресурса, на которое была превышена минимально необходимая норма.
Если на ресурс наложено ограничение типа
, то в графе Разница дается количество ресурса, которое не используется при реализации оптимального решения.
Отчет по устойчивости. Отчет по устойчивости состоит из двух таблиц (рис.3.3).
Таблица 1 содержит информацию, относящуюся к переменным:
результирующие значения переменных;
нормированная стоимость, т.е. дополнительные двойственные переменные, которые показывает, на сколько изменяется целевая функция при принудительном включении единицы этой переменной в оптимальное решение;
коэффициенты целевой функции;
допустимые значения приращения коэффициентов целевой функции, при которых сохраняется первоначальное оптимальное решение.
Рис. 3.3. Отчет по устойчивости
Таблица 2 (рис. 3.3) содержит информацию, относящуюся к ограничениям:
величина использованных ресурсовв колонке Результ. значение;
теневые цены, т.е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу. Теневая цена рассчитывается только для дефицитных ресурсов;
значения приращения ресурсов, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.
Отчет по пределам. В отчете пределам (рис. 3.4) показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.
Рис. 3.4. Отчет по пределам
Двойственная задача линейного программирования
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче.
Лекция 4 Анализ чувствительности решения задачи линейного программирования
Похожие статьи:
- Карьерные решения: анализ и воображение
- Пример решения задачи, решаемой с использованием пакета ms excel.
- Градиентный метод решения задачи нелинейного планирования.