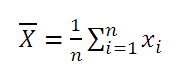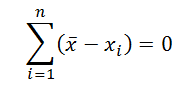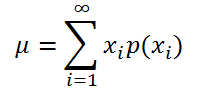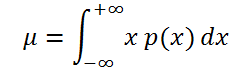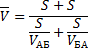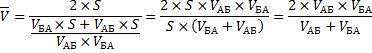Анализ числовых рядов в excel - Word и Excel - помощь в работе с программами

Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Примеры методов анализа числовых рядов в Excel

Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20). Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.

Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.

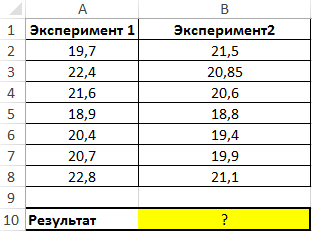
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?

Вид таблицы данных:

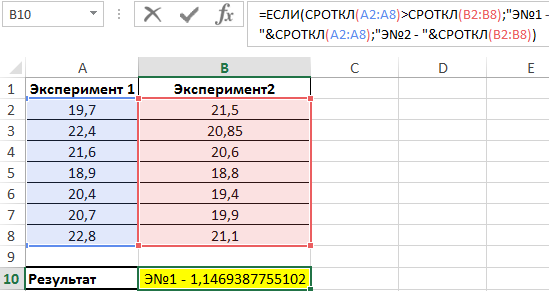
Используем следующую формулу:

Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.

Полученное значение:

В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.

Формула расчета линейного коэффициента вариации в Excel

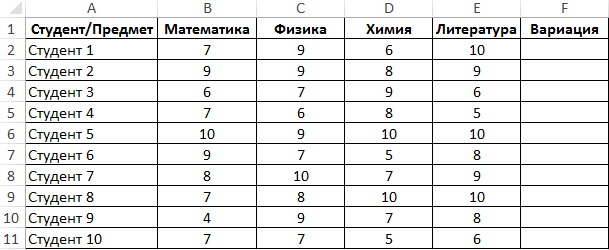
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.

Вид таблицы данных:

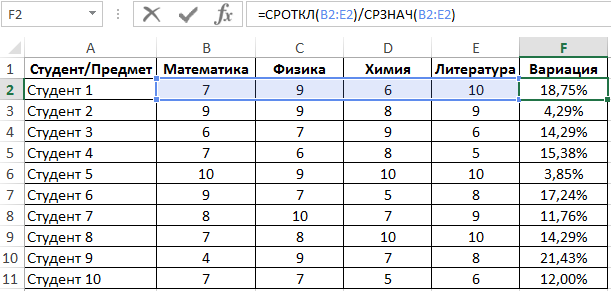
Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:

Растянем ее вниз по столбцу и получим следующие значения:

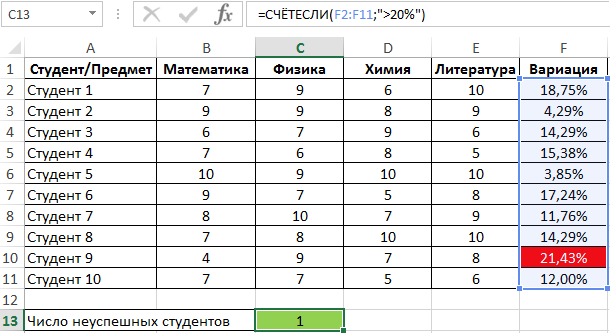
Для определения числа неуспешных студентов по указанному критерию используем функцию:

Полученный результат:

Правила использования функции СРОТКЛ в Excel

Функция имеет следующий синтаксис:

=СРОТКЛ(число1;[число2];…)

Описание аргументов:

число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
[число2];… — необязательный, принимает второе и последующие значения из исследуемого числового ряда.

Примечания:

При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ({2;5;4;7;10}).
Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.

Источник

Содержание

Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
Вопросы и ответы

Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.

Процедура прогнозирования

Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.

Способ 1: линия тренда

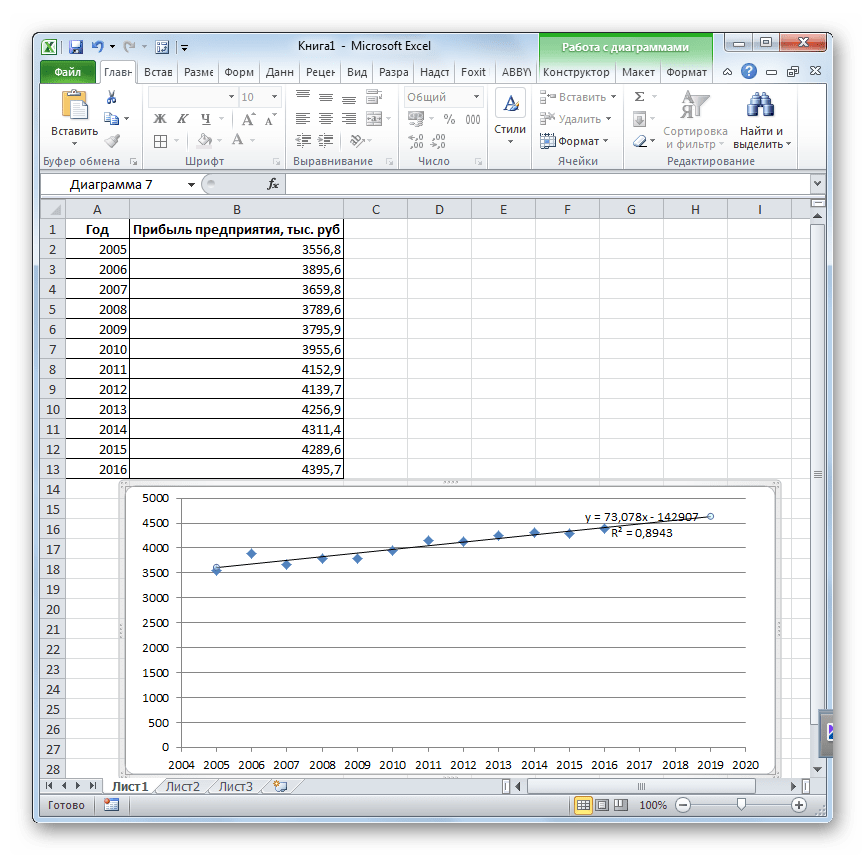
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.

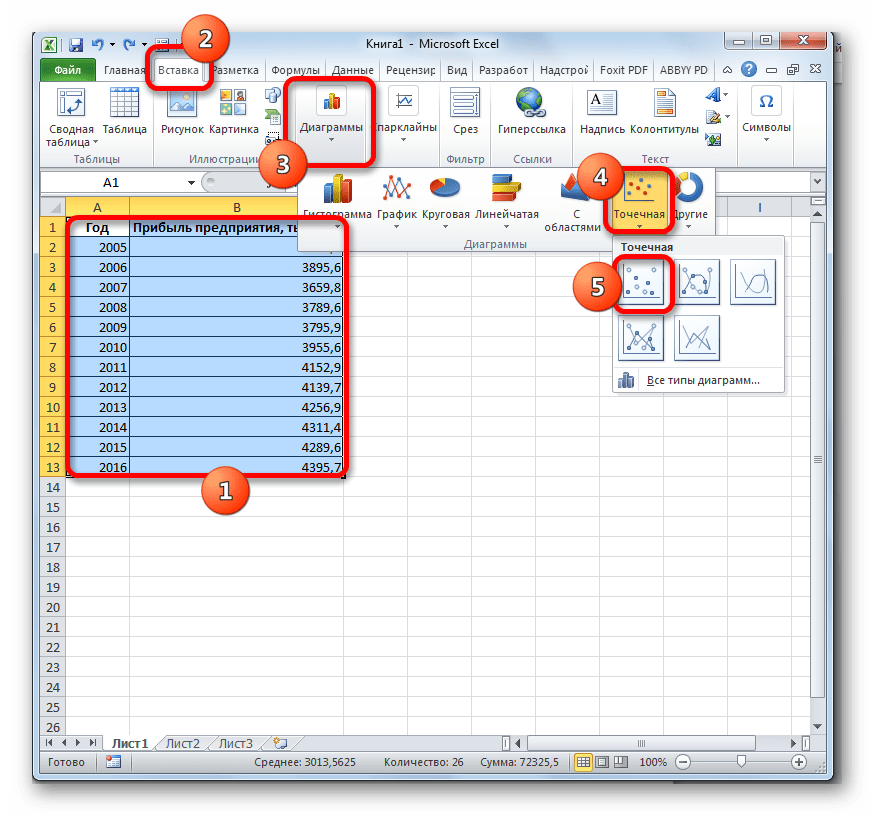
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.

Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.

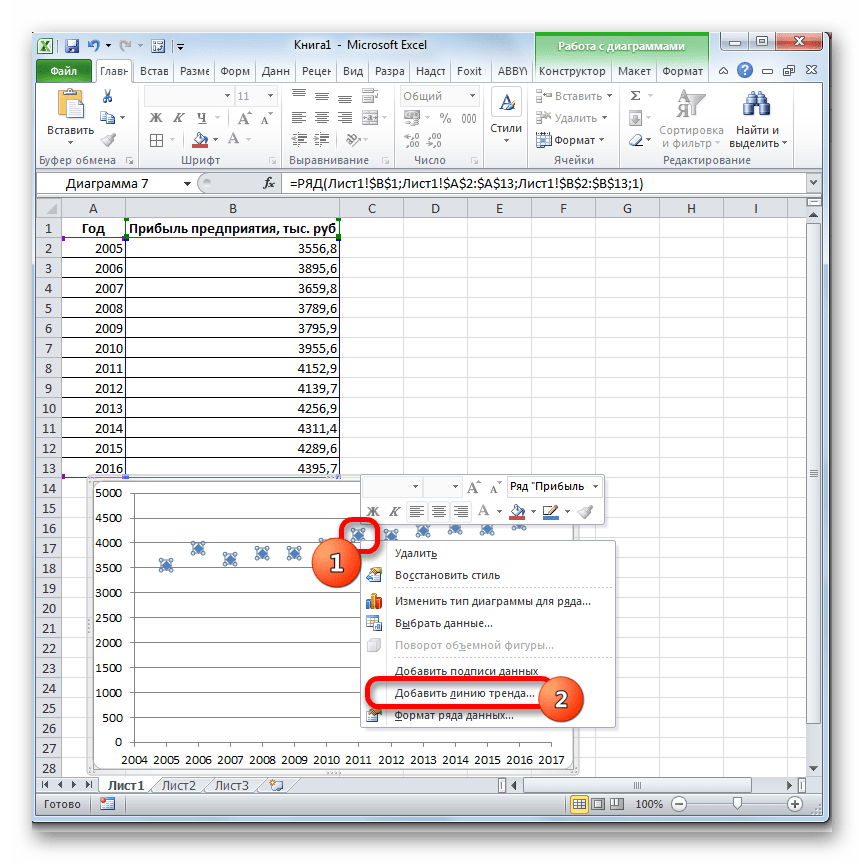
Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».

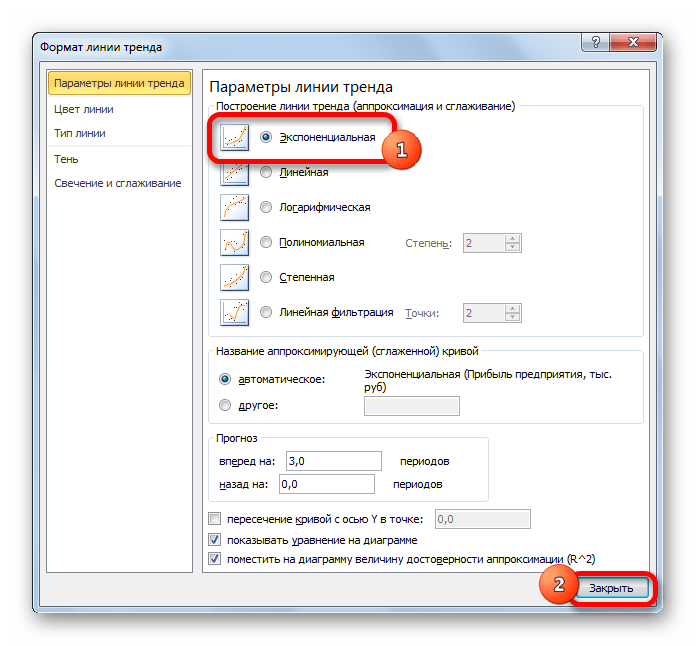
Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
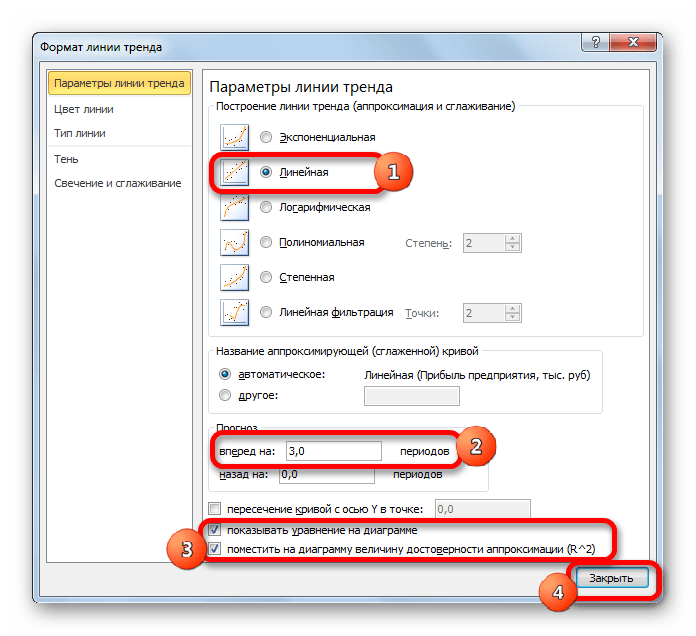
Давайте для начала выберем линейную аппроксимацию.

В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».

Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.

Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.

Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.

Урок: Как построить линию тренда в Excel

Способ 2: оператор ПРЕДСКАЗ

Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:

=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)

«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.

«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.

«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.

Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.

При вычислении данным способом используется метод линейной регрессии.

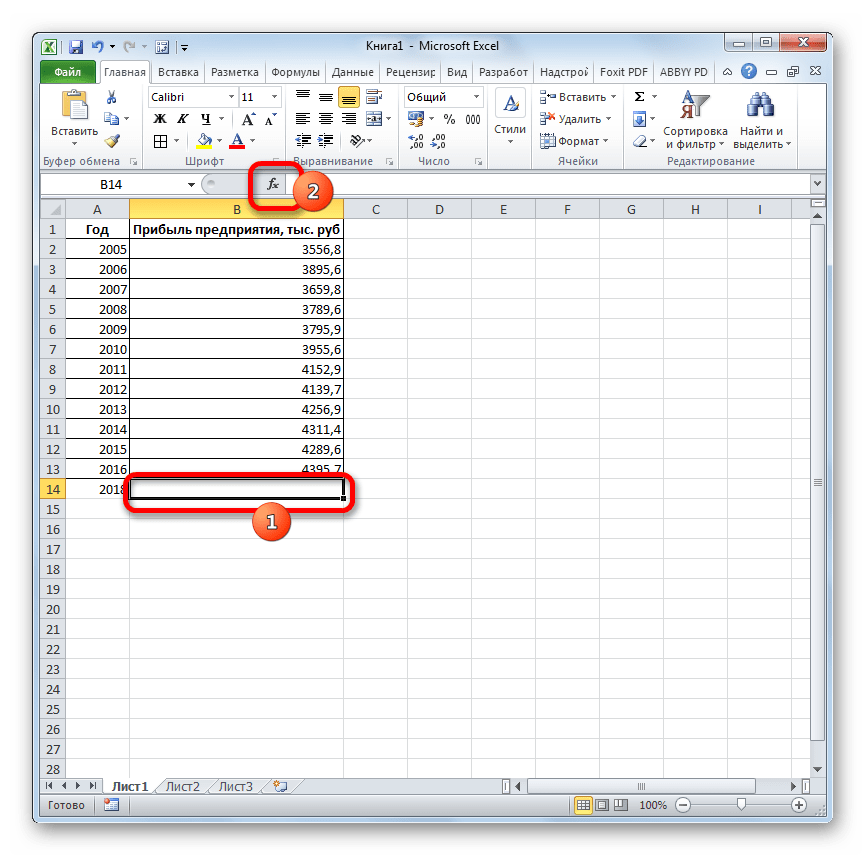
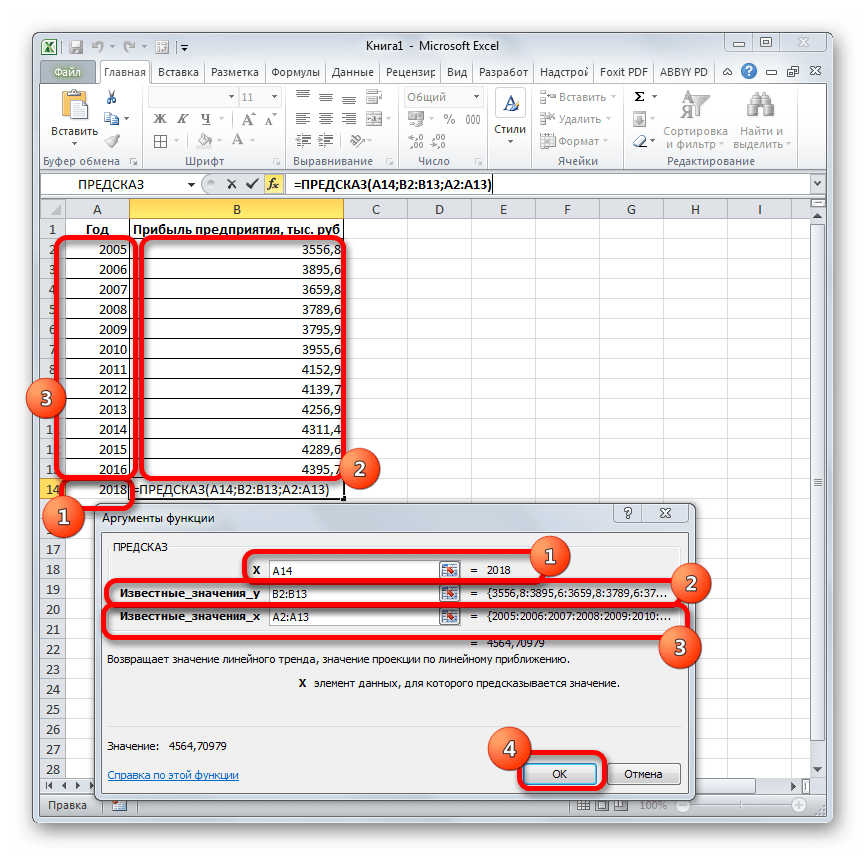
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.

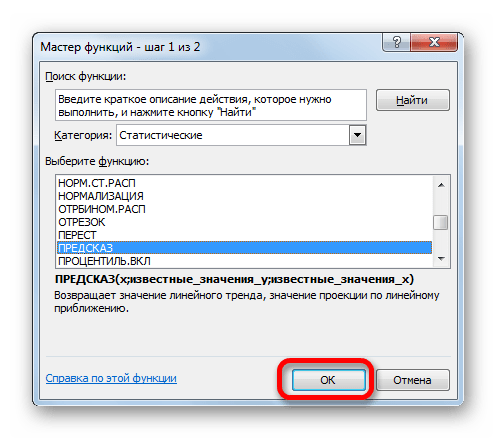
Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».

Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».

Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.

Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.

После того, как вся информация внесена, жмем на кнопку «OK».

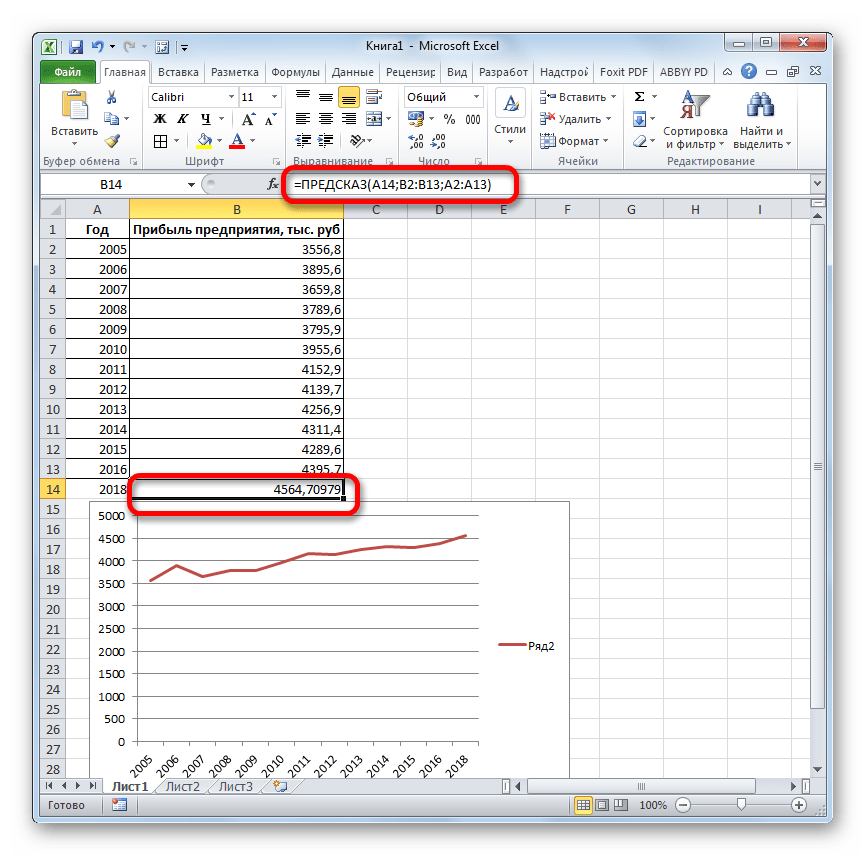
Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.

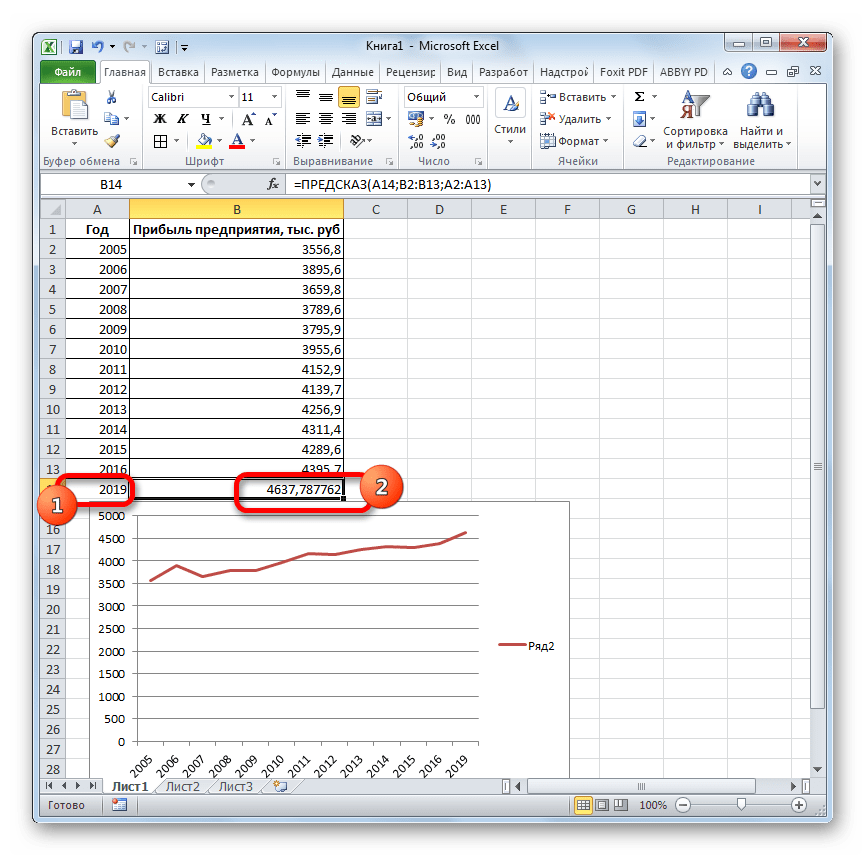
Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.

Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.

Урок: Экстраполяция в Excel

Способ 3: оператор ТЕНДЕНЦИЯ

Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:

=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.

Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.

Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.

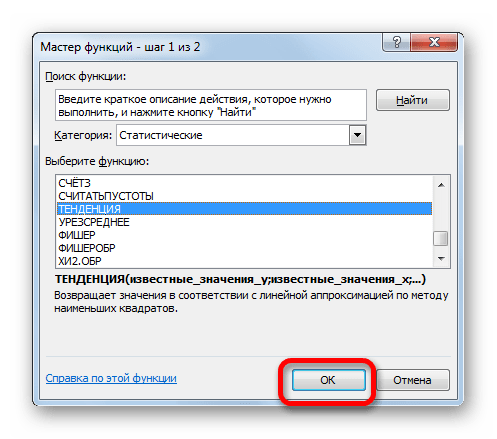
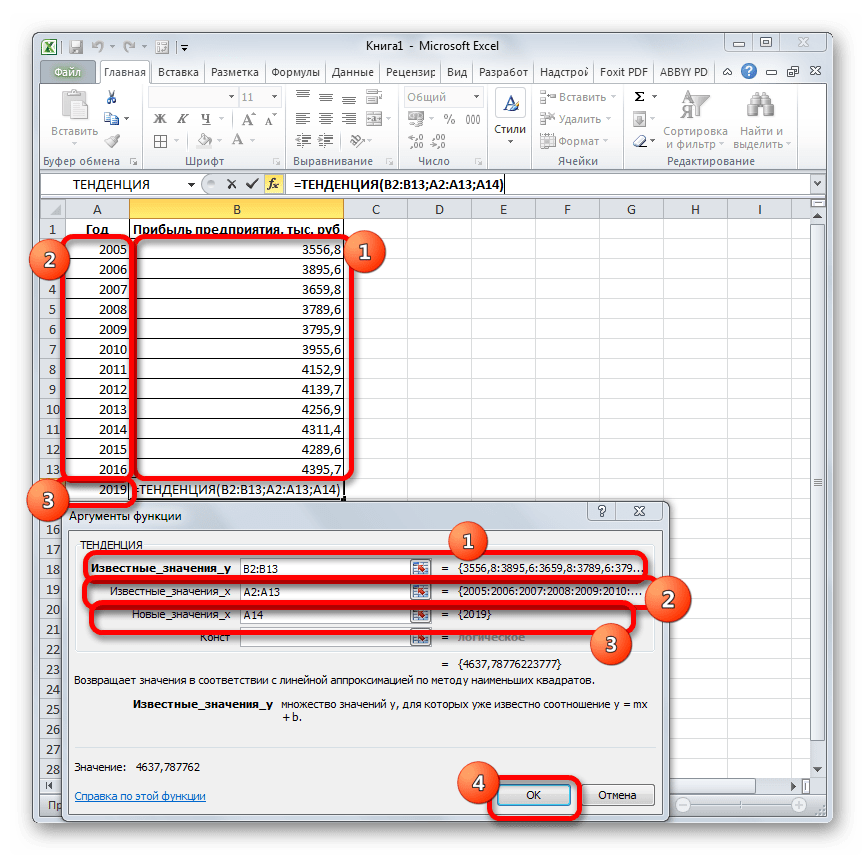
Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».

Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».

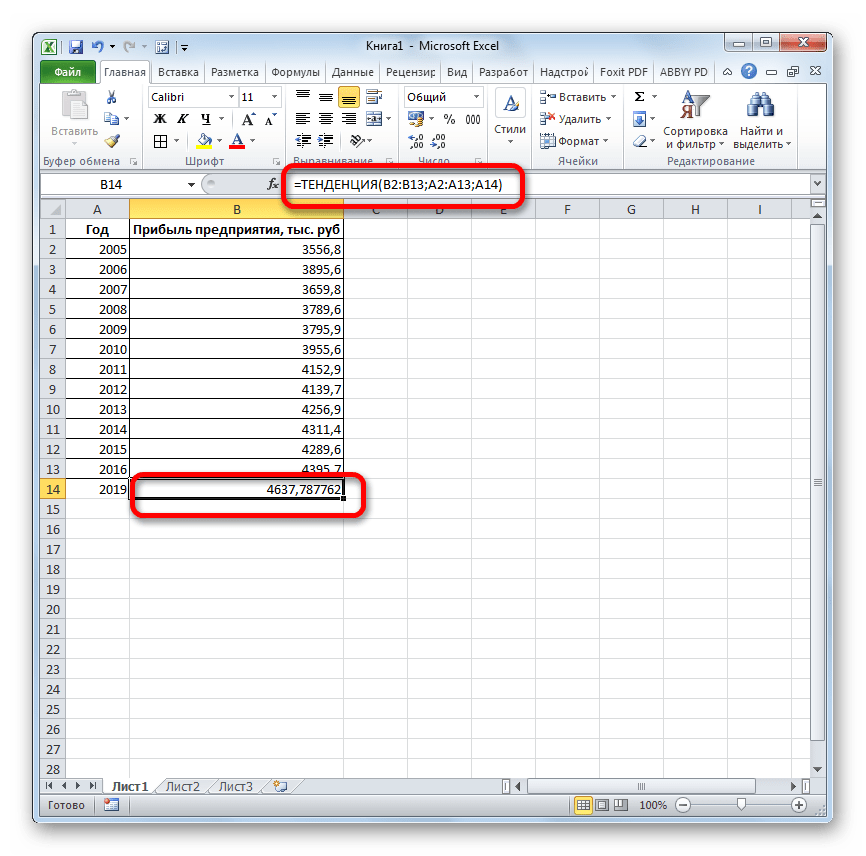
Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.

Способ 4: оператор РОСТ

Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:

=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])

Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.

Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».

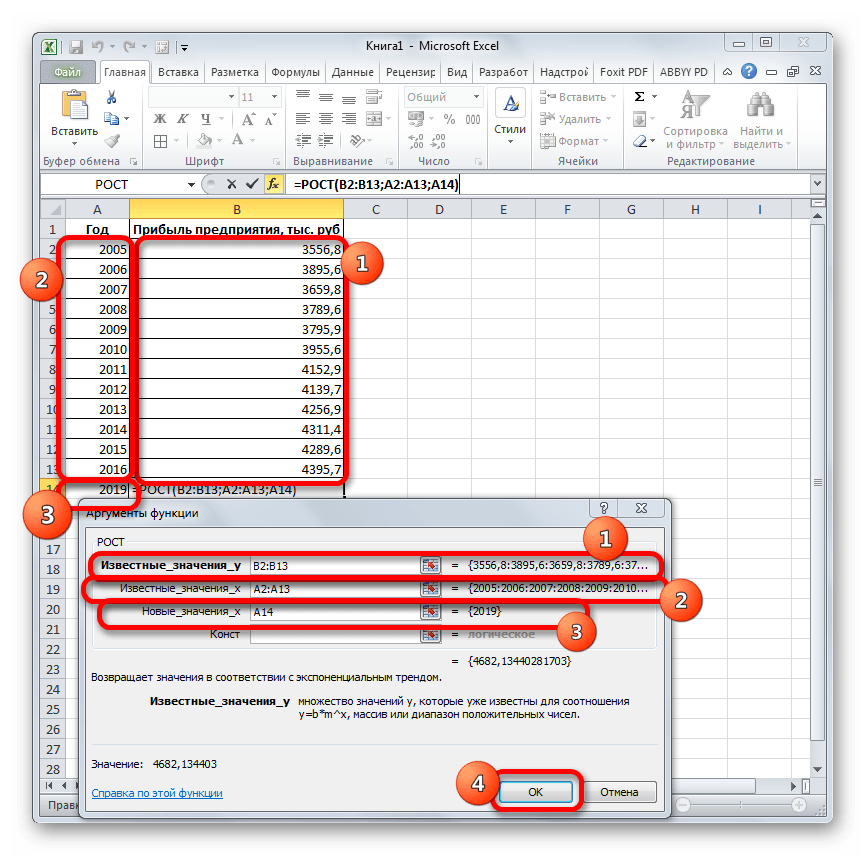
Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».

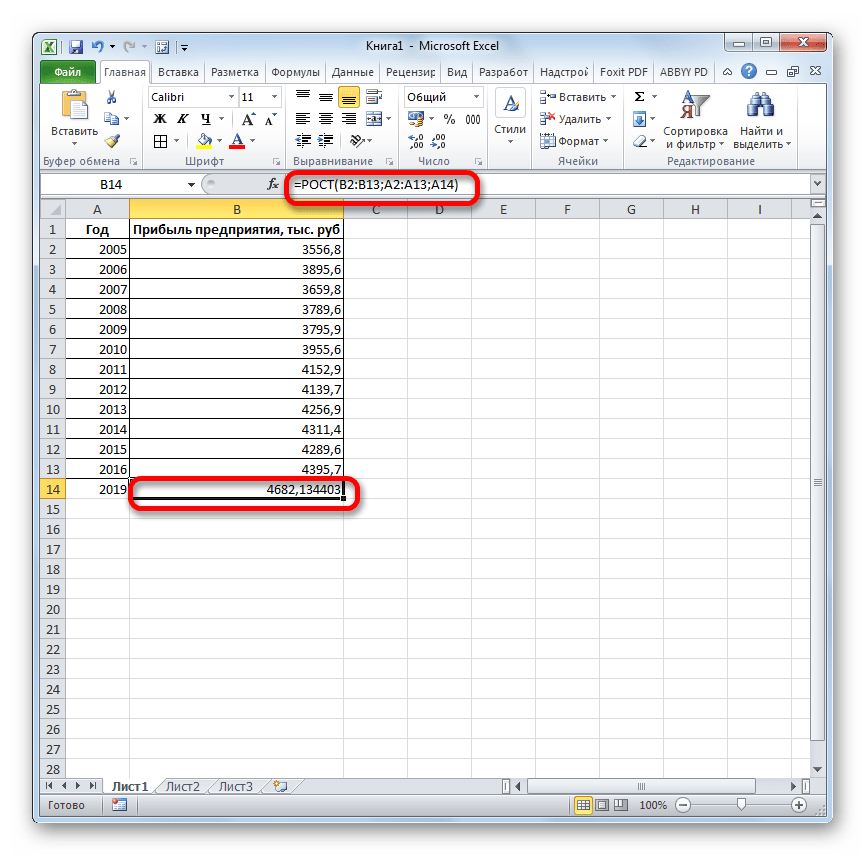
Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.

Способ 5: оператор ЛИНЕЙН

Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:

=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.

Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».

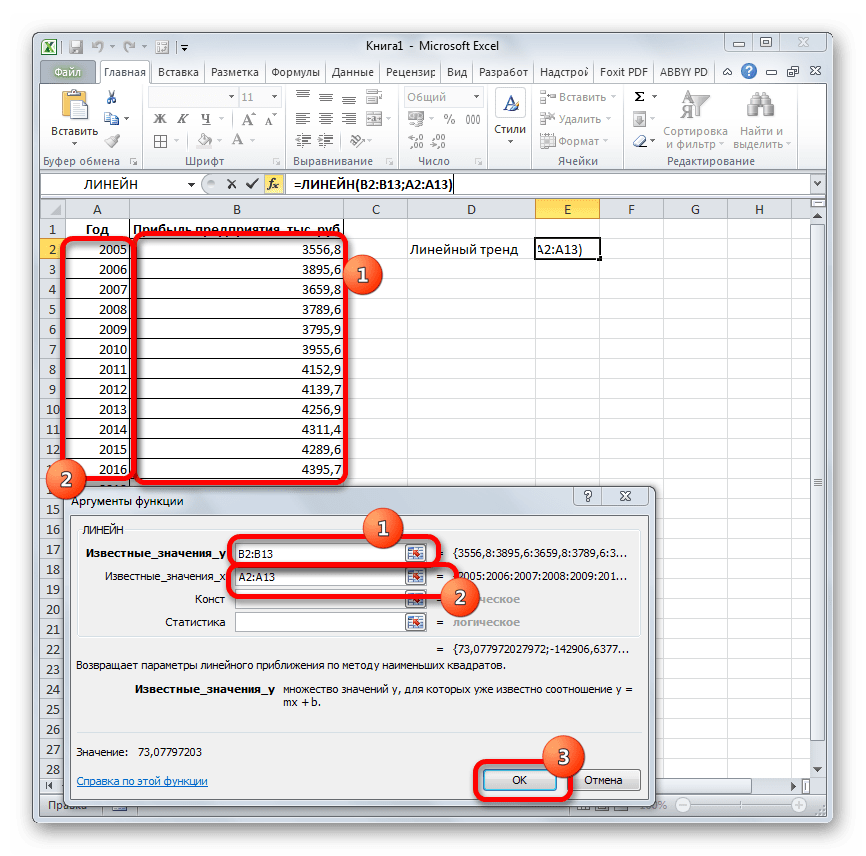
В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».

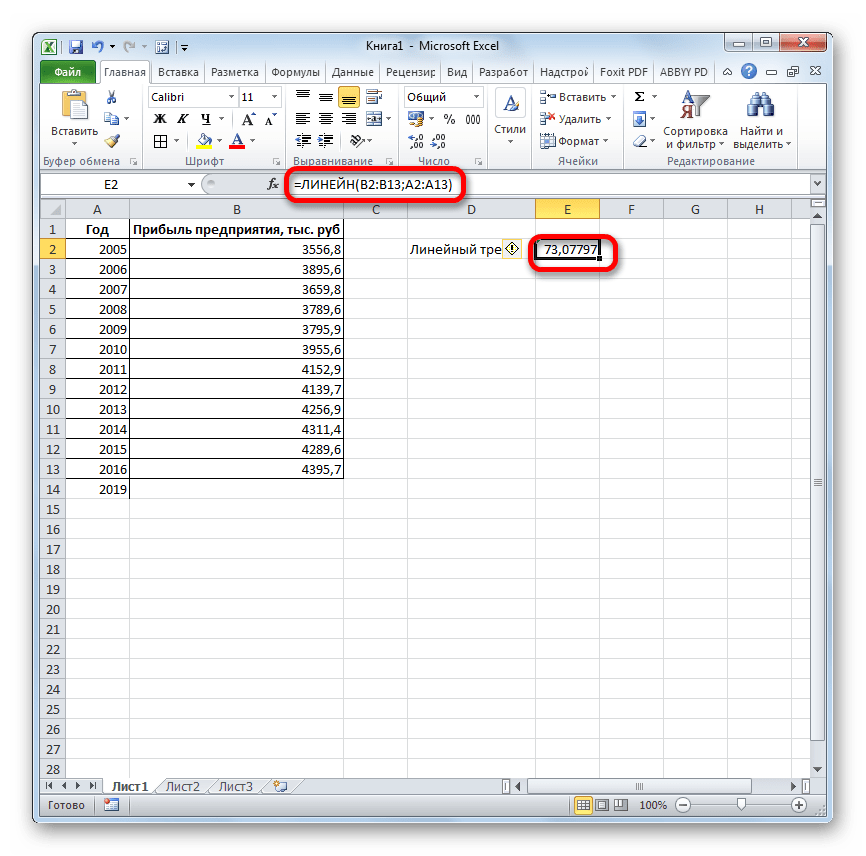
Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.

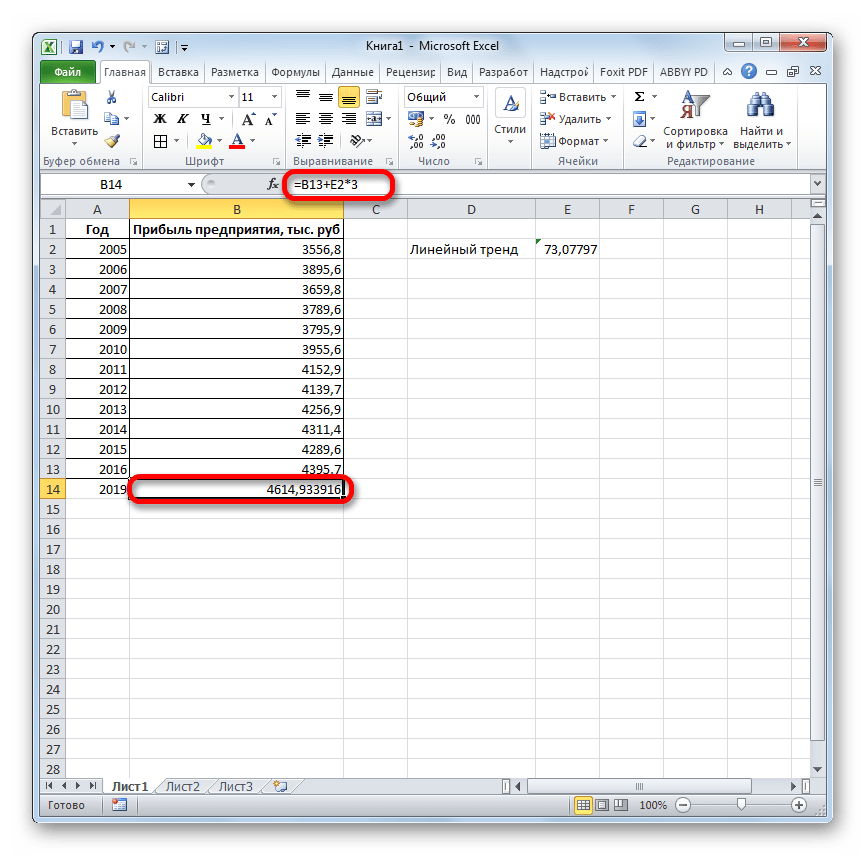
Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.

Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.

Способ 6: оператор ЛГРФПРИБЛ

Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:

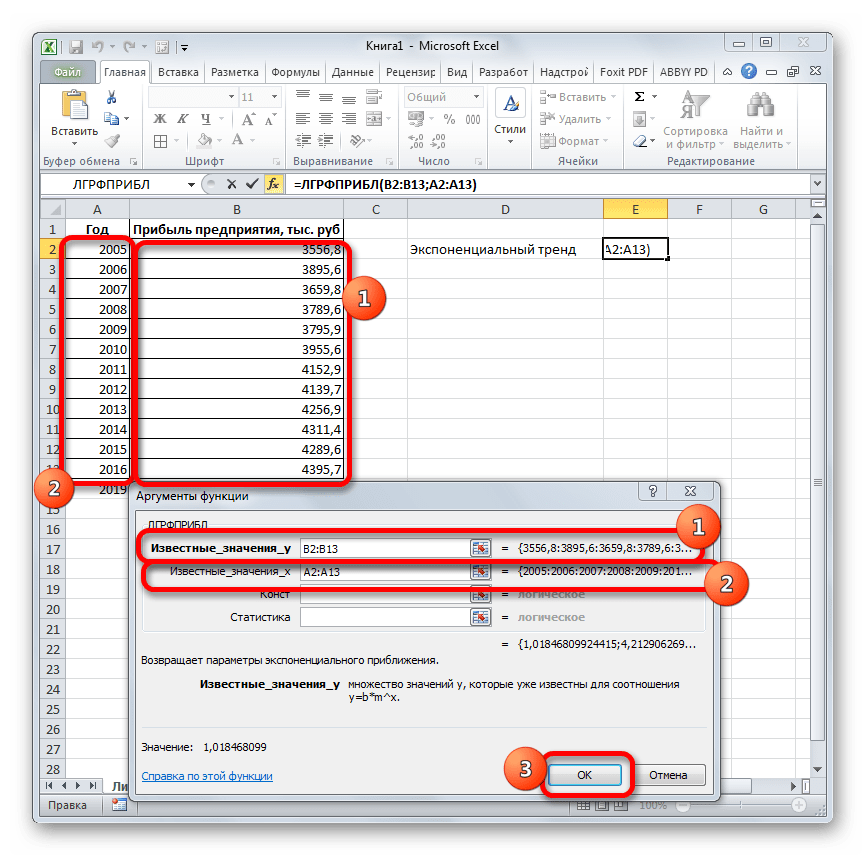
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])

Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.

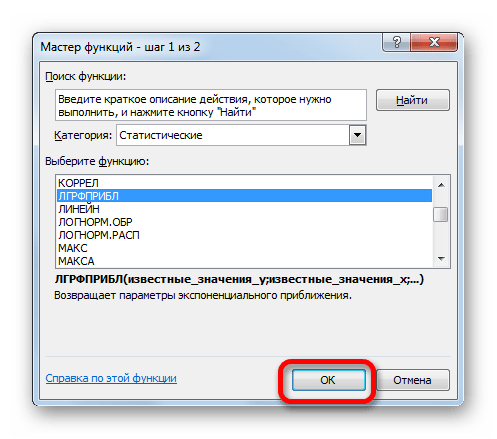
В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».

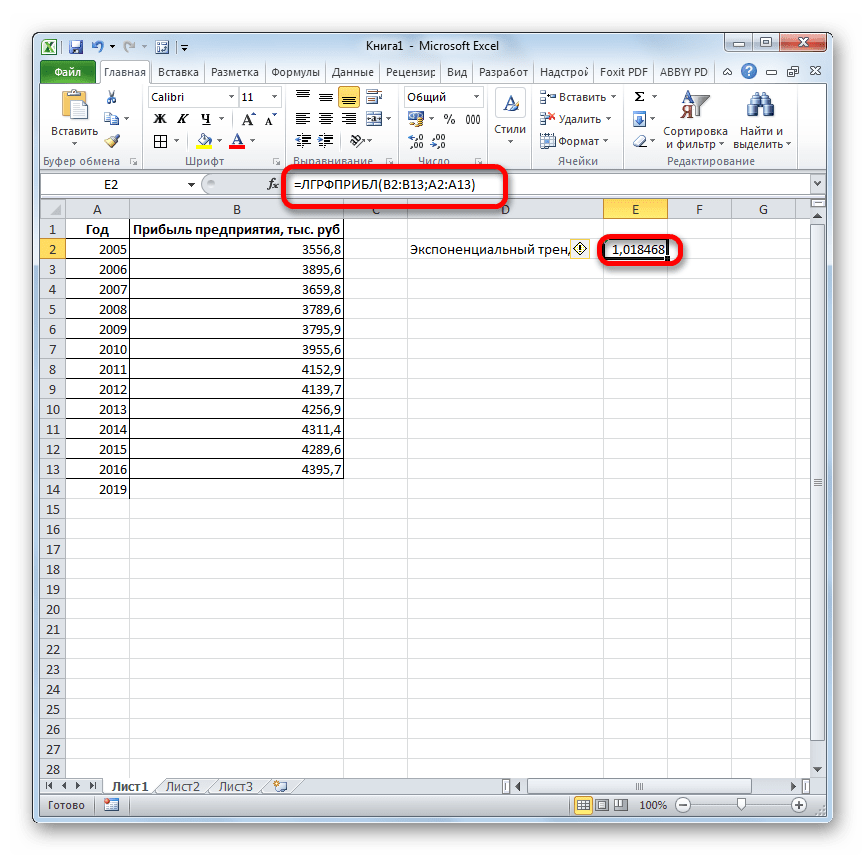
Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».

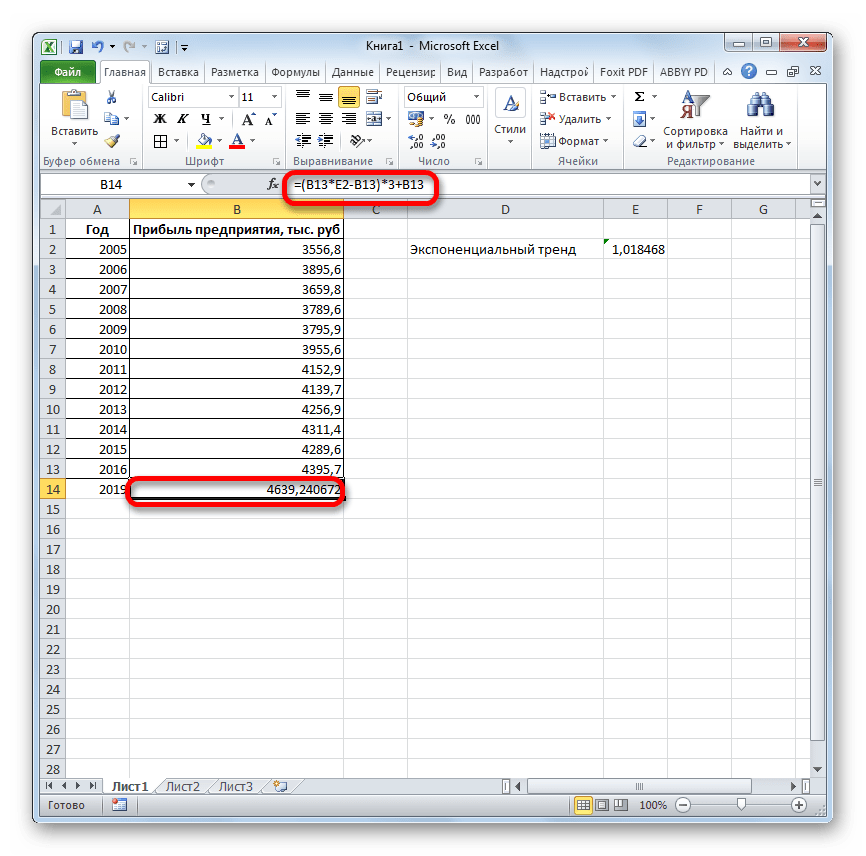
Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.

Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.

Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.

Урок: Другие статистические функции в Excel

Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.

Источник

Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше

Если вам нужно спрогнозировать расходы на следующий год или проецировать ожидаемые результаты для ряда в научном эксперименте, вы можете использовать Microsoft Office Excel для автоматического создания будущих значений, основанных на существующих данных, или для автоматического получения экстраполированных значений, основанных на вычислениях линейного тренда или тренда роста.

Вы можете заполнить ряд значений, которые соответствуют простому линейному или экспоненциальному тренду роста, с помощью маркер заполнения или последовательности. Для расширения сложных и нелинейных данных можно использовать функции или регрессионный анализ в надстройке «Надстройка «Надстройка анализа».

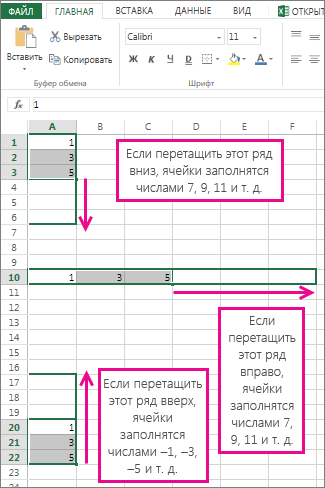
В линейном ряду шаг или разница между первым и следующим значением добавляется к начальному значению, а затем добавляется к каждому последующему значению.

Начальное значение	Расширенный линейный ряд
1, 2	3, 4, 5
1, 3	5, 7, 9
100, 95	90, 85

Чтобы заполнить ряд для линейного тренда, сделайте следующее:

Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Чтобы повысить точность ряда трендов, выберите дополнительные начальные значения.
Перетащите его в нужном направлении.

Например, если в ячейках C1:E1 выбраны начальные значения 3, 5 и 8, перетащите его вправо, чтобы заполнить значениями тенденций, или перетащите его влево, чтобы заполнить значениями убывания.

Совет: Чтобы вручную управлять тем, как создается ряд, или заполнить ряд с помощью клавиатуры, выберите команду Ряд(вкладкаГлавная, группа Редактирование, кнопка Заполнить).

В рядах роста начальное значение умножается на шаг, чтобы получить следующее значение в ряду. Результат и каждый последующий результат умножаются на шаг.

Начальное значение	Расширенный ряд роста
1, 2	4, 8, 16
1, 3	9, 27, 81
2, 3	4.5, 6.75, 10.125

Чтобы заполнить ряд для тенденции роста, сделайте следующее:

Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Чтобы повысить точность ряда трендов, выберите дополнительные начальные значения.
Удерживая нажатой правую кнопку мыши, перетащите указатель заполнения в нужном направлении, отпустите кнопку мыши, а затем на ленте нажмите кнопку контекстное меню.

Например, если в ячейках C1:E1 выбраны начальные значения 3, 5 и 8, перетащите его вправо, чтобы заполнить значениями тенденций, или перетащите его влево, чтобы заполнить значениями убывания.

При нажатии кнопки Ряд можно вручную управлять тем, как создается линейный тренд или тенденция роста, а затем заполнять значения с помощью клавиатуры.

В линейном ряду начальные значения применяются к алгоритму наименьших квадратов (y=mx+b), который создает ряд.
В рядах роста начальные значения применяются к алгоритму экспоненциальной кривой (y=b*m^x), который создает ряд.

В обоих случаях шаг игнорируется. Созданный ряд эквивалентен значениям, возвращенным функцией ТЕНДЕНЦИЯ или функцией РОСТ.

Чтобы заполнить значения вручную, сделайте следующее:

Вы выберите ячейку, в которой нужно начать ряд. Ячейка должна содержать первое значение ряда.

При выборе команды Ряд итоговые ряды заменяют исходные выбранные значения. Если вы хотите сохранить исходные значения, скопируйте их в другую строку или столбец, а затем создайте ряд, выбирая скопированные значения.
На вкладке Главная в группе Редактирование нажмите кнопку Заполнить и выберите пункт Прогрессия.
Выполните одно из указанных ниже действий.
- Чтобы заполнить ряд вниз по worksheet, щелкните Столбцы.
- Чтобы заполнить ряд по всему ряду, щелкните Строки.
В поле Шаг введите значение, на которое вы хотите увеличить ряд.

Тип ряда	Результат шага
Линейная	Значение шага добавляется к первому начальному значению, а затем к каждому последующему значению.
Геометрическая	Первое начальное значение умножается на шаг. Результат и каждый последующий результат умножаются на шаг.

В области Типвыберите линейный или Рост.
В поле Остановить значение введите значение, на которое нужно остановить ряд.

Примечание: Если ряд имеет несколько начальных значений и Excel создать тенденцию, выберите значение Тренд.

Если у вас есть данные, для которых вы хотите спрогнозировать тенденцию, можно создать линия тренда на диаграмме. Например, если в Excel есть диаграмма с данными о продажах за первые несколько месяцев года, вы можете добавить на нее линию тренда, которая отображает общий тренд продаж (увеличение или уменьшение или снижение), а также прогнозируемый тренд на месяцы вперед.

Предполагается, что вы уже создали диаграмму, основанную на существующих данных. Если это не так, см. раздел Создание диаграммы.

Щелкните диаграмму.
Щелкните ряд данных, в который вы хотите добавить линия тренда или скользящее среднее.
На вкладке Макет в группе Анализ нажмите кнопку Линия тренда ивыберите нужный тип линии тренда или скользящего среднего.
Чтобы настроить параметры и отформатирование линии тренда или скользящего среднего, щелкните линию тренда правой кнопкой мыши и выберите в меню пункт Формат линии тренда.
Выберите нужные параметры линии тренда, линии и эффекты.
- При выборе параметра Полиномиальная, введите в поле Порядок наивысшую мощность для независимой переменной.
- Если выбрано значение Скользящегосреднего , введите в поле Период количество периодов, используемых для расчета лино-среднего.

Примечания:

В поле На основе ряда перечислены все ряды данных на диаграмме, которые поддерживают линии тренда. Чтобы добавить линию тренда к другому ряду, щелкните имя в поле и выберите нужные параметры.
При добавлении скользящего среднего на точечная диаграмма скользящие средние значения основаны на порядке, за исключением значений X, относящегося к диаграмме. Чтобы получить нужный результат, перед добавлением скользящего среднего может потребоваться отсортировать значения x.

Важно: Начиная с Excel 2005 г., Excel способ вычисления значения^R2 для линейных линий тренда на диаграммах, где для перехваченной линии тренда установлено значение нуля (0). Эта корректировка исправит вычисления, которые дают неправильные значения R^2,и выровняет вычисление^R2 с функцией LINEST. В результате на диаграммах, созданных в предыдущих версиях Excel, могут отображаться разные значения ^R2. Дополнительные сведения см. в таблице Изменения внутренних вычислений линейных линий тренда на диаграмме.

Если вам нужно выполнить более сложный регрессионный анализ, в том числе вычислить и отсчитывать остаточные данные, используйте средство регрессионного анализа в надстройке «Надстройка «Надстройка анализа». Дополнительные сведения см. в окне Загрузка средства анализа.

В Excel в Интернете, вы можете проецировать значения в ряду с помощью функций или щелкнуть и перетащить его, чтобы создать линейный тренд чисел. Однако создать тенденцию роста с помощью ручки заполнения нельзя.

Вот как можно использовать его для создания линейного тренда чисел в Excel в Интернете:

Выделите не менее двух ячеек, содержащих начальные значения для тренда.

Чтобы повысить точность ряда трендов, выберите дополнительные начальные значения.
Перетащите его в нужном направлении.

Использование функции ПРОГНОЗ Функция ПРЕДСПРОС вычисляет или предсказывает будущее значение с использованием существующих значений. Предсказываемое значение — это значение y, соответствующее заданному значению x. Значения x и y известны; новое значение предсказывается с использованием линейной регрессии. Эта функция используется для предсказания будущих продаж, требований к запасам и потребительских тенденций.

Использование функции ТЕНДЕНЦИЯ или ФУНКЦИИ РОСТ Функции ТЕНДЕНЦИЯ и РОСТ могут выполнять экстраполяцию будущих значений y,которые расширяют прямую или экспоненциальный кривую, наилучшим образом описывающую существующие данные. Они также могут возвращать только значения yна основе известных значений x-длянаиболее подходящих строк или кривой. Для отстройки линии или кривой, описывающую существующие данные, используйте существующие значения x-value и y-value,возвращаемые функцией ТЕНДЕНЦИЯ или РОСТ.

Использование функции ЛИНИИСТОЛ или ФУНКЦИИ ЛОГЕСТ Функцию ЛИННЕФ или LOGEST можно использовать для вычисления прямой или экспоненциальной кривой из существующих данных. Функции LINEST и LOGEST возвращают различные статистические данные о регрессии, включая наклон и отступ линии, которая лучше всего подходит.

В следующей таблице содержатся ссылки на дополнительные сведения об этих функциях.

Функция	Описание
Прогноз	Project значения
Тенденция	Project значения, которые соответствуют прямой линии тренда
Роста	Project, которые соответствуют экспоненциальной кривой
Линейн	Расчет прямой линии из существующих данных
LOGEST	Расчет экспоненциальной кривой из существующих данных

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Нужна дополнительная помощь?

Источник

Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки .

В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки .

Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже ), т.е. среднего значения исходного распределения, из которого взята выборка .

Примечание : О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL .

Некоторые свойства среднего арифметического :

Сумма всех отклонений от среднего значения равна 0:

Если к каждому из значений x _i прибавить одну и туже константу с , то среднее арифметическое увеличится на такую же константу;
Если каждое из значений x _i умножить на одну и туже константу с , то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение . В этом случае среднее значение имеет специальное название — Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание : В англоязычной литературе имеется множество терминов для обозначения математического ожидания : expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет дискретное распределение , то математическое ожидание вычисляется по формуле:

где x _i – значение, которое может принимать случайная величина, а р(x _i ) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение , то математическое ожидание вычисляется по формуле:

где р(x) – плотность вероятности (именно плотность вероятности , а не вероятность, как в дискретном случае).

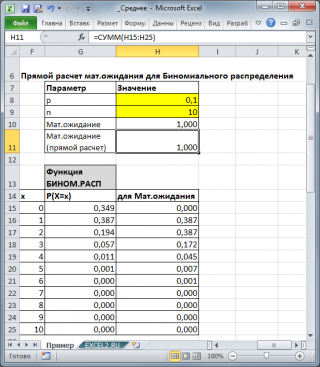
Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения ). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

Свойства математического ожидания

E[a*X]=a*E[X], где а — const

E[E[X]]=E[X] — т.к. величина E[X] — является const

E[X+Y]=E[X]+E[Y] — работает даже для случайных величин не являющихся независимыми.

СОВЕТ : Про другие показатели распределения — Дисперсию и Стандартное отклонение, можно прочитать в статье Дисперсия и стандартное отклонение в MS EXCEL .

Среднее арифметическое в Excel

Среднее арифметическое значение — самый известный статистический показатель. В этой заметке рассмотрим его смысл, формулы расчета и свойства.

Средняя арифметическая как оценка математического ожидания

Теория вероятностей занимается изучением случайных величин. Для этого строятся различные характеристики, описывающие их поведение. Одной из основных характеристик случайной величины является математическое ожидание, являющееся своего рода центром, вокруг которого группируются остальные значения.

Формула матожидания имеет следующий вид:

где M(X) – математическое ожидание

x_i – это случайные величины

То есть, математическое ожидание случайной величины — это взвешенная сумма значений случайной величины, где веса равны соответствующим вероятностям.

Математическое ожидание суммы выпавших очков при бросании двух игральных костей равно 7. Это легко подсчитать, зная вероятности. А как рассчитать матожидание, если вероятности не известны? Есть только результат наблюдений. В дело вступает статистика, которая позволяет получить приблизительное значение матожидания по фактическим данным наблюдений.

Математическая статистика предоставляет несколько вариантов оценки математического ожидания. Основное среди них – среднее арифметическое.

Среднее арифметическое значение рассчитывается по формуле, которая известна любому школьнику.

где x_i – значения переменной,
n – количество значений.

Среднее арифметическое – это соотношение суммы значений некоторого показателя с количеством таких значений (наблюдений).

Свойства средней арифметической (математического ожидания)

Теперь рассмотрим свойства средней арифметической, которые часто используются при алгебраических манипуляциях. Правильней будет вновь вернутся к термину математического ожидания, т.к. именно его свойства приводят в учебниках.

Матожидание в русскоязычной литературе обычно обозначают как M(X), в иностранных учебниках можно увидеть E(X). Встречается обозначение греческой буквой μ (читается «мю»). Для удобства предлагаю вариант M(X).

Итак, свойство 1. Если имеются переменные X, Y, Z, то математическое ожидание их суммы равно сумме их математических ожиданий.

M(X+Y+Z) = M(X) + M(Y) + M(Z)

Допустим, среднее время, затрачиваемое на мойку автомобиля M(X) равно 20 минут, а на подкачку колес M(Y) – 5 минут. Тогда общее среднее арифметическое время на мойку и подкачку составит M(X+Y) = M(X) + M(Y) = 20 + 5 = 25 минут.

Свойство 2. Если переменную (т.е. каждое значение переменной) умножить на постоянную величину (a), то математическое ожидание такой величины равно произведению матожидания переменной и этой константы.

К примеру, среднее время мойки одной машины M(X) 20 минут. Тогда среднее время мойки двух машин составит M(aX) = aM(X) = 2*20 = 40 минут.

Свойство 3. Математическое ожидание постоянной величины (а) есть сама эта величина (а).

Если установленная стоимость мойки легкового автомобиля равна 100 рублей, то средняя стоимость мойки нескольких автомобилей также равна 100 рублей.

Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

Автомойка за день в среднем обслуживает 50 автомобилей (X). Средний чек – 100 рублей (Y). Тогда средняя выручка автомойки в день M(XY) равна произведению среднего количества M(X) на средний тариф M(Y), т.е. 50*100 = 500 рублей.

Формула среднего значения в Excel

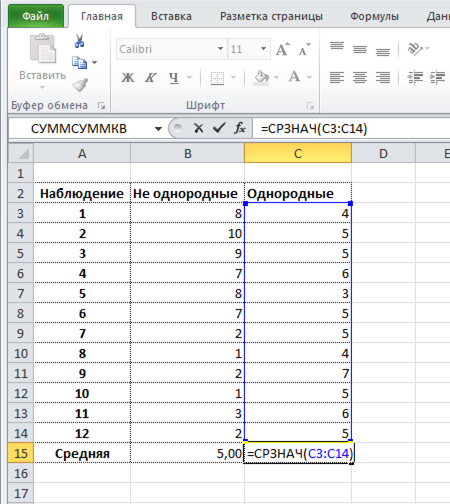
Среднее арифметическое чисел в Excel рассчитывают с помощью функции СРЗНАЧ. Выглядит примерно так.

У этой формулы есть замечательное свойство. Если в диапазоне, по которому рассчитывается формула, присутствуют пустые ячейки (не нулевые, а именно пустые), то они исключается из расчета.

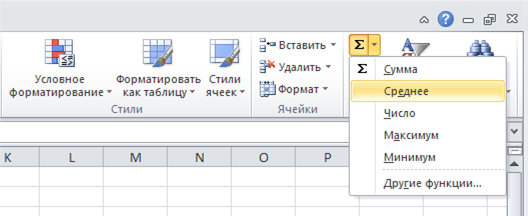
Вызвать функцию можно разными способами. Например, воспользоваться командой автосуммы во вкладке Главная:

После вызова формулы нужно указать диапазон данных, по которому рассчитывается среднее значение.

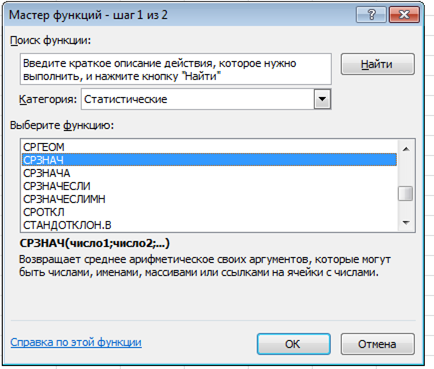
Есть и стандартный способ для всех функций. Нужно нажать на кнопку fx в начале строки формул. Затем либо с помощью поиска, либо просто по списку выбрать функцию СРЗНАЧ (в категории «Статистические»).

Средняя арифметическая взвешенная

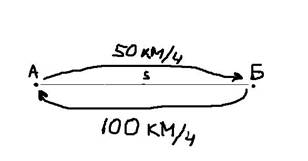
Рассмотрим следующую простую задачу. Между пунктами А и Б расстояние S, которые автомобиль проехал со скоростью 50 км/ч. В обратную сторону – со скоростью 100 км/ч.

Какова была средняя скорость движения из А в Б и обратно? Большинство людей ответят 75 км/ч (среднее из 50 и 100) и это неправильный ответ. Средняя скорость – это все пройденное расстояние, деленное на все потраченное время. В нашем случае все расстояние – это S + S = 2*S (туда и обратно), все время складывается из времени из А в Б и из Б в А. Зная скорость и расстояние, время найти элементарно. Исходная формула для нахождения средней скорости имеет вид:

Теперь преобразуем формулу до удобного вида.

Правильный ответ: средняя скорость автомобиля составила 66,7 км/ч.

Средняя скорость – это на самом деле среднее расстояние в единицу времени. Поэтому для расчета средней скорости (среднего расстояния в единицу времени) используется средняя арифметическая взвешенная по следующей формуле.

где x – анализируемый показатель; f – вес.

Аналогичным образом по формуле средневзвешенной средней рассчитывается средняя цена (средняя стоимость на единицу продукции), средний процент и т.д. То есть если средняя считается по другим усредненным значениям, нужно применить среднюю взвешенную, а не простую.

Формула средневзвешенного значение в Excel

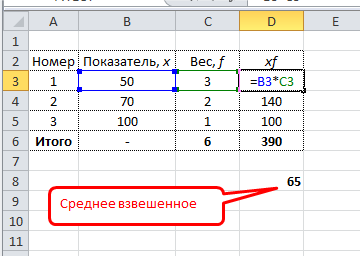
Обычная функция среднего значения в Excel СРЗНАЧ, к сожалению, считает только среднюю простую. Готовой формулы для среднего взвешенного значения в Excel нет. Однако расчет несложно сделать подручными средствами.

Самый понятный вариант создать дополнительный столбец. Выглядит примерно так.

Имеется возможность сократить количество расчетов. Есть функция СУММПРОИЗВ. С ее помощью можно рассчитать числитель одним действием. Разделить на сумму весов можно в этой же ячейке. Вся формула для расчета среднего взвешенного значения в Excel выглядит так:

Интерпретация средней взвешенной такая же, как и у средней простой. Средняя простая – это частный случай взвешенной, когда все веса равны 1.

Физический смысл средней арифметической

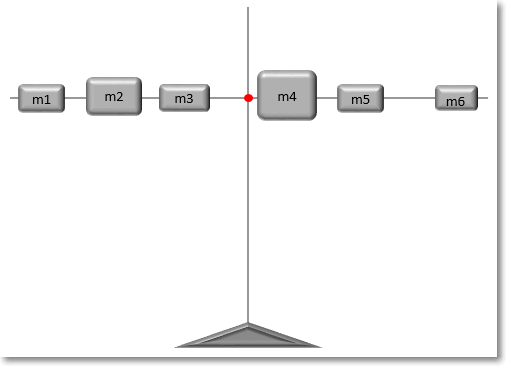
Представим, что имеется спица, на которой в разных местах нанизаны грузики различной массы.

Как отыскать центр тяжести? Центр тяжести – это такая точка, за которую можно ухватиться, и спица при этом останется в горизонтальном положении и не будет переворачиваться под действием силы тяжести. Она должна быть в центре всех масс, чтобы силы слева равнялись силам справа. Для нахождения точки равновесия следует рассчитать среднее арифметическое взвешенное расстояний от начала спицы до каждого грузика. Весами будут являться массы грузиков (m_i), что в прямом смысле слова соответствует понятию веса. Таким образом, среднее арифметическое расстояние – это центр равновесия системы, когда силы с одной стороны точки уравновешивают силы с другой стороны.

И последнее. В русском языке так сложилось, что под словом «средний» обычно понимают именно среднее арифметическое. То есть моду и медиану как-то не принято называть средним значением. А вот на английском языке слово «средний» (average) может трактоваться и как среднее арифметическое (mean), и как мода (mode), и как медиана (median). Так что при чтении иностранной литературы следует быть бдительным.

Формула математическое ожидания в MS Excel – расчет по шагам

Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже), т.е. среднего значения исходного распределения, из которого взята выборка.

Примечание: О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL.

Некоторые свойства среднего арифметического:

Сумма всех отклонений от среднего значения равна 0:

Если к каждому из значений x_i прибавить одну и туже константу с, то среднее арифметическое увеличится на такую же константу;
Если каждое из значений x_i умножить на одну и туже константу с, то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:

где x_i – значение, которое может принимать случайная величина, а р(x_i) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:

где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).

Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

Примеры методов анализа числовых рядов в Excel

Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.

Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.

Вид таблицы данных:

Используем следующую формулу:

Формула расчета линейного коэффициента вариации в Excel

Вид таблицы данных:

Растянем ее вниз по столбцу и получим следующие значения:

Для определения числа неуспешных студентов по указанному критерию используем функцию:

Правила использования функции СРОТКЛ в Excel

Функция имеет следующий синтаксис:

=СРОТКЛ( число1 ;[число2];. )

число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
[число2];… – необязательный, принимает второе и последующие значения из исследуемого числового ряда.

При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ(<2;5;4;7;10>).
Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.

1. Вычислить математическое ожидание:

1) Пуск > Все программы > Microsoft Office > Microsoft Excel

2) Так как функция математического ожидания – это т оже самое, что и функция среднего арифметического, то: в пустой ячейке вводим «=», далее нажимаем fx, выбираем функцию СРЗНАЧ, выделяем числовые данные нашей исходной таблицы.

2. Вычислить дисперсию:

Вводим =, далее – fx, “Статистические” – “ДИСП”, выделить числовые данные нашей исходной таблицы.

3. Среднее квадратичесое отклонение (не смещённое):

Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.

4. Среднее квадратическое отклонение (смещённое):

Вводим =, далее – fx, “Статистические” – “СТАНДТОТКЛОН”, выделить числовые данные нашей исходной таблицы.

Вывод: Microsoft Excel является одной из самых удобных компьютерных программ, с помощью которых можно высчитать статические данные. В этом я убедился, когда высчитывал вышеуказанные данные.

Источник

Excel содержит огромное количество самых разнообразных функций, однако не все они нужны при анализе данных. В этой статье вы узнаете о 10 наиболее популярных функций, которые будут нужны при работе с информацией. Эти функции позволяют выполнить большинство задач, которые появляются при анализе данных.

1. ВПР

Эта функция является одной из самых популярных и часто используемых в Excel. Если вам необходимо найти данные в одном столбце в таблице и получить значение из другого столбца таблицы, то эта функция вам поможет. Ее синтаксис:

ВПР (искомое значение; таблица; номер столбца; интервальный просмотр)

— Искомое значение — это то значение, которое мы будем искать в таблице с данными

— Таблица — диапазон данных, в первом столбце которого мы будем искать искомое значение

—
Номер столбца — этот параметр обозначает, на какое количество столбцов
надо сдвинуться вправо в таблице для получения результата

—
Интервальный просмотр — Может принимать параметр 0 или ЛОЖЬ, что
обозначает что совпадение между искомым значением и значением в первом
столбце таблицы должен быть точным; либо 1 или ИСТИНА, соответственно
совпадение должно быть неточным. Настоятельно рекомендую использовать
только параметр ЛОЖЬ, иначе можно получать непредсказуемые результаты.

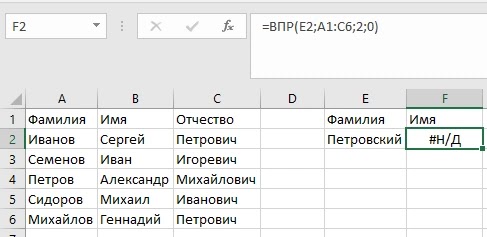
В примере выше мы ищем по фамилии Петров имя в таблице с базой данных по ФИО. В функции ВПР(E2;A1:C6;2;0) первый параметр (E2) — ссылка на ячейку с фамилией, по которой мы будем искать имя; второй параметр A1:C6 — ссылка на таблицу, в первом столбце которой мы ищем указанное в первом параметре значение; третий параметр «2» — из какого столбца справа извлекать значение; четвертый параметр «0» — точный поиск.

Если хотите изучить более подробно, как работает функция ВПР, прочитайте нашу статью «Функция ВПР в Excel».

2. ГПР

Функция ГПР выполняет туже задачу, что и ВПР, только она просматривает первую строку в поиске искомого значения и для получения результата сдвигается на указанное количество строк вниз.

Синтаксис функции следующий:

ГПР(искомое значение;таблица;номер строки;интервальный просмотр)

— Искомое значение — значение, которое мы ищем в строке.

— Таблица- диапазон данных на листе, где в первой строке мы ищем искомое значение и сдвигаемся на необходимое количество строк.

— Номер строки- числовое значение, указывающее на сколько строк вниз надо сместиться.

— Интервальный просмотр — ставьте всегда 0, тогда Эксель будет искать точное совпадение, что нам и нужно в большинстве случаев.

В примере выше мы ищем выручку за сентябрь в помесячном отчете по выручке. В формуле ГПР(A5;B1:M2;2;0) первый параметр (А5) — ссылка на месяц, по которому мы хотим получить выручку; второй параметр (B1:M2) — ссылка на таблицу, где в первой строке указаны месяцы, среди которых нам нужно найти выбранный; третий параметр «2» — из какой строки ниже мы будем получать данные; четвертый параметр «0» — ищем точное совпадение.

Если вы хотите более подробно изучить, как пользоваться функцией ГПР — прочитайте статью на нашем сайте «Функция ГПР в Excel».

3. ЕСЛИ

Функция ЕСЛИ является очень популярной в Excel. Она позволяет автоматически выполнять какое-либо действие, в зависимости от поставленного условия.

Функция ЕСЛИ выполняет проверку логического выражения и если выражение истинно, то поставляется одно значение и альтернативное, если ложь. Синтаксис следующий:

ЕСЛИ(логическое выражение; значение если истина; значение если ложь)

— Логическое выражение — выражение, которое по итогу своего вычисления должно вырнуться значение ИСТИНА или ЛОЖЬ.
— Значение, если истина — устанавливаем указанное значение, если логическое выражение вернуло ИСТИНА
— Значение, если ложь — устанавливает указанное значение, если логическое выражение вернуло ЛОЖЬ.

В примере выше мы хотим определить, получили ли мы за месяц выручку больше 500 рублей или нет. В формуле ЕСЛИ(B2>500;»Да»;»Нет») первый параметр (B2>500) проверяет, выручка за месяц больше 500 рублей или нет; второй параметр («Да») — функция вернет Да, если выручка больше 500 рублей и соответственно Нет (третий параметр), если выручка меньше.

Обратите внимание, что значения при истине или лжи могут быть не только текстовые, числовые, но также и функции(в том числе и ЕСЛИ), что позволяет реализовать достаточно сложные логические конструкции.

4. ЕСЛИОШИБКА

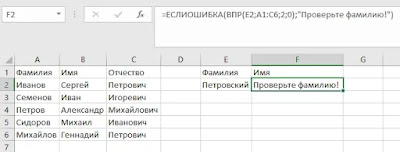
При работе с формулами в Excel, можно время от времени сталкиваться с различными ошибками. Так в примере ниже функция ВПР вернула ошибку #Н/Д из-за того, что в базе данных по ФИО нет искомой нами фамилии (более подробно об ошибке #Н/Д вы можете прочитать в этой статье: «Как исправить ошибку #Н/Д в Excel»)

Для обработки таких ситуаций отлично подойдет функция ЕСЛИОШИБКА. Ее синтаксис следующий:

ЕСЛИОШИБКА(значение; значение если ошибка)

— Значение, результат которого проверяется на ошибку.
— Значение, если ошибка — В случае, если в результате работы функции получаем ошибку, то выводится не ошибка, а данное значение.

В случае с нашим примером выше, мы можем предположить, что фамилия может быть некорректной, соответственно ЕСЛИОШИБКА вернет нам предупреждение, что бы мы проверили написание фамилии.

В примере выше, мы проверяем результат работы функции ВПР(E2;A1:C6;2;0) и в случае, если вернется ошибка, то выдаем сообщение «Проверьте фамилию!».

5. СУММЕСЛИМН

Функция СУММЕСЛИМН позволяет суммировать значения по определенным условиям. Условий может быть несколько. В Excel также есть функция СУММЕСЛИ, которая позволяет суммировать по одному критерию. Призываю вас использовать более универсальную формулу.

У функции СУММЕСЛИМН следующий синтаксис:

СУММЕСЛИМН(Диапазон суммирования; Диапазон условия 1; Условие 1;…)

— Диапазон суммирования — область листа Эксель, из которой мы суммируем данные
— Диапазон условия 1 — Диапазон ячеек, которые мы проверяем на соответствие условию
— Условие 1 — Условие, которое проверяется на соответствие в Диапазоне 1.
Обратите внимание, что диапазонов условий и соответственно условий может быть столько, сколько вам нужно.

Для примера выше мы хотим получит выручку, которую принес нам Петров в городе Москва. Формула имеет вид СУММЕСЛИМН(C2:C13;A2:A13;E2;B2:B13;F2), где C2:C13 — диапазон со значениями выручки, которые необходимо просуммировать; А2:А13 — диапазон с фамилиями, которые мы будем проверять; Е2 — ссылка на конкретную фамилию; B2:B13 — ссылка на диапазон с городами; F2 — ссылка на конкретный город.

Более подробно о функциях СУММЕСЛИМН и СУММЕСЛИ рассказано в статье «СУММЕСЛИ и СУММЕСЛИМН в Excel».

6. СЧЁТЕСЛИМН

СЧЁТЕСЛИМН очень похожа на функцию СУММЕСЛИМН, только в отличии от нее, она не суммируется значения, а только считает количество ячеек, которые соответствуют определенным условиям. Как и в случае с СУММЕСЛИМН, у СЧЁТЕСЛИМН есть упрощенная форма СЧЁТЕСЛИ, который считает количество ячеек только по одному критерию, но лучше используйте более общий вариант.

Синтаксис у функции следующий:

СЧЁТЕСЛИМН(диапазон условия 1; условие 1;…)

— Диапазон условия 1 — Диапазон ячеек, которые проверяются на соответствие определенному условию.
— Условие 1 — Условие, которое определяет какие ячейки надо учитывать при подсчете.
Обратите внимания, что диапазонов условий и соответственно условий может быть несколько.

В примере выше, мы считаем сколько в таблице ячеек, в которых фамилия — Петров, а город — Москва. В формуле СЧЁТЕСЛИМН(A2:A13;E2;B2:B13;F2) диапазон A2:A13 — диапазон фамилий, которые мы проверяем, Е2 — та фамилия, которую мы ищем в диапазоне; B2:B13 — диапазон городов и соответственно F2 — город, который мы учитываем при подсчете ячеек. Получившееся число 3 — это количество строк в таблице, где фамилия равна Иванов, а город равен Москва.

7. СЖПРОБЕЛЫ

При работе с данными в Excel, мы можем получать их из разных источников, что может привести к тому, что получаемые значения имеют «мусорную» информацию, очень часто это лишние пробелы, которые надо удалить. Можно удалять вручную, но это долго и муторно. На выручку нам приходит функция СЖПРОБЕЛЫ, которая удаляет лишние пробелы, в случае если их больше одного подряд. Синтаксис у функции очень простой:

СЖПРОБЕЛЫ(текст)

— Текст — тот текст, из которого надо убрать лишние пробелы.

Как видно из примера выше, функция успешно удалила лишние пробелы из исходной строки.

8. ЛЕВСИМВ и ПРАВСИМВ

Функции ЛЕВСИМВ и ПРАВСИМВ возвращают определенное количество знаков с начала (ЛЕВСИМВ) либо с конца (ПРАВСИМВ) строки. Эти функции нужны для получения части строки. Синтаксис у функций однотипный:

ЛЕВСИМВ(текст; количество знаков)
ПРАВСИМВ(текст; количество знаков)

— Текст — то строковое выражение, из которого мы хотим получить часть.
— Количество знаков — число символов, которое мы хотим получить.

В примере выше мы из текста «Пример текста» извлекаем 6 символов слева и получаем текст «Пример».

9. СЦЕПИТЬ

Функция СПЕПИТЬ позволяет объединить значения из нескольких ячеек. Синтаксис у функции достаточно простой:

СЦЕПИТЬ(текст1; текст2;…)

— Текст 1 — Текст, который надо соединить в одну строку
— Текст 2 — Текст, который надо соединить в одну строку
Обратите внимание, что вы можете объединить до 255 текстовых значений.

В примере выше мы объединяем фамилию и имя. В функции СЦЕПИТЬ(A2;» «;B2), первый параметр(А2) — ссылка на ячейку с фамилией; второй параметр (» «) — пробел, что бы итоговый текст смотрелся нормально; третий параметр(В2) — ссылка на ячейку с именем.

10.ЗНАЧЕН

Часто данные, которые мы получаем из внешних источников, имеют текстовый формат и мы не можем производить с ними математических действий (складывать, вычитать и т.п.). Нам требуется сначала преобразовать текст в число, для этого используйте функцию ЗНАЧЕН. Синтаксис у функции следующий:

ЗНАЧЕН(текст)

— Текст — число, представленное в текстовом формате

Как видно в примере выше, у нас есть число 12522, которое представлено в виде текста, при помощи функции ЗНАЧЕН мы преобразовали его в число 12 522, с которым в дальнейшем можем работать, как с любыми другими числами.

Спасибо, что дочитали статью. Я постарался выбрать 10 наиболее полезных функций в Excel, которые нужны при анализе данных. Жду ваши комментарии.

Источник