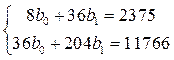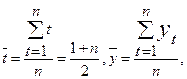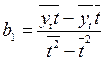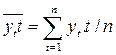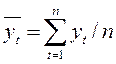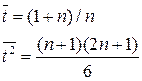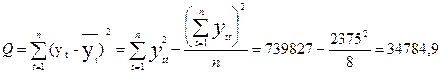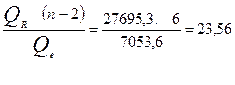Аналитическое выравнивание ряда в excel

Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.

Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.

Временные ряды в Excel

Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.

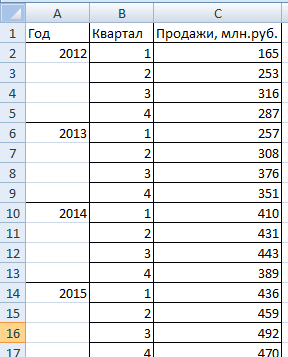
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.

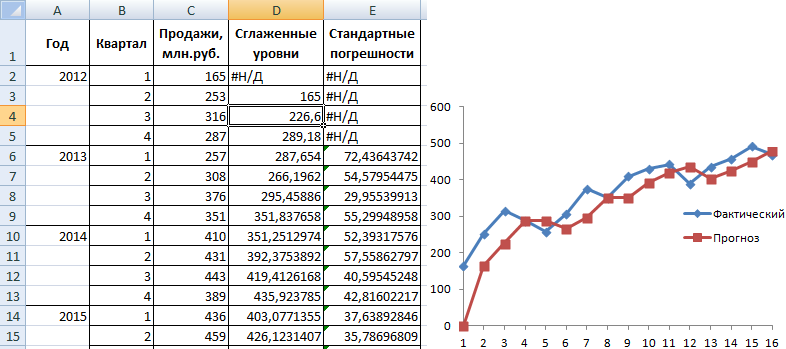
Внесем данные о реализации в таблицу Excel:

На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».

Подключение настройки «Анализ данных» детально описано здесь.

Нужная кнопка появится на ленте.

Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.

Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».

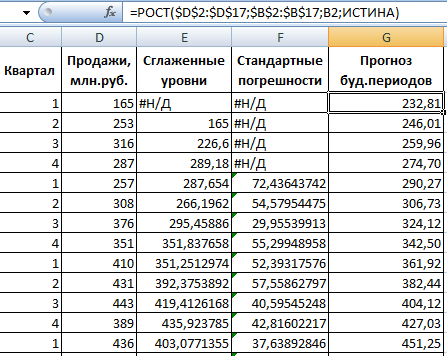
Закрываем диалоговое окно нажатием ОК. Результаты анализа:

Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).



Прогнозирование временного ряда в Excel

Составим прогноз продаж, используя данные из предыдущего примера.

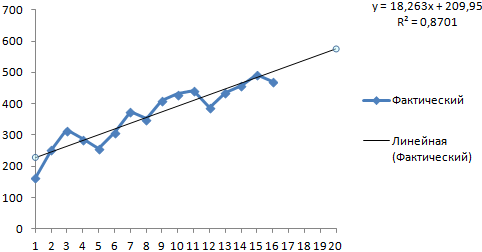
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).

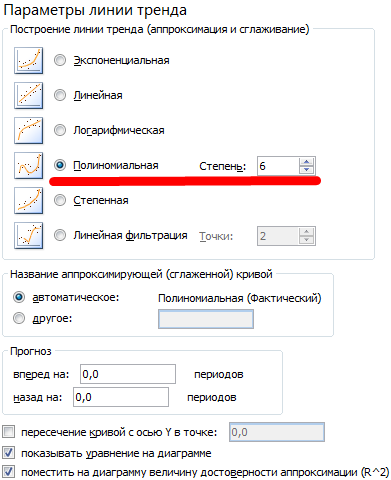
Настраиваем параметры линии тренда:

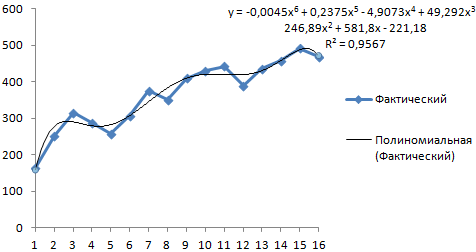
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.

R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.

Уравнение тренда – это модель формулы для расчета прогнозных значений.

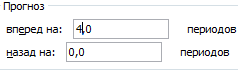
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.

Получаем достаточно оптимистичный результат:

В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.

Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.

Для линейной зависимости – ТЕНДЕНЦИЯ.

При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.

Аналитическое выравнивание временного ряда.

Рассмотрим модель временного ряда y_t = f(t) + , где f(t) — неслучайная составляющая (тренд, либо тренд и циклическая и (или) сезонная компонента, выражающая основную тенденцию).

Под выравниванием временного ряда понимают выделение неслучайной составляющей f(t), которая характеризует основную тенденцию изучаемого процесса, и выбор этой функции. Наиболее часто используются следующие функции:

f(t) = a + bt — линейная;

f(t) = e a+bt — экспоненциальная;

f(t) = a/(1 + be -ct ) — логистическая;

f(t) = C a-b(r) — Кривая Гомперца, 0 2 _adj и выбора уравнения с максимальным R 2 _adj.

Например. Для предыдущего примера построим график временного ряда с помощью «Мастера диаграмм» и добавим линию тренда.

Отметим, что, как и раньше, наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов:

— линейный тренд: y_t = a + bt, a — начальный уровень временного ряда, b — средний абсолютный прирост уровней ряда. Система нормальных уравнений имеет вид

— экспоненциальный тренд: y_t = e a+bt , е а — начальный уровень временного ряда, е b — средний в единицу времени коэффициент роста уровней ряда. Определение параметров требует предварительной линеаризации.

Другим методом выравнивания временного ряда является метод скользящей средней. Он основан на переходе от начальных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. Получаемый т.о. ряд ведет себя более гладко, чем исходный из-за устранения отклонений ряда. Рассмотрим использование этого метода на примере построения аддитивной и мультипликативной моделей временного ряда с сезонной составляющей:

(Если амплитуда колебаний приблизительно постоянна, то строят аддитивную модель, в противном случае — мультипликативную). Например, для рассматриваемого примера амплитуду можно считать приблизительно постоянной, следовательно подходящей будет аддитивная модель.

Процесс построения модели включает следующие шаги:

• 1. Выравнивание ряда методом скользящей средней.
• 2. Расчет значений сезонной составляющей .

3. Устранение сезонной составляющей и получение выравненных данных или .

• 4. Аналитическое выравнивание уровней или и расчет значений .
• 5. Расчет полученных по модели значений или .
• 6. Расчет абсолютных и (или) относительных ошибок.

Пояснения к выполнению шагов.

• 1. Проведем выравнивание исходных уровней ряда методом скользящей средней (таблица 1):
  • а) просуммируем уровни последовательно за каждые 4 квартала со сдвигом на один момент времени;
  • б) найдем скользящие средние делением на 4 полученных сумм (полученные значения уже не содержат сезонной компоненты);
  • в) приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих

средних — центрированные скользящие средние.

• 2. Оценим сезонную компоненту:
  • — для аддитивной модели — как разность между фактическими уровнями ряда y_t и центрированными скользящими средними;
  • — для мультипликативной модели — как частное от деления фактических уровней ряда на центрированные скользящие средние.

Используем эти оценки для расчета значений сезонной компоненты (таблица 2).

В моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются. Это выражается в том, что сумма значений сезонной компоненты по всем кварталам равна: нулю для аддитивной модели и числу периодов в цикле для мультипликативной модели. Определяем корректирую-щий коэффициент k и скорректированные значения сезонной компоненты: = — k или = k.

3. Исключим влияние сезонной компоненты: или .

4. Определим составляющую . Для этого проведем аналитическое выравнивание ряда с помощью линейного тренда.

5. Определим или .

6. Расчет ошибки производится по формулам соответственно: или . Для того, чтобы сравнить мультипликативную модель и другие модели, по аналогии с аддитивной моделью можно использовать сумму квадратов абсолютных ошибок .

Пример. Построим аддитивную модель по данным предыдущего примера. Таблица 1.

5 способов расчета значений линейного тренда в MS Excel

Автор: Алексей Батурин.

Это первая статья из серии «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонности», из которой вы узнаете о 5 способах расчета значений линейного тренда в Excel.

Для того, чтобы легче было научиться прогнозировать продажи с учетом роста и сезонности, я разбил 1 большую статью о расчете прогноза на 3 части:

1. 1. Расчет значений тренда (рассмотрим на примере Линейного тренда в этой статье);
   2. Расчет сезонности;
   3. Расчет прогноза;

После изучения данного материала вы сможете выбрать оптимальный способ расчета значений линейного тренда, который будет удобен для решения вашей задачи, а в последствии, и для расчета прогноза наиболее удобным для вас способом.

Линейный тренд хорошо применять для временного ряда, данные которого увеличиваются или убывают с постоянной скоростью.

Рассмотрим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.

Временной ряд продажи по месяцам (см. вложенный файл).

В этом временном ряду у нас есть 2 переменных:

Уравнение линейного тренда y(x)=a+bx, где

y — это объёмы продаж

x — номер периода (порядковый номер месяца)

a – точка пересечения с осью y на графике (минимальный уровень);

b – это значение, на которое увеличивается следующее значение временного ряда;

1-й способ расчета значений линейного тренда в Excel с помощью графика

Выделяем анализируемый объём продаж и строим график, где по оси Х — наш временной ряд (1, 2, 3… — январь, февраль, март …), по оси У — объёмы продаж. Добавляем линию тренда и уравнение тренда на график. Получаем уравнение тренда y=135134x+4594044

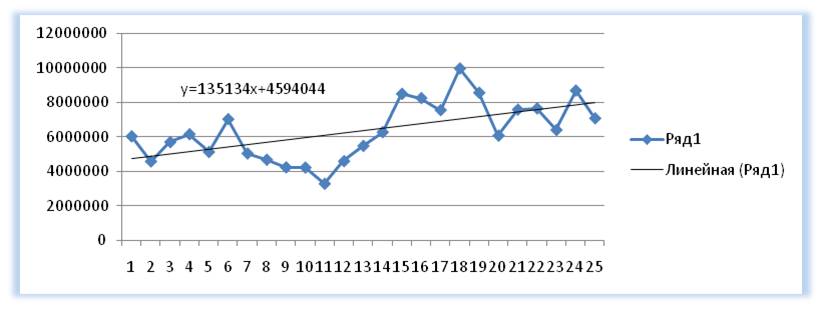
Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.

При расчете значений линейного тренде нам будут известны:

1. Время — значение по оси Х;
2. Значение «a» и «b» уравнения линейного тренда y(x)=a+bx;

Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.

Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551

27-го y=135134*27+4594044=8242686

2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН

1. Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel:

=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)

Для расчета коэффициентов в формулу вводим

известные значения y (объёмы продаж за периоды),

известные значения x (номера периодов),

вместо константы ставим 1,

вместо статистики 0,

Получаем 135135 — значение (b) линейного тренда y=a+bx;

Для того чтобы Excel рассчитал сразу 2 коэффициента (a) и (b) линейного тренда y=a+bx, необходимо

1. установить курсор в ячейку с формулой и выделить соседнюю справа, как на рисунке;
2. нажимаем клавишу F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.

Получаем 135135, 4594044 — значение (b) и (a) линейного тренда y=a+bx;

2. Рассчитаем значения линейного тренда с помощью полученных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов — x, для которых хотим рассчитать значения линейного тренда.

2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также быстрее.

3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ

Рассчитаем значения линейного тренда с помощью стандартной функции Excel:

=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)

Подставляем в формулу

1. известные значения y — это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
2. известные значения x — это номера периодов x для известных значений объёмов продаж y;
3. новые значения x — это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
4. константа — ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;

Для того чтобы рассчитать значения тренда для всего временного диапазона, в «новые значения x» вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.

4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ

Рассчитаем значения линейного тренда с помощью стандартной функции Excel:

=ПРЕДСКАЗ(x; известные значения y; известные значения x)

Вместо X поставляем номер периода, для которого рассчитываем значение тренда.

Вместо «известные значения y» — объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);

«известные значения x» — это номера периодов для каждого выделенного объёма продаж.

3-й и 4-й способ расчета значений линейного тренда быстрее, чем 1 и 2-й, однако с его помощью невозможно управлять коэффициентами тренда, как описано в статье «О линейном тренде».

5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO

2. Заходим в меню программы и нажимаем «Start_Forecast». Значения линейного тренда рассчитаны.

Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.

В следующих статье «Как самостоятельно сделать прогноз продаж с учетом роста и сезонности» мы:

О том, что еще важно знать о линейном тренде, вы можете узнать в статье «Что важно знать о линейном тренде».

Точных вам прогнозов!

Присоединяйтесь к нам!

Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

• Novo Forecast Lite — автоматический расчет прогноза в Excel .
• 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
• Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

• Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Эконометрика Методические рекомендации и задания для контрольной работы (стр. 8 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10

1) По данным задачи найти среднее значение, среднее квадратическое отклонение и коэффициенты автокорреляции (для лагов ) временного ряда;

2) найти уравнение тренда временного ряда уt, полагая что он линейный, и проверить его на уровне значимости .

3) провести сглаживание временного ряда уt методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания т = 3 года. Результаты сравнить графически;

4) выявить на уровне значимости 0,05 наличие автокорреляции возмущений временного ряда с помощью критерия Дарбина – Уотсона.

41. Урожайность картофеля уt (ц/га) в хозяйстве за 10- летний период составила:

Аналитическое выравнивание временных рядов. Оценка параметров уравнения тренда.

Как уже отмечено выше, одной из важнейших задач исследования экономического временного ряда является выявление основной тенденции изучаемого процесса, выраженной неслучайной составляющей ¦ (t) (тренда либо тренда с циклической или (и) сезонной компонентой).

Для решения этой задачи вначале необходимо выбрать вид функции:

экспоненциальная — ¦ (t) = ;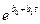

логистическая — ¦ (t)= ;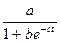

Гомперца — log ¦ (t) = a- br t , где 0 (2) = D_t + D_t – ₁ и т.д.), и порядок разностей, при котором они будут примерно одинаковыми, принимается степень полинома.

Из двух функций предпочтение обычно отдается той, при которой меньше сумма квадратов отклонений фактических данных от расчетных на основе этих функций. Но этот принцип нельзя доводить до абсурда: так, для любого ряда из n точек можно подобрать полином (n-1)-й степени, проходящий через все точки, и соответственно с минимальной – нулевой – суммой квадратов отклонений, но этом случае, очевидно, не следует говорить о выделении основной тенденции, учитывая случайный характера этих точек. Поэтому при прочих равных условиях предпочтение следует отдавать более простым функциям.

Для выявления основной тенденции чаще всего используется метод наименьших квадратов, рассмотренный в гл.3. Значения временного ряда y_t рассматриваются как зависимая переменная, а время t – как объясняющая:

где e_t – возмущения, удовлетворяющие основным предпосылкам регрессионного анализа, приведенным в §3.4, т.е. представляющие независимые и одинаково распределенные случайные величины, распределение которых предполагаем нормальным.

Напомните, что согласно методу наименьших квадратов параметры прямой ŷ_t = ¦ (t) = b₀ + b₁t находимся из системы нормальных уравнений (3.5), в которой в качестве x_i берем t:

(6.8)

Учитывая, что значения переменной t = 1,2,…,n образуют натуральный ряд чисел от 1 до n, суммы , 2 можно выразить через число членов ряда n по известным в математике формулам:

= ; 2 = . (6.9)

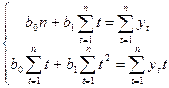
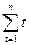
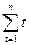
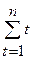
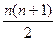
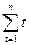
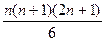
По данным табл. 6.1. найти уравнение неслучайной составляющей (тренда) для y_t , полагая тренд линейным.

Решение. По формуле (6.9)

= = 36 ; 2 = = 204.

= 213 + 171 +….+361 = 2375;

= 213 2 + 171 2 +….+ 361 2 = 739827;

= 213.1 + 171.2 +….+ 361.8 = 11766.

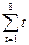
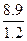
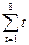
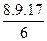
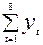
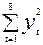
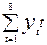
Система нормальных уравнений (6.8) имеет вид:

Откуда b₀ = 181,32; b₁ = 25,679 и уравнение тренда ŷ_t = 181,32 + 25,679t (рис 6.1), т.е. спрос ежегодно увеличивается в среднем на 25,7 ед.

При решении задачи можно было не выписывать систему нормальных уравнений, а представить уравнение регрессии в виде (3.12), т.е.

ŷ — 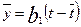, где

а коэффициент регрессии b₁ найти по формуле (3.13):

Проверим значимость полученного уравнения тренда по F – критерию на 5%-ном уровне значимости. Вычислим с помощью формулы (3.40) суммы квадратов:

а) обусловленную регрессией –

б) общую –

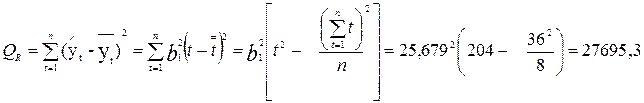
Q_e = Q – Q_R = 3478, 9 – 27695, 3 = 7053, 6.

Найдем по формуле (3.44) значение статистики:

F =

Так как F > F _0,05;1;6 ( см. табл. IV приложений), то уравнение тренда значимо.►

При применении метода наименьших квадратов для оценки парпметров экспоненциальной, логистической функций или функции Гомперца возникают сложности с решением получаемой системы нормальных уравнений, поэтому предварительно, до получения соответствующей системы, прибегают к некоторым преобразованиям этих функций ( например, логарифмированию и др.) (см. § 5.5).

Другим методом выравнивания (сглаживаний) временного ряда, т.е. выделения неслучайной составляющей, является метод скользящих средних.Он основан на переходе от наличных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени «скользит» вдоль ряда.

Получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд, из-за усреднения отклонений ряда. Действительно , если индивидуальный разброс значений члена временного ряда (y_{1 +} y₂+…. +y_m )/m около своего среднего (сглаженного) значения а будет характеризоваться существенно меньшей величиной дисперсии, равной s 2 /m.

Для усреднения могут быть использованы средняя арифметическая ( простая и с некоторыми весами), медиана и др.

►Пример 6.3. Провести сглаживание временного ряда y_t по данным табл.6.1 методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания m = 3 года.

Решение. Скользящие средние находим по формуле:

(6.10)

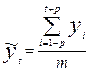
Когда m=(2p-1) – нечетное число; при m=3 p=1.

Например, при t =2 по формуле (6.10):

;

;

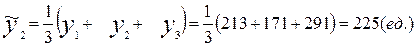
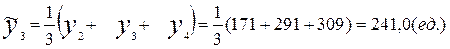
В результате получим сглаженный ряд:

t
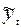	—	225,0	241,0	305,7	329,3	336,3	358,0	—

На рис.6.1 этот ряд изображен графически в виде пунктирной линии.

Метод аналитического выравнивания

Основным
содержанием метода аналитического
выравнивания временных рядов является
расчет общей тенденции развития (тренда)
как функции времени на основе математической
модели, которая наилучшим образом
отображает основную тенденцию развития
временного ряда.

В
качестве моделей обычно используют
линейную, показательную, степенную и
логарифмическую функции в зависимости
от особенностей временного ряда.

Для
оценки точности трендовой модели
используется коэффициент детерминации,
равный отношению дисперсии теоретических
данных, полученных по трендовой модели
к дисперсии эмпирических данных.
Считается, что трендовая модель адекватна
изучаемому процессу и отражает тенденцию
его развития при значениях коэффициента
детерминации близких к единице.

Порядок
построения трендовой модели с помощью
Excel2003 следующий:

1. Эмпирический
временной ряд следует представить в
виде диаграммы одного из следующих
типов: гистограмма, линейная диаграмма,
график, точечная диаграмма, диаграмма
с областями, а затем щелкнуть правой
кнопкой мыши на одном из маркеров данных
и в открывшемся контекстном меню выбрать
команду Добавить линию тренда.

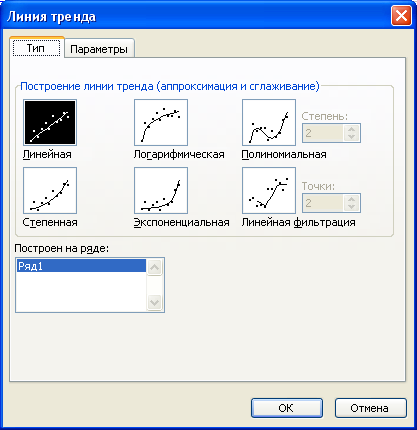
Откроется
окно диалога (рис.6.3).

Рис.
6.3. Окно выбора модели тренда

2. На
вкладке Типвыбрать требуемый вид
трендовой модели.

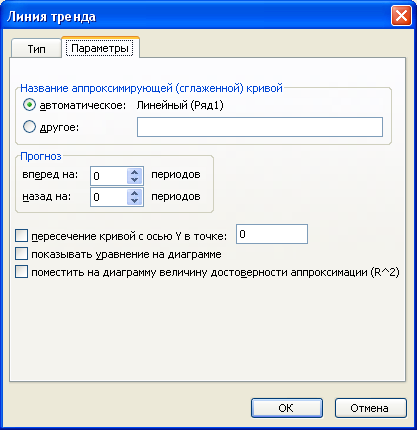
3. На
вкладке Параметры(рис. 6.4) задать
дополнительные параметры тренда:

Рис.6.4.
Дополнительные параметры модели

• Название сглаженной
  кривой– автоматическое по типу
  модели или собственное название функции.

• Прогноз–
  можно указать, на сколько периодов
  вперед (назад) требуется спроектировать
  линию тренда в будущее (прошлое).

• Если необходимо
  указать точку пересечения кривой с
  осью ординат, показать уравнение
  аппроксимирующей функции и вывести
  значение коэффициента детерминации
  следует установить соответствующие
  флажки.

Реализация
метода аналитического выравнивания в
Excel2007 проводится
аналогичным образом. Для открытия окна
диалога с настройками параметров тренда
необходимо использовать команду
контекстного менюФормат линии тренда.
Само диалоговое окно содержит те же
параметры, что и в версииExcel2003.

Использование статистических функций

Спрогнозировать
данные без использования диаграмм,
соответствующие линейным и экспоненциальным
линиям, можно с использованием
статистических функций ТЕНДЕНЦИЯ() и
РОСТ().

Функция
ТЕНДЕНЦИЯ возвращает значения в
соответствии с линейным трендом.
Аппроксимирует прямой линией (по методу
наименьших квадратов) массивы
известные_значения_yиизвестные_значения_x.
Возвращает значения y, в соответствии
с этой прямой для заданного массивановые_значения_x.

Синтаксис
функции: ТЕНДЕНЦИЯ(y; x; n_x; конст):

y-известные_значения_y– множество
значенийy, для которых
уже известна линейная зависимость;

x-известные_значения_x— множество
значенийx, для которых
уже известна линейная зависимость;

n_x-новые_значения_x– новые значенияx, для которых функция
возвращает соответствующие значенияy.

конст– логическое значение, если оно равно
0, то свободный член равен нулю, в противном
случае свободный член вычисляется
обычным образом.

Функция
РОСТ рассчитывает прогнозируемый
экспоненциальный рост на основании
имеющихся данных. Синтаксис функции:
РОСТ(y; x; n_x; конст):

y-известные_значения_y– множество
значенийy, для которых
уже известна экспоненциальная зависимость;

x-известные_значения_x— множество
значенийx, для которых
уже известна экспоненциальная зависимость;

n_x-новые_значения_x– новые значенияx, для которых функция
возвращает соответствующие значенияy.

конст– логическое значение, если оно равно
0 или отсутствует, то константа равна
единице, в противном случае вычисляется
обычным образом.

Перед
вводом формул ТЕНДЕНЦИЯ() и РОСТ()
необходимо выделить результирующие
ячейки, ввести ссылки на известные и
новые значения, при необходимости ввести
единицу в строку Константаи нажать
комбинацию клавиш <Ctrl+Shift+Enter> для
ввода данных в массив.

Соседние файлы в папке моделирование инфоком

• #

  21.03.20169.82 Кб79ArrayFormulas.xlsx
• #
• #
• #
• #
• #
• #
• #