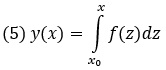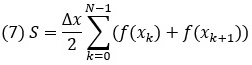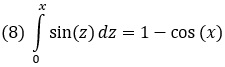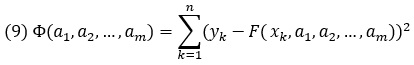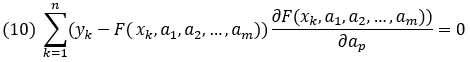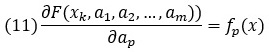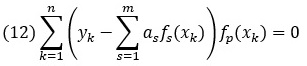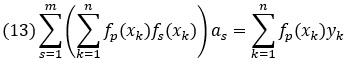Отделение корней В Excel
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Лабораторная работа
Отделение корней нелинейного уравнения
Пусть имеется нелинейное уравнение 
Требуется найти корни этого уравнения. Численный процесс приближенного решения поставленной задачи разделяют два этапа: отделение корня и уточнение корня.
Для отделения корня необходимо определить промежуток аргумента 
Этап отделения корня уравнения алгоритмизирован только для некоторых классов уравнений (наиболее известным из которых является класс алгебраических уравнений), поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с использованием всей возможной информации о функции 
Методы отделения корней
Отделение корней во многих случая можно произвести графически. Учитывая, что действительные корни уравнения F ( x )=0 – это есть точки пересечения графика функции y = F ( x ) с осью абсцисс y =0, нужно построить график функции y = F ( x ) и на оси OX отметить отрезки, содержащие по одному корню. Но часто для упрощения построения графика функции y = F ( x ) исходное уравнение заменяют равносильным ему уравнением f 1 ( x )= f 2 ( x ). Далее строятся графики функций y 1 = f 1 ( x ) и y 2 = f 2 ( x ), а затем по оси OX отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.
На практике данный способ реализуется следующим образом: например, требуется отделить корни уравнения cos(2 x )+ x -5=0 графически на отрезке [–10;10], используя Excel .
Построим график функции f (x)=cos(2 x )+x-5 в декартовой системе координат. Для этого нужно:
Ввести в ячейку A1 текст х .
Ввести в ячейку B1 текст y =cos(2 x )+ x -5.
Ввести в ячейку А2 число -10, а в ячейку А3 число -9.
Выделить ячейки А2 и А3.
Навести указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы рамка охватила диапазон ячеек А2:А22.
Ячейки автоматически заполняются цифрами :
Ввести в ячейку В2 формулу =COS(2*A2)+A2-5.
Методом протягивания заполнить диапазон ячеек В3:В22.
Вызвать «Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать «далее».
Указать диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон данных В2:В22.
Выбрать вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.
В поле «подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».
Подписать названия осей x и y соответственно, нажать «далее».
Вывести диаграмму на том же листе, что и таблица, нажать кнопку «готово».
В итоге получаем следующее (рисунок 1):
Рисунок 1 – Локализация корня
Анализируя полученное изображение графика, можно сказать, что уравнение cos(2 x )+ x -5=0 имеет один корень – это видно из пересечения графика функции y=cos(2 x )+ x -5 с осью OX. Можно выбрать отрезок, содержащий данный корень: [5;6] – отрезок локализации .
Для подтверждения полученных данных, можно решить эту же задачу вторым способом. Для этого необходимо уравнение cos(2 x )+ x -5=0 преобразовать к виду: cos(2 x )=5- x . Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y 1 =cos(2 x ) и y 2 =5- x . Для решения этой задачи в Excel необходимо выполнить следующие действия:
Вести в ячейки А1:C1 соответственно текст: « x », « y 1 =cos(2 x )», « y 2 =5- x ».
A2:A22 заполнить так же как при решении задачи первым способом.
В В2 ввести формулу =COS(2*A2).
Методом протягивания заполнить диапазон ячеек В3:В22.
В С2 ввести =5-A2.
Методом протягивания заполнить диапазон ячеек С3:С22.
С помощью Мастера диаграмм выбрать график (первый вид).
В данном случае диапазон данных следует указывать для построения двух графиков. Для этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.
Перейти на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.
Подписать ось x , выбрав диапазон А2:А22.
Подписать соответственно оси x и y .
Поместить диаграмму на имеющемся листе.
Результат представлен на рисунке 2: Анализируя полученный результат, можно сказать, что точка пересечения двух графиков попадает на тот же самый отрезок локализации [5;6] , что и при решении задачи первым способом.
Рисунок 2 – Локализация корня
Аналитический способ отделения корней
Аналитический способ отделения корней основан на следующей теореме , известной из курса математического анализа.
ТЕОРЕМА: Если непрерывная на 






В случае, когда на концах интервала функция имеет одинаковые знаки, на этом интервале корни либо отсутствуют, либо их четное число.
Для отделения корней аналитическим способом выбирается отрезок 

Б
удем вычислять значение функции F ( x ) , начиная с точки x = a , двигаясь вправо с некоторым шагом h . Если F ( x )* F (x+ h ) , то на отрезке [ x ; x + h ] существует корень (рисунок 3).
Рисунок 3 – Аналитический способ локализации корней
Доказательство существования и единственности корня на отрезке.
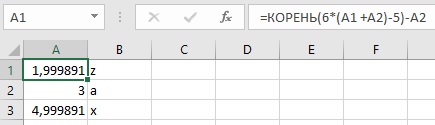
В качестве примера рассмотрим функцию f (x)=cos(2 x )+x-5 .
Ввести в ячейки А1, В1 и С1 соответственно « x », « y =cos(2 x )+ x -5» и «ответ».
В А2 и А3 ввести граничные значения отрезка изоляции.
В В2 ввести формулу =COS(2*A2)+A2-5 и методом протягивания заполнить В3.
В С2 ввести формулу =ЕСЛИ(B2*B3
Таким образом, на отрезке изоляции корень существует:
Р
исунок 4 – Проверка существования корня на отрезке
Для доказательства единственности корня на отрезке изоляции необходимо выполнить следующие действия:
Продолжить работу в том же документе MS Excel.
Заполнить D1 и E1 соответственно: « y’ =-sin(2 x )*2+1» и «ответ» (причем выражение y’ =-sin(2 x )*2+1 – это производная первого порядка от функции y =cos(2 x )+ x -5).
Ввести в D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.
Ввести в E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень не единственный»).
В
результате получаем (рисунок 5):
Рисунок 5 – Доказательство единственности корня на отрезке
Таким образом доказано существование и единственность корня на отрезке изоляции.
Рассмотрим решение задачи отделения корней уравнения
cos(2 x )+ x -5=0 аналитическим способом с шагом 1 на отрезке [-10;10].
Чтобы отделить корни уравнения аналитическим способом с помощью Excel, необходимо выполнить следующее:
Заполнить ячейки A1:D1 соответственно: « x », « y =cos(2 x )+ x -5», « h », «ответ».
В С2 ввести значение 1.
Ввести в А2 значение -10.
Ввести в А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.
В В2 ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.
В
С3 ввести формулу =ЕСЛИ(B2*B3
В результате получаем следующее (рисунок 6):
Рисунок 6 – Отделение корня
Следующий пример (рисунок 7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos ( x )=0,1 x на интервале [–10;10] с шагом 1.
Табулирование функции и построение графика осуществляется как в предыдущих примерах. Видно, что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9]; [-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].
Рисунок 7 – Отделение корней
Обратим внимание на то, что надежность рассмотренного алгоритма отделения корней уравнения зависит как от характера функции F (x), так и от выбранной величины шага h . Для повышения надежности следует выбирать при отделении корней достаточно малые значения h .
1. Выполнить отделение корней следующих функций:
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
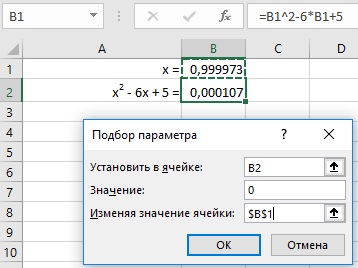
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://exceltable.com/otchety/reshenie-uravneniy
Лабораторная работа
Отделение корней
нелинейного уравнения
Пусть имеется
нелинейное уравнение .
Требуется найти
корни этого уравнения. Численный процесс приближенного решения поставленной
задачи разделяют два этапа: отделение корня и уточнение корня.
Для отделения
корня необходимо определить промежуток аргумента , где
содержится один и только один корень уравнения. Одна из точек этого промежутка
принимается за начальное приближение корня. В зависимости от метода, который
предполагается использовать для уточнения корня, требуется определение
некоторых свойств отделенного корня и поведения функции на отрезке отделения.
Например, при использовании метода деления пополам, необходимо и достаточно
установить лишь непрерывность функции на отрезке отделения.
Этап отделения
корня уравнения алгоритмизирован только для некоторых классов уравнений
(наиболее известным из которых является класс алгебраических уравнений),
поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с
использованием всей возможной информации о функции . Часто
применяется графический метод отделения действительных корней, обладающий
большой наглядностью.
Методы
отделения корней
Отделение корней
во многих случая можно произвести графически. Учитывая, что действительные
корни уравнения F(x)=0 – это есть точки пересечения графика
функции y=F(x) с осью абсцисс y=0, нужно построить
график функции y=F(x) и на оси OX отметить отрезки,
содержащие по одному корню. Но часто для упрощения построения графика функции y=F(x)
исходное уравнение заменяют равносильным ему уравнением f1(x)=f2(x).
Далее строятся графики функций y1=f1(x)
и y2=f2(x), а затем по оси OX
отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.
На практике
данный способ реализуется следующим образом: например, требуется отделить корни
уравнения cos(2x)+x-5=0 графически на отрезке [–10;10],
используя Excel.
1 способ
Построим график функции f(x)=cos(2x)+x-5
в декартовой системе координат. Для этого нужно:
1.
Ввести в
ячейку A1 текст х.
2.
Ввести в
ячейку B1 текст y=cos(2x)+x-5.
3.
Ввести в
ячейку А2 число -10, а в ячейку А3 число -9.
4.
Выделить
ячейки А2 и А3.
5.
Навести
указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий
выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы
рамка охватила диапазон ячеек А2:А22.
6.
Ячейки
автоматически заполняются цифрами :
7.
Ввести в
ячейку В2 формулу =COS(2*A2)+A2-5.
8.
Методом
протягивания заполнить диапазон ячеек В3:В22.
9.
Вызвать
«Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать
«далее».
10.
Указать
диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон
данных В2:В22.
11.
Выбрать
вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.
12.
В поле
«подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».
13.
Подписать
названия осей x и y соответственно, нажать «далее».
14.
Вывести
диаграмму на том же листе, что и таблица, нажать кнопку «готово».
В итоге получаем следующее
(рисунок 1):
Рисунок 1 – Локализация корня
Анализируя полученное
изображение графика, можно сказать, что уравнение cos(2x)+x-5=0
имеет один корень – это видно из пересечения графика функции y=cos(2x)+x-5
с осью OX. Можно выбрать отрезок, содержащий данный корень:[5;6] – отрезок локализации.
2 способ
Для подтверждения полученных
данных, можно решить эту же задачу вторым способом. Для этого необходимо
уравнение cos(2x)+x-5=0 преобразовать к виду: cos(2x)=5-x.
Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y1=cos(2x)
и y2=5-x. Для решения этой задачи в Excel необходимо
выполнить следующие действия:
1.
Вести в
ячейки А1:C1 соответственно текст: «x», «y1=cos(2x)»,
«y2=5-x».
2.
A2:A22
заполнить так же как при решении задачи первым способом.
3.
В В2
ввести формулу =COS(2*A2).
4.
Методом
протягивания заполнить диапазон ячеек В3:В22.
5.
В С2
ввести =5-A2.
6.
Методом
протягивания заполнить диапазон ячеек С3:С22.
7.
С помощью
Мастера диаграмм выбрать график (первый вид).
8.
В данном
случае диапазон данных следует указывать для построения двух графиков. Для
этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем
нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.
9.
Перейти
на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.
10.
Подписать
ось x , выбрав диапазон А2:А22.
11.
Подписать
соответственно оси x и y.
12.
Поместить
диаграмму на имеющемся листе.
Результат представлен на
рисунке 2: Анализируя
полученный результат, можно сказать, что точка пересечения двух графиков
попадает на тот же самый отрезок локализации [5;6], что и при решении задачи
первым способом.
Рисунок 2 – Локализация корня
Аналитический способ отделения
корней
Аналитический
способ отделения корней основан на следующей теореме, известной из курса математического
анализа.
ТЕОРЕМА: Если непрерывная на функция
,
определяющая уравнение , на концах отрезка
принимает значения разных знаков, т.е.
, то на этом отрезке содержится, по
крайней мере, один корень уравнения. Если же функция непрерывна
и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один
корень уравнения.
В случае, когда
на концах интервала функция имеет одинаковые знаки, на этом интервале корни
либо отсутствуют, либо их четное число.
Для отделения корней
аналитическим способом выбирается отрезок , на
котором находятся все интересующие вычислителя корни уравнения. Причем на
отрезке функция F(x) определена, непрерывна и F(a)*F(b)<0.
Требуется указать все частичные отрезки ,
содержащие по одному корню.
 |
Будем вычислять
значение функции F(x),
начиная с точки x=a, двигаясь вправо с некоторым шагом h. Если F(x)*F(x+h)<0,
то на отрезке [x;x+h] существует корень (рисунок 3).
Рисунок 3 –
Аналитический способ локализации корней
Если F(xk)=0,
xk-точный корень.
Доказательство существования
и единственности корня на отрезке.
В качестве примера рассмотрим
функцию f(x)=cos(2x)+x-5.
1. Ввести в ячейки А1, В1 и С1
соответственно «x», «y=cos(2x)+x-5» и «ответ».
2. В А2 и А3 ввести граничные
значения отрезка изоляции.
3. В В2 ввести формулу
=COS(2*A2)+A2-5 и методом протягивания заполнить В3.
4. В С2 ввести формулу
=ЕСЛИ(B2*B3<0;»корень существует»;»корень не
существует»).
Таким образом, на отрезке
изоляции корень существует:
 |
Рисунок 4 – Проверка существования корня на отрезке
Для доказательства
единственности корня на отрезке изоляции необходимо выполнить следующие
действия:
1.
Продолжить
работу в том же документе MS Excel.
2.
Заполнить
D1 и E1 соответственно: «y’=-sin(2x)*2+1» и «ответ» (причем выражение
y’=-sin(2x)*2+1 – это производная первого порядка от функции y=cos(2x)+x-5).
3.
Ввести в
D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.
4.
Ввести в
E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень
не единственный»).
В результате получаем
(рисунок 5):
Рисунок 5 –
Доказательство единственности корня на отрезке
Таким образом доказано
существование и единственность корня на отрезке изоляции.
Рассмотрим
решение задачи отделения корней уравнения
cos(2x)+x-5=0 аналитическим
способом с шагом 1 на отрезке [-10;10].
Чтобы отделить корни
уравнения аналитическим способом с помощью Excel, необходимо выполнить
следующее:
1.
Заполнить
ячейки A1:D1 соответственно: «x», «y=cos(2x)+x-5»,
«h», «ответ».
2.
В С2
ввести значение 1.
3.
Ввести в
А2 значение -10.
4.
Ввести в
А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.
5.
В В2
ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.
6.
 |
В С3 ввести формулу
=ЕСЛИ(B2*B3<0;»Корень на отрезке существует»;ЕСЛИ(B3=0;»точный
корень»;»-«)) и методом протягивания заполнить диапазон ячеек
С4:С22.
В результате получаем
следующее (рисунок 6):
Рисунок 6 –
Отделение корня
Следующий пример (рисунок
7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos(x)=0,1x на интервале [–10;10] с шагом
1.
Табулирование
функции и построение графика осуществляется как в предыдущих примерах. Видно,
что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9];
[-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].
Рисунок 7 – Отделение корней
Обратим внимание
на то, что надежность рассмотренного алгоритма отделения корней уравнения
зависит как от характера функции F(x), так и от выбранной величины шага h.
Для повышения надежности следует выбирать при отделении корней достаточно малые
значения h.
Задание
1. Выполнить отделение корней
следующих функций:
|
№ п/п |
Уравнение |
A |
B |
|
1 |
tg(x) = 1/x |
0 |
n/2 |
|
2 |
e -x = x |
0 |
1 |
|
3 |
ln(x) = 1/x |
1 |
2 |
|
4 |
2 +ln(x) = 1/x |
0 |
1 |
|
5 |
x — x3 + 1 =0 |
1 |
2 |
2. Выполнить индивидуальные задания
Вариант 1
|
1 |
ctg(x) = —x2 |
1,6 |
4,5 |
|
2 |
2ln(x)+sin(x) =e x |
0 |
2 |
|
3 |
lg(x) = 2 x-x3 |
0 |
10 |
|
4 |
cos(x) = 1/x |
0 |
p/2 |
|
5 |
cos(x) = ln(1+x) |
0 |
p/2 |
Вариант 2
|
1 |
tg(x) = 1/x—x2 |
1,6 |
4,5 |
|
2 |
2ln(x) =e x |
0 |
2 |
|
3 |
lg(x) = sin(x) |
0 |
10 |
|
4 |
cos(x)+x2 = 1/x |
0 |
p/2 |
|
5 |
cos2(x) = ln(1+x2) |
0 |
p/2 |
Вариант 3
|
1 |
cos2(x) = x |
0 |
p/2 |
|
2 |
1 — 3 x + x3=0 |
0 |
1 |
|
3 |
1 — 3x + x4=0 |
0 |
1 |
|
4 |
1 — 3 x + x5=0 |
0 |
1 |
|
5 |
tg(x) = 1/x2 |
0 |
p/2 |
Вариант 4
|
1 |
ln(x) = sin(x) |
1 |
3 |
|
2 |
e — x = sin(x) |
0 |
p/2 |
|
3 |
e x = 1 /sin(x) |
0 |
p/2 |
|
4 |
e — x = x2 |
0 |
1 |
|
5 |
2 + ln(x) = 1/x2 |
0 |
1 |
Вариант 5
|
1 |
ln(x) = Sin (x) |
0 |
p/2 |
|
2 |
x — x3 + 2 =0 |
1 |
2 |
|
3 |
x +5 = x3 |
1 |
2 |
|
4 |
x 2— 0,5 x-2=0 |
0 |
0,5 |
|
5 |
ln(x -1)+ x-2=0 |
1 |
3 |
Вариант 6
|
1 |
ln(x+3) = Sin (x) |
0 |
p/2 |
|
2 |
2x — x3 + 3 =0 |
1 |
2 |
|
3 |
x +8 = x3+x2 |
1 |
2 |
|
4 |
x — 0,5 x2+4=0 |
0 |
0,5 |
|
5 |
(x -1)2— x=0 |
1 |
3 |
Вариант 7
|
1 |
x +0,5 = e -x |
0 |
1 |
|
2 |
2 — x + x3=0 |
-2 |
0 |
|
3 |
sin(x) = 1/x |
0 |
p/2 |
|
4 |
sin(x) = x/2 |
п/2 |
п |
|
5 |
ln(x) = e -x |
0 |
2 |
Вариант 8
|
1 |
lg(x) = e — x |
0 |
1 |
|
2 |
cos(x) = x |
0 |
p/2 |
|
3 |
cos(x) = ln(x) |
0 |
p/2 |
|
4 |
cos(x) = tg(x) |
0 |
p/2 |
|
5 |
cos(x) = x3 |
0 |
p/2 |
Вариант 9
|
1 |
1 — 5 x + x3=0 |
0 |
1 |
|
2 |
1 — 5 x + x4=0 |
0 |
1 |
|
3 |
1 — 3 x + x5=0 |
1 |
2 |
|
4 |
4cos(x) = x+x2 |
0 |
p/2 |
|
5 |
cos(x) = ln(x)-x2 |
0 |
p/2 |
Вариант 10
|
1 |
ln(x) = cos (x) |
0 |
p/2 |
|
2 |
x2 — x3 + 2 =0 |
1 |
2 |
|
3 |
cosx +5 = x3 |
1 |
2 |
|
4 |
x 0,5— x=0 |
0 |
0,5 |
|
5 |
(x -1)2— x=5 |
1 |
3 |
Вариант 11
|
1 |
ln(x+3) =sin (x)-x |
0 |
p/2 |
|
2 |
2x — x3 + 3 =ln(x) |
1 |
2 |
|
3 |
cos(x) +2 = x3+x2 |
1 |
2 |
|
4 |
3x — 0,5 x2+cosx=0 |
0 |
0,5 |
|
5 |
(x -1)2— x+tg(x-1)=0 |
1 |
3 |
Вариант 12
|
1 |
x2 +0,5 = e -x |
0 |
1 |
|
2 |
2 – sin(x) + x3=0 |
-2 |
0 |
|
3 |
sin(x) = 1/x-x2 |
0 |
p/2 |
|
4 |
sin(x) = x/2+cos(x) |
п/2 |
п |
|
5 |
ln(x)-x = e -x |
0 |
2 |
Вариант 13
|
1 |
lg(x)+2sin2(x) = e — x |
0 |
1 |
|
2 |
cos(x+p/2) = x+x2 |
0 |
p/2 |
|
3 |
cos(x) = ln(x)-x2 |
0 |
p/2 |
|
4 |
cos(x) = |
0 |
p/2 |
|
5 |
cos(x) = x3-log(x2) |
0 |
p/2 |
Вариант 14
|
1 |
1 — 5 cos(x) + x3=0 |
0 |
1 |
|
2 |
1 — 5 tg(x) + x4=0 |
0 |
1 |
|
3 |
1 – 3( x-2)2 + x5=0 |
1 |
2 |
|
4 |
4cos(x) = cos(x)+x2 |
0 |
p/2 |
|
5 |
cos(x) = ln(x)-x2+x |
0 |
p/2 |
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Растеряев А.Н. 1
1МБОУ СОШ № 3 им. атамана М.И. Платова
Кожушкова Т.Ю. 1
1МБОУ СОШ № 3 им. атамана М.И. Платова
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Современное развитие науки, техники и технологий тесно связано с использованием математических методов, программного обеспечения и мощных ЭВМ, ставшим рабочим инструментом учёного, инженера, конструктора. Все это позволяет строить и исследовать математические модели сложных устройств, систем и процессов, при этом резко сократить время и стоимость инженерных разработок.
Широкое использование ЭВМ способствовало развитию вычислительной математики (прикладной математики). Как и любая наука, вычислительная математика представляет собой сплав «классической» (теоретической) науки и прикладной науки, в роли последней выступает область вычислительных методов.
Практически все, что окружает современного человека – это все так или иначе связано с математикой. Последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального программного обеспечения при решении линейных и нелинейных уравнений и их систем.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических и трансцендентных уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, методы аналитического решения показательных, логарифмических и тригонометрических уравнений. При этом многие математические задачи, например, решение неравенств и их систем, нахождение области допустимых решений функции и т. п., включают в себя этап решения уравнений.
Цель работы: Освоение приемов численного решения алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel.
Задачи:
1) Ознакомиться с историей развития аналитических и численных методов решения уравнений.
2). Изучить особенности, достоинства и недостатки аналитических и численных методов.
3). Ознакомиться с вычислительными возможностями ЭТ MS Excel и изучить средства уточнения действительных корней нелинейных уравнений.
4) Освоить приемы отделения и уточнения действительных корней нелинейных уравнений в среде ЭТ MS Excel.
5) Решить задачи численного нахождения корней алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel.
Объект исследования: нелинейные уравнения с одной переменной.
Предмет исследования: возможности ЭТ MS Excel для численного решения нелинейные уравнения с одной переменной.
ОСНОВНАЯ ЧАСТЬ
1. Краткая история развития численных методов
Вычислительная математика начала свое развитие достаточно давно и в своем развитии прошла три этапа:
I. Первый этап начался 3-4 тысячи лет назад. Жители Вавилона в 2000 г. до н.э. уже умели решать квадратные уравнения и составлять таблицы для решения кубических уравнений путем приведения общего кубического многочлена к нормальному виду. В VII в. индийцы развили последовательную алгебраическую теорию уравнений первой и второй степени. Итальянский математик Ш. Ферро (1465-1526) нашел способ решения кубических уравнений специального вида [1]. Этот научный результат стал отправным пунктом для развития алгебры и математики вообще. Другим итальянским математиком, инженером, медиком и астрологом Дж. Кардано (1506-1576) было найдено решение приведенного кубического уравнения и опубликовано в 1545 г. в его научном труде «Великое искусство». В 1591 году великий французский математик Ф. Виет (1540-1603) впервые ввел символическое обозначение не только для неизвестных, но и для коэффициентов уравнений; указал на зависимость между корнями и коэффициентами уравнений (формулы Виета). Вычислительные средства этого этапа – палочки, пальцы, камешки и как вершина – счеты (абак).
II. Второй период начался с И. Ньютона (1642-1727). В этот период решались задачи астрономии, геодезии, баллистики и расчета механических конструкций, сводящиеся либо к обыкновенным дифференциальным уравнениям, либо к алгебраическим системам с большим числом неизвестных. В 1669 г. Ньютон предложил метод касательных для приближенного решения алгебраических уравнений, а в 1676 г. – способ приближенного вычисления определенных интегралов. Вычислительные средства – таблицы элементарных функций, арифмометры и логарифмические линейки.
III. Третий период начался примерно с 1940 года. Толчком к развитию прикладной математики послужили военные задачи, требующие высокой скорости решения задач. Появились электронные вычислительные машины. Например, Colossus («Колосс») – секретный британский компьютер, спроектированный и построенный в ходе Второй мировой войны в 1943 году для расшифровки перехваченных немецких радиосообщений, зашифрованных с помощью электронно-механического устройства «Энигма» (по-гречески – загадка). Спецификацию компьютера разработали английский математик, криптоаналитик профессор Макс Ньюман (Max Newman 1897- 1984) и его коллеги. Компьютер состоял из 1500 электронных ламп (2500 в новой версии Colossus Mark II), что делало Colossus самым мощным компьютером того времени. Его ближайший конкурент имел всего 150 ламп. Это позволило сократить время расшифровки перехваченных немецких сообщений с нескольких недель до нескольких часов. Модернизация Colossus Mark II считается первым программируемым компьютером в истории ЭВМ.
2. Особенности, достоинства и недостатки аналитических и численных методов
С помощью математического моделирования решение научной задачи сводится к решению математической задачи, являющейся её моделью. Для решения математических задач используются две основные группы методов: аналитические и численные.
Аналитические методы, как правило, позволяют получить решение задачи в виде формул. В частности, если математическая задача состоит в решении нелинейных уравнений, то использование известных из курса средней школы приемов сразу приводит к цели. К сожалению, на практике это бывает достаточно редко. Например, если задача свелась к решению уравнения с одной переменной:
то при всей тривиальности этой задачи выразить корни уравнения путем аналитических преобразований не удается. Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Доказательство этого факта связано с именами математиков Абеля (1802-1829) и Галуа (1811-1832).
Аналогичные проблемы возникают также и при решении других математических задач. В частности, при вычислении определенных интегралов также часто не удается выразить первообразную через элементарные функции.
Для решения таких задач разрабатываются и применяются методы приближенных вычислений или численные методы, позволяющие свести решение математической задачи к выполнению конечного числа арифметических действий над числами. Таким образом, численные методы позволяют найти решение в виде числа или таблицы значений, найденных с заданной точностью.
Важным отличием и преимуществом аналитических методов перед численными является то, что они позволяют получить общее решение задачи в виде формулы, по которой можно изучать качественные особенности решения, а также исследовать влияние начальных условий и параметров задачи на характер решения. Численные же методы позволяют найти только частное решение задачи с конкретными значениями параметров и исходных данных, при этом численные методы обладают большей общностью.
3. Численное решение уравнений с одной переменной
Нелинейное уравнение с одной переменной в общем случае может быть записано в виде
F(x) = 0, (1)
где функция F(x) определена и непрерывна на конечном или бесконечном интервале a < x < b.
Всякое значение [a, b], обращающее функцию F(x) в нуль, т.е. когда F() = 0, называется корнем уравнения (1) или нулем функции F(x).
Нелинейные уравнения с одной переменной подразделяются на алгебраические и трансцендентные.Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.
Как было сказано выше, методы решения нелинейных уравнений делятся на две группы:
аналитические (точные) методы;
численные (приближенные) методы.
Задача численного нахождения действительных корней нелинейного уравнения (1) обычно состоит из двух этапов [2]:
отделения корней, т.е. нахождения достаточно малых окрестностей рассматриваемой области, в которых содержится один и только один искомый корень;
уточнения отделенных на первом этапе корней, т.е. их нахождение численным методом с заданной степенью точности.
В связи с этим рассмотрим вначале задачу отделения корней, а затем возможности численных методов их уточнения.
На первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то сколько их, и затем определить интервалы, в каждом из которых находится единственный корень. Одним из самых распространенных и не очень точных является графический метод.
Принимая во внимание, что действительные корни уравнения (1) – это точки пересечения графика функции F(x) с осью абсцисс, достаточно построить график функции F(x) и отметить точки пересечения графикас осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив исходное уравнение (1) равносильным ему уравнением:
F1(x)= F2(x), (2)
где функцииF1(x) и F2(x) – более простые, чем исходная функцияF(x). Тогда, построив графики функций у =F1(x) и у = F2(x), искомые корни получим как абсциссы точек пересечения этих графиков.
Покажем теперь, что найденные графически отрезки содержат один и только один корень решаемого уравнения. Предположим, что найден отрезок [a, b] такой, что
функцияF(x) непрерывна на отрезке [a, b] вместе с производной первого порядка;
значения F(x) на концах отрезка имеют разные знаки (F(a)F(b) < 0);
первая производная F (x) сохраняет определенный знак на всем отрезке.
Условия 1) и 2) гарантируют, что на интервале [a, b] находится хотя бы один корень, а из 3) следует, что F(x) на данном интервале монотонна и поэтому корень будет единственным. Такой интервал называют интервалом изоляции искомого корня ξ.
Пример 1. Графически отделить корни уравнения
x.lg x– 1 = 0. (3)
Решение. Уравнение (3) перепишем в виде равенства lg x=.
Отсюда ясно, что корни уравнения (3) могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = . Построив эти кривые (см. рис. 1), приближенно найдем единственный корень уравнения (3) или определим его содержащий отрезок [2, 3].
Рис. 1 – Графическое отделение корней (пример 1)
Убедимся, что отрезок [2, 3] содержит один и только один корень уравнения (3).
Перепишем уравнение в виде F(x) = 0, где .
Тогда F(2) = 2.lg(2) – 1 = 2.0.30103–1=0.60206 –1= –0.39794 0, т.е. на концах отрезка функция F(x) принимает значения разных знаков.
Найдем первую производную функции:
Следовательно, первая производная сохраняют свой знак на отрезке, а на концах отрезка функция F(x) принимает значения разных знаков, значит отрезок [2, 3] – отрезок изоляции искомого корня ξ.
После этого выполняется этап уточнения отделенных корней нелинейного уравнения. На каждом из найденных интервалов для поиска корня используются численные методы уточнения корня до заданной точности ε. К данным методам относятся: метод половинного деления (бисекций), метод хорд, метод касательных (Ньютона), метод последовательных приближений (итераций) и т.п.
4. Средства уточнения корней электронных таблиц Microsoft Excel
Электронные таблицы MS Excel входят в стандартный пакет формирования и обработки информации MS Office и установлены практически на каждом современном компьютере. Применение электронных таблиц упрощает работу с данными и позволяет получать результаты без проведения расчетов вручную или специального программирования. Наиболее широкое применение электронные таблицы нашли в экономических и бухгалтерских расчетах, но не все знают, что и в научно-технических задачах электронные таблицы можно использовать достаточно эффективно. Вычислительную мощь Excel обеспечивают встроенные функции, средства анализа и надстройки.
Надстройки – специальные средства, расширяющие возможности программы MS Excel. Именно надстройки делают ее удобной для использования в научно-технической работе. Хотя эти средства считаются внешними, дополнительными, доступ к ним осуществляется при помощи обычных команд командной строки (обычно через меню команд Сервис или Данные). При этом открываются специальные диалоговые окна, оформленные как стандартные диалоговые окна MS Excel.
Подключить или отключить установленные надстройки Excel можно с помощью Настройки панели быстрого доступа. Подключение надстроек увеличивает нагрузку на вычислительную систему, поэтому обычно рекомендуют подключать только те надстройки, которые реально используются.
Для уточнения корней с помощью ЭТ MS Excel можно использовать средство Подбор параметра (команда Данные → Анализ «что если») или надстройку Поиск решения.
Приведем лист MS Excel (см. рис. 2) с иллюстрацией применения средства Подбор параметра для уточнения корня уравнения (3), изолированного на отрезке [2, 3].
Рис. 2 – Графическое отделение корней уравнения двумя способами и подготовка к этапу уточнения
При подборе параметра Excel изменяет значение в одной конкретной ячейке, в нашем случае N32, до тех пор, пока вычисления по формуле в ячейке О32, ссылающейся на ячейку N32, не дадут нужного результата, а именно нуля функции (см. рис. 3).
Рис. 3 – Окно диалога средства Подбор параметра
После нажатия на кнопку OК MS Excel выведет окно диалога Результат подбора параметра (см. рис. 4). Если подобранное значение корня необходимо сохранить, то нажмите на ОК, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки, в нашем случае – ячейка N32.
Рис. 4 – Окно диалога Результат подбора параметра
Таким образом, искомое значение корня, уточненное средством Подбор параметра, составит ξ = 2,50617208. При подборе параметра Excel использует итерационный (циклический) процесс, при этом количество итераций и точность может устанавливаться пользователем.
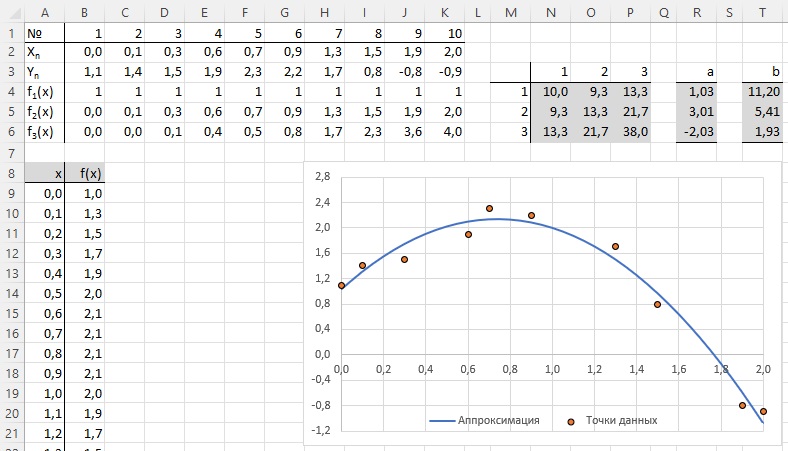
Рассмотрим теперь, как воспользоваться надстройкой Поиск решения на примере нахождения корней алгебраического уравнения х3 – 10.х + 2 = 0. На следующем листе MS Excel приведен этап графического отделения корней (см. рис. 5).
Рис. 5 – Этап графического отделения корней уравнения х3 – 10.х + 2 = 0
Анализ графика функции показывает, что решаемое уравнение имеет три действительных корня, определены отрезки изоляции искомых корней.
Для уточнения отделенных корней сформируем вторую таблицу, в которую занесем середины отрезков изоляции, которые будут взяты за начальные приближения к искомым корням. Кроме этого, таблица содержит столбец вычисленных значений функции F(x) = х3 – 10.х + 2. Далее из команды главного меню Данные следует вызвать надстройку Поиск решения. При этом откроется диалоговое окно, представленное на рис. 6.
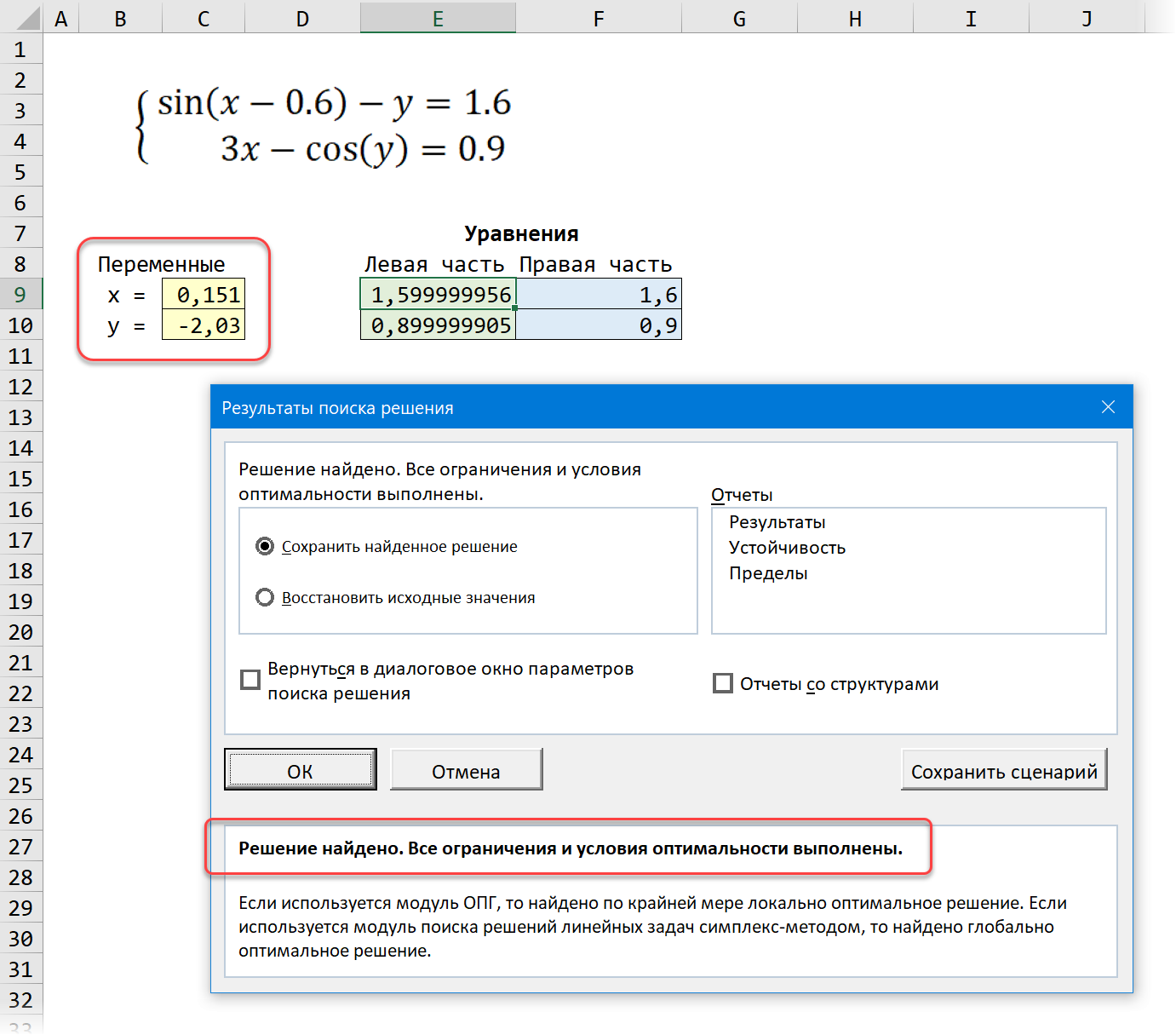
Рис. 6 – Диалоговое окно надстройки Поиск решения
Для уточнения первого корня в поле Оптимизировать целевую функцию указываем адрес ячейки D23. Поскольку необходимо найти решение уравнения F(x) = 0, то в переключателе До: записываем значение правой части уравнения (т. е. 0). В поле Изменяя ячейки переменных: заносится абсолютный адрес ячейки С23. Для запуска процесса решения задачи следует щелкнуть по кнопке Найти решение. На экране появится диалоговое окно Результаты поиска решения с информацией о том, найдено или нет искомое решение (см. рис. 7). Если решение найдено, то далее следует выбрать один из следующих возможных вариантов:
• сохранить найденное решение, т. е. заменить исходные значения в изменяемых ячейках на значения, полученные в результате решения задачи;
• восстановить исходные значения в изменяемых ячейках.
Рис. 7 – Диалоговое окно Результаты поиска решения
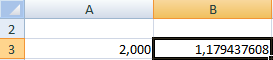
Таким образом, искомое значение первого корня, уточненное надстройкой Поиск решения, составит ξ1 = -3,257896991. Аналогично находится второй корень ξ2 = 0,200809757. Третий корень найдем с помощью средства Подбор параметра. Результаты решения представлены на рис. 8.
Рис. 8 – Результаты уточнения третьего корня
ЗАКЛЮЧЕНИЕ
В результате выполнения данной научно-исследовательской работы достигнута цель исследования – я освоил приемы численного решения алгебраических и трансцендентных уравнений в среде электронных таблиц MS Excel. При этом я ознакомился с историей развития аналитических и численных методов решения уравнений и систем уравнений, изучил особенности, достоинства и недостатки аналитических и численных методов. Кроме этого, я ознакомился с вычислительными возможностями ЭТ MS Excel и изучил такие средства уточнения действительных корней нелинейных уравнений, как средство Подбор параметра и надстройка Поиск решения. Оба эти инструмента позволяют подобрать значение искомого корня, при котором функция F(ξ) обращается в ноль. На практике в среде ЭТ MS Excel были графически отделены и уточнены корни трансцендентного уравнения x. lg x – 1 = 0 и алгебраического х3 – 10.х + 2 = 0.
Надеюсь, что полученные знания и навыки помогут мне успешно сдать ОГЭ по дисциплинам математика и информатика и ИТК.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ
1. Боголюбов А.Н. Математики. Механики. Библиографический справочник. – Киев: Наукова думка, 1983. – 638 с.
2. Б.П. Демидович, И.А. Марон. Основы вычислительной математики. – М.: Наука, 1966. – 664 с.
3. Дж. Уокенбах. Microsoft Office Excel 2007. Библия пользователя. – М.: Диалектика, 2008. – 816 с.
4. П. Дж. Бернс, Дж. Р. Николсон. Секреты Excel для Windows 95. – К.: Диалектика, 1996. – 576 с.
Просмотров работы: 1863
Книга посвящена методам решения вычислительных задач с помощью Excel: алгебраические уравнения и системы, интерполирование и аппроксимация функциональных зависимостей, дифференцирование и интегрирование, решение дифференциальных и интегральных уравнений. В книге также описываются основные приемы работы с Excel, обсуждаются способы организации документов, анализируются методы ввода и редактирования данных, изучаются возможности применения форматов и стилей, иллюстрируются принципы использования встроенных вычислительных утилит, а также даются основы программирования на VBA. Ранее по теме я опубликовал Вильям Дж. Орвис. Excel для ученых, инженеров и студентов.
Алексей Васильев. Числовые расчеты в Excel. — СПб.: Издательство «Лань», 2022. — 600 с.
Скачать краткое содержание в формате Word или pdf (конспект составляет около 3% от объема книги), примеры в архиве (внутри файл Excel с поддержкой макросов)
Купить книгу в Ozon или Лабиринте
Главная идея книги — это адаптация стандартных (или «классических») алгоритмов решения задач вычислительной математики для реализации в приложении, имеющем «ячеечную» структуру, т.е. структуру электронной таблицы. Автор использует среду Excel 2013, самой свежей версии на момент выпуска книги. Я же использую Excel 365.
Глава 5. Методы вычислений и обработка данных
Числовые формулы и циклические ссылки
Эффектный механизм вычислений основан на использовании циклических ссылок. Циклическая ссылка – это ссылка в формуле на ячейку, которая содержит формулу (т.е. ссылка в ячейке на эту же ячейку). По умолчанию такая ситуация считается ошибочной, поскольку означает, что для вычисления значения ячейки по формуле с циклической ссылкой необходимо использовать значение этой ячейки. Круг замкнулся!
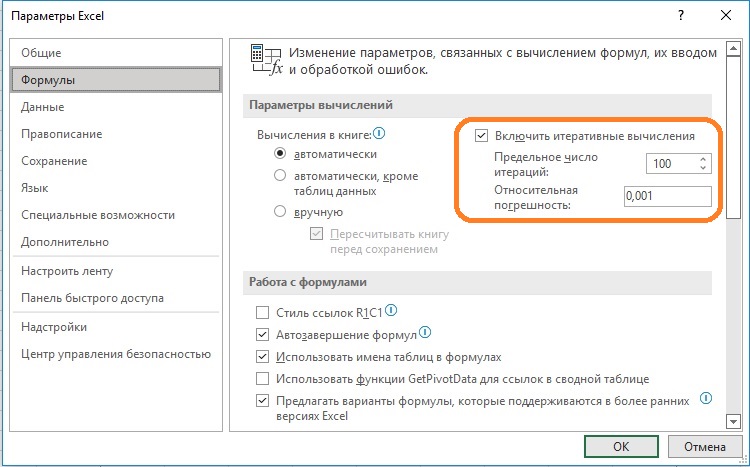
Для использования циклических ссылок пройдите Файл –> Параметры –> Формулы. Устанавливаем флажок Включить итеративные вычисления.
Рис. 1. Переход в режим использования циклических ссылок (итеративных вычислений)
В итерационном процессе начальное значение ячейки всегда равно нулю. Это нулевое значение используется в циклической ссылке для вычисления значения ячейки для первой итерации. Значение ячейки для первой итерации используется для вычисления значения ячейки для второй итерации и т.д. Предельное количество итераций определяется значением поля Предельное число итераций. Вычисления также заканчиваются, если относительная погрешность вычислений становится меньше того значения, что указано в поле Относительная погрешность.
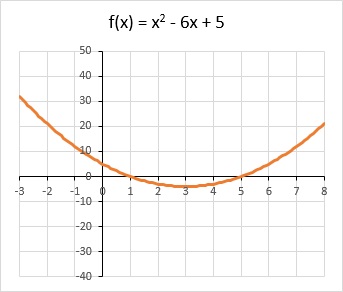
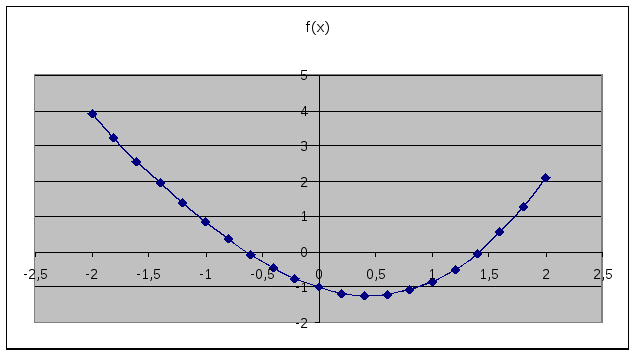
Метод последовательных итераций может применяться для решения алгебраических уравнений вида х = f(x). Например, найдем корни уравнения х2 — 6х + 5 = 0. У него два корня х = 1 и х = 5.
Рис. 2. График функции у = х2 — 6х + 5
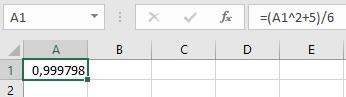
Представим уравнение в виде
В ячейку А1 введите формулу =(А1^2+5)/6
Рис. 3. Нахождение корня уравнения итерационным методом
Точность решения определяется настройками Параметров Excel (см. рис. 1). Если точности не хватило, нажмите <F9>. Итерационный процесс продолжится с текущего числового значения ячейки.
Одна из проблем итерационного процесса заключается в том, что он всегда стартует с нулевого значения в ячейке. Например, чтобы найти второй корень уравнения, его следует представим в виде…
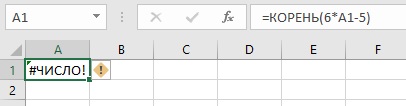
Но… при х = 0 под корнем отрицательное значение. Поэтому если в ячейку А1 ввести формулу =КОРЕНЬ(6*А1-5), получим сообщение об ошибке:
Рис. 4. Ошибка из-за того, что начальное выражение под корнем отрицательное
Изменим начальное значение. Идея состоит в том, чтобы ввести новую переменную z = х – а или х = z + а. И решить новое уравнение z = f(z + a) – a. Для переменной z начальное значение по-прежнему нулевое. В ячейку А2 введите начальное приближение для корня, а в ячейку А1 – формулу =КОРЕНЬ(6*(А1 +А2)-5)-А2.
Рис. 5. Начальное значение для итерационных вычислений задается в явном виде
В результате решения уравнения z = f(z + а) — а находим корень для z. При этом х = z + а.
Чтобы метод итераций работал нужно, чтобы в области поиска корня функции f(x) ее производная по модулю была меньше единицы.
Как минимум, это условие должно выполняться в точке начального значения поиска корня.
Утилита подбора параметра
Большинство расчетных возможностей Excel реализуется через встроенные функции. Но иногда удобнее использовать специальные утилиты или надстройки. Так, например, назначение утилиты Подбора параметра состоит в том, чтобы подобрать значение в какой-то определенной ячейке такое, что значение в другой ячейке примет нужное значение.
Чтобы запустить утилиту пройдите Данные –> Прогноз –> Анализ «что если» –> Подбор параметра. Решим с помощью этой утилиты рассмотренное выше уравнение.
Рис. 6. Решение уравнение с помощью утилиты Подбор параметра
Найден один из двух корней уравнения. Второй корень х = 5 можно найти, если изменить начальное значение в ячейке ВЗ. Например, на 8. В реальной жизни угадать, как начальное приближение влияет на результат подбора параметра, бывает крайне сложно. Еще одна проблема заключается в том, что варьируется всего одна ячейка. В этом отношении более гибкой является надстройка Поиск решения, используемая в оптимизационных задачах.
Глава 7. Избранные вычислительные задачи
Решение дифференциального уравнения
Дифференциальным называется уравнение вида F(x, y, y’, y’’, … y(n)) = 0, связывающее аргумент х, неизвестную функцию у(х) и ее производные. Порядок дифференциального уравнения определяется порядком старшей производной. Задача – найти функцию.
Рассмотрим уравнение первого порядка у'(х) = f(x, у(х)). Чтобы найти решение уравнения в числовом виде, необходимо указать начальное условие – значение функции у(х) в точке х0, т. е. указать числовое значение у0 такое, что y(x0) = y0. Дифференциальное уравнение и начальные условия – это задача Коши. Для решения дифференциального уравнения используем не самый точный, но весьма простой метод Эйлера. Чтобы найти значение функции у(х) интервал значений аргумента от х0 до х разбивается на N одинаковых частей так, что xk = х0 + kΔx, где Δx = (х – х0)/N. k = 0, 1, …, N.
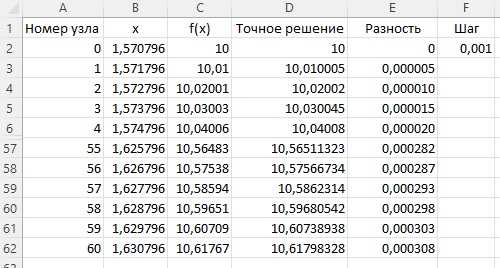
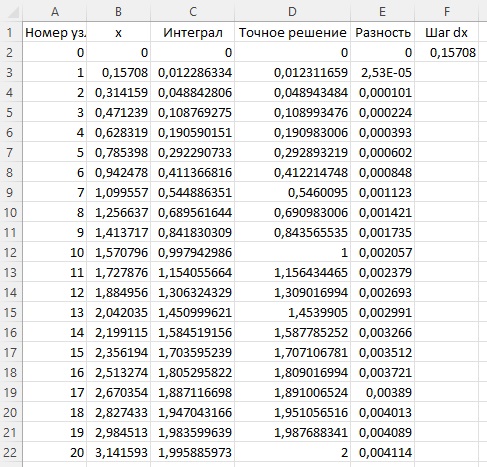
Для вычисления значения y(xN) последовательно вычисляем значения y(xk) в узловых точках xk. При этом используем рекуррентное соотношение yk+1 = yk + Δx*f(xk,yk) с начальным приближением у0 = у(х0). Эту итерационную процедуру реализуем в Excel для уравнения у'(х) = у(х)*sinx с начальным условием у(π/2) = 10. Эта задача имеет «точное» аналитическое решение
Рис. 7. Результат решения дифференциального уравнения в числовом виде
Здесь в столбце А — номер узла; В — значение аргумента в узле; С — значение искомой функции; D — точное решение уравнения; Е — разность точного и приближенного решений. В ячейке F2 указано значение для шага приращения по аргументу. Формулы см. в приложенном Excel-файле. Часть строк на рис. 7 скрыта.
Вычисление интегралов
Рассмотрим задачу о вычислении интеграла вида
Для интегрирования используем метод трапеций. Интервал интегрирования разбиваем на N частей и выбираем узловые точки xk = х0 + kΔx, где Δх = (х — x0)/N, а индекс k = 0, 1, …, N. Воспользуемся тем обстоятельством, что числовое значение интеграла равно площади под графиком функции на интервале интегрирования. Разобьем область под кривой на трапеции, с основаниями в узловых точках. Ребро трапеции в точке хk равняется f(xk). Тогда площадь области под кривой равняется (примерно) сумме площадей таких трапеции. А площадь одной трапеции равна
Таким образом, в качестве оценки для значения интеграла получаем выражение
Воспользуемся этой формулой для вычислений в Excel интеграла
Рис. 8. Результат вычисления интеграла (формулы см. в приложенном Excel-файле)
Глава 8. Диаграммы
Параметрическая кривая
Под параметрической подразумевается кривая, уравнение которой задано в параметрическом виде. Идея определения в параметрическом виде зависимости у от х состоит в том, что задается зависимость каждой из этих переменных от параметра t. А если заданы зависимости х = f1(t) и у = f2(t), то система из этих двух уравнений определяет (неявно) зависимость у(х). Такая зависимость называется параметрической. Если в системе уравнений х = f1(t) и у = f2(t) путем алгебраических преобразований удается исключить параметр t, получают явное соотношение между переменными х и у. Для построения графика для зависимости у(х) нужно предварительно вычислить координаты точек (xk, yk) (k = 0, 1, 2, …, n). Это делают, используя соотношения: xk = x(tk) = f1(tk) и yk = y(tk) = f2(tk).
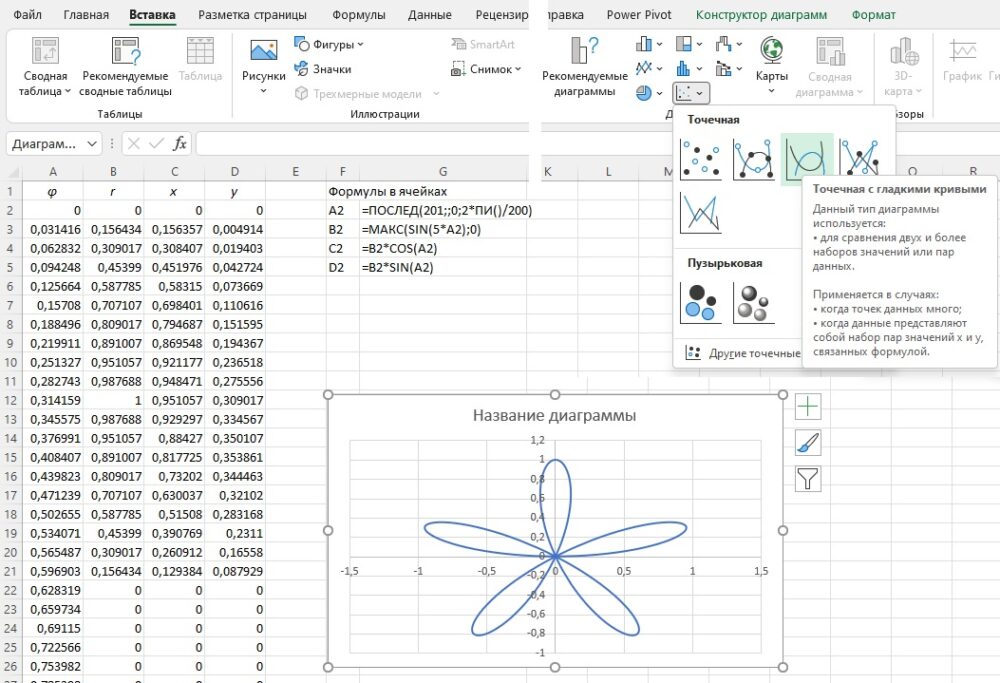
Мы построим график функции, которая в полярных координатах задана соотношением r = sin(5φ). Здесь r и φ – полярные координаты – радиус и полярный угол. Полярный угол φ может принимать значения от 0 до 2π, а радиус должен быть неотрицательным. Полярные координаты связаны с декартовыми х и у соотношениями х = rсоs(φ) и у = rsin(φ). В роли параметра выступает φ. Действительно, декартовы координаты точек на кривой определяются соотношениями x(φ) = r(φ)cos(φ) и y(φ) = r(φ)sin(φ ф), где r(φ) = sin(5 φ). Если результат, возвращаемый формулой r(φ) = sin(5 φ), меньше нуля, то присваиваем r значение 0 (r по определению неотрицательна).
Рис. 9. Параметрическая кривая; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
Выделите диапазон C2:D202, пройдите Вставить –> Диаграммы –> Точечная и выберите тип Точечная с гладкими кривыми.
Глава 10. Основы программирования в VBA
Код процедуры, демонстрирующий использование конструкции With … End With
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
Sub Getlnfo() ‘ Размер шрифта ячейки Dim FSize As Integer ‘ Название шрифта Dim FName As String ‘ Ширина и высота ячейки Dim CWidth As Integer, CHeigh As Integer ‘ Соотношение сторон ячейки Dim CScale As Double ‘ Текущая дата Dim Today As Date ‘ Текст для отображения в окне Dim txt As String ‘ Обработка активной ячейки With ActiveCell ‘ Считывание названия шрифта FName = .Font.Name ‘ Считывание размера шрифта FSize = .Font.Size ‘ Считывание ширины ячейки CWidth = .Width ‘ Считывание высоты ячейки CHeight = .Height ‘ Вычисление соотношения сторон ячейки CScale = CWidth / CHeight ‘ Определение текущей даты Today = Date ‘ Формирование текста для отображения в окне txt = «Сегодня « & Today & vbLf & vbLf txt = txt & «Параметры активной ячейки:» & vbLf & vbLf txt = txt & «Шрифт — « & FName & vbLf txt = txt & «Размер — « & FSize & vbLf txt = txt & «Ширина ячейки — « & CWidth & vbLf txt = txt & «Высота ячейки — « & CHeight & vbLf txt = txt & «Соотношение сторон — « & CScale End With ‘ Звуковое приветствие Application.Speech.Speak («Hello, glad to see you!») ‘ Отображение окна с сообщением MsgBox txt, vblnformation, «Информация об активной ячейке» ‘ Завершающая озвучка Application.Speech.Speak («Good bye!») End Sub |
Пример использования конструкции If … Then … Else
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Sub WhoAreYou() ‘ Имя пользователя Dim name As String ‘ Название для окна Dim title As String title = «Служба знакомств» ‘ Будем знакомиться? Result = MsgBox(«Хотите познакомиться?», vbYesNo, title) ‘ Проверка результата If Result = vbYes Then name = InputBox(«Kaк Вас зовут?», title) ‘ Если не указано имя, завершаем макрос If name = «» Then End ‘ Если имя указано, отображаем приветствие MsgBox «Добрый день, « & name & «! Приятно познакомиться!», vbOKOnly, title Else ‘ Знакомство не состоялось MsgBox «Очень жаль! Пока!», vbOKOnly, title End If End Sub |
Пример использования оператора выбора Case и цикла For Each … Next
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
Sub SetColor() ‘ Переменная для обозначения ячейки Dim Cell As Range ‘ Перебор ячеек в выделенном диапазоне For Each Cell In Selection With Cell ‘ Оператор выбора Select Case .Value Case 0 .Interior.Color = vbYellow .Font.Bold = True .Font.Color = vbBlue Case Is > 0 .Interior.Color = vbGreen .Font.Italic = True .Font.Color = vbWhite Case Is < 0 .Interior.Color = vbRed .Font.Bold = True .Font.Italic = True .Font.Color = vbBlack End Select End With Next Cell End Sub |
Глава 11. Создание форм и обработка событий
Чтобы создать форму в VBE пройдите Insert –> UserForm. Добавьте в форму два текстовых окна и одну кнопку.
Рис. 10. Пользовательская форма
С формой связан код в отдельном Module2:
|
Sub SimpleFormShow() With UserForm1.Label2 .Caption = .Caption & » « & ActiveCell.Address End With UserForm1.Show End Sub |
Свой код связан с кнопкой «Закрыть окно». Чтобы увидеть его дважды щелкните на кнопке:
|
Private Sub CommandButton1_Click() Unload UserForm1 End Sub |
Ключевое слово Private означает, что процедура доступна только для внутреннего вызова – вызвать эту процедуру как макрос из Excel не получится.
Обработка событий
Рассмотрим на примере формы для заполнения ячеек числами Фибоначчи. Первые два числа равны единице, а каждое следующее равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, …
Код макроса для заполнения ячеек числами Фибоначчи разместим в Module3
|
Sub Fibonacci() ‘ Отображение формы UserForm2.Show End Sub |
В макросе всего одна команда, которая отображает окно формы. Основной код связан с элементами формы.
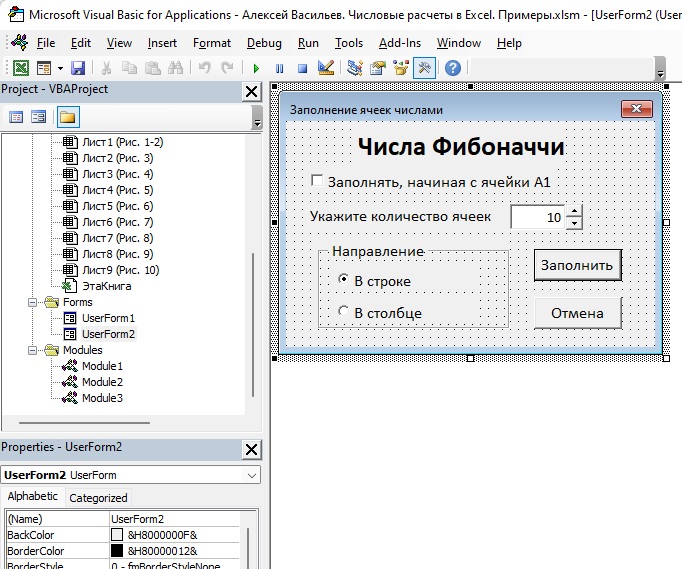
Рис. 11. UserForm2
Рассмотрим элементы формы. Свойство Caption UserForm2 = Заполнение ячеек числами. Текстовая метка Label1: Caption = Числа Фибоначчи. Далее следует элемент CheckBox1. Свойство Caption = Заполнять, начиная с ячейки А1. Свойство Value оставляем False (оно такое по умолчанию). Свойство Caption текстовой метки Label2 = Укажите количество ячеек. Справа от нее расположены элементы TextBox1 (Value = 10, Text Align = З-fmTextAlignRight) и SpinButton1 (Value = 10, Min = 3, Max = 20). Далее Frame1. Свойство Caption = Направление. Внутри два переключателя: OptionButton1 (Caption = В строке, Value = True) и OptionButton2 (Caption = В столбце, Value = False). Справа две кнопки: CommandButton1 (Caption = Заполнить, Default = True) и CommandButton2 (Caption = Отмена, Default = False).
Теперь перейдем к программированию кнопок. Начнем с самого простого кода для кнопки закрытия окна формы. Для этого дважды кликните на ней. И введите код:
|
Private Sub CommandButton2_Click() ‘ Выгрузка формы из памяти Unload UserForm2 End Sub |
Далее щелкните на числовом переключателе – SpinButton1:
|
Private Sub SpinButton1_Change() ‘ Синхронизация текстового поля со значением числового переключателя TextBox1.Text = SpinButton1.Value End Sub |
При щелчке на пиктограмме числового счетчика, в зависимости от того, какая из двух стрелок «щелкнута», значение переключателя (значение свойства Value) увеличивается/уменьшается на величину, определяемую свойством SmallChange (в нашем случае это единица) — если новое значение не выходит за допустимые пределы (задаются свойствами Мах и Min). Процедура-обработчик запускается каждый раз при щелчке на счетчике. Поэтому, если мы изменяем состояние счетчика, это автоматически скажется на состоянии текстового поля.
Обработчик для текстового поля по умолчанию реагирует на событие/процедуру TextBoxI_Change. Нам это не подходит. Мы не хотим считать событием любое изменение содержимого поля (в процессе редактирования содержимого). Нас интересует ситуация, когда пользователь закончил редактировать поле. На этот случай предусмотрена процедура с ключевым словом AfterUpdate:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Private Sub TextBox1_AfterUpdate() ‘ Переменная для запоминания значения в текстовом поле Dim num As Integer ‘ Считывание числового значения текстового поля num = Val(TextBox1.Text) With SpinButton1 ‘ Проверка попадания значения в допустимый диапазон If num >= .Min And num <= .Max Then ‘ Корректное значение присваивается числовому переключателю .Value = num Else ‘ Если значение некорректное, в текстовое поле ‘ вписывается значение числового переключателя TextBox1.Text = .Value End If End With End Sub |
На момент начала редактирования текстового поля свойство Text текстового поля TextBox1 и свойство Value числового счетчика SpinButton1 одинаковы. Следующий шаг— пользователь ввел в текстовое поле новое значение – теперь это значение свойства Text объекта TextBox1. Мы его проверяем, и, если оно попадает в допустимый интервал значений, присваиваем соответствующее значение свойству Value числового счетчика SpinButton1. Если же новое значение в текстовом поле не попадает в допустимый интервал значений, в текстовое поле необходимо вернуть старое значение. Про это значение «помнит» свойство Value числового счетчика SpinButton1. Здесь действие обратное – свойству Text текстового поля TextBox1 присваивается значение свойства Value числового счетчика SpinButton1.
В теле процедуры TextBoxI_Afterllpdate() объявляется целочисленная переменная num, которой затем командой num = Val(TextBox1.Text) присваивается значение. Мы использовали функцию Val(), которой в качестве аргумента передается текстовое представление числа, а функция в качестве результата возвращает реальное число. Текстовое представление числа считывается инструкцией TextBox1.Text из текстового поля. Таким образом, в переменную num записано новое значение в текстовом поле. Затем на сцену выходит условный оператор, в котором проверяется условие принадлежности значения переменной num интервалу от SpinButton1.Min до SpinButton1.Мах. При этом мы использовали логический оператор And. Если условие выполнено, свойству SpinButton1.Value присваивается значение num. В противном случае свойству TextBox1.Text присваивается значение SpinButton1.Value.
Код кнопки CommandButton1:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
Private Sub CommandButton1_Click() ‘ Размер массива для чисел Фибоначчи Dim N As Integer, i As Integer ‘ Объявление динамического массива Dim F() As Integer ‘ Размер массива задается значением в текстовом поле N = Val(TextBox1.Text) ‘ Определение размера массива ReDim F(1 To N) ‘ Первые два числа в последовательности Фибоначчи F(1) = 1 F(2) = 1 ‘ Заполнение массива числами Фибоначчи For i = 3 To N F(i) = F(i — 1) + F(i — 2) Next i ‘ Переменная для ссылки для начальной ячейки Dim StartCell As Range ‘ Определение начальной ячейки If CheckBox1.Value Then Set StartCell = Range(«A1») Else Set StartCell = ActiveCell End If ‘ Определение «направления»заполнения If OptionButton1.Value Then For i = 1 To N ‘ Заполнение строки ячеек StartCell.Offset(0, i — 1).Value = F(i) Next i Else ‘ Заполнение столбца ячеек For i = 1 To N StartCell.Offset(i — 1, 0).Value = F(i) Next i End If ‘ Выгрузка формы из памяти Unload UserForm2 End Sub |
В коде важный идеологический момент связан с тем, что мы сначала создаем массив из чисел Фибоначчи, а затем копируем числа из массива в ячейки рабочего листа. Поэтому предварительно определяются размеры массива (количество заполняемых ячеек), и этот массив заполняется числами. Затем мы определяем начальную ячейку заполнения и «направление» заполнения — в строке или в столбце.
Целочисленная переменная N объявляется для записи в нее размера массива. Целочисленная переменная I объявляется для использования в качестве счетчика цикла. Командой Dim F() As Integer объявляется динамический массив F() целых чисел. Затем из текстового поля инструкцией N = Val(TextBox1.Text) считывается количество заполняемых ячеек (размер массива). Чтобы выделить место под массив соответствующего размера, выполняем инструкцию ReDim F(1 То N).
Существует два типа массивов – статические и динамические. Размер статического массива должен быть известен на момент компиляции кода. Размер динамического массива определяется в процессе выполнения программы. Мы имеем дело со вторым случаем. С практической точки зрения разница между статическим и динамическим массивами в том, что размеры статического массива – константы. Например, командой Dim MyArray(1 То 100) As Integer объявляется целочисленный массив МуАггау из 100 элементов (индексы элементов массива изменяются от 1 до 100). Мы же сначала инструкцией Dim F() As Integer декларируем, что F – это массив из целых чисел, неизвестно пока какого размера. А командой ReDim F(1 То N) подтверждаем, что массив из N элементов. Предварительно, разумеется, мы присваиваем значение переменной N.
Командами F(1) = 1 и F(2) = 1 заполняются первые два элемента массива. Для заполнения прочих элементов массива используем оператор цикла с командой F(i) = F(i-1)+F(i-2) (i – индексная переменная) в теле оператора цикла (каждый следующий элемент равен сумме двух предыдущих).
Следующий этап связан с определением начальной ячейки. Для этого командой Dim StartCell As Range мы объявляем переменную StartCell типа Range. Это будет ссылка на начальную ячейку. В условном операторе проверяем, установлен ли флажок опции CheckBox1 (значение свойства Value равно True или False). В зависимости от результата проверки выполняется команда Set StartCell = Range(«A1») (начальная ячейка А1) или Set StartCell = ActiveCell (начальная ячейка – активная на момент запуска макроса). При присваивании значений объектным ссылкам используется ключевое слово Set.
Направление заполнения определяем путем проверки значения свойства OptionButtonl1.Value (выясняем, установлен переключатель OptionButton1 или нет). Если переключатель установлен, то запускается оператор цикла с командой StartCell.Offset(0,i-1).Value = F(i) в теле цикла. В противном случае запускается другой оператор цикла, в котором выполняется команда StartCell.Offset(i-1,0).Value = F(i). Этими командами ячейки рабочего листа заполняются значениями из массива F.
Метод Offset() вызывается из объекта ячейки и имеет два аргумента: смещение вдоль столбца и вдоль строки. В качестве результата возвращается ссылка на соответствующую ячейку. Так, например, инструкция StartCell.Offset(2,5).Value ссылается на ячейку, которая находится на 2 строки вниз и 5 столбцов вправо по отношению к ячейке StartCell. Функция Offset() в VBA подобна функции СМЕЩ в Excel.
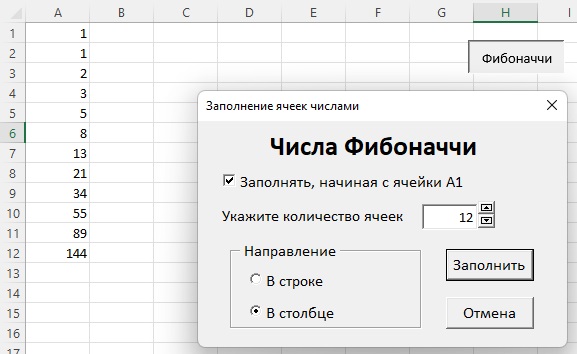
Выгрузка формы из памяти осуществляется командой Unload UserForm2. Проверяем, как работает форма.
Рис. 12. Числа Фибоначчи
Глава 12. Решение алгебраических уравнений и систем
Показано, как использовать методы половинного деления (этот метод я изложил подробнее в отдельной заметке), хорд, касательных, последовательных приближений, Ньютона, градиентного спуска, а также методы линейной алгебры.
Глава 13. Интерполирование и аппроксимация
Представлены интерполяционный полином Лагранжа (см. подробнее), интерполяционный полином Ньютона, полиномиальная интерполяция, интерполяция набором функций, интерполяция сплайнами, а также методы аппроксимации.
Методы аппроксимации. Теория
Задача аппроксимирования близка по постановке к задаче интерполирования. В обоих случаях по набору «экспериментальных» данных необходимо восстановить «наилучшее» функциональное выражение между зависимой и независимой переменными. Отличие между этими задачами состоит в том, что в задаче интерполирования накладывается условие совпадения в узловых точках табличных значений и значений интерполяционной функции. При аппроксимировании параметров для варьирования недостаточно для того, чтобы аппроксимирующая функциональная кривая в каждой узловой точке принимала предопределенное значение. Ищется функция, которая будет иметь «наименьшее отклонение» от значений в узловых точках. При этом необходимо задать «метрику», через которую определяется «цена» отклонения от значения в узловой точке. В качестве метода оптимизации часто используют метод наименьших квадратов.
Предположим, имеется выражение F(x, а1, а2, …, аm), на основе которого мы хотим аппроксимировать зависимость, заданную значениями у1, у2, …, уm в узловых точках х1, х2, …, хm. Задача состоит в том, чтобы на основе критерия вычислить параметры оптимизации а1, а2, …, аm, которые входят в выражение для функции F(x, а1, а2, …, аm).
В данном случае важно то, что количество m варьируемых параметров в аппроксимирующей функции не превышает количество n узловых точек, т.е. m ≤ n. Причем, если имеет место равенство m = n, то речь идет о задаче интерполирования.
В качестве критерия мы будем использовать метод наименьших квадратов. Для этого построим функцию, определяемую как сумма квадратов разности «экспериментальных» и «теоретических» значений в узловых точках:
Суть метода состоит в том, чтобы подобрать такие параметры а1, а2, …, аm, при которых значение выражения Φ(а1, а2, …, аm) будет минимальным. В результате получаем систему из m алгебраических трансцендентных уравнений, решая которую, находим параметры а1, а2, …, аm.
Если учесть явное выражение для функции Φ(а1, а2, …, аm), уравнения системы для определения оптимизационных параметров могут быть записаны как
Индекс p = 1, 2, …, m.
Часто аппроксимирующая функция представима в виде линейной комбинации базисных функций, и оптимизация выполняется по коэффициентам этой линейной комбинации — имеется в виду, что функция F(x, а1, а2, …, аm) = a1f1(x) + a2f2(x) + … + amfm(x), где базисные функции f1(x), f2(x), … fm(x) известны и определены однозначно.
Нередко задачу с нелинейной по параметрам оптимизации аппроксимирующей функцией удается свести к линейному случаю. Например, если по точкам (xk, yk) (k = 1, 2, …, n) мы пытаемся вычислить оптимальные параметры для функции F(x, A, b) = Аехp(bx), то можем рассмотреть набор точек (xk, In(yk)) и аппроксимировать эту зависимость линейной функцией ln(F(x, А, b)) = lnA + bx.
В этом случае мы можем значительно продвинуться в вопросе выбора оптимальных параметров а1, а2, …, аm. В частности, несложно понять, что
Тогда система для определения оптимизационных параметров записывается как
для индексов р = 1, 2, …, m. После преобразований эти уравнения можем записать в виде
Относительно параметров as (индекс s = 1, 2, …, m) — это линейная неоднородная система алгебраических уравнений, которая достаточно легко решается, в том числе и в Excel. Ее удобно записать в матричном виде. Для этого введем ряд обозначений: вектор значений табулированной функции в узловых точках
… матрица F̂ размерами mхn (m строк и n столбцов) значений базисных функций в узловых точках с элементами Fij = fi(xj) (индексы i = 1,2, …, m и j = 1, 2, …, n). Тогда систему уравнений для определения оптимизационных параметров можно в матричном виде записать как
где через
обозначен вектор, составленный из параметров оптимизации. Решение этой системы можем записать в виде
где индекс -1 обозначает обратную матрицу.
Аппроксимация в Excel
Реализуем описанную выше схему на листе Excel. Оттолкнемся от исходных данных (область В2:К3) и построим аппроксимирующую зависимость на основе полиномиального выражения второй степени. Аппроксимирующая функция имеет вид F(x) = а1 + а2х + а3х2, и задача состоит в определении по исходным данным параметров а1, а2 и а3).
Рис. 13. Построение аппроксимирующей зависимости
Построим матрицу, составленную из значений базисных функций в узловых точках. Учитывая вид аппроксимирующей функции F(x) = а1 + а2х + а3х2, понятно, что базисными функциями являются f1(x) = 1, f2(x) = х и f3(x) = х2. Значения этих функций в узловых точках вычислено в ячейках В4:К6. Это и есть та матрица, на основе которой вычисляются параметры аппроксимирующей функции. Выполним промежуточные расчеты:
Для вычисления параметров аппроксимирующей функции в ячейки R4:R6 вводим формулу массива =МУМНОЖ(МОБР(N4:P6);T4:T6). Этой формулой реализуется выражение (17). Получаем вектор-столбик с коэффициентами а. Теперь значение аппроксимирующей функции в любой точке х можно вычислить по формуле F(x) = 1,03 + 3,01х – 2,03х2 (диапазон А8:В29).
Глава 14. Дифференцирование и интегрирование
Рассмотрено: вычисление производной в узловых точках. Общие подходы к числовому интегрированию. Метод Чебышева. Метод Гаусса. Вычисление несобственных интегралов. Вычисление повторных интегралов.
Глава 15. Решение дифференциальных и интегральных уравнений
Метод последовательных приближений. Метод степенных рядов. Метод Рунге–Кутты. Метод Адамса. Метод Милна. Системы дифференциальных уравнений. Интегральные уравнения.
Глава 16. Вместо заключения
Рассмотрен бесплатный аналог Excel – приложением Open Office Calc.
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
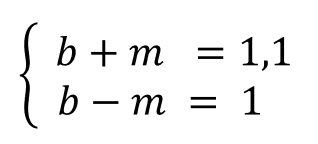
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
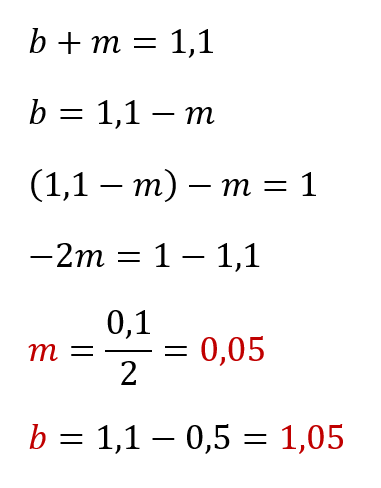
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
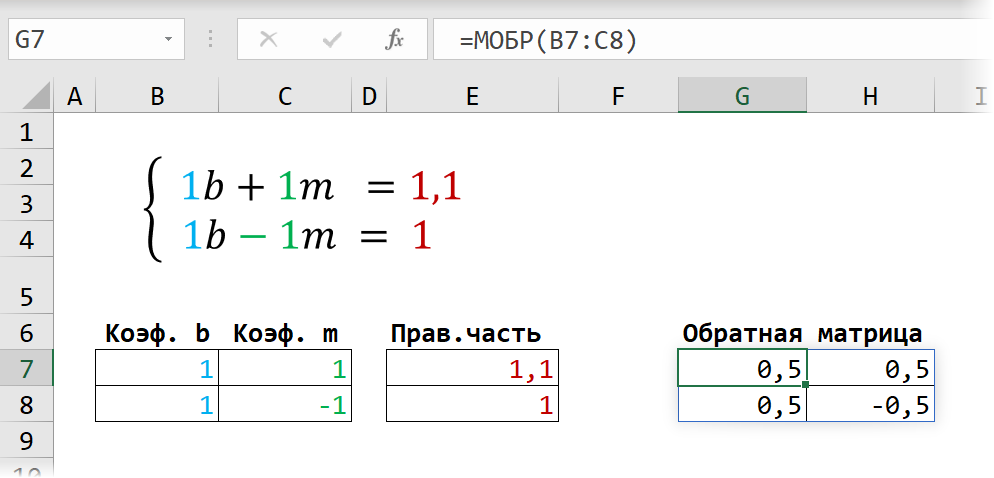
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
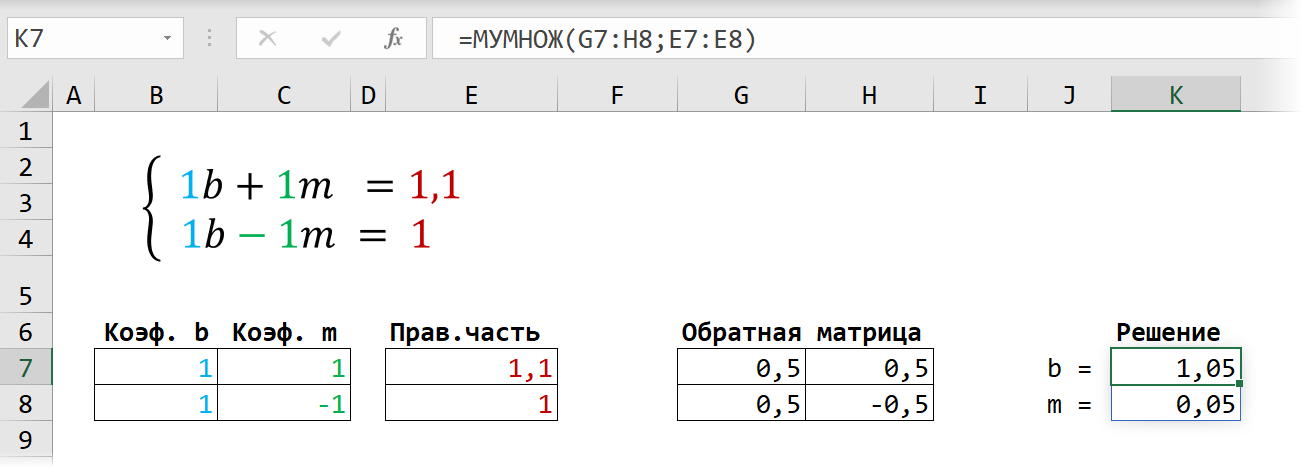
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
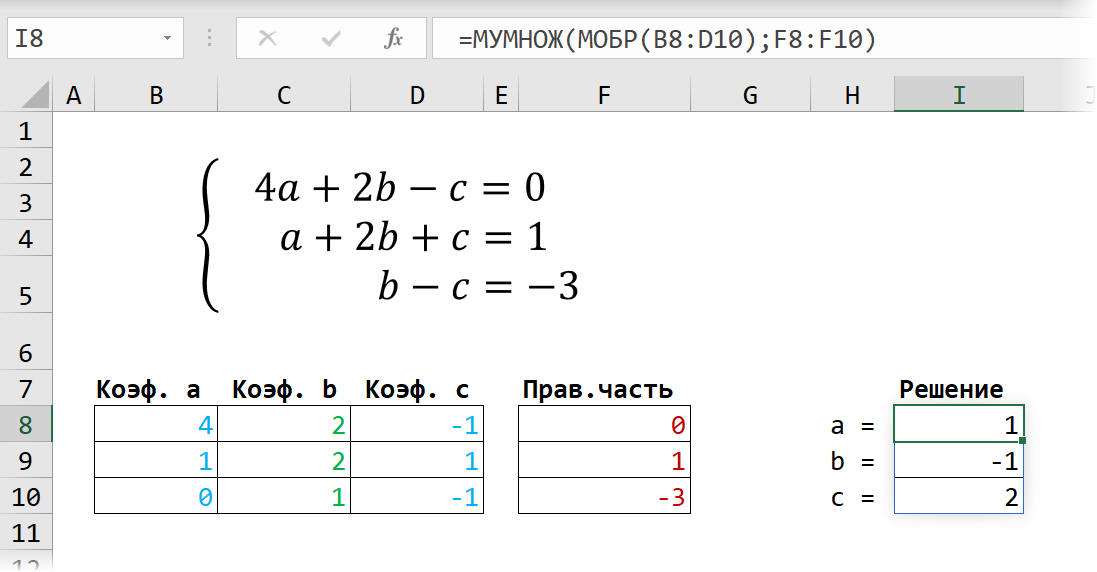
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
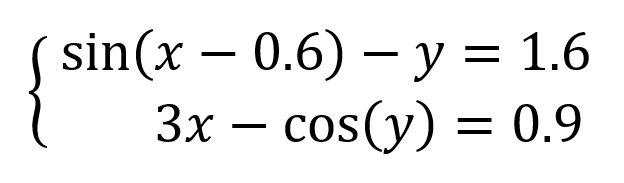
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
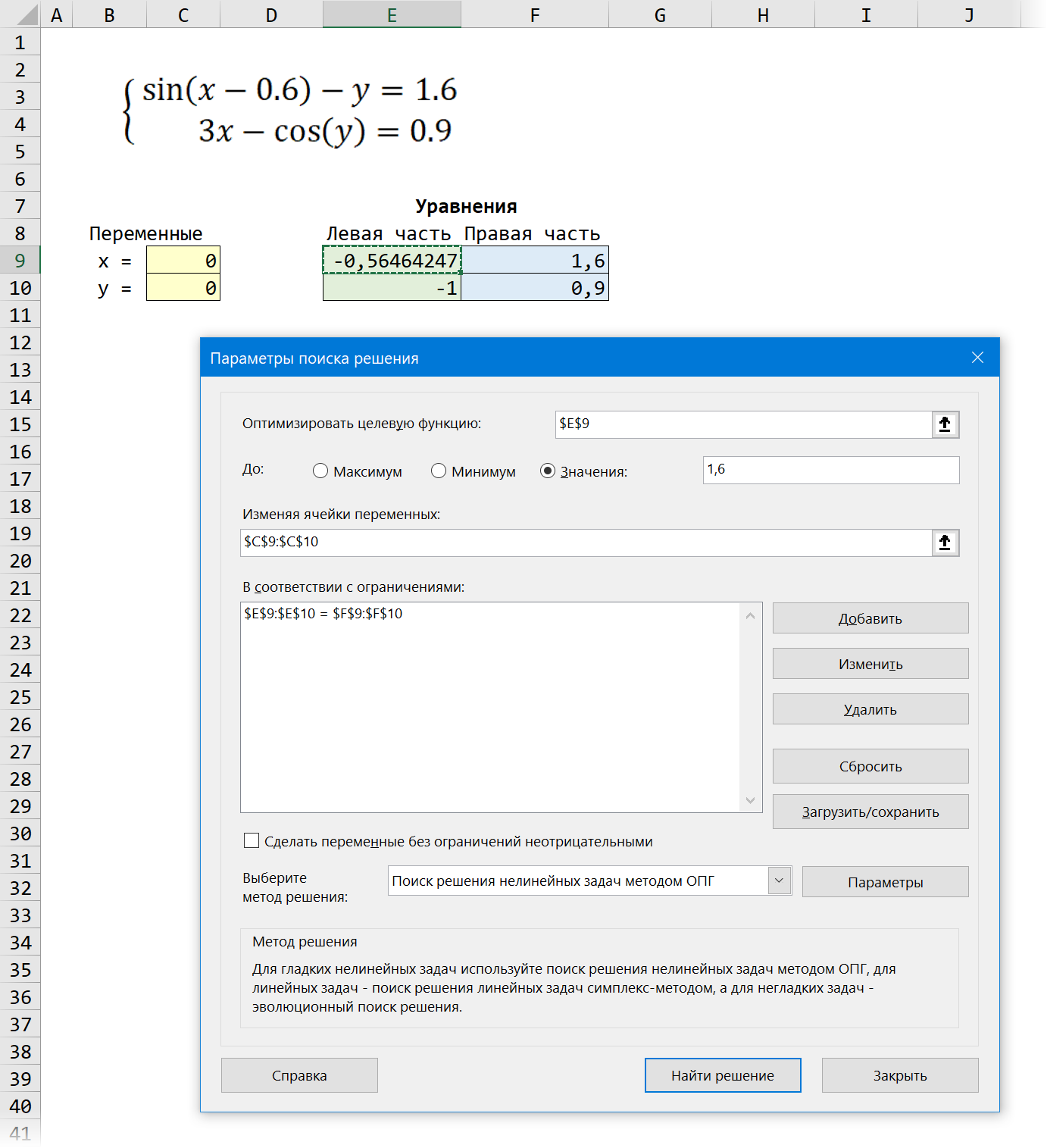
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
Тема:
Электронная таблица Microsoft
Excel.
Средства и методы решения
уравнений.
Цель работы:Освоить численный
метод решения уравнения и встроенные
средства решения уравнений..
Содержание
Лабораторная
работа №11 1
Тема:
Электронная таблица Microsoft Excel. Средства
и методы решения уравнений. 1
1
Численный метод решения нелинейных
уравнений 1
1.1 Область
локализации корней 1
1.2 Критерии
сходимости при решении уравнений 2
1.3 Метод
половинного деления (метод дихотомии) 2
Пример
решения уравнения методом дихотомии 3
2
Решение уравнений, используя “Подбор
параметра” 6
2.1 Пример
решения уравнения, используя “Подбор
параметра” 6
3
Решение уравнений и систем уравнений,
используя надстройку “Поиск решения” 9
3.1 Пример
решения уравнения, используя надстройку
“Поиск решения” 10
Задание
1. Решение уравнений численным методом 12
Задания
2. Решение уравнений встроенными
средствами “Подбор параметра” и “Поиск
решения” 12
Контрольные
вопросы 13
1 Численный метод решения нелинейных
уравнений
1.1 Область локализации корней
В
общем виде любое уравнение одной
переменной принято записывать так
,
при этом корнем (решением) называется
такое значение x*, чтооказывается
верным тождеством. Уравнение может
иметь один, несколько (включая бесконечное
число) или ни одного корня. Как легко
видеть, для действительных корней задача
отыскания решения уравнения легко
интерпретируется графически: корень
есть такое значение независимой
переменной, при котором происходит
пересечение графика функции, стоящей
в левой части уравненияf(x),
с осью абсцисс.
Например,
для уравнения
выполним преобразование и приведем его
к видуf(x)=0
т.е.
.
График этой функции представлен на
рисунке 1. Очевидно, что данное уравнение
имеет два действительных корня – один
на отрезке [-1, 0] , а второй – [1, 2].
Рисунок
1. График функции
Таким образом, можно приблизительно
определять область локализации корнейуравнения. Заметим, что отделить корень
можно не единственным образом: если
корень отделён на каком-либо отрезке,
то годится и любой меньший отрезок,
содержащий этот корень. Вообще говоря,
чем меньше отрезок, тем лучше, но при
этом не следует забывать о том, что на
отделение корня на меньших отрезках
также тратятся вычислительные усилия,
и, быть может, весьма значительные. Таким
образом, часто для начала довольствуются
весьма широким отрезком, на котором
корень отделён.
Некоторые
виды уравнений допускают аналитическое
решение. Например, степенные
алгебраические уравнения степени
n
приn ≤
4. Однако, в общем виде, аналитическое
решение, как
правило, отсутствует. В этом случае,
применяются численные
методы. Все
численные методы решения уравнений
представляют собой итерационные
алгоритмы
последовательного приближения к корню
уравнения. То есть, выбирается начальное
приближение к корню x0
и затем с помощью итерационной формулы
генерируется последовательность x1,
x2,
…,xk сходящаяся
к корню уравнения
.
1.2 Критерии сходимости при решении уравнений
-
Абсолютная
погрешность — абсолютное изменение
приближения на соседних шагах итерации -
Относительная
погрешность — относительное изменение
приближения на соседних шагах итерации -
Близость
к нулю вычисленного значения левой
части уравнения (иногда это значение
называют невязкой
уравнения,
так как для
корня невязка равна нулю)
Соседние файлы в папке m3_2012
- #
- #
12.08.2017153.09 Кб29a1.doc
- #
12.08.2017186.23 Кб9a1.htm
- #
- #
12.08.2017100.18 Кб9a10.htm
- #
- #
12.08.2017171.91 Кб11a11.htm
- #
- #
12.08.201796.27 Кб8a12.htm
- #
- #
12.08.201793.46 Кб8a13.htm
Решение уравнений
Аналитическое решение некоторых уравнений, содержащих, например тригонометрические функции может быть получено лишь для единичных частных случаев. Так, например, нет способа решить аналитически даже такое простое уравнение, как cos x=x
Численные методы позволяют найти приближенное значение корня с любой заданной точностью.
Приближённое нахождение обычно состоит из двух этапов:
1) отделение корней, т.е. установление возможно точных промежутков [a,b], в которых содержится только один корень уравнения;
2) уточнение приближённых корней, т.е. доведение их до заданной степени точности.
Мы будем рассматривать решения уравнений вида f(x)=0. Функция f(x)определена и непрерывна на отрезке [а.Ь]. Значение х0 называется корнем уравнения если f(х0)=0
Для отделения корней будем исходить из следующих положений:
- Если f(a)* f(b] < 0 , то внутри отрезка a, b существует, по крайней мере, один корень
- Если функция y = f(x) непрерывна на отрезке [a, b], и f(a)*f(b)<0 и f‘(x) на интервале (a, b) сохраняет знак, то внутри отрезка [а, b] существует единственный корень уравнения
Приближённое отделение корней можно провести и графически. Для этого уравнение (1) заменяют равносильным ему уравнением р(х) = ф(х), где функции р(х) и ф(х] более простые, чем функция f(x). Тогда, построив графики функций у = р(х) и у = ф(х), искомые корни получим, как абсциссы точек пересечения этих графиков
Метод дихотомии
Для уточнения корня разделим отрезок [а, b] пополам и вычислим значение функции f(х) в точке xsr=(a+b)/2. Выбираем ту из половин [a, xsr ] или [xsr ,b], на концах которых функция f(x) имеет противоположные знаки.. Продолжаем процесс деления отрезка пополам и проводим то же рассмотрение до тех пор, пока. длина [a,b] станет меньше заданной точности. В последнем случае за приближённое значение корня можно принять любую точку отрезка [a,b] (как правило, берут его середину). Алгоритм высокоэффективен, так как на каждом витке (итерации) интервал поиска сокращается вдвое; следовательно, 10 итераций сократят его в тысячу раз. Сложности могут возникнуть с отделением корня у сложных функций.
Для приближенного определения отрезка на котором находится корень можно воспользоваться табличным процессором, построив график функции
ПРИМЕР: Определим графически корень уравнения . Пусть f1(х) = х, a
и построим графики этих функций. (График). Корень находится на интервале от 1 до 2. Здесь же уточним значение корня с точностью 0,001(на доске шапка таблицы)
Решение в Excel,
Алгоритм для программной реализации
- а:=левая граница b:= правая граница
- m:= (a+b)/2 середина
- определяем f(a) и f(m)
- если f(a)*f(m)<0 то b:=m иначе a:=m
- если (a-b)/2>e повторяем , начиная с пункта2
Метод хорд.
Точки графика функции на концах интервала соединяются хордой. Точка пересечения хорды и оси Ох (х*) и используется в качестве пробной. Далее рассуждаем так же, как и в предыдущем методе: если f(xa) и f(х*) одного знака на интервале , нижняя граница переносится в точку х*; в противном случае – переносим верхнюю границу. Далее проводим новую хорду и т.д.
Осталось только уточнить, как найти х*. По сути, задача сводится к следующей: через 2 точки с неизвестными координатами (х1, у1) и (х2, у2) проведена прямая; найти точку пересечения этой прямой и оси Ох.
Запишем уравнение прямой по двум точках:
В точке пересечения этой прямой и оси Ох у=0, а х=х*, то есть
, откуда
процесс вычисления приближённых значений продолжается до тех пор, пока для двух последовательных приближений корня х„ и хп_1 не будет выполняться условие abs(xn-xn-1)е — заданная точность
Сходимость метода гораздо выше предыдущего
Алгоритм различается только в пункте вычисления серединной точки- пересечения хорды с осью абсцисс и условия останова (разность между двумя соседними точками пересечения)
Решение в Excel
Уравнения для самостоятельного решения: (отрезок в excel ищем самостоятельно)
(х=1,261)
(х=?)
- sin(x/2)+1=x^2 (х=1,26)
- y=sin3x*cos5x (х=?)
(х=0,756)
- x-cosx=0 (х=0,739)
- x^2+4sinx=0 (х=-1,933)
- x=(x+1)3 (х=-2,325)