Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
- линейной (у = а + bx);
- параболической (y = a + bx + cx2);
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а0 + а1х1 +…+акхк.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
Пример:
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
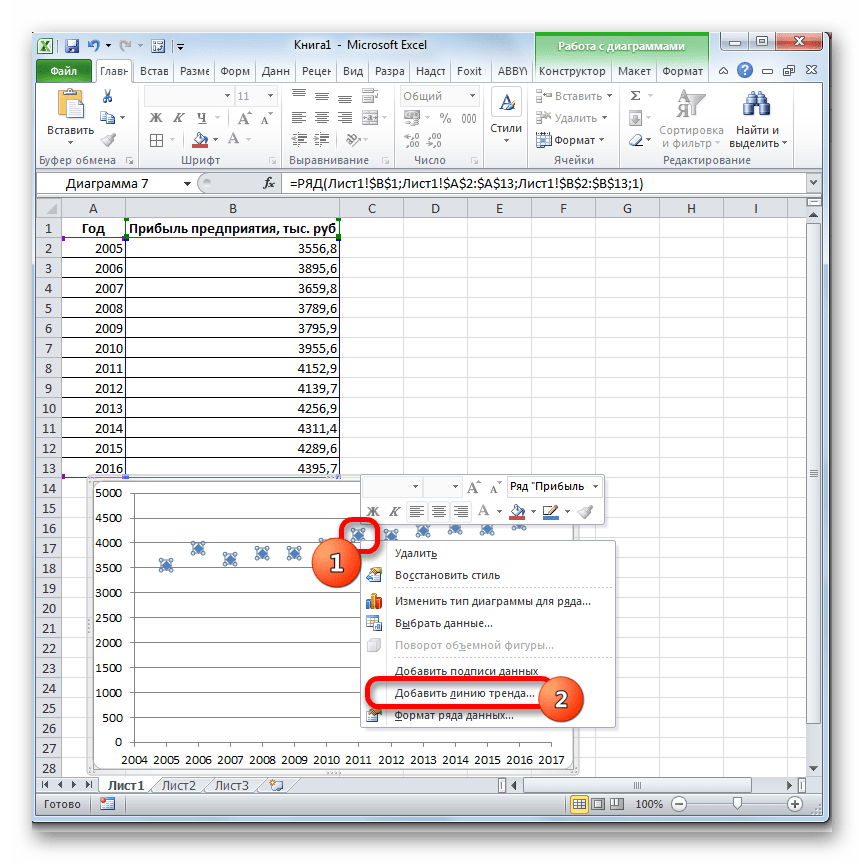
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
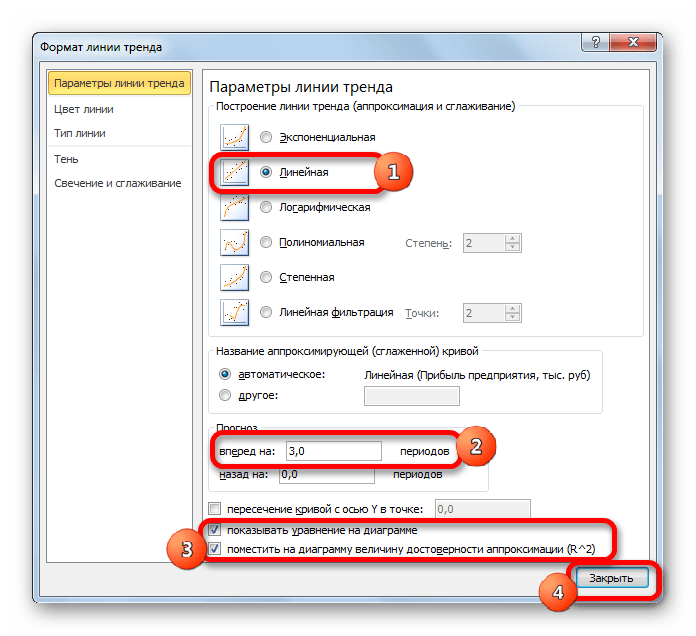
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
Лабораторная
работа №1. Аналитическое моделирование. 3
I.Статичные
аналитические модели оптимизации.
Построение в среде MS Excel. 4
Задача
линейного программирования (ЗЛП). 4
Решение
задач линейного программирования с
помощью надстройки «поиск решений» в
среде excel 6
Задача
оптимального использования ресурсов 8
Запуск
«Поиска решения» 12
Создание
отчета по результатам поиска решения 15
Индивидуальные
варианты заданий. 16
II.
Статичные аналитические модели,
описываемые уравнениями. Построение
в среде MathCad. 20
Решение
уравнений средствами Mathcad 20
Построение
графиков в MathCad 21
Рекомендации
по использованию функции root. 25
Нахождение
корней полинома 26
Символьное
решение уравнений 27
Индивидуальные
варианты заданий. 29
III.
Динамические аналитические модели.
Построение в среде MatLab. 32
Решение
обыкновенных дифференциальных уравнений
в MATLAB. 32
Решение
систем обыкновенных дифференциальных
уравнений с заданными начальными
условиями. 34
Решение
дифференциальных уравнений второго
порядка. 39
Интегрирование
систем линейных дифференциальных
уравнений в матричном виде. 40
Варианты
заданий. 43
Общие
задания. 43
Индивидуальные
задания. 45
Лабораторная
работа №2. Построение аналитической
модели по результатам эксперимента. 49
I.
Построение модели в среде Excel. 49
II.
Построение модели в среде Statistica. 52
Общие
сведения о программе Statistica. 52
Рабочее
окно пакета STATISTICA. 52
Ввод
данных эксперимента. 54
Импорт
данных из внешних программ 54
Ручной
ввод информации 58
Построение
линейной парной регрессионной модели 62
Построение
многомерной регрессионной модели 67
III.
Построение модели в среде Origin Pro. 76
Индивидуальные
варианты заданий. 84
Лабораторная
работа №3. Модели массового обслуживания. 86
I.
Построение модели в среде AnyLogic. 86
Пользовательский
интерфейс 86
Общая
информация о создании моделей в
Enterprise Library 92
Моделирование
одноканальной СМО с очередью. 95
Моделирование
многоканальной СМО с очередью. 106
Индивидуальные
варианты заданий. 113
Лабораторная
работа №4. Моделирование интеллектуальных
систем. Нейросеть обратного распространения
ошибки. 114
I.
Обзор использования пакета Excel Neural
Package. 115
II.
Обзор использования пакета Deductor. 125
III.
Обзор использования пакета STATISTICA Neural
Networks. 137
Индивидуальные
варианты заданий. 145
Лабораторная
работа №5. Моделирование интеллектуальных
систем. Нейронная сеть для кластеризации. 146
I.
Теоретические сведения. 146
II.
Проектирование карты Кохонена в пакете
Excel Neural Package. 147
III.
Проектирование карты Кохонена в пакете
Deductor. 160
IV.
Проектирование карты Кохонена в пакете
Statistica. 172
Индивидуальные
варианты заданий. 179
Лабораторная
работа №6. Моделирование интеллектуальных
систем. Система нечеткого вывода. 180
I.
Постановка задачи. 180
II.
Процесс разработки системы 181
Индивидуальные
варианты заданий. 188
Основой
методов построения аналитических
моделей является построение и программная
реализация МАТЕМАТИЧЕСКОЙ
МОДЕЛИ.
Основные
этапы использования формальных
математических методов:
анализ
ситуации и постановка задачи исследования
построение
математической модели
формирование
задачи выбора наилучшей стратегии
решение
задачи и анализ полученного решения с
возможной корректировкой модели
Анализ
ситуации позволяет выделить основные
типы параметров, описывающих состояние
системы: УПРАВЛЯЕМЫЕ,
ЦЕЛЕВЫЕ И НЕУПРАВЛЯЕМЫЕ.
Управляемые
параметры являются искомыми и их значения
определяют стратегию.
Целевые
параметры необходимы для описания
поставленных целей. Значения целевых
параметров зависят от управляемых
параметров.
Значения
неуправляемых
параметров не могут изменяться
руководством, оставаясь постоянными,
известными полностью или частично.
Разделение
параметров на 3 основные группы носит
относительный характер и может изменяться
в зависимости от ситуации.
Построение
мат. модели включает введение условных
обозначений для параметров и, самое
главное, УСТАНОВЛЕНИЕ
ЗАВИСИМОСТЕЙ,
которые связывают эти параметры. Любая
модель является абстракцией, отражающей
лишь самые важные черты, особенности
описываемой системы.
Будем
считать, что зависимости между параметрами
задаются в виде следующего набора
функций:
Wi
= F( X1,X2,…,Xn,
a1,a2,…,ak),
i=(1,m), (1.
0)
где
W — обозначения целевых параметров,
X — обозначения управляемых параметров,
а — обозначения неуправляемых
параметров,
m — число целевых параметров,
n — число управляемых параметров,
k
— число неуправляемых параметров.
I.Статичные аналитические модели оптимизации. Построение в среде ms Excel.
Задача
оптимизации, или задача выбора наилучшей
стратегии, формируется на основе мат.
модели следующим образом:
-
из
целевых параметров выбирается ОДИН,
определяющий ЦЕЛЬ функционирования
системы и, следовательно, конкретизирующий
понятие наилучшей стратегии; значение
этого параметра в зависимости от
ситуации должно быть или как можно
больше, или как можно меньше; соответствующая
функция F называется ЦЕЛЕВОЙ или
КРИТЕРИЕМ ЭФФЕКТИВНОСТИ; эта функция
позволяет сравнивать стратегии между
собой и выбирать наилучшую из них в
соответствии с поставленной целью; -
на
значения остальных (m-1) целевых параметров
накладываются ОГРАНИЧЕНИЯ вида bi <
Wi < ci, где b и c — заданные величины; эти
ограничения определяют набор ДОПУСТИМЫХ
стратегий, т.е. такие значения управляемых
параметров, при которых выполняются
СРАЗУ ВСЕ заданные условия; наилучшая
стратегия должна выбираться ТОЛЬКО из
допустимых.
В
результате задача выбора наилучшей
стратегии математически формулируется
как ЗАДАЧА ОПТИМИЗАЦИИ:
НАЙТИ
ТАКИЕ ЗНАЧЕНИЯ УПРАВЛЯЕМЫХ ПАРАМЕТРОВ,
ПРИ КОТОРЫХ ВЫПОЛНЯЮТСЯ ВСЕ ОГРАНИЧЕНИЯ
НА ЗНАЧЕНИЯ ЦЕЛЕВЫХ ПАРАМЕТРОВ И
ДОСТИГАЕТСЯ НАИБОЛЬШЕЕ (НАИМЕНЬШЕЕ)
ЗНАЧЕНИЕ ЦЕЛЕВОЙ ФУНКЦИИ.
Условная
запись:
найти
x1,x2,…,xn
так, чтобы
W
= F( x, a ) => max (min) (1.
0)
при
выполнении ограничений
bi
< Wi=F(
x,
a
) < ci
, i=(2,m)
(1.
0)
Наиболее
простой и распространенной на практике
задачей подобного типа является задача
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. Ее особенность
состоит в том, что ВСЕ функции F являются
ЛИНЕЙНЫМИ, т.е.
F(
X, a ) = a1X1
+ a2X2
+ … + anXn
(1. 0)
Соседние файлы в папке МатМод экология
- #
- #
- #
- #
- #
- #
Модель данных позволяет интегрировать данные из нескольких таблиц, эффективно создавая реляционный источник данных в книге Excel. В Excel модели данных используются прозрачно, предоставляя табличные данные, используемые в сводных таблицах и сводных диаграммах. Модель данных визуализируются как коллекция таблиц в списке полей, и в большинстве раз вы даже не узнаете, что она существует.
Прежде чем приступить к работе с моделью данных, необходимо получить некоторые данные. Для этого мы будем использовать интерфейс Get & Transform (Power Query), поэтому вам может потребоваться выполнить шаг назад и посмотреть видео, или следуйте нашему руководству по обучению по get & Transform и Power Pivot.
Где есть Power Pivot?
-
Excel 2016 & Excel для Microsoft 365 — Power Pivot включен в ленту.
-
Excel 2013 — Power Pivot входит в Office профессиональный плюс Excel 2013, но не включен по умолчанию. Дополнительные сведения о запуске надстройки Power Pivot для Excel 2013.
-
Excel 2010 — скачайте надстройку Power Pivot, а затем установите надстройку Power Pivot.
Где находится get & Transform (Power Query)?
-
Excel 2016 & Excel для Microsoft 365 . Get & Transform (Power Query) интегрировано с Excel на вкладке «Данные«.
-
Excel 2013 — Power Query — это надстройка, которая входит в Excel, но ее необходимо активировать. Перейдите к разделу «Параметры >» > надстроек, а затем в раскрывающемся списке «Управление» в нижней части панели выберите com-надстройки > Go. Проверьте microsoft Power Query Excel, а затем ОК, чтобы активировать его. На Power Query будет добавлена вкладка Power Query.
-
Excel 2010 — скачивание и установка Power Query надстройки.. После активации на ленту Power Query вкладки.
Начало работы
Сначала необходимо получить некоторые данные.
-
В Excel 2016 и Excel для Microsoft 365 используйте data >Get & Transform Data > Get Data > Get Data to import data from any number of external data sources, such as a text file, Excel workbook, website, Microsoft Access, SQL Server, or another relational database that contains multiple related tables.
В Excel 2013 и 2010 перейдите к Power Query >получения внешних данных и выберите источник данных.
-
Excel предложит выбрать таблицу. Если вы хотите получить несколько таблиц из одного источника данных, установите флажок «Включить выбор нескольких таблиц «. При выборе нескольких таблиц Excel автоматически создает модель данных.
Примечание: В этих примерах мы используем книгу Excel с вымышленными сведениями о классах и оценках учащихся. Вы можете скачать пример книги модели данных учащихся и следовать инструкциям. Вы также можете скачать версию с готовой моделью данных..
-
Выберите одну или несколько таблиц и нажмите кнопку «Загрузить «.
Если необходимо изменить исходные данные, можно выбрать параметр «Изменить «. Дополнительные сведения см. в статье «Общие сведения Редактор запросов (Power Query)».
Теперь у вас есть модель данных, которая содержит все импортированные таблицы, и они будут отображаться в списке полей сводной таблицы.
Примечания:
-
Модели создаются неявно, когда вы импортируете в Excel несколько таблиц одновременно.
-
Модели создаются явно, если вы импортируете данные с помощью надстройки Power Pivot. В надстройке модель представлена в макете с вкладками, аналогичном Excel, где каждая вкладка содержит табличные данные. Дополнительные сведения об импорте данных с помощью надстройки Power Pivotсм. в статье «Получение данных с помощью SQL Server данных».
-
Модель может содержать одну таблицу. Чтобы создать модель на основе только одной таблицы, выберите таблицу и нажмите кнопку Добавить в модель данных в Power Pivot. Это может понадобиться в том случае, если вы хотите использовать функции Power Pivot, например отфильтрованные наборы данных, вычисляемые столбцы, вычисляемые поля, ключевые показатели эффективности и иерархии.
-
Связи между таблицами могут создаваться автоматически при импорте связанных таблиц, у которых есть связи по первичному и внешнему ключу. Excel обычно может использовать импортированные данные о связях в качестве основы для связей между таблицами в модели данных.
-
Советы по сокращению размера модели данных см. в статье «Создание модели данных, оптимизированной для памяти, с помощью Excel и Power Pivot».
-
Дополнительные сведения см. в руководстве по импорту данных в Excel и созданию модели данных.
Создание связей между таблицами
Следующим шагом является создание связей между таблицами, чтобы вы могли извлекать данные из любой из них. Каждая таблица должна иметь первичный ключ или уникальный идентификатор поля, например идентификатор учащегося или номер класса. Самый простой способ — перетащить эти поля, чтобы подключить их в представлении схемы Power Pivot.
-
Перейдите в power Pivot > Manage.
-
На вкладке « Главная» выберите » Представление схемы».
-
Будут отображены все импортированные таблицы, и может потребоваться некоторое время, чтобы изменить их размер в зависимости от количества полей в каждой из них.
-
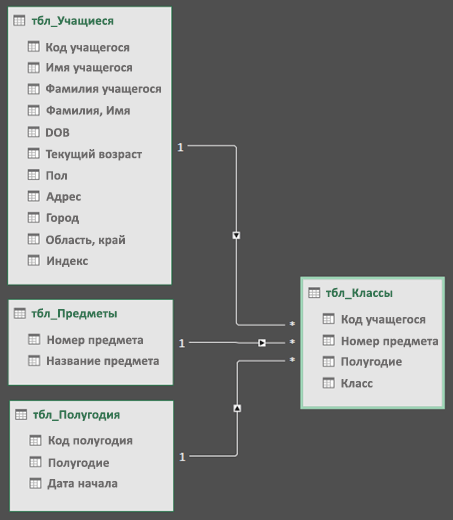
Затем перетащите поле первичного ключа из одной таблицы в следующую. В следующем примере показано представление схемы таблиц учащихся.
Мы создали следующие ссылки:
-
tbl_Students | Идентификатор учащегося > tbl_Grades | Идентификатор учащегося
Другими словами, перетащите поле «Идентификатор учащегося» из таблицы «Учащиеся» в поле «Идентификатор учащегося» в таблице «Оценки».
-
tbl_Semesters | Идентификаторы > tbl_Grades | Семестр
-
tbl_Classes | Номер класса > tbl_Grades | Номер класса
Примечания:
-
Имена полей не обязательно должны совпадать для создания связи, но они должны быть одинаковыми типами данных.
-
Соединители в представлении схемы имеют «1» с одной стороны, а «*» — с другой. Это означает, что между таблицами существует связь «один ко многим», которая определяет, как данные используются в сводных таблицах. См. дополнительные сведения о связях между таблицами в модели данных.
-
Соединители указывают только на наличие связи между таблицами. На самом деле они не показывают, какие поля связаны друг с другом. Чтобы просмотреть ссылки, перейдите в раздел Power Pivot > Manage > Design > Relationships > Управление связями. В Excel можно перейти к разделу «>данных».
-
Создание сводной таблицы или сводной диаграммы с помощью модели данных
Книга Excel может содержать только одну модель данных, но эта модель может содержать несколько таблиц, которые можно многократно использовать в книге. Вы можете добавить дополнительные таблицы в существующую модель данных в любое время.
-
В Power Pivotперейдите к разделу » Управление».
-
На вкладке « Главная» выберите сводную таблицу.
-
Выберите место размещения сводной таблицы: новый лист или текущее расположение.
-
Нажмите кнопку «ОК», и Excel добавит пустую сводную таблицу с областью списка полей справа.
Затем создайте сводную таблицу или сводную диаграмму. Если вы уже создали связи между таблицами, можно использовать любое из их полей в сводной таблице. Мы уже создали связи в образце книги модели данных учащихся.
Добавление имеющихся несвязанных данных в модель данных
Предположим, вы импортировали или скопировали много данных, которые вы хотите использовать в модели, но не добавили их в модель данных. Принудительно отправить новые данные в модель очень просто.
-
Начните с выбора любой ячейки в данных, которые необходимо добавить в модель. Это может быть любой диапазон данных, но лучше всего использовать данные, отформатированные в виде таблицы Excel .
-
Добавьте данные одним из следующих способов.
-
Щелкните Power Pivot > Добавить в модель данных.
-
Выберите Вставка > Сводная таблица и установите флажок Добавить эти данные в модель данных в диалоговом окне «Создание сводной таблицы».
Диапазон или таблица будут добавлены в модель как связанная таблица. Дополнительные сведения о работе со связанными таблицами в модели см. в статье Добавление данных с помощью связанных таблиц Excel в Power Pivot.
Добавление данных в таблицу Power Pivot данных
В Power Pivot невозможно добавить строку в таблицу, введя текст непосредственно в новой строке, как это можно сделать на листе Excel. Но можно добавить строки , скопируйте и вставьте или обновите исходные данные и обновите модель Power Pivot.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Ознакомьтесь & по преобразованию и обучению Power Pivot
Общие сведения о редакторе запросов (Power Query)
Создание модели данных, оптимизированной для памяти, с помощью Excel и Power Pivot
Руководство. Импорт данных в Excel и создание модели данных
Определение источников данных, используемых в модели данных книги
Связи между таблицами в модели данных
Чтобы оперативно мониторить и своевременно влиять на динамику реализации продукции, коммерческой службе требуются аналитические отчеты, в которых раскрываются различные аспекты процесса реализации.
Большинство современных учетных программ имеет встроенные наборы аналитических отчетов о продажах, но все они формируют показатели только по заданным параметрам отбора. Для ввода новых показателей нужно привлекать программистов.
Если пользователям такой отчетности требуется часто менять структуру отчетов о продажах или создавать новые отчеты, то для самостоятельного решения подобных задач вполне подойдет всем знакомый табличный редактор Excel.
ИНСТРУМЕНТАРИЙ EXCEL ДЛЯ СОЗДАНИЯ АНАЛИТИЧЕСКИХ ОТЧЕТОВ
В табличном редакторе Excel предусмотрен широкий выбор инструментов, с помощью которых можно создать аналитические отчеты на основе данных о реализации продукции. Для успешной работы с этими инструментами от пользователя требуется определенный уровень подготовки. Представим перечень инструментария для создания аналитических отчетов:
- продвинутый уровень — макросы, Power BI;
- хороший уровень — OLAP-кубы, Power Query/Pivot;
- средний уровень — сводные таблицы, формулы.
Рассмотрим особенности применения каждого из указанных инструментов, а также знания и навыки пользователя, которые нужны для их качественного применения.
Макросы
Работа с макросами основана на применении языка программирования VBA, который можно использовать для расширения возможностей MS Excel и других приложений MS Office. С помощью прописанных в макросе команд можно:
- проводить различные обработки и сортировки данных в файле Excel;
- получать информацию из других файлов;
- создавать сводные таблицы;
- добавлять в создаваемые отчеты дополнительные функции, которые невозможно получить обычными средствами Excel.
Чтобы создавать макросы, пользователь должен отлично знать редактор Excel, владеть языком программирования VBA. Приведу в качестве примера запись макроса, с помощью которого в файле Excel автоматически из массива данных формируется сводная таблица:
Очевидно, что работать с макросами может незначительная часть сотрудников, которые создают отчетность в Excel.
Power BI
Power BI по своей сути является отдельным программным продуктом, в который можно загрузить файлы Excel и произвести дальнейшую обработку с целью анализа и визуализации данных.
Power BI включает в себя весь функционал надстроек Excel (Power Query и Power Pivot плюс улучшенные механизмы визуализации из Power View и Power Map). Преимущества данного инструмента: с отчетами может работать сразу несколько пользователей плюс широкий диапазон визуализации показателей отчетов.
Идет тренд к интеграции Excel c Power BI. Например, в Excel 2019 появилась возможность напрямую загружать данные в функционал Power BI. Для этого в меню выбираем:
Файл > Опубликовать > Опубликовать в Power BI.
Передав файл, нажимаем кнопку «Перейти к Power BI», чтобы просмотреть загруженные данные.
Главные сложности использования Power BI: загруженные таблицы Excel нужно дополнительно обрабатывать для корректного включения их данных в отчеты, а формулы для создания отчетов в этой программе отличаются от формул Excel.
Power BI постоянно развивается, однако на сегодняшний момент использовать его для формирования аналитических отчетов достаточно трудоемко.
OLAP-кубы
OLAP (online analytical processing) — аналитическая технология обработки данных в реальном времени, при которой данные из учетной базы выгружаются в файлы Excel, а затем обрабатываются с помощью другого инструмента Excel (сводных таблиц).
Для начала работы нужно создать подключение файла Excel к данным OLAP-куба (Данные → Получение внешних данных), а затем из открывшегося окна перетащить курсором в табличную часть Excel показатели, которые требуются.
В результате будет получена сводная таблица с отчетными данными. Главное ее преимущество — возможность автоматической актуализации данных при каждом подключении к OLAP-кубу.
Power Query/Pivot
Данные инструменты являются надстройками Excel, поэтому работа с ними происходит непосредственно из меню табличного редактора.
Power Query появился в версии Excel 2013 как отдельная надстройка, требующая подключения, а с версии 2016 г. весь функционал Power Query уже встроен по умолчанию и находится на вкладке «Данные → Получить и преобразовать».
Power Query обладает значительными возможностями для целей создания отчетов. С помощью этой надстройки можно:
- загружать данные в Excel из почти 40 различных источников, среди которых базы данных (SQL, Oracle, Access, Teradata), корпоративные ERP-системы (SAP, Microsoft Dynamics, 1C), интернет-сервисы;
- собирать данные из файлов всех основных типов данных (XLSX, TXT, HTML, XM) — поодиночке и сразу из всех файлов указанной папки;
- зачищать полученные данные от лишних пробелов, столбцов или строк, повторов, служебной информации в заголовках, непечатаемых символов и т. д;
- трансформировать таблицы Excel, приводя их в желаемый вид (фильтровать, сортировать, менять порядок столбцов, транспонировать, добавлять итоги, разворачивать кросс-таблицы в плоские и сворачивать обратно);
- подставлять данные из одной таблицы в другую по совпадению одного или нескольких параметров (полностью заменяет формулу ВПР и ее аналоги).
Главная особенность Power Query: все действия по импорту и трансформации данных запоминаются в виде запроса — последовательности шагов на внутреннем языке программирования Power Query, который лаконично называется «М».
Шаги можно отредактировать, воспроизвести любое количество раз (обновить запрос). Поэтому данный инструмент может служить хорошей альтернативой создания макросов или прописания очень сложных формул при построении отчетов.
Power Pivot — надстройка Excel, предназначенная для разнопланового анализа больших объемов данных. Поэтому результат работы с Power Pivot похож на усложненные сводные таблицы.
Общие принципы работы в Power Pivot:
- внешние данные загружают в Power Pivot, который поддерживает 15 различных источников: распространенные базы данных (SQL, Oracle, Access), файлы Excel, текстовые файлы, веб-каналы данных. Если Power Query использовать как источник данных, то возможности загрузки увеличиваются многократно;
- между загруженными таблицами настраиваются связи, то есть создается Модель Данных. Это позволит строить отчеты по любым полям из имеющихся таблиц так, будто это одна таблица;
- при необходимости в Модель Данных добавляют дополнительные вычисления с помощью вычисляемых столбцов (аналог столбца с формулами в «умной» таблице) и мер (аналог вычисляемого поля в сводной таблице). Нужные вычисления записываются на специальном внутреннем языке Power Pivot, который называется DAX (Data Analysis Expressions);
- на листе Excel по Модели Данных строят интересующие отчеты в виде сводных таблиц и диаграмм.
Сводные таблицы
Первый интерфейс сводных таблиц (сводных отчетов) был включен в состав Excel в 1993 г. (в версии Excel 5.0). Этот инструмент изначально создавался для построения отчетов на основе многомерных данных. Он имеет достаточно широкие функциональные возможности.
Реализованный в Excel инструмент сводных таблиц позволяет расположить измерения многомерных данных в области рабочего листа. Упрощенно можно представлять себе сводную таблицу как отчет, лежащий сверху диапазона ячеек (хотя есть определенная привязка форматов ячеек к полям сводной таблицы).
Сводная таблица Excel имеет четыре области отображения информации: фильтр, столбцы, строки и данные. Измерения данных именуются полями сводной таблицы. Эти поля имеют собственные свойства и формат отображения.
С помощью сводных таблиц можно группировать, сортировать, фильтровать и менять расположение данных с целью получения различных аналитических выборок.
Обновление отчета производится простыми средствами пользовательского интерфейса. Данные автоматически агрегируются по заданным правилам. Не требуется дополнительный или повторный ввод какой-либо информации.
Сводные таблицы Excel являются самым востребованным инструментом при работе с многомерными данными в больших объемах информации. Этот инструмент поддерживает в качестве источника данных как внешние источники данных, так и внутренние диапазоны электронных таблиц.
Для работы со сводными таблицами не нужны знания в области программирования VBA или внутренних языков программирования надстроек Excel.
Формулы Excel
Механизм формул появился в первой версии табличного редактора. С тех пор он значительно расширился. На сегодняшний день функционал формул содержит больше сотни наименований. С учетом того что при создании отчетов формулы могут комбинироваться, количество вариантов трудно подсчитать.
Формулы отлично подходят для создания двухмерных отчетов при обработке небольшого объема данных. Преимущество формул в том, что их легко копировать или транспонировать на другие ячейки отчетов, переделать или защитить от изменений.
В редакторе Excel есть встроенный справочник по формулам, что облегчает работу пользователям со средним уровнем владения Excel. Поэтому я предлагаю рассмотреть возможности использования функционала формул при разработке аналитических отчетов из одного источника данных.
ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ФОРМУЛ ДЛЯ РАЗРАБОТКИ АНАЛИТИКИ ПРОДАЖ В EXCEL
Вне зависимости от выбора инструментария Excel при разработке аналитических отчетов о реализации продукции в первую очередь создают новую книгу и загружают в нее исходные данные из учетной программы компании для последующей их обработки.
Удобнее всего сделать это путем формирования в учетной программе реестра продаж с нужными показателями и сохранения его в виде файла формата Excel. Далее отчетность будем создавать на отдельных листах этого файла.
Возьмем самые востребованные данные о продажах, на основе которых создаются аналитические отчеты:
- наименование покупателя;
- наименование продукции;
- дата отгрузки продукции покупателю;
- регион реализации продукции;
- сумма реализации продукции;
- валовая прибыль от реализации продукции;
- маржа (процентное соотношение валовой прибыли к сумме реализации).
Материал публикуется частично. Полностью его можно прочитать в журнале «Планово-экономический отдел» № 10, 2020.
Содержание
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
- Вопросы и ответы
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
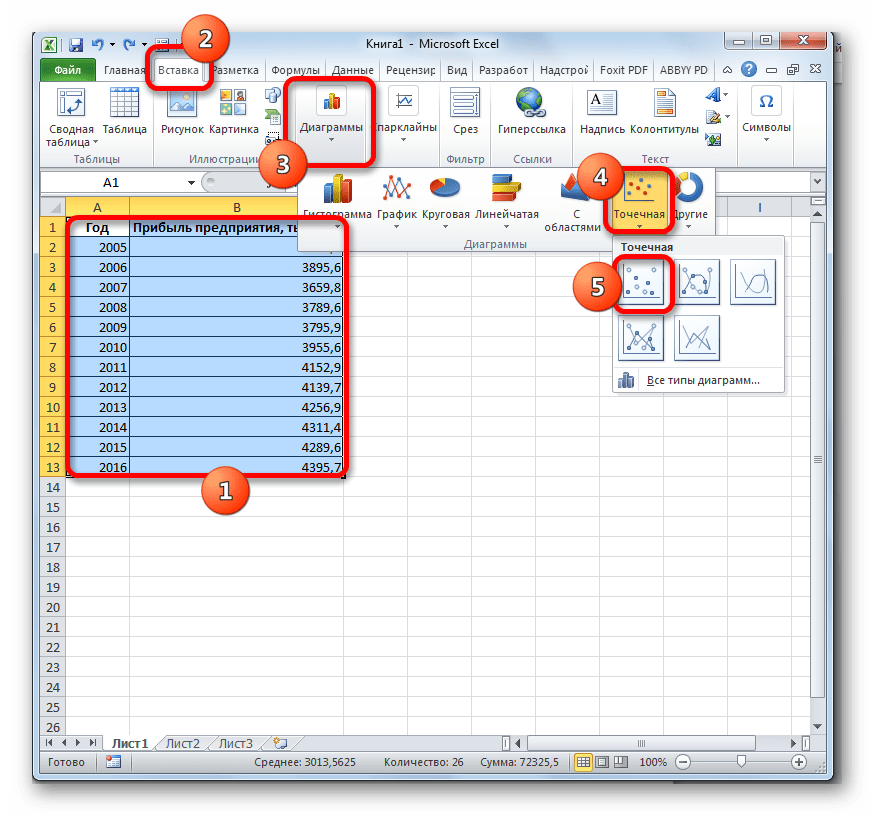
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
- Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
- Открывается окно форматирования линии тренда. В нем можно выбрать один из шести видов аппроксимации:
- Линейная;
- Логарифмическая;
- Экспоненциальная;
- Степенная;
- Полиномиальная;
- Линейная фильтрация.
Давайте для начала выберем линейную аппроксимацию.
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
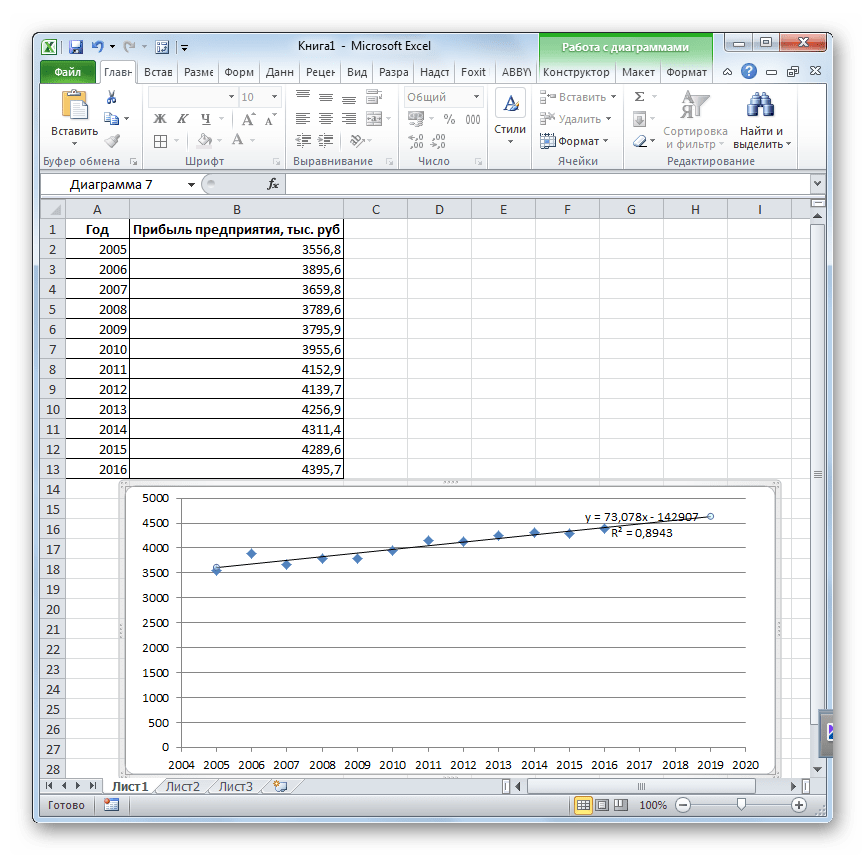
- Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
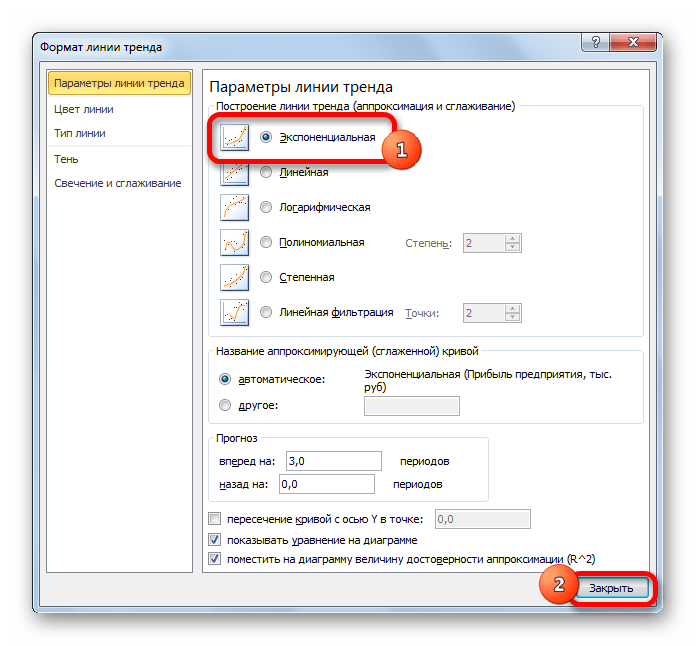
- Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Урок: Как построить линию тренда в Excel
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
=ПРЕДСКАЗ(X;известные_значения_y;известные значения_x)
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
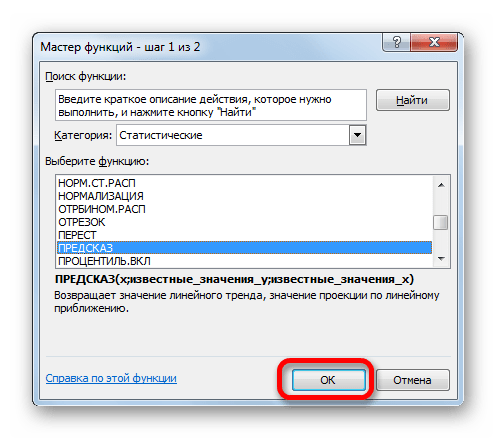
- Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
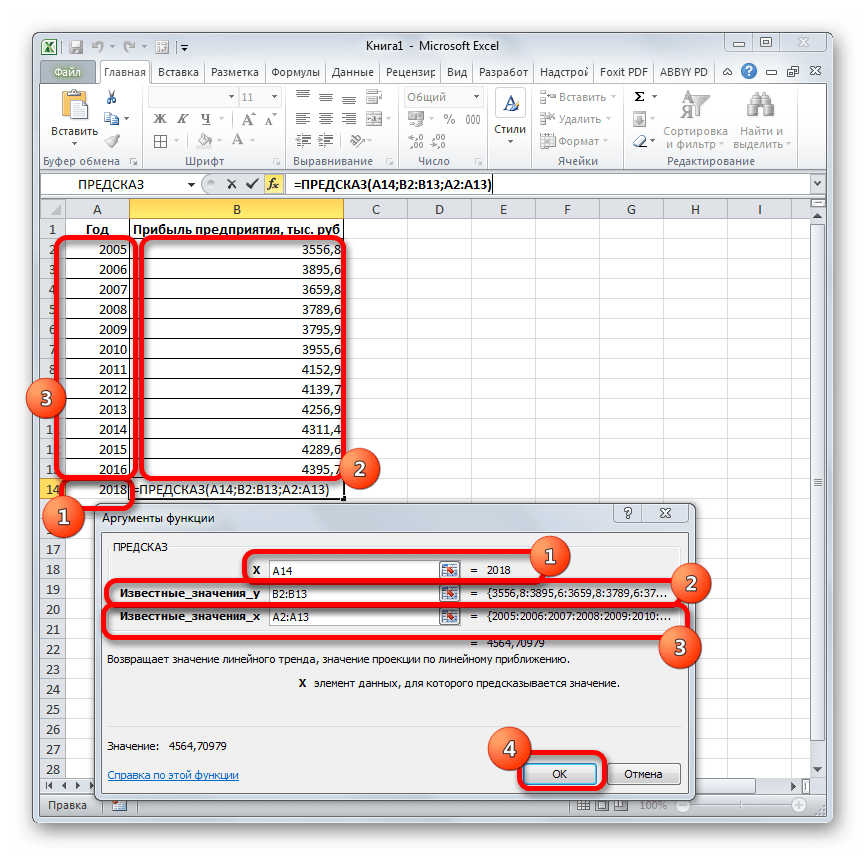
- Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
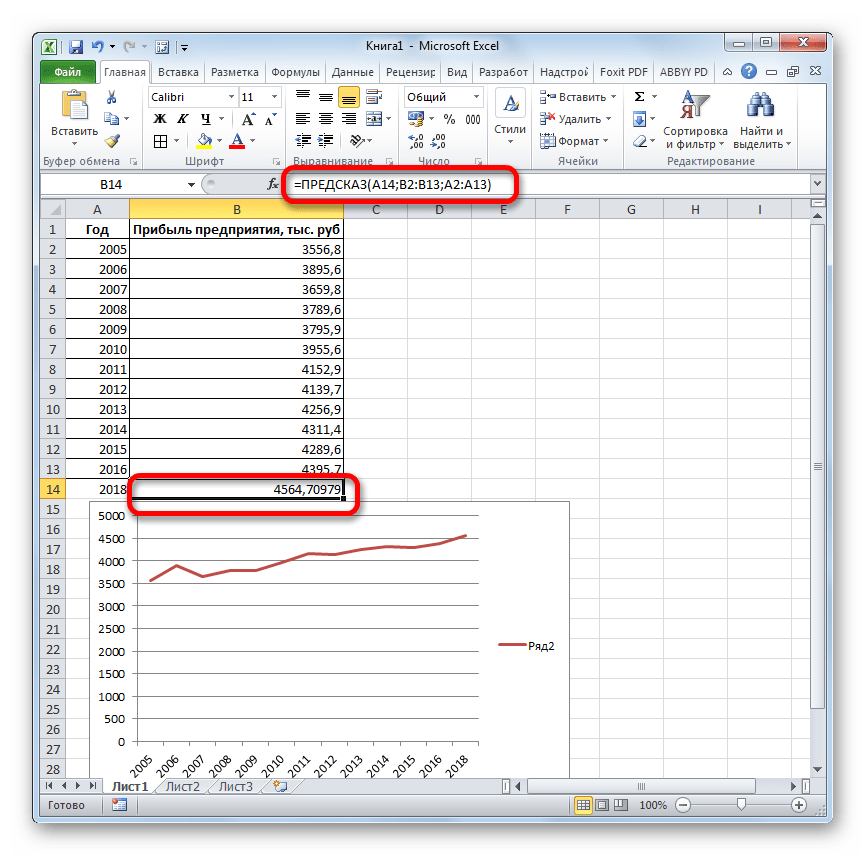
- Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
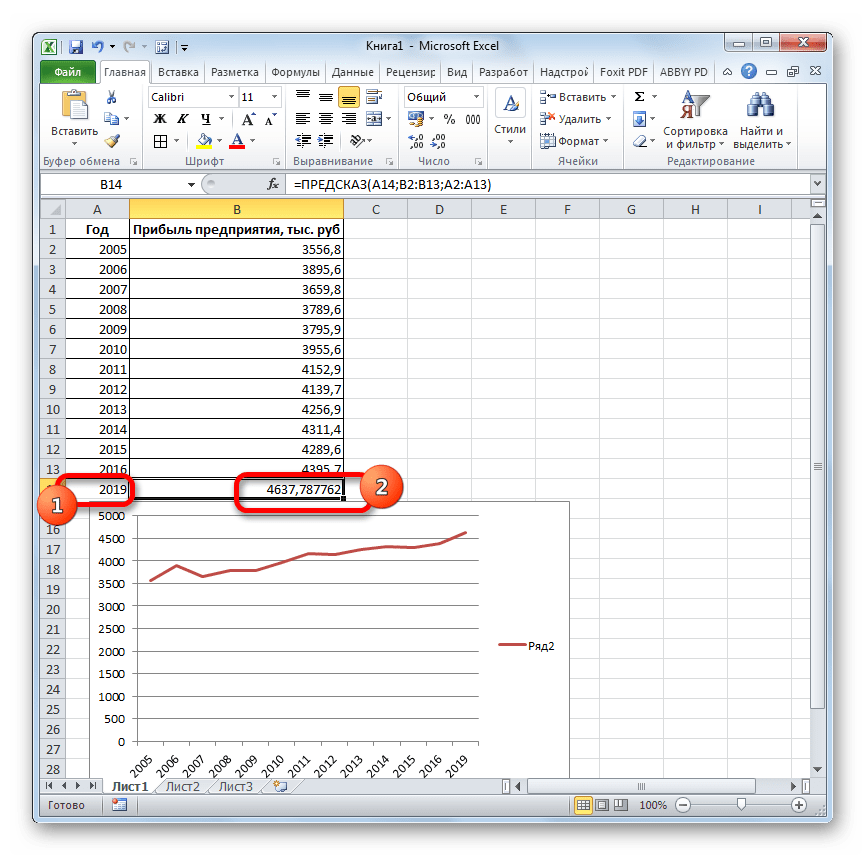
- Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
Урок: Экстраполяция в Excel
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
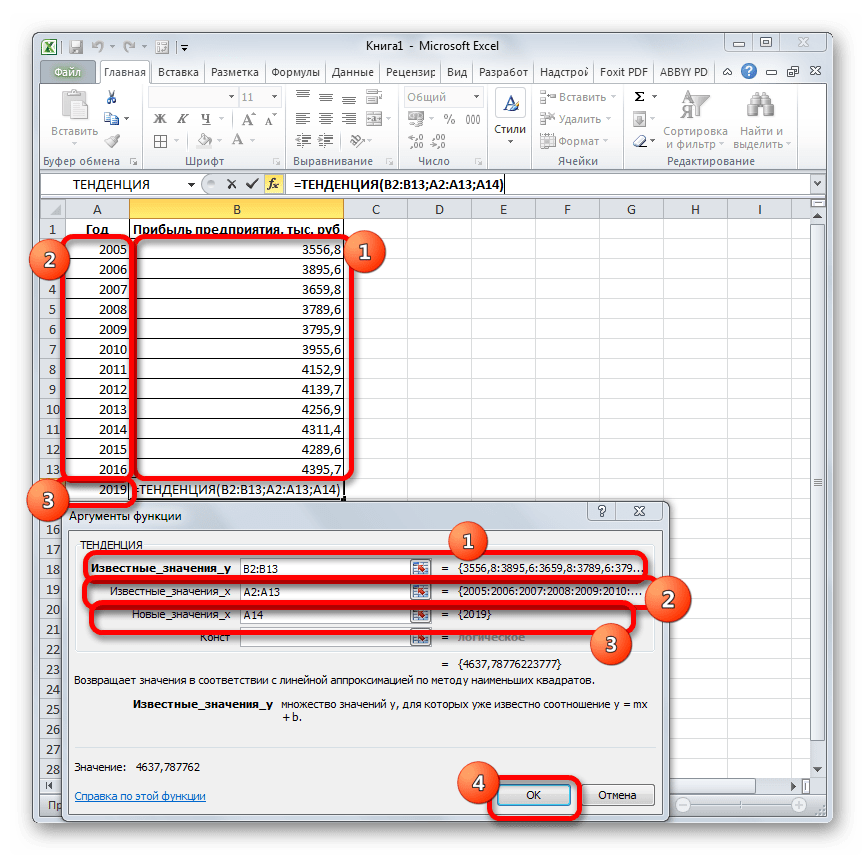
- Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
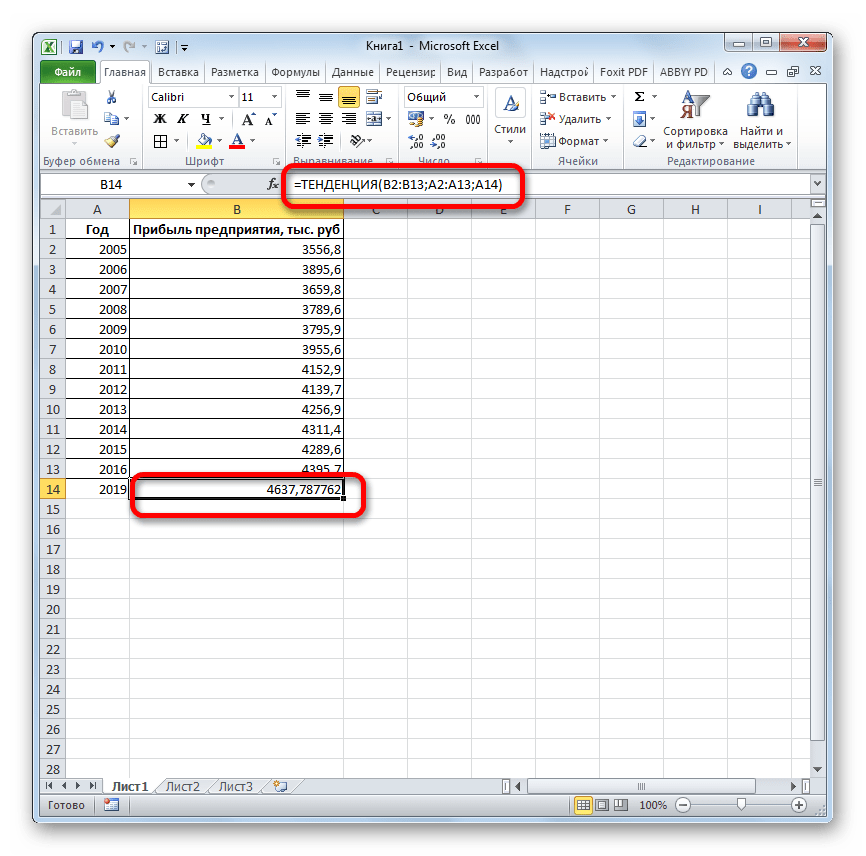
- Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
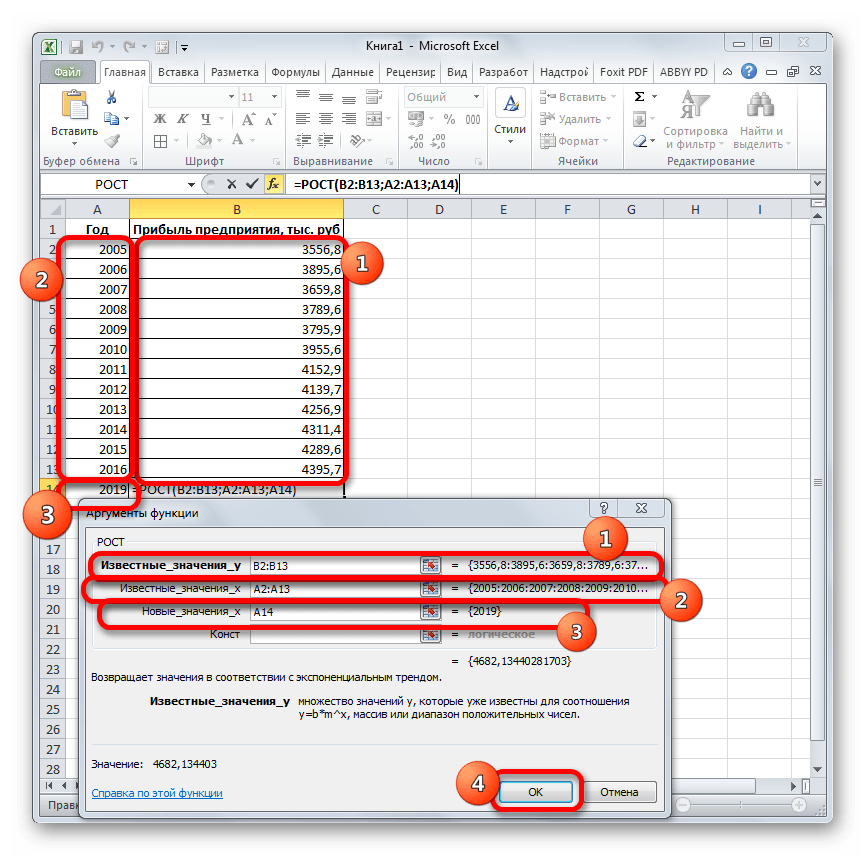
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
- Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
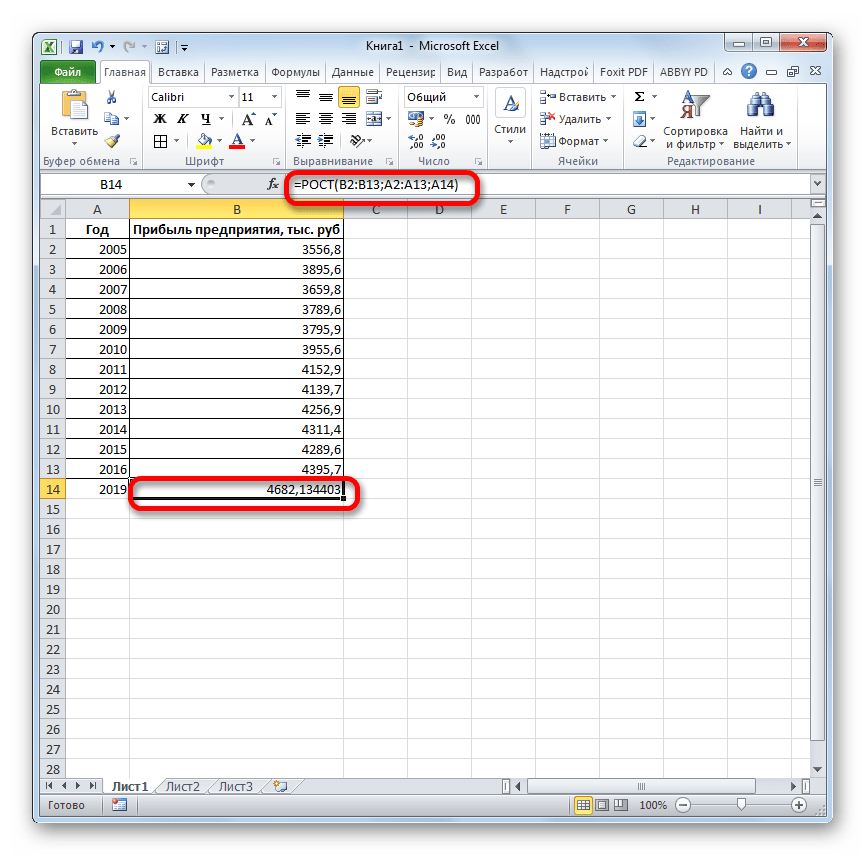
- Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
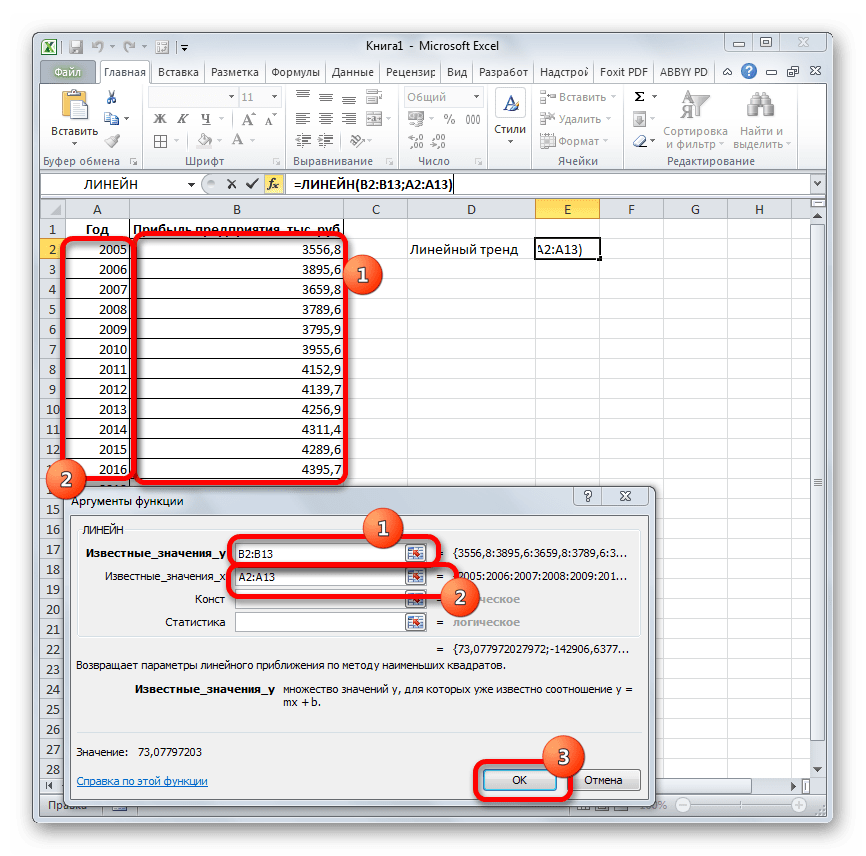
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
- В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
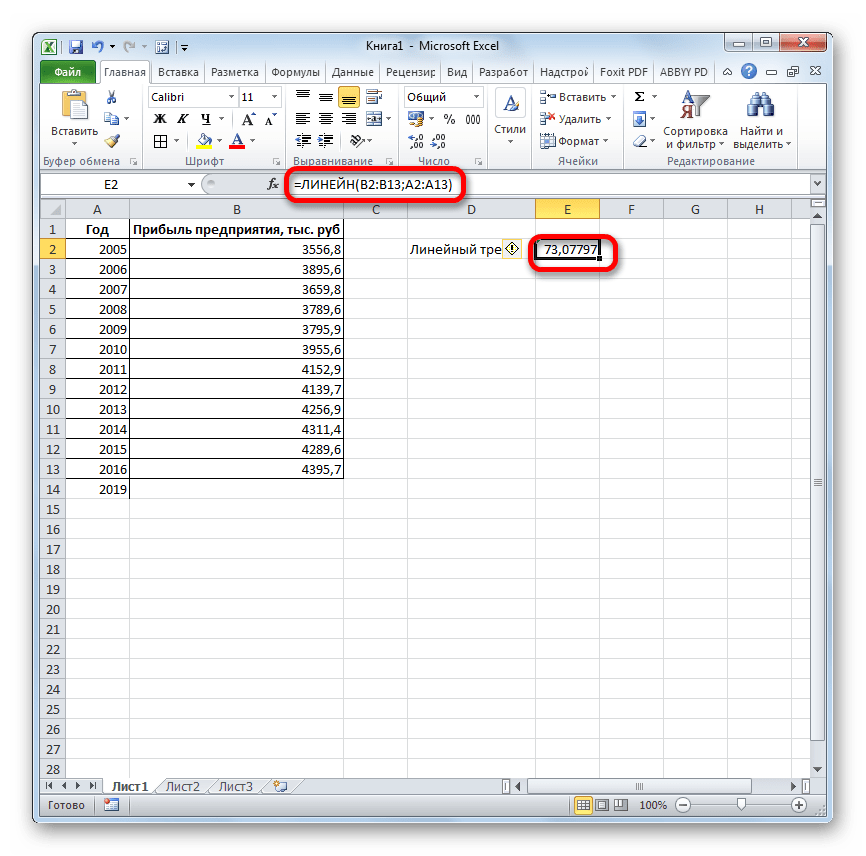
- Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
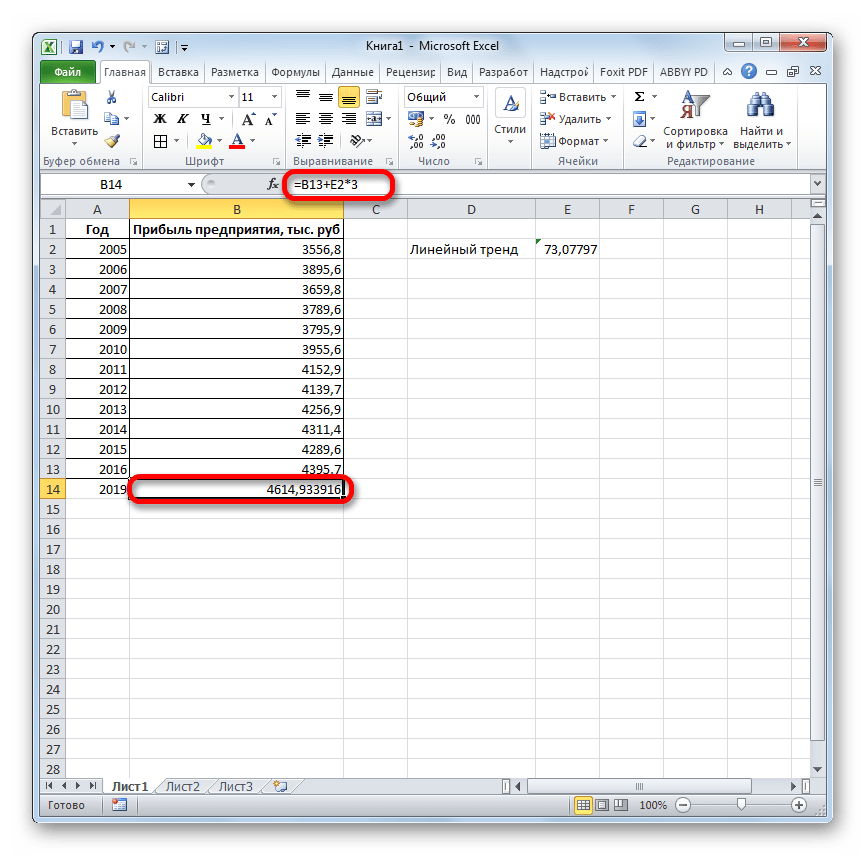
- Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
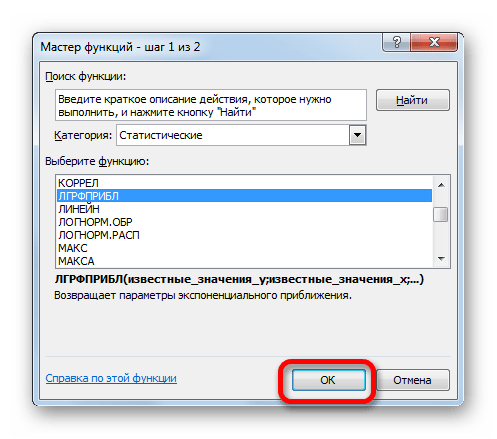
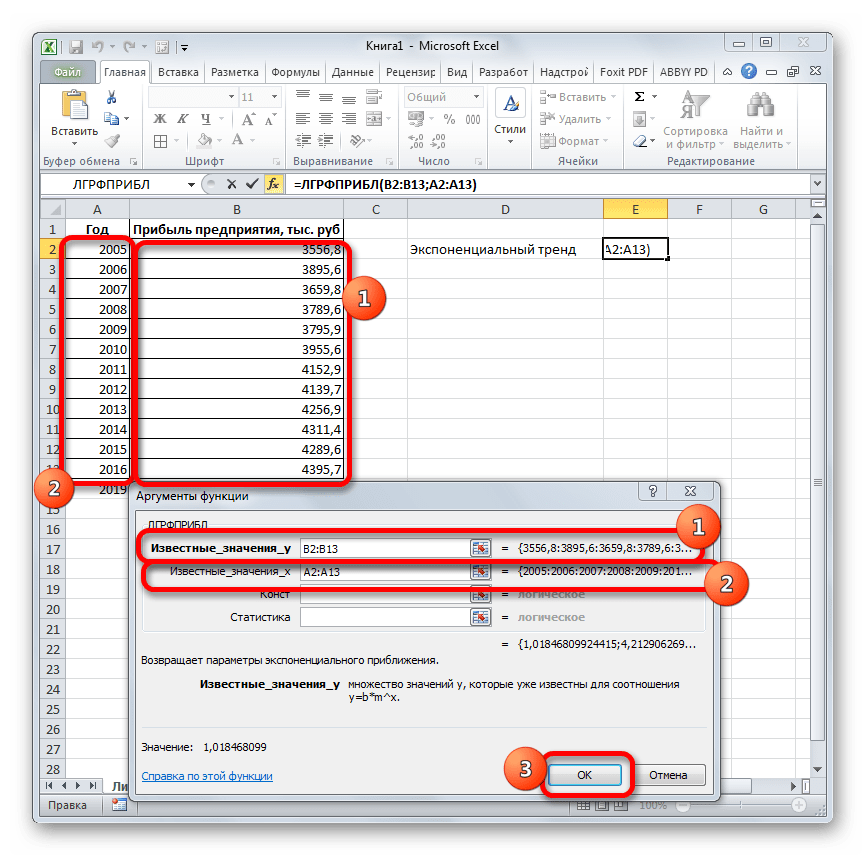
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
- Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
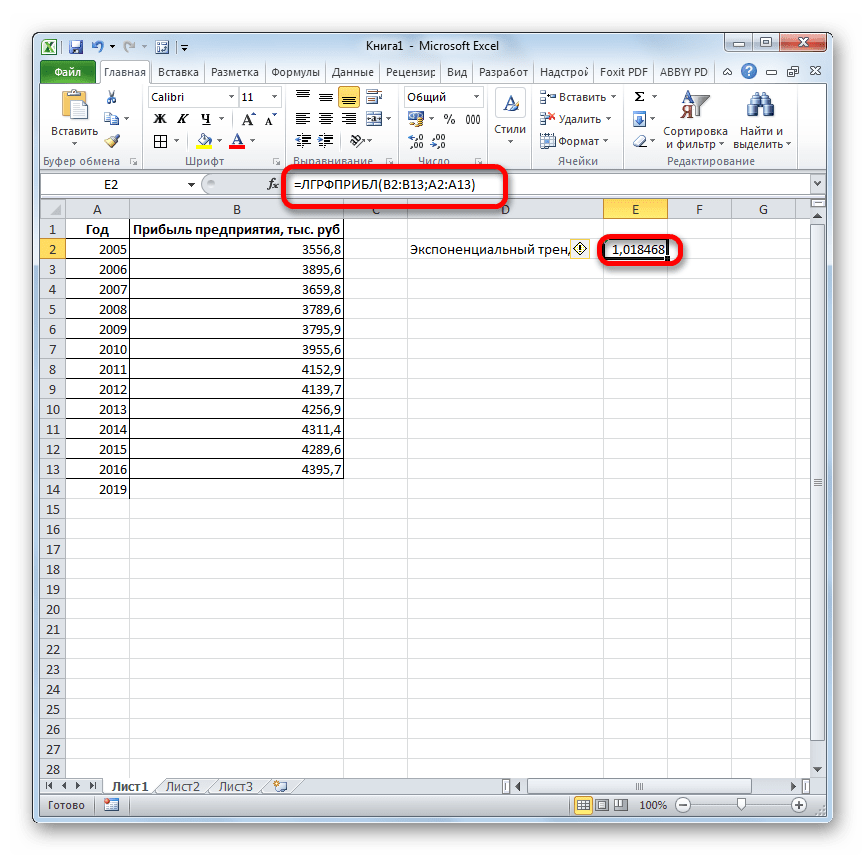
- Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
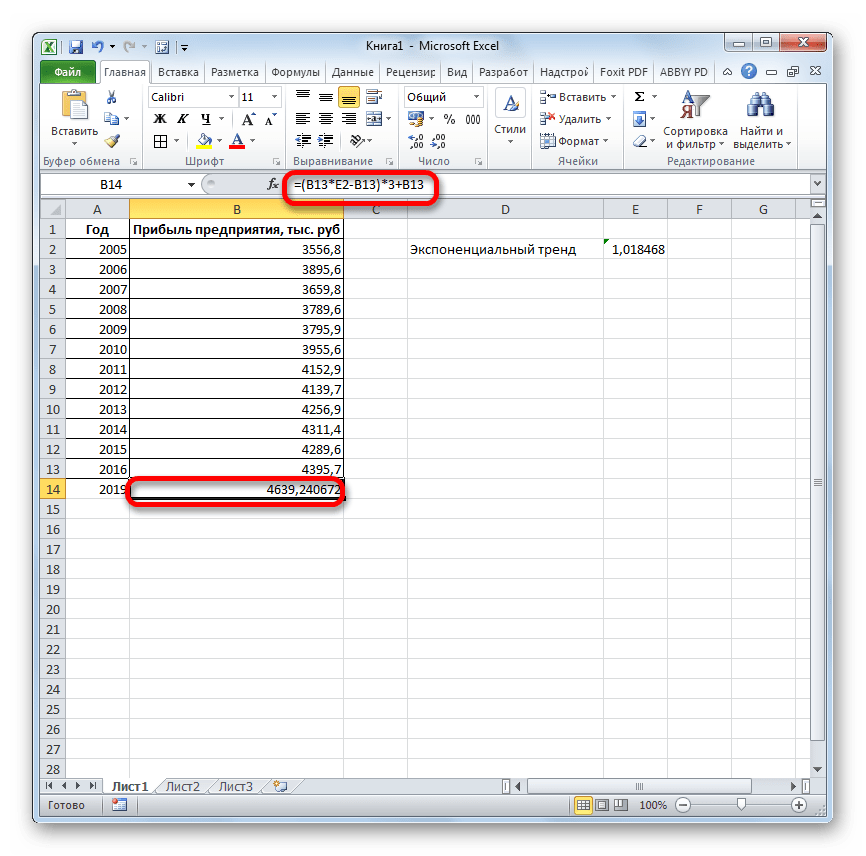
- Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Урок: Другие статистические функции в Excel
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.