05.04.11 — 12:26
Ищу аналог «поиска решений» EXEL на 1С 7.7. Есть исходники на си, но переписывать долго.
1 — 05.04.11 — 12:27
йоксель?
2 — 05.04.11 — 12:27
хотя, нет. Что за «поиск решений» я хз
3 — 05.04.11 — 12:30
4 — 05.04.11 — 12:31
сольвер использует метод градиентов.
время-деньги.
коли долго (нет времени) — закажите аутсорсерам.
но в виде вк — быстрее напорядки.
5 — 05.04.11 — 12:32
(3)Еще их кличут «Анализ данных…» (Сервис -> «Анализ данных…»)…
(0)Так то это все рассчитываемо и без этих мастеров.
6 — 05.04.11 — 12:32
Excel тогда уж…
7 — 05.04.11 — 12:35
ни у кого не возник китайский вопрос?
8 — 05.04.11 — 12:43
(4) сколько примерно времени нужно чтобы в 1-го это сделать ?
9 — 05.04.11 — 12:44
(4) задача неясно поставлена, нужно именно прикладное решение, потому самому пыхтеть придется
10 — 05.04.11 — 12:45
(3) Чтобы получить более подробные сведения об используемых алгоритмах оптимального поиска, обратитесь по адресу:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Адрес в Интернете: http://www.frontsys.com
Электронная почта: info@frontsys.com
очень помогло
11 — 05.04.11 — 12:52
(0) вот нафига делать численные методы в проге, для этого не приспособленной? мне страшно представить, сколько будет искать решение 1С для нескольких переменных при более менее сложной функции.
пишите на 1с и выносите в ВК.
ЗЫ Поиск решений в Екселе — УГ
12 — 05.04.11 — 12:58
(11) Расшифруй. Что значит «пишите на 1с и выносите в ВК». Давно у нас в 1С компилятор встроен?
13 — 05.04.11 — 12:59
(12) пардон. конечно, имел в виду в (11) «пишите на с++ и выносите в ВК»
14 — 05.04.11 — 13:06
15 — 05.04.11 — 13:06
написано специально для 1С
16 — 05.04.11 — 13:07
(15) а какая задача исходно стоит? что надо оптимизировать?
17 — 05.04.11 — 13:13
(16) расчет состава рецепта комбикорма,
из условий,
1. что полученное качество будет не хуже госта
2. процент вхождения каждого компонента состава в пределах от и до
3. Компоненты есть на складе, если компонента нет то есть список взаимозаменяемости компонентов
18 — 05.04.11 — 13:14
а по OLE в Excel запускать не вариант?
19 — 05.04.11 — 13:14
(17) качество — это содержание белка?
взаимозаменяемость по условию, а не произвольная, сильно усложняет задачу
20 — 05.04.11 — 13:15
(18) плохой вариант
21 — 05.04.11 — 13:20
(19) каждый компонент (отруби и т.д.) имеет свой показетель питательной ценности, это обменная энергия, сырой протеин, клетчатка, Лизин, и т.д.
вот в сумме эти компоненты должны давать корм с пит ценностью, для протеина от 15 до 17% , для клетчатки до 9% и т.д.
с взаимозаменяемостью, задача вообще непонятно как стоит, ведь несколько компонентов можно заменить на один и тот же, пока буду опираться на практику, то есть на примеры решений технолога,а потом выведу метод . возможно комбинатоника пригодится
22 — 05.04.11 — 13:22
кроме того в формулу оптимизации цена стремится к минимуму, нужно предусмотреть чтобы можно было приготовить корм из остатков, чтобы свести конечный остаток к минимуму. так что задача классная !
23 — 05.04.11 — 13:22
(21) а критерий оптимизации какой тогда? Стоиомсть?
24 — 05.04.11 — 13:24
в 1се есть какой-то анализ данных
25 — 05.04.11 — 13:28
(23) взависимости от выбора решения
если не нужно остатки подбивать, то стоимость -> МИн,
если нужно остатки подбить, то остатки на складе — >Мин
26 — 07.04.11 — 06:57
В общем компонента тупит(не находит решение), там где эксель справляется 
27 — 07.04.11 — 07:11
(26) исходные данные выложи
28 — 07.04.11 — 08:12
29 — 07.04.11 — 10:34
вот слил исходники с откомпиленным exe, тоже реализация метода, по примеру находит решение без проблем
http://hddfiles.ru/download/4915/
30 — 07.04.11 — 10:55
Вообщем, я так понял компонента использует метод Гомори,
ошибка в разных программах одна и таже «невозможно найти начальный базис», другими методами задача решается
31 — 07.04.11 — 13:06
(0) Да тупого перебора хватит должно хватить. Даже если на 1С реализовать.
32 — 07.04.11 — 13:09
А я прям из 1с заюзал екселевский механизм поиска решений.
33 — 07.04.11 — 13:17
(8) Пара часов, если соответствующей математикой владеешь.
34 — 07.04.11 — 13:18
(31) бугага
35 — 07.04.11 — 13:38
(34) Чо ты ржешь?
36 — 07.04.11 — 13:44
(35) какой перебор при нецелочисленной оптимизации нафих?
какая скорость перебора при нескольких переменных?
чо за фантазии?
37 — 07.04.11 — 13:56
(36) Да ладна. Ничо там страшного нету.
38 — 07.04.11 — 13:57
Если бы 1С сделал свой эксель он бы быстро набрал бы популярность. Я бы точно купил.
39 — 07.04.11 — 14:12
(37) теоретик?
40 — 07.04.11 — 14:14
(39) Хуже
41 — 08.04.11 — 05:59
(39)(40)
если даже взять целочисленно дял каждоко компонента от 0..100, и этих компонентов будет 5,
то получим 100*100*100*100*100 = 10 000 000 000 комбинаций,
если ещё проверять ограничения их штук 8, взависимости от типа смеси.
представим что 1С за 1 секунду переберет 1000 варинатов (что врядли), получи 10 000 000 секунд, получим 115 дней 
42 — 08.04.11 — 06:39
(28) что за дурацкая мода выкладывать в xlsx?
ЗЫ все же МС — дебилы
43 — 08.04.11 — 08:23
(41) Ну там можно не всё перебирать, а только то, что нужно. Автор объяснил бы поконкретнее, что именно нужно.
44 — 08.04.11 — 08:24
(43) «можно не всё перебирать, а только то, что нужно»
гы) конгениально!) только это уже будет не «тупой перебор», как ты предлагал
45 — 08.04.11 — 08:26
(44) Это будет тупой перебор того, что нужно. И не обещал я ничего. Я предположение высказал.
46 — 14.04.11 — 13:24
ну вот прошло 9 дней с момента поиска до реализации,
как ни странно компонента для 1С с http://www.openproj.ru/75/
не всё решала, ходя делфовый исходник в (написал прогу на дельфи) тестовые примеры выполняла. получилось, что
исходник на дельфи работает, а из компоненты не хочет.
Поскольку исходника компоненты небыло, пришлось самому писать, шаблон компоненты взял отсюда с мисты спасибо огромное всё довольно просто оказалось в создании компонент.
Далее из компоненты сделал лог, который показывал результаты, оказалось, что результаты сверхмалых величин разные (вот тут описал проблему В компоненте для 1С 7.7.на Delphi 6 получаются другие значение, чем на самом Del, перевел коэффициент погрешности в с -13 степени на -10 и всё пошло !!! Из-за того, что автор компоненты не учёл этого, пришлось изучить методику создания компоненты, + вспомнить математику, спасибо автору !
DmSk
47 — 14.04.11 — 13:32
чуть позже выложу исходники , для совместимости с предыдущей компонентой все названия методов оставл прежние
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
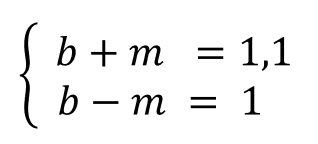
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
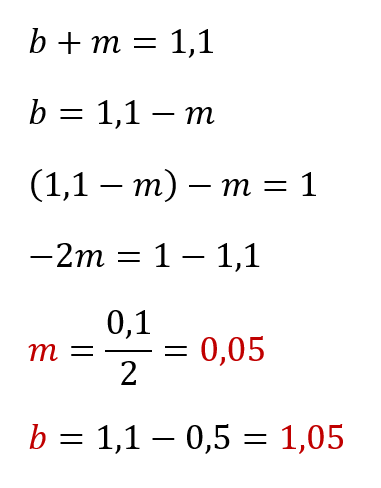
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
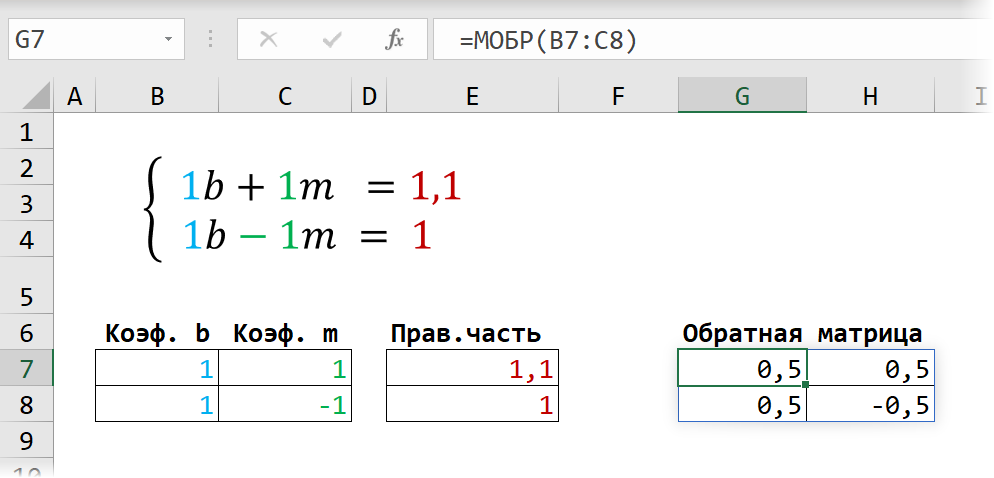
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
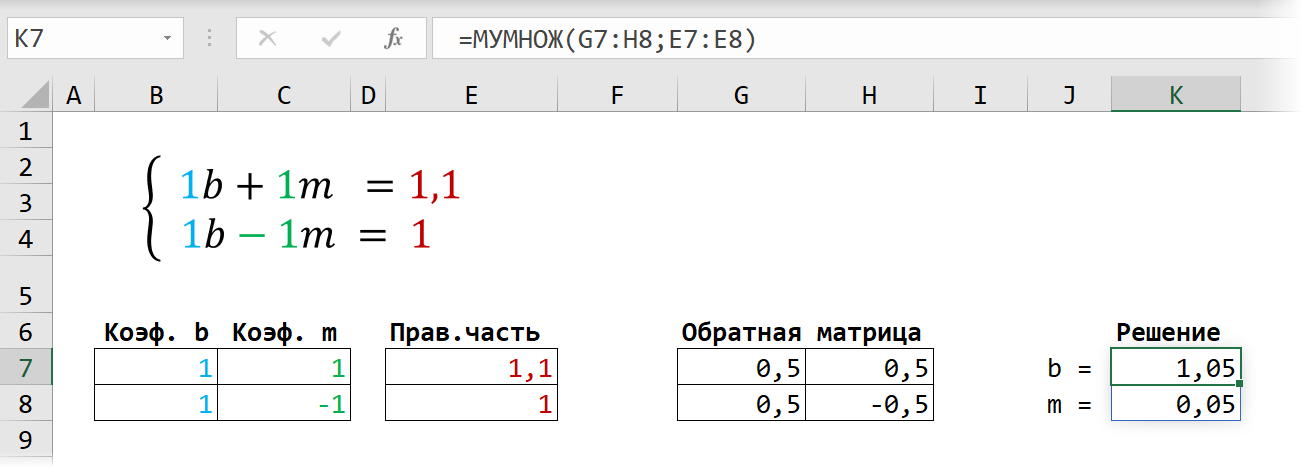
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
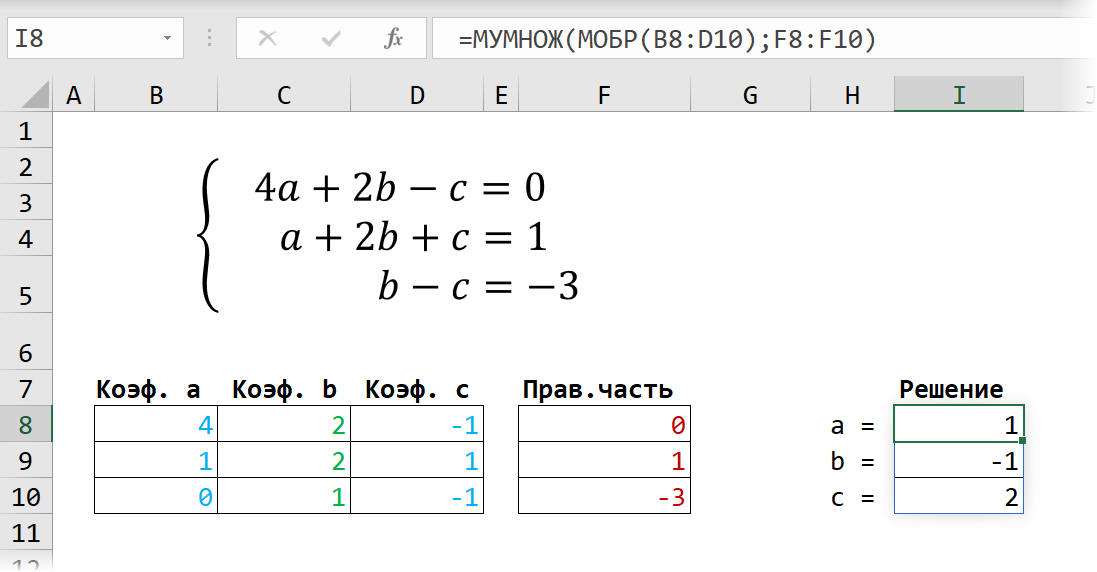
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
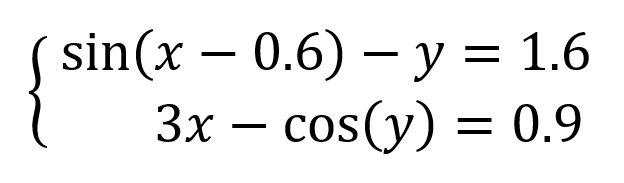
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
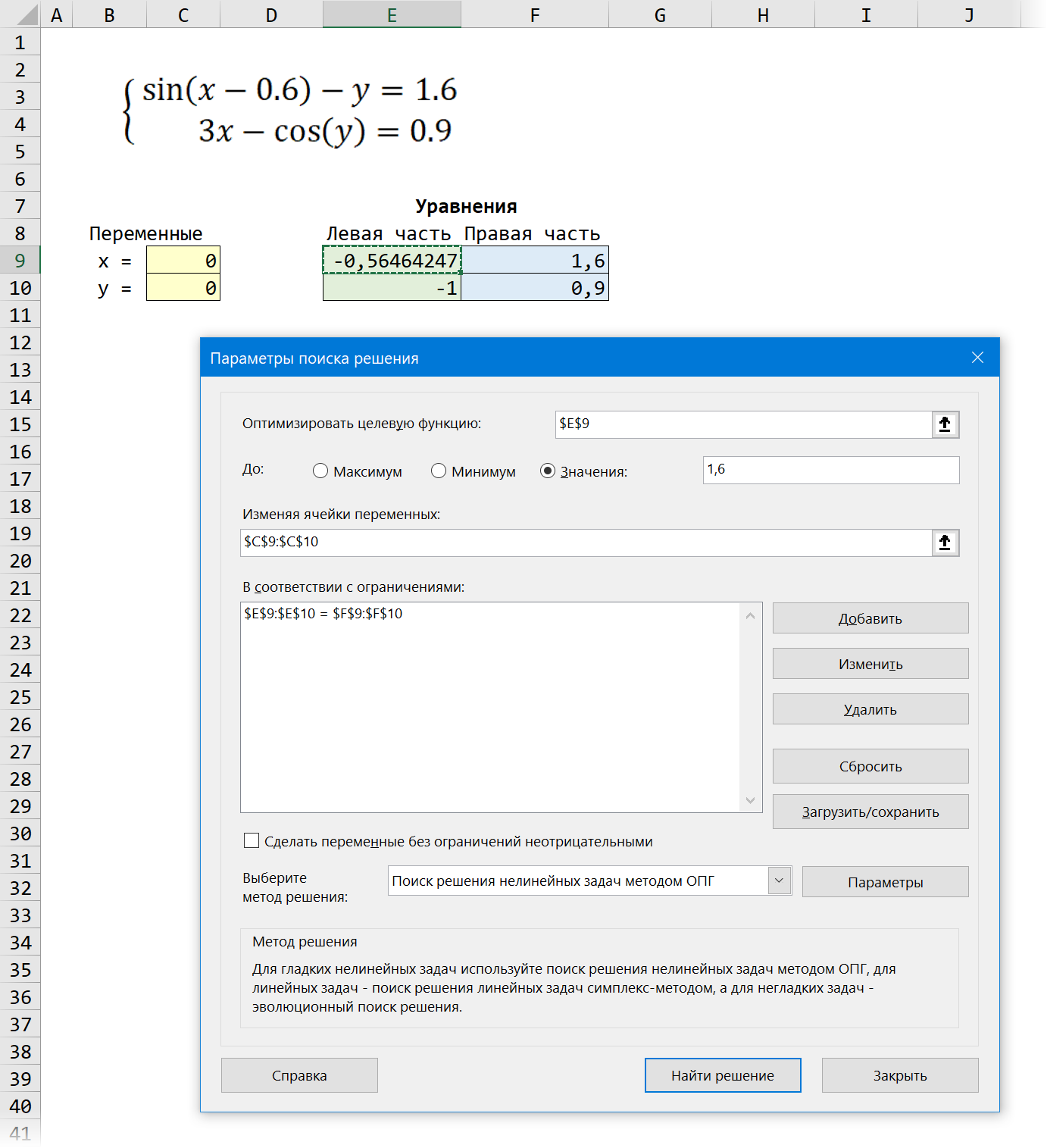
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
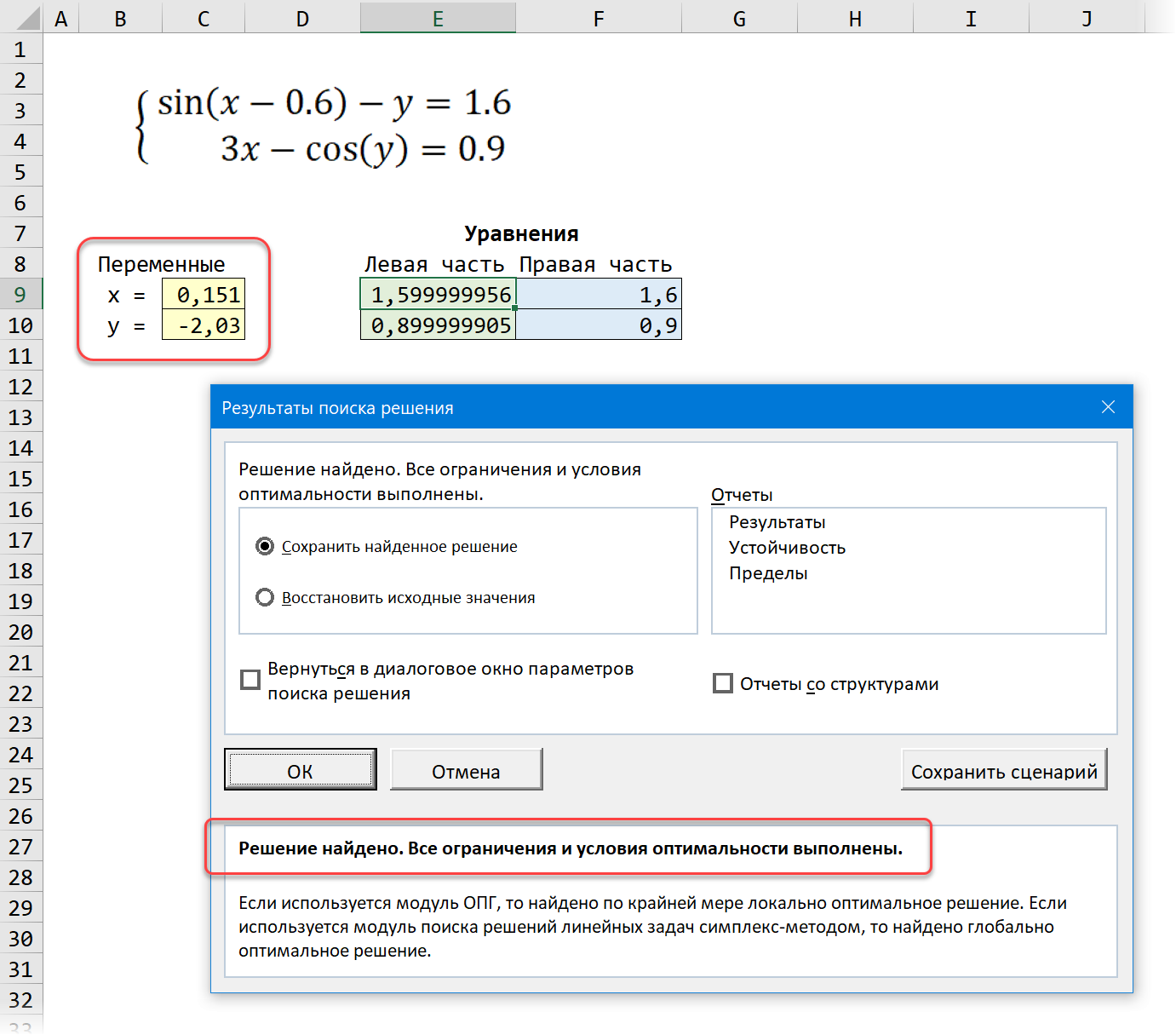
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
|
6 / 6 / 3 Регистрация: 23.06.2012 Сообщений: 51 |
|
|
1 |
|
|
14.03.2015, 08:51. Показов 4555. Ответов 6
Всем доброго времени суток. Хотелось бы узнать, возможно ли создать аналог надстройки «Поиск решений» из Excel на VB.NET? Если да, то как. Если есть специалист, разбирающийся в принципах работы данной надстройки, то с радостью приму от него информацию о том, по каким принципам и алгоритмам она работает, т.е. какие уравнения там используются и т.п. Заранее спасибо всем.
0 |
|
2079 / 1232 / 464 Регистрация: 20.12.2014 Сообщений: 3,237 |
|
|
14.03.2015, 09:42 |
2 |
|
по каким принципам и алгоритмам она работает, т.е. какие уравнения там используются и т.п. Когда-то давно делал реализацию поиска решения на VBA. В интернете есть информация по этому поводу. Нашел тогда практически весь код. Ссылки, к сожалению не сохранил, но помню, что искал не долго. А уж переделать программу с VBA на VB.NET, думаю, вполне реально.
0 |
|
6 / 6 / 3 Регистрация: 23.06.2012 Сообщений: 51 |
|
|
14.03.2015, 10:26 [ТС] |
3 |
|
К сожалению, с VBA я не знаком. Если и найду информацию, то нужно будет повтыкать ещё в код VBA, но, думаю, я разберусь. Жаль, что ссылки не сохранены, очень пригодились бы.
0 |
|
6 / 6 / 3 Регистрация: 23.06.2012 Сообщений: 51 |
|
|
14.03.2015, 15:20 [ТС] |
5 |
|
Спасибо за ссылку. С ней всё кажется попроще. А нужно ли подключать библиотеку VBA в проект, чтобы использовать код VBA? Или код нужно переработать под VB.NET? Или сделать и то, и другое?
0 |
|
2079 / 1232 / 464 Регистрация: 20.12.2014 Сообщений: 3,237 |
|
|
14.03.2015, 21:47 |
6 |
|
Мне кажется библиотеку подключать надо, потому что там специфические функции, ну и код, естественно, придется чуть подправить. Всё-таки vba и vb.net отличаются. Вот, еще ссылку нашел, правда там на английском всё, но перевести переводчиком, я думаю, сможете. Насколько я понял — это что-то типа поиска решения на разных языках программирования. Или, даже, надстройки для разных языков.
1 |
|
6 / 6 / 3 Регистрация: 23.06.2012 Сообщений: 51 |
|
|
15.03.2015, 20:13 [ТС] |
7 |
|
РешениеОгромное спасибо за ссылки. Теперь буду пытаться разобраться с ломаным машинным переводом и кодом. Очень надеюсь, что смогу разобраться без особых сложностей. Добавлено через 7 часов 38 минут
1 |
Аналог «поиск решения» для ГУгл Екселя?
Подскажите аналог стандартному в EXCEL «Поиск Решения»
Для Гугл Excel.
По сути как добавить в гугл ексель «поиск Решения»
-
Вопрос заданболее трёх лет назад
-
8773 просмотра
Подозреваю, что такого функционала в Гугл таблицах — нет. Тем не менее, вполне можно написать js макроc, который будет выполнять нужные операции.
Пригласить эксперта
-
Показать ещё
Загружается…
15 апр. 2023, в 07:16
1000 руб./за проект
15 апр. 2023, в 04:50
7000 руб./за проект
15 апр. 2023, в 03:28
5000 руб./за проект
Минуточку внимания
|
Группа: Пользователи Ранг: Прохожий Сообщений: 5
Замечаний: |
Добрый день!
Прошу помочь с формулой, голова кипит)
Мне необходимо, чтобы в одной ячейке выводился процент, который в свою очередь зависит от 3 критериев.
Например: условие 1 -ДА, условие 2 — ДА, условие 3 — ДА, то выводится 20%. Если условие 1 -ДА, условие 2 — НЕТ условие 3 — НЕТ, то выводится 10% и т.д.
Сложность в том, что вариантов этих критерии у меня 7, а выводиться все должно в одной ячейке.
Функция ЕСЛИ выдает ошибку, что слишком много аргументов для этой функции.
К сообщению приложен файл:
9435851.xlsx
(10.1 Kb)



 Сообщение было отмечено Памирыч как решение
Сообщение было отмечено Памирыч как решение
