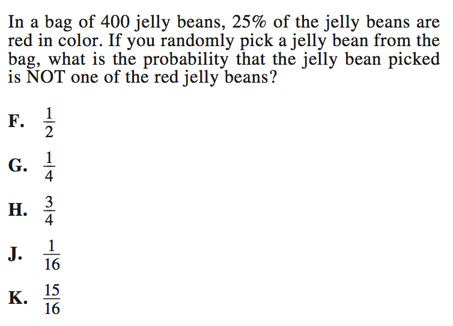Word problems are always a challenge for students. There are so many processes involved in solving word problems that it can be challenging to pinpoint concerns. Is it reading comprehension? Is it computation? Are students overly relying on key words? And the list goes on.
One of my favorite strategies is to make sure students are familar with all types of word problems. This Types of Word Problems resource is very helpful for teaching this challenging skill!
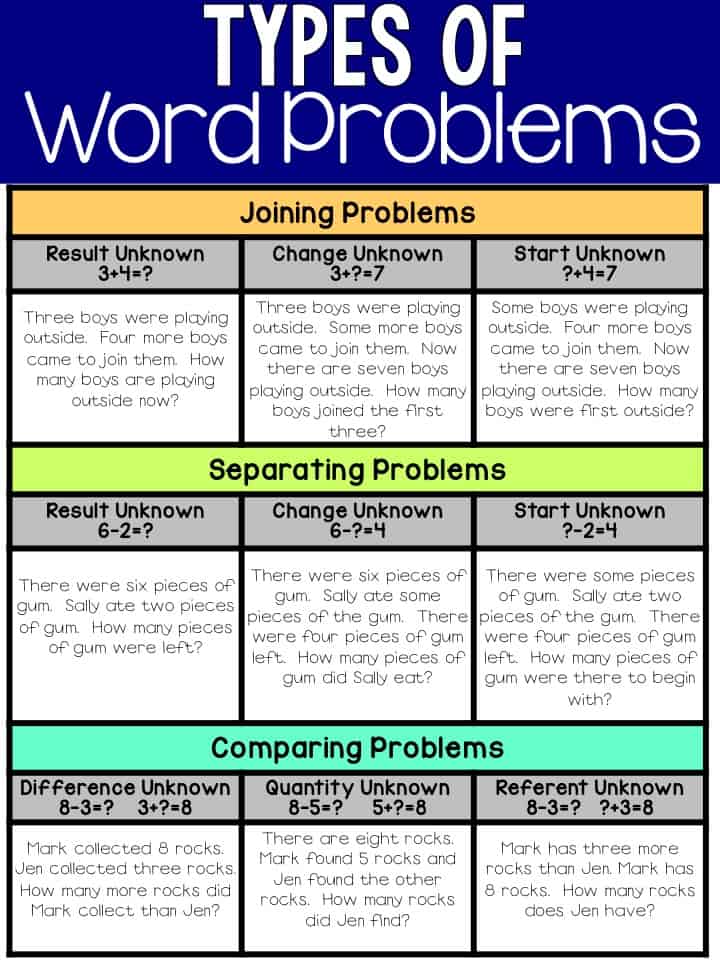
Addition and Subtraction
There are three main types of addition and subtraction problems:
- joining problems
- separating problems
- comparing problems
Students should solve problems where the result is unknown, change is unknown, or start is unknown. When I begin teaching types of word problems, I use small numbers so students can focus on the meaning of the problem, rather than computation. This also gives students the opportunity to use counters to illustrate the problem, role playing and writing their own word problems.
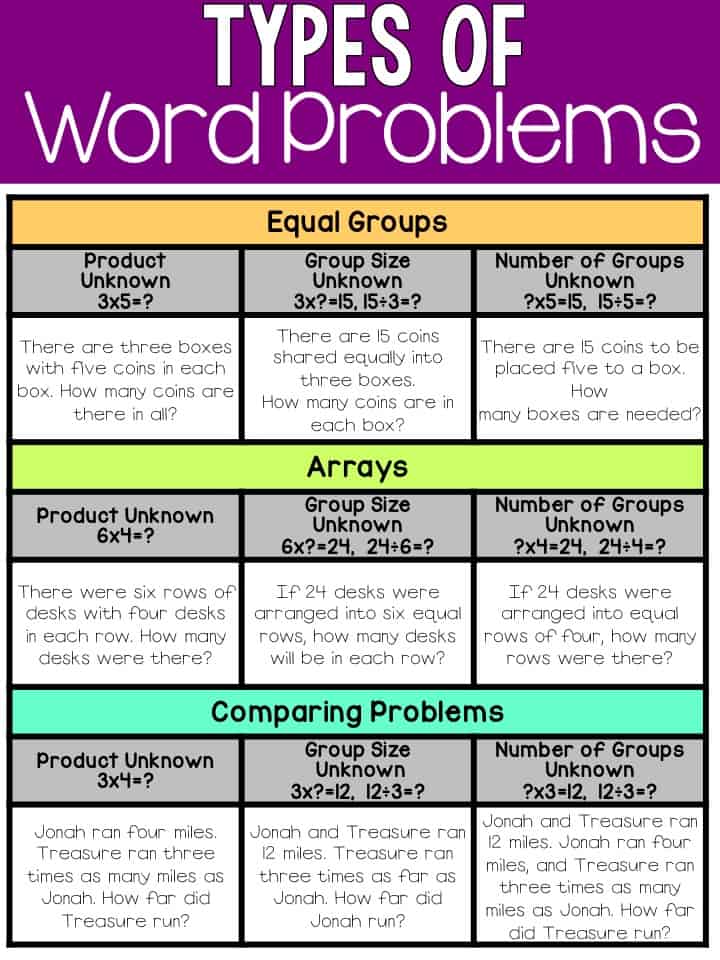
Multiplication and Division
There are also three main types of multiplication and division word problems:
- equal groups
- arrays
- comparing problems
Within each type of problem, the product may be unknown, the group size may be unknown, or the number of groups may be unknown. Once again, I use counters to have students determine which equation to use to determine how to solve the different types of problems. Students should also notice the difference between addition/subtraction problems and multiplication/division problems.
In the resource, there are posters for each type of word problem. You can display these after you introduce that type of word problem and then refer to the posters throughout the year. You can even print this in a smaller size so students can add these to their math notebooks.
A great way to help students develop an understanding of word problems is to have them write word problems. In the resource, there is a booklet is for addition and subtraction, a booklet for multiplication and division, and a booklet that combines both addition and subtraction. In the addition and subtraction booklet, I replaced all numbers with letters, because I wanted my students to not focus on a numerical answer, but the equation used to solve the problem. Over the years, I’ve found that my students’ primary focus was the answer, not the process.
When students have to write a word problem to reflect a certain style of word problem, it raises their level of thinking and problem solving significantly. This is a much more complex skill, so we typically practice writing word problems through guided practice first.
For additional practice solving different types of word problems, there are 22 addition and subtraction task cards and 18 multiplication and division task cards, for a total of 40 task cards. There are two task cards for each type of word problem, so all problem types are equally represented.
You could use the task cards as a math center or as any part of your math instruction.
This word problem practice was a huge help in allowing my students to dig even deeper with word problems. If you’re interested in checking it out, here is a link that will take you to a preview.
What are Word Problems?
Word problems are sometimes called practical problems or logical deduction questions.
These types of questions assess your ability to understand whether or not you have enough information in order to solve a problem.
Calculations for Word Problems
You normally will not be asked to perform calculations on word problems.
These types of problems usually ask you to interpret the data provided. Alternatively, the question might ask whether there is sufficient information in order to reach a certain conclusion.
Types of Word Problems
You may see these types of word problems on your standardized exam.
Please click on the links in each of the sections below to see the free exercises.
What Information Can Be Determined from the Data Provided?
These types of problems will give you a narrative paragraph or list of information.
The information will usually be provided for the total data set, as well as for subsets of the data.
You then have to decide which fact can be determined from the information provided.
Interpreting Test Scores
In order to interpret test scores, you will need to understand the concepts of raw score, mean, mode, standard deviation, percentile, and stanine.
Questions on Logical Connectives
Logical connectives are words such as: if, then, but, all, most, some, none, each, and every.
For example: Baseball practice is held every Saturday, but not if it is raining.
For questions on logical connectives, you will again see statements in a narrative paragraph or in list form.
You then have to make a small logical deduction from the information provided in order to answer the question.
Measuring Weight
These types of problems will not ask you to calculate the weight of an item.
Rather, they will ask you to identify the suitable unit of measurement for a particular item.
Be sure that you are well-versed with US units of measurement for your examination.
What Information is Missing?
These questions ask you to evaluate the data and determine which piece of missing information is needed in order to solve the problem.
Students sometimes find these types of logical deduction questions to be the most difficult.
Please click on the link above to see step-by-step instructions on how to answer “missing information” questions.
If you are looking for tips and ideas for how to teach word problems to your elementary students, then you’ve found the right place! We know that teaching elementary students how to solve word problems is important for math concept and skill application, but it sure can feel like a daunting charge without knowing about the different types, the best practices for teaching them, and common misconceptions to plan in advance for, as well as having the resources you need. All this information will make you feel confident about how to teach addition, subtraction, multiplication, and division word problems! Teaching students how to solve word problems will be so much easier!
This blog post will address the following questions:
- What is a word problem?
- What is a multi-step word problem?
- Why are elementary math word problems important?
- Why are math word problems so hard for elementary students?
- What are the types of word problems?
- How do I teach math word problems in a systematic way?
- What are the best elementary math word problem strategies I can teach my students and what are some tips for how to teach math word problems strategies?
- Do you have any helpful tips for how to teach word problems?
- What are the common mistakes I should look for that my students may make?
- How do I address my students’ common misconceptions surrounding elementary math word problems?
What is a Word Problem?
A word problem is a math situation that calls for an equation to be solved. Students must apply their critical thinking skills to determine how to solve the problem. Word problems give students the opportunity to practice turning situations into numbers. This is critical as students progress in their education, as well as in their day-to-day life. By teaching students how to solve word problems in a strategic way, you are setting them up for future success!
What is a Multi-Step Word Problem?
A multi-step word problem, also known as a two-step word problem or two-step equation word problem, is a math situation that involves more than one equation having to be answered in order to solve the ultimate question. This requires students to apply their problem solving skills to determine which operation or operations to use to tackle the problem and find the necessary information. In some cases, the situation may call for mixed operations, and in others the operations will be the same. Multi-step word problems offer students the opportunity to practice the skill of applying different math concepts with a given problem.
Why are Word Problems Important in Math?
Word problems are essential in math because they give students the opportunity to apply what they have learned to a real life situation. In addition, it facilitates students in developing their higher order thinking and critical thinking skills, creativity, positive mindset toward persevering while problem solving, and confidence in their math abilities. Word problems are an effective tool for teachers to determine whether or not students understand and can apply the concepts and skills they learned to a real life situation.
Why do Students Struggle with Math Word Problems?
Knowing why students have trouble with word problems will help you better understand how to teach them. The reason why math word problems are difficult for your students is because of a few different reasons. First, students need to be able to fluently read and comprehend the text. Second, they need to be able to identify which operations and steps are needed to find the answer. Finally, they need to be able to accurately calculate the answer. If you have students who struggle with reading or English is their second language (ESL), they may not be able to accurately show what they know and can do because of language and literacy barriers. In these cases, it is appropriate to read the text aloud to them or have it translated into their native language for assignments and assessments.
Types of Word Problems
Knowing the different types of word problems will help you better understand how to teach math word problems. Read below to learn about the four types of basic one-step addition and subtraction word problems, the subcategories within each of them, and specific examples for all of them. Two-step equation word problems can encompass two of the same type or two separate types (also known as mixed operation word problems).
1. Join
This type of word problem involves an action that increases the original amount. There are three kinds: Result unknown, change unknown, and initial quantity unknown.
Result Unknown
Example: There were 7 kids swimming in the pool. 3 more kids jumped in. How many kids are in the pool now? (7 + 3 = ?)
Change Unknown
Example: There were 8 kids swimming in the pool. More kids jumped in. Now there are 15 kids in the pool. How many kids jumped in? (8 + ? = 15)
Initial Quantity Unknown
Example: There were kids swimming in the pool. 2 kids jumped in. Now there are 6 kids in the pool. How many kids were swimming in the pool at first? (? + 2 = 6)
2. Separate
This type of word problem involves an action that decreases the original amount. There are three kinds: Result unknown, change unknown, and initial quantity unknown.
Result Unknown
Example: There were 12 kids swimming in the pool. 6 of the kids got out of the pool. How many kids are in the pool now? (12 – 6 = ?)
Change Unknown
Example: There were 9 kids swimming in the pool. Some of the kids got out of the pool. Now there are 4 kids in the pool. How many kids got out of the pool? (9 – ? = 4)
Initial Quantity Unknown
Example: There were kids swimming in the pool. 3 of the kids got out of the pool. Now there are 2 kids in the pool. How many kids were in the pool at first? (? – 3 = 2)
 |
 |
 |
 |
 |
 |
3. Part-Part-Whole
This type of word problem does not involve an action like the join and separate types. Instead, it is about defining relationships among a whole and two parts. There are two kinds: result unknown and part unknown.
Result Unknown
Example: There are 5 boys and 9 girls swimming in the pool. How many kids are in the pool? (5 + 9 = ?)
Part Unknown
Example: There are 12 kids swimming in the pool. 8 of them are girls and the rest of them are boys. How many boys are swimming in the pool? (8 + ? = 12)
4. Compare
This type of word problem does not involve an action or relationship like the three other types. Instead, it is about comparing two different unrelated items. There are two kinds: Difference unknown and quantity unknown.
Difference Unknown
Example: There are 2 kids in the pool. There are 7 kids in the yard. How many more kids are in the yard than in the pool? (2 + ? = 7 or 7 – 2 = ?)
Quantity Unknown
Example 1: There are 5 kids in the pool. There are 3 fewer kids playing in the yard. How many kids are playing in the yard? (5 – 3 = ?)
Example 2: There are 2 kids in the pool. There are 10 more kids playing in the yard than in the pool. How many kids are playing in the yard? (2 + 10 = ?)
How to Solve Word Problems in 5 Easy Steps
Here are 5 steps that will help you teach word problems to your 1st, 2nd, 3rd, 4th or 5th grade students:
- Read the problem.
- Read the problem a second time and make meaning of it by visualizing, drawing pictures, and highlighting important information (numbers, phrases, and questions).
- Plan how you will solve the problem by organizing information in a graphic organizer and writing down equations and formulas that you will need to solve.
- Implement the plan and determine answer.
- Reflect on your answer and determine if it is reasonable. If not, check your work and start back at step one if needed. If the answer is reasonable, check your answer and be prepared to explain how you solved it and why you chose the strategies you did.
5 Math Word Problem Strategies
Here are 5 strategies for how to teach elementary word problems:
Visualize
Understand the math situation and what the question is asking by picturing what you read in your head while you are reading.
Draw Pictures
Make meaning of what the word problem is asking by drawing a picture of the math situation.
Make Models
Use math tools like base-ten blocks to model what is happening in the math situation.
Highlight Important Information
Underline or highlight important numbers, phrases, and questions.
Engage in Word Study
Look for key words and phrases like “less” or “in all.” Check out this blog post if you are interested in learning more about math word problem keywords and their limitations.
10 Tips for Teaching Students How to Solve Math Word Problems
Here are 10 tips for how to teach math word problems:
- Model a positive attitude toward word problems and math.
- Embody a growth mindset.
- Model! Provide plenty of direct instruction.
- Give lots of opportunities to practice.
- Explicitly teach strategies and post anchor charts so students can access them and remember prior learning.
- Celebrate the strategies and process rather than the correct answer.
- Encourage students to continue persevering when they get stuck.
- Invite students to act as peer tutors.
- Provide opportunities for students to write their own word problems.
- Engage in whole-group discussions when solving word problems as a class.
Common Misconceptions and Errors When Students Learn How to Solve Math Word Problems
Here are 5 common misconceptions or errors elementary students have or make surrounding math word problems:
1. Use the Incorrect Operation
Elementary students often apply the incorrect operations because they pull the numbers from a word problem and add them without considering what the question is asking them or they misunderstand what the problem is asking. Early in their experience with word problems, this strategy may work most of the time; however, its effectiveness will cease as the math gets more complex. It is important to instruct students to develop and apply problem-solving strategies.
Although helpful in determining the meaning, elementary students rely solely on key words and phrases in a word problem to determine what operation is being called for. Again, this may be an effective strategy early on in their math career, but it should not be the only strategy students use to determine what their plan of attack is.
2. Get Stuck in a Fixed Mindset
Some elementary students give up before starting a word problem because they think all word problems are too hard. It is essential to instill a positive mindset towards math in students. The best way to do that is through modeling. If you portray an excitement for math, many of your students will share that same feeling.
3. Struggle with Reading Skills Component
For first and second graders (as well as struggling readers and ESL students), it is common for students to decode the text incorrectly. Along the same lines, some elementary students think they can’t solve word problems because they do not know how to read yet. The purpose of word problems is not to assess whether a child can read or not. Instead, the purpose is to assess their critical thinking and problem-solving skills. As a result, it is appropriate to read word problems to elementary students.
4. Calculate Incorrectly
You’ll find instances where students will understand what the question is asking, but they will calculate the addends or the subtrahend from the minuend incorrectly. This type of error is important to note when analyzing student responses because it gives you valuable information for when you plan your instruction.
5. Encode Response Incorrectly
Another error that is important to note when analyzing student responses is when you find that they encode their solution in writing incorrectly. This means they understand what the problem is asking, they solve the operations correctly, document their work meticulously, but then write the incorrect answer on the line.
How to Address Common Misconceptions Surrounding Math Word Problems
You might be wondering, “What can I do in response to some of these misconceptions and errors?” After collecting and analyzing the data, forming groups based on the results, and planning differentiated instruction, you may want to consider trying out these prompts:
- Can you reread the question aloud to me?
- What is the question asking us to do?
- How can we represent the information and question?
- Can we represent the information and question with an equation?
- What is our first step?
- What is our next step?
- Can you think of any strategies we use to help us solve?
- How did you find your answer?
- Can you walk me through how you found your answer step by step?
- What do we need to remember when recording our answer?
Now that you have all these tips and ideas for how to teach word problems, we would love for you to try these word problem resources with your students. They offer students opportunities to practice solving word problems after having learned how to solve word problems. You can download word problem worksheets specific to your grade level (along with lots of other math freebies) in our free printable math resources bundle using this link: free printable math activities for elementary teachers.
Check out my monthly word problem resources!
- 1st Grade Word Problems
- 2nd Grade Word Problems
- 3rd Grade Word Problems
- 4th Grade Word Problems
- 5th Grade Word Problems

The cornerstone of primary math is number sense — and primarily mastering the concept of addition and subtraction, hopefully even gaining automaticity with those addition and subtraction facts. Elementary teachers live and breathe addition and subtraction!
Teachers work all year to help children build conceptual understanding, make connections, and see relationships — working their behinds off modeling and practicing those concepts and helping kids gain a deep understanding. Then comes the mastery piece — fact fluency. It is a ton of hard work!
But the word problems. Oh, the word problems! That’s the piece that sometimes gets left by the wayside in the desperate attempt to drive home fact mastery.
It doesn’t seem too complicated at first glance because we have used story problems since Kindergarten to help students build a conceptual understanding of addition and subtraction.
But we can easily get stuck in the basic join and separate word problem set and not even realize that there are many more ways that problems can be presented.
When pushing through that quick word problem of the day, it’s easy to forget to increase the complexity of the problems we present.
Now as a fourth grade teacher, I can see how essential those early word problems are. If students didn’t learn to understand and solve complex addition and subtraction word problems in the early grades, they have a much more difficult time understanding multi step multiplication and division problems in the upper grades. They need that foundation on which to build the new concepts.
It is so important for kids to have daily opportunities to solve all different types of word problems. And not just any old problem we come up with on the fly, but varied and wide ranging.
When teaching first grade, I found myself forgetting to include all the types of word problem types. I tended to go with the familiar. So I incorporated daily word problem practice and I found it helpful to keep a chart handy so I could keep track of the problems we were working on and ensure that my students were getting exposure to all problem types.
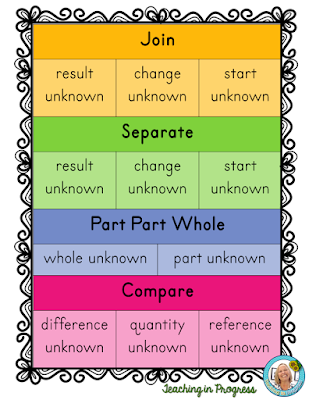
Did you know there are four different types of word problems?
And 11 subsets? Take a look at this chart based on the CGI model.
Let’s take a closer look at each type:
JOIN
Join problems involve an action, with a set being added to an existing set.
Result Unknown is the type of addition problem our kids are so familiar with when they come to us: 3 + 2 = __
We know the parts and need to find the sum. Joe had 3 pencils. Meg gave him 2 more pencils. How many pencils does Joe have now?
Change Unknown problems ramp up the complexity and throw in the missing part: 3 + __ = 5
Joe had 3 pencils. Meg gave him some more and now Joe has 5 pencils. How many pencils did Meg give Joe?
Start Unknown problems are very similar: __ + 2 = 5
Joe had some pencils. Meg gave him 2 more and now Joe has 5 pencils. How many pencils did Joe have to start?
All of these problems involve joining two sets, but once the start and change become unknown, the problem requires a deeper understanding.
SEPARATE
Separate problems also involve an action with a set being removed from an existing set.
Result Unknown again, is a familiar form of a subtraction problem: 5 — 3 = __
Joe had 5 pencils. He gave 3 of them to Meg. How many pencils does Joe have left?
Change Unknown provides for the missing part and an opportunity for deeper understanding of subtraction: 5 — __ = 2
Joe had 5 pencils. He gave some of them to Meg and now he has 2 pencils left. How many pencils did Joe give Meg?
Start Unknown is looking to find the whole: __ — 3 = 2
Joe had some pencils. He gave Meg three and now he has 2 pencils left. How many pencils did Joe have to start?
All subtraction problems, but presented in ways that allow for a more conceptual understanding of subtraction.
PART-PART WHOLE
Part part whole problems seem much like join and separate problems, but they do not involve an action. The problem is really looking at relationships between the quantities. There are two types of part-part whole problems:
Whole Unknown 2 + 3= __ Joe had 2 green pencils and 3 yellow pencils. How many pencils did Joe have altogether?
Part Unknown 2 + __= 5 or 5 — 2 = __ Joe had 5 pencils. Two are green and the rest are yellow. How many yellow pencils does Joe have?
COMPARE
Compare problems also look at relationships between quantities. But here we are not looking at a set and its subsets, but the relationship between two distinct sets.
Difference Unknown compares two sets. 5 — 3 = __ or 3 + __ = 5
Joe had 5 pencils. Meg had 3
pencils. How many more pencils did
Joe have than Meg?
Quantity Unknown 3 + 2 = __
Joe had 3 pencils. Meg had 2
more pencils than Joe. How
many pencils did Meg have?
Reference Unknown 5 — 3 = __
Joe had 5 pencils. He had 3 more than Meg. How many pencils did
Meg have?
Each type of problem requires a different level of thinking and problem solving.
If you do daily word problem practice and would like to ensure that you cover all problems types, or if you haven’t incorporated a word problem of the day and would like to start, grab this freebie! It contains a copy of the problem type poster and some word problems with work mats to get you started!
Solving word problems in elementary school is an essential part of the math curriculum. Here are over 30 math word problems to practice with children, plus expert guidance on how to solve them.
This blog is part of our series of blogs designed for teachers, schools and parents supporting home learning.
What is a word problem?
A word problem in math is a math question written as one sentence or more that requires children to apply their math knowledge to a ‘real-life’ scenario.
This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem.
For example:
Isn’t brilliant arithmetic enough?
In short, no. Students need to build good reading comprehension, even in math. Overtime math problems become increasingly complex and require students to possess deep conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
As students progress through their mathematical education, they will need to be able to apply mathematical reasoning and develop mathematical arguments and proofs using math language. They will also need to be dynamic, applying their math knowledge to a variety of increasingly sophisticated problems.
To support this schools are adopting a ‘mastery’ approach to math
“Teaching for mastery”, is defined with theses component:
- Math teaching for mastery rejects the idea that a large proportion of people ‘just can’t do math’.
- All students are encouraged by the belief that by working hard at math they can succeed.
- Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other.
- Significant time is spent developing deep knowledge of the key ideas that are needed to support future learning. The structure and connections within the mathematics are emphasized, so that students develop deep learning that can be sustained.
(The Essence of Maths Teaching for Mastery, 2016)
Mastery helps children to explore math in greater depth
Fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learned the number skills appropriate to their grade level/age, they should be progressed to the next grade level/age of number skills.
The mastery approach encourages exploring the breadth and depth of these math concepts (once fluency is secure) through reasoning and problem solving.
How to teach children to solve word problems?
Here are two simple strategies that can be applied to many word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
Let’s see how this can be applied to word problems to help achieve the answer.
Solving a simple word problem
There are 28 students in a class.
The teacher has 8 liters of orange juice.
She pours 225 milliliters of orange juice for every student.
How much orange juice is left over?
1. What do you already know?
- There are 1,000ml in 1 liter
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
The bar model, also known as strip diagram, is always a great way of representing problems. However, if you are not familiar with this, there are always other ways of drawing it out.
Read more: What is a bar model
For example, for this question, you could draw 28 students (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 liters’ marked at the top.
Now to put the math to work. This is a 5th grade multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
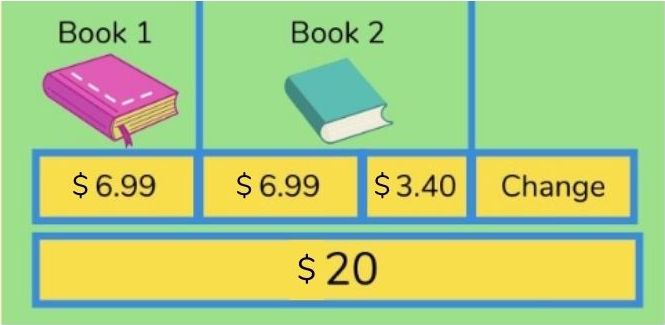
Solving a more complex, mixed word problem
Mara is in a bookshop.
She buys one book for $6.99 and another that costs $3.40 more than the first book.
She pays using a $20 bill.
What change does Mara get? (What is the remainder?)
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the math to work using what we already know and what we’ve drawn to break down the steps.
Mara is in a bookshop.
She buys one book for $6.99 and another that costs $3.40 more than the first book. 1) $6.99 + ($6.99 + $3.40) = $17.38
She pays using a $20 bill.
What change does Mara get? 2) $20 – $17.38 = $2.62
Math Word Problems For Kindergarten to Grade 5
The more children learn about math as they go through elementary school, the trickier the word problems they face will become.
Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each elementary grade.
Word problems in kindergarten
Throughout kindergarten a child is likely to be introduced to word problems with the help of concrete resources (manipulatives, such as pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.
An example of a word problem for kindergarten would be
Chris has 3 red bounce balls and 2 green bounce balls. How many bounce balls does Chris have in all?
Word problems 1st grade
First grade is a continuation of kindergarten when it comes to word problems, with children still using concrete resources to help them understand and visualize the problems they are working on
An example of a word problem for first grade would be:
A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?
Word problems in 2nd grade
In second grade, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the adding and subtracting within 100, adding up to 4- two-digit numbers at a time.
This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.
Second grade word problem: Geometry properties of shape
Shaun is making shapes out of plastic straws.
At the vertices where the straws meet, he uses blobs of modeling clay to fix them together
Here are some of the shapes he makes:
| Shape | Number of straws | Number of blobs of modeling clay |
| A | 4 | 4 |
| B | 3 | 3 |
| C | 6 | 6 |
One of Sean’s shapes is a triangle. Which is it? Explain your answer.
Answer: shape B as a triangle has 3 sides (straws) and 3 vertices, or angles (clay)
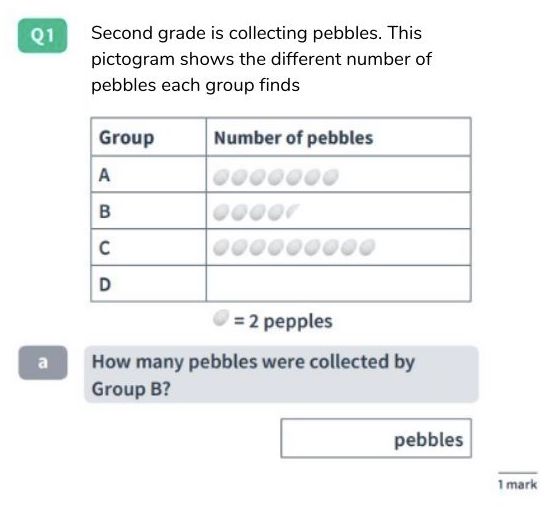
Second grade word problem: Statistics
2nd grade is collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.
Word problems in 3rd grade
At this stage of their elementary school career, children should feel confident using the written method for addition and subtraction. They will begin multiplying and dividing within 100.
This year children will be presented with a variety of problems, including 2-step problems and be expected to work out the appropriate method required to solve each one.
3rd grade word problem: Number and place value
My number has four digits and has a 7 in the hundreds place.
The digit which has the highest value in my number is 2.
The digit which has the lowest value in my number is 6.
My number has 3 fewer tens than hundreds.
What is my number?
Answer: 2,746
Word problems in 4th grade
One and two-step word problems continue in fourth grade, but this is also the year that children will be introduced to word problems containing decimals.
Fourth grade word problem: Fractions and decimals
Stan, Frank and John are washing their cars outside their houses.
Stan has washed 0.5 of his car.
Frank has washed 1/5 of his car.
Norm has washed 2/5 of his car.
Who has washed the most?
Explain your answer.
Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.4)
Word problems in 5th grade
In fifth grade children move on from 2-step word problems to multi-step word problems. These will include fractions and decimals.
Here are some examples of the types of math word problems in fifth grade will have to solve.
5th grade word problem – Ratio and proportion
The Angel of the North is a large statue in England. It is 20 meters tall and 54 meters wide.
Ally makes a scale model of the Angel of the North. Her model is 40 centimeters tall. How wide is her model?
Answer: 108cm
Fifth grade word problem – Algebra
Amina is making designs with two different shapes.
She gives each shape a value.
Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
Fifth grade word problem: Measurement
There are 28 students in a class.
The teacher has 8 liters of orange juice.
She pours 225 milliliters of orange juice for every student.
How much orange juice is left over?
Answer: 1.7 liters or 1,700ml
Topic based word problems
The following examples give you an idea of the kinds of math word problems your child will encounter in elementary school
Place value word problem fourth grade
This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37
Download free number and place value word problems for grades 2, 3, 4 and 5
Addition and subtraction word problem grade 2
Sam has 64 sweets. He gets given 12 more. He then gives 22 away. How many sweets is he left with? Answer: 54
Download free addition and subtraction word problems for for grades 2, 3, 4 and 5
Addition word problem grade 2
Sammy thinks of a number. He subtracts 70. His new number is 12. What was the number Sammy thought of? Answer: 82
Subtraction word problem fifth grade
The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC
Multiplication word problem third grade
Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108
Download free multiplication word problems for grades 2, 3, 4 and 5.
Division word problem fifth grade
A factory produces 3,572 paint brushes every day. They are packaged into boxes of 19. How many boxes does the factory produce every day? Answer: 188
Download free division word problems for grades 2, 3, 4 and 5.
Free resource: Use these four operations word problems to practice addition, subtraction, multiplication and division all together.
Fraction word problem fourth grade
At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3
Download free fractions and decimals word problems for grades 2, 3, 4 and 5.
Money word problem second grade
Lucy and Noor found some money on the playground at recess. Lucy found 2 dimes and 1 penny, and Noor found 2 quarters and a dime. How many cents did Lucy and Noor find? Answer: Lucy = $0.21, Noor = $0.60; $0.21 + $0.61 = $0.81
Area word problem 3rd grade
A rectangle measures 6cm by 5cm.
What is its area? Answer: 30cm2
Perimeter word problem 3rd grade
The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many meters has she swum? Answer: 108m
Ratio word problem 5th grade (crossover with measurement)
A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
PEMDAS word problem fifth grade
Draw a pair of parentheses in one of these calculations so that they make two different answers. What are the answers?
50 – 10 × 5 =
50 – 10 × 5 =
Volume word problem fifth grade
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
Remember: The word problems can change but the math won’t
It can be easy for children to get overwhelmed when they first come across word problems, but it is important that you remind them that while the context of the problem may be presented in a different way, the math behind it remains the same.
Word problems are a good way to bring math into the real world and make math more relevant for your child. So help them practice, or even ask them to turn the tables and make up some word problems for you to solve.
Do you have students who need extra support in math?
Give your fourth and fifth grade students more opportunities to consolidate learning and practice skills through personalized elementary math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Programs are available for fourth grade and fifth grade, and you can try 6 lessons absolutely free.
Heeey you awesome teacher friend!
I have told you a million times: I am NOT a math person.
I am an avid reader.
And learner above all.
Oh and I want the best for my students.
Year after year, I look …
I read…
I find ways…
I reflect.
About word problems.
Do you feel that when you think you have done a good job teaching word problems, then your students start guessing the heck out of the answers?
Add!
Subtract!
Lord have mercy on my soul.
I know you can relate.
It almost seems like my efforts have been in vain.
Seriously.
In NC we have a document released by the state in which the clear distinctions among the problems are made. You can find this document HERE!
There are also clear distinctions between the kind of of problems that our students need to master by the end of Kindergarten, first grade, and second grade.
My students struggle every year with word problems. And every year I make an effort to go out of my way to teach them (and make sure that they have learned) different ways to solve them.
I am a firm BELIEVER in the gradual release of responsibility model.
Do you remember your professors in college talking about it? They were not kidding.
Well here’s a picture, just in case you are a visual learner like me.
It all begins with showing the kids how “I do it.”
Well, if I want to show the kids how “I do it,” might as well know the how and why. Right?
I mentioned before that there are different kinds of distinctions among the word problem types.
They are called CGI word problems. The research behind the problem types is clearly outlined on
Children’s Mathematics ~ Cognitively Guided Instruction (or CGI)
Yes, I know. What a geek.
#Notageek #IjustlovewhatIdo
As I am reading this book, there were 4 guiding principles that TRULY made me aware and reflect about the way I teach word problems.
Yes. Obviously. Duuuh. Four different types of word problems.
Was I teaching my students to identify the relationships and actions in word problems?
Are you?
How to go about it?
Classifying. Relationships. Actions. Described in problems.
Drop mic.
And how come I am able to teach text structure in reading, and I was neglecting text structure in math?
Huge light bulb moment teacher friends.
RELATIONSHIPS – ACTIONS – STRUCTURE.
So let’s go back to the gradual release model.
These are some of the anchor charts that I have used this year to introduce different types of word problems in whole group lessons during our math workshop time.
I color code to show my students the relationships in number bonds, bar models, number sentences, and actual sentences. Labeling everything, plays a VERY important part in conceptual understanding. I make sure to teach my students that the number sentence comes with understanding. We must understand before we actually figure out a “plus” or a “minus.”
Bar Models
So what are the type of word problems and what kind of strategies can we teach our students?
I really believe that there is not right or wrong way. Our students come to us already with a great deal of experiences.
I do believe, however, that there are ways that make my students’ understanding deeper, like bar models or number bonds.
I made this set of posters for my classroom, but more importantly for my students. These posters give us a visual, a point of reference, and a starting point to learn how to identify (and see) RELATIONSHIPS.
You can grab them for FREE by clicking HERE!! {There are 11 posters in
So, why are word problems so hard for kids to solve?
Simple.
We have to help them change the mindset of looking for the answer first. These are the set of steps that we follow in order to avoid looking for the answer first:
1.Read the problem
2. Identify the who and the what (We label and color here)
3. Draw unit bars with the help of manipulatives (Connecting cubes win by a landslide)
4. Reread problem, double check for information, adjust the bars. (This is why connecting cubes are better)
5. Decide on the question mark. (Label and color the question)
6. Work the number sentence out (see? this is towards the end)
7. Write a sentence to answer the question mark.
I really need to make an anchor chart with these steps and keep it up the whole year. These are the steps recommended by Singapore math experts. They are the bomb.
Let’s go back to the gradual release.
I have already told you about the “I do.”
I made these Color, label, cut, and paste mats to do during small groups during guided math. This is the “we do” part. It takes time and patience. The a-ha moment is priceless.
For the “you do it together” and ” you do it alone”, I ask my student to apply their strategies learned from the “I do” and “we do” stages by using task cards.
Simple and effective way to check for understanding. Hello formative assessment.
So what’s next?
Word problems are hard to understand. They make an important part of our classroom. As of recently, I have created a problem solving corner, where I hope that my students can see themselves as true problem solvers and mathematicians.
I hang posters with problem types that we have already practiced over and over.
There are connecting cubes, base ten blocks, coins, shapes, counters, and many other things in our problem solving corner. I hope to add more supplies based on observations and the suggestions of my students.
I continue to look for literature that supports problem solving in Math. Let me know if you have a fave!
Just in case you are interested in these activities, you may check them out from my TPT store.
You can learn more by clicking HERE!!
Thank you for reading teacher friends, I hope that you found this post useful.
Until next time!
Though the majority of ACT math problems use diagrams or simply ask you to solve given mathematical equations, you will also see approximately 15-18 word problems on any given ACT (between 25% and 30% of the total math section). This means that knowing how best to deal with word problems will help you significantly when taking the test. Though there are many different types of ACT word problems, most of them are not nearly as difficult or cumbersome as they may appear.
This post will be your complete guide to ACT word problems: how to translate your word problems into equations and diagrams, the different types of word problems you’ll see on the test, and how best to go about solving your word problems for test day.
What Are Word Problems?
A word problem is any problem that is based mostly or entirely on written description and does not provide you with an equation, diagram, or graph. You must use your reading skills to translate the words of the question into a workable math problem and then solve for your information.
Word problems will show up on the test for a variety of reasons. Most of the time, these types of questions act to test your reading and visualization skills, as well act as a medium to deliver questions that would otherwise be untestable. For instance, if you must determine the number of sides of an unknown polygon based on given information, a diagram would certainly give the game away!
Translating Word Problems Into Equations or Drawings
In order to translate your word problems into actionable math equations that you can solve, you’ll need to know and utilize some key math terms. Whenever you see these words, you can translate them into the proper action. For instance, the word “product” means “the value of two or more values that have been multiplied together,” so if you need to find “the product of a and b,” you’ll need to set up your equation with $a * b$.
|
Key Terms |
Mathematical Action |
|
Sum, increased by, added to, total of |
+ |
|
Difference, decreased by, subtracted from |
— |
|
Product, times |
* or x |
|
Divided by |
/ or ÷ |
|
Equals, is, are, equivalent, same |
= |
|
Is less than |
< |
|
Is greater than |
> |
|
Is less than or equal to |
≤ |
|
Is greater than or equal to |
≥ |
Let’s take a look at this in action with an example problem:
We have two different cable companies that each have different rates for installation and different monthly fees. We are asked to find out how many months it will take for the cost for each company to be the «same,» which means we must set the two rates equal.
Uptown Cable charges 120 dollars for installation plus 25 dollars a month. We do not know how many months we’re working with, so we will have:
$120 + 25x$
Downtown Cable charges 60 dollars for installation and 35 dollars per month. Again, we don’t know how many months we’re working with, but we know they will be the same, so we will have:
$60 + 35x$
And, again, because we are finding the amount of months when the cost is the «same,» we must set our rates equal.
$120 + 25x = 60 + 35x$
From here, we can solve for $x$, since it is a single variable equation.
[Note: the final answer is G, 6 months]
Learning the language of ACT word problems will help you to unravel much of the mystery of these types of questions.
Typical ACT Word Problems
ACT word problems can be grouped into two major categories: word problems where you must simply set up an equation and word problems in which you must solve for a specific piece of information.
Word Problem Type 1: Setting Up an Equation
This is the less common type of word problem on the test, but you’ll generally see it at least once or twice. You’ll also usually see this type of word problem first. For this type of question, you must use the given information to set up the equation, even though you don’t need to solve for the missing variable.
Almost always, you’ll see this type of question in the first ten questions on the test, meaning that the ACT test-makers consider them fairly “easy.” This is due to the fact that you only have to provide the set-up and not the execution.
We consider a “profit” to be any money that is gained, so we must always subtract our costs from our earnings. We know that Jones had to invest 10 million starting capital, so he is only making a profit if he has earned more than 10 million dollars. This means we can eliminate answer choices C, D, and E, as they do not account for this 10 million.
Now each boat costs Jones 7,000 dollars to make and he sells them for 20,000. This means that he earns a profit of:
$20,000 — 7,000$
$13,000$ per boat.
If $x$ represents our number of boats, then our final equation will be:
$13,000x — 10,000,000$
Our final answer is A, $13,000x — 10,000,000$
Word Problem Type 2: Solving for Your Information
Other than the few set-up word questions you’ll see, the rest of your ACT word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of ACT math topics, including averages, single variable equations, and probabilities, among others. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
This question is a rare example of a time in which not every piece of given information is needed to solve the problem. For most ACT word questions, all your given information will come into play at some point, but this is not the case here (though you can use all of your information, should you so choose).
For example, we are told that 25% of a given set of jelly beans are red. 25% translates to $1/4$ because 25% is the same as $25/100$ (or $1/4$). If we are being asked to find how many jelly beans are NOT red, then we know it would be $3/4$ because 100% is the same as 1, and 1 — $1/4$ = $3/4$.
So we didn’t need to know that there were 400 jellybeans to know that our final answer is H, $3/4$.
Alternatively, we could use all of our given information and find 25% of 400 in order to find the remaining jelly beans.
$400 * {1/4}$ or $400/4$
$100$
If 100 jellybeans are red, then 400 — 100 = 300 jelly beans are NOT red. This means that the not-red jelly beans make up,
$300/400$
$3/4$ of the total number of jelly beans.
Again, our final answer is H, $3/4$
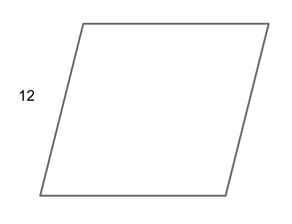
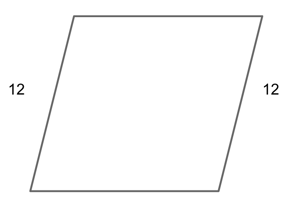
You might also be given a geometry problem as a word problem, which may or may not be set up with a scenario as well.
Geometry questions will be presented as word problems typically because the test-makers felt the problem would be too easy to solve had you been given a diagram.
The test-makers didn’t give us a diagram, so let’s make ourselves one and fill it in with what we know so far.
We know from our studies of parallelograms that opposite side pairs will be equal, so we know that the opposite side of our given will also be 12.
Now we can use this information to subtract from our total perimeter.
$72 — 12 — 12$
$48$
Again, opposite sides will be equal and we know that the sum of the two remaining sides will be 48. This means that each remaining side will be:
$48/2$
$24$
Now we have four sides in the pairings of 12 and 24.
Our final answer is C, 12, 12, 24, 24.
Now, how do we put our knowledge to its best effect? Let’s take a look.
ACT Math Strategies for Your Word Problems
Though you’ll see word problems on a myriad of different types of ACT math topics, there are still a few techniques you can apply to solve your word problems as a whole.
#1: Draw It Out
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what, exactly, you’re working with. For instance, let’s look at how a picture can help you solve a ratio/division problem:
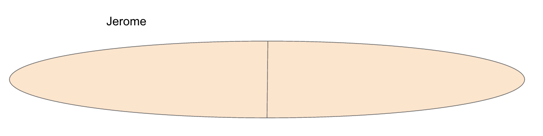
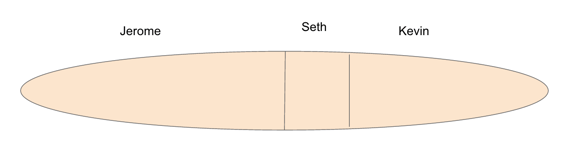
Let’s start by first drawing our sandwich and Jerome’s portion of it.
Now let’s divvy off Kevin’s portion and, by the remainder, Seth’s as well.
By seeing the problem visually, we can see that the ratio of Jerome’s share, to Kevin’s, to Seth’s will go in descending order of size. This let’s us eliminate answer choices A, B, and C, and leaves us with answer choices D and E.
Just by drawing it out and using process of elimination, and without knowing anything else about ratios, we have a 50-50 shot of guessing the right answer. And, again, without knowing anything else about fractions or ratios, we can make an educated guess between the two options. Since Jerome’s share doesn’t look twice as large as Kevin’s, our answer is probably not E.
This leaves us with our final answer D, 3:2:1.
[Note: for a breakdown on how to solve this problem using fractions and ratios instead of using a diagram and educated guessing, check out our guide to ACT fractions and ratios.]
As for geometry problems, remember—you’re often given a word problem as a word problem because it would be too simple to solve had you had a diagram to work with from the get-go. So take back the advantage and draw the picture yourself. Even a quick and dirty sketch can help you visualize the problem much easier than you can in your head and help keep all your information clear.
#2: Memorize Important Terms
If you’re not used to translating English words into mathematical equations, then ACT word problems can sound like so much nonsense and leave you floundering to set up the proper equation. Look to the chart and learn how to translate your keywords into their math equivalents. Doing so will help you to understand exactly what the problem is asking you to find.
There are free ACT math questions available online, so memorize your terms and then practice on real ACT word problems to make sure you’ve got your definitions down and can apply them to real problems.
#3: Underline and Write Out the Key Information
The key to solving a word problem is bringing together all the relevant pieces of given information and putting them in the right places. Make sure you write out all your givens on the diagram you’ve drawn (if the problem calls for a diagram) and that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline them in the problem and then write them out yourself before you set up your equation, so take a moment to perform this step.
#4: Pay Close Attention to Exactly What Is Being Asked of You
Little is more frustrating than solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of $x$ or $x + y$? Better to make sure before you start what you’re supposed to find than realize two minutes down the line that you have to solve the problem all over again.
#5: Brush Up on Any Specific Math Topic in Which You Feel Weak
You are likely to see both diagram/equation problems and word problems for any given ACT math topic on the test. Many of the topics can swing either way, which is why there are so many different types of word problems and why you’ll need to know the ins and outs of any particular math topic in order to solve its corresponding word problem. For example, if you don’t know how to properly set up a system of equations problem, you will have a difficult time of it when presented with a word problem on the topic.
So understand that solving a word problem is a two-step process: it requires you to both understand how word problems themselves work and to understand the math topic in question. If you have any areas of mathematical weakness, now is a good time to brush up on them, or else the word problem might be trickier than you were expecting.
All set? Time to shine!
Test Your Knowledge
Now to put your word problem know-how to the test with real ACT math problems.
Answers: K, C, A, E
Answer Explanations:
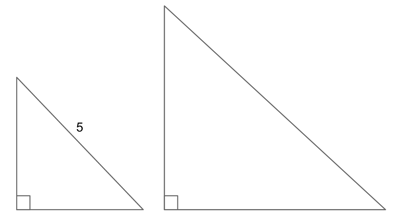
1) First, let us make a sketch of what we have, just so we can keep our measurements straight. We know we have two triangles, one smaller than the other, and the hypotenuse of the smaller triangle is 5.
Now our triangles are in a ratio of 2:5, so if the hypotenuse of the smaller triangle is 5, we can find the hypotenuse of the larger triangle by setting them up in a proportion.
$2/5 = 5/x$
$2x = 25$
$x = 12.5$
Our final answer is K, 12.5.
2) Because we are dealing with a hypothetical number that is increasing and decreasing based on percentage, we can solve this problem in one of two ways—by using algebra or by plugging in our own numbers.
Solving Method 1: Algebra
If we assign our hypothetical number as $x$, we can say that $x$ is increased by 25% by saying:
$x + 0.25x$
Which gives us:
$1.25x$
Now, we can decrease this value by 20% by saying:
$1.25x — (1.25x * 0.2)$
$1.25x — 0.25x$
This leaves us with:
$1x$ or 100% of our original number.
Our final answer is C, 100%.
Solving Method 2: Plugging in Numbers
Alternatively, we can use the same basic process, but make it a little simpler by using numbers instead of variables.
Let’s say our original number is 100. (Why 100? Why not! Our number can literally be anything and 100 is an easy number to work with.)
So if we need to increase 100 by 25%, we first need to find 25% of 100 and then add that to 100.
$100 + (0.25)100$
$100 + 25$
$125$
Now we need to decrease this value by 20%, so we would say:
$125 — (0.2)125$
$125 — 25$
$100$
We are left with the same number we started with, which means we are left with 100% of the number we started with.
Again, our final answer is C, 100%.
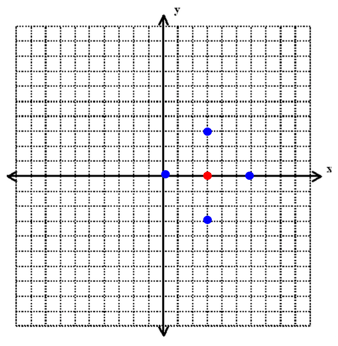
3) Let’s first begin by drawing a picture of our scene. We know that one vertex of the square is at (3, 0), so we can mark it on a coordinate plane.
Now, we are told that each side of the square is 3 cm long. To make life simple, we can start by marking all the possible vertexes attached to our known vertex at (3, 0) straight up, down, and side to side. If no answers match, we can then look to vertexes at different angles.
Our possible vertexes are:
(0, 0), (6, 0), 3, 3) and (3, -3)
One of our possible vertexes is at (6, 0 and this matches one of our answer choices, so we can stop here.
Our final answer is A, (6, 0).
4) We are told that Ms. Lopez throws out the lowest test score and then averages the remaining scores. Because Victor’s scores are already in ascending order, we can throw out the first score of 62.
Now to find the average of the remaining 4 scores, let us add them together and then divide by the number of scores.
$(78 + 83 + 84 + 93)/4$
$338/4$
$84.5$
Our final answer is E, 84.5.

Picture: John Morris/Flickr
The Take-Aways
Word problems comprise a significant portion of the ACT, so it’s a good idea to understand how they work and how to translate the words into a proper equation. But remember that translating your word problems is still only half the battle.
You must also supplement this knowledge of how to solve word problems with a solid understanding of the math topic in question. For example, it won’t do a lot of good if you can translate a probability word problem if you don’t understand exactly how probabilities work. So be sure to not only learn how to approach your word problems, but also hone your focus on any math topics you feel you need to improve upon. You can find links to all of our ACT math topic guides here to help your studies.
What’s Next?
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
When most people hear “word problems,” they often think of the popular example of trains traveling at different speeds, or unrealistic applications of math. However, word problems represent how most people use math in everyday life, and the SAT includes these problems to test students’ ability to reason logically and solve problems.
For many students, the hardest part of a word problem is figuring out exactly what the word problem is asking of you. Not all word problems are created the same though, so we’re going to break down what you need to know so that you feel confident solving them on the SAT.
Types of Math Word Problems on the SAT
You could divide math word problem in a few different ways. You could do it by topic, for example, such as using the SAT subscores as your guide. Or you could do it by the type of solution the problem requires of you. We’re going to focus on the second way, simply because trying to divide word problems by topic would mean we’d have to cover virtually every math topic the SAT covers, which is way more than we could fit in a single post.
Creating an equation or a formula. In these problems, you’ll be given some information about a scenario and asked to come up with an equation or formula that represents that scenario. In fact, looking for the word “represents” in the question might tip you off that you’re dealing with a problem of this type. These are almost exclusively found in the multiple-choice questions, with different equations or formulas listed as the answer choices.
Solving for a value. This is the most common form of word problem. Based on the information in the word problem, you’ll need to come up with at least one specific value that satisfies the requirements of the problem. Examples include finding “how much” or “how many” of something in the problem, or finding minimums and maximum values.
Defining or interpreting. For these problems, you are often asked to interpret what a variable or a constant means in the situation described, or you might be asked what kinds of conclusions can be drawn from a survey. These types of problems often have no “math” involved, and instead ask you to think logically about a situation.
Tip: Being able to identify problems by type on the SAT is a useful prep exercise and can help you on the day you take the test. You may want to use the Math section from a free practice SAT test and circle all of the word problems. Then, read each word problem and assign it to one of the types. Doing this will help you see the commonalities between different types of questions and will allow you to spend less time on the actual test wondering what type of question you’re dealing with!
How to Approach SAT Math Word Problems
For every SAT Math word problem, there are two things to consider. The first is what we discussed above, which is to figure out what type of problem you’re dealing with to best identify what you need to do. Once you know whether you need to provide a definition, write an equation, or solve for a value, you’ve taken the first step.
The next step will be to do the math that you’ve identified you need to do based on the type of word problem. Let’s take a look at each one:
Write an equation/formula. For problems of this type and for problems that ask you to solve for a specific value, you will often need to understand how to “translate” a word problem into an equation, diagram, or graph that you can work with. Luckily, the SAT is very particular about how it uses words in its word problems, so you can always be sure that certain words are meant to relate to specific mathematical concepts. Here are some of the common phrases used by test makers to clue you in to what kind of math you’re looking for:
| Word/phrase | Mathematical meaning/symbol |
| Is, will be, is equal to, is the same as | Equals, = |
| Plus, sum, increased by, added to, received | Addition, + |
| Minus, fewer, difference, decreased by | Subtraction, – |
| Times, product, multiplied by, of | Multiplication, x |
| Divided by, quotient, per, for | Division, ÷ |
| More than, greater than | Inequality, > |
| At least, minimum | Inequality, ≥ |
| Fewer than, less than | Inequality, < |
| At most, maximum | Inequality, ≤ |
| What, how many | Variable, x (or any other letter) |
Solve for a value. With these problems, you might be given an equation as part of your information, but most likely you have to write an equation or formula and solve for the answer. You may benefit from drawing a diagram on some of these questions, especially if the word problem refers to geometric shapes but doesn’t already include one. This can help you visualize the information you’re looking for (the measure of an angle, for example) and help you focus on the right concepts to find the solution.
When translating a word problem into a diagram, make sure you follow the set-up as described in the word problem to the best of your ability, and don’t be fooled by your own diagram. For example, a problem may mention a right triangle, so you draw one. You may end up drawing a diagram that looks like a 45-45-90 triangle, but the problem is actually dealing with a 30-60-90 triangle. By labeling all of the information on your diagram and making a mental note that your drawings aren’t to scale, you can quickly make sense of most problems.
Defining and interpreting. With these types of problems, you often have the equation or formula given to you, and you just need to explain how a part of it works. If you’re not sure, consider whether you’re being asked about a constant or a variable, and eliminate any choices that don’t correspond to the type of value you’re looking at. You can also test the equation with different numbers to see how the value in question influences the equation.
Some problems involve your knowledge of statistical topics, such as understanding how to draw conclusions from surveys, or what factors affect standard deviation. For many of these problems, you’ll need to review these concepts in order to form the correct conclusion.
Examples of SAT Math Word Problems
The following example problems come from the College Board’s free SAT practice tests.
Example of Creating an Equation/Formula
How to solve: We can tell we need to come up with our own formula based on the answer choices and the word “represents” in the problem’s question. We need to find the formula that represents what the original price of a laptop was in terms of p, what Alma paid for it.
Let’s make x the original price of the laptop. In this case, x would be multiplied by .8 to get to the sales price (representing the 20% discount). The sales prices would then be multiplied by 1.08 to account for sales tax. This means that p=(1.08)(0.8)(x). We need to isolate x, so we need to divide both sides by 1.08 and 0.8. That gives us D as the correct answer.
Alternate method: Many problems requiring you to create your own equation are not too difficult, but they can get tricky when there are several steps involved or several variables. You can substitute a number for the variable you’re solving for to find the solution that way. For example, you can set $100 to be the original price of the laptop. Multiply it by .8 to find the sales price, and then by 1.08 to find the price that Alma paid. Then plug the price Alma paid into the answer choices to find the correct answer.
Example of Solving for a Value
How to solve: The word “maximum” tips us off that we are looking for a specific value and that we’ll be dealing with an inequality (see above). Given the information in the problem, we can write this inequality to start: (weight of driver) + (weight of truck) + (14x, or the weight of the boxes) ≤ 6000.
Because we’re told that the weight of the driver and the truck equals 4,500, we can replace that part of the equation: 4500 + 14x ≤ 6000. Now, all we need to do is solve for x. Subtract 4500 from both sides to get 14x ≤ 1500. Then divide both sides by 14 to get x ≤ 107.14… The answer is thus 107.
Note: Pay close attention to how you need to round when working with inequalities. Although this particular decimal probably wouldn’t have made you think to round up, if the result of the division had been 107.9999 you should still round down in this case because the number you’re looking for needs to be less than that value.
Example of Defining/Interpreting
How to solve: Again, the use of the word “interpretation” lets us know what type of problem we’re dealing with. In this case, 12 is a coefficient for the variables n and h, which are the number of landscapers and the number of hours respectively. We can thus rule out choices B and D, since those answers define 12 as a constant in place of these variables.
Since this equation is used to calculate the price of a job, we can be sure 12 represents a dollar amount as reflected in choices A and C. To figure out how things are affected, we can substitute simple numbers for n and h. When both are equal to 1 (there is one landscaper who works for one hour), then 12nh=12(1)(1)=12. When we increase both of these numbers to two, then 12nh=12(2)(2)=48. We can thus rule out C, because the price increased by more than 12 when we added another hour. Choice A is the best interpretation.
How to solve: This is an interpretation problem dealing with statistical concepts rather than interpreting an equation. To be able to “solve” you’d need to know what factors contribute to a reliable conclusion and see what was missing from this survey set-up. In this case, the correct answer is D.
In order for reliable conclusions to be drawn, a sample must be selected at random from the population to ensure that the sample is representative of the population, which in this case is the entire town. By choosing people at the same restaurant on one day, the researcher is possibly biasing their results by narrowing their sample to “people who like this one restaurant.” Because the sample is not representative, choice D identifies the factor that makes the conclusion unreliable. The other choices are factors that, given what we know from the problem, don’t negatively impact the conclusion.
SAT Math Word Problems Tips
As you may have noticed in the last example, you’ll still need to be familiar with math concepts and understand how they might show up in different situations to really feel confident taking any problem on. Here are a couple of other tips worth mentioning:
For most problems, there is more than one way to solve it. We showed this with the first example, where we provided an alternate method for solving a problem. If you find yourself stumped on a problem (we’ve all been there!), then move on to other problems and return to the one that tripped you up later. You may find that you see what you need to do more clearly.
Read carefully. The SAT test makers put a lot of care into how they write math word problems. Be sure to carefully read the question so that you don’t misread something and solve for the wrong thing. (The test makers may even include the answers that result from these common misreadings in the choices!). It’s difficult to read a question correctly once you’ve misread it. If you’re a fast reader who tends to skip over things, try mouthing the words silently as you read. It will force you to slow down just enough that you won’t miss anything, but not so much that you won’t have time to finish the test.
In general, preparing for the SAT Math section requires a multi-faceted approach. You need to be able to identify the types of questions you’re dealing with, know mathematical concepts and how to use them, and deal with other testing issues like rushing through the end or dealing with test anxiety. To help you get started, check out our free SAT Guide that includes 8 of our best test prep tips!
For more information about preparing for the SAT, check out these posts below:
30 SAT Math Formulas You Need to Know
25 Tips and Tricks for the SAT
5 Common SAT Math Mistakes to Avoid
Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!
We explain what a word problem is and give examples of the types of word problems your child might be challenged with in each primary-school maths year group, from Year 1 to Year 6.
What is a word problem?
A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation.
Word problems are seen as a crucial part of learning in the primary curriculum, because they require children to apply their knowledge of various different concepts to ‘real-life’ scenarios.
Word problems also help children to familiarise themselves with mathematical language (vocabulary like fewer, altogether, difference, more, share, multiply, subtract, equal, reduced, etc.).
Teachers tend to try and include word problems in their maths lessons at least twice a week.
What is RUCSAC?
In the classroom children might be taught the acronym RUCSAC (Read, Understand, Choose, Solve, Answer, Check) to help them complete word problems.
By following the acronym step by step children learn to apply a structured, analytical strategy to their calculations. They will need to understand what the problem is asking them to find out by reading the question carefully, choosing the correct mathematical operation to help them solve the query and finally checking their answer by using the inverse operation.
Word problem examples for Years 1 to 6
The following are example word problems that apply to each primary year group.
Year 1
In Year 1 a child would usually been given apparatus to help them with a problem (counters, plastic coins, number cards, number lines or picture cards).
Sarah wants to buy a teddy bear costing 30p. How many 10p coins will she need?
Brian has 3 sweets. Tom has double this number of sweets. How many sweets does Tom have?
Year 2
In Year 2, children continue to use apparatus to help them with problem-solving.
Faye has 12 marbles. Her friend Louise has 9 marbles. How many marbles do they both have altogether?
Three children are each given 5 teddy bears. How many teddy bears do they have altogether?
Year 3
In Year 3, some children may use apparatus, but on the whole children will tend to work out word problems without physical aids. Teachers will usually demonstrate written methods for the four operations (addition, subtraction, multiplication and division) to support children in their working out of the problems.
A jumper costs £23. How much will 4 jumpers cost?
Sarah has 24 balloons. She gives a quarter of them away to her friend. How many balloons does she give away?
Children will also start to do two-step problems in Year 3. This is a problem where finding the answer requires two separate calculations, for example:
I have £34. I am given another £26. I divide this money equally into four different bank accounts. How much money do I put in each bank account?
- In this case, the first step would be to add £34 and £26 to make £60.
- The second step would be to divide £60 by 4 to make £15.
Year 4
Children should feel confident in an efficient written method for each operation at this stage. They will continue to be given a variety of problems and have to work out which operation and method is appropriate for each. They will also be given two-step problems.
I have 98 marbles. I share them equally between 6 friends. How many marbles does each friend get? How many marbles are left over?
Year 5
Children will continue to do one-step and two-step problems. They will start to carry out problem-solving involving decimals.
My chest of drawers is 80cm wide and my table is 1.3m wide. How much wall space do they take up when put side by side?
There are 24 floors of a car park. Each floor has room for 45 cars. How many cars can the car park fit altogether?
Year 6
In Year 6 children solve ‘multi-step problems’ and problems involving fractions, decimals and percentages.
Sarah sees the same jumper in two different sales:
In the first sale, the original price of the jumper is £36.15, but has been reduced by a third.
In the second sale, the jumper was priced at £45, but now has 40% off.
How much does each jumper cost and which one is the cheapest?
In the past, calculators were sometimes used for solving two-step problems like the one above, but the new curriculum does not include the use of calculators at any time during primary school.
We recommend reading any word problem at least three times. By the conclusion of the third reading, you should be magically whisked away to your home in Kansas.
Read it once…
…to get a general idea of what’s going on. Is the problem about money? Height and width? Distances? Money? Yeah, we already said money, but it’s important. Can you draw a picture in the margin that helps you visualize the problem?
Twice…
…to translate from English into math. Read the problem carefully this time, figuring out which pieces of information are important and which ones aren’t. Then ignore the unnecessary bits. This may sound a bit harsh, but they’re big boys. They’ll get over it.
Three times…
…a lady. Wait, that’s not it.
…to make sure you answered the right question. To be sure, read the question one last time before drawing a box around your final answer. Even if this method of double-checking saves you only once out of every 100 times, it’ll help you in the long run. One out of 100 is better than zero out of 100, but now we’re moving into some advanced mathematics.
Sample Problem
The local department store was having a sale. Holla! Gabe bought a pair of shoes for $21, although they would’ve been cheaper if he’d bought penny loafers. He also bought some shirts that were on sale for 25% off their normal retail price of $18 each. Gabe, always the bargain hunter, spent $75 total. How many shirts did he buy? Also, does he really think any of them will go with those shoes?
Read the problem:
Once…
…for a general idea of what’s going on: Gabe went shopping and spent money. Sounds like an old familiar story. Time for an intervention, friends of Gabe. Preferably before he maxes out his Diner’s Club card.
Now we need to figure out how many shirts he bought, so we read the problem:
Twice…
…to translate from English into math. Remember, we can translate a bit at a time, sort of like how Gabe pays for some of his major purchases when he has them on layaway. Sheesh, Gabe. Get a hold of yourself.
(total amount Gabe spent) = (amount he spent on shoes) + (amount he spent on shirts)
We know he spent $75 total, of which $21 was spent on shoes. This gives us the equation:
$75 = 21 + (amount he spent on shirts)
The problem has gotten smaller. It’s depressing when that happens with cake, but great when it happens to a word problem. Now all we need to do is come up with a symbolic expression for how much Gabe spent on shirts, or the cost per shirt times the number of shirts:
(amount he spent on shirts) = (cost per shirt)(number of shirts)
Since the shirts are 25% off their normal price of $18, they cost $18 – 0.25(18) = $13.50 each. What a deal, and real polyester, too!
We need to introduce a variable for the number of shirts; s will do the trick nicely.
(amount he spent on shirts) = 13.5s
When we plug this into the earlier equation, we find that:
75 = 21 + 13.5s
Finally, we’ve reduced this thing to a super-simple-looking equation! Good riddance, vestiges of language! Begone, nouns and verbs!
Things look much nicer now, right? No worrying about shirts or shoes or prices or Gabe’s uncontrollable shopping addiction. For the moment, we can forget about the word problem and solve the equation. The answer is s = 4, by the way. In case you were interested.
Three times…
…to make sure we’re answering the right question. We want to know how many shirts Gabe bought. Is that the answer we arrived at? We found that s = 4, and s was the number of shirts Gabe bought, so we’re all done. Four new shirts for Gabe, and three of them feature a Hawaiian pattern. Gabe, if you insist on buying far more clothes than you need, can’t you at least have a decent fashion sense?
When translating from English into math, some information can be ignored. We don’t care that «the local department store was having a sale.» Gabe might, but we certainly don’t. We care about statements that tell us numbers, and statements that tell us what the question is. Any extraneous information has been placed there simply as a decoy. We’re not going to fall for that. Wait a second…two for one? We’ll grab our jacket and meet you there.
Some people find it helpful to underline the important pieces of information in a word problem. You’re like an actor highlighting in a script the lines that are important for him to remember. Unlike an actor, however, you can always look back at the original problem if you draw a blank. Also, you don’t need to wear any stage makeup.
In the problem we just did, the important bits might look something like this:
The local department store was having a sale. Gabe bought a pair of shoes for $21 and some shirts that were on sale for 25% off their normal retail price of $18 each. If Gabe spent $75 total, how many shirts did he buy?
As you practice, you’ll become better at figuring out which parts of the word problem you can ignore and which parts are important.