Алгоритмы которые использует excel - Word и Excel - помощь в работе с программами

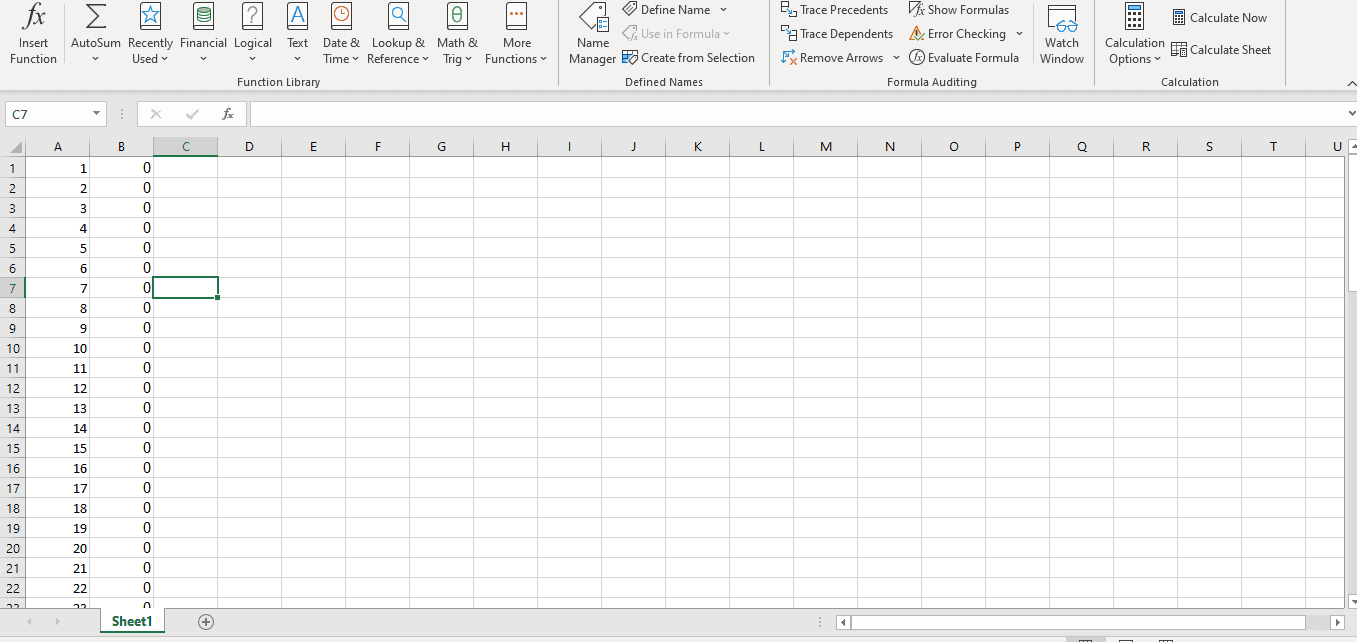
Линейные алгоритмы в MS Excel

В рамках табличного процессора MS Excel возможна реализация линейных алгоритмов, главным назначением которых является вычисление функций зависящих от одного и более параметра. Для реализации линейного алгоритма в раках MS Excel используются формулы, записанные в рамках синтаксиса программы.

Формулы – это математические выражения, записанные в ячейки листа MS Excel используя стандартный для него синтаксис в рамках которых выполняется вычисления. В MS Excel формулы начинаются со знака равенства (=). Например, формула вычисления разницы меду 10 и отношением 12 к 3 имеет вид «=10-12/3». Формула может содержать такие элементы, как: функция, ссылка, оператор, контакта.

Функция – это стандартная формула, которая возвращает результат выполнения определенных действий над значениями, выступающими в качестве аргументов. Например, функция COS(ЧИСЛО) – возвращает косинус от заданного числа. Использование функции позволяет упростить линейное выражение в ячейках листа, что значительно уменьшает длину формул.

Константа – это постоянное (не вычисляемое) значение. Например, число 2 или текст «Сумма» являются константами. Выражение или результаты вычисления заданного выражения константами не являются, контактна может быть прописана в отдельной ячейке листа MS Excel.

Основные функции, которые могут понадобиться при выполнении практических заданий в MS Excel при изучении дисциплины, представлены в таблице 1.

Основные функции MS Excel

Функция	Результат выполнения функции	Пример
ABS(число)	Модуль числа или модуль от результата вычисления выражения, записанного в качестве аргумента функции	= ABS(-2) функция вернет значение 2 = ABS(10-3*2) функция вернет значение 4
ПИ()	Возвращает число 3,14159265358979, которое является математической константой π с точностью до 15 цифр.	= ПИ() функция вернет значение 3,14159265358979
COS(число)	Возвращает косинус заданного числа или косинус от результата вычисления выражения, записанного в качестве аргумента функции. Считается, что аргументом функции является угол в радианах.	= COS(0) функция вернет значение 1 = COS(ПИ()) функция вернет значение -1
SIN(число)	Возвращает синус заданного числа или синус от результата вычисления выражения, записанного в качестве аргумента функции. Считается, что аргументом функции является угол в радианах.	= SIN(0) функция вернет значение 0 = SIN(ПИ()/2) функция вернет значение 1
TAN(число)	Возвращает тангенс заданного числа или тангенс от результата вычисления выражения, записанного в качестве аргумента функции. Считается, что аргументом функции является угол в радианах.	= TAN(0) функция вернет значение 0 = TAN(ПИ()/4) функция вернет значение 1
EXP(число)	Возвращает значение «e», возведенное в степень, которая записана в аргументе функции как число или выражение.	= EXP(0) функция вернет значение 1 = EXP(1) функция вернет значение числа «е» приблизительно 2,71828
LN(число)	Возвращает натуральный логарифм числа или натуральный логарифм от результата вычисления выражения, записанного в качестве аргумента функции. Аргумент функции должен быть положительным вещественным числом.	=LN(EXP(1)) функция вернет значение 1 =LN(3) функция вернет значение натурального логарифма от 3 (1,098612)
КОРЕНЬ(число)	Возвращает положительное значение квадратного корня числа или выражения, записанного в качестве аргумента функции. Аргумент функции должен быть больше 0.	=КОРЕНЬ(4) функция вернет значение 2 =КОРЕНЬ(16+ABS(-9)) функция вернет значение 5

В таблице 1 приведен далеко не полный список математических и тригонометрических функций, являющихся стандартными для MS Excel. Более подробную информацию о функциях можно получить в справке программы.

В формулах используются простые математические операции:

Сложение в MS Excel – «+», пример «=В3+143» (складывает значение ячейки B3 и число 143).

Вычитание в MS Excel – «-», пример «=B3-143» (вычитает из значения ячейки B3 и число 143).

Умножение в MS Excel – «*», пример «=B3*143» (умножает значение ячейки B3 на число 143).

Деление в MS Excel – «/», пример «=B3/143» (делит значение ячейки B3 на число 143).

Возведение в степень в MS Excel – «^»,«=B3^143» (возводит значение ячейки B3 в степень 143).

Пример реализации линейного алгоритма в MS Excel

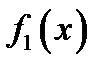
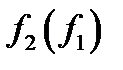
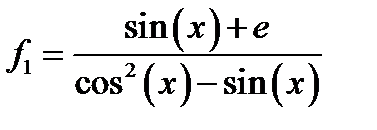
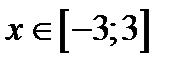
Рассмотрим на примере реализацию линейного алгоритма в MS Excel: необходимо рассчитать по формулам величину значений функций и : , , отрезок разбивает с шагом 0,5.

Реализация линейного алгоритма в MS Excel:

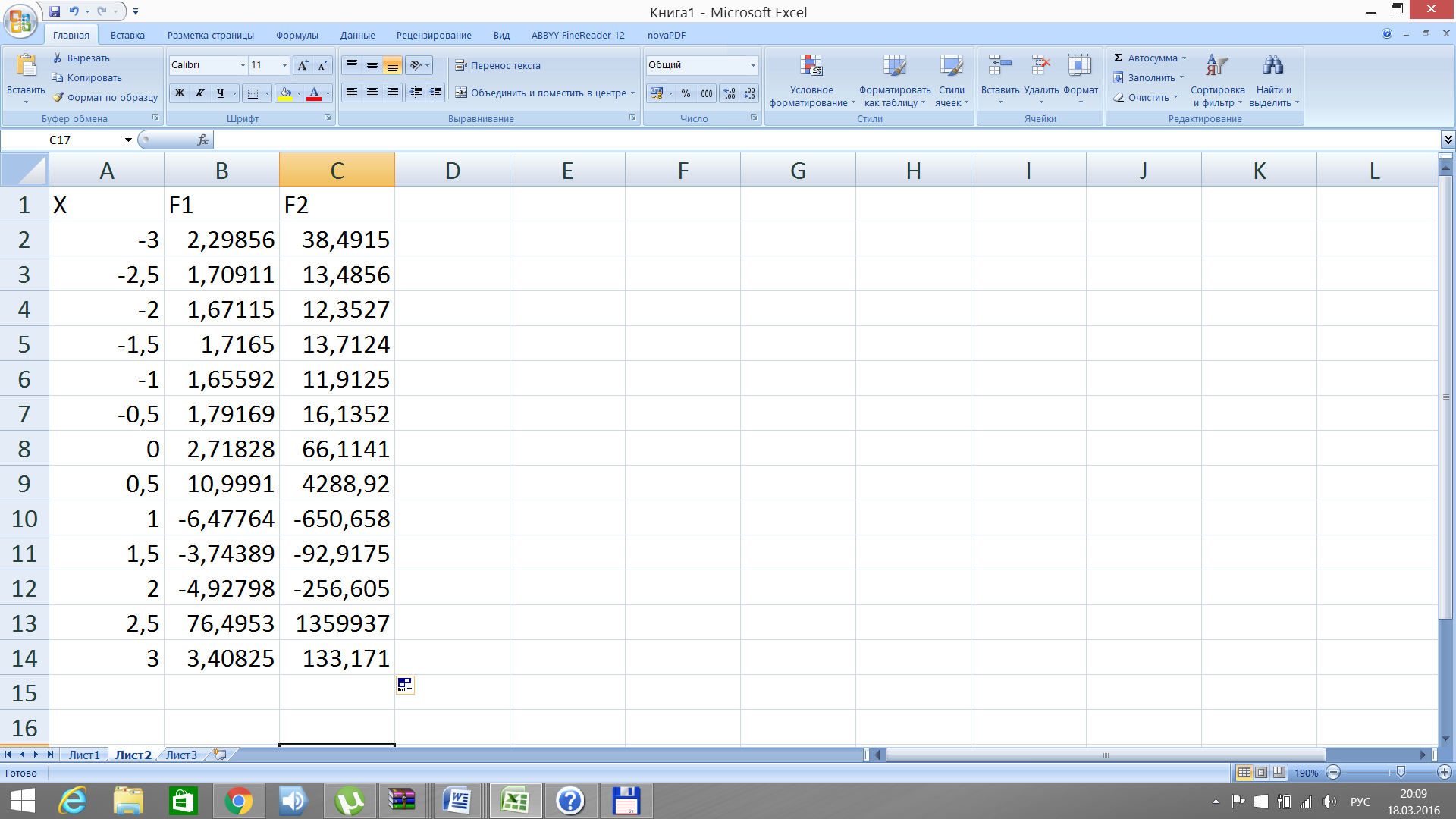
1. Создадим на листе 1 в ячейках А1, B1, C1 заголовок таблицы данных для реализации линейного алгоритма X, F1, F2 соответственно (рис. 3).

2. Заполним столбец А значениями аргумента функции X с шагом 0,5 (рис. 3) начиная с ячейки A2.

Рис. 3. Структура линейного алгоритма в MS Excel

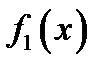
3. Запишем выражение используя синтаксис MS Excel в ячейке В2. Для формулы выражения записанного в В2 аргументом x является значение, записанное в ячейке A2. Выражение в ячейке В2 имеет вид (рис. 4): =(SIN(A2)+EXP(1))/(COS(A2)^2-SIN(A2)).

Рис. 4. Вычисление

После записи формулы выражения 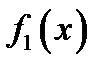в ячейке В2, нажимаем Enter и растягиваем формулу на весь диапазон аргумента x.

4. Запишем выражение используя синтаксис MS Excel в ячейке С2. Для формулы выражения записанного в С2 аргументом является значение, вчисленное в ячейке В2. Выражение в ячейке С2 имеет вид (рис. 5): =3*(B2^3+B2^2-2*B2).

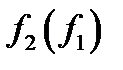
Рис. 5. Вычисление

После записи формулы выражения 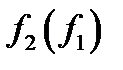в ячейке C2, нажимаем Enter и растягиваем формулу на весь диапазон аргумента x.

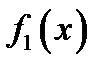
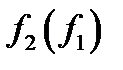
После завершения реализации линейного алгоритма о вычислении двух функций и структура вычисления линейного алгоритма имеет вид представленный на рис. 6.

Рис. 6. Результат реализации линейного алгоритма

Рассмотренный выше пример, является примером реализации части задания № 1 самостоятельной работы, в рамках задания 1 еще необходимо построить и отформатировать диаграммы, что будет рассмотрено в разделе 4 (см. раздел 4, Построение простой точечной диаграммы в MS Excel).

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Источник

РЕАЛИЗАЦИЯ АЛГОРИТМОВ С ПОМОЩЬЮ МАКРОСОВ В EXCEL

Цель работы: получить практические навыки разработки функций для реализации линейных, разветвляющихся и простейших циклических алгоритмов с помощью макросов в Excel.

Теоретические сведения

Реализация линейных и разветвляющихся алгоритмов

В Visual Basic for Application для задания значения переменной используется оператор присваивания. Этот оператор имеет следующий вид:

Выражение может быть арифметическим, текстовым или логическим.

Для записи выражений используются арифметические, текстовые и логические операции (операторы).

Арифметические операторы служат для выполнения арифметических действий над числами (таблица 16.1).

Таблица 16.1 ‑ Арифметические операторы

Арифметический оператор	Действие	Пример
+ (знак плюс)	Сложение	3+3
– (знак минус)	Вычитание Унарный минус	3–1 –1
* (звездочка)	Умножение	3*3
/ (косая черта) (обратная черта)	Деление Целочисленное деление	5/8 (результат 0.625) 58 (результат 0)
% (знак процента)	Процент	20%
^ (крышка)	Возведение в степень	3^2 (аналогично 3*3)

Для объединения нескольких текстовых строк в единую последовательность букв служит текстовый оператор &. Например, выражение «Энергетический » & «факультет» эквивалентно записи «Энергетический факультет».

Для записи разветвляющихсяалгоритмов используется оператор If(Если), который имеет две формы записи.

1. Однострочная запись:

Ifусловие Then [оператор]

If условие Then [оператор 1] [Elseоператор 2]

2. Многострочная запись:

If условие Then

End If

В однострочном операторе условие и выполняемые при соблюдении условия действия располагаются в одной строке. В том случае, если при выполнении условия требуется выполнение блока операторов, используется многострочный оператор.

После имени конструкции If должно следовать логическое выражение, содержащее условие. Для создания сложных условий используются логические операции And (И) и Or (Или). В качестве условия могут выступать следующие логические выражения: сравнение переменной с другой переменной, константой или функцией; любая переменная; выражение; поле базы данных; функция, принимающие значения True (Истина) или False (Ложь).

Конструкция If…Then (Тогда)…Else (Также)аналогична конструкции If. Then, но позволяет задать действия, исполняемые как при выполнении условий, так и в случае их невыполнения.

Команда Ifможет проверить только одно условие. Если требуется осуществить переход управления в зависимости от результатов проверки нескольких условий, то дополнительное условие можно задать с помощью оператора Else If (Также Если). Оно будет анализироваться только в том случае, если предыдущее условие ложно.

Ключевое слово End If обозначает конец многострочной конструкции и его наличие в команде в этом случае обязательно. Если указанное условие выполняется, то есть результат проверки равен True (Истина), то выполняются операторы, следующие за ключевым словом Then. Если условие не выполняется, то Visual Basic переходит к выполнению операторов, следующих за указанным оператором.

В качестве примера приведем функцию определения корней квадратного уравнения:

Function Корни(a, b, c)

d = b ^ 2 — 4 * a * c

x1 = (-b + d ^ (1 / 2)) / (2 * a)

x2 = (-b — d ^ (1 / 2)) / (2 * a)

Корни = «x1=» + str(x1) + «; x2=» + str(x2)

Корни = «корней нет»

Конструкция Select Сase позволяет обрабатывать в программе несколько условий и аналогична блоку конструкций If…Then…Else. Эта конструкция состоит из анализируемого выражения и набора операторов Case (в случае) на каждое возможное значение выражения. Работает эта конструкция следующим образом. Сначала вычисляется значение заданного в конструкции выражения. Затем полученное значение сравнивается со значениями, задаваемыми в операторах Сase конструкции. Если найдено искомое значение, выполняются команды, приписанные данному оператору Case. После завершения выполнения конструкций управление будет передано конструкции, следующей за ключевым словом End Select. Запись конструкции Select Case следующая:

Select Case сравниваемое значение

CASE значение 1

CASE значение 2

End Select

В начале конструкции расположены ключевые слова Select Case, указывающие, что расположенный рядом с ними параметр “сравниваемое значение” будет проверяться на несколько значений. Далее следуют группы команд, начинающиеся с ключевого слова Case. Если параметр “сравниваемое значение” равен значению, указанному в текущем операторе Case, то будут выполняться команды, расположенные между этим и следующим ключевым словом Case.

В качестве примера воспользуемся конструкцией Select Case для выбора удельного активного сопротивления и расчета полного активного сопротивления R в зависимости от заданной марки провода воздушной линии электропередачи:

Источник

Реализацию алгоритма вычислительной задачи в
электронных таблицах Excel возможно, так как они
выполняют необходимые требования, предъявляемые
к среде реализации алгоритма [Глущенко Ю. В.
Обоснование использования языка
программирования в учебном процессе (в печати)].

Для реализации вычислительных алгоритмов
необходимо уметь реализовывать базовые
структуры алгоритмов. На примерах задач,
приводящих к базовым структурам, разберемся с
реализацией вычислительного процесса базовых
структур в электронных таблицах. Можно
предложить следующий алгоритм:

Составление спецификаций переменных заданного
алгоритма в виде таблицы, в столбцах которой
будут Имя переменной в алгоритме, назначение,
тип, диапазон, адрес в Excel, вид реализации.
Разработка таблиц ВводаИнформации.
Разработка таблицы подзадачи
ОбработкаИнформации.
Разработка таблицы ВыводаРезультата.
Тестирование построенных таблиц.

Линейные алгоритмы

ЗАДАЧА. Задан алгоритм в виде:

НАЧАЛО_АЛГОРИТМА

Ввести значения сторон треугольника а, в, с.
Вычислить значение полупериметра р = (а+в+с)/2
Вычислить площадь треугольника S=(p*(p-а)*(р-в)*(р-с)).
Вывести значение S.

КОНЕЦ_АЛГОРИТМА

Реализовать вычисления по заданному алгоритму
в Excel.

РЕШЕНИЕ.

1. Спецификация переменных исходного
алгоритма:

№ п/п.	Имя перем. в алгоритме	Назначение	Тип	Диапазон	Адрес	Вид реализации
Переменные входного потока
1	А	Сторона тр-ка	Вещ	0, +	B3	<число>
2	В	Сторона тр-ка	Вещ	0, +	B4	<число>
3	С	Сторона тр-ка	Вещ	0, +	В5	<число>
Переменные блока обработки информации
4	Р	полупериметр	Вещ	0, +	Е3	<формула>
5	S	Площадь тр-ка	Вещ	0, +	Е4	<формула>
Переменные выходного потока.
6	S	Площадь тр-ка	Вещ	0, +	Н3	<формула>

2. Разработка таблицы ВводаИнформации

Таблица ВводаИнформации должна содержать
значения переменных входного потока. Ее
реализация показана на Рис. 1.

3. Разработка таблицы подзадачи
ОбработкаИнформации

В данной таблице необходимо провести
вычисления полупериметра и площади. Оба эти
параметра вводятся с помощью формул в
соответствующие ячейки. Реализация данной
таблицы приведено на Рис. 1.

4. Разработка таблицы ВыводаРезультатов

Таблица ВыводаРезультатов должна содержать
значения переменных выходного потока. Ее
реализация показана на Рис. 1.

5. Тестирование разработанных таблиц

Для тестирования полученных таблиц строим
таблицу теста по следующему шаблону:

№ п/п.	Имя	Назначение	Значение/результат
1	А	Входной поток	1	3	1
2	В	1	4	1
3	С	4	5	2
4	Р	Промежуточные	3	6	2
5	S	Выходной поток	Ошибка	6	0

ЗАДАЧА РЕШЕНА.

Задачи для самостоятельной работы можно найти
в Приложении 1.

Алгоритм ветвления

ЗАДАЧА. Задан алгоритм в виде:

НАЧАЛО_АЛГОРИТМА

Ввести значение переменной Х.
ЕСЛИ Х не больше 0,
ТО Y:=Х*Х, ИНАЧЕ Y:=Х+1.
Вывести значение переменной Y.

КОНЕЦ_АЛГОРИТМА

Реализовать вычисления по заданному алгоритму
в Excel.

РЕШЕНИЕ.

1. Спецификация переменных исходного
алгоритма:

2. Разработка таблицы ВводаИнформации

Таблица ВводаИнформации должна содержать
значения переменных входного потока. В нашем
случае значение X. Ее реализация показана на Рис. 2.

3, 4. Разработка таблицы подзадачи
ОбработкаИнформации.

В данной задаче можно (и нужно) объединить
задачи ОбработкиИнфориации и ВыводаРезультатов,
построив только таблицу ВыводаРезультатов. Ее
реализация показана на Рис. 2.

5. Тестирование разработанной таблицы.

Для тестирования полученной таблицы
необходимо взять минимум три значения Х:

слева от ветвления,
в точке ветвления,
справа от точки ветвления.

Значения берутся так, чтобы просто было
проверить результат. Поэтому построим таблицу
тестирования в виде:

Имя переменной	ЗНАЧЕНИЕ/РЕЗУЛЬТАТ
Слева от точки ветвления	В точке ветвления	Справа от точки ветвления
X	-5	0	2
Y	25	0	3

ЗАДАЧА РЕШЕНА.

Задачи для самостоятельной работы можно найти
в Приложении 2.

Циклические алгоритмы

ЗАДАЧА. Задан алгоритм в виде:

НАЧАЛО_АЛГОРИТМА

Ввести значение целочисленной переменной
1<=N<=10.
S:= 0 {Начальное значение
сумматора равно нулю}.
I:= 0 {Начальное
значение индекса цикла равно нулю}.
I:=I+1 {Текущее значение индекса
цикла}.
S:=S+I
{накопление
суммы}.
ЕСЛИ N>I то идти на п.4
{конец цикла с постусловием}
Вывести значение
S
{Вывод результата}.

КОНЕЦ_АЛГОРИТМА

Реализовать вычисления по заданному алгоритму
в Excel.

РЕШЕНИЕ.

1. Спецификация переменных исходного
алгоритма:

№ п/п.	Имя переменной в алгоритме.	Назначение	Тип	Диапазон	Адрес	Реализация
Переменные входного потока
1	N	ПВхП	ц	1..10	B3	<число>
Индекс цикла
1	i	индекс	ц	1..N	А10:A50	<массив>
5	S	ПВхдП	ц	<=55	B10:B50	<формула>
Переменные выходного потока.
5	S	ПВхдП	ц	<=55	Е3	<формула>

2. Разработка таблицы ВводаИнформации

Таблица ВводаИнформации должна содержать
значения переменных входного потока. В нашем
случае значение N. Ее реализация показана на Рис. 3.

3. Разработка таблицы подзадачи
ОбработкаИнформации

Реализация обработки информации возможна лишь
с использованием циклического алгоритма.
В случае с Excel данную задачу необходимо разбить
на три:

Построение столбца индексов цикла.
Построение столбца элементов массива.

ЗАДАЧА №1 ПОСТРОЕНИЕ СТОЛБЦА ИНДЕКСА ЦИКЛА.

Данную задачу сформулируем в виде:

Построить столбец значений индекса цикла в
интервале [1..N (задано)]. При этом с изменением
значения N в ячейке В3 должно изменяться и
количество значений индекса цикла в расчетной
таблице.
Эта задача решается в столбце А начиная со строки
№10.

Важно отметить, что протяжку можно вести до
любого номера строки лишь бы при всех изменениях
N протяжка формулы захватывала все строки
изменения значения индекса цикла. Необходимо
только помнить, что при протяжке увеличивается
объем файла, то есть чем глубже протянем формулу,
тем большим будет объем полученного файла и,
возможно, медленнее будет работать Excel с этим
файлом.

Рис. 3.

ПЕРВАЯ ЗАДАЧА РЕШЕНА

ЗАДАЧА №2. ПОСТРОЕНИЕ СТОЛБЦА ЭЛЕМЕНТОВ ЦИКЛА.

Здесь под элементом цикла будем понимать
текущее значение S, зависящее от значения индекса
цикла.
Сформулируем задачу в следующем виде:
Для каждого значения индекса цикла определить
текущее значение S.
Столбец В дает нам текущие значения S=f(<индекс
цикла>), при этом протяжка формулы в столбце В
должна быть не меньше протяжки в столбце А.

Рис. 3.

ВТОРАЯ ЗАДАЧА РЕШЕНА.

4. Разработка таблицы подзадачи
ВыводРезультатов

Для решения данной задачи следует понять, что
выходным значением S будет наибольшее из
значений в ячейках В [10…]. Конечное значение
интервала в В определяется протяжкой формул в
задачах №№1, 2. Пусть формулы протянули до строки
№50. Естественно, наибольшим S будет для
наибольшего значения индекса цикла, так как на
каждом шаге прибавляется число большее 1.
Следовательно, в ячейку Е3 необходимо ввести
формулу

Е3 =>[=МАКС(b10:b50)]

Рис. 3.

И если помнить, что значение пустой ячейки Excel
воспринимает как «0», то…

ТРЕТЬЯ ЗАДАЧА РЕШЕНА.

5. Тестирование полученных таблиц

Для тестирования полученной таблицы строим
таблицу теста по следующему шаблону:

№ п/п.	Имя	назначение	Значение/результат
1	N	Вход	1	5	7	9	10
2	S	Выход	1	15	28	45	55

ЗАДАЧА РЕШЕНА.

Задачи для самостоятельной работы можно найти
в Приложении 3.

Источник

Большинство типовых
вычислительных алгоритмов в Excel оформлены
в виде стандартных функций и вызываются
с помощью программы Мастер функций (см.
подразд. 1.9). Самые популярные
из них:

ЕСЛИ() – позволяет
предусмотреть разные варианты заполнения
ячейки;
СУММ(), ПРОИЗВЕД()
– соответственно суммирование и
перемножение значений из одного или
нескольких блоков;
СУММПРОИЗВ() –
суммирование произведений соответствующих
элементов двух или нескольких массивов;
СРЗНАЧ(), СРГЕОМ()
– расчет соответственно среднего
арифметического и геометрического по
числам в заданных блоках;
СЧЕТ() – определение
количества чисел в заданном блоке.

Более сложные
алгоритмы оформлены в виде команд и
заказываются через меню Сервис. Наиболее
важные из них:

Подбор параметра…
– нахождение аргумента, при котором
функция примет нужное значение;
Поиск решения…
– решение систем уравнений и задач
оптимизации;
Пакет анализа –
содержит программы, необходимые при
статистической обработке данных.

Если нужная для
вычислений команда отсутствует в меню,
ее можно установить с помощью команды
Сервис Надстройки…

6.1. Общие сведения о функции если()

Функция ЕСЛИ()
позволяет предусмотреть разные способы
заполнения одной и той же ячейки. То,
каким из них следует воспользоваться
в данный момент, Excel определяет
самостоятельно по тому, выполняется
или нет при введенных данных указанное
в функции условие. Стандартный формат
функции имеет следующий вид:

ЕСЛИ(Логическое_выражение;
Значение_если_истина;Значение_если_ложь)

Здесь:

Логическое_выражение
– это условие, которое при одних
значениях введенных данных выполняется,
при других – нет;
Значение_если_истина
– алгоритм, по которому определяется
значение функции, когда условие
оказывается правильным;
Значение_если_ложь
– алгоритм, по которому определяется
значение функции, когда условие
оказывается неправильным.

В роли алгоритмов,
которые выбирает функция ЕСЛИ(), могут
выступать расчетные выражения, другие
функции, ссылки на ячейки, где находится
нужная информация, текстовые строки и
т. п.

Рассмотрим действие
этой функции на конкретных примерах.

6.2. Выбор из двух вариантов по одному условию

Пример

Поставщик ввел
оптовую скидку на цену для больших
партий товара. Надо составить шаблон
для расчета стоимости любой партии
товара.

Составим таблицу
из констант, необходимых для расчета.
В ячейки А1:А4 введем названия констант:
«ОбъемПартии», «ОптБарьер»,
«РознЦена», «ОптЦена». Присвоим
ячейкам В1:В4 такие же имена (удобно
пользоваться командой Вставка 
Имя 
Создать…). В ячейку С1 введем
текст «СтоимПартииТовара».

Сделаем активной
ячейку С2 и вызовем через Мастер функций
функцию ЕСЛИ(). В окне аргументов в
текстовые поля введем следующие значения:

В поле
«Логическое_выражение:» вводится
условие, по которому Excel будет выбирать
нужный вариант действий. Его можно
составить так:

ОбъемПартии<=ОптБарьер

В поле
«Значение_если_истина:» указывается
способ, по которому следует рассчитывать
функцию, если условие оказалось
правильным при тех данных, которые
введены во влияющие ячейки в данный
момент. Для нашего примера этот аргумент
выглядит следующим образом:

ОбъемПартии*
РознЦена

В поле
«Значение_если_ложь:» указывается,
как рассчитывать функцию, если условие
не выполняется. Для нашего примера
следует ввести

ОбъемПартии*ОптЦена

Расчетный шаблон
готов. Чтобы проверить его, введите
удобные для устных расчетов числа в
ячейки В1:В4 и проверьте, правильно ли
функция ЕСЛИ() выбрала формулу для
заполнения ячейки С2. Введите в В1 другой
объем партии, при котором требуется
использовать другую цену при расчете
стоимости покупки. Если в обоих случаях
получены верные результаты, можно
красиво отформатировать ячейки А1:С4
(см.
подразд. 1.13–1.16) и пользоваться
этим шаблоном, меняя только значения
констант в В1:В4.

Пример

В таблице значений
функции y = 2cos(x
+ 2)e^0,5^xнадо отметить символом «*» строку
с минимальным значением.

Введем в ячейки
А1 и В1 подписи «X» и
«Y», в блок А2:А11 –
значения аргументов, в блок В2:В11 –
формулу расчета функции. Столбец С
зарезервируем для заказанной в условии
метки. В ячейкуD1 введем
текст «минимум», в ячейкеD2
с помощью функции МИН() найдем это
значение в блоке В2:В11.

Выделим ячейку С2
и вызовем через Мастер функций функцию
ЕСЛИ(). Условие, по которому Excel выбирает
нужный вариант действий, составим так:
В2=$D$2. В строку второго
аргумента вводим символ «*» (без
кавычек), в третий – пробел и нажмем
после этого <ОК>. С помощью протяжки
скопируем полученную формулу на блок
С2:С11.

Задание

Посмотрите, какой
вид приняла функция в разных ячейках
этого блока.

Рассмотрим функцию
ЕСЛИ() в той строке, в которой появилась
«*». Значение функции y
в этой строке минимально. Левая и
правая части условия оказались
одинаковыми, т. е. первый аргумент –
правильный. Поэтому для заполнения
своей ячейки функция ЕСЛИ выбрала то,
что указано во втором аргументе. Для
значений функцииув других строках
условие, введенное в функцию ЕСЛИ(),
оказывается неверным, поэтому она
заполняет свои ячейки по варианту
третьего аргумента. В нашем случае это
пробел, который невидим на экране,
поэтому ячейки кажутся пустыми.

Измените аргументы,
введенные в А2:А11. «*» переместилась
в другую строку, хотя формулы в С2:С11 не
были изменены (после изменения данных
каждая функция ЕСЛИ() автоматически
проверила свой первый аргумент заново
и приняла новое управляющее решение,
каким правилом пользоваться для
заполнения своей ячейки).

Задание

В ячейку А1 введите
формулу:

=ЕСЛИ(С3=37;»СЕНО»;»СОЛОМА»)

Определите влияющую
ячейку (команда
Сервис 
Зависимости 
Влияющие ячейки) и введите в
нее такое число, при котором СОЛОМА
превратится в СЕНО.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Время на прочтение
1 мин

Количество просмотров 6.7K

Педагог-новатор Виктор Федорович Шаталов в 70-х годах прошлого века разработал систему обучения с использованием опорных сигналов — взаимосвязанных ключевых слов, условных знаков, рисунков и формул с кратким выводом [1].

Опорным алгоритмом в Excel будем называть набор изображений и алгоритмов (формул), особым образом расположенных на Excel-листе, который помогает активизировать мышление обучающихся.

Приведу пример использования опорного алгоритм в Excel, например, при изучении алгоритма Диффи-Хелмана на занятии по криптографии.

Следуя методике Шаталова последовательность действий такова:

Первый этап. Образно-эмоциональное объяснение учителем материала. Также можно использовать просмотр видео-урока из Академии Хана по основам криптографии:

Второй этап. Сжатое изложение учебного материала с помощью Excel-алгоритма.

Рис. Опорный Excel-алгоритм Диффи-Хелмана

Расшифровка алгоритма:

Имеются два простых числа 13 и 7, которые знают Элис и Боб (и открыт для Ив).
Элис и Боб придумывают два числа — 3 и 10 соответственно.
Далее начинается обмен:
Элис отправляет 5 -> =ОСТАТ(F17^C6;F16)
Боб вычисляет общий ключ 12 -> =ОСТАТ(E5^H6;F16)
Боб отправляет 4 -> =ОСТАТ(F17^H6;F16)
Боб вычисляет общий ключ 12 -> =ОСТАТ(F7^C6;F16)
В итоге они имеют общий ключ 12, который не знает Ив.

Далее… закрепление материала, решение задач, использование программы CrypTool, обмен по сети между обучающимися зашифрованными сообщениями.

Подобные Excel-алгоритмы можно встретить в сети, например, Цезаря, Вижинера, Энигму, однако названия этой методике в педагогике не нашел.

Ссылки:

» ru.wikipedia.org/wiki/Шаталов,_Виктор_Фёдорович
» ru.wikipedia.org/wiki/Протокол_Диффи_—_Хеллмана

Источник

A Бразильский математик по имени Ренато Джанелла говорит, что можно предсказать номера лотереи используя теории вероятностей и сложную математику. Джанелла написала исследование под названием Геометрия шанса: номера лотереи следуют прогнозируемой закономерности. Это исследование предполагает, что не все комбинации чисел имеют одинаковую вероятность выпадения вничью.

Следовательно, можно предсказать шаблоны или комбинации чисел которые имеют больше шансов появиться в розыгрыше лотереи. Но что делать, если вы не разбираетесь в сложной математике? Если вам нужен более простой способ предугадывать номера лотереи, вы можете использовать алгоритмы с использованием Excel. Я покажу вам, как вы можете создать свой документ, чтобы у вас был список чисел, которые имеют больше шансов появиться в розыгрыше.

Содержание

Объяснение алгоритма предсказания лотерейных номеров
Действительно ли работает алгоритм предсказания лотерейного номера?
Как создать формулу алгоритма прогнозирования лотереи с помощью Excel
Определение вероятности лотереи в Excel
Использование двухбарабанных лотерей
Использовать этот готовый алгоритм лотереи Excel Загрузить
Заключительные мысли об алгоритме прогнозирования лото
Часто задаваемые вопросы

Объяснение алгоритма предсказания лотерейных номеров

Алгоритм — это комбинация инструкций которые помогут вам решить сложную задачу. Каждый компьютер использует алгоритмы для работы. Алгоритм предсказания лотереи использует большую комбинацию чисел, чтобы помочь вам выбрать правильный набор чисел.

Вы можете использовать Excel для создания своего алгоритма. Все, что вам нужно сделать, это ввести правильную команду в электронную таблицу Excel, и она проанализирует для вас сотни или тысячи чисел. Этот алгоритм процесса дает вам список прогнозируемых чисел которые, скорее всего, сыграют вничью.

Преимущество использования Excel для создания алгоритмов прогнозирования заключается в том, что вы можете использовать этот метод для любой лотереи в мире. Так что, если вы хотите попробовать свои силы в самых популярных онлайн-лотереях, таких как MegaMillions or Американский пауэрбол ты можешь используйте свои алгоритмы прогнозирования, чтобы увеличить свои шансы на победу.

Помимо MegaMillions или US Powerball, вы можете использовать алгоритмы прогнозирования, чтобы увеличить свои шансы для других наших лучшие онлайн-лотереи по странам.

Действительно ли работает алгоритм предсказания лотерейного номера?

Следует помнить один фактор: ни один алгоритм предсказания лотереи не может гарантировать выигрыш джекпота. Но это значительно увеличивает ваши шансы на победу. даже если вы выиграете меньшие призы с других ярусов.

С другой стороны, алгоритм предсказания лотереи работает для определенной цели и будет работать для того, для чего он предназначен. Его задача — предоставить вам комбинацию цифр который с большей вероятностью появится в розыгрыше, вместо того, чтобы давать вам случайные числа. Но опять же, это не может гарантировать победу.

Как только вы будете готовы; Играйте с лучшими лотерейными сайтами!

Как создать формулу алгоритма прогнозирования лотереи с помощью Excel

Теперь, когда вы знаете больше об алгоритмах предсказания лотереи, я хотел бы показать вам, как вы можете сделать это самостоятельно. используя Microsoft Excel. Эта программа является мощным инструментом и идеально подходит для людей, которые не умеют писать коды или не имеют опыта программирования. Кроме того, вам не нужны обширные навыки работы с Excel, чтобы создать собственный алгоритм прогнозирования. Чтобы начать, выполните следующие действия.

Откройте Excel — создайте свой документ

Откройте новую книгу в Microsoft Excel. Чтобы вам было легче читать, вы можете добавить цветные заголовки or выделить определенные разделы. Но если вы хотите создать простую электронную таблицу, вам не нужно ничего добавлять.

Заполните свой первый столбец

Начните с ввода 1 в ячейке A1 , а затем 2 в ячейке A2. Взгляните на снимок экрана, который я предоставил ниже, чтобы помочь вам.

Как я уже упоминал ранее, вы можете использовать этот алгоритм для любой лотереи по всему миру. В этом примере я хотел бы использовать лотерею, в которой 70 шаров в основном барабане. Поэтому вам нужно номер столбца A от 1 до 70.

Вы можете ввести эти числа вручную, но это займет время. Итак, выделите первую и вторую ячейку (A1-A2), и вокруг ячеек появится зеленая рамка. Там будет маленькая точка в правом нижнем углу коробки. Нажмите на маленькую точку, а затем перетащите зеленую рамку до ячейки A70. в этом столбце будут введены числа от 1 до 70.

Если вы играете в другую лотерею, например Американский пауэрбол с барабаном из 69 шаров, тогда вы должны ввести числа от 1 до 69 в столбце A. Взгляните на скриншоты, которые я предоставил ниже, чтобы помочь вам.

Введите свою функцию в столбец B

Теперь, когда ваша первая строка заполнена, введите следующее формула в ячейку B1:

= СЧЁТЕСЛИ (U72: AO6000; A1), Двойной щелчок U72: AO6000 и нажмите клавишу F4 сделать формулу абсолютной. Если у вас нет клавиши F4, вы можете используйте свою цифровую клавиатуру. Убедитесь, что вы скопировали эту функцию полностью до ячейка B70. В столбце B должны быть нули.

Выделите свой диапазон от B1 до B70. Теперь нажмите кнопку «Домой» в верхнем левом углу экрана и перейдите к Вкладка «Стили» , чтобы выбрать Условное форматирование. Нажмите Верхние / нижние правила , а затем выберите Выше среднего. Выберите нужный текст. Эта функция выделит числа, которые выше среднего в вашем алгоритме после следующего шага.

Введите другую формулу в столбец U71

Найдите столбец U71 и введите следующую формулу:

= СЛУЧМЕЖДУ (1; 70)

Как только вы введете формулу, появится случайное число между 1 и 70 это диапазон в основном барабане вашей лотереи. Когда я ввел формулу, я получил число 34. Вы можете получить другое число, когда введете формулу. Теперь скопируйте эту ячейку с помощью нажатие Ctrl + C.

Вверху столбца A вы увидите значок коробка с U71. В этом блоке вам нужно ввести следующую формулу: U72: AO6000

Теперь нажмите Ctrl + V, чтобы вставить эту формулу во всех ячейках вашего документа. Просто не забудьте использовать Параметр «Вставить значения».

Вы увидите ряды и ряды чисел!

Выделенные числа в столбце B

Теперь вы увидите список номеров под Выделенный столбец B. В этом столбце выделены числа, выглядят выше среднего. На листе Excel также подсчитано, во сколько раз число в столбце A появляется в книге.

Повторите процесс, используя выделенные числа.

Приведенный выше процесс создает электронную таблицу с тысячи чисел, которые рандомизированы. На этом листе вы можете выбрать частые числа, которые появляются так что вы можете использовать их в своем лотерейном билете. Однако у вас все еще слишком много выделенных чисел.

Следовательно, вам нужно сузить числа, повторив процесс, упомянутый выше, четыре раза. Откройте новую таблицу Excel, но оставьте открытой книгу алгоритмов. Вместо того, чтобы вводить числа от 1 до 70 в столбце A, вы используйте выделенные числа в вашей предыдущей книге. Теперь у вас будет меньше чисел для работы.

Просто скопируйте значения из предыдущей книги, введите их в столбец A и повторите шаги:

Введите формулу СЧЁТЕСЛИ… в столбец B
Перейдите к U71 и введите = RANDBETWEEN (1; 70)
Введите U72: AO6000 в поле ячейки над столбцом A.
Скопируйте ячейку, как раньше, и вставьте

Если у вас все еще слишком много выделенных чисел в столбце B, просто повторяйте процессы, пока не получите количество номеров, необходимое для выбранной вами лотереи.

Определение вероятности лотереи в Excel

Большинство лотерей имеют один шанс на миллион на победу. Некоторые игроки выбирают лотереи, которые дают им больше шансов на выигрыш. обычно более мелкие лотереи, такие как Chispazo в Мексике. Эта лотерея имеет вероятность 1 из 98,280 XNUMX шансов на получение приза джекпота.

Чтобы узнать, какова вероятность выигрыша в вашей любимой лотерее, просто откройте новую таблицу Excel и выполните следующие простые шаги:

В столбце C1 введите выбранный вами диапазон номеров лотереи. Например, Powerball США имеет диапазон от 1 до 69. Поэтому введите 69 в столбце C.
Для столбца D1 введите количество цифр, которое нужно выбрать. Для лотереи Powerball США вам нужно выбрать пять чисел, поэтому введите цифру 5 в свой столбец.
В ячейке E1 введите в этой формуле = COMBIN (C1, D1) и нажмите клавишу ВВОД. Формула даст вероятность выбранной вами лотереи.

С помощью этих шагов вы можете решить, будет ли это лучшая лотерея для вас, исходя из ваших шансов на выигрыш.

Использование двухбарабанных лотерей

Вы хотите определить свои шансы на выигрыш с помощью лотереи с двумя барабанами? Затем вы можете добавить определенную информацию в свою электронную таблицу Excel, чтобы получить ответ. Следуй этим шагам:

В ячейке C1 введите выбранный вами диапазон номеров лотереи. Если вы играете в MegaMillions, наберите 70 в этой ячейке.
Вы должны выбрать пять чисел в основном барабане, чтобы выиграть MegaMillions, поэтому в ячейке D1 введите 5.
Используйте формулу = КОМБИНАТ (C1; D1) в ячейке E1, чтобы определить свою вероятность.
Добавьте второй диапазон номеров барабана в ячейку F1, который будет равен 25, если вы играете в MegaMillions.
В ячейке G1 введите эту формулу = E1 * F1, чтобы получить фактическое шансы лотереи если бы вы выбрали 5 номеров плюс ваш бонусный номер.

Использовать этот готовый алгоритм лотереи Excel Загрузить

Если вы не хотите создавать свою таблицу каждый раз, когда хотите играть в лотерею, тогда скачать эту готовую электронную таблицу Excel, которую я сделал. Готовый лист Excel сэкономит ваше время, потому что вам не придется вводить все формулы.

Если вы играете в лотерею, отличную от лотереи в загруженной таблице Excel, просто измените числа в столбце A и убедитесь, что формулы соответствуют измененным ячейкам.

Попробуйте алгоритм лотереи на Lottoland!

Заключительные мысли об алгоритме прогнозирования лото

Использование алгоритм предсказания в Excel это идеальная стратегия для выбора чисел. Поэтому вместо того, чтобы выбирать случайные числа для игры в любимую лотерею, вы можете использовать алгоритмы, созданные Excel, чтобы увеличить свои шансы.

Не забывайте, что нужно повторите процесс четыре раза используя метод, описанный в этой статье, чтобы сузить круг ваших оценок. Каждый раз, когда вы используете этот метод, ваши числа будут другими. Таким образом, вы можете создать несколько таблиц, если хотите сыграть в более чем одну лотерею или купить более одного лотерейного билета.

Часто задаваемые вопросы

Может ли Excel предсказать выигрышные номера лотереи?

Ни одна программа не может предсказать точные выигрышные номера лотереи, потому что они не могут определить будущее. Excel поможет вам создать алгоритм, который поможет вам выбрать числа, которые могут отображаться в лотерее, но не могут предсказать выигрышные числа.

Можете ли вы составлять комбинации номеров лотереи в Excel?

Да, вы можете использовать Excel для создания комбинаций чисел. Вы можете использовать формулу =COMBIN для создания комбинаций. Например, если у вас есть лотерея с диапазоном чисел от 1 до 52, и вам нужно выбрать 6 шаров, используйте формулу =СОЕДИНЕНИЕ(52,6)

Есть ли другие инструменты, которые вы можете использовать для создания номеров лотереи в Excel?

Да, есть и другие инструменты, которые вы можете использовать в Excel. Самым популярным из них является KuTools for Excel, который поможет вам легко генерировать номера лотереи.

Может ли кто-нибудь использовать Excel для предсказания номеров лотереи?

Да, любой может использовать Excel, чтобы получить номера лотереи, необходимые для игры в предпочитаемую им игру. Все, что вам нужно, это компьютер или ноутбук с установленным на нем Excel. В Интернете есть множество руководств, в которых предлагаются различные формулы. Все, что вам нужно сделать, это следовать инструкциям, и вы получите свои алгоритмы лотереи.

Что произойдет, если формулы лотереи Excel не работают?

Иногда Excel не распознает используемые вами формулы. Возможно, вам придется изменить некоторые настройки. Убедитесь, что в вашем Excel включена функция автоматического суммирования. Щелкните ячейку и на вкладке «Числа» на домашней ленте убедитесь, что для нее установлено значение «Общие», а не «Текст».

Источник