Алгоритм решения задачи при excel - Word и Excel - помощь в работе с программами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Содержание

Поиск решения задач в Excel с примерами
Решение задач оптимизации в Excel
Решение финансовых задач в Excel
Решение эконометрики в Excel
Решение логических задач в Excel
Решение математических задач в Excel
Линейное программирование в Excel

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Решение задач оптимизации в Excel

В Excel для решения задач оптимизации используются следующие команды:

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Оформим исходные данные в виде таблицы:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Дано 2 диапазона значений:

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Источник

Линейное программирование в Excel

В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel» внизу окна:

Для того чтобы решить задачу ЛП в табличном процессоре Microsoft Excel , необходимо выполнить следующие действия:
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
· переменных,
· целевой функции (ЦФ),
· ограничений,
· граничных условий;
b) ввести исходные данные в экранную форму:
· коэффициенты ЦФ,
· коэффициенты при переменных в ограничениях,
· правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
· формулу для расчета ЦФ,
· формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения» ):
· целевую ячейку,
· направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения» ):
· ячейки со значениями переменных,
· граничные условия для допустимых значений переменных,
· соотношения между правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения» );
b) запустить задачу на решение (в окне «Поиск решения» );
c) выбрать формат вывода решения (в окне «Результаты поиска решения» ).

Рассмотрим подробно использование MS Excel на примере решения следующей задачи.

Фабрика «GRM pic» выпускает два вида каш для завтрака — «Crunchy» и «Chewy». Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.

Управляющему производством Джою Дисону необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.

Цех	Необходимый фонд рабочего времени чел.-ч/т	Общий фонд рабочего времени чел.-ч. в месяц
«Crunchy»	«Chewy»
А. Производство	10	4	1000
В. Добавка приправ	3	2	360
С. Упаковка	2	5	600

Доход от производства 1 т «Crunchy» составляет 150 ф. ст., а от производства «Chewy» — 75 ф, ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.

а) Сформулировать модель линейного программирования, максимизирующую общий доход фабрики за месяц.

б) Решить ее c помощью MS Excel.

Ввод исходных данных
Создание экранной формы и ввод исходных данных

Экранная форма для решения в MS Excel представлена на рисунке 1.

В экранной форме на рисунке 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи 1 соответствуют ячейки B4 (x₁), C4 (x₂), коэффициентам ЦФ соответствуют ячейки B6 (c₁=150), C6 (c₂=75), правым частям ограничений соответствуют ячейки D18 (b₁=1000), D19 (b₂=360), D20 (b₃=600) и т.д.

Ввод зависимостей из формальной постановки задачи в экранную форму

Для ввода зависимостей определяющих выражение для целевой функции и ограничений используется функция MS Excel СУММПРОИЗВ , которая вычисляет сумму попарных произведений двух или более массивов.

Одним из самых простых способов определения функций в MS Excel является использование режима «Вставка функций» , который можно вызвать из меню «Вставка» или при нажатии кнопки f_x (рисунок 2) на стандартной панели инструментов.

Рисунок 2

Так, например, выражение для целевой функции из задачи 1 определяется следующим образом:
· курсор в поле D6;
· нажав кнопку f_x , вызовите окно «Мастер функций — шаг 1 из 2»;
· выберите в окне «Категория» категорию «Математические»;
· в окне «Функция» выберите функцию СУММПРОИЗВ (рис. 3);

Рисунок 3
· в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение B$4:C$4 , а в строку «Массив 2» — выражение B6:C6 (рис. 4);

Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи ( B3, C3 ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения ( B13, C13 — 1-е ограничение; B14, С14 — 2-е ограничение и B15, С15 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.
Таблица 1.

Формулы, описывающие ограничения модели (1)

Левая часть ограничения	Формула Excel
10x₁+4x₂ или B3×B13+C3×C13	=СУММПРОИЗВ(B4:C4;B13:C13))
3x₁+2x₂ или B3×B14+C3×C14	=СУММПРОИЗВ(B4:C4;B14:C14))
2x₁+5x₂ или B3×B15+C3×C15	=СУММПРОИЗВ(B4:C4;B15:C15)

Дальнейшие действия производятся в окне «Поиск решения» , которое вызывается из меню «Сервис» (рис.5):

· поставьте курсор в поле «Установить целевую ячейку» ;

· введите адрес целевой ячейки $D$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры;

· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».

Ввод ограничений и граничных условий
Задание ячеек переменных

В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $B$4:$С$4 . Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных

В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1).
· Нажмите кнопку «Добавить» , после чего появится окно «Добавление ограничения» (рис.6).
· В поле «Ссылка на ячейку» введите адреса ячеек переменных $B$4:$С$4 . Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
· В поле знака откройте список предлагаемых знаков и выберите ≥ .
· В поле «Ограничение» введите 0.

Рис.6 — Добавление условия неотрицательности переменных задачи (1)

Задание знаков ограничений ≤ , ≥ , = .
· Нажмите кнопку «Добавить» в окне «Добавление ограничения» .
· В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $B$18 . Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
· В соответствии с условием задачи (1) выбрать в поле знака необходимый знак, например, ≤ .
· В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $D$18 .
· Аналогично введите ограничения: $B$19 , $B$20 .
· Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK .

Окно «Поиск решения» после ввода всех необходимых данных задачи (1) представлено на рис. 5.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 5).

Решение задачи
Установка параметров решения задачи

Задача запускается на решение в окне «Поиск решения» . Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 7).

Рис. 7 — Параметры поиска решения, подходящие для большинства задач ЛП

Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «OK» .

Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить» .

После запуска на решение задачи ЛП на экране появляется окно «Результаты поиска решения» с сообщением об успешном решении задачи, представленном на рис. 8.

Рис. 8 -. Сообщение об успешном решении задачи

Появление иного сообщения свидетельствует не о характере оптимального решения задачи, а о том, что при вводе условий задачи в MS Excel были допущены ошибки, не позволяющие MS Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие MS Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы» . Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «OK» . После этого в экранной форме появляется оптимальное решение задачи (рис. 9).

Источник

МОУ «Детчинская средняя общеобразовательная школа»

Проект решения задачи

по спецкурсу «Решение текстовых задач»

Подготовили учащиеся

8 класса

Росколотенко А.

Проверила

Герасимова О. Н.

Детчино 2011

Задача 18

Построить таблицы по приведённым ниже данным (рис. 1, рис. 2).
Определить средний балл экзаменационной сессии по курсам и по факультету.
Результаты округлить до одного десятичного знака после запятой, используя функцию ОКРУГЛ().
Определить рейтинг (место по уровню успеваемости) каждого курса, используя функцию РАНГ().
Результаты вычислений представить в графическом виде.
Используя табличные данные на рис. 2, сформировать и заполнить ведомость итогов экзаменационной сессии по факультету.

1 курс	2 курс	3 курс	4 курс	5 курс
Балл	Количество оценок	Балл	Количество оценок	Балл	Количество оценок	Балл	Количество оценок	Балл	Количество оценок
5	23	5	27	5	32	5	28	5	34
4	57	4	60	4	58	4	63	4	62
3	18	3	14	3	10	3	9	3	6
2	7	2	9	2	4	2	1	2

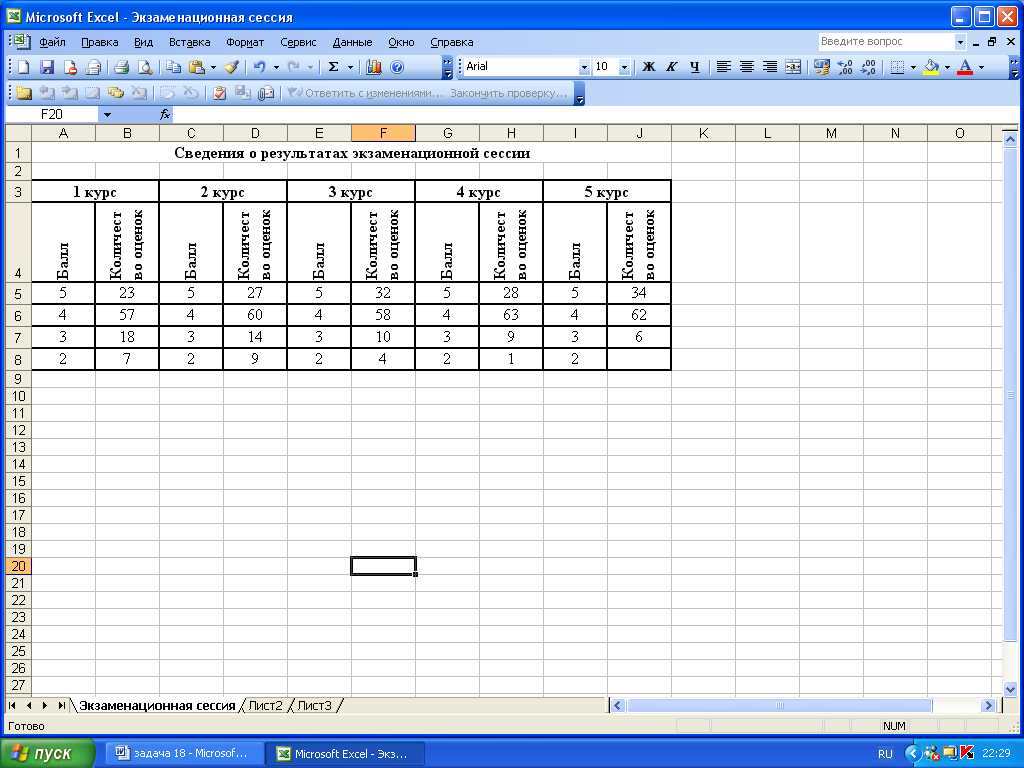
Рис. 1. Сведения о результатах экзаменационной сессии

курс	Средний балл	Рейтинг
1
2
3
4
5
По факультету

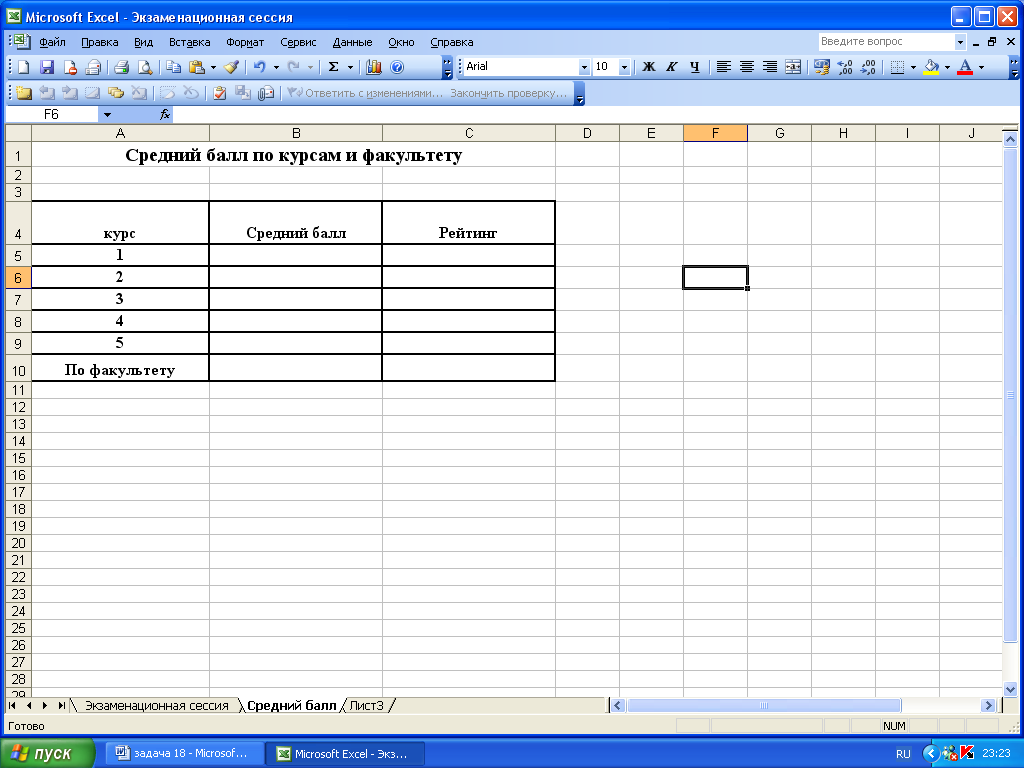
Рис. 2. Средний балл по курсам и по факультету

Алгоритм решения задачи:

Запустить табличный процессор MS Excel.
Создать книгу с именем «Экзаменационная сессия».
Лист 1 переименовать в лист «Экзаменационная сессия».
На рабочем листе «Экзаменационная сессия» MS Excel создать таблицу «Сведения о результатах экзаменационной сессии».
Заполнить таблицу «Результаты экзаменационной сессии» данными (рис. 1).

Рис. 3. Расположение таблицы «Сведения о результатах экзаменационной сессии» на рабочем листе «Экзаменационная сессия» MS Excel

6. Разработать структуру шаблона таблицы «Средний балл по курсам и факультету» (рис. 4.)

Колонка электронной таблицы	Наименование (реквизит)	Тип данных	Формат данных
Длина	Точность
A	Курс	текстовый	20
B	Средний балл	числовой	2	1
C	Рейтинг	числовой	1	0

Рис. 4. Структура шаблона таблицы «Средний балл по курсам и факультету»

7. Лист 2 переименовать в лист с названием «Средний балл».

8. На листе «Средний балл» создать таблицу «Средний балл по курсам и факультету» (данные с рис. 2.)

Рис. 5. Расположение таблицы «Средний балл по курсам и по факультету» на рабочем листе MS Excel

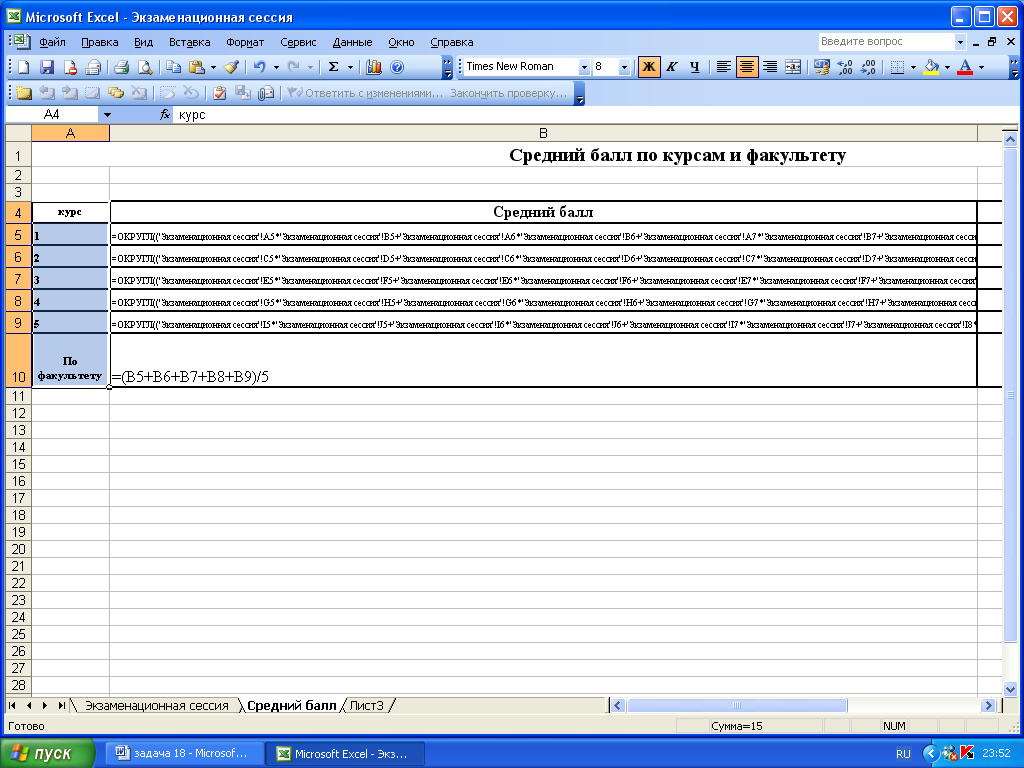
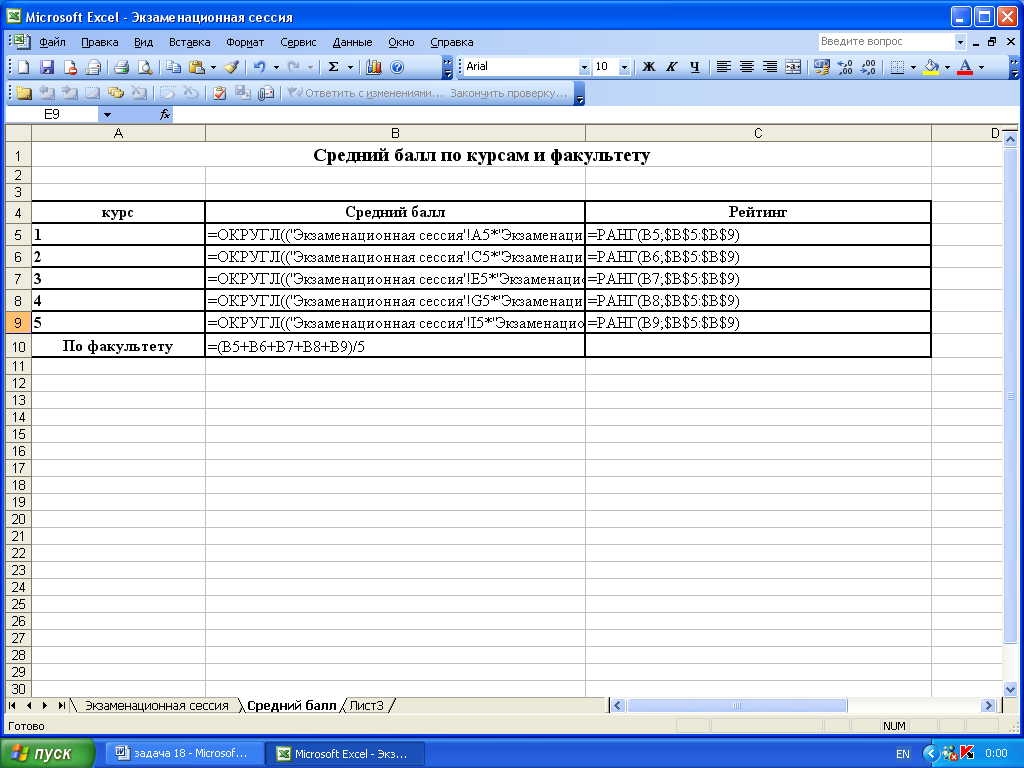
9. В колонке В5 написать формулу для вычисления среднего балла и округлить полученный результат до одного знака после запятой с помощью функции ОКРУГЛ (данные для вычислений возьмем с первого листа т. е. с листа «Экзаменационная сессия»): =ОКРУГЛ((‘Экзаменационная сессия’!A5*’Экзаменационная сессия’!B5+’Экзаменационная сессия’!A6*’Экзаменационная сессия’!B6+’Экзаменационная сессия’!A7*’Экзаменационная сессия’!B7+’Экзаменационная сессия’!A8*’Экзаменационная сессия’!B8)/(‘Экзаменационная сессия’!B5+’Экзаменационная сессия’!B6+’Экзаменационная сессия’!B7+’Экзаменационная сессия’!B8);1), нажмём ENTER. В ячейки В5 средний балл вычислен.

Рис.6. Формулы для вычисления среднего балла на рабочем листе MS Excel

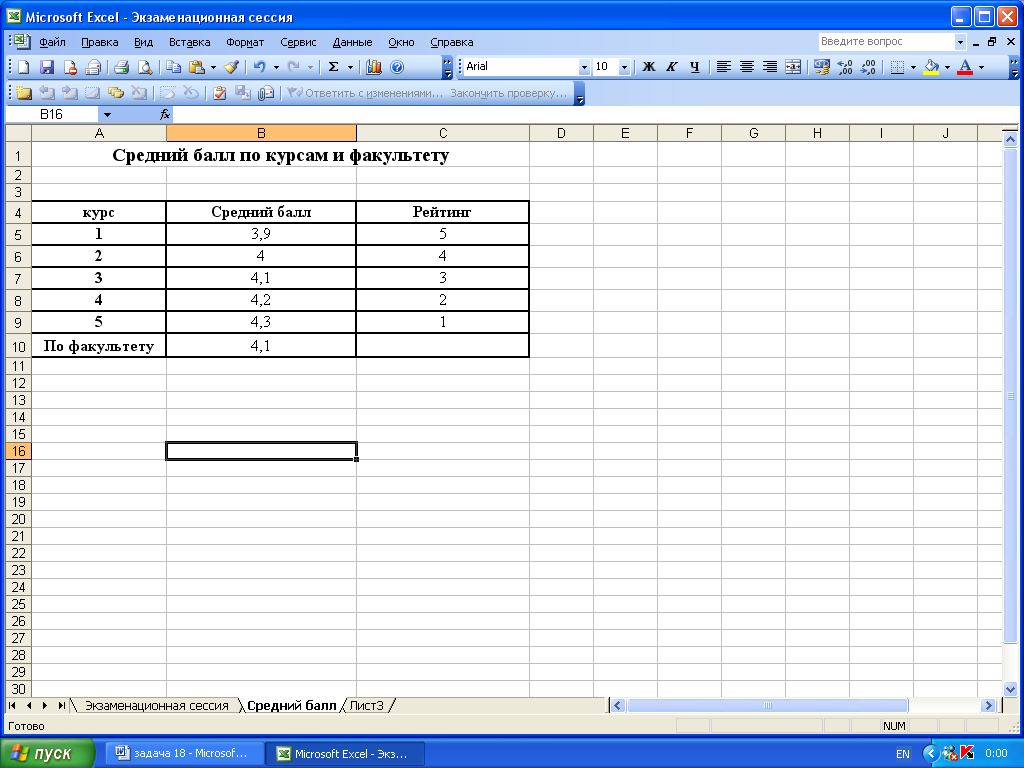
10. С помощью автозаполнения растянем формулу до ячейки В9 и вычислим средние баллы по всем курсам.

11. В ячейки В10 напишем формулу для вычисления среднего балла по факультету: =(B5+B6+B7+B8+B9)/5.

Рис.7. Вычисление среднего балла в на рабочем листе MS Excel

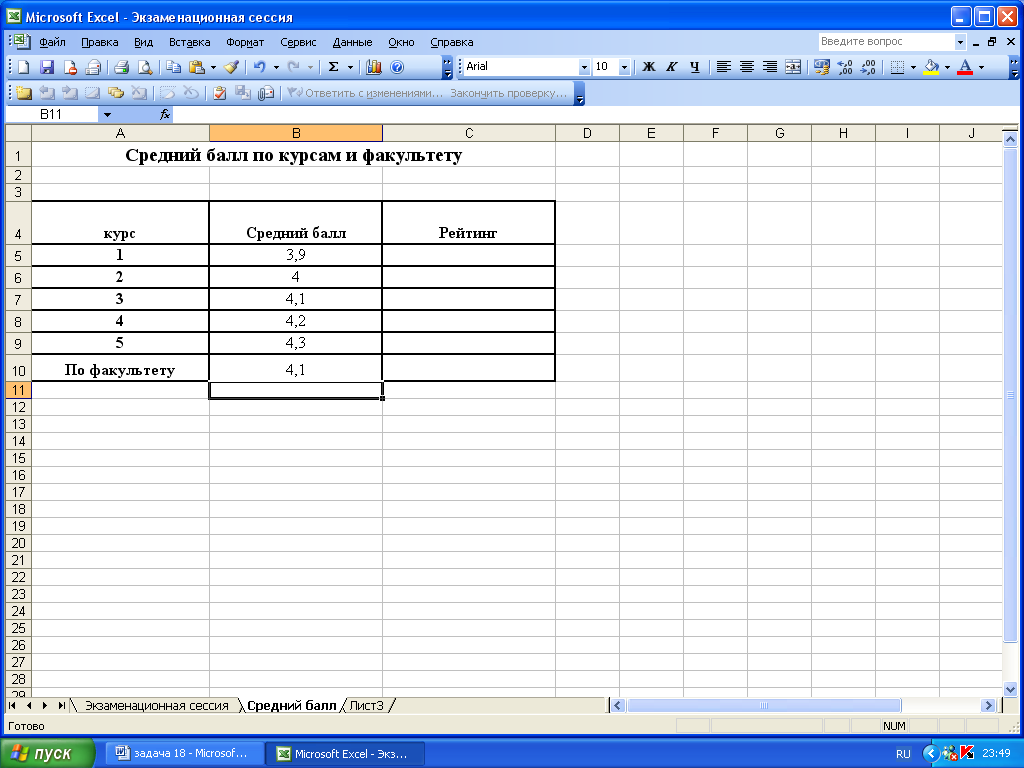
12. В ячейки С5 напишем формулу для вычисления рейтинга по курсам: =РАНГ(B5;$B$5:$B$9).

13. С помощью автозаполнения растянем формулу до ячейки С5.

Рис.8. Формулы для вычисления среднего балла и рейтинга на рабочем листе MS Excel

Рис.9. Вычисление среднего балла и рейтинга в на рабочем листе MS Excel

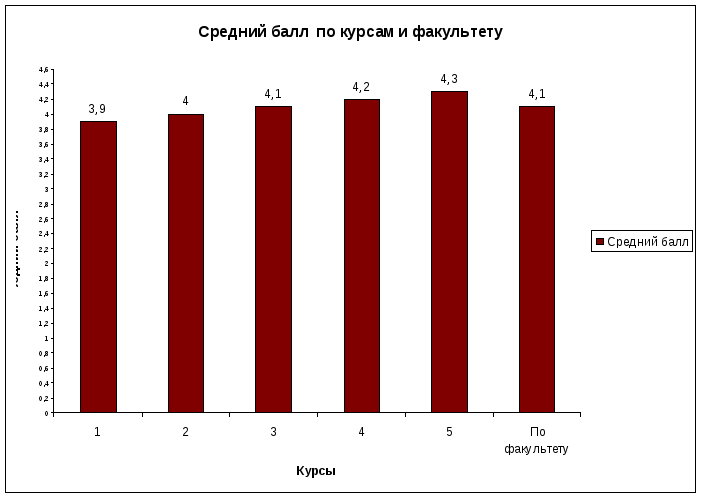
14. Результаты вычислений среднего балла и рейтинга представим в графическом виде. Выделим столбцы «Курс» и «Средний балл» и с помощью Мастера диаграмм построим график функции «Средний балл по курсам и факультету». Выберем тип диаграммы – гистограмма.

Рис.10. Диаграмма «Средний балл по курсам и факультету»

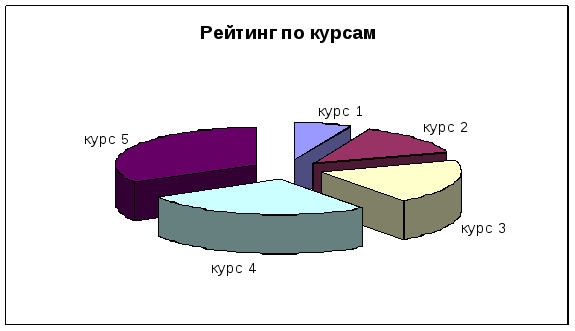
15. Выделим столбцы «Курс» и «Рейтинг» и с помощью Мастера диаграмм построим график функции «Рейтинг по курсам». Выберем тип диаграммы – круговая.

Рис.11. Диаграмма «Рейтинг по курсам»

16. Листу 3 дадим название «Итоговая ведомость».

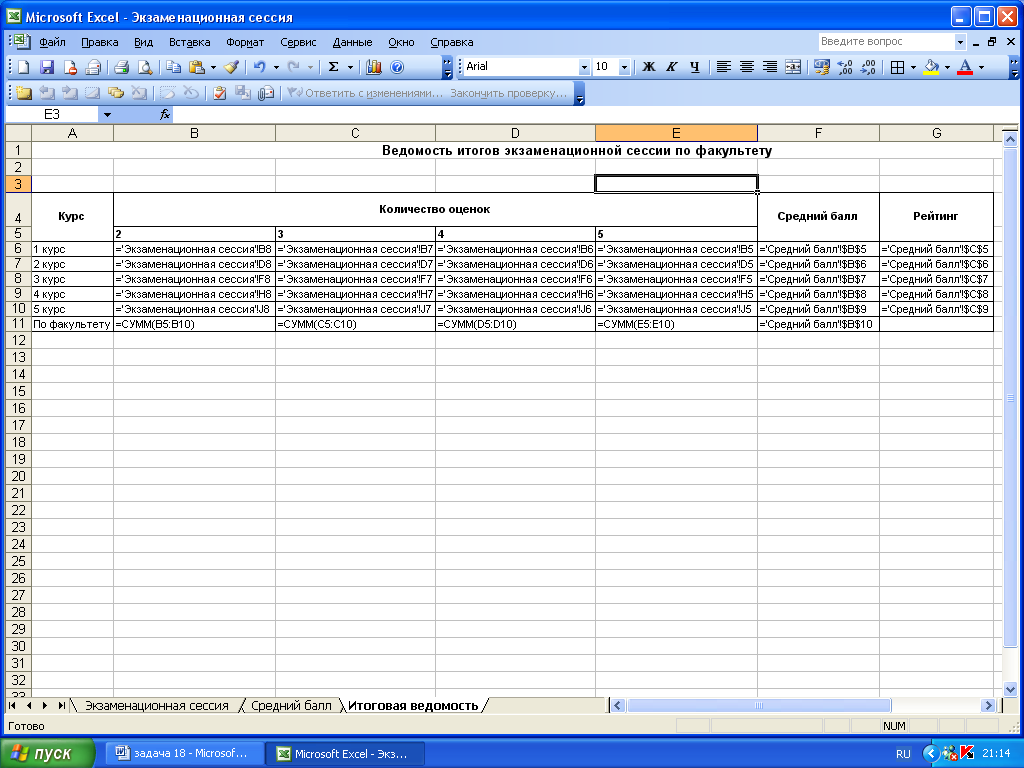
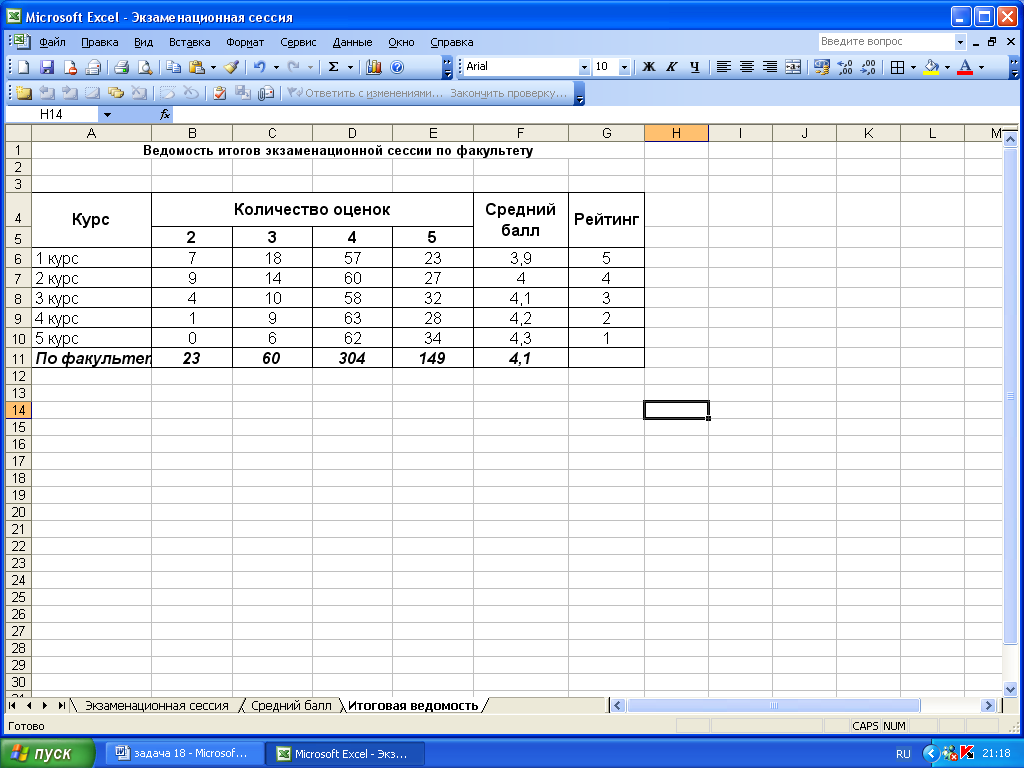
17. На листе «Итоговая ведомость» построим таблицу «Ведомость итогов экзаменационной сессии по факультету»

18. С помощью формул свяжем таблицы «Сведения о результатах экзаменационной сессии» и «Средний балл по курсам и факультету». Данные отобразим в таблице «Ведомость итогов экзаменационной сессии по факультету».

19. В ячейки В6 запишем формулу для переноса количества «2» для первого курса: =’Экзаменационная сессия’!B8. Аналогичными формулами заполним диапазон ячеек В6:Е10. С помощью этих формул количество «2», «3», «4», «5» перенесётся из таблицы «Сведения о результатах экзаменационной сессии» в таблицу «Ведомость итогов экзаменационной сессии по факультету».

20. В ячейки F6 пропишем формулу для переноса среднего балла для каждого курса из таблицы «Средний балл по курсам и факультету» в таблицу «Ведомость итогов экзаменационной сессии по факультету»: =’Средний балл’!$B$5. Аналогичными формулами заполним ячейки F7:F10.

21. Для вычисления рейтинга по курсам в ячейки G6 запишем формулу которая свяжет таблицы «Средний балл по курсам и факультету» и «Ведомость итогов экзаменационной сессии по факультету»: =’Средний балл’!$C$5. Аналогичными формулами заполним диапазон ячеек F7:F10.

22. В ячейках B11, C11, D11, E11 с помощью автосуммы подсчитаем количество «2», «3», «4», «5» по факультету.

23. В ячейки F11 запишем формулу для среднего балла по факультету (данные возьмем из таблицы «Средний балл по курсам и факультету»: =’Средний балл’!$B$10.

Рис.12. Формулы для составления «Ведомости итогов экзаменационной сессии по факультету» на рабочем листе MS Excel

Рис.13. «Ведомость итогов экзаменационной сессии по факультету»

Источник

Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике

Содержание

Как включить функцию “Поиск решения”
Подготовительный этап
Применение функции и ее настройка
Заключение

Как включить функцию “Поиск решения”

Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:

Открываем меню “Файл”, кликнув по соответствующему названию.
Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.

Подготовительный этап

Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.

Итак, у нас есть данные про продаже товаров, представленные в табличном виде.

И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.

Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.

Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.

Применение функции и ее настройка

Формула готова. Теперь нужно применить саму функцию.

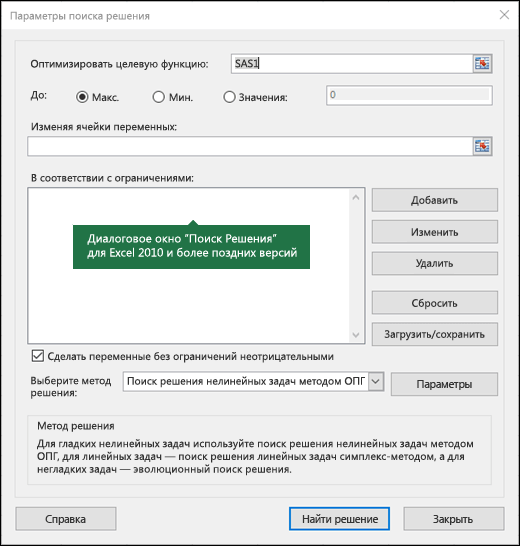
Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
Теперь наша таблица полностью готова в соответствии с поставленной задачей.

Заключение

Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.

Источник

«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.

Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.

Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.

В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).

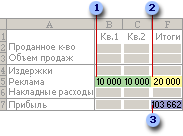
1. Ячейки переменных

2. Ячейка с ограничениями

3. Целевая ячейка

После выполнения процедуры получены следующие значения.

На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
Выполните одно из следующих действий.
- Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
- Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
- Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
- В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
1. В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
2. В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
3. Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
4. Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
5. Выполните одно из указанных ниже действий.
  - Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
  - Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
    Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.
    
    Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
6. В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
7. Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
- Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
- Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
- Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
- Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
- Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.

После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
- Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
- Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.

В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.

В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.

При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.

Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.

В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.

Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
Симплекс-метод. Используется для линейных задач.
Эволюционный метод Используется для негладких задач.

В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).

переменных

с ограничениями

цель

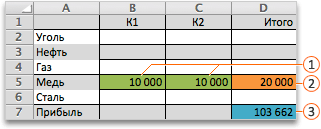
В результате выполнения получены следующие значения:

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.

Примечание: Целевая ячейка должна содержать формулу.

Выполните одно из следующих действий.

Задача	Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных	Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных	Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение	Щелкните Значение, а затем введите нужное значение в поле.

В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.

Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.

В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.

Для этого выполните следующие действия:

В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.

Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
Выполните одно из указанных ниже действий.

Задача	Необходимые действия
Принять ограничение и добавить другое	Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения	Нажмите кнопку ОК.

Нажмите кнопку Найти решение и выполните одно из следующих действий:

Задача	Необходимые действия
Сохранить значения решения на листе	В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения	Щелкните Восстановить исходные значения.

Примечания:

Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.

В диалоговом окне Показать предварительное решение выполните одно из следующих действий:

Задача	Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения	Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение	Нажмите кнопку Продолжить.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.

Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:

Задача	Необходимые действия
Настроить время решения и число итераций	На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить. Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность	На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости	На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.

Задача

Необходимые действия

Настроить время решения и число итераций

На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.

Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.

Задать точность

На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.

Задать степень сходимости

На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.

Нажмите кнопку ОК.
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.

При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.

Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.

В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.

В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:

Метод решения	Описание
Нелинейный метод обобщенного понижающего градиента (ОПГ)	Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции.
Поиск решения линейных задач симплекс-методом	Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *.
Эволюционный поиск решения	Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных.

Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.

Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.

Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».

Дополнительная справка по надстройке «Поиск решения»

За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:

Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.

Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Использование «Решения» для бюджетов с использованием средств на счете вех

Использование «Решение» для определения оптимального сочетания продуктов

Введение в анализ гипотетических вариантов

Полные сведения о формулах в Excel

Рекомендации, позволяющие избежать появления неработающих формул

Обнаружение ошибок в формулах

Сочетания клавиш в Excel

Функции Excel (по алфавиту)

Функции Excel (по категориям)

Источник