8 bit data word - Word и Excel - помощь в работе с программами

from Wikipedia, the free encyclopedia

This article is not adequately provided with supporting documents (for example individual proofs ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

A data word or just a word is a certain amount of data that a computer can process in one step in the arithmetic-logic unit of the processor . If a maximum amount of data is meant, its size is called word width, processing width or bus width.

In programming languages, however , the data word is a platform-independent data unit or the designation for a data type and generally corresponds to 16 bits or 32 bits (see examples ).

Twice a word — in context — is a double word (English double word , short DWord ) or long word referred. For four times a word there is in English also have the designation quadruple word , short Quad Word or QWord . The data unit with half the word width is correspondingly referred to as a half word .

Smallest addressable unit

Depending on the system, the word length can differ considerably, with the variants in computers produced so far, starting from 4 bits, almost always following a power of two , i.e. a respective doubling of the word length. (Exceptions to this were, for example, the mainframe computers TR 4 and TR 440 from the 1960s / 1970s with 50 and 52-bit wide words.)

In addition to the largest possible number that can be processed in one computing step, the word length primarily determines the size of the maximum directly addressable memory . Therefore, a tendency towards longer word lengths can be seen:

The first main processors only had 4-bit data words ( nibbles ). With 4 bits you can map 16 states, this is sufficient for the representation of the ten digits 0 to 9. Many digital clocks and simple pocket calculators still have 4-bit CPUs today .
In the 1970s, the 8-bit CPUs established themselves and dominated the market for home users until around 1990 . With 8 bits it was now possible to store 256 different characters in one data word. The computers now used alphanumeric inputs and outputs, which were much more legible and opened up new possibilities. The resulting 8-bit character sets , e.g. B. EBCDIC or the various 8-bit extensions to the 7-bit ASCII — Codes have been preserved in part to the 32-bit era, and simple text files are still often in an 8-bit format.
Since then, the word length is within the x86 — processor family has repeatedly doubled:
- With its first models, this had a 16-bit architecture ,
- which was soon followed by the 32-bit architecture of numerous PC processors, e. B. in the Pentium , Athlon , G4 and Core Duo processors.
- Currently (as of 2019) the 64-bit architecture is common, e.g. B. the Athlon-64 -, G5 -, newer Pentium-4 -, Core-2-Duo -, the Intel-Core-i-series as well as various server processors (e.g. Itanium , UltraSparc , Power4 , Opteron , newer Xeon ).

Different meanings

In programming languages for x86 systems, the size of a word has not grown , partly out of habit, but mainly in order to maintain compatibility with previous processors, but is now colloquially used to denote a bit sequence of 16 bits, i.e. the status of the 8086 processor.

For later x86 processors the designations Doppelwort / DWORD (English double word , also long word / Long ) and QWORD (English quad word ) were introduced. When changing from 32-bit architectures and operating systems to 64-bit , the meaning of long has been separated:

In the Windows world , the width of such a long word remained 32 bits
in the Linux world it was expanded to 64 bit.

In other computer architectures (e.g. PowerPC , Sparc ) a word often means a bit sequence of 32 bits (the original word length of these architectures), which is why the designation half-word is used there for sequences of 16 bits.

Examples

Processors of the IA-32 -80×86- architecture

Data width	Data type	Processor register
4 bits = ½ byte	Nibble	no registers of their own
8 bits = 1 byte	byte	z. B. the registers AL and AH
16 bits = 2 bytes	Word	z. B. the register AX
32 bits = 4 bytes	Double word	z. B. the register EAX
64 bits = 8 bytes	Quadruple Word	z. B. the register MM0
128 bits = 16 bytes	Double Quadruple Word	z. B. the register XMM0

The term Word (or word) is also used in the Windows API for a 16-bit number.

PLC

When programming programmable logic controllers (PLC), the IEC 61131-3 standard defines the word sizes as follows:

Data width	Bit data types	Integer data types	Range of values
unsigned	signed
8 bits = 1 byte	BYTE (byte)	(U) SINT (short integer)	0..255	−128..127
16 bits = 2 bytes	WORD (word)	(U) INT (integer)	0..65 535	−32 768..32 767
32 bits = 4 bytes	DWORD (double word)	(U) DINT (Double Integer)	0..2 ³² -1	-2 ³¹ ..2 ³¹ -1
64 bits = 8 bytes	LWORD (long word)	(U) LINT (Long Integer)	0..2 ⁶⁴ -1	-2 ⁶³ ..2 ⁶³ -1

If the letter U is placed in front of an integer data type (e.g. U DINT), this means “unsigned” (unsigned), without U the integer values are signed .

Individual evidence

↑ http://www.wissen.de/lexikon/ververarbeitungbreite
↑ QuinnRadich: Windows Data Types (BaseTsd.h) — Win32 apps. Retrieved January 15, 2020 (American English).
↑ May, Cathy .: The PowerPC architecture: a specification for a new family of RISC processors . 2nd Edition. Morgan Kaufman Publishers, San Francisco 1994, ISBN 1-55860-316-6 .
↑ Agner Fog: Calling conventions for different C ++ compilers and operating systems: Chapter 3, Data Representation (PDF; 416 kB) February 16, 2010. Accessed August 30, 2010.
↑ Christof Lange: API programming for beginners . 1999. Retrieved December 19, 2010.

Источник

From Wikipedia, the free encyclopedia

In computing, a word is the natural unit of data used by a particular processor design. A word is a fixed-sized datum handled as a unit by the instruction set or the hardware of the processor. The number of bits or digits^[a] in a word (the word size, word width, or word length) is an important characteristic of any specific processor design or computer architecture.

The size of a word is reflected in many aspects of a computer’s structure and operation; the majority of the registers in a processor are usually word-sized and the largest datum that can be transferred to and from the working memory in a single operation is a word in many (not all) architectures. The largest possible address size, used to designate a location in memory, is typically a hardware word (here, «hardware word» means the full-sized natural word of the processor, as opposed to any other definition used).

Documentation for older computers with fixed word size commonly states memory sizes in words rather than bytes or characters. The documentation sometimes uses metric prefixes correctly, sometimes with rounding, e.g., 65 kilowords (KW) meaning for 65536 words, and sometimes uses them incorrectly, with kilowords (KW) meaning 1024 words (2¹⁰) and megawords (MW) meaning 1,048,576 words (2²⁰). With standardization on 8-bit bytes and byte addressability, stating memory sizes in bytes, kilobytes, and megabytes with powers of 1024 rather than 1000 has become the norm, although there is some use of the IEC binary prefixes.

Several of the earliest computers (and a few modern as well) use binary-coded decimal rather than plain binary, typically having a word size of 10 or 12 decimal digits, and some early decimal computers have no fixed word length at all. Early binary systems tended to use word lengths that were some multiple of 6-bits, with the 36-bit word being especially common on mainframe computers. The introduction of ASCII led to the move to systems with word lengths that were a multiple of 8-bits, with 16-bit machines being popular in the 1970s before the move to modern processors with 32 or 64 bits.^[1] Special-purpose designs like digital signal processors, may have any word length from 4 to 80 bits.^[1]

The size of a word can sometimes differ from the expected due to backward compatibility with earlier computers. If multiple compatible variations or a family of processors share a common architecture and instruction set but differ in their word sizes, their documentation and software may become notationally complex to accommodate the difference (see Size families below).

Uses of words[edit]

Depending on how a computer is organized, word-size units may be used for:

Fixed-point numbers: Holders for fixed point, usually integer, numerical values may be available in one or in several different sizes, but one of the sizes available will almost always be the word. The other sizes, if any, are likely to be multiples or fractions of the word size. The smaller sizes are normally used only for efficient use of memory; when loaded into the processor, their values usually go into a larger, word sized holder.
Floating-point numbers: Holders for floating-point numerical values are typically either a word or a multiple of a word.
Addresses: Holders for memory addresses must be of a size capable of expressing the needed range of values but not be excessively large, so often the size used is the word though it can also be a multiple or fraction of the word size.
Registers: Processor registers are designed with a size appropriate for the type of data they hold, e.g. integers, floating-point numbers, or addresses. Many computer architectures use general-purpose registers that are capable of storing data in multiple representations.
Memory–processor transfer: When the processor reads from the memory subsystem into a register or writes a register’s value to memory, the amount of data transferred is often a word. Historically, this amount of bits which could be transferred in one cycle was also called a catena in some environments (such as the Bull GAMMA 60 [fr]).^[2]^[3] In simple memory subsystems, the word is transferred over the memory data bus, which typically has a width of a word or half-word. In memory subsystems that use caches, the word-sized transfer is the one between the processor and the first level of cache; at lower levels of the memory hierarchy larger transfers (which are a multiple of the word size) are normally used.
Unit of address resolution: In a given architecture, successive address values designate successive units of memory; this unit is the unit of address resolution. In most computers, the unit is either a character (e.g. a byte) or a word. (A few computers have used bit resolution.) If the unit is a word, then a larger amount of memory can be accessed using an address of a given size at the cost of added complexity to access individual characters. On the other hand, if the unit is a byte, then individual characters can be addressed (i.e. selected during the memory operation).
Instructions: Machine instructions are normally the size of the architecture’s word, such as in RISC architectures, or a multiple of the «char» size that is a fraction of it. This is a natural choice since instructions and data usually share the same memory subsystem. In Harvard architectures the word sizes of instructions and data need not be related, as instructions and data are stored in different memories; for example, the processor in the 1ESS electronic telephone switch has 37-bit instructions and 23-bit data words.

Word size choice[edit]

When a computer architecture is designed, the choice of a word size is of substantial importance. There are design considerations which encourage particular bit-group sizes for particular uses (e.g. for addresses), and these considerations point to different sizes for different uses. However, considerations of economy in design strongly push for one size, or a very few sizes related by multiples or fractions (submultiples) to a primary size. That preferred size becomes the word size of the architecture.

Character size was in the past (pre-variable-sized character encoding) one of the influences on unit of address resolution and the choice of word size. Before the mid-1960s, characters were most often stored in six bits; this allowed no more than 64 characters, so the alphabet was limited to upper case. Since it is efficient in time and space to have the word size be a multiple of the character size, word sizes in this period were usually multiples of 6 bits (in binary machines). A common choice then was the 36-bit word, which is also a good size for the numeric properties of a floating point format.

After the introduction of the IBM System/360 design, which uses eight-bit characters and supports lower-case letters, the standard size of a character (or more accurately, a byte) becomes eight bits. Word sizes thereafter are naturally multiples of eight bits, with 16, 32, and 64 bits being commonly used.

Variable-word architectures[edit]

Early machine designs included some that used what is often termed a variable word length. In this type of organization, an operand has no fixed length. Depending on the machine and the instruction, the length might be denoted by a count field, by a delimiting character, or by an additional bit called, e.g., flag, or word mark. Such machines often use binary-coded decimal in 4-bit digits, or in 6-bit characters, for numbers. This class of machines includes the IBM 702, IBM 705, IBM 7080, IBM 7010, UNIVAC 1050, IBM 1401, IBM 1620, and RCA 301.

Most of these machines work on one unit of memory at a time and since each instruction or datum is several units long, each instruction takes several cycles just to access memory. These machines are often quite slow because of this. For example, instruction fetches on an IBM 1620 Model I take 8 cycles (160 μs) just to read the 12 digits of the instruction (the Model II reduced this to 6 cycles, or 4 cycles if the instruction did not need both address fields). Instruction execution takes a variable number of cycles, depending on the size of the operands.

Word, bit and byte addressing[edit]

The memory model of an architecture is strongly influenced by the word size. In particular, the resolution of a memory address, that is, the smallest unit that can be designated by an address, has often been chosen to be the word. In this approach, the word-addressable machine approach, address values which differ by one designate adjacent memory words. This is natural in machines which deal almost always in word (or multiple-word) units, and has the advantage of allowing instructions to use minimally sized fields to contain addresses, which can permit a smaller instruction size or a larger variety of instructions.

When byte processing is to be a significant part of the workload, it is usually more advantageous to use the byte, rather than the word, as the unit of address resolution. Address values which differ by one designate adjacent bytes in memory. This allows an arbitrary character within a character string to be addressed straightforwardly. A word can still be addressed, but the address to be used requires a few more bits than the word-resolution alternative. The word size needs to be an integer multiple of the character size in this organization. This addressing approach was used in the IBM 360, and has been the most common approach in machines designed since then.

When the workload involves processing fields of different sizes, it can be advantageous to address to the bit. Machines with bit addressing may have some instructions that use a programmer-defined byte size and other instructions that operate on fixed data sizes. As an example, on the IBM 7030^[4] («Stretch»), a floating point instruction can only address words while an integer arithmetic instruction can specify a field length of 1-64 bits, a byte size of 1-8 bits and an accumulator offset of 0-127 bits.

In a byte-addressable machine with storage-to-storage (SS) instructions, there are typically move instructions to copy one or multiple bytes from one arbitrary location to another. In a byte-oriented (byte-addressable) machine without SS instructions, moving a single byte from one arbitrary location to another is typically:

LOAD the source byte
STORE the result back in the target byte

Individual bytes can be accessed on a word-oriented machine in one of two ways. Bytes can be manipulated by a combination of shift and mask operations in registers. Moving a single byte from one arbitrary location to another may require the equivalent of the following:

LOAD the word containing the source byte
SHIFT the source word to align the desired byte to the correct position in the target word
AND the source word with a mask to zero out all but the desired bits
LOAD the word containing the target byte
AND the target word with a mask to zero out the target byte
OR the registers containing the source and target words to insert the source byte
STORE the result back in the target location

Alternatively many word-oriented machines implement byte operations with instructions using special byte pointers in registers or memory. For example, the PDP-10 byte pointer contained the size of the byte in bits (allowing different-sized bytes to be accessed), the bit position of the byte within the word, and the word address of the data. Instructions could automatically adjust the pointer to the next byte on, for example, load and deposit (store) operations.

Powers of two[edit]

Different amounts of memory are used to store data values with different degrees of precision. The commonly used sizes are usually a power of two multiple of the unit of address resolution (byte or word). Converting the index of an item in an array into the memory address offset of the item then requires only a shift operation rather than a multiplication. In some cases this relationship can also avoid the use of division operations. As a result, most modern computer designs have word sizes (and other operand sizes) that are a power of two times the size of a byte.

Size families[edit]

As computer designs have grown more complex, the central importance of a single word size to an architecture has decreased. Although more capable hardware can use a wider variety of sizes of data, market forces exert pressure to maintain backward compatibility while extending processor capability. As a result, what might have been the central word size in a fresh design has to coexist as an alternative size to the original word size in a backward compatible design. The original word size remains available in future designs, forming the basis of a size family.

In the mid-1970s, DEC designed the VAX to be a 32-bit successor of the 16-bit PDP-11. They used word for a 16-bit quantity, while longword referred to a 32-bit quantity; this terminology is the same as the terminology used for the PDP-11. This was in contrast to earlier machines, where the natural unit of addressing memory would be called a word, while a quantity that is one half a word would be called a halfword. In fitting with this scheme, a VAX quadword is 64 bits. They continued this 16-bit word/32-bit longword/64-bit quadword terminology with the 64-bit Alpha.

Another example is the x86 family, of which processors of three different word lengths (16-bit, later 32- and 64-bit) have been released, while word continues to designate a 16-bit quantity. As software is routinely ported from one word-length to the next, some APIs and documentation define or refer to an older (and thus shorter) word-length than the full word length on the CPU that software may be compiled for. Also, similar to how bytes are used for small numbers in many programs, a shorter word (16 or 32 bits) may be used in contexts where the range of a wider word is not needed (especially where this can save considerable stack space or cache memory space). For example, Microsoft’s Windows API maintains the programming language definition of WORD as 16 bits, despite the fact that the API may be used on a 32- or 64-bit x86 processor, where the standard word size would be 32 or 64 bits, respectively. Data structures containing such different sized words refer to them as:

WORD (16 bits/2 bytes)
DWORD (32 bits/4 bytes)
QWORD (64 bits/8 bytes)

A similar phenomenon has developed in Intel’s x86 assembly language – because of the support for various sizes (and backward compatibility) in the instruction set, some instruction mnemonics carry «d» or «q» identifiers denoting «double-«, «quad-» or «double-quad-«, which are in terms of the architecture’s original 16-bit word size.

An example with a different word size is the IBM System/360 family. In the System/360 architecture, System/370 architecture and System/390 architecture, there are 8-bit bytes, 16-bit halfwords, 32-bit words and 64-bit doublewords. The z/Architecture, which is the 64-bit member of that architecture family, continues to refer to 16-bit halfwords, 32-bit words, and 64-bit doublewords, and additionally features 128-bit quadwords.

In general, new processors must use the same data word lengths and virtual address widths as an older processor to have binary compatibility with that older processor.

Often carefully written source code – written with source-code compatibility and software portability in mind – can be recompiled to run on a variety of processors, even ones with different data word lengths or different address widths or both.

Table of word sizes[edit]

key: bit: bits, c: characters, d: decimal digits, w: word size of architecture, n: variable size, wm: Word mark
Year	Computer architecture	Word size w	Integer sizes	Floatingpoint sizes	Instruction sizes	Unit of address resolution	Char size
1837	Babbage Analytical engine	50 d	w	—	Five different cards were used for different functions, exact size of cards not known.	w	—
1941	Zuse Z3	22 bit	—	w	8 bit	w	—
1942	ABC	50 bit	w	—	—	—	—
1944	Harvard Mark I	23 d	w	—	24 bit	—	—
1946 (1948) {1953}	ENIAC (w/Panel #16^[5]) {w/Panel #26^[6]}	10 d	w, 2w (w) {w}	—	— (2 d, 4 d, 6 d, 8 d) {2 d, 4 d, 6 d, 8 d}	— — {w}	—
1948	Manchester Baby	32 bit	w	—	w	w	—
1951	UNIVAC I	12 d	w	—	1⁄2w	w	1 d
1952	IAS machine	40 bit	w	—	1⁄2w	w	5 bit
1952	Fast Universal Digital Computer M-2	34 bit	w?	w	34 bit = 4-bit opcode plus 3×10 bit address	10 bit	—
1952	IBM 701	36 bit	1⁄2w, w	—	1⁄2w	1⁄2w, w	6 bit
1952	UNIVAC 60	n d	1 d, … 10 d	—	—	—	2 d, 3 d
1952	ARRA I	30 bit	w	—	w	w	5 bit
1953	IBM 702	n c	0 c, … 511 c	—	5 c	c	6 bit
1953	UNIVAC 120	n d	1 d, … 10 d	—	—	—	2 d, 3 d
1953	ARRA II	30 bit	w	2w	1⁄2w	w	5 bit
1954 (1955)	IBM 650 (w/IBM 653)	10 d	w	— (w)	w	w	2 d
1954	IBM 704	36 bit	w	w	w	w	6 bit
1954	IBM 705	n c	0 c, … 255 c	—	5 c	c	6 bit
1954	IBM NORC	16 d	w	w, 2w	w	w	—
1956	IBM 305	n d	1 d, … 100 d	—	10 d	d	1 d
1956	ARMAC	34 bit	w	w	1⁄2w	w	5 bit, 6 bit
1956	LGP-30	31 bit	w	—	16 bit	w	6 bit
1957	Autonetics Recomp I	40 bit	w, 79 bit, 8 d, 15 d	—	1⁄2w	1⁄2w, w	5 bit
1958	UNIVAC II	12 d	w	—	1⁄2w	w	1 d
1958	SAGE	32 bit	1⁄2w	—	w	w	6 bit
1958	Autonetics Recomp II	40 bit	w, 79 bit, 8 d, 15 d	2w	1⁄2w	1⁄2w, w	5 bit
1958	Setun	6 trit (~9.5 bits)^[b]	up to 6 tryte		up to 3 trytes		4 trit^?
1958	Electrologica X1	27 bit	w	2w	w	w	5 bit, 6 bit
1959	IBM 1401	n c	1 c, …	—	1 c, 2 c, 4 c, 5 c, 7 c, 8 c	c	6 bit + wm
1959 (TBD)	IBM 1620	n d	2 d, …	— (4 d, … 102 d)	12 d	d	2 d
1960	LARC	12 d	w, 2w	w, 2w	w	w	2 d
1960	CDC 1604	48 bit	w	w	1⁄2w	w	6 bit
1960	IBM 1410	n c	1 c, …	—	1 c, 2 c, 6 c, 7 c, 11 c, 12 c	c	6 bit + wm
1960	IBM 7070	10 d^[c]	w, 1-9 d	w	w	w, d	2 d
1960	PDP-1	18 bit	w	—	w	w	6 bit
1960	Elliott 803	39 bit
1961	IBM 7030 (Stretch)	64 bit	1 bit, … 64 bit, 1 d, … 16 d	w	1⁄2w, w	bit (integer), 1⁄2w (branch), w (float)	1 bit, … 8 bit
1961	IBM 7080	n c	0 c, … 255 c	—	5 c	c	6 bit
1962	GE-6xx	36 bit	w, 2 w	w, 2 w, 80 bit	w	w	6 bit, 9 bit
1962	UNIVAC III	25 bit	w, 2w, 3w, 4w, 6 d, 12 d	—	w	w	6 bit
1962	Autonetics D-17B Minuteman I Guidance Computer	27 bit	11 bit, 24 bit	—	24 bit	w	—
1962	UNIVAC 1107	36 bit	1⁄6w, 1⁄3w, 1⁄2w, w	w	w	w	6 bit
1962	IBM 7010	n c	1 c, …	—	1 c, 2 c, 6 c, 7 c, 11 c, 12 c	c	6 b + wm
1962	IBM 7094	36 bit	w	w, 2w	w	w	6 bit
1962	SDS 9 Series	24 bit	w	2w	w	w
1963 (1966)	Apollo Guidance Computer	15 bit	w	—	w, 2w	w	—
1963	Saturn Launch Vehicle Digital Computer	26 bit	w	—	13 bit	w	—
1964/1966	PDP-6/PDP-10	36 bit	w	w, 2 w	w	w	6 bit 7 bit (typical) 9 bit
1964	Titan	48 bit	w	w	w	w	w
1964	CDC 6600	60 bit	w	w	1⁄4w, 1⁄2w	w	6 bit
1964	Autonetics D-37C Minuteman II Guidance Computer	27 bit	11 bit, 24 bit	—	24 bit	w	4 bit, 5 bit
1965	Gemini Guidance Computer	39 bit	26 bit	—	13 bit	13 bit, 26	—bit
1965	IBM 1130	16 bit	w, 2w	2w, 3w	w, 2w	w	8 bit
1965	IBM System/360	32 bit	1⁄2w, w, 1 d, … 16 d	w, 2w	1⁄2w, w, 11⁄2w	8 bit	8 bit
1965	UNIVAC 1108	36 bit	1⁄6w, 1⁄4w, 1⁄3w, 1⁄2w, w, 2w	w, 2w	w	w	6 bit, 9 bit
1965	PDP-8	12 bit	w	—	w	w	8 bit
1965	Electrologica X8	27 bit	w	2w	w	w	6 bit, 7 bit
1966	SDS Sigma 7	32 bit	1⁄2w, w	w, 2w	w	8 bit	8 bit
1969	Four-Phase Systems AL1	8 bit	w	—	?	?	?
1970	MP944	20 bit	w	—	?	?	?
1970	PDP-11	16 bit	w	2w, 4w	w, 2w, 3w	8 bit	8 bit
1971	CDC STAR-100	64 bit	1⁄2w, w	1⁄2w, w	1⁄2w, w	bit	8 bit
1971	TMS1802NC	4 bit	w	—	?	?	—
1971	Intel 4004	4 bit	w, d	—	2w, 4w	w	—
1972	Intel 8008	8 bit	w, 2 d	—	w, 2w, 3w	w	8 bit
1972	Calcomp 900	9 bit	w	—	w, 2w	w	8 bit
1974	Intel 8080	8 bit	w, 2w, 2 d	—	w, 2w, 3w	w	8 bit
1975	ILLIAC IV	64 bit	w	w, 1⁄2w	w	w	—
1975	Motorola 6800	8 bit	w, 2 d	—	w, 2w, 3w	w	8 bit
1975	MOS Tech. 6501 MOS Tech. 6502	8 bit	w, 2 d	—	w, 2w, 3w	w	8 bit
1976	Cray-1	64 bit	24 bit, w	w	1⁄4w, 1⁄2w	w	8 bit
1976	Zilog Z80	8 bit	w, 2w, 2 d	—	w, 2w, 3w, 4w, 5w	w	8 bit
1978 (1980)	16-bit x86 (Intel 8086) (w/floating point: Intel 8087)	16 bit	1⁄2w, w, 2 d	— (2w, 4w, 5w, 17 d)	1⁄2w, w, … 7w	8 bit	8 bit
1978	VAX	32 bit	1⁄4w, 1⁄2w, w, 1 d, … 31 d, 1 bit, … 32 bit	w, 2w	1⁄4w, … 141⁄4w	8 bit	8 bit
1979 (1984)	Motorola 68000 series (w/floating point)	32 bit	1⁄4w, 1⁄2w, w, 2 d	— (w, 2w, 21⁄2w)	1⁄2w, w, … 71⁄2w	8 bit	8 bit
1985	IA-32 (Intel 80386) (w/floating point)	32 bit	1⁄4w, 1⁄2w, w	— (w, 2w, 80 bit)	8 bit, … 120 bit 1⁄4w … 33⁄4w	8 bit	8 bit
1985	ARMv1	32 bit	1⁄4w, w	—	w	8 bit	8 bit
1985	MIPS I	32 bit	1⁄4w, 1⁄2w, w	w, 2w	w	8 bit	8 bit
1991	Cray C90	64 bit	32 bit, w	w	1⁄4w, 1⁄2w, 48 bit	w	8 bit
1992	Alpha	64 bit	8 bit, 1⁄4w, 1⁄2w, w	1⁄2w, w	1⁄2w	8 bit	8 bit
1992	PowerPC	32 bit	1⁄4w, 1⁄2w, w	w, 2w	w	8 bit	8 bit
1996	ARMv4 (w/Thumb)	32 bit	1⁄4w, 1⁄2w, w	—	w (1⁄2w, w)	8 bit	8 bit
2000	IBM z/Architecture (w/vector facility)	64 bit	1⁄4w, 1⁄2w, w 1 d, … 31 d	1⁄2w, w, 2w	1⁄4w, 1⁄2w, 3⁄4w	8 bit	8 bit, UTF-16, UTF-32
2001	IA-64	64 bit	8 bit, 1⁄4w, 1⁄2w, w	1⁄2w, w	41 bit (in 128-bit bundles)^[7]	8 bit	8 bit
2001	ARMv6 (w/VFP)	32 bit	8 bit, 1⁄2w, w	— (w, 2w)	1⁄2w, w	8 bit	8 bit
2003	x86-64	64 bit	8 bit, 1⁄4w, 1⁄2w, w	1⁄2w, w, 80 bit	8 bit, … 120 bit	8 bit	8 bit
2013	ARMv8-A and ARMv9-A	64 bit	8 bit, 1⁄4w, 1⁄2w, w	1⁄2w, w	1⁄2w	8 bit	8 bit
Year	Computer architecture	Word size w	Integer sizes	Floatingpoint sizes	Instruction sizes	Unit of address resolution	Char size
key: bit: bits, d: decimal digits, w: word size of architecture, n: variable size

^[8]^[9]

Notes[edit]

^ Many early computers were decimal, and a few were ternary
^ The bit equivalent is computed by taking the amount of information entropy provided by the trit, which is $log _{2}(3)$ . This gives an equivalent of about 9.51 bits for 6 trits.
^ Three-state sign

References[edit]

^ ^a ^b Beebe, Nelson H. F. (2017-08-22). «Chapter I. Integer arithmetic». The Mathematical-Function Computation Handbook — Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. p. 970. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721.
^ Dreyfus, Phillippe (1958-05-08) [1958-05-06]. Written at Los Angeles, California, USA. System design of the Gamma 60 (PDF). Western Joint Computer Conference: Contrasts in Computers. ACM, New York, NY, USA. pp. 130–133. IRE-ACM-AIEE ’58 (Western). Archived (PDF) from the original on 2017-04-03. Retrieved 2017-04-03. […] Internal data code is used: Quantitative (numerical) data are coded in a 4-bit decimal code; qualitative (alpha-numerical) data are coded in a 6-bit alphanumerical code. The internal instruction code means that the instructions are coded in straight binary code.
As to the internal information length, the information quantum is called a «catena,» and it is composed of 24 bits representing either 6 decimal digits, or 4 alphanumerical characters. This quantum must contain a multiple of 4 and 6 bits to represent a whole number of decimal or alphanumeric characters. Twenty-four bits was found to be a good compromise between the minimum 12 bits, which would lead to a too-low transfer flow from a parallel readout core memory, and 36 bits or more, which was judged as too large an information quantum. The catena is to be considered as the equivalent of a character in variable word length machines, but it cannot be called so, as it may contain several characters. It is transferred in series to and from the main memory.
Not wanting to call a «quantum» a word, or a set of characters a letter, (a word is a word, and a quantum is something else), a new word was made, and it was called a «catena.» It is an English word and exists in Webster’s although it does not in French. Webster’s definition of the word catena is, «a connected series;» therefore, a 24-bit information item. The word catena will be used hereafter.
The internal code, therefore, has been defined. Now what are the external data codes? These depend primarily upon the information handling device involved. The Gamma 60 [fr] is designed to handle information relevant to any binary coded structure. Thus an 80-column punched card is considered as a 960-bit information item; 12 rows multiplied by 80 columns equals 960 possible punches; is stored as an exact image in 960 magnetic cores of the main memory with 2 card columns occupying one catena. […]
^ Blaauw, Gerrit Anne; Brooks, Jr., Frederick Phillips; Buchholz, Werner (1962). «4: Natural Data Units» (PDF). In Buchholz, Werner (ed.). Planning a Computer System – Project Stretch. McGraw-Hill Book Company, Inc. / The Maple Press Company, York, PA. pp. 39–40. LCCN 61-10466. Archived (PDF) from the original on 2017-04-03. Retrieved 2017-04-03. […] Terms used here to describe the structure imposed by the machine design, in addition to bit, are listed below.
Byte denotes a group of bits used to encode a character, or the number of bits transmitted in parallel to and from input-output units. A term other than character is used here because a given character may be represented in different applications by more than one code, and different codes may use different numbers of bits (i.e., different byte sizes). In input-output transmission the grouping of bits may be completely arbitrary and have no relation to actual characters. (The term is coined from bite, but respelled to avoid accidental mutation to bit.)
A word consists of the number of data bits transmitted in parallel from or to memory in one memory cycle. Word size is thus defined as a structural property of the memory. (The term catena was coined for this purpose by the designers of the Bull GAMMA 60 [fr] computer.)
Block refers to the number of words transmitted to or from an input-output unit in response to a single input-output instruction. Block size is a structural property of an input-output unit; it may have been fixed by the design or left to be varied by the program. […]
^ «Format» (PDF). Reference Manual 7030 Data Processing System (PDF). IBM. August 1961. pp. 50–57. Retrieved 2021-12-15.
^ Clippinger, Richard F. [in German] (1948-09-29). «A Logical Coding System Applied to the ENIAC (Electronic Numerical Integrator and Computer)». Aberdeen Proving Ground, Maryland, US: Ballistic Research Laboratories. Report No. 673; Project No. TB3-0007 of the Research and Development Division, Ordnance Department. Retrieved 2017-04-05.{{cite web}}: CS1 maint: url-status (link)
^ Clippinger, Richard F. [in German] (1948-09-29). «A Logical Coding System Applied to the ENIAC». Aberdeen Proving Ground, Maryland, US: Ballistic Research Laboratories. Section VIII: Modified ENIAC. Retrieved 2017-04-05.{{cite web}}: CS1 maint: url-status (link)
^ «4. Instruction Formats» (PDF). Intel Itanium Architecture Software Developer’s Manual. Vol. 3: Intel Itanium Instruction Set Reference. p. 3:293. Retrieved 2022-04-25. Three instructions are grouped together into 128-bit sized and aligned containers called bundles. Each bundle contains three 41-bit instruction slots and a 5-bit template field.
^ Blaauw, Gerrit Anne; Brooks, Jr., Frederick Phillips (1997). Computer Architecture: Concepts and Evolution (1 ed.). Addison-Wesley. ISBN 0-201-10557-8. (1213 pages) (NB. This is a single-volume edition. This work was also available in a two-volume version.)
^ Ralston, Anthony; Reilly, Edwin D. (1993). Encyclopedia of Computer Science (3rd ed.). Van Nostrand Reinhold. ISBN 0-442-27679-6.

Источник

Уважаемые коллеги, мы рады предложить вам, разрабатываемый нами учебный курс по программированию ПЛК фирмы Beckhoff с применением среды автоматизации TwinCAT. Курс предназначен исключительно для самостоятельного изучения в ознакомительных целях. Перед любым применением изложенного материала в коммерческих целях просим связаться с нами. Текст из предложенных вам статей скопированный и размещенный в других источниках, должен содержать ссылку на наш сайт heaviside.ru. Вы можете связаться с нами по любым вопросам, в том числе создания для вас систем мониторинга и АСУ ТП.

Типы данных в языках стандарта МЭК 61131-3

Уважаемые коллеги, в этой статье мы будем рассматривать важнейшую для написания программ тему — типы данных. Чтобы читатели понимали, в чем отличие одних типов данных от других и зачем они вообще нужны, мы подробно разберем, каким образом данные представлены в процессоре. В следующем занятии будет большая практическая работа, выполняя которую, можно будет потренироваться объявлять переменные и на практике познакомится с особенностями выполнения математических операций с различными типами данных.

Простые типы данных

В прошлой статье мы научились записывать цифры в двоичной системе счисления. Именно такую систему счисления используют все компьютеры, микропроцессоры и прочая вычислительная техника. Теперь мы будем изучать типы данных.

Любая переменная, которую вы используете в своем коде, будь то показания датчиков, состояние выхода или выхода, состояние катушки или просто любая промежуточная величина, при выполнении программы будет хранится в оперативной памяти. Чтобы под каждую используемую переменную на этапе компиляции проекта была выделена оперативная память, мы объявляем переменные при написании программы. Компиляция, это перевод исходного кода, написанного программистом, в команды на языке ассемблера понятные процессору. Причем в зависимости от вида применяемого процессора один и тот же исходный код может транслироваться в разные ассемблерные команды (вспомним что ПЛК Beckhoff, как и персональные компьютеры работают на процессорах семейства x86).

Как помните, из статьи Знакомство с языком LD, при объявлении переменной необходимо указать, к какому типу данных будет принадлежать переменная. Как вы уже можете понять, число B0₁₆ будет занимать гораздо меньший объем памяти чем число 4 C4E5 01E7 7A90₁₆. Также одни и те же операции с разными типами данных будут транслироваться в разные ассемблерные команды. В TwinCAT используются следующие типы данных:

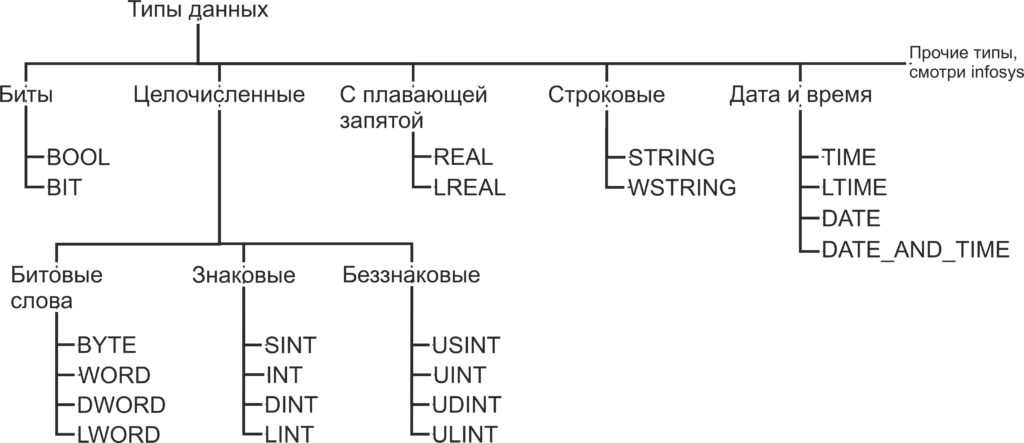
Классификация типов данных TwinCAT 3

Биты

BOOL — это простейший тип данных, как уже было сказано, этот тип данных может принимать только два значения 0 и 1. Так же в TwinCAT, как и в большинстве языков программирования, эти значения, наравне с 0 и 1, обозначаются как TRUE и FALSE и несут в себе количество информации, соответствующее одному биту. Минимальным объемом данных, который читается из памяти за один раз, является байт, то есть восемь бит. Поэтому, для оптимизации скорости доступа к данным, переменная типа BOOL занимает восемь бит памяти. Для хранения самой переменной используется нулевой бит, а биты с первого по седьмой заполнены нулями. Впрочем, на практике о таком нюансе приходится вспоминать достаточно редко.

BIT — то же самое, что и BOOL, но в памяти занимает 1 бит. Как можно догадаться, операции с этим типом данных медленнее чем с типом BOOL, но он занимает меньше места в памяти. Тип данных BIT отсутствует в стандарте МЭК 61131-3 и поддерживается исключительно в TwinCAT, поэтому стоит отдавать предпочтение типу BOOL, когда у вас нет явных поводов использовать тип BIT.

Целочисленные типы данных

BYTE — тип данных, по размеру соответствующий одному байту. Хоть с типом BYTE можно производить математические операции, но в первую очередь он предназначен для хранения набора из 8 бит. Иногда в таком виде удобнее, чем побитно, передавать данные по цифровым интерфейсам, работать с входами выходами и так далее. С такими вопросами мы будем знакомится далее по мере изучения курса. В переменную типа BYTE можно записать числа из диапазона 0..255 (0..2⁸-1).

WORD — то же самое, что и BYTE, но размером 16 бит. В переменную типа WORD можно записать числа из диапазона 0..65 535 (0..2¹⁶-1). Тип данных WORD переводится с английского как «слово». Давным-давно термином машинное слово называли группу бит, обрабатываемых вычислительной машиной за один раз. Была уместна фраза «Программа состоит из машинных слов.». Со временем этим термином перестали пользоваться в прямом его значении, и сейчас под термином «машинное слово» обычно подразумевается группа из 16 бит.

DWORD — то же самое, что и BYTE, но размером 32 бит. В переменную типа DWORD можно записать числа из диапазона 0..4 294 967 295 (0..2³²-1). DWORD — это сокращение от double word, что переводится как двойное слово. Довольно часто буква «D» перед каким-либо типом данных значит, что этот тип данных в два раза длиннее, чем исходный.

LWORD — то же самое, что и BYTE, но размером 64 ;бит. В переменную типа LWORD можно записать числа из диапазона 0..18 446 744 073 709 551 615 (0..2⁶⁴-1). LWORD — это сокращение от long word, что переводится как длинное слово. Приставка «L» перед типом данных, как правило, означает что такой тип имеет длину 64 бита.

SINT — знаковый тип данных, длинной 8 бит. В переменную типа SINT можно записать числа из диапазона -128..127 (-2⁷..2⁷-1). В отличии от всех предыдущих типов данных этот тип данных предназначен для хранения именно чисел, а не набора бит. Слово знаковый в описании типа означает, что такой тип данных может хранить как положительные, так и отрицательные значения. Для хранения знака числа предназначен старший, в данном случае седьмой, разряд числа. Если старший разряд имеет значение 0, то число интерпретируется как положительное, если 1, то число интерпретируется как отрицательное. Приставка «S» означает short, что переводится с английского как короткий. Как вы догадались, SINT короткий вариант типа INT.

USINT — беззнаковый тип данных, длинной 8 бит. В переменную типа USINT можно записать числа из диапазона 0..255 (0..2⁸-1). Приставка «U» означает unsigned, переводится как беззнаковый.

Остальные целочисленные типы аналогичны уже описанным и отличаются только размером. Сведем все целочисленные типы в таблицу.

Тип данных	Нижний предел	Верхний предел	Занимаемая память
BYTE	0	255	8 бит
WORD	0	65 535	16 бит
DWORD	0	4 294 967 295	32 бит
LWORD	0	2⁶⁴-1	64 бит
SINT	-128	127	8 бит
USINT	0	255	8 бит
INT	-32 768	32 767	16 бит
UINT	0	65 535	16 бит
DINT	-2 147 483 648	2 147 483 647	32 бит
UDINT	0	4 294 967 295	32 бит
LINT	-2⁶³	-2⁶³-1	64 бит
ULINT	0	-2⁶⁴-1	64 бит

Выше мы рассматривали целочисленные типы данных, то есть такие типы данных, в которых отсутствует запятая. При совершении математических операций с целочисленными типами данных есть некоторые особенности:

Округление при делении: округление всегда выполняется вниз. То есть дробная часть просто отбрасывается. Если делимое меньше делителя, то частное всегда будет равно нулю, например, 10/11 = 0.
Переполнение: если к целочисленной переменной, например, SINT, имеющей значение 255, прибавить 1, переменная переполнится и примет значение 0. Если прибавить 2, переменная примет значение 1 и так далее. При операции 0 — 1 результатом будет 255. Это свойство очень схоже с устройством стрелочных часов. Если сейчас 2 часа, то 5 часов назад было 9 часов. Только шкала часов имеет пределы не 1..12, а 0..255. Иногда такое свойство может использоваться при написании программ, но как правило не стоит допускать переполнения переменных.

Подробно такие нюансы разбираются в пособиях по дискретной математике. Мы на них пока что останавливаться не будем, но о приведенных двух особенностях не стоит забывать при написании программ.

Можно встретить упоминания о данных с фиксированной запятой, это такие данные, в которых количество знаков после запятой строго фиксировано. В TwinCAT типы данных с фиксированной запятой отсутствуют в чистом виде. TwinCAT поддерживает типы данных с плавающей запятой, то есть количество знаков до и после запятой может быть любым в пределах поддерживаемого диапазона.

Типы данных с плавающей запятой

REAL — тип данных с плавающей запятой длинной 32 бита. В переменную типа REAL можно записать числа из диапазона -3.402 82*10³⁸..3.402 82*10³⁸.

LREAL — тип данных с плавающей запятой длинной 64 бита. В переменную типа LREAL можно записать числа из диапазона -1.797 693 134 862 315 8*10³⁰⁸..1.797 693 134 862 315 8*10³⁰⁸.

При присваивании значения типам REAL и LREAL присваиваемое значение должно содержать целую часть, разделительную точку и дробную часть, например, 7.4 или 560.0.

Так же при записи значения типа REAL и LREAL использовать экспоненциальную (научную) форму. Примером экспоненциальной формы записи будет Me+P, в этом примере

M называется мантиссой.
e называется экспонентой (от англ. «exponent»), означающая «·10^» («…умножить на десять в степени…»),
P называется порядком.

Примерами такой формы записи будет:

1.64e+3 расшифровывается как 1.64e+3 = 1.64*10³ = 1640.
9.764e+5 расшифровывается как 9.764e+5 = 9.764*10⁵ = 976400.
0.3694e+2 расшифровывается как 0.3694e+2 = 0.3694*10² = 36.94.

Еще один способ записи присваиваемого значения переменной типа REAL и LREAL, это добавить к числу префикс REAL#, например, REAL#7.4 или REAL#560. В таком случае можно не указывать дробную часть.

Старший, 31-й бит переменной типа REAL представляет собой знак. Следующие восемь бит, с 30-го по 23-й отведены под экспоненту. Оставшиеся 23 бита, с 22-го по 0-й используются для записи мантиссы.

В переменной типа LREAL старший, 63-й бит также используется для записи знака. В следующие 11 бит, с 62 по 52-й, записана экспонента. Оставшиеся 52 бита, с 51-го по 0-й, используются для записи мантиссы.

При записи числа с большим количеством значащих цифр в переменные типа REAL и LREAL производится округление. Необходимо не забывать об этом в расчетах, к которым предъявляются строгие требования по точности. Еще одна особенность, вытекающая из прошлой, если вы хотите сравнить два числа типа REAL или LREAL, прямое сравнение мало применимо, так как если в результате округления числа отличаются хоть на малую долю результат сравнения будет FALSE. Чтобы выполнить сравнение более корректно, можно вычесть одно число из другого, а потом оценить больше или меньше модуль получившегося результата вычитания, чем наибольшая допустимая разность. Поведение системы при переполнении переменных с плавающей запятой не определенно стандартом МЭК 61131-3, допускать его не стоит.

Строковые типы данных

STRING — тип данных для хранения символов. Каждый символ в переменной типа STRING хранится в 1 байте, в кодировке Windows-1252, это значит, что переменные такого типа поддерживают только латинские символы. При объявлении переменной количество символов в переменной указывается в круглых или квадратных скобках. Если размер не указан, при объявлении по умолчанию он равен 80 символам. Для данных типа STRING количество содержащихся в переменной символов не ограниченно, но функции для обработки строк могут принять до 255 символов.

Объем памяти, необходимый для переменной STRING, всегда составляет 1 байт на символ +1 дополнительный байт, например, переменная объявленная как «STRING [80]» будет занимать 81 байт. Для присвоения константного значения переменной типа STRING присваемый текст необходимо заключить в одинарные кавычки.

Пример объявления строки на 35 символов:

sVar : STRING(35) := 'This is a String'; (*Пример объявления переменной типа STRING*)

WSTRING — этот тип данных схож с типом STRING, но использует по 2 байта на символ и кодировку Unicode. Это значит что переменные типа WSTRING поддерживают символы кириллицы. Для присвоения константного значения переменной типа WSTRING присваемый текст необходимо заключить в двойные кавычки.

Пример объявления переменной типа WSTRING:

wsVar : WSTRING := "This is a WString"; (*Пример объявления переменной типа WSTRING*)

Если значение, присваиваемое переменной STRING или WSTRING, содержит знак доллара ($), следующие два символа интерпретируются как шестнадцатеричный код в соответствии с кодировкой Windows-1252. Код также соответствует кодировке ASCII.

Код со знаком доллара	Его значение в переменной
$<восьмибитное число>	Восьмибитное число интерпретируется как символ в кодировке ISO / IEC 8859-1
‘$41’	A
‘$9A’	©
‘$40’	@
‘$0D’, ‘$R’, ‘$r’	Разрыв строки
‘$0A’, ‘$L’, ‘$l’, ‘$N’, ‘$n’	Новая строка
‘$P’, ‘$p’	Конец страницы
‘$T’, ‘$t’	Табуляция
‘$$’	Знак доллара
‘$’ ‘	Одиночная кавычка

Такое разнообразие кодировок связанно с тем, что у всех из них первые 128 символов соответствуют кодовой таблице ASCII, но в статье для каждого случая кодировка указывалась так же, как она указана в infosys.

Пример:

VAR CONSTANT 
	sConstA  : STRING :='Hello world';



  


                       
  



	sConstB  : STRING :='Hello world $21';   (*Пример объявления переменной типа STRING с спец символом*)
END_VAR

Типы данных времени

TIME — тип данных, предназначенный для хранения временных промежутков. Размер типа данных 32 бита. Этот тип данных интерпретируется в TwinCAT, как переменная типа DWORD, содержащая время в миллисекундах. Нижний допустимый предел 0 (0 мс), верхний предел 4 294 967 295 (49 дней, 17 часов, 2 минуты, 47 секунд, 295 миллисекунд). Для записи значений в переменные типа TIME используется префикс T# и суффиксы d: дни, h: часы, m: минуты, s: секунды, ms: миллисекунды, которые должны располагаться в порядке убывания.

Примеры корректного присваивания значения переменной типа TIME:

TIME1 : TIME := T#14ms;
TIME1 : TIME := T#100s12ms; // Допускается переполнение в старшем отрезке времени.
TIME1 : TIME := t#12h34m15s;

Примеры некорректного присваивания значения переменной типа TIME, при компиляции будет выдана ошибка:

TIME1 : TIME := t#5m68s;   // Переполнение не в старшем отрезке времени недопустимо
TIME1 : TIME := 15ms;   // Пропущен префикс T#
TIME1 : TIME := t#4ms13d;   // Не соблюден порядок записи временных отрезок

LTIME — тип данных аналогичен TIME, но его размер составляет 64 бита, а временные отрезки хранятся в наносекундах. Нижний допустимый предел 0, верхний предел 213 503 дней, 23 часов, 34 минуты, 33 секунд, 709 миллисекунд, 551 микросекунд и 615 наносекунд. Для записи значений в переменные типа LTIME используется префикс LTIME#. Помимо суффиксов, используемых для записи типа TIME для LTIME, используются µs: микросекунды и ns: наносекунды.

Пример:

LTIME1 : LTIME := LTIME#1000d15h23m12s34ms2us44ns; (*Пример объявления переменной типа LTIME*)

TIME_OF_DAY (TOD) — тип данных для записи времени суток. Имеет размер 32 бита. Нижнее допустимое значение 0, верхнее допустимое значение 23 часа, 59 минут, 59 секунд, 999 миллисекунд. Для записи значений в переменные типа TOD используется префикс TIME_OF_DAY# или TOD#, значение записывается в виде <часы : минуты : секунды> . В остальном этот тип данных аналогичен типу TIME.

Пример:

TIME_OF_DAY#15:36:30.123
tod#00:00:00

Date — тип данных для записи даты. Имеет размер 32 бита. Нижнее допустимое значение 0 (01.01.1970), верхнее допустимое значение 4 294 967 295 (7 февраля 2106), да, здесь присутствует возможный компьютерный апокалипсис, но учитывая запас по верхнему пределу, эта проблема не слишком актуальна. Для записи значений в переменные типа TOD используется префикс DATE# или D#, значение записывается в виде <год — месяц — дата>. В остальном этот тип данных аналогичен типу TIME.

DATE#1996-05-06
d#1972-03-29

DATE_AND_TIME (DT) — тип данных для записи даты и времени. Имеет размер 32 бита. Нижнее допустимое значение 0 (01.01.1970), верхнее допустимое значение 4 294 967 295 (7 февраля 2106, 6:28:15). Для записи значений в переменные типа DT используется префикс DATE_AND_TIME # или DT#, значение записывается в виде <год — месяц — дата — час : минута : секунда>. В остальном этот тип данных аналогичен типу TIME.

DATE_AND_TIME#1996-05-06-15:36:30
dt#1972-03-29-00:00:00

На этом раз мы заканчиваем рассмотрение типов данных. Сейчас мы разобрали не все типы данных, остальные можно найти в infosys по пути TwinCAT 3 → TE1000 XAE → PLC → Reference Programming → Data types.

Следующая статья будет целиком состоять из практической работы, мы напишем калькулятор на языке LD.

Источник

16 bits.
Data structures containing such different sized words refer to them as WORD (16 bits/2 bytes), DWORD (32 bits/4 bytes) and QWORD (64 bits/8 bytes) respectively.

Contents

1 Is a word 16 or 32 bits?
2 Is a word always 32 bits?
3 Can a word be 8 bits?
4 How many bits are in a name?
5 What is 64-bit system?
6 What is an 8 bit word?
7 What is 64-bit word size?
8 How big is a word in 64-bit?
9 What is word in C?
10 What is a Dataword?
11 How many values can 10 bits represent?
12 How do you write kilobytes?
13 What is a bit in a horse’s mouth?
14 How many bits is a letter?
15 What is a collection of 8 bits called?
16 Is my computer 32 or 64?
17 What is meant by 32-bit?
18 Do I need 32 or 64-bit?
19 What is better 8-bit or 16 bit?
20 What does 8-bit 16 bit 32 bit microprocessor mean?

Is a word 16 or 32 bits?

In x86 assembly language WORD , DOUBLEWORD ( DWORD ) and QUADWORD ( QWORD ) are used for 2, 4 and 8 byte sizes, regardless of the machine word size. A word is typically the “native” data size of the CPU. That is, on a 16-bit CPU, a word is 16 bits, on a 32-bit CPU, it’s 32 and so on.

Is a word always 32 bits?

The Intel/AMD instruction set concept of a “Word”, “Doubleword”, etc. In Intel docs, a “Word” (Win32 WORD ) is 16 bits. A “Doubleword” (Win32 DWORD ) is 32 bits. A “Quadword” (Win32 QWORD ) is 64 bits.

Can a word be 8 bits?

An 8-bit word greatly restricts the range of numbers that can be accommodated. But this is usually overcome by using larger words. With 8 bits, the maximum number of values is 256 or 0 through 255.

How many bits are in a name?

Find the 8-bit binary code sequence for each letter of your name, writing it down with a small space between each set of 8 bits. For example, if your name starts with the letter A, your first letter would be 01000001.

What is 64-bit system?

An operating system that is designed to work in a computer that processes 64 bits at a time.A 64-bit operating system will not work in a 32-bit computer, but a 32-bit operating system will run in a 64-bit computer. See 64-bit computing.

What is an 8 bit word?

A byte is eight bits, a word is 2 bytes (16 bits), a doubleword is 4 bytes (32 bits), and a quadword is 8 bytes (64 bits).

What is 64-bit word size?

Bits and Bytes
Each set of 8 bits is called a byte. Two bytes together as in a 16 bit machine make up a word , 32 bit machines are 4 bytes which is a double word and 64 bit machines are 8 bytes which is a quad word.

How big is a word in 64-bit?

8 bytes
Data structures containing such different sized words refer to them as WORD (16 bits/2 bytes), DWORD (32 bits/4 bytes) and QWORD (64 bits/8 bytes) respectively.

What is word in C?

A word is an integer number of bytes for example, one, two, four, or eight. When someone talks about the “n-bits” of a machine, they are generally talking about the machine’s word size. For example, when people say the Pentium is a 32-bit chip, they are referring to its word size, which is 32 bits, or four bytes.

What is a Dataword?

A data word is a standard unit of data. For example, most IBM compatible computers have an eight bit word known as byte. Data, Measurements, Word.

How many values can 10 bits represent?

1024
Binary number representation

Length of bit string (b)	Number of possible values (N)
8	256
9	512
10	1024
…

How do you write kilobytes?

In the International System of Units (SI) the prefix kilo means 1000 (10³); therefore, one kilobyte is 1000 bytes. The unit symbol is kB.

What is a bit in a horse’s mouth?

By definition, a bit is a piece of metal or synthetic material that fits in a horse’s mouth and aids in the communication between the horse and rider.Most horses are worked in a bridle with a bit; however, horse owners who don’t care for bits will use a hackamore, or “bitless” bridle.

How many bits is a letter?

eight bits
Computer manufacturers agreed to use one code called the ASCII (American Standard Code for Information Interchange). ASCII is an 8-bit code. That is, it uses eight bits to represent a letter or a punctuation mark. Eight bits are called a byte.

What is a collection of 8 bits called?

A collection of eight bits is called Byte.

Is my computer 32 or 64?

Click Start, type system in the search box, and then click System Information in the Programs list. When System Summary is selected in the navigation pane, the operating system is displayed as follows: For a 64-bit version operating system: X64-based PC appears for the System Type under Item.

What is meant by 32-bit?

32-bit, in computer systems, refers to the number of bits that can be transmitted or processed in parallel.For microprocessors, it indicates the width of the registers and it can process any data and use memory addresses that are represented in 32-bits.

Do I need 32 or 64-bit?

For most people, 64-bit Windows is today’s standard and you should use it to take advantage of security features, better performance, and increased RAM capability. The only reasons you’d want to stick with 32-bit Windows are: Your computer has a 32-bit processor.

What is better 8-bit or 16 bit?

In terms of color, an 8-bit image can hold 16,000,000 colors, whereas a 16-bit image can hold 28,000,000,000. Note that you can’t just open an 8-bit image in Photoshop and convert it to 16-bit.More bits means bigger file sizes, making images more costly to process and store.

What does 8-bit 16 bit 32 bit microprocessor mean?

The main difference between 8 bit and 16 bit microcontrollers is the width of the data pipe. As you may have already deduced, an 8 bit microcontroller has an 8 bit data pipe while a 16 bit microcontroller has a 16 bit data pipe.A 16 bit number gives you a lot more precision than 8 bit numbers.

Источник

I’ve done some research.
A byte is 8 bits and a word is the smallest unit that can be addressed on memory. The exact length of a word varies. What I don’t understand is what’s the point of having a byte? Why not say 8 bits?

I asked a prof this question and he said most machines these days are byte-addressable, but what would that make a word?

Peter Cordes

317k45 gold badges583 silver badges818 bronze badges

asked Oct 13, 2011 at 6:17

Byte: Today, a byte is almost always 8 bit. However, that wasn’t always the case and there’s no «standard» or something that dictates this. Since 8 bits is a convenient number to work with it became the de facto standard.

Word: The natural size with which a processor is handling data (the register size). The most common word sizes encountered today are 8, 16, 32 and 64 bits, but other sizes are possible. For examples, there were a few 36 bit machines, or even 12 bit machines.

The byte is the smallest addressable unit for a CPU. If you want to set/clear single bits, you first need to fetch the corresponding byte from memory, mess with the bits and then write the byte back to memory.

By contrast, one definition for word is the biggest chunk of bits with which a processor can do processing (like addition and subtraction) at a time – typically the width of an integer register. That definition is a bit fuzzy, as some processors might have different register sizes for different tasks (integer vs. floating point processing for example) or are able to access fractions of a register. The word size is the maximum register size that the majority of operations work with.

There are also a few processors which have a different pointer size: for example, the 8086 is a 16-bit processor which means its registers are 16 bit wide. But its pointers (addresses) are 20 bit wide and were calculated by combining two 16 bit registers in a certain way.

In some manuals and APIs, the term «word» may be «stuck» on a former legacy size and might differ from what’s the actual, current word size of a processor when the platform evolved to support larger register sizes. For example, the Intel and AMD x86 manuals still use «word» to mean 16 bits with DWORD (double-word, 32 bit) and QWORD (quad-word, 64 bit) as larger sizes. This is then reflected in some APIs, like Microsoft’s WinAPI.

answered Oct 13, 2011 at 6:51

DarkDustDarkDust

90.4k19 gold badges188 silver badges223 bronze badges

What I don’t understand is what’s the point of having a byte? Why not say 8 bits?

Apart from the technical point that a byte isn’t necessarily 8 bits, the reasons for having a term is simple human nature:

economy of effort (aka laziness) — it is easier to say «byte» rather than «eight bits»
tribalism — groups of people like to use jargon / a private language to set them apart from others.

Just go with the flow. You are not going to change 50+ years of accumulated IT terminology and cultural baggage by complaining about it.

FWIW — the correct term to use when you mean «8 bits independent of the hardware architecture» is «octet».

answered Oct 13, 2011 at 6:47

Stephen CStephen C

692k94 gold badges792 silver badges1205 bronze badges

BYTE

I am trying to answer this question from C++ perspective.

The C++ standard defines ‘byte’ as “Addressable unit of data large enough to hold any member of the basic character set of the execution environment.”

What this means is that the byte consists of at least enough adjacent bits to accommodate the basic character set for the implementation. That is, the number of possible values must equal or exceed the number of distinct characters.
In the United States, the basic character sets are usually the ASCII and EBCDIC sets, each of which can be accommodated by 8 bits.
Hence it is guaranteed that a byte will have at least 8 bits.

In other words, a byte is the amount of memory required to store a single character.

If you want to verify ‘number of bits’ in your C++ implementation, check the file ‘limits.h’. It should have an entry like below.

#define CHAR_BIT      8         /* number of bits in a char */

WORD

A Word is defined as specific number of bits which can be processed together (i.e. in one attempt) by the machine/system.
Alternatively, we can say that Word defines the amount of data that can be transferred between CPU and RAM in a single operation.

The hardware registers in a computer machine are word sized.
The Word size also defines the largest possible memory address (each memory address points to a byte sized memory).

Note – In C++ programs, the memory addresses points to a byte of memory and not to a word.

answered May 29, 2012 at 18:12

It seems all the answers assume high level languages and mainly C/C++.

But the question is tagged «assembly» and in all assemblers I know (for 8bit, 16bit, 32bit and 64bit CPUs), the definitions are much more clear:

byte  = 8 bits 
word  = 2 bytes
dword = 4 bytes = 2Words (dword means "double word")
qword = 8 bytes = 2Dwords = 4Words ("quadruple word")

answered Feb 3, 2013 at 18:38

johnfoundjohnfound

6,8014 gold badges30 silver badges58 bronze badges

Why not say 8 bits?

Because not all machines have 8-bit bytes. Since you tagged this C, look up CHAR_BIT in limits.h.

answered Oct 13, 2011 at 6:19

cnicutarcnicutar

177k25 gold badges361 silver badges391 bronze badges

A word is the size of the registers in the processor. This means processor instructions like, add, mul, etc are on word-sized inputs.

But most modern architectures have memory that is addressable in 8-bit chunks, so it is convenient to use the word «byte».

answered Oct 13, 2011 at 6:21

VoidStarVoidStar

5,1611 gold badge30 silver badges44 bronze badges

In this context, a word is the unit that a machine uses when working with memory. For example, on a 32 bit machine, the word is 32 bits long and on a 64 bit is 64 bits long. The word size determines the address space.

In programming (C/C++), the word is typically represented by the int_ptr type, which has the same length as a pointer, this way abstracting these details.

Some APIs might confuse you though, such as Win32 API, because it has types such as WORD (16 bits) and DWORD (32 bits). The reason is that the API was initially targeting 16 bit machines, then was ported to 32 bit machines, then to 64 bit machines. To store a pointer, you can use INT_PTR. More details here and here.

answered Oct 13, 2011 at 6:39

npclaudiunpclaudiu

2,3911 gold badge16 silver badges18 bronze badges

The exact length of a word varies. What I don’t understand is what’s the point of having a byte? Why not say 8 bits?

Even though the length of a word varies, on all modern machines and even all older architectures that I’m familiar with, the word size is still a multiple of the byte size. So there is no particular downside to using «byte» over «8 bits» in relation to the variable word size.

Beyond that, here are some reasons to use byte (or octet¹) over «8 bits»:

Larger units are just convenient to avoid very large or very small numbers: you might as well ask «why say 3 nanoseconds when you could say 0.000000003 seconds» or «why say 1 kilogram when you could say 1,000 grams», etc.
Beyond the convenience, the unit of a byte is somehow as fundamental as 1 bit since many operations typically work not at the byte level, but at the byte level: addressing memory, allocating dynamic storage, reading from a file or socket, etc.
Even if you were to adopt «8 bit» as a type of unit, so you could say «two 8-bits» instead of «two bytes», it would be often be very confusing to have your new unit start with a number. For example, if someone said «one-hundred 8-bits» it could easily be interpreted as 108 bits, rather than 100 bits.

¹ Although I’ll consider a byte to be 8 bits for this answer, this isn’t universally true: on older machines a byte may have a different size (such as 6 bits. Octet always means 8 bits, regardless of the machine (so this term is often used in defining network protocols). In modern usage, byte is overwhelmingly used as synonymous with 8 bits.

answered Feb 10, 2018 at 22:17

BeeOnRopeBeeOnRope

59k15 gold badges200 silver badges371 bronze badges

Whatever the terminology present in datasheets and compilers, a ‘Byte’ is eight bits. Let’s not try to confuse enquirers and generalities with the more obscure exceptions, particularly as the word ‘Byte’ comes from the expression «By Eight». I’ve worked in the semiconductor/electronics industry for over thirty years and not once known ‘Byte’ used to express anything more than eight bits.

answered Feb 3, 2013 at 18:04

A group of 8 bits is called a byte ( with the exception where it is not for certain architectures )

A word is a fixed sized group of bits that are handled as a unit by the instruction set and/or hardware of the processor. That means the size of a general purpose register ( which is generally more than a byte ) is a word

In the C, a word is most often called an integer => int

answered Oct 13, 2011 at 6:23

tolitiustolitius

22k6 gold badges69 silver badges81 bronze badges

Reference:https://www.os-book.com/OS9/slide-dir/PPT-dir/ch1.ppt

The basic unit of computer storage is the bit. A bit can contain one of two
values, 0 and 1. All other storage in a computer is based on collections of bits.
Given enough bits, it is amazing how many things a computer can represent:
numbers, letters, images, movies, sounds, documents, and programs, to name
a few. A byte is 8 bits, and on most computers it is the smallest convenient
chunk of storage. For example, most computers don’t have an instruction to
move a bit but do have one to move a byte. A less common term is word,
which is a given computer architecture’s native unit of data. A word is made up
of one or more bytes. For example, a computer that has 64-bit registers and 64-
bit memory addressing typically has 64-bit (8-byte) words. A computer executes
many operations in its native word size rather than a byte at a time.
Computer storage, along with most computer throughput, is generally measured
and manipulated in bytes and collections of bytes.
A kilobyte, or KB, is 1,024 bytes
a megabyte, or MB, is 1,024 2 bytes
a gigabyte, or GB, is 1,024 3 bytes
a terabyte, or TB, is 1,024 4 bytes
a petabyte, or PB, is 1,024 5 bytes
Computer manufacturers often round off these numbers and say that a
megabyte is 1 million bytes and a gigabyte is 1 billion bytes. Networking
measurements are an exception to this general rule; they are given in bits
(because networks move data a bit at a time)

answered Apr 13, 2020 at 9:00

LiLiLiLi

3833 silver badges11 bronze badges

If a machine is byte-addressable and a word is the smallest unit that can be addressed on memory then I guess a word would be a byte!

answered Oct 13, 2011 at 6:19

K-balloK-ballo

79.9k20 gold badges159 silver badges169 bronze badges

The terms of BYTE and WORD are relative to the size of the processor that is being referred to. The most common processors are/were 8 bit, 16 bit, 32 bit or 64 bit. These are the WORD lengths of the processor. Actually half of a WORD is a BYTE, whatever the numerical length is. Ready for this, half of a BYTE is a NIBBLE.

answered Feb 9, 2018 at 17:59

In fact, in common usage, word has become synonymous with 16 bits, much like byte has with 8 bits. Can get a little confusing since the «word size» on a 32-bit CPU is 32-bits, but when talking about a word of data, one would mean 16-bits. Microcontrollers with a 32-bit word size have taken to calling their instructions «longs» (supposedly to try and avoid the word/doubleword confusion).

answered Oct 13, 2011 at 12:52

Brian KnoblauchBrian Knoblauch

20.4k15 gold badges61 silver badges92 bronze badges

Источник

Electronic Circuits: Digital

Louis E. FrenzelJr., in Electronics Explained (Second Edition), 2018

Maximum Decimal Value for N Bits

The number of bits in a binary word determines the maximum decimal value that can be represented by that word. This maximum value is determined with the formula:

M=2N−1

where M is the maximum decimal value and N is the number of bits in the word.

For example, what is the largest decimal number that can be represented by 4 bits?

M=2N−1=16−1=15

With 4 bits, the maximum possible number is binary 1111 or decimal 15.

The maximum decimal number that can be represented with 1 byte is 255 or 11111111. An 8-bit word greatly restricts the range of numbers that can be accommodated. But this is usually overcome by using larger words.

There is one important point to know before you leave this subject. The formula M = 2^N − 1 determines the maximum decimal quantity (M) that can be represented with a binary word of N bits. This value is 1 less than the maximum number of values that can be represented. The maximum number of values that can be represented (Q) is determined with the formula:

Q=2N

With 8 bits, the maximum number of values is 256 or 0 through 255.

Table 5.1 gives the number of bits in a binary number and the maximum number of states that can be represented.

Table 5.1. Number of Bits in Binary Number and Maximum Number of States

Number of Bits	Maximum States
8	256
12	4096 (4 K)
16	65,536 (64 K)
20	1,048,576 (1 M)
24	16,777,216 (16 M)
32	4,294,967,296 (4 G)

G, gigabits = 1,0737,41,824; K, kilobits = 1024; M, megabits = 1,048,576.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128116418000059

Serial I/O Primer

Louis E. FrenzelJr, in Handbook of Serial Communications Interfaces, 2016

Asynchronous versus Synchronous Transmission

Asynchronous serial data is usually sent one binary word at a time. Each is accompanied by start and stop bits that define the beginning and end of a word. Figure 2.10 shows one byte with a start bit that transitions from 1 to 0 for one bit time. The byte bits follow. A 0 to 1 transition or a low signal is the stop bit the end of the word. Some standards use two stop bits. Note that a 1 is low (−12V) and a 0 is high (+12V).

Figure 2.10. Asynchronous data transmission.

Asynchronous transmission is very reliable but is inefficient because of the start and stop bits. These bits also slow transmission. However, for some applications, the lack of speed is not a disadvantage where reliability is essential.

Many serial interfaces and protocols use this asynchronous method. It is so widely used that the basic process has been incorporated into a standard integrated circuit known as a universal asynchronous receiver transmitter or UART. Figure 2.11 shows the basic arrangement. Data to be transmitted is usually derived from a computer or embedded controller and sent to the UART over a parallel bus and stored temporarily in a buffer memory. It is then sent to another buffer register over the UARTs internal bus. The byte to be sent is then loaded into a shift register where start, stop, and parity bits are added. Parity is usually optional and odd or even parity may be selected. A clock then transmits to word serially in NRZ format.

Figure 2.11. The UART is at the heart of most asynchronous interfaces.

Received data comes in serially to the lower shift register. The start, stop, and parity bits are monitored and actions are taken accordingly. The received byte is then transferred in parallel to the buffer and then to an external microcontroller or a PC. Control logic provides input and output control signals used in some protocols. While UARTs are available as an IC today, they are more likely to be integrated into an embedded controller or other IC.

The overhead of the stop and start bits can be eliminated or at least minimized by using synchronous transmission. Each data word is transmitted directly one after the other in a block where the beginning or end is defined by selected bits or words. Digital counters keep track of word boundaries by counting bits and words. Synchronous transmission is faster than asynchronous because there are fewer overhead bits. However, synchronous transmission does have its overhead. Data is transmitted in blocks or frames of words and special fields define the beginning and end of each frame. These codes take the form of multibit words that form the packet overhead.

The term “asynchronous” also refers to the random start of any transmission. In most data communications systems, data is transmitted in packets, usually synchronous. However, it is not known when a packet will begin or end as it is not tied to any timing convention. Data is just sent when needed.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128006290000024

The digital computer

Martin Plonus, in Electronics and Communications for Scientists and Engineers (Second Edition), 2020

8.2.3 Communicating with a computer: Programming languages

Programming languages provide the link between human thought processes and the binary words of machine language that control computer actions, in other words, instructions written by a programmer that the computer can execute. A computer chip understands machine language only, that is, the language of 0’s and 1’s. Programming in machine language is incredibly slow and easily leads to errors. Assembly languages were developed that express elementary computer operations as mnemonics instead of numeric instructions. For example, to add two numbers, the instruction in assembly language is ADD. Even though programming in assembly language is time consuming, assembly language programs can be very efficient and should be used especially in applications where speed, access to all functions on board, and size of executable code are important. A program called an assembler is used to convert the application program written in assembly language to machine language. Although assembly language is much easier to use since the mnemonics make it immediately clear what is meant by a certain instruction, it must be pointed out that assembly language is coupled to the specific microprocessor. This is not the case for higher-level languages. Higher languages such as C/C ++, JAVA, and scripting languages like Python, were developed to reduce programming time, which usually is the largest block of time consumed in developing new software. Even though such programs are not as efficient as programs written in assembly language, the savings in product development time when using a language such as C has reduced the use of assembly language programming to special situations where speed and access to all a computer’s features is important. A compiler is used to convert a C program into the machine language of a particular type of microprocessor. A high-level language such as C is frequently used even in software for 8-bit controllers, and C ++ and JAVA are often used in used in the design of software for 16-, 32-, and 64-bit microcontrollers.

Fig. 8.1 illustrates the translation of human thought to machine language by use of programming languages.

Fig. 8.1. Programming languages provide the link between human thought statements and the 0’s and 1’s of machine code which the computer can execute.

Single statements in a higher-level language, which is close to human thought expressions, can produce hundreds of machine instructions, whereas a single statement in the lower-level assembly language, whose symbolic code more closely resembles machine code, generally produces only one instruction.

Fig. 8.2 shows how a 16-bit processor would execute a simple 16-bit program to add the numbers in memory locations X, Y, and Z and store the sum in memory location D. The first column shows the binary instructions in machine language. Symbolic instructions in assembly language, which have a nearly one-to-one correspondence with the machine language instructions, are shown in the next column. They are quite mnemonic and should be read as “Load the number at location X into the accumulator register; add the number at location Y to the number in the accumulator register; add the number at location Z to the number in the accumulator register; store the number in the accumulator register at location D.” The accumulator register in a microcontroller is a special register where most of the arithmetic operations are performed. This series of assembly language statements, therefore, accomplishes the desired result. This sequence of assembly statements would be input to the assembler program that would translate them into the corresponding machine language (first column) needed by the computer. After assembly, the machine language program would be loaded into the machine and the program executed. Because programming in assembly language involves many more details and low-level details relating to the structure of the microcomputer, higher-level languages have been developed. FORTRAN (FOR—mula TRANslator) was one of the earlier and most widely used programming languages and employs algebraic symbols and formulas as program statements. Thus the familiar algebraic expression for adding numbers becomes a FORTRAN instruction; for example, the last column in Fig. 8.2 is the FORTRAN statement for adding the three numbers and is compiled into the set of corresponding machine language instructions of the first column.

Fig. 8.2. Three types of program instructions. Machine language gives instructions as 0’s and 1’s and is the only language that the computer understands. Assembly language is more concise but still very cumbersome when programming. A high-level language such as FORTRAN or C facilitates easy programming.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128170083000085

THE GUIDANCE OF MISSILES BY RADIO REMOTE-CONTROL

JEAN MARCUS, in Radio Remote-Control and Telemetry and their Application to Missiles, 1966

VII.4.2.1 General Remarks

The remote-control instructions are in the form of a succession of binary words, which are transmitted cyclically. Each order is therefore characterized by a digital word, which can be decomposed into two syllables: address and command. The “address” syllable indicates the component at which the order itself is directed. With a five-digit address, for example, thirty-two different combinations are available. To each of these address digits can be attached additional digits as a check upon the address which is transmitted. When the instructions are of the “yes-no” type, the command syllable consists of two digits, either 11 or 00, which indicate that the command is or is not to be executed. A progressive type of remote control can be obtained by including enough digits in the “command” syllable, making due allowance for the accuracy of the order.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9781483200866500102

Processing Elements

Lars Wanhammar, in DSP Integrated Circuits, 1999

11.2.3 One’s-Complement Representation

One’s-complement representation as just discussed is a diminished-radix complement representation with R = r^k − Q = 1 − Q for r = 2 and k = 0. A normalized W_d-bit binary word in one’s-complement representation is interpreted as

(11.10)x=−x01−Q+∑i=1Wd−1xi2−i

The values lie in the range − 1 + Q ≤ x ≤ l − Q where Q=2−Wd+1. Also, in one’s-complement representation, the zero value has a redundant binary representation which reduces the value range and complicates the checking for zero. The values + 1 and − 1 can not be represented. Numbers having the same magnitude, but different signs, are represented by different binary words. For example, we have

+0.82812510=0.1101011C−0.82812510=1.0010101C010=0.0000001Cor1.1111111C

For x > 0, one’s-complement representation has the same binary words as, for example, signed-magnitude representation. For x < 0, the values are the bit-complement of the corresponding positive values. Addition and subtraction in one’s-complement representation are more complicated to implement than in binary offset and two’s-complement representations, which will be discussed later.

Example 11.1

Show that the negative value of a number, x, in one’s-complement representation can be obtained by inverting all bits in the binary word.

We have from Equation (11.10)

y=−x=−−x01−Q+∑i=1Wd−1xi2−i=x01−Q−∑i=1Wd−1xi2−i+∑i=1Wd−11−xi2−i=−1−x01−Q+∑i=1Wd−11−xi2−i=−x¯01−Q+∑i=1Wd−1x¯i2−i

Hence, the sign of a number in one’s-complement representation can be changed by just taking the bit-complement. Thus, subtraction can be accomplished by addition of the bit-complemented word.

A change of sign is easier in signed-magnitude representation compared to binary offset and two’s-complement representations, since using these representations, changing the sign of a number is done by taking the bit-complement and adding 1 to the least-significant position. Multiplication using one’s-complement is more difficult to implement than with two’s-complement or binary offset since an end-around-carry is required.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780127345307500118

Designs and Error-Correcting Codes

K.T. Phelps, C.A. Rodger, in Encyclopedia of Physical Science and Technology (Third Edition), 2003

III Constant Weight Codes

A constant weight code (CW) with parameters n, d, w is a set C of binary words of length n all having weight w such that the distance between any two codewords is at least d. All nontrivial (n, d, w) CW codes have d ≤ 2w. Let A(n, d, w) be the largest number of codewords in any CW code with these parameters. The classic problem then is to detemine this number or find the best upper and lower bounds on A(n, d, w).

Binary CW codes have found application in synchronization problems, in areas such as optical codedivision multiple-acces (CDMA) communications systems, frequency-hopping spread-spectrum communications, modile radio, radar and sonar signal design, and the construction of protocol sequences for multiuser collision channel without feedback. Constant weight codes over other alphabets have received some attention, but so far there have been few applications. We will only discuss the binary CW codes.

Constant weight codes have been extensively studied, and a good reference is MacWilliams and Sloane (1977). Eric Raines and Neil Sloane maintain a table of the best known lower bounds on A(n, d, w) on the web site: http://www.research.att.com/njas/codes/Andw/. We will present an overview of this topic with an emphasis on the connections with designs.

Since the sum of any two binary words of the same weight always has even weight, we have A(n,2δ − 1, w) = A(n,2δ,w). We will assume from now on that the distance d is even. We also have A(n, d, w) = A(n, d, n − w), since whenever two words are distance d apart, so are their complements. This means one only needs to consider the case w ≤ n/2.

The connection between CW codes and designs is immediate. In terms of sets, a CW code is just a collection of w subsets of an n set where the intersection of any two w subsets contains at most t=w−d2 elements. Equivalently, a CW code is a partial Sw−d2+1,w,n Steiner system. We then have

A(n,d,w)≤n(n−1)…(n−w+d/2)w(w−1)…(d/2)

with equality if and only if a Steiner system S(w−d2+1,w,n)exists.

The interest in CW codes also comes from the problem of finding linear (or nonlinear) codes (n, M, d) of maximum size M. Obviously, A(n, d, w) is an upper bound on the number of words of a given weight in such a maximum code. Conversely, such codes (or their cosets) can give lower bounds for A(n, d, w). In particular, the stronger version of the Hamming Bound (given in the section on perfect codes) was originally proved using A(n,2t + 2,2t + 1).

A(n,2t + 2,2t + 1) is just the number of blocks in a maximum partial S(t + 1,2t + 1,n) design or packing. If C is a t-error-correcting code, then for any c ∈ C, the number of blocks in a neighborhood packing ∣NS(c)∣ ≤ A(n,2t + 2,2t + 1). The number of words that are distance t + 1 from c but not distance t from any other codeword is

(nt+1)−(2t+1t+1)|NS(c)|≥(nt+1)−(2t+1t+1)A(2t+2,2t+1).

Each such word is distance t + 1 from at most ⌊n/t + 1⌋ other codewords. Thus, summing over all c ∈ C, each such word is counted at most this many times. This gives a stronger version of the Hamming bound:

|C|((∑i=0t(ni))+(nt+1)−(2t+1t+1)A(n,2t+2,2t+1)⌊n/(t+1)⌋)≤2n.

Constant weight codes cannot be linear, since this would mean the zero vector was in the code, but one can have a code with all nonzero words having the same weight. These codes are sometime referred to as linear equidistant codes. The dual of the Hamming code (also called the simplex code) is an example of such a code. In fact, it has been proved that the only such codes are formed by taking several copies of a simplex code. The proofs that all such codes are generalized simplex codes come explicitly from coding theory (Bonisoli, 1983) and also implicitly from results on designs and set systems (Teirlinck, 1980). There is a close connection between linear equidistant codes and finite geometries. The words of a simplex code correspond to the hyperplanes of projective space [over GF (2)] just as the words of weight 3 in the Hamming code correspond to lines in this projective space. [For connections between codes and finite geometries, see Black and Mullin (1976).]

Another variation on CW codes are optical orthogonal codes (OOC) which were motivated by an application to optical CDMA communication systems. Briefly, an (n, w, t_a,t_b) OOC is a CW code, C, of length n and weight w such that for any c = (c₀,c₁,…,c_n−1) ∈ C, and each y ∈ C, c ≠ y and each i ≢ 0 (mod n),

(1)∑j=0n−1cjcj+i≤ta,

and

(2)∑j=0n−1cjyj+i≤tc.

Equation (1) is the autocorrelation property, and Eq. (2) is the cross-correlation property. Most research has focused on the case where t_a = t_c = t, in which case we refer to an (n, w, t) OOC. Again, one can refomulate these properties in terms of (partial) designs or packings. In this case, an OOC is a collection of w subsets of the integers (mod n), such that for subsets c, b ∈ C,

(3)c+i∩c+j≤tai≠j,

and

(4)c+i∩b+j≤tc.

Here, c + i = {x + i (mod n) ∣ x ∈ c}.

An OOC code is equivalent to a cyclic design or packing. A code or packing is said to be cyclic if every cyclic shift of a codeword (or block) is another codeword. The set of all cyclic shifts of a codeword is said to be an orbit. A representative from that orbit is often called a base block. An (n, w, t) OOC is a set of base blocks for a cyclic (partial) S(t + 1,w, n) design or packing (assuming t < w). Conversely, given such a cyclic partial S(t + 1,w, n) design or packing, one can form an (n, w, t) OOC by taking one representative block or codeword from each orbit.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B0122274105001678

Compression

StéphaneMallat , in A Wavelet Tour of Signal Processing (Third Edition), 2009

Shannon Entropy

The Shannon theorem [429] proves that entropy is a lower bound for the average bit rate R_X of any prefix code.

Theorem 10.1:

Shannon. Let X be a source with symbols {xk}1≤k≤K that occur with probabilities {pk}1≤k≤K that occur with probabilities {pk}l≤k≤K. The average bit rate R_X of a prefix code satisfies

(10.4)RX≥ϰ(X)=−Σk=1Kpklog2pk.

Moreover, there exists a prefix code such that

and H(X) is called the entropy of X.

Proof.

This theorem is based on the Kraft inequality given by Lemma 10.1.

Lemma 10.1:

Kraft. Any prefix code satisfies

(10.6)Σk=1K2−lk≤1.

Conversely, if {lk}1≤k≤K is a positive sequence that satisfies (10.6), then a sequence of binary words {wk}1≤k≤K of length {lk}1≤k≤K exists that satisfies the prefix condition.

To prove (10.6), we construct a full binary tree T the leaves of which are at the depth m = max{l₁, l₂, …, l_k}. Inside this tree, we can locate node n_k at depth l_k that codes the binary word w_k. We denote T_k to the subtree with the root of n_k, as illustrated in Figure 10.2. This subtree has a depth m – l_k and thus contains 2m−lk nodes at the level m of T. There are 2^m nodes at the depth m of T and the prefix condition implies that the subtrees T₁, …, T_K have no node in common, so

FIGURE 10.2. The leaves at depth m of tree T are regrouped as sets S_k of 2m−lk nodes that are the leaves of tree T_k, having its root n_k at depth l_k. Here, m = 4 and l₁ = 2, so S₁ has 2² nodes.

Σk=1K2m−lk≤2m,

which proves (10.6).

Conversely, we consider {lk}1≤k≤K that satisfies (10.6), with l1≤l2≤…≤lk and m = max{l₁, l₂, …, l_K}. Again, we construct a full binary tree T with leaves at depth m. Let S₁ be the 2^m–l1 first nodes at level m, S₂ be the next 2^m–l2 nodes, and so on, as illustrated in Figure 10.2. Since Σk=1K 2m−lk≤2m, the sets {Sk}1≤k≤K, have fewer than 2^m elements and can thus be constructed at level m of the tree. The nodes of a set S_k are the leaves of a subtree T_k of T. The root n_k of T_k is at depth l_k and corresponds to a binary word w_k. By construction, all these subtrees T_k are distinct, so {wk}1≤k≤K is a prefix code where each code word w_k has a length l_k. This finishes the lemma proof.

To prove the two inequalities (10.4) and (10.5) of the theorem, we consider the minimization of

RX=Σk=1Kpklk

under the Kraft inequality constraint

Σk=1K2−lk≤1.

If we admit noninteger values for l_k, we can verify with Lagrange multipliers that the minimum is reached for l_k = – log₂ p_k. The value of this minimum is the entropy lower bound:

RX=Σk=1Kpklk=−Σk=1Kpklogpk=ϰ(X),

which proves (10.4).

To guarantee that l_k is an integer, the Shannon code is defined by

(10.7)lk=−⌈log2pk⌉,

where ⌈x⌉ is the smallest integer larger than x. Since lk≥−log2pk, the Kraft inequality is satisfied:

Σk=1K2−lk≤Σk=1K2log2pk=1.

Lemma 10.1 proves that there exists a prefix code with binary words w_k that have length w_k. For this code,

RX=Σk=1Kpklk≤Σk=1Kpk(−log2pk+1)=ϰ(X)+1,

which proves (10.5).

The entropy H(X) measures the uncertainty as to the outcome of the random variable X, and

0≤ϰ(X)≤log2K.

The maximum value log₂ K corresponds to a sequence with a uniform probability distribution p_k = 1/K for 1≤k≤K. Since no value is more probable than any other, the uncertainty as to the outcome of X is maximum. The minimum entropy value H(X) = 0 corresponds to a source where one symbol x_k occurs with probability 1. There is no uncertainty as to the outcome of X because we know in advance that it will be equal to x_k.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123743701000148

Dynamic Range

Morgan Jones, in Valve Amplifiers (Fourth Edition), 2012

Precision

Computers use binary numbers, so if we make our numerical measurement more precise by using smaller quantising levels, there must be more of them, and a binary word comprising more bits is required. CD used a 16-bit word, and because there are two possible states for each bit, the total number of different levels that can be described by a 16 bit word is 2¹⁶=65,536. Similarly, a 24 bit system can describe 2²⁴=16,777,216 different levels, but requires one-and-a-half times as much memory to store each word (24/16=1½).

As a rule of thumb (ignoring dither), the Dynamic Range (DR) of a digital system is:

DRdB=6n

where n=number of bits.

Thus, a 16 bit system has a theoretical dynamic range of 6×16=96 dB and a 24 bit system 144 dB (never achieved because Analogue to Digital Convertors (ADCs) simply aren’t that good).

We could decide to be more precise by making more numerical measurements. Sampling twice as often doubles the memory required.

To sum up, a more precise description generates more data, requiring more memory, and this will become significant later.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780080966403000034

Vector Quantization Techniques in Image Compression

A. Gersho, … S.-W. Wu, in Handbook of Visual Communications, 1995

6.1.5 Performance and Complexity of Vector Quantization

VQ is often loosely described as the optimal way to quantize a vector. Specifically, consider any encoding system that operates in any way on the components of the input vector and generates a binary word (or a set of binary words) with a total of up to N possible distinct values, and an associated decoding system that reproduces an approximation to this vector from the binary data. Such an encoding method can never provide superior performance (and generally will give inferior performance) to a suitably designed VQ coding scheme with a codebook of size N [1]. The proof is simply to note that the given decoder can be used to generate a unique VQ codebook whose associated VQ decoder exactly replicates the given decoder operation. Then, by replacing the given encoder with a nearest neighbor encoder based on this codebook, the VQ will necessarily match or exceed the performance of the original coding scheme.

In general, in encoding a waveform or an image, the performance of VQ improves as the dimension increases. In fact, even if a sequence of samples are statistically independent, the average distortion per pixel decreases (slightly) as the dimension is increased. Asymptotically as the dimension approaches infinity, VQ theoretically can approach the ultimate distortion–rate performance bounds studied in information theory. Intuitively, it is clear that the benefit from increasing the dimension in coding a group of pixels in an image is the ability it provides to exploit more spatial correlation among the samples. In this chapter we use the term correlation in a general sense to include nonlinear as well as linear statistical interdependency among samples.

While VQ offers the best rate–distortion performance possible for coding a block of signal samples or parameters, it has possibly the worst complexity of any effective coding scheme. The complexity of performing a nearest neighbor search is proportional to the codebook size N and therefore grows exponentially with the dimension k for a fixed rate r. This is not a problem for moderate codebook sizes, but it is a sufficient obstacle to prevent direct VQ of an image block with sufficient size to adequately exploit spatial correlation. For example, suppose the rate of 0.25 bit per pixel (bpp) is specified. Then, for an 8 × 8 block, the codebook size is N = 65536, and for a 16 × 16 block, the size is N = 10¹⁹. Thus a complexity barrier is quickly reached as the dimension grows for a given coding resolution.

The complexity problem does not eliminate VQ as a viable coding method, but it does generally limit the direct use of full search VQ to the role of a building block in a complete coding system. Thus other methods for eliminating redundancy, i.e., for exploiting the extensive spatial correlation in an image, are generally required prior to the quantization stage. When VQ is applied, the vectors usually represent a set of features extracted from an image rather than image pixels themselves. Alternatively, many coding systems can be viewed as a particular form of structurally constrained VQ that, in effect, performs VQ on large-dimension vectors by forcing constraints on the encoder and decoder mappings. These schemes may not resemble the paradigm of encoding via an exhaustive search through a single codebook.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780080918549500117

Data Handling

W. Bolton, in Programmable Logic Controllers (Sixth Edition), 2015

12.1 Registers and Bits

A register is where data can be stored (see Section 8.1 for an initial discussion of registers). In a PLC there are a number of such registers. Each data register can store a binary word of usually 8 or 16 bits. The number of bits determines the size of the number that can be stored. The binary system uses only two symbols, 0 and 1 (see Chapter 3). Thus we might have the 4-bit number 1111. This is the denary number, that is, the familiar number system based on 10s, of 2⁰ + 2¹ + 2² + 2³ = 1 + 2 + 4 + 8 = 15. Thus a 4-bit register can store a positive number between 0 and 2⁰ + 2¹ + 2² + 2³ or 2⁴ − 1 = 15. An 8-bit register can store a positive number between 0 and 2⁰ + 2¹ + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ + 2⁷ or 2⁸ − 1, that is, 255. A 16-bit register can store a positive number between 0 and 2¹⁶ − 1, that is, 65,535.

Thus a 16-bit word can be used for positive numbers in the range 0 to 65,535. If negative numbers are required, the most significant bit is used to represent the sign, a 1 representing a negative number and a 0 a positive number; the format used for negative numbers is two’s complement. Two’s complement is a way of writing negative numbers so that when we add, say, the signed equivalent of +5 and –5, we obtain 0. Thus in this format, 1011 represents the negative number −5 and 0101 the positive number +5; 1011 + 0101 = (1)0000 with the (1) for the 4-bit number being lost. See Chapter 3 for further discussion.

The binary coded decimal (BCD) format is often used with PLCs when they are connected to devices such as digital displays. With the natural binary number there is no simple link between the separate symbols of a denary number and the equivalent binary number. You have to work out the arithmetic to decipher one number from the other. With the BCD system, each denary digit is represented, in turn, by a 4-bit binary number (four is the smallest number of binary bits that gives a denary number greater than 10, that is, 2ⁿ > 10). To illustrate this idea, consider the denary number 123. The 3 is represented by the 4-bit binary number 0011, the 2 by the 4-bit number 0010, and the 1 by 0001. Thus the BCD number of 123 is 0001 0010 0011. BCD is a convenient system for use with external devices that are arranged in denary format, such as decade switches (thumbwheel switches) and digital displays. Then four binary bits can be used for each denary digit. PLCs therefore often have inputs or outputs that can be programmed to convert BCD from external input devices to the binary format needed inside the PLC and from the binary format used internally in the PLC to BCD for external output devices (see Section 12.3).

The thumbwheel switch is widely used as a means of inputting BCD data manually into a PLC. It has four contacts that can be opened or closed to give the four binary bits to represent a denary number (Figure 12.1). The contacts are opened or closed by rotating a wheel using one’s thumb. By using a number of such switches, data can be input in BCD format.

Figure 12.1. Thumbwheel switch.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128029299000121

Источник

Smallest addressable unit

Different meanings

Examples

Processors of the IA-32 -80×86- architecture

PLC

Individual evidence

Uses of words[edit]

Word size choice[edit]

Variable-word architectures[edit]

Word, bit and byte addressing[edit]

Powers of two[edit]

Size families[edit]

Table of word sizes[edit]

See also[edit]

Notes[edit]

References[edit]

Типы данных в языках стандарта МЭК 61131-3

Простые типы данных

Биты

Целочисленные типы данных

Типы данных с плавающей запятой

Строковые типы данных

Типы данных времени

Is a word 16 or 32 bits?

Is a word always 32 bits?

Can a word be 8 bits?

How many bits are in a name?

What is 64-bit system?

What is an 8 bit word?

What is 64-bit word size?

How big is a word in 64-bit?

What is word in C?

What is a Dataword?

How many values can 10 bits represent?

How do you write kilobytes?

What is a bit in a horse’s mouth?

How many bits is a letter?

What is a collection of 8 bits called?

Is my computer 32 or 64?

What is meant by 32-bit?

Do I need 32 or 64-bit?

What is better 8-bit or 16 bit?

What does 8-bit 16 bit 32 bit microprocessor mean?

Electronic Circuits: Digital

Maximum Decimal Value for N Bits

Serial I/O Primer

Asynchronous versus Synchronous Transmission

The digital computer

8.2.3 Communicating with a computer: Programming languages

THE GUIDANCE OF MISSILES BY RADIO REMOTE-CONTROL

VII.4.2.1 General Remarks

Processing Elements

11.2.3 One’s-Complement Representation

Designs and Error-Correcting Codes

III Constant Weight Codes

Compression

Shannon Entropy

Theorem 10.1:

Proof.

Lemma 10.1:

Dynamic Range

Precision

Vector Quantization Techniques in Image Compression

6.1.5 Performance and Complexity of Vector Quantization

Data Handling

12.1 Registers and Bits