Related Pages
2-Step Word Problems And Bar Models
More Math Word Problems
Algebra Word Problems
More Singapore Math Word Problems
Example:
There were 42 mangoes in each crate. 12 such crates of mangoes were delivered to a factory.
4 mangoes were rotten and had to be thrown away. The remaining mangoes were packed into
boxes of 10 mangoes each. How many boxes of mangoes were there?
Solution:
Step 1: Find the total number of mangoes delivered.
12 × 42 = 504
The total number of mangoes delivered was 504.
Step 2: Find the number of remaining mangoes.
504 – 4 = 500
Step 3: Find the number of boxes of mangoes.
500 ÷ 10 = 50
There were 50 boxes of mangoes.
Example:
There were 9500 spectators at a football match. 6375 of them were men. Of the remaining spectators,
there were 4 times as many children as women. How many children were there?
Solution:
Step 1: Find the number of women and children.
9500 – 6375 = 3125
There were 3125 women and children.
Step 2: Find the number of women.
3125 ÷ 5 = 625
There were 625 women.
Step 3: Find the number of children.
625 × 4 = 2500
There were 2500 children.
How to use bar models to solve a word problem that involves “three times as many” and “4 more”?
Example:
Claire loves animals. She has three times as many goldfish as she has chickens. She has four more
hamsters than chickens. Altogether, she has 49 animals (just goldfish, hamsters and chickens).
How many more goldfish does she have than hamsters?
- Show Video Lesson
How to solve a problem involving “8 less than twice as many.”?
Example:
Steve collects baseball cards. He has 8 fewer than twice as many Padres cards as Giants cards.
He has three times as many Dodgers cards as Giants cards. Altogether, he has 82 cards. How
many Padres cards does he have?
- Show Video Lesson
Visual Problem Solving — Singapore Style
Example:
2 tablets and 4 mini-tablets cost a total of $2,480. A tablet and a mini-tablet cost $870 all together.
How much does a mini-tablet cost?
-
Show Video Lesson
A model drawing involving multiples is used to solve a complex word problem
Example:
Billy, Robert, and DJ had 210 model cars. Billy had twice as many cars as Robert. Robert had 3 times
as many models as DJ. How many model cars did Billy have?
- Show Video Lesson
How to use a Singapore style model drawing involving fractions to solve a complex story problem?
Example:
At the school talent show, 1/3 of the people were boys, 3/6 were girls, and the rest were adults. If there were 50 more girls than adults, how many people were there in total?
- Show Video Lesson
Example:
Bernardo is 5 times older than Irma. Irma is five years older than Oswaldo. If the sum of their ages is 65 years, how old will Oswaldo be in 7 years?
- Show Video Lesson
Visual problem solving using Singapore methods via model drawing which includes multiples, division, subtraction, and logical reasoning
Example:
Cameron scored 5 times as many points as Lars in a basketball game. Mike scored an amount equal to
the 6th multiple of 9. If the 3 boys scored a total of 126 points, how many points did Cameron score?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Comparison word problems in elementary schools
Students may start solving comparison word problems as early as first
grade. Then, these problems get more and more challenging in 4th or 5th
grade. There are two types of comparison in math: additive and
multiplicative.
Next we show some examples commonly used in elementary schools.
Additive comparison
In additive comparison, the problem may have the following expressions where x can be a whole number.
- How much more?
- How much less?
- x more
- x less
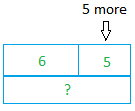
Example #1
Darline has 6 candies. Sylvia has 5 more. How many candies does Sylvia have? Here is the model for this problem.
Sylvia has 6 + 5 candies or 11 candies.
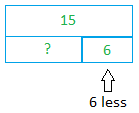
Example #2
John has 15 books. Peter has 6 less. How many books does Peter have? Here is the model for this problem.
Peter has 15 — 6 or 9 books
Multiplicative comparison
In multiplicative comparison, the problem may have the following expressions where x can be a whole number.
- x times as many
- x times more … than
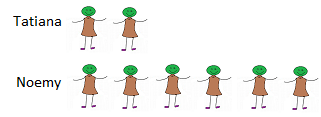
Example #3
Noemy has 3 times as many dolls as Tatiana. Tatiana has 2 dolls. How many dolls does Noemy have?
Step 1
Draw a model for this situation.
Step 2
Use the model to write an equation. Let n be the number of dolls Noemy has.
n = 3 x 2
Step 3
Solve the equation. n = 3. so Noemy has 6 dolls.
A challenging comparing word problem in elementary school.
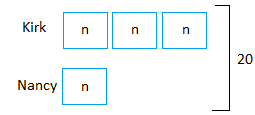
Example #4
Kirk has 3 times as many baseball cards as Nancy. Together, they have 20 baseball cards. How many cards does Kirk have?
Step 1
Draw a box with the letter n in it to show that Nancy has an unknown number of cards. Kirk has 3 times as many cards as Nancy, so draw three identical boxes to represent Kirk’s cards.
Step 2
Use a model to write an equation. There are 4 equal boxes and each box has n cards.
To get the total numbers of cards, you need to do 4 x n. This amount must equal to 20 cards. So 4 x n = 20
Step 3
Solve the equation to find n.
4 times what number is equal to 20? Since 4 x 5 = 20, n = 5.
Nancy has 5 baseball cards.
Step 4
Find how many cards Kirk has. Kirk has 3 times as many as Nancy or 3 x 5.
Kirk has 15 cards.
Example #5
Kirk has 3 times as many baseball cards as Nancy. Together, they have 20 baseball cards. How many cards does Kirk have?
Recent Articles
-
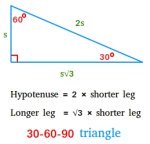
30-60-90 Triangle
Apr 03, 23 05:08 PM
What is a 30-60-90 triangle? Definition, proof, area, and easy to follow real-world examples.
Read More
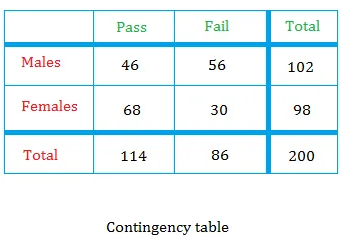
-
Calculate the Conditional Probability using a Contingency Table
Mar 29, 23 10:19 AM
Learn to calculate the conditional probability using a contingency table. This contingency table can help you understand quickly and painlessly.
Read More
Click here to see ALL problems on Percentage-and-ratio-word-problems
| Question 970375: There are 3 times as many boys as girls in a room. If 4 boys and four girls leave the room, then there will be 5 times as many boys as girls in the room. In total, how many boys and girls were in the room originally? (Scroll Down for Answer!) |
Did you know that Algebra.Com OR get immediate PAID help on: |
Answer by MathTherapy(10301)

(Show Source):
You can put this solution on YOUR website!
There are 3 times as many boys as girls in a room. If 4 boys and four girls leave the room, then there will be 5 times as many boys as girls in the room. In total, how many boys and girls were in the room originally?
Original numbers:
-
#1
Hello everyone,
This is a somewhat specific question pertaining to English. I am taking the GMAT in a week, and the Quantitative part systematically pops up such expressions:
«Of the 2,500 voters participating in a local election, three times as many voted for candidate A as for candidate B, and twice as many people voted for candidate A as for candidate C. «
Now, English is not my first language and I have a really hard time — that is half a minute or so, which is a lot on the GMAT — understanding what they actually mean: does 3A=B or does 3B=A; 2A=C or 2C=A?
The only way I am currently able to somehow understand what they tell me is to identify — more or less intuitively — which variable is greater (here, A) and multiply the other one by the given factor (here, 3B and 2C).
Could any of you please suggest some other way to understand such phrases? Maybe there is some relatively straightforward way of rephrasing such expressions so that it becomes clear?
Thanks in advance,
Liviu
-
#2
English is not my first language too, but I think it is 3B=1A and 2C=1A.
The candidates who voted for B were 3 times the candidates that voted for A.
Well, I might be wrong, wait for natives to be sure!!
-
#3
It is 3A=B and 2A=C. The subject immediately following «three times as many» or whatever the factor is, are the ones to be multiplied. «
Five times as many went to see East of B
ucharest as went to see Mr Bean’s Holiday.» More people went to see East of Bucharest. Note the verb and object that comes immediately after «times as many», it’s the people or things that did this action that need to be multiplied.
-
#4
It is 3A=B and 2A=C. The subject immediately follows «three times as many» or whatever the factor is, are the ones to be multiplied. «
Five times as many went to seeEast of B
ucharest as went to see Mr Bean’s Holiday.» More people went to see East of Bucharest. Note the verb and object comes immediately after «many», it’s the people or things that did this action that need to be multiplied.
Sorry, I was incorrect!!
-
#5
IrishStar, I sympathize with your confusion. In thinking how to explain it, I realized how confusing it must be! Yet I had taken its understanding for granted.
-
#6
This seems more like algebra than English, but I’ll give it a shot.
Three times as many people voted for A as for B:
3A=B
Twice as many people voted for A as for C:
2A=C
-
#7
This seems more like algebra than English, but I’ll give it a shot.
Three times as many people voted for A as for B:
3A=BTwice as many people voted for A as for C:
2A=C
This is confusing.
To me, it’s the exact opposite. For example, if 300 people voted for A and 100 people voted for B, three times as many people voted for A as for B. In that case, I’d say 3B=A.
The same holds for «twice as many» in my way of seeing it. If 200 people voted for A and 100 people voted for C, then twice as many people voted for A as for C, and 2C=A.
-
#8
Thanks all for answering.
This is actually what I thought of in the first place. I usually simplify like this: 3 times A is B and twice A is C. Hence, 3A=B and 2A=C. HOWEVER, the problem is that the answer key says the opposite. I wanted to post the link, but there might be some issues with such content becoming publicly available; I will copy relevant parts of the question / key.
«Of the 2,500 voters participating in a local election, three times as many voted for candidate A as for candidate B, and twice as many people voted for candidate A as for candidate C. If each voter chose either candidate, A, B, or C, or abstained, and 300 voters abstained, how many people voted for candidate C?»
«[..] Try B next. If C = 600, then A = 1,200, and B = 400. 600 + 1,200 + 400 + 300 = 2,500. (B) is the answer.»
According to the Princeton Review answer key (also, IrishStar and JamesM), it is 3B that equals A and 2C that equals A. However, others (Matching Mole, tomandjerryfan and me) think that 3 times A is B and twice A is C.
So, I’m quite confused as to who makes the mistake here.. Any other ideas?
-
#9
For me, three times as many people voted for A as for B means that more people voted for A than for B. Therefore, algebraically we would need to multiply the A by 3, which would be expressed as 3A.
The same goes for my understanding of the second sentence.
-
#10
Let’s suppose A had 1,200 votes; then B had 400 and C had 600 — total 2,200 votes. Just then extend to 2,500 voters and you get the result: A = 1,364, B = 455 and C = 681
-
#11
Well, «300 voters abstained»..
However, my question here is more about how to correctly interpret «three times as many voted for candidate A as for candidate B, and twice as many people voted for candidate A as for candidate C«. Is it 3B that equals A and 2C that equals A, as the answer key asserts, or 3A=B and 2A=C as others think.
After logical consideration, I agree with JamesM: «300 people voted for A and 100 people voted for B, three times as many people voted for A as for B. In that case, I’d say 3B=A.» But first hunch intuition based on English tells me the inverse. So, is there a standardized and straightforward way to deal with such phrases?
-
#12
For me, three times as many people voted for A as for B means that more people voted for A than for B. Therefore, algebraically we would need to multiply the A by 3, which would be expressed as 3A.
I would disagree. You say — and I agree — that more people voted for A and less people voted for B. When A is bigger than B, you’d need to adjust B by a certain factor >1 in order for the result to equal the bigger A. So following this logic, it is 3B that equals A. In this equation, B is indeed small and A is big.
-
#13
«Of the 2,500 voters participating in a local election, three times as many voted for candidate A as for candidate B, and twice as many people voted for candidate A as for candidate C. «
The confusion in interpreting this is surprising.
Take it slowly.
Three times as many voted for A as for B.
A got three times as many votes as B.
A got three votes for every one vote that B got.
If A got 30 votes, B got 10 votes
Now repeat for A and C.
Twice as many people voted for A as for C
A got twice as many votes as C
A got two votes for every one vote that C got.
If A got 30 votes, C got 15 votes.
-
#14
I would disagree. You say — and I agree — that more people voted for A and less people voted for B. When A is bigger than B, you’d need to adjust B by a certain factor >1 in order for the result to equal the bigger A. So following this logic, it is 3B that equals A. In this equation, B is indeed small and A is big.
landroni: You are correct.
A = 3B
A = 2C
-
#15
I would disagree. You say — and I agree — that more people voted for A and less people voted for B. When A is bigger than B, you’d need to adjust B by a certain factor >1 in order for the result to equal the bigger A. So following this logic, it is 3B that equals A. In this equation, B is indeed small and A is big.
You would think that English isn’t my first language!
I understand it now. If A = 300 and B = 100, then A is 3 times larger than B. We need to multiply B by 3 to arrive at three times its size, which is A.
But if you want a standardized/straightforward way of dealing with these types of problems, I suggest you wait for the math experts!
-
#16
You would think that English isn’t my first language!
Most definitely not. As JamesM said, this is confusing.
panjadrum: thanks. This is a relatively straightforward way to tackle such phrases:
Three times as many voted for A as for B:
=>A got 3, while B got 1.
=>3:1 ratio
=>I’d need to multiply B by 3 to get it equal A
=>3B=A
Next time, I’ll try to take it easier ~_-. Thanks all for answering this English problem.. using Math.
-
#17
Three times as many voted for candidate A as for candidate B — A is three times as big as B:
A/B=3
A=3B
-
#18
«Times» in a verbal math problem means «multiply»
Word problems involving «four times as many as»
Someone asked for help to explain the concepts of multiplicative word problems involving «as many as», like the ones below:
1) Haley had four times as many dollars as her sister. Together they had $60. How much money does Haley have?
2) Rachel had 5 times as many dollars as her sister, Nora. They had a total of $90. How much money did each of them have?
The BAR MODEL is an excellent tool for helping children understand what is going on in these types of word problems.
In (1), draw a bar for Haley and another for her sister. Divide Haley’s bar into four parts, and make the other bar just one such part long.
Haley |—|—|—|—|
Sister |—|
Now you will see that the TOTAL needs divided into FIVE equal parts — and from then on it is easy-peasy.
Additionally, you can use Thinking Blocks website to build such bar models INTERACTIVELY.
For problems like (1) and (2) above, choose the fourth model from the left (rightmost) in the top row that is bluish in color. Then click «Start modeling» button. Video tutorials exist also. This is not my site, but it’s a very nice interactive tool for this concept!
Popular posts from this blog
Never give up! A story by 8-year old Savannah
This is a wonderful story by a girl about her experiences with math… have your kids read it! Note how she learns when the teacher allows her to correct her mistakes in a test. I definitely advocate that. In fact, I give my kids HALF of the points they COULD have gotten at first, if they get a test question correct when they revise it. Tests should be LEARNING tools, and help children learn, just like everything else we do in teaching them, and NOT «scary judgment devices». https://blackwomenrockmath.com/blog/f/never-give-up
Workbook for kids — savings and finances
It’s financial literacy month (April), so here’s a free nice workbook: A Kid’s Guide to Saving: An Interactive Workbook With 14 pages, the guide includes: A calculator that illustrates the magic of compound interest for a child’s understanding Budgeting worksheets to calculate how much to save and set savings goals A quiz to test their learning with a certificate of completion at the end
Mathematical dot-to-dot
Interesting! This is a mathematical dot-to-dot that’s different from the routine…you can have your middle or high school students review integer operation, the order of operations, percentages, exponents, and other topics with these dot-to-dots.😊 https://mathshko.com/2020/01/04/number-dot-to-dot/