Привет! В этой статье посмотрим некоторые задачи из 26 задания ЕГЭ по информатике.
Стоит отменить, что задачи из 26 задания являются одними из самых сложных во всем экзамене, и найти какой-то конкретный шаблон для всех типов задач не получится.
Но обычно в 26 задании нужно использовать сортирку.
Решать задачи будем преимущественно на языке Python.
Задача (Классическая, Демо 2021)
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов.
Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар – 50, поэтому ответ для приведённого примера:
Решение:
Первый способ (с помощью Excel).
Решим задачу с помощью Excel. Чтобы открыть текстовый файл в программе Excel, выбираем Файл->Открыть, выбираем нужную папку и указываем, чтобы в папке были видны все типы файлов.
И выбираем наш текстовый файл.
Выскочит окно Мастер текстов (импорт). Здесь оставляем выбранный пункт с разделителями и кликаем Далее.
В следующем окне поставим ещё галочку пробел. В итоге Символами-разделителем будут знак табуляции и пробел.
Кликаем ещё раз Далее и Готово.
Наши данные вставятся, как нужно!
Число 8200 (размер свободного места) нужно запомнить или записать на черновике. Число 970 (количество файлов) нам в принципе не нужно при таком подходе решения.
Теперь удаляем первую строчку. Выделяем две ячейки в первой строчке, через контекстное меню мыши нажимаем Удалить…. Выбираем ячейки, со сдвигом вверх.
1. Найдём максимальное количество файлов.
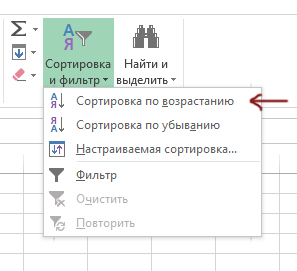
Выделяем весь столбец A и сортируем его по возрастанию.
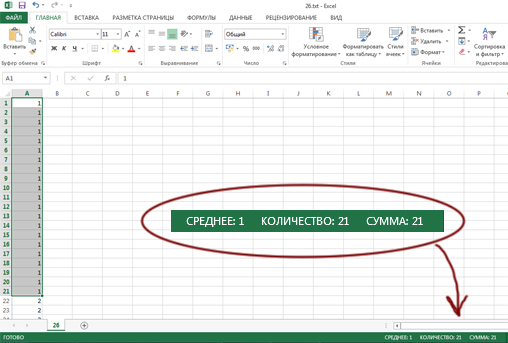
Теперь выделяем ячейки сверху мышкой, а справа в нижней части программы будет показываться сумма выделенных ячеек.
Мы должны выделить максимальное количество ячеек, но чтобы сумма не превышала число 8200.
Получается максимальное количество файлов, которое можно сохранить, равно 568.
2. Найдём максимальный размер файла при максимальном количестве файлов.
Если мы сохраним максимальное количество файлов, то у нас ещё останется свободное место 8200-8176=24, т.к. сумма выделенных ячеек равна 8176.
Мы можем заменить наибольший файл (последняя выделенная ячейка равная 29) ещё большим файлом, размер которого не превышает 24+29=53.
Если покрутим таблицу вниз, то найдём такой файл размером 50. Это и будет наибольший файл при максимальном количестве файлов.
Ответ получается 568 50.
Второй способ (с помощью Python).
f=open('26.txt') st = f.readline().split() s=int(st[0]) n=int(st[1]) a=[] #Записываем данные в список a for i in range(n): x=int(f.readline()) a.append(x) #Сортируем список a.sort() b=[] for i in range(n): if sum(b) + a[i] <= s: b.append(a[i]) else: break b=b[:-1] for i in range(len(a)-1, -1, -1): if sum(b) + a[i] <= s: b.append(a[i]) break print(len(b), b[-1])
В начале подвязываемся к файлу. С помощью команды readline() считываем первую строчку. С помощью команды split() разбиваем строчку по пробелу на два числа. Переменная st — это список. В st[0] — будет подстрока с первым числом, в st[1] со вторым.
Переменная s — это размер свободного пространства на диске, n — это количество пользователей. Мы должны использоваться функцию int(), чтобы перевести из текстового типа данных в целый числовой.
Заводим пустой список a. В него мы будем помещать все значения объёмов пользователей, которые идут ниже по файлу. Зачитываем последующие числа в список a, превращая их в целый тип данных.
Команда .sort() сортирует (раскладывает по порядку) по возрастанию элементы списка.
Заводим список b. В него будем класть элементы, которые записываем на диск. Т.к. числа отсортированы, то, начиная с самого маленького файла, мы сможем заполнить диск максимальным количеством файлов.
С помощью цикла пробегаемся по всем элементам. В начале проверяем, есть ли место для очередного элемента, а потом записываем элемент в список b. Таким образом, сможем найти максимальное количество.
Чтобы найти максимальный элемент при максимальном количестве, удаляем из списка b последний самый большой элемент.
Пробегаемся по списку a, начиная с конца. Ищем кем можно заменить удалённый элемент. Мы идём с конца, поэтому в приоритете будут самый большие элементы.
После того, как найденный элемент будет умещаться в список b, можно печатать ответ.
Ответ:
Задача (Двумерные списки)
В лесничестве саженцы сосны высадили параллельными рядами, которые пронумерованы идущими подряд натуральными числами. Растения в каждом ряду пронумерованы натуральными числами начиная с единицы.
По данным аэрофотосъёмки известно, в каких рядах и на каких местах растения не прижились. Найдите ряд с наибольшим номером, в котором есть ровно 13 идущих подряд свободных мест для посадки новых сосен, таких, что непосредственно слева и справа от них в том же ряду растут сосны. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: наибольший номер ряда и наименьший номер места для посадки из числа найденных в этом ряду подходящих последовательностей из 13 свободных мест.
Входные данные.
В первой строке входного файла находится число N — количество прижившихся саженцев сосны (натуральное число, не превышающее 20 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 100 000: номер ряда и номер места в этом ряду, на котором растёт деревце.
Выходные данные.
Два целых неотрицательных числа: наибольший номер ряда и наименьший номер места в выбранной последовательности из 13 мест, подходящих для посадки новых сосен.
Типовой пример организации входных данных:
7
40 3
40 7
60 33
50 125
50 129
50 68
50 72
Для приведённого примера, при условии, что необходимо 3 свободных места, ответом является пара чисел: 50; 69.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
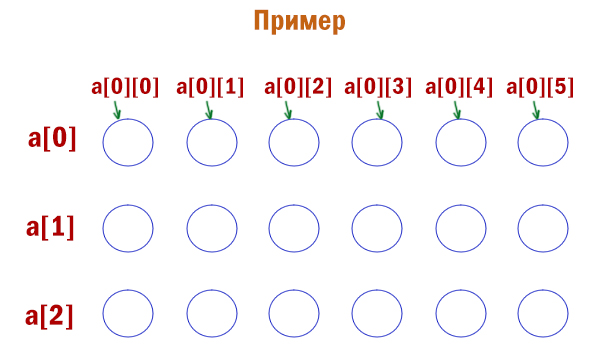
f=open('26_dm.txt') n=int(f.readline()) a=[0]*100001 for i in range(0, 100001): a[i]=[] #Заполняем списки for i in range(0, n): s=f.readline() b=s.split() a[int(b[0])].append(int(b[1])) #Сортируем списки for i in range(0, len(a)): a[i].sort() flag_stop=0 for i in range(len(a)-1, -1, -1): for j in range(0, len(a[i])-1): if a[i][j+1]-a[i][j]==14: print(i, a[i][j]+1) flag_stop=1 break if flag_stop==1: break
Всего у нас может быть сто тысяч рядов. Поэтому мы заводим 100000 списков. Каждый список — это очередной ряд. Но в программе завели 1000001, т.к. нулевой список использоваться не будет.
В каждый ряд добавляются номера деревьев. Это и будут элементы для каждого списка. Если не будет деревьев в ряду, то список останется пустым.
В программе мы сортируем каждый список, чтобы числа все шли в порядке возрастания.
Если в каком-нибудь списке числа имеют разницу в 14 единиц, то значит между ними ровно 13 свободных мест. Например, числа 10 и 24. Между ними 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23. Всего 13 чисел.
Чтобы проанализировать двумерный массив, используем вложенные циклы. Ряды перебираем сверху вниз. Как только найдём нужный ряд, выйдем из цикла, и в переменной i будет наибольший нужный ряд.
Сами же ряды перебираем в порядке возрастания. Как только между числами разница будет в 14 единиц, то значение j+1 наименьший свободный номер из промежутка в 13 деревьев.
Чтобы вовремя выйти из вложенных циклов, используем дополнительный флаг (переменную flag_stop).
Ответ:
Задача (Демо 2023)
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки — подарок упаковывается в одну из коробок, та в свою очередь в другую коробоку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее количество коробок, которое можно использовать для упаковки одного подарка, и максимально возможную длину стороны самой маленькой коробки, где будет находиться подарок. Размер подарка позволяет поместить его в самую маленькую коробку.
Выходные данные
В первой строке входного файла находится число N — количество коробок в магазине (натуральное число, не превышающая 10 000). В следующих N строках находятся значения длин сторон коробок (все числа натуральные, не превышающие 10 000), каждое — в отдельной строке.
Запишите в ответе два целых числа: сначала наибольшее количество коробок, которое можно использовать для упаковки одного подарка, затем максимально возможную длину стороны самой маленькой коробки в таком наборе.
Типовой пример организации данных во входном файле.
5
43
40
32
40
30
Пример входного файла приведён для пяти коробок и случая, когда минимальная допустимая разница между длинами сторон коробок, подходящих упаковки «матрёшки», составлят 3 единицы.
При таких исходных данных условию задачи удовлетворяют наборы коробок с длинами сторон 30, 40 и 43 или 32, 40 и 43 соответственно, т.е. количество коробок равно 3, а длина стороны самой маленькой коробки равна 32.
Типовой пример имеет иллюстративный характер. Для выполнения задания используйте данные из прилагаемых файлов.
Решение:
f=open('26.txt') n=int(f.readline()) a=[] for i in range(n): x=int(f.readline()) a.append(x) a.sort(reverse=True) k=1 p=a[0] for i in range(1, len(a)): if p-a[i]>=3: k=k+1 p=a[i] print(k, p)
В начале считываем все числа в массив (список) a. Сортируем их в порядке убывания.
Приступаем собирать упаковку. Начинаем с самой большой упаковки. Большую упаковку точно можно взять в наш подарок. Переменная p — это размер последний коробки, которую мы взяли. Переменная k — количество коробок в подарке на текущий момент времени.
Если следующая коробка подходит по условию, то мы её берём в наш подарок. Кто-то может подумать, что, может быть, выгоднее взять не самую большую коробку, а предпоследнего размера. Но все размеры, которые будут подходить для предпоследнего элемента, точно будут подходить и для последнего, и количество упаковок точно не будет меньше, если мы берём самую большую коробку.
Дубликаты не влияют на ответы.
Если мы начинаем с самой большой коробки, то в самом конце в переменной p окажется максимальный размер самой маленькой коробки.
Ответ:
Задача (Разные типы товаров)
На закупку товаров типов A, B, C, D и E выделена определённая сумма денег. Эти товары есть в продаже по различной цене. Необходимо на выделенную сумму закупить как можно больше товаров пяти типов (по общему количеству). Если можно разными способами купить максимальное количество пяти типов товаров, то нужно выбрать способ, при котором будет закуплено как можно больше товаров типа A. Если при этих условиях есть несколько способов закупки, нужно потратить как можно меньше денег.
Определите, сколько будет закуплено товаров типа A и сколько денег останется.
Входные данные представлены в файле следующим образом. Первая строка входного файла содержит два целых числа: N – общее количество товаров и M – сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк содержит целое число (цена товара в рублях) и символ (латинская буква), определяющий тип товара. Все данные в строках входного файла отделены одним пробелом.
Запишите в ответе два числа: сначала количество закупленных товаров типа A, затем оставшуюся неиспользованной сумму денег.
Пример входного файла:
6 110
40 E
50 A
50 D
30 C
20 B
10 A
В данном случае можно купить не более четырёх товаров, из них не более двух товаров типа A. Минимальная цена такой покупки 110 рублей (покупаем товары 10 A, 20 B, 30 C, 50 A). Останется 0 рублей. Ответ: 2 0.
Решение:
f=open('26-rtt.txt') s=f.readline().split() n=int(s[0]) m=int(s[1]) X, Y, Z = [], [], [] for i in range(n): s=f.readline().split() X.append((int(s[0]), s[1])) X.sort() sm=0 for i in range(n): if sm+X[i][0]<= m: sm=sm+X[i][0] Y.append(X[i]) else: if X[i][1]=='A': Z.append(X[i]) j=0 for i in range(len(Y)-1, -1, -1): if Y[i][1]=='A': continue if sm - Y[i][0] + Z[j][0] <= m: sm = sm - Y[i][0] + Z[j][0] Y[i] = Z[j] else: break j=j+1 count = 0 for i in range(len(Y)): if Y[i][1]=='A': count=count+1 print(count, m-sm)
В этом решении участвуют три списка. Список X — это все товары из нашего файла. Каждый товар — это отдельный список, состоящий из двух элементов: стоимости и типа товара.
После того, как список X укомплектован, сортируем его по первому значению (по цене). Таким образом, самые дешёвые товары всех типов будут находится в начале, самые в дорогие в конце. Так мы сможем найти максимальное количество, которое можно закупить на указанную сумму.
Список Y — это те товары, которые мы взяли при вычислении предыдущего шага. Переменная sm — это та сумма, которую потратим при нахождении максимального количества товаров в независимости от типа товаров.
Список Z — это те товары, которые мы НЕ взяли в предыдущем шаге, но только с типами A.
Основной секрет данной задачи заключается в том, что мы будем убирать по очереди один элемент из списка уже взятых товаров типа В и добавлять один товар типа A из списка не взятых товаров. Т.к. мы всегда один элемент убираем и один прибавляем, то количество остаётся одинаковым, т.е. максимальным. Тем самым мы стараемся сделать товаров типа A как можно больше.
Нужна максимальная экономия при заменах, чтобы можно было сделать как можно больше замен, и при это осталось как можно больше денег. Для этого всегда меняем самый большой элемент из списка Y, на самый маленький элемент из списка Z
При заменах меняем и значение суммы выбранных элементов (переменная sm).
Когда замены больше невозможны, то остаётся только посчитать количество элементов с типом A в списке Y.
Ответ:
Задача (Интересный шаблон)
Предприятие производит оптовую закупку изделий A и C, на которую выделена определённая сумма денег. У поставщика есть в наличии партии этих изделий различных модификаций по различной цене. На выделенные деньги необходимо приобрести как можно больше изделий C (независимо от модификации). Закупать можно любую часть каждой партии. Если у поставщика закончатся изделия C, то на оставшиеся деньги необходимо приобрести как можно больше изделий A. Известна выделенная для закупки сумма, а также количество и цена различных модификаций данных изделий у поставщика. Необходимо определить, сколько будет закуплено изделий A и какая сумма останется неиспользованной. Если возможно несколько вариантов решения (с одинаковым количеством закупленных изделий A), нужно выбрать вариант, при котором оставшаяся сумма максимальна.
Входные данные представлены в файле следующим образом. Первая строка входного файла содержит два целых числа: N – общее количество партий изделий у поставщика и S – сумма выделенных на закупку денег (в рублях). Каждая из следующих N строк описывает одну партию изделия: сначала записана буква A или C (тип изделия), а затем – два целых числа: цена одного изделия в рублях и количество изделий в партии. Все данные в строках входного файла разделены одним пробелом.
В ответе запишите два целых числа: сначала количество закупленных изделий типа A, затем оставшуюся неиспользованной сумму денег.
Пример входного файла:
4 1000
A 14 12
C 30 7
A 40 24
C 50 15
В данном случае сначала нужно купить изделия C: 7 изделий по 30 рублей и 15 изделий по 50 рублей. На это будет потрачено 960 рублей. На оставшиеся 40 рублей можно купить 2 изделия A по 14 рублей. Таким образом, всего будет куплено 2 изделия A и останется 12 рублей. В ответе надо записать числа 2 и 12.
Решение:
Создадим список. Каждый элемент списка будет является тоже списком из трёх элементов: тип изделия, цена изделия и количество изделий данной модификации.
Нам потребуется отсортировать строчки файла сначала по типу изделия, т.к. нужно приобрести как можно больше изделий типа C. После этого нужно сделать сортировку второго уровня, отсортировать строчки по цене. Ведь так мы сможем взять максимальное количество изделий на выделенную сумму.
Рассмотрим интересный шаблон для подобного рода задач.
a=[] a.append((5, 1, 6)) a.append((7, 7, 3)) a.append((3, 4, 5)) a.append((3, 1, 2)) a.append((3, 3, 2)) a.sort(key=lambda d: (d[0], d[1])) print(a)
Получается результат:
Видим, что сначала элементы расположились по первому числу, затем уже по второму.
Напишем решение для нашей задачи.
f=open('26_4.txt') st=f.readline().split() n=int(st[0]) s=int(st[1]) k=0 a=[] for i in range(n): st=f.readline().split() if st[0]=='A': st[0]='D' if st[0]=='C': st[0]='B' a.append((st[0], int(st[1]), int(st[2]))) a.sort(key=lambda d:(d[0], d[1])) for i in range(len(a)): for j in range(a[i][2]): if s-a[i][1]>=0: s=s-a[i][1] if a[i][0] == 'D': k=k+1 print(k, s)
Т.к. нужно в начале набрать изделий типа С как можно больше, то хотелось бы видеть именно в начале этот тип после сортировки. Чтобы добиться желаемого, обозначим букву С за букву B, а букву A за D. Сортировку по цене делаем в возрастающем порядке.
Далее пробегаемся в цикле по отсортированному списку. Во вложенном цикле покупаем один товар конкретной модификации, пока это можно сделать. Посчитываем количество товаров типа A.
Ответ:
Задача (Бинарный поиск)
В текстовом файле записан набор натуральных чисел, не превышающих 109. Гарантируется, что все числа различны. Необходимо определить, сколько в наборе таких пар чётных чисел, что их среднее арифметическое тоже присутствует в файле, и чему равно наибольшее из средних арифметических таких пар.
Входные данные.
Первая строка входного файла содержит целое число N — общее количество чисел в наборе. Каждая из следующих N строк содержит одно число.
В ответе запишите два целых числа: сначала количество пар, затем наибольшее среднее арифметическое.
Пример входного файла:
6
3
8
14
11
2
17
В данном случае есть две подходящие пары: 8 и 14 (среднее арифметическое 11), 14 и 2 (среднее арифметическое 8). В ответе надо записать числа 2 и 11.
Решение:
f=open('26_6.txt') n=int(f.readline()) k=0 mx=0 a=[] for i in range(n): x=int(f.readline()) a.append(x) a.sort() for i in range(0, len(a)-1): if a[i]%2==0: for j in range(i+1, len(a)): if a[j]%2==0: sr = (a[i] + a[j]) // 2 # Бинарный поиск l=0 r=len(a)-1 index=0 while(l <= r): index = (r + l) // 2 if a[index] == sr: k=k+1 mx=max(mx, a[index]) break if a[index] < sr: l=index+1 else: r=index-1 print(k, mx)
В начале записываем все числа в массив. Сортируем все числа, как обычно в 26 задании из ЕГЭ по информатике.
После идут два вложенных цикла — мы перебираем все пары в массиве a. Берём только чётные числа.
Чтобы найти число в отсортированном массиве воспользуемся «бинарным поиском». Об этом приёме подробно рассказано в этой статье.
Ответ:
Надеюсь, Вам повезёт при решении 26 задания на ЕГЭ по информатике.
Александр, будут ли разборы задач с чередующимися красными и синими коробками(как в 4 варианте сборника Крылова и Чуркиной)? Писал в школе пробник по этому варианту, и набрал 95 баллов, спасибо вам за отличные уроки, это очень эффективная подготовка
Спасибо за отзыв!) Посмотрю эту задачку, если что, разберу.
Александр, полагаю, у вас опечатка в задаче с «Интересным шаблоном».
Последняя строчка решения: «Посчитываем количество товаров типа С.» — В задаче говориться о типах А.
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
Источники:
Демонстрационная версия ЕГЭ−2021 по информатике;
Демонстрационная версия ЕГЭ−2022 по информатике.
2
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 4000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
3
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 5000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
4
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 6000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
5
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
Задание 26
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 3000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
Ответ:
Пройти тестирование по этим заданиям
- ЕГЭ по информатике
Способ решения задания №26 ЕГЭ по информатике (без использования программирования) с помощью MS Excel.
Автор: Черноиванова Екатерина Вадимовна
→ скачать презентацию
ЗАДАНИЕ
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше,чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер
имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.Входные данные находятся в файле.
Связанные страницы:
ЕГЭ информатика 26 задание разбор, теория, как решать.
Обработка целочисленной информации с использованием сортировки, (В) — 2 балла
Е26.17 В магазине для упаковки подарков есть N кубических коробок.
В магазине для упаковки подарков есть N кубических коробок. Самой интересной считается упаковка подарка по принципу матрёшки – подарок упаковывается в одну из коробок, та в свою очередь в другую коробку и т.д. Одну коробку можно поместить в другую, если длина её стороны хотя бы на 3 единицы меньше длины стороны другой коробки. Определите наибольшее …
Читать далее
Е26.16 В лесополосе осуществляется посадка деревьев.
В лесополосе осуществляется посадка деревьев. Причем саженцы высаживают рядами на одинаковом расстоянии. Через какое-то время осуществляется аэросъемка, в результате которой определяется, какие саженцы прижились. Необходимо определить ряд с максимальным номером, в котором есть подряд ровно 11 неприжившихся саженцев, при условии, что справа и слева от них саженц прижились. В ответе запишите сначала наибольший номер ряда, затем …
Читать далее
Е26.15 определить номер ряда с наибольшим количеством светлых точек в нечётных позициях
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 10 000 на 10 000 точек. При попадании каждой частицы на экран в протоколе фиксируются координаты попадания: номер ряда (целое число от 1 до 10 000) и номер позиции в ряду (целое число от 1 до 10 000). Точка экрана, в …
Читать далее
Е26.14 сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя. По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а …
Читать далее
Е26.13 определить максимальную длину такой группы и номер ряда
При проведении эксперимента заряженные частицы попадают на чувствительный экран, представляющий из себя матрицу размером 10 000 на 10 000 точек. При попадании каждой частицы на экран в протоколе фиксируются координаты попадания: номер ряда (целое число от 1 до 10 000) и номер позиции в ряду (целое число от 1 до 10 000). Точка экрана, в …
Читать далее
Е26.12 определите цену самого дорогого товара, не участвующего в распродаже
В магазине электроники раз в месяц проводится распродажа. Из всех товаров выбирают К товаров с самой большой ценой и делают на них скидку в 20%, затем ещё М товаров с самой большой ценой и делают на них скидку 10%. По заданной информации о цене каждого из товаров и количестве товаров, на которые будет скидка, определите …
Читать далее
Е26.11 числа в паре имеют разную чётность, а их сумма тоже присутствует в файле
В текстовом файле записан набор натуральных чисел, не превышающих 109. Гарантируется, что все числа различны. Необходимо определить, сколько в наборе таких пар чисел, что числа в паре имеют разную чётность, а их сумма тоже присутствует в файле, и чему равна наибольшая из сумм таких пар. Входные данные Первая строка входного файла содержит целое число N …
Читать далее
Е26.10 Причем файлы размером больше 400 МБ записывает на диск A
Системный администратор раз в неделю создаёт архив пользовательских файлов. Причем файлы размером больше 400 МБ записывает на диск A, а меньшего размера на диск F. Известно, какой объём занимает файл каждого пользователя. Системный администратор старается сохранить как можно больше файлов. Необходимо найти, сколько файлов на каждом диске может сохранить системный администратор и максимальный размер сохраненного …
Читать далее
Е26.9 Спутник «М305» проводит измерения солнечной активности
Спутник «М305» проводит измерения солнечной активности, результат каждого измерения представляет собой натуральное число. Перед обработкой серии измерений из неё исключают K наибольших и K наименьших значений (как недостоверные). По заданной информации о значении каждого из измерений, а также количестве исключаемых значений, определите наибольшее достоверное измерение, а также целую часть среднего значения всех достоверных измерений. Входные …
Читать далее
Е26.8 чему равно наибольшее из средних арифметических таких пар
В текстовом файле записан набор натуральных чисел, не превышающих 109. Гарантируется, что все числа различны. Необходимо определить, сколько в наборе таких пар чётных чисел, что их среднее арифметическое тоже присутствует в файле, и чему равно наибольшее из средних арифметических таких пар. Входные данные Первая строка входного файла содержит целое число N – общее количество чисел …
Читать далее
Информатика. ЕГЭ
Задания для подготовки
Задачи разных лет из реальных экзаменов, демо-вариантов, сборников задач и других источников
Задание 26. Информатика. 2022-1
Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся двум соседним белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наибольшим номером, в котором есть два соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наименьший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.
Входные данные
В первой строке входного файла находится число (N) — количество рядов пикселей (натуральное число, не превышающее ( 10~000)). Каждая из следующих (N) строк содержит два натуральных числа, не превышающих (100~000): номер ряда и номер чёрного пикселя в ряду.
Выходные данные
Два целых неотрицательных числа: номер ряда и наименьший номер пикселя в выбранной паре.
Пример входного файла:
(7)
(20 ,, 10)
(20 ,, 13)
(30 ,, 45)
(40 ,, 17)
(40 ,, 20)
(40 ,, 30)
(40 ,, 33)
Условию задачи удовлетворяют три пары чисел: (20) и (11), (40) и (18), (40) и (31). Ответ для приведённого примера:
(40) (18)
Файл с данными
Показать решение…
Задание 26. Информатика. 2022-2
Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся двум соседним белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наименьшим номером, в котором есть два соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наибольший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.
Входные данные
В первой строке входного файла находится число (N) — количество рядов пикселей (натуральное число, не превышающее ( 10~000)). Каждая из следующих (N) строк содержит два натуральных числа, не превышающих (100~000): номер ряда и номер чёрного пикселя в ряду.
Выходные данные
Два целых неотрицательных числа: номер ряда и наибольший номер пикселя в выбранной паре.
Пример входного файла:
(7)
(30 ,, 45)
(40 ,, 17)
(40 ,, 20)
(40 ,, 30)
(40 ,, 33)
(50 ,, 10)
(50 ,, 13)
Условию задачи удовлетворяют три пары чисел: (40) и (19), (40) и (32), (50) и (12). Ответ для приведённого примера:
(40) (32)
Файл с данными
Показать решение…
Задание 26. Информатика. 2022-3
Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный всем имеющимся трём соседним подряд идущим белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наибольшим номером, в котором есть три соседних пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наименьший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.
Входные данные
В первой строке входного файла находится число (N) — количество рядов пикселей (натуральное число, не превышающее ( 10~000)). Каждая из следующих (N) строк содержит два натуральных числа, не превышающих (100~000): номер ряда и номер чёрного пикселя в ряду.
Выходные данные
Два целых неотрицательных числа: номер ряда и наименьший номер пикселя в выбранной паре.
Пример входного файла:
(7)
(20 ,, 10)
(20 ,, 14)
(30 ,, 45)
(40 ,, 17)
(40 ,, 21)
(40 ,, 30)
(40 ,, 34)
Условию задачи удовлетворяют три пары чисел: (20) и (11), (40) и (18), (40) и (31). Ответ для приведённого примера:
(40) (18)
Файл с данными
Показать решение…
Задание 26. Информатика. 2022-4
Для хранения двумерного цифрового растрового чёрно-белого изображения Петя сохранил в текстовом файле информацию и позициях всех пикселей чёрного цвета на изображении (номера рядов пикселей и номера чёрных пикселей в ряду). Для редактирования изображения Пете нужно изменить цвет с белого на чёрный трём соседним подряд идущим белым пикселям, таким что слева и справа от них в том же ряду пиксели чёрные.
Найдите ряд с наименьшим номером, в котором есть три соседних подряд идущих белых пикселя, удовлетворяющих требованию Пети. Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому условию. В ответе запишите два целых числа: номер ряда и наибольший номер пикселя в ряду из найденных в этом ряду подходящий пар белых пикселей.
Входные данные
В первой строке входного файла находится число (N) — количество рядов пикселей (натуральное число, не превышающее ( 10~000)). Каждая из следующих (N) строк содержит два натуральных числа, не превышающих (100~000): номер ряда и номер чёрного пикселя в ряду.
Выходные данные
Два целых неотрицательных числа: номер ряда и наибольший номер пикселя в выбранной паре.
Пример входного файла:
(7)
(30 ,, 45)
(40 ,, 17)
(40 ,, 21)
(40 ,, 30)
(40 ,, 34)
(50 ,, 10)
(50 ,, 14)
Условию задачи удовлетворяют три пары чисел: (40) и (20), (40) и (33), (50) и (13). Ответ для приведённого примера:
(40) (33)
Файл с данными
Показать решение…
Задание 26. Информатика. 2022-5
Илье необходимо перенести файлы с одного компьютера на другой при помощи внешнего жёсткого диска.
Объём диска может быть меньше, чем требуется для переноса файлов за один раз. Свободный объём на диске и размеры файлов известны.
По заданной информации об объёме файлов на компьютере и свободном объёме на диске определите максимальное число файлов, которые могут быть перенесены за один раз на внешний жесткий диск, а также максимальный размер файла, записанного на этот диск, при условии, что перенесено наибольшее возможное число файлов.
Входные данные
В первой строке входного файла находятся два числа: (S) — размер свободного места на диске (натуральное число, не превосходящее (100~000)) и (N) — количество файлов, которые надо перенести (натуральное число, не превышающее (10~000)). В следующих (N) строках находятся значения объёмов указанных файлов (все числа натуральные, не превышающие (100)), каждое в отдельной строке.
Выходные данные
Запишите в ответе два числа: сначала наибольшее число файлов, которые могут быть перенесены на внешний жёсткий диск за один раз, затем максимальный размер перенесённого файла, при условии, что перенесено наибольшее возможное число файлов. Если вариантов переноса несколько, выберите тот, при котором будет перенесён наибольший файл.
Пример входного файла:
(100) (4)
(80)
(30)
(50)
(40)
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов: (30) и (40), (30) и (50) или (40) и (50). Наибольший объём файла из перечисленных пар — (50), поэтому ответ для приведённого примера:
(2) (50)
Файл с данными
Показать решение…

В задание №26
Тема: Обработка массива целых чисел из файла. Сортировка.
Проверяется yмение обрабатывать целочисленную информацию с использованием сортировки
Примеры заданий:
Задание 26 Простое задание (Решу ЕГЭ)
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные:
В первой строке входного файла находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 10 000) и N — количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера:
2 50
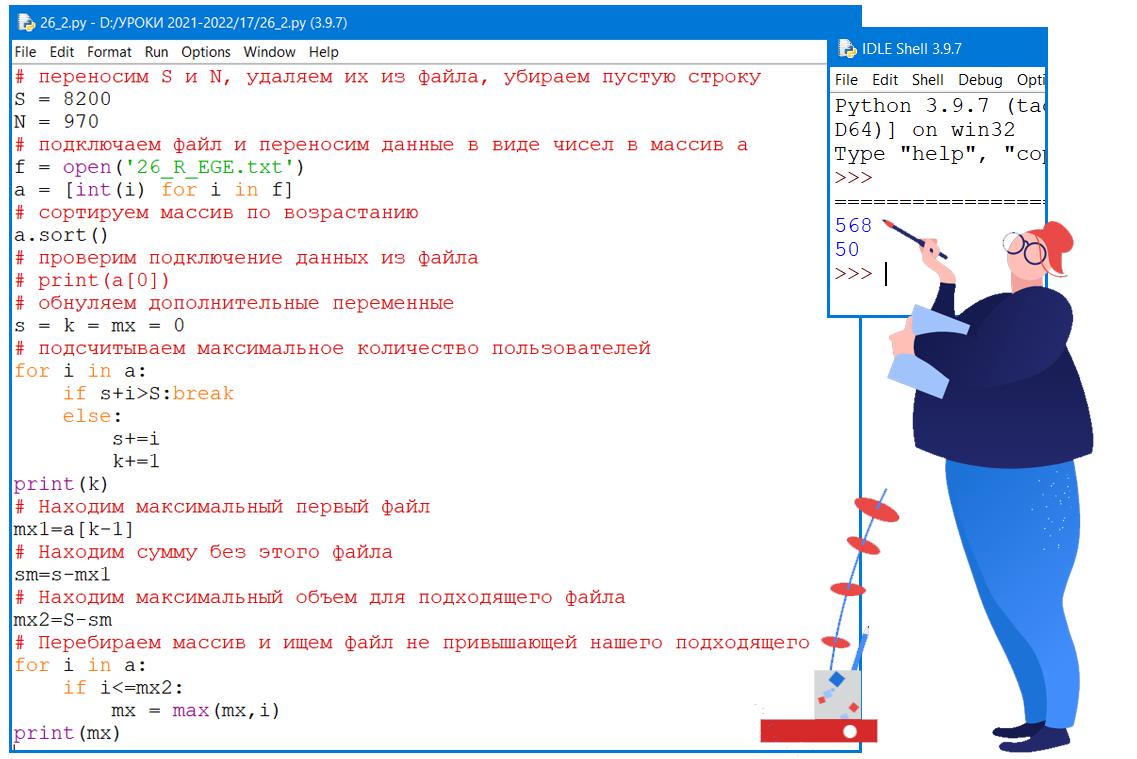
Проще всего 26-е задание решать в Excel. Можно решить задание и
с помощью программы, но это будет посложнее. На ЕГЭ решение через программы не рекомендуется.
Здесь и далее во всех задачах этого класса предполагается, что не все файлы могут быть сохранены на диске, то есть хотя бы для одного файла места не хватит.
Решаем с помощью Excel
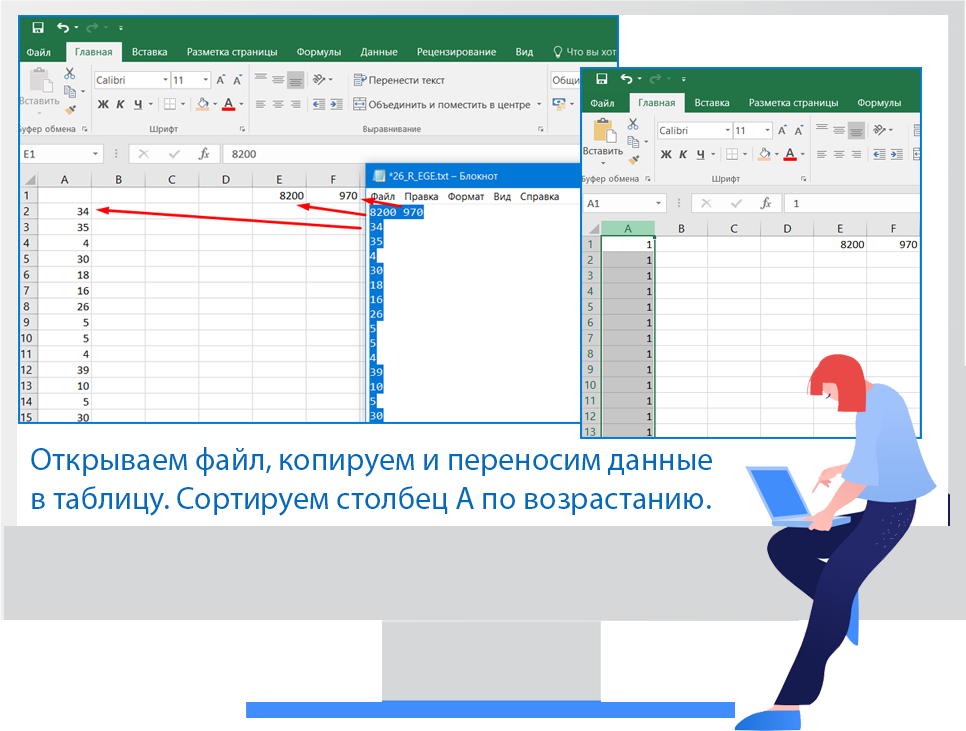
- Сначала загружаем данные в электронную таблицу, отрываем файл, копируем (Ctrl+A) и вставляем в Excel (Ctrl+V), для удобства переносим первую строку, которая содержит не такие данные, как все остальные и сортируем по возрастанию столбец А
- Далее начинаем выделять ячейки первого столбца, отслеживая значение суммы в строке состояния, нужно выделить наибольшее количество данных, сумма которых не больше, чем 8200
- Получили:
— Количество строк 568 (это первый ответ)
— Сумма 8176
— Последний наибольший файл 29 - Попробуем заменить наибольший файл ещё большим, так как наш архив (8200) это позволяет сделать:
— убираем наш наибольший 29 из общей суммы 8176-29=8147
— из исходного объема архива отнимаем полученное 8200-8147=53, получается что нам надо поискать файл такого или немного поменьше размера. - Спускаемся по списку и находим, что нам подходит первый файл размером 50
Мы нашли максимальное количество файлов 568 и максимальный файл 50
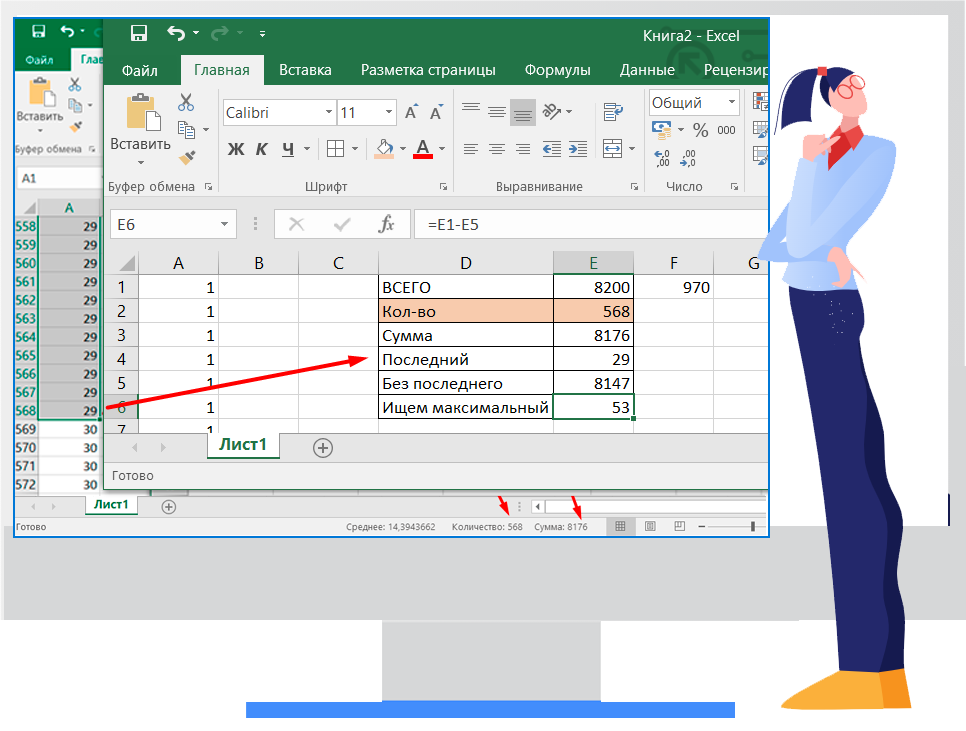
Ответ: 56850
Задание 26 демо (ФИПИ-2022)
Организация засаживает ряды саженцев, которые идут параллельно друг другу.
Известно,какие места в рядах уже заняты саженцами. Найдите ряд с наибольшим номером(нумерация рядом идет по возрастанию), в котором есть 13 подряд
свободных мест, таких что слева и справа от них в том же ряду места уже засажены (заняты). Гарантируется, что есть хотя бы один ряд, удовлетворяющий этому
условию. В ответе запишите два целых числа: максимальный номер ряда и наименьший номер
места из найденных в этом ряду подходящих пар свободных мест.
Входные данные:
В первой строке входного файла 26 (3).txt находится число N – количество занятых
мест (натуральное число, не превышающее 10 000). Каждая из следующих N строк
содержит два натуральных числа, не превышающих 100 000: номер ряда и номер
занятого места.
Выходные данные:
Два целых неотрицательных числа: Максимальный номер ряда, где нашлись обозначенные в задаче места и минимальный номер подходящего свободного места.
Типовой пример организации входных данных:
7
40 3
40 7
60 33
50 125
50 129
50 68
50 72
Для приведённого примера, при условии, что необходимо
3 свободных места, ответом является пара чисел: 50; 69.
Типовой пример имеет иллюстративный характер. Для
выполнения задания используйте данные из прилагаемых
файлов.
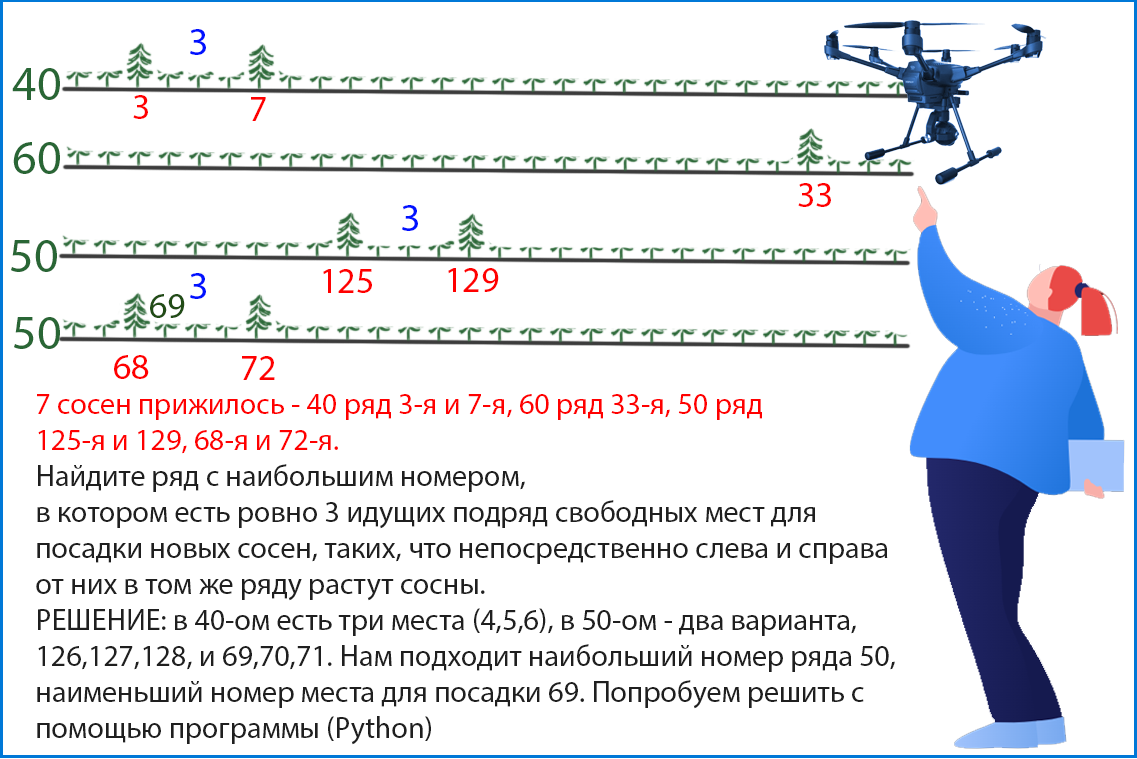
Решаем с помощью Excel
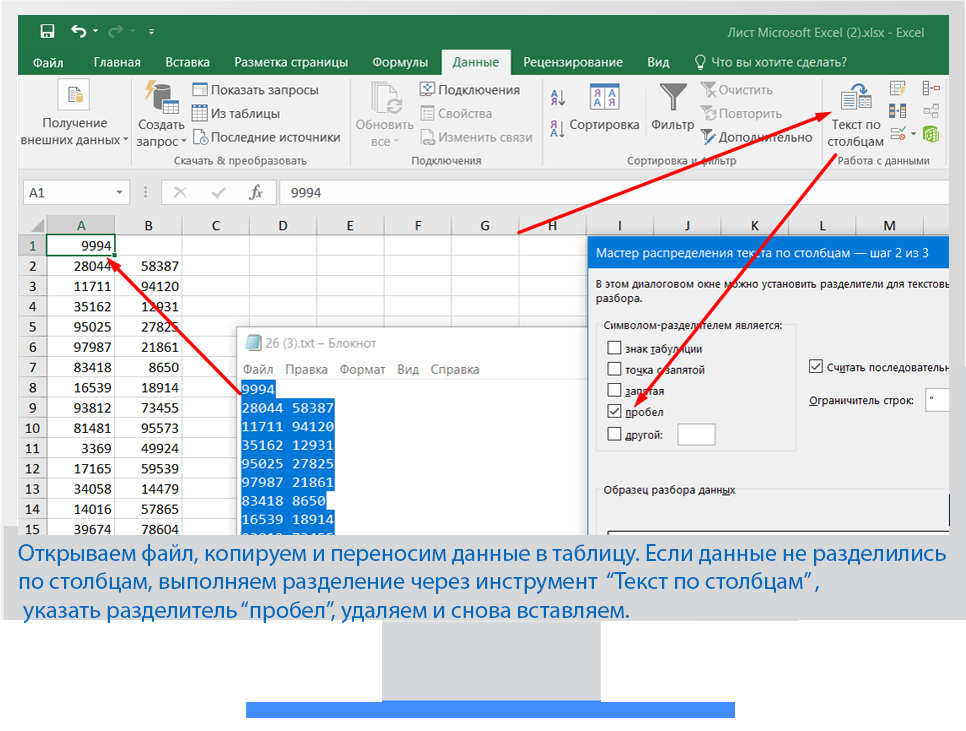
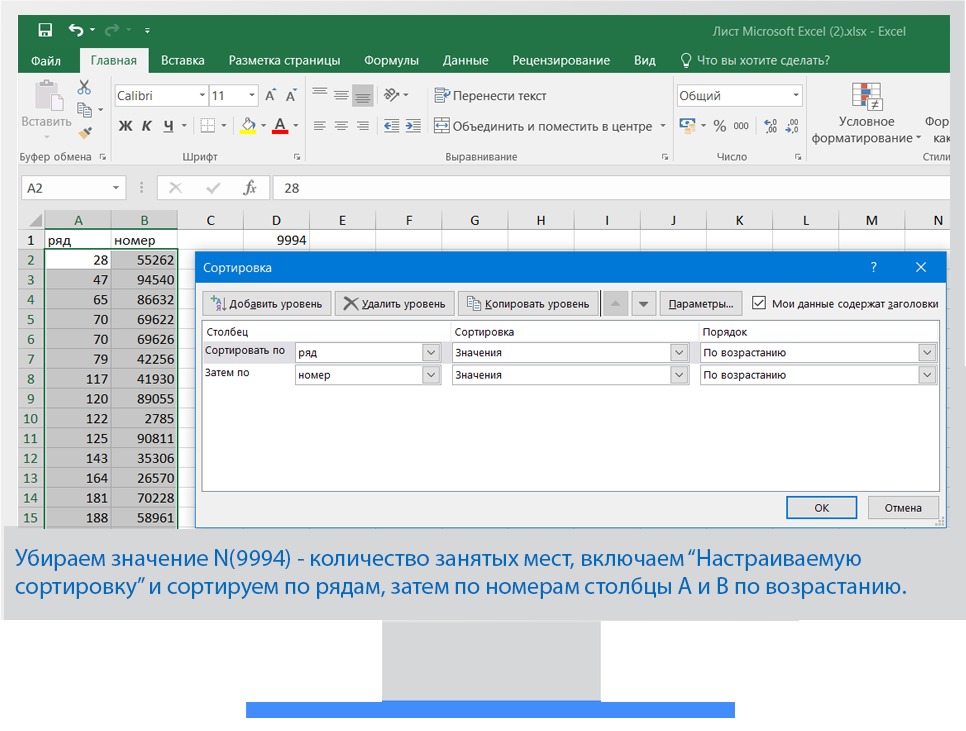
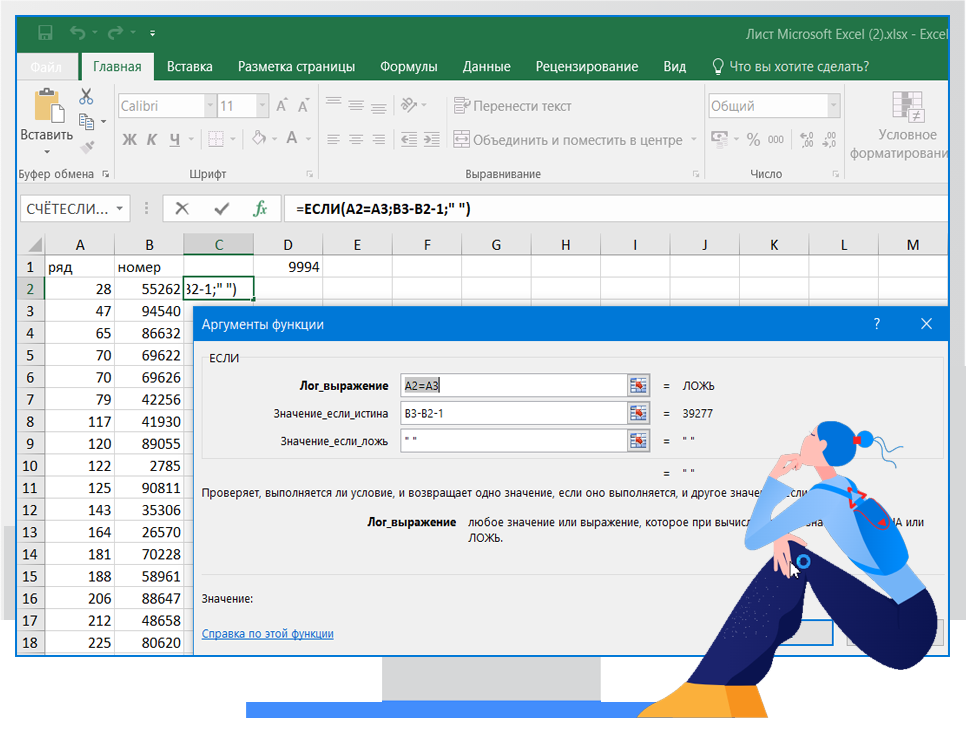
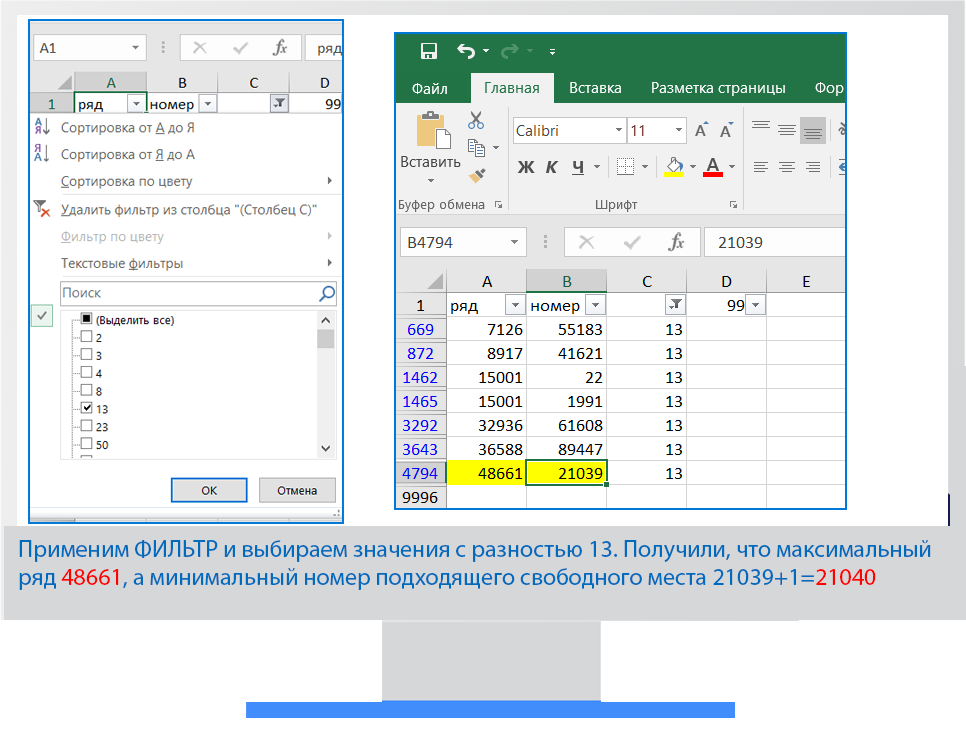
Задание 26 Товар/Скидки (Решу ЕГЭ)
Как нас обманывают в магазинах 🙂
Продавец предоставляет покупателю, делающему большую закупку, скидку по следующим правилам:
- — на каждый второй товар стоимостью больше 50 рублей предоставляется скидка 25%;
- — общая стоимость покупки со скидкой округляется вверх до целого числа рублей;
- — порядок товаров в списке определяет продавец и делает это так, чтобы общая сумма скидки была наименьшей.
По известной стоимости каждого товара в покупке необходимо определить общую стоимость покупки с учётом скидки и стоимость самого дорогого товара, на который будет предоставлена скидка.
Входные данные:
Первая строка входного файла содержит число N — общее количество купленных товаров. Каждая из следующих N строк содержит одно целое число — стоимость товара в рублях.
Выходные данные:
В ответе запишите два целых числа: сначала общую стоимость покупки с учётом скидки, затем стоимость самого дорогого товара, на который будет предоставлена скидка.
Типовой пример организации входных данных:
6
125
50
490
215
144
320
В данном случае товар стоимостью 50 не участвует в определении скидки, остальные товары продавцу выгодно расположить в таком порядке цен: 490, 125, 215, 144, 320. Тогда скидка предоставляется на товары стоимостью 125 и 144. Стоимость этих двух товаров со скидкой составит 201,75 руб., после округления — 202 руб. Общая стоимость покупки составит:
50 + 490 + 215 + 320 + 202 = 1277 руб.
Самый дорогой товар, на который будет получена скидка, стоит 144 руб. В ответе нужно записать числа 1277 и 144.
Решаем с помощью Excel
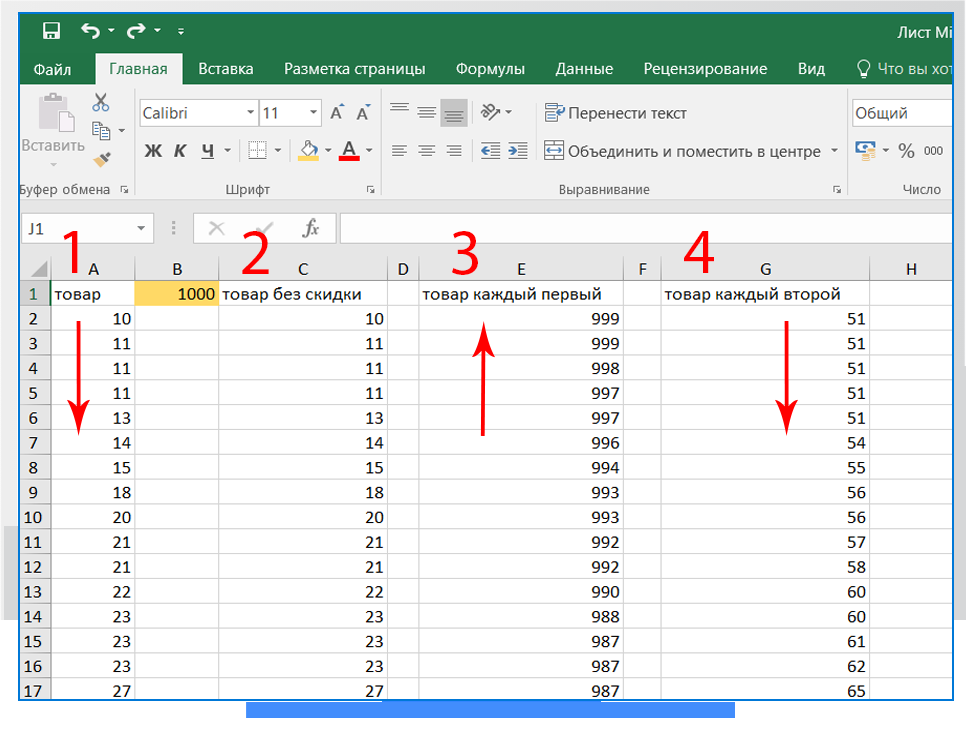
- Отрываем файл, копируем (Ctrl+A) и вставляем в Excel (Ctrl+V), убираем первое число(N — общее количество купленных товаров) и сортируем по возрастанию
- Копируем диапазон товаров меньше 50, на который скидка не действует, переносим в отдельный столбец (С)
- Копируем диапазон от 50 и более, переносим в отдельные столбцы (Е и G)
- Столбец Е сортируем по убыванию, это будет более дорогой ПЕРВЫЙ товар, столбец G оставляем по возрастанию, это будет ВТОРОЙ по списку товар, на который действует скидка 25%
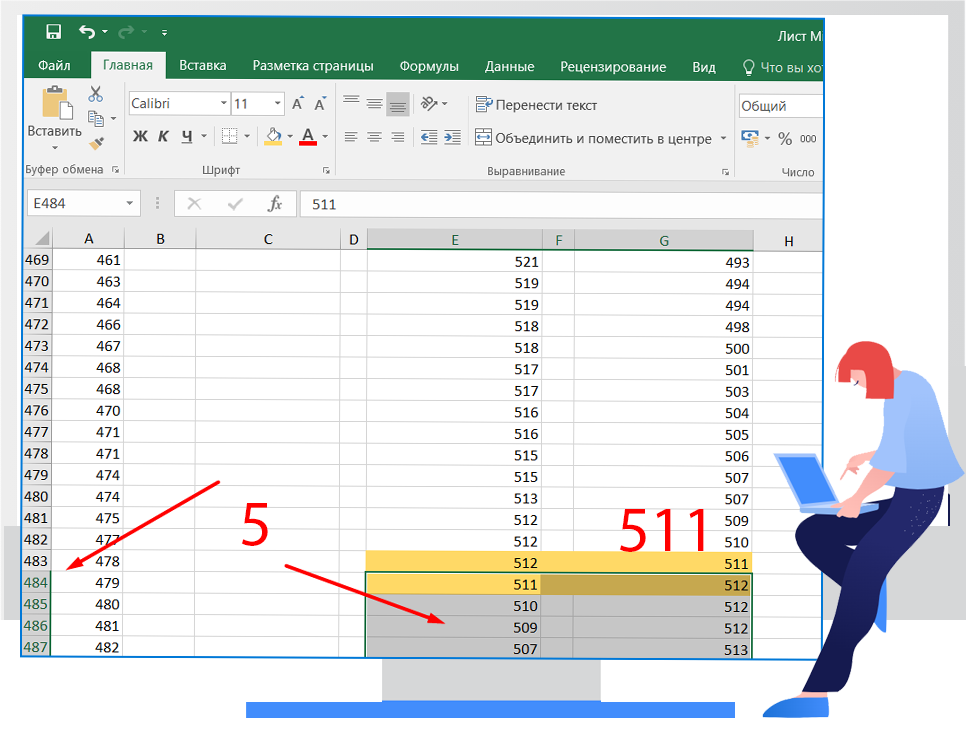
- Выделив столбец Е, мы видим, что ли количество товаров 965, делим его пополам и находим середину, между двумя столбцами, нижнюю половину удаляем
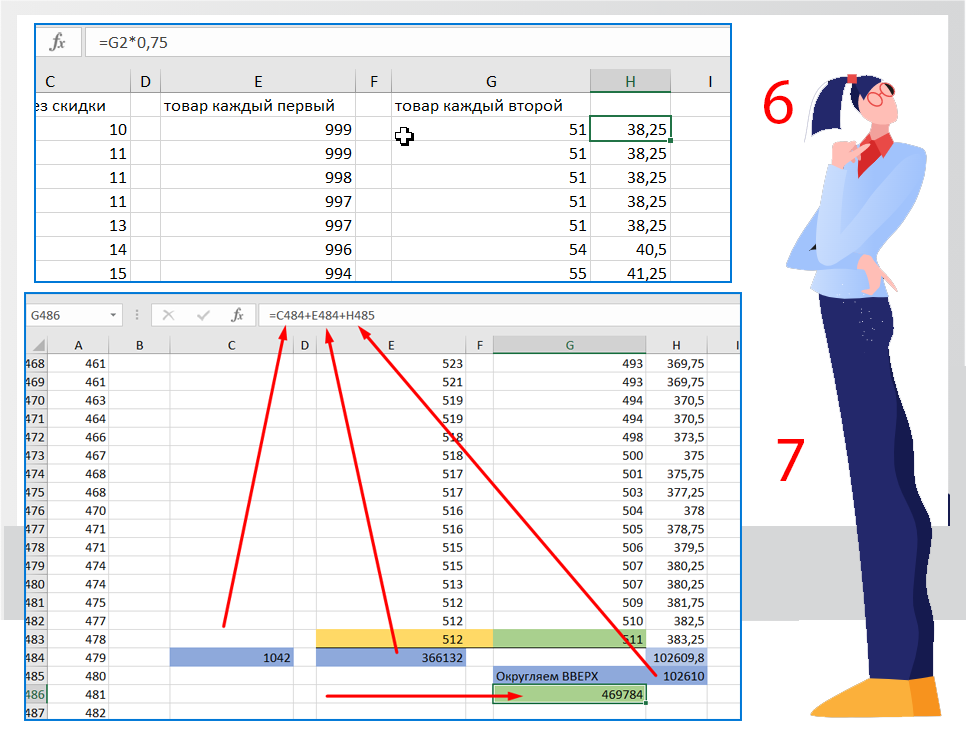
Мы нашли Самый дорогой товар, на который будет получена скидка, стоит 511 руб. - В ячейку Н2 вставляем формулу для переоценки каждого второго товара, т.е. цену умножаем на 0,75 (скидка 25%)
- Суммируем наш товар:
— сумма товара без скидки до 50 рублей 1042
— сумма КАЖДОГО ПЕРВОГО 366132
— сумму товара со скидкой округляем ВВЕРХ 102610
Сумма всего товара 469784
Ответ: 469784 511
Задание 26 Груз(Решу ЕГЭ)
Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы массой от 200 до 210 кг грузят в первую очередь, гарантируется, что все такие грузы поместятся. На оставшееся после этого место стараются взять как можно больше грузов. Если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу. Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т. д. Известны количество грузов, масса каждого из них и грузоподъёмность грузовика. Необходимо определить количество и общую массу грузов, которые будут вывезены при погрузке по вышеописанным правилам.
Входные данные:
Первая строка входного файла содержит два целых числа: N — общее количество грузов и M — грузоподъёмность грузовика в кг. Каждая из следующих N строк содержит одно целое число — массу груза в кг.
Выходные данные:
В ответе запишите два целых числа: сначала максимально возможное количество грузов, затем их общую массу.
Решаем с помощью Excel
- Отрываем файл, копируем (Ctrl+A) и вставляем в Excel (Ctrl+V), перемещаем первую ячейку (N — общее количество грузов и M — грузоподъёмность грузовика в кг) и сортируем по возрастанию данные в столбце А
- выбираем диапазон от 200 до 210 кг, можно его скопировать и вставить в отдельный столбик. Подсчитаем сумму и количество груза.
- Находим массу груза без главного 10000-2669=7331. В столбце А выделяем диапазон, который на превышает полученное число, фиксируем количество (110) и массу последнего большого груза (123).
- Стараются взять как можно больше грузов, если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу. Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т. д.
- Постараемся найти такой груз, что бы грузоподъемность была наибольшей и количество грузов не поменялось. Будем подбирать
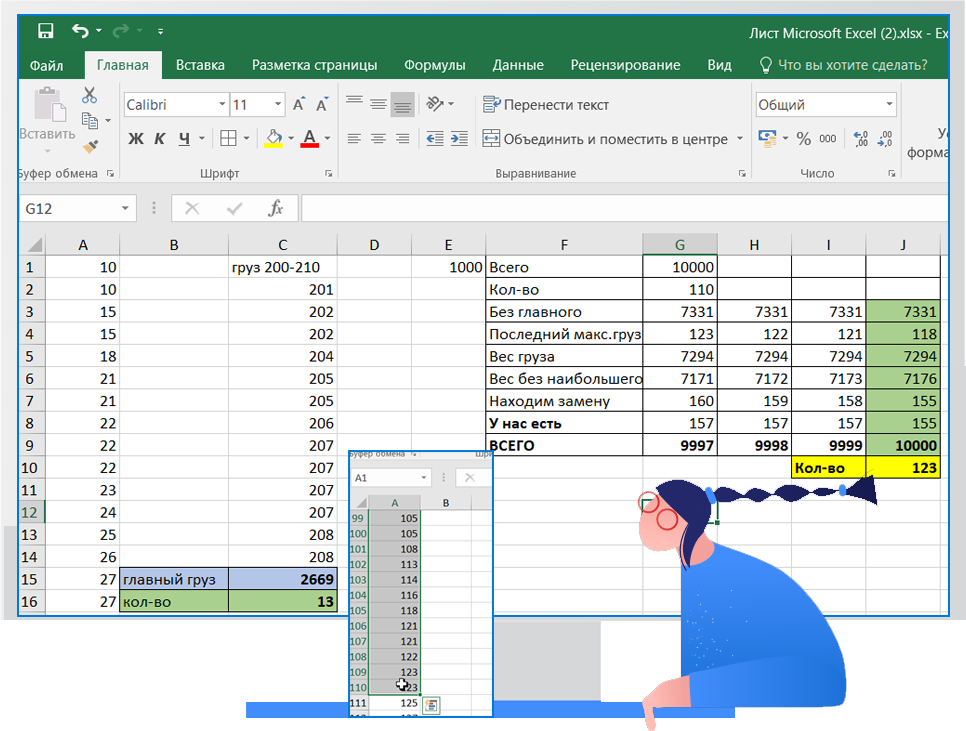
Ответ: 123 10000
На уроке рассмотрен материал для подготовки к ЕГЭ по информатике, разбор 26 задания. Объясняется тема о программной обработке целочисленной информации с использованием алгоритмов сортировки.
26-е задание: «Обработка целочисленной информации с использованием сортировки»
Уровень сложности
— высокий,
Требуется использование специализированного программного обеспечения
— да,
Максимальный балл
— 2,
Примерное время выполнения
— 35 минут.
Проверяемые элементы содержания: Умение обрабатывать целочисленную информацию с использованием сортировки
Выполнение 26 задания ЕГЭ
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
26_1.
26_1. Демоверсия варианта ЕГЭ по информатике 2021, ФИПИ:
Задание выполняется с использованием прилагаемых файлов
Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов.
Известно, какой объём занимает файл каждого пользователя.
По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные.
В первой строке входного файла находятся два числа: S – размер свободного места на диске (натуральное число, не превышающее 10 000) и N – количество пользователей (натуральное число, не превышающее 1000). В следующих N строках находятся значения объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Пример входного файла:
100 4 80 30 50 40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар – 50, поэтому ответ для приведённого примера:
2 | 50
Ответ: 568 | 50
✍ Решение:
-
Проанализируем возможное решение:
- Чтобы вычислить максимальное число пользователей, чьи файлы можно сохранить в архиве, необходимо брать файлы с наименьшим объемом , пока суммарный объем этих файлов меньше свободного объема диска. Т.е. для нижеуказанного примера, будем брать
30 + 40. Файл объемом 50 мы взять уже не сможем, так как70 + 50 = 120, а это уже больше указанного объема диска (100):
100 4 80 30 50 40
100 - 70 = 30
30 - 40 <= запаса (30) 40 - 40 <= запаса (30) 50 - 40 <= запаса (30) 80 - 40 > запаса (30), не подходит
Теперь построим алгоритм на языках программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
Ответ: 568 | 50
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
26_2.
26_2:
Задание выполняется с использованием прилагаемых файлов
В магазине электроники раз в месяц проводится распродажа. Из всех товаров выбирают K товаров с самой большой ценой и делают на них скидку в 20%. По заданной информации о цене каждого из товаров и количестве товаров, на которые будет скидка, определите цену самого дорогого товара, не участвующего в распродаже, а также целую часть от суммы всех скидок.
Входные и выходные данные.
В первой строке входного файла 26-k1.txt находятся два числа, записанные через пробел: N – общее количество цен (натуральное число, не превышающее 10 000) и K – количество товаров со скидкой. В следующих N строках находятся значения цены каждого из товаров (все числа натуральные, не превышающие 10 000), каждое в отдельной строке.
Запишите в ответе два числа: сначала цену самого дорогого товара, не участвующего в распродаже, а затем целую часть от суммы всех скидок.
Пример входного файла:
10 3 1800 3600 3700 800 2600 2500 1800 1500 1900 1200
При таких исходных данных ответ должен содержать два числа – 2500 и 1980.
Пояснение: скидка будет на товары стоимостью 3700, 3600, 2600. Тогда самый дорогой товар без скидки стоит 2500, а сумма скидок 740+720+520 = 1980.
Ответ: 9000 | 190680
✍ Решение:
-
Теперь построим алгоритм на языках программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Public user contributions licensed under
cc-wiki license with attribution required
Слайд 1
Решение задач по теме «Обработка целочисленной информации» Выполнила: Черноиванова Екатерина Вадимовна
Слайд 2
Задание Системный администратор раз в неделю создаёт архив пользовательских файлов. Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный объём архивируемых файлов. Известно, какой объём занимает файл каждого пользователя. По заданной информации об объёме файлов пользователей и свободном объёме на архивном диске определите максимальное число пользователей , чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранён в архиве, при условии, что сохранены файлы максимально возможного числа пользователей . Входные данные находятся в файле. Пример взят с сайта РешуЕГЭ. https://ege.sdamgia.ru/
Слайд 3
Пример Пример входного файла: 100 4 80 30 50 40 При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объём файла из перечисленных пар — 50, поэтому ответ для приведённого примера: 2 50 (2 файла, максимум 50) Пример взят с сайта РешуЕГЭ. https://ege.sdamgia.ru/
Слайд 4
Решение на Паскаль Ответ 568 50 Пример взят с сайта РешуЕГЭ. https://ege.sdamgia.ru/
Слайд 5
Решение в MS EXCEL Скопировать данные на EXCEL -лист ( C trl+A Ctrl+C Ctrl+V ) Удалить в Excel первую строку Выделить столбец и отсортировать по возрастанию данные Выделять элементы, начиная с первого, чтобы сумма не превышала заданного значения Запомнить номер строки, для числа, которое вошло в сумму последним (Это первый ответ) От возможной суммы отнять найденную сумму и прибавить значение последнего элемента. Получим объём максимального файла, который можем добавить, ищем ближайший размер к нему из данных.
1.
ЗАДАНИЕ №26
35 минут
2.
ПРО РЕШЕНИЕ 26-ГО ЗАДАНИЯ
Проще всего 26-е задание решать в Excel. Можно решить задание и
с помощью программы, но это будет очень сложно. Если Вам
интересно, в курсе выложен файл с решением 26-го задания с
помощью программ на Питоне.
На ЕГЭ решение через программы не рекомендуется.
3.
1: РАЗБОР
В магазине электроники раз в месяц проводится распродажа. Из всех
товаров выбирают K товаров с самой большой ценой и делают на них
скидку в 20%. По заданной информации о цене каждого из товаров и
количестве товаров, на которые будет скидка, определите цену самого
дорогого товара, не участвующего в распродаже, а также целую часть от
суммы всех скидок.
Входные и выходные данные. В первой строке входного файла 1.txt
находятся два числа, записанные через пробел: N – общее количество
цен (натуральное число, не превышающее 10 000) и K – количество
товаров со скидкой. В следующих N строках находятся значения цены
каждого из товаров (все числа натуральные, не превышающие 10 000),
каждое в отдельной строке. Запишите в ответе два числа: сначала цену
самого дорогого товара, не участвующего в распродаже, а затем целую
часть от суммы всех скидок.
4.
1: РАЗБОР
Пример входного файла:
10 3
1800
3600
3700
800
2600
2500
1800
1500
1900
1200
При таких исходных данных ответ должен содержать два числа – 2500 и 1980. Пояснение: скидка будет на товары стоимостью
3700, 3600, 2600. Тогда самый дорогой товар без скидки стоит 2500, а сумма скидок 740+720+520 = 1980.
5.
1: РАЗБОР
План решения задачи:
1) скопировать данные из текстового файла в Excel,
подредактировать их, если нужно;
2) определить, чем равно K (второе число в текстовом файле);
3) отсортировать числа по убыванию;
4) найти K + 1 число в списке – по условию к этой цене уже не
будет применяться скидка;
5) для первых K чисел (товаров) посчитать скидку;
6) посчитать сумму всех скидок.
6.
1: РАЗБОР
Начнём поэтапно решать задачу.
1) Откроем текстовый файл. Он выглядит так:
Здесь 1000 – количество товаров (чисел) в файле,
100 – количество товаров со скидкой.
Если Вы нажмёте Ctrl + A, Вы выделите все строчки файла. После этого
нажимаем Ctrl + C (копируем строчки).
7.
1: РАЗБОР
В Excel переходим в ячейку A1 и нажимаем Ctrl + V (вставляем
данные в файл).
Первая ячейка нам не нужна, там
содержится не цена, а общее количеств
товаров и количество товаров со скидкой
Поэтому ячейку можно переименовать:
8.
1: РАЗБОР
2) Второе число в файле равно 100. Т.е. к K самым дорогим товарам
применяется скидка.
3) Отсортируем числа по убыванию, чтобы понять, к каким товарам
применяется скидка.
Для этого выделим
ячейки A2-A1001 и
перейдём во вкладку
Data.
9.
1: РАЗБОР
Нажмём на Sort:
10.
1: РАЗБОР
Настройки сортировки: от большего к меньшему (Largest to
Smallest). Нажимаем ОК. Данные в столбце А теперь
отсортированы по убыванию.
11.
1: РАЗБОР
4) Первые 100 товаров – самые дорогие, на них будет скидка. На
101 товар скидка не действует. Т.к. числа начинаются со 2-й
строчки, 101-й товар находится в строчке 102.
Его цена – 9000.
12.
1: РАЗБОР
Есть ещё один способ понять, выделили ли Вы все нужные ячейки или
нет. При выделении смотрите в правый нижний угол Excel. Там
отображается среднее арифметическое значений ячеек, их количество
выделенных и сумма их значений:
Здесь среднее арифметическое равно 5317, 647059, количество
выделенных ячеек – 34, сумма их значений – 180800.
13.
1: РАЗБОР
5) Определим скидку на первые 100 товаров. Скидка составляет 20% от стоимости, т.е. чтобы
узнать скидку, цену умножем на 0.2.
Растягиваем формулу на первые 100 товаров (тянем за зелёный квадратик в правом нижнем
углу ячейки с формулой скидки).
Получаем:
14.
1: РАЗБОР
6) Считаем суммарную скидку. Скидка находится в ячейках B2B101, поэтому формула для суммы выглядит так:
= SUM(B2:B101)
15.
1: РАЗБОР
Ответ: 9000 190680
16.
2: САМОСТОЯТЕЛЬНО
Спутник «Фотон» проводит измерения солнечной активности, результат
каждого измерения представляет собой натуральное число. Перед
обработкой серии измерений из неё исключают K наибольших и K
наименьших значений (как недостоверные). По заданной информации о
значении каждого из измерений, а также количестве исключаемых значений,
определите наибольшее достоверное измерение, а также целую часть
среднего значения всех достоверных измерений.
Входные и выходные данные. В первой строке входного файла 2.txt находятся
два числа, записанные через пробел: N – общее количество измерений
(натуральное число, не превышающее 10 000) и K – количество исключаемых
минимальных и максимальных значений. В следующих N строках находятся
значения каждого из измерений (все числа натуральные, не превышающие
1000), каждое в отдельной строке. Запишите в ответе два числа: сначала
наибольшее достоверное измерение, а затем целую часть среднего значения
всех достоверных измерений.
17.
2: САМОСТОЯТЕЛЬНО
Пример входного файла:
10 2
34
50
43
44
23
9
39
5
38
36
При таких исходных данных ответ должен содержать 2 числа – 43 и 35. Пояснение: будут отброшены значения 5, 9, 44, 50.
Тогда наибольшее оставшееся значение равно 43, а среднее значение из оставшихся равно (23+34+36+38+39+43):6 = 35,5.
18.
2: САМОСТОЯТЕЛЬНО
Ответ:
957 501
Формула для среднего арифметического (при условии, что первая
строка таблицы содержит не число, а название колонки):
=AVERAGE(A52:A951)
19.
3: САМОСТОЯТЕЛЬНО
Системный администратор раз в неделю создаёт архив пользовательских файлов.
Выделяемый объем памяти рассчитывается, как общий объем файлов за вычетом
количественно 10% файлов – 5% составляют самые мелкие файлы и 5 % составляют
самые крупные файлы.
Известно, какой объём занимает файл каждого пользователя.
Определите объем выделенного дискового пространства и размер самого крупного
из сохраненных файлов. В случае, если 5% является нецелым числом, берется целая
часть от деления количества файлов на 20.
Входные данные.
В первой строке входного файла 3.txt находится число N – количество пользователей
(натуральное число, 20 ≤ N ≤ 10000). В следующих N строках находятся значения
объёмов файлов каждого пользователя (все числа натуральные, не превышающие
100), каждое в отдельной строке.
Запишите в ответе два числа: сначала объем сохраненных файлов, затем размер
наибольшего сохраненного файла.
20.
3: САМОСТОЯТЕЛЬНО
Пример входного файла (для вычета 20% файлов):
10
50
33
44
17
92
58
42
10
52
88
При таких исходных данных можно сохранить 8 файлов – 50, 33, 44, 17, 58, 42, 52, 88. Поэтому ответ
должен содержать два числа – 384 и 88.
21.
3: САМОСТОЯТЕЛЬНО
Ответ: 496209 96
22.
4: РАЗБОР
Магазин предоставляет оптовому покупателю скидку по следующим
правилам:
− на каждый второй товар ценой больше 100 рублей предоставляется скидка
10 %;
− общая цена покупки со скидкой округляется вверх до целого числа рублей;
− порядок товаров в списке определяет магазин и делает это так, чтобы общая
сумма скидки была наименьшей.
Вам необходимо определить общую цену закупки с учётом скидки и цену
самого дорогого товара, на который будет предоставлена скидка.
Входные данные. Первая строка входного файла 4.txt содержит число N –
общее количество купленных товаров. Каждая из следующих N строк
содержит одно целое число – цену товара в рублях. В ответе запишите два
целых числа: сначала общую цену покупки с учётом скидки, затем цену самого
дорогого товара, на который предоставлена скидка.
23.
4: РАЗБОР
Пример входного файла
7
225
160
380
95
192
310
60
В данном случае товары с ценой 60 и 95 не участвуют в определении скидки, остальные товары
магазину выгодно расположить в таком порядке цен: 380, 160, 225, 192, 310. Скидка предоставляется на
товары ценой 160 и 192. Суммарная цена этих двух товаров со скидкой составит 316,8 руб., после
округления – 317 руб. Общая цена покупки составит: 60 + 95 + 317 + 380 + 225 + 310 = 1387 руб. Самый
дорогой товар, на который будет получена скидка, стоит 192 руб. В ответе нужно записать числа 1387 и
192.
24.
4: РАЗБОР
Обратите внимание на условие задачи: порядок товаров в списке
определяет магазин и делает это так, чтобы общая сумма скидки была
наименьшей.
Очевидно, что магазину выгоднее всего сделать скидку на самые
дешёвые товары. Но т.к. по условию скидка предоставляется на товары
ценой больше 100 рублей, нам потребуется:
1) отсортировать цены по убыванию
2) определить, на какие товары может быть скидка (цена больше 100
рублей)
3) сделать скидку на половину товаров из пункта 2 (причём на самую
дешёвую половину)
25.
4: РАЗБОР
Данные после сортировки
Выделили товары ценой больше 100 рублей
Количество товаров ценой
больше 100 рублей — 921
26.
4: РАЗБОР
Т.к. 921 товар имеет цену больше 100 рублей, скидка будет
предоставлена на 921 / 2 = 460 товаров (округление вниз, т.к.
скидка на каждый второй товар, не на каждый первый).
Выделяем цветов 460 самых дешёвых товаров дороже 100 рублей.
Самый дорогой товар со скидкой – 550.
27.
4: РАЗБОР
Осталось посчитать суммарную стоимость скидкой. Сделать это можно
несколькими способами:
1) посчитать общую сумму без скидок, вычесть из этой суммы скидку
на 460 товаров;
2) посчитать сумму, исключив 460 товаров со скидкой, посчитать сумму
на 460 товаров со скидкой, сложить получившиеся суммы.
Выбрать можно любой удобный Вам способ. В презентации будет
рассмотрен первый способ, т.к. в нём потребуется выполнить меньше
действий.
28.
4: РАЗБОР
Осталось посчитать суммарную стоимость скидкой. Сделать это можно
несколькими способами:
1) посчитать общую сумму без скидок, вычесть из этой суммы скидку
на 460 товаров
2) посчитать сумму, исключив 460 товаров со скидкой, посчитать сумму
на 460 товаров со скидкой, сложить получившиеся суммы.
Выбрать можно любой удобный Вам способ. В презентации будет
рассмотрен первый способ, т.к. в нём потребуется выполнить меньше
действий.
29.
4: РАЗБОР
Формула для ячейки С2:
=SUM(A2:A1001)
Формула для ячейки D2:
=SUM(A463:A922)*0,1
(подсчитали общую сумму товаров, на которые будет действовать скидка, и
определили скидку: это 10% от общей суммы, т.е. 0.1 от суммы)
Формулы для ячейки E2:
=C2-D2
Т.к. по условию чек округляется в большую сторону, итоговая сумма будет
499078.
30.
4: РАЗБОР
Ответ: 499078 550
31.
5: САМОСТОЯТЕЛЬНО
Магазин предоставляет оптовому покупателю скидку по следующим
правилам:
− на каждый третий товар ценой больше 150 рублей предоставляется скидка
20%;
− общая цена покупки со скидкой округляется вверх до целого числа рублей;
− порядок товаров в списке определяет магазин и делает это так, чтобы общая
сумма скидки была наименьшей.
Вам необходимо определить общую цену закупки с учётом скидки и цену
самого дорогого товара, на который будет предоставлена скидка.
Входные данные. Первая строка входного файла 5.txt содержит число N –
общее количество купленных товаров. Каждая из следующих N строк
содержит одно целое число – цену товара в рублях. В ответе запишите два
целых числа: сначала общую цену покупки с учётом скидки, затем цену самого
дорогого товара, на который предоставлена скидка.
32.
5: САМОСТОЯТЕЛЬНО
Пример входного файла
7
225
160
380
95
192
310
60
В данном случае товары с ценой 60 и 95 не участвуют в определении скидки, остальные товары
магазину выгодно расположить в таком порядке цен: 380, 160, 225, 192, 310. Скидка предоставляется на
товары ценой 160 и 192. Суммарная цена этих двух товаров со скидкой составит 281,6 руб., после
округления – 282 руб. Общая цена покупки составит: 60 + 95 + 282 + 380 + 225 + 310 = 1352 руб. Самый
дорогой товар, на который будет получена скидка, стоит 192 руб. В ответе нужно записать числа 1352 и
192.
33.
5: САМОСТОЯТЕЛЬНО
Ответ: 497024 439
Количество товаров ценой выше 150: 869
Скидка будет предоставлена на 869 / 3 = 289,6666 = 289 товаров
34.
6: РАЗБОР
ВНИМАНИЕ! ЗАДАНИЕ ЭТОГО ТИПА БЫЛО В ДЕМОВЕРСИИ ЕГЭ
Для перевозки партии грузов различной массы выделен грузовик, но его
грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы
массой от 180 до 200 кг грузят в первую очередь. На оставшееся после этого место
стараются взять как можно большее количество грузов. Если это можно сделать
несколькими способами, выбирают тот способ, при котором самый большой из
выбранных грузов имеет наибольшую массу. Если и при этом условии возможно
несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй
по величине груз, и т.д. Известны количество грузов, масса каждого из них и
грузоподъёмность грузовика. Необходимо определить количество и общую массу
грузов, которые будут вывезены при погрузке по вышеописанным правилам.
Входные данные представлены в файле 6.txt следующим образом. В первой строке
входного файла записаны два целых числа: N – общее количество грузов и M –
грузоподъёмность грузовика в кг. Каждая из следующих N строк содержит одно целое
число – массу груза в кг. В ответе запишите два целых числа: сначала максимально
возможное количество грузов, затем их общую массу.
35.
6: РАЗБОР
Пример организации исходных данных во входном файле:
6 700
100
185
120
160
140
300
В данном случае сначала нужно взять груз массой 185 кг. Остается 515 кг. После этого можно вывезти
ещё максимум 3 груза. Это можно сделать четырьмя способами: 100 + 120 + 140, 100 + 140 + 160, 100 +
120 + 160, 120 + 140 + 160. Выбираем способ, при котором вывозится груз наибольшей возможной
массы. Таких способов три: 100 + 120 + 160, 100 + 140 + 160, 120 + 140 + 160. Из этих способов выбираем
те, при которых больше масса второго по величине груза, то есть 100 + 140 + 160 и 120 + 140 + 160. Их
них нужно выбрать вариант 120 + 140 + 160, так как в этом случае третий по величине груз наиболее
тяжёлый. Всего получается 4 груза общей массой 605 кг. Ответ: 4 605.
36.
6: РАЗБОР
План решения задачи:
1) отсортировать список грузов по убыванию
2) посчитать, сколько останется свободного места, если загрузить
все обязательные грузы (вес от 180 до 200 кг)
3) посчитать максимальное количество грузов как можно
меньшей массы, которое можно загрузить на оставшееся место
4) если осталось ещё какое-то место, попытаться заменить
последний загруженный груз на груз из списка незагруженных
(максимального веса)
37.
6: РАЗБОР
1) Сортируем список грузов по убыванию
2) Посчитаем, сколько останется
свободного места, если загрузить вс
обязательные грузы (вес от 180
до 200 кг)
Свободного места остаётся:
10000 – 3018 = 6982 кг
38.
6: РАЗБОР
3) Теперь попытаемся набрать наибольшее количество
необязательных грузов. Для упрощения работы можно
продублировать столбец с грузами, удалив из него грузы с массой
180-200 кг.
39.
6: РАЗБОР
Грузы массой 20-128 дают в сумме 6904 кг. Максимальное
количество необязательных грузов – 102.
4) Попытаемся заменить верхний груз (128) на груз большей массы,
т.к. ещё осталось свободное место.
6982 – 6904 = 78 кг – можно добавить.
40.
6: РАЗБОР
Текущая максимальная масса – 128 кг, поэтомугруз 128 кг можно
заменить на груз 128 + 78 = 206 кг. Такой груз есть.
41.
6: РАЗБОР
Получившееся количество грузов:
16 обязательных грузов (масса 180-200 кг)
102 необязательных груза
Итого: количество грузов: 16 + 102 = 118
Масса грузов:
3018 обязательных грузов (масса 180-200 кг)
6982 необязательных грузов
Итого: 3018 + 6982 = 10000
Ответ: 118 10000
42.
6: РАЗБОР
Важно: в этом задании нашёлся груз массы 206, в результате
свободного места не осталось. Если бы ещё оставалось свободное
место, нужно было бы попытаться заменить на бОльший второй
максимальный груз, затем третий максимальный груз и т.д.
Груз, который мы удалили из списка загружаемых (в этом примере
– груз 128), может быть погружен снова (на него можно заменить
второй по массе груз, третий и т.д.).
43.
6: РАЗБОР
Пример: предположим, у нас нет груза весом ровно 206 кг, есть
только груз весом 204 кг:
После замены:
44.
6: РАЗБОР
Остались 2 кг. Поэтому 126 можно заменить на 128.
45.
7: САМОСТОЯТЕЛЬНО
Для перевозки партии грузов различной массы выделен грузовик, но его
грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы
массой от 310 до 320 кг грузят в первую очередь. На оставшееся после этого место
стараются взять как можно большее количество грузов. Если это можно сделать
несколькими способами, выбирают тот способ, при котором самый большой из
выбранных грузов имеет наибольшую массу. Если и при этом условии возможно
несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй
по величине груз, и т.д. Известны количество грузов, масса каждого из них и
грузоподъёмность грузовика. Необходимо определить количество и общую массу
грузов, которые будут вывезены при погрузке по вышеописанным правилам.
Входные данные представлены в файле 7.txt следующим образом. В первой строке
входного файла записаны два целых числа: N – общее количество грузов и M –
грузоподъёмность грузовика в кг. Каждая из следующих N строк содержит одно целое
число – массу груза в кг. В ответе запишите два целых числа: сначала максимально
возможное количество грузов, затем их общую массу.
46.
7: САМОСТОЯТЕЛЬНО
Пример организации исходных данных во входном файле:
6 720
100
315
120
160
140
300
В данном случае сначала нужно взять груз массой 315 кг. Остается 405 кг. После этого можно
вывезти ещё максимум 3 груза. Это можно сделать тремя способами: 100 + 120 + 140, 100 +
140 + 160, 100 + 120 + 160. Выбираем способ, при котором вывозится груз наибольшей
возможной массы. Таких способов два: 100 + 120 + 160, 100 + 140 + 160. Из этих способов
выбираем тот, при котором больше масса второго по величине груза, то есть 100 + 140 + 160.
Всего получается 4 груза общей массой 715 кг. Ответ: 4 715.
47.
7: САМОСТОЯТЕЛЬНО
Ответ: 113 9999
48.
8: САМОСТОЯТЕЛЬНО
Системный администратор раз в неделю создаёт архив пользовательских файлов.
Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный
объём архивируемых файлов. Известно, какой объём занимает файл каждого
пользователя. Администратор сохраняет файлы по следующему правилу: выбирается
файл максимального размера, который может быть записан на диск, затем
выбирается файл минимального размера, который может быть записан на диск.
Данный сценарий повторяется до тех пор, пока на диск нельзя будет записать ни
одного из оставшихся файлов.
Входные данные представлены в файле 8.txt следующим образом. В первой строке
входного файла находятся два числа: S – размер свободного места на диске
(натуральное число, не превышающее 10 000) и N – количество пользователей
(натуральное число, не превышающее 1000). В следующих N строках находятся
значения объёмов файлов каждого пользователя (все числа натуральные, не
превышающие 100), каждое в отдельной строке.
Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы
могут быть помещены в архив, затем размер последнего сохраненного файла.
49.
8: САМОСТОЯТЕЛЬНО
Пример организации исходных данных во входном файле:
100 5
80
30
10
5
7
При таких исходных данных можно сохранить файлы трех
пользователей. Объёмы этих трёх файлов 80, 5 и 10. Последний
выбранный файл имеет размер 10 , поэтому ответ для приведённого
примера: 3 10.
50.
8: САМОСТОЯТЕЛЬНО
Ответ: 573 229
51.
9: САМОСТОЯТЕЛЬНО
В магазине Пятэльдодео на черную пятницу решено провести одну из двух акций. Первая
акция – 30% скидки на 70% самых дешевых товаров, 40% процентов скидки на оставшиеся
товары. Вторая акция – 40% скидки на 50% самых дешевых товаров, 35% процентов скидки на
оставшиеся товары. Определите, какая акция принесет больше прибыли, если предположить,
что все товары будут проданы.
В качестве ответа нужно привести разницу в прибыли двух акций и стоимость самого дорогого
товара, реализованного при проведении выбранной акции. В форму записать целые части
найденных чисел.
Входные данные. В первой строке входного файла 9.txt находится число N – количество
товаров кратное 20 (натуральное число, 20 ≤ N ≤ 10000). В следующих N строках находятся
значения – стоимость товаров (целое число не большее 1000).
Пример входного файла (все значения с новой строки):
20
4 13 4 23 22 20 8 6 5 12 48 22 50 12 63 23 4 8 9 11
При таких исходных данных ответ должен содержать 2 числа – 1 и 40.
52.
9: САМОСТОЯТЕЛЬНО
Ответ: 63792 600
53.
10: САМОСТОЯТЕЛЬНО
Системный администратор раз в неделю создаёт архив пользовательских файлов.
Однако объём диска, куда он помещает архив, может быть меньше, чем суммарный
объём архивируемых файлов. Известно, какой объём занимает файл каждого
пользователя. По заданной информации об объёме файлов пользователей и
свободном объёме на архивном диске определите максимальное число
пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер
имеющегося файла, который может быть сохранён в архиве, при условии, что
сохранены файлы максимально возможного числа пользователей.
Входные данные. В первой строке входного файла 10.txt находятся два числа: S –
размер свободного места на диске (натуральное число, не превышающее 10 000) и N
– количество пользователей (натуральное число, не превышающее 1000). В
следующих N строках находятся значения объёмов файлов каждого пользователя (все
числа натуральные, не превышающие 100), каждое в отдельной строке. Запишите в
ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть
помещены в архив, затем максимальный размер имеющегося файла, который может
быть сохранён в архиве, при условии, что сохранены файлы максимально
возможного числа пользователей.
54.
10: САМОСТОЯТЕЛЬНО
Пример входного файла:
100 4
80
30
50
40
При таких исходных данных можно сохранить файлы максимум двух
пользователей. Возможные объёмы этих двух файлов 30 и 40, 30 и 50
или 40 и 50. Наибольший объём файла из перечисленных пар – 50,
поэтому ответ для приведённого примера:
2 50
55.
10: САМОСТОЯТЕЛЬНО
Ответ: 2797 51
56.
11: РАЗБОР
Системный администратор раз в неделю создаёт архив пользовательских файлов. Известно,
какой объём занимает файл каждого пользователя. Сохраняются файлы всех пользователей.
Каждый файл в архиве может быть либо сжат, либо сохранен в исходном состоянии. Сжатый
файл занимает в памяти 80% от исходного. Для архива выделяется объем, равный 90% от
общего объема файлов пользователей до сжатия.
Для ускорения процесса создания архива как можно наибольшее возможное количество
файлов сохраняется без сжатия.
Определите максимально возможное количество файлов, которое может быть сохранено без
сжатия, и максимально возможный размер такого файла.
Входные данные. В первой строке входного файла 11.txt записано натуральное число N –
количество пользователей (20 ≤ N ≤ 10000). В следующих N строках записаны значения
объёмов файлов каждого пользователя (все числа натуральные, не превышающие 100),
каждое в отдельной строке.
Запишите в ответе два числа: сначала количество несжатых файлов, затем наибольший
размер сохраненного без сжатия файла.
57.
11: РАЗБОР
Пример входного файла:
7
13
17
5
55
61
9
10
При таких исходных данных ответ должен содержать 2 числа – 5 и 17.
58.
11: РАЗБОР
1) отсортируем файлы по возрастанию и определим, сколько места
бдет занимать файл в архиве
59.
11: РАЗБОР
2) отсортируем файлы по возрастанию и определим, сколько места
будет занимать файл в архиве (в ячейку С2 записываем значение
А2, а формулу из ячейки C3 тиражируем на весь столбец).
60.
11: РАЗБОР
3) определим сумму всех файлов без сжатия
4) определим сумму сжатия (формулу из ячейки D2 тиражируем на
весь столбец):
61.
11: РАЗБОР
5) определим, сколько всего места потребуется на диске (формула
из ячейки Е2 тиражируется на весь столбец):
62.
11: РАЗБОР
6) определим максимальный размер архива (по условию – 90% от
всех файлов без сжатия):
63.
11: РАЗБОР
Получается, что если файлы с 1 по 6808 не сжаты (в таблице это
файлы с 2 по 6809), то итоговый размер получится равным
489695,6.
64.
11: РАЗБОР
Попытаемся заменить файл весом 71 на файл с большим весом.
Для этого файл с весом 71 занесём в архив, а файл с весом 99
вынесем из архива:
(можно записать просто как
489695,6 – 71 + 71*0,8 + 99 – 99*0,8 )
65.
11: РАЗБОР
Ответ: 6808 99